Что такое контур электрической цепи. Как определить независимые контуры. Какие законы применяются для расчета контуров. Какие методы используются для анализа контуров электрических цепей.
Определение контура электрической цепи
Контур электрической цепи — это замкнутый путь, проходящий по нескольким ветвям электрической схемы. Основные свойства контура:
- Замкнутость — начальная и конечная точки контура совпадают
- Проходит по нескольким ветвям схемы
- Содержит несколько узлов соединения ветвей
- Может включать источники ЭДС и потребители электроэнергии
Контур является важным понятием в теории электрических цепей, так как позволяет применять законы Кирхгофа для расчета токов и напряжений.
Виды контуров электрических цепей
Различают следующие основные виды контуров:
- Простой контур — не содержит других контуров внутри себя
- Сложный контур — включает в себя другие контуры
- Независимый контур — содержит хотя бы одну новую ветвь, не входящую в другие контуры
- Зависимый контур — может быть получен из других контуров
Количество независимых контуров в схеме определяется по формуле:
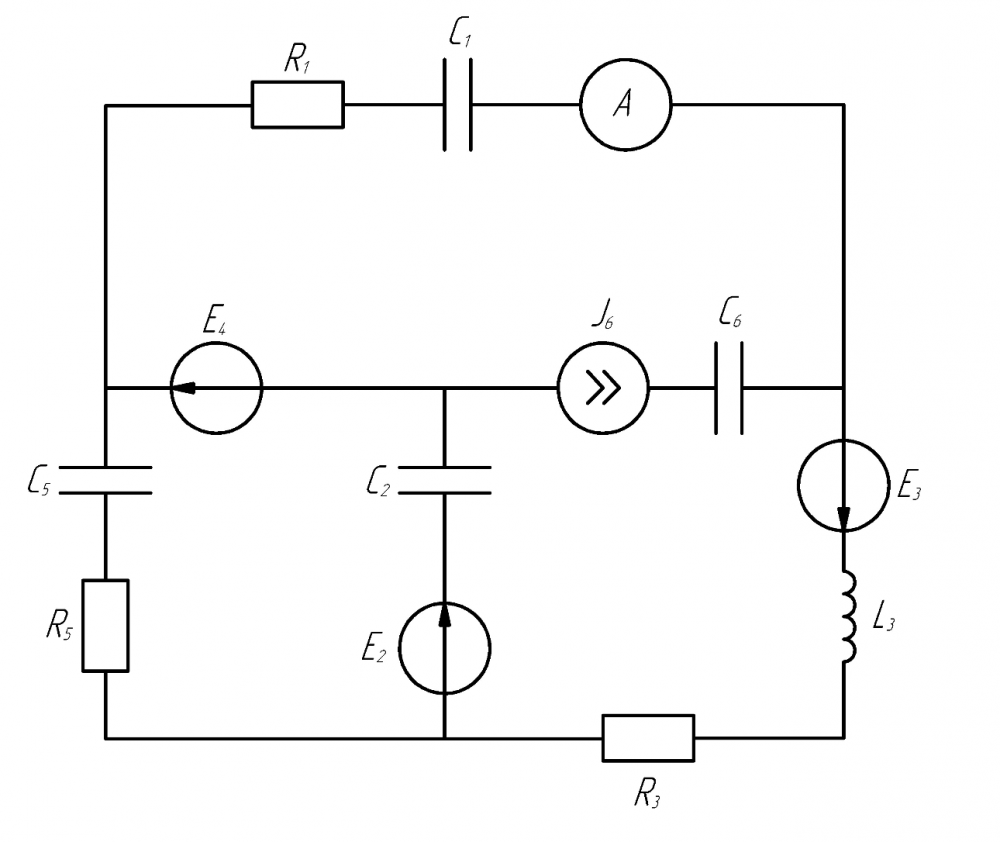
N = B — У + 1
где N — число независимых контуров, B — число ветвей, У — число узлов схемы.
Как определить независимые контуры в схеме
Для определения независимых контуров в электрической схеме можно использовать следующий алгоритм:
- Подсчитать общее число ветвей B и узлов У в схеме
- Рассчитать число независимых контуров N по формуле N = B — У + 1
- Выбрать простой контур в качестве первого независимого
- Выбирать следующие контуры так, чтобы каждый содержал хотя бы одну новую ветвь
- Продолжать выбор контуров, пока их число не достигнет N
Важно выбирать контуры так, чтобы каждый новый контур отличался от предыдущих хотя бы одной ветвью. Это обеспечит независимость системы уравнений при расчете цепи.
Применение законов Кирхгофа к контурам
Для расчета токов и напряжений в контурах электрических цепей применяются два закона Кирхгофа:
Первый закон Кирхгофа (для узлов)
Алгебраическая сумма токов, сходящихся в узле, равна нулю:
∑I = 0
Этот закон применяется для составления уравнений в узлах схемы.
Второй закон Кирхгофа (для контуров)
Алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжений на сопротивлениях:
∑E = ∑IR
Этот закон позволяет составить уравнения для независимых контуров схемы.
Применение законов Кирхгофа дает систему линейных уравнений, решение которой позволяет найти токи во всех ветвях схемы.
Методы расчета контуров электрических цепей
Основные методы анализа контуров электрических цепей:
Метод контурных токов
Суть метода:
- В каждом независимом контуре задается контурный ток
- Составляются уравнения по второму закону Кирхгофа для каждого контура
- Решается система уравнений относительно контурных токов
- Определяются реальные токи в ветвях
Преимущество метода — меньшее число уравнений по сравнению с методом узловых потенциалов.
Метод узловых потенциалов
Алгоритм метода:
- Выбирается узел с нулевым потенциалом
- Составляются уравнения по первому закону Кирхгофа для остальных узлов
- Решается система относительно потенциалов узлов
- Определяются токи в ветвях по закону Ома
Метод эффективен для цепей с большим числом узлов.
Метод наложения
Основные шаги:
- Рассматривается действие каждого источника в отдельности
- Определяются частичные токи от каждого источника
- Находится алгебраическая сумма частичных токов
Метод удобен при анализе влияния отдельных источников.
Особенности расчета сложных контуров
При расчете сложных контуров электрических цепей следует учитывать следующие особенности:
- Необходимо правильно выбрать независимые контуры
- Важно согласовать направления токов и ЭДС в уравнениях
- Следует проверять полученные результаты по энергетическому балансу
- Для сложных схем эффективно применение компьютерных методов расчета
- При наличии управляемых источников требуется модификация методов
Корректный учет этих особенностей позволяет получить достоверные результаты при анализе сложных электрических схем.
Применение теории контуров в электротехнике
Теория контуров электрических цепей находит широкое применение в различных областях электротехники:
- Расчет и проектирование электрических сетей
- Анализ работы электронных схем
- Моделирование электромагнитных процессов
- Разработка систем электроснабжения
- Создание устройств релейной защиты и автоматики
Понимание свойств контуров позволяет эффективно решать задачи анализа и синтеза электрических цепей различного назначения.
Заключение
Контур является фундаментальным понятием в теории электрических цепей. Умение правильно выделять и анализировать контуры позволяет эффективно применять законы Кирхгофа и другие методы расчета. Это дает возможность решать широкий круг практических задач в области электротехники и электроники.
Контур электрической цепи это | Домострой
Эл.цепь называется линейной, если она содержит только линейные элементы.
Линейный элемент – это сопротивление, которое не зависит от протекающего тока и действующего напряжения.
Точка на схеме называется узлом, если в ней соединяются 2 или более проводов.
Ветвь эл.цепи – ее участок, состоящий из одного или нескольких элементов, соединенных так, что по ним протекает один и тот же ток.
Контур эл.цепи – это замкнутый путь, проходящий по нескольким ветвям.
1 закон:
Сумма втекающих в узел токов равна сумме вытекающих из узла токов.
Закон
Алгебраическая сумма ЭДС в контуре равна алгебраической сумме напряжений на всех элементах этого
Контура.
Билет №9
Первый закон Кирхгофа)
Первый закон Кирхгофа или закон токов Кирхгофа гласит: сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Так как токи, которые вытекают из узла берутся с отрицательным знаком, то существует другая формулировка первого закона Кирхгофа: алгебраическая сумма токов в узле равна нулю.
Так как токи, которые вытекают из узла берутся с отрицательным знаком, то существует другая формулировка первого закона Кирхгофа: алгебраическая сумма токов в узле равна нулю.
Рассмотрим схему на рисунке 1.
Здесь ток I1— полный ток, притекающий к узлу А, а токи I2 и I3 — токи, вытекающие из узла А. Следовательно, можно записать:
Аналогично для узла B
Предположим, что I4 = 2 мА и I5 = 3 мА, получим
I3 = 2 + 3 = 5 мА
Приняв I2 = 1 мА, получим
Далее можно записать для узла C
и для узла D
Математическая запись)
Первый закон Кирхгофа
В любом узле электрической цепи алгебраическая сумма токов равна нулю
,
где m – число ветвей подключенных к узлу.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус».
3.(применение к расчету цепей)
Метод непосредственного применения законов Кирхгофа для расчета электрической цепи заключается в составлении системы из В уравнений с В неизвестными (B — количество ветвей в рассматриваемой цепи) по двум законам Кирхгофа и последующем их решении.
Билет №10
Второй закон Кирхгофа)
Второй закон Кирхгофа.
Второй закон (правило) Кирхгофа — алгебраическая сумма напряжений на элементах контура электрической цепи равна нулю.
Контур электрической цепи — замкнутый проводящий ток путь образованный элементами электрической цепи.
Математическая запись)
Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках
где n – число источников ЭДС в контуре;
m – число элементов с сопротивлением Rk в контуре;
Uk=RkIk – напряжение или падение напряжения на k-м элементе контура.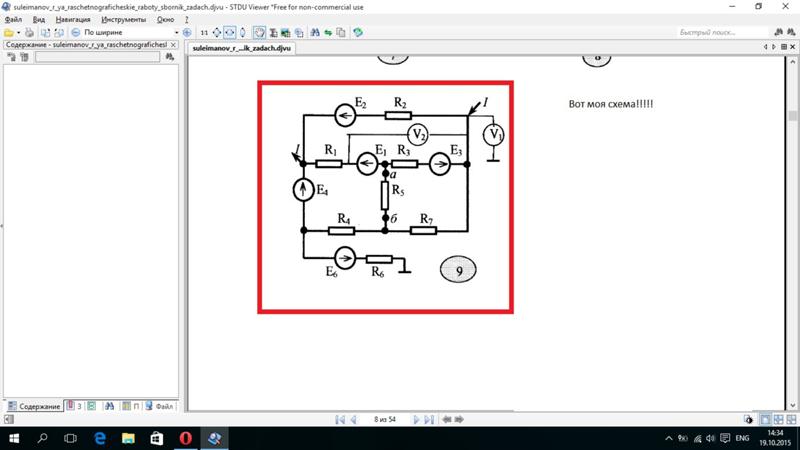
3.(применение к расчету цепей)
Метод непосредственного применения законов Кирхгофа для расчета электрической цепи заключается в составлении системы из В уравнений с В неизвестными (B — количество ветвей в рассматриваемой цепи) по двум законам Кирхгофа и последующем их решении.
Билет №11
Последовательное соединение резисторов)
Контур — электрическая цепь
Контур электрической цепи представляет собой любой замкнутый путь, проходящий по нескольким ветвям. [1]
Контур электрической цепи представляет собой замкнутый путь, проходящий по нескольким ветвям. [2]
Контуром электрической цепи называется замкнутый путь, образуемый одной или несколькими ветвями. Если внутри площади выбранного контура не лежат другие ветви, связывающие между собой точки, принадлежащие тому же контуру, то такой контур будем называть простым, или ячейкой. [3]
Контуром электрической цепи называют любой замкнутый путь, проходящий по нескольким ветвям. [4]
[4]
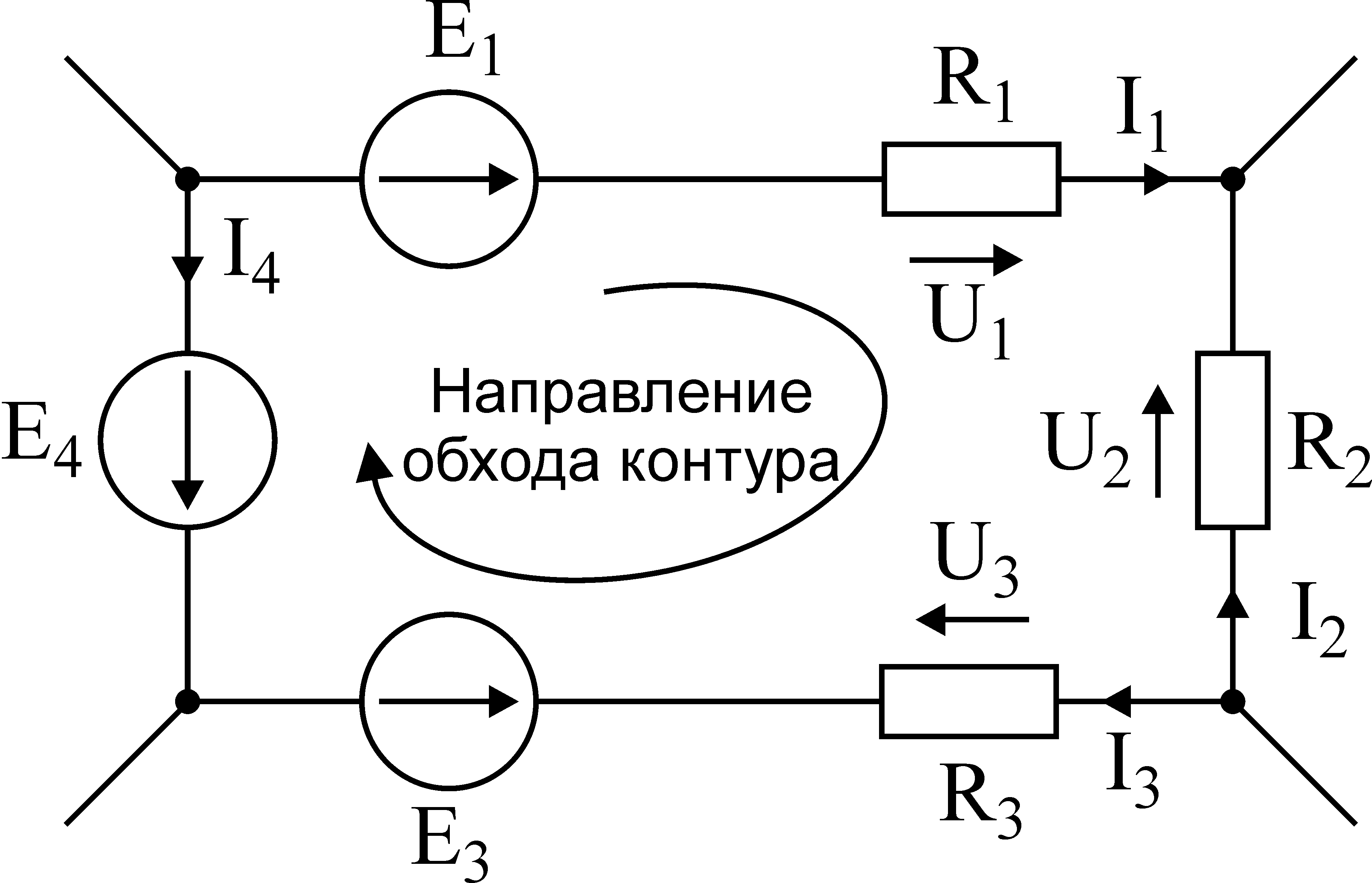
Для контура электрической цепи , изображенного на рис. 2.2, стрелками показаны положительные направления токов. Источники электрической энергии, внутренними сопротивлениями которых можно пренебречь или внутренние сопротивления которых учтены в значениях сопротивлений ветвей н, г2, г3, обозначены кружками со стрелками, показывающими направления действия ЭДС. [5]
Систему контуров электрической цепи системы будем выбирать так, чтобы ветвь, содержащая нагрузку, входила лишь в один из соответствующих контуров трехфазной системы. Это объясняется тем, что активное сопротивление нагрузки следует считать величиной того же порядка, что и индуктивное сопротивление статорных цепей. Поэтому уравнения Кирхгофа для контуров, содержащих нагрузку, будут формально описывать быстрые процессы, а медленные процессы и отвечающие им медленные переменные окажутся скрытыми. Для выделения скрытых переменных необходимо преобразовать уравнения цепей, что равносильно введению контуров, включающих только цепи статоров двух машин. [6]
[6]
Потенциальная диаграмма контура электрической цепи показывает распределение электрического потенциала вдоль его обхода, если по оси абсцисс отложены в принятом масштабе величины сопротивлений между отдельными точками контура электрической цепи, а по оси ординат — соответствующие величины электрического потенциала. [8]
Кирхгофа для узлов и контуров электрической цепи . [10]
При уменьшении токов в контурах электрических цепей энергия поля может быть полностью или частично возвращена или преобразована в другие виды энергии. [11]
Примерами дифференцирующих звеньев могут служить контуры электрических цепей , состоящие из активного и индуктивного сопротивлений или из емкостного и активного сопротивлений. [13]
График распределения потенциала вдоль какого-либо контура электрической цепи называют потенциальной диаграммой. [15]
Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.
Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.
Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
Узел – место соединения трёх и
более ветвей.Точки К и Е не являются узлами.
Контур электрический — это… Что такое Контур электрический?
- Контур электрический
- контур электрической цепи, любой замкнутый путь, проходящий по нескольким ветвям электрической цепи (См. Электрическая цепь).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Контур
- Контурная съёмка
Смотреть что такое «Контур электрический» в других словарях:
КОНТУР ЭЛЕКТРИЧЕСКИЙ — (контур электрической цепи) любой замкнутый путь, проходящий по нескольким ветвям электрической цепи.
 Иногда термин контур электрический используют как синоним термина колебательный контур … Большой Энциклопедический словарь
Иногда термин контур электрический используют как синоним термина колебательный контур … Большой Энциклопедический словарьконтур электрический — (контур электрической цепи), любой замкнутый путь, проходящий по нескольким ветвям электрической цепи. Иногда термин «контур электрический» используют как синоним термина «колебательный контур». * * * КОНТУР ЭЛЕКТРИЧЕСКИЙ КОНТУР ЭЛЕКТРИЧЕСКИЙ… … Энциклопедический словарь
КОНТУР ЭЛЕКТРИЧЕСКИЙ — (контур электрич. цепи), любой замкнутый путь, проходящий по неск. ветвям электрич. цепи. Иногда термин К. э. используют как синоним термина колебательный контур … Естествознание. Энциклопедический словарь
КОНТУР — (фр. contour, от contourner обертывать, очерчивать). Очертание, профиль, очерк. В рисовании: линия, которая определяет внешнюю форму предмета. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. КОНТУР набросок,… … Словарь иностранных слов русского языка
КОНТУР — (1) замкнутая цепь проводников, по которой течёт электрический ток; (2) очертание какого либо предмета, линия, очерчивающая систему точек на плоскости млн.
 форму конфигурации в пространстве … Большая политехническая энциклопедия
форму конфигурации в пространстве … Большая политехническая энциклопедияЭЛЕКТРИЧЕСКИЙ ФИЛЬТР — электрическая цепь, состоящая из конденсаторов и катушек индуктивности (или активных сопротивлений), соединённых определённым образом с целью выделения только полезных сигналов и подавления колебаний др. полосы частот («частота среза»), которые… … Большая политехническая энциклопедия
Электрический конденсатор — У этого термина существуют и другие значения, см. Конденсатор (значения). См. также: варикап Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик … Википедия
электрический контур — elektrinis kontūras statusas T sritis fizika atitikmenys: angl. electric circuit vok. elektrischer Kreis, m rus. электрический контур, m pranc. circuit électrique, m … Fizikos terminų žodynas
Электрический фильтр — Фильтр в электронике устройство для выделения желательных компонент спектра электрического сигнала и/или подавления нежелательных.

Электрический фильтр (электрич. устройство) — Фильтр в электронике устройство для выделения желательных компонент спектра электрического сигнала и/или подавления нежелательных. Содержание 1 Типы фильтров 2 Принцип работы пассивных аналоговых фильтров … Википедия
Как определить независимые контуры
Независимый контур – это замкнутый участок электрической цепи, проложенный через ветви цепи, содержащий хотя бы одну новую ветвь, неиспользованную при поиске других независимых контуров.
Независимый контур содержит не менее одной новой ветви. Он и не получается из контуров, которые уже были выбраны, как независимые путем удаления из этих контуров общих ветвей.
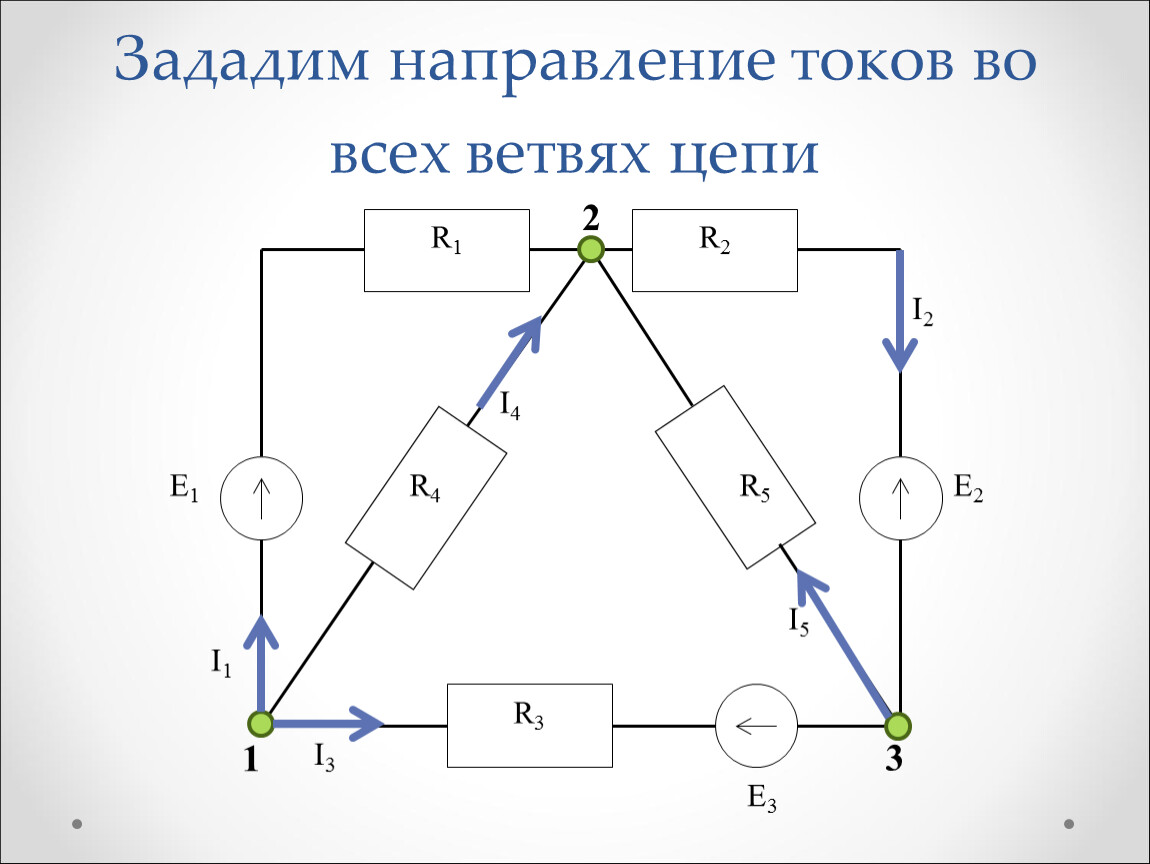
На рисунке независимыми контурами являются:
При свертке параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из сворачиваемых.
Если параллельно соединены n одинаковых сопротивлений (Рис. 3.3), эквивалентное сопротивление в n раз меньше сопротивления любой из ветвей.
Если на участке цепи параллельно соединены лишь два элемента (Рис. 3.4), выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно определить как отношение произведения двух сопротивлений к их сумме:
4. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
К основным законам электрических цепей относятся закон Ома и законы Кирхгофа.
Если в ветви не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (Рис. 4.1):
Закон Ома для ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветви.
В частности, ток в ветви, изображенной на Рис. 4.2, равен:
.
Первый закон Кирхгофа
В любом узле цепи алгебраическая сумма токов равна нулю. При этом, токи, направленные к узлу, принято считать положительными, токи, направленные от узла, принято считать отрицательными (Рис. 4.3).
По первому закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема. Но не все они будут независимыми. Если схема содержит узлов, независимыми будут уравнений. Оставшееся уравнение будет являться следствием всех предыдущих.
Второй закон Кирхгофа
В любом замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической сумме ЭДС, включенных в контур.
При этом, положительными считаются те напряжения и ЭДС, которые совпадают с направлением обхода контура, отрицательными считаются напряжения и ЭДС, которые противоположны направлению обхода контура. Направление обхода контура можно выбирать произвольно.
Алгоритм составления уравнения по второму закону Кирхгофа для замкнутого контура цепи
Для заданного контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа составляется в следующем порядке:
- Задается направление токов в ветвях (Рис. 4.4 б).
- Выбирается направление обхода контура (Рис. 4.4 в).
- Записывается уравнение, в левой части которого – сумма падений напряжений на сопротивлениях ветвей. В правой части – сумма ЭДС контура.
Примечание: Падение напряжения на сопротивлении ветви записывается в соответствии с известным уже законом Ома (1.1):
Применение второго закона Кирхгофа для незамкнутого участка цепи
Второй закон Кирхгофа справедлив только для замкнутого контура. При этом, любой незамкнутый участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве незамкнутого участка.
При этом, любой незамкнутый участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве незамкнутого участка.
Незамкнутый участок цепи abcd изображен на Рис. 4.5 а.
Дополняем участок до замкнутого контура, добавляя напряжение между незамкнутыми точками c и d (Рис. 4.5 б). Теперь для контура abcd можно записать второй закон Корхгофа:
Применение законов Кирхгофа при наличии в цепи источника тока
Источник тока имеет бесконечно большое сопротивление, поэтому не образует замкнутого контура и не может входить в уравнения второго закона Кирхгофа. Однако, в уравнениях первого закона Кирхгофа источник тока должен содержаться обязательно.
При необходимости записать уравнение по второму закону Кирхгофа для контура, содержащего источник тока, его заменяют напряжением на выводах источника тока.
Написать уравнение по первому закону Кирхгофа для узла a и уравнение по второму закону Кирхгофа для контура abcd (Рис. 4.6 а).
4.6 а).
Уравнение по первому закону Кирхгофа для узла a содержит источник тока и имеет вид:
Для того чтобы написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его выводах (Рис. 4.6 б), задаем направление обхода контура против часовой стрелки и получаем:
Для упрощения расчетов источник тока с параллельным сопротивлением можно заменить на эквивалентный источник ЭДС (Рис. 4.7). После расчета необходимо обязательно вернуться к исходной схеме.
Независимый контур цепи
В принципе, по второму закону Кирхгофа можно составить столько уравнений, сколько контуров содержит цепь. Но не все эти уравнения будут независимыми. Для определения независимости уравнений по второму закону Кирхгофа вводится такое понятие как независимый контур цепи.
Независимый контур цепи – это такой контур, который содержит хотя бы одну новую ветвь, не вошедшую в другие контуры цепи.
Независимые контуры в общем случае выбираются произвольно, но проще всего выбирать их так, чтобы они совпадали с ячейками цепи (Рис. 4.8 б).
Если схема содержит ветвей и узлов, число независимых контуров равно
.
Схема на Рис. 4.8 б содержит три независимых контура.
5. СИСТЕМА УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ
Законы Кирхгофа можно использовать для расчета токов в ветвях цепи. Главное требование при этом – получение системы независимых уравнений, в которой число неизвестных равно количеству токов, подлежащих определению.
Алгоритм составления системы уравнений по законам Кирхгофа
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 266
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 602
- БГУ 153
- БГУИР 391
- БелГУТ 4908
- БГЭУ 962
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 119
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1967
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 300
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 409
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 497
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 130
- ИжГТУ 143
- КемГППК 171
- КемГУ 507
- КГМТУ 269
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2909
- КрасГАУ 370
- КрасГМУ 630
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 139
- КубГУ 107
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 367
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 330
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 636
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 454
- НИУ МЭИ 641
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 212
- НУК им.
 Макарова 542
Макарова 542 - НВ 777
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1992
- НГУЭУ 499
- НИИ 201
- ОмГТУ 301
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 119
- РАНХиГС 186
- РОАТ МИИТ 608
- РТА 243
- РГГМУ 118
- РГПУ им. Герцена 124
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 122
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 130
- СПбГАСУ 318
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 147
- СПбГПУ 1598
- СПбГТИ (ТУ) 292
- СПбГТУРП 235
- СПбГУ 582
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 193
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 380
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1655
- СибГТУ 946
- СГУПС 1513
- СибГУТИ 2083
- СибУПК 377
- СФУ 2423
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 324
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 306
Полный список ВУЗов
Чтобы распечатать файл, скачайте его (в формате Word).
Метод контурных токов – один из основных и широко применяемых на практике методов. Он заключается в определении по второму закону Кирхгофа контурных токов. Для каждого контура цепи задают ток, который остается неизменным.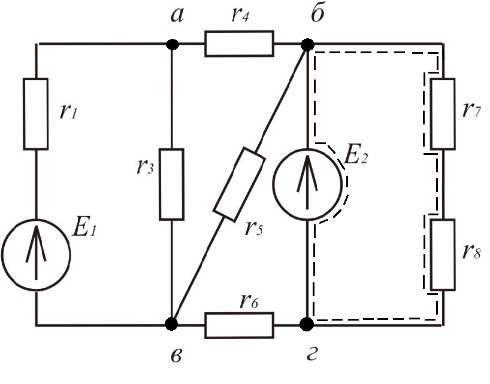 В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно.
В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно.
Контурные токи, проходя через узел, остаются непрерывными. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа.
Рис.28. Иллюстрация к методу контурных токов.
На рис.28 показана цепь с двумя независимыми контурами, следовательно, и с двумя контурными токами I11иI22.
Токи в ветвях I1иI2равны контурным токам:
Ток I3равен сумме этих двух контурных токов:
По второму закону Кирхгофа для первого контура цепи:
r11– сумма всех сопротивлений, входящих в контурI, называетсясобственным сопротивлением контура.
r12– сопротивление ветви, общей для контураIиII;
E11=E1-E2– алгебраическая сумма всех э.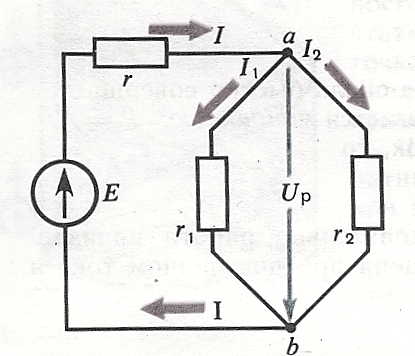 д.с., содержащихся в первом контуре; со знаком «-» берется э.д.с., действующая навстречу контурному току рассматриваемого контура.
д.с., содержащихся в первом контуре; со знаком «-» берется э.д.с., действующая навстречу контурному току рассматриваемого контура.
Аналогично для второго контура рис.28.
Уравнения, составленные по методу контурных токов, всегда записывают в виде системы. Для схемы рис.28:
В результате решения системы находят контурные токи, а затем токи ветвей.
Если заданная электрическая цепь содержит nнезависимых контуров, то на основании второго закона Кирхгофа получаетсяnконтурных уравнений:
(29)
Собственные сопротивления riiвходят в уравнения (29) со знаком «+», поскольку обход контура принимается совпадающим с положительным направлением контурного токаIii. Общие сопротивленияrikвойдут в уравнения со знаком «-», когда токиIiиIkнаправлены в них встречно.
Число уравнений, составляемых по методу контурных токов, определяется по формуле:
где Nb– число ветвей электрической цепи;
Nи. т.– число идеальных источников тока.
т.– число идеальных источников тока.
Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
Решим пример 2 параграфа 11, используя метод контурных токов.
Цепь содержит три контура, через которые протекают контурные токи.
При наличии источников тока надо так направлять контурные токи, чтобы они протекали через данные источники. Но через один источник тока не может протекать два контурных тока.
На рис.1 обозначены положительные направления контурных токов. Очевидно, что I11=J1;I22=-J2
Контурный ток I33– неизвестен, для него составляем уравнение:
В правой части уравнения стоит «0», т.к. отсутствует контурная э.д.с.
В результате решения определяем I33=16,25 мА
Структура электрической цепи
К структурным или
топологическим свойствам цепи относятся
такие ее особенности, которые не связаны
с характеристиками входящих в нее
активных и пассивных элементов. К ним
относятся следующие понятия: ветвь,
узел, контур.
К ним
относятся следующие понятия: ветвь,
узел, контур.
Ветвью электрической цепи называют участок, элементы которого включены последовательно друг за другом и обтекаются одним и тем же током.
Узлом электрической цепи называют место соединения нескольких ветвей. Узел связывает не менее трех ветвей и является точкой разветвления.
Ветви считаются соединенными последовательно, если они обтекаются одним и тем же током. Ветви считаются соединенными параллельно, если они присоединены к одной и той же паре узлов. Таким образом, при последовательном соединении элементов общим параметром для них является ток, при параллельном – напряжение между узлами.
Контуром
электрической
цепи называется совокупность следующих
друг за другом ветвей. Узлы, в которых
эти ветви соединяются, являются точками
разветвления. При обходе замкнутого
контура
начальная и конечная точки совпадают. В дальнейшем под контуром понимается
замкнутый контур.
В дальнейшем под контуром понимается
замкнутый контур.
Цепь, в которой отсутствуют разветвления, называют одноконтурной, при наличии разветвлений – многоконтурной. Многоконтурная цепь характеризуется числом независимых контуров. Совокупность независимых контуров определяется тем, что каждый из последующих контуров, начиная от элементарного, отличается по меньшей мере одной новой ветвью. Число независимых контуров может быть определено по формуле Эйлера:
(1.8)
где m – количество ветвей,
n – количество узлов, причем m > n всегда.
Пример.
В цепи на рис. 1.10. четыре узла: a, b, c, d; шесть ветвей: ab, bd, bc, ad, dc, ac. Т.о., количество независимых контуров по формуле Эйлера определится следующим образом:
p = 6 — 4 + 1 = 3.
Это могут быть
следующие контуры: abcd,
dbc, adc или
abd,
dbca, adc и
другие.
-
Законы Кирхгофа
Законы Кирхгофа являются основой теории линейных цепей и представляют собой так же, как и закон Ома, обобщение опытных данных.
I закон Кирхгофа (для токов): алгебраическая сумма токов в узле равна нулю, или сумма притекающих и сумма истекающих токов одинаковы. Как правило, при суммировании притекающие токи берутся со знаком «+», а истекающие – со знаком «–».
(1.8)
II закон Кирхгофа (для напряжений): алгебраическая сумма ЭДС всех источников, встречающихся при обходе контура, равна алгебраической сумме напряжений на всех потребителях. В алгебраической форме
. (1.8)
В сумму со знаком
«+» входят ЭДС содействующих источников
(т.е. тех источников, которые действуют
в направлении, согласном с обходом
контура) и со знаком «–» ЭДС
противодействующих источников. При
суммировании напряжений потребителей
со знаком «+» берутся напряжения на всех
потребителях, токи которых направлены
согласно с обходом контура, и со знаком
«–» берутся напряжения всех остальных
потребителей. Направление обхода контура
выбирается произвольно.
При
суммировании напряжений потребителей
со знаком «+» берутся напряжения на всех
потребителях, токи которых направлены
согласно с обходом контура, и со знаком
«–» берутся напряжения всех остальных
потребителей. Направление обхода контура
выбирается произвольно.
-
Преобразование линейных пассивных электрических цепей
Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем.
При последовательном соединении роль эквивалентного сопротивления (или сопротивления эквивалентного потребителя) играет сумма сопротивлений всех потребителей (рис. 1.11.).
(1.10) Это следует из II закона Кирхгофа:
(1. 11)
11)
При двух последовательно соединенных потребителях:
(1.12)
При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
. (1.13)
Это следует из I закона Кирхгофа:
При двух параллельно соединенных потребителях:
(1.14)
Таким образом, для расчета цепей с последовательно включенными потребителями целесообразно их свойства выражать значениями сопротивлений, а для параллельно включенных – значениями проводимостей.
Определение эквивалентного сопротивления при смешанном соединении потребителей выполняется путем постепенного упрощения (сворачивания) исходной цепи.
Пример.
Параллельное соединение R1 и R2:
Последовательное соединение R12 и R3:
Последовательное соединение R4 и R5:
Параллельное соединение R123 и R45:
Последовательное соединение Rас и R6:
Таким образом, эквивалентное сопротивление
Более сложными
являются взаимные преобразования
потребителей, соединенных звездой или
треугольником. К таким преобразованиям
следует обращаться в тех случаях, когда
в цепи, подлежащей упрощению, нельзя
выделить параллельное или последовательное
соединения потребителей.
К таким преобразованиям
следует обращаться в тех случаях, когда
в цепи, подлежащей упрощению, нельзя
выделить параллельное или последовательное
соединения потребителей.
В узлах a, b, c и треугольник , и звезда на рис. 1.14. соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены.
Выразим Uab треугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.
Заменим в первом уравнении токи I3 и I2 на соответствующие выражения:
По закону Ома напряжение Uab для соединения потребителей треугольником:
(1.15)
Теперь получим выражение для этого же напряжения при соединении потребителей звездой:
(1.16)
Для эквивалентности данных цепей при произвольных значениях токов Ia и Ib необходимо равенство напряжений Uab для соединения потребителей треугольником и звездой. Это возможно только при одинаковых коэффициентах уравнений (1.15) и (1.16), т.е.
(1.17)
Аналогично можно получить выражения для определения :
(1.18)
Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника.
Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений (1.17) и (1.18) через проводимости:
(1.19)
или через сопротивления:
(1.20)
Следовательно, сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.
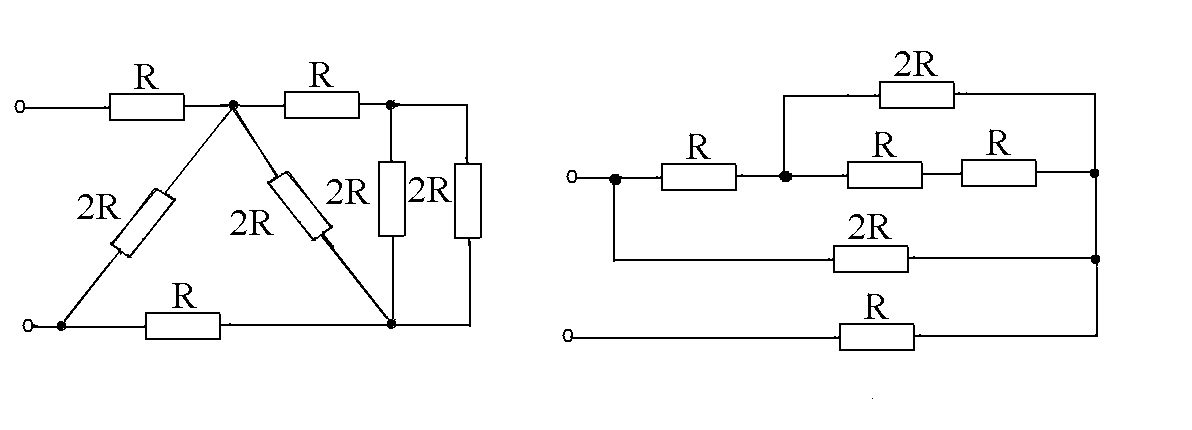
3.Раскройте понятия схема электрической цепи, узел, ветвь, контур. Приведите пример. Укажите количество узлов, ветвей и независимых контуров в электрической цепи (рисунок 1)
Графическое изображение электрической цепи, содержащее условные обозначения ее элементов, называется схемой электрической цепи.
Участок, вдоль которого ток один и тот же, называется ветвью электрической цепи.
Место соединения ветвей называется узлом электрической цепи.
Узел образуется при соединении в одной точке не менее трех ветвей, например на схеме рис. 3.16 к узлу 6 подключены четыре ветви.Всего узлов четыре 1,3,4,6.
Ветви, не содержащие источников электрической энергии, называются пассивными, а ветви, в которые входят источники,—активными.
Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром электрической цепи. Контур не включающий в себя остальные называется назависимым контуром электрической цепи.
На рис. 3.16 таких контуров четыре:1-2-3-1; 1-3-6-1; 3-4-6-3, 4-5-6-4.
На схемах стрелками отмечаются положительные направления ЭДС напряжений и токов. Направление ЭДС может быть указано обозначением полярности зажимов источника: внутри источника ЭДС направлена от отрицательного зажима к положительному (так же как и ток).
Рисунок 1-Схема электрической цепи
В предложенной схеме (рисунок 1)
количество узлов 3
количество ветвей 5
количество независимых контуров3
4.Сформулируйте первый и второй законы Кирхгофа. Приведите примеры в общем виде.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлу электрической цепи: алгебраическая сумма токов в ветвях соединённых в один узел равна нулю:
∑ I = 0 , (1)
где I – ток в ветви,А.
В эту сумму токи входят с разными знаками, в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например для схемы 1 уравнения имеют вид:
Узел 1: — I1 – I2 + I3 =0
Узел 3: I1 + I2 – I7 – I4 = 0
Узел 4: I4 – I5 + I6 = 0
Узел 6: — I3 + I7 + I5 – I6 = 0
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Пример:
2 R1 3 R4 4
I1 I7 I4
I2 I5
E1 R2 E2 R5 E3
R3 I3 R7 I6 R6
1 6 5
Рисунок 1-Схема электрической цепи
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей: в контуре электрической цепи алгебраическая сумма ЭДС , входящих в контур,равна алгебраической сумме падений напряжений на пассивных элементах этого контура:
∑ E = ∑IR, (2)
где I – ток в ветви,А;
Е-ЭДС,В;
R-сопротивление, Ом.
При этом положительными считаются токи и ЭДС, направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на схеме 1:
для 1-2-3-1
I1R1 – I2R2 = E1
для 3-4-6-3
I4R4 + I5R5 – I7R7 = -E2
для 1-3-6-1
I7R7 + I2R2 + I3R3 = E2
для 6-5-4-6
I6R6 + I5R5 = E3
Электротехника. Уравнения Кирхгофа — Botva-Project
Разберем на примере домашнего задания, как пользоваться уравнениями Кирхгофа при расчете электрических цепей.
Задается электрическая схема, в которой известны значения всех сопротивлений и ЭДС источников напряжения. То есть все R и E заданы.
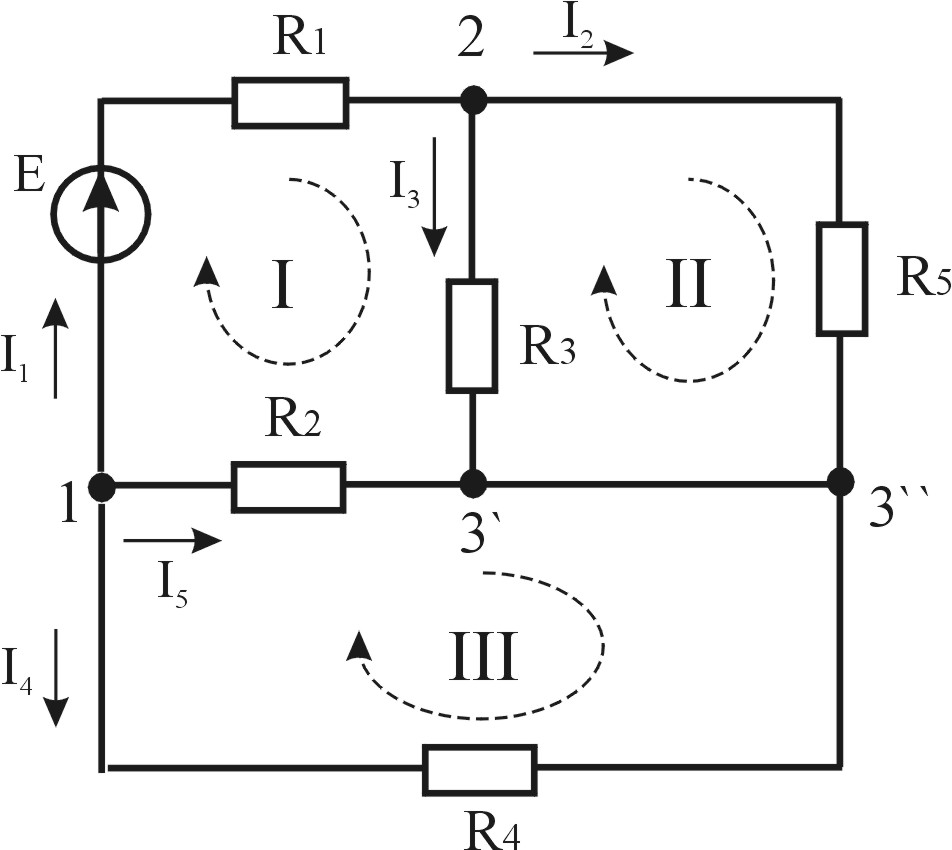
Первым делом, нужно определить, сколько в схеме узлов, независимых контуров и ветвей.
Узел — это просто точка, где сходится три и больше проводов. Иногда составители заданий хитрят и отмечают жирной точкой углы схем, не ведитесь, это провокация. Узлом считается только то место, где проводов не меньше трех. В нашем случае узлов 4. Нумеруем их в произвольном порядке.
Число независимых контуров мы определяем по количеству геометрических фигур, составляющих схему. Обычно это не составляет труда, хотя встречаются и замороченные схемы, где не сразу становится очевидным количество контуров. То есть мысленно делаем заливку каждого участка схемы, и количество получившихся цветов соответствует количеству независимых контуров. Просим прощения за косноязычность, но стараемся объяснять, что называется, «на пальцах», чтобы было понятно. Вот контуры в нашей схеме.
Ветвь — это участок провода между двумя узлами. Участки 1-2, 1-4, 1-3, 2-4, 2-3, 3-4 — это ветви нашей схемы. Всего получается 6 ветвей. В каждой из них течет свой ток, который надо обозначить на схеме. Направление стрелки, указывающей ток, выбираем произвольно (разве что, мы любим в ветвях с источниками напряжения выбирать направления токов туда же, куда указывают стрелки ЭДС). А вообще, направление стрелок ни на что не влияет, в результате расчета часть токов получится со знаком «плюс» (значит, направление соответствует выбранному), а часть токов — со знаком «минус» (значит, направление тока противоположно). Вот наши токи на схеме. Заодно выберем направление обхода в каждом контуре. Направление можно выбирать произвольно, но мы рекомендуем всегда брать направление по часовой стрелке во всех контурах. Меньше будете путаться.
Подведем промежуточный итог. Мы изучили данную схему, посчитали количество узлов (четыре), количество независимых контуров (три), количество ветвей (шесть), пронумеровали узлы, контуры, выбрали направление обхода и расставили стрелки токов в ветвях (шесть токов в соответствии с количеством ветвей).
Перейдем непосредственно к уравнениям Кирхгофа.
Первый закон Кирхгофа гласит: сколько тока пришло в узел, столько и должно выйти. Напоминает закон сохранения чего-угодно и по сути им и является. То есть сумма токов, вошедших в узел, равна сумме токов вышедших из узла. На практике это выглядит так: смотрим на любой узел, записываем, какие токи текут в ветвях, составляющих этот узел (из определения узла понятно, что их должно быть не меньше трех), входящие токи берем с плюсом, исходящие — с минусом. В сумме должен получиться ноль. Число уравнений, записанных по первому закону Кирхгофа, должно быть на единицу меньше, чем количество узлов в схеме. То есть из четырех узлов выбираем любые три. Исключительно из любви к прекрасному возьмем подряд узлы 1, 2, 3.
Смотрим на узел 1. В нем сходятся ветви 1,3,5, ток I1 входит (+), ток I3 выходит (-), ток I5 выходит (-).
Получаем первое уравнение.
Узел 2. В нем сходятся ветви 1,2,4, ток I1 выходит (-), ток I2 входит (+), ток I4 выходит (-).
Второе уравнение.
Узел 3. В нем сходятся ветви 4,5,6, ток I4 входит (+), ток I5 входит (+), ток I6 выходит (-).
Третье уравнение.
Аналогично можно записать уравнение по первому закону Кирхгофа для узла 4, но это уже будет избыточное уравнение. Нам нужно только три, но, подчеркиваем, что выбрать можно любые три узла.
Второй закон Кирхгофа простыми словами сводится к следующему: сумма напряжений на каждом резисторе внутри контура должна быть равна ЭДС этого контура. На практике это выглядит так: берем по очереди каждый контур, в левой части уравнения пишем напряжения на резисторах. Как мы помним из закона Ома U=IR, то есть напряжение на резисторе равно произведению силы тока в ветви на сопротивление резистора. ЭДС контура — это источники напряжения Е в нашей схеме. В общем, проще показать на примере, чем объяснить.
Уравнений пишем ровно столько, сколько в цепи независимых контуров, то есть три. Начинаем по порядку.
Контур I. Направление обхода мы выбрали по часовой стрелке. Ток I1 мы направили в другую сторону, поэтому падение напряжения на резисторе R1 берется с минусом. В резисторе R2 ток тот же и тоже берется с минусом. Ток I2 течет без сопротивления, игнорируем его, ток I3 — то же самое. ЭДС в контуре одна — E1, и направление также противоположно выбранному направлению обхода, значит, в правую часть уравнения записываем E1 со знаком минус.
Для контура I уравнение Кирхгофа выглядит так:
Контур II обходим тоже по часовой стрелке. Ток I4 течет через сопротивление R4 в направлении, совпадающем с направлением обхода. Токи I2 и I6 текут без сопротивлений, так что в уравнение не входят. ЭДС в правой части уравнения: E1 с плюсом, E3 с плюсом, E4 с плюсом.
Уравнение получается таким:
И наконец контур III. Ток I5 через резистор R5 с минусом, токи I3 и I6 не участвуют. ЭДС E2 с минусом.
Получаем
Окончательно получаем систему из шести уравнений (как раз столько, сколько у нас неизвестных токов в наших ветвях).
Эта система имеет одно решение, так что, решив ее любым доступным вам методом (мы предпочитаем решать в MathCad, поскольку меньше риск арифметической ошибки и проще вносить исправления, если понадобится), вы определите все неизвестные токи в цепи.
В следующих разделах мы обсудим методы проверки расчета электрической схемы, а также рассмотрим другие способы решения, такие как метод контурных токов, метод межузловых потенциалов, метод эквивалентного генератора.
Надеемся, материал был полезен.
Всегда ваша, Botva-Project
определение, элементы, схемы. Топология и методы расчета
Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!
Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.
Электрические цепи
Электрическая цепь – это совокупность устройств, по которым течет электрический ток.
Рассмотрим самую простую электрическую цепь. Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:
Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.
Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.
Электрическая цепьКстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.
По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.
Элементы электрических цепей
Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.
Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.
Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.
Существуют условные обозначения для изображения элементов цепи на схемах.
Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.
Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.
Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.
При решении задач и анализе схем используют следующие понятия:
- Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
- Узел – соединение ветвей цепи;
- Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
Чтобы понять, что есть что, взглянем на рисунок:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Классификация электрических цепей
По назначению электрические цепи бывают:
- Силовые электрические цепи;
- Электрические цепи управления;
- Электрические цепи измерения;
Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.
Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.
Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.
Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.
Расчет электрических цепей
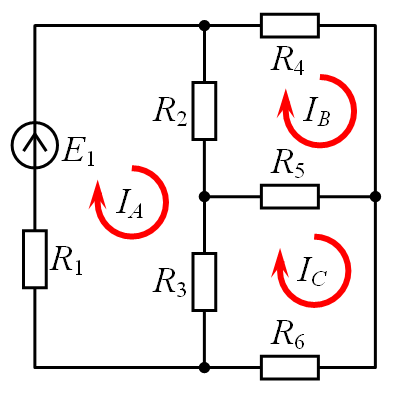
Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:
Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов
Какую бы цепь Вам ни понадобилось рассчитать, наши специалисты всегда помогут справится с заданиями. Мы найдем все токи по правилу Кирхгофа и решим любой пример на переходные процессы в электрических цепях. Получайте удовольствие от учебы вместе с нами!
Что такое электрическая цепь?
Электрическая схема представляет собой соединение электрических компонентов. Электрическая цепь состоит из батарей, резисторов, катушек индуктивности, конденсаторов, переключателей или транзисторов. Электрическая сеть состоит из замкнутого контура. Цепь — это замкнутый путь, по которому электроны текут по проволоке. Пока медная проволока находится в свободном доступе, электроны дрейфуют между атомами, но никогда не покидают медь.
Однако, когда мы подключаем этот медный провод к батарее, свободные электроны будут двигаться к положительному полюсу батареи.Эта толкающая сила называется Электродвижущая сила (E.M.F). E.M.F. выражается в вольтах. И обычно это называется напряжением. В результате этого напряжения происходит движение электронов. Это движение известно как электронный ток или электрический ток . Мы можем измерить ток, подключив амперметр между медным проводом и источником напряжения.
Полная цепь — это бесконечный цикл электронов. Если мы возьмем провод и закрутим его, он образует непрерывный путь, по которому электроны могут течь вечно.Это основная концепция схемы.
Электрическая цепь в основном состоит из
- Электрические источники, обеспечивающие напряжение и ток, такие как батареи. Они источник электронов.
- Переключатели, резисторы, потенциометры, конденсаторы, которые используются для управления электричеством.
- Устройства защиты в цепях высокого напряжения. Это автоматический выключатель, предохранитель и др.
- Провода, по которым проходит электрический ток из одной точки в другую в цепи.
- Нагрузкой в цепи может быть двигатель, светодиод, лампа и т. Д.
Вот некоторые основные свойства электрических цепей:
- Контур всегда замкнутый.
- Цепь всегда состоит из источника энергии,
- Направление потока тока — от положительной клеммы к отрицательной клемме источника.
- Направление потока электронов от отрицательной клеммы к положительной клемме источника.
Принципиальная схема
Принципиальная схема — это визуальное отображение электрической цепи.Принципиальные схемы бывают двух типов:
- Иллюстрированное изображение: Иллюстрированное изображение выполнено с использованием базовых изображений. Диаграмма этого типа дает аудитории менее техническое представление.
Наглядная принципиальная схема
- Схема: На этих схемах используются стандартные промышленные символы. Эти диаграммы используются для представления схемы электрику или любой другой технической аудитории.
Схема
Условные обозначения принципиальных схем
На принципиальной схеме есть сотни символов.Некоторые основные символы:
Предположим, мы хотим нарисовать простую схему, в которой батарея подключена к светодиоду таким образом, что положительная клемма батареи подключена к положительной клемме светодиода, а отрицательная клемма батареи подключена к отрицательной клемме светодиода. Тогда это можно представить как:
Типы цепей
В основном есть три типа цепей:
-
Обрыв цепи
Если в простой цепи одна клемма отключена, ток через эту цепь не протекает.Это состояние называется обрывом цепи или отсутствием нагрузки.
Обрыв цепи
-
Замкнутый контур
Электрическая цепь имеет источник электродвижущей силы и нагрузку. Эта нагрузка действует как токопроводящий путь. Если ток протекает через нагрузку, это считается замкнутой цепью. Если в простой цепи ток может течь от одного вывода батареи к другому без какого-либо прерывания, это называется замкнутой цепью.
Замкнутый контур
-
Короткое замыкание
Если положительная клемма аккумулятора напрямую соединена с отрицательной клеммой без какого-либо сопротивления между ними, это называется коротким замыканием.
Короткое замыкание
Помимо вышеуказанных схем, компоненты в электрической цепи могут быть расположены двумя различными способами: последовательно и параллельно.
Цепь серииЕсли в цепи компоненты соединены последовательно, тогда цепь называется последовательной схемой. В последовательной цепи ток через каждый компонент одинаков, а подаваемое напряжение представляет собой сумму напряжений на каждом компоненте. Если провод соединяет батарею с одной лампой, со следующей лампой, а затем обратно с батареей, говорят, что лампы соединены последовательно.
Последовательное соединение двух ламп
Параллельная цепь
Если в цепи компоненты соединены параллельно, тогда цепь называется параллельной цепью. В параллельной цепи напряжение на каждом компоненте будет одинаковым, а общий приложенный ток представляет собой сумму тока, протекающего через каждый компонент. Если лампа подключена к батарее, а другая лампа подключена в отдельном шлейфе с первой лампой, то лампа подключается параллельно.
Параллельное соединение двух ламп
Здесь напряжение на каждой лампочке будет таким же, как напряжение, подаваемое батареей.Ток через каждую лампу будет разделен, значит, если мы приложим к цепи 5А, 5А будет током, протекающим через каждую лампу.
Таким образом работают последовательные и параллельные цепи, и у них есть свои собственные свойства деления тока и напряжения.
Электрические цепи есть повсюду вокруг нас, в наших мобильных телефонах, в наших компьютерах, в вентиляторах и фонариках. Трудно предположить практическое использование электричества без электрических цепей. Мы все зависим от этих сложных цепей вокруг нас.
Что такое электрическая цепь?
В Уроке 1 обсуждалась концепция разности электрических потенциалов. Электрический потенциал — это количество электрической потенциальной энергии на единицу заряда, которым обладал бы заряженный объект, если бы он был помещен в электрическое поле в заданном месте. Концепция потенциала — это величина, зависящая от местоположения — она выражает количество потенциальной энергии на основе заряда, так что оно не зависит от количества заряда, фактически присутствующего на объекте, обладающем электрическим потенциалом.Разность электрических потенциалов — это просто разница в электрических потенциалах между двумя разными точками в пределах электрического поля.
Чтобы проиллюстрировать концепцию разности электрических потенциалов и природу электрической цепи, рассмотрим следующую ситуацию. Предположим, что есть две металлические пластины, ориентированные параллельно друг другу, и каждая заряжена зарядом противоположного типа — одна положительная, а другая отрицательная. Такое расположение заряженных пластин создаст электрическое поле в области между пластинами, которое направлено от положительной пластины к отрицательной пластине.Положительный тестовый заряд, помещенный между пластинами, будет двигаться от положительной пластины к отрицательной пластине. Это движение положительного испытательного заряда от положительной пластины к отрицательной могло бы происходить без потребности в подаче энергии в виде работы; это произойдет естественным образом и, таким образом, снизит потенциальную энергию заряда. Положительная пластина будет местом с высоким потенциалом, а отрицательная пластина — местом с низким потенциалом. Между этими двумя точками будет разница в электрическом потенциале.
Теперь предположим, что две противоположно заряженные пластины соединены металлической проволокой. Что случилось бы? Проволока служит своего рода зарядной трубкой, по которой может течь заряд. Со временем можно было представить себе положительные заряды, перемещающиеся от положительной пластины через зарядную трубку (провод) к отрицательной пластине. То есть положительный заряд естественным образом двигался бы в направлении электрического поля, созданного расположением двух противоположно заряженных пластин.По мере того, как положительный заряд покидает верхнюю пластину, пластина будет становиться менее заряженной, как показано на анимации справа. Когда положительный заряд достигнет отрицательной пластины, эта пластина станет менее отрицательно заряженной. Со временем количество положительного и отрицательного заряда на двух пластинах будет постепенно уменьшаться. Поскольку электрическое поле зависит от количества заряда, присутствующего на объекте, создающем электрическое поле, электрическое поле, создаваемое двумя пластинами, будет постепенно уменьшаться в силе с течением времени.В конце концов, электрическое поле между пластинами станет настолько маленьким, что не будет наблюдаемого движения заряда между двумя пластинами. Пластины в конечном итоге теряют заряд и достигают того же электрического потенциала. При отсутствии разности электрических потенциалов не будет потока заряда.
Приведенная выше иллюстрация приближается к демонстрации значения электрической цепи. Однако, чтобы быть истинной цепью, заряды должны постоянно проходить через полный цикл, возвращаясь в свое исходное положение и снова циклически проходя через него.Если бы существовало средство перемещения положительного заряда с отрицательной пластины обратно вверх на положительную пластину, то движение положительного заряда вниз через зарядную трубку (то есть провод) происходило бы непрерывно. В таком случае будет установлена цепь или петля.
Обычное лабораторное занятие, которое иллюстрирует необходимость полного цикла, использует аккумуляторный блок (набор D-элементов), лампочку и несколько соединительных проводов. Это упражнение включает наблюдение за эффектом подключения и отключения провода при простом расположении аккумуляторной батареи, лампочек и проводов.Когда все подключения к аккумуляторной батарее выполнены, лампочка загорится. Фактически, зажигание лампочки происходит сразу после окончательного подключения. Нет заметной временной задержки между моментом последнего подключения и моментом, когда лампочка загорается.
Тот факт, что лампочка горит и продолжает гореть, свидетельствует о том, что заряд проходит через нить накаливания лампочки и что электрическая цепь была установлена.Цепь — это просто замкнутый контур, по которому могут непрерывно перемещаться заряды. Чтобы продемонстрировать, что заряды движутся не только через нить накаливания лампочки, но и через провода, соединяющие аккумуляторную батарею и лампочку, мы изменили описанное выше действие. Компас помещают под проволоку в любом месте так, чтобы его стрелка совпадала с проволокой. После окончательного подключения к аккумуляторной батарее загорается лампочка, и стрелка компаса отклоняется. Игла служит детектором движущихся зарядов внутри провода.Когда он отклоняется, заряды движутся по проводу. А если отсоединить провод от аккумуляторной батареи, лампочка больше не горит, а стрелка компаса вернется в исходное положение. Когда лампочка загорается, заряд проходит через электрохимические элементы батареи, провода и нити накаливания лампочки; стрелка компаса определяет движение этого заряда. Можно сказать, что есть ток — поток заряда в цепи.
Электрическая цепь, представленная комбинацией батареи, лампочки и проводов, состоит из двух отдельных частей: внутренней цепи и внешней цепи.Часть схемы, содержащая электрохимические элементы батареи, является внутренней схемой. Часть схемы, в которой заряд перемещается за пределы аккумуляторной батареи через провода и лампочку, является внешней схемой. В Уроке 2 мы сосредоточимся на движении заряда по внешней цепи. В следующей части Урока 2 мы исследуем требования, которые должны быть выполнены, чтобы заряд протекал через внешнюю цепь.
Электрическая цепь — Energy Education
Рисунок 1: Пример замкнутой цепи (щелкните, чтобы увеличить). [1]Электрическая цепь представляет собой соединение компонентов, которые могут проводить электрический ток. В простых электрических цепях есть проводники (обычно провода), компонент, который подает питание (например, аккумулятор или розетка), и компонент, который поглощает энергию, называемый нагрузкой. Лампочка может быть примером нагрузки, и всегда должен быть обратный путь, чтобы электроны могли вернуться к источнику питания от нагрузки. Каждая цепь предназначена для подачи питания на одну или несколько нагрузок.Например, в бумбоксе питание идет на динамики. Точно так же мощность в лампе идет на лампочку. Схема позволяет заряду уходить с одной стороны источника питания и возвращаться с другой стороны источника питания.
Цепи могут быть включены последовательно, параллельно или их комбинация называется последовательно-параллельной цепью. [2] Чтобы узнать больше об этих различных схемах, посетите: последовательная и параллельная схемы.
На рисунке 1 цепь замкнута (заряд может уходить из источника питания, проходить через лампочку и возвращаться к источнику питания), и лампочка действует как нагрузка.Обратите внимание, что показания вольтметра показывают 0 В, потому что падение напряжения на электрическом переключателе равно 0. [1]
Обрыв цепи
Рисунок 2: Пример разомкнутой цепи (щелкните, чтобы увеличить). [1]Разрыв цепи (как на рисунке 2) имеет физический разрыв в пути проводимости, где ток падает до 0, а сопротивление становится бесконечным (слишком большим для измерения омметром). Однако напряжение можно измерить, потому что вольтметр подключается через открытую клемму. [3] Обратите внимание, что обрыв цепи не является истинной цепью, потому что заряд с одной стороны источника питания не может уйти и вернуться на другую сторону источника питания.
На Рисунке 2 переключатель поднят, поэтому цепь размыкается, что означает, что ток не проходит полный путь и лампочка не работает. Вольтметр все еще может быть подключен и отображает показание 18 вольт из-за наличия двух последовательно соединенных 9-вольтных батарей. [1]
Не имеет значения, где находится разрыв в электрической цепи, любое прерывание пути остановит электрический ток от перемещения по его пути.Это основа электрического переключателя, о котором говорилось выше.
Короткое замыкание
Рисунок 3. Пример короткого замыкания (щелкните, чтобы увеличить). [1] .Короткое замыкание (показано на рисунке 3) — это непреднамеренное соединение с низким сопротивлением между двумя или более точками в цепи. Поскольку ток увеличивается по мере уменьшения сопротивления (заданного законом Ома), это приведет к протеканию большого количества тока через «короткое замыкание». Этот более высокий ток, если он больше, чем может безопасно выдержать калибр провода, может вызвать ожог пути тока из-за высоких температур и может вызвать пожар.Это приводит к тому, что замыкает цепь. [3] Защитные устройства, такие как предохранители и автоматические выключатели, используются в случае короткого замыкания для предотвращения опасности поражения электрическим током и связанных с ним повреждений.
На рисунке 3 присутствует короткое замыкание. Хотя часть тока все еще проходит через лампочку, путь, идущий в обход лампочки, обеспечивает самое низкое сопротивление для цепи. Это более низкое сопротивление соответствует значительно большему току. Это большое количество тока превышает номинальный ток провода, тем самым разрушая переключатель и сжигая часть пути тока. [1]
Моделирование петель
Университет Колорадо любезно разрешил нам использовать следующую симуляцию Фета. Это моделирование исследует, как батареи работают в электрической цепи:
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 Университет Колорадо (2011).Комплект для конструирования цепей (только DC), виртуальная лаборатория [онлайн]. Доступно http://phet.colorado.edu/en/simulation/circuit-construction-kit-dc-virtual-lab
- ↑ R.T. Пэйнтер, «Основные электрические компоненты и счетчики», в Введение в электричество , 1-е изд. Нью-Джерси: Прентис-Холл, 2011, гл. 4, сек. 4.3, с. 155-160.
- ↑ 3,0 3,1 R.T. Пэйнтер, «Основные электрические компоненты и счетчики», в Введение в электричество , 1-е изд. Нью-Джерси: Прентис-Холл, 2011, гл.4, сек. 4.4, с. 160-162.
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
I. Качественное исследование последовательных и параллельных цепей
Электрическая цепь состоит из полного замкнутого пути (или путей) для электрического тока. «Последовательная» цепь имеет только один путь для прохождения электричества. «Параллельная» цепь имеет два или более пути для электричества.
Сначала вы подключите простую схему, которая позволит вам проверять материалы на проводимость.Затем будут подключены некоторые цепи, чтобы продемонстрировать влияние последовательных и параллельных цепей на компоненты в цепи.
ПРОЦЕДУРА:
1. Подключите печатную плату, как показано на рисунке, и обратите внимание, что лампочка загорится, когда вы коснетесь зондов вместе.
2. Коснитесь концами другого незакрепленного провода зондами. Обратите внимание, что лампочка горит ярко. Это показатель хорошей электропроводности, поскольку ток через лампочку напрямую зависит от яркости.
3. Проверьте несколько других предметов и запишите свои результаты. Включите монету, кожу и стакан с водой. Убедитесь, что зонды контактируют с измеряемым материалом, но не друг с другом. Перечислите проверенные материалы и свои выводы об их проводимости.
4. Подключите цепь заново, как показано на схеме ниже. Это последовательная или параллельная схема?
|
5. Теперь отсоедините провод №2 и подсоедините его к лампочке №2.Подключите другой провод от лампочки №2 к лампочке №1. На рисунке показана схема. Как яркость каждой лампы соотносится с яркостью лампы на этапе 4 процедуры. Почему она отличается? Откручиваем одну лампочку. Что происходит и почему? |
|
6. Подключите показанную схему. Покажите на схеме или на эскизе путь (и) текущего потока. Это последовательная или параллельная схема? Откручиваем одну лампочку. Опишите, что происходит и почему. |
II.Количественное исследование напряжения, тока и закона Ома.
Электрический ток — это скорость электрического заряда, измеряемая в амперах. Ток переносит электрическую энергию по проводникам. Напряжение (В) — это мера энергии на единицу заряда между двумя точками в цепи. Можно думать о напряжении как об эффективной «разнице давлений», которая вызывает протекание тока. Сопротивление (R) является противодействием току и измеряется в омах. На практике резисторы принимают форму лампочек, тостеров, нагревателей и других устройств, которые используют электрическую энергию для выполнения полезных задач, а также являются нежелательной формой сопротивления в электропроводке, которая передает электрическую энергию вам.
В этом лабораторном упражнении будет использован законОма для определения напряжения, тока или сопротивления в цепи. Закон Ома просто гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению в цепи:
или в символьной форме
I = V / R или эквивалентно R = V / IСимволы и приборы: В принципиальных схемах будут использоваться следующие символы.
|
Провод имеет практически нулевое сопротивление в большинстве практических случаев. «Батарея» будет подключать лабораторные столы к центральной электросети постоянного тока. Один и тот же лабораторный измеритель будет использоваться как для амперметра, так и для вольтметра. Вам нужно будет выбрать правильную функцию с помощью переключателя. |
Амперметр всегда подключается последовательно в цепи.Несоблюдение этого правила приведет к перегоранию предохранителей или повреждению счетчиков. Напомним, что ток имеет только один путь для прохождения в последовательном соединении, поэтому амперметр измеряет ток, протекающий через последовательно включенные элементы схемы. Используемые амперметры будут измерять в миллиамперах или 10 -3 ампер.
Вольтметр всегда подключается параллельно элементам цепи, которые он проверяет, и измеряет изменение напряжения на них.
ПРОЦЕДУРА:
(Надлежащая маркировка принципиальных схем является частью вашего отчета.)
А. Закон Ома
1. Подключите цепь, как показано, с установленным амперметром, соблюдая правильную полярность. Установите селекторный переключатель измерителя на миллиампер постоянного тока. «Аккумулятором» в этом случае будут круглые розетки Flex Lab на лабораторном столе, которые подключены к источнику постоянного тока — НЕ ПОДКЛЮЧАЙТЕ ПИТАНИЕ, пока схема не будет одобрена инструктором.
2. После утверждения подайте питание, подключив провода к розеткам постоянного тока, и запишите показания амперметра в миллиамперах.Повторите измерение тока каждого из остальных резисторов, поместив их в цепь вместо первого.
3. Отсоедините провода питания и выньте амперметр из цепи. Переключите его на постоянное напряжение и подключите параллельно резистору. Подключите напряжение постоянного тока и измерьте напряжение на резисторе. Повторите то же самое для других резисторов.
4. Теперь у вас есть измерения напряжения и тока для каждого резистора. Используйте закон Ома, чтобы рассчитать сопротивление для каждого резистора и сравнить рассчитанное значение, полученное из маркировки на резисторе или из цветового кода на резисторе.
B. Распределение тока.
1. Сформируйте последовательную цепь, показанную ниже. Поскольку вы снова будете использовать измеритель в качестве амперметра, переустановите его селекторный переключатель на миллиамперы постоянного тока. Перед подачей питания убедитесь, что это правильно.
2. Последовательно подключите амперметр к точкам 1, 2, 3 и 4 и запишите текущее значение в каждой точке. Обратите внимание, что обычный ток в этой цепи считается направленным по часовой стрелке, а электроны будут циркулировать против часовой стрелки.Какие выводы можно сделать о токе в последовательной цепи по результатам измерений?
C. Распределение напряжения
Цепь, подключенная к Части B, теперь будет использоваться для измерения напряжений. Будут использоваться соединения, показанные ниже, но поскольку вы будете использовать один и тот же измеритель для амперметра и вольтметра, амперметр не будет на месте, когда вы будете измерять напряжения.
1. Измерьте напряжение на каждом резисторе по очереди и во всей цепи, как показано на V4.Запишите результаты.
2. Сравните сумму напряжений на отдельных резисторах с напряжением во всей цепи. Что можно сделать по поводу напряжения в последовательной цепи?
3. Используйте напряжения на каждом резисторе, полученные в шаге 1 выше, и токи, полученные из раздела B выше, вместе с законом Ома, чтобы получить значения для отдельных сопротивлений. Сравните значения с указанными значениями для резисторов.
4.Из общего напряжения, измеренного на этапе 1, и общего тока, измеренного в разделе B, вычислите эквивалентное сопротивление всей цепи, состоящей из трех последовательно включенных резисторов. Сравните этот результат с суммой R A + R B + R C .
ВОПРОСОВ:
1. Какие функции выполняет провод? Связаны ли с вашим аппаратом изоляторы? Что они делают?
2. Что, если что, по проводам течет?
3.Почему должно быть два подключения к аккумулятору и к лампочке?
4. Если у вас есть прибор на 120 вольт и через него протекает ток 2 ампера, какова потребляемая мощность в ваттах? Какое у него сопротивление в Ом?
5. Почему розетки в вашем доме подключены параллельно, а не последовательно?
Electrical Circuits — Christopher Gray, Engineering
Основным требованием к полезности электрических технологий является то, что вы должны иметь возможность заставить электроны двигаться, когда и когда вы этого хотите.Чтобы электричество текло, у него должны быть Источник и Путь. Источник обеспечивает электроны и мотивацию (напряжение), чтобы заставить их двигаться. Примерами источников являются батареи, генераторы, топливные элементы и солнечные панели. Путь может быть любым материалом с высокой электропроводностью (проводником), который проходит от источника к земле или обратно к источнику. Обычные примеры проводников — медь, алюминий и золото. Уберите или отключите источник или путь, и электричество не будет течь.Короткое замыкание
Короткое замыкание создается, когда создается токопроводящий путь между источником и землей или обратно к источнику. Короткое замыкание позволяет электричеству течь с очень небольшим сопротивлением. Энергия источника преобразуется в электрическую энергию (электричество), когда электроны проходят через проводник. Если вы используете аккумулятор в качестве источника, он очень быстро разрядится. Энергия не может быть создана или уничтожена, только преобразована из одной формы в другую (Закон сохранения энергии).Без чего-либо еще в цепи, чтобы использовать эту электрическую энергию, ее нужно как-то высвобождать. Электрическая энергия преобразуется в тепловую. Проводник и батарея нагреются, и тепловая энергия будет излучаться или отводиться. Поскольку при коротком замыкании выделяется много тепла, они представляют серьезную опасность возгорания и ожога. Чтобы избежать этих негативных последствий, было разработано множество компонентов безопасности для предотвращения коротких замыканий. Провода покрыты изоляционными (с низкой проводимостью) материалами, такими как пластик.Предохранители, автоматические выключатели и «индикаторы замыкания на землю» используются для прекращения подачи электроэнергии в случае обнаружения короткого замыкания.
Полная схема
Полная схема имеет источник и путь, но также имеет компонент, называемый нагрузкой, который использует электрическую энергию. Нагрузки могут преобразовывать электрическую энергию в механическую, тепловую или электромагнитную энергию. Например, вы можете создать цепь, которая соединяет каждую сторону батареи с лампочкой с помощью проводов.Электричество течет от батареи через лампочку (излучающую свет), а затем обратно в батарею. Это похоже на схему, которую вы можете найти в фонарике. Электрическая энергия используется лампочкой для получения света. Поскольку провод (проводник) все еще имеет некоторое сопротивление, часть энергии все равно будет преобразовываться в тепло, и лампочка, скорее всего, будет выделять тепло (инфракрасное излучение) в дополнение к видимому свету. Эффективность схемы показывает, сколько энергии используется и сколько тратится впустую.Люминесцентные лампы более эффективны, чем лампы накаливания, но современные светодиодные лампы эффективнее их обоих. Лампы накаливания производят больше всего тепла, а светодиодные лампы — меньше всего тепла.Хорошая полная цепь
Хотя полная схема может быть безопасной и выполнять работу, она не будет работать долго, если вы не добавите некоторые компоненты управления. Возьмем для примера схему фонарика. Он будет излучать свет, но без переключателя для включения и выключения он будет светить, когда он вам не нужен, а батареи скоро разрядятся и перестанут зажигать, когда вам это нужно.Чтобы сделать это хорошей законченной схемой, вам нужно добавить переключатель, чтобы вы могли включать его, когда вам это нужно, и выключать, чтобы сохранить батарею на будущее. Некоторыми примерами компонентов управления являются переключатели, резисторы, потенциометры, конденсаторы, трансформатор (не роботы из научной фантастики), преобразователи и транзисторы. Цель всего этого — обеспечить подачу нужного количества электричества в нужные места в нужное время.Серия и параллельные цепи
Цепи серии
В последовательной цепи создается путь, который позволяет электричеству течь от источника через каждый компонент и обратно к источнику, так что есть только один путь для электронов.Электричество проходит через ряд компонентов, выстроенных один за другим. Это простая для понимания схема, потому что вы не дали электричеству выбора, когда оно пойдет. Рассчитать напряжение, сопротивление и ток в последовательной цепи довольно просто. Когда две или более батареи соединены последовательно, их напряжения складываются (две батареи на 9 вольт, соединенные последовательно, дают 18 вольт). Резисторы, соединенные последовательно, также просто складываются, чтобы получить общее сопротивление цепи (100 Ом + 50 Ом + 80 Ом = 230 Ом).Как только вы узнаете общее напряжение и полное сопротивление, вы можете использовать закон Ома для расчета тока, протекающего по цепи.
Параллельные цепи
Когда создается цепь, которая обеспечивает более одного возможного пути прохождения электричества, это называется параллельной цепью. Простая параллельная схема может включать лампочки, подключенные к одной и той же батарее, так что есть два пути, по которым может течь электричество, по одному через каждую лампочку.Часть электричества проходит через первую лампочку, а часть электричества проходит через вторую лампочку. Распределяя электричество таким образом, и если оба пути идентичны, обе лампы получают одинаковое количество напряжения от батареи. Когда батареи размещаются параллельно, их напряжения НЕ суммируются, а скорее продлевается срок службы батарей (две батареи на 9 вольт, включенные параллельно, будут обеспечивать 9 вольт в цепи в течение более длительного времени, чем одна батарея на 9 вольт). Когда вы предоставляете более одного пути для прохождения тока через несколько нагрузок, вы фактически снижаете общее сопротивление в цепи.Расчет общего сопротивления в параллельной цепи более сложен (1 / R t = 1 / R 1 + 1 / R 2 …), но помните, что общее сопротивление всегда будет ниже, чем наименьшее сопротивление из любая ветка. Например, если одна ветвь имеет фонарь с сопротивлением 1000 Ом, а другая ветвь — всего 100 Ом, то общее сопротивление будет меньше 100 Ом. Еще сложнее рассчитать ток в параллельных цепях. Как только вы узнаете общее напряжение и общее сопротивление, вы можете рассчитать общий ток, протекающий по цепи, но это не скажет вам, сколько тока протекает через любую одну нагрузку.Ток в каждой ветви параллельной цепи будет обратно пропорционален величине сопротивления в этой ветви по сравнению с общим сопротивлением (ветвь с сопротивлением 100 Ом будет иметь в 10 раз больше тока, чем ветвь с сопротивлением 1000 Ом).
Параллельные и последовательные схемы
По мере того, как вы работаете со все более и более сложными электрическими цепями, очень важно находить схемы, в которых есть компоненты как в параллельном, так и в последовательном соединении.Чтобы рассчитать напряжение, сопротивление и ток в такой сложной цепи, вы должны сначала найти общее сопротивление в каждой из параллельных цепей, прежде чем вы сможете рассчитать общее сопротивление для всей цепи. Затем, исходя из общего напряжения, необходимо рассчитать падение напряжения в каждой параллельной цепи.
Основная анатомия электрической цепи — Основное электричество
Термин круговая означает круговое путешествие или петлю. Это петля, по которой движутся электроны.Чтобы электроны могли течь, в цепи должны присутствовать некоторые основные компоненты:
Источник: Это устройство, которое преобразует другие формы энергии в электрическую. Он обеспечивает ЭДС, которая проталкивает электроны по цепи. Другими словами, это источник электрического давления. Некоторыми примерами являются батареи, солнечные элементы, генераторы и термопары.
Переключатели: Переключатели — это устройства, управляющие размыканием и замыканием цепей.Замкнутая цепь — это цепь, которая имеет завершенный путь для прохождения тока. Если в цепи есть разрыв, в котором не может протекать ток, у нас будет разрыв цепи .
Предохранители и прерыватели:
Рисунок 14. Самостоятельное изображение предохранителя. Используется по лицензии Creative Commons-Share Alike 3.0 Unported.Предохранители и прерыватели используются на пути тока для защиты. Они предназначены для преднамеренного открытия, если сила тока превышает определенный рейтинг.Например, если предохранитель или прерыватель рассчитан на 15 ампер, а ток в цепи превышает 15 ампер, они «сработают» или разомкнутся, что приведет к разрыву цепи.
Предохранители отличаются от автоматических выключателей тем, что при срабатывании их необходимо заменить. Автоматический выключатель можно сбросить и использовать повторно.
Нагрузка: Это устройство, которое преобразует электрическую энергию в другие формы энергии. Это также известно как разность потенциалов. Это часть схемы, которая выполняет полезную работу.Некоторые примеры — фонари, обогреватели и двигатели.
Рис. 15. Электрические шины в распределительной стойке для изображения большого здания, [email protected]. Используется по лицензии Creative Commons-Share Alike 3.0 Unported.Проводники: Они завершают путь прохождения электронов.
Проводники могут иметь вид:
- Провод
- Шина
- Медь
- Алюминий
Полярность и направление тока
Ранее мы говорили о термине полярность , который представляет собой заряд в одной точке по отношению к другой.
В электрических цепях мы часто ссылаемся на полярность различных точек в цепи. Это важно понимать при подключении счетчиков и некоторых устройств, чувствительных к полярности.
Ток проходит через нагрузку от отрицательного к положительному. Ток течет через источник от положительного к отрицательному.
постоянного тока и переменного тока
Пока что цепи, которые мы обсуждали, имеют неизменную полярность. Электроны текут только в одном направлении. Это известно как постоянного тока (DC) .Примерами являются батареи, термопары, генераторы постоянного тока и солнечные элементы.
Переменный ток (AC) постоянно и через определенные промежутки времени меняет свое направление. AC производится генераторами. Переменный ток, используемый в наших домах, составляет 60 циклов переменного тока. Это означает, что он меняет полярность 120 раз в секунду, производя 60 полных циклов. Более подробно это будет рассмотрено в будущих уроках.
электрических цепей
электрических цепейДалее: Закон Ома вверх: электрический ток Предыдущее: Электрический ток Батарея — это устройство, имеющее положительных и отрицательных Терминал.Какой-то процесс, обычно химическая реакция, происходит внутри аккумулятор, который заставляет положительный заряд перемещаться к положительному выводу, и наоборот . Этот процесс продолжается до тех пор, пока электрическое поле между двумя выводами не станет достаточно сильный, чтобы препятствовать дальнейшей миграции заряда.
Электрическая цепь — проводящий путь, внешний к аккумулятору, что позволяет заряжать поток с одного терминала к другому. Простая схема может состоять из одножильный металлический провод, соединяющий положительную и отрицательную клеммы.Более реалистичная схема имеет несколько точек разветвления, поэтому заряд может много разных путей между двумя терминалами.
Предположим, что (положительный) заряд движется вокруг внешнего цепь, от плюса к отрицательный вывод электрическим полем, установленным между терминалы. Работа, проделанная с зарядом этим полем за время его путешествие, в чем разница по электрическому потенциалу между положительной и отрицательной клеммами. Обычно мы называем напряжением батареи: e.грамм. , когда мы говорим о 6-вольтовой батарее, на самом деле мы имеем в виду что разность потенциалов между двумя его выводами составляет 6 В. Примечание. Разд. 5, что электрические работы, выполненные на заряде полностью не зависит от маршрута между терминалы. Другими словами, хотя в целом многие различные пути через внешнюю цепь, по которым заряд может проходить по порядку чтобы добраться от положительного к отрицательному выводу аккумулятор, электрическая энергия которого заряд, приобретаемый в этом путешествии, всегда один и тот же.Поскольку при анализе электрические цепи, нас в первую очередь интересует энергия ( т.е. , в преобразовании химической энергии батареи в тепловая энергия в каком-либо электронагревательном элементе или механическом энергия в некоторых электродвигателях, и т. д. ), Отсюда следует, что свойство батареи, которое нас в первую очередь волнует, — это ее напряжение . Следовательно, нам не нужно отображать электрическое поле. генерируется батареей, чтобы вычислить, сколько энергии это поле дает заряд, который идет по какой-то подключенной к нему внешней цепи.Все, что нам нужно знать, это разность потенциалов между двумя клеммами. батареи. Очевидно, это огромное упрощение.
Этот раздел касается только установившихся электрических цепей
питается от аккумуляторов постоянного напряжения. Таким образом, скорость, с которой электрические
заряд перетекает с положительной клеммы аккумуляторной батареи на внешнюю
контур должен соответствовать скорости, с которой заряд перетекает из контура в
отрицательный полюс аккумуляторной батареи, иначе заряд будет накапливаться в
либо аккумулятор, либо цепь, которые не соответствуют установившемуся режиму
ситуация.Скорость, с которой заряд вытекает из положительного вывода
называется электрическим током , истекающим из батареи. Так же,
скорость, с которой заряд течет в отрицательный вывод, называется током
течет в аккумулятор. Конечно, эти два тока должны быть одинаковыми в
установившееся состояние.
Электрический ток измеряется в амперах (А), которые
эквивалент кулонов в секунду:
| (124) |
Мы можем определить электрический ток, протекающий в любой конкретной точке внешняя схема следующим образом.Если заряд проходит мимо этой точки в бесконечно малом интервале времени, то
| (125) |
По соглашению направление тока принимается равным положительные заряды должны переместиться, чтобы учесть поток заряда. В установившемся режиме ток во всех точках внешней цепи должен остаются неизменными во времени. Мы называем этот тип цепи постоянного тока (DC) цепь, потому что ток всегда течет в одном и том же направлении.Там есть второй тип цепи, называемый цепью переменного тока (AC), в который периодически меняет направление тока.
Рассмотрим простую схему, в которой протекает постоянный ток. вокруг одного проводящего провода, соединяющего положительный и отрицательный клеммы аккумуляторной батареи напряжения. Предположим, что ток равен переносятся положительными зарядами, протекающими по внешней цепи от положительного к отрицательный терминал. На самом деле ток переносятся отрицательными зарядами ( i.е. , электронами), протекающими в обратном направлении. направление, но для большинства целей мы можем спокойно игнорировать этот довольно неудобный факт. Каждый заряд, протекающий по внешней цепи, испытывает потенциальное падение. Чтобы снова обтекать цепь, заряд должен быть поднятым до потенциала положительной клеммы батареи. Этот процесс происходит внутри батареи, поскольку заряд мигрирует из отрицательный к положительной клемме. Энергия требуется для перемещения заряда между двумя терминалами, полученный из энергия, выделяемая в результате химических реакций, происходящих внутри аккумулятор.
Простая трасса, описанная выше, в некоторой степени аналогична небольшому горнолыжному курорту. Заряды, протекающие по внешнему контуру, похожи на людей, катающихся на лыжах. вниз по горнолыжному склону. Заряды стекают по градиенту электрического потенциал так же, как люди спускаются по градиенту гравитационного потенциала. Обратите внимание, что хорошие лыжники, которые спускаются прямо по склону, приобретают именно та же гравитационная энергия, что и у бедных лыжников, которые катаются из стороны в сторону. В обоих случаях общая приобретенная энергия зависит только от разница в высоте между верхом и низом склона.Аналогичным образом, сборы при обтекании внешнего контура приобретают одинаковую электрическую энергию независимо от маршрута они берут, потому что приобретаемая энергия зависит только от разности потенциалов между двумя выводами аккумуляторной батареи. Когда-то люди на нашем горнолыжном курорте достичь дна склон, они должны быть подняты наверх на подъемнике прежде, чем они снова смогут спуститься по нему на лыжах. Таким образом, подъемник на нашем курорте играет аналогичную роль. роль батареи в нашей цепи. Конечно, подъемник должен расходовать негравитационную энергию, чтобы поднять лыжников на вершину склона, всего за таким же образом, как батарея должна расходовать неэлектрическую энергию для перемещения зарядов вверх до потенциальной градиент.

