Что такое логические элементы и для чего они используются. Какие основные виды логических элементов существуют. Как работают базовые логические элементы И, ИЛИ, НЕ. Где применяются логические элементы в современной электронике.
Что такое логические элементы и зачем они нужны
Логические элементы — это базовые электронные схемы, которые выполняют простейшие логические операции над входными сигналами. Они являются основой цифровой электроники и используются для создания более сложных цифровых устройств.
Основные функции логических элементов:
- Обработка двоичных сигналов (0 и 1)
- Выполнение базовых логических операций (И, ИЛИ, НЕ и др.)
- Преобразование и коммутация цифровых сигналов
- Построение комбинационных и последовательностных логических схем
Логические элементы позволяют реализовать любые цифровые устройства — от простых до сложнейших микропроцессоров. Они лежат в основе работы всей современной цифровой техники.
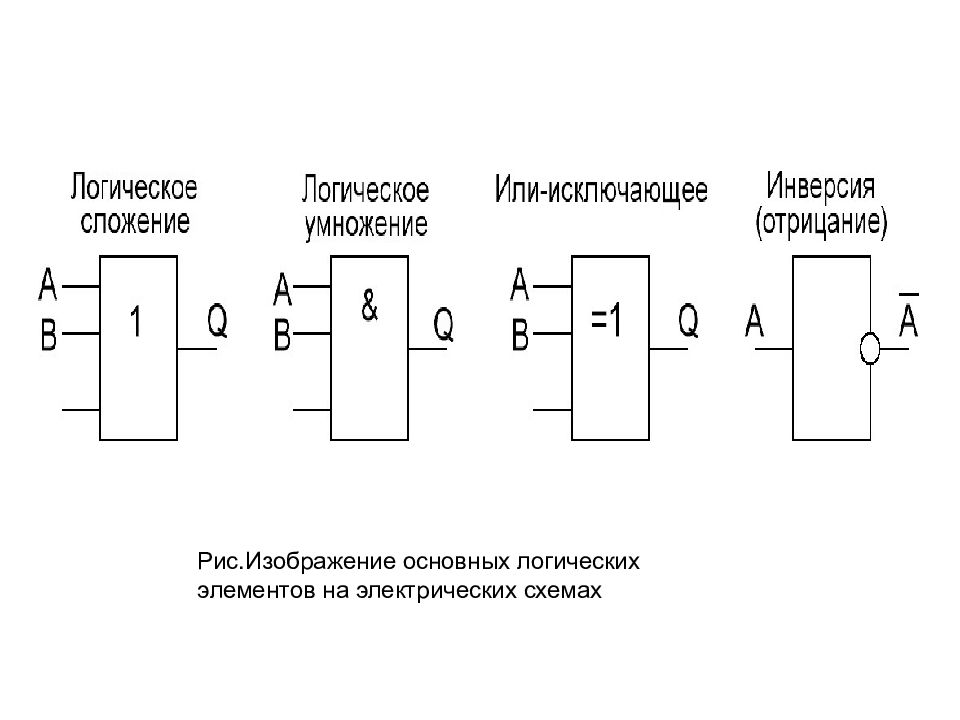
Основные виды логических элементов
Существует несколько базовых видов логических элементов, на основе которых строятся более сложные схемы:
- И (AND)
- ИЛИ (OR)
- НЕ (NOT)
- И-НЕ (NAND)
- ИЛИ-НЕ (NOR)
- Исключающее ИЛИ (XOR)
- Эквивалентность (XNOR)
Рассмотрим принцип работы трех основных логических элементов подробнее.
Логический элемент И (AND)
Элемент И имеет два или более входа и один выход. Выходной сигнал равен 1 только тогда, когда все входные сигналы равны 1. В остальных случаях выход равен 0.
Таблица истинности для элемента И с двумя входами:
| Вход A | Вход B | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Как видно из таблицы, выход элемента И равен 1 только при единичных сигналах на всех входах.
Логический элемент ИЛИ (OR)
Элемент ИЛИ также имеет несколько входов и один выход. Выходной сигнал равен 1, если хотя бы на одном из входов присутствует 1. Выход равен 0 только если все входы равны 0.
Таблица истинности для элемента ИЛИ с двумя входами:
| Вход A | Вход B | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Таким образом, элемент ИЛИ выдает единичный сигнал при наличии хотя бы одной единицы на входе.
Логический элемент НЕ (NOT)
Таблица истинности для элемента НЕ:
| Вход A | Выход Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Элемент НЕ выполняет простейшую логическую операцию инверсии входного сигнала.
Как работают логические элементы на транзисторах
Логические элементы реализуются на базе полупроводниковых транзисторов. Рассмотрим принцип работы элемента И-НЕ на биполярных транзисторах:
- Входные сигналы подаются на базы транзисторов
- При подаче логического нуля транзистор закрыт
- При подаче логической единицы транзистор открывается
- Выходной сигнал снимается с коллектора
- Выход элемента И-НЕ равен нулю только если все транзисторы открыты
Таким образом, комбинируя транзисторные ключи, можно реализовать любые логические функции. Современные логические элементы выполняются по интегральной технологии на одном кристалле.
Где применяются логические элементы
Логические элементы являются основой для построения всех цифровых устройств. Основные области их применения:
- Процессоры и микроконтроллеры
- Оперативная и постоянная память
- Цифровые схемы управления
- АЦП и ЦАП
- Коммутаторы и мультиплексоры
- Шифраторы и дешифраторы
- Счетчики и регистры
- Сумматоры и арифметико-логические устройства
Логические элементы используются во всех современных электронных устройствах — компьютерах, смартфонах, бытовой технике, автомобильной электронике и т.д. Они позволяют создавать сложнейшие цифровые системы из простейших логических блоков.
Преимущества современных логических элементов
Современные интегральные логические элементы обладают рядом важных преимуществ:
- Высокое быстродействие (время переключения порядка наносекунд)
- Низкое энергопотребление
- Высокая степень интеграции (миллионы элементов на кристалле)
- Высокая надежность
- Низкая стоимость при массовом производстве
Это позволяет создавать сверхбыстрые и энергоэффективные цифровые устройства с огромными вычислительными возможностями.
Перспективы развития логических элементов
Основные направления совершенствования логических элементов:
- Уменьшение размеров транзисторных структур до единиц нанометров
- Увеличение плотности размещения элементов на кристалле
- Снижение энергопотребления
- Повышение рабочих частот до сотен гигагерц
- Разработка элементов на новых физических принципах (спинтроника, фотоника и др.)
Развитие технологий логических элементов обеспечивает постоянный рост производительности вычислительных систем и появление новых классов цифровых устройств.
Заключение
Логические элементы являются фундаментальной основой современной цифровой электроники. Они позволяют реализовать сложнейшие вычислительные алгоритмы с помощью простых логических операций. Развитие технологий производства логических элементов обеспечивает непрерывный прогресс в области электроники и вычислительной техники.
Логические элементы и их релейные эквиваленты
Дата Автор ElectricianКомментироватьПросмотров: 18 599
С помощью логических элементов довольно легко реализуются функции алгебры логики, которая является костяком устройств автоматики и вычислительных машин. Логические элементы могут реализовываться огромным количеством способов в зависимости от надобности и состоять из полупроводниковых, релейных, интегральных, пневматических и других элементов и схем.
Между величинами, входящими и выходящими из логического элемента, существует определенная зависимость, которая называется функциональной и обозначается как y = f(x) для устройств с одной переменной и как y = f(x1, x2) для устройств с двумя переменными величинами. В этой записи Х называют независимую переменную или аргумент, а Y – зависимая переменная, так как ее значение напрямую зависит от значения аргумента Х.
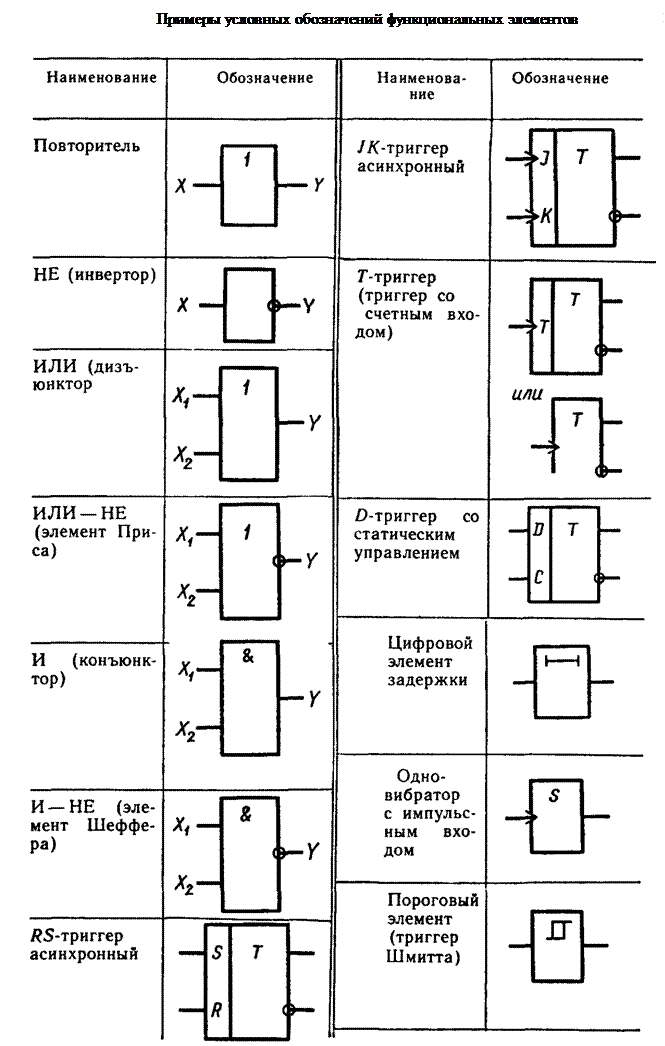
Ниже показана таблица логических элементов и эквивалентных им положений контактов реле:
Функция повторения
Реализуется логическим элементом повторителем (пункт 1 в таблице). Повторитель можно сравнить с нормально открытым контактом реле. При открытом контакте Х=0 и, соответственно Y=0, то есть цепь находится в непроводящем состоянии, а при закрытом наоборот Х=1 и Y=1, то есть цепь находится в проводящем состоянии.
Функция отрицания
Реализует данную функцию логический элемент НЕ или как его часто называют – инвертор (пункт 2 в таблице). Его сравнивают с нормально закрытым контактом реле, когда при отсутствии напряжения на катушке управления (Х=0) его контакт находится в проводящем состоянии (Y=1). При подаче напряжения на катушку (Х=1) контакт размыкается и разрывает цепь (Y=0).
Функция логического сложения
В схемотехнике носит название дизъюнкция или функция ИЛИ (пункт 3 в таблице). Реализуема эта функция логическим элементом дизъюнктором. Суть данной операции заключается в логическом суммировании входных сигналов X для получения результирующего сигнала на выходе Y. Описывается данная зависимость простой формулой X1 + X2 = Y. Вот примеры – 0+0=1, 1+0=1,0+1=1,1+1=1. На примере обычного реле – это два параллельно подключенных нормально разомкнутых контакта. Если один контакт разомкнут, то проводимость цепи обеспечит второй, замкнутый контакт. Для того что бы цепь оказалась разорванной, необходимо разомкнуть оба контакта.
Суть данной операции заключается в логическом суммировании входных сигналов X для получения результирующего сигнала на выходе Y. Описывается данная зависимость простой формулой X1 + X2 = Y. Вот примеры – 0+0=1, 1+0=1,0+1=1,1+1=1. На примере обычного реле – это два параллельно подключенных нормально разомкнутых контакта. Если один контакт разомкнут, то проводимость цепи обеспечит второй, замкнутый контакт. Для того что бы цепь оказалась разорванной, необходимо разомкнуть оба контакта.
Функция логического умножения
В схемотехнике носит название конъюнкция или функция И (пункт 4 в таблице). Реализует ее специальный логический элемент – конъюктор. Данная функция – логическое перемножение сигналов:
Если сравнить с реле – то это два последовательно включенные нормально открытые контакты. А при таком подключении контактов реле проводимость можно получить только в случае, когда оба контакта замкнуты.
Функция равнозначности
Имеет следующий вид — X1≡X2 = Y или в виде логических символов: 0≡0 =1; 1≡0 = 0; 0≡1 = 0; 1≡1 = 1.
Значения 1 будет только при условии, что X1 = X2. Эквивалентом в релейной схеме будет два последовательно включенных переключающихся контакта (пункт 5 в таблице).
Функция неравнозначности
Противоположная функции равнозначности (пункт 6 в таблице) и часто носит название функции сложности по модулю m2:
Posted in Станки с ЧПУ, СхемотехникаЛогические элементы
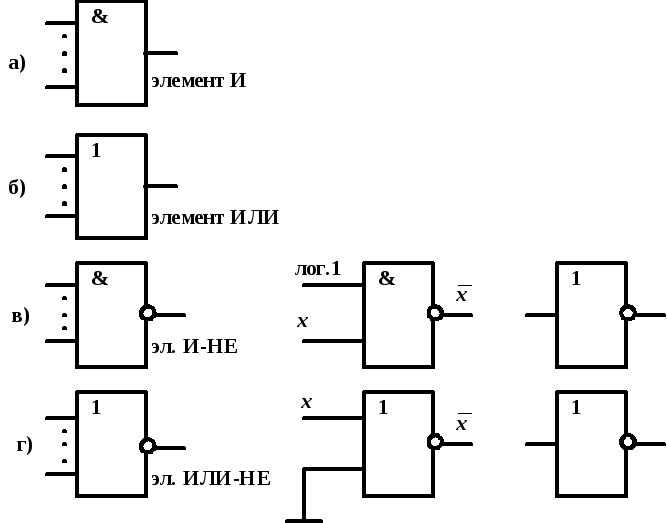
Любые цифровые микросхемы строятся на основе простейших логических элементов «НЕ», «ИЛИ», «И». В настоящее время используется несколько технологий построения логических элементов:
- транзисторно-транзисторная логика (ТТЛ, TTL)
- логика на основе комплементарных МОП транзисторов (КМОП, CMOS)
- логика на основе сочетания комплементарных МОП и биполярных транзисторов (BiCMOS)
Простейшим логическим элементом является инвертор, который работает в соответствии со следующей таблицей:
| Рис 1 Таблица истинности логического инвертора | |
Рис 2 Изображение логического инвертора
на принципиальных схемах.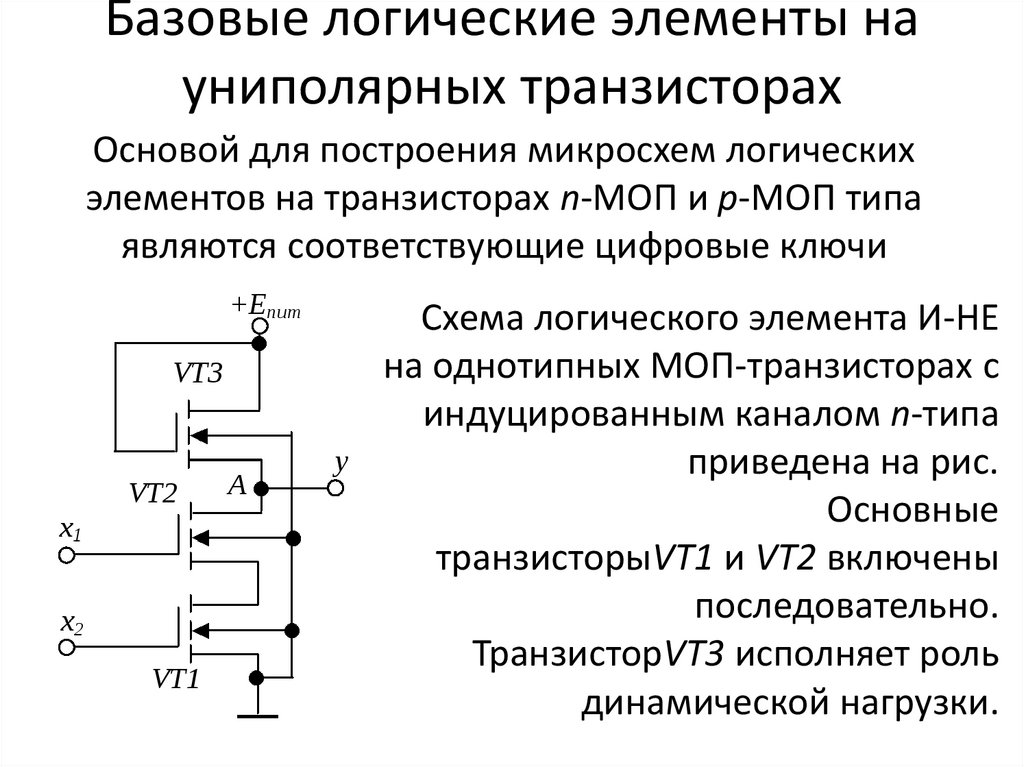 |
Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно:
| Рис 3 Таблица истинности схемы, выполняющей логическую функцию «И-НЕ». | |
| Рис 4 Изображение схемы, выполняющей логическую функцию «И-НЕ». |
Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:
| Рис 5 Таблица истинности схемы, выполняющей логическую функцию «ИЛИ-НЕ». | |
Рис 6 Изображение схемы, выполняющей
логическую функцию «ИЛИ-НЕ».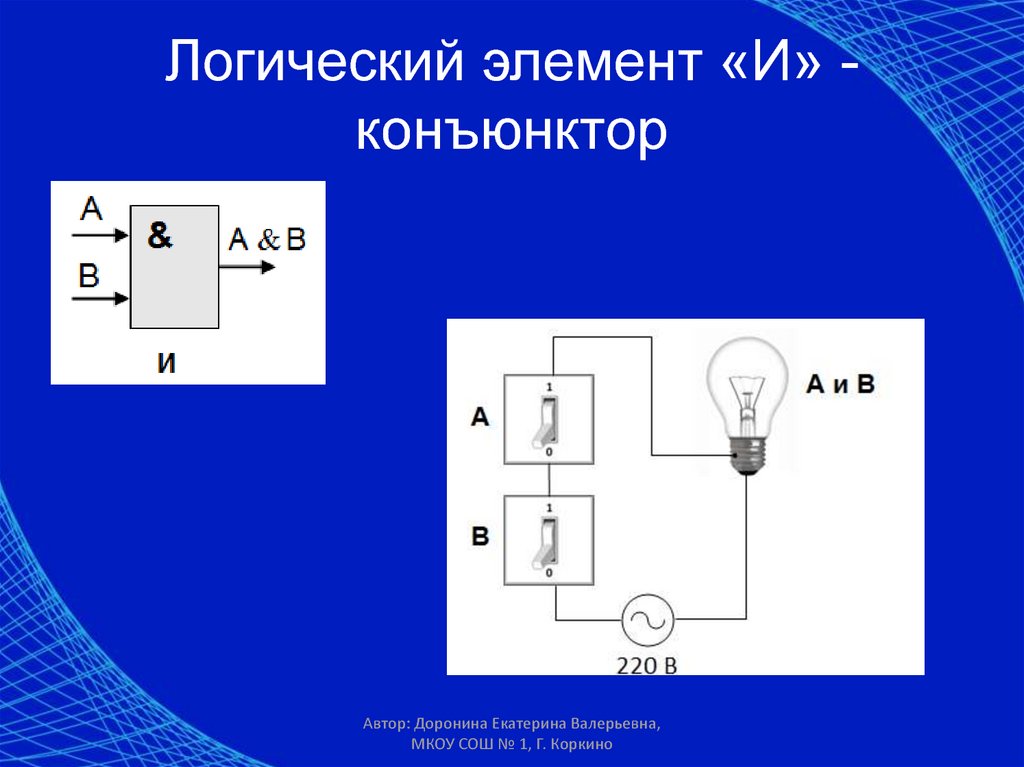 |
Построение произвольной таблицы истинности.
Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем «И» «ИЛИ» «НЕ».
При построении схемы, реализующей произвольную
таблицу истинности, каждый выход анализируется
(и строится схема) отдельно. Для реализации
таблицы истинности при помощи логических
элементов «И» достаточно рассмотреть только
те строки таблицы истинности, которые содержат
логические «1» в выходном сигнале. Строки,
содержащие в выходном сигнале логический 0 в
построении схемы не участвуют. Каждая строка,
содержащая в выходном сигнале логическую
«1», реализуется схемой логического «И»
с количеством входов, совпадающим с количеством
входных сигналов в таблице истинности. Входные
сигналы, описанные в таблице истинности
логической «1» подаются на вход этой схемы
непосредственно, а входные сигналы, описанные в
таблице истинности логическим «0» подаются
на вход через иверторы.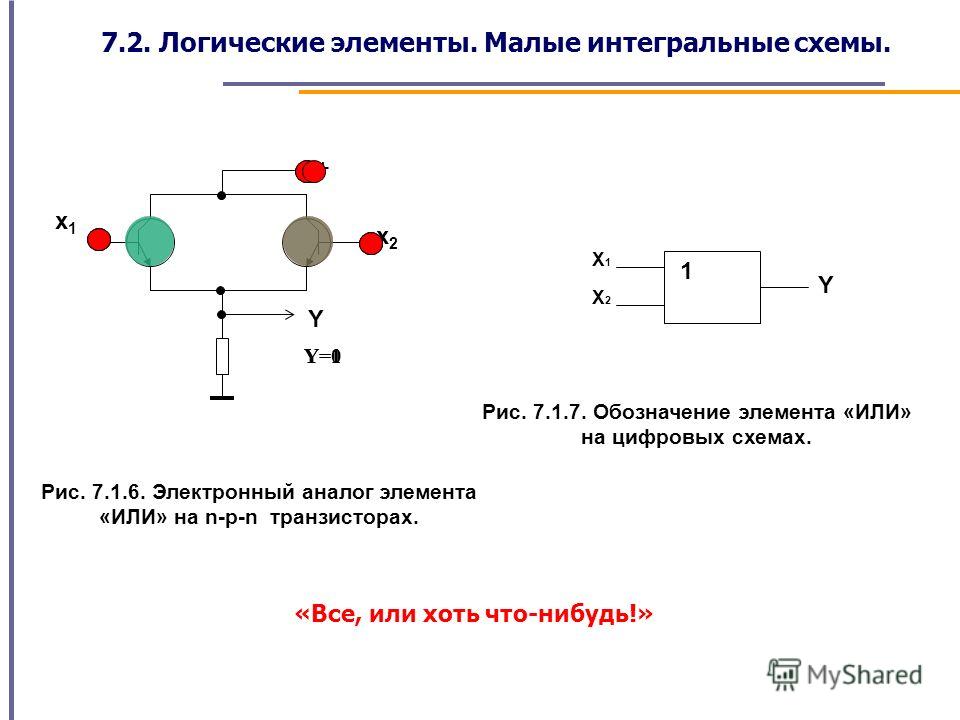
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 7:
Рисунок 7 Произвольная таблица истинности.
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные красным цветом. Эти строки реализуются микросхемой D2 на рисунке 8. Каждая строка реализуется своей схемой «И», затем выходы этих схем объединяются Для построения схемы, реализующей сигнал Out2, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3.
Рисунок 8. Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 7.
[Содержание] [Вперёд]
Логические вентилии как они работают
By Øyvind Nydal Dahl 7 комментариев
Логические элементы являются основными строительными блоками цифровой электроники. Это компоненты, которые мы используем для «работы» с 1 и 0. Вы можете комбинировать их для создания других строительных блоков, таких как триггеры, сумматоры и многое другое.
Основные логические элементы: И, НЕ-И, ИЛИ, ИЛИ, исключающее ИЛИ, исключающее ИЛИ и НЕ.
Элемент И
Элемент И принимает два (или более) входа и выдает 1 (ВЫСОКИЙ/истина), если все входы равны 1. В противном случае он выдает 0 (НИЗКИЙ/ложь).
Таблица истинности приведена ниже, но все, что вам действительно нужно помнить, это то, что элемент И требует 1 на входе A и на входе B, чтобы выдать 1. Q
If you want to use it in a circuit, IC 4081 содержит 4 логических элемента И.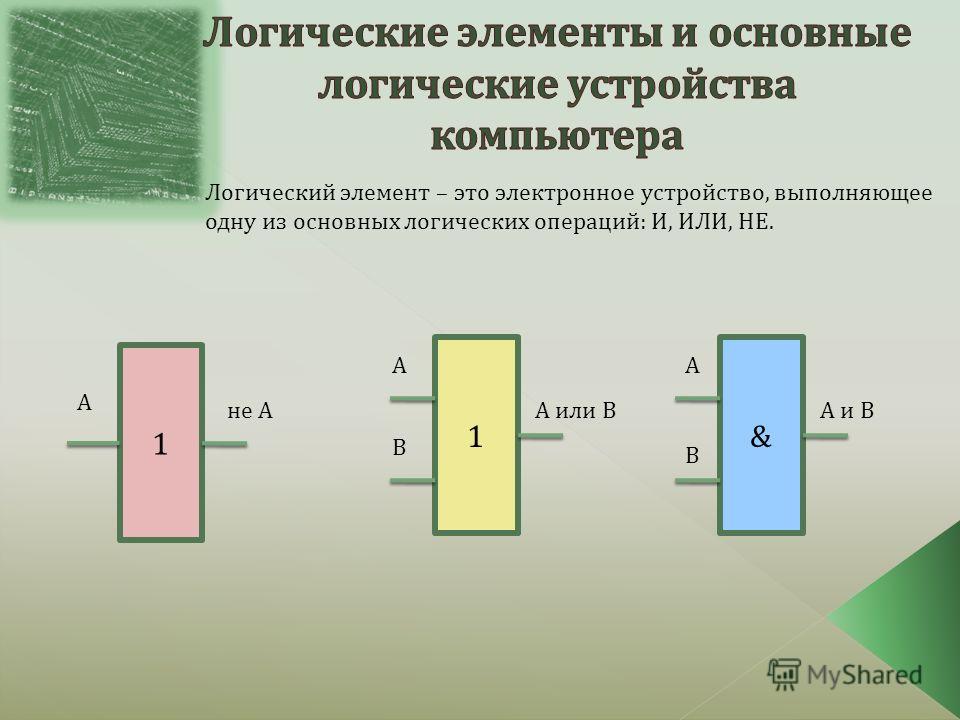
Элемент НЕ/Инвертор
Простейшим логическим элементом является элемент НЕ. В качестве входных данных требуется один бит (A). И дает на выходе (Q) то, чего НЕТ на входе. Таким образом, если на входе есть 1, его выход равен 0. И если на входе есть 0, его выход равен 1. Это также называется 9.0071 инвертор .
| Вход A | Выход Q |
|---|---|
| 0 | 1 |
| 1 | 0 |
Элемент ИЛИ
Элемент ИЛИ принимает два (или более) входа и выдает 1, если любой из входов равен 1. В противном случае он выдает 0.
Таблица истинности приведена ниже, но все, что вам действительно нужно помнить, это то, что вентилю ИЛИ требуется 1 на входе A 9.0017 or input B to give out 1.
| Input A | Input B | Output Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
, если вы хотите использовать его в контуре, IC 4071.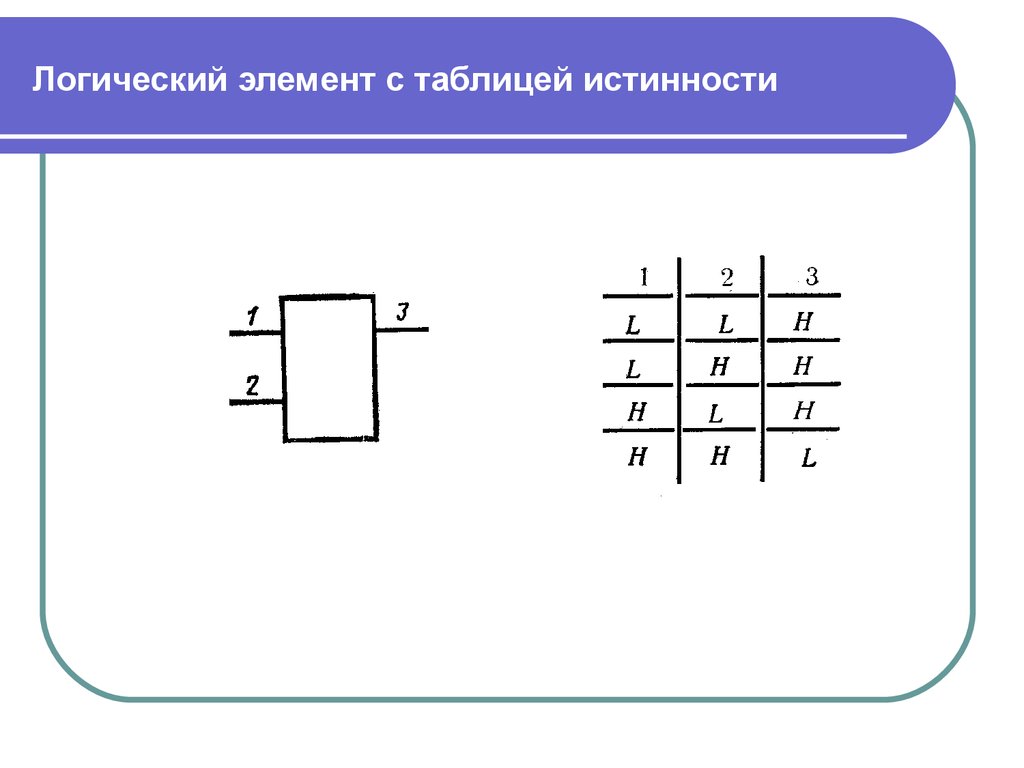
Вентиль И-НЕ
Вентиль И-НЕ (или НЕ-И) работает противоположно вентилю И. Это похоже на то, как если бы на выходе вентиля И был вентиль НЕ:
Таблицу истинности вы найдете ниже. Но все, что вам нужно помнить, это то, что единственный раз, когда выход логического элемента И-НЕ равен 0, это когда оба входа равны 1.
Вентиль ИЛИ
Вентиль ИЛИ (или НЕ ИЛИ) работает в противоположном направлении по отношению к вентилю ИЛИ. Это как если бы на выходе вентиля ИЛИ был вентиль НЕ.
Ниже вы найдете таблицу истинности. Но все, что вам нужно помнить, это то, что единственный раз, когда выход вентиля ИЛИ-НЕ равен 1, это когда оба входа равны 0.
| Input A | Input B | Output Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Если вы хотите использовать вентили ИЛИ-НЕ в схеме, IC 4001 содержит 4 вентиля ИЛИ-НЕ.
Элемент XOR
Элемент XOR (или исключающее ИЛИ) выдает 1, если один из двух его входов равен 1, но не оба. Вы также можете посмотреть на это таким образом — если два входа отличаются друг от друга, выход верен.
| Input A | Input B | Output Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Если вы хотите использовать вентили XOR в схеме, IC 4070 содержит 4 вентиля XOR.
Вентиль XNOR
Вентилятор XNOR (или Исключающее НЕ ИЛИ) работает как вентиль XOR с инвертором на выходе. Другой способ взглянуть на это — заметить, что выход становится равным 1, если два его входа равны — либо две единицы, либо два нуля.
| Input A | Input B | Output Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Если вы хотите использовать вентили XNOR в схеме, вы найдете четыре из них в Circuit Gates Logic 4073.
Логический вентиль может быть построен на транзисторах и обычно представляет собой интегральную схему (ИС).
Есть две классические серии IC, которые содержат много одинаковых функций; серии 7400 и серии 4000.
Серия 7400 — самая старая серия.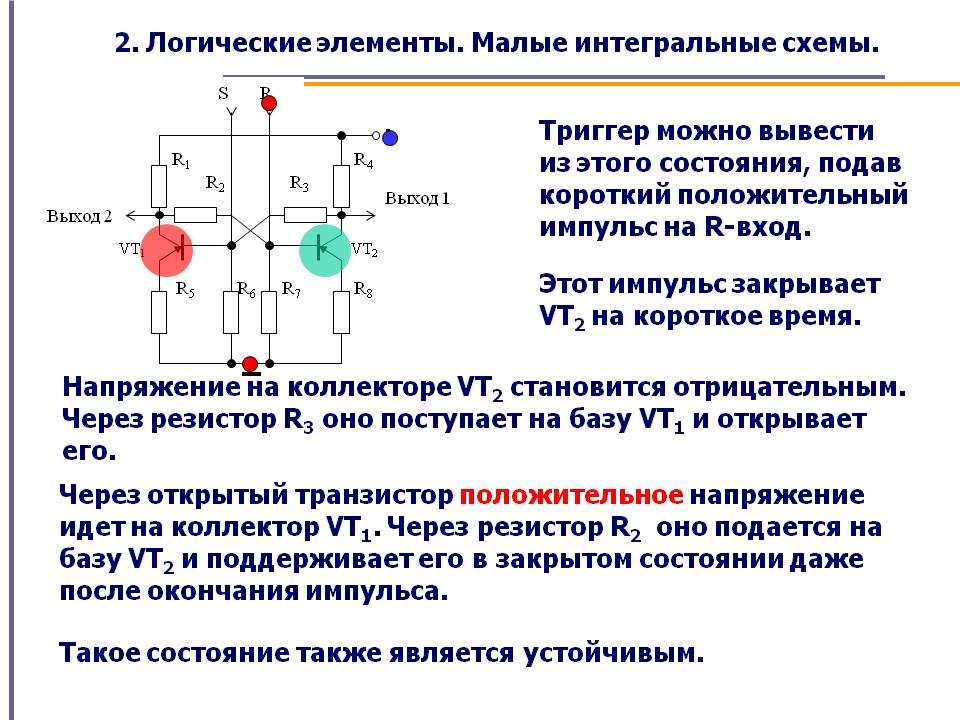 Серия 4000 была представлена как более экономичная и более универсальная альтернатива 7400. Но сегодня существует несколько семейств серии 7400, некоторые из которых обладают такими же свойствами, как и серия 4000.
Серия 4000 была представлена как более экономичная и более универсальная альтернатива 7400. Но сегодня существует несколько семейств серии 7400, некоторые из которых обладают такими же свойствами, как и серия 4000.
Посмотрите мой список распространенных микросхем серии 4000 с выводами, пояснениями и примерами схем для получения дополнительной информации.
Полный список ИС серии 4000 (Википедия)
Полный список ИС серии 7400 (Википедия)
Дополнительные учебные пособия по Logic Gates
Рубрики: Logic Gates
Взаимодействие с читателем
Логические элементы — определение, типы, использование
Электропроводность полупроводникового материала находится где-то между проводимостью проводника, такого как металлическая медь, и изолятора, такого как стекло. При повышении температуры его удельное сопротивление уменьшается, в то время как металлы имеют противоположный эффект. Проводимость кристаллической структуры можно модифицировать благоприятным образом, вводя в нее примеси (легирование). Когда в одном и том же кристалле существуют две отдельные легированные области, образуется полупроводниковый переход. Поведение носителей заряда, таких как электроны, ионы и электронные дырки, в этих соединениях лежит в основе диодов, транзисторов и большинства современных электронных устройств.
Когда в одном и том же кристалле существуют две отдельные легированные области, образуется полупроводниковый переход. Поведение носителей заряда, таких как электроны, ионы и электронные дырки, в этих соединениях лежит в основе диодов, транзисторов и большинства современных электронных устройств.
Полупроводники включают кремний, германий, арсенид галлия и элементы так называемой металлоидной лестницы периодической таблицы. Арсенид галлия является вторым по распространенности полупроводником после кремния и используется в лазерных диодах, солнечных элементах, интегральных схемах микроволнового диапазона и других устройствах. Кремний является важным компонентом в производстве почти всех электрических цепей.
Логические элементы
Логические элементы представляют собой простую коммутационную схему, которая определяет, может ли входной импульс пройти на выход в цифровых схемах.
Строительными блоками цифровой схемы являются логические вентили, которые выполняют множество логических операций, необходимых для любой цифровой схемы. Они могут принимать два или более входных данных, но производить только один выходной сигнал.
Они могут принимать два или более входных данных, но производить только один выходной сигнал.
Сочетание входов, подаваемых на логический элемент, определяет его выход. Логические вентили используют булеву алгебру для выполнения логических процессов. Логические вентили можно найти почти в каждом цифровом гаджете, который мы используем на регулярной основе. Логические вентили используются в архитектуре наших телефонов, ноутбуков, планшетов и запоминающих устройств.
Булева алгебра
Булева алгебра — это тип логической алгебры, в котором символы представляют логические уровни.
Цифры (или символы) 1 и 0 относятся к логическим уровням в этой алгебре; в электрических цепях логическая 1 будет представлять замкнутый переключатель, высокое напряжение или состояние «включено» устройства. Разомкнутый выключатель, низкое напряжение или состояние «выключено» устройства будет представлено логическим 0.
В любой момент времени цифровое устройство будет находиться в одном из этих двух бинарных состояний. Лампочку можно использовать для демонстрации работы логического вентиля. Когда на выключатель подается логический 0, он выключается, а лампочка не горит. Переключатель находится в состоянии ON, когда применяется логическая 1, и лампочка загорается. В интегральных схемах (ИС) широко используются логические элементы.
Лампочку можно использовать для демонстрации работы логического вентиля. Когда на выключатель подается логический 0, он выключается, а лампочка не горит. Переключатель находится в состоянии ON, когда применяется логическая 1, и лампочка загорается. В интегральных схемах (ИС) широко используются логические элементы.
Таблица истинности: Выходы для всех мыслимых комбинаций входов, которые могут применяться к логическим элементам или схемам, перечислены в таблице истинности. Когда мы вводим значения в таблицу истинности, мы обычно выражаем их как 1 или 0, где 1 обозначает истинную логику, а 0 обозначает ложную логику.
Типы логических элементов
Логический элемент представляет собой цифровой элемент, позволяющий передавать данные. Логические вентили используют логику, чтобы определить, передавать сигнал или нет. С другой стороны, логические вентили управляют потоком информации на основе набора правил. Обычно используются следующие типы логических вентилей:
- AND
- OR
- NOT
- NOR
- NAND
- XOR
- XNOR
Basic Logic Gates
AND Gate
An AND gate has a single output and two or more inputs.
- Когда все входы равны 1, выход этого элемента равен 1.
- Булева логика элемента И: Y=A.B , если есть два входа A и B.
Символ элемента И и истинность таблица выглядит следующим образом:
| Input | Output | ||
| A | B | A AND B | |
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 09003 | 09003 | 09003 |
| 1 | 1 | 1 | |
Символ и Врата
Следовательно, в и ворот, высокие выходы.
Схема ИЛИ
В схеме ИЛИ можно использовать два или более входа и один выход.
- Логика этого элемента такова, что если хотя бы один из входов равен 1, выход будет равен 1.
- Выход элемента ИЛИ будет задан следующей математической процедурой, если есть два входа A и B: Y =А+В
| Input | Output | ||||||||
| A | B | A OR B | |||||||
| 0 | 0 | 0 | |||||||
| 0 | 1 | 1 | |||||||
| 1 | 09003 | 1 | 09003 | 1 200934 | 0 9003 | 1 200934 | 9002 0 9003 | 0034 | 1 |
| 1 | 1 | 1 | |||||||
Symbol of OR gate
Therefore, in the OR gate, the output is high when any of the inputs is высокий.
Вентиль НЕ
Вентиль НЕ является базовым вентилем с одним входом и одним выходом.
- Когда на входе 1, на выходе 0, и наоборот. Вентиль НЕ иногда называют инвертором из-за его особенностей.
- Если имеется только один вход A, выход можно рассчитать с помощью логического уравнения Y=A’.
| Input | Output |
| A | Not A |
| 0 | 1 |
| 1 | 0 |
Символ ворот НЕ
Логический элемент НЕ, как показывает его таблица истинности, инвертирует входной сигнал.
Универсальные логические элементы
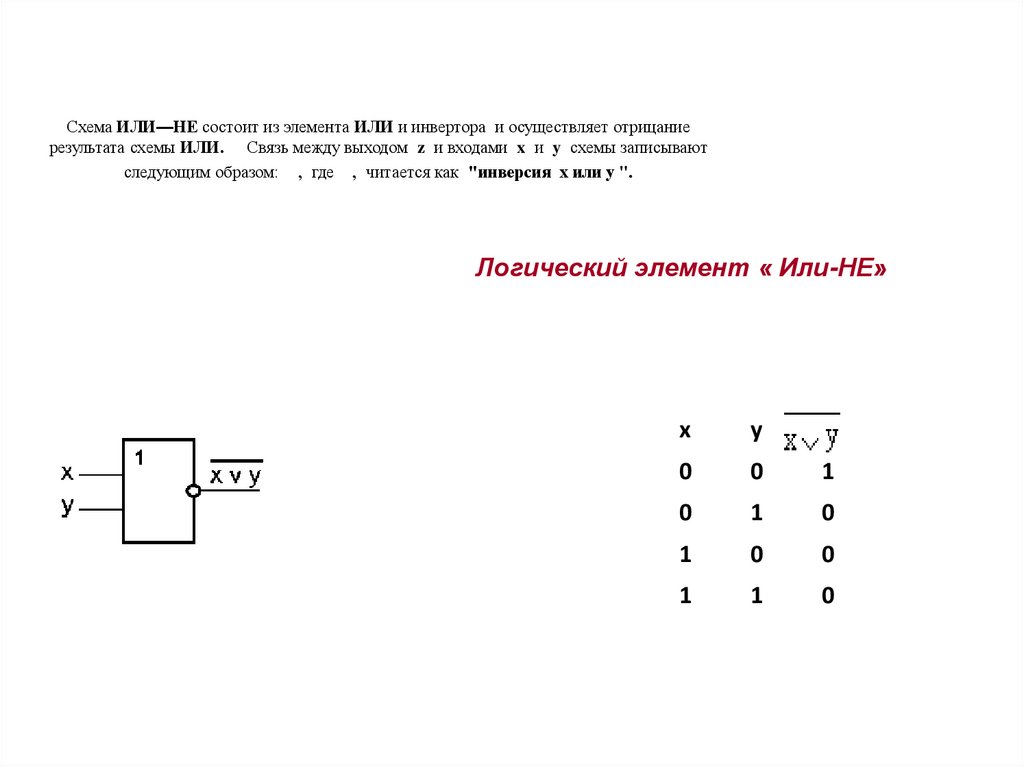
Элемент ИЛИ-НЕ
Элемент ИЛИ-НЕ, иногда называемый элементом НЕ-ИЛИ, состоит из элемента ИЛИ, за которым следует элемент НЕ.
- Выход этого элемента равен 1 только тогда, когда все его входы равны 0. В качестве альтернативы, когда на всех входах низкий уровень, на выходе высокий уровень.
- Булев оператор для вентиля ИЛИ-ИЛИ: Y=(A+B)’, если есть два входа A и B.
| Input | Output | ||
| A | B | A NOR B | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 09003 | 09003 | 09003 |
| 1 | 1 | 0 | |
Символ NOR GATE
. полярно противоположны воротам ИЛИ. Вентиль ИЛИ-ИЛИ иногда называют универсальным вентилем, поскольку его можно использовать для реализации вентилей ИЛИ, И и НЕ.
Вентиль И-НЕ
Вентиль И-НЕ, иногда известный как вентиль НЕ-И, по существу представляет собой вентиль НЕ, за которым следует вентиль И.
- Выход этого элемента равен 1, только если ни один из входов не равен 1. В качестве альтернативы, когда все входы не высокие и хотя бы один низкий, выход высокий.
- If there are two inputs A and B, the Boolean expression for the NAND gate is Y=(A.B)’
| Input | Output | |
| A | Б | А НЕ-И Б |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Символ NAND GATE
. Сравнивая их таблицы истины, мы сможем, что их выходы — это Полос. Вентиль И-НЕ известен как универсальный вентиль, потому что его можно использовать для реализации вентилей И, ИЛИ и НЕ.
Сравнивая их таблицы истины, мы сможем, что их выходы — это Полос. Вентиль И-НЕ известен как универсальный вентиль, потому что его можно использовать для реализации вентилей И, ИЛИ и НЕ.
Прочие логические элементы
Элемент исключающее ИЛИ
Элемент Исключающее ИЛИ или Исключающее ИЛИ представляет собой цифровой логический элемент, который принимает более двух входов, но выводит только одно значение.
- Если какой-либо из входов «Высокий», выход XOR Gate — «Высокий». Если оба входа «Высокий», выход — «Низкий». Если оба входа — «Низкий», выход «Низкий»
- Логическое уравнение для вентиля XOR имеет вид Y=A’.B+A.B’, если есть два входа A и B.
| Input | Output | |||||
| A | B | A XOR B | ||||
| 0 | 0 | 0 | ||||
| 0 | 1 | 1 | ||||
| 1 | 0 | 1 | 00003 | 9000 2 | 00003 | 9003 9000 2 0 0003 | 9003 9000 2 .
| 1 | 1 | 0 | ||||
Символ xor Gate
его выходные данные основаны на логике или затворе, как мы видим.
Вентиль XNOR
Вентиль Exclusive-NOR или EX-NOR представляет собой цифровой логический вентиль, который принимает более двух входов, но выводит только один.
- Если оба входа имеют «высокий уровень», выход XNOR Gate является «высоким». Если оба входа имеют «низкий уровень», выходной сигнал «высокий». «Низкий»
- Если есть два входа A и B, то логическое уравнение вентиля XNOR: Y=A.B+A’B’.
| Input | Output | |
| A | B | A XNOR B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Symbol of XNOR gate
Таблица истинности показывает, что его выходы основаны на логической схеме вентиля НЕ-ИЛИ.
Использование логических элементов
- Логические элементы используются в различных технологиях. Это компоненты микросхем (ИС), которые являются компонентами компьютеров, телефонов, ноутбуков и других электронных устройств.
- Логические элементы можно комбинировать различными способами, и миллионы таких комбинаций необходимы для создания новейших гаджетов, спутников и даже роботов.
- Простые комбинации логических вентилей также можно найти в охранной сигнализации, зуммерах, выключателях и уличных фонарях. Поскольку эти ворота могут выбирать запуск или остановку на основе логики, они часто используются в различных секторах.
- Логические вентили также важны для передачи данных, вычислений и обработки данных. Даже транзисторно-транзисторная логика и схемы КМОП широко используют логические вентили.
Решенные примеры логических вентилей – определение, типы, использование
Вопрос 1: Что такое логические вентили?
Ответ:
Логические элементы представляют собой цифровые схемы, которые выполняют логические операции над предоставленными им входными данными и производят соответствующие выходные данные.
 .
.

