Что такое таблица истинности и как ее построить. Как выполнять логические операции и составлять сложные логические выражения. Какие основные виды логических функций существуют. Как анализировать таблицы истинности и применять их на практике.
Что такое таблица истинности и для чего она нужна
Таблица истинности — это инструмент в математической логике и цифровой схемотехнике для описания логических функций. Она показывает, какие значения принимает логическая функция при всех возможных комбинациях значений входных переменных.
Основные цели использования таблиц истинности:
- Наглядное представление работы логических функций и выражений
- Анализ поведения логических схем при различных входных сигналах
- Проверка эквивалентности логических выражений
- Минимизация логических функций
- Синтез логических схем по заданной таблице истинности
Таким образом, таблицы истинности являются фундаментальным инструментом при работе с логическими функциями и проектировании цифровых устройств.
Основные логические операции и их таблицы истинности
Рассмотрим базовые логические операции и соответствующие им таблицы истинности:
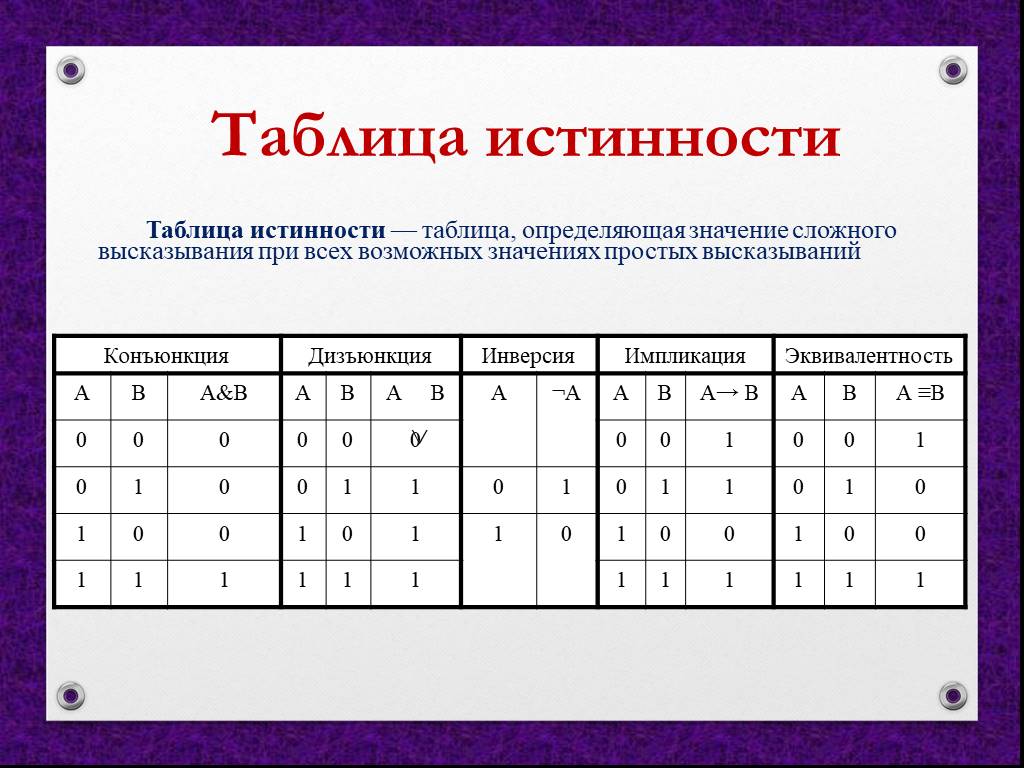
Операция НЕ (отрицание, инверсия)
Это унарная операция, которая инвертирует входное значение:
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Операция И (конъюнкция)
Результат истинен только если истинны оба операнда:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция ИЛИ (дизъюнкция)
Результат истинен если истинен хотя бы один из операндов:
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Эти базовые операции являются основой для построения более сложных логических выражений и функций.
Как построить таблицу истинности для сложного логического выражения
При построении таблицы истинности для сложного логического выражения следует придерживаться определенного алгоритма:
- Определите количество входных переменных в выражении.
- Создайте столбцы для всех входных переменных и для результирующего выражения.
- Заполните столбцы входных переменных всеми возможными комбинациями значений (0 и 1).
- Разбейте сложное выражение на подвыражения и создайте для них дополнительные столбцы.
- Вычисляйте значения подвыражений последовательно, используя уже известные значения.
- В последнем столбце вычислите значение всего выражения.
Рассмотрим пример построения таблицы истинности для выражения:
F = (A OR B) AND (NOT A OR NOT B)
| A | B | A OR B | NOT A | NOT B | NOT A OR NOT B | F |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Такой подход позволяет наглядно представить работу сложного логического выражения и проанализировать его поведение при различных входных данных.
Анализ таблиц истинности: что можно узнать
Анализ таблиц истинности позволяет получить важную информацию о логической функции или выражении:
- Определить, является ли функция постоянной (всегда 0 или всегда 1)
- Выявить, зависит ли функция от всех входных переменных
- Найти условия, при которых функция принимает истинное или ложное значение
- Проверить, является ли функция самодвойственной (инвариантной относительно замены 0 на 1 и наоборот)
- Определить, сохраняет ли функция константу 0 или 1
- Выявить симметричность функции относительно некоторых переменных
Например, анализируя таблицу истинности выше, можно сделать следующие выводы:
- Функция F не является постоянной, так как принимает как значение 0, так и 1
- F зависит от обеих переменных A и B
- F принимает истинное значение, когда только одна из переменных A или B истинна
- F не является самодвойственной
Такой анализ помогает лучше понять свойства логической функции и может быть полезен при оптимизации логических схем.
Практическое применение таблиц истинности
Таблицы истинности находят широкое применение в различных областях:
Цифровая схемотехника
В проектировании цифровых устройств таблицы истинности используются для:
- Описания работы логических элементов и микросхем
- Синтеза комбинационных схем по заданной логической функции
- Минимизации логических выражений для оптимизации схем
- Анализа работы существующих схем
Программирование
В программировании таблицы истинности помогают:
- Разрабатывать и отлаживать сложные условные конструкции
- Оптимизировать булевы выражения в условиях
- Тестировать логику работы программ
Искусственный интеллект
В области ИИ таблицы истинности применяются для:
- Представления знаний в экспертных системах
- Обучения и тестирования нейронных сетей
- Реализации логического вывода в системах ИИ
Таким образом, понимание и умение работать с таблицами истинности является важным навыком для специалистов в области информационных технологий и смежных областях.
Сложные логические функции и их таблицы истинности
Помимо базовых логических операций, существуют более сложные логические функции, которые часто используются в цифровой схемотехнике и программировании. Рассмотрим некоторые из них:
Исключающее ИЛИ (XOR)
Эта функция возвращает истину, когда значения операндов различны:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Импликация
Логическая операция, соответствующая союзу «если…, то…»:
| A | B | A → B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Эквивалентность
Функция, возвращающая истину, когда оба операнда имеют одинаковое значение:
| A | B | A ↔ B |
|---|---|---|
| 0 | 1 | |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Понимание этих функций и умение строить для них таблицы истинности расширяет возможности работы со сложными логическими выражениями и схемами.
Минимизация логических функций с помощью таблиц истинности
Одно из важных применений таблиц истинности — минимизация логических функций. Это процесс упрощения логического выражения с целью уменьшения количества операций и переменных, при сохранении функциональности.
Основные методы минимизации с использованием таблиц истинности:
- Метод карт Карно
- Метод Квайна-Мак-Класки
- Метод Петрика
Рассмотрим пример минимизации функции с помощью карты Карно:
Пусть дана функция F(A,B,C) = A’B’C + A’BC + AB’C + ABC
Построим таблицу истинности:
| A | B | C | F |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Используя карту Карно, можно минимизировать эту функцию до вида:
F(A,B,C) = C
Этот пример демонстрирует, как таблицы истинности могут быть использованы для значительного упрощения логических выражений, что важно для оптимизации цифровых схем и программного кода.
(курс 68 ч.) §11. Логические выражения
Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, углубленный уровень)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, углубленный уровень) | §11. Логические выражения
Содержание урока
Формализация
Таблицы истинности
Составление условий
Логические схемы
Выводы
Вопросы и задания
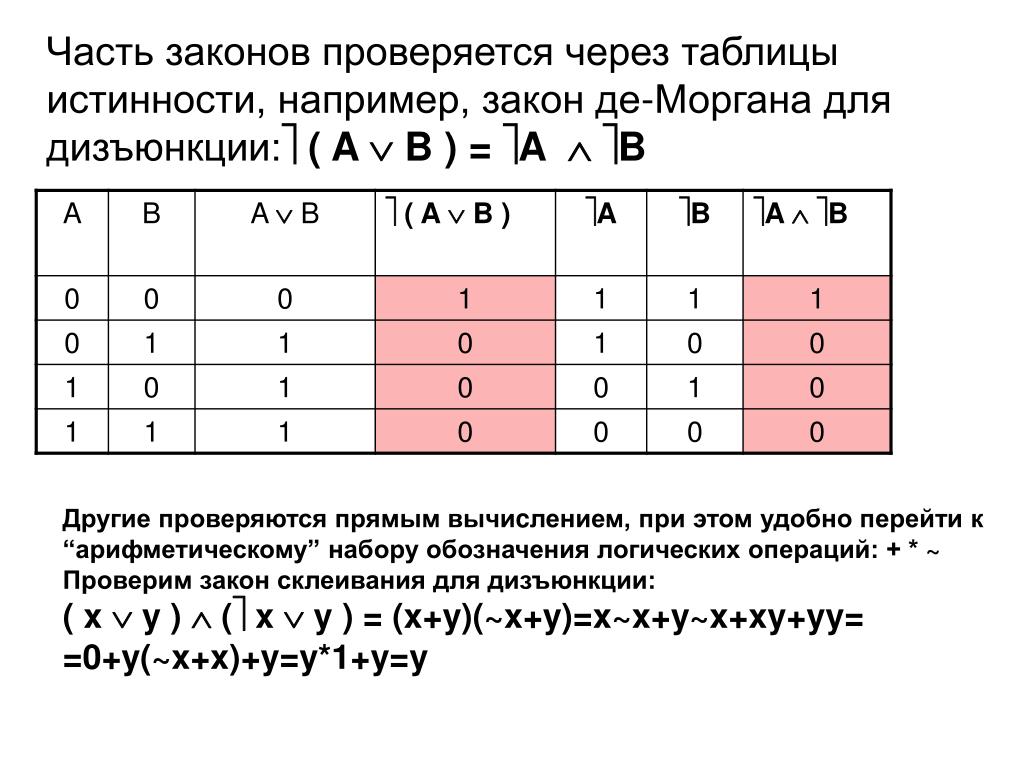
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
X = А • B + А • В.
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).
Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).
Рис. 2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 23 = 8 строк, для каждой из них нужно знать, чему равно значение функции.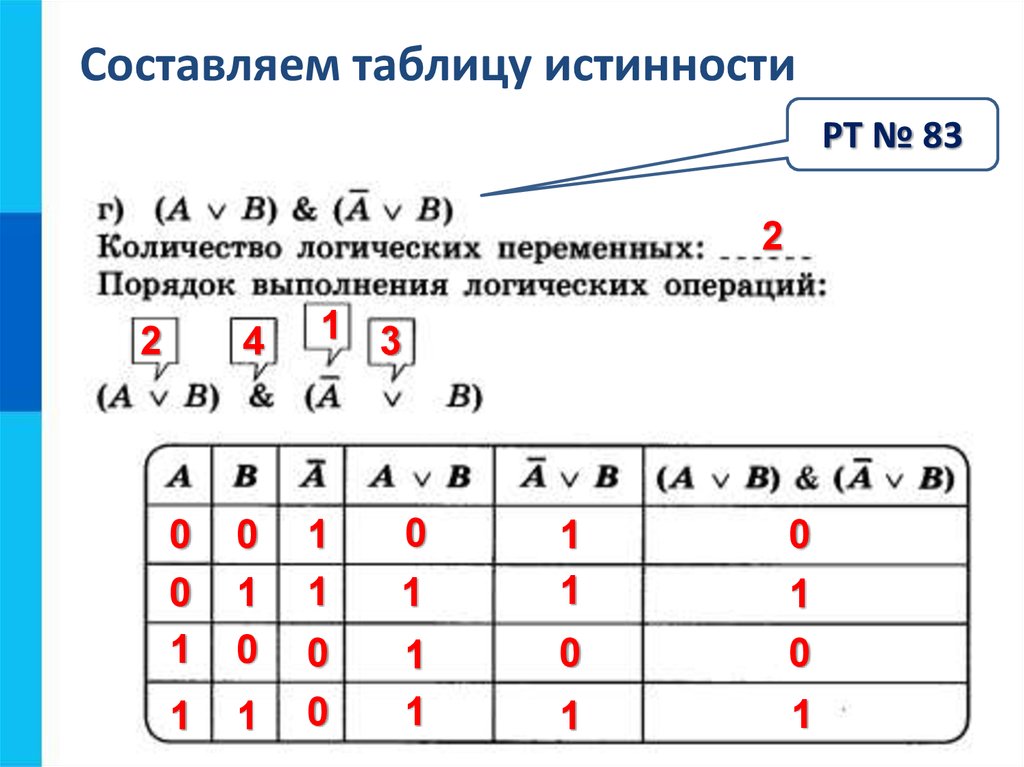
В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
а) А + В + C;
б) A • С + В;
в) А + B • С;
г) А • В • C;
д) A • B + C.
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке.
Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
а) А + B + C;
б) A • С • В;
в) А • B • C;
г) A + В + С;
д) A + B + C.
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).
Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
а) A + В + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + В + C.
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные).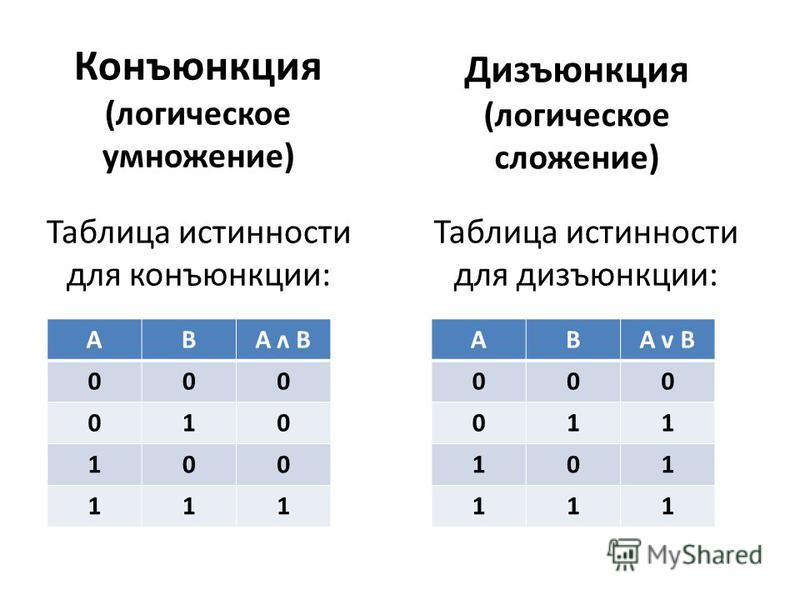
Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
а) 1 + В + 0;
в) 0 + B + 0;
д) 0 + В + 0.
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).
Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
а) А • B + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + B + C.
Следующая страница Составление условий
Cкачать материалы урока
для логических операций и выражений, как строить
Содержание:
- Что такое таблицы истинности
- Логические операции
- Логические выражения
- Инверсия
- Конъюнкция
- Дизъюнкция
- Правила составления таблицы истинности
- Примеры построения таблицы истинности
Содержание
- Что такое таблицы истинности
- Логические операции
- Логические выражения
- Инверсия
- Конъюнкция
- Дизъюнкция
- Правила составления таблицы истинности
- Примеры построения таблицы истинности
Что такое таблицы истинности
Определение
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.
Таблица истинности необходима для совершения логических операций. Она включает в себя n+1 столбцы и 2n строки, где n — число используемых переменных. В первых n столбцах представлены разные значения аргументов функции, а в n+1 столбце представлены значения функции, которые она принимает на данном наборе аргументов.
Набором называется совокупность значений переменных. А = 0, В = 1. В случае, когда количество переменных n, число различных наборов будет равно 2N. Например, для трех переменных число разных наборов будет равно 23 = 8.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).
Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции.
Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.
Логические операции
Определение
Логические операции — построение из одного или нескольких высказываний нового высказывания.
Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний.
К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.
Логические выражения
Определение
Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».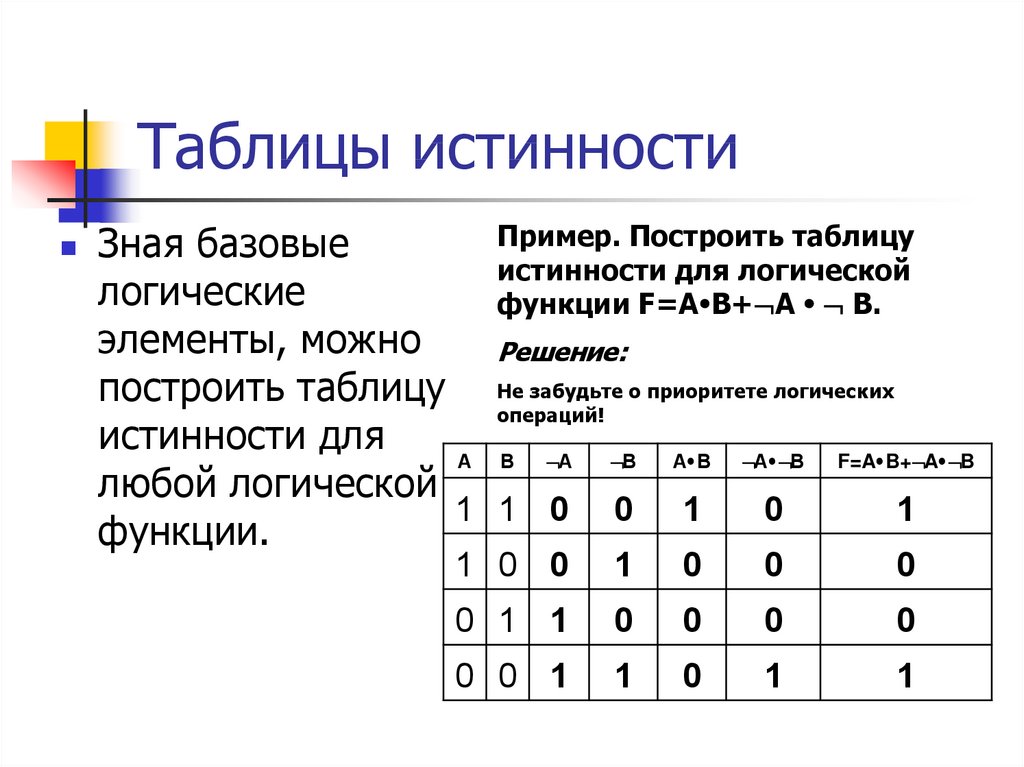
Их можно разделить на два типа:
- выражения, использующие операции сравнения и принимающие логические значения. Например, выражение a < b, где a = 12, а b = 9, равно значению «ложь»;
- логические выражения, которые связаны с логическими величинами и операциями. Например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина.
В логические выражения могут входить функции, алгебраические операции, операции сравнения и логические операции. Для таких случаев существует алгоритм выполнения действий. За исключением тех случаев, когда в логическом выражении присутствуют скобки, влияющие на порядок выполнения операций.
- вычисляется существующие функциональные зависимости;
- вычисляются алгебраические операции в обычном порядке;
- вычисляются операции сравнения в любом порядке;
- вычисляются логические операции начиная с операции отрицания. Следом вычисляется операция логического умножения, логического сложения, в последнюю очередь выполняются операции импликации и эквивалентности.
Инверсия
Определение
Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.
Если данное высказывание обозначается буквой A, то отрицание исходного высказывания обозначается следующим образом \([\overline{A}]\). Кроме этого возможно использование условного обозначения \(\neg A\). Читаться это будет как «не А», «А ложно», «неверно, что А», «отрицание А».
Унарной в данном случае называется операция, которая используется относительно одной величины.
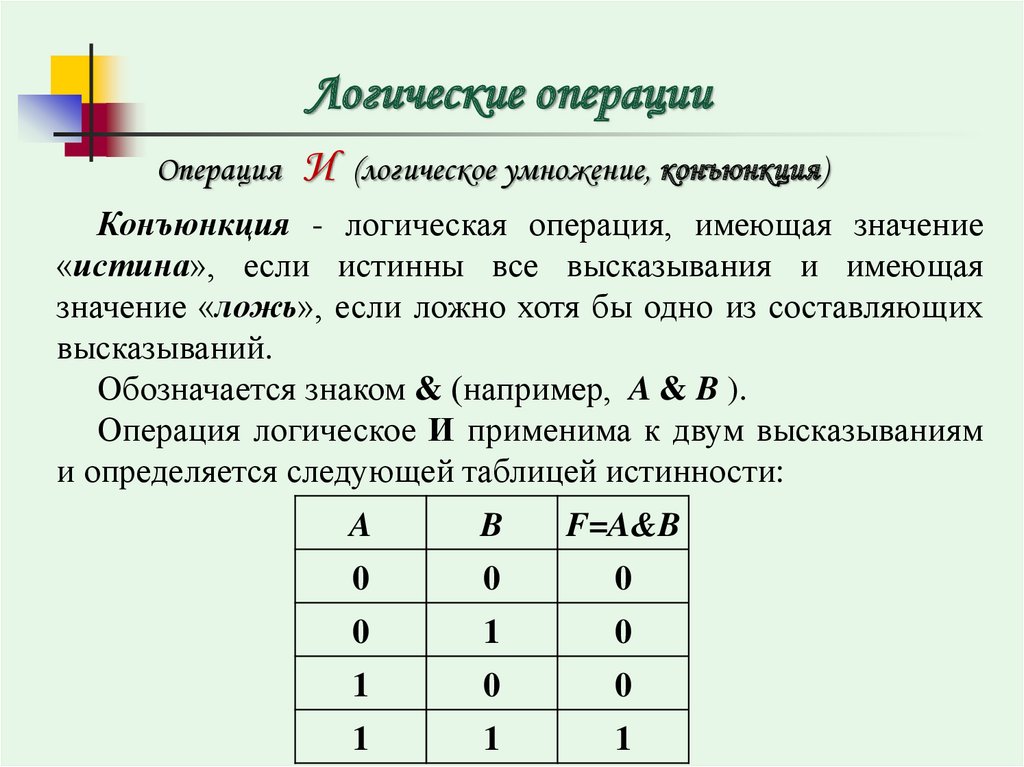
Конъюнкция
Определение
Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины. Конъюнкция соединяет логические высказывания при помощи связки «и».
Связка изображается символом ∧.
Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.
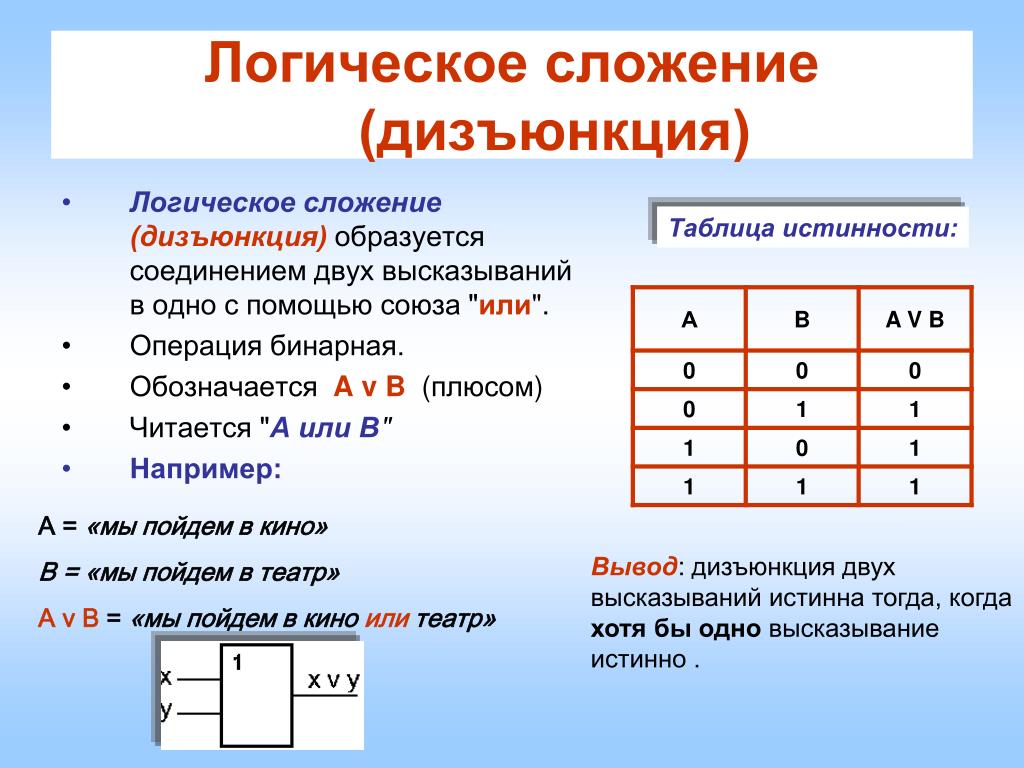
Дизъюнкция
Определение
Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨.
Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.
Правила составления таблицы истинности
Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.
Строить таблицы истинности необходимо по следующему алгоритму:
- Вычислить число переменных в выражении (n).
- Вычислить общее количество логических операций в выражении.
- Определить последовательность, в которой будут выполняться логические операции.
- Установить количество столбцов в таблице — количество переменных и количество операций.
- Внести в шапку таблицы переменные и операции, соблюдая последовательность, определенную в пункте 3.
- Высчитать количество строк в таблице, используя формулу m = 2n
- Занести в таблицу наборы входных переменных. Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2n−1.
- Заполнить таблицу, совершая логические операции.
Примеры построения таблицы истинности
Задача
Построим таблицу истинности и решим выражение\( F = (A \vee B) \wedge (¬A \vee ¬B)\). Будем пользоваться приведенным выше алгоритмом.
- Число переменных в выражении n = 2.
- Общее количество логических операций в выражении — 5.
- Последовательность выполнения логических операций — 1, 5, 2, 4, 3.
- Количество столбцов — 7. Логические переменные (А и В) + логические операции \(\vee\), \(\wedge\), \(¬\), \(\vee\) , \(¬\) = 2 +5 = 7.
- Количество строк — 5, исходя из m =2n, таким образом 22 = 4, 4+1 (строка заголовков столбцов) = 5.
- Заполним таблицу.
Решение
| А | В | \(А \vee В\) | ¬А | ¬В | \(¬А \vee ¬В\) | \((A \vee B) \wedge (¬A \vee ¬B)\) |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0 при A = B = 0 и A = B = 1
Задача
Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge ¬Z\)
- Число переменных в выражении n = 3.
- Общее количество логических операций в выражении — 3.
- Последовательность выполнения логических операций — 3, 2, 1.
- Количество столбцов — 6. Логические переменные (X, Y, Z) + логические операции\( \vee\), \(\wedge\), ¬ = 3 + 3 = 6.
- Количество строк — 9, исходя из m =2n, таким образом 23 = 8, 8+1 (строка заголовков столбцов) = 9.
- Заполним таблицу.
Решение
| X | Y | Z | ¬Z | \(Y \wedge ¬Z\) | \(X \vee Y \wedge ¬Z\) |
| 0 | 0 | 0 | q | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0, при X = Y = Z = 0; при X = Y = 0 и Z = 1.
Насколько полезной была для вас статья?
Рейтинг: 2.58 (Голосов: 26)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
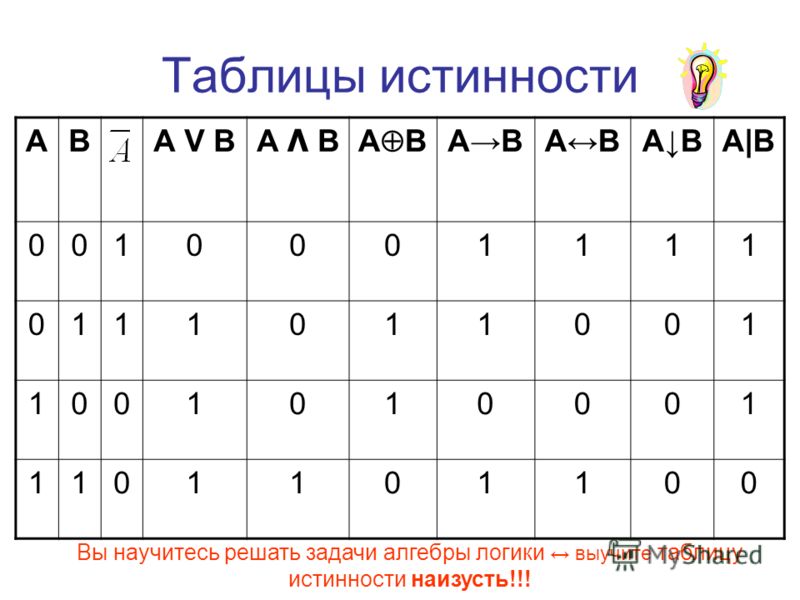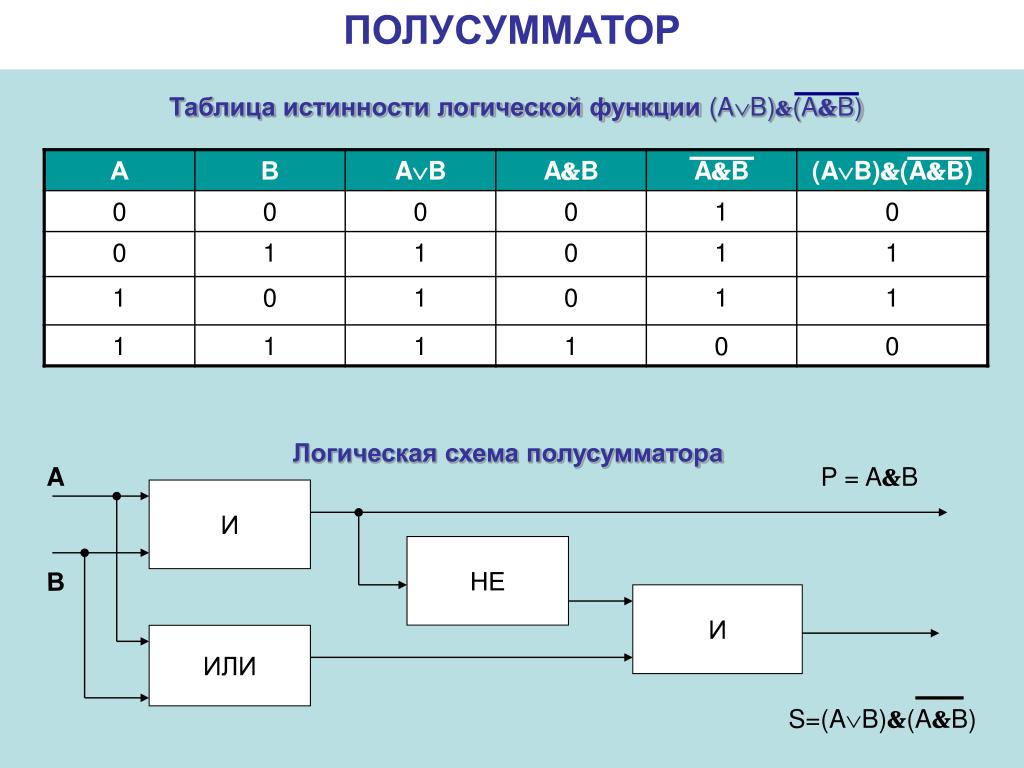Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.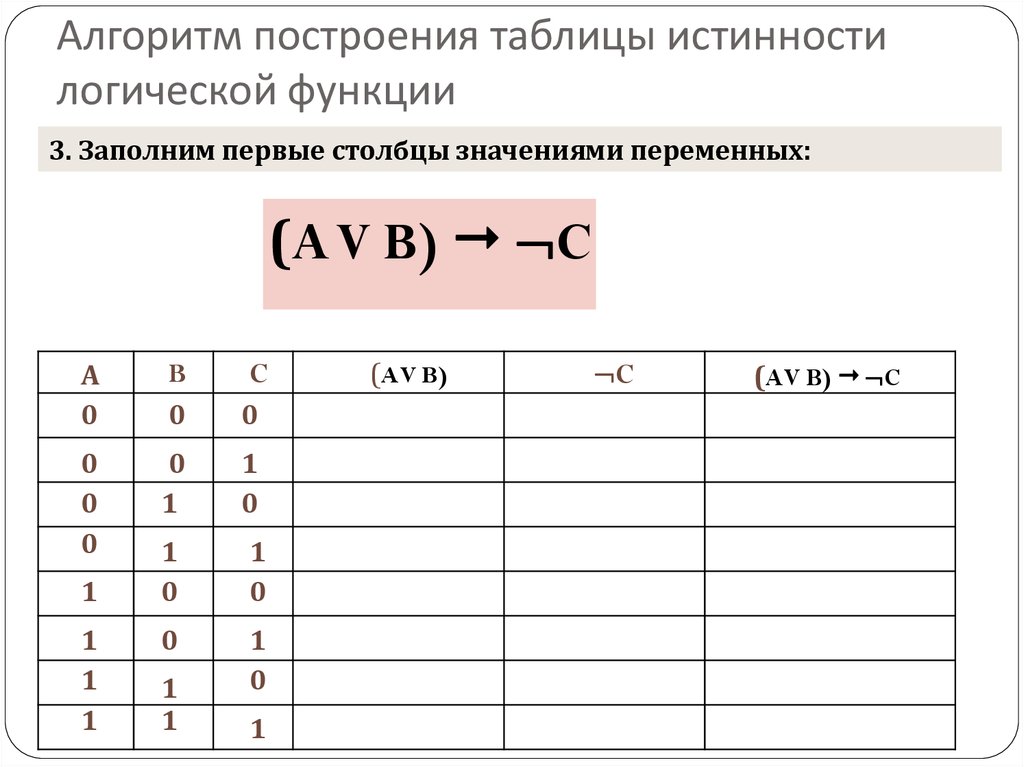
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.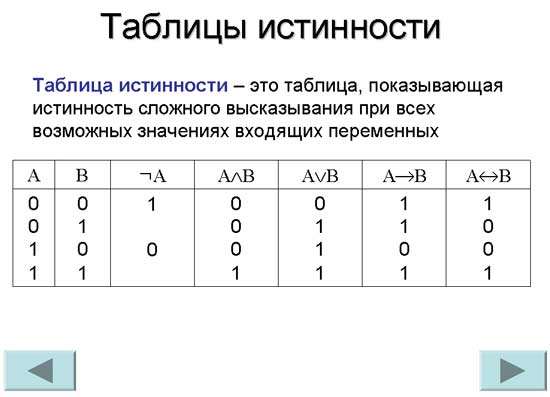
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Общая функция логического выражения и каждой отдельной логики также может быть выражена в форме таблицы, которая называется таблицей истинности. Логическое выражение цифровой схемы используется для построения таблицы истинности для соответствующей функции. Таблица истинности состоит из входов и выходов. Общее количество входов, доступных для цифровой логической схемы, составляет входы и строится для каждого возможного состояния или комбинации. Функция каждого логического элемента и всей цифровой схемы представляет собой выход. Эти выходы определяются для каждого возможного состояния или комбинации входов.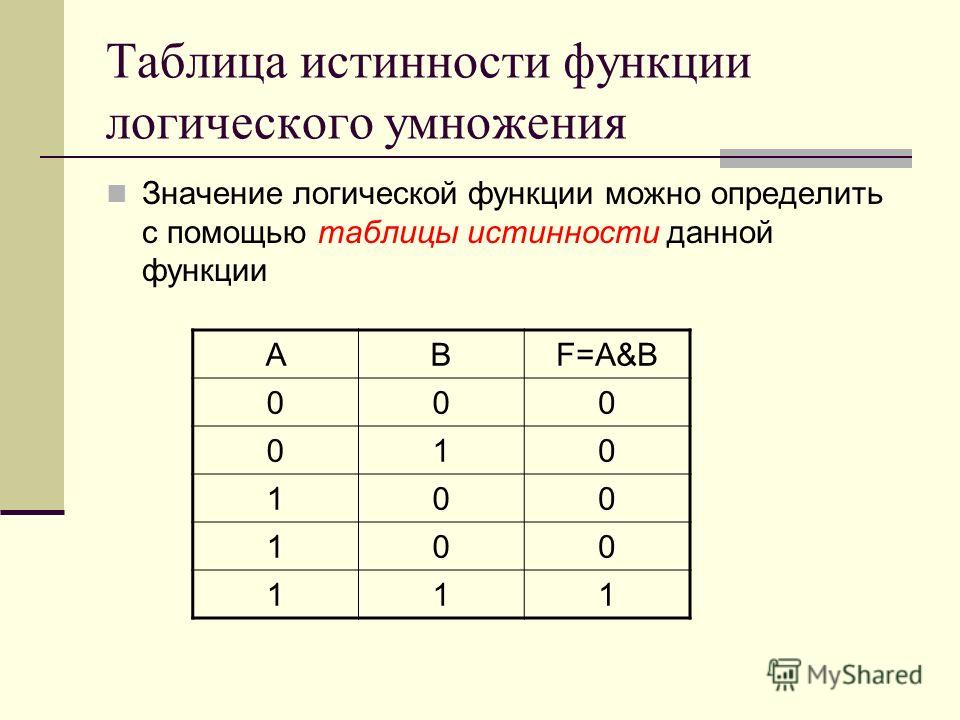
Как уже известно из предыдущих статей, состояния входа и выхода логических элементов представлены в виде данных логической логики, который имеет только два состояния, т. е. «ВКЛ» = «1» = «ИСТИНА» и «ВЫКЛ» = «0» = « ЛОЖНЫЙ». Однако в таблицах истинности чаще всего состояния представлены логическими типами «1» и «0», которые также равны битовым значениям. Комбинации состояний для двух входов (X и Y):
Однако в этой статье для простоты не используется логический элемент или схема с более чем тремя входами. Таблицы истинности, построенные для двух и трех входов, представляют собой логику, которую можно использовать для построения таблиц истинности для цифровой схемы, имеющей любое количество входов.
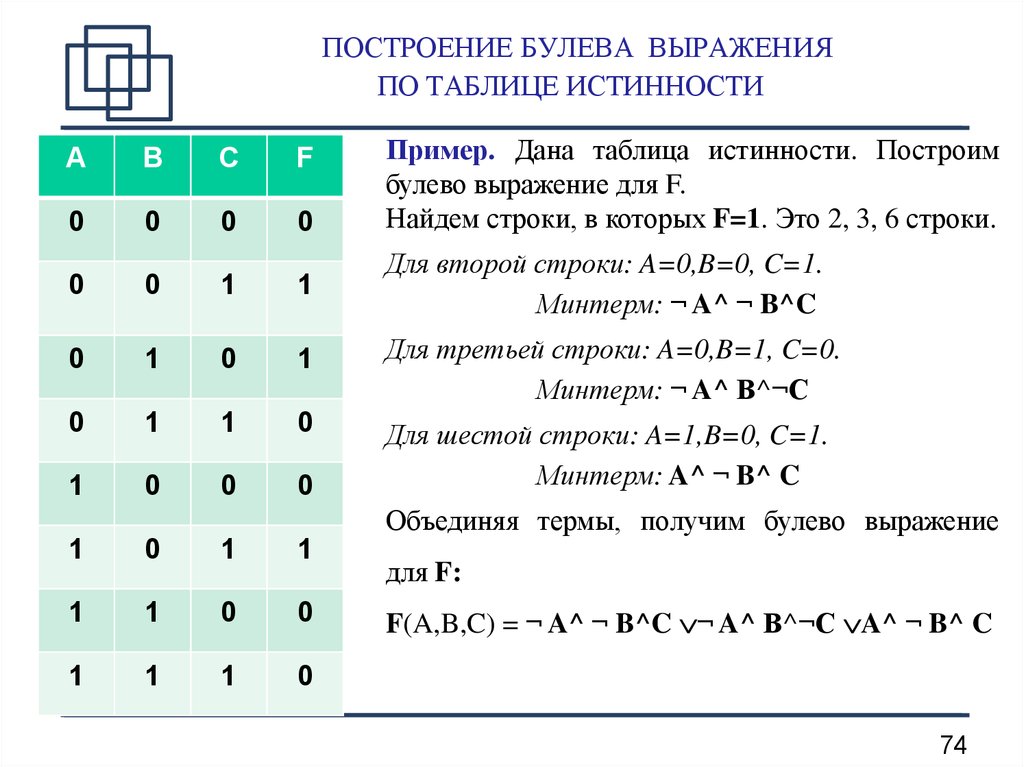
д. Из-за их важности в логических схемах они доступны в цифровых микросхемах. пакеты и настоящим включены в статью.
