Что такое логические элементы ЭВМ. Как устроены базовые логические операции. Почему компьютер оперирует нулями и единицами. Какие бывают логические функции.
Что такое логические элементы и для чего они нужны
Логические элементы — это базовые «кирпичики», из которых строится вся логика работы компьютера. Они выполняют простейшие логические операции над двоичными сигналами (0 и 1). Комбинируя эти элементы, можно создавать сложные электронные схемы, способные выполнять вычисления и обрабатывать информацию.
Основные типы логических элементов:
- И (AND) — выполняет логическое умножение
- ИЛИ (OR) — выполняет логическое сложение
- НЕ (NOT) — выполняет инверсию (отрицание)
- Исключающее ИЛИ (XOR)
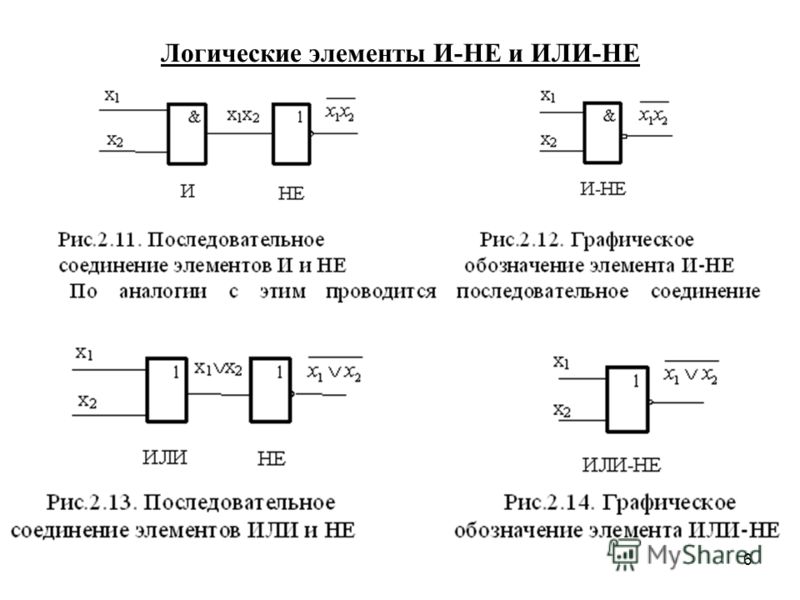
- И-НЕ (NAND)
- ИЛИ-НЕ (NOR)
Из этих базовых элементов строятся более сложные узлы — регистры, счетчики, сумматоры и т.д. Они в свою очередь образуют функциональные блоки процессора, памяти и других устройств компьютера.
Почему компьютеры работают в двоичной системе

- Простота реализации — электронные схемы легко переводятся в два состояния (есть сигнал/нет сигнала)
- Помехоустойчивость — промежуточные состояния легко отфильтровываются
- Экономичность — требуется меньше элементов для кодирования информации
- Удобство выполнения логических операций
При этом двоичная система позволяет закодировать любую информацию — числа, текст, изображения, звук. Главное преимущество — простота обработки сигналов электронными схемами.
Базовые логические операции
Логическое умножение (И, AND)
Операция И возвращает 1 только если все входные сигналы равны 1. В остальных случаях результат 0.
Таблица истинности для двух входов:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическое сложение (ИЛИ, OR)
Операция ИЛИ возвращает 1, если хотя бы один из входных сигналов равен 1. Результат 0 только если все входы 0.
Таблица истинности для двух входов:
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Отрицание (НЕ, NOT)
Операция НЕ инвертирует входной сигнал — превращает 0 в 1 и наоборот.
Таблица истинности:
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Как строятся сложные логические схемы
Комбинируя базовые логические элементы, можно создавать схемы любой сложности. Например, сложение двух одноразрядных двоичных чисел реализуется так:
- Два входа складываются через элемент XOR — получаем сумму без учета переноса
- Те же входы подаются на элемент AND — получаем бит переноса
- Если есть перенос с предыдущего разряда, он складывается с суммой через еще один XOR
Таким образом, используя простейшие логические элементы, можно построить полноценный одноразрядный сумматор. А объединяя такие сумматоры, получаем многоразрядные вычислительные схемы.
Зачем нужны таблицы истинности
Таблица истинности — это полное описание работы логического элемента или схемы. Она показывает результат для всех возможных комбинаций входных сигналов.
Таблицы истинности позволяют:
- Проверить корректность работы схемы
- Оптимизировать логические выражения
- Сравнивать разные реализации одной функции
- Находить эквивалентные схемы
Для сложных схем с большим числом входов таблицы становятся громоздкими. В этом случае используют другие методы анализа — карты Карно, диаграммы Вейча и т.д.

Как логические элементы реализуются на физическом уровне
В современных компьютерах логические элементы реализуются на основе транзисторов. Основные технологии:
- TTL (транзисторно-транзисторная логика) — используются биполярные транзисторы
- КМОП (комплементарная металл-оксид-полупроводниковая структура) — применяются полевые транзисторы
Каждый логический элемент содержит несколько транзисторов, соединенных определенным образом. Например, элемент И-НЕ в TTL-логике состоит из двух транзисторов и нескольких резисторов.
Современные процессоры содержат миллиарды транзисторов, образующих сложнейшие логические схемы. При этом базовые принципы работы остаются неизменными на протяжении десятилетий.
Какую роль играет булева алгебра
Булева алгебра — это раздел математической логики, изучающий операции над логическими величинами. Она лежит в основе проектирования цифровых схем.
Основные области применения булевой алгебры в цифровой электронике:
- Описание работы логических схем
- Оптимизация логических выражений
- Минимизация количества элементов в схемах
- Анализ и синтез комбинационных схем
Законы и теоремы булевой алгебры позволяют преобразовывать логические выражения, находить эквивалентные схемы, упрощать сложные функции. Это критически важно для создания эффективных цифровых устройств.
Урок 1. Логический анализ языка
Первый урок нашего курса мы посвятим сложной, но очень важной теме – логическому анализу языка. Сразу стоит оговориться, что эта тема многим может показаться абстрактной, нагруженной терминологией, неприменимой на практике. Не пугайтесь! Логический анализ языка – это основа любой логической системы и правильного рассуждения. Те термины, которые мы здесь узнаем, станут нашим логическим алфавитом, без знания которого просто нельзя пойти дальше, но постепенно мы научимся пользоваться им с лёгкостью.
Во введении к курсу было сказано, что логика концентрируется только на той части человеческого знания, которая выражена в языковой форме. Всем известно, что язык – это основной канал коммуникации между людьми, главный способ передачи информации и трансляции знаний. При этом язык – настолько тонкий инструмент, что он позволяет не только наилучшим образом выражать и передавать наши мысли, но и скрывать их, запутывать, обманывать. Поэтому логика ставит перед собой задачу прояснить работу языка. Не занимается ли тем же самым языкознание? И да, и нет. Безусловно, филологи проясняют, как работает язык на разных уровнях: фонетическом, лексическом, синтаксическом. Также они анализируют регулярности в языковом употреблении, и на основе этого анализа разрабатываются правила орфографии, грамматики, пунктуации, произношения. Эти правила призваны унифицировать использование языка и сделать его более лёгким и понятным.
Не занимается ли тем же самым языкознание? И да, и нет. Безусловно, филологи проясняют, как работает язык на разных уровнях: фонетическом, лексическом, синтаксическом. Также они анализируют регулярности в языковом употреблении, и на основе этого анализа разрабатываются правила орфографии, грамматики, пунктуации, произношения. Эти правила призваны унифицировать использование языка и сделать его более лёгким и понятным.
Логики под прояснением работы языка понимают нечто совершенно иное. В отличие от языкознания, логика стремится как можно больше абстрагироваться от конкретной языковой оболочки и содержания высказываний и перейти к независимым от них универсальным логическим законам и правилам рассуждения. Философ и логик Людвиг Витгенштейн говорил, что язык переодевает мысли (Витгенштейн Л. Логико-философский трактат. М.: Канон+, 2008, с. 72). Так вот, задача логического анализа языка снять языковую одежду и выявить тот скелет или каркас, который под ней скрыт. Логики называют этот скелет логической формой. Если говорить просто, логическая форма – это то, что остаётся от высказывания после того, как мы убрали всё его конкретное содержание. Именно концентрация на логических формах высказываний и логических отношениях между ними делает логику универсальной, применимой к любому рассуждению, независимо от его предмета.
Если говорить просто, логическая форма – это то, что остаётся от высказывания после того, как мы убрали всё его конкретное содержание. Именно концентрация на логических формах высказываний и логических отношениях между ними делает логику универсальной, применимой к любому рассуждению, независимо от его предмета.
Выявление логических форм так важно, потому что оно способно дать нам полезную информацию о рассуждении, даже если мы не разбираемся в теме. Только по форме высказываний можно определить, корректно ли рассуждение, правильно ли дано определение, правильно ли используются понятия, не пытаются ли нас намеренно запутать и т.д. Поэтому главная задача этого урока – научиться отвлекаться от содержания высказываний и выявлять их логические формы.
Содержание
- Язык как система знаков
- Треугольник Фреге
- Виды языковых выражений
- Примеры логического анализа предложений
- Упражнения
- Проверочные вопросы на усвоение материала
Язык как система знаков
Чтобы научиться этому, сначала необходимо понять, что для логиков представляет собой язык. Начнём с того, что они видят в языке, прежде всего, знаковую систему. Буквы, слова, предложения – всё это знаки. Согласно знаменитому определению основоположника науки о знаках – семиотики – Чарльза Пирса, знак – «это нечто, что обозначает что-либо для кого-нибудь в определенном отношении или объеме» (Пирс Ч.С. Избранные философские произведения, М.: Логос, 2000, с. 177). Это довольно запутанное определение можно представить в виде квадрата:
Начнём с того, что они видят в языке, прежде всего, знаковую систему. Буквы, слова, предложения – всё это знаки. Согласно знаменитому определению основоположника науки о знаках – семиотики – Чарльза Пирса, знак – «это нечто, что обозначает что-либо для кого-нибудь в определенном отношении или объеме» (Пирс Ч.С. Избранные философские произведения, М.: Логос, 2000, с. 177). Это довольно запутанное определение можно представить в виде квадрата:
В естественном языке знаками будут слова, словосочетания и предложения. «Авокадо», «тренер сборной Германии по футболу», «Александр Сергеевич Пушкин», «Кошки много спят» – всё это знаки. Я пишу их в кавычках специально, чтобы показать, что речь идёт именно о знаках – сочетаниях букв и звуков, которые нечто для нас обозначают. То, что знак обозначает, называется десигнатом. Десигнатами могут быть предметы, люди, абстрактные сущности, состояния, ситуации, положения дел в мире – в общем, всё что угодно. Слово «апельсин» обозначает для меня конкретный предмет. Слово «Иван» – конкретного человека. Предложение «Сегодня выпал снег» – положение дел. Интерпретатор – это человек, который воспринимает нечто (в случае языка – письменные символы и звуковые сочетания) как знак чего-то. Интерпретанта – это то, как человек реагирует на знак (например, если я вижу на перекрёстке знак «Стоп», то я останавливаю свою машину).
Слово «Иван» – конкретного человека. Предложение «Сегодня выпал снег» – положение дел. Интерпретатор – это человек, который воспринимает нечто (в случае языка – письменные символы и звуковые сочетания) как знак чего-то. Интерпретанта – это то, как человек реагирует на знак (например, если я вижу на перекрёстке знак «Стоп», то я останавливаю свою машину).
Отношение знаков к десигнатам описывается семантикой. Отношения знаков между собой – синтактикой. Отношение знаков к интерпретатору и интерпретанте – прагматикой. Логика не занимается прагматикой, так как последняя всегда связана с конкретной ситуацией, от которой логика стремится абстрагироваться. Зато изучение семантики и синтактики становятся её важными разделами.
Далее, язык состоит не просто из знаков, но знаков определённого рода – знаков-символов. Знаки-символы связаны со своими десигнатами произвольным образом. Например, буквы произвольным образом связаны со звуками (и это хорошо видно из наличия разных алфавитов), слова произвольно связаны с обозначаемыми предметами и явлениями (по-русски мы говорим «собака», по-английски – «dog», по-французски – «chien»; выбранное слово произвольно и ничего не говорит нам о животном, которое мы так называем), предложения произвольно связаны с выражаемыми мыслями (одну и ту же мысль можно передать с помощью совершенно разных предложений).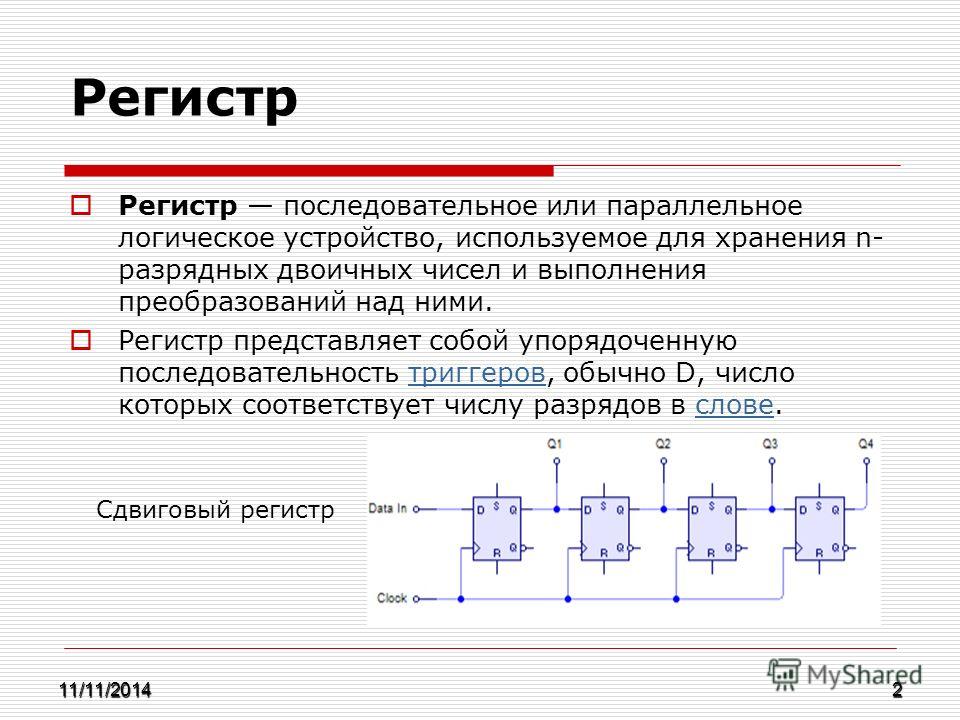
Кроме того, помимо знаков-символов есть и другие. Например, если знак копирует объект, это иконический знак 🐶. Иконические знаки также называют знаками-копиями и знаками-изображениями. А если знак указывает на объект, это индексальный знак или просто знак-признак (вспомните значок фирмы Nike или Adidas). Когда же знак символизирует объект, находясь в условной связи с ним, это уже знак-символ (как в примере со словами «собака», «dog» и т.д.)
Каждый тип знака обладает своими преимуществами, способными создать максимальный эффект. Те же иконические знаки и знаки-символы очень легко воспринимаются и создают в сознании наблюдателя конкертный образ и позволяют соотнести его с изначальным объектом без каких-либо усилий.
Треугольник Фреге
Один из основоположников современной логики Готлоб Фреге заметил, что знаки обладают определённой двойственностью. С одной стороны, они обозначают какие-то объекты, а с другой – передают интерпретатору некоторую дополнительную информацию о них. Например, возьмём словосочетание «автор “Войны и мира”». Это знак, обозначающий Льва Толстого. Помимо того, что этот знак указывает на конкретного человека, он также сообщает нам, что этот человек написал определённую книгу. Фреге назвал значением тот объект, который знак обозначает, и смыслом – ту дополнительную информацию, которую он несёт. Так появился треугольник Фреге:
Например, возьмём словосочетание «автор “Войны и мира”». Это знак, обозначающий Льва Толстого. Помимо того, что этот знак указывает на конкретного человека, он также сообщает нам, что этот человек написал определённую книгу. Фреге назвал значением тот объект, который знак обозначает, и смыслом – ту дополнительную информацию, которую он несёт. Так появился треугольник Фреге:
Интересно отметить, далеко не все знаки обладают этими двумя характеристиками. Например, знак «нынешний король Франции» не имеет никакого значения, так как он обозначает несуществующий предмет, зато обладает смыслом. В то же время какой-нибудь знак «а» может обладать значением, которое я хочу ему придать, но не выражает никакого смысла. Помимо этого, различение значения и смысла понятно, когда речь идёт о словах и словосочетаниях. Но как быть с предложениями? Логики считают, что повествовательные предложения тоже обладают значением и смыслом. Поскольку они утверждают нечто о мире, то их значением будет «истина» либо «ложь», а смыслом – собственно описанная ими ситуация. Допустим, дано предложение: «Павлов открыл и описал действие условных рефлексов». Значение этого предложения – «истина». Смысл – тот факт, что Павлов открыл и описал действие условных рефлексов. При этом предложения, как и слова, могут не иметь значения. Например, возьмём предложение «Все дети Джона лысы». По идее, оно должно быть либо истинным, либо ложным. Однако что если у Джона нет детей? В таком случае мы не можем приписать ему никакого значения.
Допустим, дано предложение: «Павлов открыл и описал действие условных рефлексов». Значение этого предложения – «истина». Смысл – тот факт, что Павлов открыл и описал действие условных рефлексов. При этом предложения, как и слова, могут не иметь значения. Например, возьмём предложение «Все дети Джона лысы». По идее, оно должно быть либо истинным, либо ложным. Однако что если у Джона нет детей? В таком случае мы не можем приписать ему никакого значения.
Поскольку знаки произвольны, то для удобства при анализе мы можем заменять их более простыми символами. Они будут иметь то же значение, но будут абстрагироваться от смысла. Соответственно, выражения языка будут рассматриваться в зависимости не от их содержания, а от той семантической функции, которую они выполняют. Выявление семантических функций и замена выражений простыми символами – очень важная процедура, так как по большому счёту она и представляет собой процесс отвлечения от содержания высказываний и переход на уровень логических форм.
Игра на эффект Cтрупа
Чтобы вы смогли понять, насколько иногда нам сложно отделять знак, его значение и смысл, предлагаем сыграть в игру по мотивам эффекта Струпа.
В психологии эффектом Струпа (англ. Stroop effect) называют задержку реакции при прочтении слов, когда цвет слов не совпадает с написанными словами (к примеру, слово «красный» написано синим). Эффект назван в честь Джона Ридли Струпа, впервые опубликовавшего этот тест на английском в 1935 году. До этого этот эффект был опубликован в Германии в 1929 году. Это исследование стало одним из наиболее цитируемых исследований в истории экспериментальной психологии.
Сейчас мы вам предлагаем пройти нашу модификацию данного теста.
Cтатистика На весь экран
Виды языковых выражений
В зависимости от выполняемых ими семантических функций языковые выражения делятся на следующие виды:
Расшифруем, что это всё обозначает. Итак, языковые выражения делятся на два типа: предложения и термины.
Предложение – это знаковая форма для передачи мыслей. Если мысль представляет собой вопрос, то она выражается вопросительным предложением. Если мы имеем дело с императивом, то – побудительным предложением. Если же речь идёт о суждении, то есть мысли об утверждении или отрицании наличия некоторой ситуации в мире, то его выражают с помощью повествовательных предложений. Стоит отметить, что логика в основном концентрируется на изучении как раз повествовательных предложений, так как они выступают главным способом передачи знания о мире. Мы в этом курсе также будем говорить по большей части именно о них.
Термины – это значимые части предложений или, если говорить проще, слова и словосочетания. Они в свою очередь делятся на термины логические, то есть термины, которые что-то говорят о логическом устройстве предложений, и термины дескриптивные, то есть термины, которые что-то описывают, несут какую-то информацию о положении дел в мире. Дескриптивные термины различаются в зависимости от того, что именно они обозначают. Имена обозначают какой-то один единственный объект. Например, «Елизавета II» обозначает ровно одного человека. При этом именем может быть и словосочетание: «нынешняя королева Великобритании» тоже обозначает ровно одного человека. Предикаты обозначают свойства, состояния, отношения: «быть красным», «быть английской королевой», «граничить с», «знать иностранный язык» и т.д. В естественном языке предикатам соответствуют нарицательные существительные, прилагательные, глаголы. Функторы обозначают качественные и количественные характеристики предметов. К ним относятся знаки математических операций, физические величины и т.п.: «корень из», «натуральный логарифм от», «масса», «скорость».
Имена обозначают какой-то один единственный объект. Например, «Елизавета II» обозначает ровно одного человека. При этом именем может быть и словосочетание: «нынешняя королева Великобритании» тоже обозначает ровно одного человека. Предикаты обозначают свойства, состояния, отношения: «быть красным», «быть английской королевой», «граничить с», «знать иностранный язык» и т.д. В естественном языке предикатам соответствуют нарицательные существительные, прилагательные, глаголы. Функторы обозначают качественные и количественные характеристики предметов. К ним относятся знаки математических операций, физические величины и т.п.: «корень из», «натуральный логарифм от», «масса», «скорость».
Логические термины – это то, на что, прежде всего, обращает внимание логик, сталкиваясь с какими-то рассуждениями. В этом курсе мы тоже попытаемся научиться видеть их и использовать это умение. Итак, логические термины делятся на предицирующие связки, пропозициональные связки и кванторы.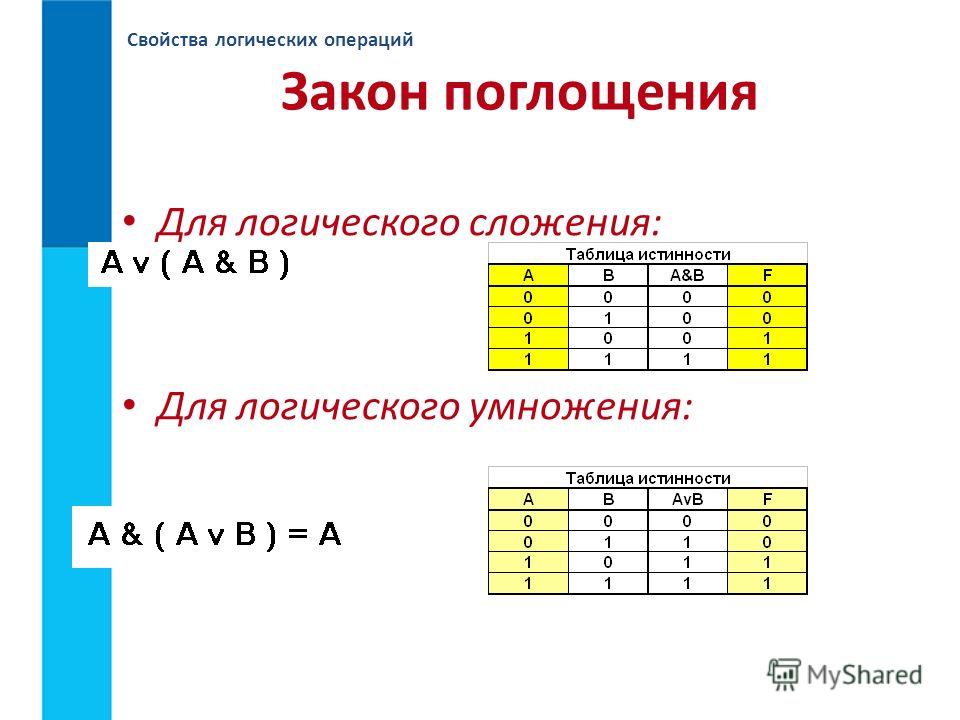 Предицирующие связки – это связки «есть» и «не есть». В естественном языке они могут выражаться разными словами («являться», «выступать» и т.д.) или даже опускаться («Сократ – человек»). Пропозициональные связки выражают отношения между различными предложениями или между компонентами одного предложения. К этим связкам относятся: «и», «или», «неверно, что», «если…, то», «если и только если». Кванторы передают информацию о количестве предметов. Квантор общности выражается словами «все», «ни один», «каждый», «любой». Квантор существования передаётся словами «существует», «некоторые», «большинство», «какой-нибудь».
Предицирующие связки – это связки «есть» и «не есть». В естественном языке они могут выражаться разными словами («являться», «выступать» и т.д.) или даже опускаться («Сократ – человек»). Пропозициональные связки выражают отношения между различными предложениями или между компонентами одного предложения. К этим связкам относятся: «и», «или», «неверно, что», «если…, то», «если и только если». Кванторы передают информацию о количестве предметов. Квантор общности выражается словами «все», «ни один», «каждый», «любой». Квантор существования передаётся словами «существует», «некоторые», «большинство», «какой-нибудь».
Примеры логического анализа предложений
Посмотрим, как вся эта теория работает на практике. Возьмём несколько предложений и рассмотрим их компоненты с точки зрения семантических функций.
Начнём с предложения: «Катя пошла в кино, а Люда осталась дома зубрить сопромат». Во-первых, это сложное предложение состоит из двух простых: «Катя пошла в кино», «Люда осталась дома зубрить сопромат». Между собой они соединяются союзом «а», который в логике приравнивается к пропозициональной связке «и». То есть мы получаем два повествовательных предложения, связанных пропозициональной связкой «и». Для удобства мы можем заменить наши простые предложения знаками «р» и «q», тогда логическая форма этого предложения будет выглядеть следующим образом: «р и q».
Между собой они соединяются союзом «а», который в логике приравнивается к пропозициональной связке «и». То есть мы получаем два повествовательных предложения, связанных пропозициональной связкой «и». Для удобства мы можем заменить наши простые предложения знаками «р» и «q», тогда логическая форма этого предложения будет выглядеть следующим образом: «р и q».
Теперь посмотрим на предложение: «Петя пошёл на занятия или прогулял их». Хотя это предложение простое, в логике оно будет разбиваться на две части: «Петя пошёл на занятия» и «Петя прогулял занятия», соединённые пропозициональной связкой «или». К тому же предложение «Петя прогулял занятия» эквивалентно предложению «Петя не пошёл на занятия» или «Неверно, что Петя пошёл на занятия». Таким образом, наше предложение будет выглядеть для логика так: «Петя пошёл на занятия, или неверно, что Петя пошёл на занятия». Заменяем предложения на простые знаки и получаем логическую форму: «р или неверно, что р». Кстати, предложения такой формы всегда истинны. Логическая форма предложения «Если бросить камень в окно, то оно разобьётся» – «если р, то q». Логическая форма предложения «Я выйду за тебя, если и только если ты подаришь мне кольцо с брильянтом» – «р, если и только если q». И так далее.
Кстати, предложения такой формы всегда истинны. Логическая форма предложения «Если бросить камень в окно, то оно разобьётся» – «если р, то q». Логическая форма предложения «Я выйду за тебя, если и только если ты подаришь мне кольцо с брильянтом» – «р, если и только если q». И так далее.
Вы, наверное, уже обратили внимание, что сейчас мы только выделяли простые предложения и пропозициональные связки между ними, но не затрагивали другие термины внутри предложений. Примерно в таком духе работает логика высказываний. В её рамках простые предложения заменяются короткими символами «p», «q», «r», «s» и т.д. и выявляются те пропозициональные связки, которые соединяют их между собой («и», «или», «неверно, что», «если, то»). В принципе даже такой поверхностный анализ может быть очень полезным, так как он помогает прояснить отношения между высказываниями в ходе рассуждения: выявлять парадоксы, тавтологии, противоречия и отсекать ложные высказывания, исходя только из их формы.
Безусловно, логический анализ может идти и глубже и затрагивать не только отношения между предложениями, но и отношения между логическими и нелогическими терминами внутри простых предложений. К логическим системам, которые основаны на таком более детальном анализе, относятся логика предикатов и силлогистика. Попробуем проанализировать несколько простых предложений, определяя семантические функции входящих в них терминов, чтобы получить представление, как они работают.
Возьмём предложение: «Все динозавры вымерли». «Все» – это квантор общности. «Динозавры» – это предикат, так как этот термин обозначает свойство «быть динозавром», которое присуще целому классу объектов. «Вымерли» – это тоже предикат, обозначающий свойство «быть вымершим». Чтобы записать логическую форму этого предложения, мы можем заменить предикаты буквами S и P. Попробуем: «Все S P». Получилось что-то странное и не имеющее особого смысла. Проблема в том, что мы пропустили предицирующую связку «есть». Хотя в естественном языке в этом предложении слова «есть» нет и не может быть, с точки зрения логики предицирующая связка «есть» здесь присутствует. Она связывает между собой два предиката: «быть динозавром» и «быть вымершим». В итоге мы получаем: «Все S есть P».
Хотя в естественном языке в этом предложении слова «есть» нет и не может быть, с точки зрения логики предицирующая связка «есть» здесь присутствует. Она связывает между собой два предиката: «быть динозавром» и «быть вымершим». В итоге мы получаем: «Все S есть P».
Теперь возьмём предложение: «Некоторые дети часто плачут, но Аня – плачет редко». В этом предложении две части. Начнём с первой. «Некоторые» – это квантор существования, то есть он как бы говорит нам: «Существуют такие объекты, которым присуще быть детьми и часто плакать». «Дети» и «часто плакать» – предикаты, не забываем о невидимой предицирующей связке «есть». Получаем: «Некоторые S есть P». Перейдём ко второй части. «Аня» – это имя, оно обозначает одного-единственного конкретного человека. «Плакать редко» эквивалентно «не плакать часто». Это значит, что мы имеем здесь тот же предикат, что и в первой части – «плакать часто» и предицирующую связку «не есть».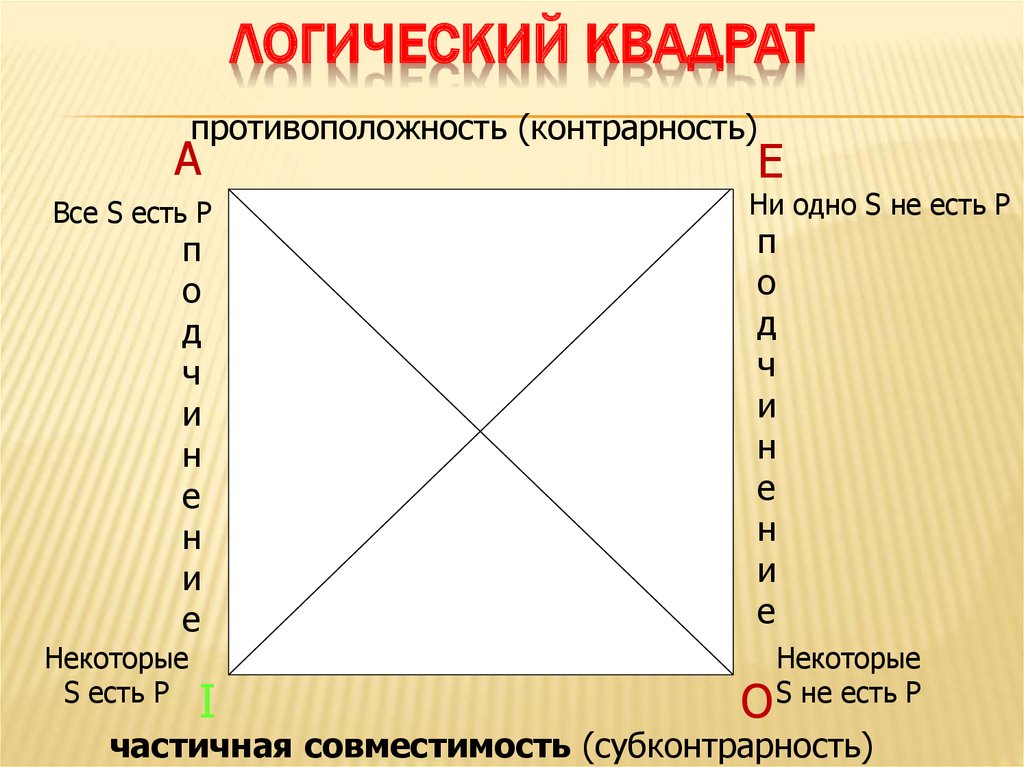 Логическая форма этого предложения: «а не есть P». Союз «но» представляет собой пропозициональную связку «и». В итоге: «Некоторые S есть P, и а не есть P».
Логическая форма этого предложения: «а не есть P». Союз «но» представляет собой пропозициональную связку «и». В итоге: «Некоторые S есть P, и а не есть P».
Таким образом и происходит логический анализ языковых выражений. Сначала определяются семантические функции предложений и слов, затем предложения, имена, предикаты и функторы заменяются короткими удобными символами, которые позволяют отвлечься от конкретного содержания, и выявляются те логические термины, которые связывают их между собой. Это даёт нам возможность проверить, насколько данное рассуждение корректно с точки зрения его логической формы. Естественно, чем более детальный логический анализ языка проводится, тем более сложной будет логическая система. Но одновременно и тем более тонким инструментом для разбора рассуждений она окажется. Конечно, примеры анализа, приведённые выше, могут показаться сложными и не до конца ясными. В этом нет ничего страшного: когда мы перейдём к конкретным темам, их значение прояснится. На сегодня важно запомнить, что за словами естественного языка нужно научиться видеть их семантические функции, за предложениями – их логические формы. Это станет ключом к умению логично рассуждать.
На сегодня важно запомнить, что за словами естественного языка нужно научиться видеть их семантические функции, за предложениями – их логические формы. Это станет ключом к умению логично рассуждать.
Напоследок, предлагаем вам несколько несложных логических задач. Попробуйте представить их решение в виде пошагового рассуждения. Где это возможно, абстрагируйтесь от содержания предложений и перейдите на уровень логических форм.
Упражнения
«Живописная» экспертиза (Из книги Сергея Быльцова «Логические головоломки и задачи»)
Одному коллекционеру принесли картину, якобы принадлежащую перу кисти Антонио Канале, прозванному Каналетто. Коллекционер не был большим знатоком живописи и потому пригласил на экспертизу трёх специалистов. Эксперты высказали о картине следующие суждения:
- Первый: Это не только не Каналетто, но даже и не Гварди.
- Второй: Это не Каналетто, но это настоящий Алессандро Маньяско.
- Третий: Конечно, это не Маньяско, это, несомненно, Антонио Канале.
Впоследствии объективными методами авторство картины было установлено, и оказалось, что один из экспертов сказал правду, другой ошибся, а третий был прав наполовину. Кто автор картины?
Принцесса и Иванушка
В этом упражнении вам необходимо найти принцессу, исходя из имеющихся данных на табличках. История такова: в поисках принцессы, похищенной Кощеем, Иванушка оказался в старинном замке. Преодолев массу препятствий, он очутился в помещении, из которого вели три двери. Иванушка знал, что за какой-то из них находится принцесса, за другой сидит тигр, а за оставшейся дверью никого нет.
Cтатистика На весь экран
Предлагаем вам также пройти упражнение, которое отлично показывает, что наш мозг может находить и понимать смысл слов, даже если его пытаются намеренно запутать. Это происходит потому, что мы читаем не по буквам и слогам, а слова целиком и кроме того, смысл слов мы понимаем благодаря соседним словам и словосочетаниям, с которыми наш мозг сталкивался раньше.
Cтатистика На весь экран
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Cтатистика На весь экран
Ксения Галанина
← Логическое мышление2 Понятие в логике →
НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Ключевые слова: логический, выражение, истина, ложь, алгебра, представление, переменная, значение, функция, инверсия, дизъюнкция, конъюнкция, таблица, очередь
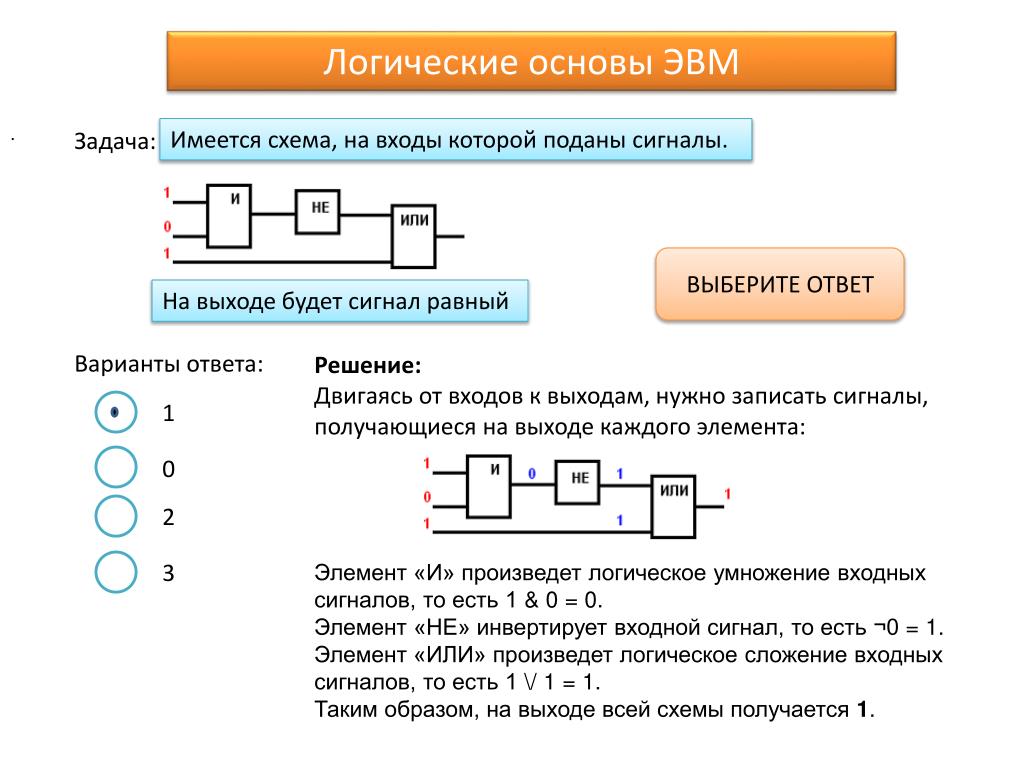
intuit.ru/2010/edi»>Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица»
. За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.intuit.ru/2010/edi»>Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
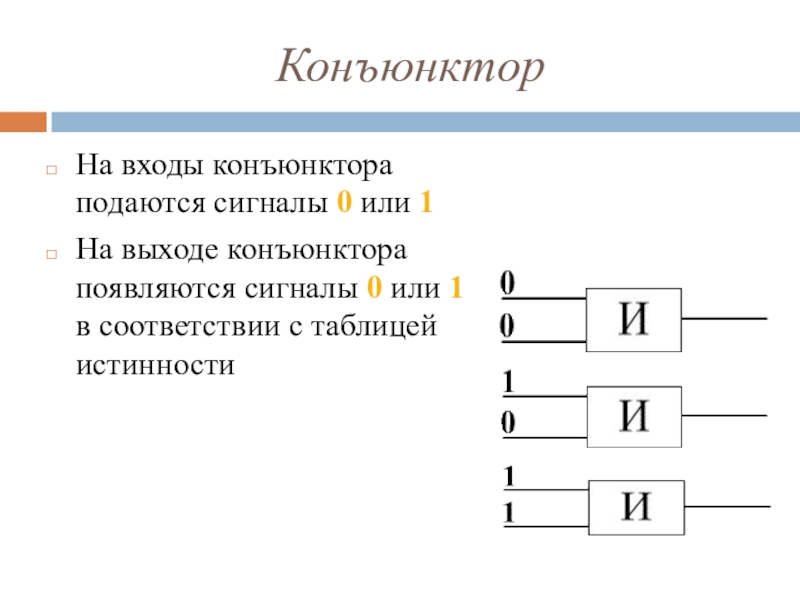
Логическое умножение (конъюнкция) — функция И
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например, ;
- на выходе схемы ( ) — такое ее состояние, когда через сопротивление R ток не протекает.
Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.
Рис. 1.1. Трёх-входовой логический элемент И
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — , и . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и , и , и . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
- либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
- либо ;
- либо — с использованием знака конъюнкции;
- либо , но при этом из контекста должно быть ясно, что между переменными , и производится логическое умножение.
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа — и . Количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или , или . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа — и . Количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или , или . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая , то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо — с использованием знака дизъюнкции.
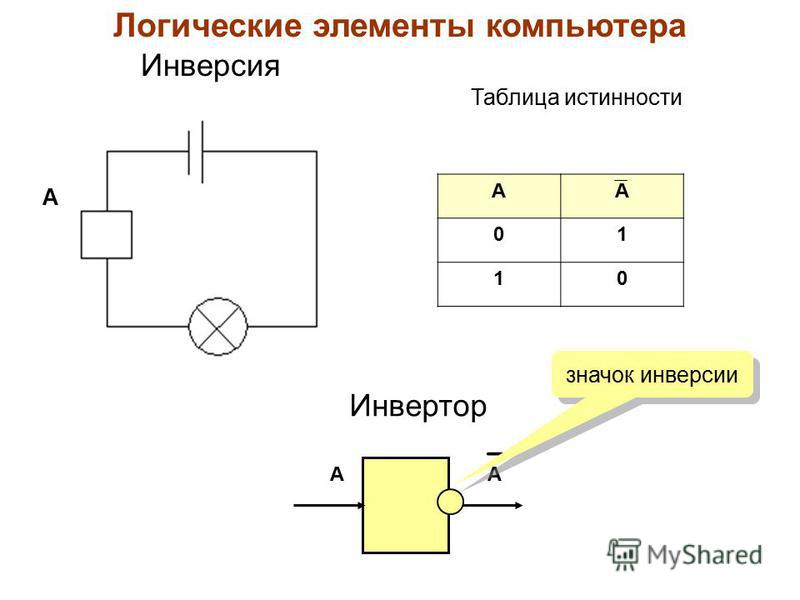
Логическое отрицание (инверсия) — функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход — . Количество вариантов для единственной логической переменной равно . Очевидно, что через сопротивление R ток протекает ( ) тогда, когда не замкнут, т.е. . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет
только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет
только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
Рис. 1.3. Логический элемент НЕ
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:
К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
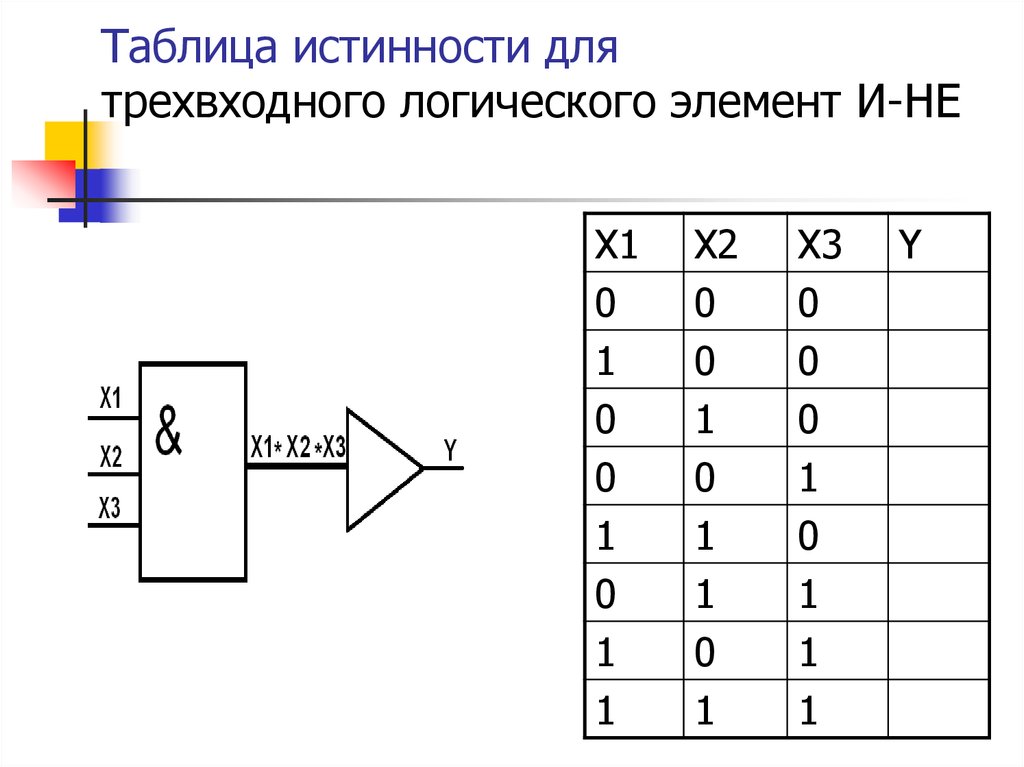
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
- либо ;
- либо ;
- либо .
Логическая функция и элемент ИЛИ-НЕ
intuit.ru/2010/edi»>В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо .
Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
Логическое определение и значение — Merriam-Webster
лог·i·кал ˈlä-ji-kəl
1
а(1)
: относящийся к, вовлекающий или соответствующий логике
логический вывод
(2)
: хорошо разбирается в логике
б
: формально истинное или достоверное : аналитическое, дедуктивное
логическое утверждение
логически мыслящий
логичность
ˌlä-jə-ka-lə-tē
существительное
логически
ˈlä-ji-k(ə-)lē
наречие
логичность
ˈlä-ji-kəl-nəs
существительное
Синонимы
- аналитический
- аналитический
- когерентный
- последовательное
- хороший
- рациональное
- разумный
- разумный
- звук
- действительный
- обоснованный
- well-grounded
Просмотреть все синонимы и антонимы в тезаурусе
Примеры предложений
Так как она помогла нам раньше, это . Логично предположить, что она нам снова поможет.
Он кажется логичным выбором для этой работы.
Она не смогла дать мне логического объяснения своему поведению.
Логично предположить, что она нам снова поможет.
Он кажется логичным выбором для этой работы.
Она не смогла дать мне логического объяснения своему поведению.
Недавние примеры в Интернете
Если проведение кампании по соблюдению правил невозможно без миллионов долларов, то следующие логический шаг будет устранять это неравенство.
— Ирина Александр, New York Times , 8 марта 2023 г.
Переход к пенсионному возрасту для социального обеспечения и других механизмов пенсионного обеспечения представляет собой логический следующий шаг. — Крис Кароса, Forbes , 7 марта 2023 г.
Ходатайство о принуждении к даче показаний, поданное прокуратурой, является логический следующий шаг в уголовном расследовании, когда прокуратура пытается заставить свидетеля или третью сторону подчиниться повестке большого жюри.
— Роберт Коста, CBS News , 23 февраля 2023 г.
Это изменение знаменует собой следующий логический шаг для BT Sport, а также более широкую трансформацию нашего потребительского бизнеса.
— Георг Салаи, The Hollywood Reporter , 21 февраля 2023 г.
Это изменение отмечает следующие логический шаг для BT Sport, а также более широкую трансформацию нашего потребительского бизнеса.
— Патрик Фратер, Variety , 21 февраля 2023 г.
Bing уже может генерировать таблицы и диаграммы для базовых данных, но преобразование их в наглядную графику для презентаций или даже для использования в Excel — логический следующий шаг.
— Крис Кароса, Forbes , 7 марта 2023 г.
Ходатайство о принуждении к даче показаний, поданное прокуратурой, является логический следующий шаг в уголовном расследовании, когда прокуратура пытается заставить свидетеля или третью сторону подчиниться повестке большого жюри.
— Роберт Коста, CBS News , 23 февраля 2023 г.
Это изменение знаменует собой следующий логический шаг для BT Sport, а также более широкую трансформацию нашего потребительского бизнеса.
— Георг Салаи, The Hollywood Reporter , 21 февраля 2023 г.
Это изменение отмечает следующие логический шаг для BT Sport, а также более широкую трансформацию нашего потребительского бизнеса.
— Патрик Фратер, Variety , 21 февраля 2023 г.
Bing уже может генерировать таблицы и диаграммы для базовых данных, но преобразование их в наглядную графику для презентаций или даже для использования в Excel — логический следующий шаг. — Том Уоррен, The Verge , 10 февраля 2023 г.
Конечно, клиенты не могли воспроизвести внешний вид дома, и линейка продуктов была следующей 9.0089 логический шаг .
— Линди Сигал, Harper’s BAZAAR , 26 января 2023 г.
Что если разделение доходов, следующий логический шаг в компенсации спортсменам, уничтожит большую часть этой сделки с правами на СМИ?
— Зак Остерман, The Indianapolis Star , 12 января 2023 г.
Узнать больше
— Том Уоррен, The Verge , 10 февраля 2023 г.
Конечно, клиенты не могли воспроизвести внешний вид дома, и линейка продуктов была следующей 9.0089 логический шаг .
— Линди Сигал, Harper’s BAZAAR , 26 января 2023 г.
Что если разделение доходов, следующий логический шаг в компенсации спортсменам, уничтожит большую часть этой сделки с правами на СМИ?
— Зак Остерман, The Indianapolis Star , 12 января 2023 г.
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «логический». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Первое известное использование
15 век, в значении, определенном в смысле 1a(1)
Путешественник во времени
Первое известное использование логический был в 15 веке
Посмотреть другие слова из того же века логика
логический
логическое следствие
Посмотреть другие записи рядом
Процитировать эту запись
Стиль
MLAЧикагоAPAMМерриам-Вебстер
«Логично». Словарь Merriam-Webster.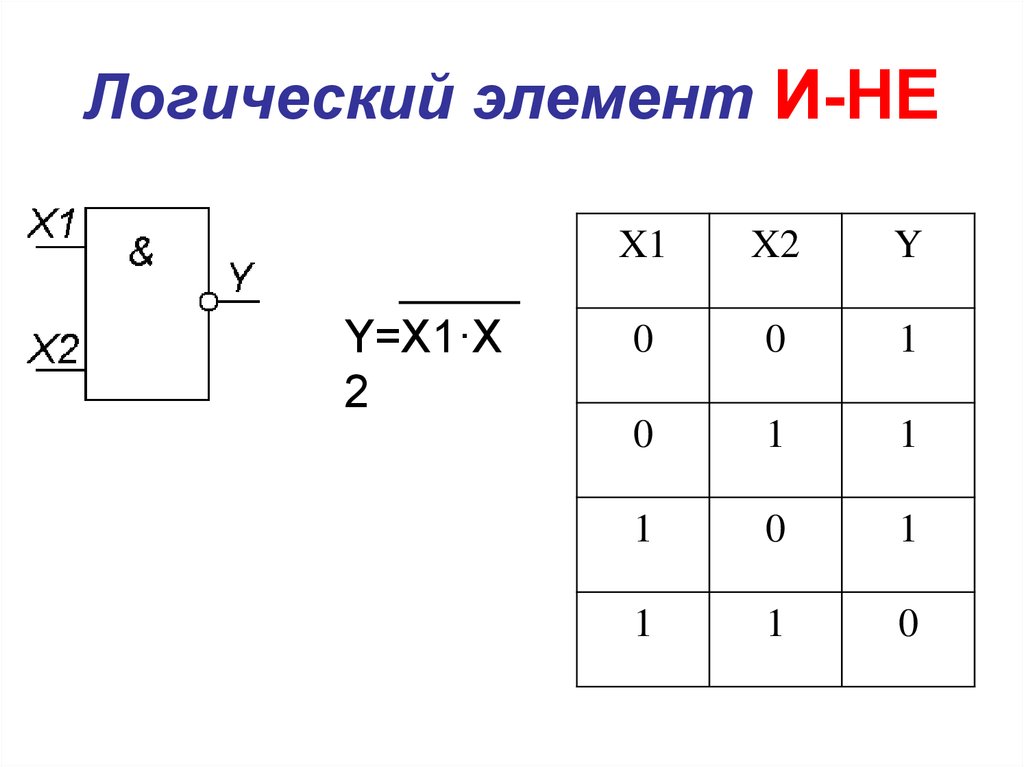 com , Merriam-Webster, https://www.merriam-webster.com/dictionary/logical. По состоянию на 10 марта 2023 г.
com , Merriam-Webster, https://www.merriam-webster.com/dictionary/logical. По состоянию на 10 марта 2023 г.
Копия цитирования
Детское определение
логическое
прилагательное
лог·i·кал ˈläj-i-kəl
1
: или относящиеся к логике : используемые в логике
2
: в соответствии с правилами логики
a логический аргумент
3
: опытный в логике
а логический мыслитель
4
: в соответствии с тем, что можно разумно ожидать
a логический результат действия
логически
-k(ə-)lē
наречие
логичность
-kəl-nəs
существительное
Еще от Merriam-Webster о
логическомНглиш: Перевод логического для говорящих на испанском языке
Britannica English: Перевод логического для говорящих на арабском языке
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
Логическое определение и значение | Словарь.com
- Основные определения
- Синонимы
- Викторина
- Связанное содержимое
- Примеры
- Британский
Показывает уровень оценки в зависимости от сложности слова.
[ loj-i-kuhl ]
/ ˈlɒdʒ ɪ kəl /
Сохранить это слово!
См. синонимы для: логично / логично на Thesaurus.com
Показывает уровень обучения в зависимости от сложности слова.
прилагательное
в соответствии или в согласии с принципами логики: логический вывод.
рассуждение в соответствии с принципами логики, как человека или разума: логическое мышление.
разумный; следовало ожидать: война была логическим следствием таких угроз.
логических или относящихся к ним.
ДРУГИЕ СЛОВА ДЛЯ логического
1, 3 действительный.
См. синонимы к слову логичный на Thesaurus.com
ПРОТИВОПОЛОЖНОСТИ К логическому
1-3 неразумный.
См. антонимы к слову логический на Thesaurus.com
ВИКТОРИНА
ВСЕ ЗА(У)Р ЭТОГО БРИТАНСКОГО ПРОТИВ. АМЕРИКАНСКИЙ АНГЛИЙСКИЙ ВИКТОРИНА
Между тем, как люди говорят по-английски в США и Великобритании, огромная разница. Способны ли ваши языковые навыки определить разницу? Давай выясним!
Вопрос 1 из 7
Правда или ложь? Британский английский и американский английский различаются только сленговыми словами.
Происхождение логического
От средневекового латинского слова logicālis, датируемого 1490–1500 гг. ; см. логику, -al 1
; см. логику, -al 1
ДРУГИЕ СЛОВА ИЗ лог. ·кал·ли, наречие·пер·лог·и·каль, прилагательноеги·пер·лог·и·кальность, существительное
гипер·пер·лог·и·кальность, сущ. кал, прилагательноене·логичность, существительноене·лог·и·кальность, существительное·вер·логичность, прилагательноео·вер·логичность, существительное·вер· лог·и·каль·и·ти, существительное пред·лог·и·каль, прилагательноеква·си-лог·и·каль, прилагательноесу·пер·лог·и·каль, прилагательноесу·пер·лог·и·каль·и· ты, существительное, непонятный, логический, прилагательное
Слова рядом логический
logging, logging stone, Logi, логия, логика, логический, логический атомизм, логическое следствие, логическая константа, логическая конструкция, логическая форма
Dictionary.com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc., 2023
Слова, относящиеся к логическому
убедительный, связный, неотразимый, последовательный, убедительный, интеллектуальный, законный, ясный, необходимый, очевидный, правдоподобный, рациональный, актуальный, разумный , действительный, мудрый, аналитический, аналитический, ясный, здравомыслящий
Как использовать логический в предложении
-
Есть также несколько логических аргументов в пользу этого.

Основные моменты Суперкубка: Bacs празднуют чемпионство, Том Брэди становится MVP|Дес Билер, Марк Маске, Чак Калпеппер|8 февраля 2021 г.|Washington Post
-
Для них модель «это просто способ понять конкретный процесс или конкретный вопрос, который нас интересует, — сказал Кучарски, — и проработка логических следствий наших предположений».
Тяжелые уроки моделирования пандемии коронавируса|Джордана Чепелевич|28 января 2021 г.|Журнал Quanta
-
В комнате с шестью выходами кажется, что наиболее логичным будет для толпы разделить поровну все шесть.
Хотите выбраться живым? Следуйте за муравьями — Выпуск 95: Побег|Конор Мирвольд|28 января 2021|Наутилус
-
Когда Шекспировский театр ушел, логичным выбором было бы придерживаться более исторической работы — оглянуться назад.
Джанет Гриффин из театра Фолджер объявляет о завершении карьеры после десятилетий преданности Шекспиру|Питер Маркс|27 января 2021 г.|Washington Post
-
наслаждаться нашей обычной деятельности гораздо раньше.
Предвидение лучших результатов для здоровья для всех|Джейсон Спарапани|26 января 2021|MIT Technology Review
-
Если следовать этой цепочке рассуждений до ее логического завершения, путь к достижению мира во всем мире состоит в том, чтобы дать всем атомные бомбы.
Санта терпит неудачу еще раз|P. Дж. О’Рурк|27 декабря 2014 г.|DAILY BEAST
-
Доведенное до логического завершения суждение «не я» может привести к тому, что мы будем считать других людей вообще не людьми!
Фергюсон, иммиграционная служба и «Мы против США». Их’|Джин Робинсон|27 ноября 2014 г.|DAILY BEAST
-
Если достоверность мудрости неопределенности сама по себе ненадежна, сила определения рушится по логическим стандартам.
Рождение романа|Ник Ромео|27 ноября 2014 г.|DAILY BEAST
-
Объявление войны ИГИЛ, таким образом, кажется логичным следующим шагом.
Рэнд Пол объявляет войну ИГИЛ и разрешает боты на земле|Оливия Нуцци|24 ноября 2014 г.
 |DAILY BEAST
|DAILY BEAST -
Если вы были эмоциональны, вы ясно видели в нем фюрера, но любой, кто был разумен и логичен воспринимался как враг.
Крестный отец правого радио|Кейтлин Диксон|23 ноября 2014 г.|DAILY BEAST
-
Педантичный, лишенный воображения и самонадеянный Теобальд был логичным выбором на роль Короля-болвана в 1728 году.
Письмо мистера Сиббера мистеру Поупу|Колли Сибберу
-
Тетя Ри была привилегированным персонажем, но ее логический метод допроса был неудобен.
Рамона|Хелен Хант Джексон
-
Вероятно, он не открыл для себя этого сознательно: результат, во всяком случае, был логичен и очевиден.
Волна|Алджернон Блэквуд
-
Логическое и тщательное обоснование содержания Декларации очевидно.
Святое наследие: жизнь Вирджинии|Дороти М. Торпи
-
Я знал, что от некоторых из них он отказался, потому что это звучало нелогично, но другие части, похоже, произвели на него впечатление.