Как рассчитать общее сопротивление параллельно соединенных резисторов. Какие особенности имеет параллельное соединение резисторов. Как изменяется общее сопротивление при параллельном подключении. Какие формулы используются для расчета параллельных резисторов.
Что такое параллельное соединение резисторов
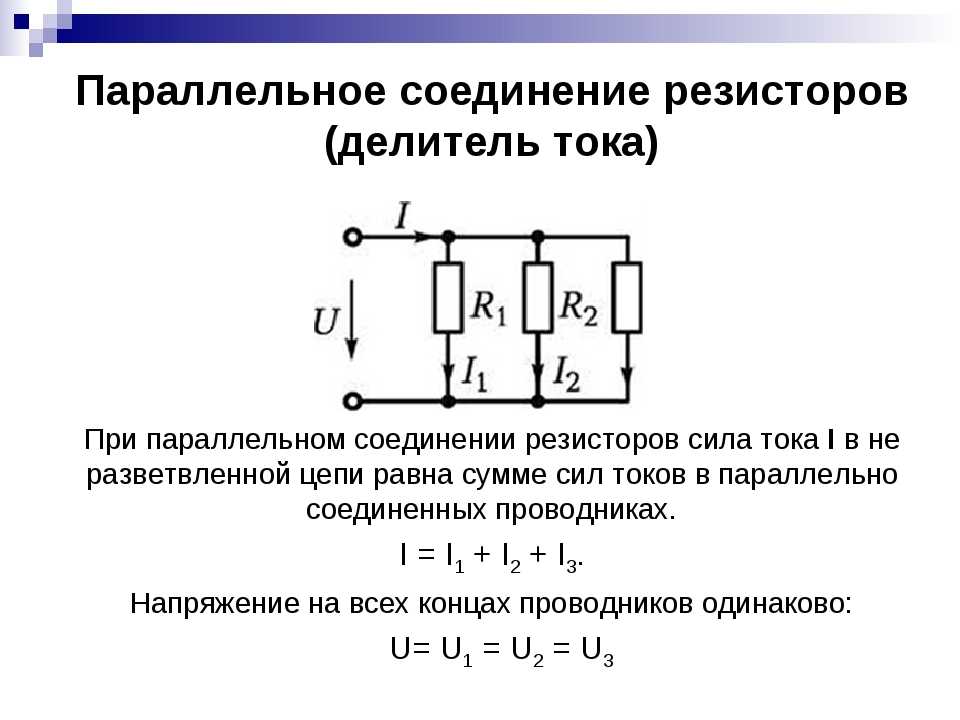
Параллельное соединение резисторов — это способ подключения, при котором все резисторы подсоединяются к одним и тем же точкам электрической цепи. При этом через каждый резистор протекает отдельный ток, а напряжение на всех резисторах одинаково.
Основные особенности параллельного соединения резисторов:
- Напряжение на всех резисторах одинаково и равно напряжению источника
- Общий ток равен сумме токов через каждый резистор
- Общее сопротивление всегда меньше сопротивления резистора с наименьшим номиналом
- Добавление параллельных ветвей уменьшает общее сопротивление
Формула для расчета параллельного соединения резисторов
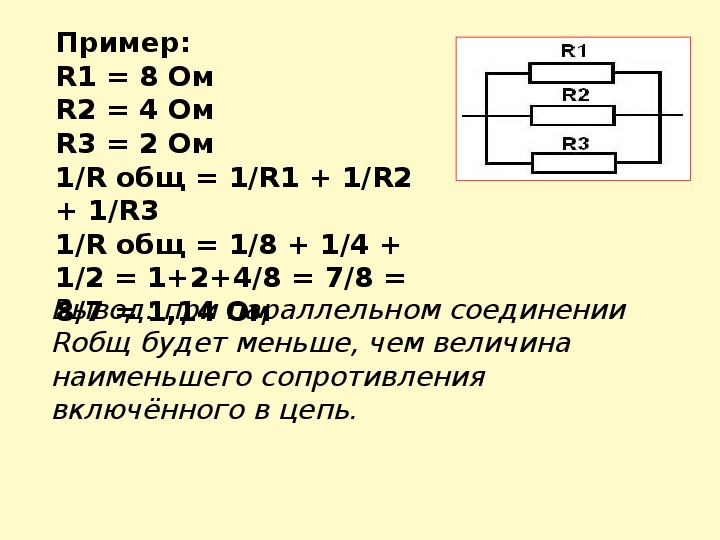
Для расчета общего сопротивления параллельно соединенных резисторов используется следующая формула:
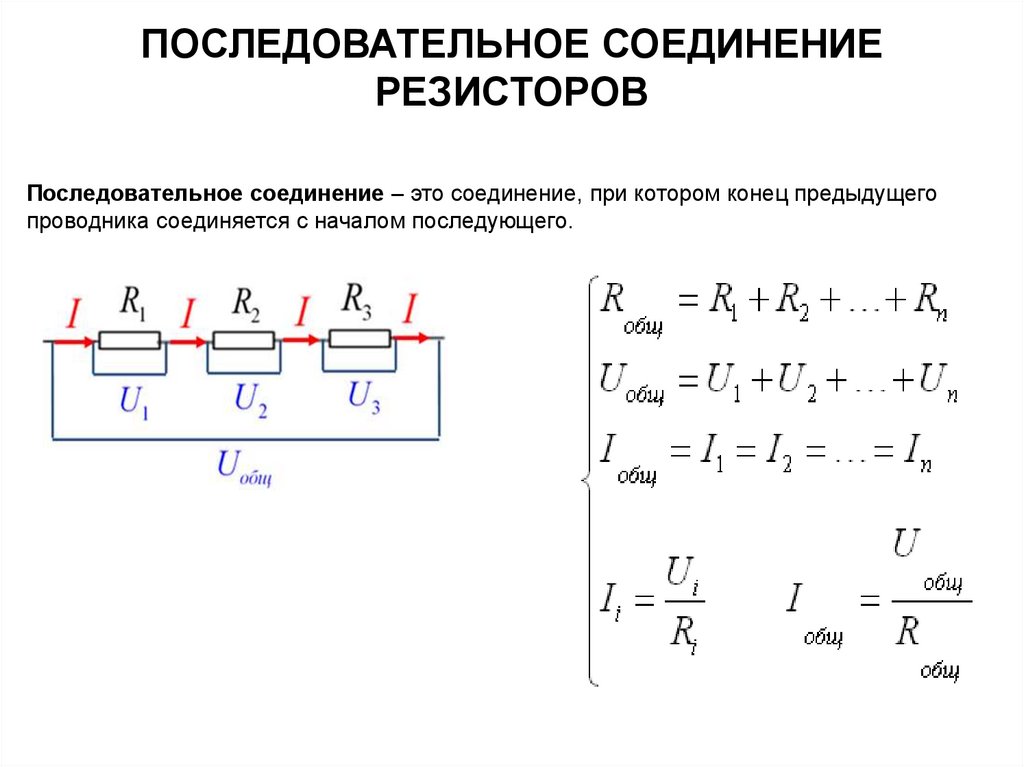
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где R — общее сопротивление, R1, R2, R3, Rn — сопротивления отдельных резисторов.
Для двух параллельных резисторов формула упрощается:
R = (R1 * R2) / (R1 + R2)
Расчет параллельного соединения двух резисторов
Рассмотрим пример расчета общего сопротивления для двух параллельно соединенных резисторов номиналом 100 Ом и 200 Ом:
- Подставляем значения в формулу: R = (100 * 200) / (100 + 200)
- Выполняем вычисления: R = 20000 / 300 = 66.67 Ом
Таким образом, общее сопротивление двух параллельных резисторов 100 Ом и 200 Ом составляет 66.67 Ом.
Особенности параллельного соединения одинаковых резисторов
При параллельном соединении нескольких одинаковых резисторов расчет можно упростить. В этом случае общее сопротивление равно:
R = R1 / n
Где R1 — номинал одного резистора, n — количество резисторов.
Например, для 4-х параллельно соединенных резисторов по 100 Ом:
R = 100 / 4 = 25 Ом
Как изменяется общее сопротивление при параллельном подключении
При параллельном соединении резисторов общее сопротивление всегда уменьшается. Это происходит потому, что добавление параллельных ветвей создает дополнительные пути для протекания тока.
Основные закономерности:
- Общее сопротивление всегда меньше сопротивления резистора с наименьшим номиналом
- Чем больше параллельных резисторов, тем меньше общее сопротивление
- При добавлении параллельной ветви уменьшение сопротивления становится все менее заметным
Преимущества и недостатки параллельного соединения резисторов
Параллельное соединение резисторов имеет как преимущества, так и недостатки:
Преимущества:
- Позволяет получить сопротивление меньше номинала имеющихся резисторов
- Обеспечивает резервирование — при выходе из строя одного резистора цепь продолжит работать
- Общее сопротивление не превышает сопротивление наименьшего резистора
Недостатки:
- Сложность точного расчета при большом количестве резисторов
- Увеличение общего тока в цепи
- Необходимость использовать резисторы с большей мощностью
Применение параллельного соединения резисторов
Параллельное соединение резисторов широко применяется в электронике и электротехнике для решения различных задач:
- Получение нестандартных номиналов сопротивлений
- Увеличение мощности резистивного элемента
- Создание делителей тока
- Обеспечение резервирования в ответственных цепях
- Создание шунтов для измерительных приборов
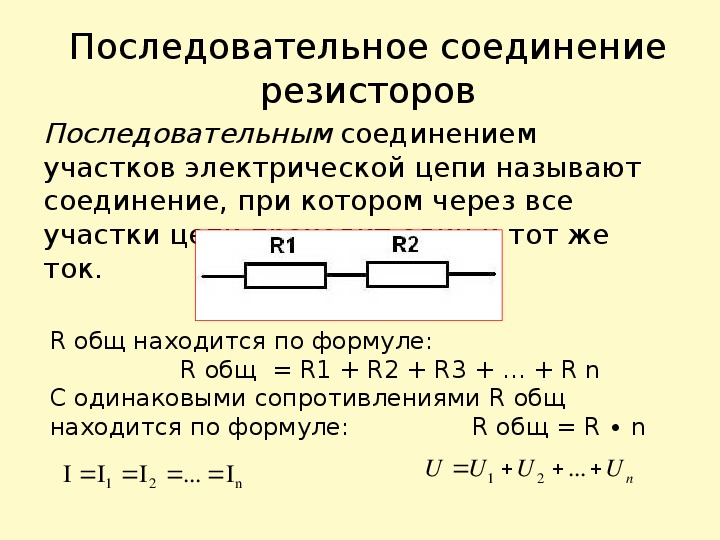
Сравнение параллельного и последовательного соединения резисторов
Параллельное и последовательное соединение резисторов имеют существенные различия:
| Параметр | Параллельное соединение | Последовательное соединение |
|---|---|---|
| Общее сопротивление | Меньше наименьшего резистора | Больше наибольшего резистора |
| Напряжение | Одинаково на всех резисторах | Сумма напряжений на резисторах |
| Ток | Сумма токов через резисторы | Одинаков для всех резисторов |
Как рассчитать токи в параллельных ветвях
Для расчета токов в параллельных ветвях можно использовать закон Ома. Зная напряжение и сопротивление каждой ветви, ток рассчитывается по формуле:
I = U / R
Где I — ток, U — напряжение, R — сопротивление ветви.
Пример расчета для двух параллельных резисторов 100 Ом и 200 Ом при напряжении 10 В:
- Ток через резистор 100 Ом: I1 = 10 / 100 = 0.1 А
- Ток через резистор 200 Ом: I2 = 10 / 200 = 0.05 А
- Общий ток: I = I1 + I2 = 0.1 + 0.05 = 0.15 А
Практические советы по использованию параллельных резисторов
При использовании параллельного соединения резисторов следует учитывать несколько практических аспектов:
- Используйте резисторы с запасом по мощности, так как общий ток увеличивается
- Для точного расчета учитывайте допуски резисторов
- При большом количестве резисторов используйте калькуляторы или программы для расчета
- Помните, что реальные резисторы имеют паразитные параметры, которые могут влиять на результат
- При высоких частотах учитывайте индуктивность соединительных проводов
Заключение
Параллельное соединение резисторов — важный способ построения электрических цепей, позволяющий решать различные практические задачи. Понимание принципов работы и методов расчета параллельных цепей необходимо для грамотного проектирования электронных устройств.
Основные моменты, которые следует помнить о параллельном соединении резисторов:
- Общее сопротивление всегда меньше сопротивления наименьшего резистора
- Напряжение на всех резисторах одинаково
- Общий ток равен сумме токов через отдельные резисторы
- Для расчета используется формула обратных величин
- При добавлении параллельных ветвей общее сопротивление уменьшается
Зная эти принципы и используя соответствующие формулы, можно эффективно применять параллельное соединение резисторов в различных электронных схемах.

Тормозные модули и резисторы
Тормозные модули и резисторы
Полное соответствие между преобразователями SINUS PENTA, тормозными модулями и резисторами
Преобразователи SINUS PENTA имеют встроенный тормозной модуль до размера S32 включительно.
Для типоразмеров от S41 до S90 поставляются внешние тормозные модули.
Santerno поставляет также полный спектр тормозных резисторов для любых применений.
Конфигурации
Встроенный тормозной модуль в преобразователях SINUS PENTA S05-S32
Все SINUS PENTA до размера S32 имеют встроенный тормозной модуль
BU200 для S60
BU200 – это специальный тормозной модуль для преобразователей размера S60
(BU200 может также использоваться вместо BU700 для преобразователей размеров S41-S51)
BU700 2T-4T для S41-S51 – BU600 5T-6T для S42-S52
BU700 – это специальный тормозной модуль для преобразователей класса 2T-4T размеров S41-S51
BU600 – это специальный тормозной модуль для преобразователей класса 5T-6T размеров S42-S52
BU1440 для модульных преобразователей размеров S65-S90
BU1440 – это тормозной модуль для всех модульных преобразователей размеров S65, S70, S75, S80, S90
Тип подключения
А – Один резистор
B – Два и более параллельно включенных резисторов
C – Два последовательно включенных резистора
D – Четыре резистора (параллельное включение двух цепочек по два последовательно включенных резистора)
E – Шесть резисторов (параллельное включение трех цепочек по два последовательно включенных резистора)
F – Восемь резисторов (параллельное включение четырех цепочек по два последовательно включенных резистора)
MD – Два блока, каждый из которых содержит тормозной модуль и четыре резистора (параллельное включение двух цепочек по два последовательно включенных резистора)
ME – Два блока, каждый из которых содержит тормозной модуль и шесть резисторов (параллельное включение трех цепочек по два последовательно включенных резистора)
MF – Два блока, каждый из которых содержит тормозной модуль и восемь резисторов (параллельное включение четырех цепочек по два последовательно включенных резистора)
MG – Два блока, каждый из которых содержит тормозной модуль и десять резисторов (параллельное включение пяти цепочек по два последовательно включенных резистора)
MH – Два блока, каждый из которых содержит тормозной модуль и двенадцать резисторов (параллельное включение шести цепочек по два последовательно включенных резистора)
O – Четыре блока, каждый из которых содержит тормозной модуль и тормозной резистор
P – Пять блоков, каждый из которых содержит тормозной модуль и тормозной резистор
Q – Шесть блоков, каждый из которых содержит тормозной модуль и тормозной резистор
R – Семь блоков, каждый из которых содержит тормозной модуль и тормозной резистор
S – Восемь блоков, каждый из которых содержит тормозной модуль и тормозной резистор
V – Два блока, каждый из которых содержит тормозной модуль и два параллельно включенных резистора
X – Три блока, каждый из которых содержит тормозной модуль и два параллельно включенных резистора
Y – Четыре блока, каждый из которых содержит тормозной модуль и два параллельно включенных резистора
W – Пять блоков, каждый из которых содержит тормозной модуль и два параллельно включенных резистора
Z – Шесть блоков, каждый из которых содержит тормозной модуль и два параллельно включенных резистора
ЗАГРУЗКИ
Каталог — Аксессуары
Что такое резистор
Что такое резистор и расчет резистора.
- Что такое резистор
- Закон Ома
- Резисторы параллельно
- Резисторы последовательно
- Размеры и материал влияет
- Изображение резистора
- Обозначения резисторов
- Цветовой код резистора
- Типы резисторов
Что такое резистор
Резистор — это электрический компонент, который снижает электрический ток.
Способность резистора уменьшать ток называется сопротивлением и измеряется в омах (обозначение: Ω).
Если провести аналогию с потоком воды по трубам, резистор представляет собой тонкую трубку, которая уменьшает поток воды.
Закон Ома
Ток резистора I в амперах (А) равен напряжению резистора V в вольтах (В).
деленное на сопротивление R в омах (Ом):
Потребляемая мощность резистора P в ваттах (Вт) равна току резистора I в амперах (A).
умноженное на напряжение резистора V в вольтах (В):
P = I × V
Потребляемая мощность резистора P в ваттах (Вт) равна квадрату силы тока резистора I в амперах (A).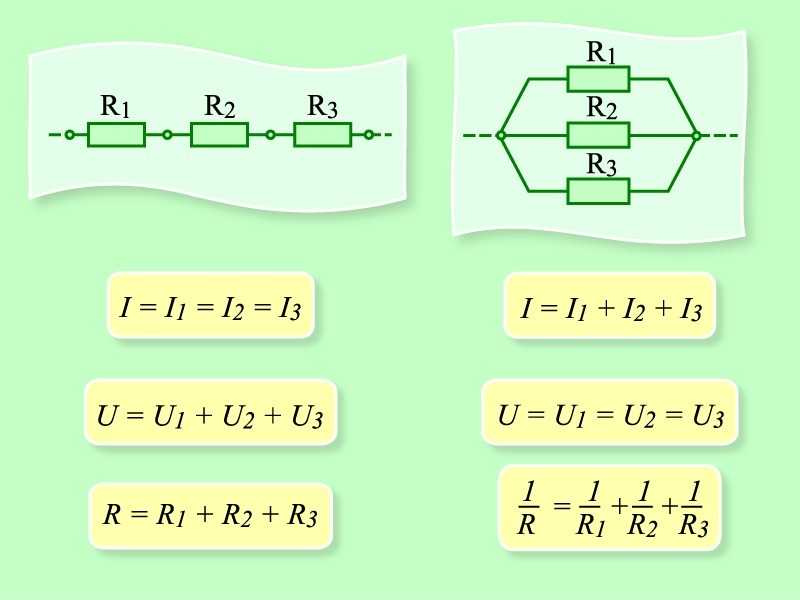
умноженное на сопротивление резистора R в омах (Ом):
P = I 2 × R
Потребляемая мощность резистора P в ваттах (Вт) равна квадрату напряжения резистора V в вольтах (В).
деленное на сопротивление резистора R в омах (Ом):
P = V 2 / R
Резисторы параллельно
Общее эквивалентное сопротивление резисторов, включенных параллельно R Total , определяется как:
Поэтому, когда вы добавляете резисторы параллельно, общее сопротивление уменьшается.
Резисторы последовательно
Общее эквивалентное сопротивление резисторов в серии R total является суммой значений сопротивлений:
R всего = R 1 + R 2 + R 3 + …
Поэтому, когда вы добавляете резисторы последовательно, общее сопротивление увеличивается.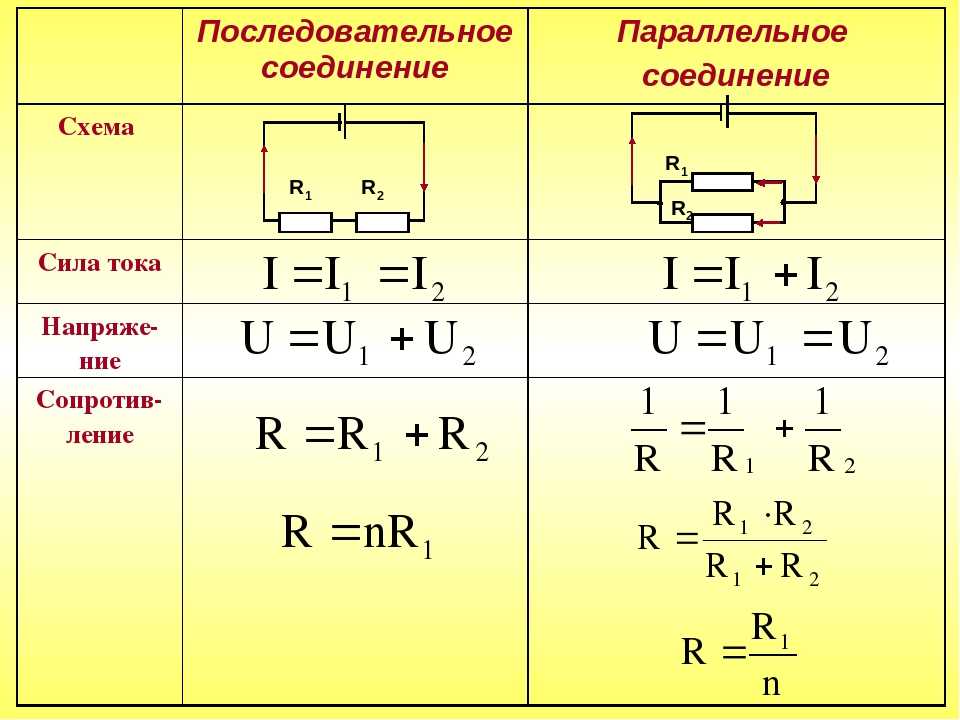
Размеры и материал влияет
Сопротивление резистора R в Ом (Ом) равно удельному сопротивлению ρ в Ом-метрах (Ом ∙ м), умноженному на длину резистора l в метрах (м), деленному на площадь поперечного сечения резистора A в квадратных метрах (м 2. ):
Изображение резистора
Обозначения резисторов
| Резистор (IEEE) | Резистор снижает ток. | |
| Резистор (IEC) | ||
| Потенциометр (IEEE) | Регулируемый резистор — имеет 3 вывода. | |
| Потенциометр (IEC) | ||
| Переменный резистор / реостат (IEEE) | Регулируемый резистор — имеет 2 вывода. | |
| Переменный резистор / реостат (IEC) | ||
| Подстроечный резистор | Пресест резистор | |
| Термистор | Терморезистор — изменение сопротивления при изменении температуры | |
| Фоторезистор / светозависимый резистор (LDR) | Изменяет сопротивление в зависимости от света |
Цветовой код резистора
Сопротивление резистора и его допуски отмечены на резисторе полосами цветного кода, которые обозначают значение сопротивления.
Есть 3 типа цветовых кодов:
- 4 полосы: цифра, цифра, множитель, допуск.
- 5 полос: цифра, цифра, цифра, множитель, допуск.
- 6 диапазонов: цифра, цифра, цифра, множитель, допуск, температурный коэффициент.
Расчет сопротивления 4-х полосного резистора
R = (10 × цифра 1 + цифра 2 ) × множитель
Расчет сопротивления 5-ти или 6-ти полосного резистора
R = (100 × цифра 1 + 10 × цифра 2 + цифра 3 ) × множитель
Типы резисторов
| Переменный резистор | Переменный резистор имеет регулируемое сопротивление (2 клеммы) |
| Потенциометр | Потенциометр имеет регулируемое сопротивление (3 клеммы) |
| Фоторезистор | Снижает сопротивление при воздействии света |
| Силовой резистор | Силовой резистор применяется в цепях большой мощности и имеет большие габариты. |
| Поверхностный монтаж (SMT / SMD) резистор |
Резисторы SMT / SMD имеют небольшие габариты. Резисторы устанавливаются на печатную плату (PCB), этот метод быстрый и требует небольшой площади платы. |
| Сеть резисторов | Сеть резисторов — это микросхема, содержащая несколько резисторов с одинаковыми или разными номиналами. |
| Углеродный резистор | |
| Чип резистор | |
| Металлооксидный резистор | |
| Керамический резистор |
Подтягивающий резистор
В цифровых схемах подтягивающий резистор — это обычный резистор, который подключен к источнику высокого напряжения (например, + 5 В или + 12 В) и устанавливает уровень входа или выхода устройства на «1».
Подтягивающий резистор устанавливает уровень на «1», когда вход / выход отключен. Когда вход / выход подключен, уровень определяется устройством и отменяет подтягивающий резистор.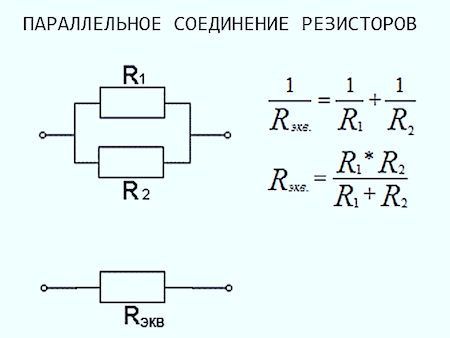
Понижающий резистор
В цифровых схемах понижающий резистор — это обычный резистор, который подключен к земле (0 В) и устанавливает уровень входа или выхода устройства на «0».
Понижающий резистор устанавливает уровень на «0», когда вход / выход отключен. Когда вход / выход подключен, уровень определяется устройством и перекрывает понижающий резистор.
Электрическое сопротивление ►
Смотрите также
- Электрическое сопротивление
- Обозначения резисторов
- Ом
- Закон Ома
- Конденсатор
- Катушка индуктивности
Параллельные резисторы — Справочник по электронике
Резистор — это пассивный компонент с двумя выводами, который вносит определенное электрическое сопротивление в цепь. Они используются практически во всех схемах мира и в различных конфигурациях. ‘ Параллельные резисторы ’ относится к конфигурации, когда ток может проходить одновременно по нескольким цепям, содержащим резисторы .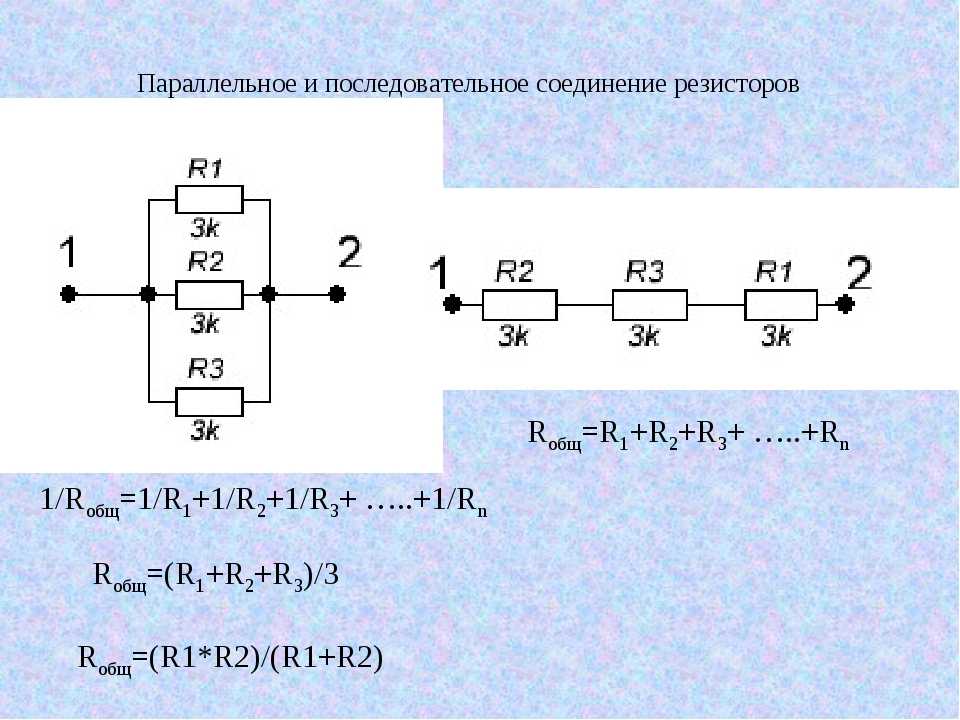 Это также обычно называют конфигурацией параллельного резистора.
Это также обычно называют конфигурацией параллельного резистора.
Резисторы могут быть соединены последовательно, параллельно или в комбинации последовательно и параллельно.
Когда резисторы подключены параллельно, они уменьшают общее эквивалентное сопротивление ниже значения резистора с наименьшим номиналом.
Большинство цепей являются сложными и имеют как последовательные, так и параллельные участки. Параллельная конфигурация означает, что электрический ток проходит по цепи более чем по одному пути. Эти пути обычно называют ветвями .
Величина тока, протекающего через каждую ветвь, определяется сопротивлением каждой ветви. Через ветвь с более высоким сопротивлением будет протекать меньший ток, чем через ветвь с меньшим сопротивлением.
В то же время, чем больше ответвлений, тем больше общий ток. Когда к цепи добавляются новые ответвления, общее эквивалентное сопротивление параллельной цепи уменьшается, даже если все ответвления имеют одинаковое сопротивление. Это приводит к увеличению общего тока через систему.
Это приводит к увеличению общего тока через систему.
Если использовать аналогию с водой, протекающей по трубе, то если бы мы добавили вторую трубу, сопротивление потоку воды уменьшилось бы, и благодаря второй трубе через систему прошло бы больше воды.
Оказывается, электрический ток течет по проводникам примерно так же, как вода по трубам. Более параллельные ответвления уменьшают общее сопротивление системы и тем самым увеличивают ток через всю систему.
Формула эквивалентного сопротивления для резисторов, включенных параллельно: 9{-1}
Содержание – Резисторы, включенные параллельно
В нашем последнем уроке мы рассматривали последовательное соединение резисторов. Изучая резисторы параллельно, мы можем анализировать влияние резистивных компонентов в более сложных схемах.
Обзор резисторов в серии
Это может показаться небольшим изменением, но резисторы, соединенные последовательно, имеют совсем другое эквивалентное сопротивление, чем те же резисторы, соединенные параллельно.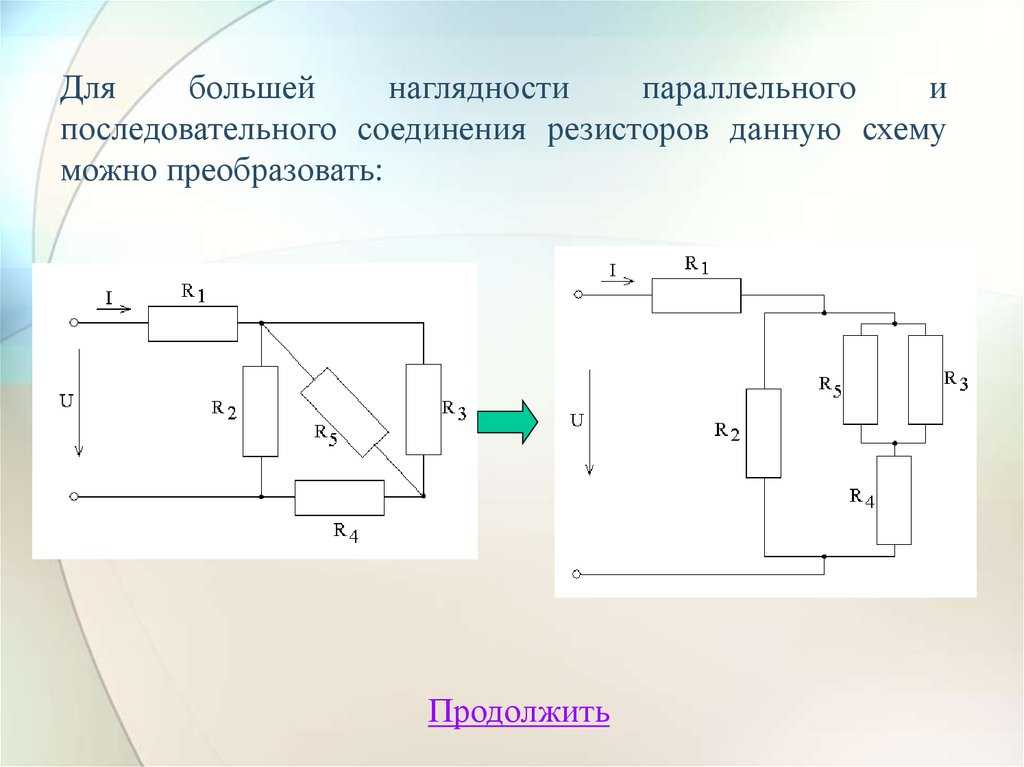
В последовательной цепи общее сопротивление просто добавляет:
R_{TSeries} = R_1 + R_2 + R_3 +...+ R_N R 1 представляет сопротивление резистора R 1 ; R2 представляет собой сопротивление резистора R2 и так далее. Общее эквивалентное сопротивление последовательной цепи обозначается R Tсерия , которое равно сумме номиналов всех резисторов, включенных последовательно.
Суммарный ток в последовательной цепи зависит от R Tseries и определяется законом Ома:
I = \frac{V}{R_{TSeries}} Параллельные резисторы
Напряжение
Рассмотрим схему с двумя параллельными резисторами. R 1 и R 2 расположены параллельно друг другу. Наш источник напряжения — это батарея, которая обеспечивает 1,5 Вольта. R 1 и R 2 подключаются непосредственно к клеммам аккумулятора. Если бы мы измерили напряжение на любом из резисторов, мы бы обнаружили, что падение напряжения на обоих резисторах составляет 1,5 В. Это имеет смысл, потому что они оба подключены непосредственно к клеммам аккумулятора.
Это имеет смысл, потому что они оба подключены непосредственно к клеммам аккумулятора.
Сразу видно, что оба пути тока имеют одинаковое напряжение .
Давайте внесем ясность в нашу дискуссию, внимательно изучив напряжение как в последовательных, так и в параллельных цепях. Как и в последовательной цепи, напряжение батареи определяет общее напряжение в цепи. В последовательной цепи напряжение равно сумме напряжений каждого компонента:
V_Tseries = V_1 + V_2 + V_3 + ...+V_N
В параллельной цепи падение напряжения на каждом пути равно общему приложенному напряжению. Мы можем использовать этот факт для расчета общего тока и тока в каждом пути.
V_Tparallel = V_1 = V_2 = V_3 = V_N
Ток
Что насчет тока? В последовательной цепи был только один путь прохождения тока. Поскольку ток определяется сопротивлением каждого пути, последовательная цепь имеет только одно значение тока, и оно одинаково для всех компонентов в этой цепи.
I_{Tseries}= I_1=I_2= \frac{V_T}{R_T} В параллельной цепи теперь есть несколько путей прохождения тока. На приведенной выше схеме ток может течь от положительной клеммы батареи через резистор R 9.0045 1 или R 2 . На этот раз у течения есть выбор. Если сопротивления путей различны, ток будет разным для каждого пути .
Однако общий ток во всей цепи по-прежнему определяется общим сопротивлением цепи. Как и в случае с последовательными цепями, мы можем объединить вклады резисторов, чтобы найти общее сопротивление цепи. Мы назовем это эквивалентным сопротивлением или R eq 9.0046 . Если мы сможем найти Req, мы сможем использовать закон Ома, чтобы найти ток в цепи. Начнем с определения полного тока I T как суммы токов от каждого из двух путей:
I_T = I_1 + I_2
Где I 1 — это ток через R 1 и I 2 — ток через R 2 . Общий ток в цепи — это просто сумма токов в каждом пути.
В параллельной цепи есть несколько путей прохождения тока. Каждый путь может иметь различный ток, в зависимости от сопротивления этого пути. Общий ток представляет собой сумму токов для каждого пути.
Из закона Ома мы знаем, что ток по каждому пути будет определяться напряжением и сопротивлением на этом пути. Мы также знаем, что ток во всей цепи зависит от закона Ома с использованием R eq . как эквивалентное напряжение для цепи. На этот раз напряжение на каждом пути одинаковое:
I_1 =\frac{V_{источник}}{R_1},I_2=\frac{V_{источник}}{R_2}, I_T =\frac{V_{источник }}{R_{eq}} Воспользуемся для нахождения полного эквивалентного сопротивления. 9{-1}
В этом случае мы предполагаем, что каждая ветвь либо имеет только один резистор, и мы обозначаем общее сопротивление этой ветви как R 1 , R 2 или R 3 . Если ветвь имеет более одного резистора, то сопротивление ветви добавляется, как и в последовательной цепи. R 1 , R 2 и R 3 представляют общее комбинированное сопротивление каждой ветви.
R 1 , R 2 и R 3 представляют общее комбинированное сопротивление каждой ветви.
Также находим интересный факт:
Параллельно общее сопротивление часто менее сопротивления каждого компонента. Более параллельные пути тока уменьшают общее сопротивление.
Пример 1. Два резистора, включенных параллельно
Рис. 1. Два резистора, включенных параллельноДавайте ответим на следующие вопросы для приведенной выше схемы:
1) Каково общее сопротивление цепи?
Чтобы найти полное сопротивление, мы можем использовать формулу, используя обратную величину сопротивления.
R_T = \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}} = \frac{1}{\frac{1}{5 \Omega}+\frac{1 }{10 \Омега}} = 3,33 \Омега В качестве двойной проверки мы подтверждаем, что общее сопротивление меньше, чем сопротивление любого пути тока.
2) Какова сила тока в каждой цепи и во всей цепи?
Чтобы найти ток в цепи, сначала мы должны найти ток для каждого пути, а затем просуммировать ток в каждом пути. Имейте в виду, что падение напряжения одинаково во всех параллельных цепях тока.
Имейте в виду, что падение напряжения одинаково во всех параллельных цепях тока.
I_1 = \frac{V_1}{R_1} = \frac{1.5V}{5\Omega}=.3A I_2 = \frac{V_2}{R_2} = \frac{1.5V}{10 \Omega } = 0,15 А 92}{3,33} = 0,675 Вт Пример 2. Три резистора, соединенных параллельно
Добавим в нашу схему третий резистор. Мы увидим, что добавление третьего резистора изменит наше общее сопротивление, общий ток и общую рассеиваемую мощность. Напряжение на каждом пути такое же, как напряжение батареи.
1) Каково общее сопротивление цепи?
На этот раз нам нужно рассмотреть три резистора.
R_T = \frac{1}{\frac{1}{R_1}+\frac{1}{R_2} + \frac{1}{R_3}} = \frac{1}{\frac{1}{ 5 \Omega}+\frac{1}{10 \Omega}+\frac{1}{12\Omega}} = 2,61\Omega 2) Какова сила тока в каждой цепи и во всей цепи?
Как и в первом примере, мы можем найти общий ток, просуммировав ток каждого пути.
I_1 = \frac{V_1}{R_1} = \frac{1.5V}{5\Omega} = .3A I_2 = \frac{V_2}{R_2} = \frac{1. 5V}{10\Omega } = 0,15 А
5V}{10\Omega } = 0,15 А Для первых двух резисторов схема идентична схеме из первого примера. Теперь, когда у нас есть третий резистор, мы также должны добавить ток с этого пути. Третий резистор изменит общий ток в цепи. 92(12\Омега) = 0,1875 Вт
P_T = P_1 + P_2 + P_3 = 0,45 Вт + 0,225 Вт + 0,1875 Вт = 0,8625 Вт
4) Как добавление третьего резистора изменило схему?
Добавление третьего резистора уменьшило общее сопротивление цепи с 3,33 Ом до 2,61 Ом.
Общий ток увеличен с 0,45 до 0,575 ампер.
Общая рассеиваемая мощность увеличена с 0,645 Вт до 0,8625 Вт.
Урок 0 : Введение в Модуль 3
Урок 1 : Введение в цепи постоянного тока
Урок 2 : серии и параллельные схемы
Урок 3 : DC Power Sources and Anductors
Урок 4 : Резисторы, конденсации и индукторы
4 Урок 5: Резисторы, включенные последовательно
Урок 6: Резисторы, включенные параллельно
Урок 7: Делители напряжения
Урок 8: Закон тока Кирхгофа
Урок 9: Закон о напряжениях Кирхоффа
Урок 10: Конденсаторы
Урок 11: Диэлектрические материалы
Урок 12: Конденсаторы в паралле
Урок 13: Казин в серии в паралле
. Урок 14: Конденсаторы в последовательном и параллельном соединении
Урок 14: Конденсаторы в последовательном и параллельном соединении
Компоненты электроники: Соединение резисторов в последовательном и параллельном соединении
Существует два основных способа соединения резисторов в электронной схеме: последовательно (натянуты встык) и параллельно (бок о бок). ). Ниже объясняется, как рассчитать общее сопротивление сети резисторов, соединенных последовательно и параллельно.
Вам нужно будет напрячь свои мыслительные способности, когда будете выполнять математические расчеты, необходимые для расчета параллельных резисторов. Математика не очень сложная, но и не тривиальная.
Соединить резисторы последовательно
Рассчитать общее сопротивление для двух или более резисторов, соединенных встык, т. е. последовательно, очень просто: нужно просто сложить значения сопротивления, чтобы получить общее сопротивление.
Например, если вам нужно сопротивление 1100 Ом и вы не можете найти резистор на 1100 Ом, вы можете последовательно соединить резистор на 1000 Ом и резистор на 100 Ом.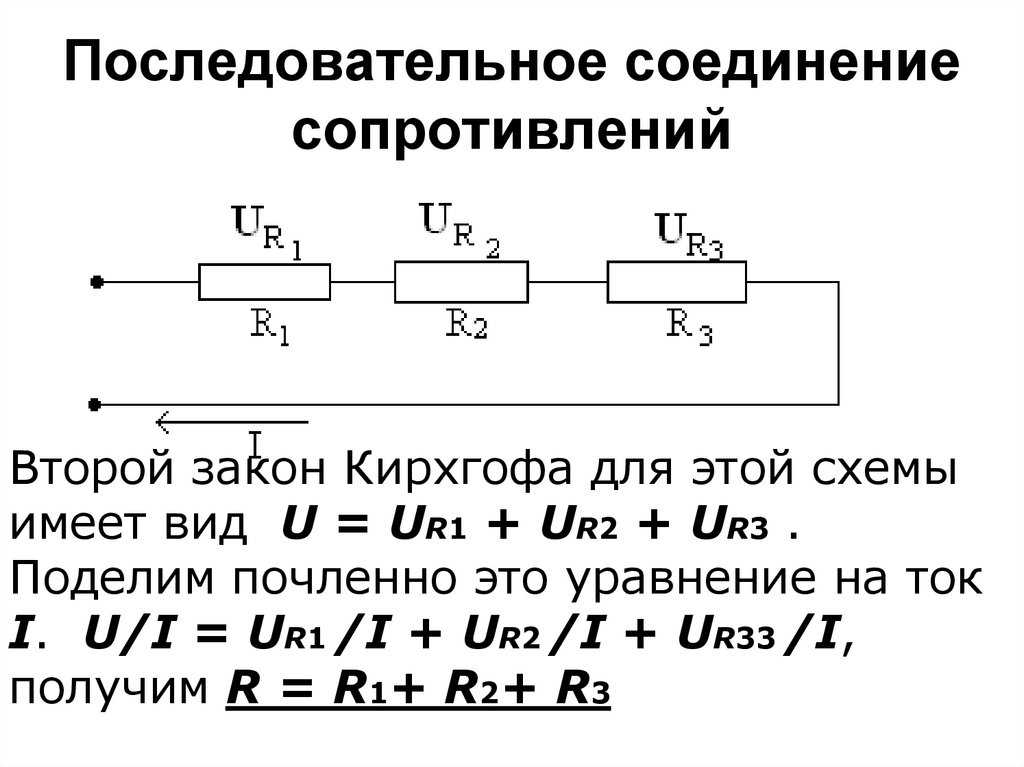 Сложив эти два сопротивления, вы получите общее сопротивление 1100 Ом.
Сложив эти два сопротивления, вы получите общее сопротивление 1100 Ом.
При желании вы можете подключить более двух резисторов последовательно. Вы просто продолжаете складывать все сопротивления, чтобы получить общее значение сопротивления. Например, если вам нужно сопротивление 1800 Ом, вы можете использовать последовательно резистор на 1 кОм и восемь резисторов на 100 Ом.
Здесь две цепи имеют одинаковое сопротивление. Схема слева выполняет работу с одним резистором; схема справа делает это с тремя. Таким образом, схемы эквивалентны.
Каждый раз, когда вы видите два или более резистора, соединенных последовательно в цепи, вы можете заменить один резистор, номинал которого представляет собой сумму отдельных резисторов. Точно так же каждый раз, когда вы видите один резистор в цепи, вы можете заменить два или более резисторов последовательно, если их значения в сумме соответствуют желаемому значению.
Общее сопротивление последовательно соединенных резисторов всегда больше, чем сопротивление любого из резисторов в отдельности. Это потому, что каждый резистор добавляет свое собственное сопротивление к общему.
Это потому, что каждый резистор добавляет свое собственное сопротивление к общему.
Соединить резисторы параллельно
Вы также можете соединить резисторы параллельно, чтобы создать эквивалентные сопротивления. Однако расчет общего сопротивления для резисторов, соединенных параллельно, немного сложнее, чем расчет сопротивления для резисторов, соединенных последовательно.
При параллельном соединении двух резисторов ток может протекать через оба резистора одновременно. Хотя каждый резистор выполняет свою работу по сдерживанию тока, общее сопротивление двух параллельно соединенных резисторов всегда меньше, чем сопротивление любого из резисторов, потому что ток проходит двумя путями.
Итак, как рассчитать общее сопротивление для резисторов, включенных параллельно? Очень осторожно. Вот правила:
-
Первый, самый простой случай: Параллельные резисторы одинакового номинала. В этом случае вы можете рассчитать общее сопротивление, разделив значение одного из отдельных резисторов на количество резисторов, включенных параллельно.
 Например, общее сопротивление двух параллельно соединенных резисторов по 1 кОм составляет 500 Ом, а общее сопротивление четырех резисторов по 1 кОм составляет 250 Ом.
Например, общее сопротивление двух параллельно соединенных резисторов по 1 кОм составляет 500 Ом, а общее сопротивление четырех резисторов по 1 кОм составляет 250 Ом. К сожалению, это единственный простой случай. Математика, когда резисторы, соединенные параллельно, имеют неравные значения, более сложна.
-
Если используются только два резистора разных номиналов, расчет не так уж плох:
В этой формуле R1 и R2 — номиналы двух резисторов.
Вот пример, основанный на параллельном соединении резисторов 2 кОм и 3 кОм:
-
Для трех и более резисторов, включенных параллельно, расчет начинает выглядеть как ракетостроение:
Точки в конце выражения означают, что вы продолжаете складывать обратные величины сопротивлений для всех имеющихся у вас резисторов.
В случае, если вы достаточно сумасшедший, чтобы действительно хотеть заниматься такой математикой, вот пример для трех резисторов номиналами 2 кОм, 4 кОм и 8 кОм:
Как видите, окончательный результат равен 1 142,857 Ом.