Что представляет собой магнитное поле Земли. Каковы его основные параметры и характеристики. Как образуется магнитное поле нашей планеты. Какую роль играет магнитосфера для жизни на Земле. Как изменяется магнитное поле со временем.
Что такое магнитное поле Земли и каковы его основные характеристики
Магнитное поле Земли — это область вокруг нашей планеты, в которой действуют магнитные силы. Оно простирается на десятки тысяч километров в космическое пространство и образует магнитосферу Земли.
Основные характеристики геомагнитного поля:
- Напряженность на поверхности Земли составляет от 25 до 65 мкТл (микротесла)
- Магнитные полюса не совпадают с географическими и смещены на сотни километров
- Северный магнитный полюс находится в Южном полушарии, а южный — в Северном
- Ось магнитного диполя наклонена примерно на 11° к оси вращения Земли
- Конфигурация поля близка к полю магнитного диполя, помещенного в центр планеты
Магнитное поле Земли не является постоянным — оно медленно изменяется со временем. Это явление называется вековыми вариациями геомагнитного поля.

Как возникает магнитное поле нашей планеты
Существование магнитного поля Земли обусловлено процессами, происходящими в ее жидком внешнем ядре. Согласно современным представлениям, основной механизм генерации геомагнитного поля связан с конвекцией электропроводящего вещества во внешнем ядре планеты.
Ключевые факторы образования магнитного поля Земли:
- Вращение планеты вокруг своей оси
- Конвективные течения в жидком внешнем ядре
- Высокая электропроводность вещества ядра
- Эффект динамо — самоподдерживающийся механизм генерации магнитного поля
Конвекция в ядре создает упорядоченные течения проводящей жидкости, которые при взаимодействии с вращением планеты порождают электрические токи. Эти токи, в свою очередь, генерируют магнитное поле.
Какую роль играет магнитосфера для жизни на Земле
Магнитное поле Земли выполняет важнейшую защитную функцию для нашей планеты и жизни на ней. Основные аспекты влияния магнитосферы:
- Защита от космической радиации и солнечного ветра
- Удержание атмосферы от рассеивания в космическое пространство
- Формирование радиационных поясов Ван Аллена
- Влияние на миграцию и навигацию некоторых видов животных
- Образование полярных сияний
Без магнитного поля жизнь на Земле в ее нынешнем виде была бы невозможна. Магнитосфера отклоняет большую часть заряженных частиц солнечного ветра, предотвращая разрушение озонового слоя и защищая биосферу от губительного космического излучения.

Как изменяется магнитное поле Земли со временем
Геомагнитное поле нашей планеты не является постоянным — оно медленно эволюционирует с течением времени. Основные типы изменений магнитного поля Земли:
- Вековые вариации — медленные изменения в масштабе десятилетий и столетий
- Инверсии — полное обращение магнитных полюсов местами
- Экскурсы — кратковременные резкие изменения конфигурации поля
- Джерки — резкие изменения скорости вековых вариаций
В настоящее время наблюдается постепенное ослабление магнитного поля Земли. За последние 200 лет его напряженность уменьшилась примерно на 10%. Некоторые ученые полагают, что это может быть признаком подготовки к очередной инверсии магнитного поля планеты.
Методы изучения и измерения геомагнитного поля
Для исследования магнитного поля Земли используется целый комплекс различных методов:
- Наземные магнитные обсерватории
- Аэромагнитная и морская магнитная съемка
- Спутниковые магнитные измерения
- Палеомагнитные исследования горных пород
- Археомагнитные измерения древних артефактов
Современные спутники позволяют проводить высокоточные измерения магнитного поля на разных высотах и составлять детальные карты его распределения. Палеомагнитные данные дают информацию об эволюции поля на протяжении миллионов лет.

Влияние магнитных бурь на земную магнитосферу
Магнитные бури — это кратковременные возмущения магнитного поля Земли, вызванные взаимодействием магнитосферы с потоками солнечного ветра и корональными выбросами массы. Основные эффекты магнитных бурь:
- Усиление электрических токов в магнитосфере и ионосфере
- Изменение формы магнитосферы
- Ускорение частиц в радиационных поясах
- Генерация геомагнитно-индуцированных токов на поверхности Земли
- Усиление полярных сияний
Сильные магнитные бури могут оказывать влияние на работу спутников, энергетических и навигационных систем. Изучение динамики магнитных бурь важно для прогнозирования космической погоды и обеспечения безопасности технологической инфраструктуры.
Применение знаний о магнитном поле Земли
Понимание структуры и динамики геомагнитного поля имеет важное практическое значение во многих областях:
- Навигация и ориентирование
- Геологоразведка и поиск полезных ископаемых
- Прогнозирование космической погоды
- Изучение глубинного строения Земли
- Археологические и геофизические исследования
- Разработка систем защиты от космического излучения
Данные о магнитном поле Земли используются для создания точных навигационных карт, калибровки компасов и магнитометров, а также для изучения глобальных геофизических процессов. Исследование геомагнетизма остается одним из важнейших направлений в науках о Земле.

Магнитное поле — Циклопедия
Магнитное поле — это компонент электромагнитного поля, возникающий в присутствии переменного во времени электрического поля. Кроме того, магнитное поле может создаваться током заряженных частиц или магнитными моментами электронов в атомах (постоянные магниты). С точки зрения квантовой теории поля, электромагнитное взаимодействие передается безмассовым бозонным фотоном (частица, которую можно представить как квантовое возбуждение электромагнитного поля). Основной характеристикой магнитного поля является его сила, которая определяется вектором магнитной индукции [math]\vec{\mathbf{B}}[/math] (вектором индукции магнитного поля). В СИ магнитная индукция измеряется в теслах (TL), в системе СГС — в гауссах. Эффекты магнитных полей обычно проявляются в постоянных магнитах, которые притягивают магнитные материалы, такие как железо, и притягивают или отталкивают другие магниты.
В специальной теории относительности электрическое и магнитное поля — это два взаимосвязанных аспекта одного и того же объекта, называемого электромагнитным тензором.
В повседневной жизни магнитные поля чаще всего встречаются как невидимая сила, создаваемая постоянными магнитами, которые взаимодействуют с ферромагнитными материалами, такими как железо, кобальт или никель. Магнитные поля очень широко используются во всех современных технологиях, в частности в области электротехники и электромеханики. Торсионные магнитные поля используются как в электродвигателях, так и в генераторах. Взаимодействие магнитных полей в электрических устройствах, таких как трансформаторы, присутствует в магнитных цепях. Магнитные силы предоставляют информацию о носителях заряда в материале благодаря эффекту Голе. Земля создает собственное магнитное поле, которое защищает озоновый слой Земли от солнечного ветра и играет важную роль в навигации по компасу.
[править] Формирование магнитного поля
[править] Постоянные магниты
В отличие от электрических зарядов, магнитные заряды, которые создавали бы магнитное поле аналогичным образом, не наблюдаются. Теоретически такие заряды, называемые магнитными монополями, могут существовать. В этом случае электрическое и магнитное поля будут полностью симметричными.
Наименьшей единицей, которая может генерировать магнитное поле, является магнитный диполь. Магнитный диполь отличается тем, что у него всегда есть два полюса, в которых силовые линии поля начинаются и заканчиваются. Микроскопические магнитные диполи связаны со спинами элементарных частиц. Частицы с ненулевым спином, такие как протоны, нейтроны и электроны, являются элементарными магнитами. Величина дипольного магнетизма может быть выражена магнитным дипольным моментом, который обычно называют магнитным моментом и обозначают буквой [math]\mathbf{m}[/math]. Магнитный момент макроскопического куска вещества можно вычислить как векторную сумму магнитных моментов его атомов.
[править] Модель Гильберта и H-поле
Магнитное поле H, созданное двумя магнитными зарядами.В этой модели диполь рассматривается как два магнитных заряда, и создаваемое ими поле похоже на поле электрического диполя, то есть его линии начинаются на севере и заканчиваются на юге без бесконечности, точно так же, как линии электрического поля начинаются с положительного заряда и заканчиваются отрицательным.
Модель Гильберта предполагает допустимые значения напряженности магнитного поля как внутри, так и снаружи магнита, включая тот факт, что его направление противоположно направлению вектора намагниченности. Однако у модели полюса есть ограничения из-за того, что она фактически основана на понятии плотности магнитного заряда. Таким образом, это не может объяснить ни того факта, что полюса магнита нельзя отделить друг от друга, ни магнитных свойств движущихся электрических зарядов
[править] Модель Ампера и B-поле
В этой модели диполь рассматривается как небольшой замкнутый контур, по которому непрерывно течет ток[1]. В такой модели создаваемое ею поле будет соленоидным, что означает, что ее силовые линии не имеют ни начала, ни конца, а будут закручены по контуру, проходящему через ее ядро. Магнитный момент такого диполя будет [math]\mathbf{m} = \mathrm{I}\mathbf{S}[/math], где I — ток в цепи, а S — его площадь поперечного сечения. Вот такой магнит будет перпендикулярен контуру. Важной особенностью поля B является то, что в отличие от H-поля, линии которого всегда направлены от одного полюса к другому, его линии внутри магнита имеют противоположное направление.
Магнитный момент такого диполя будет [math]\mathbf{m} = \mathrm{I}\mathbf{S}[/math], где I — ток в цепи, а S — его площадь поперечного сечения. Вот такой магнит будет перпендикулярен контуру. Важной особенностью поля B является то, что в отличие от H-поля, линии которого всегда направлены от одного полюса к другому, его линии внутри магнита имеют противоположное направление.
Подводя итог и формализуя результат, можно сказать, что если силовая линия B-поля попадает в определенную область пространства, она всегда выходит из нее позже, то есть
- [math]\oint_S \mathbf{B} \cdot \mathrm{d}\mathbf{A} = 0,[/math]
где интеграл вычисляется по замкнутой поверхности S, а произведение B·dA положительно, когда линия выходит на поверхность, и отрицательно, когда она покидает ее.
На самом деле современная модель ближе к истине. Для многих частиц, таких как переходные металлы или двухатомные молекулы, основной вклад в магнитный момент вносит орбитальный момент электрона[2]. Однако другой источник, то есть момент, возникающий при раскручивании электронов и ядер, такой моделью не объясняется, поскольку спин — чисто квантовое явление и не имеет близких аналогов в мире.
Однако другой источник, то есть момент, возникающий при раскручивании электронов и ядер, такой моделью не объясняется, поскольку спин — чисто квантовое явление и не имеет близких аналогов в мире.
[править] Электрические заряды
Одиночный заряд, двигаясь равномерно и прямо, создает вокруг себя магнитное поле, линии которого замыкаются и закручиваются вокруг оси, совпадающей с направлением движения заряда. Его значение можно записать следующим образом:[math]\mathbf{B} = \mathbf{E} \cdot \mathrm{v}[/math][3]. Как можно понять из релятивистских соображений, величина поля будет зависеть от системы отсчета наблюдателя, движущегося с той же скоростью и в том же направлении, что и заряд. Таким образом, в теории относительности электрическое и магнитное поля являются компонентами одного и того же электромагнитного поля.
Поскольку электрический ток представляет собой набор большого количества движущихся зарядов, он также создает магнитное поле. Однако такая система не может создавать электрическое поле, потому что она электрически нейтральна. 2},[/math]
2},[/math]
Направление поля можно определить по правилу Ампера или правилу правой руки. Такое поле также является вихрем, то есть его силовые линии замкнуты. В крайнем случае бесконечного прямого проводника магнитное поле будет обладать осевой и поступательной симметрией.
Чтобы сконцентрировать магнитное поле, цепь переделывается в катушку, таким образом образуя соленоид, в котором внутреннее поле усиливается, а внешнее поле ослабляется. Если внутрь соленоида поместить ферромагнитный сердечник, образуется электромагнит. Для бесконечного соленоида поле внутри него можно записать по формуле:
- [math]B=\mu_0nI[/math]
где n — количество витков провода на единицу длины, I — ток в цепи. Эта формула также верна для соленоида конечной длины, если точка измерения находится достаточно далеко от его концов.
Магнитное поле также создается переменным электрическим полем. Согласно закону электромагнитной индукции переменное магнитное поле создает переменное электрическое поле, которое также является вихревым. Взаимное создание электрического и магнитного полей на переменных магнитных и электрических полях приводит к возможности распространения электромагнитных волн в пространстве.
Взаимное создание электрического и магнитного полей на переменных магнитных и электрических полях приводит к возможности распространения электромагнитных волн в пространстве.
Магнитные и электрические поля человека — Альтернативный взгляд Salik.biz
Электрическое поле человека существует на поверхности тела и снаружи, вне его. Электрическое поле вне тела человека обусловлено главным образом трибозарядами, то есть зарядами, возникающими на поверхности тела вследствие трения об одежду или о какой-либо диэлектрический предмет, при этом на теле создается электрический потенциал порядка нескольких вольт. Электрическое поле непрерывно меняется во времени: во-первых, происходит нейтрализация трибозарядов — они стекают с высокоомной поверхности кожи с характерными временами ~ 100 — 1000 с; во-вторых, изменения геометрии тела вследствие дыхательных движений, биения сердца и т.п. приводят к модуляции постоянного электрического поля вне тела.
Еще одним источником электрического поля вне тела человека является электрическое поле сердца. Приблизив два электрода к поверхности тела, можно бесконтактно и дистанционно зарегистрировать такую же кардиограмму, что и традиционным контактным методом. Отметим, что этот сигнал ни много раз меньше, чем поле трибозарядов.
Приблизив два электрода к поверхности тела, можно бесконтактно и дистанционно зарегистрировать такую же кардиограмму, что и традиционным контактным методом. Отметим, что этот сигнал ни много раз меньше, чем поле трибозарядов.
В медицине бесконтактный метод измерения электрических полей, связанных с телом человека, нашел свое применение для измерения низкочастотных движений грудной клетки.
При этом на тело пациента подается переменное электрическое напряжение частотой — 10 МГц, а несколько антенн-электродов подносят к грудной клетке на расстоянии 2-5 см. Антенна и тело представляют собой две обкладки конденсатора. Перемещения грудной клетки меняет расстояние между обкладками, то есть емкость этого конденсатора и, следовательно, емкостной ток, измеряемый каждой антенной. На основании измерений этих токов можно построить карту перемещений грудной клетки во время дыхательного цикла. В норме она должна быть симметрична относительно грудины. Ее симметрия нарушена и с одной стороны амплитуда движений мала, то это может свидетельствовать, например, о скрытом переломе ребра, при котором блокируется сокращение мышц с соответствующей стороны грудной клетки.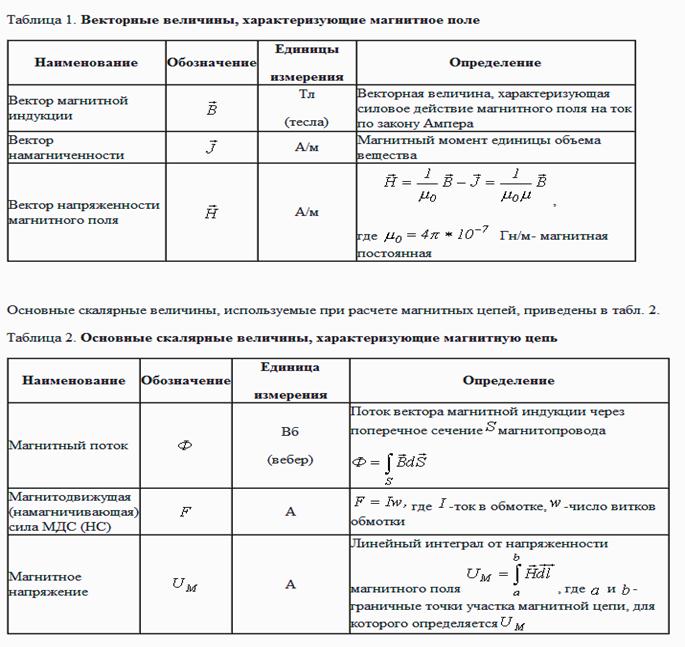
Контактные измерения электрического поля в настоящее время находят наибольшее применение в медицине: в кардиографии и электроэнцефалографии. Основной прогресс в этих исследованиях обусловлен применением вычислительной техники, в том числе персональных компьютеров. Они позволяют получать электрокардиограммы высокого разрешении (ЭКГ ВР).
Как известно, амплитуда сигнала ЭКГ не более 1 мВ, а ST-сегмента еще меньше, причем сигнал маскируется электрическим шумом, связанным с нерегулярной мышечной активностью. Поэтому применяют метод накопления — то есть суммирование многих последовательно идущих сигналов ЭКГ. Для этого ЭВМ сдвигает каждый последующий сигнал так, чтобы его R-пик был совмещен с R-пиком предыдущего сигнала, и прибавляет его к предыдущему, и так для многих сигналов в течение нескольких минут. При этой процедуре полезный повторяющийся сигнал увеличивается, а нерегулярные по мехи гасят друг друга. За счет подавления шума удается выделить тонкую структуру ST-комплекса, которая важна для прогноза риска мгновенной смерти.
В электроэнцефалографии, используемой для целей нейрохирургии, персональные компьютеры позволяют строить в реальном времени мгновенные карты распределения электрического поля мозга с использованием потенциалов от 16 до 32 электродов, размещенных на обоих полушариях, через временные интервалы порядка нескольких мс.
Построение каждой карты включает в себя четыре процедуры:
1) измерение электрического потенциала во всех точках, где стоят электроды;
2) интерполяцию (продолжения) измеренных значений на точки, лежащие между электродами;
3) сглаживание получившейся карты;
4) раскрашивание карты в цвета, соответствующие определенным значениям потенциала. Получаются эффектные цветные изображения. Такое представление в квазицвете, когда всему диапазону значений поля от минимального до максимального ставят в соответствие набор цветов, например от фиолетового до красного, сейчас очень распространено, поскольку сильно облегчает врачу анализ сложных пространственных распределений. В результате получается последовательность карт, из которой видно, как по поверхности коры перемещаются источники электрического потенциала.
В результате получается последовательность карт, из которой видно, как по поверхности коры перемещаются источники электрического потенциала.
Персональный компьютер позволяет строить карты не только мгновенного распределения потенциала, но и более тонких параметров ЭЭГ, которые давно апробированы в клинической практике. К ним в первую очередь относится пространственное распределение электрической мощности тех или иных спектральных составляющих ЭЭГ (α, Я, γ, δ, и θ-ритмы). Для построения такой карты в определенном временном окне измеряют потенциалы в 32 точках скальпа, затем по этим записям определяют частотные спектры и строится пространственное распределение отдельных спектральных компонент.
Карты α, δ, Я ритмов сильно отличаются. Нарушения симметрии таких карт между правым и левым полушарием может быть диагностическим критерием в случае опухолей мозга и при некоторых других заболеваниях.
Таким образом, в настоящее время разработаны бесконтактные методы регистрации электрического поля, которое создает тело человека в окружающем пространстве, и найдены некоторые приложения этих методов в медицине. Контактные измерения электрического поля получили новый импульс в связи с развитием персональных ЭВМ — их высокое быстродействие позволило получать карты электрических полей мозга.
Контактные измерения электрического поля получили новый импульс в связи с развитием персональных ЭВМ — их высокое быстродействие позволило получать карты электрических полей мозга.
Магнитное поле человека
Магнитное поле тела человека создается токами, генерируемыми клетками сердца и коры головного мозга. Оно исключительно мало — 10 млн. — 1 млрд. раз слабее магнитного поля Земли. Для его измерения используют квантовый магнитометр. Его датчиком является сверхпроводящий квантовый магнитометр (СКВИД), на вход которого включены приемы и с катушки. Этот датчик измеряет сверхслабый магнитный поток, пронизывающий катушки. Чтобы СКВИД работал, его надо ох ладить до температуры, при которой появляется сверхпроводимость, т.е. до температуры жидкого гелия (4 К). Для этого его и приемные катушки помещают в специальный термос для хранения жидкого гелия — криостат, точнее, в его узкую хвостовую часть, которую удается максимально близко поднести к телу человека.
В последние годы после открытия «высокотемпературной сверхпроводимости» появились СКВИДы, которые достаточно охлаждать до температуры жидкого азота (77 К). Их чувствительность достаточна для измерения магнитных полей сердца.
Их чувствительность достаточна для измерения магнитных полей сердца.
Магнитное поле, создаваемое организмом человека, на много порядков меньше, чем магнитном поле Земли, его флуктуации (геомагнитный шум) или поля технических устройств.
Существуют два подхода к устранению влияния шумов. Наиболее радикальный — создание сравнительно большого объема (комнаты), в котором магнитные шумы резко уменьшены с помощью магнитных экранов. Для наиболее тонких биомагнитных исследований (на мозге) шумы необходимо с шикать примерно в миллион раз, что может быть обеспечено многослойными стопками из магнитомягкого ферромагнитного сплава (например, пермаллоя). Экранированная комната — дорогостоящее сооружение, и лишь крупнейшие научные центры могут позволить себе се сооружение. Количество таких комнат в мире в настоящее время исчисляется единицами.
Есть и другой, более доступный способ ослабить влияние внешних шумов. Он основан на том, что в большинстве своем магнитные шумы в окружающем нас пространстве порождаются хаотическими колебаниями (флуктуациями) земного магнитного поля и промышленными электроустановками. Вдали от резких магнитных аномалий и электрических машин магнитное поле хотя и флуктуирует со временем, но пространственно однородно, слабо меняясь на расстояниях, сравнимых с размерами человеческого тела. Собственно же биомагнитные поля быстро ослабевают при удалении от живого организма. Это означает, что внешние поля, хотя и намного более сильные, имеют меньшие градиенты (т.е. скорость изменения с удалением от объекта), чем биомагнитные поля.
Вдали от резких магнитных аномалий и электрических машин магнитное поле хотя и флуктуирует со временем, но пространственно однородно, слабо меняясь на расстояниях, сравнимых с размерами человеческого тела. Собственно же биомагнитные поля быстро ослабевают при удалении от живого организма. Это означает, что внешние поля, хотя и намного более сильные, имеют меньшие градиенты (т.е. скорость изменения с удалением от объекта), чем биомагнитные поля.
Приемное устройство прибора со сквидом в качестве чувствительного элемента изготовляется так, что оно чувствительно только к градиенту магнитного поля, — в этом случае прибор называют градиометром. Однако часто внешние (шумовые) поля обладают все же заметными градиентами, тогда приходится применять прибор, измеряющий вторую пространственную производную индукции магнитного поля — градиометр второго порядка. Такой прибор можно применять уже в обычной лабораторной обстановке. Но все же и градиометры предпочтительно применять в местах с «магнитно-спокойной» обстановкой, и некоторые исследовательские группы работают в специально сооружаемых немагнитных домах в сельской местности.
В настоящее время интенсивные биомагнитные исследования ведутся как в магнитоэкранированных комнатах, так и без них, с применением градиометров. В широком спектре биомагнитных явлений есть много задач, допускающих разный уровень ослабления внешних шумов.
Что такое поле в физике
Когда в пространстве распределена какая-либо физическая величина, то говорят, что в пространстве задано поле этой величины.
Если распределена скалярная величина, то поле называют скалярным. Такое поле математики описывают скалярной функцией.
А если в области распределена векторная величина, тогда поле называется векторным. Его описывают с помощью векторной функции.
Скалярное поле
К примеру, мы можем измерять температуру зимой в различных точках комнаты.
При этом, чем ближе к батарее центрального отопления и чем выше к потолку, тем выше будет температура. А в точках у пола и в отдалении от нагретой батареи температура будет ниже на несколько градусов.
Рассмотрим трехмерное пространство (рис. 1) и какую-нибудь точку, расположенную в этом пространстве. Обозначим точку большой латинской буквой, например P.
Рис. 1. Каждой точке в трехмерном пространстве в соответствие поставлены три числа на осях
Этой точке поставлены в соответствие три числа x, y, z, лежащие на осях Ox, Oy, Oz. Такие числа называют координатами точки. Обычно математики записывают координаты точки рядом с ее названием: \(\large P\left( x ; y ; z \right)\).
Мы можем дополнительно поставить в соответствие этой точке четвертое число – температуру t в градусах Цельсия (рис. 2).
Рис. 2. Пример распределения температуры в комнате, во время сезона отопления
Составим таблицу, в которой будут содержаться координаты точек пространства и температура в этих точках. Так мы упорядочим информацию о распределении температуры в комнате.
По такой таблице можно построить графики, на которых изобразим, как именно температура будет зависеть от какой-либо координаты пространства.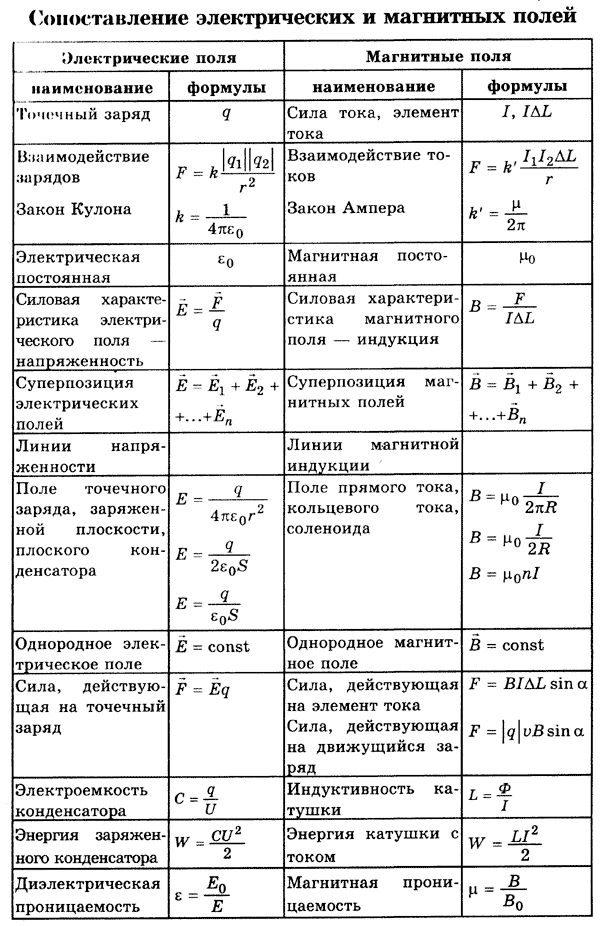
Эта таблица и графики содержат информацию о поле температур.
Так как распределенная по комнате температура является скалярной величиной, то поле температуры называют скалярным. А таблица задает скалярную функцию, описывающую распределение температуры в комнате.
Такая функция связывает координаты точки и значение физической величины – температуры в этой точке.
Это обычная функция, наподобие тех, с которыми вам приходилось решать примеры на школьной математике. Только эта функция зависит не от одной переменной x, а от трех переменных величин — координат x, y, z точек, расположенных в трехмерном пространстве.
\[\large \varphi = f \left( x ; y ; z \right)\]
А четвертая величина – температура, будет являться значением этой функции. Наподобие числа «y» для функции одной переменной «x».
Векторное поле
Предположим, что в углу комнаты лежит большой магнит. А мы ходим по комнате со шнурком, к одному концу которого привязан железный гвоздь. Второй конец шнурка держим в горизонтально вытянутой руке.
Второй конец шнурка держим в горизонтально вытянутой руке.
Расхаживая по комнате, мы заметим, что в некоторой области комнаты шнурок с гвоздем отклоняется от вертикального положения в сторону магнита.
Чем ближе мы подходим к магниту, тем сильнее он притягивает гвоздь. Тем больше усилий нужно приложить, чтобы удержать шнурок в руке.
Такие поля, наподобие поля, созданного магнитом, называют силовыми полями.
Поля силовые – это векторные поля, так как распределенная по комнате и измеренная в различных точках комнаты сила – это векторная величина.
Теперь каждой точке комнаты мы можем поставить в соответствие не только координаты точки, но и вектор F силы, действующей на гвоздь в этой точке.
Составим таблицу и запишем в нее координаты каждой выбранной точки комнаты и координаты вектора силы, с которой магнит действует на гвоздь в этой точке.
У вектора силы в каждой отдельной точке будут свои характеристики — длина и направление. Поэтому, таблица, содержащая информацию о силе в каждой точке комнаты, будет содержать 6 строк. Три строки – это координаты точки, и три строки – координаты вектора.
Три строки – это координаты точки, и три строки – координаты вектора.
Такая таблица задает функцию, которую математики называют сокращенно «вектор-функцией».
Вектор-функцию, описывающую векторное поле, можно обозначить так:
\(\large \overrightarrow{A \left( P \right)} \) – вектор-функция. Подробнее можно записать ее таким способом:
\[\large \boxed{ \overrightarrow{A \left( P \right)} = A_{x}\left( x ; y ; z \right) \cdot \vec{i} + A_{y}\left( x ; y ; z \right) \cdot \vec{j} + A_{z}\left( x ; y ; z \right) \cdot \vec{k} }\]
\( A_{x}\left( x ; y ; z \right) ; A_{y}\left( x ; y ; z \right) ; A_{z}\left( x ; y ; z \right) \) – это компоненты (части) вектор функции.
\( \vec{i} ; \vec{j} ; \vec{k} \) – орты.
Обычно в школе такие функции не изучают. Но вы теперь знаете, что кроме обычных — скалярных функций, существуют вектор-функции.
Из записи видно, что векторная функция отличается от скалярной тем, что имеет три компоненты (части). Каждая компонента (часть) зависит от трех координат точки P пространства.
Какое поле называют стационарным
Многие процессы, происходящие вокруг нас, изменяются во времени. Например, температура в полдень жаркого летнего дня будет выше, чем температура перед закатом этого же дня. Иными словами, скалярная величина – температура воздуха на улице, а значит и, ее поле, изменяются со временем.
В противоположность этому, поле температуры в закрытом помещении зимой изменяться не будет. Конечно, если батареи центрального отопления будут иметь одинаковую температуру в течение продолжительного времени.
Величины и процессы, изменяющиеся во времени, называют нестационарными. А стабильные, не изменяющиеся с течением времени величины – стационарными.
Если поле не изменяется с течением времени, его называют стационарным. А если изменяется – тогда нестационарным.
Все ли поля можно почувствовать
Мы можем чувствовать поле температур, благодаря тому, что на коже у нас содержатся особые рецепторы, способные воспринимать температуру окружающей среды.
Однако, не все поля люди могут ощущать. Например, мы невосприимчивы к магнитным и электрическим полям, потому, что у нас нет органа, способного улавливать их изменения.
Как же тогда мы узнали о электрических и магнитных полях? Мы нашли тех, кто может чувствовать эти поля.
Некоторые рыбы способны улавливать изменение электрического поля. Например, электрический скат (рис. 3) улавливает электрические сигналы и благодаря этому прекрасно ориентируется. У него есть для этого специальные органы, в отличие от человека. Отдельные скаты способны генерировать электрические разряды напряжением до 200 вольт.
Рис. 3. Электрический скат умеет чувствовать электрическое поле
Электрический угорь (рис. 4) может достигать 2,5 метров в длину. Он способен не только улавливать электрические поля, но и генерировать мощные электрические разряды напряжением до 860 Вольт и силой тока до 1 Ампера. Использует их, преимущественно охотясь на добычу, или спасаясь от других хищников.
Рис. 4. Электрический угорь чувствует электрическое поле и может вырабатывать электрические импульсы
Способность улавливать изменение электрического поля называют электрорецепцией. Ее обнаружили у некоторых рыб, амфибий и млекопитающих – утконоса и ехидны. Она используется для охоты, общения и улавливания магнитного поля земли.
Перелетные птицы, например, журавли (рис. 5), содержат орган, способный улавливать изменение магнитного поля Земли. Благодаря этому они ориентируются в пространстве во время перелетов в теплые края.
Рис. 5. Перелетные птицы ориентируются по магнитному полю Земли
Как мы можем обнаружить поле без помощи животных?
Для обнаружения электрического поля мы будем использовать электрический заряд. Потому, что поле действует электрической силой на заряды, помещенные в него.
А, чтобы обнаружить магнитное поле, мы можем воспользоваться небольшим магнитом, или железным предметом. Потому, что магнитное поле будет воздействовать на них.
Как обозначают поля на рисунках
Рассмотрим часть карты мира. Обратим внимание на то, что области частей карты закрашены различными цветовыми оттенками (рис. 6).
Рис. 6. Различные уровни высот на карте раскрашены разными цветами
Так же, в одном из углов карты можно заметить разноцветную табличку, наподобие, нарисованной поверх карты на рисунке. На ней нарисована шкала высот и глубин и, рядом с каждым оттенком записаны цифры, обозначающие высоту или глубину в метрах.
Примечание: Высоты и глубины на местности обозначают с помощью областей, имеющих различные цвета, для наглядности. Чем ближе к красному цвету, тем выше, а чем ближе к фиолетовому, тем глубже.
По краям цветовых областей проведены тонкие границы, они ограничивают области, имеющие одинаковый уровень высот. Такие границы называют линиями уровня.
Высота или уровень – это скалярная величина. Поэтому, мы можем сказать, что с помощью цветных областей и линий на их границах задано поле, описывающее распределение высот на поверхности Земли.
Скалярное поле можно изобразить с помощью линий уровня.
Вспомним теперь пример с магнитом и гвоздиком. В каждой точке комнаты можно нарисовать вектор силы, с которой магнит притягивает железный гвоздь (рис. 7).
Рис. 7. Силы выстраиваются вдоль некоторых линий, их называют силовыми линиями поля
Чем ближе к магниту, тем больше сила притяжения, тем длиннее векторы. Можно обратить внимание, что векторы силы как бы располагаются вдоль некоторых линий. Они дополнительно проведены пунктиром на рисунке. Видно, так же, что эти линии искривлены.
Такие линии, вдоль которых выстаиваются векторы силы, называют силовыми линиями. Силовые поля – векторные.
Векторные поля изображают с помощью силовых линий. Вдоль таких линий выстраиваются векторы сил. Эти линии имеют и другие названия.
Связь между скалярными и векторными полями
Скалярному полю можно поставить в соответствие векторное поле. Вернемся к примеру обозначения высот на карте (рис. 6). Мы знаем, что на карте имеются области, на которых присутствуют резкие перепады высот. На таких участках есть несколько градаций цветовых оттенков, а области, имеющие различные цвета, в таких местах располагаются чаще.
6). Мы знаем, что на карте имеются области, на которых присутствуют резкие перепады высот. На таких участках есть несколько градаций цветовых оттенков, а области, имеющие различные цвета, в таких местах располагаются чаще.
Чтобы обозначить резкие перепады высот, придумали использовать специальный вектор – вектор градиента. Он описывает, как быстро изменяется скалярная величина – например, высота на карте местности.
Этот вектор обозначают так:
\[\large \boxed{ \overrightarrow{grad \left( h \right)} }\]
Примечание: Градиент, от слова градация – его можно перевести, как сорт, или изменчивость. Например, градации яркости имеют различные оттенки серого цвета. В школьной физике вектор градиента обычно не рассматривают.
Градиент направлен в сторону наибольшего возрастания физической величины. А длина вектора градиента равна скорости, с которой возрастает физ. величина в этом направлении.
На разных участках карты присутствуют различные перепады высот, где-то высота изменяется быстрее, а где-то — медленнее. Значит, в различных областях местности вектор градиента будет иметь разную длину.
Значит, в различных областях местности вектор градиента будет иметь разную длину.
А если в пространстве распределена векторная величина, то говорят, что задано поле такой физ. величины.
Так, мы получили два связанных поля – скалярное поле высоты и векторное поле градиента, описывающее скорость изменения высоты в различных областях местности.
Для примера, описывая электрическое поле мы будем использовать две величины – скалярную — потенциал электростатического поля и векторную – напряженность электрического поля. Эти величины связаны между собой с помощью вектора градиента.
Однородные и неоднородные поля
Поле однородное, если в каждой точке пространства оно имеет одно и то же значение распределенной величины.
Например, температура во всех точках пространства имеет одно и то же значение. Или, электрическое поле действует на помещенный в него заряд во всех точках пространства с одной и той же силой.
Однородные силовые поля изображают прямыми линиями, расстояние между которыми не изменяется (рис. 8а).
8а).
Рис. 8. Линии однородного – а) и неоднородного – б) поля
Распределенные заряды могут создавать однородные поля. Электрическое поле, существующее между двумя заряженными параллельными плоскостями, однородное.
Если же в разных точках пространства поле действует на пробный заряд с различными силами, тогда поле называют неоднородным. Линии неоднородных полей кривые и расстояние между ними изменяется (рис. 8б).
Поле неоднородное, если в разных точках пространства оно имеет различные значения распределенной величины.
Например, поле магнита – это неоднородное поле, потому, что сила воздействия магнита возрастает по мере приближения к нему. Электрическое поле вокруг точечного заряда, так же неоднородное, потому, что сила воздействия на пробный заряд возрастает с уменьшением расстояния до заряда, создавшего поле.
По силовым линиям можно узнать величину поля. Чем гуще располагаются линии поля в какой-либо области, тем больше величина поля в этой области.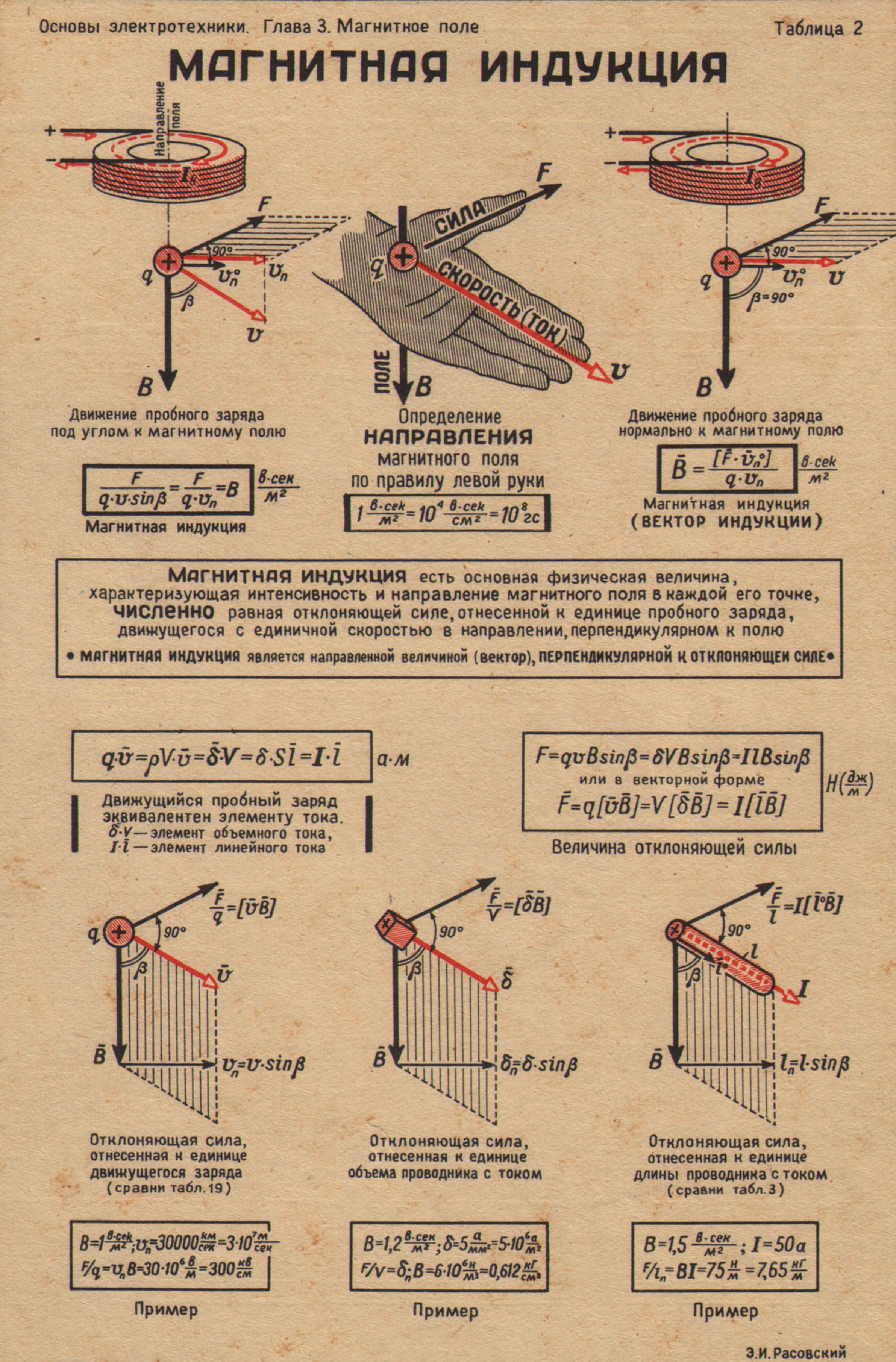
Примеры скалярных полей
Это поля распределения скалярных величин — плотности, давления, гравитационного и электростатического потенциалов, температуры, высот и т. п.
Поле плотности зарядов
Когда в трехмерном пространстве распределены заряды, мы можем говорить о плотности такого распределения. Плотность зарядов – величина скалярная. Ее распределение задает скалярное поле, описывается скалярной функцией.
Поле плотности тел
Если в пространстве распределена масса, то существует плотность распределения массы. Плотность тела – это скалярная функция, она задает скалярное поле.
Поле давления звуковой волны
Пусть в газе или жидкости распределяется звуковая волна. Звуковые волны являются поперечными волнами. По мере распространения волны в газе или жидкости возникают области сгущения и разряжения. Потому, что колеблется давление. Оно в различных точках пространства отличается. То есть, оно зависит от положения точки в пространстве. Когда скалярная величина – давление, распределена в пространстве, ее распределение описывается скалярной функцией. Эта функция задает скалярное поле.
Эта функция задает скалярное поле.
Поле гравитационного потенциала — распределение потенциальной энергии
По закону всемирного тяготения, тела, имеющие массу, взаимно притягиваются. А если есть взаимодействие, то имеется потенциальная энергия такого взаимодействия. Распределение потенциальной энергии задается скалярной функцией, эта функция описывает скалярное поле и называется гравитационным потенциалом.
Поле распределения электрического потенциала
Заряды, находящиеся на некотором расстоянии, притягиваются, или отталкиваются. Значит, существует потенциальная энергия их взаимодействия. Распределение энергии описывается потенциалом системы заряженных частиц. Электрический потенциал является скалярной функцией, описывающей скалярное поле.
Примеры векторных полей
Это поля распределения векторных величин – сил, скоростей и т. д.
Гравитационное поле сил
Сила всемирного тяготения – это вектор, значит поле, описывающее гравитационное притяжение тел, будет векторным.
Поле скоростей потока жидкости
Когда жидкость течет, одни ее части в потоке двигаются быстрее других. Это значит, что скорости частиц жидкости различаются. Распределение скоростей частиц потока можно описать полем. Скорость – это вектор, значит, поле скоростей потока жидкости – это векторное поле.
Поле Кулоновских сил
Нам известно, что покоящиеся заряды притягиваются, или отталкиваются благодаря Кулоновским силам. Силы такого взаимодействия распределяются в пространстве и задают поле. Это электростатическое поле, оно является векторным полем напряженности.
Поле магнитных сил
Движущиеся заряды взаимодействуют благодаря магнитным полям. Индукция магнитного поля описывает, как сила взаимодействия изменяется в пространстве. Поэтому, индукция магнитного поля является вектор-функцией, задающей векторное магнитное поле.
Примечание: По сути, индукция магнитного поля – это сила, действующая на движущийся заряд со стороны других движущихся зарядов.
Выводы
- Все измеряемые нами величины можно разделить на скалярные, не имеющие направления и, векторные – направление имеющие.
- Говорят, что задано поле физической величины, когда эта величина распределена в пространстве.
- В пространстве могут распределяться не только скалярные величины, но и векторные величины.
- Если в пространстве распределена скалярная величина, то поле называют скалярным, а если — векторная величина, то поле — векторное.
- Поле стационарное, если оно не изменяется со временем. А если изменяется – тогда поле нестационарное.
- Люди могут ощущать не все поля. Но обнаружить поле можно с помощью тел, или приборов, чувствительных к этим полям. Например, электрическое поле можно обнаружить по его действию на заряды.
- Поля на рисунках удобно изображать с помощью специальных линий. Скалярные поля удобно обозначать с помощью линий уровня.
- Векторные поля изображают с помощью линий, вдоль которых направлены распределенные в пространстве векторы.
 Такие линии носят название силовых линий, линий напряженности поля, линий индукции поля.
Такие линии носят название силовых линий, линий напряженности поля, линий индукции поля. - Векторные и скалярные поля можно связать. Для этого можно использовать специальный вектор – вектор градиента.
- Однородное поле в каждой точке пространства оно имеет одно и то же значение распределенной величины. Однородные силовые поля изображают прямыми линиями, расстояние между которыми сохраняется.
- Неоднородное поле в разных точках пространства оно имеет различные значения распределенной величины. Неоднородные поля изображают кривыми линиями, расстояние между ними изменяется.
- Чем гуще располагаются линии поля в какой-либо области, тем больше его значение в этой области.
Основные электрические и магнитных величины
Единицы основных электрических и магнитных величин
|
Наименование величины |
Уравнение |
Наименование |
Обозначение |
|
Сила электрического тока |
|
Ампер |
А |
|
Электрический заряд |
Кулон |
Кл |
|
|
Удельное поверхностное сопротивление |
Ом |
Ом |
|
|
Удельная электрическая проводимость |
Сименс на метр |
См/м |
|
|
Удельное объемное сопротивление |
Ом ·метр |
Ом·м |
|
|
Абсолютная диэлектрическая проницаемость |
Фарада на метр |
Ф/м |
|
|
Электрическая постоянная |
Фарада на метр |
Ф/м |
|
|
Магнитная индукция |
Тесла |
Тл |
|
|
Напряженность магнитного поля |
Ампер на метр |
А/м |
|
|
Абсолютная магнитная проницаемость |
Генри на метр |
Гн/м |
|
|
Магнитная постоянная |
Генри на метр |
Гн/м |
Основные электрические и магнитных величины — 5. 0 out of
5
based on
1 vote
0 out of
5
based on
1 vote
Магнитное поле — МАГНИТ СТАНДАРТ
Как известно, появление магнитных взаимодействий происходит за счет движения заряженных частиц. Стационарные магнитные поля возникают вокруг проводников с постоянным электрическим током.
В зависимости от направления, по которому движутся заряженные частицы, два проводника, расположенные в непосредственной близости, могут взаимно отталкиваться или притягиваться. Это обуславливается силами, которые создают возникающие магнитные поля.
Основные характеристики магнитного поля, используемые в системах СИ и СГС
Магнитное поле имеет следующие основные характеристики:
- Напряженность (H). Для измерения значения этой векторной величины в международной системе СИ используются амперы на метр (А/м). В системе «Сантиметр-Грамм-Секунда» для этого применяются Эрстеды (Э). Взаимосвязь выглядит следующим образом: 1 А/м = 4π/103 Э. 1 А/м ≈ 0,0125663 Э.
- Индукция (B).
 Для измерения значения этой векторной величины в международной системе СИ используются Теслы (Тл). В системе «Сантиметр-Грамм-Секунда» для этого применяются Гауссы (Гс). Взаимосвязь выглядит следующим образом: 1 Тл = 10000 Гс.
Для измерения значения этой векторной величины в международной системе СИ используются Теслы (Тл). В системе «Сантиметр-Грамм-Секунда» для этого применяются Гауссы (Гс). Взаимосвязь выглядит следующим образом: 1 Тл = 10000 Гс.
Магнитная индукция в системе «Сантиметр-Грамм-Секунда»
В системе СГС связь индукции и напряженности в присутствии магнитного материала определяется следующим соотношением:
B=H+4πI
В этой формуле I — магнитный момент единицы объема материала (намагниченность). В системе СГС для измерения этой величины используются Гауссы (Гс).
Индукция характеризует поле, возникающее в веществе. Напряженность определяет параметры внешних магнитных полей и магнитных полей в вакууме. Величина B также может использоваться для внешних магнитных полей.
В вакууме значения индукции и напряженности равны (по системе СГС).
Магнитная индукция в международной системе СИ
В системе СИ используется следующее соотношение:
B=µ0(H+I)
В этой формуле µ0 — магнитная проницаемость вакуума. µ0 = 4π*10-7 Гн/м.
µ0 = 4π*10-7 Гн/м.
Векторы индукции, намагниченности и напряженности
На рисунке 1 показаны векторы намагниченности, индукции и напряженности в постоянном магните при отсутствии внешнего поля.
Рисунок 1 — Намагниченность, индукция и напряженность в постоянном магните.
Напряженность — это поле, создаваемое самим магнитом. Вектор H направлен противоположно вектору I. Напряженность иначе называется размагничивающим полем.
Таблица характеристик магнитного поля
Характеристика СИ СГС Связь между СИ и СГС Напряженность (Н) А/м (ампер на метр) Э (Эрстед) 1 А/м = 4π/1000 Э 1 А/м ≈ 0,0125663 Э 1 Э ≈ 79,57 А/м Магнитный поток (Ф) Вб (Вебер) Гс*см2 (Максвелл) 1 Вб = 100000000 Гс*см2 Индукция (В) Тл (Тесла) Гс (Гаусс) 1 Т = 10000 Гс 1 Гс = 0,0001 Т Намагниченность (I) А/м (ампер на метр) Гс (Гаусс) 1 А/м = 0,001 Гс 1 Гс = 1000 А/м
Магнитный диполь
На рисунке 2 представлены силовые линии магнитного поля, которые создают магнитные диполи (рамки с током).
Рисунок 2 — Силовые линии магнитного диполя.
Постоянный магнит можно также рассматривать как рамку с током. Создаваемые в окружающем пространстве силовые линии идентичны.
Вращающееся магнитное поле — Карта знаний
-
Вращающееся магнитное поле. Обычно под вращающимся магнитным полем понимается магнитное поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается с постоянной угловой скоростью. Впрочем, вращающимися называют и магнитные поля магнитов, вращающихся относительно оси, не совпадающей с их осью симметрии (например, магнитные поля звезд или планет).
Вращающееся магнитное поле создают, накладывая два или более разнонаправленных переменных, зависящих от времени по синусоидальному закону, магнитных поля одинаковой частоты, но сдвинутых друг относительно друга по фазе.

Это было на практике осуществлено независимо в 1888 году итальянским физиком Г. Феррарисом и сербским инженером Н. Тесла. Применяется в синхронных и асинхронных машинах.
Разность фаз для двухфазных систем (два перпендикулярных электромагнита) должна составлять 90°, а для 3-фазных (три электромагнита, направленных в одной плоскости под углом 120° друг к другу) 120°.
Источник: Википедия
Связанные понятия
Кольца Гельмгольца (катушки Гельмгольца) — две соосно расположенные одинаковые радиальные катушки, расстояние между центрами которых равно их среднему радиусу. В центре системы имеется зона однородного магнитного поля. Используются для получения постоянного, переменного или импульсного магнитного поля с зоной однородности, которое обычно используется в экспериментах, а также для калибровки датчиков магнитной индукции, намагничивания и размагничивания постоянных магнитов, размагничивания стальных. ..
Инклинатор — прибор, служащий для измерения величины наклонения силы земного магнетизма.
Квадрупо́льная ли́нза — устройство для фокусировки пучков заряженных частиц с помощью магнитного или реже электрического поля квадрупольной конфигурации.
Лого́метр — магнитоэлектрический электроизмерительный прибор для измерения отношения сил двух электрических токов.
Га́мма — внесистемная единица измерения напряжённости магнитного поля, применяемая в геофизике и в измерениях космических магнитных полей. Обозначается греческой буквой γ.
..
Инклинатор — прибор, служащий для измерения величины наклонения силы земного магнетизма.
Квадрупо́льная ли́нза — устройство для фокусировки пучков заряженных частиц с помощью магнитного или реже электрического поля квадрупольной конфигурации.
Лого́метр — магнитоэлектрический электроизмерительный прибор для измерения отношения сил двух электрических токов.
Га́мма — внесистемная единица измерения напряжённости магнитного поля, применяемая в геофизике и в измерениях космических магнитных полей. Обозначается греческой буквой γ.
Упоминания в литературе
Однако, в отличие от Бэббиджа и Гершеля, Тесла не хотел создавать вращающееся магнитное поле путем механического вращения магнита под ротором: эффективный двигатель должен преобразовать электричество в движение, не движение в движение. Как в таком случае Тесла мог использовать электрический ток для создания вращающегося магнитного поля?
Двигатели переменного тока делятся на синхронные, асинхронные и коллекторные. В синхронных двигателях обмотка статора подключается к сети переменного тока, а обмотка ротора (в большинстве конструкций) – к источнику постоянного тока. В результате взаимодействия магнитных полей статора и ротора возникает крутящий момент, под действием которого ротор вращается синхронно с вектором напряжённости магнитного поля статора, т. е. частота вращения ротора жёстко связана с частотой питающего тока. Синхронные электродвигатели применяют в электроприводах, не требующих регулирования частоты вращения при отсутствии значительных перегрузок на валу двигателя (напр., для привода насосов, компрессоров, вентиляторов и т. д.). Наиболее распространены асинхронные электродвигатели. Они просты в изготовлении, надёжны в эксплуатации и потому являются основными двигателями в электроприводе.
Как в таком случае Тесла мог использовать электрический ток для создания вращающегося магнитного поля?
Двигатели переменного тока делятся на синхронные, асинхронные и коллекторные. В синхронных двигателях обмотка статора подключается к сети переменного тока, а обмотка ротора (в большинстве конструкций) – к источнику постоянного тока. В результате взаимодействия магнитных полей статора и ротора возникает крутящий момент, под действием которого ротор вращается синхронно с вектором напряжённости магнитного поля статора, т. е. частота вращения ротора жёстко связана с частотой питающего тока. Синхронные электродвигатели применяют в электроприводах, не требующих регулирования частоты вращения при отсутствии значительных перегрузок на валу двигателя (напр., для привода насосов, компрессоров, вентиляторов и т. д.). Наиболее распространены асинхронные электродвигатели. Они просты в изготовлении, надёжны в эксплуатации и потому являются основными двигателями в электроприводе. В асинхронном двигателе вращающееся магнитное поле, возникающее при прохождении переменного тока по обмоткам статора, взаимодействует с током, наведённым магнитным полем статора в обмотках ротора, в результате возникают механические усилия, заставляющие ротор вращаться в сторону вращения магнитного поля. Частота вращения ротора асинхронного электродвигателя зависит от частоты вращения магнитного поля статора (определяется частотой питающего тока), числом пар полюсов двигателя и уменьшается с увеличением нагрузки. Направление вращения асинхронного электродвигателя изменяют переключением любых двух фаз обмотки статора. Коллекторные двигатели позволяют плавно регулировать частоту вращения в широких пределах, но они дороже и менее надёжны, чем синхронные и асинхронные электродвигатели. Мощность электродвигателей – от долей ватта до нескольких десятков мегаватт.
В асинхронном двигателе вращающееся магнитное поле, возникающее при прохождении переменного тока по обмоткам статора, взаимодействует с током, наведённым магнитным полем статора в обмотках ротора, в результате возникают механические усилия, заставляющие ротор вращаться в сторону вращения магнитного поля. Частота вращения ротора асинхронного электродвигателя зависит от частоты вращения магнитного поля статора (определяется частотой питающего тока), числом пар полюсов двигателя и уменьшается с увеличением нагрузки. Направление вращения асинхронного электродвигателя изменяют переключением любых двух фаз обмотки статора. Коллекторные двигатели позволяют плавно регулировать частоту вращения в широких пределах, но они дороже и менее надёжны, чем синхронные и асинхронные электродвигатели. Мощность электродвигателей – от долей ватта до нескольких десятков мегаватт.
Связанные понятия (продолжение)
Дипо́ль — идеализированная система, служащая для приближённого описания поля, создаваемого более сложными системами зарядов, а также для приближенного описания действия внешнего поля на такие системы. Дипольное приближение, выполнение которого обычно подразумевается, когда говорится о поле диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка. Полученные функции будут эффективно…
Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток).
Магнесин — бесконтактная магнитоэлектрическая машина, являющаяся индикаторной системой синхронной связи. Термин «магнесин» образован слиянием от греческих слов «magnetis» — магнит и «synchronos» — одновременный. Применяется для синхронизации поворота осей механизмов, находящихся на небольшом расстоянии друг от друга и с практическим отсутствием момента сопротивления на валу приёмника.
Дипольное приближение, выполнение которого обычно подразумевается, когда говорится о поле диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка. Полученные функции будут эффективно…
Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток).
Магнесин — бесконтактная магнитоэлектрическая машина, являющаяся индикаторной системой синхронной связи. Термин «магнесин» образован слиянием от греческих слов «magnetis» — магнит и «synchronos» — одновременный. Применяется для синхронизации поворота осей механизмов, находящихся на небольшом расстоянии друг от друга и с практическим отсутствием момента сопротивления на валу приёмника. Магнитная линза — устройство электронной оптики, линза для фокусировки электронов.
Гальвано́метр (от фамилии учёного Луиджи Гальвани и слова др.-греч. μετρέω — «измеряю») — высокочувствительный прибор для измерения силы малых постоянных электрических токов. В отличие от обычных микроамперметров шкала гальванометра может быть проградуирована не только в единицах силы тока, но и в единицах напряжения, единицах других физических величин. Шкала может иметь условную, безразмерную градуировку, например, при использовании в качестве нуль-индикаторов.
Квантова́ние Дира́ка — эвристический аргумент, предложенный П. Дираком и показывающий, что однозначность предсказаний квантовой механики с электрическими зарядами может быть сохранена в теории, включающей магнитные монополи, лишь при условии совместного квантования магнитного и электрического зарядов.
Магнитная линза — устройство электронной оптики, линза для фокусировки электронов.
Гальвано́метр (от фамилии учёного Луиджи Гальвани и слова др.-греч. μετρέω — «измеряю») — высокочувствительный прибор для измерения силы малых постоянных электрических токов. В отличие от обычных микроамперметров шкала гальванометра может быть проградуирована не только в единицах силы тока, но и в единицах напряжения, единицах других физических величин. Шкала может иметь условную, безразмерную градуировку, например, при использовании в качестве нуль-индикаторов.
Квантова́ние Дира́ка — эвристический аргумент, предложенный П. Дираком и показывающий, что однозначность предсказаний квантовой механики с электрическими зарядами может быть сохранена в теории, включающей магнитные монополи, лишь при условии совместного квантования магнитного и электрического зарядов. Магнито́метр — (от гр. μαγνητό — магнит + гр. μετρεω измеряю), прибор для измерения характеристик магнитного поля и магнитных свойств материалов. В зависимости от измеряемой величины различают приборы для измерения напряжённости поля (эрстедметры), направления поля (инклинаторы и деклинаторы), градиента поля (градиентометры), магнитной индукции (тесламетры), магнитного потока (веберметры, или флюксметры), коэрцитивной силы (коэрцитиметры), магнитной проницаемости (мю-метры), магнитной восприимчивости…
Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой.
Магнито́метр — (от гр. μαγνητό — магнит + гр. μετρεω измеряю), прибор для измерения характеристик магнитного поля и магнитных свойств материалов. В зависимости от измеряемой величины различают приборы для измерения напряжённости поля (эрстедметры), направления поля (инклинаторы и деклинаторы), градиента поля (градиентометры), магнитной индукции (тесламетры), магнитного потока (веберметры, или флюксметры), коэрцитивной силы (коэрцитиметры), магнитной проницаемости (мю-метры), магнитной восприимчивости…
Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость…
Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость…Подробнее: Силовые линии векторного поля
Магнитное реле (англ. magnetic relay) — реле, которое реагирует на изменение магнитных величин (напряженности магнитного поля, магнитной индукции, магнитного потока) или магнитных характеристик материалов (магнитной проницаемости, остаточной магнитной индукции, кэрцитивной силы и т.п.). Измерительный механизм — совокупность элементов средства измерений, которые обеспечивают необходимое перемещение указателя (стрелки, светового пятна и т. д.) Инфракрасная головка самонаведения (Тепловая головка самонаведения, ТГС; англ. Heatseeker) — головка самонаведения, работающая на принципе улавливания волн инфракрасного диапазона, излучаемых захватываемой целью. Представляет собой оптико-электронный прибор, предназначенный для идентификации цели на окружающем фоне и выдачи в автоматическое прицельное устройство (АПУ) сигнала захвата, а также для измерения и выдачи в автопилот сигнала угловой скорости линии визирования.
Эффект де Хааза — ван Альфена — явление периодического изменения магнитной восприимчивости с ростом магнитного поля при низких температурах. Впервые обнаружен де Хаазом и ван Альфеном в 1930 году.
Магнитная сборка Хальбаха — особая конфигурация постоянных магнитов, характеризующаяся тем, что магнитное поле с одной из её сторон практически полностью отсутствует благодаря особому расположению элементов сборки.Повторение последовательности элементов (на передней поверхности вектор намагничивания: влево, вверх, вправо, вниз, влево) воспроизводит описываемый эффект.
Ионная циклотронная ловушка представляет собой один из вариантов масс-анализатора в масс-спектрометрии, в основе которого лежит принцип ионного циклотронного резонанса.
Представляет собой оптико-электронный прибор, предназначенный для идентификации цели на окружающем фоне и выдачи в автоматическое прицельное устройство (АПУ) сигнала захвата, а также для измерения и выдачи в автопилот сигнала угловой скорости линии визирования.
Эффект де Хааза — ван Альфена — явление периодического изменения магнитной восприимчивости с ростом магнитного поля при низких температурах. Впервые обнаружен де Хаазом и ван Альфеном в 1930 году.
Магнитная сборка Хальбаха — особая конфигурация постоянных магнитов, характеризующаяся тем, что магнитное поле с одной из её сторон практически полностью отсутствует благодаря особому расположению элементов сборки.Повторение последовательности элементов (на передней поверхности вектор намагничивания: влево, вверх, вправо, вниз, влево) воспроизводит описываемый эффект.
Ионная циклотронная ловушка представляет собой один из вариантов масс-анализатора в масс-спектрометрии, в основе которого лежит принцип ионного циклотронного резонанса. Ионы удерживаются магнитным полем в ловушке Пеннинга, двигаясь по кругу под действием силы Лоренца.
Ви́гглер (от англ. wiggle — вихлять, изгибаться, ёрзать) — устройство для генерации синхротронного излучения в электронном накопителе-синхротроне.
Эффект Литтла — Паркса был обнаружен в 1962 году Уильямом А. Литтлом и Роландом Д. Парком в экспериментах с тонкостенными сверхпроводящими цилиндрами помещёнными в параллельное магнитное поле. Это одно из первых указаний на важность куперовского спаривания.
Магнитосопротивление (магниторезистивный эффект) — изменение электрического сопротивления материала в магнитном поле. Впервые эффект был обнаружен в 1856 Уильямом Томсоном. В общем случае можно говорить о любом изменении тока через образец при том же приложенном напряжении и изменении магнитного поля. Все вещества в той или иной мере обладают магнетосопротивлением.
Ионы удерживаются магнитным полем в ловушке Пеннинга, двигаясь по кругу под действием силы Лоренца.
Ви́гглер (от англ. wiggle — вихлять, изгибаться, ёрзать) — устройство для генерации синхротронного излучения в электронном накопителе-синхротроне.
Эффект Литтла — Паркса был обнаружен в 1962 году Уильямом А. Литтлом и Роландом Д. Парком в экспериментах с тонкостенными сверхпроводящими цилиндрами помещёнными в параллельное магнитное поле. Это одно из первых указаний на важность куперовского спаривания.
Магнитосопротивление (магниторезистивный эффект) — изменение электрического сопротивления материала в магнитном поле. Впервые эффект был обнаружен в 1856 Уильямом Томсоном. В общем случае можно говорить о любом изменении тока через образец при том же приложенном напряжении и изменении магнитного поля. Все вещества в той или иной мере обладают магнетосопротивлением. Для сверхпроводников, способных без сопротивления проводить электрический ток, существует критическое магнитное поле, которое разрушает…
Для сверхпроводников, способных без сопротивления проводить электрический ток, существует критическое магнитное поле, которое разрушает…Подробнее: Магнетосопротивление
Ловушка Пеннинга — устройство, использующее однородное статическое магнитное поле и пространственно неоднородное электрическое поле для хранения заряженных частиц. Этот тип ловушек часто используется при точных измерениях свойств ионов и стабильных субатомных частиц, обладающих электрическим зарядом. В недавнем прошлом подобная ловушка успешно использовалась при физической реализации квантового компьютера и квантовых вычислений. Ловушки Пеннинга также применялись при создании так называемого «квазиатома… Гироскопический тренажёр — малогабаритный спортивный тренажёр, принцип работы которого основан на свойствах роторного гироскопа. Используется для создания нагрузки мышц и суставов кисти руки. Для достижения высоких степеней раскручивания ротора гироскопического тренажёра задействуются мышцы предплечья, плеча и плечевого пояса.
Пинч (англ. pinch — сужение, сжатие) — эффект сжатия токового канала под действием магнитного поля, индуцированного самим током. Сильный ток, протекающий в плазме, твёрдом или жидком металле создаёт магнитное поле. Оно действует на заряженные частицы (электроны и/или ионы), что может сильно изменить распределение тока. При больших токах сила Ампера приводит к деформации проводящего канала, вплоть до разрушения. В природе наблюдается в молниях .
Для достижения высоких степеней раскручивания ротора гироскопического тренажёра задействуются мышцы предплечья, плеча и плечевого пояса.
Пинч (англ. pinch — сужение, сжатие) — эффект сжатия токового канала под действием магнитного поля, индуцированного самим током. Сильный ток, протекающий в плазме, твёрдом или жидком металле создаёт магнитное поле. Оно действует на заряженные частицы (электроны и/или ионы), что может сильно изменить распределение тока. При больших токах сила Ампера приводит к деформации проводящего канала, вплоть до разрушения. В природе наблюдается в молниях .Подробнее: Пинч-эффект
Самоорганизующаяся система — кибернетическая (или динамическая) адаптивная система, в которой запоминание информации (накопление опыта) выражается в изменении структуры системы. Враща́тельное движе́ние — вид механического движения. При вращательном движении материальная точка описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной… Оптический изолятор — оптический прибор, пропускающий свет в прямом направлении, но поглощающий в обратном. Оптические изоляторы применяются в оптических линиях связи для защиты резонаторов лазерных передатчиков от отражённых сигналов, а также как входной элемент оптических усилителей. Униполярный генератор — разновидность электрической машины постоянного тока. Содержит проводящий диск, постоянное магнитное поле, параллельное оси вращения диска, 1 токосъёмник на оси диска и 2-й токосъёмник у края диска. Вращение плоскости поляризации поперечной волны — физическое явление, заключающееся в повороте поляризационного вектора линейно-поляризованной поперечной волны вокруг её волнового вектора при прохождении волны через анизотропную среду. Волна может быть электромагнитной, акустической, гравитационной и т. д. Тахогенера́тор (от др.-греч. τάχος — «быстрый», «скорость» и лат. generator «производитель») — электрическая микромашина, измерительный генератор постоянного или переменного тока, предназначенный для преобразования мгновенного значения частоты (угловой скорости) вращения вала в однозначно связанный со скоростью электрический сигнал. Магни́тный монопо́ль — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд является источником статического магнитного поля совершенно так же, как электрический заряд является источником статического электрического поля. Индукционный прибор — электрический прибор, в котором используется наведение вихревых токов в немагнитном проводящем элементе (обычно — алюминиевом диске). Этот принцип действия применяется в электросчётчиках, тахометрах, фазочувствительных реле и т. д. Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны. Бетатронные колебания — быстрые поперечные колебания, совершаемые частицей в фокусирующих магнитных полях ускорителя. Бетатронные колебания — основной предмет изучения электронной оптики, раздела физики ускорителей. Электромагни́тная инду́кция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении во времени магнитного поля или при движении материальной среды в магнитном поле. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей… Стеллара́тор — тип реактора для осуществления управляемого термоядерного синтеза. Название происходит от лат. stella — звезда, что должно указывать на схожесть процессов, происходящих в стеллараторе и внутри звёзд. Изобретён Л. Спитцером в 1950 году, первый образец построен под его руководством в следующем году в рамках секретного проекта «Маттерхорн». Векторное управление является методом управления синхронными и асинхронными двигателями, не только формирующим гармонические токи (напряжения) фаз (скалярное управление), но и обеспечивающим управление магнитным потоком ротора. Первые реализации принципа векторного управления и алгоритмы повышенной точности нуждаются в применении датчиков положения (скорости) ротора. Дипольный магнит (поворотный магнит) — в физике ускорителей, магнитный элемент, создающий однородное магнитное поле. Используется, в первую очередь, для создания ведущего поля, задающего траекторию пучка заряженных частиц, а также в системах впуска/выпуска пучка, для коррекции равновесной орбиты и пр. Измери́тельная ли́ния — устройство для исследования распределения электрического поля вдоль СВЧ-линии передачи. Представляет собой отрезок коаксиальной линии или волновода с перемещающимся вдоль него индикатором, отмечающим узлы (пучности) электрического поля. Магни́тное ква́нтовое число́ (m) — квантовое число, параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы). Магнитное квантовое число характеризует ориентацию в пространстве орбитального момента импульса электрона или пространственное расположение атомной орбитали. Оно принимает целые значения от -l до +l, где l — орбитальное квантовое число, то есть имеет ровно столько значений, сколько орбиталей существует… Электромеха́ника — раздел электротехники, в котором рассматриваются общие принципы электромеханического преобразования энергии и их практическое применение для проектирования и эксплуатации электрических машин. Ондуля́тор (от фр. onduler — волноваться, колебаться) — устройство для генерации когерентного синхротронного излучения в электронном накопителе-синхротроне. Гироско́п (от др.-греч. γῦρος «круг» + σκοπέω «смотрю») — устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено, относительно инерциальной системы отсчета. Простейший пример гироскопа — юла (волчок). Эффект Фарадея (продольный магнитооптический эффект Фарадея) — магнитооптический эффект, который заключается в том, что при распространении линейно-поляризованного света через оптически неактивное вещество, находящееся в магнитном поле, наблюдается вращение плоскости поляризации света. Теоретически, эффект Фарадея может проявляться и в вакууме в магнитных полях порядка 1011—1012 Гс. Генера́тор переме́нного то́ка (устаревшее «альтерна́тор») — электрическая машина, преобразующая механическую энергию в электрическую энергию переменного тока. Большинство генераторов переменного тока используют вращающееся магнитное поле. Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела. Углова́я ско́рость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Для вращения в двухмерном пространстве угловая скорость выражается числом, в трёхмерном пространстве представляется псевдовектором (аксиальным вектором), а в общем случае — кососимметрическим тензором.ОСНОВНЫЕ КОНЦЕПЦИИ | ANSHS Класс физики
ОСНОВНЫЕ ПОНЯТИЯ
МАГНИТНОЕ ПОЛЕ
магнитное поле земли
• Магнитное поле — это центральное понятие, используемое при описании магнитных явлений.
• Область или пространство вокруг намагниченного тела или токоведущей цепи, в которой может быть обнаружена результирующая магнитная сила.
• Магнитное поле состоит из воображаемых линий потока, исходящих от движущихся или вращающихся электрически заряженных частиц.Примеры включают спин протона и движение электронов по проводу в электрической цепи.
- Магнитное поле или линии потока движущейся заряженной частицы
МАГНИТНАЯ СИЛА
Магнитное поле объекта может создавать магнитную силу на других объектах с помощью магнитных полей. Эта сила и есть то, что мы называем магнетизмом.
Когда магнитное поле применяется к движущемуся электрическому заряду, например, движущемуся протону или электрическому току в проводе, сила, действующая на заряд, называется силой Лоренца.
Притяжение
Когда два магнита или магнитных объекта находятся близко друг к другу, возникает сила, которая притягивает полюса друг к другу.
- Сила притягивает N к S
Магниты также сильно притягивают ферромагнитные материалы, такие как железо, никель и кобальт.
Отталкивание
Когда два магнитных объекта имеют одинаковые полюса, обращенные друг к другу, магнитная сила раздвигает их.
- Сила раздвигает магнитные объекты
Магнитное и электрическое поля
Магнитное и электрическое поля одинаковы и различны.Они также взаимосвязаны.
Сходство электрических зарядов и магнетизма
Так же, как положительный (+) и отрицательный (-) электрические заряды притягиваются друг к другу, полюса N и S магнита притягиваются друг к другу.
В электричестве, как заряды, отталкиваются, и в магнетизме, как полюса.
Различные электрические заряды и магнетизм
Магнитное поле является дипольным полем. Это означает, что у каждого магнита должно быть два полюса.
С другой стороны, положительный (+) или отрицательный (-) электрический заряд может существовать отдельно.Электрические заряды называются монополями, поскольку они могут существовать без противоположного заряда.
• Монополь — одиночный магнитный полюс или электрический заряд
• Диполь — пара противоположных полюсов
• Так называемый магнитный момент является мерой силы диполя. Магнитные моменты выражаются кратными магнетонам Бора. Магнетон Бора имеет значение 9,27 x 10-24 джоулей / тесла.
ФОРМЫ МАГНЕТИЗМА
ДИАМАГНЕТИЗМ
— свойство объекта, которое заставляет его создавать слабое магнитное поле в противовес приложенному извне магнитному полю.Это форма магнетизма, которая проявляется веществом только в присутствии внешнего магнитного поля.
ПАРАМАГНЕТИЗМ
— это форма магнетизма, которая возникает только в присутствии внешнего магнитного поля. Парамагнитные материалы притягиваются к магнитным полям, следовательно, имеют относительную магнитную проницаемость больше единицы (или, что то же самое, положительную магнитную восприимчивость).
МОЛЕКУЛЯРНЫЙ МАГНИТ
— Одномолекулярный магнит или SMM — это объект, состоящий из молекул, каждая из которых ведет себя как отдельный суперпарамагнетик.Это отличается от магнита на основе молекул, в котором группа молекул ведет себя как магнит.
ФЕРРОМАГНЕТИЗМ
— это «нормальная» форма магнетизма, знакомая большинству людей, которая проявляется в подковообразных магнитах и магнитах на холодильник. Он отвечает за большую часть магнитного поведения, встречающегося в повседневной жизни. Согласно классическому тексту о ферромагнетизме, притяжение между магнитом и ферромагнитным материалом — это «качество магнетизма, впервые явное для древнего мира и для нас сегодня».
АНТИФЕРРОМАГНЕТИЗМ
— магнитные моменты атомов или молекул, обычно связанные со спинами электронов, выстраиваются по регулярной схеме с соседними спинами (на разных подрешетках), направленными в противоположных направлениях.
ФЕРРИМАГНЕТИЗМ
— ферримагнетик — это материал, в котором магнитные моменты атомов на разных подрешетках противоположны, как в антиферромагнетизме; однако в ферримагнетиках противодействующие моменты не равны, и спонтанная намагниченность сохраняется.
МЕТАМАГНЕТИЗМ
— это увеличение намагниченности материала при небольшом изменении внешнего магнитного поля. Метамагнитное поведение может иметь совершенно разные физические причины для разных типов метамагнетиков.
СУПЕРПАРАМАГНЕТИЗМ
— это форма магнетизма, которая возникает только в присутствии внешнего магнитного поля.
МАГНИТНЫЕ ПОЛЯ и СИЛЫ
Те же ситуации, которые создают магнитные поля (заряд, движущийся в токе или в атоме, и собственные магнитные диполи), также являются ситуациями, в которых магнитное поле оказывает влияние, создавая силу.Ниже приводится формула движущегося заряда; для сил на собственном диполе см магнитный диполь.
Когда заряженная частица движется через магнитное поле B, она ощущает силу F, заданную перекрестным произведением:
где — электрический заряд частицы, — вектор скорости частицы, — магнитное поле. Поскольку это перекрестное произведение, сила перпендикулярна как движению частицы, так и магнитному полю. Отсюда следует, что магнитная сила не действует на частицу; он может изменить направление движения частицы, но не может вызвать ее ускорение или замедление.Величина силы
где — угол между векторами и.
Одним из инструментов для определения направления вектора скорости движущегося заряда, магнитного поля и прилагаемой силы является маркировка указательного пальца «V», среднего пальца «B» и большого пальца «F» правой рукой. . При создании конфигурации, подобной оружию (средний палец пересекает указательный), пальцы представляют вектор скорости, вектор магнитного поля и вектор силы соответственно.См. Также правило правой руки.
Закон Ленца определяет направление индуцированной электродвижущей силы (ЭДС) и тока, возникающего в результате электромагнитной индукции. Немецкий физик Генрих Ленц сформулировал ее в 1834 году.
Нравится:
Нравится Загрузка …
магнитных терминов, используемых в магнитных цепях. Определение и формулы
Магнит и магнетизм Важные термины, определения и формулы
Магнитное поле или магнитная индукция (B)
Магнит или электромагнит создает магнитное поле.Поле, в котором магнит притягивает или отталкивает магнитные материалы, такие как железо, сталь и т. Д., Может быть определено как сила, действующая на движущийся заряд,
F = qxvx B
Где
- F = Сила,
- V = скорость частиц,
- B = величина поля.
Полезно знать:
Это векторная величина, а единица магнитного поля в системе СИ — Тесла, где 1 Тесла = (Ньютон x секунда) / (кулон x метр) 10000 Гаусс.Формула для магнитного поля в СИ: B = µ ○ (H + M), а в CGS — B = H + 4π M.
Провод, по которому проходит постоянный ток или постоянный магнит, создает магнитостатическое (канцелярское) поле и его величина и направление остаются прежними. При переменном токе или пульсирующем постоянном токе проводник создает переменное магнитное поле, которое непрерывно меняет свое направление и величину.
Также прочтите
Напряженность магнитного поля (H)
Величина намагничивающей силы (сколько силы она имеет для намагничивания, магнитные материалы, такие как железо, сталь и т. Д.) Называется силой магнитного поля, которая обозначается ( ЧАС).Он обратно пропорционален длине провода и прямо пропорционален току, проходящему по нему. В системе СИ единица измерения напряженности магнитного поля — Ампер / метр (А / м), это векторная величина, а формула СИ для напряженности магнитного поля:
H = NI / 1c
, где 1c = магнитный путь в метрах.
Магнитный поток (Φ)
Проще говоря, Магнитное поле x площадь, перпендикулярная магнитному полю (B), называется Магнитным потоком, который обозначается Φ или Φ м или Φ B .Или это величина магнитного поля или магнитных силовых линий, проходящих через поверхность, такую как проводящая область, пространство, воздух и т. Д. В системе СИ единица измерения магнитного потока — Wb (Вебер). Формула для нахождения магнитного потока в системе СИ:
Φ = BAc
Где
Ac = площадь в м 2
И единица измерения CGS и формула для Магнитного потока — Максвелл (M), а Φ = BAc Ac = площадь в см 2 соответственно.
Намагничивание (M)
Состояние намагничиваемого материала или процесс намагничивания магнитных материалов.Это плотность дипольных моментов постоянного магнита или электромагнита в магнитных материалах. Или магнитный момент (м) на единицу объема (v) магнитным полем называется намагниченностью. Единица намагничивания в системе СИ — ампер / метр (А / м), также это векторная величина. Формула SI для намагничивания:
M = m / V
, где
- m = общий магнитный момент
- и V = объем в м 3 .
Единица CGS и формула намагничивания: Emu / cm 3 и M = m / V соответственно, где m = общий магнитный момент, V = объем в см 3 и EMU = электромагнитные единицы.Это также может быть определено как M = (N / V) x m → M = nm ……. (N / V) = п. Где «m» — это магнитный момент, а «n» — это плотность магнитных моментов.
Магнитная проницаемость вакуума (µ ○ )
Говоря забавными словами, Пермь = Разрешение и способность — это особенность или умение что-то делать. Т.е. проницаемость (µ) — это способность материала, при помощи которого он легко намагничивается?
Магнитная проницаемость вакуума
Это величина сопротивления магнитному полю при формовании в вакууме.
Единица проницаемости в системе СИ — (H · м −1 ) или Ньютон на квадратный ампер (N · A −2 ). Единица СИ и формулы для магнитной проницаемости вакуума: Ньютон / Ампер 2 и µ ○ = 4πx10 -7 ≈ 1,2566370614 Г · м -1 соответственно. Единица CGS магнитной проницаемости вакуума — 1.
Полезно знать: Противоположность магнитной проницаемости — это магнитная относительность.
Полезно знать: известное магнитное соотношение: B = µH, где µ — проницаемость, которая является скалярной величиной, B — магнитное поле, а H — сила намагничивания или напряженность магнитного поля.
Индуктивность (L)
Индуктивность — это свойство проводника, катушки или провода, которое препятствует изменению тока, протекающего через них. Изменение тока, протекающего по проводнику, создает напряжение, называемое обратной ЭДС или электродвижущей силой.
Равномерность Изменение тока, протекающего через проводник или катушку, вызывает напряжение, которое называется самоиндуцированной ЭДС, а в любых соседних катушках или проводниках это называется взаимной индуктивностью. В системе СИ единица индуктивности (л) — Генри «H», формула:
L = µ ○ µN 2 Ac / 1c
Где
- N = число витков
- Ac = площадь в м 2
- 1c = магнитный путь в метрах
Единица измерения CGS и формула индуктивности — Генри «H» (Джозеф Генри) и L = 0.4π µN 2 Ac / 1c x10 -8 соответственно
где;
- L = индуктивность
- N = витки
- Ac = площадь в см 2
- 1c = магнитный путь в см.
Полезно знать : 1 H = 1 Вт / А (Один Генри = 1 Вебер на Ампер)
Формула собственной индуктивности
L = µ ○ (N 2 xA) / л
Где:
- L = в Генри
- μ ο = проницаемость свободного пространства (4.π.10 -7 )
- N = количество витков
- A = площадь внутренней сердцевины (π.r 2 ) в м 2
- l = длина катушки в метрах
Формула взаимной индуктивности
M = μ ο μ r N 1 N 2 A / l
Где:
- µ o = проницаемость .π.10 -7 )
- µ r = относительная проницаемость сердечника из мягкого железа
- N = количество витков катушки
- A = площадь поперечного сечения в м 2
- l = длина катушек в метрах
Связанные сообщения:
Voltage или E.М.Ф. (В)
Разница электрических потенциалов между двумя точками называется напряжением. Или работа, совершаемая на единицу заряда в статическом электрическом поле по перемещению заряда между двумя точками, поэтому уравнение принимает вид
В = Вт / q или E / q.
Где;
- В = напряжение
- E = энергия в джоулях
- q = заряд в кулонах
Или электрическая потенциальная энергия на единицу заряда называется напряжением.
По закону Ома напряжение = V = I x R, где I = ток в амперах и R = сопротивление в омах (Ом)
Единицей измерения напряжения в системе СИ является вольт (В) или джоуль на кулон.Где 1 В = 1 Джоуль / 1 Кулон
Формула СИ для напряжения:
В = -N dΦ / dt
Где;
- N = количество витков катушки
- dΦ = скорость изменения потока
- t = время
Полезно знать: Другие связанные слова, используемые для напряжений и ЭДС: Разница электрических потенциалов , Электрическое напряжение , Электрическое давление, разность потенциалов, Pd, ЭДС, электродвижущая сила и это скалярная величина, и это тип электрической энергии.
В следующей таблице показаны все вышеперечисленные основные термины, используемые в магнитных цепях с единицами измерения SI и CGS и формулами.
| Количество | Обозначение | Единица СИ | Уравнение СИ | Единица CGS | Фактор 9709 9047 9703 9047 9703 9047 Преобразование 9703 9047 9047 Уравнение 9047 CGS 970 | B | Тесла (T) | B = µ ○ (H + M) | Gauss (G) | B = H + 4π M | 1T = 10 4 G | |
| Магнитное поле Прочность | H | Ампер / метр (А / м) | H = NI / 1c 1c = магнитный путь в м | Эрстед Oe | H = 0.4πNI / 1c 1c = магнитный путь в см | 1A / м = 4πx10 -3 Oe | |||||
| Магнитный поток | Φ | Weber (Wb) | Φ = BA000 м 2 | Максвелл M | Φ = BAc Ac = площадь в см 2 | 1Wb = 10 8 M | |||||
| Намагниченность | M намагниченность | M / м) | M = m / V m = Общий магнитный момент, V = объем в м 3 | Emu / cm 3 Где EMU = Электромагнитные блоки | M = m / V м = общий магнитный момент, V = объем в см 3 | 1A / м = 10- 3 emu / cm 3 | |||||
| Магнитная проницаемость вакуума | µ ○ | Ньютон / Ампер 2 | µ ○ 90 179 = 4πx10 -7 ≈ 1.2566370614 H · м −1 | 1 | — | 4πx10 -7 | |||||
| Индуктивность | L | Генри | L = µ ○ N = Ac Оборотов Ac = Площадь, м 2 1c = Магнитный путь, м | Генри | L = 0,4π мкН 2 Ac / 1c x10 -8 N = Оборотов Ac = Площадь в см 2 1c = магнитный путь в см | 1 | |||||
| Напряжение или ЭДС | В | Вольт | В = — NdΦ / dt N = Оборотов | В = -10 -8 xNxdΦ / dt N = Оборотов | 1 |
Ниже приводится таблица в формате изображения для справки.
Похожие сообщения:
Магнитное поле из-за стержневого магнита | Примечания, видео, контроль качества и тесты | 12 класс> Физика> Основы магнетизма
Магнитное поле стержневого магнита
Магнитное поле стержневого магнита
Можно рассчитать напряженность магнитного поля в любой точке вокруг стержневого магнита. Однако важны измерения в двух точках: в точке на оси и в точке на экваториальной линии стержневого магнита.3} $$
Ссылка
Ману Кумар Хатри, Манодж Кумар Тхапа и др. Принципы физики . Катманду: публикация Ayam PVT LTD, 2010.
S.K. Гаутам, Дж. М. Прадхан. Учебник по физике . Катманду: публикация Сурьи, 2003.
.20.1 Магнитные поля, силовые линии и сила — Физика
20.1 Магнитные поля, силовые линии и сила — Физика | OpenStaxSkip к ContentPhysics20.1 Магнитные поля, силовые линии и сила- Предисловие
-
- Введение
- 1.1 Физика: определения и приложения
- 1.2 Научные методы
- 1.3 Язык физики: физические величины и единицы
- Ключевые термины
- Резюме раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Задача производительности
-
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- 2 Движение в одном измерении
- Введение
- 2.1 Относительное движение, расстояние и смещение
- 2.2 Скорость и скорость
- 2.3 Графики зависимости положения от времени
- 2.4 Графики зависимости скорости от времени
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
-
- Элементы концепции
- Элементы критического мышления
- Проблемы
- Задача производительности
-
- Множественный выбор
- Краткий ответ
- Расширенный ответ
-
- Введение
- 3.1 Ускорение
- 3.2 Представление ускорения с помощью уравнений и графиков
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- 14 Задача производительности
- Краткий ответ
- Расширенный ответ
- Введение
- 4.1 Сила
- 4,2 Первый закон движения Ньютона: инерция
- 4,3 Второй закон движения Ньютона
- 4,4 Третий закон движения Ньютона
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
-
- Элементы концепции
- Критические элементы Элементы
- Проблемы
- Задача производительности
-
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 5.1 Сложение и вычитание векторов: графические методы
- 5.2 Сложение и вычитание векторов: аналитические методы
- 5.3 Движение снаряда
- 5.4 Наклонные плоскости
- 5.5 Простое гармоническое движение
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
- Элементы концепции
- Элементы критического мышления
- Проблемы
- Задача производительности
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Элементы концепции
- Элементы критического мышления
- Проблемы с производительностью
- Задачи
- Множественный выбор
- Краткий ответ
- Расширенный ответ
- Введение
- 7.1 Законы движения планет Кеплера
- 7.2 Закон всемирного тяготения Ньютона и общая теория относительности Эйнштейна
- Ключевые термины
- Резюме раздела
- Ключевые уравнения
-
- Элементы концепции
- Элементы концепции
- Задачи для критического мышления
- Задачи для выполнения задач
-
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 8.1 Линейный импульс, сила и импульс
- 8.2 Сохранение импульса
- 8.3 Упругие и неупругие столкновения
- Ключевые термины
- Резюме раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Критическое мышление 166 Проблемы с производительностью
Задача
- Множественный выбор
- Краткий ответ
- Расширенный ответ
- Введение
- 9.1 Работа, мощность и теорема работы-энергии
- 9.2 Механическая энергия и сохранение энергии
- 9.3 Простые машины
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Задача производительности
-
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 10.1 Постулаты специальной теории относительности
- 10.2 Последствия специальной теории относительности
- Ключевые термины
- Краткое изложение раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- 14 Выборочная задача 9066
- Краткий ответ
- Расширенный ответ
- Введение
- 11.1 Температура и тепловая энергия
- 11.2 Тепло, удельная теплоемкость и теплопередача
- 11.3 Фазовое изменение и скрытая теплота
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Элементы критического мышления
- Задача производительности
-
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 12.1 Нулевой закон термодинамики: тепловое равновесие
- 12.2 Первый закон термодинамики: тепловая энергия и работа
- 12.3 Второй закон термодинамики: энтропия
- 12.4 Приложения термодинамики: тепловые двигатели, тепловые насосы и холодильники
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Задача производительности
-
- Множественный выбор
- Короткий ответ
- 146
- Введение
- 13.1 Типы волн
- 13.2 Свойства волн: скорость, амплитуда, частота и период
- 13.3 Взаимодействие с волнами: суперпозиция и интерференция
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
-
- Элементы концепции
- Элементы для критического мышления
- Проблемы
- Задача производительности
-
- Множественный выбор
- Краткий ответ
- Расширенный ответ
- Введение
- 14.1 Скорость звука, частота и длина волны
- 14.2 Интенсивность звука и уровень звука
- 14.3 Эффект Доплера и звуковые удары
- 14.4 Звуковые помехи и резонанс
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
-
- Элементы концепции
- Элементы критического мышления
- Проблемы
- Задача производительности
-
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение .1 Электромагнитный спектр
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- 14 Задание на выполнение нескольких задач
- Введение
- 16,1 Отражение
- 16.2 Refraction
- 16.3 Линзы
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
-
- Элементы концепции
- Элементы критического мышления
- Проблемы
- Задача производительности
-
- Выбор ответа
-
- Расширенный отклик
- Введение
- 17.1 Понимание дифракции и интерференции
- 17.2 Приложения дифракции, интерференции и когерентности
- Ключевые термины
- Резюме раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Задача производительности 67
- 907 907 Ответ
- Расширенный ответ
- Введение
- 18.1 Электрические заряды, сохранение заряда и перенос заряда
- 18.2 Закон Кулона
- 18.3 Электрическое поле
- 18.4 Электрический потенциал
- 18.5 Конденсаторы и диэлектрики
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
-
- Концептуальные элементы
- Критически важные задачи для мышления
- Задачи для критического мышления 9016
-
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 19.1 Закон Ома
- 19.2 Последовательные схемы
- 19.3 Параллельные схемы
- 19.4 Электроэнергия
- Ключевые термины
- Резюме раздела
22.3 Магнитные поля и линии магнитного поля — College Physics
22.3 Линии — колледж физики | OpenStaxSkip к контенту- Предисловие
- 1 Введение: Природа науки и физики
- Введение в науку и область физики, физических величин и единиц измерения
- 1.1 Физика: Введение
- 1.2 Физические величины и единицы
- 1.3 Точность, прецизионность и значащие числа
- 1.4 Приближение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
Одномерная кинематика - 2.1 Смещение
- 2.2 Векторы, скаляры и системы координат
- 2.3 Время, скорость и скорость
- 2.4 Ускорение
- 2.5 Уравнения движения для постоянного ускорения в одном измерении
- 2.6 Основы решения проблем для одномерной кинематики
- 2.7 Падающие объекты
- 2.8 Графический анализ одномерного движения
- Глоссарий
- Краткое содержание раздела Вопросы
- Задачи и упражнения
- Введение в двумерную кинематику
- 3.1 Кинематика в двух измерениях: введение
- 3.2 Сложение и вычитание векторов: графические методы
- 3.3 Сложение и вычитание векторов: аналитические методы
- 3.4 Движение снаряда
- 3.5 Добавление скоростей
- Глоссарий
- Краткое содержание раздела
- Задачи и упражнения
- Введение в динамику: законы движения Ньютона
- 4.1 Развитие концепции силы
- 4.2 Первый закон движения Ньютона: инерция
- 4.3 Второй закон движения Ньютона: концепция системы
- 4.4 Третий закон движения Ньютона: симметрия сил
- 4.5 Примеры нормалей, натяжения и других сил
- 4.6 Стратегии решения проблем
- 4.7 Дальнейшие применения законов движения Ньютона
- 4.8 Расширенная тема: Четыре основных силы — Введение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение: дальнейшие применения законов Ньютона
- 5.1 Трение
- 5.2 Силы сопротивления
- 5.3 Упругость: напряжение и деформация
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 6.1 Угол вращения и угловая скорость
- 6.2 Центростремительное ускорение
- 6.3 Центростремительная сила
- 6.4 Фиктивные силы и неинерциальные системы координат: сила Кориолиса
- 6.5 Универсальный закон тяготения Ньютона
- 6.6 Спутники и законы Кеплера: аргумент в пользу простоты
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в линейный импульс и столкновения
- 8.1 Линейный импульс и сила
- 8.2 Импульс
- 8.3 Сохранение импульса
- 8.4 Упругие столкновения в одном измерении
- 8.5 Неупругие столкновения в одном измерении
- 8.6 Столкновения точечных масс в двух измерениях
- 8.7 Введение в ракетное движение
- Глоссарий
- Резюме раздела Концептуальные вопросы
- Задачи и упражнения
- Введение в статику и крутящий момент
- 9.1 Первое условие равновесия
- 9.2 Второе условие равновесия
- 9.3 Стабильность
- 9.4 Приложения статики, включая стратегии решения проблем
- 9.5 Простые механизмы
- 9.6 Силы и моменты в мышцах и суставах
- Глоссарий
- Резюме раздела
- Концептуальные вопросы Задачи и упражнения
- Введение во вращательное движение и угловой момент
- 10.1 Угловое ускорение
- 10.2 Кинематика вращательного движения
- 10.3 Динамика вращательного движения: вращательная инерция
- 10.4 Кинетическая энергия вращения: новый взгляд на работу и энергию
- 10,5 Угловой момент и его сохранение
- 10,6 Столкновения двух протяженных тел
- 10.7 Гироскопические эффекты: векторные аспекты углового момента
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в статику жидкостей
- 11.1 Что такое жидкость?
- 11.2 Плотность
- 11.3 Давление
- 11.4 Изменение давления в зависимости от глубины в жидкости
- 11.5 Принцип Паскаля
- 11.6 Измерение манометрического давления, абсолютного давления и давления
- 11.7 Принцип Архимеда
- 11.8 Принцип Архимеда в адгезии жидкости и адгезии : Поверхностное натяжение и капиллярное действие
- 11.9 Давление в теле
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в динамику жидкости Биологические и медицинские приложения
- 12.1 Расход и его связь со скоростью
- 12.2 Уравнение Бернулли
- 12.3 Наиболее общие приложения уравнения Бернулли
- 12.4 Вязкость и ламинарный поток; Закон Пуазейля.
- Введение в температуру, кинетическую теорию и законы газа
- 13.1 Температура
- 13.2 Термическое расширение твердых тел и жидкостей
- 13.3 Закон идеального газа
- 13.4 Кинетическая теория: атомное и молекулярное объяснение давления и температуры
- 13,5 фазовые изменения
- 13,6 Влажность, испарение и кипение
- Введение в методы теплопередачи
- 14.1 Тепло
- 14.2 Изменение температуры и теплоемкость
- 14.3 Фазовое изменение и скрытая теплота
- 14.4 Методы теплопередачи
- 14.5 Проводимость
- 14.6 Конвекция
- 14.7 Излучение
- Глоссарий
- Вопросы по концепции
- Вопросы по концепции И упражнения
- Введение в термодинамику
- 15.1 Первый закон термодинамики
- 15.2 Первый закон термодинамики и некоторые простые процессы
- 15.3 Введение во второй закон термодинамики: тепловые двигатели и их эффективность
- 15.4 Совершенный тепловой двигатель Карно: новый закон термодинамики
- 15.5 Приложения термодинамики: тепловые насосы и холодильники
- 15,6 Энтропия и второй закон термодинамики: Беспорядок и недоступность энергии
- 15.7 Статистическая интерпретация энтропии и второй закон термодинамики: основное объяснение
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
Базовые количества
| (1) |
| Ампер | (7) |
Ток одинаков на всех компонентах, проводящих электричество, это от до переменной .
Плотность тока ,
| (8) |
| (9) |
| (10) |
| (11) |
Напряжение — это энергия на заряд, а электрическое поле — это сила на заряд.
Напряжение измеряется как разница в двух точках электрическое поле или цепь (или точка относительно эталона точка называется земля ), т.е.е., это по переменной .
Мощность — это скорость преобразования энергии. Преобразование 1 Джоуля энергии за 1 секунду соответствует мощности 1 Вт:
| (12) |
| (13) |
Энергия также может быть измерена в киловатт-часов (кВтч) Джоули.
- Электрическая сила на единицу заряда — электрическое поле; Энергия на единицу заряда — это напряжение напряжение.
- Сила тяжести на единицу массы — гравитационное поле; Энергия на единицу массы равна . Хотя это количество не явно определенное, оно аналогично напряжению в электрическом поле.
Интенсивность магнитного эффекта (линий на единицу площади в магнитной поле или поток) измеряется плотностью магнитного потока в теслах.Магнитное поле Земли составляет от 25 до 65 мкТесла, аппарат МРТ составляет 1,5 или 3 тесла.
Магнитный поток через площадь (в нормальном направление области)
| (16) |
Когда и находятся в одном направлении (), а если 1 тесла и 1 квадратный метр, то поток 1 Weber .
В магнитном поле на заряд действует сила движется со скоростью:
| (17) |

