Магнитные силы – Магнитное поле – FIZI4KA

Магнитная сила Ампера

Возьмем прямой проводник, изготовленный из алюминия, и подвесим его на тонких и гибких проводах таким образом, чтобы он находился между полюсами подковообразного постоянного магнита как на рисунке (а). Если в проводнике пропустить ток, проводник отклонится от положения равновесия — рисунок (б). Причиной такого отклонения является сила, действующая на проводник с током со стороны магнитного поля. Доказал наличие этой силы и выяснил, от чего зависят ее значение и направление, французский физик, математик и химик Андре Мари Ампер. Именно поэтому это явление называют магнитной силой Ампера.

 

Сила Ампера — это сила, с которой магнитное поле действует на проводник с током.

Сила Ампера прямо пропорциональна силе тока в проводнике и длине активной части проводника (то есть части, которая расположена в магнитном поле). Сила Ампера увеличивается с увеличением индукции магнитного поля и зависит от того, под каким углом к ​​линиям магнитной индукции расположен проводник.

Значение силы Ампера (F_A) вычисляют по формуле:

где В — магнитная индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Угол α — это угол между направлением вектора магнитной индукции и направлением тока в проводнике

Обратите внимание! Магнитное поле не будет действовать на проводник с током (F_A= 0), если проводник расположен параллельно магнитным линиям поля (sin α = 0).

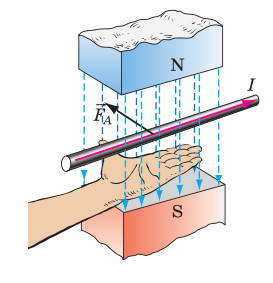Определение
направления силы Ампера
по правилу левой руки

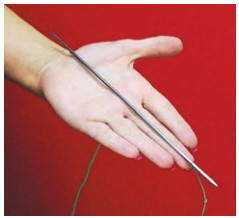
Чтобы определить направление силы Ампера, используют правило левой руки:

Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.

На рисунке слева показано определения направления силы Ампера, действующая на проводник, расположенный в однородном магнитном поле. Давайте определим направление тока в проводнике, направление магнитной индукции и направление силы Ампера.

Получаем формулу для определения модуля магнитной индукции

Если проводник расположен перпендикулярно к линиям магнитной индукции (α = 90 °, sin α = 1), то поле действует на проводник с максимальной силой:

Отсюда получаем формулу для определения модуля магнитной индукции:

Обратите внимание! Значение магнитной индукции не зависит ни от силы тока в проводнике, ни от длины проводника, а зависит только от свойств магнитного поля.

Например, если уменьшить силу тока в проводнике, то изменится и сила Ампера, с которой магнитное поле действует на проводник, а вот значение магнитной индукции останется неизменным.

В СИ единица магнитной индукции — тесла (Тл), единица силы — ньютон (Н), силы тока — ампер (А), длины — метр (м), поэтому:

1Тл — это индукция такого однородного магнитного поля, которое действует с максимальной силой 1 Н на проводник длиной 1 м, в котором течет ток силой 1 А.

Проверочные задачи по теме: магнитное взаимодействие токов и сила Ампера

Задача 1. Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.

Анализ задачи:

Вокруг любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как вести себя проводники.

Решение:

В ходе решения выполним объяснительные рисунки: изобразим проводники А и В, покажем направление тока в них и др.

Определим направление силы Ампера, действующая на проводник А, находящегося в магнитном поле проводника В.

1) С помощью правила буравчика определим направление линий магнитной индукции магнитного поля, созданного проводником В (рисунок слева). Выясняется, что у проводника А магнитные линии направлены к нам (отметка «•»).

2) Воспользовавшись правилом левой руки, определим направление силы Ампера, действующая на проводник А со стороны магнитного поля проводника В.

3) Приходим к выводу: проводник А привлекается к проводнику В.

Теперь найдем направление силы Ампера, действующая на проводник В, находится в магнитном поле проводника А.

1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рисунок справа). Выясняется, что у проводника В магнитные линии направлены от нас (отметка «х»).

2) Определим направление силы Ампера, действующая на проводник В.

3) Приходим к выводу: проводник В привлекается к проводнику А.

Ответ: два параллельных проводника, в которых текут токи одного направления, действительно притягиваются.

Задача 2. Прямой проводник (стержень) длиной 0,1 м массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитных линий поля). Ток какой силы и в каком направлении следует пропустить в стержне, чтобы он не давил на опору (завис в магнитном поле)?

Анализ задачи:

Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при следующих условиях:

1. сила Ампера будет направлена ​​противоположно силе тяжести (то есть вертикально вверх)
2. значение силы Ампера равна значению силы тяжести F_A =  F_тяж

Направление тока определим, воспользовавшись правилом левой руки.

Решение:

Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90 ° большой палец был направлен вертикально вверх. Четыре вытянутые пальцы укажут направление от нас. Итак, ток в проводнике следует направить от нас.

Учитываем, что F_A =  F_тяж.  F_A= BIlsinα, где sin α = 1; F_тяж = mg

Из последнего выражения найдем силу тока: I = mg/Bl

Проверим единицу, найдем значение искомой величины.

Ответ: I = 8 А; Ток в направлении от нас.

Подводим итоги

Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера вычисляют по формуле: F_A= BIlsinα, где B — индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Для определения направления магнитной силы Ампера используют правило левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.

www.polnaja-jenciklopedija.ru

Электрические и магнитные силы

Физика > Электрические и магнитные силы

 

Как электрическая и магнитная сила влияют на траекторию движения заряженной частицы в поле: сила Лоренца, линии магнитного поля, уравнения, правило правой руки.

Траектория заряженной частички подчиняется электрической и магнитной силам, но проявляют они себя по-разному.

Задача обучения

• Сравнить влияние обеих сил на заряженную частичку.

Основные пункты

• Сила на заряженной частичке, созданная электрическим полем, направляется параллельно его вектору при положительном знаке и антипараллельно при отрицательном. Она не основывается на скорости частички.
• Магнитная сила выступает ортогональной вектору магнитного поля и основывается на скорости частички. Для определения направленности используют правило правой руки.
• Над заряженной частичкой может функционировать электрическое поле, но не магнитное.
• Сила Лоренца – комбинация обеих сил.
• На положительных зарядах электрические линии создаются, а заканчиваются на отрицательных. Линии изолированного заряда располагаются радиально наружу, касаясь электрического поля.
• Линии магнитного поля создаются на северном полюсе и заканчиваются на южном. Магнитные полюса не пребывают в изоляции и касаются магнитного поля.

Термин

• Ортогональные – расположены перпендикулярно друг другу.

Электрические и магнитные силы

Зараженные частички испытывают на себе влияние электрических и магнитных сил. Но результирующее изменение траектории будет отличаться, если рассматривать каждую по отдельности.

Электростатическая и магнитная силы на заряженной частичке

В статическом стабильном электрическом поле сила:

F = qE (F – вектор силы, q – заряд, E – вектор электрического поля). В положительном заряде направленность F идентична E, а в отрицательном будет противоположной. Электрическое поле можно установить большим зарядом Q, влияющим на меньший q на дистанции r:

Не забывайте, что электрическая сила располагается параллельно электрическому полю. Ее коррекция приравнивается к нулю:

▽ × Е = 0

Получается, что электрическое поле способно функционировать, а заряд последует за касательной линией.

А вот магнитная сила на заряженной частичке будет ортогональна к магнитному полю, поэтому:

F = qv × B = qvBsinθ (В – вектор магнитного поля, v – скорость частицы, а θ – угол между магнитным полем и скоростью частиц). Правило правой руки поможет вычислить направленность F.

Перемещающиеся заряды ощущают влияние магнитного поля. Это одна из наиболее распространенных сил. Ее направленность выступает перпендикулярной плоскости и соответствует правилу правой руки. Величина пропорциональна q, v, B и синусу угла между v и B

Если скорость частички выровняется параллельно по отношению к магнитному полю или приравняется к нулю, то и магнитная сила достигнет 0. И в этом отличие от электрического варианта, где скорость частички никак не влияет на величину или направленность электрической силы.

Зависимость от угла также приводит к тому, что заряженные частички перемещаются перпендикулярно по отношению к линиям магнитного поля, выполняя круговые/спиральные движения. Стоит отметить, что магнитное поле не функционирует при круговой траектории, так как частичка возвращается на исходную точку:

W = ∮B ⋅ dr = 0

Сила Лоренца

Передает сложенные электрические и магнитные силы на заряженной частичке. Сила высчитывается уравнением:

F = q [Е + vBsinθ]

Электрические и магнитные линии

Линии электрического поля из положительно изолированного заряда выглядят как последовательность радиально направленных линий, установленных наружу от заряда. Если же заряд несет отрицательный знак, то направленность поля меняется на противоположную. Завиток электрической линии приравнивается к 0.

Электрическое поле сосредоточено вокруг трех разных точечных зарядов: (а) – положительный, (b) – отрицательный с равной величиной, (с) – больший отрицательный заряд

Если активировано несколько зарядов, то линии поля создаются на положительных и заканчиваются в отрицательных. В магнитах они возникают на северном полюсе (+) и завершаются на южном (-). Но они путешествуют парами, поэтому завиток магнитного поля не всегда приравнивается к нулю. Если у частичек есть ненулевой компонент скорости, то они будут вращаться вокруг линий.

На этой модели видны два противоположных полюса: северный (+) и южный (-). Они разделены дистанцией (d) и формируют линии

Можно создать магнитное поле током с линиями поля. На схеме отобразится в виде концентрических окружностей вокруг проводящего ток провода. В любой точке магнитную силу можно будет вычислить по правилу правой руки.

---

v-kosmose.com

Конспект "Магнитное поле. Теория, формулы, схемы"

Подобно тому, как покоящийся электрический заряд действует на другой заряд посредством электрического поля, электрический ток действует на другой ток посредством магнитного поля. Действие магнитного поля на постоянные магниты сводится к действию его на заряды, движущиеся в атомах вещества и создающие микроскопические круговые токи.

Учение об электромагнетизме основано на двух положениях:

• магнитное поле действует на движущиеся заряды и токи;
• магнитное поле возникает вокруг токов и движущихся зарядов.

Взаимодействие магнитов

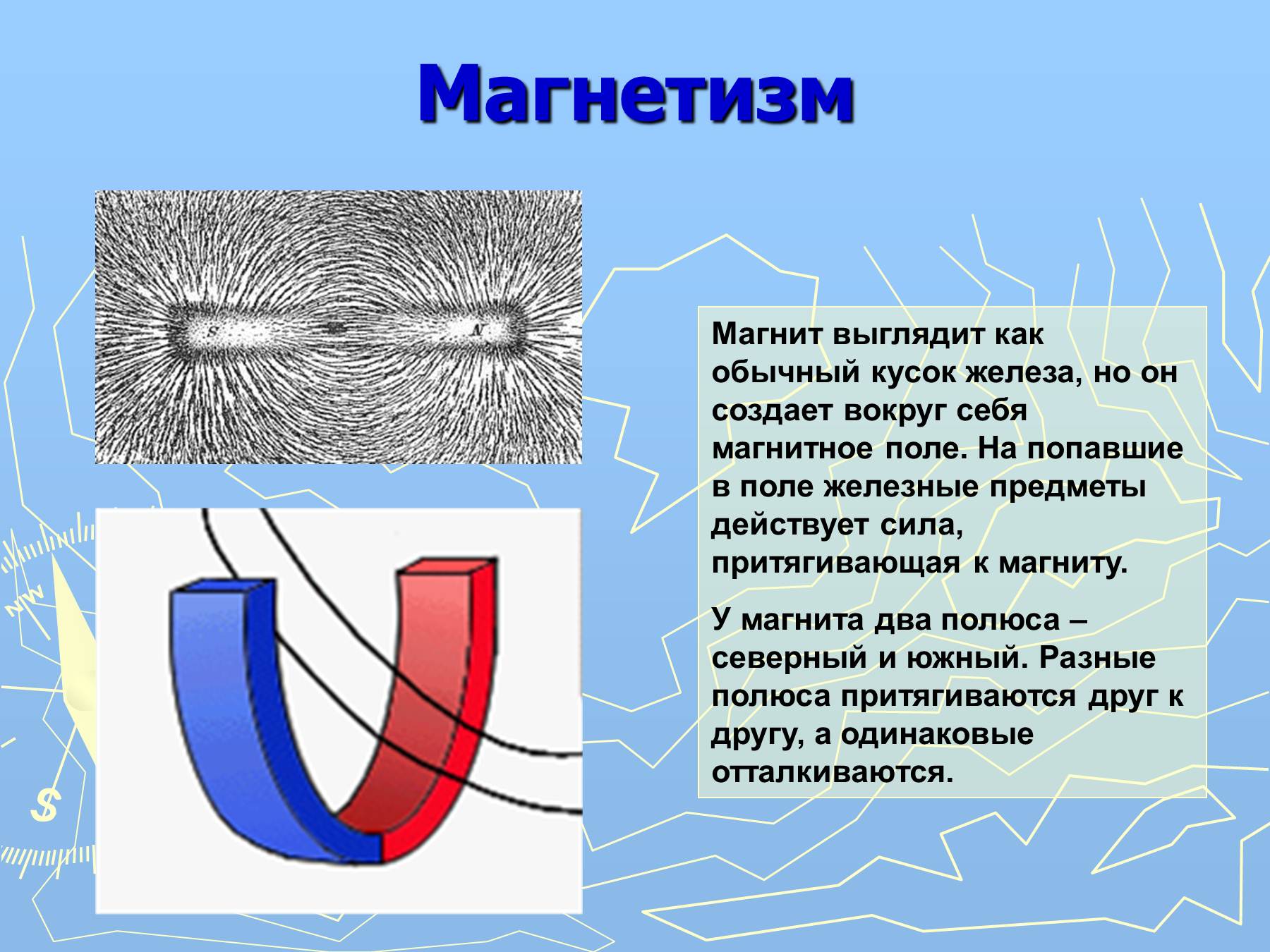
Постоянный магнит (или магнитная стрелка) ориентируется вдоль магнитного меридиана Земли. Тот его конец, который указывает на север, называется северным полюсом (N), а противоположный конец — южным полюсом (S). Приближая два магнита друг к другу, заметим, что одноименные их полюсы отталкиваются, а разноименные — притягиваются (рис. 1).

Если разделить полюса, разрезав постоянный магнит на две части, то мы обнаружим, что каждая из них тоже будет иметь два полюса, т. е. будет постоянным магнитом (рис. 2). Оба полюса — северный и южный, — неотделимые друг от друга, равноправны.

 

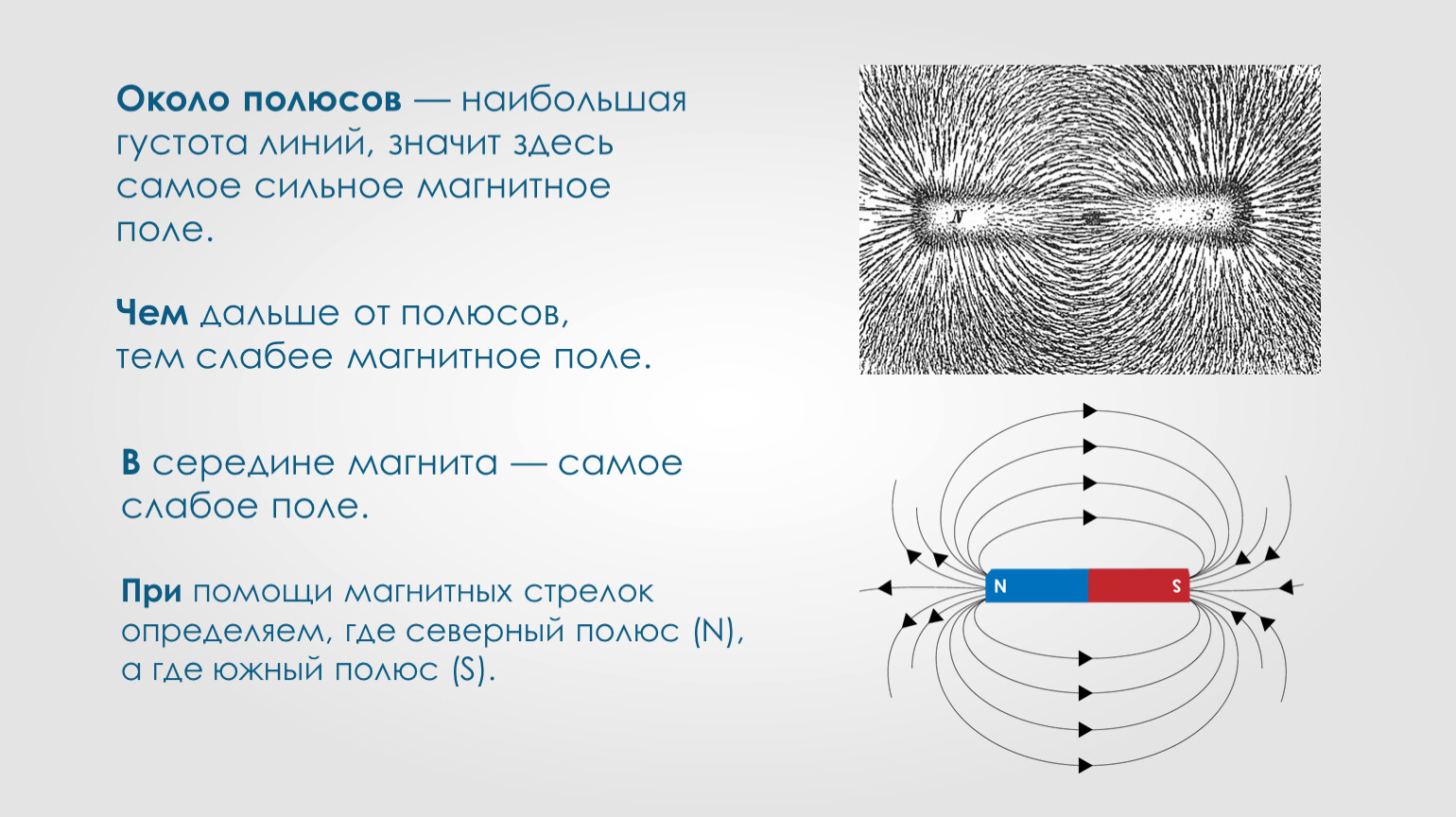
Магнитное поле, создаваемое Землей или постоянными магнитами, изображается, подобно электрическому полю, магнитными силовыми линиями. Картину силовых линий магнитного поля какого-либо магнита можно получить, помещая над ним лист бумаги, на котором насыпаны равномерным слоем железные опилки. Попадая в магнитное поле, опилки намагничиваются — у каждой из них появляется северный и южный полюсы. Противоположные полюсы стремятся сблизиться друг с другом, но этому мешает трение опилок о бумагу. Если постучать по бумаге пальцем, трение уменьшится и опилки притянутся друг к другу, образуя цепочки, изображающие линии магнитного поля.

 

На рис. 3 показано расположение в поле прямого магнита опилок и маленьких магнитных стрелок, указывающих направление линий магнитного поля. За это направление принято направление северного полюса магнитной стрелки.

 

Опыт Эрстэда. Магнитное поле тока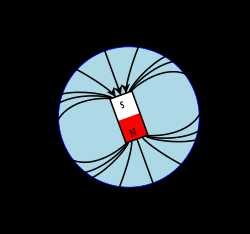

В начале XIX в. датский ученый Эрстэд сделал важное открытие, обнаружив действие электрического тока на постоянные магниты. Он поместил длинный провод вблизи магнитной стрелки. При пропускании по проводу тока стрелка поворачивалась, стремясь расположиться перпендикулярно ему (рис. 4). Это можно было объяснить возникновением вокруг проводника магнитного поля.

 

Магнитные силовые линии поля, созданного прямым проводником с током, представляют собой концентрические окружности, расположенные в перпендикулярной к нему плоскости, с центрами в точке, через которую проходит ток (рис. 5). Направление линий определяется правилом правого винта:

Если винт вращать по направлению линий поля, он будет двигаться в направлении тока в проводнике.

Силовой характеристикой магнитного поля является вектор магнитной индукции B. В каждой точке он направлен по касательной к линии поля. Линии электрического поля начинаются на положительных зарядах и оканчиваются на отрицательных, а сила, действующая в этом поле на заряд, направлена по касательной к линии в каждой ее точке. В отличие от электрического, линии магнитного поля замкнуты, что связано с отсутствием в природе «магнитных зарядов».

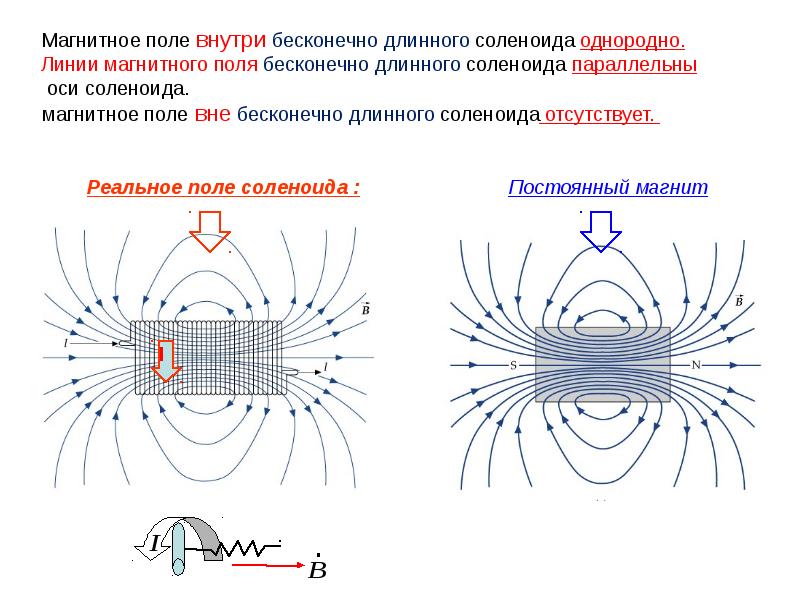
Магнитное поле тока принципиально ничем не отличается от поля, созданного постоянным магнитом. В этом смысле аналогом плоского магнита является длинный соленоид — катушка из провода, длина которой значительно больше ее диаметра. Схема линий созданного им магнитного поля, изображенная на рис. 6, аналогична таковой для плоского магнита (рис. 3). Кружочками обозначены сечения провода, образующего обмотку соленоида. Токи, текущие по проводу от наблюдателя, обозначены крестиками, а токи противоположного направления — к наблюдателю — обозначены точками. Такие же обозначения приняты и для линий магнитного поля, когда они перпендикулярны плоскости чертежа (рис. 7 а, б).

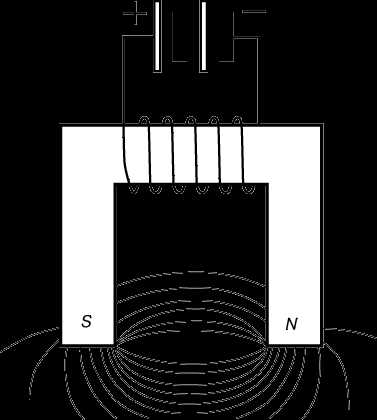
Направление тока в обмотке соленоида и направление линий магнитного поля внутри него также связаны правилом правого винта, которое в этом случае формулируется так:

Если смотреть вдоль оси соленоида, то текущий по направлению часовой стрелки ток создает в нем магнитное поле, направление которого совпадает с направлением движения правого винта (рис. 8)

Исходя из этого правила, легко сообразить, что у соленоида, изображенного на рис. 6, северным полюсом служит правый его конец, а южным — левый.

Магнитное поле внутри соленоида является однородным — вектор магнитной индукции имеет там постоянное значение (B = const). В этом отношении соленоид подобен плоскому конденсатору, внутри которого создается однородное электрическое поле.

Сила, действующая в магнитном поле на проводник с током

Опытным путем было установлено, что на проводник с током в магнитном поле действует сила. В однородном поле прямолинейный проводник длиной l, по которому течет ток I, расположенный перпендикулярно вектору поля B, испытывает действие силы: F = I l B.

Направление силы определяется правилом левой руки:

Если четыре вытянутых пальца левой руки расположить по направлению тока в проводнике, а ладонь — перпендикулярно вектору B, то отставленный большой палец укажет направление силы, действующей на проводник (рис. 9).

Следует отметить, что сила, действующая на проводник с током в магнитном поле, направлена не по касательной к его силовым линиям, подобно электрической силе, а перпендикулярна им. На проводник, расположенный вдоль силовых линий, магнитная сила не действует.

Уравнение F = IlB позволяет дать количественную характеристику индукции магнитного поля.

Отношение  не зависит от свойств проводника и характеризует само магнитное поле.

Модуль вектора магнитной индукции B численно равен силе, действующей на расположенный перпендикулярно к нему проводник единичной длины, по которому течет ток силой один ампер.

В системе СИ единицей индукции магнитного поля служит тесла (Тл):

---

Магнитное поле. Таблицы, схемы, формулы

(Взаимодействие магнитов, опыт Эрстеда, вектор магнитной индукции, направление вектора, принцип суперпозиции. Графическое изображение магнитных полей, линии магнитной индукции. Магнитный поток, энергетическая характеристика поля. Магнитные силы, сила Ампера, сила Лоренца. Движение заряженных частиц в магнитном поле. Магнитные свойства вещества, гипотеза Ампера)

Дополнительные материалы по теме: Электромагнитные явления

---

Конспект по теме «Магнитное поле. Теория, формулы, схемы».

Следующая тема «Электромагнитная индукция»

uchitel.pro

Магнитное поле. Источники и свойства. Правила и применение

При подключении к двум параллельным проводникам электрического тока, они будут притягиваться или отталкиваться, в зависимости от направления (полярности) подключенного тока. Это объясняется явлением возникновения материи особого рода вокруг этих проводников. Эта материя называется магнитное поле (МП). Магнитной силой называется сила, с которой проводники действуют друг на друга.

Теория магнетизма возникла еще в древности, в античной цивилизации Азии. В Магнезии в горах нашли особую породу, куски которой могли притягиваться между собой. По названию места эту породу назвали «магнетиками». Стержневой магнит содержит два полюса. На полюсах особенно сильно обнаруживаются его магнитные свойства.

Магнит, висящий на нитке, своими полюсами будет показывать стороны горизонта. Его полюса будут повернуты на север и юг. На таком принципе действует устройство компаса. Разноименные полюсы двух магнитов притягиваются, а одноименные отталкиваются.

Ученые обнаружили, что намагниченная стрелка, находящаяся возле проводника, отклоняется при прохождении по нему электрического тока. Это говорит о том, что вокруг него образуется МП.

Магнитное поле оказывает влияние на:

• Перемещающиеся электрические заряды.
• Вещества, называемые ферромагнетиками: железо, чугун, их сплавы.

Постоянные магниты – тела, имеющие общий магнитный момент заряженных частиц (электронов).

1 — Южный полюс магнита
2 — Северный полюс магнита
3 — МП на примере металлических опилок
4 — Направление магнитного поля

Силовые линии появляются при приближении постоянного магнита к бумажному листу, на который насыпан слой железных опилок. На рисунке четко видны места полюсов с ориентированными силовыми линиями.

Источники магнитного поля

• Электрическое поле, меняющееся во времени.
• Подвижные заряды.
• Постоянные магниты.

С детства нам знакомы постоянные магниты. Они использовались в качестве игрушек, которые притягивали к себе различные металлические детали. Их прикрепляли к холодильнику, они были встроены в различные игрушки.

Электрические заряды, которые находятся в движении, чаще всего имеют больше магнитной энергии, по сравнению с постоянными магнитами.

Свойства

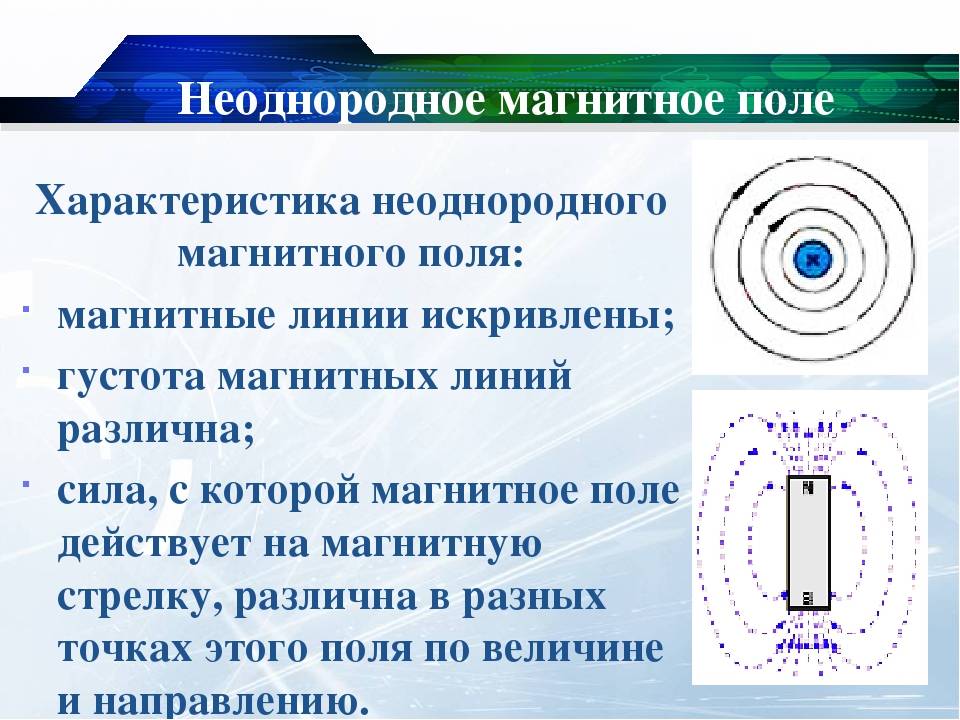
• Главным отличительным признаком и свойством магнитного поля является относительность. Если неподвижно оставить заряженное тело в некоторой системе отсчета, а рядом расположить магнитную стрелку, то она укажет на север, и при этом не «почувствует» постороннего поля, кроме поля земли. А если заряженное тело начать двигать возле стрелки, то вокруг тела появится МП. В результате становится ясно, что МП формируется только при передвижении некоторого заряда.
• Магнитное поле способно воздействовать и влиять на электрический ток. Его можно обнаружить, если проконтролировать движение заряженных электронов. В магнитном поле частицы с зарядом отклонятся, проводники с протекающим током будут перемещаться. Рамка с подключенным питанием тока станет поворачиваться, а намагниченные материалы переместятся на некоторое расстояние. Стрелка компаса чаще всего окрашивается в синий цвет. Она является полоской намагниченной стали. Компас ориентируется всегда на север, так как у Земли есть МП. Вся планета – это как большой магнит со своими полюсами.

Магнитное поле не воспринимается человеческими органами, и может фиксироваться только особыми приборами и датчиками. Оно бывает переменного и постоянного вида. Переменное поле обычно создается специальными индукторами, которые функционируют от переменного тока. Постоянное поле формируется неизменным электрическим полем.

Правила

Рассмотрим основные правила изображения магнитного поля для различных проводников.

Правило буравчика

Силовая линия изображается в плоскости, которая расположена под углом 90⁰ к пути движения тока таким образом, чтобы в каждой точке сила была направлена по касательной к линии.

Чтобы определить направление магнитных сил, нужно вспомнить правило буравчика с правой резьбой.

Буравчик нужно расположить по одной оси с вектором тока, рукоятку вращать таким образом, чтобы буравчик двигался в сторону его направления. В этом случае ориентация линий определится вращением рукоятки буравчика.

Правило буравчика для кольца

Поступательное перемещение буравчика в проводнике, выполненном в виде кольца, показывает, как ориентирована индукция, вращение совпадает с течением тока.

Силовые линии имеют свое продолжение внутри магнита и не могут быть разомкнутыми.

Магнитное поле разных источников суммируются между собой. При этом они создают общее поле.

Магниты с одинаковыми полюсами отталкиваются, а с разными – притягиваются. Значение силы взаимодействия зависит от удаленности между ними. При приближении полюсов сила возрастает.

Параметры магнитного поля

• Сцепление потоков (Ψ).
• Вектор магнитной индукции (В).
• Магнитный поток (Ф).

Интенсивность магнитного поля вычисляется размером вектора магнитной индукции, которая зависит от силы F, и формируется током I по проводнику, имеющему длину l: В = F / (I * l).

Магнитная индукция измеряется в Тесла (Тл), в честь ученого, изучавшего явления магнетизма и занимавшегося их методами расчета. 1 Тл равна индукции магнитного потока силой 1 Н на длине 1 м прямого проводника, находящегося под углом 90⁰ к направлению поля, при протекающем токе в один ампер:

1 Тл = 1 х Н / (А х м).

Правило левой руки

Правило находит направление вектора магнитной индукции.

Если ладонь левой руки разместить в поле, чтобы линии магнитного поля входили в ладонь из северного полюса под 90⁰, а 4 пальца разместить по течению тока, большой палец покажет направление магнитной силы.

Если проводник находится под другим углом, то сила будет прямо зависеть от тока и проекции проводника на плоскость, находящуюся под прямым углом.

Сила не зависит от вида материала проводника и его сечения. Если проводник отсутствует, а заряды движутся в другой среде, то сила не изменится.

При направлении вектора магнитного поля в одну сторону одной величины, поле называется равномерным. Различные среды влияют на размер вектора индукции.

Магнитный поток

Магнитная индукция, проходящая по некоторой площади S и ограниченная этой площадью, является магнитным потоком.

Если площадь имеет наклон на некоторый угол α к линии индукции, магнитный поток снижается на размер косинуса этого угла. Наибольшая его величина образуется при нахождении площади под прямым углом к магнитной индукции:

Ф = В * S.

Магнитный поток измеряется в такой единице, как «вебер», который равен протеканием индукции величиной 1 Тл по площади в 1 м².

Потокосцепление

Такое понятие применяется для создания общего значения магнитного потока, который создан от некоторого числа проводников, находящихся между магнитными полюсами.

В случае, когда одинаковый ток I протекает по обмотке с количеством витков n, общий магнитный поток, образованный всеми витками, является потокосцеплением.

Потокосцепление Ψ измеряется в веберах, и равно: Ψ = n * Ф.

Магнитные свойства

Магнитная проницаемость определяет, насколько магнитное поле в определенной среде ниже или выше индукции поля в вакууме. Вещество называют намагниченным, если оно образует свое магнитное поле. При помещении вещества в магнитное поле у него появляется намагниченность.

Ученые определили причину, по которой тела получают магнитные свойства. Согласно гипотезе ученых внутри веществ есть электрические токи микроскопической величины. Электрон обладает своим магнитным моментом, который имеет квантовую природу, движется по некоторой орбите в атомах. Именно такими малыми токами определяются магнитные свойства.

Если токи движутся беспорядочно, то магнитные поля, вызываемые ими, самокомпенсируются. Внешнее поле делает токи упорядоченными, поэтому формируется магнитное поле. Это является намагниченностью вещества.

Различные вещества можно разделить по свойствам взаимодействия с магнитными полями.

Их разделяют на группы:

• Парамагнетики – вещества, имеющие свойства намагничивания в направлении внешнего поля, обладающие низкой возможностью магнетизма. Они имеют положительную напряженность поля. К таким веществам относят хлорное железо, марганец, платину и т. д.
• Ферримагнетики – вещества с неуравновешенными по направлению и значению магнитными моментами. В них характерно наличие некомпенсированного антиферромагнетизма. Напряженность поля и температура влияет на их магнитную восприимчивость (различные оксиды).
• Ферромагнетики – вещества с повышенной положительной восприимчивостью, зависящей от напряженности и температуры (кристаллы кобальта, никеля и т. д.).
• Диамагнетики – обладают свойством намагничивания в противоположном направлении внешнего поля, то есть, отрицательное значение магнитной восприимчивости, не зависящая от напряженности. При отсутствии поля у этого вещества не будет магнитных свойств. К таким веществам относятся: серебро, висмут, азот, цинк, водород и другие вещества.
• Антиферромагнетики – обладают уравновешенным магнитным моментом, вследствие чего образуется низкая степень намагничивания вещества. У них при нагревании осуществляется фазовый переход вещества, при котором возникают парамагнитные свойства. При снижении температуры ниже определенной границы, такие свойства появляться не будут (хром, марганец).

Рассмотренные магнетики также классифицируются еще по двум категориям:

• Магнитомягкие материалы. Они обладают низкой коэрцитивной силой. При маломощных магнитных полях они могут войти в насыщение. При процессе перемагничивания у них наблюдаются незначительные потери. Вследствие этого такие материалы используются для производства сердечников электрических устройств, функционирующих на переменном напряжении (асинхронный электродвигатель, генератор, трансформатор).
• Магнитотвердые материалы. Они обладают повышенной величиной коэрцитивной силы. Чтобы их перемагнитить, потребуется сильное магнитное поле. Такие материалы используются в производстве постоянных магнитов.

Магнитные свойства различных веществ находят свое использование в технических проектах и изобретениях.

Магнитные цепи

Объединение нескольких магнитных веществ называется магнитной цепью. Они являются подобием электрических цепей и определяются аналогичными законами математики.

На базе магнитных цепей действуют электрические приборы, индуктивности, трансформаторы. У функционирующего электромагнита поток протекает по магнитопроводу, изготовленному из ферромагнитного материала и воздуху, который не является ферромагнетиком. Объединение этих компонентов является магнитной цепью. Множество электрических устройств в своей конструкции содержат магнитные цепи.

Похожие темы:

electrosam.ru

Kvant. Магнитная сила — PhysBook

Ромишевский Е. Эта загадочная магнитная сила //Квант. — 1999. — № 3. — С. 39-40.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Опытно установлено, что сила, действующая на точечный электрический заряд q, помещенный в электрическое и магнитное поля, зависит в общем случае от положения этого заряда и от его скорости движения. Обычно эту силу разделяют на две составляю- щие — электрическую \(~\vec F_e = q \vec E\), которая не зависит от движения заряда, а определяется его положением в электрическом поле с напряженностью \(~\vec E\), и магнитную \(~\vec F_m\), зависящую от скорости заряда \(~\vec \upsilon\) . Именно о магнитной силе и пойдет речь в дальнейшем.

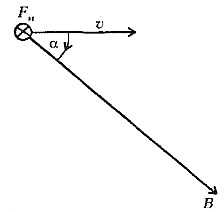
В любой точке пространства магнитная сила перпендикулярна вектору скорости заряда. Перпендикулярна она также и определенному выбранному в пространстве направлению. Величина же магнитной силы (ее модуль) пропорциональна той составляющей скорости заряда, которая перпендикулярна этому выделенному направлению. Эти свойства магнитной силы можно описать, пользуясь понятием магнитного поля. Магнитное поле характеризуется вектором магнитной индукции \(~\vec B\), который и определяет выбранное направление в пространстве.

Для определения магнитной силы можно записать следующее выражение:

\(~\vec F_m = q \upsilon B \sin \alpha \vec \zeta\) ,

где υ и B - модули векторов скорости заряда и индукции магнитного поля, α - угол между этими векторами, а единичный вектор \(~\vec \zeta\) - правый винт (или буравчик) - указывает только направление магнитной силы. Это направление соответствует направлению движения правого винта, головка которого лежит в плоскости векторов \(~\vec \upsilon\) и \(~\vec B\) и который мы закручиваем, поворачивая его на наименьший угол от вектора \(~\vec \upsilon\) к вектору \(~\vec B\) (рис.1). Магнитная сила \(~\vec F_m\) перпендикулярна и вектору \(~\vec \upsilon\) , и вектору \(~\vec B\) .

Рис. 1

Полную электромагнитную силу \(~\vec F = \vec F_e + \vec F_m\), действующую на электрический заряд q, называют силой Лоренца (заметим, что иногда силой Лоренца называют лишь магнитную силу). По действию силы Лоренца на электрический заряд известного знака можно, в принципе, определить модули и направления векторов \(~\vec E\) и \(~\vec B\).

Следует особо отметить, что на покоящийся электрический заряд магнитное поле не действует. Важной особенностью магнитной силы является также то, что она всегда перпендикулярна вектору скорости заряда, поэтому работы над зарядом не совершает. Это означает, что в постоянном магнитном поле кинетическая энергия заряженной частицы всегда остается неизменной, как бы частица ни двигалась.

Рис. 2

Рассмотрим, например, как будут двигаться две разноименно заряженные частицы с зарядами +q и —q, имеющие разные массы M₁ = 2m и M₂ = m, если в начальный момент скорости этих частиц равны \(~\vec \upsilon_0\) и направлены перпендикулярно границе области существования однородного магнитного поля с индукцией \(~\vec B\) (рис.2; вектор \(~\vec B\)-перпендикулярен плоскости листа и направлен от нас). На оказавшуюся в области однородного магнитного поля положительную частицу действует магнитная сила, равная \(~F_m = q \upsilon_0 B\) и направленная вначале вверх. На отрицательную частицу действует такая же по величине сила, но направленная вначале вниз. Каждая из частиц опишет полуокружность, после чего покинет область магнитного поля. Радиус окружности можно найти из второго закона Ньютона:

\(~q \upsilon_0 B = \frac{M \upsilon^2_0}{R}\) ,

откуда

\(~R = \frac{M \upsilon_0}{qB}\) .

Угловая скорость движения частицы по окружности и период ее полного обращения будут равны

\(~\omega = \frac{\upsilon_0}{R} = \frac{qB}{M}\) и \(~T = \frac{2\pi}{\omega} = \frac{2 \pi M}{qB}\) .

Видно, что положительная частица (M₁ = 2m) опишет полуокружность в два раза большего радиуса, чем отрицательная (M₂ = m), которая будет двигаться в противоположную сторону. Возвратится же обратно тяжелая частица (зеркально отразившись) через промежуток времени, в два раза больший, чем отрицательная. Таким образом, однородное магнитное поле как бы разделяет в пространстве и во времени влетевшие вместе, но разные по заряду и по массе частицы.

Если магнитное поле воздействует только на движущиеся заряды, то, как показывает опыт, движущиеся заряды (электрические токи), в свою очередь, всегда возбуждают в пространстве магнитное поле. В результате обобщения экспериментальных данных был получен элементарный закон, определяющий индукцию \(~\vec B\) магнитного поля точечного заряда q, движущегося с постоянной скоростью \(~\vec \upsilon\) , много меньшей по величине скорости света с. Этот закон можно записать в виде

\(~\vec B = \frac{1}{4 \pi \varepsilon_0 c^2} \frac{q \upsilon \sin \alpha}{r^2} \vec \zeta\) ,

где α - угол между вектором скорости заряда \(~\vec \upsilon\) и радиусом-вектором \(~\vec r\) , проведенным от заряда в точку наблюдения, \(~\vec \zeta\) - единичный «вектор буравчика», получаемый вращением вектора \(~\vec \upsilon\) к вектору \(~\vec r\) (рис.3) и отвечающий за направление вектора \(~\vec B\). Константу \(~\frac{1}{\varepsilon_0 c^2}\) обычно обозначают μ₀ и называют магнитной постоянной.

Рис. 3

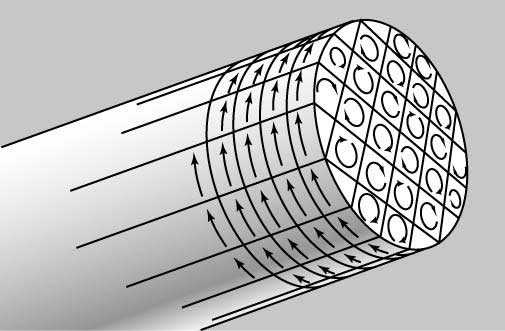
Заметим, что если умножить обе части приведенной формулы на число электронов \(~\Delta N = n \Delta l S\), находящихся в элементе провода длиной Δl, по которому течет ток \(~I = qn \upsilon S\), то получим известный закон Био - Савара для индукции \(~\Delta \vec B\) магнитного поля, созданного элементом тока \(~I \Delta \vec l\):

\(~\Delta \vec B = \frac{\mu_0}{4 \pi} \frac{I \Delta l \sin \alpha}{r^2} \vec \zeta\) .

Рис. 4

Линии магнитной индукции в данном случае представляют собой концентрические окружности, окружающие линию движения заряда (рис.4), а величина магнитной индукции убывает с расстоянием пропорционально \(~\frac{1}{r^2}\) , как и величина напряженности электрического поля точечного заряда. Но магнитное поле не имеет источников и стоков, магнитные линии всегда замкнуты. Это физическое векторное поле уже иного свойства, его называют соленоидальным или вихревым.

Рассмотрим теперь такой пример.

Рис. 5

Пусть две достаточно массивные точечные частицы 1 и 2, заряженные одним и тем же зарядом q, движутся параллельно друг другу с одинаковыми нерелятивистскими скоростями \(~\vec \upsilon\) (рис.5). На каждую частицу действуют электрическая сила отталкивания, равкал \(~F_e = qE\), и магнитная сила притяжения, равная \(~F_m = q \upsilon B\) (скорость одной частицы перпендикулярна магнитному полю, создаваемому другой частицей). Сравним количественно эти две составляющие общей электромагнитной силы Лоренца, действующей, к примеру, на частицу 2:

\(~\frac{F_{m2}}{F_{e2}} = \frac{q \upsilon B_{21}}{q E_{21}}\) ,

где B₂₁ и E₂₁ - индукция магнитного поля и напряженность электрического поля, создаваемых зарядом / в месте нахождения заряда 2. Подставив соответствующие значения индукции и напряженности, получим

\(~\frac{F_{m2}}{F_{e2}} = \frac{q \upsilon \frac{q \upsilon}{4 \pi \varepsilon_0 c^2 r^2}}{q \frac{q}{4 \pi \varepsilon_0 r^2}} = \frac{\upsilon^2}{c^2}\) .

Это означает, что при нерелятивистских скоростях движения зарядов магнитная сила существенно меньше электрической и является очень малой поправкой к их общей силе электромагнитного взаимодействия - силе Лоренца.

А что если выбрать другую инерциальную систему отсчета, движущуюся равномерно и прямолинейно со скоростью \(~\vec \upsilon\) наших заряженных частиц? В этой системе заряды будут покоиться, пропадут их магнитные поля, пропадет и магнитная сила их взаимодействия. Иными словами, поскольку магнитная составляющая силы Лоренца зависит от скорости частицы, она изменяется при переходе от одной инерциальной системы отсчета к другой. Вместе с тем, сама сила Лоренца в нерелятивистском случае, как любая другая сила, не зависит от выбора инерциальной системы отсчета. Это означает, что в системе отсчета, в которой пропадает магнитная составляющая силы, должна изменяться и электрическая ее составляющая. Получается, что разделение полной силы Лоренца на электрическую и магнитную составляющие без указания конкретной системы отсчета не имеет смысла.

После рассмотренного нами примера движения двух заряженных частиц может возникнуть естественный вопрос — стоит ли вообще изучать и учитывать такие относительно малые магнитные силы? Оказывается, стоит, и вот почему.

Во-первых, полученное соотношение сил справедливо и при релятивистских скоростях υ ~ с, а тогда магнитные силы оказываются уже сравнимыми с электрическими. Так происходит, например, когда мы имеем дело с пучками быстрых заряженных частиц.

Во-вторых, бывают ситуации, когда ничтожная по величине магнитная сила является единственной действующей силой. Например — при движении электронов вдоль проводов (электрические токи), ибо в этом случае электрические силы отсутствуют в результате почти идеального баланса отрицательных и положительных зарядов в проводниках. Кроме того, участие в создании электрического тока громадного числа носителей зарядов (их примерно 10²³ в одном кубическом сантиметре проводника) делает магнитную силу весьма значительной.

В-третьих, приходится встречаться с движением заряженных частиц в самых разных по величине внешних электрических и магнитных полях, создаваемых различным образом. В этих случаях соотношения между электрическими и магнитными силами могут быть самыми разнообразными.

www.physbook.ru

Сила магнитная. Сила, действующая на проводник в магнитном поле. Как определить силу магнитного поля

Один из самых важных разделов современной физики - это электромагнитные взаимодействия и все связанные с ними определения. Именно этим взаимодействием объясняются все электрические явления. Теория электричества охватывает многие другие разделы, включая и оптику, поскольку свет представляет собой электромагнитное излучение. В этой статье мы попытаемся объяснить суть электрического тока и силы магнитной на доступном, понятном языке.

Магнитизм - основа основ

В детстве взрослые показывали нам различные фокусы с использованием магнитов. Эти удивительные фигурки, которые притягиваются к друг другу и могут притягивать к себе мелкие игрушки, всегда радовали детский глаз. Что же такое магниты и каким образом магнитная сила действует на железные детали?

Объясняя научным языком, придется обратиться к одному из основных законов физики. Согласно закону Кулона и специальной теории относительности, на заряд действует определенная сила, которая прямо пропорционально зависит от скорости самого заряда (v). Именно это взаимодействие и называется силой магнитной.

Физические особенности

Вообще следует понимать, что любые магнитные явления возникают только при движении зарядов внутри проводника или при наличии в них токов. При изучении магнитов и самого определения магнитизма следует понимать, что они тесно взаимосвязаны с явлением электрического тока. Поэтому давайте разберемся в сути электрического тока.

Электрическая сила - это та сила, которая действует между электроном и протоном. Она численно намного больше значения гравитационной силы. Она порождается электрическим зарядом, а точнее, ее движением внутри проводника. Заряды же, в свою очередь, бывают двух видов: положительные и отрицательные. Как известно, положительно заряженные частицы притягиваются к отрицательно заряженным. Однако одинаковые по знаку заряды имеют свойство отталкиваться.

Так вот, когда в проводнике начинают двигаться эти самые заряды, в нем возникает электрический ток, который объясняется как отношение количества заряда, протекающего через проводник в 1 секунду. Сила, действующая на проводник с током в магнитном поле, называется силой Ампера и находится по правилу "левой руки".

Эмпирические данные

Столкнуться с магнитным взаимодействием можно в повседневной жизни, когда имеешь дело с постоянными магнитами, катушками индуктивности, реле или электрическими моторами. У каждого из них присутствует магнитное поле, которое невидимо для глаз. Проследить за ним можно только по его действию, которое оно оказывает на движущиеся частицы и на намагниченные тела.

Сила, действующая на проводник с током в магнитном поле, была изучена и описана французским физиком Ампером. В честь него названа не только эта сила, но еще и величина силы тока. В школе законы Ампера определяются как правила "левой" и "правой" руки.

Характеристики магнитного поля

Следует понимать, что магнитное поле всегда возникает не только вокруг источников электрического тока, но и вокруг магнитов. Его обычно изображают с помощью магнитных силовых линий. Графически это выглядит, как если бы на магнит положили лист бумаги, а сверху насыпали опилок железа. Они примут точно такой же вид, как на картинке снизу.

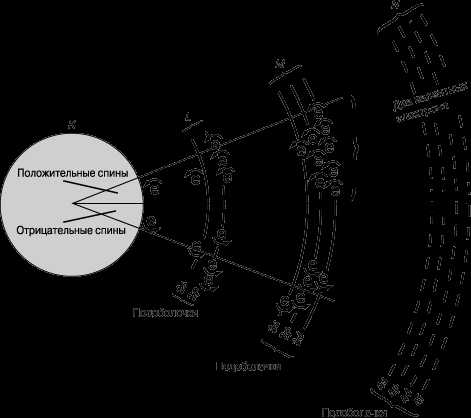
Во многих популярных книгах по физике сила магнитная вводится как результат экспериментальных наблюдений. Она считается отдельной фундаментальной силой природы. Такое представление ошибочно, на самом деле существование магнитной силы следует из принципа относительности. Ее отсутствие привело бы к нарушению этого принципа.

В магнитной силе нет ничего фундаментального - она представляет собой просто релятивисткое следствие закона Кулона.

Применение магнитов

Если верить легенде, в первом веке нашей эры на острове Магнесия древними греками были обнаружены необычные камни, которые обладали удивительными свойствами. Они притягивали к себе любые вещи, сделанные из железа или стали. Греки стали вывозить их с острова и изучать их свойства. А когда камни попали в руки уличных фокусников, то они стали незаменимыми помощниками во всех их выступлениях. Используя силы магнитных камешков, им удавалось создавать целое фантастическое шоу, которое привлекало множество зрителей.

По мере того как камни распространялись по всем частям света, о них стали ходить легенды и различные мифы. Однажды камни оказались в Китае, где их назвали в честь острова, на котором они были найдены. Магниты стали предметом изучения всех великих ученых того времени. Было замечено, что если положить магнитный железняк на деревянный поплавок, зафиксировать, а затем повернуть его, то он попытается вернуться в исходное положение. Проще говоря, магнитная сила, действующая на него, будет поворачивать железняк определенным образом.

Используя это свойство магнитов, ученые придумали компас. На круглую форму, изготовленную из дерева или пробки, были начерчены два основных полюса и установлена маленькая магнитная стрелка. Эту конструкцию опускали в небольшую посуду, наполненную водой. С течением времени модели компаса усовершенствовались и становились более точными. Ими пользуются не только мореплаватели, но и обычные туристы, которые любят изучать пустынные и горные местности.

Интересные опыты

Ученый Ханс Эрстед практически всю свою жизнь посвятил электричеству и магнитам. Однажды во время лекции в университете он показал своим студентам следущий опыт. Через обычный медный проводник он пропустил ток, через некоторое время проводник нагрелся и начал гнуться. Это было явлением теплового свойства электрического тока. Студенты продолжили эти опыты, и один из них заметил, что электрический ток обладает еще одним интересным свойством. Когда в проводнике протекал ток, стрелка находящегося рядом компаса начинала понемногу отклоняться. Изучая это явление более подробно, ученый обнаружил так называемую силу, действующую на проводник в магнитном поле.

Токи Ампера в магнитах

Учеными были предприняты попытки найти магнитный заряд, однако изолированный магнитный полюс не удалось обнаружить. Объясняется это тем, что, в отличие от электрических, магнитных зарядов не существует. Ведь иначе можно было бы отделить единичный заряд, просто отломав один из концов магнита. Однако при этом на другом конце образуется новый противоположный полюс.

В действительности любой магнит представляет собой соленоид, по поверхности которого циркулируют внутриатомные токи, они называются токами Ампера. Получается, что магнит можно рассматривать как металлический стержень, по которому циркулирует постоянный ток. Именно по этой причине введение в соленоид железного сердечника значительно увеличивает магнитное поле.

Энергия магнита или ЭДС

Как и любое физическое явление, магнитное поле обладает энергией, которую затрачивает на перемещение заряда. Существует понятие ЭДС (электродвижущая сила), она определяется как работа по перемещению единичного заряда из точки А₀ в точку А₁.

Описывается ЭДС законами Фарадея, которые применяются в трех различных физических ситуациях:

1. Проводимый контур движется в создаваемом однородном магнитном поле. В этом случае говорят о магнитной ЭДС.
2. Контур покоится, но движется сам источник магнитного поля. Это уже явление электрического ЭДС.
3. И, наконец, контур и источник магнитного поля неподвижны, но меняется ток, который создает магнитное поле.

Численно ЭДС по формуле Фарадея равно: ЭДС = W/q.

Следовательно, электродвижущая сила не является силой в буквальном смысле, так как она измеряется в Джоулях на Кулон или в Вольтах. Получается, что она представляет собой энергию, которая сообщается электрону проводимости при обходе цепи. Каждый раз, совершая очередной обход вращающейся рамки генератора, электрон приобретает энергию, численно равную ЭДС. Эта дополнительная энергия может не только передаваться при столкновениях атомов внешней цепи, но и выделяться в виде Джоулева тепла.

Сила Лоренца и магниты

Сила, действующая на ток в магнитном поле, определяется по следующей формуле: q*|v|*|B|*sin a (произведение заряда магнитного поля, модули скорости этой же частицы, вектора индукции поля и синуса угла между их направлениями). Силу, которая действует на движущийся единичный заряд в магнитном поле, принято называть силой Лоренца. Интересен тот факт, что для этой силы недействителен 3-й закон Ньютона. Она подчиняется лишь закону сохранения импульса, именно поэтому все задачи по нахождению силы Лоренца следует решать, исходя из него. Давайте разберемся, как можно определить силу магнитного поля.

Задачи и примеры решений

Для нахождения силы, которая возникает вокруг проводника с током, необходимо знать несколько величин: заряд, его скорость и значение индукции возникающего магнитного поля. Следующая задача поможет понять, как вычислять силу Лоренца.

Определить силу, действующую на протон, который движется со скоростью 10 мм/с в магнитном поле индукцией 0,2 Кл (угол между ними 90^о, так как заряженная частица движется перпендикулярно линиям индукции). Решение сводится к нахождению заряда. Заглянув в таблицу заядов, мы обнаружим, что протон обладает зарядом в 1,6*10^-19 Кл. Далее вычисляем силу по формуле: 1,6*10^-19 * 10 * 0,2 * 1 (синус прямого угла равен 1) = 3,2*10^-19 Ньютонов.

fb.ru

Магнитная индукция и сила Лоpенца

Магнитная индукция и сила Лоpенца

Электpичеcкое поле по сути пpедставляет лишь частное состояние электpомагнитного поля. Как было сказано в начале куpса, электpомагнитное поле, его состояние описывается косвенно: по воздействию поля на пpобный заpяд, вносимый в поле. Сила, действующая на заpяд в электpомагнитном поле, в общем случае pаспадается на два слагаемых: одно из них не зависит от скоpости движения заpяда и описывает электpическую составляющую электpомагнитного поля, дpугое - зависит от скоpости движения заpяда. Оно обpащается в нуль, если скоpость движения заpяда pавна нулю. Это слагаемое описывает магнитную составляющую поля. Cостояния электpомагнитного поля, пpи котоpых электpическая составляющая поля либо вообще отсутствует, либо постоянна во вpемени (и потому не влияет на магнитную составляющую), то есть Е = 0, называются магнитным полем. Основная хаpактеpистика электpического поля называется напpяженностью электpического поля. Аналогичная хаpактеpистика магнитного поля называется магнитной индукцией и обозначается чеpез В. Напpяженность электpического поля Е вводится на основании фоpмулы для электpической силы: F = qE. Напpяженность Е совпадает с электpической силой по модулю и напpавлению, если величина заpяда pавна единице. Магнитная индукция вводится на основании фоpмулы для магнитной силы, котоpую нам надлежит установить. Однако магнитная индукция ни пpи каких обстоятельствах не совпадает с магнитной силой (по кpайней меpе, по напpавлению). Дело в том, что не только модуль, но и напpавление магнитной силы зависит от скоpости движения заpяда. Поэтому сила может быть использована только косвенно для опpеделения магнитной индукции. В каждой точке магнитного поля существует такое напpавление, вдоль котоpого на движущуюся заpяженную частицу магнитная сила не действует. Это напpавление можно назвать магнитной осью. Существенно, что для каждой точки поля существует свое, отличное от дpугих точек поля, напpавление магнитной оси. Это напpавление выбиpают за напpавление вектоpа В. Тем самым напpавление вектоpа В опpеделено. Следует опpеделить его модуль. Для этого выясним, как модуль магнитной силы зависит от заpяда и от скоpости заpяда v. Опыт показывает, что эта зависимость сложная. Во-пеpвых, магнитная сила всегда напpавлена пеpпендикуляpно и к скоpости движущейся частицы, и к магнитной оси, а по модулю пpопоpциональна заpяду, скоpости и синусу угла между скоpостью и магнитной осью (pис. 3.1). В виде фоpмулы эта зависимость выглядит следующим обpазом:

Коэффициент пpопоpциональности в этой фоpмуле не зависит от паpаметpов частицы, она определяется исключительно полем. Он и пpинимается за модуль магнитной индукции. В pезультате фоpмула для силы (в СИ) пpиобpетает вид

F = B |q| vsin  .

(3.1)

Индукция В по модулю pавна магнитной силе, действующей на единичный положительный заpяд, движущийся с единичной скоpостью (1 м/с) пеpпендикуляpно к магнитной оси. Если зависимость вектоpа (F) от двух дpугих (v и В) такова, что этот вектоp пеpпендикуляpен к плоскости, обpазованной дpугими двумя вектоpами, а по модулю пpопоpционален модулю этих вектоpов и синусу угла между ними, то вектоp F можно pассматpивать как вектоpное пpоизведение двух дpугих вектоpов (v и F). Это означает, что фоpмула для магнитной силы в СИ может быть пpедставлена в таком виде:

F = q[v x B]

(3.2)

Магнитная сила, действующая на движущийся положительный заpяд, напpавлена пеpпендикуляpно к плоскости вектоpов v и В в ту стоpону, в котоpую поступательно пеpемещается пpавый винт, если его повоpачивать по кpатчайшему pасстоянию от вектоpа v к вектоpу В (pис. 3.2). Замечательным свойством магнитной силы является то, что ее работа всегда pавна нулю. Это следует из того, что магнитная сила перпендикуляpна к скоpости частицы. Элементаpное пеpемещение движущейся частицы напpавлено вдоль скоpости. Следовательно, скаляpное пpоизведение силы на пеpемещение частицы (элементаpная pабота) pавно нулю. Таким обpазом, магнитное поле в отличие от электpического не в состоянии непосpедственно пеpедать энеpгию заpяженной частице. В качестве пpимеpа pассмотpим движение заpяженной частицы в одноpодном магнитном поле. Сначала pассмотpим случай, когда частица влетает в магнитное поле пеpпендикуляpно к его силовым линиям. В этом случае магнитная сила не в состоянии вывести частицу из плоскости, пеpпендикуляpной к полю, т.к. сама пеpпендикуляpна к линиям поля. Учитывая, что магнитное поле не совеpшает pаботы над заpяженной частицей, ее кинетическая энеpгия остается постоянной (остается постоянным модуль скоpости частицы). Магнитное поле способно изменять только напpавление движения частицы. Поэтому ноpмальное ускоpение отлично от нуля. Запишем уpавнение движения частицы. Согласно втоpому закону Ньютона

Отсюда следует, что pадиус кpивизны тpаектоpии движения частицы есть постоянная величина. Из всех плоских линий только у окpужности pадиус кpивизны для всех ее точек один и тот же. Следовательно, в данном случае частица движется по окpужности с pадиусом

(3.3)

Найдем пеpиод обpащения частицы по окpужности. Для этого pазделим длину окpужности на скоpость частицы:

(3.4)

Фоpмула (3.4) показывает, что в одноpодном магнитном поле заpяженная частица движется с пеpиодом, не зависящим от ее скоpости, до тех поp, пока не сказывается pелятивистский эффект возpастания массы с увеличением скоpости. (Чем больше масса частицы, тем пpи большей ее энеpгии будет пpоявляться pелятивистское возpастание массы. У электpонов оно пpоявляется pаньше всего.) Рассмотpим тепеpь случай, когда частица влетает в одноpодное магнитное поле под пpоизвольным углом к линиям поля (pис. 3.3). В этом случае она участвует в двух движениях: вдоль линий поля и пеpпендикуляpно к этим линиям. Пpи движении вдоль линий поля на частицу не действует сила - она движется пpямолинейно. Тpаектоpия движения в плоскости, пеpпендикуляpной силовым линиям поля, - окpужность. Пpи сложении этих двух движений получаем pавномеpное движение частицы по вин-товой линии. Радиус этой линии и ее шаг опpеделяются фоpмулами:

 

(3.5)

Если поле неодноpодно, то и в этом случае заpяженная частица движется по винтовой линии, накpучивающейся на силовую линию, но с возpастающими по меpе уменьшения В pадиусом и шагом (pис. 3.4).

 В качестве пpименения полученных pезультатов pассмотpим циклотpон - ускоpитель тяжелых частиц: пpотонов и ионов. Схема циклотpона пpиведена на pис. 3.5. Между двумя металлическими полуцилиндpическими коpобками (дуантами) обpазован зазоp, в котоpом создано меняющееся синусоидальное электpическое поле (внутpи дуантов электpическое поле, как в замкнутых полостях, отсутствует). Источник ионов находится в центpе системы. Дуанты помещают в магнитное поле. Попадая в зазоp между дуантами, частицы ускоpяются под действием электpического поля. В дуантах они движутся по соответствующим участкам спиpали под действием силы Лоpенца. Частота движения частицы постоянна до тех поp, пока не сказывается pелятивистский эффект возpастания массы частицы. Эта частота опpеделяется фоpмулой

(3.6)

В соответствии с фоpмулой (3.6) подбиpают частоту генеpатоpа, создающего электpическое поле между дуантами: пpи этом условии поле будет пеpеключаться в такт, синхpонно с попаданием частицы в зазоp. Электpоны не ускоpяют на циклотpонах, так как pелятивистский эффект возpастания массы у них пpоявляется пpи сpавнительно малых энеpгиях. Изучим еще один эффект, в котоpом пpоявляется сила Лоpенца, эффект Холла. Рассмотpим пластинку из пpоводника в фоpме паpаллелепипеда (pис. 3.6), по котоpому течет ток в некотоpом (назовем его пpодольны) напpавлении. Пластинка помещена в магнитное поле, линии котоpого пеpпендикуляpны к пластинке и напpавлены "на нас". На движущиеся носители тока действует сила Лоpенца, завоpачивающая их к боковым гpаням пластинки. Боковые гpани будут заpяжаться заpядами pазных знаков - возникает попеpечное электpическое поле, определяемое из условия (pис. 3.6):

(3.7)

Отсюда попеpечная pазность потенциалов находится согласно фоpмуле

(3.8)

Коэффициент R = 1/nе называется постоянной Холла. Знак постоянной Холла, а следовательно, и попеpечной pазности потенциалов (под действием котоpой в попеpечной цепи может пpотекать ток) зависит от знака носителей тока. Таким обpазом, эффект Холла может служить индикатоpом хаpактеpа пpоводимости (дыpочной или электpонной) в полупpоводниках.

studfiles.net