Что такое мгновенные значения тока и напряжения в цепях переменного тока. Как рассчитать амплитуду, частоту и фазу синусоидальных сигналов. Какие существуют методы анализа цепей переменного тока. Как связаны между собой мгновенные, действующие и средние значения.
Основные характеристики синусоидальных токов и напряжений
Синусоидальные токи и напряжения являются основой электроэнергетических систем переменного тока. Их мгновенные значения непрерывно изменяются во времени по синусоидальному закону:
i(t) = Im sin(ωt + φi)
u(t) = Um sin(ωt + φu)
где:
- Im, Um — амплитудные значения тока и напряжения
- ω — угловая частота
- φi, φu — начальные фазы тока и напряжения
Расчет параметров синусоидальных сигналов
Для полного описания синусоидального сигнала необходимо знать три основных параметра:
- Амплитуда (Im или Um) — максимальное значение сигнала
- Частота (f) или угловая частота (ω = 2πf) — число колебаний в секунду
- Начальная фаза (φ) — сдвиг синусоиды относительно начала координат
Как рассчитать эти параметры по мгновенным значениям?

- Амплитуда определяется как максимальное значение сигнала
- Частоту можно найти по периоду колебаний: f = 1/T
- Фазу удобно определять в момент перехода сигнала через ноль
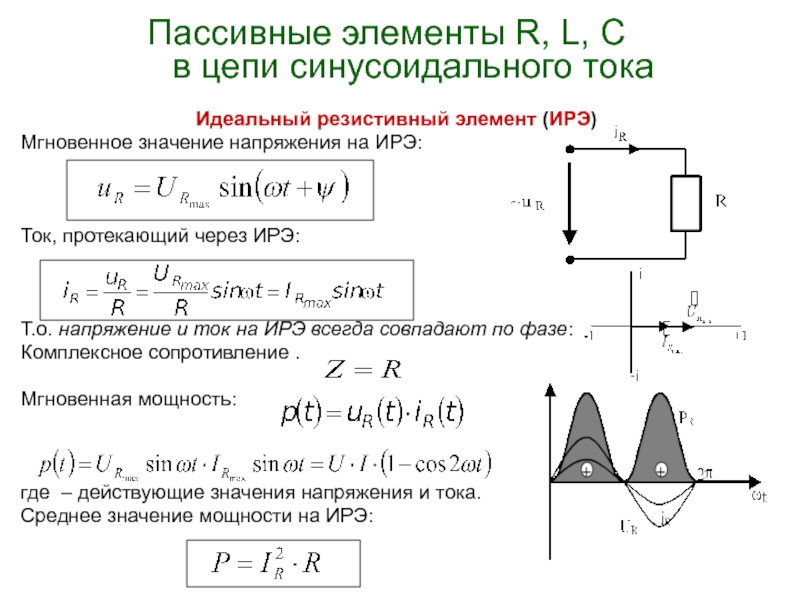
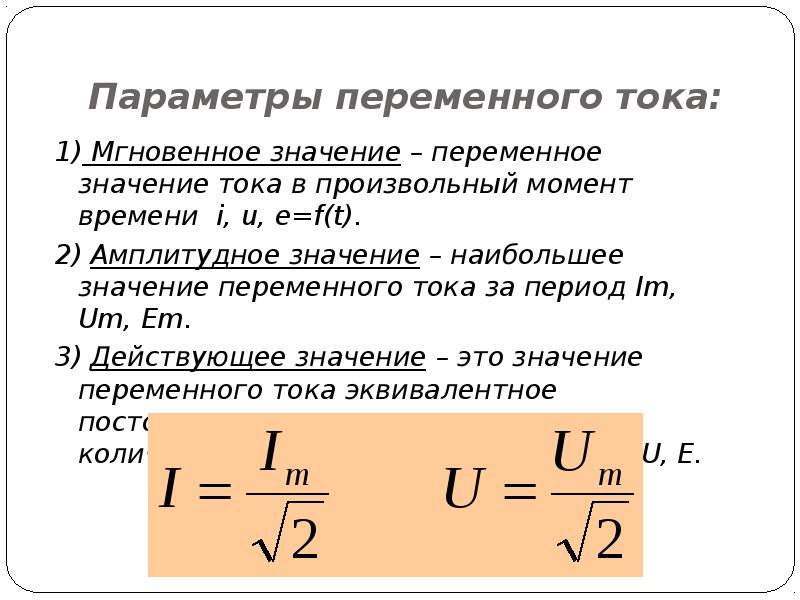
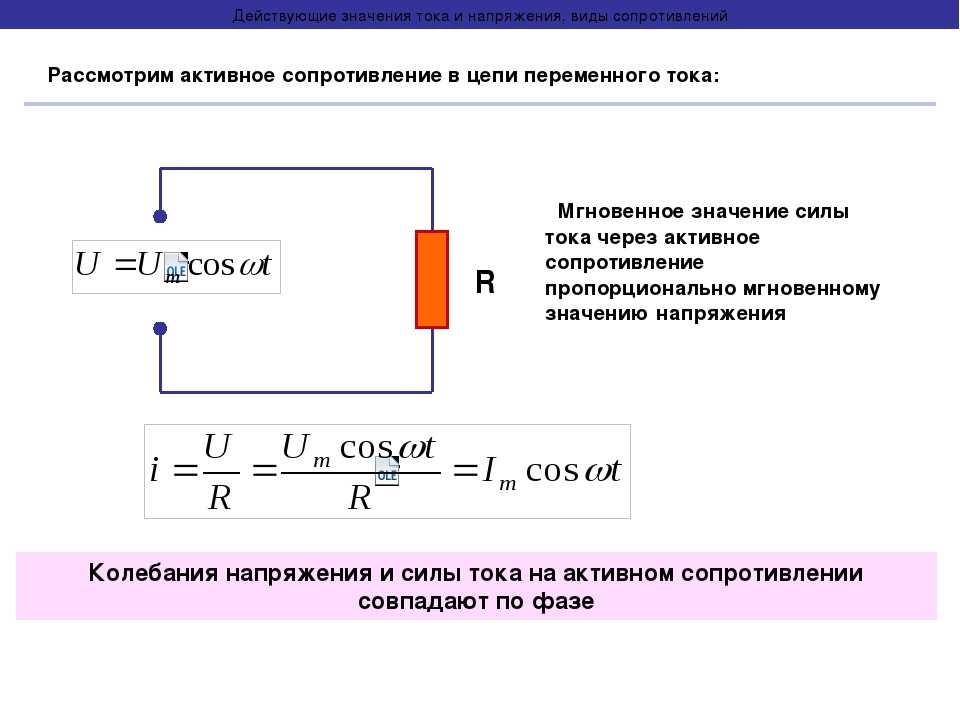
Действующие и средние значения синусоидальных величин
Помимо мгновенных значений, важную роль играют действующие и средние значения синусоидальных токов и напряжений:
- Действующее значение: I = Im/√2, U = Um/√2
- Среднее значение за полупериод: Iср = 2Im/π, Uср = 2Um/π
Действующие значения широко используются на практике, так как характеризуют тепловое и силовое действие переменного тока. Большинство измерительных приборов показывают именно действующие значения.
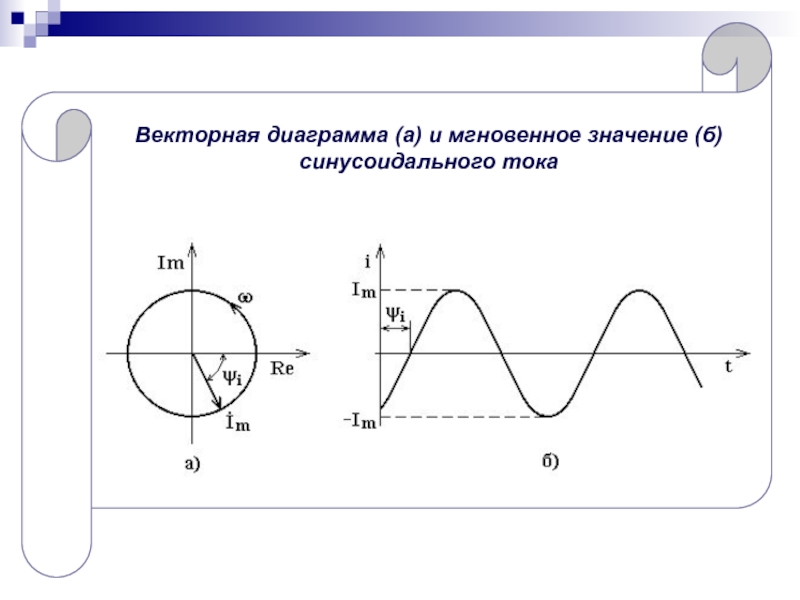
Векторные диаграммы синусоидальных величин
Удобным способом графического представления синусоидальных токов и напряжений являются векторные диаграммы. На них синусоидальные величины изображаются векторами, длина которых равна амплитуде, а угол поворота — начальной фазе.
Векторные диаграммы позволяют наглядно показать:
- Сдвиг фаз между током и напряжением
- Соотношения между напряжениями на различных элементах цепи
- Результат сложения нескольких синусоидальных величин
Анализ цепей переменного тока символическим методом
Для расчета сложных цепей переменного тока часто применяется символический метод. Его суть заключается в следующем:
- Синусоидальные токи и напряжения заменяются комплексными числами
- Расчет цепи выполняется по законам Ома и Кирхгофа для комплексных величин
- Полученные комплексные значения преобразуются обратно в синусоидальные
Преимущества символического метода:
- Упрощение расчетов сложных цепей
- Возможность применения методов расчета цепей постоянного тока
- Наглядное представление амплитуд и фаз на комплексной плоскости
Мощность в цепях синусоидального тока
В цепях переменного тока различают следующие виды мощности:
- Активная мощность P — средняя за период мощность, преобразуемая в другие виды энергии
- Реактивная мощность Q — характеризует обмен энергией между источником и реактивными элементами
- Полная мощность S — произведение действующих значений тока и напряжения
Соотношение между ними:
S2 = P2 + Q2
Коэффициент мощности определяется как:
cosφ = P/S
Резонанс в электрических цепях переменного тока
Резонанс — это явление резкого возрастания амплитуды колебаний при совпадении частоты внешнего воздействия с собственной частотой системы. В электрических цепях различают:
- Резонанс напряжений — в последовательном колебательном контуре
- Резонанс токов — в параллельном колебательном контуре
При резонансе:
- Реактивная мощность равна нулю
- Коэффициент мощности равен единице
- Ток и напряжение совпадают по фазе
Трехфазные цепи синусоидального тока
Трехфазная система состоит из трех однофазных цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые друг относительно друга на 120°. Преимущества трехфазных цепей:
- Экономия проводникового материала
- Создание кругового вращающегося магнитного поля
- Возможность получения двух уровней напряжения
Различают соединение фаз звездой и треугольником. При симметричной нагрузке:
- Треугольник: Iл = √3Iф, Uл = Uф
Влияние высших гармоник на форму синусоидальных сигналов
Реальные токи и напряжения часто отличаются от идеальной синусоиды из-за наличия высших гармоник. Это приводит к следующим негативным последствиям:
- Увеличение потерь в электрических машинах и трансформаторах
- Ложные срабатывания устройств защиты и автоматики
- Нагрев нулевого провода в трехфазных системах
- Помехи в линиях связи и измерительных цепях
Для борьбы с высшими гармониками применяют:
- Фильтры гармоник
- Схемы с умножением фаз
- Активные компенсаторы искажений
1.3 Мгновенные значения тока и напряжения первичной обмотки трансформатора т1 и их волновая диаграмма.
Рассчитаем мгновенные значения тока и напряжения на индуктивности L6
:
Напряжение на индуктивности:
Рис 3. Волновая диаграмма тока
Рис 4. Волновая диаграмма напряжения
1.4 Расчет ИГК методом эквивалентного источника относительно первичной обмотки трансформатора.
Размыкаем ветвь с катушкой L6:
Определим токи методом контурных токов:
Составим уравнение по второму закону Кирхгофа для 3 контура (см. рис. 5):
Итак,
полученное значении тока
полностью совпадает со значением,
полученным в пункте 1. 1.
1.
1.5 Определение индуктивностей и взаимных индуктивностей.
U
Расчет взаимных индуктивностей и индуктивностей катушек:
2. Расчет четырехполюсника.
2.1 Расчет токов и напряжений методом входного сопротивления, построение векторной диаграммы токов и напряжений.
R1 = 40 Ом
R2 = 26 Ом
R3 = 60 Ом
L0 = 100 мГн
Определим входное сопротивление четырехполюсника:
Определим входное напряжение и ток:
Найдем токи и напряжения:
Векторные диаграммы токов и напряжений выглядят следующим образом:
2.
 2. Определение мгновенных значений uвх, iвх и uвых, фазового сдвига между входным и выходным напряжением, а также отношения их действующих значений.
Действующие
значения:
2. Определение мгновенных значений uвх, iвх и uвых, фазового сдвига между входным и выходным напряжением, а также отношения их действующих значений.
Действующие
значения:
Сдвиг по фазе между выходным и входным напряжением:
Отношение действующих значений:
2.3. Определение реактивного сопротивления, которое необходимо подключить к выходным зажимам четырехполюсника, чтобы uвх и iвых совпадали по фазе.
Для получения резонанса, подключим параллельно выходным зажимам емкостную нагрузку.
Входное сопротивление в этом случае будет иметь вид:
Условием резонанса является равенство нулю мнимой части входного сопротивления:
Корни
квадратного уравнения: С1=86.5
мкФ и С2=3. 2
мкФ
2
мкФ
Будем рассматривать емкость С1.
Zвх(С1)=34.74 Ом
Определим добротность:
Заметим, что входной ток при резонансе в данном случае оказывается больше, чем в электромагнитной системе, не испытывающей резонанс. Отношение действующих значений входных токов в этих двух случаях равно:
2.4. Определение передаточных функций.
Заменим S на:
2.5. Амплитудно- и фазочастотные характеристики, определение uвых при заданном uвх.
Рис 11. ФЧХ
Определим Uвых:
Полученное
значение выходного напряжения совпадает
с найденным в п. 2.2.
2.2.
3. Расчет установившихся значений напряжений и токов в электрических цепях при несинусоидальном воздействии.
3.1. Расчет iвх(t ) и uвых(t) частотным методом, представив входное напряжение в виде ряда Фурье.
Входное напряжение задано формулой (ряд Фурье):
где k – целое нечетное число.
Входное воздействие можно записать в виде:
Рассчитаем выходное напряжение частотным методом:
Определим входное сопротивление:
Рассчитаем входной ток:
3. 2
Построение графиков напряжения и тока.
2
Построение графиков напряжения и тока.
3.3 Определение действующих значений несинусоидальных токов, активной мощности, реактивной мощности, коэффициента формы кривых.
Действующие значения сигналов:
Активная мощность:
Полная мощность:
Реактивная мощность:
Рассчитаем коэффициенты формы кривых:
3.4 Эквивалентные синусоиды.
Определим коэффициент мощности:
Тогда соответствующие эквивалентные синусоиды будут иметь вид:
4. Расчет переходных процессов классическим методом.
4. 1
Переходная и импульсная характеристика
для входного тока и выходного напряжения.
1
Переходная и импульсная характеристика
для входного тока и выходного напряжения.
Применим метод входного переходного сопротивления. Характеристическое уравнение при заданных параметрах элементов схемы:
Решение будет иметь вид: (4.1)
Найдем начальные и вынужденные значения тока. Ток в момент времени t=0+ протекает через резисторы R2 и R3:
Определим вынужденный ток:
Определим постоянную А, для этого запишем уравнение 4.1 в момент времени t=0+:
Подставим найденные значения в уравнение 4.1:
Аналогичным образом рассчитаем uвых(t):
Покажем связь между переходной и передаточной функциями:
Полученные
значения совпадают.
Полученное значение должно совпадать с . Покажем это:
Действительно, значения совпадают.
Покажем связь импульсной характеристики с АЧХ:
Данное выражение совпадает с выражением для W(S), полученным в п. 2.4.
Сообщество Экспонента
- вопрос
- 19.10.2022
Математика и статистика, Цифровая обработка сигналов, Финансы
u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка
u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка
- вопрос
- 19.10.2022
Математика и статистика, Цифровая обработка сигналов, Финансы, Другое
u = (y³)/3 + 8xy — 9y — 4x² — 10
u = (y³)/3 + 8xy — 9y — 4x² — 10
2 Ответа
- Публикация
- 18.10.2022
Другое
Введение В настоящее время существует три основных подхода при построении криптографической системы:
— алгоритмы с открытыми ключами;
— симметричные алгоритмы с закрытыми ключами (блочные шифры). ..
..
Аннотация статьи
Разработан алгоритм генерации ключей шифрования в симметричных криптографических системах с закрытыми ключами, без использования передачи ключей по сетям связи.
An algorithm has been developed for generating encryption keys in symmetric cryptographic systems with private keys, without using key transmission over communication networks.
Ключевые слова: шифрование, симметричные криптографические системы, одноразовые блокноты, алгоритм генерации ключей, интернет вещи, (IoT), приемно-контрольные приборы.
- шифрование
18.10.2022
- Отвеченный вопрос
- 17.10.2022
Изображения и видео, Цифровая обработка сигналов, Верификация и валидация, Математика и статистика, Системы управления, Другое, Автоматизация испытаний
Здравствуйте,Необходимо смоделировать теплопередачу в емкости с водой, через которую проложена труба. Имеется разница температур жидкости в трубе и в емкости. Подскажите инструменты, статиьи, видео и…
Имеется разница температур жидкости в трубе и в емкости. Подскажите инструменты, статиьи, видео и…
Здравствуйте,Необходимо смоделировать теплопередачу в емкости с водой, через которую проложена труба. Имеется разница температур жидкости в трубе и в емкости. Подскажите инструменты, статиьи, видео и…
2 Ответа
- MATLAB
- теплопередача
- теплообмен
17.10.2022
- вопрос
- 15.10.2022
Цифровая обработка сигналов, Автоматизация испытаний, Системы управления, Электропривод и силовая электроника
Всем привет! Мультиметр не выдает окна с графиками после моделирования, может кто сталкивался таким? Желаемые измеряемые величины естественно перенес в правый столбец и ничего( Симулинк ве…
Всем привет! Мультиметр не выдает окна с графиками после моделирования, может кто сталкивался таким? Желаемые измеряемые величины естественно перенес в правый столбец и ничего(
Симулинк ве. -5;…
-5;…
Сроду не программировал и сразу кинули в matlab. Не знаю в чем здесь проблема. Буду рад если поможете. Извиняюсь за такое кол-во строк кода 🙁
- Построение пилота
12.10.2022
- вопрос
- 11.10.2022
Математика и статистика, Радиолокация, Робототехника и беспилотники, Цифровая обработка сигналов, ПЛИС и СнК, Глубокое и машинное обучение(ИИ), Системы управления, Биология, Изображения и видео, Системы связи, Автоматизация испытаний, Другое, Финансы, Встраиваемые системы, Электропривод и силовая электроника
1. Вопрос глобальный. Зачем он нужен?2. Если я создаю pcode функции, внутри которой вызываются другие функции, код которых содержится в других файлах, то в итоговом файле будет всё, или надо делать pc…
1. Вопрос глобальный. Зачем он нужен?2. Если я создаю pcode функции, внутри которой вызываются другие функции, код которых содержится в других файлах, то в итоговом файле будет всё, или надо делать pc. ..
..
1 Ответ
- MATLAB
11.10.2022
- вопрос
- 22.09.2022
Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
7 Ответов
- вопрос
- 20.09.2022
Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
1 Ответ
- MATLAB
20.09.2022
- Публикация
- 15.09.2022
Системы управления, Другое
Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
Мгновенное значение переменного тока и класс 12 по физике JEE_Main
Ответ
Проверено
216,6 тыс.+ просмотров
Подсказка: В цепи переменного тока значения электродвижущей силы и тока непрерывно изменяются во времени. Таким образом, мы не можем рассчитать мощность напрямую. средняя мощность для синусоидальной функции будет получена путем усреднения за один период. Средняя мощность цепи переменного тока также известна как истинная мощность электрической цепи. 90}\].
Средняя мощность цепи переменного тока также известна как истинная мощность электрической цепи. 90}\].
Используемая формула: Мы знаем, что мощность равна произведению напряжения на время. Среднюю мощность вычисляем по формуле \[{P_{av}} = {V_{rms}} \times {i_{rms}}\cos \phi \].
Полное пошаговое решение:
Дано: \[i = \dfrac{1}{{\sqrt 2 }}\sin \left( {100\pi t} \right)Ампер\] и \[e = \dfrac{1}{{\sqrt 2}}\sin\left({100\pi t + \dfrac{\pi}}{3}} \right)Вольт\]
, т. е. \[{i_0} = \ dfrac{1}{{\sqrt 2 }}\] и \[{V_0} = \dfrac{1}{{\sqrt 2 }}\]. 90}\]
\[ \Rightarrow {P_{av}} = \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{1} {8}Вт\]
\[\следовательно {P_{av}} = \dfrac{1}{8}Вт\]
Следовательно, средняя мощность, потребляемая в цепи переменного тока, равна \[\следовательно {P_{av} } = \dfrac{1}{8}W\].
Дополнительная информация: Для цепей переменного тока мгновенная мощность постоянно меняется с различными промежутками времени. Кривая зависимости мощности от времени синусоидальна. Поскольку мы получаем этот тип кривой, т. Е. Это затрудняет измерение мощности. Вычисляя среднее или среднее значение мощности, Поэтому удобнее вычислять. Среднее значение мгновенной мощности за фиксированное количество циклов, средняя мощность синусоидальной кривой задается просто как: \[{P_{av}} = {V_{rms}} \times {i_{rms}}\cos \фи\].
Кривая зависимости мощности от времени синусоидальна. Поскольку мы получаем этот тип кривой, т. Е. Это затрудняет измерение мощности. Вычисляя среднее или среднее значение мощности, Поэтому удобнее вычислять. Среднее значение мгновенной мощности за фиксированное количество циклов, средняя мощность синусоидальной кривой задается просто как: \[{P_{av}} = {V_{rms}} \times {i_{rms}}\cos \фи\].
Примечание: Студенты должны быть внимательны при расчете среднеквадратичных значений тока и напряжения. Они должны быть осторожны, чтобы найти разность фаз между напряжением и током. В вопросе приведены среднеквадратичные значения. Не используйте \[\dfrac{1}{{\sqrt 2 }}\] как \[{V_{rms}}\] и \[{i_{rms}}\] в формуле. Здесь \[\dfrac{1}{{\sqrt 2 }}\]является \[{i_0}\] для тока, а \[\dfrac{1}{{\sqrt 2 }}\]является \[{V_0} \].
Недавно обновленные страницы
Рассчитать изменение энтропии, связанное с преобразованием класса 11 химии JEE_Main
Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC Класс 11 2 Для химической реакции JEE03
rm2Clg to rmCrmlrm2rmg знаки химии класса 11 JEE_Main
Изменение энтальпии для перехода жидкой воды класса 11 химии JEE_Main
Рассчитать изменение энтропии, связанное с конверсией химии класса 11 JEE_Main
Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC Класс 11 2 Для химической реакции JEE03
rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main
Изменение энтальпии перехода жидкой воды 11 класса химии JEE_Main
Тенденции сомнений
Мгновенные, пиковые, средние и среднеквадратичные значения переменного тока и напряжения
- Автор Балсара Джей
- Последнее изменение 19-07-2022
Как правило, мы знаем, что есть два типа тока, которые мы используем в нашей повседневной жизни, а именно. \((1)\) Постоянный ток \(\left({{\rm{DC}}} \right)\) и \((2)\) Переменный ток \(\left({{\rm{AC}) }} \right).\) Постоянный ток просто означает однонаправленный поток заряда. В цепи ток просто продолжает течь в том же направлении, основываясь на приложенной к нему разности потенциалов с той же единицей величины, что и источник или нагрузка. Напротив, переменный ток — это электрический ток, который меняет свое направление и меняет свою величину в течение фиксированных интервалов времени. Графики ниже показывают четкую разницу в характере постоянного и переменного тока. 9{{\rm{nd}}}}\) изображение).
\((1)\) Постоянный ток \(\left({{\rm{DC}}} \right)\) и \((2)\) Переменный ток \(\left({{\rm{AC}) }} \right).\) Постоянный ток просто означает однонаправленный поток заряда. В цепи ток просто продолжает течь в том же направлении, основываясь на приложенной к нему разности потенциалов с той же единицей величины, что и источник или нагрузка. Напротив, переменный ток — это электрический ток, который меняет свое направление и меняет свою величину в течение фиксированных интервалов времени. Графики ниже показывают четкую разницу в характере постоянного и переменного тока. 9{{\rm{nd}}}}\) изображение).
Итак, если значения напряжения и тока постоянно изменяются со временем, то как мы можем рассчитать величину тока в определенное время? Как мы даем оценки источнику или инструментам? Прочитав эту статью, вы узнаете о различных типах значений тока и напряжения в случае переменного тока.
Исследование мощности в цепях переменного тока здесь
Разница между постоянным и переменным током
| DEMEAR TUCCE | Чередовый ток | |
| Магнитуна и направление тока не изменяются со временем | Масштабирование и направление.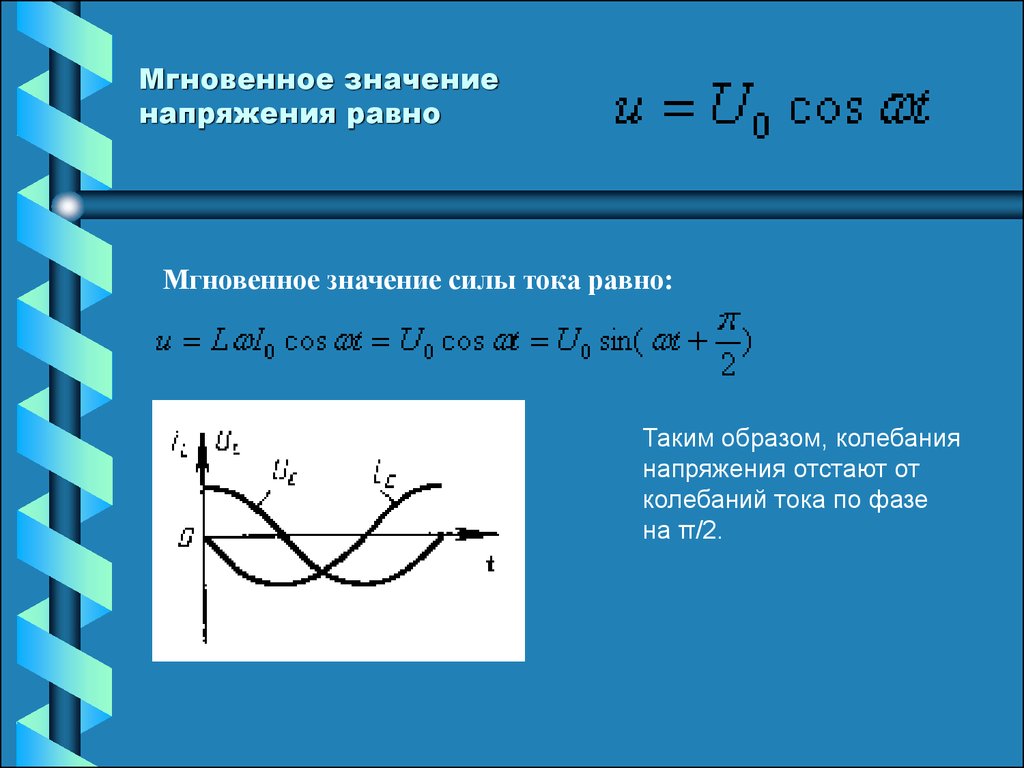 на большие расстояния на большие расстояния | Безопасно передавать переменный ток на большие расстояния |
| Не имеет частоты | Его частота составляет около \({\rm{50}}\,{\rm{Гц}} \) или \({\rm{60}}\,{\rm{Гц}}\) в зависимости от страны | |
| Движение электронов однонаправленное | Движение электронов продолжает изменяться в зависимости от изменения полярности | |
| Создано с помощью химических реакций | Создано с помощью непрерывного изменения магнитного потока | |
| Мгновенное значение и пиковое значение Как известно, значения тока и напряжения в случае переменного тока изменяются со временем. Следовательно, в каждый момент времени существуют разные значения тока и напряжения в зависимости от характера волны переменного тока. Обычно источник подает переменное напряжение в соответствии с уравнением \(V = {V_0}\sin (\omega t)\) Здесь \({V_0}\) — максимальное значение (пиковое значение) подаваемого напряжения, \(\omega \) — угловая частота, а \(t\) — время. Для тока мы рассматриваем различные схемы, потому что он работает по-разному для резисторов, конденсаторов и катушек индуктивности. Разность фаз между током и напряжением, когда источник переменного тока приложен к резистору, равна нулю. Следовательно, мгновенное значение тока в резисторе будет \(i = {i_0}\sin (\omega t).\) Для аналогичного случая в конденсаторе ток опережает напряжение на угол \({\frac{\pi {2}},\) следовательно, мгновенное значение тока через конденсатор равно \(i = {i_0} \sin \left( {\omega t + \frac{\pi }{2}} \right)\) а для индуктора напряжение опережает ток на тот же угол. Следовательно, мгновенное значение тока через индуктор будет \(i = {i_0}\sin \left( {\omega t – \frac{\pi }{2}} \right).\) Но для комбинации резистора, конденсатора и катушки индуктивности мгновенный ток обычно записывается как \(i = {i_0} \sin (\omega t – \varphi )\). Среднее значениеСреднее значение — это среднее значение переменного тока во времени. Поскольку переменный ток имеет одинаковые значения как в положительном, так и в отрицательном направлении, его средние значения всегда равны нулю. 9{\ frac {T} {2}} \) \ (\ поэтому \ langle V \ rangle = \ frac {{2 {V_0}}} {\ pi} \) \ (\ langle V \ rangle = 0,637{V_0}\) Следовательно, среднее значение за полупериод в \(0,637\) раз больше его пикового значения. Это было среднее значение для синусоидальной формы волны. Далее в этой статье мы также рассмотрим средние значения других сигналов. Среднеквадратичное значение Среднеквадратичное значение означает среднеквадратичное значение, которое означает значение установившегося тока или напряжения постоянного тока, которое выделяет такое же количество тепла в данном резисторе за заданное время, как и переменный ток. \(\следовательно {V_{rms}} = \frac{{{V_0}}}{{\sqrt 2 }}\) То же самое будет и в случае тока если это синусоидальная волна. Следовательно, среднеквадратичное значение напряжения и тока для синусоидального сигнала примерно в \(0,71\) раз превышает его пиковое значение. Среднее значение и среднеквадратичное значение для сигналов треугольной и прямоугольной формыНа диаграмме показан сигнал треугольной формы. Уравнение треугольной формы волны будет иметь вид \(V = \frac{{4{V_0}}}{T}t\) 92} \) \(\следовательно {V_{rms}} = {V_0}\) Следовательно, среднеквадратичное значение меандра также равно его пиковому значению. Резюме Из этой статьи мы узнали о мгновенных значениях переменного тока и напряжения, а также научились находить средние значения и среднеквадратичные значения для различных типов сигналов. Для синусоидальной волны: Для треугольной волны: Часто задаваемые вопросы Q.1. Как найти пиковое значение по среднеквадратичному значению? Q.2. Что такое пиковое, среднее и среднеквадратичное значение? Q.3. В чем разница между переменным током и переменным напряжением? Q.4. Как переменный ток влияет на напряжение? Q.5. Сколько вольт переменного тока? |

 Следовательно, для любого времени \(t,\) мы можем получить мгновенное значение напряжения через пиковое напряжение.
Следовательно, для любого времени \(t,\) мы можем получить мгновенное значение напряжения через пиковое напряжение.  Где \(\varphi\) — разность фаз между током и напряжением, которая изменяется в зависимости от величины подключенных компонентов и способа их подключения.
Где \(\varphi\) — разность фаз между током и напряжением, которая изменяется в зависимости от величины подключенных компонентов и способа их подключения.  Как следует из названия, шаг за шагом, сначала нам нужно возвести количество в квадрат, затем взять его средние значения и, наконец, получить из них корень. 92}}{2}} \)
Как следует из названия, шаг за шагом, сначала нам нужно возвести количество в квадрат, затем взять его средние значения и, наконец, получить из них корень. 92}}{2}} \) 
 Среднее значение представляет собой среднее значение переменного тока за фиксированное время, тогда как среднеквадратичное значение представляет собой среднеквадратичное значение данного уравнения.
Среднее значение представляет собой среднее значение переменного тока за фиксированное время, тогда как среднеквадратичное значение представляет собой среднеквадратичное значение данного уравнения. 
