Мощность цепи переменного тока с активным сопротивлением. Сопротивление в цепях переменного тока: виды, расчет, влияние на мощность — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Какие виды сопротивлений существуют в цепях переменного тока. Как рассчитать активное, реактивное и полное сопротивление. Как сопротивление влияет на мощность в цепи переменного тока. Что такое коэффициент мощности.

Содержание

Виды сопротивлений в цепях переменного тока

В цепях переменного тока существует несколько видов сопротивлений:

Активное сопротивление (R) — сопротивление, на котором происходит необратимое преобразование электрической энергии в тепловую
Реактивное сопротивление (X) — сопротивление, обусловленное наличием в цепи катушек индуктивности и конденсаторов
Полное сопротивление (Z) — общее сопротивление цепи переменного тока, учитывающее как активную, так и реактивную составляющие

Какие основные отличия между этими видами сопротивлений?

Активное сопротивление не зависит от частоты тока и приводит к потерям энергии. Реактивное сопротивление зависит от частоты и не приводит к потерям энергии — она лишь накапливается в магнитном или электрическом поле. Полное сопротивление учитывает оба эффекта и определяет общее противодействие цепи протеканию переменного тока.

Расчет активного сопротивления

Активное сопротивление в цепи переменного тока рассчитывается по формуле:

R = U / I

где U — действующее значение напряжения, I — действующее значение тока.

Активное сопротивление измеряется в Омах (Ом) и не зависит от частоты переменного тока.

Как рассчитать активное сопротивление на практике? Измерьте действующие значения напряжения и тока с помощью вольтметра и амперметра переменного тока. Затем разделите напряжение на ток.

Расчет реактивного сопротивления

Реактивное сопротивление катушки индуктивности рассчитывается по формуле:

X_L = 2πfL

где f — частота переменного тока, L — индуктивность катушки.

Реактивное сопротивление конденсатора:

X_C = 1 / (2πfC)

где C — емкость конденсатора.

Реактивное сопротивление измеряется в Омах и зависит от частоты переменного тока.

Расчет полного сопротивления

Полное сопротивление цепи переменного тока рассчитывается по формуле:

Z = √(R² + X²)

где R — активное сопротивление, X — реактивное сопротивление.

Полное сопротивление также измеряется в Омах и учитывает как активную, так и реактивную составляющие.

Влияние сопротивления на мощность в цепи переменного тока

Сопротивление оказывает значительное влияние на мощность в цепи переменного тока:

На активном сопротивлении выделяется активная мощность: P = I²R
На реактивном сопротивлении выделяется реактивная мощность: Q = I²X
Полная мощность в цепи: S = I²Z

Как сопротивление влияет на коэффициент мощности? Коэффициент мощности определяется отношением активной мощности к полной:

cos φ = P / S = R / Z

Чем больше активное сопротивление по сравнению с реактивным, тем выше коэффициент мощности.

Коэффициент мощности в цепях переменного тока

Коэффициент мощности — важный параметр, характеризующий эффективность передачи энергии в цепи переменного тока. Он определяется как:

cos φ = P / S

где P — активная мощность, S — полная мощность.

Коэффициент мощности может принимать значения от 0 до 1. Чем ближе он к единице, тем эффективнее передача энергии в цепи.

Как повысить коэффициент мощности? Основные способы:

Уменьшение реактивной мощности за счет компенсации индуктивной нагрузки конденсаторами
Снижение потребления реактивной мощности путем замены недогруженных асинхронных двигателей
Применение синхронных двигателей вместо асинхронных

Резонанс в цепях переменного тока

Резонанс — это явление резкого возрастания амплитуды колебаний в цепи переменного тока при определенной частоте.

Различают два вида резонанса:

Резонанс напряжений — в последовательной RLC-цепи
Резонанс токов — в параллельной RLC-цепи

При резонансе напряжений реактивное сопротивление катушки равно реактивному сопротивлению конденсатора:

X_L = X_C

Резонансная частота определяется формулой:

f₀ = 1 / (2π√LC)

Как резонанс влияет на сопротивление цепи? При резонансе полное сопротивление цепи становится равным активному сопротивлению, а ток достигает максимального значения.

Применение сопротивлений в цепях переменного тока

Сопротивления в цепях переменного тока имеют широкое практическое применение:

Активные сопротивления используются для преобразования электрической энергии в тепловую (нагревательные приборы)
Катушки индуктивности применяются в фильтрах, трансформаторах, дросселях
Конденсаторы используются для накопления энергии, фильтрации, компенсации реактивной мощности

Где еще применяются сопротивления в цепях переменного тока? В системах электроснабжения для ограничения токов короткого замыкания, в измерительной технике для создания делителей напряжения, в радиотехнике для согласования сопротивлений и т.д.

Методы измерения сопротивлений в цепях переменного тока

Существует несколько методов измерения сопротивлений в цепях переменного тока:

Метод амперметра-вольтметра
Мостовой метод
Резонансный метод
Метод ваттметра

Метод амперметра-вольтметра основан на законе Ома и заключается в измерении тока и напряжения с последующим расчетом сопротивления.

Мостовой метод использует мостовые схемы для сравнения измеряемого сопротивления с эталонным.

Как выбрать оптимальный метод измерения? Это зависит от требуемой точности, диапазона измерений, наличия оборудования и других факторов.

4. Электрическая цепь с активным сопротивлением

Электрический ток проводимости в металлах представляет собой направленное движение свободных электронов. Скорость электронов и направление их движения определяется значением и полярностью приложенного к проводнику напряжения.

При движении электроны сталкиваются с атомами проводника, и их кинетическая энергия превращается в тепловую энергию, которая идет на нагрев проводника и рассеивание в окружающую среду. Этот активный процесс является необратимым и количественно определяется сопротивлением R. Поэтому его называют активным сопротивлением. Как правило, различают активное и омическое сопротивления. При рассмотрении цепей переменного тока сопротивление R называют активным, так как оно больше сопротивления постоянному току. При рассмотрении цепей постоянного тока сопротивление R называют омическим.

(Если через один и тот же проводник пропускать переменный и постоянный ток, то для того, чтобы выделилось одно и то же количество теплоты, величина переменного тока должна быть больше, чем постоянного).

Элементы электрической цепи, обладающие только активным сопротивлением R, называют резисторами. Все элементы электрической цепи – провода, обмотки, реостаты – обладают активным сопротивлением, все они нагреваются при пропускании тока.

Кроме активного сопротивления существует еще индуктивное, емкостное, реактивное, полное.

Пусть к зажимам цепи с активным сопротивлением R приложено напряжение источника питания.

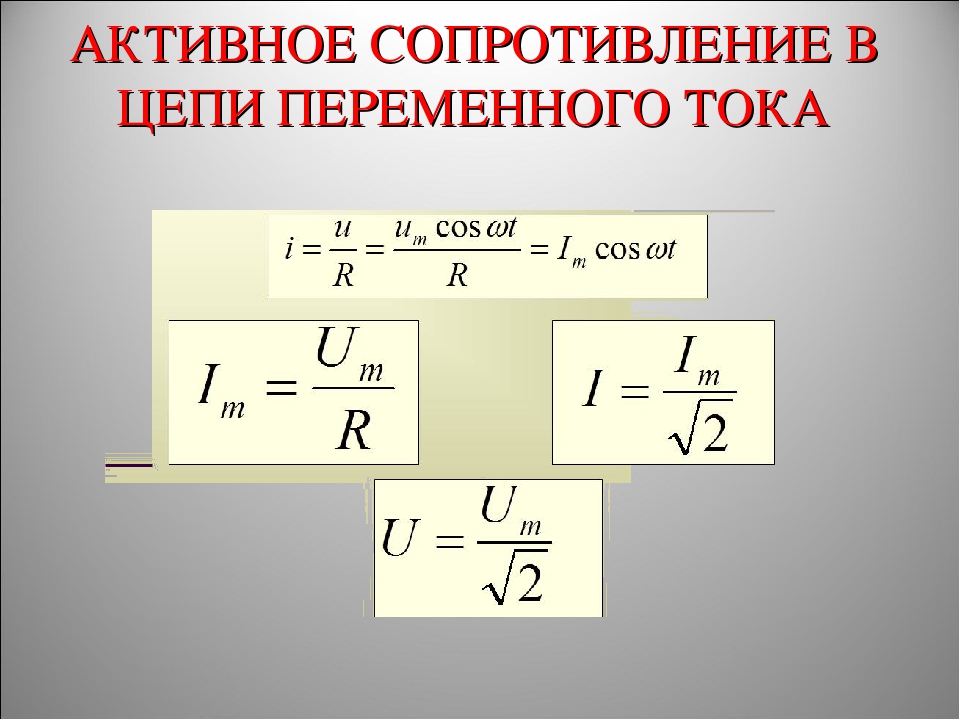
По закону Ома для мгновенных значений для этой цепи

, отсюда

– закон Ома для амплитудных значений.

Разделив левую и правую части этого выражения на , получим

– закон Ома для действующих значений

( , – связь действующего значения с амплитудным).

– закон Ома в комплексной форме.

Комплексное действующее значение тока .

Поскольку ток и напряжение совпадают по фазе, как видно из формул для мгновенных значений, то можно представить изменение тока и напряжения на временной диаграмме следующим образом:

5.

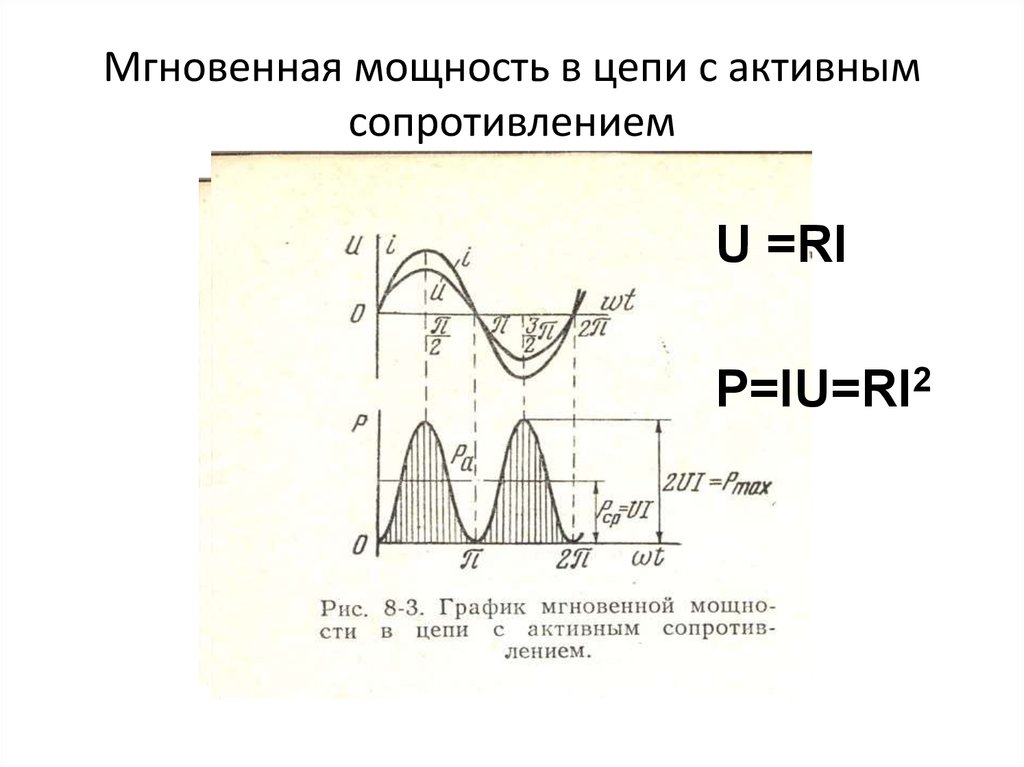
Мощность в цепи с активным сопротивлением

Мгновенная мощность

Мощность определяет скорость расхода энергии, и для цепей переменного тока также является переменной величиной.

Т.к. , то

Из формулы видно:мгновенная мощность остается всегда положительной и колеблется около уровня UI (см. график).

С энергетической точки зрения, положительная мощность – это мощность, которая поступает из генератора в нагрузку, а отрицательная – та, которая возвращается обратно. Первая мощность называется активной, вторая – реактивной. Через активное сопротивление проходит только активная мощность.

Средняя мощность

Для определения расхода энергии за длительное время пользуются средним значением мощности. Такую мощность еще называют активной

P = UI.

Активная мощность обозначается [P], единица измерения Ватт (Вт), (кВт), (МВт).

6. Электрическая цепь с индуктивностью

Индуктивность можно определить как меру магнитной инерции элемента в отношении электромагнитного поля. По смыслу индуктивность в электротехнике можно сравнить с массой в механике. Чем больше индуктивность элемента, тем медленнее и тем большую энергию магнитного поля он запасает.

Индуктивностью, индуктивным сопротивлением обладают в разной мере все элементы электрической цепи переменного тока. Особенно велика она у обмоток или катушек, состоящих из большого числа витков. В цепях постоянного тока индуктивность равна нулю, поскольку ток не меняется со временем и проявляется лишь при переходных режимах.

Рассмотрим электрическую цепь, состоящую из источника и катушки индуктивности.

Под действием синусоидального напряжения в цепи протекает синусоидальный ток

В результате этого вокруг катушки возникает переменное магнитное поле, и в катушке наводится э. д.с. самоиндукции.

Если R = 0, то напряжение источника целиком идет на уравновешивание этой э.д.с. Следовательно,

Т.к. по закону электромагнитной индукции , то

или , где .

Сопоставив выражения для мгновенных значений тока и напряжения, можно видеть, что напряжение в цепи с индуктивностью опережает по фазе ток на .

Т.О, временная диаграмма для тока и напряжения выглядит:

Векторная диаграмма тока и напряжения для цепи с индуктивностью

– индуктивное сопротивление цепи;

: видно, что с увеличением частоты увеличивается индуктивное сопротивление.

Закон Ома для цепи с индуктивностью

Закон Ома для амплитудных значений для цепи с индуктивностью: .

Разделив левую и правую части этого выражения на , получим закон Ома для действующих значений .

Закон Ома в комплексной форме

j обеспечивает сдвиг фаз на между I и U на комплексной плоскости.

2.2. Цепь переменного тока с активным сопротивлением

Известно, что сопротивление одного и того же проводника переменному току больше, чем постоянному току. Это объясняется явлением поверхностного эффекта, сущность которого заключается в следующем. Электрические заряды, обуславливающие постоянный ток, распределяются по сечению проводника равномерно, примерно так, как показано на рис. 2.3, а. При прохождении по проводнику переменного тока, создаваемый им переменный магнитный поток вытесняет электрические заряды из центральной части проводника к его периферийным слоям (рис. 2.3, б).

а) постоянный ток б) переменный ток

Рис. 2.3 Распределение электрических зарядов по сечению проводника

Чем выше частота тока в цепи, тем ближе к поверхности проводника располагаются электрические заряды. При этом плотность зарядов на поверхности проводника увеличивается и его сопротивление возрастает. Сопротивление проводника постоянному току называют омическим сопротивлением, а его сопротивление переменному току – активным сопротивлением. К активным сопротивлениям относят электрические лампы накаливания, электрические печи, различные нагревательные приборы и провода, где электрическая энергия почти целиком превращается в тепловую энергию.

Рассмотрим цепь, состоящую из активной нагрузки с сопротивлением R (рис. 2.4), к зажимам которой приложено переменное напряжение.

(2.5)

Рис. 2.4 Цепь переменного тока с активной нагрузкой.

Мгновенное значение тока в цепи определяется по закону Ома

(2.6)

где

Сравнивая между собой выражения (2. 5) и (2.6), отметим, что в цепи переменного тока с активным сопротивлением напряжение и ток совпадают по фазе друг с другом.

Мгновенная мощность такой цепи равна произведению мгновенных значений тока и напряжения.

(2.7)

Построим волновую и векторную диаграммы цепи переменного тока с активным сопротивлением (рис. 2.5).

Рис. 2.5 Волновая и векторная диаграммы цепи переменного тока с активным сопротивлением.

Как видно из волновой диаграммы, потребление мощности в сети с активной нагрузкой периодически изменяется от нуля до максимального значения и опять до нуля. При этом знак мощности всё время остаётся положительным. Это означает, что в активной нагрузке происходит процесс необратимого преобразования электрической энергии в тепловую энергию.

Мощность цепи переменного тока принято оценивать по среднему значению мгновенной мощности за период:

Следовательно, в цепи переменного тока с активным сопротивлением активная мощность определяется как произведение действующих значений тока и напряжения:

Многие элементы электрических установок состоят из индуктивных катушек, обладающих индуктивностью L. При включении такой катушки в цепь переменного тока, в ней мгновенно проявляется действие ЭДС самоиндукции — , препятствующее изменению тока. Величина этой ЭДС настолько значительна, что на ее уравновешивание затрачивается основная часть напряжения, приложенного к катушке, и лишь его небольшая часть приходится на падение напряжения в активном сопротивлении катушки. Поэтому часто активное сопротивление катушки приравнивается к нулю, и такую катушку называют идеальной катушкой индуктивности. Цепь переменного тока с такой катушкой называется цепью с индуктивной нагрузкой (рис. 2.6).

Рис. 2.6 Цепь переменного тока с индуктивной нагрузкой.

К зажимам цепи подведено синусоидальное напряжение u. Под действием этого напряжения в цепи возникает ток, мгновенное значение которого равно (2.8.)

Ток возбуждает в катушке ЭДС самоиндукции, пропорциональную скорости изменения тока в цепи

(2. 9)

В любой момент времени ЭДС самоиндукции — уравновешивается напряжением на зажимах цепи u

(2.10)

Подставляя (2.8) и (2.10) в (2.9), имеем:

(2.11)

где амплитудное значение напряжения:

(2.12)

Разделив обе части уравнения (2.12) на , получим выражение закона Ома для цепи с идеальной катушкой индуктивности.

(2.13)

Рассмотрим размерность знаменателя выражения (2.13)

Обозначим и назовем индуктивным сопротивлением идеальной катушки. Его величина зависит от индуктивности катушки и частоты питающего тока.

Сравнивая между собой уравнения (2. 8) и (2.11) делаем вывод: в цепи переменного тока с индуктивной нагрузкой напряжение опережает ток на угол в 90°.

Мгновенная мощность цепи определяется как произведение мгновенных значений тока и напряжения, т.е.

Таким образом, мгновенная мощность в цепи переменного тока с индуктивностью изменяется во времени с удвоенной частотой по отношению к частоте тока.

Построим векторную и волновую диаграммы цепи с индуктивным сопротивлением (рис. 2.7).

Рис. 2.7 Векторная и волновая диаграммы цепи переменного тока с индуктивным сопротивлением.

Анализ волновой диаграммы позволяет сделать следующие выводы:

В течение первой и третьей четвертей периода переменного тока при его изменении от нуля до амплитудного значения, мощность положительна. Это означает, что энергия, посылаемая источником во внешнюю цепь, запасается в катушке индуктивности в форме энергии магнитного поля

В течении второй и четвёртой четвертей периода, при изменении тока от амплитудного значения до нуля, мощность отрицательна. Это означает, что катушка индуктивности возвращает запасенную энергию источнику.

Таким образом, в цепи переменного тока с идеальной катушкой индуктивности происходит периодический обмен энергией между внешним источником и магнитным полем катушки. Средняя активная мощность за период оказывается равной нулю, т.е. источник в такой цепи не расходует энергии и, следовательно, в индуктивности не происходит необратимого преобразования электрической энергии в другие виды энергии.

Мощность цепи с идеальной катушкой оценивают по величине индуктивной мощности Q_L, измеряемой в ВАр (вольт-ампер реактивный) и характеризующей интенсивность обмена энергией между генератором и магнитным полем катушки

Индуктивная мощность в отличие от активной мощности не может быть использована в практических целях.

Сопротивление в цепях переменного тока — Цепи переменного тока

Цепи переменного тока

Введение

Как правило, формы сигналов переменного напряжения и тока ряда электронных устройств существенно не отличаются от синусоиды. Дальше, несинусоидальные сигналы могут быть разделены на синусоидальные для целей анализ. Поэтому во всех обсуждениях напряжений и токов в следующем сечения, синусоида будет использоваться как основа математического анализа.

В следующих разделах влияние свойств электрической цепи будут осмотрены. Эти свойства схемы или параметры схемы сопротивление, индуктивность и емкость. Необходимо указать, что это невозможно построить чисто резистивный, чисто индуктивный или чисто емкостная цепь. При обсуждении чистого сопротивления, чистой индуктивности или чистая емкость, мы рассматриваем гипотетические схемы.

Чистая резистивная цепь

Чистая резистивная цепь.

Синусоидальное напряжение подается на сопротивление, как показано на рисунке выше. Показаны результирующие временные вариации форм тока и напряжения. на рисунке ниже. По этим формам сигналов можно сделать следующие выводы:
1. Обе волны синусоидальные и имеют одинаковую частоту.
2. Волны совпадают по фазе.

Синфазный ток и напряжение.

Соотношения формы сигнала на рисунке выше могут быть выражены математически. Напряжение, приложенное к сопротивлению цепи чистого сопротивления, равно

Применяя закон Ома в любой момент,

где

На рисунке ниже показаны две векторные диаграммы. В одном фазор тока и напряжение phasor показаны как максимальные значения. В другом они показаны как эффективные ценности. Поскольку эти вращающиеся векторы времени представляют собой синусоиды, было бы правильнее использовать максимальные значения. На практике удобнее использовать эффективные значения, и, кроме того, эффективные значения на это указывают традиционные показания счетчика.

Векторная диаграмма максимальных и эффективных значений.

Таким образом, закон Ома можно применить к эффективным величинам фазора. ток и векторное напряжение. Проводимость G можно использовать в Уравнения закона Ома для векторного тока и напряжения, как и при постоянном токе. схемы.

Для демонстрации зависимости переменного тока и напряжения по закону Ома от сопротивления приведен следующий пример.

Пример 1: Напряжение, приложенное к сопротивлению чистого цепь сопротивления v = 150 sin 377 t . Сопротивление 800 Ом. Рассчитайте (1) максимальное значение тока, (2) мгновенный ток при t = 0,002 с, и (3) действующее значение тока.

Решение:

2. Расчет мгновенного напряжения при t = 0,002 с,

Мгновенный ток

Мгновенный ток также можно рассчитать напрямую

Также

Средняя мощность, рассеиваемая на сопротивлении, определяется уравнением

В этом уравнении напряжение и ток даны как эффективные значения. Это здесь следует отметить, что В и I указывают действующие значения переменного тока напряжение и ток, соответственно, если только они не указаны для обозначения максимальные или средние значения. Cos θ — коэффициент мощности, а θ — фазовый угол между током и напряжением. Поскольку в цепь чистого сопротивления ток и напряжение совпадают по фазе, угол θ = 0 и cos θ = 1. Предыдущее уравнение поэтому сводится к уравнению для чисто резистивной цепи

15.4 Мощность в цепи переменного тока – University Physics Volume 2

Глава 15. Цепи переменного тока

Цели обучения

К концу раздела вы сможете:

Опишите, как средняя мощность от цепи переменного тока может быть выражена через пиковый ток и напряжение и среднеквадратичное значение тока и напряжения
Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности

Элемент схемы рассеивает или производит мощность в соответствии с [латекс]P=IV,[/латекс], где I — ток через элемент, а В — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность [латекс]p\left(t\right)=i\left(t\right)v\left(t\right)[/latex] также зависит от времени. Сюжет р ( т ) для различных элементов схемы показан на рисунке 15.16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15.7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.

Рисунок 15.16 График мгновенной мощности для различных элементов схемы. (a) Для резистора [латекс]{P}_{\text{ave}}={I}_{0}{V}_{0}\text{/}2,[/latex], тогда как для ( б) конденсатор и (в) катушка индуктивности [латекс] {P} _ {\ text {аве}} = 0.

[/латекс] (г) для источника [латекс] {P} _ {\ text { ave}}={I}_{0}{V}_{0}\left(\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi \right)\text{/}2 ,[/latex], который может быть положительным, отрицательным или нулевым, в зависимости от [latex]\varphi .[/latex]

Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем 9.{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\left(\omega t-\varphi\right)\phantom{\ правило {0.2em} {0ex}} \ text {sin} \ phantom {\ правило {0.2em} {0ex}} \ omega t \ phantom {\ правило {0.2em} {0ex}} дт. [/латекс]

Используя тригонометрическое соотношение [латекс]\фантом{\правило{0.2em}{0ex}}\текст{sin}\фантом{\правило{0.2em}{0ex}}\left(AB\right)=\phantom{ \rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}A\text{cos}\phantom{\rule{0.2em}{0ex}}B-\ фантом {\ правило {0. 2em} {0ex}} \ текст {sin} \ фантом {\ правило {0.2em} {0ex}} B \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ phantom{\rule{0.2em}{0ex}}A,[/latex] получаем 9{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t\text{cos}\phantom{\rule{0.2em }{0ex}}\omega tdt=0.[/latex]

Следовательно, средняя мощность, связанная с элементом схемы, равна

[латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0} \ phantom {\ rule {0.2em} {0ex} }\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]

В инженерных приложениях [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi[/латекс] известен как коэффициент мощности , равный 9.0147 , что является величиной, на которую мощность, подаваемая в цепи, меньше теоретического максимума цепи из-за несовпадения фазы напряжения и тока. Для резистора [латекс]\варфи =0,[/латекс], поэтому средняя рассеиваемая мощность равна

.
[латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0}. [/latex]
Сравнение p ( t ) и [латекс]{P}_{\text{ave}}[/latex] показано на рис. 15.16(d). Чтобы [латекс]{P}_{\text{ave}}=\left(1\text{/}2\right){I}_{0}{V}_{0}[/latex] выглядел как его аналог на постоянном токе, мы используем среднеквадратичные значения {0ex}}{V}_{\text{rms}}[/latex] тока и напряжения. По определению это 9{2}\влево(т\вправо)дт.[/латекс]
С [латекс] я \ влево (т \ вправо) = {I} _ {0} \ фантом {\ правило {0.2em} {0ex}} \ текст {грех} \ фантом {\ правило {0.2em} {0ex }}\left(\omega t-\varphi\right)\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}v\left(t \right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t,[/latex] получаем
[латекс] {I} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} {I} _ {0} \ phantom {\ rule {0.2em} {0ex}} \ text {и}\phantom{\rule{0.2em}{0ex}}{V}_{\text{rms}}=\frac{1}{\sqrt{2}}{V}_{0}.[/ латекс] 9{2}Р.[/латекс]
Это уравнение еще раз подчеркивает, почему для обсуждения выбрано среднеквадратичное значение, а не пиковые значения. Оба уравнения для средней мощности верны для уравнения 15.13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника составляет [латекс]110\sqrt{2}\phantom{\rule{0.2em}{0ex}}\text{V}=\text{156 В}\text{.}[/latex] Потому что большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, покажет 110 В.
Для конденсатора и катушки индуктивности [латекс]\varphi =\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{ 0ex}}-\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{rad,}[/latex] соответственно. Поскольку [latex]\text{cos}\pi \text{/}2=\text{cos}\left(\text{−}\pi \text{/}2\right)=0,[/latex] мы найдите из уравнения 15.12, что средняя мощность, рассеиваемая любым из этих элементов, равна [латекс] {P} _ {\ text {аве}} = 0. [/латекс] Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода и затем разрядите его обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках рис. 15.16, (б) и (в), которые показывают p( t) колеблется синусоидально около нуля.
Фазовый угол генератора переменного тока может иметь любое значение. Если [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi > 0,[/latex] генератор вырабатывает энергию; если [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ phantom {\ rule {0.2em} {0ex }}\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]
Для генератора в цепи RLC ,
9{2}R,[/латекс]
, что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс. {4} \ текст {рад} \ текст{/} \ текст {s} \ справа) t \ справа][/латекс] 9{-6}\phantom{\rule{0.2em}{0ex}}\text{F}[/latex] и [латекс]R=5.00\phantom{\rule{0.2em}{0ex}}\text{ Ω}[/латекс]. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?
Стратегия
Среднеквадратичное напряжение — это амплитуда напряжения, умноженная на [latex]1\text{/}\sqrt{2}[/latex]. Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, потому что у нас есть импеданс цепи Z , среднеквадратичное значение напряжения [латекс] {V} _ {\ text {среднеквадратичное значение}} [/латекс] и сопротивление R .
Решение
Показать ответ
Поскольку [латекс]{V}_{0}=4.00\phantom{\rule{0.2em}{0ex}}\text{V,}[/latex] среднеквадратичное напряжение генератор
[латекс] {V} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} \ left (4. {1\text{/}2}\hfill \\ & =7.07\phantom{\rule{0.2em}{0ex }}\text{Ω}\text{.}\hfill \end{массив}[/latex] 9{2}\text{/}R,[/latex], где 90 117 В 90 118 заменяет среднеквадратичное значение напряжения.
Проверьте свои знания
Вольтметр переменного тока, подключенный к клеммам генератора переменного тока частотой 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
Показать решение
[латекс]v\left(t\right)=\left(10.0\phantom{\rule{0.2em}{0ex}}\text{V}\right)\phantom{\rule{0.2 em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}90\pi t[/latex]
Проверьте свои знания
Покажите, что среднеквадратичное значение напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока со среднеквадратичным значением тока равно [латекс]{I}_{\text{среднеквадратичное значение}}[/латекс] по [латексу] {I} _ {\ text {rms}} R, {I} _ {\ text {rms}} {X} _ {C}, \ phantom {\ rule {0.2em} {0ex}} \ text{and}\phantom{\rule{0.2em}{0ex}}{I}_{\text{rms}}{X}_{L},[/latex] соответственно. Определить эти значения для компонентов Цепь RLC уравнения 15.12.
Show Solution
2,00 В; 10,01 В; 8,01 В
Резюме
Средняя мощность переменного тока находится путем умножения среднеквадратичных значений тока и напряжения.
Закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на импеданс.
Средняя мощность, подаваемая на Цепь RLC зависит от фазового угла.
Коэффициент мощности находится в диапазоне от –1 до 1.
Концептуальные вопросы
При каком значении фазового угла [latex]\varphi[/latex] между выходным напряжением источника переменного тока и током средняя выходная мощность источника максимальна?
Обсудите разницу между средней мощностью и мгновенной мощностью.
Показать решение
Мгновенная мощность — это мощность в данный момент времени. Средняя мощность — это мощность, усредненная по циклу или числу циклов.
Средний переменный ток, подаваемый в цепь, равен нулю. Несмотря на это, мощность рассеивается в цепи. Объяснять.
Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?
Показать решение
Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.
Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Задачи
ЭДС источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0. 2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{рад/с}\text{.}[/latex] Вычислить среднюю выходную мощность источника, если он подключен через (a) конденсатор [латекс]20\text{-}\mu \text{F}[/латекс], (б) катушку индуктивности 20 мГн и (в) [латексный ]50\text{-}\text{Ом}[/latex] резистор.
Расчет среднеквадратичного значения тока для источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0.2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{rad/s}[/latex] при соединении через (a) [латекс] 20\text{-}\mu \text{F}[/latex] конденсатор, (b) катушка индуктивности 20 мГн и (c) [латекс]50\text{-}\text{Ом}[/latex ] резистор.
Показать решение
а. 0,89 А; б. 5,6 А; в. 1,4 А
Катушка индуктивности 40 мГн подключена к источнику переменного тока частотой 60 Гц, амплитуда напряжения которого составляет 50 В. Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет?
Для цепи РЛК серии амплитуда напряжения и частота источника 100 В и 500 Гц соответственно; [латекс] R = 500 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс]; и [латекс] L = 0,20 \ фантом {\ правило {0,2em} {0ex}} \ текст {H} [/латекс]. Найдите среднюю мощность, рассеиваемую на резисторе, при следующих значениях емкости: (а) [латекс]С=2,0 мкМ \текст{F}[/латекс] и (б) [латекс]С=0,20\фантом{\ правило{0.2em}{0ex}}\mu \text{F}\text{.}[/latex]
Показать раствор
а. 7,3 Вт; б. 6,3 Вт
Источник переменного тока с амплитудой напряжения 10 В отдает электрическую энергию мощностью 0,80 Вт при выходном токе 2,5 А. Каков фазовый угол [латекс]\varphi[/латекс] между ЭДС и током?
Цепь серии RLC имеет импеданс [латекс]60\фантом{\правило{0.2em}{0ex}}\текст{Ом}[/латекс] и коэффициент мощности 0,50, при этом напряжение отстает от текущий. а) Следует ли последовательно с элементами включить конденсатор или катушку индуктивности, чтобы повысить коэффициент мощности цепи? б) При каком реактивном сопротивлении катушки индуктивности коэффициент мощности увеличится до единицы?
Показать раствор
а.