Что такое закон Ома и как он связан с мощностью в электрических цепях. Как рассчитать мощность по сопротивлению. Какие формулы применяются для расчета мощности в различных случаях. Где используется закон Ома на практике.
Закон Ома: основные понятия и формулировка
Закон Ома — один из фундаментальных законов электротехники, устанавливающий связь между силой тока, напряжением и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году.
Формулировка закона Ома гласит: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
Математически закон Ома выражается формулой:
I = U / R
где:
- I — сила тока (в амперах, А)
- U — напряжение (в вольтах, В)
- R — сопротивление (в омах, Ом)
Связь закона Ома с мощностью электрического тока
Мощность электрического тока — это работа, совершаемая током за единицу времени. Она характеризует скорость преобразования электрической энергии в другие виды энергии.
Формула для расчета мощности:
P = U * I
где P — мощность (в ваттах, Вт).
Подставив в эту формулу выражение для силы тока из закона Ома, получим формулу для расчета мощности через напряжение и сопротивление:
P = U^2 / R
Формулы для расчета мощности в различных случаях
Существует несколько формул для расчета мощности в зависимости от известных параметров цепи:
- P = U * I — если известны напряжение и сила тока
- P = I^2 * R — если известны сила тока и сопротивление
- P = U^2 / R — если известны напряжение и сопротивление
Эти формулы позволяют рассчитать мощность, зная любые два из трех параметров: напряжение, силу тока или сопротивление.
Практическое применение закона Ома для расчета мощности
Закон Ома и формулы для расчета мощности широко применяются на практике в электротехнике и электронике. Вот некоторые примеры:
- Расчет мощности электроприборов
- Определение необходимого сечения проводов
- Подбор номиналов резисторов в электронных схемах
- Расчет КПД электрических устройств
- Проектирование систем электроснабжения
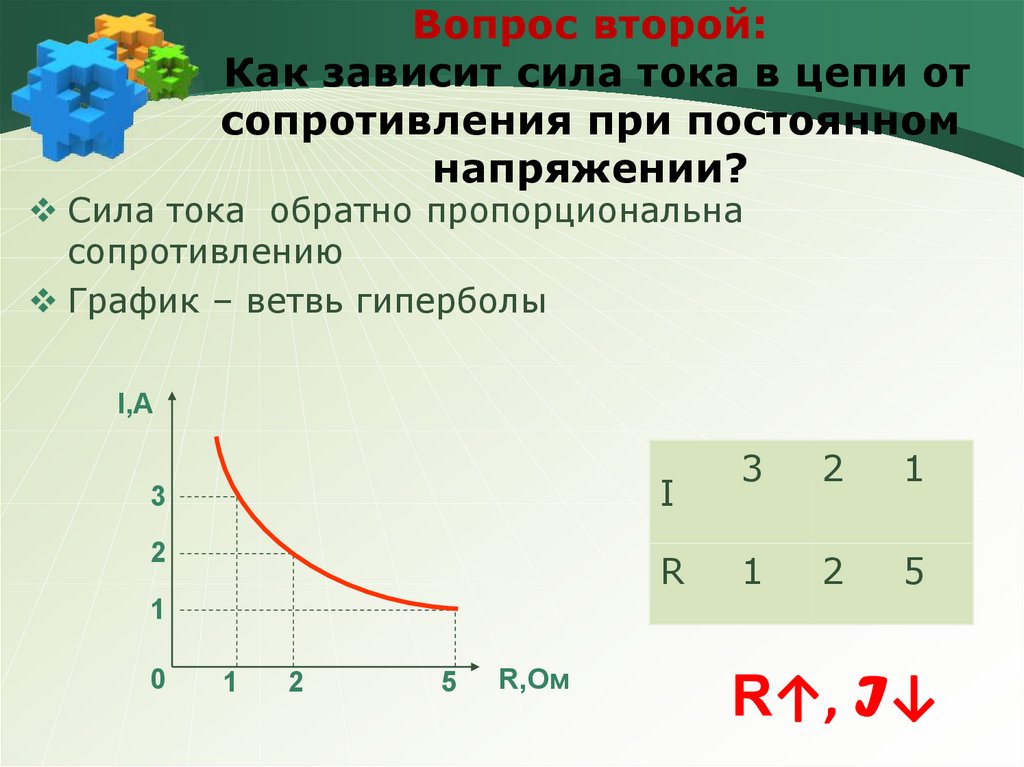
Зависимость мощности от сопротивления при постоянном напряжении
При постоянном напряжении мощность, выделяемая на сопротивлении, обратно пропорциональна величине этого сопротивления. Это следует из формулы P = U^2 / R.
Графически эта зависимость выглядит как гипербола:
«` «`Как видно из графика, при увеличении сопротивления мощность уменьшается, стремясь к нулю при бесконечно большом сопротивлении.
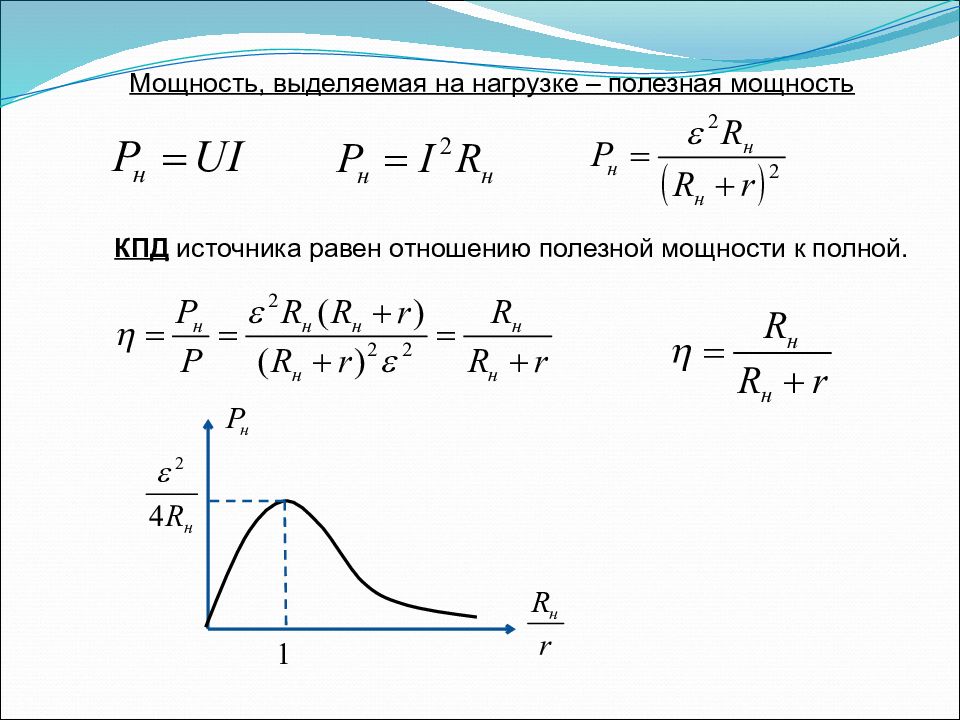
Максимальная мощность в цепи с источником ЭДС
В цепи с источником ЭДС и внутренним сопротивлением максимальная мощность на нагрузке достигается при равенстве сопротивления нагрузки внутреннему сопротивлению источника. Это называется согласованием нагрузки.
Формула для расчета максимальной мощности:
P_max = (E^2) / (4 * R_внутр)
где E — ЭДС источника, R_внутр — его внутреннее сопротивление.
Закон Джоуля-Ленца и тепловая мощность
Закон Джоуля-Ленца связывает количество теплоты, выделяемой в проводнике при прохождении электрического тока, с параметрами цепи:
Q = I^2 * R * t
где Q — количество теплоты, t — время.
Тепловая мощность, выделяемая на участке цепи:
P = I^2 * R
Эта формула идентична одной из формул для расчета электрической мощности, что показывает эквивалентность электрической и тепловой мощности в проводнике.
Применение закона Ома в бытовых электроприборах
В быту мы постоянно сталкиваемся с проявлениями закона Ома и зависимости мощности от сопротивления. Вот несколько примеров:
- Электрические чайники и обогреватели используют большую мощность за счет низкого сопротивления нагревательного элемента
- Светодиодные лампы потребляют меньше энергии из-за высокого внутреннего сопротивления
- Регуляторы яркости света работают на принципе изменения сопротивления в цепи
- Предохранители защищают технику, разрывая цепь при превышении допустимой силы тока
Ограничения закона Ома и нелинейные элементы
Закон Ома применим не ко всем элементам электрических цепей. Существуют так называемые нелинейные элементы, для которых зависимость между током и напряжением не является линейной. К ним относятся:
- Полупроводниковые диоды
- Транзисторы
- Газоразрядные лампы
- Терморезисторы
Для таких элементов расчет мощности требует использования более сложных моделей и формул.
Заключение
Закон Ома и связанные с ним формулы для расчета мощности являются основополагающими в электротехнике. Понимание взаимосвязи между током, напряжением, сопротивлением и мощностью позволяет эффективно проектировать и анализировать электрические цепи, а также оптимизировать работу электрооборудования.
Несмотря на свою простоту, закон Ома остается одним из самых важных и широко используемых законов в области электричества и электроники, находя применение как в сложных промышленных системах, так и в бытовых приборах.
Мощность резистора
151
Сегодня поговорим о мощности резисторов. Это тоже очень важный параметр. Я уже рассказывал о том что такое резистор, и какие виды и типы резисторов бывают. Но подробно про мощность мы не говорили.
Мощность резистора — это максимально допустимое значение мощности электрического тока (единица измерения Ватт), которое резистор может пропустить через себя без перегрева и выхода из строя. Резистор в зависимости от своего сопротивления и тока проходящего через него превращает часть электрической энергии в тепло. Это и называется мощностью рассеивания резистора.
Какая мощность будет выделяться (рассеиваться) на резисторе
Как я уже написал чуть выше, мощность рассеивания резистора зависит от его сопротивления и силы тока, проходящего по нему. Для расчета мощности, которая будет рассеиваться в виде тепла на резисторе используется формула: P = I² * R
- P — мощность в Ватт
- I — Сила тока в Ампер
- R — Сопротивление в Ом
Для примера рассчитаем мощность которая будет рассеиваться на резисторе в схеме с подключением светодиода.
Вот схема подключения:
Про то как рассчитать номинал резистора для подключения светодиода и силу тока в цепи, а так же как управлять светодиодом с помощью Ардуино я писал в этой статье. В нашем примере используется резистор на 150 Ом и сила тока в цепи составляет 20 миллиампер или 0.02 ампера. Теперь мы можем рассчитать мощность, которая будет рассеиваться на резисторе.
P = I² * R = 0.02² * 150 = 0.0004 * 150 = 0.06 Ватт
Это значит что на нашем резисторе будет рассеиваться 0.06 Ватт. Это совсем не много, поэтому подойдет практически любой резистор кроме самых маломощных SMD элементов.
Если фактическая рассеиваемая мощность превышает допустимую для резистора, то он будет перегреваться и в итоге сгорит. Это не только разорвет электрическую цепь, но и может стать причиной пожара. Поэтому старайтесь использовать резисторы с заявленной мощностью больше чем необходимая в 1.5-2 раза.
Как определить мощность резистора
Как я уже писал в других статьях, обычно резисторы — это мелкие элементы, поэтому на их корпусе сложно описать все их параметры.
Для описания номинала и класса точности используется цветовая маркировка или специальная маркировка для SMD резисторов. А для того что бы понять какой мощности резистор нужно его измерить. Вот схема которая поможет узнать мощность резисторов в зависимости от их размера:
Так же существуют резисторы рассчитанные и на более высокие мощности. Они уже крупнее, поэтому их мощность и номинал написаны на корпусе «человеческим языком». Вот керамические резисторы или даже высокомощные с радиатором для рассеивания тепла:
Керамические резисторы с сопротивлением 10 Ом и мощностью 10 ВаттРезистор с радиатором на 10 Ом и мощностью 50 ВаттМощность SMD резисторов
Показатель максимальной мощности в маркировку на таких маленьких корпусах поместить было просто не возможно. Но мы все равно можем определить максимальную мощность смд резистора при помощи штангенциркуля, ну или хотя бы обычной линейки. Дело в том что мощность зависит от размера корпуса smd резистора.
Поэтому они делятся на типоразмеры и обозначаются цифрами, которые означают длину и ширину корпуса в дюймах. Вот таблица с помощью которой вы сможете определить допустимую мощность резистора в smd исполнении:
| Размер в дюймах | Длинна в мм | Ширина в мм | Мощность при 70°C в Ватт |
| 0075 | 0,3 | 0,15 | 0,02 |
| 01005 | 0,4 | 0,2 | 0,03 |
| 0201 | 0,6 | 0,3 | 0,05 |
| 0402 | 1 | 0,5 | 0,063 |
| 0603 | 1,6 | 0,8 | 0,1 |
| 0805 | 2,0 | 1,25 | 0,125 |
| 1206 | 3,2 | 1,6 | 0,25 |
| 1210 | 3,2 | 2,5 | 0,5 |
| 1218 | 3,2 | 4,8 | 1 |
| 1812 | 4,5 | 3,2 | 0,75 |
| 2010 | 5 | 2,5 | 0,75 |
| 2512 | 6,4 | 3,2 | 2 |
Обратите внимание что при последовательном и параллельном подключении резисторов, рассеиваемая мощность рассчитывается для каждого резистора отдельно.
Мощность выделяемая на внутреннем сопротивлении источника тока
С. Н. Карташов
Мощность, выделяемая во внешней цепи с потребителями С.Н.КАРТАШОВ ,с. Маис, Пензенская обл.
Предлагаемые задачи рассматриваются с учениками 10-х и 11-х классов на заседании школьного физического кружка. Они требуют знаний по теме «Законы постоянного тока», умения исследовать функции на экстремум при помощи производной, а также навыков программирования на компьютере.
ЗАДАЧА 1. Найдите зависимость мощности, выделяемой во внешней цепи, от числа одинаковых потребителей (лампочек), соединённых параллельно. ЭДС источника , его внутреннее сопротивление r .
Решение
Пусть сопротивления всех лампочек
одинаковы R 1 = R 2 = … = R n , P – мощность, выделяемая во внешней цепи, P 1
– мощность, выделяемая на каждой лампочке.
Очевидно, что P = nP 1 ; P 1 = I 1 2 R 1 , где I 1 – ток, проходящий
через каждую лампочку.
Сила тока в неразветвлённой цепи:
(1)
Применяя первое правило Кирхгофа, имеем
(2)
С учётом (2) имеем для мощности
Полная мощность, выделяемая во внешней цепи:
(3)
Нетрудно заметить, что если n , то P 0. Это означает, что при неограниченном увеличении количества лампочек мы не достигнем бесконечного увеличения мощности, выделяемой во внешней цепи. Напротив, мощность будет стремиться к нулю.
Из формулы (3) следует также, что если r 0, то P n 2 /R . То есть, если источник тока идеален (r = 0), то мощность возрастает прямо пропорционально числу потребителей в цепи. Но внутреннее сопротивление источника тока не может быть равно нулю, поэтому достигнуть бесконечного увеличения мощности во внешней цепи за счёт увеличения числа потребителей невозможно. Напротив, достигнув максимума, мощность, выделяемая во внешней цепи, начнёт уменьшаться с ростом потребителей.
Для получения полной картины
зависимости мощности Р от количества
потребителей n , можно предложить учащимся
построить график зависимости P (n ) на
компьютере ( = 20 В, r = 0,5 Ом, R 1 = 100 Ом).
В рубрике
«Дополнительные материалы» на сайте газеты приводим
авторскую компьютерную программу WATT для
построения вышеупомянутой зависимости (среда
программирования QBasic , компьютер Celeron 1300).
Изменяя внутреннее сопротивление r при неизменных и R 1 , делаем вывод: мощность P , выделяемая во внешней цепи, убывает с ростом r . Изменяя R 1 при неизменных и r , делаем вывод: от сопротивления одной лампочки максимум мощности P не зависит. Этот максимум сдвигается вправо при увеличении R 1 и сдвигается влево при уменьшении
ЗАДАЧА 2. При каком значении R мощность, выделяемая во внешней цепи, максимальна? ЭДС источника тока , внутреннее сопротивление r .
Решение
Получим формулу зависимости мощности P , выделяемой во внешней цепи, от внешнего сопротивления R и исследуем функцию P (r ) на экстремум при помощи производной.
По закону Ома для полной цепи, ток I =/(R + r
), мощность, выделяемая во внешней цепи:Дифференцируем P по R :
Найдём критические точки из условия P» = 0:
(R + r ) 2 – 2R (R + r ) = 0;
(R + r ) · (R + r – 2R ) = 0;
(R + r ) · (r – R ) = 0.
Имеем две критические точки R = –r и R = r . Но т.к. R > 0, то R = –r не имеет смысла.
Производная P» меняет знак с
«+» на «–» в точке R = r , следовательно, R = r – точка минимума.
Итак, мощность максимальна, если R = r , т.е. внутреннее сопротивление источника тока равно внешнему сопротивлению. Это означает, что применительно к задаче 1 максимум мощности наблюдается при
Рассчитаем максимум мощности, используя формулу (3) и условие r = R 1 /n :
(4)
При = 12 В, r = 0,4 Ом и R 1 = 20 Ом имеем n max = R 1 /r = 50 ламп.
Согласно формуле (4), P max = 90
Вт. Всё это очень хорошо согласуется с
результатами компьютерного эксперимента. Кроме
того, из этой формулы следует, что максимум
мощности зависит от внутреннего сопротивления
обратно пропорционально, в чём легко убедиться,
используя компьютерную программу WATT ,
приведённую на сайте газеты .
2 и скопируем её в
ячейки В5–В30. Графики, построенные с помощью
таблицы Excel и программы WATT, совпадают
(максимум мощности 200 Вт получается, если внешнее
сопротивление цепи равно внутреннему
сопротивлению источника тока). В рубрике
«Дополнительные материалы» к № 9/2008 на сайте
газеты приведена программа «Мощность»,
аналогичная программе WATT , но на более
продвинутом языке VisualBasic 6.0, результат расчёта
с её помощью, а также таблица МicrosoftExcel.
Сергей Николаевич Карташов –
учитель физики высшей квалификационной
категории, выпускник физфака МПГУ им. В.И.Ленина
1993 г. Педагогический стаж 14 лет. Ученики Сергея
Владимировича занимают призовые места на
районных олимпиадах по физике и математике.
Педагогическое кредо: моделирование физических
процессов на компьютере, индивидуальная работа с
сильными детьми. Один закончил физфак МГУ им.
М.В.Ломоносова, ещё один учится в университете им.
Н.Э.Баумана. В 2002 г. Сергей Владимирович был
награждён почётной грамотой МОиН РФ.
Доброго вам времени суток! Рад снова видеть вас на уроке. Сегодня нас ждёт разговор об одном свойстве электрического тока, которое может быть и полезным, и вредным. Ранее уже упоминалось, что для переноса заряда по проводнику необходимо затратить некоторое количество энергии. Так же мы говорили о том, что источником этой энергии для электрической цепи являются источники тока. А куда же эта энергия девается, ведь электроны только переносят её из точки А в точку В и отдают либо узлам решётки материала, либо, если электрон ну оооочень везучий, возвращают её на противоположный электрод батареи? Стоит сразу заметить, что число таких «везучих» электронов очень близко к нулю, то есть вероятность электрона достигнуть лампочки во Владивостоке, вылетев из розетки в Москве, практически равна нулю (оп-па, какая подсказочка к задаче ). Это объясняется очень просто: ЭДС источника всегда уменьшается, значит, энергия пропадает куда-то… Но это нарушало бы закон сохранения энергии.
Действительно, энергия не может пропадать в никуда, она лишь преобразуется из одного вида в другой. На этом принципе работают источники тока: какой-то вид энергии (химическая, световая, механическая и т.д.) преобразуются в электрическую энергию. Имеет место и обратное преобразование: зарядка аккумулятора приводит к восстановлению электролита, электрическая лампочка излучает свет, а динамик наушников – звук. Эти процессы и характеризуют работу электрического тока. Давайте для наглядности остановимся на обыкновенной лампе накаливания. Известно, что их существует большое количество: разнообразные размеры и формы, рабочее напряжение, некоторые лампы светят ярче, некоторые тусклее. Неизменным остаётся только принцип их работы. Рассмотрим внутреннее строение такой лампы:
Рисунок 6.1 – Внутреннее строение лампы накаливания
Обычная лампочка, которую сейчас пытаются заменить на так называемую «энергосберегающую», состоит из:
- 1.
Стеклянная колба. - 2. Полость колбы (вакуумированная или наполненная газом).
- 3. Нить накаливания (вольфрам или его сплав).
- 4. Первый электрод.
- 5. Второй электрод.
- 6. Крючки-держатели нити накаливания.
- 7. Ножка лампы (выполняет функцию держателя).
- 8. Внешний вывод для подключения (токоввод), имеющий внутри предохранитель, который защищает колбу от разрыва в момент перегорания нити накала.
- 9. Корпус цоколя (держатель лампы в патроне).
- 10. Изолятор цоколя (стекло).
- 11. Второй внешний вывод для подключения (токоввод).
Стеклянная колба.Как легко заметить к электрической части лампы (то есть той части, по которой протекает ток), можно отнести далеко не все составляющие. Можно сказать, что лампа состоит из проводника, который посредством специальной системы может подключаться к электрической цепи. Принцип работы лампы накаливания основан на эффекте электромагнитного теплового излучения. Однако излучение может приходиться на разные области спектра: от инфракрасного до видимого.
Чтобы обеспечить излучение в видимой области спектра, согласно закону Планка (зависимость длины волны излучения от температуры), необходимо подобрать температуры, при которой происходит излучение преимущественно белого света. Этому условию удовлетворяет диапазон температур от 5500 до 7000 градусов Кельвина. При температуре 5770К спектр излучения лампы будет совпадать со спектром излучения Солнца, что наиболее привычно человеческому глазу.
Однако нагревания до таких высоких температур не выдерживает ни один из известных металлов. Наиболее тугоплавкие металлы вольфрам и осмий имеют температуру плавления 34100С (3683К) и 30450С (3318К), соответственно. Поэтому все лампы накаливания излучают только бледно-желтый свет, однако, реально воспринимаемый цвет может быть искажён адаптацией глаза к условиям освещения. Излучение «холодного» белого света является одним из преимуществ «энергосберегающих» ламп перед лампами накаливания.
Колба с газом или вакуумом необходима для защиты нити накала от воздействия атмосферного воздуха.
Газовая среда состоит в основном из смеси инертных газов (смесь азота N2 с аргоном Ar являются наиболее распространёнными в силу малой себестоимости и большой молярной массы, которая уменьшает потери тепла, возникающие при этом за счёт теплопроводности). Особой группой являются галогенные лампы накаливания. Принципиальной их особенностью является введение в полость колбы галогенов или их соединений. В такой лампе испарившийся с поверхности тела накала металл вступает в соединение с галогенами, и затем возвращается на поверхность нити за счёт температурного разложения получившегося соединения. Такие лампы имеют большую температуру спирали, больший КПД и срок службы, меньший размер колбы и другие преимущества. Но вернемся к току, который протекает по нити накаливания…
Ранее мы говорили, что перенос единичных зарядов в проводнике из точки А в точку В производится под действием электрического напряжения, которое совершает работу. При различных значениях напряжения и величине заряда, выполняется различная работа, следовательно, необходимо оценить величину скорости передачи (преобразования) энергии.
Эта величина называется электрической мощностью и характеризует выполненную работу за единицу времени:
Работа электрического тока при переносе одного заряда численно равна значению напряжения на участке АВ ( : потенциальная энергия поля равна произведению разности потенциалов на перенесённый заряд), тогда:
Умножив значение мощности для одного заряда на число перенесённых зарядов, получим значение мощности электрического тока:
Учитывая, что отношение величины заряда ко времени равно величине протекающего тока, получим:
Величина электрической мощности измеряется в ваттах (Вт) или в вольт-амперах (ВА), однако, эти величины не являются тождественными. Хотя произведение силы тока, выраженной в амперах на напряжение, выраженное в вольтах, даёт величину вольт-амперы, она используется для характеристики несколько «другой» мощности, которую мы рассмотрим позже, так как она пока не связана с изучаемыми характеристиками.
Тогда работа тока равна мощности, умноженной на время:
Величина работы электрического тока измеряется в джоулях (Дж) .
Применяя закон Ома и следствия из него, получим еще два выражения для вычисления электрической мощности:
При помощи этих формул и известных значений любых двух величин из четырех (напряжение, ток, сопротивление, мощность) можно найти остальные две величины. Кроме того, эти формулы выражают так называемую постоянную мощность. Кроме неё, можно дать характеристику мгновенной мощности , которая в различные моменты времени может изменять своё значение:
Обычно для выделения величины, зависящей от времени (мгновенное значение) используют строчные буквы алфавита, а для выделения величин, характеризующие постоянные или усреднённые значения – прописные . Мгновенной работы, разумеется, не существует.
Так же следует запомнить, что электроны, перемещающиеся по проводнику, сталкиваются с узлами кристаллической решётки, отдают им свою энергию, которая выделяется в виде тепла, поэтому практически вся электрическая энергия в проводнике переходит в тепловую, но при высоких температурах нагрева (электрическая лампа) часть энергии расходуется еще и на световое излучение.
Кроме того, раз на любом участке проводника существует преобразование мощности в тепло, значит, не вся мощность, выделяемая источником, (а она эквивалентна мощности тока, только вместо значения напряжения в формулу 6.1 необходимо подставить значение ЭДС источника) поступает в нагрузку. Нагрузкой в электротехнике называется потребитель (приемник) электрической энергии, в данном случае – лампа накаливания. Тогда для характеристики эффективности системы (устройства, машины, электрической цепи) в отношении преобразования или передачи энергии вводится коэффициент полезного действия (КПД). Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой, обозначается обычно η («эта»). КПД является безразмерной величиной и часто измеряется в процентах. Математически определение КПД может быть записано в виде:
где A – работа, выполненная потребителем,
Q – энергия, отданная источником.
В силу закона сохранения энергии КПД всегда меньше единицы или равен ей, то есть невозможно получить полезной работы больше, чем затрачено энергии.
Разность ∆Q=A-Q называется потерями мощности . Из формулы 6.3 видно, что потери мощности будут возрастать при увеличении сопротивления проводника, поэтому чтобы получить как можно больше теплового излучения в лампах используется тонкая бифилярная (двойная) спираль, сопротивление которой довольно велико. Нить имеет толщину порядка 50 микрон, чтобы компенсировать относительно малое удельное сопротивление металла. Стоит отметить, что КПД ламп накаливания составляет не более 15%, то есть более 85% мощности рассеивается в виде тепла (инфракрасное излучение).
На этом наш урок закончен, надеюсь, что он вам понравился, не забывайте подписываться на обновления . До свидания!
Задачки на сегодня.
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt . Электрическое поле на выделенном участке совершает работу
выражающей закон Ома для однородного участка цепи с сопротивлением R , умножить на I Δt , то получится соотношение
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.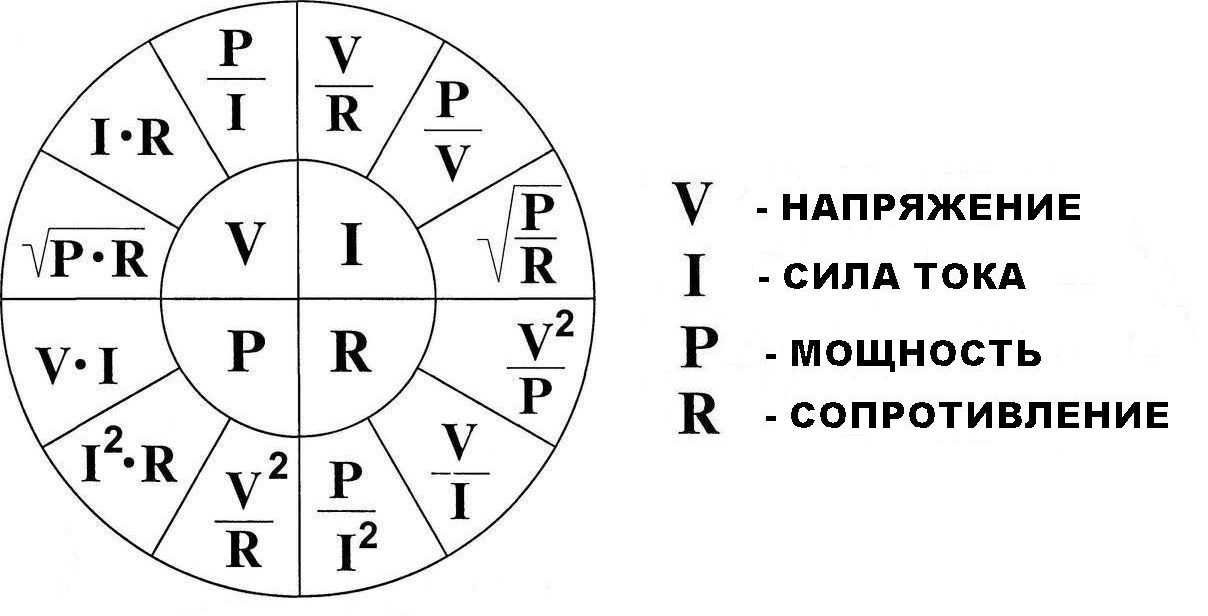
Джоулем и Эмилием Ленцем и носит название закона Джоуля-Ленца .
Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt , за которое эта работа была совершена:
Работа электрического тока в СИ выражается в Джоулях (Дж), мощность — в Ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R . Закон Ома для полной цепи записывается в виде
Первый член в левой части ΔQ = R I 2 Δt — тепло, выделяющееся на внешнем участке цепи за время Δt , второй член ΔQ ист = r I 2 Δt — тепло, выделяющееся внутри источника за то же время.
Выражение I Δt равно работе сторонних сил ΔA ст, действующих внутри источника.
При протекании электрического тока по замкнутой цепи работа сторонних сил ΔA ст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ ) и внутри источника (ΔQ ист ) .
ΔQ + ΔQ ист = ΔA ст = I Δ |
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами , действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
Внешняя цепь может представлять собой не только проводник с сопротивлением R , но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки . Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем.
Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
Во внешней цепи выделяется мощность
Отношение равное
называется коэффициентом полезного действия источника .
На рис. 1.11.1 графически представлены зависимости мощности источника P ист, полезной мощности P , выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной , и внутренним сопротивлением r . Ток в цепи может изменяться в пределах от I = 0 (при ) до (при R = 0).
Из приведенных графиков видно, что максимальная мощность во внешней цепи P max , равная
достигается при R = r . При этом ток в цепи
а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т.
е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
Мощность и внутреннее сопротивление
Мощность и внутреннее сопротивлениеДалее: Примеры работы Вверх: Электрический ток Предыдущий: Энергия в цепях постоянного тока Рассмотрим простую схему, в которой батарея ЭДС и внутренних сопротивление управляет током через внешний резистор сопротивления (см. рис. 17). Внешний резистор обычно называют в качестве нагрузочного резистора . Это может означать либо электрический свет, электрический нагревательный элемент или, может быть, электродвигатель. основная цель схема заключается в передаче энергии от батареи к нагрузке, где она фактически делает что-то полезное для нас ( напр. , освещение лампочка или поднятие тяжестей). Посмотрим, насколько внутреннее сопротивление батареи мешает этому процессу.
Эквивалентное сопротивление цепи (поскольку сопротивление нагрузки равно
последовательно с внутренним сопротивлением), поэтому ток, протекающий в
схема задается
| (145) |
Выходная мощность ЭДС просто
| (146) |
Мощность, рассеиваемая в виде тепла на внутреннем сопротивлении батареи, равна
| (147) |
Аналогично, мощность, передаваемая в нагрузку, равна
| (148) |
Обратите внимание, что
| (149) |
Таким образом, часть выходной мощности батареи немедленно теряется по мере рассеивания тепла.
внутреннее сопротивление аккумулятора. Остаток передается в нагрузку. Пусть
а также . Это следует из
уравнение (148) что
| (150) |
Функция монотонно возрастает от нуля при увеличивается в диапазоне, достигает максимальное значение при , а затем монотонно убывает с ростом В диапазоне . Другими словами, если сопротивление нагрузки изменяется при постоянна, а затем передаваемая мощность достигает максимума ценность
| (151) |
когда . Это очень важный результат в электротехнике. Передача мощности между источником напряжения и внешней нагрузкой наиболее эффективна, когда сопротивление нагрузки соответствует внутреннему сопротивлению источника напряжения.
Если сопротивление нагрузки слишком низкое, то большая часть выходной мощности напряжения
источник рассеивается в виде тепла внутри самого источника. Если сопротивление нагрузки
слишком велик, то ток, протекающий в цепи, слишком мал для
передавать энергию в нагрузку с заметной скоростью. Отметим, что в оптимальном случае
, всего половина выходной мощности источника напряжения
передается в нагрузку. Другая половина рассеивается в виде тепла внутри
источник.
Между прочим, инженеры-электрики называют процесс, при котором сопротивление
нагрузка согласована с нагрузкой источника питания согласование импеданса (импеданс — это просто причудливое название сопротивления). Далее: Примеры работы Вверх: Электрический ток Предыдущий: Энергия в цепях постоянного тока Ричард Фицпатрик 2007-07-14
Справедливость, сила и сопротивление | EG Press
Справедливость, сила и сопротивление – международный рецензируемый журнал, продвигающий критический анализ и объединяющий теорию, политику и активизм.
Работая над социальной справедливостью, государственной подотчетностью и освобождением от наказания, журнал в первую очередь является средством для обеспечения доступности и продвижения сложных исследований и научных исследований, которые можно использовать для критического информирования современных дебатов и политики. Первоначально основанный в Европейской группе по изучению отклонений и социального контроля, журнал предлагает ученым, практикам и активистам критически осмыслить концепции справедливости и власти, а также их последствия для жизни людей, наиболее затронутых социальными проблемами. вредит. Сосредоточение внимания на сопротивлении отражает стремление перенести это важнейшее знание в социальные действия, использовать способы, которыми можно противостоять преступлениям и вреду сильных мира сего, в частности, и поддерживать более широкое понимание того, как смягчить пенитенциарный экспансионизм и смягчить вред и насилие. .
Редакторы приветствуют теоретические, нормативные и эмпирические исследования с междисциплинарной точки зрения, включая социологию, земиологию, географию, право, историю, криминологию, пенологию, философию, социальную политику и социальную теорию от ученых и активистов.
Журнал также стремится улучшить общение и сотрудничество в критических и радикальных сетях. Следовательно, он приветствует открытые материалы в следующих формах:
- Исследовательские статьи объемом 6000-8000 слов
- Интервенции (включая краткие статьи, новости кампании, личные размышления и (авто)биографические рассказы) объемом до 2000 слов
- Рецензии на книги объемом до 2000 слов
Журнал также публикует и приветствует идеи для тематических специальных выпусков.
Тематика журнала включает ряд тем, включая критический анализ социального вреда; теории государственной власти, авторитета и легитимности; гендерное и расовое насилие; политика социального контроля; класс, бедность и маргинализация; наследие колониализма, неоколониализма и постколониализма; пенитенциарная политика и пенитенциарная практика; вред сильных мира сего; криминализация; сравнительные исследования и интернационалистские точки зрения; аболиционистские взгляды, социальные движения, вовлеченные в прямую борьбу сопротивления и оспаривания; интервенционистские стратегии и радикальные альтернативы, продвигающие права человека, социальную справедливость и демократическую подотчетность.
С 2021 года (Том 5) Справедливость, сила и сопротивление будет опубликовано Policy Press совместно с Европейской группой по изучению отклонений и социального контроля. Информацию о журнале можно найти здесь: Политика Press | Справедливость, сила и сопротивление (bristoluniversitypress.co.uk)
Пожалуйста, направляйте запросы на подписку и обновления, касающиеся 2021 (том 5), дистрибьютору Policy Press, Turpin Distribution Ltd:
Turpin Distribution Ltd
Pegasus Drive
Страттонский бизнес -парк
Biggleswade
Бедфордшир
SG18 8TQ, UK
TEL: +44 (0) 1767 6019
TEL: +44 (0) 1767 6019
TEL: +44 (0) 1767 604619
TEL: +44 (0) 1767 604619
.
Электронная почта: [email protected]
Тарифы на подписку на 2021 год доступны по адресу: https://bristoluniversitypress.co.uk/journals/subscribe. С прессой Policy можно связаться по адресу: pp-journals@bristol .
