Как рассчитать мощность при параллельном соединении резисторов. Какие формулы используются для вычисления общей мощности и мощности отдельных элементов. Чем отличается параллельное соединение от последовательного с точки зрения мощности.
Основные принципы параллельного соединения резисторов
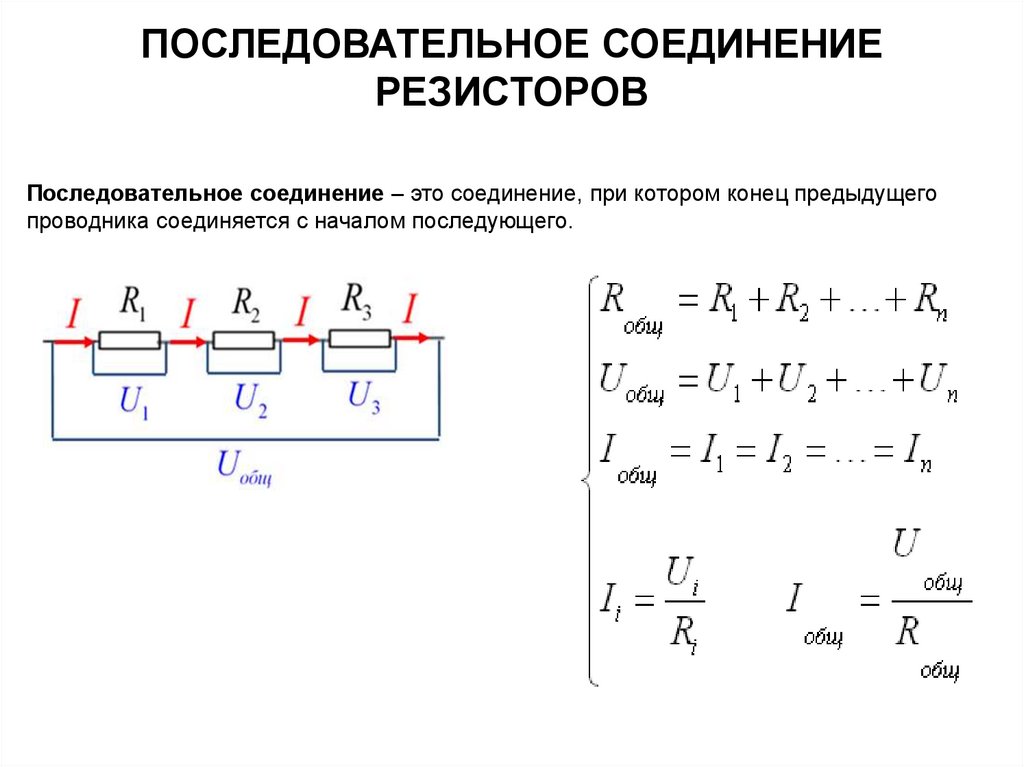
При параллельном соединении резисторов все элементы подключаются к одним и тем же двум точкам электрической цепи. Это приводит к следующим важным особенностям:
- Напряжение на всех резисторах одинаково и равно общему напряжению цепи
- Общий ток делится между параллельными ветвями
- Общее сопротивление цепи уменьшается
Эти свойства оказывают существенное влияние на распределение мощности в параллельной цепи.
Формула расчета мощности при параллельном соединении
Общая мощность при параллельном соединении резисторов рассчитывается по формуле:
P = P1 + P2 + … + Pn
Где P — общая мощность цепи, P1, P2, …, Pn — мощности отдельных резисторов.
Мощность каждого резистора можно вычислить по формуле:
P = U^2 / R
Где U — напряжение на резисторе (одинаковое для всех), R — сопротивление резистора.
Особенности распределения мощности в параллельной цепи
При параллельном соединении мощность распределяется между резисторами обратно пропорционально их сопротивлениям. Это означает, что:
- Резистор с меньшим сопротивлением потребляет большую мощность
- Резистор с большим сопротивлением потребляет меньшую мощность
Такое распределение мощности является следствием того, что ток в параллельных ветвях обратно пропорционален их сопротивлению при одинаковом напряжении.
Сравнение с последовательным соединением
В отличие от параллельного, при последовательном соединении резисторов:
- Ток через все резисторы одинаковый
- Напряжение распределяется пропорционально сопротивлениям
- Общее сопротивление цепи увеличивается
Это приводит к тому, что при последовательном соединении мощность распределяется пропорционально сопротивлениям резисторов — больший резистор потребляет большую мощность.

Пример расчета мощности в параллельной цепи
Рассмотрим пример расчета мощности для параллельного соединения трех резисторов:
- R1 = 100 Ом
- R2 = 200 Ом
- R3 = 300 Ом
- Напряжение U = 12 В
Мощности отдельных резисторов:
P1 = U^2 / R1 = 12^2 / 100 = 1,44 Вт
P2 = U^2 / R2 = 12^2 / 200 = 0,72 Вт
P3 = U^2 / R3 = 12^2 / 300 = 0,48 Вт
Общая мощность цепи:
P = P1 + P2 + P3 = 1,44 + 0,72 + 0,48 = 2,64 Вт
Как видим, резистор с наименьшим сопротивлением (R1) потребляет наибольшую мощность.
Практическое применение параллельного соединения
Параллельное соединение резисторов широко применяется в электротехнике и электронике. Основные области применения:
- Создание делителей тока
- Регулировка общего сопротивления цепи
- Подключение нескольких потребителей к одному источнику питания
- Создание эквивалентных сопротивлений
Понимание принципов распределения мощности при параллельном соединении важно для правильного проектирования и эксплуатации электрических цепей.
Влияние температуры на мощность в параллельной цепи
При расчете мощности в реальных параллельных цепях важно учитывать температурную зависимость сопротивления. С ростом температуры сопротивление металлических проводников увеличивается, что приводит к изменению распределения мощности:
- Резистор, нагревающийся сильнее, увеличивает свое сопротивление
- Это приводит к уменьшению тока через него и снижению выделяемой мощности
- В результате происходит саморегуляция температуры элементов
Этот эффект может быть как полезным (предотвращение перегрева), так и нежелательным (изменение характеристик цепи). При точных расчетах его необходимо учитывать.
Расчет мощности в сложных параллельных цепях
В реальных электрических схемах часто встречаются сложные параллельно-последовательные соединения. Для расчета мощности в таких цепях используется следующий алгоритм:
- Разбить схему на простые параллельные и последовательные участки
- Рассчитать эквивалентные сопротивления для каждого участка
- Определить токи и напряжения на всех элементах
- Вычислить мощности отдельных элементов и участков
- Сложить мощности для получения общей мощности цепи
Для сложных цепей часто применяют компьютерное моделирование, позволяющее учесть все нюансы распределения мощности.
Заключение
Расчет мощности при параллельном соединении резисторов — важная задача в электротехнике. Правильное понимание принципов распределения мощности позволяет:

- Оптимально проектировать электрические цепи
- Предотвращать перегрузку и выход из строя элементов
- Эффективно управлять энергопотреблением устройств
Применение современных методов расчета и моделирования позволяет точно рассчитывать мощность даже в сложных параллельных цепях с учетом реальных характеристик элементов.
Расчет мощности при параллельном соединении
/
/
Расчет мощности при параллельном соединении
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
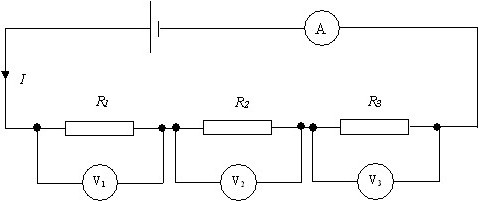
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при
Мощность тока при параллельном и последовательном соединении
Автор На чтение 11 мин. Опубликовано
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
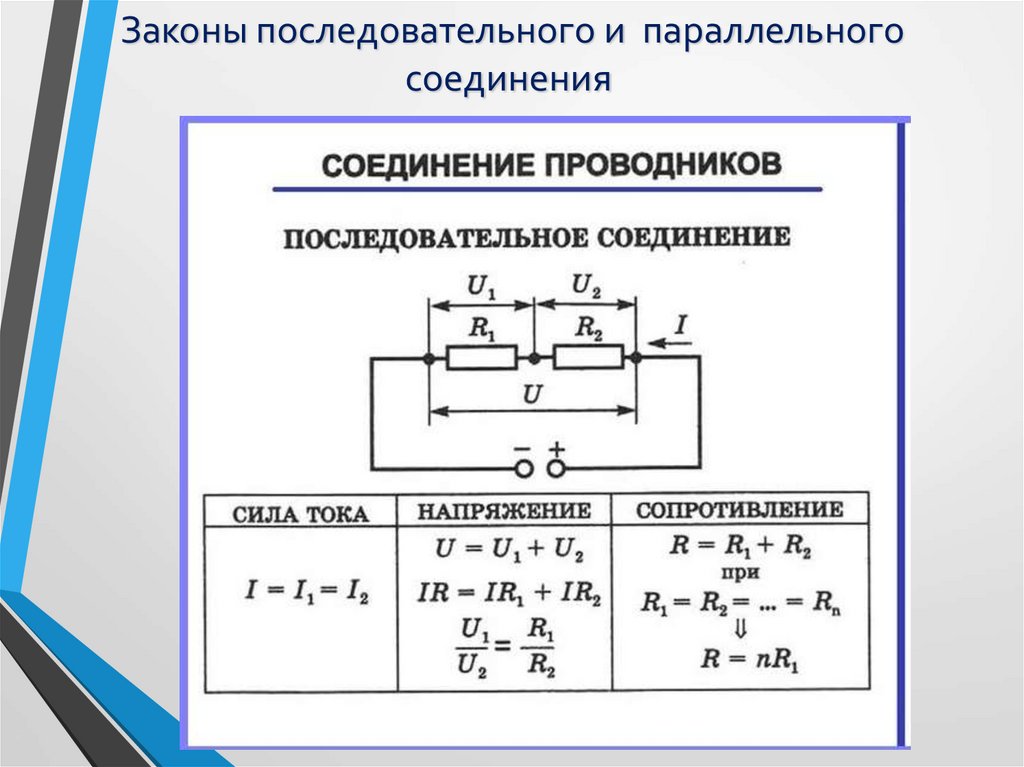
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
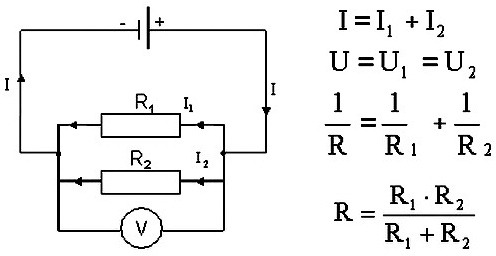
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Применение
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторов
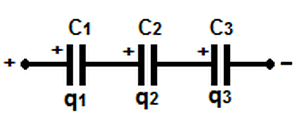
При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
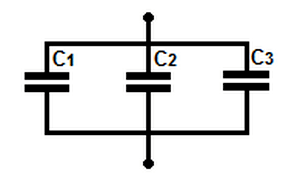
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
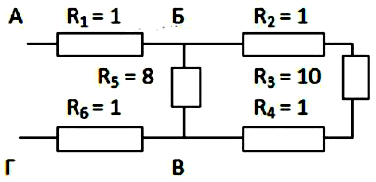
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Мощность электрического тока при параллельном соединении
Автор На чтение 2 мин. Опубликовано

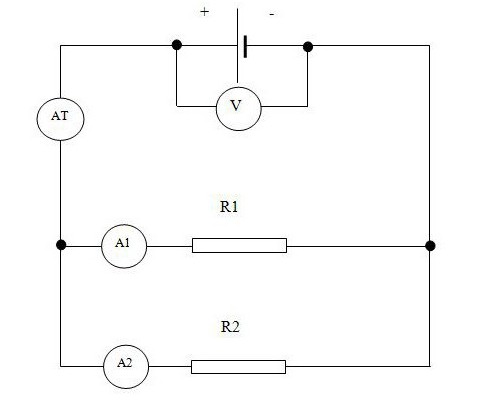
Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).

Рис. 1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении

Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений

Для двух параллельно соединенных сопротивлений

Для ветвей с одинаковым сопротивлением где n количество ветвей
Ток при параллельном соединении

Мощность при параллельном соединении

Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам

Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:

т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость

и эквивалентное сопротивление
Для двух резисторов

Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой

в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
| Рисунок 1.9.1. |
По закону Ома, напряжения и на проводниках равны
Общее напряжение на обоих проводниках равно сумме напряжений 1 и 2:
где – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения 1 и 2 на обоих проводниках одинаковы:
Сумма токов 1 + 2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы и ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу за время Δ подтекает заряд Δ, а утекает от узла за то же время заряд 1Δ + 2Δ. Следовательно, = 1 + 2.
| Рисунок 1.9.2. |
Записывая на основании закона Ома
где – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
| Рисунок 1.9.3. |
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
| Рисунок 1.9.4. |
Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
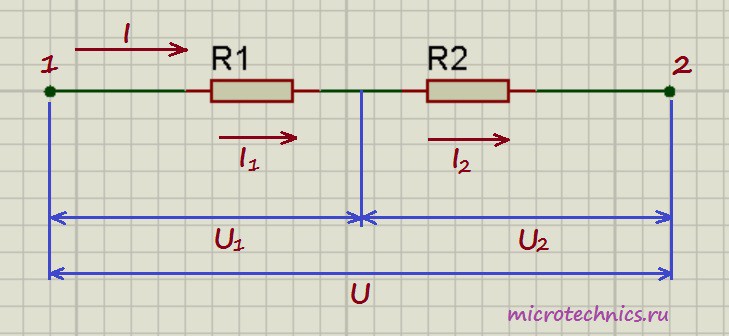
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
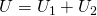
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
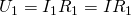
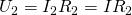
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
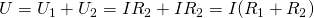
Но для общего напряжение также справедлив закон Ома:
Здесь  – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
– это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
Общее сопротивление будет равно:

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны ( ), то общее сопротивление цепи составит:
), то общее сопротивление цепи составит:

 в данной формуле равно количеству элементов цепи.
в данной формуле равно количеству элементов цепи.
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
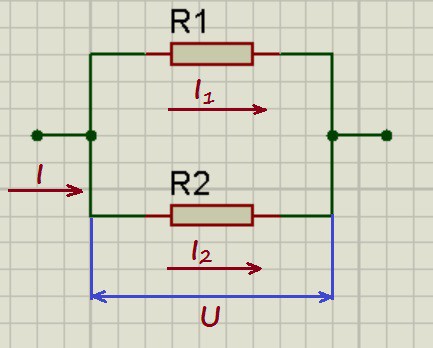
При параллельном соединении напряжения на проводниках равны:
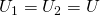
А для токов справедливо следующее выражение:
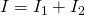
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
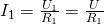
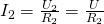
Подставим эти выражения в формулу общего тока:
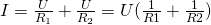
А по закону Ома ток:
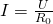
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
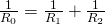
Данную формулу можно записать и несколько иначе:
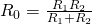
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Как определить мощность резисторов. Мощность резисторов при параллельном соединении
Все электронные устройства содержат резисторы, являющиеся их основным элементом. С его помощью изменяют величину тока в электрической цепи. В статье приведены свойства резисторов и методы расчёта их мощности.
Назначение резистора
Для регулировки тока в электрических цепях применяются резисторы. Это свойство определено законом Ома:
I=U/R (1)
Из формулы (1) хорошо видно, что чем меньше сопротивление, тем сильнее возрастает ток, и наоборот, чем меньше величина R, тем больше ток. Именно это свойство электрического сопротивления используется в электротехнике. На основании этой формулы создаются схемы делителей тока, широко применяющиеся в электротехнических устройствах.
В этой схеме ток от источника делится на два, обратно пропорциональных сопротивлениям резисторов.
Кроме регулировки тока, резисторы используются в делителях напряжения. В этом случае опять используется закон Ома, но немного в другой форме:
U=I∙R (2)
Из формулы (2) следует, что при увеличении сопротивления увеличивается напряжение. Это свойство используется для построения схем делителей напряжения.
Из схемы и формулы (2) ясно, что напряжения на резисторах распределяются пропорционально сопротивлениям.
Изображение резисторов на схемах
По стандарту резисторы изображаются прямоугольником с размерами 10 х 4 мм и обозначаются буквой R. Часто указывается мощность резисторов на схеме. Изображение этого показателя выполняется косыми или прямыми чёрточками. Если мощность более 2 Ватт, то обозначение производится римскими цифрами. Обычно это делается для проволочных резисторов. В некоторых государствах, например в США, применяются другие условные обозначения. Для облегчения ремонта и анализа схемы часто приводится мощность резисторов, обозначение которых выполняется по ГОСТ 2.728-74.
Технические характеристики устройств
Основная характеристика резистора – номинальное сопротивление Rн, которое указывается на схеме возле резистора и на его корпусе. Единица измерения сопротивления – ом, килоом и мегаом. Изготавливаются резисторы с сопротивлением от долей ома и до сотен мегаомов. Существует немало технологий производства резисторов, все они имеют и преимущества, и недостатки. В принципе, не существует технологии, которая позволила бы абсолютно точно изготавливать резистор с заданным значением сопротивления.
Второй важной характеристикой является отклонение сопротивления. Оно измеряется в % от номинального R. Существует стандартный ряд отклонения сопротивления: ±20, ±10, ±5, ±2, ±1% и далее вплоть до значения ±0,001%.
Следующей важной характеристикой является мощность резисторов. При работе они нагреваются от проходящего по ним тока. Если рассеиваемая мощность будет превышать допустимое значение, то устройство выйдет из строя.
Резисторы при нагревании изменяют своё сопротивление, поэтому для устройств, работающих в широком диапазоне температур, вводится ещё одна характеристика – температурный коэффициент сопротивления. Он измеряется в ppm/°C, то есть 10-6 Rн/°C (миллионная часть от Rн на 1°C).
Последовательное соединение резисторов
Резисторы могут соединяться тремя разными способами: последовательным, параллельным и смешанным. При последовательном соединении ток поочерёдно проходит через все сопротивления.
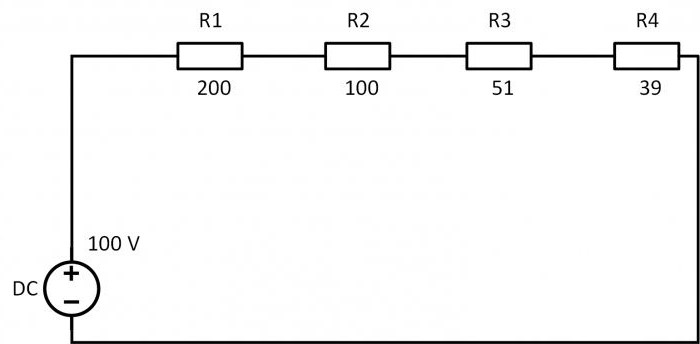
При таком соединении ток в любой точке цепи один и тот же, его можно определить по закону Ома. Полное сопротивление цепи в этом случае равно сумме сопротивлений:
R=200+100+51+39=390 Ом;
I=U/R=100/390=0,256 А.
Теперь можно определить мощность при последовательном соединении резисторов, она рассчитывается по формуле:
P=I2∙R= 0,2562∙390=25,55 Вт.
Аналогично определяется мощность остальных резисторов:
P1= I2∙R1=0,2562∙200=13,11 Вт;
P2= I2∙R2=0,2562∙100=6,55 Вт;
P3= I2∙R3=0,2562∙51=3,34 Вт;
P4= I2∙R4=0,2562∙39=2,55 Вт.
Если сложить мощность резисторов, то получится полная P:
P=13,11+6,55+3,34+2,55=25,55 Вт.
Параллельное соединение резисторов
При параллельном соединении все начала резисторов подключаются к одному узлу схемы, а концы – к другому. При таком соединении ток разветвляется и течёт по каждому устройству. Величина тока, согласно закону Ома, обратно пропорциональна сопротивлениям, а напряжение на всех резисторах одинаково.
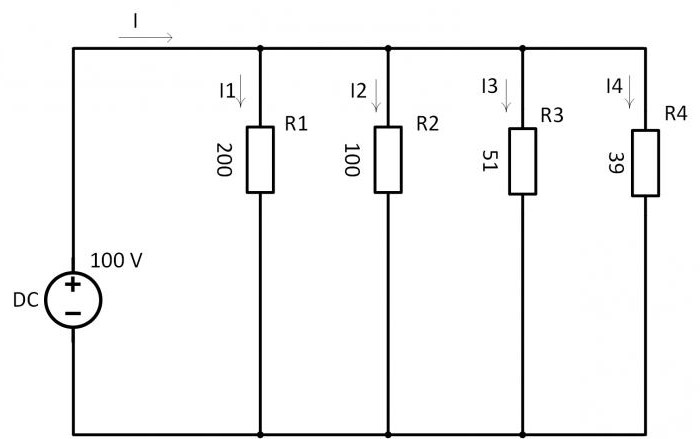
Прежде чем найти ток, нужно рассчитать полную проводимость всех резисторов по общеизвестной формуле:
1/R=1/R1+1/R2+1/R3+1/R4=1/200+1/100+1/51+1/39=0,005+0,01+0,0196+0,0256= 0,06024 1/Ом.
Сопротивление – величина, обратная проводимости:
R=1/0,06024= 16,6 Ом.
Воспользовавшись законом Ома, находят ток через источник:
I= U/R=100∙0,06024=6,024 A.
Зная ток через источник, находят мощность параллельно соединённых резисторов по формуле:
P=I2∙R=6,0242∙16,6=602,3 Вт.
По закону Ома рассчитывается ток через резисторы:
I1=U/R1=100/200=0,5 А;
I2=U/R2=100/100=1 А;
I3=U/R1=100/51=1,96 А;
I1=U/R1=100/39=2,56 А.
Немного по другой формуле можно рассчитать мощность резисторов при параллельном соединении:
P1= U2/R1=1002/200=50 Вт;
P2= U2/R2=1002/100=100 Вт;
P3= U2/R3=1002/51=195,9 Вт;
P4= U2/R4=1002/39=256,4 Вт.
Если всё это сложить, то получится мощность всех резисторов:
P= P1+ P2+ P3+ P4=50+100+195,9+256,4=602,3 Вт.
Смешанное соединение
Схемы со смешанным соединением резисторов содержат последовательное и одновременно параллельное соединение. Эту схему несложно преобразовать, заменив параллельное соединение резисторов последовательным. Для этого заменяют сначала сопротивления R2 и R6 на их общее R2,6, используя формулу, приведённую ниже:
R2,6=R2∙R6/R2+R6.
Точно так же заменяются два параллельных резистора R4, R5 одним R4,5:
R4,5=R4∙R5/R4+R5.
В результате получается новая, более простая схема. Обе схемы приведены ниже.
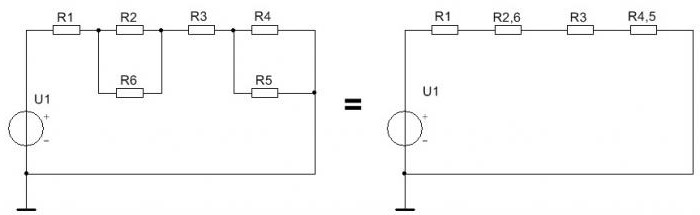
Мощность резисторов на схеме со смешанным соединением определяется по формуле:
P=U∙I.
Для расчёта по этой формуле сначала находят напряжение на каждом сопротивлении и величину тока через него. Можно использовать другой метод, чтобы определить мощность резисторов. Для этого используется формула:
P=U∙I=(I∙R)∙I=I2∙R.
Если известно только напряжение на резисторах, то применяют другую формулу:
P=U∙I=U∙(U/R)=U2/R.
Все три формулы часто используются на практике.
Расчёт параметров схемы
Расчёт параметров схемы заключается в нахождении неизвестных токов и напряжений всех ветвей на участках электрической цепи. Имея эти данные, можно рассчитать мощность каждого резистора, входящего в схему. Простые методы расчёта были показаны выше, на практике же дело обстоит сложнее.
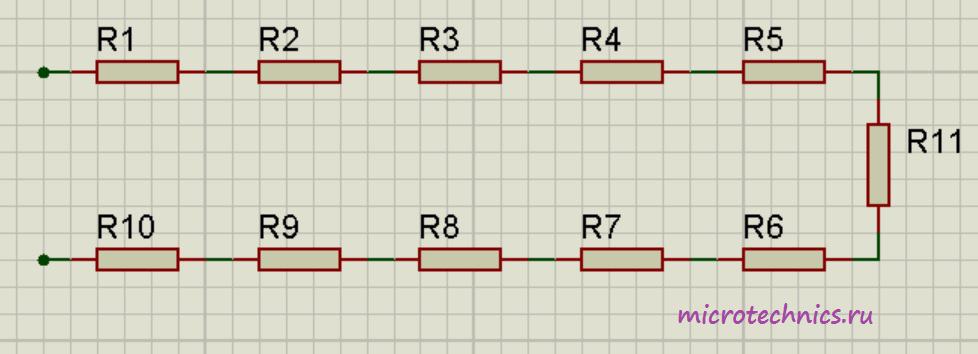
В реальных схемах часто встречается соединение резисторов звездой и треугольником, что создаёт значительные трудности при расчётах. Для упрощения таких схем были разработаны методы преобразования звезды в треугольник, и наоборот. Этот метод проиллюстрирован на схеме, представленной ниже:
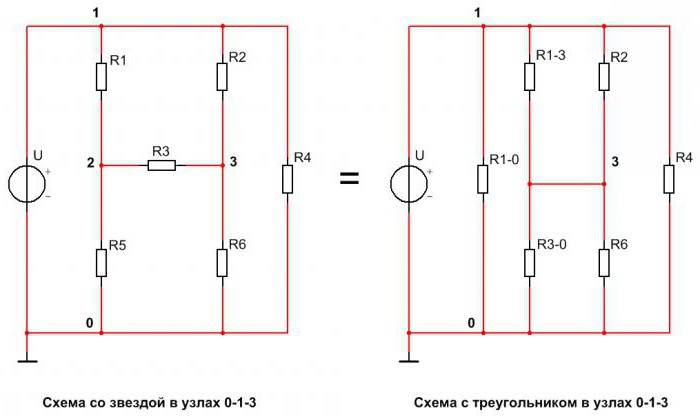
Первая схема имеет в своём составе звезду, подключенную к узлам 0-1-3. К узлу 1 подсоединён резистор R1, к узлу 3 – R3, а к узлу 0 – R5. На второй схеме к узлам 1-3-0 подключены резисторы треугольника. К узлу 1 подключены резисторы R1-0 и R1-3, к узлу 3 – R1-3 и R3-0, а к узлу 0 – R3-0 и R1-0. Эти две схемы полностью эквивалентны.
Для перехода от первой схемы ко второй рассчитываются сопротивления резисторов треугольника:
R1-0=R1+R5+R1∙R5/R3;
R1-3=R1+R3+R1∙R3/R5;
R3-0=R3+R5+R3∙R5/R1.
Дальнейшие преобразования сводятся к вычислению параллельно и последовательно соединённых сопротивлений. Когда будет найдено полное сопротивление цепи, находят по закону Ома ток через источник. Используя этот закон, несложно найти токи во всех ветвях.
Как определить мощность резисторов после нахождения всех токов? Для этого используют общеизвестную формулу: P=I2∙R, применяя её для каждого сопротивления, найдём их мощности.
Экспериментальное определение характеристик элементов схемы
Для экспериментального определения нужных характеристик элементов требуется собрать заданную схему из реальных компонентов. После этого с помощью электроизмерительных приборов выполняют все необходимые измерения. Этот метод трудоёмкий и дорогостоящий. Разработчики электрических и электронных устройств для этой цели используют моделирующие программы. С помощью них производятся все необходимые вычисления, и моделируется поведение элементов схемы в различных ситуациях. Только после этого собирается опытный образец технического устройства. Одной из таких распространённых программ является мощная система моделирования Multisim 14.0 фирмы National Instruments.
Как определить мощность резисторов с помощью этой программы? Это можно сделать двумя методами. Первый метод – это измерить ток и напряжение с помощью амперметра и вольтметра. Перемножив результаты измерений, получают искомую мощность.
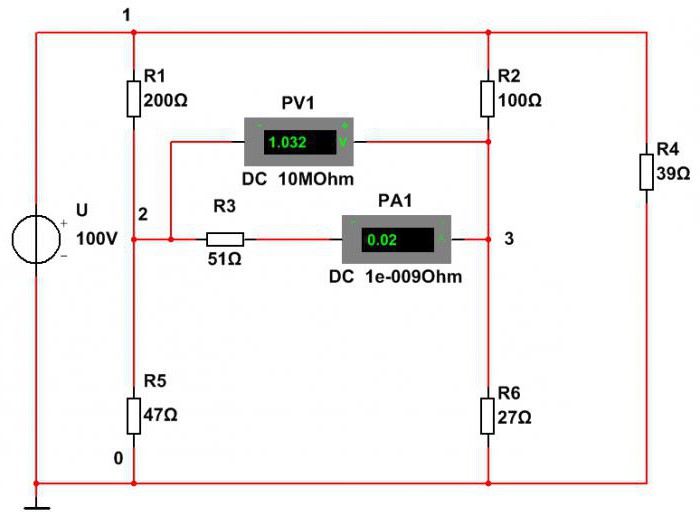
Из этой схемы определяем мощность сопротивления R3:
P3=U∙I=1,032∙0,02=0,02064 Вт=20,6 мВт.
Второй метод – это непосредственное измерение мощности при помощи ваттметра.
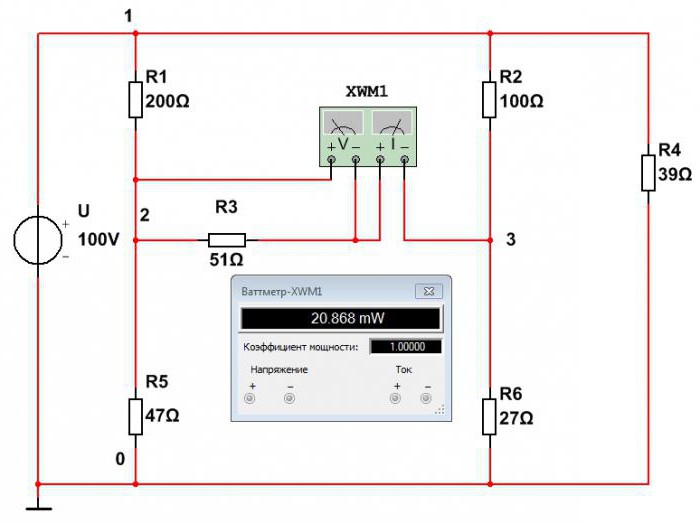
Из этой схемы видно, что мощность сопротивления R3 равна P3=20,8 мВт. Расхождение из-за погрешности в первом методе больше. Точно так же определяются мощности остальных элементов.
Мощность тока при параллельном и последовательном соединении — Topsamoe.ru
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Применение
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Расчет мощности при параллельном и последовательном соединении
Оптимальным источником энергии, для нагрева испарительной емкости, является квартирная электрическая сеть, напряжением 220 В. Можно просто использовать для этих целей бытовую электроплиту. Но, при нагреве на электроплите, много энергии расходуется на бесполезный нагрев самой плиты, а также излучается во внешнюю среду, от нагревательного элемента, не совершая при этом, полезной работы. Эта, понапрасну затрачиваемая энергия, может достигать приличных значений – до 30-50 %, от общей затраченной мощности на нагрев куба. Поэтому использование обычных электроплит, является нерациональным с точки зрения экономии. Ведь за каждый лишний киловатт энергии, приходится платить. Наиболее эффективно использовать врезанные в испарительную емкость эл. ТЭНы. При таком исполнении, вся энергия расходуется только на нагрев куба + излучение от его стенок вовне. Стенки куба, для уменьшения тепловых потерь, необходимо теплоизолировать. Ведь затраты на излучение тепла, от стенок самого куба могут так же, составлять до 20 и более процентов, от всей затрачиваемой мощности, в зависимости от его размеров. Для использования в качестве нагревательных элементов врезанных в емкость, вполне подходят ТЭНы, от бытовых эл.чайников, или другие подходящие по размерам. Мощность таких ТЭНов, бывает разная. Наиболее часто применяются ТЭНы с выбитой на корпусе мощностью 1.0 кВт и 1.25 кВт. Но есть и другие.
Поэтому мощность 1-го ТЭНа, может не соответствовать по параметрам, для нагрева куба и быть больше или меньше. В таких случаях, для получения необходимой мощности нагрева, можно использовать несколько ТЭНов, соединенных последовательно или последовательно-параллельно. Коммутируя различные комбинации соединения ТЭНов, переключателем от бытовой эл. плиты, можно получать различную мощность. Например имея восемь врезанных ТЭНов, по 1.25 кВт каждый, в зависимости от комбинации включения, можно получить следующую мощность.
Такого диапазона вполне хватит для регулировки и поддержания нужной температуры при перегонке и ректификации. Но можно получить и иную мощность, добавив количество режимов переключения и используя различные комбинации включения.
Последовательное соединение 2-х ТЭНов по 1.25 кВт и подключение их к сети 220В, в сумме дает 625 Вт. Параллельное соединение, в сумме дает 2.5 кВт.
Рассчитать можно по следующей формуле.
Мы знаем напряжение, действующее в сети, это 220В. Далее мы так же знаем мощность ТЭН, выбитую на его поверхности допустим это 1,25 кВт, значит, нам нужно узнать силу тока, протекающую в этой цепи. Силу тока, зная напряжение и мощность, узнаем из следующей формулы.
Сила тока = мощность, деленная на напряжение в сети.
Записывается она так: I = P / U.
Где I – сила тока в амперах.
P – мощность в ваттах.
U – напряжение в вольтах.
При подсчете нужно мощность, указанную на корпусе ТЭН в кВт, перевести в ватты.
1,25 кВт = 1250Вт. Подставляем известные значения в эту формулу и получаем силу тока.
I = 1250Вт / 220 = 5,681 А
Далее зная силу тока подсчитываем сопротивление ТЭНа, по следующей формуле.
R = U / I, где
R – сопротивление в Омах
U – напряжение в вольтах
I – сила тока в амперах
Подставляем известные значения в формулу и узнаем сопротивление 1 ТЭНа.
R = 220 / 5.681 = 38,725 Ом.
Далее подсчитываем общее сопротивление всех последовательно соединенных ТЭНов. Общее сопротивление равно сумме всех сопротивлений, соединенных последовательно ТЭНов
Rобщ = R1+ R2 + R3 и т.д.
Таким образом, два последовательно соединенных ТЭНа, имеют сопротивление равное 77,45 Ом. Теперь нетрудно подсчитать мощность выделяемую этими двумя ТЭНами.
P = U 2 / R где,
P – мощность в ваттах
U 2 – напряжение в квадрате, в вольтах
R – общее сопротивление всех посл. соед. ТЭНов
P = 624,919 Вт, округляем до значения 625 Вт.
Далее при необходимости можно подсчитать мощность любого количества последовательно соединенных ТЭНов, или ориентироваться на таблицу.
В таблице 1.1 приведены значения для последовательного соединения ТЭНов.
| Кол-во ТЭН | Мощность (Вт) | Сопротивление (Ом) | Напряжение (В) | Сила тока (А) |
| 1 | 1250,000 | 38,725 | 220 | 5,68 |
| Последовательное соединение | ||||
| 2 | 625 | 2 ТЭН = 77,45 | 220 | 2,84 |
| 3 | 416 | 3 ТЭН =1 16,175 | 220 | 1,89 |
| 4 | 312 | 4 ТЭН=154,9 | 220 | 1,42 |
| 5 | 250 | 5 ТЭН=193,625 | 220 | 1,13 |
| 6 | 208 | 6 ТЭН=232,35 | 220 | 0,94 |
| 7 | 178 | 7 ТЭН=271,075 | 220 | 0,81 |
| 8 | 156 | 8 ТЭН=309,8 | 220 | 0,71 |
В таблице 1.2 приведены значения для параллельного соединения ТЭНов.
| Кол-во ТЭН | Мощность (Вт) | Сопротивление (Ом) | Напряжение (В) | Сила тока (А) |
| Параллельное соединение | ||||
| 2 | 2500 | 2 ТЭН=19,3625 | 220 | 11,36 |
| 3 | 3750 | 3 ТЭН=12,9083 | 220 | 17,04 |
| 4 | 5000 | 4 ТЭН=9,68125 | 220 | 22,72 |
| 5 | 6250 | 5 ТЭН=7,7450 | 220 | 28,40 |
| 6 | 7500 | 6 ТЭН=6,45415 | 220 | 34,08 |
| 7 | 8750 | 7 ТЭН=5,5321 | 220 | 39,76 |
| 8 | 10000 | 8 ТЭН=4,840 | 220 | 45,45 |
Еще один немаловажный плюс, который дает последовательное соединение ТЭНов, это уменьшенный в несколько раз протекающий через них ток, и соответственно малый нагрев корпуса нагревательного элемента, тем самым не допускается пригорание браги во время перегонки и не привносит неприятного дополнительного вкуса и запаха в конечный продукт. Так же ресурс работы ТЭНов, при таком включении, будет практически вечным.
Расчеты выполнены для ТЭНов, мощностью 1.25 кВт. Для ТЭНов другой мощности, общую мощность нужно пересчитать согласно закона Ома, пользуясь выше приведенными формулами.

Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).

Рис. 1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении

Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений

Для двух параллельно соединенных сопротивлений

Для ветвей с одинаковым сопротивлением где n количество ветвей
Ток при параллельном соединении

Мощность при параллельном соединении

Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам

Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:

т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость

и эквивалентное сопротивление
Для двух резисторов

Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой

в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
Статьи, Схемы, Справочники
Часть 2. Лабораторные работы Мощность тока в проводниках при их последовательном и параллельном соединении Цель работы: сравнить мощность тока в двух проводниках при их последовательном и параллельном подключении. Оборудование: батарейка 1 , амперметр, вольтметр, два резистора с сопротивлениями, отличающимися в несколько раз, ключ, соединительные провода. А для сравнения значений мощности тока в проводниках при их параллельном соединении удобнее использовать формулу потому что при этом напряжение на концах проводников одинаково.
Поиск данных по Вашему запросу:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Перейти к результатам поиска >>>
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Последовательное и параллельное соединение конденсаторов
Мощность тока в проводниках при их последовательном и параллельном соединении
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение. При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого.
Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них. Рассмотрим некоторое количество резисторов, соединенных последовательно.
Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения. Это соединение можно рассмотреть иначе.
Все резисторы можно заменить одним эквивалентным резистором. Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе. Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений.
Следствием первых двух правил будет являться третье правило. Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме.
Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры.
Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы. В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников резисторов , соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше. Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:. После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:.
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать. При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок.
Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их. При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов.
Конденсаторы , находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:.
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:. Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:. Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов.
А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:.
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме. Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4.
Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно. Остальные два сопротивления первый и шестой подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек. Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов.
Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий. Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы. Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом.
Законы, открытые им, действуют и поныне, а понять их сможет практически каждый. Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:. Теперь необходимо определиться , как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:.
Здесь I — ток в цепи в амперах, U — напряжение, подводимое к цепи в вольтах, R — сопротивление цепи в омах, P — электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R нагрузки.
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки. Если мы возьмем, к примеру, паяльник с сопротивлением спирали Ом и подключим его к осветительной розетке с напряжением В, то ток через паяльник будет составлять:.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:. Все рассмотренные выше случаи являются простыми — один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному.
Существует три типа соединения нагрузки:. В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра?
Последовательное и параллельное соединение резисторов
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее , чем у любого резистора из этой цепи. При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи. Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним. Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:. Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов. Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью.
Мощность при параллельном и последовательном соединении резисторов
Если вам нужно большее напряжение, чем могут выдать ваши источники питания, можно соединить выходы источников последовательно. Если вам нужен больший ток, чем могут выдать ваши источники питания, можно соединить выходы источников параллельно. Однако при этом нужно соблюдать некоторые меры предосторожности. В параллельной и последовательной конфигурациях можно использовать измерительные входы. На рис. Последовательное соединение выходов с использованием измерительных входов. Параллельное соединение выходов с использованием измерительных входов.
Расчет мощности при последовательном соединении
Регистрация Вход. Ответы Mail. Вопросы – лидеры Возможна ли дружба между процессор amd phenom ii x6 t и видеокартой rx 8gb 1 ставка. Помогите подобрать видеокарту Лидеры категории Антон Владимирович Искусственный Интеллект.
Последовательное и параллельное соединение. Применение и схемы
Резисторы между собой могут быть соединены двумя основными способами: последовательно и параллельно. Смешанное соединение резисторов является их комбинацией. Сочетания любых соединений резисторов можно привести к одному резистору, расчетом сопротивления которого R мы сейчас займемся. Параллельное соединение резисторов. Давайте рассчитаем общее сопротивление такой цепи рисунок 1.
Последовательное и параллельное соединение
Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения — параллельное. Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам. А — Последовательное соединение. В — Параллельное соединение. Рисунок 1 — Последовательное и параллельное соединение. Как мы видим из рисунка 1, параллельное соединение — это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы — в другой узел.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение. При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток.
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка. Закон Джоуля – Ленца. В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла. Работа и мощность электрического тока.
Наша жизнь, зачастую, бывает очень стремительна, и каждая минута может быть на вес золота. Поэтому время полезно и нужно беречь. Если у Вас на даче собралась большая семья и Вам нужно оперативно всех накормить горячим обедом, то одной электрической плитки может не хватить. Предположим, что у Вас есть две одинаковые электрические плитки.
By : adminтеория, формулы, подключение и расчет силы тока
 Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы. Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой. Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом. Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы. Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой. Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом. Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Основные электрические величины цепи
Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:
- Электрическое напряжение, согласно научному определению, это разность потенциалов
 между двумя точками электрической цепи. Измеряется в вольтах (В). Между клеммами бытовой розетки, к примеру, оно равно 220 В, на батарейке вольтметр покажет 1,5 В, а зарядное устройство вашего планшета или смартфона выдает 5 В. Напряжение бывает переменным и постоянным, но в нашем случае это несущественно.
между двумя точками электрической цепи. Измеряется в вольтах (В). Между клеммами бытовой розетки, к примеру, оно равно 220 В, на батарейке вольтметр покажет 1,5 В, а зарядное устройство вашего планшета или смартфона выдает 5 В. Напряжение бывает переменным и постоянным, но в нашем случае это несущественно. - Электрический ток – упорядоченное движение электронов в электрической цепи. Ближайшая аналогия – ток воды в трубопроводе. Измеряется в амперах (А). Если цепь не замкнута, ток существовать не может.
- Электрическое сопротивление. Величина измеряется в омах (Ом) и характеризует способность проводника или электрической цепи сопротивляться прохождению электрического тока. Если продолжить аналогию с водопроводом, то новая гладкая труба будет иметь маленькое сопротивление, забитая ржавчиной и шлаками – высокое.
- Электрическая мощность. Эта величина характеризует скорость преобразования электрической энергии в любую другую и измеряется в ваттах (Вт). Кипятильник в 1000 Вт вскипятит воду быстрее стоваттного, мощная лампа светит ярче и т.д.
Взаимная зависимость электрических величин
Теперь необходимо определиться, как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:
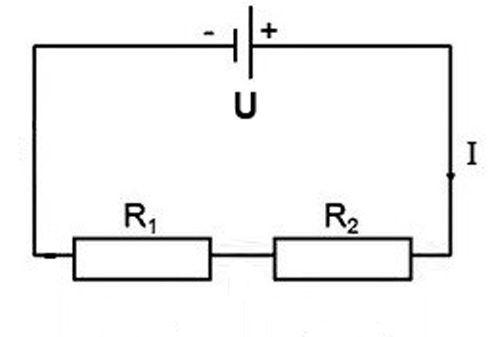 Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R (нагрузки).
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки. Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
220 / 100 = 2,2 А.
Какова мощность этого паяльника? Воспользуемся формулой 2:
2,2 * 220 = 484 Вт.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т.д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
60 / 220 = 0,27 А или 270 мА.
Сопротивление спирали лампы в рабочем режиме:
220 / 0,27 = 815 Ом.
Схемы с несколькими проводниками
Все рассмотренные выше случаи являются простыми – один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному. Существует три типа соединения нагрузки:
- Параллельное.
- Последовательное.
- Смешанное.
Параллельное соединение проводников
В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра? Верно, 180 Вт. Быстренько подсчитываем сначала ток через люстру:
180 / 220 = 0,818 А.
А затем и ее сопротивление:
220 / 0,818 = 269 Ом.
Перед этим мы вычисляли сопротивление одной лампы (815 Ом) и ток через нее (270 мА). Сопротивление же люстры оказалось втрое ниже, а ток — втрое выше. А теперь пора взглянуть на схему трехрожкового светильника.
Схема люстры с тремя лампами
Все лампы в нем соединены параллельно и подключены к сети. Получается, при параллельном соединении трех ламп общее сопротивление нагрузки уменьшилось втрое? В нашем случае — да, но он частный – все лампы имеют одинаковые сопротивление и мощность. Если каждая из нагрузок будет иметь свое сопротивление, то для подсчета общего значения простого деления на количество нагрузок мало. Но и тут есть выход из положения – достаточно воспользоваться вот этой формулой:
1/Rобщ. = 1/R1 + 1/R2 + … 1/Rn.
Для удобства использования формулу можно легко преобразовать:
Rобщ. = (R1*R2*… Rn) / (R1+R2+ … Rn).
Здесь Rобщ. – общее сопротивление цепи при параллельном включении нагрузки. R1 … Rn – сопротивления каждой нагрузки.
Почему увеличился ток, когда вы включили параллельно три лампы вместо одной, понять несложно – ведь он зависит от напряжения (оно осталось неизменным), деленного на сопротивление (оно уменьшилось). Очевидно, что и мощность при параллельном соединении увеличится пропорционально увеличению тока.
Последовательное соединение
 Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Последовательно соединенная нагрузка
Расчет сопротивления при последовательном соединении проводников исключительно прост:
Rобщ. = R1 + R2.
Те же три шестидесятиваттные лампы, соединенные последовательно, составят уже 2445 Ом (см. расчеты выше). Какими будут последствия увеличения сопротивления цепи? Согласно формулам 1 и 2 становится вполне понятно, что мощность и сила тока при последовательном соединении проводников упадет. Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Последовательное соединение трех ламп в гирлянду
Общее напряжение, приложенное ко всей цепи, так и осталось 220 В. Но оно поделилось между каждой из ламп пропорционально их сопротивлению! Поскольку лампы у нас одинаковой мощности и сопротивления, то напряжение поделилось поровну: U1 = U2 = U3 = U/3. То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше. Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
- Измеряете сопротивление каждой из ламп.
- Рассчитываете общее сопротивление цепи.
- По общим напряжению и сопротивлению рассчитываете ток в цепи.
- По общему току и сопротивлению ламп вычисляете падение напряжения на каждой из них.
Хотите закрепить полученные знания? Решите простую задачу, не заглядывая в ответ в конце:
В вашем распоряжении есть 15 однотипных миниатюрных лампочек, рассчитанных на напряжение 13,5 В. Можно ли из них сделать елочную гирлянду, подключаемую к обычной розетке, и если можно, то как?
Смешанное соединение
С параллельным и последовательным соединением проводников вы, конечно, без труда разобрались. Но как быть, если перед вами оказалась примерно такая схема?
Смешанное соединение проводников
Как определить общее сопротивление цепи? Для этого вам понадобится разбить схему на несколько участков. Вышеприведенная конструкция достаточно проста и участков будет два — R1 и R2,R3. Сначала вы рассчитываете общее сопротивление параллельно соединенных элементов R2,R3 и находите Rобщ.23. Затем вычисляете общее сопротивление всей цепи, состоящей из R1 и Rобщ.23, соединенных последовательно:
- Rобщ.23 = (R2*R3) / (R2+R3).
- Rцепи = R1 + Rобщ.23.
Задача решена, все очень просто. А теперь вопрос несколько сложнее.
Сложное смешанное соединение сопротивлений
Как быть тут? Точно так же, просто нужно проявить некоторую фантазию. Резисторы R2, R4, R5 соединены последовательно. Рассчитываем их общее сопротивление:
Rобщ.245 = R2+R4+R5.
Теперь параллельно к Rобщ.245 подключаем R3:
Rобщ.2345 = (R3* Rобщ.245) / (R3+ Rобщ.245).
Ну а дальше все очевидно, поскольку остались R1, R6 и найденное нами Rобщ.2345, соединенные последовательно:
Rцепи = R1+ Rобщ.2345+R6.
Вот и все!
Ответ на задачу о елочной гирлянде
Лампы имеют рабочее напряжение всего 13.5 В, а в розетке 220 В, поэтому их нужно включать последовательно.
Поскольку лампы однотипные, напряжение сети разделится между ними поровну и на каждой лампочке окажется 220 / 15 = 14,6 В. Лампы рассчитаны на напряжение 13,5 В, поэтому такая гирлянда хоть и заработает, но очень быстро перегорит. Чтобы реализовать задумку, вам понадобится минимум 220 / 13,5 = 17, а лучше 18-19 лампочек.
Схема елочной гирлянды из миниатюрных ламп накаливания
Параллельные цепи — преимущества, мощность, ток, напряжение и эффективное сопротивление
Введение
В этом уроке мы рассмотрим параллельные схемы. Посмотрим, почему они так распространены. Мы также рассмотрим напряжение, мощность, ток и эффективное сопротивление.

 Активность, показывающая, что параллельно включенные лампы одинаково ярки, потому что они всегда подключены к одному источнику напряжения.
Активность, показывающая, что параллельно включенные лампы одинаково ярки, потому что они всегда подключены к одному источнику напряжения.
Преимущество параллельных цепей перед последовательными цепями
Если мы хотим подключить две лампочки к одной и той же батарее, очевидный способ их подключения — последовательно.Это означает, что обе лампы находятся на одном и том же проводящем пути от одной клеммы батареи к другой.
Проблема с последовательным соединением двух лампочек заключается в том, что обе лампы тусклые, и если вы выключите одну лампочку, они обе погаснут.

 Анимация, показывающая, что ток, потребляемый от батареи, увеличивается по мере того, как больше компонентов подключаются параллельно.
Анимация, показывающая, что ток, потребляемый от батареи, увеличивается по мере того, как больше компонентов подключаются параллельно.
Параллельное подключение ламп дает два преимущества.
- Все они получают полное напряжение батареи, поэтому все они яркие
- Все они находятся в собственном проводящем контуре, поэтому вы можете выключить одну лампочку, не затрагивая другие.
Параллельные схемы в доме
Дома все ваши приборы подключены параллельно друг другу. Это означает, что все они получают полное сетевое напряжение, и вы можете включить телевизор, не включая микроволновую печь.

 Анимация, показывающая, как все наши бытовые приборы подключаются параллельно друг другу.
Анимация, показывающая, как все наши бытовые приборы подключаются параллельно друг другу.
Как это работает?
Электрические кабели в вашем доме состоят из трех жил. Мы пока проигнорируем Землю и сконцентрируемся на двух из них: живом и нейтральном.В Европе лайв коричневый, а нейтральный синий. В США жить может быть черным, красным или желтым; а нейтральный обычно бывает белым или белым с желтыми полосами.
Между фазой и нейтралью есть напряжение, потому что они косвенно подключены к электростанции. Каждая электрическая розетка в вашем доме подключена к фазе и нейтрали. Металлические штыри вилки обеспечивают электрическое соединение с розеткой. Штепсель, опять же с проводом под напряжением и нулевым проводом, соединяет вилку с устройством.
Каждый прибор имеет собственное соединение между фазой и нейтралью, поэтому каждый прибор можно включать отдельно, и на него подается полное напряжение.
Параллельное добавление всегда увеличивает общий ток
Даже если все приборы в вашем доме подключены к одному напряжению, все они потребляют разные токи. Электрическая духовка быстро передает энергию, поэтому потребляемый ею ток будет большим. Телевизор передает энергию довольно медленно, поэтому потребляемый им ток будет довольно небольшим.

 Действие для визуализации увеличения тока, потребляемого батареей, при параллельном добавлении дополнительного компонента.
Действие для визуализации увеличения тока, потребляемого батареей, при параллельном добавлении дополнительного компонента.
Все эти токи должны добавляться к источнику питания, поскольку он должен обеспечивать их все одновременно. Чем больше подключено устройств, тем больше потребляемый ток.
Почему ток не «расщепляется» на переходах в параллельных цепях
Часто говорят, что ток разделяется на переходах в параллельных цепях, но с этой идеей нужно быть очень осторожным.Это часто может привести к постоянному заблуждению.

 Анимация, объясняющая, почему о разделении тока на стыках лучше не думать.
Анимация, объясняющая, почему о разделении тока на стыках лучше не думать.
Первое, что следует помнить, это то, что заряды не начинаются с батареи, а затем проходят через пустые провода, пока не дойдут до места соединения, а затем нужно решить, что делать. Заряды уже есть повсюду в цепи, и все они начинают очень медленно течь повсюду одновременно.
Другая проблема в том, что нет «течения», которое могло бы течь.Чем больше устройств вы подключаете параллельно, тем больше ток, потребляемый от источника питания. Один и тот же ток не просто разделяется по-разному.
Иногда проще представить компоненты как активные объекты, требующие тока от источника питания. Если схема настроена так, что иногда эти токи должны протекать по одному проводу, вам необходимо их сложить.
Расчет токов в параллельных цепях
При параллельном подключении лампочек на них должно быть одинаковое напряжение.Вы можете относиться к ним так, как будто каждый из них находится в своей собственной цепи (что, если рассматривать схему как смысловую петлю, так и есть).

 Анимация, показывающая, как рассчитать токи в параллельных цепях.
Анимация, показывающая, как рассчитать токи в параллельных цепях.
Если лампы разные, то лампа с меньшим сопротивлением потребляет больший ток и будет ярче. Это просто закон Ома: малое сопротивление означает большой ток.
Это стратегия:
- рассчитать ток через каждую лампочку по закону Ома
- сложите токи, чтобы найти ток, потребляемый от батареи
Вы можете рассчитать ток, используя уравнение закона Ома V = IR.Сначала вам нужно переставить его так, чтобы I = V / R, и помните, что V — это просто напряжение батареи.
Параллельное соединение всегда снижает эффективное сопротивление
Батарея параллельной цепи не «знает», что к ней подключено. Все, что он чувствует, — это общее сопротивление (или, если вам нравится общий спрос на ток). Сопротивление, которое испытывает аккумулятор, называется эффективным сопротивлением цепи.

 Анимация, в которой сопротивления параллельно объясняются как дыры в ванне.
Анимация, в которой сопротивления параллельно объясняются как дыры в ванне.По мере того, как вы добавляете все больше и больше компонентов параллельно, ток, потребляемый от источника питания, становится все больше и больше. Если ток становится больше, сопротивление должно уменьшаться. Таким образом, добавляя сопротивления, вы фактически уменьшаете эффективное сопротивление, что кажется странным.
Неважно, насколько велико сопротивление, добавление его параллельно всегда снижает эффективное сопротивление. Для объяснения этого есть пара аналогий.
Если у вас есть ванна с отверстием на дне, она опустеет.Если вы добавите еще одно отверстие, независимо от его размера, ванна всегда опустеет быстрее.
Или представьте себе огромную толпу, покидающую стадион через главные ворота. Если открываются даже крошечные боковые ворота, то количество людей, покидающих стадион каждую минуту, возрастает.
Эмпирические правила расчета эффективного сопротивления параллельных цепей

 График, иллюстрирующий некоторые практические правила для эффективного сопротивления параллельных цепей.
График, иллюстрирующий некоторые практические правила для эффективного сопротивления параллельных цепей.
- Общее сопротивление всегда меньше наименьшего сопротивления (потому что вы всегда можете представить себе, как сначала строите схему с наименьшим сопротивлением, а затем эффективное сопротивление продолжает уменьшаться по мере добавления большего сопротивления).
- Два идентичных резистора имеют эффективное сопротивление, равное половине их значения (поскольку добавление второго сопротивления удваивает ток, поэтому сопротивление уменьшается вдвое).
- Три одинаковых резистора имеют эффективное сопротивление, равное трети их номинала, и так далее.
- Очень большое сопротивление и очень маленькое сопротивление параллельно имеют эффективное сопротивление немного меньше, чем маленькое сопротивление (маленькое сопротивление похоже на большое отверстие в ванне, добавление еще одного крошечного отверстия все равно увеличивает общую скорость потока. )

 Игра Попрактикуйтесь в эффективном сопротивлении параллельных резисторов.Ведите космический вездеход над черной дырой, используя только квадраты с эффективным сопротивлением менее 10 Ом.
Игра Попрактикуйтесь в эффективном сопротивлении параллельных резисторов.Ведите космический вездеход над черной дырой, используя только квадраты с эффективным сопротивлением менее 10 Ом.
Расчет эффективного сопротивления параллельных цепей

 Анимация, показывающая, как использовать формулу для расчета эффективного сопротивления.
Анимация, показывающая, как использовать формулу для расчета эффективного сопротивления.
Формула для расчета эффективного сопротивления параллельных цепей выглядит довольно сложной, возможно, поэтому параллельные цепи часто преподаются после последовательных цепей, хотя параллельные цепи гораздо более распространены и полезны.
Эту формулу довольно легко вывести, если вы не против иметь дело с дробями.
Использовать формулу не так уж сложно. Просто подставьте свои значения сопротивления, а затем сложите дроби.
Будьте осторожны, после того, как вы сложите дроби, вы получите не R с эффективностью , а с 1 / R с эффективностью , поэтому вам нужно перевернуть результат, чтобы найти эффективное сопротивление.
В качестве проверки убедитесь, что результат меньше наименьшего сопротивления.
Расчет эффективного сопротивления путем расчета полного потребляемого тока

 Рисунок, поясняющий, как вычислить эффективное сопротивление, вычислив полный ток, потребляемый от батареи.
Рисунок, поясняющий, как вычислить эффективное сопротивление, вычислив полный ток, потребляемый от батареи.
Вместо того, чтобы использовать формулу, мы можем рассчитать общий ток, потребляемый от источника питания, а затем использовать R эффективное = V аккумулятор / I всего для расчета эффективного сопротивления.
Фактически это то, что делает формула, но иногда вопрос дает вам токи через компоненты, а не их сопротивления, поэтому быстрее использовать этот метод, чем сначала рассчитывать сопротивления, а затем использовать формулу.
Вернуться к объяснению электроснабжения
.динамиков в параллельном калькуляторе — Geoff the Gray Geek
- Home
- Home AV
- Подключение оборудования
- Подключение динамиков
- Подключение динамиков
- Подключение оборудования
- Аудио калькуляторы
- Электрические калькуляторы
- Аудио калькуляторы
- Электрические калькуляторы
Search
 Geoff the Gray Geek
Geoff the Gray Geek 

- Home Оборудование
- Conne Подключение динамиков
- Подключение оборудования

Часто задаваемые вопросы по подключению динамиков

Симуляторы селекторного переключателя динамиков

Общие сведения об импедансе динамиков

Как подключить видеомагнитофон к телевизору с плоским экраном
-

Общие сведения о мощности усилителя

Общие сведения о чувствительности динамика

Как несколько динамиков разделяют мощность

Импеданс динамика меняет мощность усилителя2

2 Общее представление о динамике
Обзор работы, энергии и мощности: термины и формулы
условия
Консервативная сила
Любая сила, сохраняющая механическую энергию, в отличие от неконсервативной сила. См. Заявление о консервации механических энергия.
Консервативная система
Система, в которой сохраняется энергия.
Энергия
Умение делать работу.
Кинетическая энергия
Энергия движения.
Неконсервативная сила
Любая сила, не сохраняющая механическую энергию, в отличие от консервативная сила.
Независимость от пути
Собственность консервативных сил, утверждающая, что работа выполняется на любом пути между двумя заданными очков то же самое.
Потенциальная энергия
Энергия конфигурации консервативной системы. Для формул видеть Определение потенциальной энергии, гравитационной потенциальная энергия, и Определение потенциальной энергии в зависимости от положения сила.
Общая механическая энергия
Сумма кинетической и потенциальной энергии консервативного система. См. Определение полной механической энергии.
работай
Сила, приложенная на расстоянии. Для формул см. Работу, выполненную постоянной сила, параллельная перемещению, и работа, выполняемая любым постоянная сила, и работа, выполняемая позиционно-зависимой силой.
Джоуль
Единицы работы, эквивалентные Ньютон-метру.Также единицы энергии.
Мощность
Выполненная работа за единицу времени. Формулы см. В разделе Формула среднего мощность, Определение мгновенной мощности и формула для мгновенной мощности.
Ватт
Единица мощности; равно джоуль в секунду.
Формулы
| Работа, выполняемая постоянной силой, параллельной перемещению | W = Fx |
| Работа, выполняемая любой постоянной силой | W = Fx cos θ |
| Теорема работы-энергии | W = ΔK |
| Формула для средней мощности |  = =  |
| Определение мгновенной мощности | P =  |
| Формула мгновенной мощности | P = Fv cos θ |
| Работа, выполняемая силами, зависящими от позиции | W =  F ( x ) dx усилие. F ( x ) dx усилие. |
| Определение потенциальной энергии. | ΔU = — Вт |
| Гравитационно потенциальная энергия. | U G = мг / час |
| Заявление о сохранении механической энергии. | Δ ( U + K ) = 0 |
| Определение полной механической энергии. | U + K = E |
| Определение потенциальной энергии с учетом силы, зависящей от положения. | ΔU = —  F ( x ) dx F ( x ) dx |

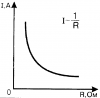
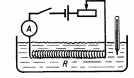
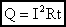
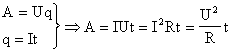
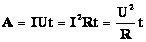
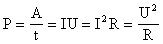
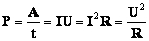

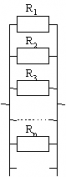
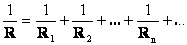
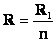
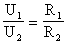 – чем больше сопротивление, тем больше напряжение.
– чем больше сопротивление, тем больше напряжение.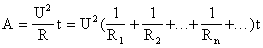 .
.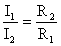 – чем больше сопротивление, тем меньше сила тока.
– чем больше сопротивление, тем меньше сила тока.