Мощность резистора формула. Мощность резистора: формулы расчета, зависимость от соединения и практическое применение

Как рассчитать мощность резистора. Какие формулы используются для последовательного и параллельного соединения. От чего зависит мощность резистора. Как определить мощность по внешнему виду.

Основные формулы для расчета мощности резистора

Мощность резистора — это важный параметр, который необходимо учитывать при проектировании электрических схем. Существует несколько формул для расчета мощности резистора:

• P = I^2 * R, где I — сила тока, R — сопротивление
• P = U^2 / R, где U — напряжение
• P = U * I

Выбор конкретной формулы зависит от того, какие параметры известны. Рассмотрим каждую формулу подробнее.

Расчет мощности через ток и сопротивление

Формула P = I^2 * R удобна, когда известны значения тока и сопротивления. Например, если через резистор 100 Ом протекает ток 0.1 А, мощность составит:

P = 0.1^2 * 100 = 0.01 * 100 = 1 Вт

Расчет мощности через напряжение и сопротивление

Формула P = U^2 / R применяется при известном напряжении и сопротивлении. Для резистора 1 кОм под напряжением 10 В мощность будет:

P = 10^2 / 1000 = 100 / 1000 = 0.1 Вт

Расчет мощности через напряжение и ток

Формула P = U * I используется, когда известны напряжение и ток. При напряжении 5 В и токе 0.5 А мощность составит:

P = 5 * 0.5 = 2.5 Вт

Мощность при последовательном соединении резисторов

При последовательном соединении резисторов общая мощность рассчитывается как сумма мощностей отдельных резисторов:

P общ = P1 + P2 + P3 + …

Это связано с тем, что через все резисторы протекает одинаковый ток, но падение напряжения на каждом резисторе разное. Рассмотрим пример:

Пусть имеется 3 резистора по 100 Ом, соединенных последовательно. Общее сопротивление 300 Ом. При напряжении 30 В ток составит 0.1 А. Мощность каждого резистора:

P1 = P2 = P3 = 0.1^2 * 100 = 1 Вт

Общая мощность: P общ = 1 + 1 + 1 = 3 Вт

Особенности расчета мощности при параллельном соединении

При параллельном соединении резисторов напряжение на всех элементах одинаковое, но токи различаются. Общая мощность также равна сумме мощностей отдельных резисторов:

P общ = P1 + P2 + P3 + …

Однако расчет усложняется тем, что токи через резисторы разные. Рассмотрим пример:

Имеется 3 резистора 100, 200 и 300 Ом, соединенных параллельно. При напряжении 10 В токи составят:

I1 = 10 / 100 = 0.1 А I2 = 10 / 200 = 0.05 А I3 = 10 / 300 = 0.033 А

Мощности отдельных резисторов:

P1 = 10 * 0.1 = 1 Вт P2 = 10 * 0.05 = 0.5 Вт P3 = 10 * 0.033 = 0.33 Вт

Общая мощность: P общ = 1 + 0.5 + 0.33 = 1.83 Вт

От чего зависит мощность резистора

Мощность резистора зависит от нескольких ключевых факторов:

• Сопротивление резистора
• Напряжение, приложенное к резистору
• Сила тока, протекающего через резистор
• Температура окружающей среды
• Способ охлаждения резистора

Рассмотрим влияние каждого фактора подробнее.

Влияние сопротивления на мощность

Чем выше сопротивление резистора при неизменном напряжении, тем меньше мощность. Это следует из формулы P = U^2 / R. Например, при напряжении 10 В:

Для 100 Ом: P = 10^2 / 100 = 1 Вт Для 1 кОм: P = 10^2 / 1000 = 0.1 Вт

Зависимость мощности от напряжения

Мощность прямо пропорциональна квадрату напряжения. При увеличении напряжения вдвое мощность возрастает в 4 раза. Например, для резистора 100 Ом:

При 5 В: P = 5^2 / 100 = 0.25 Вт При 10 В: P = 10^2 / 100 = 1 Вт

Влияние силы тока на мощность

Мощность также прямо пропорциональна квадрату тока. Удвоение тока приводит к четырехкратному увеличению мощности. Для резистора 100 Ом:

При токе 0.1 А: P = 0.1^2 * 100 = 1 Вт При токе 0.2 А: P = 0.2^2 * 100 = 4 Вт

Как определить мощность резистора по внешнему виду

Мощность резистора можно приблизительно оценить по его размерам и конструкции:

• Маленькие резисторы обычно рассчитаны на мощность 0.125 — 0.25 Вт
• Резисторы среднего размера — 0.5 — 2 Вт
• Крупные резисторы — от 3 Вт и выше
• Резисторы с радиатором или керамическим корпусом — высокомощные, от 5 Вт

Однако точное значение мощности можно узнать только из маркировки или документации.

Практическое применение расчета мощности резисторов

Расчет мощности резисторов необходим в следующих случаях:

• Выбор компонентов при проектировании схем
• Определение допустимой нагрузки в существующих схемах
• Расчет системы охлаждения для мощных резисторов
• Оптимизация энергопотребления устройств

Рассмотрим несколько практических примеров.

Выбор резистора для светодиода

Допустим, нужно подключить светодиод к источнику 12 В. Рабочий ток светодиода 20 мА, падение напряжения 2 В. Рассчитаем необходимое сопротивление:

R = (12 — 2) / 0.02 = 500 Ом

Мощность резистора:

P = (12 — 2)^2 / 500 = 0.2 Вт

Следовательно, подойдет резистор на 0.25 Вт или выше.

Расчет нагрузки для блока питания

Пусть имеется блок питания 5 В, 2 А. Нужно рассчитать минимальное сопротивление нагрузки:

R = U / I = 5 / 2 = 2.5 Ом

Мощность нагрузки составит:

P = 5 * 2 = 10 Вт

Это значение нужно учитывать при выборе компонентов и проектировании системы охлаждения.

Типичные ошибки при расчете мощности резисторов

При расчете мощности резисторов часто допускаются следующие ошибки:

• Неучет температурного коэффициента сопротивления
• Игнорирование импульсных нагрузок
• Пренебрежение саморазогревом резистора
• Неправильный выбор формулы расчета

Рассмотрим, как избежать этих ошибок.

Учет температурного коэффициента

Сопротивление резистора меняется с температурой. Для точных расчетов нужно учитывать температурный коэффициент сопротивления (ТКС). Например, для резистора с ТКС 0.01%/°C при нагреве на 50°C сопротивление изменится на:

0.01% * 50 = 0.5%

Учет импульсных нагрузок

При импульсных нагрузках пиковая мощность может значительно превышать среднюю. Нужно выбирать резистор с запасом по мощности или использовать специальные импульсные резисторы.

Расчет саморазогрева

При протекании тока резистор нагревается, что меняет его сопротивление. Для точных расчетов нужно учитывать тепловое сопротивление резистора и окружающей среды.

Современные тенденции в расчете мощности резисторов

В последние годы наблюдаются следующие тенденции в области расчета и применения мощных резисторов:

• Использование компьютерного моделирования
• Применение новых материалов с улучшенными характеристиками
• Миниатюризация компонентов при сохранении мощности
• Разработка интеллектуальных систем контроля мощности

Эти тенденции позволяют создавать более эффективные и надежные электронные устройства.

Компьютерное моделирование

Современные САПР позволяют моделировать тепловые режимы резисторов с высокой точностью. Это помогает оптимизировать конструкцию и избежать перегрева.

Новые материалы

Применение нанотехнологий позволяет создавать резисторы с улучшенными характеристиками. Например, углеродные нанотрубки обеспечивают высокую теплопроводность и стабильность параметров.

Таким образом, расчет мощности резисторов — важная задача при проектировании электронных устройств. Правильный выбор компонентов обеспечивает надежность и эффективность схемы. Современные методы расчета и новые материалы открывают новые возможности для создания высокотехнологичных устройств.

Расчет мощности при параллельном соединении

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

• P₁ = I 2 x R₁ = 0,256 2 x 200 = 13,11 Вт;
• P₂ = I 2 x R₂ = 0,256 2 x 100 = 6,55 Вт;
• P₃ = I 2 x R₃ = 0,256 2 x 51 = 3,34 Вт;
• P₄ = I 2 x R₄ = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

• 1/R = 1/R₁+1/R₂+1/R₃+1/R₄ = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
• Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
• Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
• Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
• Расчет силы тока для каждого резистора выполняется по формулам: I₁ = U/R₁ = 100/200 = 0,5A; I₂ = U/R₂ = 100/100 = 1A; I₃ = U/R₃ = 100/51 = 1,96A; I₄ = U/R₄ = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P₁ = U 2 /R₁ = 100 2 /200 = 50 Вт; P₂ = U 2 /R₂ = 100 2 /100 = 100 Вт; P₃ = U 2 /R₃ = 100 2 /51 = 195,9 Вт; P₄ = U 2 /R₄ = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р₁+Р₂+Р₃+Р₄ = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

• Первая формула для последовательного вида соединения.
• Далее, для параллельной схемы.
• И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

Мощность резистора: обозначение на схеме, как увеличить, что делать, если нет подходящего

Всех приветствую, кто заглянул на огонек. Речь в обзоре пойдет, как вы наверно уже догадались, о том, как сделать простую резистивную USB нагрузку для длительного тестирования емкости повербанков (ПБ), анализа качества кабелей и сетевых адаптеров.

Это одна из нескольких возможных статей о самостоятельном изготовлении резистивной нагрузки (на балластных резисторах), при удачном раскладе возможно руки дойдут и до электронной нагрузки, с регулировкой и стабилизацией тока.

Данная нагрузка служит уже достаточно давно и постоянно мелькает в моих обзорах, поэтому если заинтересовало, прошу под кат. В последнее время, такая самоделка уже не очень актуальна, т.к. появились бюджетные электронные нагрузки, поэтому имеет смысл доплатить и купить готовую.

Я же покупал еще по старому курсу, да и электронных нагрузок особо не было. Поэтому, если нужна именно резистивная, то приступим…

Возможные пути приобретения/изготовления резистивной нагрузки:

1) купить готовую плату-нагрузку с резисторами: Плюсы: + готовое работающее устройство (минимум телодвижений) + не нужны штекеры и провода (минимум потерь) + переключатель на 1А/2А (индикация) + небольшие размеры + небольшая стоимость Минусы: — очень сильно нагревается (около 180°С при токе 1А и около 230°С при токе 2А) и начинает жутко вонять (судя по отзывам, сам такой не имею) — не имеет корпуса, токоведущие/нагревающиеся части открыты (можно обжечься/прожечь что-нибудь, закоротить) — сложно прикрепить радиатор Так как изготовление хорошего нагрузочного модуля отнимает силы и время, то можно воспользоваться данной приблудой, но оставлять без присмотра не стоит 2) найти в закромах мощные резисторы (советские ПЭВ, ППБ и подобные), рассеиваемая им мощность для продолжительной работы должна быть не менее 10 Вт Плюсы: + меньший, но все равно достаточно высокий нагрев + не нужно покупать/средняя стоимость (наличие дома/покупка в магазе) + регулировка сопротивления, т.е. можно плавно изменять ток в широких пределах (только некоторые резюки, либо небольшая доработка) Минусы: — нужно припаивать штекер и провода — большие размеры — невозможность крепления радиатора (на большинстве) — нет переключателя (можно переделать, нужен второй резистор) — не имеет корпуса, токоведущие/нагревающиеся части также открыты (можно обжечься/прожечь что-нибудь) Я не имею таких резисторов в наличие, поэтому выбор за вами.

3) покупка резисторов 25-100 Вт в металлическом корпусе для отвода тепла и сборка своего модуля с кожухом

Плюсы: + средний нагрев (могут без опаски работать без доп. радиаторов) + средняя стоимость + возможность крепления дополнительного радиатора Минусы: — нужно припаивать штекер и провода — большие размеры — нет переключателя (можно переделать, нужен второй резистор) При этом они могут работать и без дополнительного охлаждения, но при этом неплохо греются, в пределах нормы, конечно. Я включал 25W резюки на полную разрядку моего ПБ — выдержали, но сильно грелись. Я рекомендую купить 100W резисторы, тогда дополнительный радиатор может совсем не пригодиться.

Итак, если решили собрать самодельный стенд из похожих резисторов, то приступим. Необходимые компоненты:

1) два резистора 25-100W по 4,7 Ом каждый. Как на зло, цены поднялись и многих номиналов уже не стало в продаже. Но наебайке есть 25W, 100W. Ищем по «Power resistor». 2) выключатель, я покупал тут 3) разборный USB штекер «папа», к примеру тут или тут 4) небольшой кусок медного многожильного провода большого сечения, к примеру, акустический провод 5) небольшой алюминиевый радиатор (по желанию) 6) пластиковая коробка

Номиналы резисторов рассчитываются по знакомой всем формуле закона Ома — I=U/R или R=U/I, где R – сопротивление (Ом), I –ток (А) и U – напряжение (V). К примеру, нам нужен ток 2А, поэтому для нагрузки 5V адаптеров нам нужен резюк 2,5Ома, т.к. 5/2=2,5 Ом.

Для 1А рассчитываем аналогично — 5/1=5 Ом. Так как большинство адаптеров/БП снижают напряжение под нагрузкой, то необходимо делать поправку на это и считать в среднем от 4,8V. Тогда на ток 2А нужен будет резюк R= U/I=4,8V/2А=2,4Ома, а для 1А — R= U/I=4,8V/1А=4,8Ома.

Также нужно помнить, что соединительные провода, выключатель и USB штекер также имеют некоторое сопротивление. Напомню одну хитрость, что при последовательном соединении резисторов общее сопротивление складывается, а при параллельном – будет чуть меньше самого маленького резистора.

Общее сопротивление нескольких резисторов можно посчитать здесь.

Чтобы не искать подходящие номиналы и не мудрить со схемой, я рекомендую сделать по моему варианту, правда с другими номиналами – 2 резистора по 4,7 Ом и небольшой выключатель. Для 1А будет задействован один резистор, для 2А – два в параллель. При этом, если мощность резистора или сопротивление не подходят, можете группировать несколько по указанным выше формулам. В своем нагрузочном модуле я использовал 2 резистора: 5,1Ом и 6Ом, т.к. я их выиграл на аукционе наEbay’ки за копейки, на другие номиналы тогда аукционов не было. При соединении параллельно, я получаю 2,7Ома для тока в 2А (в действительности 1,75А), а для тока в 1А (0,95А)задействую 1 резюк на 5,1 Ом. Они чуток не подходят, идеальный вариант был бы при использовании двух резюков по 4,7Ома, но таких лотов на аукционе не было.

Непосредственная сборка:

До этого пользовался вот таким простеньким модулем, он годился даже для длительных нагрузок, хотя при длительной работе он сильно нагревался, но не вонял и не перегорал (доставать, правда, его не удобно, можно было обжечься). Как только приехал второй резюк на 6 Ом, начал собирать стенд. Вот размеры типичных 25W резисторов в алюминиевом корпусе: Обратная сторона неровная и покрыта лаком, к тому же проушины для крепления имеют заусенцы, поэтому резисторы могут неплотно прилегать к радиатору, я рекомендую пройтись нулевой наждачкой: Сам радиатор я взял из старых запасов. Это распиленный пополам радиатор от бюджетных кулеров GlacialTech для процессоров на Socket A. В сервис центрах по ремонту компьютеров и бытовой техники за 50-100р вам отдадут целую пачку, на любой вкус и цвет. Можно использовать цельный радиатор, температура нагрева будет еще меньше. Мой нагрузочный стенд на 2А (точнее 1,75А) выше 70гр не нагревается. К тому же, к цельному радиатору можно приспособить небольшой вентилятор, тогда можно гонять модуль на высоких токах. При использовании 100Вт резисторов радиатор может вообще не понадобиться. Вот тот самый радиатор: Подошва у радиатора неровная, лучше отшлифовать. Можно оставить и так, теплообмен будет чуть похуже. Размеры моего радиатора: Вот что нам понадобится для изготовления модуля (наждачная бумага/шкурка на 1000/2000, стекло, в качестве идеально ровной поверхности, дрель, сверла, метчики для нарезки резьбы и машинное масло): Идеально полировать с пастой ГОИ не имеет особого смысла, хватит и 2000 наждачки. Затем сверлим отверстия и метчиком нарезаем резьбу (как это делать рассказывать не буду, см. в интернете). Если нет подходящего инструмента, то используйте термоклей/термоскотч/термопрокладки (ссылки внизу), сверлить ничего не придется. От себя добавлю, чтобы не сломать инструмент, капайте масло и через два полных оборота метчика, делайте пол оборота назад. Так вы 100% не сломаете метчик. По возможности пройдите чистовым метчиком (смотрите по количеству рисок на нем). Получается в итоге что-то вроде этого: В качестве кожуха я использовал защитный экран от старого холодильника. Можно использовать что угодно: от органики до любых пластиковых штуковин. Оргстекло небольшой толщины легко гнется при нагреве, я как-то гнул его над жалом мощного паяльника, только потом края придется немного подровнять. В общем, используем все, что есть под рукой. Перед окончательной сборкой пройдитесь по отверстиям сверлом большего диаметра, чтобы убрать заусенцы, иначе резюки плотно прилегать не будут (раззенковать): Далее намазываем тонкий слой термопасты на резисторы, можно просто выдавить каплю пасты, при затяжке она сама расползется. Я использовал российскую «народную» термопасту КПТ-8 (покупается в магазинах электрики): У нее средняя эффективность, со временем она подсыхает, но зато стоит копейки и продается в любых магазинах радиоэлектроники, для нашего модуля сгодится. Прикручиваем винты и загибаем вывода резисторов (можно до крепежа): Как видите, излишки термопасты вылезли наружу, они мешать не будут: Берем штекер USB «папа», желательно с позолоченными контактами (см. предыдущие пункты) и акустический провод с медными (не омедненными!) жилами толстого сечения. Для защиты от термического и механического воздействия я натянул термоусадку. Так как провод толстый, ножиком раздраконьте выходное отверстие: Берем выключатель, он будет вкл/выкл режим «2А». Подойдет любой силовой. Я использовал простенький KCD11, рассчитанный на 220V и 3А. В качестве окантовки использовал старый кабель-канал, немного срезав края. В одном из них вырезаем окошко под выключатель. Затем припаиваем выключатель к выводам резисторов: Сам провод припаиваем к резистору, который будет работать на 1А «по умолчанию». В моем случае это резистор 5,1 Ома. Если вы используете два одинаковых резюка по 4,7Ом, то припаиваем к любому: Одна сторона выводов будет соединена через выключатель, т.е. в положении «выкл» ток – 1А, в положении «вкл» — 2А, т.к. включается второй резюк в параллель. Получается вот такая простая схема: Далее прикручиваем кожух: Ставим верхнюю планку из того же кабель-канала или чего-нибудь похожего на место проема. Получается довольно неплохо: Ну и подклеиваем режимы работы, бумага и скотч в помощь: В итоге при хорошем адаптере имеем следующее (0,95А и 1,75А): Температура радиатора при токе 2А (1,75А) ни разу не поднималась выше 70°С, при 0,95А в районе 60°С:

Итого: устройство работает, сильно не нагревается, не воняет, свои функции выполняет на 100%. Да, с номиналами чуток не повезло, но ничего страшного. Все мои обзоры ПБ протестированы именно с этой нагрузкой, при желании можно расширить диапазон токов, к примеру, на 0,5А/1А/1,5А/2А/2,5А…

Кисулька:

Мощность при параллельном соединении формула

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно.

Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов

В жизни последовательное соединение резисторов имеет вид:

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

• Общее номинальное сопротивление составного резистора обозначено как Rобщ.
• Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
• Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом.

Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом.

Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов

Можно соединять резисторы и параллельно:

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

  Акб обратная полярность что это

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

1. Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
2. Измерение сопротивления при параллельном соединении
3. Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
4. При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Резистор – это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала.

Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов.

О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.

Последовательное соединение резисторов – это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи.

При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам.

Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.

  Температура плавления клея для клеевого пистолета

• На фотографии можно увидеть параллельное подключение резисторов.
• Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:
• — R(общ) – общее сопротивление;
• — R1, R2, R3 и Rn – параллельно подключенные резисторы.
• Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:
• — R(общ) – общее сопротивление;
• — R1, R2 – параллельно подключенные резисторы.
• В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:
• — R(общ) – общее сопротивление;
• — R – номинал параллельно подключенного резистора;
• — n – количество соединенных элементов.
• Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.
• Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:
• После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.

Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью.

В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением.

Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.

Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.

При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

1. Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
2. Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

  Как открутить болт с фиксатором резьбы

• Общее сопротивление R рассчитывается по формуле:
• Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Обозначение мощности резистора на схеме, как её увеличить, что делать, если нет подходящего по мощности резистора

Обозначение мощности резистора на схеме, как её увеличить, что делать, если нет подходящего по мощности резистора

Резистор — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления, предназначенный для линейного преобразования силы тока в напряжение и напряжения в силу тока, ограничения тока, поглощения электрической энергии и др. Весьма широко используемый компонент практически всех электрических и электронных устройств.

В схемах радиоэлектронной аппаратуры одним из наиболее часто встречающихся элементов является резистор, другое его название это сопротивление. У него есть целый ряд характеристик, среди которых есть мощность. В этой статье мы поговорим о резисторах, что делать, если у вас нет подходящего по мощности элемента, и почему они сгорают.

Характеристики резисторов

1. Основной параметр резистора – это номинальное сопротивление.

2. Второй параметр, по которому его выбирают – это максимальная (или предельная) рассеиваемая мощность.

3. Температурный коэффициент сопротивления – описывает, насколько изменяется сопротивление, при изменении его температуры на 1 градус Цельсия.

4. Допустимое отклонение от номинала. Обычно разброс параметров резистора от одного заявленного в пределах 5-10%, это зависит от ГОСТ или ТУ по которому он произведен, существуют и точные резисторы с отклонением до 1%, обычно стоят дороже.

5. Предельное рабочее напряжение, зависит от конструкции элемента, в бытовых электроприборах с напряжением питания 220В могут применяться практически любые резисторы.

6. Шумовые характеристики.

7. Максимальная температура окружающей среды. Это такая температура, которая может быть при достижении максимальной рассеиваемой мощности самого резистора. Об этом подробнее поговорим позже.

8. Влаго- и термоустойчивость.

Есть еще две характеристики, о которых начинающие чаще всего не знают, это:

1. Паразитная индуктивность.

2. Паразитная ёмкость.

Оба параметра зависят от типа и конструктивных особенностей резистора. Индуктивность имеет в любом проводнике, вопрос в её величины. Типовые величины паразитных индуктивностей и емкостей приводить бессмысленно. Паразитные составляющие следует учитывать при проектировании и ремонте высокочастотных приборах.

На низких частотах (например, в пределах звукового диапазона до 20 кГц), существенного влияния в работу схемы они не вносят. В высокочастотных приборах, с рабочими частотами в сотни тысяч и выше герц существенное влияние вносит даже расположение дорожек на плате и их форма.

• Мощность резистора
• Из курса физики многие отлично помнят формулу мощности для электричества, это: P=U*I
• Отсюда следует, что она линейно зависит от тока и напряжения. Ток же через резистор зависит от его сопротивления и приложенного к нему напряжению, то есть:
• I=U/R
• Падение напряжения на резисторе (сколько на его выводах остаётся напряжения от приложенного к цепи, в которой он установлен), так же зависит от тока и сопротивления:
• I=U/R
• Теперь объясним простыми словами, что такое мощность у резистора и куда она выделяется.

У любого металла есть своё удельное сопротивление, это такая величина, которая зависит от структуры этого самого металла. Когда носители зарядов (в нашем случае электроны), под воздействием электрического тока протекают через проводник, они сталкиваются с частицами, из которого состоит металл.

В результате этих столкновений затрудняется движение тока. Если очень обобщенно сказать, то получается, так, что чем плотнее структура металла, тем сложнее протекать току (тем больше сопротивление).

На картинке пример кристаллической решетки, для наглядности.

Из-за этих столкновений выделяется тепло. Это можно представить, как если бы вы шли через толпу (большое сопротивление), где вас еще и толкают, или если бы шли по пустому коридору, где вы сильнее вспотеете?

То же самое происходит и с металлом. Мощность выделяется в виде тепла. В некоторых случаях это плохо, потому что так снижается коэффициент полезного действия прибора. В других ситуациях – это полезное свойство, например в работе ТЭНов. В лампах накаливания за счет своего сопротивления спираль раскаляется до яркого свечения.

Но как это относится к резисторам?

Дело в том, что резисторы применяют для ограничения тока при питании каких-либо устройств, или элементов цепи, или для задания режимов работы полупроводниковым приборам. Из формулы выше станет ясно, что ток снижается, за счет снижения напряжения. Лишнее напряжение можно сказать, что сгорает в виде тепла на резисторе, мощность при этом считается по той же формуле, что и общая мощность:

P=U*I

Здесь U – это количество вольт «сожженных» на резисторе, а I – это ток, который через него протекает.2/1=144/1=144 Вт.

Всё сходится. Резистор будет выделять тепло с мощностью в 144Вт. Это условные значения, взятые в качестве примера. На практике таких резисторов вы не встретите в радиоэлектронной аппаратуре, исключением являются большие сопротивления для регулирования двигателей постоянного тока или пуска мощных синхронных машин в асинхронном режиме.

Какие бывают резисторы и как они обозначаются на схеме

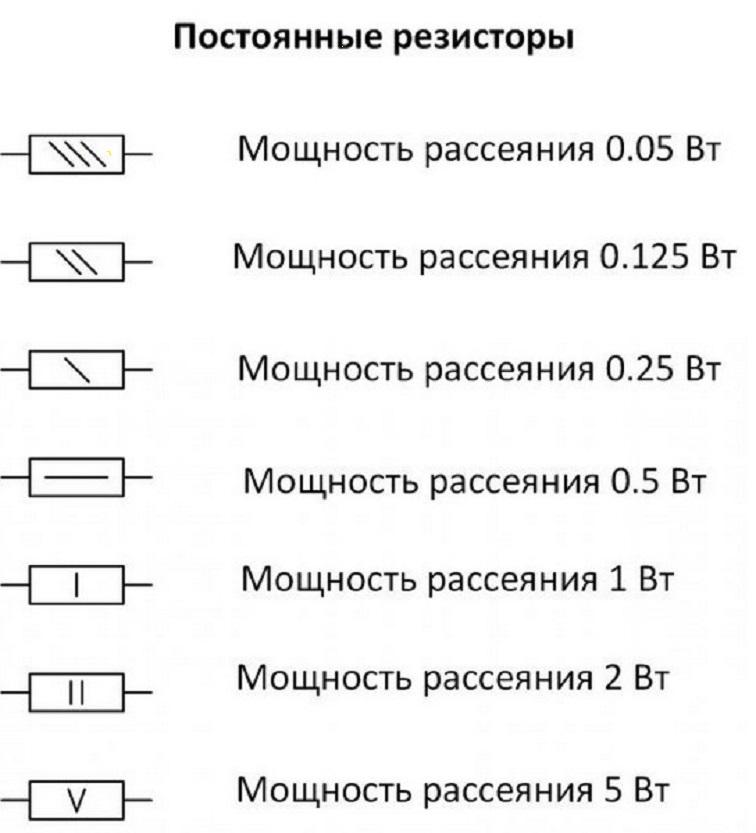
Ряд мощностей резисторов стандартен: 0.05 (0.62) – 0.125 – 0.25 – 0.5 – 1 – 2 – 5

Это типовые номиналы распространенных резисторов, бывают и большие значения, или другие величины. Но этот ряд наиболее распространен. При сборке электроники используют схему электрическую принципиальную, с порядкового номера элементов. Реже указываться номинальное сопротивление, еще реже указывается номинальное сопротивление и мощность.

Чтобы быстро определить мощность резистора на схеме были введены соответствующие УГО (условные графические обозначения) по ГОСТ. Внешний вид таких обозначений и их расшифровка представлены в таблице ниже.

Вообще эти данные, а также название конкретного типа резистора указываются в перечне элементов, там же указывается и разрешенный допуск в %.

Внешне, они отличаются размером, чем мощнее элемент, тем больше его размер. Больший размер увеличивает площадь теплообмена резистора с окружающей средой. Поэтому тепло, которое выделяется при прохождении тока через сопротивление, быстрее отдаётся воздуху (если окружающая среда воздух).

Это значит, что резистор может греться с большей мощностью (выделять определенное количество тепла в единицу времени). Когда температура сопротивления достигает определенного уровня, сначала начинает выгорать внешний слой с маркировкой, дальше сгорает резистивный слой (пленка, проволока или что-то другое).

Чтобы вы оценили, как сильно может греться резистор, взгляните на нагрев спирали разобранного мощного резистора (более 5 Вт) в керамическом корпусе.

В характеристиках был такой параметр, как допустимая температура окружающей среды. Она указывается, для правильного подбора элемента.

Дело в том, что раз мощность резистора ограничена способностью отдать тепло и, при этом, не перегреться, а для отдачи тепла, т.е.

охлаждения элемента путем конвекции или принудительным потоком воздуха должна быть как можно большая разница температур элемента и окружающей среды.

Поэтому если вокруг элемента слишком жарко он быстрее нагреется и сгорит, даже если электрическая мощность на нем ниже максимально рассеиваемой. Нормальной температурой является 20-25 градусов Цельсия.

Что делать, если нет резистора нужной мощности?

Частой проблемой радиолюбителей является отсутствия резистора нужной мощности. Если у вас есть резисторы мощнее, чем нужно – ничего страшного в этом нет, можно ставить не задумываясь. Лишь бы он влез по размеру. Если все имеющиеся резисторы по мощности меньше, чем нужно – это уже проблема.

На самом деле решить этот вопрос достаточно просто. Вспомните законы последовательного и параллельного соединения резисторов.

1. При последовательном соединении резисторов сумма падений напряжений на всей цепочке равняется сумме падений на каждом из них. А ток, протекающий через каждый резистор равен общему току, т.е. в цепи из последовательно соединенных элементов протекает ОДИН ток, но приложенные к каждому из них напряжения РАЗНЫЕ, определяются по закону Ома для участка цепи (см. выше) Uобщ=U1+U2+U3

2. При параллельном соединении резисторов падение на всех напряжения равны, а ток, протекающий в каждой из ветвей обратно пропорционален сопротивлению ветви. Общий ток цепочки из параллельно соединенных резисторов равен сумме токов каждой из ветвей.

На этой картинке изображено всё вышесказанное, в удобной для запоминания форме.

Так, как при последовательном соединении резисторов снизится напряжение на каждом из них, а при параллельном соединении ток, то если P=U*I

Мощность, выделяемая на каждом из них, снизится соответствующим образом.

Поэтому, если у вас нет резистора 100 Ом на 1 Вт, его можно почти всегда заменить 2 резисторами на 50 Ом и 0.5 Вт соединенными последовательно, или 2 резисторами на 200 Ом и 0.5 Вт соединенными параллельно.

Я не просто так написал «ПОЧТИ ВСЕГДА».

Дело в том, что не все резисторы одинаково хорошо переносят ударные токи, в некоторых цепях, например связанные с зарядом конденсаторов большой ёмкости, в первоначальный момент времени переносят большую ударную нагрузку, которая может повредить его резистивный слой. Такие связки нужно проверять на практике или путем долгих расчетов и чтением технической документации и ТУ на резисторы, чем почти никогда и никто не занимается.

Заключение

Мощность резистора – это величина не менее важная, чем его номинальное сопротивление. Если не уделять внимания подбору сопротивлений нужно мощности, то они будут перегорать и сильно греться, что плохо в любой цепи.

При ремонте аппаратуры, особенно китайской, ни в коем случае не пытайтесь ставить резисторы меньшей мощности, лучше поставить с запасом, если есть такая возможность поместить его по габаритам на плате.

Для стабильной и надежной работы радиоэлектронного устройства нужно подбирать мощность, как минимум, с запасом в половину от предполагаемой, а лучше в 2 раза больше. Это значит, что если по расчетам на резисторе выделяется 0.9-1 Вт, то мощность резистора или их сборки должна быть не меньше, чем 1.5-2 Вт.

Ранее ЭлектроВести писали, что JinkoSolar объявила, что она установила новый рекорд эффективности для монокристаллических PERC-панелей, который составил 24,38%.

Компания также разработала модуль мощностью 469,3 Вт.

Кроме того, китайский производитель фотоэлектрических элементов поравнялся с фирмой Trina Solar, которая на прошлой неделе заявила о рекордном 24,58% показателе КПД монокристаллических панелей n-типа.

Резистор

Радиоэлектроника для начинающих

Резистор служит для ограничения тока в электрической цепи, создания падений напряжения на отдельных её участках и пр. Применений очень много, всех и не перечесть.

Другое название резистора – сопротивление. По сути, это просто игра слов, так как в переводе с английского resistance – это сопротивление (электрическому току).

Когда речь заходит об электронике, то порой можно встретить фразы типа: «Замени сопротивление», «Два сопротивления сгорели». В зависимости от контекста под сопротивлением может подразумеваться именно электронная деталь.

На схемах резистор обозначается прямоугольником с двумя выводами. На зарубежных схемах его изображают чуть-чуть иначе. «Тело» резистора обозначают ломаной линией – своеобразная стилизация под первые образцы резисторов, конструкция которых представляла собой катушку, намотанную высокоомным проводом на изоляционном каркасе.

Рядом с условным обозначением указывается тип элемента (R) и его порядковый номер в схеме (R1). Здесь же указано его номинальное сопротивление. Если указана только цифра или число, то это сопротивление в Омах.

Иногда, рядом с числом пишут Ω – так, греческой заглавной буквой «Омега» обозначают омы. Ну, а, если так, – 10к, то этот резистор имеет сопротивление 10 килоОм (10 кОм – 10 000 Ом).

Про множители и приставки «кило», «мега» можете почитать здесь.

Не стоит забывать о переменных и подстроечных резисторах, которые всё реже, но ещё встречаются в современной электронике. Об их устройстве и параметрах я уже рассказывал на страницах сайта.

Основные параметры резисторов

• Номинальное сопротивление.
  Это заводское значение сопротивления конкретного прибора, измеряется это значение в Омах (производные килоОм – 1000 Ом, мегаОм – 1000000 Ом). Диапазон сопротивлений простирается от долей Ома (0,01 – 0,1 Ом) до сотен и тысяч килоОм (100 кОм – 1МОм). Для каждой электронной цепи необходимы свои наборы номиналов сопротивлений. Поэтому разброс значений номинальных сопротивлений столь велик.
• Рассеиваемая мощность.
  Более подробно о мощности резистора я уже писал здесь.
  При прохождении электрического тока через резистор происходит его нагрев. Если пропускать через него ток, превышающий заданное значение, то токопроводящее покрытие разогреется настолько, что резистор сгорает. Поэтому существует разделение резисторов по рассеиваемой мощности.
  На графическом обозначении резистора внутри прямоугольника мощность обозначается наклонной, вертикальной или горизонтальной чертой. На рисунке обозначено соответствие графического обозначения и мощности указанного на схеме резистора.
  
  К примеру, если через резистор потечёт ток 0,1А (100 mA), а его номинальное сопротивление 100 Ом, то необходим резистор мощностью не менее 1 Вт. Если вместо этого применить резистор на 0,5 Вт, то он вскоре выйдет из строя. Мощные резисторы применяются в сильноточных цепях, например, в блоках питания или сварочных инверторах.
  Если необходим резистор мощностью более 2 Вт (5 Вт и более), то внутри прямоугольника на условном графическом обозначении пишется римская цифра. Например, V – 5 Вт, Х – 10 Вт, XII – 12 Вт.
• Допуск.
  При изготовлении резисторов не удаётся добиться абсолютной точности номинального сопротивления. Если на резисторе указано 10 Ом, то его реальное сопротивление будет в районе 10 Ом, но никак не ровно 10. Оно может быть и 9,88 и 10,5 Ом. Чтобы как-то обозначить пределы погрешности в номинальном сопротивлении резисторов, их делят на группы и присваивают им допуск. Допуск задаётся в процентах. Если вы купили резистор на 100 Ом c допуском ±10%, то его реальное сопротивление может быть от 90 Ом до 110 Ом. Узнать точное сопротивление этого резистора можно лишь с помощью омметра или мультиметра, проведя соответствующее измерение. Но одно известно точно. Сопротивление этого резистора не будет меньше 90 или больше 110 Ом.
  Строгая точность номиналов сопротивлений в обычной аппаратуре важна не всегда. Так, например, в бытовой электронике допускается замена резисторов с допуском ±20% от того номинала, что требуется в схеме. Это выручает в тех случаях, когда необходимо заменить неисправный резистор (например, на 10 Ом). Если нет подходящего элемента с нужным номиналом, то можно поставить резистор с номинальным сопротивлением от 8 Ом (10-2 Ом) до 12 Ом (10+2 Ом). Считается так (10 Ом/100%) * 20% = 2 Ом. Допуск составляет -2 Ом в сторону уменьшения, +2 Ом в сторону увеличения.
  Для тех, кто ещё не знает, существует ещё одна возможность подобрать необходимое сопротивление – его можно составить, соединив вместе несколько резисторов разных номиналов. Об этом читайте в статье про соединение резисторов.
  Существует аппаратура, где такой трюк не пройдёт – это прецизионная аппаратура. К ней относится медицинское оборудование, измерительные приборы, электронные узлы высокоточных систем, например, военных. В ответственной электронике используются высокоточные резисторы, допуск их составляет десятые и сотые доли процента (0,1-0,01%). Иногда такие резисторы можно встретить и в бытовой электронике.
  Стоит отметить, что в настоящее время в продаже можно встретить резисторы с допуском не более 10% (обычно 1%, 5% и реже 10%). Высокоточные резисторы имеют допуск в 0,25…0,05%.
• Температурный коэффициент сопротивления (ТКС).
  Под влиянием внешней температуры или собственного нагрева из-за протекающего тока, сопротивление резистора меняется. Иногда в тех пределах, которые нежелательны для работы схемы. Чтобы оценить изменение сопротивления из-за воздействия температуры, то есть термостабильность резистора, используется такой параметр, как ТКС (Температурный Коэффициент Сопротивления). За рубежом принято сокращение T.C.R.
  В маркировке резистора величина ТКС, как правило, не указывается. Для нас же необходимо знать, что чем меньше ТКС, тем лучше резистор, так как он обладает лучшей термостабильностью. Более подробно о таком параметре, как ТКС, я рассказывал тут.

Первые три параметра основные, их надо знать!

Перечислим их ещё раз:

• Номинальное сопротивление (маркируется как 100 Ом, 10кОм, 1МОм…)
• Рассеиваемая мощность (измеряется в Ваттах: 1 Вт, 0,5 Вт, 5 Вт…)
• Допуск (выражается в процентах: 5%, 10%, 0,1%, 20%).

Так же стоит отметить конструктивное исполнение резисторов.

Сейчас можно встретить как микроминиатюрные резисторы для поверхностного монтажа (SMD-резисторы), которые не имеют выводов, так и мощные, в керамических корпусах.

Существуют и невозгораемые, разрывные и прочее. Перечислять можно очень долго, но основные параметры у них одинаковые: номинальное сопротивление, рассеиваемая мощность и допуск.

В настоящее время номинальное сопротивление резисторов и их допуск маркируют цветными полосами на корпусе самого элемента.

Как правило, такая маркировка применяется для маломощных резисторов, которые имеют небольшие габариты и мощность менее 2…3 ватт.

Каждая фирма-изготовитель устанавливает свою систему маркировки, что вносит некоторую путаницу. Но в основном присутствует одна устоявшаяся система маркировки.

Новичкам в электронике хотелось бы рассказать и о том, что кроме резисторов, цветовыми полосами маркируют и миниатюрные конденсаторы в цилиндрических корпусах. Иногда это вызывает путаницу, так как такие конденсаторы ложно принимают за резисторы.

Таблица цветового кодирования

Рассчитывается сопротивление по цветным полосам так. Например, три первых полосы – красные, последняя четвёртая золотистого цвета. Тогда сопротивление резистора 2,2 кОм = 2200 Ом.

Первые две цифры согласно красному цвету – 22, третья красная полоса, это множитель. Стало быть, по таблице множитель для красной полосы – 100. На множитель необходимо умножить число 22. Тогда, 22 * 100 = 2200 Ом.

Золотистая полоса соответствует допуску в 5%. Значит, реальное сопротивление может быть в пределе от 2090 Ом (2,09 кОм) до 2310 Ом (2,31 кОм).

Мощность рассеивания зависит от размеров и конструктивного исполнения корпуса.

На практике широкое распространение имеют резисторы с допуском 5 и 10%. Поэтому за допуск отвечают полосы золотого и серебристого цвета. Понятно, что в таком случае, первая полоса находится с противоположной стороны элемента. С неё и нужно начинать считывание номинала.

Но, как быть, если резистор имеет небольшой допуск, например 1 или 2% ? С какой стороны считывать номинал, если с обеих сторон присутствуют полосы красного и коричневого цветов?

Этот случай предусмотрели и первую полосу размещают ближе к одному из краёв резистора. Это можно заметить на рисунке таблицы. Полоски, обозначающие допуск расположены дальше от края элемента.

Конечно, бывают случаи, когда нет возможности считать цветовую маркировку резистора (забыли таблицу, стёрта/повреждена сама маркировка, некорректное нанесение полос и пр.).

В таком случае, узнать точное сопротивление резистора можно только, если измерить его сопротивление мультиметром или омметром. В таком случае вы будете 100% знать его реальную величину. Также при сборке электронных устройств рекомендуется проверять резисторы мультиметром для того, чтобы отсеить возможный брак.

Главная » Радиоэлектроника для начинающих » Текущая страница

Также Вам будет интересно узнать:

Простой способ определить Vf светодиода, чтобы выбрать подходящий резистор

Вы неправильно понимаете, как работает светодиод, так как Vf — это не напряжение, которое вы кладете на светодиод, чтобы заставить его работать, а напряжение, которое появляется (падает) на светодиод, когда ток пропускается через него.

Если вы посмотрите на соответствующий лист данных, вы увидите Vf (min), Vf и Vf (max), заданные для определенного тока, и это означает, что, если вы подадите указанный ток через светодиод, вы можете ожидать Vf падать где-нибудь между Vf (мин) и Vf (макс.), причем Vf является типичным значением.

Итак, ответ на ваш вопрос:

• Источником питания является любой источник переменного напряжения, R обеспечивает балласт для светодиода, снижая его чувствительность к изменениям источника питания.
• Это не даст светодиоду испускать свой волшебный дым, если вы случайно запустите источник питания слишком далеко, и его значение [R] не критично, в разумных пределах.
• Например, если вы используете резистор 1000 Ом и пытаетесь протолкнуть 20 мА через светодиод, эти 20 мА также должны пройти через R, поэтому R будет падать:
•  E = IR = 0,02 A × 1000 Ом = 20 вольт, E = IRзнак равно0.02A×1000Ωзнак равно20 вольт,
• и вам понадобится запас для светодиодов.
• «A» — это амперметр, используемый для измерения тока через светодиод, а «V» — вольтметр, используемый для измерения напряжения на светодиоде.

При использовании, то, что вам нужно сделать, это запустить источник питания с нуля вольт, а затем провернуть его до тех пор, пока амперметр не покажет 20 миллиампер, тогда напряжение, отображаемое на вольтметре, будет Vf для этого конкретного диода при данном конкретном токе и температуре окружающей среды. температура.

1. Возвращаясь к вашему вопросу, способ определить, какое значение последовательного сопротивления является «правильным» для вашего светодиода, состоит в том, чтобы сначала определить его Vf при желаемом прямом токе (если), а затем использовать закон Ома для определения значения сопротивления, так:
2. R =  Vс — VеяеR = Вs-Веяе
3. Если предположить, что Vs (напряжение питания) составляет 12 вольт, то Vf равно 2 вольтам, а If — 20 мА, мы получим
4. R =  12 В- 2 В0,02 А= 500 ОмR = 12В-2В0.02Aзнак равно500 Ом
5. Затем, чтобы определить мощность рассеиваемого резистора, мы можем написать:
6. Pd = (Vs — Vf) × If = 10 В × 0,02 А = 0,2 Вт  Pd = (Vs — Vf)×Если знак равно 10V×0.02Aзнак равно0,2 Вт
7. 510 Ом — это самое близкое значение E24 (+/- 5%), которое будет сохраняться, если на консервативной стороне 20 мА, и резистор 1/4 Вт должен быть в порядке.
8. Утиный суп, а? 😉

Какая реальная мощность резисторов-обманок, или, почему мощность, написанная на корпусе резистора отличается от реальной

Какая реальная мощность резисторов-обманок, или, почему мощность, написанная на корпусе резистора отличается от реальной

Многие наши клиенты при покупке резисторов-обманок задают следующий вопрос: «Почему мощность, указанная на сайте, отличается от мощности, которая указана на корпусе самого резистора?»

Многие наши клиенты при покупке резисторов-обманок задают следующий вопрос: «Почему мощность, указанная на сайте, отличается от мощности, которая указана на корпусе самого резистора?»

 

Для примера возьмем резистор-обманку 17W. Как видим, на его корпусе указано 27W.

 

 

Дело в том, что резистор-обманка представляет собой обычный резистор со своими характеристиками. У резистора есть максимальная излучаемая мощность, которая зависит от размера и типа резистора. И есть реально потребляемая мощность, она зависит от сопротивления и напряжения. На корпусе же указана именно максимальная излучаемая мощность. Поэтому подбирать резистор необходимо именно по мощности, которая дана на сайте.

Для примера возьмем резистор-обманку 32W. На корпусе указаны максимальная излучаемая мощность 50W и сопротивление 6 Ом.

По закону Ома для участка цепи I = U/R.

U(напряжение) в сети составляет 14V, соответственно, I (сила тока) = 14V/6Ом=2,3А.

Мощность рассчитываем по формуле W = I * U=2,3А*14V=32 Вт. Это те самые 32W, которые указаны на сайте.

 

 

Так, если Вы решили установить светодиодную лампу с цоколем, к примеру, P21W,  Ваш автомобиль оснащен бортовым компьютером, либо же при установке светодиодов увеличилась частота мерцания «поворотников», необходимо выбирать резистор либо на 17 или 20 Вт., в зависимости от потребляемой мощности светодиодной лампы, которая, обычно, не превышает 5 Вт. Если мы суммируем потребляемую мощность резистор (17Вт.) и потребляемую мощность светодиодной лампы (3-5 Вт.), получаем число, близкое к 21 Вт. В этом случае бортовой компьютер воспримет светодиодную лампу и резистор как штатную лампу накаливания и не выдаст ошибку. Аналогичное произойдет с частотой мерцания «поворотников», которая не будет превышать штатной.

Что такое мощность резистора? | joyta.ru

Номинальная мощность резистора определяет, какое максимальное количество энергии может рассеять резистор без риска перегрева.

Как вытекает из закона Ома, электрическая мощность связана с напряжением и током:

 P = I * U

Если электрическая мощность, выделяемая на резисторе, не превышает его номинальную рассеиваемую мощность, температура резистора будет стабильной. Следует отметить, что температура на самом резисторе распределена не равномерно. Его корпус немного теплее, чем выводы, а самая высокая температура в центре корпуса.

Чем выше скорость теплоотдачи в окружающую среду, тем ниже температура на резисторе. Крупные резисторы с большой площадью поверхности, как правило, могут рассеивать значительное количество тепловой мощности.

Если мощность выделяемая на резисторе превышает его номинальную мощность, то резистор может быть поврежден. Это может иметь несколько последствий:

• изменение значения сопротивления,
• снижение срока службы,
• полный выход из строя в результате обрыва цепи,
• в экстремальных случаях чрезмерная мощность может даже стать причиной возгорания.

Определение: мощность резистора — номинальная мощность, которую может рассеять резистор, сохраняя при этом свою работоспособность.

Мощность резистора

Номинальная мощность резистора определяется для определенной температуры окружающей среды на открытом воздухе. Обратите внимание, что на практике количество энергии, которую резистор может рассеять без повреждения  сильно зависит от условий эксплуатации и, следовательно, не равна номинальной мощности.

Например, повышение температуры окружающей среды может значительно уменьшить номинальную мощность резистора.

Hantek 2000 — осциллограф 3 в 1

Портативный USB осциллограф, 2 канала, 40 МГц….

Это следует учитывать при разработке схем. Обычно резисторы рассчитаны для работы при температуре до 70°С, выше этого значения резистор значительно снижает свою номинальную рассеиваемую мощность. Это иллюстрируется кривой ухудшения параметров.

Наряду с влиянием температуры окружающей среды, есть еще несколько факторов, влияющих на изменение номинального значения мощности резистора. Наиболее важные факторы приведены ниже:

Корпус

Скорость теплоотдачи ограничивается из-за установки резистора в корпус прибора. Корпус ограничивает воздушный поток и, следовательно, отвод тепла путем конвекции. Излучаемое тепло будет удаляться неэффективно, потому что стенки корпуса действуют как тепловой барьер. Влияние корпуса на степень потери тепла сильно зависит от размера, формы, материала и толщины стенок.

Принудительное охлаждение

Увеличение теплопередачи посредством принудительной конвекции позволяет получить более высокую рассеиваемую мощность, чем путем обычной естественной конвекции.

Это может быть достигнуто путем создания воздушного потока, или даже жидкостным охлаждением. Некоторые мощные резисторы имеют ребристый корпус, чтобы создать большую поверхность для рассеивания тепла.

Группировка компонентов

На печатной плате резисторы зачастую расположены близко друг к другу. В таком случае тепловое излучение одного резистора будет оказывать влияние на показатель мощности рядом расположенных резисторов.

В заключении хотелось бы отметить, что для большинства электронных схем номинальная мощность резисторов не является ключевым параметром, поскольку эти резисторы рассеивают малое количество энергии от одного ватта и меньше.

Однако в силовой электронике мощность является важной характеристикой. Типичной областью применения мощных резисторов являются источники питания, динамические тормоза, преобразователи мощности, усилители и нагреватели.

Мощность переменного тока. Мощность тока через катушку, резистор, конденсатор

 

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

 

Мощность тока через резистор

 

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

 

Мощность тока через конденсатор

 

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

 

Мощность тока через катушку

 

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

 

Мощность тока на произвольном участке

 

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Определение мощности резистора: можно ли узнать по размеру детали

Главная База знаний Электроника

Резисторы есть в любой электрической схеме. Но в разных схемах протекают различной величины ток. Не могут же одни и те же элементы работать при 0,1 А и при 100 А. Ведь при прохождении тока сопротивление греется.

Чем выше ток, тем более интенсивный нагрев. Значит, и резисторы должны быть на разную величину тока. Так и есть. Отображает их способность работать при различных токах такой параметр, как мощность резистора. На деталях покрупнее она указывается прямо на корпусе.

Для мелких корпусов есть другой метод определения (см. ниже).

Что такое мощность резистора

Мощность определяется как произведение силы тока на сопротивление: P = I * R и измеряется в ваттах (закон Ома). Рассеиваемая мощность резистора — это максимальный ток, который сопротивление может выдерживать длительное время без ущерба для работоспособности. То есть, этот параметр надо выбирать для каждой схемы отдельно — по максимальному рабочему току.

Как определить мощность резистора по внешнему виду: надо знать соответствие размеров и мощностей

Физически рассеиваемая мощность резистора — это то количество тепла, которое его корпус может «отдать» в окружающую среду и не перегреться при этом до фатальных последствий. При этом, нагрев не должен слишком сильно влиять на сопротивление резистора.

Стандартный ряд мощностей резисторов и их обозначение на схемах

Обратите внимание, что резисторы одного номинала могут быть с разной мощностью рассеивания. Этот параметр зависит от технологии изготовления, материала корпуса. Есть определенный ряд мощностей и их графическое обозначение по ГОСТу.

Графическое обозначение мощности резисторов на схеме — черточки и римские цифры, нанесенные на поверхность сопротивления. Самое малое стандартное значение 0,05 Вт, самое большое — 25 Вт, но есть и более мощные. Но это уже специальная элементная база и в бытовой аппаратуре не встречается.

Как обозначаются мощность маломощных резисторов надо просто запомнить. Это косые линии на прямоугольниках, которыми обозначают сопротивления на схемах.

Количество косых черточек обозначает количество четвертей дюйма. При номиналах сопротивлений от 1 Вт на изображении ставятся римские цифры: I, II, III, V, VI и т.д.

Цифра эта и обозначает мощность резистора в ваттах. Тут немного проще, так как соответствие прямое.

Как определить по внешнему виду

На принципиальной схеме указана нужная мощность резистора — тут все понятно. Но как определить мощность сопротивления по внешнему виду на печатной плате? Вообще, чем больше размер корпуса, тем больше тепла он рассеивает. На достаточно крупных по размеру сопротивлениях указывается номинальное сопротивление и его мощность в ваттах.

Тут есть некоторая путаница, но не все так страшно. На отечественных сопротивлениях рядом с цифрой ставят букву В. В зарубежных ставят W. Но эти буквы есть не всегда. В импортных может стоять V или SW перед цифрой. Еще в импортных может тоже стоять буква B, а в отечественных МЛТ может не стоять ничего или буква W. Запутанная история, конечно. Но с опытом появляется хоть какая-то ясность.

Как определить мощность резистора: стоит в маркировке

А ведь есть маленькие резисторы, на которых и номинал-то с трудом помещается. В импортных он нанесен цветными полосками. Как у них узнать мощность рассеивания?

В старом ГОСТе была таблица соответствий размеров и мощностей. Резисторы отечественного производства по прежнему делают в соответствии с этой таблицей. Импортные, кстати, тоже, но они по размерам чуть меньше отечественных.

Тем не менее их также можно идентифицировать. Если сомневаетесь, к какой группе отнести конкретный экземпляр, лучше считать что он имеет более низкую способность рассеивать тепло. Меньше шансов, что деталь скоро перегорит.

Тип резистора Диаметр, мм Длинна, ммРассеиваемая мощность, Вт

ВС	2,5	7,0	0,125
УЛМ, ВС	5,5	16,5	0,25
ВС	5,5	26,5	0,5
7,6	30,5	1
9,8	48,5	2
25	75	5
30	120	10
КИМ	1,8	3,8	0,05
2,5	8	0,125
МЛТ	2	6	0,125
3	7	0,125
4,2	10,8	0,5
6,6	13	1
8,6	18,5	2

С размерами сопротивлений и их мощностью вроде понятно. Не все так однозначно. Есть резисторы большого размера с малой рассеивающей способностью и наоборот. Но в таких случаях, проставляют этот параметр в маркировке.

Мощность SMD-резисторов

SMD-компоненты предназначены для поверхностного монтажа и имеют миниатюрные размеры. Мощность резисторов SMD определяется по размерам. Также она есть в характеристиках, но необходимо знать серию и производителя. Таблица мощности СМД резисторов содержит наиболее часто встречающиеся номиналы.

Размеры SMD-резисторов — вот по какому признаку можно определить мощность этих элементов

Код imperialКод metrikДлинна inch/mmШирина inch/mmВысота inch/mmМощность, Вт

0201	0603	0,024/0,6	0,012/0,3	0,01/0,25	1/20 (0,05)
0402	1005	0,04/1,0	0,02/0,5	0,014/0,35	1/16 (0,062)
0603	1608	0,06/1,55	0,03/0,85	0,018/0,45	1/10 (0,10)
0805	2112	0,08/2,0	0,05/1,2	0,018/0,45	1/8 (0,125)
1206	3216	0,12/3,2	0,06/1,6	0,022/0,55	1/4 (0,25)
1210	3225	0,12/3,2	0,10/2,5	0,022/0,55	1/2 (0,50)
1218	3246	0,12/3,2	0,18/4,6	0,022/0,55	1,0
2010	5025	0,20/2,0	0,10/2,5	0,024/0,6	3/4 (0,75)
2512	6332	0,25/6,3	0,12/3,2	0,024/0,6	1,0

В общем-то, у этого типа радиоэлементов нет другого оперативного способа определения тока, при котором они могут работать, кроме как по размерам. Можно узнать по характеристикам, но их найти не всегда просто.

Как рассчитать мощность резистора в схеме

Чтобы рассчитать мощность резисторов в схеме, кроме сопротивления (R) необходимо знать силу тока (I). На основании этих данных можно рассчитать мощность. Формула обычная: P = I² * R. Квадрат силы тока умножить на сопротивление. Силу тока подставляем в Амперах, сопротивление — в Омах.

Если номинал написан в килоомах (кОм) или мегаомах (мОм),  его переводим в Омы. Это важно, иначе будет неправильная цифра.

Схема последовательного соединения резисторов

Для примера рассмотрим схему на рисунке выше. Последовательное соединение сопротивлений характерно тем, что через каждый отдельный резистор цепи протекает одинаковый ток.

Значит мощность сопротивлений будет одинаковой. Последовательно соединенные сопротивления просто суммируется: 200 Ом + 100 Ом + 51 Ом + 39 Ом = 390 Ом. Ток рассчитаем по формуле: I = U/R.

Подставляем данные: I = 100 В / 390 Ом = 0,256 А.

По расчетным данным определяем суммарную мощность сопротивлений: P = 0,256² * 390 Ом = 25,549 Вт.  Аналогично рассчитывается мощность каждого из резисторов. Например, рассчитаем мощность резистора R2 на схеме. Ток мы знаем, его номинал тоже.

Получаем: 0,256А² * 100 Ом = 6,55 Вт. То есть, мощность этого резистора должна быть не ниже 7 Вт. Брать с более низкой мощностью точно не стоит — быстро перегорит.

Если позволяет конструктив прибора, то можно поставить резистор большей мощности, например, на 10 Вт.

Есть резисторы серии МЛТ, в которых мощность рассеивания тепла указана сразу после названия серии без каких-либо букв. В данном случае — МЛТ-2 означает, что мощность этого экземпляра 2 Вт, а номинал 6,8 кОм.

При параллельном подключении расчет аналогичен. Нужно только правильно рассчитать ток, но это тема другой статьи. А формула расчета мощности резистора от типа соединения не зависит.

Как подобрать резистор на замену

Если вам необходимо поменять резистор, брать надо либо той же мощности, либо выше. Ни в коем случае не ниже — ведь резистор и без того вышел из строя. Происходит это обычно из-за перегрева. Так что установка резистора меньшей мощности исключена. Вернее, вы его поставить можете. Но будьте готовы к тому, что скоро его снова придется менять.

Примерно определить мощность резистора можно по размерам

Если место на плате позволяет, лучше поставить деталь с большей мощностью рассеивания, чем была у заменяемой детали. Или поднять резистор той же мощности повыше (можно вообще не подрезать выводы) — чтобы охлаждение было лучше. В общем, при замене резистора, мощность берем либо ту же, либо выше на шаг.

Источник: https://elektroznatok.ru/info/elektronika/moshhnost-rezistora

Мощность SMD резистора. Как узнать?

Радиоэлектроника для начинающих

Также, как и выводные резисторы, SMD-резисторы для монтажа на поверхность рассчитаны на определённую мощность рассеивания. Но, как её узнать?

На самом деле, определить мощность SMD резистора не так уж и сложно. Мощность рядовых чип-резисторов, которых в современной электронике огромное множество, можно определить исходя из их размеров.

Далее представлена таблица №1, в которой указано соответствие типоразмера SMD-резистора и его мощности рассеивания. Отмечу, что в таблице указан типоразмер в дюймовой системе кодировки, а реальные размеры указаны в миллиметрах (длина и ширина). Сделано это исходя из удобства.

Дело в том, что до сих пор наибольшее распространение получила система кодирования типоразмера чип-резисторов в дюймах. Её используют все: производители, поставщики и магазины. А для того, чтобы определить типоразмер, а, следовательно, и мощность, мы должны замерить длину и ширину резистора обычной линейкой или другим более точным инструментом, шкала которого проградуирована в миллиметрах.

Если у вас на руках имеется SMD-резистор, мощность которого требуется узнать, то, сделав замеры обычной линейкой, можно быстро определить его типоразмер и соответствующую ему мощность рассеивания.

Таблица №1. Соответствие мощности SMD-резистора и его типоразмера.

Типоразмер (дюймовый, inch)	Мощность (Power Rating at 70°C)	Мощность, Вт.	Длина (L) /Ширина (W), мм.
0075	1/50W	0,02 Вт	0,3/0,15
01005	1/32W	0,03 Вт	0,4/0,2
0201	1/20W	0,05 Вт	0,6/0,3
0402	1/16W, 1/8W	0,063 Вт; 0,125 Вт	1,0/0,5
0603	1/10W, 1/5W	0,1 Вт; 0,2 Вт	1,6/0,8
0805	1/8W, 1/4W	0,125 Вт; 0,25 Вт	2,0/1,25
1206	1/4W, 1/2W	0,25 Вт; 0,5 Вт	3,2/1,6
1210	1/2W	0,5 Вт	3,2/2,5
1218	1W; 1,5W	1 Вт; 1,5 Вт	3,2/4,8
1812	1/2W, 3/4W	0,5 Вт; 0,75 Вт	4,5/3,2
2010	3/4W	0,75 Вт	5,0/2,5
2512	1W; 1,5W; 2W	1 Вт; 1,5 Вт; 2 Вт	6,4/3,2
Мощность SMD-резисторов с широкими электродами (Long side termination chip resistors)
0406	0,25…0,3W	0,25…0,3 Вт	1,0/1,6
0612	0,75…1W	0,75…1 Вт	1,6/3,2
1020	1W	1 Вт	2,5/5,0
1218	1W	1 Вт	3,2/4,6
1225	2W	2 Вт	3,2/6,4

В таблице №1 также указаны типовые мощности и для SMD-резисторов с широкими боковыми электродами (выводами). В документации такие резисторы называются Long Side Termination Chip Resistors или Wide Terminal Chip Resistors.

Хочу обратить внимание на то, что в колонке (Мощность, Power Rating at 70°C) для некоторых типоразмеров указано несколько значений мощности. Дело в том, что производители выпускают разные серии SMD-резисторов. В одной серии мощность резисторов для типоразмера 1206 нормирована на уровне 0,5 Вт, а в другой 0,25 Вт.

Например, чип-резисторы серии CRM фирмы Bourns® рассчитаны на повышенную мощность: CRM0805 (0,25W), CRM1206 (0,5W), CRM2010 (1W). Используются такие в импульсных источниках питания в качестве токовых датчиков, токоограничительных резисторов, снабберов (демпфирующих резисторов).

Такое положение дел нужно учитывать, если вы собираетесь использовать резистор, мощность которого была определена исходя из размеров. При этом, нужно остановиться на наименьшем значении мощности, взятом из таблицы №1.

Если этим пренебречь, то может случится так, что вам попадётся резистор с меньшей мощностью, например, 0,25W вместо 0,5W, а это уже чревато его перегревом и выходом из строя при работе в реальной схеме.

Хотелось бы отметить, что сведения в таблице №1 в основном относятся к стандартным SMD-резисторам, то есть таким, которые широко и в большом количестве используются при производстве электроники.

Как правило, это чип резисторы на основе толстой плёнки (thick film chip resistors), так как они являются самыми дешёвыми, и, как следствие, самыми распространёнными. Примером могут служить серии стандартных толстоплёночных SMD резисторов D/CRCW e3 (Vishay®), ERJ (Panasonic) или RC (Yageo).

Не секрет, что существует огромное количество узкоспециализированных SMD-резисторов, которые имеют свои особенности.

К таким можно отнести резисторы, которые работают при повышенных температурах (до 230°C), в условии агрессивной среды (Antisulfur), миллиомные чип резисторы, SMD резисторы-перемычки.

Если такие резисторы и встречаются на печатных платах от потребительской электроники, то, как правило, их количество невелико, они применяются в определённых цепях электронных схем.

Их характеристики, в том числе и мощность рассеивания, может существенно отличатся от усреднённых значений, которые приведены в таблице №1 и являются типовыми для стандартных SMD-резисторов, количество которых в электронной схеме может быть просто огромным.

Типовые мощности тонкоплёночных резисторов (Thin film chip resistors) также соответствуют значениям из таблицы №1. Резисторы для некоторых областей применения, например, для автомобильной электроники (avtomotive grade), могут иметь мощность чуть выше той, что указана в таблице №1.

Как узнать мощность резисторных SMD-сборок?

Для резисторных SMD-сборок мощность в технической документации указывается на элемент (per element), а иногда ещё и на сборку вцелом (per package). Обычно, чип-сборка состоит из набора 2, 4, или 8 резисторов стандартного типоразмера. Например, набор типоразмера 0408 соответствует четырём SMD резисторам типоразмера 0402.

Так вот, типовая мощность одного резистора в такой сборке мало чем отличается от стандартной мощности отдельного SMD-резистора такого же типоразмера.

Так, для резисторных SMD-сборок 0202 (0201 × 2) мощность на элемент обычно составляет 0,03W (1/32W). Для тех, кто ещё не знает, сборка типоразмера 0202, – это два резистора 0201 в наборе.

Для сборок 0404 (0402 × 2), 0408 (0402 × 4) мощность на элемент обычно не превышает значения в 0,063W (1/16W).

Для сборок 0606 (0603 × 2), 0612 (0603 × 4), 0616 (0602 × 8) мощность на элемент составляет 0,063…0,125W.

Чип-сборка типоразмера 0612 на 4 резистора с выводами типа convex (т.е. выпуклыми). Мощность на элемент 0,1W.

На следующем фото резисторная чип-сборка 8×1206 с материнской платы старого, но очень крутого промышленного компьютера. На современных платах наборы такого типоразмера встречаются очень редко.

Ориентировочная мощность такой сборки 0,25W на элемент. Это если исходить из соображения, что типовая мощность для типоразмера 1206 составляет минимум 0,25W.

Хотя, стоит иметь ввиду, что в документации на стандартные современные сборки типоразмера 4×1206 минимальная мощность обычно 0,125W (1/8W) на элемент, что в 2 раза меньше. Так что, тут можно и поспорить, но я всё же остановлюсь на значении в 0,25W.

В англоязычной тех. документации мощность рассеивания называется Power Dissipation (иногда Rated dissipation), а обозначается как P70. Нижнему индексу (70) соответствует температура окружающей среды, при которой резистор способен долговременно выдерживать указанную мощность.

Каждая серия резисторов рассчитана на работу в определённом интервале температур. В большинстве своём, рабочая температура обычных чип-резисторов на основе толстой плёнки (thick film) лежит в интервале от -55°C до +155°C. Но, для микроминиатюрных типоразмеров от 0075 до 0201 максимальная температура, как правило, ограничена на уровне +125°C.

Как уже говорилось, в технической документации мощность SMD-резисторов указывается для температуры окружающей среды +70°C. Если резистор, эксплуатируется при температуре выше +70°C, то мощность, которая выделяется на нём в процессе работы должна быть снижена. Проще говоря, при повышенной температуре резистор просто не успевает охлаждаться.

На графике снижения мощности (Power Derating Curve) по шкале Rated Load (%) указан процент от номинальной мощности, которую способен выдержать SMD-резистор при соответствующей температуре окружающей среды (Ambient Temperature, °C).

Так, при температуре в +120°C мощность должна быть снижена до уровня 40% для изделий, рассчитанных на работу в температурном диапазоне -55°C…+155°C. Если у нас резистор на 1 ватт, то при данной температуре он способен долговременно выдерживать мощность в 0,4 ватта. Нетрудно заметить, что температура в 155°C соответствует нулевой мощности.

Приведённый график является типовым для стандартных толстоплёночных резисторов. Для специализированных SMD-резисторов график снижения мощности может существенно отличаться. Например, так он выглядит для резисторов серии PHT (Vishay).

Это высокостабильные тонкоплёночные чип резисторы для работы при повышенной температуре окружающей среды (от -55°C до +215°C). Даже к установке таких резисторов на печатную плату предъявляются определённые требования, чтобы эффективно отводить тепло от резистивного слоя.

Мощные SMD-резисторы

Существует мнение, что максимальная мощность рассеивания SMD резисторов ограничена их физическими размерами и параметрами резистивного слоя, например, сечением. И это так. Несмотря на это, среди резисторов для поверхностного монтажа есть и модели повышенной мощности.

К таким можно отнести чип резисторы серии PCAN (Vishay). Особенностью данных резисторов является подложка из нитрида алюминия (aluminum nitride, AlN), которая обладает повышенной теплопроводностью.

90% тепла от резистивного слоя SMD-резистора проходит через тело компонента, то есть через его подложку (substrate). Керамика на основе алюмонитрида (нитрида алюминия) обладает высокой теплопроводностью, что позволяет быстрее отводить тепло от резистивного слоя.

К тому же, керамика на основе алюмонитрида нетоксична.

Кроме этого нижняя часть контактных электродов данных чип-резисторов имеет увеличенную площадь, за счёт которой удаётся уменьшить тепловое сопротивление между проводящим слоем резистора и контактными площадками на печатной плате.

Такое сочетание технических решений позволяет преодолеть мощностные ограничения для стандартных типоразмеров смд-резисторов. Для сравнения, приведу значения мощности рассеивания для четырёх типоразмеров, доступных в данной серии.

Тонкоплёночные прецизионные чип резисторы повышенной мощности серии PCAN (Vishay)
Типоразмер, inch	Мощность, W
0603	0,5
0805	1
1206	2
2512	6

Как видим, для типоразмера 2512 мощность составляет 6 Вт. Стандартный SMD-резистор такого же типоразмера, как правило, имеет мощность не более 1 или 2 Вт.

Так же есть чип-резисторы с более скромными характеристиками, например, серии PHP (Vishay). В ней уже используется подложка из рядового, хотя, и высокочистого оксида алюминия (alumina, Al2O3), который широко используется в качестве материала для подложки в стандартных SMD-резисторах.

Из особенностей: увеличенная площадь нижних электродов Wraparound-типа. Допустимая мощность для типоразмера 2512 данной серии составляет 2,5 Вт. Это на 0,5…1,5 ватта больше, чем у стандартных резисторов аналогичного размера.

Работа чип-резисторов на таких мощностях возможна с одной оговоркой, – это соблюдение правил монтажа на печатную плату. Об этом прямо сообщается в технической документации на серию.

Какие бы технические ухищрения не использовались для увеличения мощностных характеристик SMD-резисторов, но тепло всё равно отводить куда-то надо. Именно поэтому, к таким резисторам предъявляются особые требования монтажа их на плату.

Основными способами отвода избытка тепла от резистивного слоя SMD-резистора являются соединительные контакты медных проводников, поверхность печатной платы и внешнее охлаждение.

В печатных платах под поверхностный монтаж элементов, избытки тепла от элементов отводятся в толщу платы и медные полигоны, которые служат своеобразным радиатором. В некоторых случаях может применятся принудительное внешнее охлаждение (например, вентиляторы).

Главная » Радиоэлектроника для начинающих » Текущая страница

Также Вам будет интересно узнать:

Источник: https://go-radio.ru/moshchnost-smd-rezistorov.html

Как определить мощность резистора

Здравствуйте, уважаемые читатели сайта sesaga.ru. Резистор является самым используемым радиокомпонентом, без которого не обходится ни одна электронная схема. Основными параметрами резистора являются электрическое сопротивление, мощность и допуск.

Если с сопротивлением и допуском все понятно, то определение мощности малогабаритных резисторов вызывает некоторые трудности, особенно на первых порах занятием радиолюбительством.

В статье о цветовой и цифровой маркировке резисторов я уже рассказывал о мощности резисторов, но судя по Вашим м, этот параметр был раскрыт не полностью.

В этой статье я постараюсь устранить этот пробел.

Итак.

Резисторы бывают разного устройства и конструкции, но в большинстве случаев они представляют собой небольшой цилиндр из фарфора или какого-нибудь другого изолятора, на который нанесен токопроводящий слой, обладающий определенным электрическим сопротивлением. В других конструкция на цилиндр наматывается требуемое количество витков тонкой проволоки из сплавов, обладающих большим сопротивлением.

Резисторы применяют согласно мощности, на которую он рассчитан, и которую может выдержать без риска быть испорченным при прохождении через него электрического тока.

Поэтому на схемах внутри прямоугольника прописывают условные обозначения, указывающие мощность резистора в ваттах (Вт): двойной косой чертой обозначают резистор мощностью 0,125 Вт; прямой чертой, расположенной вдоль значка резистора, обозначают мощность 0,5 Вт; римской цифрой обозначается мощность от 1 Вт и выше.

Как правило, резисторы разной мощности отличаются размерами и чем больше мощность резистора, тем размер его больше. На крупногабаритных резисторах величина мощности указывается на корпусе в виде цифрового значения, а вот малогабаритные резисторы приходится определять на «глаз».

Но все же определить мощность того или иного резистора не так уж и трудно, так как габаритные размеры соответствуют стандарту, которого стараются придерживаться все производители электронных компонентов. В Советском Союзе даже выпускались таблицы для определения мощности резисторов по их размерам: диаметру и длине.

На отечественных резисторах типа МЛТ и некоторых зарубежных мощностью 1Вт и выше величина мощности указывается на корпусе цифровым значением. На остальных импортных резисторах рядом с цифрой дополнительно ставят латинскую букву W.

Правда, встречаются некоторые зарубежные экземпляры, где после цифрового значения может стоять другая буква. Как правило, подобную маркировку ставит производитель, который сам изготавливает некоторые компоненты для своей аппаратуры, не придерживаясь стандартов.

Однако с размерами есть небольшой нюанс, который надо знать: габариты отечественных и импортных резисторов одинаковой мощности немного отличаются друг от друга — отечественные резисторы чуть больше своих зарубежных собратьев.

Это объясняется тем, что отечественные радиокомпоненты выпускаются с некоторым запасом по мощности, тогда как у зарубежных аналогов такого запаса нет. Поэтому при замене отечественных резисторов зарубежными, зарубежный аналог следует брать на порядок мощнее.

Есть еще один тип резисторов, выпускаемые как зарубежными, так и отечественными производителями, габариты которых не подходят под стандартные размеры. Как правило, это низкоомные высокоточные резисторы, имеющие допуск по номинальному сопротивлению от 1% и ниже. Такие резисторы применяются в измерительных приборах, медицинском, военном или высокоточном оборудовании.

Если с крупногабаритными резисторами все понятно, то малогабаритные резисторы мощностью 0,5 Вт и ниже приходится различать только исходя из их размеров. Но и в этом случае сложного ничего нет, так как на первое время достаточно в качестве образца иметь по одному резистору с мощностями от 0,125Вт до 0,5Вт, чтобы сравнивать их с искомыми резисторами.

А в дальнейшем, когда придет опыт, Вы сможете без труда определять мощность резисторов по их габаритам.

Ну и в довершении статьи картинка с резисторами отечественного и зарубежного производства в порядке возрастания их мощности. А чтобы легче было ориентироваться в габаритах, на каждой картинке предоставлена спичка, относительно которой можно судить о размерах того или иного резистора.

И еще надо сказать о замене: резистор мощностью 0,125Вт можно заменить резистором мощностью 0,125Вт и выше. Лишь бы позволял размер платы. А вот резистор мощностью 0,5Вт нельзя заменить резисторами 0,125Вт и 0,25Вт, так как их мощность меньше и в процессе работы они могут перегреться и выйти из строя.

• И по традиции видеоролик, где показывается еще один вариант определения мощности резисторов.
• Удачи!

Источник: https://sesaga.ru/kak-opredelit-moshhnost-rezistora.html

Как проверить резистор мультиметром

При работе с электрической схемой возникают ситуации, когда необходимо проверить сопротивление резистора.

Это может понадобиться при проверке исправности или подгонке его величины под требуемое значение, которое отличается от номинального.

Проверять сопротивление можно, не выпаивая резистор, или после его выпайки. В этой статье я расскажу, как правильно проверить резистор мультиметром.

Содержание статьи

Для того, чтобы узнать сопротивление резистора, нужно воспользоваться обычным мультиметром.

Принцип измерений основан на законе Ома, который гласит, что сила тока находится в прямой пропорциональной зависимости от напряжения и обратно пропорциональной от сопротивления.

Определение сопротивления происходит косвенным путем по формуле R = U/I. То есть, при известных напряжении и силе тока легко определить сопротивление.

Если ранее применялись стрелочные тестеры, то сегодня радиолюбители для проверки исправности резисторов чаще всего используют цифровые мультиметры с круговым переключателем, с помощью которого выставляется тип рабочего режима и диапазон измерений.

Цифровой тестер для проверки резисторов

Для измерения величины R переключатель выставляют в диапазон Ω. В комплекте к такому прибору идет один комплект щупов, имеющих разную расцветку. Принято красный щуп вставлять в отверстие com, а черный – VΩCX+.

Как проверить резистор не выпаивая: визуальная проверка

Процесс проверки резистора на работоспособность непосредственно на плате без полной выпайки является довольно трудоемким занятием, поэтому предварительно можно определить сгоревшую деталь визуально. Прежде всего осматривают корпус на предмет повреждений и сколов, надежности закрепления выводов.

О неисправностях свидетельствуют:

• Потемнение корпуса. Сгоревший резистор имеет потемневшую поверхность – полностью или частично в виде колечек. Слабое потемнение не свидетельствует о неисправности, а только о перегреве, который не привел к полному выходу детали из строя.
• Появление характерного запаха.
• Стирание маркировки.
• Наличие на плате сгоревших дорожек

Если условия позволяют, то неисправный резистор выпаивают, а на его место впаивают новый с таким же номиналом.

Внимание! Осмотр не гарантирует точного определения исправности, резистор может выглядеть как новый даже при оборванном контакте.

Подготовка мультиметра к проведению измерений: какие установить настройки

Перед измерениями прибор готовят к работе. Для этого его включают и концы щупов закорачивают между собой. Если на дисплее появляются нули, то прибор исправен и в цепи нет обрыва. На дисплее могут отражаться не нули, а доли Ома.

Подготовка прибора к проверке

При разомкнутых щупах на исправном мультиметре отображается цифра 1 и диапазон измерений. Кабельные шнуры подключают в соответствии с тем режимом, который вам необходим, – «Прозвонка» или «Измерение».

Как прозвонить резистор

Режим «Прозвонка» (имеется не во всех тестерах) применяется, чтобы убедиться, что в цепях, идущих через резистор или параллельных ему, отсутствует короткое замыкание. Для его установки регулятор поворачивают к значку диода. Если между точками установки щупов есть токопроводящая цепь, то через динамик генерируется звуковой сигнал.

Режим прозвонки

Этот режим применяют только для резисторов, номинал которых не превышает 70 Ом. Для деталей с большим номиналом его использовать не имеет смысла, поскольку сигнал настолько слаб, что его можно не услышать.

Как определить номинал резистора по маркировке

Для определения работоспособности желательно знать номинал. Как определить номинал резистора по цветовой маркировке, мы подробно рассказали в этой статье.

Немного дополним информацию о способах маркировки SMD резисторов. Из-за малого размера на них практически невозможно нанести традиционную цветовую маркировку, поэтому предусмотрена особая система идентификации. В обозначение входят: 3 или 4 цифры, 2 цифры и буква.

В первой системе первые две или три цифры характеризуют численное значение резистора, а последняя является показателем множителя, обозначающим степень, в которую возводят 10 для получения окончательного результата. Если сопротивление ниже 1 Ом, то для определения местонахождения запятой служит символ R. Например, сопротивление 0,05 Ом выглядит как 0R05.

Высокоточные (прецизионные) резисторы имеют очень малые размеры, поэтому нуждаются в компактной маркировке. Она состоит из трех цифр – первые две являются кодом, а третья – множителем.

Каждому коду соответствует трехзначное значение сопротивления, определяемое по таблице.

Такая маркировка выполняется в соответствии со стандартом EIA-96, разработанным для резисторов с допуском по сопротивлению не выше 1%.

Таблица кодов для прецизионных резисторов

Код	Значение	Код	Значение	Код	Значение	Код	Значение	Код	Значение	Код	Значение
01	100	17	147	33	215	49	316	65	464	81	681
02	102	18	150	34	221	50	324	66	475	82	698
03	105	19	154	35	226	51	332	67	487	83	715
04	107	20	158	36	232	52	340	68	499	84	732
05	110	21	162	37	237	53	348	69	511	85	750
06	113	22	165	38	243	54	357	70	523	86	768
07	115	23	169	39	249	55	365	71	536	87	787
08	118	24	174	40	255	56	374	72	549	88	806
09	121	25	178	41	261	57	383	73	562	89	825
10	124	26	182	42	267	58	392	74	576	90	845
11	127	27	187	43	274	59	402	75	590	91	866
12	130	28	191	44	280	60	412	76	604	92	887
13	133	29	196	45	287	61	422	77	619	93	909
14	137	30	200	46	294	62	432	78	634	94	931
15	140	31	205	47	301	63	443	79	649	95	953
16	143	32	210	48	309	64	453	80	665	96	976

Проверка сопротивления постоянного резистора

После подготовки прибора к работе приступают к измерениям. Для этого выпаивают одну из ножек сопротивления. Один из щупов подсоединяется к запаянной ножке, второй – к свободной. Если резистор исправен, то на дисплее появится показание, соответствующее номинальному значению в пределах допуска.

Как проверяют сопротивление резистора

При обрыве цепи на экране горит «1».

Внимание! Регулятором перед измерением выставляют переключатель на ближайшее к номиналу значение большего достоинства. Если регулятором была выполнена настройка на значение, меньшее, чем номинал детали, то на дисплее результаты измерений отображаться не будут, поскольку срабатывает внутренняя блокировка тестера.

Если с одной стороны от резистора в схеме впаян конденсатор, то ножку с этой стороны условно можно считать свободно висящей. И в этом случае можно провести измерения, не выпаивая резистор.

СМД-резисторы – компоненты поверхностного монтажа, измерение сопротивления которых осложняется их малыми размерами. Их обычно проверяют, как и все постоянные резисторы, выпайкой одной ножки.

Проверка переменного резистора

Проверка без выпайки из схемы переменных резисторов, имеющих как минимум три ножки, более сложная, по сравнению с проверкой постоянного резистора.

Переменный резистор

Наиболее легким вариантом является положение резистора в самом начале схемы, поскольку одна из крайних «ножек» подключается через емкость. Поэтому по постоянному току приравнивается к свободно висящей. Такой способ измерения позволяет определить общее сопротивление, которое присутствует между крайними контактами.

Провести точные измерения сопротивления резистора позволяет его выпайка из схемы. Аналогично выпаянной, проверяется и новая деталь. Этапы измерений:

• Мультиметр включают в режим измерения.
• Щупальца подсоединяют к крайним ножкам. Это позволяет определить общее сопротивление. Значение на дисплее не должно отличаться от номинала более чем на положенный допуск. Величина допуска характеризуется последним кольцом в цветовой маркировке. Она выражается в процентах от номинального значения.
• Если общее сопротивление соответствует номинальному, то измеряют сопротивление между средней и крайней ножками. После подсоединения «крокодилов» вращают ручку переменного резистора в одном из направлений. Сопротивление либо плавно возрастает до ранее установленного общего значения, либо снижается до нулевого значения. При самой частой неисправности (пропадании контакта токосъемника) прибор показывает бесконечность.

Видео: как проверить резистор мультиметром

Другие материалы по теме

Анатолий Мельник

Специалист в области радиоэлектроники и электронных компонентов. Консультант по подбору деталей в компании РадиоЭлемент.

Источник: https://www.RadioElementy.ru/articles/kak-proverit-rezistor-multimetrom/

Все о резисторах. Определение, типы резисторов и их номинал

КатегорииСправочная Статьи для новичков

Привет. Сегодня статья будет посвящена такому радиоэлементу как резистор, или как было принято называть его ранее сопротивление.

Основной задачей резисторов является создание сопротивления электрическому току. Для более наглядной визуализации, давайте представим электрический ток, как воду, которая течет по трубе.

В конце этой трубы установлен кран, который полностью откручен, и он просто пропускает через себя водный поток.

Стоит нам немного начать закрывать кран, как мы сразу увидим, что поток стает слабее вплоть до того момента, когда течь воды полностью остановится.

По такому принципу и работают резисторы, только вместо трубы у нас электрический проводник, вместо воды ток, а вместо крана наш резистор. Чем больше номинал резистора, тем больше он делает сопротивление электрическому току. Сопротивление резистора измеряется такой единицей измерения как Ом.

Так как в схемах могут использоваться очень большие резисторы, номинал которых может составлять порядка 1000 -1000000 Ом, то для облегчения вычислений используют производные единицы, такие как кОм, мОм и гОм.

Для большего понимания этих единиц измерения, привожу следующую расшифровку:

• 1кОм = 1000 Ом;
• 1 мОм = 1000 кОм;
• 1гОм = 1000 мОм;

На практике все очень просто. Если нам попался резистор с надписью 1,8 кОм, то проведя не сложные вычисления, увидим, что номинал в Омах будет соответствовать 1800 Ом.

По принципу работы, резисторы делятся на постоянные и переменные.

Из самих названий можно догадаться, что постоянные резисторы в процессе работы никогда не меняют своего номинала. Переменные же резисторы, могут менять свой номинал в процессе работы, и используются для выполнения какой-то настройки. Примером для использования переменных резисторов может быть ручки управления громкостью, тембром на магнитофонах.

Постоянные резисторы

Поговорим более детально о постоянных резисторах. На практике, обозначение номинала резисторов наносится на корпусе. Это может быть буквенно–цифровой код или обозначение цветными полосками (цветовая маркировка резисторов). Как узнать номинал резистора по цветовой маркировке, можем узнать из этой статьи.

Что касается буквенно-цифрового обозначения, то его принято обозначать такими способами:

1. Буква R – означает, что номинал резистора будет измеряться в Омах. Очень важным является позиция этой буквы. Если на резисторе надпить типа 12R то номинал резистора будет 12Ом. Если же буква будет в начале R12, то сопротивление будет 0,12Ом. Также возможно обозначение типа 12R1, что будет означать 12,1 Ом.
2. Буква K – означает, что номинал резистора будет измеряться в кОмах. Действуют теже правила что и для предыдущего примера. 12K = 12кОм, K12 = 0,12 кОм и 12К1 = 12,1кОм.
3. Буква М– означает, что номинал резистора будет измеряться в мОмах. 12М = 12мОм, М12 = 0,12 мОм и 12М1 = 12,1мОм.

Так же на корпусе резистора обозначают такую величину как отклонение от номинала.

При массовом производстве сопротивлений, в виду не совершенства технологий производства, сопротивления могут иметь некоторые отклонения от заявленного номинала.

Это возможное отклонение обозначается на корпусе резистора в виде ±0,7% или ±5%. Цифры могут быть разные, в зависимости от метода производства.

Мощность резисторов

В процессе работы, при больших нагрузках резистор выделяет тепло. Если в схему, где идут большие нагрузки поставить резистор маленькой мощности, то он быстро разогреется и сгорит. Чем больше по размерам резистор, тем больше его мощность. На рисунке ниже видно обозначение мощности резисторов на схемах.

Обозначение мощности резисторов на схеме

Резисторы разной мощности

Переменные резисторы

Как говорилось ранее, переменные резисторы используются для плавной регулировки силы тока и напряжения в пределах номинала резистора. Переменные резисторы бывают построечные и регулировочные.

С помощью регулировочных резисторов проводятся постоянные пользовательские регулировки аппаратуры (регулировка звука, яркости тембра и др.), а построечные используются для настройки аппаратуры в режиме наладки во время сборки техники.

Для регулировочных резисторов приемлемо наличия удобной ручки, построечные же обычно регулируются отверткой.

Переменный резистор

Подстроечные резисторы

Если на переменном резисторе написано что он имеет номинал 10кОм, то это означает, что он производит регулировку в пределах от до 10 кОм. В среднем положении ручки его номинал будет приблизительно около 5 кОм, в крайнем или 0 или 10 кОм.

Если Вам необходимо рассчитать номинал своего резистора, то советуем Вам воспользоватся нашим онлайн калькулятором цветовой маркировки резисторов.

Весь инструмент и расходники, которые я использую в ремонтах находится здесь.
Если у Вас возникли вопросы по ремонту телевизионной техники, вы можете задать их на нашем новом форуме . (4

Источник: https://my-chip.info/vse-o-rezistorax-opredelenie-tipy-rezistorov-i-ix-nominal/

Резисторы в цепях переменного тока

Физика > Резисторы в цепях переменного тока

 

Изучите напряжение и силу цепи переменного тока, в которую включен резистор: формула закона Ома для определения тока и напряжения цепи, схема постоянного тока.

В цепи переменного тока с резистором и источником питания используют закон Ома (V = IR).

Задача обучения

• Используйте закон Ома для вычисления тока и напряжения.

Основные пункты

• В переменном напряжении (V = V₀sin(2πνt)) ток задается как: I =V₀/R · sin(2πνt). Это выражение происходит из закона Ома: V = IR.
• Чаще всего вместо источника постоянного тока используют переменное напряжение.
• Рассеиваемая мощность:  P = V²₀/R · sin (2πνt). Так что средняя мощность переменного тока: V²₀/2R

Термин

• Закон Ома: в электрической цепи с сопротивлениями постоянный ток выступает прямо пропорциональным напряжению.

Постоянный ток представляет собою перемещение электрического заряда в едином направлении. Это обычное состояние цепи со стабильным напряжением. Но чаще всего используют переменный ток, который периодически меняет направление. Если источник меняется с периодами (особенно синусоидально), то схему именуют цепью переменного тока. Конечно, частоты переменного тока, которые используют в домах и предприятиях, отличаются по всему миру.

(а) – Постоянные ток и напряжение остаются стабильными во времени. (b) – График напряжения и тока, основывающихся на времени, для мощности переменного тока в 60Гц. Они синусоидальные и расположены в фазе для простой схемы сопротивления. Частоты и пиковые напряжения источников сильно отличаются

Мы уже рассматривали закон Ома:

I = V/R (I – ток, V – напряжение, R – сопротивление цепи). Его можно использовать для цепей переменного и постоянного тока. Поэтому при переменном напряжении, заданном:

V = V₀sin (2πνt), где V₀ – пиковое напряжение, а ν – частота в герцах, ток в цепи определяется как:

I = V₀/R ⋅ sin (2πνt).

В этом примере мы располагаем резистором и источником напряжения в цепи, где ток и напряжение считаются разными. Ток в резисторе перемещается назад/вперед без разности фаз, как и напряжение.

Давайте взглянем на идеальный резистор, светлеющий и тускнеющий 120 раз в секунду. Колебание светового потока говорит о колебании мощности. Так как P = IV, используем указанные выше формулы, чтобы рассмотреть зависимость мощности от времени:

P = V²₀/R ⋅ sin (2πνt).

Чтобы отыскать среднюю мощность, потребляемую схемой, необходимо взять среднее время от функции:

Выходит, что:

---

Номинальная мощность резистора

и мощность резисторов

Когда электрический ток проходит через резистор из-за наличия на нем напряжения, электрическая энергия теряется резистором в виде тепла, и чем больше этот ток, тем горячее становится резистор. Это известно как номинальная мощность резистора .

Резисторы

оцениваются по значению их сопротивления и электрической мощности, выраженной в ваттах (Вт), которую они могут безопасно рассеивать, в основном в зависимости от их размера.Каждый резистор имеет максимальную номинальную мощность, которая определяется его физическим размером, как правило, чем больше площадь его поверхности, тем большую мощность он может безопасно рассеивать в окружающем воздухе или в радиаторе.

Резистор может использоваться при любой комбинации напряжения (в пределах разумного) и тока при условии, что его «номинальная рассеиваемая мощность» не превышается с номинальной мощностью резистора, указывающей, сколько мощности резистор может преобразовать в тепло или поглотить без какого-либо повреждения. сам. Номинальная мощность резистора иногда называется номинальной мощностью резистора и определяется как — количество тепла, которое резистивный элемент может рассеивать в течение неопределенного периода времени без ухудшения его характеристик.

Номинальная мощность резисторов может сильно варьироваться от менее одной десятой ватта до многих сотен ватт в зависимости от их размера, конструкции и окружающей рабочей температуры. У большинства резисторов максимальная номинальная резистивная мощность указана для температуры окружающей среды от +70 ^до C или ниже.

Электрическая мощность — это скорость использования или потребления энергии (преобразование в тепло) во времени. Стандартная единица измерения электрической мощности — Вт, , обозначение Вт, , номинальная мощность резисторов также указывается в ваттах.Как и в случае с другими электрическими величинами, к слову «ватт» добавляются префиксы, когда они обозначают очень большую или очень маленькую мощность резистора. Вот некоторые из наиболее распространенных из них:

Электроагрегаты

Установка	Символ	Значение	Аббревиатура
милливатт	мВт	1/1000 ватта	10 -3 Вт
киловатт	кВт	1000 Вт	10 3 Вт
мегаватт	МВт	1000000 Вт	10 6 Вт

Мощность резистора (P)

Мы знаем из закона Ома, что когда ток проходит через сопротивление, на нем падает напряжение, производя продукт, связанный с мощностью.

Другими словами, если сопротивление подвергается действию напряжения или если оно проводит ток, то оно всегда будет потреблять электроэнергию, и мы можем наложить эти три величины мощности, напряжения и тока в треугольник, называемый Треугольник мощности с мощностью, которая будет рассеиваться в виде тепла в резисторе вверху, с потребляемым током и напряжением на нем внизу, как показано.

Треугольник мощности резистора

Приведенный выше треугольник мощности отлично подходит для расчета мощности, рассеиваемой в резисторе, если мы знаем значения напряжения на нем и тока, протекающего через него.Но мы также можем рассчитать мощность, рассеиваемую сопротивлением, используя закон Ома.

Закон

Ом позволяет рассчитать рассеиваемую мощность с учетом значения сопротивления резистора. Используя закон Ома, можно получить два альтернативных варианта приведенного выше выражения для мощности резистора, если нам известны только два значения: напряжение, ток или сопротивление:

[P = V x I] Мощность = Вольт x Ампер

[P = I ² x R] Мощность = ток ² x Ом

[P = V ² ÷ R] Мощность = Вольт ² ÷ Ом

Рассеиваемая электрическая мощность любого резистора в цепи постоянного тока может быть рассчитана по одной из следующих трех стандартных формул:

• Где:
• В — напряжение на резисторе в вольтах
• Я находится в токе, протекающем через резистор, в Амперах
• R — сопротивление резистора в Ом (Ом)

Поскольку номинальная рассеиваемая мощность резисторов связана с их физическими размерами, 1/4 (0.Резистор 250) Вт физически меньше, чем резистор 1 Вт, и резисторы с одинаковым омическим сопротивлением также доступны с разной мощностью или номинальной мощностью. Угольные резисторы, например, обычно производятся с номинальной мощностью 1/8 (0,125) Вт, 1/4 (0,250) Вт, 1/2 (0,5) Вт, 1 Вт и 2 Вт.

Вообще говоря, чем больше их физический размер, тем выше его номинальная мощность. Однако всегда лучше выбирать резистор определенного размера, который способен рассеивать мощность, в два или более раз превышающую расчетную.Когда требуются резисторы с более высокой номинальной мощностью, обычно используются резисторы с проволочной обмоткой для рассеивания чрезмерного тепла.

Тип	Номинальная мощность	Устойчивость
Металлическая пленка	Очень низкий, менее 3 Вт	Высокий 1%
Углерод	Low менее 5 Вт	Низкая 20%
Проволочная	Высокая до 500 Вт	Высокий 1%

Силовые резисторы

Силовые резисторы с проволочной обмоткой бывают самых разных конструкций и типов, от стандартных меньших типов в алюминиевом корпусе мощностью 25 Вт, установленных на радиаторе, как мы видели ранее, до более крупных трубчатых керамических или фарфоровых резисторов мощностью 1000 Вт, используемых для нагревательных элементов.

Типичный силовой резистор

Сопротивление резисторов с проволочной обмоткой очень низкое (низкое омическое сопротивление) по сравнению с резисторами с углеродной или металлической пленкой. Диапазон сопротивления силового резистора составляет от менее 1 Ом (R005) до всего 100 кОм, поскольку для более высоких значений сопротивления потребуется тонкая проволока, которая легко выйдет из строя.

Низкоомные резисторы малой мощности обычно используются для датчиков тока, где, согласно закону Ома, ток, протекающий через сопротивление, вызывает падение напряжения на нем.

Это напряжение можно измерить, чтобы определить значение тока, протекающего в цепи. Этот тип резистора используется в тестовом измерительном оборудовании и регулируемых источниках питания.

Мощные резисторы с проволочной обмоткой большего размера изготовлены из коррозионно-стойкой проволоки, намотанной на фарфоровый или керамический каркас сердечника, и обычно используются для рассеивания высоких пусковых токов, например, возникающих в цепях управления двигателем, электромагнита или управления лифтом / краном, а также в цепях торможения двигателя.

Обычно эти типы резисторов имеют стандартную номинальную мощность до 500 Вт и обычно соединяются вместе, образуя так называемые «блоки сопротивлений».

Еще одной полезной особенностью силовых резисторов с проволочной обмоткой является использование нагревательных элементов, подобных тем, которые используются для электрических каминов, тостеров, утюгов и т.д. Используемая проволока обычно изготавливается из никель-хрома (нихрома), допускает температуру до 1200 ^o C.

Все резисторы, углеродистые, металлопленочные или проволочные, подчиняются закону Ома при расчете максимальной мощности (мощности).Также стоит отметить, что при параллельном подключении двух резисторов их общая номинальная мощность увеличивается. Если оба резистора имеют одинаковое номинальное значение и одинаковую мощность, то общая номинальная мощность удваивается.

Пример номинальной мощности резистора №1

Какова максимальная номинальная мощность в ваттах постоянного резистора, напряжение на выводах которого составляет 12 вольт, а через него протекает ток 50 миллиампер.

Учитывая, что нам известны указанные выше значения напряжения и тока, мы можем подставить эти значения в следующее уравнение: P = V * I.

Пример номинальной мощности резистора №2

Рассчитайте максимальный безопасный ток, который может пройти через резистор 1,8 кОм с номинальной мощностью 0,5 Вт.

Опять же, поскольку мы знаем номинальную мощность резистора и его сопротивление, теперь мы можем подставить эти значения в стандартное уравнение мощности: P = I ² R.

Все резисторы имеют максимальную рассеиваемую мощность , которая представляет собой максимальное количество мощности, которое они могут безопасно рассеивать без ущерба для себя.Резисторы, мощность которых превышает их максимальную номинальную мощность, как правило, довольно быстро сгорают в дыму и повреждают цепь, к которой они подключены. Если резистор должен использоваться с номинальной мощностью, близкой к максимальной, тогда потребуется какой-либо радиатор или охлаждение.

Номинальная мощность резистора — важный параметр, который следует учитывать при выборе резистора для конкретного применения. Задача резистора — противостоять току, протекающему по цепи, и он делает это, рассеивая нежелательную мощность в виде тепла.Выбор резистора с малой мощностью, когда ожидается большая рассеиваемая мощность, приведет к перегреву резистора, разрушив как резистор, так и цепь.

До сих пор мы рассматривали резисторы, подключенные к постоянному источнику постоянного тока, но в следующем руководстве о резисторах мы рассмотрим поведение резисторов, подключенных к источнику синусоидального переменного тока, и покажем, что напряжение, ток и, следовательно, все мощности, потребляемые резистором, используемым в цепи переменного тока, синфазны друг с другом.

Основы: Рассеивание мощности и электронные компоненты

Постоянно существующей проблемой в проектировании электронных схем является выбор подходящих компонентов, которые не только выполняют свои намеченные задачи, но и выживут в предсказуемых условиях эксплуатации.Большая часть этого процесса — убедиться, что ваши компоненты будут оставаться в пределах своих безопасных рабочих ограничений с точки зрения тока, напряжения и мощности. Из этих трех «силовая» часть часто является самой сложной (как для новичков, так и для экспертов), потому что безопасная рабочая зона может очень сильно зависеть от особенностей ситуации.

Далее мы познакомим вас с некоторыми основными концепциями рассеяния мощности в электронных компонентах, чтобы понять, как выбирать компоненты для простых схем с учетом ограничений мощности.

— НАЧАЛО ПРОСТОГО —

Давайте начнем с одной из самых простых схем, которую только можно вообразить: батарея, подключенная к единственному резистору:

Здесь у нас одна батарея на 9 В и одна батарея на 100? (100 Ом) резистор, соединенный проводами, чтобы сформировать полную цепь.

Достаточно просто, правда? Но теперь вопрос: если вы действительно хотите построить эту схему, насколько «большой» из 100? резистор нужно ли использовать, чтобы убедиться, что он не перегревается? То есть, можем ли мы просто использовать «обычный» резистор ¼ W, как показано ниже, или нам нужно увеличить?

Чтобы это выяснить, нам необходимо рассчитать мощность, рассеиваемую резистором.
Вот общее правило расчета рассеиваемой мощности:

Правило питания: P = I × V
Если ток I протекает через данный элемент в вашей цепи, теряя при этом напряжение V , то мощность, рассеиваемая этой цепью Элемент является произведением этого тока и напряжения: P = I × V .

В сторону :
Каким образом ток, умноженный на напряжение, может дать нам измерение «мощности»?

Чтобы понять это, нам нужно помнить, что физически представляют ток и напряжение.

Электрический ток — это скорость протекания электрического заряда через цепь, обычно выражаемая в амперах, где 1 ампер = 1 кулон в секунду. (Кулон — это единица измерения электрического заряда в системе СИ.)

Напряжение или, более формально, электрический потенциал — это потенциальная энергия на единицу электрического заряда через рассматриваемый элемент схемы. В большинстве случаев вы можете думать об этом как о количестве энергии, которое «расходуется» в элементе на единицу проходящего заряда.Электрический потенциал обычно измеряется в вольтах, где 1 вольт = 1 джоуль на кулон. (Джоуль — единица энергии в системе СИ.)

Итак, если мы возьмем ток, умноженный на напряжение, это даст нам количество энергии, которое «израсходовано» в элементе на единицу заряда, умноженное на количества этих единиц заряда, проходящих через элемент в секунду. :

1 ампер × 1 вольт =
1 (кулон / секунда) × 1 (джоуль / кулон) =
1 джоуль / секунда

Результирующая величина выражается в единицах один джоуль в секунду: скорость потока энергии, более известная как мощность.Единица измерения мощности в системе СИ — ватт, где 1 ватт = 1 джоуль в секунду.

Итак, у нас есть

1 ампер × 1 вольт = 1 ватт

Снова на нашу трассу! Чтобы использовать правило мощности ( P = I × V ), нам нужно знать как ток через резистор, так и напряжение на резисторе.

Во-первых, мы используем закон Ома ( В = I × R ), чтобы найти ток через резистор.
• Напряжение на резисторе В = 9 В.
• Сопротивление резистора R = 100 Ом.

Следовательно, ток через резистор равен:

I = В / R = 9 В / 100? = 90 мА

Затем мы можем использовать правило мощности ( P = I × V ), чтобы найти мощность, рассеиваемую резистором.
• Ток через резистор I = 90 мА.
• Напряжение на резисторе В = 9 В.

Следовательно, мощность, рассеиваемая на резисторе, составляет:

P = I × В = 90 мА × 9 В = 0,81 Вт

Так вы можете использовать резистор на 1/4 Вт?

Нет, потому что он, скорее всего, выйдет из строя из-за перегрева.
100? резистор в этой схеме должен быть рассчитан не менее чем на 0,81 Вт. Обычно выбирается следующий больший доступный размер, в данном случае 1 Вт.

Резистор мощностью 1 Вт обычно поставляется в гораздо более крупном физическом корпусе, как показано здесь:

(1 Вт, резистор 51 Ом, для сравнения размеров.)

Поскольку резистор на 1 Вт физически намного больше, он должен быть в состоянии справиться с рассеиванием большей мощности за счет большей площади поверхности и более широких выводов. (Он все еще может сильно нагреваться на ощупь, но не должен нагреваться настолько, чтобы выйти из строя.)

Вот альтернативное расположение, которое работает с четырьмя 25? резисторы в серии (а в сумме все равно 100?).В этом случае ток через каждый резистор по-прежнему составляет 90 мА. Но поскольку на каждом резисторе имеется только четверть напряжения, на каждом резисторе рассеивается только четверть меньшей мощности. Для такой схемы достаточно, чтобы четыре резистора были рассчитаны на 1/4 Вт.

В сторону: прорабатываем этот пример.

Поскольку четыре резистора включены последовательно, мы можем сложить их значения, чтобы получить их общее сопротивление, равное 100 Ом. Использование закона Ома с этим общим сопротивлением снова дает нам ток 90 мА.И снова, поскольку резисторы включены последовательно, одинаковый ток (90 мА) должен протекать через каждый обратно к батарее. Напряжение через каждые 25? резистор тогда В = I × R , или 90 мА × 25? = 2,25 В. (Чтобы еще раз убедиться, что это разумно, обратите внимание, что напряжения на четырех резисторах в сумме составляют 4 × 2,25 В = 9 В.)

Мощность на каждого человека 25? резистор P = I × В = 90 мА × 2,25 В? 0,20 Вт, безопасный уровень для использования с резистором 1/4 Вт.Интуитивно понятно, что если разделить 100? резистор на четыре равные части, каждая из которых должна рассеивать четверть общей мощности.

— ЗА РЕЗИСТОРАМИ —

Для нашего следующего примера давайте рассмотрим следующую ситуацию: предположим, что у вас есть схема, которая принимает входной сигнал от источника питания 9 В и имеет встроенный линейный регулятор для понижения напряжения до 5 В, где все работает. Ваша нагрузка на конце 5 В может достигать 1 А.

Как выглядит мощность в этой ситуации?

Регулятор, по сути, действует как большой переменный резистор, который регулирует свое сопротивление по мере необходимости для поддержания постоянного выходного напряжения 5 В. Когда выходная нагрузка составляет 1 А, выходная мощность, обеспечиваемая регулятором, составляет 5 В × 1 А = 5 Вт, а мощность, потребляемая в цепи источником питания 9 В, составляет 9 Вт. Напряжение, падающее на стабилизаторе. составляет 4 В, а при 1 А, это означает, что 4 Вт рассеивается линейным регулятором — также разница между входной и выходной мощностью.

В каждой части этой схемы соотношение мощности задается следующим образом: P = I × V . Две части — регулятор и нагрузка — это места, где рассеивается мощность. А в части цепи, подключенной к источнику питания, P = I × V описывает подачу мощности в систему — напряжение увеличивается на по мере прохождения тока по источнику питания.

Кроме того, стоит отметить, что мы, , не сказали, , какая нагрузка тянет этот 1 А.Энергия потребляется, но это не обязательно означает, что она преобразуется в (просто) тепловую энергию — например, это может быть питание двигателя или набора зарядных устройств для аккумуляторов.

Кроме того:
Хотя такая установка линейного регулятора напряжения, как эта, представляет собой очень распространенную установку для электроники, стоит отметить, что это также невероятно неэффективная схема : 4/9 входной мощности просто сгорает. как тепло, даже при работе на более низких токах.

— КОГДА НЕТ ПРОСТОЙ СПЕЦИФИКАЦИИ «МОЩНОСТЬ» —

Далее, немного более сложная часть: убедиться, что ваш регулятор может справиться с мощностью. В то время как на резисторах четко указана их мощность, на линейных регуляторах это не всегда. В нашем примере с регулятором выше предположим, что мы используем регулятор L7805ABV от ST (техническое описание здесь).

(Фото: типичный корпус TO-220, тип, который обычно используется для линейных регуляторов средней мощности)

L7805ABV — линейный стабилизатор 5 В в корпусе TO-220 (аналогичный показанному выше), рассчитанный на 1.Выходной ток 5 А и входное напряжение до 35 В.

Наивно, вы можете предположить, что вы можете подключить это прямо к входу 35 В и рассчитывать на выход 1,5 А, что означает, что регулятор будет излучать мощность 30 В * 1,5 А = 45 Вт. Но это крошечный пластиковый пакет; на самом деле он не может справиться с такой большой мощностью. Если вы посмотрите в таблицу данных в разделе «Абсолютные максимальные характеристики», чтобы попытаться определить, с какой мощностью он может справиться, все, что там написано, является «внутренне ограниченным», что само по себе далеко не ясно.

Оказывается, существует фактическая номинальная мощность, но обычно она несколько «спрятана» в таблице данных. Вы можете понять это, посмотрев на пару связанных спецификаций:

• T _OP , Диапазон рабочих температур перехода: от -40 до 125 ° C

• R _thJA , Термическое сопротивление переход-окружающая среда: 50 ° C / Вт

• R _thJC , Термическое сопротивление переходной коробки: 5 ° C / Вт

Рабочий диапазон температур перехода, T _OP , определяет, насколько горячим может быть «переход» — активная часть интегральной схемы регулятора, прежде чем он перейдет в режим теплового отключения.(Тепловое отключение — это внутренний предел, который делает мощность регулятора «внутренне ограниченной».) Для нас это максимум 125 ° C.

Тепловое сопротивление переход-окружающая среда R _thJA (часто обозначается как? _JA ), сообщает нам, насколько нагревается переход, когда (1) регулятор рассеивает заданное количество мощности и (2) регулятор находится внутри на открытом воздухе при заданной температуре окружающей среды. Предположим, нам нужно спроектировать наш регулятор для работы только в скромных коммерческих условиях, температура которых не превышает 60 ° C.Если нам нужно поддерживать температуру перехода ниже 125 ° C, то максимальное повышение температуры, которое мы можем допустить, составляет 65 ° C. Если у нас есть R _thJA 50 ° C / Вт, то максимальная рассеиваемая мощность, которую мы можем допустить, составляет 65/50 = 1,3 Вт, если мы хотим предотвратить переход регулятора в состояние теплового отключения. Это значительно ниже 4 Вт, которые можно было бы ожидать при токе нагрузки 1 А. Фактически, мы можем выдержать только 1,3 Вт / 4 В = 325 мА среднего выходного тока, не отправляя регулятор в состояние теплового отключения.

Это, однако, относится к случаю, когда ТО-220 излучает в окружающий воздух — почти наихудшая ситуация. Если мы сможем добавить радиатор или иным образом охладить регулятор, мы сможем добиться большего.

Противоположный конец спектра представлен другой термической спецификацией: корпус с термическим сопротивлением, R _thJC . Это указывает, какую разницу температур можно ожидать между переходом и внешней стороной корпуса TO-220: всего 5 ° C / Вт. Это соответствующий номер , если вы можете быстро отвести тепло от корпуса, например, если у вас есть очень хороший радиатор, подключенный к внешней стороне корпуса TO-220.С большим радиатором и идеальным соединением с этим радиатором при мощности 4 Вт температура перехода повысится всего на 20 ° C по сравнению с температурой вашего радиатора. Это представляет собой абсолютный минимум нагрева, который можно ожидать в идеальных условиях.

В зависимости от технических требований вы можете начать с этого момента, чтобы построить полный бюджет мощности, чтобы учесть теплопроводность каждого элемента вашей системы, от самого регулятора до термоинтерфейса между ним и радиатором, к тепловой связи радиатора с окружающим воздухом.Затем вы можете проверить соединения и относительную температуру каждого компонента с помощью бесконтактного инфракрасного термометра с точечным считыванием. Но часто бывает лучше переоценить ситуацию и посмотреть, есть ли лучший способ сделать это.

В данной ситуации можно подумать о переходе на стабилизатор для поверхностного монтажа, который обеспечивает лучшую управляемую мощность (за счет использования печатной платы в качестве радиатора), или, возможно, стоит подумать о добавлении силового резистора (или стабилитрона) до Регулятор понижает большую часть напряжения за пределами блока регулятора , уменьшая нагрузку на него.Или, что еще лучше, посмотрите, есть ли способ построить вашу схему без каскада линейного регулятора с потерями.

— ПОСЛЕ СЛОВА —

Мы рассмотрели основы понимания рассеяния мощности в нескольких простых схемах постоянного тока.

Принципы, которые мы рассмотрели, являются довольно общими, и их можно использовать для понимания энергопотребления в большинстве типов пассивных элементов и даже в большинстве типов интегральных схем. Однако существуют реальные ограничения, и можно потратить всю жизнь на изучение нюансов энергопотребления, особенно при более низких токах или высоких частотах, когда малые потери, которыми мы пренебрегли, становятся важными.

В цепях переменного тока многие вещи ведут себя по-разному, но правило мощности все еще сохраняется в большинстве случаев: P (t) = I (t) × В (t) для изменяющихся во времени тока и напряжения. И не все регуляторы работают с потерями: импульсные источники питания могут преобразовывать (например) 9 В постоянного тока в 5 В постоянного тока с КПД 90% или выше — это означает, что при хорошем дизайне может потребоваться всего около 0,6 А при 9 В для производят 5 В при 1 А. Но это уже отдельная история.

Номинальная мощность резисторов и мощность

Номинальная мощность резистора может быть выражена как максимальная мощность, которую резистор может выдержать.Номинальная мощность резистора — это спецификация для резистора, отличного от сопротивления

Ом. Если резистор имеет номинальную мощность 1 Вт, то мы не должны подавать на резистор более 1 Вт.

Когда электрический ток проходит через резистор из-за наличия на нем разности потенциалов, электрическая энергия теряется в виде тепловой энергии резистором. Если ток, протекающий через резистор, меньше, выделяемое тепло будет незначительным, а если приложить больший ток, количество тепла будет больше.

Таким образом, иногда номинальная мощность резистора также может быть указана как количество теплового элемента, которое может рассеиваться в течение неопределенного времени. Если мощность не превышает мощность резистора, значит, характеристики резистора не ухудшаются.

Но если мощность, подаваемая на резистор, превышает его максимальную номинальную мощность, он расплавит резистор и воспламенится дымом и, таким образом, повредит цепь. У большинства резисторов максимальная номинальная резистивная мощность указана для температуры окружающей среды 70 градусов Цельсия.

Единицы номинальной мощности

Номинальная мощность резистора рассчитывается в ваттах. Количество электроэнергии в ваттах обозначается заглавной буквой «W». Большинство резисторов имеют номинальную мощность в ваттах. Но иногда мы сталкиваемся с номинальной мощностью, такой как мВт, кВт или МВт.

мВт — это сокращение от Milli Watt. 1 мВт = 1/1000 Вт.

кВт — это сокращение от киловатта. 1кВт = 1000 Вт.

МВт — это аббревиатура от Mega Watt. 1 МВт = 1000000 Вт.

Расчет номинальной мощности

Формула номинальной мощности резистора можно рассчитать с помощью простого уравнения, которое включает напряжение и ток, приложенные к резистору.

P = V × I

Мощность — это произведение напряжения и тока, приложенного к резистору.

Если ток, приложенный к резистору, составляет 1 А, а подаваемое напряжение составляет 12 В, и резистор работает нормально, тогда мощность через резистор будет

.

P = 12 × 1 = 12 Вт

Таким образом, этот резистор будет нормально работать без ухудшения характеристик при 12 Вт. Однако максимальная мощность, то есть номинальная мощность, может составлять 15 Вт, 16 Вт или что-либо выше 12 Вт.

Теперь, пойдя дальше, нам понадобится закон Ома, который равен

.

В = I × R

Итак, мы можем записать формулу мощности как

P = V × I

P = I × R × I

P = I

² × R

Если мы знаем значение сопротивления и ток, протекающий через него, мы можем легко найти мощность.

Если значение сопротивления резистора 100 Ом и приложенный ток 0,5 А, то мощность будет

P = 0,25 × 100

P = 25 Вт

Таким образом, мощность через резистор будет 25 Вт.

Но что, если мы не знаем величину протекающего тока, а знаем подаваемое напряжение. Тогда нам снова понадобится закон Ома

.

P = V × I

P = V × V / R [потому что I = V / R]

Если значение подаваемого напряжения составляет 6 В, а сопротивление резистора 30 Ом, мощность будет

.

P = 6 × 6/30 = 6 / 5Вт

Таким образом, мощность на резисторе будет 6/5 Вт.

Резистор Мощность

Номинальная мощность или номинальная мощность резистора в основном зависят от физических размеров резистора. Если размер резистора большой, номинальная мощность будет больше, и это в основном зависит от площади поверхности резистора.

Резисторы

, мощность которых превышает их максимальную номинальную мощность, как правило, очень быстро вспыхивают дымом и повреждают цепь, к которой они подключены. Если резистор должен использоваться почти на максимальную мощность, тогда потребуется какая-то форма радиатора или охлаждения.

Рассеиваемая мощность резистора — это главное, что следует проверять при использовании резистора в определенных схемах. Каждый раз перед подключением резисторов необходимо проверять мощность, подаваемую источником. Резисторы взорвутся и повредят другие части схемы, что нежизнеспособно.

Большинство используемых нами резисторов имеют мощность 1/2 Вт, 1/3 Вт, 1/4 Вт и 1/8 Вт для низковольтных приложений. На рисунке ниже показана кривая снижения мощности. Эта кривая показывает, как номинальная мощность резистора падает при повышении его температуры.

Кривая снижения мощности

Номинальная мощность резистора падает после температуры 70 ° C. Следовательно, необходимо выбрать подходящую мощность резистора для данного приложения. Обычно при температуре выше 100 ° C предпочтительны резисторы высокой мощности.

Заключение

Номинальная мощность зависит также от размера резистора. Рассеивание мощности начинается с повышения температуры, и мощность также увеличивается. Для приложений с более высоким напряжением резисторы с проволочной обмоткой имеют хорошую номинальную мощность и специально разработаны для работы при температурах выше 300 ° C в течение более короткого периода времени.

Мощность и энергия

• Изучив этот раздел, вы сможете:
• Выполните расчеты мощности, напряжения, тока и сопротивления.
• • с использованием соответствующих единиц и подразделов.
• Различайте мощность и энергию в электрических цепях.

Мощность резисторов

Когда через резистор протекает ток, электрическая энергия преобразуется в ТЕПЛОВУЮ энергию.Тепло, генерируемое в компонентах цепи, каждый из которых обладает хотя бы некоторым сопротивлением, рассеивается в воздухе вокруг компонентов. Скорость рассеивания тепла называется МОЩНОСТЬЮ, обозначается буквой P и измеряется в ваттах (Вт).

Количество рассеиваемой мощности может быть вычислено с использованием любых двух величин, используемых в расчетах по закону Ома. Помните, как и в любой формуле, в формуле должны использоваться ОСНОВНЫЕ КОЛИЧЕСТВА, то есть ВОЛЬТЫ, ОМЫ и АМПЕРЫ (не милли, мег и т. Д.).

Чтобы найти мощность P, используя V и I

Чтобы найти мощность P, используя V и R

Чтобы найти мощность P, используя I и R

Перед тем, как начать, подумайте об этих нескольких советах, они упростят задачу, если следовать им.

1. Разработайте ответы с помощью карандаша и бумаги; в противном случае легко запутаться на полпути и получить неправильный ответ.

2.Конечно, ответ — это не просто число, это будет определенное количество ватт (или несколько или несколько единиц ватт). Не забудьте указать правильную единицу измерения (например, Вт или мВт и т. Д.), А также число, иначе ответ не имеет смысла.

3. Преобразуйте все вспомогательные единицы, такие как мВ или кОм, в ватты, указав их в соответствующей формуле. Ошибка здесь даст действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.

4. Хотя структура этих формул мощности кажется очень похожей на формулы закона Ома, есть небольшое различие — они содержат некоторые элементы в квадрате (I ² и V ² ).Будьте очень осторожны при использовании трюка с треугольником для транспонирования этих формул. Если вам нужно связать мощность с сопротивлением, то I или V необходимо возвести в квадрат (умножить на себя). Однако вы можете построить треугольник, который соответствует любой из формул для получения R, как показано ниже.

Не забудьте загрузить нашу брошюру «Подсказки по математике», в которой показано, как использовать калькулятор с показателями степени и инженерной нотацией, чтобы иметь дело с этими частями и каждый раз получать правильный ответ.

У вас нет научного калькулятора? Буклет «Подсказки по математике» объясняет, что вам нужно (и что вам не нужно, чтобы не тратить деньги без надобности). Если вы не хотите покупать научный калькулятор, вы всегда можете получить его бесплатно в сети. Пользователи ПК могут попробовать Calc98 на сайте www.calculator.org/download.html. Какой бы калькулятор вы ни выбрали, прочтите инструкции, чтобы ознакомиться с методами работы, которые вам следует использовать, поскольку они варьируются от калькулятора к калькулятору.

Важно помнить о влиянии рассеивания мощности в компонентах: чем больше мощность, тем больше тепла должно рассеиваться компонентом. Обычно это означает, что компоненты, рассеивающие большое количество энергии, нагреваются, а также они будут значительно больше по размеру, чем типы с низким энергопотреблением. Если компоненту требуется рассеивать больше энергии, чем он предназначен, он не сможет достаточно быстро избавиться от выделяемого тепла. Его температура повысится, и перегрев может вызвать полный отказ компонента и, возможно, повреждение других компонентов и самой печатной платы (PCB).В качестве меры предосторожности резисторы большой мощности часто устанавливают вне печатной платы с помощью более длинных выводных проводов, заключенных в керамические гильзы. Резисторы с проволочной обмоткой большой мощности могут даже быть заключены в металлический радиатор и прикреплены болтами к большой металлической поверхности, такой как корпус оборудования, чтобы избавиться от нежелательного тепла. Примеры резисторов большой мощности показаны на странице конструкции резистора.

Компоненты, такие как резисторы, имеют определенную номинальную мощность, указанную производителем (в ваттах или милливаттах).Этот рейтинг (параметр) необходимо проверять при замене компонента, чтобы не произошло завышения рейтинга. Это важный фактор безопасности при обслуживании электронного оборудования.

TIP

Тепло, выделяемое резисторами большой мощности, является основной причиной преждевременного выхода из строя многих цепей. Либо сам резистор выходит из строя из-за «разомкнутой цепи», особенно в резисторах с проволочной обмоткой. В резисторах из углеродного состава длительный перегрев может привести к изменению значения. Это может увеличиваться в типах с высоким сопротивлением или более опасно уменьшаться (позволяя увеличить ток) в типах с низким сопротивлением.Увеличение тока, вызванное этим уменьшением сопротивления, только ускоряет процесс, и в конечном итоге резистор (а иногда и другие связанные компоненты) сгорает!

Энергия в резисторах

Если определенное количество мощности рассеивается в течение определенного времени, то ЭНЕРГИЯ рассеивается. Энергия (мощность x время) измеряется в Джоулях, и, включив время (t) в формулы мощности, можно рассчитать энергию, рассеиваемую компонентом или схемой.

Рассеиваемая энергия = Pt или VIt или V ² t / R или даже I ² Rt Джоулей

Обратите внимание, что в формулах для энергии такие величины, как мощность, время, сопротивление, ток и напряжение, должны быть преобразованы в их основные единицы, например.грамм. Ватты, секунды, Ом, Амперы, Вольт и т. Д. Никаких дополнительных единиц или нескольких единиц! Как описано в буклете «Советы по математике».

Все вышеперечисленные единицы являются частью интегрированной системы международно стандартизированных единиц; Система S.I. (Système International d´Unités). Эта система устанавливает основные единицы для любых электрических, механических и физических свойств и их отношения друг к другу. Он также включает в себя стандартную форму кратных и подкратных чисел, описанную в буклете «Подсказки по математике».

3.5: Рассеивание мощности в цепях резисторов

Задачи обучения

• Рассеиваемая мощность в цепях резисторов.

Мы можем найти напряжения и токи в простых схемах, содержащих резисторы и источники напряжения или тока. Мы должны проверить, подчиняются ли эти переменные схемы принципу сохранения энергии: поскольку схема является замкнутой системой, она не должна рассеивать или создавать энергию. На данный момент наш подход состоит в том, чтобы сначала исследовать потребление / создание мощности цепи резистора.Позже мы докажем , что из-за KVL и KCL все цепи сохраняют электроэнергию.

Как определено на [ссылка], мгновенная мощность, потребляемая / создаваемая каждым элементом схемы, равна произведению его напряжения и тока. Общая мощность, потребляемая / создаваемая цепью, равна сумме мощностей каждого элемента.

\ [P = \ sum_ {k} v_ {k} i_ {k} \]

Напомним, что ток и напряжение каждого элемента должны соответствовать соглашению, согласно которому положительный ток определен для входа на клемму положительного напряжения.При таком соглашении положительное значение v _k i _k соответствует потребляемой мощности, отрицательное значение — создаваемой мощности. Поскольку общая мощность в цепи должна быть равна нулю ( P = 0), некоторые элементы схемы должны создавать мощность, а другие потреблять ее.

Рассмотреть простую последовательную схему следует в [ссылка]. При выполнении наших расчетов мы определили ток i _out , протекающий через клеммы положительного напряжения обоих резисторов, и нашли его равным:

\ [i_ {out} = \ frac {v_ {in}} {R_ {1} + R_ {2}} \]

Напряжение на резисторе R ₂ является выходным напряжением, и мы нашли его равным:

\ [v_ {out} = \ frac {R_ {2}} {R_ {1} + R_ {2}} v_ {in} \]

Следовательно, вычисление мощности для этого резистора дает

\ [P_ {2} = \ frac {R_ {2}} {(R_ {1} + R_ {2}) ^ {2}} v_ {in} ^ {2} \]

Следовательно, этот резистор рассеивает мощность, потому что P ₂ положительный.{2} Р \]

Поскольку резисторы имеют положительное значение, резисторы всегда рассеивают мощность . Но куда девается мощность резистора? При сохранении мощности рассеиваемая мощность должна где-то поглощаться. Ответ не предсказывается непосредственно теорией цепей, но физикой. Ток, протекающий через резистор, нагревает его; его мощность рассеивается теплом.

Удельное сопротивление

Физический провод имеет сопротивление и, следовательно, рассеивает мощность (нагревается, как резистор в цепи).Фактически, сопротивление провода длиной L и площадью поперечного сечения A определяется как:

\ [R = \ frac {\ rho L} {A} \]

Величина ρ известна как удельное сопротивление и представляет сопротивление материала единичной длины с единичной площадью поперечного сечения, составляющего провод. Удельное сопротивление измеряется в ом-метрах. Большинство материалов имеют положительное значение для ρ , что означает, что чем длиннее провод, тем больше сопротивление и, следовательно, рассеиваемая мощность. { 2} \]

Мы пришли к выводу, что оба резистора в нашей примерной схеме потребляют мощность, что указывает на источник напряжения как на производителя энергии.{2} \]

Это довольно общий результат: источники вырабатывают энергию, а элементы схемы, особенно резисторы, потребляют ее.

Но где источники берут энергию? Опять же, теория цепей не моделирует построение источников, но теория утверждает, что все источников должны получать энергию для работы.

11,3 Мощность и энергия | Электрические схемы

Начнем с расчета эквивалентного сопротивления резисторов.{2}} {\ text {9,8}} \\ & = \ текст {3,67} \ текст {Ω} \ end {выровнять *}

Теперь мы можем найти неизвестное сопротивление, сначала вычислив эквивалентную параллельную сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {5} + \ frac {1} {3} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,65} \ text {Ω} \ end {выровнять *} \ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ R_ {4} & = R_ {s} — R_ {p} \\ & = \ text {3,67} — \ text {0,65} \\ & = \ текст {3,02} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать общий ток:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {6} {\ text {3,67}} \\ & = \ текст {1,63} \ текст {А} \ end {выровнять *}

Это ток в последовательном резисторе и во всем параллельном соединении.{2} (\ text {3,02}) \\ & = \ текст {0,89} \ текст {W} \ end {выровнять *}

Затем мы находим напряжение на этих резисторах и используем его, чтобы найти напряжение на параллельная комбинация:

\ begin {align *} V & = IR \\ & = (\ text {1,63}) (\ text {3,02}) \\ & = \ текст {4,92} \ текст {V} \ end {выровнять *} \ begin {align *} V_ {T} & = V_ {1} + V_ {p} \\ V_ {p} & = V_ {T} — V_ {1} \\ & = \ text {6} — \ text {4,92} \\ & = \ текст {1,08} \ текст {V} \ end {выровнять *}

Это напряжение на каждом из параллельных резисторов.{2}} {\ text {3}} \\ & = \ текст {3,5} \ текст {W} \ end {выровнять *}

ресурсов

Последовательная цепь

Глобусы, соединенные последовательно

В последовательной цепи одна за другой подключены две или более нагрузки.

У тока есть только один путь, по которому оно может течь.

Примером последовательной схемы является набор огней на елку.Все шары ставятся один за другим.

Путь только один, поэтому ток будет одинаковым в любой точке цепи.

Принципиальная схема, показывающая три последовательно включенных резистора

Общее сопротивление в последовательной цепи будет равно сумме каждого отдельного сопротивления в цепи.

Чем больше нагрузок помещено в цепь, тем больше сопротивление.

Общее сопротивление для последовательной цепи рассчитывается по следующей формуле:

R _T = R ₁ + R ₂ + R ₃

Закон напряжения Кирхгофа

Вольтметр на каждом резисторе в последовательной цепи т

Закон Кирхгофа расширяет закон Ома в отношении напряжений на сопротивлениях в последовательной цепи. Общее напряжение питания будет равно сумме падений напряжения на каждом резисторе.

Общее падение напряжения (В _T ) рассчитывается по формуле:

V _T = V ₁ + V ₂ + V ₃

Если известны как ток, так и каждое значение сопротивления, то можно использовать закон Ома для расчета падения напряжения на каждом резисторе.

Например:

В ₁ = IR ₁

Рассеиваемая мощность

Мощность, рассеиваемая в последовательной цепи, зависит от напряжения питания, приложенного к цепи, и тока, протекающего в цепи.Ток зависит от общего сопротивления цепи.

Из раздела о мощности вы знаете формулу рассеиваемой мощности:

P = VI

Мощность, рассеиваемая в каждом отдельном компоненте, зависит от сопротивления компонента. Общая рассеиваемая мощность будет равна сумме мощности, рассеиваемой каждым отдельным сопротивлением. В зависимости от известных значений комбинации формулы мощности, а также закона Ома могут использоваться для расчета рассеиваемой мощности (или любого другого неизвестного значения).

Пример

Если значения на приведенной выше схеме:

В _Т = 20 В

R ₁ = 50 Ом

R ₂ = 20 Ом

R ₃ = 100 Ом

Общее сопротивление можно рассчитать следующим образом:

R _T = R ₁ + R ₂ + R ₃

R _T = 50 + 20 + 100

R _T = 170 Ом

Какая общая рассеиваемая мощность?

Вы можете рассчитать текущий расход, а затем рассчитать мощность.Вместо этого вы можете использовать подстановку, чтобы получить формулу.

В формуле P = VI замените I на V _T / R _T , чтобы получить формулу

P _T = V _T x V _T / R _T , что совпадает с

P _T = V _T ² / R _T

P _T = 20 ² /170

P _T = 0,235 Вт или 235 мВт

.