Мощный калькулятор онлайн. Мощный онлайн-калькулятор: все инструменты для сложных вычислений

Как выбрать лучший онлайн-калькулятор для сложных математических расчетов. Какие функции должен иметь продвинутый калькулятор. Обзор популярных веб-инструментов для математических вычислений.

Что такое мощный онлайн-калькулятор и зачем он нужен

Мощный онлайн-калькулятор — это многофункциональный веб-инструмент для выполнения сложных математических вычислений. В отличие от простых калькуляторов, он позволяет решать уравнения, строить графики функций, выполнять матричные операции и многое другое.

Основные преимущества использования мощных онлайн-калькуляторов:

• Доступность с любого устройства, подключенного к интернету
• Широкий набор математических функций
• Возможность сохранения и экспорта результатов
• Удобный интерфейс для ввода сложных выражений
• Постоянные обновления и добавление новых возможностей

Ключевые функции продвинутого онлайн-калькулятора

Чтобы считаться по-настоящему мощным, онлайн-калькулятор должен обладать следующим функционалом:

Базовые арифметические операции

Любой калькулятор должен уметь складывать, вычитать, умножать и делить числа. Но продвинутые инструменты предлагают дополнительные возможности:

• Работа с дробями и процентами
• Вычисление факториалов
• Операции с комплексными числами
• Преобразование единиц измерения

Алгебраические вычисления

Мощный калькулятор позволяет решать уравнения и системы уравнений, выполнять операции с матрицами, находить собственные значения и векторы. Какие алгебраические функции должны быть доступны:

• Решение линейных и нелинейных уравнений
• Разложение на множители
• Операции с матрицами (сложение, умножение, обращение)
• Нахождение определителей
• Решение систем линейных уравнений

Возможности для анализа функций

Продвинутый математический калькулятор должен предоставлять инструменты для исследования функций. Какие функции анализа необходимы:

• Построение графиков функций
• Вычисление пределов
• Нахождение производных и интегралов
• Разложение в ряд Тейлора
• Поиск экстремумов функций

С помощью этих инструментов можно визуализировать поведение функций и находить их важные свойства.

Статистические расчеты

Для обработки и анализа данных необходимы статистические функции. Какие возможности должен предоставлять мощный калькулятор:

• Вычисление среднего, медианы, моды
• Расчет дисперсии и стандартного отклонения
• Построение гистограмм и диаграмм рассеяния
• Корреляционный и регрессионный анализ
• Проверка статистических гипотез

Тригонометрические функции

Мощный калькулятор должен уметь работать с тригонометрическими и гиперболическими функциями. Какие возможности должны быть доступны:

• Вычисление синуса, косинуса, тангенса
• Обратные тригонометрические функции
• Перевод градусов в радианы и обратно
• Гиперболические функции
• Тригонометрические тождества

Популярные онлайн-калькуляторы с продвинутыми функциями

Рассмотрим несколько популярных веб-инструментов, предлагающих широкие возможности для математических вычислений:

Wolfram Alpha

Wolfram Alpha — это не просто калькулятор, а целая база знаний. Он может решать уравнения, строить графики, выполнять статистический анализ и многое другое. Особенности Wolfram Alpha:

• Понимание естественного языка при вводе запросов
• Визуализация результатов в виде графиков и диаграмм
• Огромная база данных по разным областям знаний
• Возможность получения пошаговых решений

Desmos

Desmos специализируется на построении графиков функций. Его основные возможности:

• Построение графиков нескольких функций
• Анимация графиков
• Исследование поведения функций
• Решение уравнений графическим методом

GeoGebra

GeoGebra сочетает возможности графического калькулятора и инструментов для геометрических построений. Что умеет GeoGebra:

• Построение графиков функций
• Геометрические построения
• Работа с векторами и матрицами
• Статистические расчеты
• 3D-визуализация

Как выбрать подходящий онлайн-калькулятор

При выборе мощного онлайн-калькулятора стоит обратить внимание на следующие аспекты:

• Набор доступных математических функций
• Удобство интерфейса и ввода выражений
• Возможность сохранения и экспорта результатов
• Наличие мобильной версии или приложения
• Поддержка и обновления

Выбор конкретного инструмента зависит от ваших потребностей и типа решаемых задач. Для базовых расчетов подойдет простой научный калькулятор, а для сложного анализа может потребоваться специализированное ПО.

Заключение

Мощные онлайн-калькуляторы значительно упрощают выполнение сложных математических вычислений. Они доступны с любого устройства, постоянно обновляются и предлагают широкий набор функций. При выборе калькулятора важно учитывать свои потребности и специфику решаемых задач.

Инженерный калькулятор онлайн

Современный уклад жизни требует постоянной динамики. Производя расчеты на калькуляторе, мы заметно экономим свое время, не рискуем в чем-то ошибиться и получаем точный результат. Благодаря изобретению данного устройства, многие люди забыли что такое недостачи и погрешности в расчетах. Однако калькулятор калькулятору рознь, и если примитивные вычислительные функции можно сделать на математической модели, то сложнейшие расчеты возможно совершить только при помощи инженерной. Отныне приобретать данное чудо современной техники не нужно – достаточно обратиться за помощью к нашему инженерному калькулятору онлайн! Программа работает без дополнительной установки – достаточно зайти на электронную страницу и начать действовать.

Градусы Радианы

Memory: 0

• MC
• MR
• MS
• M+
• M-

• (
• ,
• )
• ←
• AC

• 7
• 8
• 9
• ÷
• abs

• 4
• 5
• 6
• ×
• mod

• 1
• 2
• 3
• -

• 0
• .
• +/-
• +

• =

• sin
• sin-1
• π
• n!

• cos
• cos-1
• e^x
• x2

• tan
• tan-1
• ln
• x3

• sinh
• sinh-1
• log
• xy

• cosh
• cosh-1
• logyx
• √x

• tanh
• tanh-1
• 10x
• y√x

Функции инженерного калькулятора онлайн

Калькулятор математического типа поможет вам совершить только примитивные расчеты. С его помощью можно сделать то, чему нас учили в начальных классах средней школы:

• сложение;
• вычитание;
• деление;
• умножение;
• вычитание процентов;
• возведение числа в степень;
• нахождение корня квадратного.

Инженерный калькулятор онлайн включает в себя все эти и дополнительные функции, которые необходимы для проведения сложных расчетов. Теперь вам не придется тратить дополнительные деньги на покупку этого устройства, ведь сделать вычисления можно на нашем сайте.

Помимо вышеперечисленных, наш универсальный калькулятор поможет вам выполнить такие расчеты:

Нахождение:

• синуса угла;
• тангенса;
• косинуса;
• котангенса;
• арксинуса;
• арктангенса;
• арккосинуса;
• арккотангенса.

Интерфейс инженерного калькулятора онлайн

Выполнить все вышеперечисленные расчеты достаточно просто. Наш инженерный калькулятор онлайн обладает понятным интерфейсом, а потому работать с ним весьма удобно. По своему виду он полностью имитирует настоящий калькулятор, поэтому долгого изучения функций вам не потребуется. Несмотря на это мы прилагаем подробную инструкцию и описание каждой клавиши.

Пользоваться нашей программой выгодно еще и потому, что расчеты производятся моментально – вам не нужно обновлять страницу сайта, ведь калькулятор работает во флеш-режиме. Ежедневно нашей программой пользуется огромное количество людей. Среди них ученики высших заведений, преподаватели, архитекторы-проектировщики, ученые и другие люди, заинтересованные в точности расчетов. Инженерный калькулятор онлайн не требует скачивания и установки дополнительных плагинов, а потому вы можете начать пользоваться им прямо сейчас!

Похожие калькуляторы

Стандартный калькулятор Калькулятор дробей Калькулятор процентов

Калькулятор онлайн, бесплатный многофункциональный калькулятор

В современной жизни многие из нас довольно часто пользуются онлайн калькулятором. Такое явление в интернете можно смело назвать мощным калькулятором и одним из самых удачных. Используя его, можно произвести вычисления самого разного рода, начиная от простых и заканчивая самыми сложными (проценты, логарифмы, тригонометрические функции о др.).
Также использование такого калькулятора позволяет легко построить графики различной сложности. Поэтому, его могут использовать и школьники, и студенты, и преподаватели математики, и аспиранты. Такое онлайн чудо широко используется в бухгалтерии, в современном бизнесе, а также в иных направлениях, которые связаны с постоянными вычислениями различной сложности.
Использование онлайн калькулятора очень удобно. Ведь вы можете им пользоваться с любого компьютерного устройства, находясь в любом месте, а самое главное, в любое время. Ведь некоторые из нас иногда предпочитают работать в ночное время. Заметим, для этого только нужен доступ к интернету. Также вы должны знать, что использование такого калькулятора всегда происходит бесплатно. Не стоит также волноваться за своевременную регистрацию. Она в данном случае, совершенно не нужна.
Вам не стоит переживать по поводу того, что онлайн калькулятор сложный в использовании. Поверьте, вы самостоятельно разберетесь во всех его функциях, не смотря на то, что инструкции на русском языке нет. Вы сможете найти в окне самого онлайн калькулятора специальный видеоурок, который даст возможность узнать, как работает калькулятор. Правда, некоторым пользователям этого будет не совсем достаточно, для того, чтобы воспользоваться всеми функциями такого помощника.
Но расстраиваться вам не стоит. Сегодня на многих сайтах можно найти прекрасные подсказки по использованию онлайн калькулятором. Пользователям на самом доступном языке разъясняют все обозначения, все математические тонкости, а также предлагают примеры вычислений. Благодаря этому, вы самостоятельно можете во всем разобраться. Единственное, что каждому из нас понадобиться разное время на то, чтобы все понять. Для удобства, мы рекомендуем просто скачать подобную инструкцию и иметь ее всегда под рукой. Благодаря своей уникальности, на нем можно выполнять, как самые простые вычисления (сложения, вычитания, деление и пр.), так и самые сложные, которые используют в работе ученые и инженеры.
Для того чтобы задавать необходимые функции нужно использовать мышку (как для обычного компьютера), а также кнопки на клавиатуре. Наводите на нужные кнопочки и легко получаете правильный ответ за очень короткое время. Заметим, что при использовании такого Online калькулятора, вы никогда не будете получать неправильные ответы. Поэтому, смело пользуйтесь таким компьютерным «гением». Это намного упростит и облегчит вашу работу. Мы советуем пользоваться вышеупомянутым калькулятором и учащимся старших классов. Это позволит детям быстрее разобраться во всех математических премудростях онлайн «умельца». Будучи студентами ВУЗов, они легко и быстро будут справляться с заданиями различной сложности.

В списке ниже указаны все клавиши калькулятора и выполняемые ими операции.

Клавиша	Символ	Операция
pi	pi	Постоянная pi
е	е	Число Эйлера
%	%	Процент
( )	( )	Открыть/Закрыть скобки
,	,	Запятая
sin	sin(α)	Синус угла
cos	cos(β)	Косинус
tan	tan(y)	Тангенс
sinh	sinh()	Гиперболический синус
cosh	cosh()	Гиперболический косинус
tanh	tanh()	Гиперболический тангенс
sin-1	asin()	Обратный синус
cos-1	acos()	Обратный косинус
tan-1	atan()	Обратный тангенс
sinh-1	asinh()	Обратный гиперболический синус
cosh-1	acosh()	Обратный гиперболический косинус
tanh-1	atanh()	Обратный гиперболический тангенс
x2	^2	Возведение в квадрат
х3	^3	Возведение в куб
xy	^	Возведение в степень
10x	10^()	Возведение в степень по основанию 10
ex	exp()	Возведение в степень числа Эйлера
√x	sqrt(x)	Квадратный корень
3√x	sqrt3(x)	Корень 3-ей степени
y√x	sqrt(x,y)	Извлечение корня
log2x	log2(x)	Двоичный логарифм
log	log(x)	Десятичный логарифм
ln	ln(x)	Натуральный логарифм
logyx	log(x,y)	Логарифм
I / II		Сворачивание/Вызов дополнительных функций
Unit		Конвертер величин
Matrix		Матрицы
Solve		Уравнения и системы уравнений
		Построение графиков
Дополнительные функции (вызов клавишей II)
mod	mod	Деление с остатком
!	!	Факториал
i / j	i / j	Мнимая единица
Re	Re()	Выделение целой действительной части
Im	Im()	Исключение действительной части
|x|	abs()	Модуль числа
Arg	arg()	Аргумент функции
nCr	ncr()	Биноминальный коэффициент
gcd	gcd()	НОД
lcm	lcm()	НОК
sum	sum()	Суммарное значение всех решений
fac	factorize()	Разложение на простые множители
diff	diff()	Дифференцирование
Deg		Градусы
Rad		Радианы

Онлайн-калькулятор по математике

Примеры решенийРанг матрицы Умножение матриц Метод Гаусса Найти производную Найти интегралРешение СЛАУ методом Крамера Диф уравнения онлайнОпределитель матрицы Точки разрыва функции

В ниже приведенных онлайн-калькуляторах решение сохраняется в формате Word с отображением всех исходных формул.

Аналитическая геометрия

1. Длина отрезка по координатам x,y. Простенький калькулятор, вычисляющий длину вектора по формуле
2. Аналитическая геометрия. Мощный по своим характеристикам онлайн-калькулятор, который по координатам пирамиды определяет площадь грани, уравнения плоскостей, углы и др.
3. По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
4. Площадь треугольника по координатам вершин.
5. Уравнение прямой по координатам вершин.
6. Угол между двумя прямыми
7. Внутренние углы треугольника
8. Расстояние от точки до прямой
9. Множество точек на плоскости (Составить уравнение множества точек на плоскости)
10. Условие коллинеарности векторов
11. Скалярное произведение векторов
12. Векторное произведение
13. Момент силы относительно начала координат
14. Площадь параллелограмма, построенного на векторах
15. Объем пирамиды, построенной на векторах
16. Объем параллелограмма, построенного на векторах
17. Угол между двумя плоскостями
18. Уравнение параллельной прямой. Составляется уравнение прямой, проходящей через точку параллельно данной прямой.
19. Уравнение перпендикулярной прямой.

Онлайн-калькулятор по аналитической геометрии

Линейная алгебра

1. Определитель матрицы.
2. Матричный калькулятор: 3A-BC+A-1
3. Методы решения системы уравнений: метод Гаусса, метод Крамера, метод обратной матрицы и другие.
4. Координаты вектора в новом базисе. Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
5. Приведение кривой второго порядка к каноническому виду
6. Собственные числа матрицы
7. Выделение полного квадрата (a•x² + b•x + c = 0)
8. Метод неопределенных коэффициентов (преобразовать в сумму простейших дробей):
9. Формула дискриминанта. Данный вид калькулятора используется для нахождения дискриминанта и корней функции.
10. Деление многочленов столбиком. Данная процедура, в частности, поможет при нахождении интегралов.
11. Решение пределов.
12. Точки разрыва функции.
13. Построить график функции.

Раскрыть скобки и упростить выражение, (x²/3 — 3x + 12)(x + 2)

Степенные ряды

1. Определить сходимость или расходимость ряда
2. Определить область сходимости степенного ряда
3. Разложить в ряд Тейлора
4. Разложение функции в ряд Фурье: Разложить в ряд Фурье функцию f(x)=1+x на отрезке [-1, 1]. Построить графики частичных сумм S₀, S₁, S₂.

Комплексные числа

1. Действия с комплексными числами
2. Комплексные числа в тригонометрической и показательной формах
3. Извлечение корня из комплексных чисел используется, например, при нахождении уравнений типа w3 - z = 0.

Интегральное исчисление

1. Площадь фигуры, ограниченной линиями:
2. Вычисление интегралов (Таблица интегралов)
3. Работа силы при перемещении вдоль дуги линии: Найти работу силы F при перемещении вдоль дуги линии L от точки M₀ до точки M₁.

Дифференциальное исчисление

1. Найти производную (Таблица производных) cosx + e^sinx+x3x
2. Дифференциал функции
3. Правило Лопиталя при вычислении пределов.
4. Уравнение касательной к графику функции, уравнение нормали
5. Наибольшее и наименьшее значение функции одной переменной. Калькулятор вычисляет экстремум функции. Интервалы возрастания и убывания функции. Интервалы выпуклости и вогнутости графика функции. Точки перегиба.
6. Асимптоты функции. Определение наклонных, вертикальных и горизонтальных асимптот.
7. Построение графика функции методом дифференциального исчисления

Дифференциальные уравнения

1. Дифференциальные уравнения: , .
2. Линейные дифференциальные уравнения (решение однородных дифференциальных уравнений y''-2y'+y = e2x)

Функции нескольких переменных

1. Частные производные.
2. Экстремум функции двух переменных: нахождение минимума и максимума функции
3. Касательная плоскость и нормаль к поверхности.
4. Метод множителей Лагранжа для поиска локальных экстремумов функции.
5. Градиент функции: градиент в точке, производная по направлению вектора. Нахождение полного дифференциала функции.

Теория вероятностей

1. Системы случайных величин. Полезный калькулятор при изучении темы на условные ряды распределения X,Y.
2. Корреляционная таблица — этот тип калькулятора используется для нахождения ковариация и коэффициента корреляции.
3. см. другие онлайн-калькуляторы по теории вероятностей

С помощью сервиса WolframAlpha можно бесплатно решать многие математические задачи. Решение бесплатное и автоматическое с возможностью сохранять результаты вычислений в формате pdf. Есть возможность показать ход решения (Show steps).

Найти корни уравнения	x2 — 3x + 4 = 0
Разложить на множители	x2 — 3x + 4 = 0

С помощью калькулятора Web2 можно быстро вычислить некоторые математические выражения и находить пределы, производные и интегралы. x,x=infinity

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

6 лучших научных онлайн-калькуляторов

В настоящее время почти каждый имеет доступ к калькулятору под рукой. Большинство телефонов имеют встроенное приложение-калькулятор, и во многих повседневных ситуациях этого более чем достаточно, чтобы помочь вам, если вы застряли в пробке.

Но не все калькуляторы одинаковы. Научные и графические калькуляторы значительно мощнее, чем то, что вы, вероятно, найдете лежащим в вашем доме или на вашем телефоне по умолчанию.

Вот шесть лучших научных онлайн-калькуляторов, которые вы можете найти.

web2.0calc возглавляет список, и не зря. web2.0calc — это простой и удобный научный калькулятор, который вы можете найти в Интернете.

Он устроен так же, как физический калькулятор, чтобы помочь вам понять, как его использовать с первого взгляда, но это не единственный способ его использования. Вы можете так же легко ввести свой ответ сверху, и калькулятор автоматически проанализирует ваше выражение.

web2.0calc великолепен, потому что он не просто дает вам ответ. Всякий раз, когда вы вводите выражение, оно расширяет его для вас, а затем выражает решение различными способами, например, дробью и десятичным числом.

Если вы пытаетесь улучшить свои математические навыки, на веб-странице также есть серия формул, а также математический форум, на который вы хотите задать любые вопросы.

Далее следует графический калькулятор Desmos. Немного сложнее в использовании, чем просто калькулятор, вы можете найти время, чтобы освоиться с графическим калькулятором Desmos. Но не волнуйтесь, если вы не знакомы с этим инструментом, он прост в освоении и невероятно эффективен.

Desmos Graphing Calculator — это, как следует из названия, графический калькулятор. По умолчанию сетки чисел и математических символов нет. Вместо этого предполагается, что вы будете печатать свои выражения, которые Desmos Graphing Calculator отображает очень быстро.

Калькулятор поддерживает несколько выражений на одной оси и позволяет увеличивать и уменьшать масштаб по мере необходимости. Desmos Graphing Calculator также включает возможность добавления таблиц и выражений. Вы даже можете добавить на график папки с выражениями или изображениями, если хотите.

В то время как некоторые из калькуляторов в этом списке сосредотачиваются на том, чтобы хорошо делать одну вещь, Good Calculators делает шаг вперед. Good Calculators — это веб-сайт, на котором собраны различные калькуляторы для всех ваших нужд.

На целевой странице даже есть обычный калькулятор, если он вам действительно нужен, но Good Calculators определенно не останавливается на достигнутом. Здесь доступно огромное количество различных калькуляторов, таких как калькуляторы заработной платы и подоходного налога, калькуляторы ипотеки и калькуляторы амортизации.

Связано: Лучшие финансовые сайты, которые помогут вам оставаться на вершине рынка

После того, как вы выберете одну из этих категорий, Good Calculators перечислит множество различных калькуляторов, которые помогут удовлетворить ваши конкретные потребности. На примере категории «Калькуляторы амортизации» вы можете посмотреть, среди прочего, калькуляторы амортизации автомобилей, аннуитета и MACRS.

Независимо от вашего выбора, Good Calculators включает в себя подробные объяснения того, как и что вам нужно вводить в каждое поле, чтобы максимально использовать их калькуляторы. Вы никогда не почувствуете, что Good Calculators просто бросили вас в обширную форму или кучу полей, которые нужно заполнить без руководства.

Symbolab — следующая запись в этом списке, и не зря. Если вы хотите узнать больше о математике, то Symbolab — лучший калькулятор для использования.

Связано: Лучшие веб-сайты для закладок для изучения математики шаг за шагом

Symbolab предоставляет вам поле, в которое вы можете вводить свои математические задачи, но, в отличие от других калькуляторов, способ ввода чисел по умолчанию — это их печатать. Для математических символов вверху есть из чего выбрать, и вы даже можете выбрать конкретное действие, например «найти x».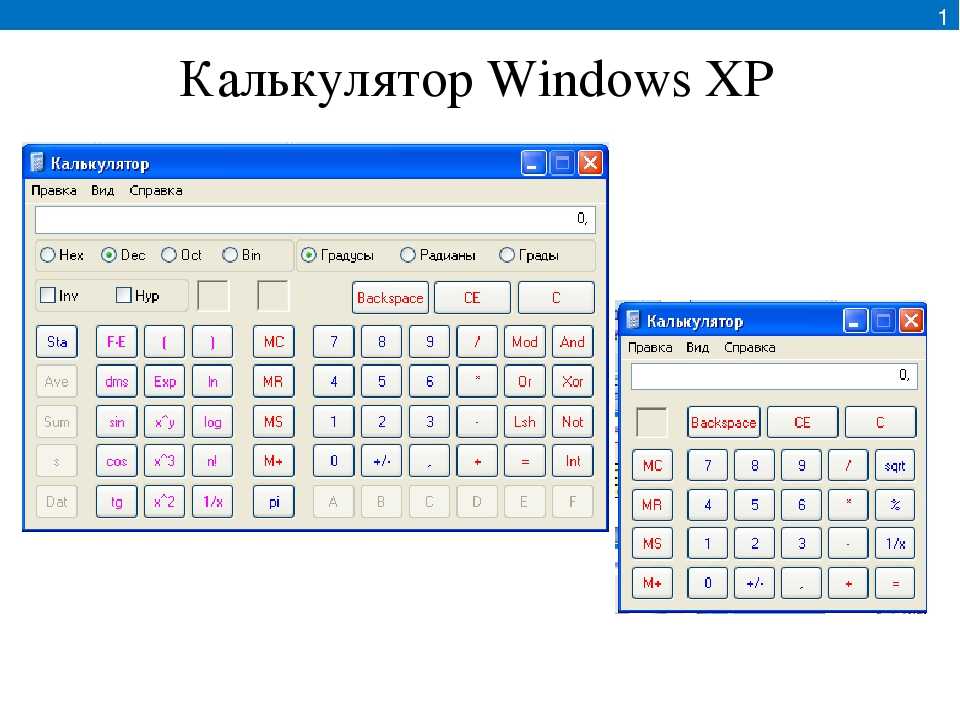

Где Symbolab действительно сияет, так это в том, как он предлагает вам решение. Вместо того, чтобы просто дать вам ответ, Symbolab также покажет вам шаги, которые были предприняты для достижения этого решения. Это делает изучение математики значительно проще, чем просто принимать ответ за чистую монету или работать в обратном направлении, чтобы изучить процесс самостоятельно.

Если вы по-прежнему получили другой ответ, Symbolab позволяет вам ввести его, чтобы проверить правильность вашего ответа, а веб-страница также может определить тип проблемы и дать вам другие ответы того же типа для практики.

WolframAlpha следующий и, возможно, самый мощный в этом списке. WolframAlpha — это не только коагулятор, но и база знаний. Это просто означает, что WolframAlpha может дать вам много информации о любом введенном вами выражении, а не только о решении.

WolframAlpha автоматически показывает ваше выражение в виде графика, в альтернативных формах и на числовой прямой.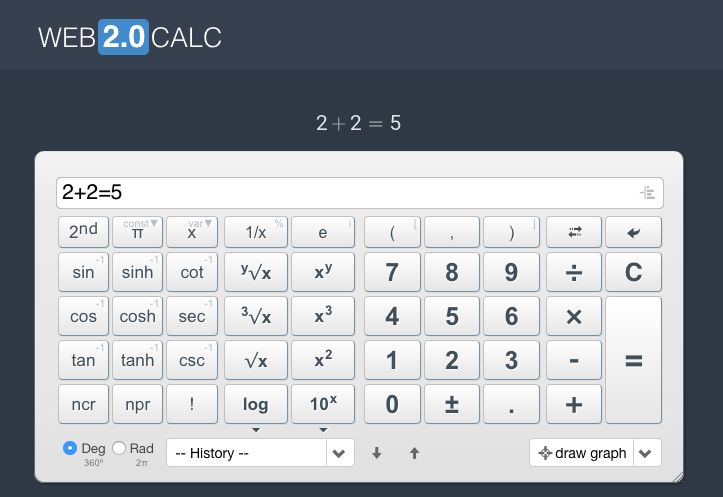 Он также автоматически генерирует вопросы, непосредственно связанные с введенным вами выражением, которые должны помочь вам узнать больше о нем и о том, как оно работает.

Связанный: Как сделать повседневную жизнь проще с Wolfram Alpha

WolframAlpha также имеет множество премиальных функций, доступных тем, кто вносит ежемесячную плату. Эти функции включают в себя пошаговые решения для выражений, практические задачи с подсказками, управляемые калькуляторы для финансов и многое другое, а также широкий спектр других функций.

Наконец, Calculator.net попал в список. Calculator.net имеет множество функций и в значительной степени представляет собой комбинацию многих уже перечисленных калькуляторов.

Calculator.net имеет простой интерфейс, напоминающий научный калькулятор, и хотя вы не можете вводить выражения с помощью клавиатуры, это все же довольно мощный инструмент.

Инструмент отличается разнообразием доступных калькуляторов. Выбор действительно огромен, и у вас не возникнет проблем с их изучением.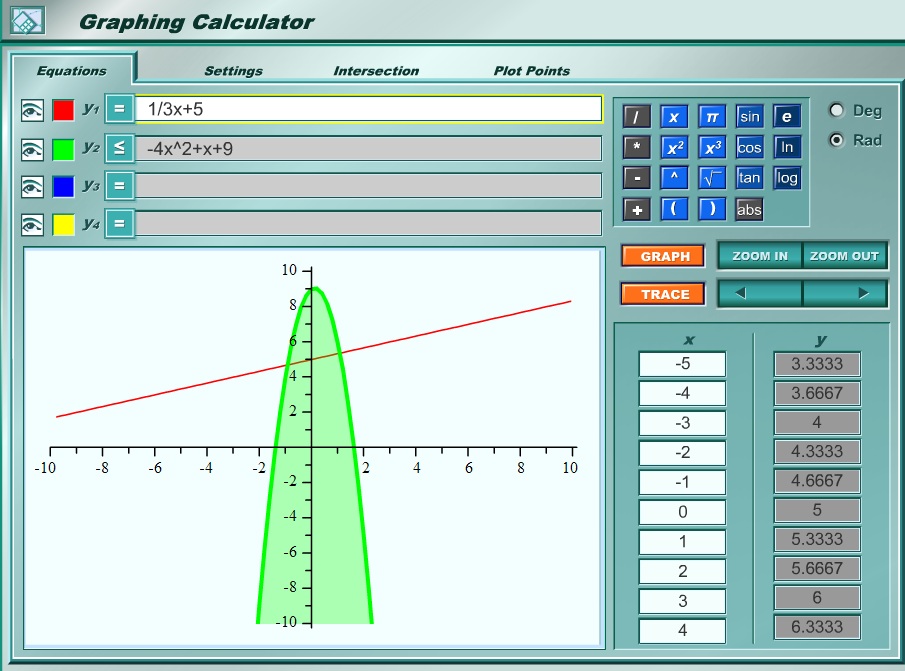

Есть объяснения того, как все они работают, поэтому вам не нужно беспокоиться о том, что вы делаете. Calculator.net — это быстро и всесторонне.

Онлайн-калькуляторы — не единственный способ

Онлайн-калькуляторы могут помочь вам добиться гораздо большего, чем то, чего вы можете достичь с помощью обычного калькулятора, лежащего под рукой или в вашем телефоне по умолчанию. Но это не значит, что это всегда лучший способ.

Везде, куда бы вы ни посмотрели, доступно множество феноменальных услуг, и как только вы откроете для них глаза, вы обязательно увидите, как много их предлагается.

Hypercalc — калькулятор, который не переполняется на MROB

Hypercalc — интерпретируемый калькулятор с открытым исходным кодом, разработанный для вычисления чрезвычайно больших чисел (таких как ваш номер телефона, поднятый в степени факториала валового мирового продукта) без переполненный.

Он хранит и манипулирует числами, используя формат индекса уровня; как таковой может выйти далеко за пределы bc, dc, MACSYMA/maxima, Mathematica и Maple, все из которых используют большая библиотека. Например, Hypercalc может сказать вам, является ли 128 ^{48 1024} больше, чем 8 ^{88 888} .

получить исходный код perl здесь

или же

используйте HyperCalc из вашего браузера

Содержание

Обзор: версии и функции

Справочная информация: предотвращение переполнения

Перл Гиперкальций

HyperCalc JavaScript от Kenny TM~ Chan

Неинтуитивные результаты при работе с огромными числами

---

Обзор: версии и функции

Было три проявления Hypercalc:

• Исходная версия Palm Pilot, больше не поддерживается

• Версия Perl (потому что Perl правит!) для терминала/консоли в системах UNIX, Linux, Mac OS и Cygwin. Исходный код здесь

• Отличный Javascript HyperCalc, который был переведен с Perl Кенни ТМ~ Чан.

Все версии Hypercalc используют внутреннее представление, подобное индекс уровня.

Версии Perl и JavaScript предоставляют историю команд (ввод и подстановка результата, как в Maxima). Другие функции варьируются в зависимости от следует:

Особенности Perl Hypercalc HyperCalc JavaScript Пользовательские переменные ДА ДА Пользовательские функции (используйте BASIC) ДА Повторное использование входных и выходных выражений (история команд) ДА ДА Совместим со всем оборудованием нет ДА (используйте веб-браузер) Максимальная точность 300 цифр 16 цифр Полностью программируемый ДА нет Неопределенность (пример: 100(4)+20(3) = 120(7) ) ДА нет Ввод и вывод Base-60 (пример: 1:20:32 + 5:39 = 1:26:11) ДА нет

Версии Perl и JavaScript доступны под лицензией бесплатная (бесплатная) лицензия GPL, но без гарантии или поддерживать.

---

Фон: предотвращение переполнения

Основное преимущество Hypercalc заключается в том, что он не «переполняется»: для больших чисел его диапазон намного больше, чем у портативного калькуляторы, приложения-калькуляторы для телефонов, числовые библиотеки, такие как gmp, или математическое программное обеспечение, такое как Mathematica. Вот краткое сравнение (подробнее на моей странице форматов с плавающей запятой):

название год максимальное значение Ранние научные калькуляторы (например, TI SR-50) 1974 9,99×10 99 Двоичный код IEEE 75464 1985 1,80×10 308 Высококачественные научные калькуляторы (например, TI-89) 1990-е 9,99×10 999 ПАРИ/ГП 1985 4,3×10 2525222 Mathematica 1988 1,44×10 323228010 Клен 1980 1,0×10 2147483646 Библиотека GMP (при условии, что «длинный» — 64 бита) 1991 10 1,777×10 20 Максима 1982 ≈ 10 10 10000000000 = 10↑↑4 Hypercalc 1998 10↑↑(10 10 )

Я начал изучать очень большие числа, такие как 2 ⁶⁵⁵³⁶ , в начале 1970-х с использованием калькулятора Texas Instruments SR-50, и приходилось вручную логарифмировать, извлекать дробные части и вычислять мантиссы и т. д. Я сделал свою собственную библиотеку BIGNUM в язык ассемблера для Apple II и снова на более поздних машинах. Такой подход ограничен памятью компьютера (на моей странице больших чисел я называют это пределом класса 2).

Я всегда хотел портативный калькулятор, который мог бы вычислять огромные числа. проблем, и Palm Pilot был первое устройство, которое действительно сделало это возможным. Я создал Palm OS HyperCalc в октябре 1998 года и заработал примерно через неделю.

Экран моего пилота треснул, и я увидел, что платформа не будет длиться слишком долго. Что еще более важно, я хотел иметь возможность копировать и вставлять числа и результаты в другие файлы во время работы над моим веб-сайтом. страницы. Поэтому я создал значительно более мощную версию Perl в лето 1999. Я сохранил и значительно расширил его на протяжении лет, добавив расширенную точность (до 295 цифр) позже в 1999 году, Интерпретатор BASIC в конце 2005 г., форматирование base-60 в конце 2007 г., расчет неопределенности в 2011 г. ( 3,467778644301262713584883219130 ) С3 =

Существует обширная встроенная справка, доступ к которой можно получить, набрав help в Подсказка гипервычисления. После начальной вводной страницы справки просто нажмите Enter несколько раз, чтобы увидеть справку по десяти конкретным темам.

---

HyperCalc JavaScript от Kenny TM~ Chan

Чтобы использовать HyperCalc из веб-браузера, перейдите сюда: JavaScript для гиперкалькулятора. Есть подробное руководство в формате PDF: Руководство по JavaScript для HyperCalc

---

Неинтуитивные результаты при работе с большими числами 9100))

Это явно неправильно — и даже не кажется хорошим приближение. В чем дело?

Давайте попробуем вычислить правильный ответ сами. Нам надо выразить ответ как 10 в степени 10 в степени чего-то, потому что это стандартный формат, который использует калькулятор, и мы собирается увидеть, сколько ошибок он сделал. Итак, мы хотим вычислить

27 ^{10 10 100}

как «башню» степеней 10. Первый шаг — выразить силу 27 в степени 10 с произведением в показателе степени по формуле х ^г = 10 ^{(log(x) . г)} :

27 ^{10 10 100} = 10 ^{(лог ₁₀ 27 . 10 10 100}

1 3) log ₁₀ 27 составляет около 1,43, поэтому мы имеем

27 ^{10 10 100} = 10 ^{1,43 . 10 10 100}

Теперь у нас есть основание 10, но показатель степени еще нуждается в доработке. Следующий шаг состоит в том, чтобы выразить произведение в виде суммы в следующем более высоком показателе степени; на этот раз мы используем формулу x ^. y = 10 ^{(log(x) + log(y))} :

10 ^{1,43 . 10 10 100} = 10 ^{10 (log ₁₀ 1,43 + 10 100 )}

3 log ₁₀ 1,43 составляет около 0,155, и если мы добавим это к 10 ¹⁰⁰ , мы получим

10 ^{10 (0,155 + 10 100 )} = 10 ^{10 1000 . .. 000.155}
= 10 ^{10 (1.000 … 000155 9гуголплекс достаточно точно увидеть погрешность калькулятора — и посмотрите, какая погрешность мала! калькулятор должен иметь по крайней мере 104 цифры точности, чтобы быть может обрабатывать значение «1.000…000155» — но оно имеет только 16 цифр точности. Эти 16 цифр занимают 1 и первая пятнадцать нулей — так что, когда калькулятор дойдет до шага, на котором мы добавление 0,155 к 1,0 . 10 100 , это просто округляет ответ до 1,0×10 100 — и выдает ответ, который мы видели, когда выполняли расчет: 9100)) = 10 10 1,00 × 10 100}

Первоначальная версия Hypercalc для Palm имела дисплей, похожий на калькулятор. короткий широкий прямоугольник, дающий достаточно места для отображения одной строки текста около 30 или 40 символов. Учитывая эту ограниченную область отображения, даже если бы он имел необходимые 104 цифры точности, он не имел бы места для вывода на экран всех 104 цифр, поэтому ответ отображаемый будет по-прежнему выглядеть так же.

Более того, независимо от того, сколько цифр мы пытаемся отобразить, всегда будет еще большее число, чем мы будем в состоянии справиться. Например, для Hypercalc потребуется чуть более миллион цифр точности, чтобы отличить

27 ^{10 10 1000000}   от   10 ^{10 10 1000000}

и если мы просто добавим еще одну десятку к этой башне показателей, вся надежда избегания округления теряется!

Для получения дополнительной информации по этому вопросу см. мое обсуждение «парадокс силовой башни» и Номера класса 3 и Разделы чисел класса 4 моих больших чисел страницы.

---

Домашние страницы Роберта Мунафо на AWS © 1996-2022 Роберт П. Мунафо. о   контакт
Эта работа находится под лицензией Creative Commons Attribution-NonCommercial 4.0 Международная лицензия. Подробности здесь.
Эта страница была написана на «неудобочитаемом» языке разметки RHTF и последний раз обновлялась 12 ноября 2020 года. Калькуляторы Abacus (лат. « board ») представляли собой желобчатую доску с подвижными счетными метками, сделанными из костей или камней. Сообщается, что он датируется 3000 г. до н.э. в древности Вавилон до появления снова в 5 веке Греция .

Перенесемся в 21 век, и у нас есть не только калькуляторы, которые помещаются в маленькие компьютеры, но и продвинутые, которые не требуют, чтобы пользователи устанавливали их на свой компьютер.

Вот 10 лучших веб-сайтов для выполнения расчетов, начиная от основных математических операций и заканчивая решением сложных финансовых вопросов.

1. Desmos

Desmos — это расширенный научный онлайн-калькулятор. Он имеет пользовательский интерфейс с вкладками и кнопками для выполнения расчетов в градусах и радианах, углах, значениях круговой диаграммы, процентах, степенях и круглых числах.

РЕКЛАМА

Он также имеет вкладку для ввода букв и специальных символов, например. скобки напрямую. Что еще круче, так это его меню настроек, в котором есть параметры для режима Брайля, режима проектора, обратного контраста (темный режим) и т. д. можно управлять как с клавиатуры, так и с помощью кнопок мыши. Он имеет отображение математических формул, поддержку больших чисел, средство решения уравнений и виджеты калькулятора.

Он достаточно мощный для решения задач по дифференциальному и интегральному исчислению, теории чисел, стандартным функциям, статистике, графикам, комплексным числам и т. д. который предлагает группу из 300+ бесплатных, высокофункциональных калькуляторов для решения всех видов математических и бизнес-задач. В нем есть калькуляторы для заработной платы и подоходного налога, выхода на пенсию, контрактов, кредитов, Forex, 2D и 3D-форм, среднего балла, логистики, продаж и инвестиций, управления человеческими ресурсами и нескольких других категорий расчетов.

Бесплатные онлайн-калькуляторы

4. GeoGebra

GeoGebra — это многофункциональная онлайн-платформа с открытым исходным кодом, созданная для объединения алгебры, геометрии, электронных таблиц, статистики, графиков и математических вычислений в одном простом в использовании пакете. с тех пор стала ведущим поставщиком программного обеспечения для динамической математики для поддержки обучения STEM.

Простой в использовании интерфейс с авторским инструментом для создания интерактивных учебных ресурсов на многих языках для людей во всем мире.

GeoGebra Scientific Calculator

5. Calculator-1.com

Calculator-1.com — это большой, простой и удобный онлайн-калькулятор для использования на работе, в школе и в личных целях. Он имеет функции для выполнения не только основных математических расчетов, но и процентных ставок по кредитам и ипотечным платежам, коммунальных платежей и счетов за работу.

Бесплатный удобный калькулятор

6. Symbolab

Symbolab — это современный онлайн-калькулятор для решения практически любых математических задач. В нем есть кнопки и готовые вкладки для построения графиков, касательных, матриц, многомерного исчисления, множеств и т. д.

Использование Symbolab удобно, поскольку оно имеет кнопки, которые можно легко щелкнуть, чтобы заполнить поле задачи, а затем отредактировать, чтобы сохранить значения задачи.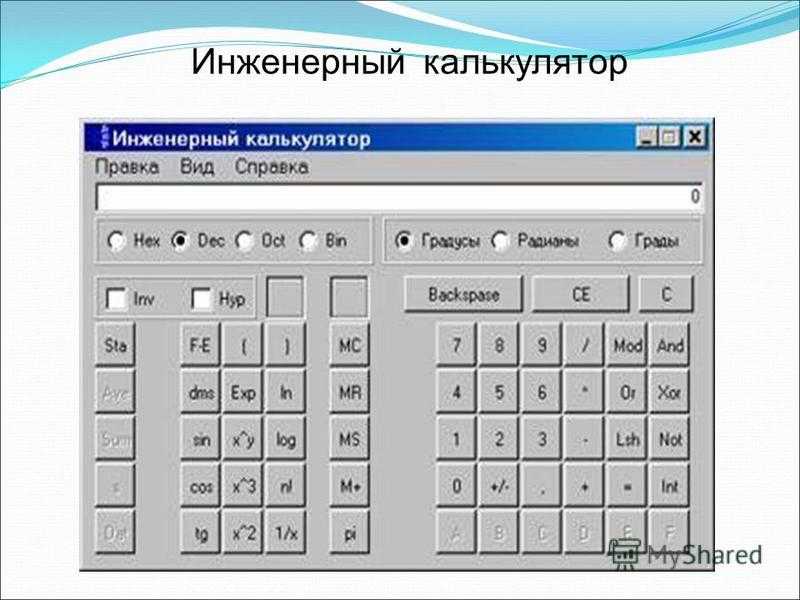

Усовершенствованный онлайн-калькулятор

7. Мета-калькулятор

Мета-калькулятор — это комплексный сложный научный онлайн-калькулятор и средство решения уравнений. Он имеет все основные функции и кнопки, включая функции sin, cos, tan, sech, перестановки и комбинации, общие кратные и т. д.

Он также может решать линейные уравнения, которые могут содержать до 6 уравнений с 2 ​​или 3 переменными и кнопка памяти для будущих расчетов.

Онлайн-калькулятор с функцией решения уравнений

8. Онлайн-калькулятор

Онлайн-калькулятор — это онлайн-калькулятор, созданный с мыслью о том, что «каждому в какой-то момент нужен калькулятор». В сочетании с возможностью быстрой загрузки он предлагает пользователям различные экраны для различных типов расчетов в виде таких модулей, как калькулятор ИМТ, конвертер расстояний, конвертер размеров колец, калькулятор патио, научный калькулятор, конвертер веса, секундомер, средство выбора случайных имен и т. д.

Бесплатный онлайн-калькулятор

9. Calculator.net

Calculator.net — это веб-сайт, на котором размещено 200+ различных калькуляторов, единственной целью которых является предоставление быстрых, всеобъемлющих и бесплатных онлайн-калькуляторов, которые удобны в использовании.

Калькуляторы сгруппированы в финансовые, например. автокредит, инфляция, оплата, процентная ставка, зарплата, калькулятор налога с продаж; Фитнес и здоровье калории, ИМТ, темп, зачатие беременности, калькуляторы жировых отложений; Математика калькуляторы треугольников, стандартных отклонений, процентов, дробей; и другие GPA, бетон, калькуляторы подсети, генератор паролей; и т. д.

Финансовые онлайн-калькуляторы

10. Bankrate

Bankrate — это независимая поддерживаемая рекламой платформа для издателей и служб сравнения с множеством онлайн-калькуляторов, которые позволяют пользователям выполнять расчеты, связанные с финансами, начиная от ипотечных кредитов и заканчивая пенсионными планами и налоговая декларация.