Напряжение это сила. Напряжение и сила тока: что опаснее для человека и как они связаны

Что такое напряжение и сила тока в электрической цепи. Как напряжение и сила тока связаны между собой. Какой параметр опаснее для человека — напряжение или сила тока. Какие значения напряжения и тока считаются опасными для жизни.

Что такое напряжение и сила тока

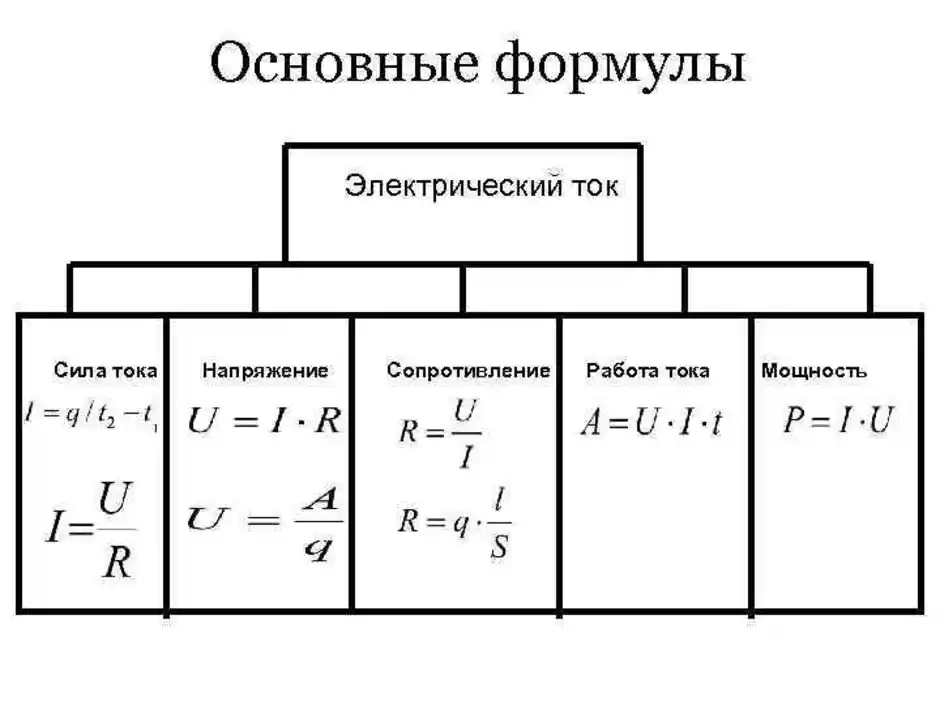
Напряжение и сила тока — два ключевых параметра, характеризующих электрический ток. Чтобы разобраться, что опаснее для человека, давайте сначала определим, что они собой представляют:

• Напряжение — это разность электрических потенциалов между двумя точками электрической цепи. Измеряется в вольтах (В). Напряжение можно представить как «электрическое давление», заставляющее электроны двигаться по проводнику.
• Сила тока — это количество электричества, проходящее через поперечное сечение проводника за единицу времени. Измеряется в амперах (А). Сила тока показывает, насколько интенсивно движутся электроны в цепи.

Как связаны напряжение и сила тока

Напряжение и сила тока тесно связаны между собой. Их взаимосвязь определяется законом Ома:

I = U / R

Где:

• I — сила тока (А)
• U — напряжение (В)
• R — сопротивление проводника (Ом)

То есть при постоянном сопротивлении, чем выше напряжение, тем больше сила тока. И наоборот, чем ниже напряжение, тем меньше сила тока.

Что опаснее для человека — напряжение или сила тока

Многие ошибочно полагают, что опасность поражения электрическим током определяется только напряжением. На самом деле главную опасность представляет именно сила тока, проходящего через тело человека.

Сила тока оказывает непосредственное воздействие на организм:

• Вызывает сокращение мышц
• Нарушает работу нервной системы
• Может привести к фибрилляции сердца
• Вызывает ожоги тканей

При этом напряжение играет важную роль, так как от него зависит, какой ток будет протекать через тело человека.

Какие значения силы тока опасны для человека

Рассмотрим, какое воздействие оказывают различные значения силы тока на организм человека:

• 0,6-1,5 мА — порог ощущения. Легкое покалывание.
• 2-3 мА — ощутимый ток. Болезненные ощущения.
• 5-7 мА — судорожное сокращение мышц. Трудно самостоятельно оторваться от проводника.
• 20-25 мА — паралич дыхательных мышц. Остановка дыхания.
• 100 мА — фибрилляция сердца. Высокая вероятность смертельного исхода.

Как видим, смертельно опасным может быть ток всего в 100 мА. При этом бытовая розетка способна выдать ток до 16 А, что в 160 раз больше смертельного значения!

Какое напряжение считается опасным

Хотя опасность определяется в первую очередь силой тока, существуют общепринятые безопасные и опасные уровни напряжения:

• До 42 В переменного тока — считается безопасным напряжением
• 42-380 В — опасное напряжение
• Свыше 380 В — особо опасное напряжение

Однако даже низкое напряжение может быть опасным при определенных условиях, например при повышенной влажности.

Почему опасно высокое напряжение

Высокое напряжение представляет опасность по нескольким причинам:

• Способно пробить защитные средства (кожу, одежду)
• Вызывает более сильный ток через тело человека
• Может вызвать дуговой разряд на расстоянии
• Приводит к более серьезным ожогам

Поэтому работы с высоковольтным оборудованием требуют особых мер предосторожности.

От чего зависит сопротивление тела человека

Сила тока, проходящего через тело человека, зависит не только от напряжения, но и от сопротивления тела. На сопротивление влияют следующие факторы:

• Состояние кожи (сухая, влажная, поврежденная)
• Площадь контакта
• Путь прохождения тока через тело
• Длительность воздействия
• Индивидуальные особенности организма

При неблагоприятных условиях сопротивление тела может снизиться в десятки раз, что увеличивает опасность поражения.

Как защититься от поражения электрическим током

Для защиты от поражения электрическим током следует соблюдать следующие меры безопасности:

• Использовать защитное заземление оборудования
• Применять устройства защитного отключения (УЗО)
• Работать с электроприборами только сухими руками
• Не касаться одновременно электроприбора и заземленных предметов
• Регулярно проверять исправность изоляции проводов
• При работе с электроустановками использовать средства индивидуальной защиты

Соблюдение этих простых правил поможет избежать опасных ситуаций при обращении с электричеством.

Заключение

Подводя итог, можно сказать, что хотя напряжение и сила тока тесно связаны, именно сила тока представляет основную опасность для человека. При этом высокое напряжение повышает риск поражения, так как способствует увеличению силы тока через тело. Поэтому при работе с электричеством важно учитывать оба эти параметра и соблюдать необходимые меры предосторожности.

Напряжение это сила приложенная

Автор На чтение 11 мин. Опубликовано 12.12.2019

изучаем сопротивление материалов

Напряжения

, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м 2 (МПа = 10 6 Н/м 2 , кгс/см 2 =98 066 Па ≈ 10 5 Па, тс/м 2 и т. д.).

Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆vec[/math]. Полное среднее напряжение на этой площадке [math]vec <р>= ∆vec/∆A [/math]. Найдем предел этого отношения при [math]∆A o 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.

Полное напряжение [math]vec p[/math], как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σ_n и касательное к площадке – касательное напряжение [math] au_n[/math]. Здесь n – нормаль к выделенной площадке 1 .

Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math] au_, au_[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением [math]vec p [/math], а с его составляющими [math]σ_x, au _, au _ [/math] . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.

Тензор напряжений

Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений

$$ T _sigma = left[matrix <
sigma _x & au _ & au _ \
au _ & sigma _y & au _ \ au _ & au _ & sigma _z
>
ight]$$

Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.

При повороте осей координат, совпадающих с нормалями к граням выделенного

элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

В каждой точке можно провести три взаимно-перпендикулярных главных площадки.

При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).

Связь внутренних усилий и напряжений

Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.

Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:

Продольное усилие на площадке dA: dN = σ_zdA
Поперечная сила вдоль оси х:

dQ _x = [math] au [/math] dA
Поперечная сила вдоль оси y: dQ _y = [math] au [/math] dA
Элементарные моменты вокруг осей x,y,z: $$egindM _x = σ _z dA cdot y \ dM _y = σ _z dA cdot x \ dM _z = dM _k = au _ dA cdot x – au _ dA cdot y end$$

Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.

1 Проекция вектора полного напряжения на нормаль к данной площадке называется нормальным напряжением и обознача­ется через σ_n.

Напряжение – мера распределения внутренних сил по сечению.

, где– внутренняя сила, выявленная на площадке.

Полное напряжение .

Нормальное напряжение – проекция вектора полного напряжения на нормаль обозначается через σ. , где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается.

Касательное напряжение – составляющие напряжения в плоскости сечения. , где(для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига.

7. Закон Гука для одноосного напряжённого состояния в точке и закон Гука для чистого сдвига. Модули упругости первого и второго рода, их физический смысл, математический смысл и графическая интерпретация. Коэффициент Пуассона.

– закон Гука для одноосного напряжённого состояния в точке.

Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см 2 .

– закон Гука для сдвига.

G– модуль сдвига (модуль упругости II рода). Размерность модуляGтакая же, как и у модуля Е, т.е. кГ/см 2 ..

μ – коэффициент Пуассона (коэффициент пропорциональности). . Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала).

8. Центральное растяжение (сжатие) прямого бруса. Определение внутренних продольных сил методом сечений. Правило знаков для внутренних продольных сил. Привести примеры расчёта внутренних продольных сил.

Брус испытывает состояние центрального растяжения (сжатия) в том случае, если в его поперечных сечениях возникают центральные продольные силы N_z(т.е. внутренняя сила, линия действия которой направлена по осиz), а остальные 5 силовых факторов равны нулю (Q_x=Q_y=M_x=M_y=M_z=0).

Правило знаков для N_z: истинная растягивающая сила – «+», истинная сжимающая сила – «-».

9. Центральное растяжение (сжатие) прямого бруса. Постановка и решение задачи об определении напряжений в поперечных сечениях бруса. Три стороны задачи.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

Постановка: Прямой брус из однородного материала, растянутый (сжатый) центральными продольными силами N. Определить напряжение, возникающее в поперечных сечениях бруса, деформации и перемещения поперечных сечений бруса в зависимости от координатzэтих сечений.

10. Центральное растяжение (сжатие) прямого бруса. Определение деформаций и перемещений. Жёсткость бруса при растяжении (сжатии). Привести примеры соответствующих расчётов.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

.

При центральном растяжении (сж.) бруса в поперечном направлении в сечении возникает только нормальное напряжение σ_z, постоянное во всех точках поперечного сечения и равноеN_z/F. , гдеEF– жёсткость бруса при растяжении (сжатии). Чем больше жёсткость бруса, тем меньше деформируется бус при одной и той же силе. 1/(EF) – податливость бруса при растяжении (сжатии).

11. Центральное растяжение (сжатие) прямого бруса. Статически неопределимые системы. Раскрытие статической неопределимости. Влияние температурного и монтажного факторов. Привести примеры соответствующих расчётов.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

Если число линейно-независимых уравнений статики меньше числа неизвестных, входящих в систему этих уравнений, то задача по определению этих неизвестных становится статически неопределимой. (На сколько удлинится одна часть, на столько сожмётся вторая).

Нормальные условия – 20º С. .f(σ,ε,tº,t)=0 – функциональная зависимость между 4 параметрами.

12. Опытное изучение механических свойств материалов при растяжении (сжатии). Принцип Сен-Венана. Диаграмма растяжения образца. Разгрузка и повторное нагружение. Наклёп. Основные механические, прочностные и деформационные характеристики материала.

Механические свойства материалов вычисляют с помощью испытательных машин, которые бывают рычажными и гидравлическими. В рычажной машине усилие создаётся при помощи груза, действующего на образец через систему рычагов, а в гидравлической – с помощью гидравлического давления.

Принцип Сен-Венана: Характер распределения напряжения в поперечных сечениях достаточно удалённых (практически на расстояния, равные характерному поперечному размеру стержня) от места приложения нагрузок, продольных сил не зависит от способа приложения этих сил, если они имеют один и тот же статический эквивалент. Однако в зоне приложения нагрузок закон распределения напряжения может заметно отличаться от закона распределения в достаточно удалённых сечениях.

Если испытуемый образец, не доводя до разрушения, разгрузить, то в процессе разгрузки зависимость между силой Р и удлинением Δlобразец получит остаточное удлинение.

Если образец был нагружен на участке, на котором соблюдается закон Гука, а затем разгружен, то удлинение будет чисто упругим. При повторном нагружении пропадёт промежуточная разгрузка.

Наклёп (нагартовка) – явление повышения упругих свойств материала в результате предварительного пластического деформирования.

Предел пропорциональности – наибольшее напряжение, до которого материал следует закону Гука.

Предел упругости – наибольшее напряжение, до которого материал не получает остаточных деформаций.

Предел текучести – напряжение, при котором происходит рост деформации без заметного увеличения нагрузки.

Предел прочности – максимальное напряжение, которое может выдержать образец, не разрушаясь.

13. Физический и условный пределы текучести материалов при испытании образцов на растяжение, предел прочности. Допускаемые напряжения при расчёте на прочность центрально растянутого (сжатого) бруса. Нормативный и фактический коэффициенты запаса прочности. Привести числовые примеры.

В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести принимается условно величина напряжения, при котором остаточная деформация ε_ост=0,002 или 0,2%. В некоторых случаях устанавливается предел ε_ост=0,5%.

max|σ_z|=[σ].,n>1(!) – нормативный коэффициент запаса прочности.

– фактический коэффициент запаса прочности.n>1(!).

14. Центральное растяжение (сжатие) прямого бруса. Расчёты на прочность и жёсткость. Условие прочности. Условие жёсткости. Три типа задач при расчёте на прочность.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

15.Обобщённый закон Гука для трёхосного напряжённого состояния в точке. Относительная объёмная деформация. Коэффициент Пуассона и его предельные значения для однородного изотропного материала.

,,. Сложив эти уравнения, получим выражение объёмной деформации:. Это выражение позволяет определить предельное значение коэффициента Пуассона для любого изотропного материала. Рассмотрим случай, когда σ_x=σ_y=σ_z=р. В этом случае:. При положительном р величина θ должна быть также положительной, при отрицательном р изменение объёма будет отрицательным. Это возможно только в том случае, когда μ≤1/2. Следовательно, значение коэффициента Пуассона для изотропного материала не может превышать 0,5.

16. Соотношение между тремя упругими постоянными для изотропного материала (без вывода формулы).

,,.

17. Исследование напряжённо-деформированного состояния в точках центрально-растянутого (сжатого) прямого бруса. Закон парности касательных напряжений.

,.

– закон парности касательных напряжений.

18. Центральное растяжение (сжатие) бруса из линейно-упругого материала. Потенциальная энергия упругой деформации бруса и её связь с работой внешних продольных сил, приложенных к брусу.

А=U+K. (В результате работы накапливается потенциальная энергия деформированного телаU, кроме того, работа идёт на совершение скорости массе тела, т. е. преобразуется в кинетическую энергию).

Если центральное растяжение (сжатие) бруса из линейно-упругого материала производится очень медленно, то скорость перемещения центра масс тела будет весьма малой. Такой процесс нагружения называется статическим. Тело в любой момент находится в состоянии равновесия. В этом случае А=U, и работа внешних сил целиком преобразуется в потенциальную энергию деформации.,,.

Для улучшения этой статьи желательно ? : Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Wikimedia Foundation . 2010 . Смотреть что такое «Механическое напряжение» в других словарях: механическое напряжение — деформация напряженное состояние воздействие — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы деформациянапряженное состояниевоздействие EN… … Справочник технического переводчика механическое напряжение — Stress (Mechanical) Механическое напряжение Мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий. Механическое напряжение в точке тела измеряется отношением упругой силы, возникающей в теле при деформации, к … Толковый англо-русский словарь по нанотехнологии. – М. механическое напряжение — įtempis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, susijęs su v >Penkiakalbis aiškinamasis metrologijos terminų žodynas механическое напряжение — įtempis statusas T sritis fizika atitikmenys: angl. stress vok. Beanspruchung, f; Spannung, f rus. механическое напряжение, n; напряжение, n pranc. contrainte, f; contrainte mécanique, f … Fizikos terminų žodynas механическое напряжение — įtempis statusas T sritis Energetika apibrėžtis V >Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas механическое напряжение — mechaninis įtempis statusas T sritis chemija apibrėžtis V >Chemijos terminų aiškinamasis žodynas механическое напряжение — mechaninis įtempis statusas T sritis fizika atitikmenys: angl. mechanical stress vok. mechanische Biegespannung, f rus. механическое напряжение, n pranc. contrainte mécanique, f … Fizikos terminų žodynas механическое напряжение, приводящее к отказу (оборудования) — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN stress to failureSTOF … Справочник технического переводчика Касательное механическое напряжение — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия Нормальное механическое напряжение — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия

Понятие силы тока, мощности, напряжения

При рассмотрении понятий силы тока, напряжения, мощности, нужно осознавать то, что все эти три параметра неразрывно связанны.
 

Мощность – это отношение производимой за определенный отрезок времени работы к данному отрезку времени. Единицей измерения является Ватт. 1 киловатт равен 1000 ватт.
 

Сила тока – это устремленное перемещение заряженных частиц. Выражает количество заряда, что пробегает сквозь разрез проводника за единицу времени. Единицей измерения является Ампер.
 

Напряжение – это отношение работы, выполненной электрическим полем для перенесения заряда, к значению переносимого заряда на полосе цепи. Этот параметр выражает работу, проделанную полем для передачи заряда между двумя точками. Единицей измерения является Вольт.
 

Можно провести аналогию описываемых параметров “силы”, “мощности” и “напряжения” с течением воды, где число ампер (сила тока) – это объем воды, пробегающей за единицу времени (обусловливается расходованием электричества, иными словами зависит от того, насколько сильно открыт кран), количество ватт (мощность) – это, к примеру, действие по приведению в движение лопастей турбины (давление перемноженное на силу тока), а значение вольт (напряжение) – это напор воды в трубопроводе. Стало быть, на блоке питания принципиальной является мощность, то есть, выдержит ли прибор, на батарейке – напряжение, потянет ли пользователь. На устройствах для электросети с установленным напряжением (220 вольт у нас) максимум силы тока, при перемножении этого показателя на значение напряжения, параллельно является и максимумом мощности.
 

Как же вычислить мощность с помощью величины напряжения и силы тока?
 

«Мощность» = «Сила тока» (Амперы) умножить на «Напряжение» (Ватты).
 

Как провести расчет силы тока по мощности и напряжению?
 

Исходя из предыдущей формулы, можем найти значение силы тока:
 

«Сила тока» = «Мощность» (Вольт-ампер) разделить на «Напряжение» (Ватты).
 

Существует еще пара значимых факторов, ежели речь идет об электричестве:
 

— Типичные розетки предусмотрены для силы тока числом 16 ампер. Так, как напряжение в электросети 220 вольт, значит, граничная мощность равна: 16 ампер умножить на 220 вольт = 3520 ватт (3,52 киловатт).
— В производстве розеток, в основном, используют 16-амперные автоматы. Из этого следует, что, когда на линии электропередачи с 16-амперным автоматом сила тока превысит 16 ампер (либо мощность возрастет свыше 3,52 киловатт), прибор автоматически вырубится. 

 

В частности, если в вашем доме проведена индивидуальная линия для кухонных розеток, то во время подсоединения к данной линии сразу двух электрообогревателей, с мощностью обоих в 2 киловатта, автомат разъединит электрическую цепь.

Что такое сила тока и напряжение

Меня всегда интересовала тема электрического тока и электронных микросхем.

И я никак не мог понять электрический ток. Ну, то есть я не мог понять, что значит вот это выражение «сила тока» или «напряжение». Что вообще значит разность потенциалов, и почему что-то куда-то от этого течёт.18. Если с нулями написать — 6 240 000 000 000 000 000 зарядов электрона составляют 1 кулон. То есть есть туча электронов, которые и переносят этот заряд. На каждый электрон приходится по одному заряду.

И вот как только я осознал, что ампер — это количество зарядов, сразу стали понятны все эти параллельные и перпендикулярные соединения.

Течёт себе по проводу 1 кулон зарядов, притёк он такой к развилке параллельного соединения — дальше по одной развилке потекла половина заряда и по другой — тоже половина (если там одинаковые лампочки, например). Потом они после этой развилки вместе слились — и снова бац — один кулон этих частиц с зарядом.

Вот и получается, что количество зарядов гуляет по цепи одинаковое количество. И поэтому то, что называют силой тока — это количество зарядов. То есть термин «сила тока» — очень хреновый термин. Количество зарядов за секунду — куда длинней звучит, но при этом куда проще.

Дальше переходим к напряжению. И его тоже я понять не мог. Естественно. Мне же его объясняли так же, как и силу тока. То есть хреново.

Что такое напряжение? Напряжение — это энергия, которая высвобождается, когда единичный заряд «сползает» от высокого потенциала к низкому. Чтобы у этого заряда был заряд, его туда нужно «затолкать». Работа (или энергия), которая затрачивается на то, чтобы этот заряд туда «загнать» в идеальном мире равна той энергии, которая высвободится. Поэтому её тоже можно назвать напряжением )

То есть вот есть у нас провод длиной 10 метров. Слева избыток заряда, справа — недостаток. Задача — обеспечить равновесие. Напряжение — это энергия, которая высвободится, пока заряды будут бежать от одного конца к другому.

По этой причине напряжение можно представить как цикл энергичных пинков под задницу зарядам. 😆 И они такие побежали. А кто не побежит? )

Напряжение измеряется в джоулях на кулон. Или — что то же самое — в вольтах. Иными словами, кулон (количество зарядов) получает пинок в 1 джоуль и бежит из точки А в точку Б. И если он добежал до точки Б, говорят, что между точками А и Б — разница потенциалов была равна 1 вольт.

Теперь лучше всего сделать паузу, выпить кофейку или чайку и посмотреть вот это гениальное видео, в котором автор Михаил Майоров очень наглядно показал электрический ток в аналогии с током воды. Очень рекомендую: всего 18 минут, а очень круто показано.

Собственно, после просмотра этого видео у меня в голове появилось хоть какое-то соображение, что к чему )

А следующим весомым шагом стала книга «Искусство схемотехники» (The Art of Electronics) авторов П. Хоровиц и У. Хилл (Paul Horowitz, Winfield Hill). Конкретно по данному вопросу нужно читать страницу 9 их шикарной книги ) Очень рекомендую. В сети найти можно, а если ищется с трудом — то она есть вот тут: http://nnm-club.me/forum/viewtopic.php?t=754538

Сопромат.in.ua: Напряжения

Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м² (МПа = 10⁶ Н/м², кгс/см²=98 066 Па ≈ 10⁵Па, тс/м² и т. д.).

Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.

\textstyle \vec{p} = \lim_{\Delta A \to 0} {\Delta\vec{R}\over \Delta A}

Полное напряжение [math]\vec p[/math], как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σ_n и касательное к площадке – касательное напряжение [math]\tau_n[/math]. Здесь n – нормаль к выделенной площадке.

Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_{nx}, \tau_{ny}[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

$$\vec{p} = \left[\matrix{\sigma _n \\ \tau _{nx} \\ \tau _{nx}} \right]$$

Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением [math]\vec p [/math], а с его составляющими [math]σ_x,\tau _{xy}, \tau _{xz} [/math] . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.

Тензор напряжений

При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – [math]σ_x,\tau _{xy}, \tau _{xz} [/math]

Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений

$$ T _\sigma = \left[\matrix{
\sigma _x & \tau _{yx} & \tau _{zx} \\
\tau _{xy} & \sigma _y & \tau _{zy} \\ \tau _{xz} & \tau _{yz} & \sigma _z
}\right]$$

Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.

При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

Площадка, на которой касательные напряжения равны нулю, называется главной площадкой.

Нормальное напряжение на главной площадке называется главным напряжением

Нормаль к главной площадке называется главной осью напряжений .

В каждой точке можно провести три взаимно-перпендикулярных главных площадки.

При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).

Связь внутренних усилий и напряжений

Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.

Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:

Продольное усилие на площадке dA: dN = σ_zdA
Поперечная сила вдоль оси х: dQ _x = [math]\tau {zx}[/math] dA
Поперечная сила вдоль оси y: dQ _y = [math]\tau {zy}[/math] dA
Элементарные моменты вокруг осей x,y,z: $$\begin{array}{lcr} dM _x = σ _z dA \cdot y \\ dM _y = σ _z dA \cdot x \\ dM _z = dM _k = \tau _{zy} dA \cdot x — \tau _{zx} dA \cdot y \end{array}$$

Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.

---

---

Связанные статьи

метки: напряжения

Сила тока и напряжение: что опаснее — простыми словами о важных вещах! | Электрика для всех

Сегодня мы поговорим о самых важных в электрике и электронике понятиях — силе тока и напряжении. Это ключевые вещи, поэтому если вы до сих пор не разобрались, чем они отличаются — давайте устраним эту проблему и разложим вольты с амперами по полочкам раз и навсегда вместе!

Какой насос качает электричество?

Главное, что вам нужно понять — электричество есть везде, весь мир держится на электричестве и даже то, что вы стоите на полу, а не проваливаетесь через него, это также заслуга электричества. Поэтому говорить о том, что в розетке есть электричество, а в кирпиче нет некорректно. Причина, по которой розетка может ударить вас током, если засунуть внутрь гвоздь в том, что есть источник электрического тока, который через провода подключен к розетке.

Представьте ведро с водой — можно засунуть в ведро трубу, но вода так и останется внутри. Для того, чтобы заставить её течь, нужен насос. Источник тока — батарейка, аккумулятор, подстанция — это и есть насос, который берёт неподвижный электрический ток и начинает его толкать по проводам, создавая потенциал.

Напряжение толкает ток, а его количество — это и есть сила

Потенциал или напряжение это то же, что, например, высота, с который вы льёте воду из ведра: чем выше поднять ведро, тем сильнее вода будет бить по земле или вашей ладони. Напряжение может быть без тока, так же, как вода в ведре необязательно падает вниз, даже если ведро поднять очень высоко: мешают стенки ёмкости или изоляция. Переверните ведро и вода потечёт. Количество воды, которое протекает через устье ведра или трубу — это и есть сила тока.

Чем выше напряжение, тем сильнее оно давит на электричество. Если давление очень высокое, даже изолятор может не выдержать и прорваться, как прорывается воздух при разряде молнии — это называется пробой изоляции. И, конечно, чем выше напряжение — тем большее количество тока течёт через проводники, то есть сила тока прямо зависит от напряжения.

Заметьте, как неудачно выбран термин — миллионы людей спотыкаются об это слово «сила тока», которое не имеет смысла и всех путает, тогда как это не «сила» тока, а попросту его количество!

Наше тело и электричество: току всё равно, через что протекать

Теперь нетрудно понять, что именно опасно в электричестве. Это именно напряжение — чем выше давление тока, тем легче он прорывает защиту нашей кожи, которая пробивается уже при 70 вольтах. А дальше ток течёт через ткани нашего тела, насыщенные водой, без особых трудностей, поражая нервную систему и, особенно, сердце.

Будьте осторожны и помните — электричество это энергия, которая может выполнить работу, а может стать причиной разрушения, если с ней не дружить.

Спасибо за просмотр и лайк!

Механическое напряжение — это… Что такое Механическое напряжение?

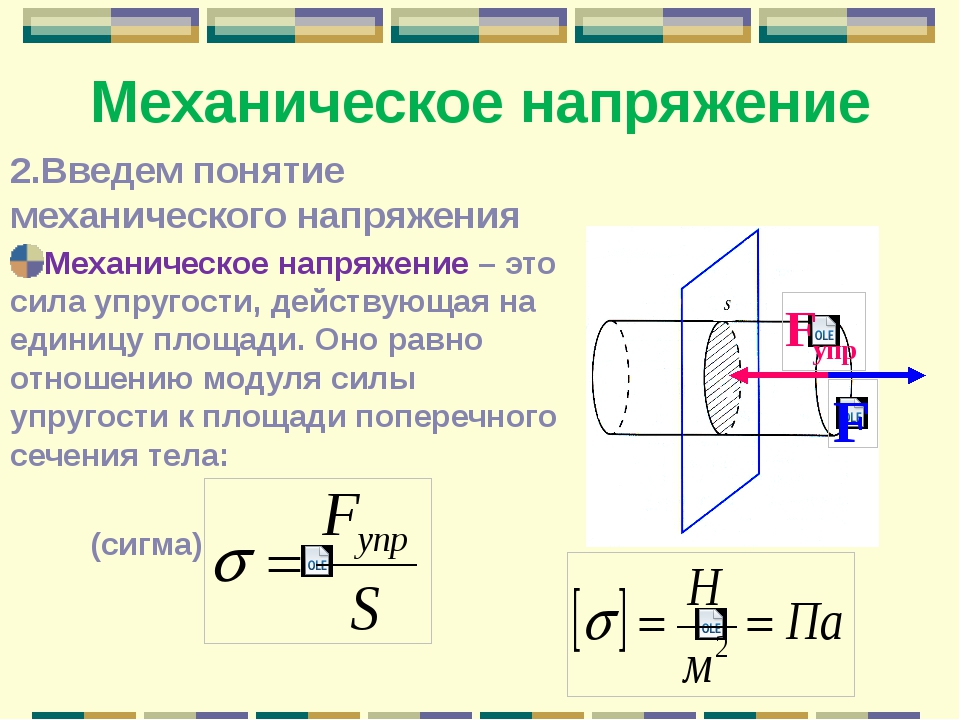
У этого термина существуют и другие значения, см. Напряжение.

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается ).
• Касательное механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В системе СИ механическое напряжение измеряется в паскалях.

Тензор механического напряжения

Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ.

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений равны отношению компоненты силы , действующей на элементарную площадку к её площади:

Здесь под понимаются компоненты вектора, образованного из нормали к элементарной площадке и её площади :

Таким образом сила, действующая на некий объём V равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма (в отсутствие объёмных сил):

См. также

Электрическое напряжение: объяснение простыми словами

Электрическое напряжение: объяснение простыми словами

Электрическим напряжением обозначается физическая величина, равная разности потенциалов между двумя точками электрического поля при перемещении единичного заряда. Для простых пользователь такое обозначение не всегда понятно. Поэтому в этой статье мы попытаемся простым, доступным языком рассказать, что собой представляет электрическое напряжение, как оно измеряется и для чего это нужно.

Что такое разность потенциалов?

Для начала проанализируем рисунок:

В первой бутылке вода находится на уровне 300 мм, а во второй – на отметке 150 мм. Разница между уровнями воды в обоих емкостях составляет 150 мм. Если рассматривать это с точки зрения науки об электричестве, это и есть разность потенциалов.

Однако, что будет, если соединить обе бутылки шлангом, а внутрь поместить обычный пластиковый шарик?

Из школьного урока физики о принципе соединяющихся сосудах знаем, что из бутылки, где уровень воды больше, жидкость постепенно перетечет в бутылку с более низким уровнем. Под воздействием потока воды шарик внутри соединяющего шланга будет перемещаться. Процесс перетекания завершится после того, как в обоих бутылках уровень жидкости уравновесится, станет одинаковым.

Иными словами, в ситуации, когда в соединенных между собой емкостях уровень жидкости станет одинаковым, результатом разности потенциалов станет ноль. Шарик останется на месте за счет электродвижущей силы, которая, по итогам эксперимента, равна нулю.

Что такое электродвижущая сила?

Аналогично напряжению, единицей измерения электродвижущей силы (ЭДС) является Вольт.

Для проведения следующего эксперимента понадобится вольтметр (прибор, измеряющий вольты) и обычная батарейка.

При исходном замере прибор покажет 1.5 В (Вольта). Однако это не является напряжением – значение указывает на величину электродвижущей силы.

На следующем этапе эксперимента к батарейке подключаются две лампочки. А напряжение измеряется в разных участках электроцепи.

Внимание следует уделить следующим показателям: напряжение для одной лампочки составляет 1 Вольт, для другой же это значение 0.3 Вольта.

Напряжение в используемых нами осветительных устройствах напрямую зависит от их мощности, измеряемой в Ваттах.

Мощность=Напряжение*ток (Р=U*I)

Из этого следует, что чем больше будет значение мощности лампы, тем большее напряжение будет на ней.

Однако, как же получается: если мощность батарейки 1.5 Вольта, к которой подключены лампочки, разделена на 1 Вольт и 0.3 Вольта, куда направились еще 0.2 Вольта? Дело в том, что каждая батарейка наделена своим внутренним сопротивлением, поэтому недостающие 0.2 Вольта были направлены именно сюда.

Резюме

Электродвижущей силой определена физическая величина, характеризующая в источниках тока работу сторонних силовых ресурсов. Посредством электродвижущей силы мы можем определять, как переносится заряд от источника тока по всей электрической цепи. Напряжение показывает этот процесс лишь на отдельном участке этой цепи. Если проще: напряжение – это внешнее силовое воздействие, способствующее перемещению шарика в шланге, соединяющим сосуды из выше приведенного примера. В электричестве напряжение обозначено силой, которая обеспечивает перемещение электронов между атомами.

Рассмотрим еще один пример

Представьте, что вам по силам будет поднять камень, вес которого составляет 40 кг. Это означает, что вы обладаете подъемной силой, равной 40 кг – в электричестве это обозначается как электродвижущая сила. Вы следуете и на своем пути вам попадается камень весом 20 кг. Вы его также берете и переносите на расстояние 10 метров. Для осуществления этого действия вам понадобилось определенное количество энергии, что в электричестве представляется как напряжение. Далее вам попадается камень весом в 30 кг. Следовательно, для его переноса из одного места в другое вам понадобится больше энергии, чем для камня, масса которого не превышала 20 кг. Однако подъемная сила (в электричестве ЭДС), независимо от веса переносимого вами камня, остается всегда одинаковой. При этом, вес камня определяет количество энергии, которая тратится на проведение этого действия (в электричестве это обозначено напряжением). Таким образом, на каждом отрезке вашего пути вы будете испытывать разное напряжение в зависимости от веса камня, который вы намерены перенести.

Ток зависит от напряжения

Закон Ома:

Исходя из приведенной формулы следует: ток является прямо пропорциональным напряжению и обратно пропорциональным сопротивлению. Иными словами, чем больше величина электрического тока, тем больше напряжение, и наоборот.

Исследование напряжения в воздушной линии электропередачи высокого напряжения методом конечных элементов

Основные моменты

•

Нормальный рабочий ток при симметричном расстоянии.

•

Случайный рабочий ток при симметричном расстоянии.

•

Нормальный рабочий ток при несимметричном расстоянии.

•

Случайный рабочий ток при несимметричном расстоянии.

Реферат

Отказ линии передачи — серьезная проблема в развивающихся странах. Основная причина выхода из строя высоковольтной воздушной линии электропередачи в энергосистеме — продолжительный перегрузочный ток. Определение сегментов линии, на которых возникает высокое напряжение из-за продолжительного чрезмерного тока при различных схемах разнесения линий и условий прохождения тока, может привести нас к анализу зон высокого напряжения для эффективного проектирования линий передачи.В этом контексте механическое напряжение на воздушной линии электропередачи высокого напряжения, возникающее в результате чрезмерных или нормальных токов, было вычислено с использованием метода конечных элементов. Исследуются несколько сегментов длинной линии передачи с симметричным и несимметричным шагом при случайном и нормальном линейном токе. В нем определяются отрезки прямых с высоким натяжением. Максимальное суммарное натяжение наблюдается в средних сегментах как симметричной, так и несимметричной линии передачи.При этом максимальное натяжение на единицу находится в начальном и нижнем сегментах. Тем не менее, изменение величины обнаруживается для симметричного и несимметричного расстояния. Настоящее исследование может предоставить технические рекомендации инженерам-проектировщикам и техническим специалистам линий передачи относительно рисков и решений, связанных с системами линий электропередач.

Ключевые слова

Метод конечных элементов

Линия электропередачи

Натяжение

Симметричный интервал

Несимметричный интервал

Случайный ток

Рекомендуемые статьи Цитирующие статьи (0)

Полный текст

© 2019 Elsevier Ltd.Все права защищены.

Рекомендуемые статьи

Цитирующие статьи

Использование силы TENSION

Парадоксальный подход к созданию альянсов дома, в зале заседаний, в университетском городке и в сообществах.

Бренда Наоми Розенберг
Самиа Мустафа Бахсун

Мир находится в состоянии повышенной эмоциональной тревожности. Заголовки от Красного моря до Миссисипи гласят: «Страх смешивается с гневом, поскольку Фергюсон готовится к новым волнениям», «Страхи холокоста преследуют израильтян, готовящихся к возможной войне», «Попытки девочек из Колорадо присоединиться к ИГИЛ вселяют страх в мусульманское сообщество. , »« Рост гнева по поводу принятия мусульманских беженцев и унижение из-за того, что они не находятся в розыске, поскольку бегущие сирийские беженцы не допускаются в Европу ».

«МЫ НАХОДИМСЯ В КРИТИЧЕСКИЙ МОМЕНТ В ИСТОРИИ. МЫ МОЖЕМ ВЫБРАТЬ САМОУНИЧТОЖЕНИЕ ИЛИ СОЗДАТЬ НОВЫЙ ДИСКУРС И БЫТЬ В ПРИСУТСТВИИ ЛУЧШИХ ИЗ НАШЕГО ЧЕЛОВЕЧЕСТВА »Бренда и Самиа

Бренда и Самиа видят необходимость в тектоническом сдвиге в том, как лидеры ведут и решают проблемы.

Эта книга знакомит с их парадоксальным и эволюционным подходом к трансформации конфликтов и межкультурным коммуникациям — «Тектоническое лидерство». Слово «тектонический» происходит от греческого слова «тектон», что означает «строитель» и используется геологами для вывода очень значительных или значительных изменений в структуре земли.
Они используют тектонику земных плит (большие участки земной поверхности, которые смещаются) как метафору для визуализации человеческих взаимодействий. Они признают, что взаимодействие людей в конфликтных ситуациях похоже на линии разлома между тектоническими плитами. Плиты взаимодействуют и создают трение на своих границах, вызывая землетрясения, когда превышается естественная упругость окружающих пород. Взаимодействие с людьми аналогичным образом может создавать линии разлома. Когда давление, создаваемое напряжением и страхом, становится невыносимым, высвобождаемая энергия подобна цунами, вызывая массовую истерию, разжигая ненависть и страх, разделяя нации, разрушая предприятия и сообщества, угнетая людей и разжигая войны.Их модель лидерства — «Тектоническое лидерство» использует силу напряжения и использует напряжение как возможность сообщить тем, кто находится в конфликте, о самых глубоких страхах, боли и ранах, передаваемых между поколениями, которые разделяют людей и отравляют наш мир. В книге «Обуздание силы напряжения» рассказывается о личном путешествии авторов как еврея и араба, а также рассказы других тектонических лидеров о том, как они напрямую справились с напряжением, которое их разделяло, и использовали его для установления более тесных отношений. Посредством пошагового процесса и включенных в него упражнений книга демонстрирует, как можно ступить на линию разлома и обуздать силу напряжения: использовать напряжение для соединения, а не разделения, вовлечения, а не отчуждения, сочувствия и не разрушать, информировать и не запугивать, вводить новшества и не подражать.
Эти истории показывают, как тектонические лидеры работают с напряжением, чтобы разрушить негативные нарративы, укрепить доверие, расширить границы, не меняя основных убеждений, и создать партнерство, несмотря на разногласия.

ОБ АВТОРАХ

Бренда и Самиа не историки, политики, психологи или философы. Это две женщины из совершенно разных профессий, происхождения, культур, идеологий и убеждений, которые разделяют разочарование в связи с неразрешенным конфликтом на глобальном и местном уровнях; двое активистов встревожены отсутствием эффективного руководства в эти неспокойные времена.Бренда Наоми Розенберг была первой женщиной-вице-президентом по моде в универмагах J.L. Hudson в Мичигане (ныне Macy’s) и старшим вице-президентом по мерчандайзингу и маркетингу модной одежды в универмагах Federated Allied. Сегодня она работает миротворцем на полную ставку. Бренда идентифицирует себя как еврейский сионист и является активным членом Американского израильского комитета политических действий (AIPAC). Она является вице-президентом Американского еврейского комитета в Детройте, штат Мичиган. Бренда удостоена 18 местных, национальных и международных наград за свои межконфессиональные усилия.Она стала первой еврейской женщиной, прочитавшей проповедь в Рамадан в американской мечети, и была участницей дискуссии Исламского общества Северной Америки (ISNA) по исцелению разногласий между шиитами и суннитами. Бренда является соавтором книги « Дружба и вера: МУДРОСТЬ женщин» , создавая союзы во имя мира. Она вдохновила соавторов создания «Воссоединения детей Авраама» — мультимедийного инструментария для мира.

Самиа Мусфа Бахсун — руководитель сферы телекоммуникаций, международный предприниматель, светский мусульманин, пропалестинский активист и общественный организатор.Самиа провела большую часть своей взрослой жизни, строя телекоммуникационные сети по всему миру. Бахсун имеет ливанское мусульманское происхождение, родился и вырос в Дакаре (Сенегал), он является американским иммигрантом с 1979 года. Самиа с раннего возраста подвергалась воздействию вопросов расы, этнической принадлежности, веры, пола и политики. из 14 ярых палестинских правозащитников и антиизраильских боевиков. Самиа отказалась от каких-либо перспектив мира, пока не объединилась с Брендой Розенберг, чтобы стать соучредителем Tectonic Leadership.Самиа тренирует молодых арабских предпринимателей и является судьей Форума предпринимателей Массачусетского технологического института (Панарабский регион). Иммигрант и натурализованный гражданин, предприниматель в секторе высоких технологий, владелец малого бизнеса, Самиа является членом руководящего комитета NJ Main Street Alliance, продвигая политику инноваций, создания рабочих мест, образования и иммиграционной реформы. Она является лауреатом Премии Дэвида Сарноффа в области правозащитной деятельности в 2013 году.

ПОХВАЛА ЗА ПРИНЯТИЕ СИЛЫ НАПРЯЖЕНИЯ

«Эта книга — замечательное свидетельство и инструмент.Действительно, большая часть его силы как инструмента заключается именно в свидетельских показаниях. Бренда и Самиа не позволили себе оставаться пленниками, порабощенными собственной болью, но показали / показали, как очень болезненное на самом деле может быть инструментом для исцеления. Их работа напоминает слова великого хасидского мастера Суси из Анипола о том, что только когда один знает боль другого, можно научиться любить другого. Боль уменьшает нас, если ведет к эгоцентризму и нечувствительности к другим; но он может облагородить нас, когда позволяет нам быть еще более сострадательными по отношению к другим.Пусть пример Самии и Бренды и дальше вдохновляет людей во всем мире быть целителями и освободителями, а не пленниками и жертвами ». Раввин Давид Розен KSG CBE Международный директор по межрелигиозным вопросам, AJC

«Причина, по которой я считаю, что Tectonic Leadership работает, заключается в том, что оно готово использовать реальное напряжение и устранять сам вред и боль, которые испытывает человек. Если вы не обращаетесь к слону в комнате, если вы не обращаете внимания на настоящую боль, то все, что мы делаем, — это маскируем ее.Мы накладываем пластырь на эту огромную рану, а пластырь недостаточно большой. Мы должны что-то сделать, чтобы исправить этот вред ». Рашид Байдун, руководитель отдела тектоники, координатор восстановительного правосудия в средней школе Стаут, Дирборн, штат Мичиган. Конфликт долгое время был определяющим фактором публичного самовыражения. Часто это используется во вред противоположной точке зрения, что приводит к крику, дезинформации и общей путанице. Однако конфликт также может быть использован как позитивная сила для перемен и возможность встретиться с другими людьми и обменяться взглядами и мнениями таким образом, чтобы это было выгодно отдельным лицам, группам, организациям и даже странам.Использование силы напряжения дает нам возможность сосредоточиться на том, как сделать это путем для людей, занятых попытками сделать мир лучше и пытающихся начать коммуникативную модель, которая уступает место результатам. Динамика может быть подходящей не для всех, но нельзя отрицать влияние на взгляды и мнения отдельных людей. Есть 11-я заповедь — Не стойте праздно. Эта книга Бренды и Самии дает нам инструменты для участия в этом процессе, и к ней нельзя относиться легкомысленно. Сила напряжения может побуждать к переменам.Шери Шифф Межконфессиональный активист

«Концепция тектонического лидерства, которое переходит в напряженность конфликта, чтобы трансформировать его, отражает то, что я обнаружил в моей собственной работе по трансформации конфликтов, особенно связанных с конфликтами идентичностей. Авторы предоставляют новый язык, инструменты общения и идеи, чтобы продвинуть этот совместный путь к миру и надежде ». Преподобный Дэн Баттри, активист за глобальный мир. Глобальный консультант по вопросам мира и справедливости с международными министерствами американских баптистских церквей.

«НАПРЯЖЕНИЕ, КОТОРЫЕ РАЗЛИЧАЕТ НАС, УДЕРЖИВАЕТ КЛЮЧ, КОТОРЫЙ МОЖЕТ СВЯЗАТЬ НАС». Бренда и Самиа

Натяжение струны и сила в теннисных ракетках

Большинство теннисистов очень осторожно выбирают теннисную ракетку, но многие не понимают, что натяжка ракетки может иметь более глубокое влияние на их игру, чем тщательно подобранная рама.

Как минимум, каждый теннисист должен понимать основные компромиссы между комфортом, мощностью, контролем и вращением в зависимости от натяжения струн.Любая приличная теннисная ракетка будет иметь рекомендуемый диапазон натяжения струны, например, от 58 до 68 фунтов. Когда мы говорим о низком или высоком напряжении, имеет смысл ограничиться не более чем 10% за пределами этого диапазона, потому что при очень низком напряжении некоторые нормальные корреляции нарушаются.

В пределах рекомендуемого диапазона натяжения для данного набора струн меньшее натяжение обеспечивает значительно меньшую нагрузку на руку. Более свободные струны также производят немного большую мощность, но они бьют дальше, в первую очередь потому, что мяч остается на струнах дольше, что заставляет его покидать ракетку по более высокой траектории, так как при большинстве ударов ракетка наклоняется вверх и поднимается по мере продвижения вперед.Более высокое напряжение обеспечивает значительно больший контроль на заданном уровне вершины вращения.

Topspin улучшает контроль, заставляя мяч падать быстрее, когда он летит вперед. Для качания с заданной скоростью и углом вверх некоторые струны производят большее вращение при более низком натяжении, некоторые — при более высоком натяжении с разницей порядка 10% или меньше. Когда замах игрока касается струн сзади мяча, одновременно отбрасывая его вперед, как это обычно бывает при замахе большинства продвинутых игроков, более быстрый замах увеличивает как вращение, так и силу.Слегка уменьшенная мощность, более низкая траектория выхода мяча и повышенный контроль в результате более высокого натяжения струны позволяют игрокам качаться быстрее, не ударяя долго, а когда они качаются быстрее при заданном угле удара вверх, они производят большее вращение.

Ключ к пониманию того, почему более низкое натяжение струн дает немного большую мощность, — это сравнение отдачи энергии, обеспечиваемой струнами, с отдачей от мяча.

Энергия удара и возврат энергии

Если вы прочитаете официальные правила тенниса, вы найдете раздел, в котором указано, что мяч, брошенный на бетон со 100 дюймов, должен отскочить на расстояние от 53 до 58 дюймов.При любом столкновении часть энергии теряется на вибрацию и трение, а в случае с теннисным мячом огромные потери теряются на деформацию материалов мяча. Когда мяч ударяется о бетон, часть его сжимается, и резина накапливает часть этой энергии, которая затем высвобождается, когда мяч разжимается. Если бы вся эта энергия была сохранена с идеальной эффективностью, мяч отскочил бы обратно на 100 дюймов (в вакууме), но в соответствии с конструкцией теннисного мяча он рассеивает около 45% этой энергии. Супербол лучше сохраняет свою энергию сжатия, и он будет отскакивать намного выше при падении с той же высоты, но мяч, который мог бы отскочить до 100% своей первоначальной высоты, по-прежнему физически невозможен.Если бы такой мяч был возможен, он бы отскакивал вечно.

Теннисный мяч возвращает только 55% своей энергии удара, но струны возвращают более 90%. Когда мяч сталкивается со струнами, обе в некоторой степени деформируются. Чем больше струны накапливают энергию столкновения, деформируясь, как батут, тем меньше мяч накапливает энергии за счет сплющивания. Чтобы получить наибольшую отдачу от столкновения, мы хотим, чтобы струны хранили как можно больше общей энергии, потому что они будут отдавать более 90% ее, тогда как почти половина любой энергии, хранящейся в шаре, будет потрачена впустую. .Более свободные струны легче деформируются, таким образом сохраняя больше энергии столкновения и сводя к минимуму потери мячом.

На этом этапе идеально звучат более свободные струны. В конце концов, мы все должны знать, что энергию нельзя тратить зря. Итак, почему при данном уровне верхнего вращения более слабые струны вызывают потерю контроля?

Control и Topspin

По мере того, как более слабое основание струны сжимается сильнее, мяч остается на струнах дольше, и в течение этого времени любые незначительные изменения в положении вашей ракетки могут изменить траекторию мяча.Мяч недостаточно долго висит на ваших струнах, чтобы вы могли сознательно с ним что-нибудь сделать. Ваш мозг не может выполнить какие-либо действия за несколько доступных миллисекунд, но этих нескольких миллисекунд достаточно, чтобы произошло непреднамеренное движение, особенно когда удар не по центру оказывает поворачивающее усилие на головку ракетки.

Различия в мощности и компромиссы между комфортом и контролем надежно применяются в пределах данного набора струн при данном уровне верхнего вращения, но более жесткие струны, такие как большинство полиэфиров и все кевлары / арамиды, ведут себя так, как если бы они были более тугими, а некоторые струны , такие как многие сополиэфиры, производят значительно больше прядения, чем другие.Среди струн с высоким потенциалом вращения одни производят большее вращение при более низком натяжении, а другие — более сильное вращение при более высоком натяжении. В результате различия, возникающие в результате изменения натяжения, нельзя сравнивать для разных типов струн; более жесткая струна или струна, которая дает лучшее вращение при более низком натяжении, может обеспечить, по крайней мере, такой же контроль при более низком натяжении, как и другая струна при более высоком натяжении. Таким образом, более жесткие струны часто натягиваются слабее, потому что они ведут себя так, как если бы они были более тугими, в том числе по их влиянию на руку.

Если вам нравится быстро замахиваться мячом и использовать топспин, вы получите лучшую комбинацию вращения и контроля, используя струны с высоким потенциалом вращения, которые производят больше вращения при более высоком натяжении, и натягивая их туго, но если ваша рука требует уменьшите натяжение для комфорта, вам следует поэкспериментировать со струнами, которые производят большее вращение при уменьшении натяжения, и если ни одна из них не достаточно мягкая, вам, возможно, придется довольствоваться меньшим потенциалом вращения, чтобы ваша рука была здоровой. Данные о спиновом потенциале струн очень ограничены; вы можете принести пользу себе и многим другим, написав производителям струн, попросив их протестировать свои струны и включить эту информацию на свои этикетки.

Дополнительные ресурсы:

Сила здорового напряжения

Сила здорового напряжения | Книга Тима Арнольда

Дайте вашей организации навыки, необходимые для преодоления хронических проблем и противоречивых ценностей.

Часто лидеры и команды имеют четкое видение, но не могут воплотить его в жизнь.

Они застревают из-за…

• Противоречивые значения.
• Дивизион внутри команды.
• Сопротивление переменам.

Сила здорового напряжения помогает лидерам выйти из тупика, предлагая простой план из 4 шагов, который позволяет им объединить свою команду, вызвать перемены и жить своими ценностями.

Сила здорового напряжения помогла сотням организаций и тысячам лидеров перейти от выживания к процветанию.

Загрузите первую главу книги «Сила здорового напряжения» бесплатно!

Скачать первую главу

Купите книгу Тима онлайн на Amazon

«Тим Арнольд сделал то, что смогли сделать несколько авторов книг по лидерству.Он предложил ценные инструменты в рамках легкодоступной модели и в нескольких необходимых словах. Эта книга более практична, чем многие книги по лидерству, которые у меня есть вместе взятые. Покупка, сила здорового напряжения, была небольшой платой за дивиденды, которые она принесет в результате лидерства групп и организаций. Я очень рекомендую это ».

• Невин Харпер
• Доцент
• Университет Виктории

Скачать бесплатно главу

Получите первую главу книги The Power of Healthy Tension ,
и ежемесячно отправляйте советы руководству прямо на свой почтовый ящик.

Авторские права © 2021 Leaders for Leaders.
Все права защищены. Сайт сделан с ♥ от Frame

5 виртуальных ледоколов оживят вашу следующую онлайн-встречу

Механика

ньютонов — Мощность и работа силы натяжения вращающегося тела

механика Ньютона — Сила и работа силы натяжения вращающегося тела — Physics Stack Exchange

Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 3 года, 4 месяца назад

Просмотрено 193 раза

$ \ begingroup $

---

Хотите улучшить этот вопрос? Добавьте подробности и проясните проблему, отредактировав этот пост.

Закрыт 3 года назад.

Предположим, что у нас есть тело, вращающееся на безмассовой струне с постоянной скоростью. Что уж говорить о проделанной работе этого напряжения. Тем более, какая мощность связана с этой работой.

У меня нет проблем с мощностью, поскольку это скалярное произведение силы натяжения и вектора скорости, которые перпендикулярны. Значит, он равен нулю.

У меня вопрос по поводу работы.Это тоже ноль? Потому что в каждой точке окружности смещение также перпендикулярно силе натяжения. Правильно ли это мышление или чего-то не хватает, чего я не вижу?

Qmechanic ♦

147k2828 золотых знаков347347 серебряных знаков17431743 бронзовых знака

Создан 20 дек.

Янушянуш

911 золотой знак66 серебряных знаков1010 бронзовых знаков

$ \ endgroup $ 1 $ \ begingroup $

Натяжение уравновешивает центробежную силу и направлено к центру круга.Угол между ним и вектором скорости равен 90 °, поэтому W = Fx (cos∅) и ∅ = 90 °, поэтому W = 0. Поскольку P = W / t => P также равно 0.

Создан 20 дек.

$ \ endgroup $ Physics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Взаимосвязь между натяжением струны и силой: бадминтон

Относительно натяжения струны и силы / контроля: струна в ракетке для бадминтона подчиняется закону Гука, и приращение растяжения пропорционально приложенной дополнительной силе.(При чрезвычайно высоком натяжении струна может выйти за пределы линейной части кривой напряжения-деформации, но я подозреваю, что ракетка уже сломалась!) Поэтому вы можете подумать, что волан ударил с одинаковой скоростью головки ракетки двумя ракетками с разными натяжение струн должно отскакивать с одинаковой скоростью: энергия в двух ракетках одинакова, волан один и тот же, и струны растягиваются на одинаковую величину (поскольку приложенная сила одинакова в обоих случаях и согласно теории Гука. Закон полученного расширения будет таким же).Однако опыт или общепринятое мнение не об этом говорят. И это тоже не то, что нам показывает физика, а именно. Удар челнока создает силу, которая является дополнительной к силе, уже приложенной к струне из-за ее натяжения. Более высокое натяжение означает более высокую начальную силу, так что при ударе струна с более высоким натяжением подвергается более высокой общей силе (чем струна с более низким натяжением) — струна пытается вернуться к своей ненатянутой длине. .Хотя дополнительная сила — это то, что вызывает дополнительное удлинение струны, возвращающая сила, которая отталкивает волан от струн, пропорциональна общей силе, возникающей из-за начального натяжения струн и из-за удара о волан. Возвратная сила действует на волан только в течение короткого времени, пока волан не покинет струны или пока струны не вернутся к своей исходной длине; однако в течение этого короткого времени сила, действующая на челнок, представляет собой сумму силы, обусловленной начальным натяжением, и силы, обусловленной ударом о челнок.Чем выше первое, тем больше восстанавливающая сила, отталкивающая челнок. Таким образом, физика, кажется, говорит нам, что более высокое натяжение струны приводит к тому, что по волану ударяют сильнее — поэтому он должен быстрее отрываться от ракетки. Но это не то, что нам говорит опыт, и это также не то, что показали лабораторные эксперименты. Почему это может быть? Причина в том, что большее усилие действует в течение более короткого времени (чем меньшее усилие в ракетке, натянутой при более низком натяжении)? Действительно ли это так? Или это как-то связано с изгибом ракетки?

Трамп наращивает усилия, чтобы удержать власть по мере роста напряженности

Президент Трамп усиливает свои попытки свергнуть победу Джо Байдена на выборах, настаивая на том, чтобы судьи, республиканские законодатели и местные власти в нескольких штатах на полях сражений игнорировали вердикты избирателей. и присудить ему голоса выборщиков, необходимые ему на второй срок.

Он почти наверняка потерпит неудачу, говорят эксперты и даже некоторые республиканские чиновники. Штаты находятся в процессе подтверждения результатов, а команда юристов Трампа до сих пор не смогла продвинуть его безосновательное дело в судах штата и федеральных судах. Тем не менее, эти усилия представляют собой чрезвычайную атаку на американскую демократию, возглавляемую самим президентом и, по крайней мере, с молчаливого одобрения его партии.

Несколько республиканцев в Конгрессе признали победу Байдена, и в четверг пять губернаторов-республиканцев встретились с избранным президентом.Но партийные лидеры, в том числе лидер большинства в Сенате Митч МакКоннелл (республиканец) и лидер меньшинства палаты представителей Кевин Маккарти (республиканец Бейкерсфилд), не высказались против отказа Трампа уступить или, как минимум, призвали его позволить Байдену получить брифинги по национальной безопасности и федеральные ресурсы, как правило, предоставляются для обеспечения плавного перехода — на этот раз в условиях смертельной пандемии и экономического кризиса.

Байден выразил уверенность в неизбежности приведения его к присяге в качестве следующего президента, но его терпение истощается.Выступая перед журналистами после встречи с двухпартийной группой губернаторов по поводу пандемии COVID-19, он скептически отозвался о последних маневрах Трампа, но сказал, что еще не готов подать в суд, чтобы получить доступ к информации и ресурсам, обычно доступным президенту. избранный.

«Трудно понять, как думает этот человек, — сказал Байден. «Остальному миру посылается невероятно разрушительный сигнал о том, как функционирует демократия. Я думаю, что это … ну, я не знаю его мотивов, но это совершенно безответственно.

На вопрос, почему он не обратился в суд, он сказал: «Я делаю суждение, основанное на многолетнем опыте того, как добиться успеха с оппозицией. Я считаю, что мы продвинемся дальше, фактически работая с коллегами-республиканцами ».

Советники Байдена со все возрастающей остротой обращают внимание на риски для здоровья и национальной безопасности, препятствующие переходу. В долгосрочной перспективе раскольническая позиция Трампа и теории заговора могут оставить неизгладимую рану; некоторые опросы уже показывают, что большинство избирателей-республиканцев считают, что переизбранию президента помешало мошенничество, несмотря на отсутствие у него доказательств.

«Это невероятно, — сказал Ларри Даймонд, старший научный сотрудник Стэнфордского университета. «Они не добьются успеха, но нашей демократии будет нанесен большой ущерб».

Рудольф Джулиани и другие адвокаты президента Трампа в четверг в штаб-квартире Республиканского национального комитета распространили теории заговора о мошенничестве на выборах.

(Жаклин Мартин / Associated Press)

Это не остановило президента или его союзников.

Рудольф В.Джулиани, бывший мэр Нью-Йорка, и группа юристов правого толка, известных продвижением теорий заговора, провели в четверг пресс-конференцию в штаб-квартире Республиканского национального комитета. Они рассказывали истории о заговоре демократов по всей стране, включающем незаконное голосование и международное вмешательство в выборы — через неделю после того, как федеральный совет назвал выборы этого года «самыми безопасными в истории Америки».

В какой-то момент Джулиани предположил, что «существовал централизованный план по осуществлению этих различных актов мошенничества с избирателями, в особенности в отношении больших городов», контролируемых демократами.Позже он процитировал «Мой кузен Винни», комедийный фильм 1992 года о необычном адвокате, которого играет Джо Пеши, хотя критики Джулиани издевались над ним в социальных сетях как над тем же незадачливым адвокатом.

Президент, который не появлялся на публике в течение нескольких дней и пропустил редкий брифинг в Белом доме для прессы об обострении кризиса с коронавирусом, поддержал Джулиани изнутри Белого дома. «Открытый и закрытый случай мошенничества с избирателями», — ложно написал он в Твиттере. «Огромные цифры!»

Крис Кребс, бывший сотрудник службы внутренней безопасности, возглавлявший совет, опровергавший лживые заявления Трампа о выборах, а затем уволенный президентом, выразил тревогу.«Эта пресс-конференция была самой опасной 1 час 45 минут телепередач в истории Америки», — написал он в Твиттере. «И, возможно, самый безумный».

Майкл Гвин, официальный представитель Байдена, отверг обвинения Джулиани, заявив, что они были опровергнуты в суде и дискредитированы даже официальными лицами в администрации Трампа.

«Как бы сильно ни старались Трамп и бешеный Джулиани, они не могут опровергнуть волю американского народа, который решительно избрал Джо Байдена следующим президентом Соединенных Штатов», — говорится в заявлении Гвина.

Избранный президент Джо Байден говорит о переходе в четверг в Уилмингтоне, Делавэр.

(Эндрю Харник / Associated Press)

Кампания Трампа заплатила 3 ​​миллиона долларов за пересчет голосов в двух сильно демократических округах Висконсина — Дэйн и Милуоки, — хотя шансов отменить победу Байдена в штате мало. Очередной пересчет голосов в Грузии, где Байден выиграл с еще более узким отрывом, не изменил результата, заявили в четверг официальные лица штата.

В Мичигане Трамп также поддерживает усилия по блокированию сертификации подавляющего большинства голосов сторонников Байдена в округе Уэйн, который включает Детройт, и, как сообщается, пригласил некоторых республиканских законодателей штата на встречу в Белом доме в пятницу.

Союзники Трампа предприняли надуманные попытки добиться того, чтобы законодательные органы, контролируемые республиканцами, в штатах, выигранных Байденом, проигнорировали голосование и назначили сторонников Трампа в коллегию выборщиков 14 декабря. После пресс-конференции Джулиани Сидни Пауэлл, один из юристов. в своей команде, изложил стратегию в телефонном интервью Fox Business.

«Все выборы — откровенно говоря, во всех колеблющихся штатах — должны быть отменены, а законодательные органы должны убедиться, что избиратели выбраны для Трампа», — сказал Пауэлл.

Адвокаты Трампа обратились к федеральному судье с просьбой отклонить результат Пенсильвании в пользу Байдена. «В конечном итоге истцы будут искать средства правовой защиты, чтобы Трамп был объявлен победителем законных голосов, поданных в Пенсильвании на всеобщих выборах 2020 года, и, таким образом, получателем голосов избирателей Пенсильвании», — говорится в заявлении в среду.

Более сильное давление на организаторов выборов оказали сторонники президента.

Государственный секретарь штата Аризона Кэти Хоббс заявила, что ее семья и ее сотрудники столкнулись с угрозами насилия. Трамп и другие избранные должностные лица «увековечивают дезинформацию и поощряют других не доверять результатам выборов, нарушая присягу, которую они принесли», — сказала она.

«Давно пора им остановиться, — сказал Хоббс, демократ. «Их слова и действия имеют последствия.

Рут Бен-Гиат, историк из Нью-Йоркского университета и эксперт по диктатурам, сказала, что Трамп, похоже, пытается совершить самоубийство, в котором избранный лидер цепляется за власть. «Он никогда не использовал демократический сценарий», — сказала она. «Он всегда придерживался авторитарного сценария».

Упорные попытки принять участие в выборах вызваны самим президентом, по словам высокопоставленного сотрудника избирательной кампании, который на условиях анонимности выступил на условиях анонимности для обсуждения деликатных внутренних вопросов.

«Он тот, кто этого не отпускает», — сказал чиновник о Трампе, который наделил Джулиани полномочиями над высшими должностными лицами избирательной кампании после встречи на прошлой неделе, потому что «Руди говорит ему то, что он хочет услышать».

Чиновник подтвердил, что имели место «несколько напряженных ситуаций», поскольку старшие советники кампании Джейсон Миллер и Джастин Кларк выразили разочарование Джулиани и Дженной Эллис, другим советником по правовым вопросам на пресс-конференции в четверг. Два юриста открыли магазин в Арлингтоне, штат Вирджиния., штаб-квартира на прошлой неделе; больше, чем другие помощники, на встречах с президентом они поощряли его шансы на отмену результатов выборов.

Хотя многие сотрудники незаметно начали процесс поиска своей следующей работы, немногие готовы признать это публично или покинуть кампанию или администрацию, пока они все еще находятся на заработной плате.

«Мы должны немного подождать с этим», — сказал чиновник. «Но не так много людей, которые думают, что Руди приносит нам много пользы.”

Не только официальные лица предвыборной кампании Трампа разделяют ложные надежды. Глава Администрации общих служб продолжает отказываться признать Байдена избранным президентом, тем самым блокируя федеральные ресурсы для своей переходной команды.