Напряжение и напряженность электрического поля: формулы, примеры расчета, единицы измерения

Что такое напряжение и напряженность электрического поля. Как рассчитать напряжение и напряженность. Какие формулы используются для расчета. В каких единицах измеряются эти величины. Примеры решения задач на расчет напряжения и напряженности.

Что такое напряжение электрического поля

Напряжение электрического поля — это физическая величина, характеризующая работу электрического поля по перемещению единичного положительного заряда из одной точки поля в другую. Напряжение обозначается буквой U и измеряется в вольтах (В).

Напряжение электрического поля равно отношению работы сил электрического поля по перемещению заряда к величине этого заряда:

U = A / q

где A — работа сил электрического поля, q — величина перемещаемого заряда.

Формулы для расчета напряжения электрического поля

Основные формулы для расчета напряжения электрического поля:

• U = φ1 — φ2 — напряжение равно разности потенциалов двух точек поля
• U = E * d — для однородного электрического поля
• U = ∫E * dl — для неоднородного электрического поля

где φ1 и φ2 — потенциалы точек поля, E — напряженность электрического поля, d — расстояние между точками, dl — элемент пути.

Что такое напряженность электрического поля

Напряженность электрического поля — это силовая характеристика электрического поля, равная отношению силы, действующей на пробный точечный заряд, помещенный в данную точку поля, к величине этого заряда.

Напряженность обозначается буквой E и измеряется в вольтах на метр (В/м).

Напряженность электрического поля определяется по формуле:

E = F / q

где F — сила, действующая на заряд q, помещенный в данную точку поля.

Формулы для расчета напряженности электрического поля

Основные формулы для расчета напряженности электрического поля:

• E = k * Q / r^2 — для точечного заряда
• E = σ / (2ε0) — для бесконечной заряженной плоскости
• E = λ / (2πε0r) — для бесконечной заряженной нити

где k — коэффициент пропорциональности, Q — величина заряда, r — расстояние от заряда, σ — поверхностная плотность заряда, λ — линейная плотность заряда, ε0 — электрическая постоянная.

Единицы измерения напряжения и напряженности электрического поля

Напряжение электрического поля измеряется в вольтах (В). 1 вольт равен напряжению, при котором заряд в 1 кулон совершает работу в 1 джоуль.

Напряженность электрического поля измеряется в вольтах на метр (В/м). 1 В/м — это напряженность такого однородного поля, в котором на заряд в 1 кулон действует сила в 1 ньютон.

Как связаны напряжение и напряженность электрического поля

Напряжение и напряженность электрического поля связаны следующим соотношением:

U = E * d

где U — напряжение, E — напряженность, d — расстояние между точками поля.

Это соотношение справедливо для однородного электрического поля. Из него следует, что напряженность численно равна напряжению, приходящемуся на единицу длины:

E = U / d

Примеры решения задач на расчет напряжения электрического поля

Задача 1. Определить напряжение между двумя точками однородного электрического поля напряженностью 200 В/м, находящимися на расстоянии 5 см друг от друга.

Решение:

Дано: E = 200 В/м d = 5 см = 0,05 м

Найти: U — ?

Используем формулу U = E * d

U = 200 В/м * 0,05 м = 10 В

Ответ: напряжение между точками равно 10 В.

Примеры решения задач на расчет напряженности электрического поля

Задача 2. Определить напряженность электрического поля точечного заряда 5 нКл на расстоянии 10 см от него.

Решение:

Дано: Q = 5 нКл = 5 * 10^-9 Кл r = 10 см = 0,1 м k = 9 * 10^9 Н*м^2/Кл^2

Найти: E — ?

Используем формулу E = k * Q / r^2

E = 9 * 10^9 * 5 * 10^-9 / (0,1)^2 = 4500 В/м

Ответ: напряженность электрического поля равна 4500 В/м.

Практическое применение расчета напряжения и напряженности электрического поля

Расчет напряжения и напряженности электрического поля имеет важное практическое значение:

• При проектировании электрических сетей и устройств
• В электроэнергетике для определения потерь при передаче электроэнергии
• В электронике при разработке полупроводниковых приборов
• В физике плазмы и ускорительной технике
• При создании систем электростатической защиты

Понимание этих величин позволяет правильно рассчитывать параметры электрических цепей и устройств, обеспечивать их надежную и безопасную работу.

Какие факторы влияют на напряжение и напряженность электрического поля

На величину напряжения и напряженности электрического поля влияют следующие основные факторы:

• Величина зарядов, создающих поле
• Расстояние от зарядов
• Диэлектрическая проницаемость среды
• Геометрия проводников и электродов
• Наличие проводящих и диэлектрических тел в поле

Учет этих факторов позволяет управлять параметрами электрического поля и создавать поля с нужными характеристиками для различных практических применений.

Формула напряжения электрического поля в физике

Содержание:

• Определение и формула напряжения электрического поля
• Единицы измерения напряжения электрического поля
• Примеры решения задач

Определение и формула напряжения электрического поля

Определение

Скалярную физическую величину, численно равную работе, которую совершает электростатические и сторонние силы, перемещая единичный положительный заряд, называют напряжением (падением напряжения) на участке цепи. Напряжение обозначают буквой U. Математическая формулировка определения напряжения имеет вид:

$$U=\frac{A}{q}(1)$$

где A — работа, которую совершает сила над зарядом qна некотором участке цепи.

Пусть пробный заряд (q>0) перемещается в однородном электрическом поле под воздействием сил рассматриваемого поля из точки 1 в точку 2 на расстояние d (рис.1) в направлении поля.

Работа, которую совершают силы поля за счет его потенциальной энергии, равна:

$$A=\overline{F d}=F d=E q d(2)$$

где E – напряженность электрического поля. Из определения напряжения электрического поля и выражения (2) получаем, что формулой для расчета напряжения однородного поля можно считать:

$$U=E d(3)$$

При перемещении положительного заряда из точки (1), имеющей потенциал $\varphi_{1}$ в точку (2) c потенциалом $\varphi_{2}$ напряжение между этими двумя точками поля равноразности потенциалов этих точек:

$$U=\varphi_{1}-\varphi_{2}(4)$$

В электростатическом поле напряжение между двумя точками не зависит от формы пути, который соединяет данные точки. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю. Поэтому для электростатического поля имеется возможность ввода разности потенциалов, которая однозначно определена действующим полем и служит характеристикой поля.

Зная напряженность поля в каждой точке можно вычислитьразность напряжение между двумя любыми точками:

$$U=\int_{1}^{2} E_{s} d s(5)$$

E_s – проекция вектора напряженности поля на направление ds, ds – элемент перемещения заряда. {-3}(B)$$

Ответ. $U = 0,12 B$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Бесконечно длинная, прямая нить заряжена равномерно с линейной плотностью т. Каково напряжение поля между двумя точками, если одна точка в два раза дальше от нити, чем первая?

Решение. Напряженность поля, которое создает бесконечно длинная, прямая нить, равномерно заряженная по длине, находится при помощи теоремы Гаусса:

$$\int \bar{E} d \bar{S}=\frac{\tau h}{\varepsilon_{0}} \rightarrow E 2 \pi r h=\frac{\tau h}{\varepsilon_{0}} \rightarrow E=\frac{\tau}{2 \pi r \varepsilon_{0}}$$

поле нити имеет цилиндрическую симметрию (рис.2).

Основой для нахождения напряжения будет формула:

$$U=\int_{r_{1}}^{r_{2}} \frac{\tau}{2 \pi r \varepsilon_{0}} d r=\frac{\tau}{2 \pi \varepsilon_{0}} \ln \left(\frac{r_{2}}{r_{1}}\right)=\frac{\tau}{2 \pi \varepsilon_{0}} \ln ?|2|$$

Ответ. $U=\frac{\tau}{2 \pi \varepsilon_{0}} \ln ?|2|$

Читать дальше: Формула работы.

Электрический заряд, напряжение, напряженность, потенциал

Любой физический объект в окружающем нас мире состоит из огромного количества элементарных частиц, обладающих зарядами. Элементарная частица протон имеет элементарный электрический заряд, которому приписывают (условно) положительный знак, элементарная частица электрон имеет элементарный отрицательный заряд.

---

Содержание:

• • Электрический заряд
  • Напряженность
  • Потенциал, напряжение
•  

• ---

Электрический заряд

Под электрическим зарядом понимают физическую величину, которая характеризует способность тел (объектов) вступать в электрическое взаимодействие. Электрический заряд обозначается через q (иногда для обозначения используют заглавную букву Q) и в Международной системе единиц (СИ) измеряется в Кулонах, [Кл].

Электрический заряд – дискретная величина, кратная элементарному электрическому заряду одного электрона (по модулю) e = 1,60217*10^-9 Кл.

где N – целое число.

С физической точки зрения 1 кулон [Кл] соответствует электрическому заряду, проходящему через поперечное сечение проводника при силе тока 1 Ампер  за 1 секунду.

Заряды существуют в двух видах: положительные (+) и отрицательные (-). Одноименные заряды отталкиваются, а разноименные – притягиваются.

Сила взаимодействия зарядов направлена вдоль прямой, соединяющей их, пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними (рисунок 1).

Рис. 1. Сила взаимодействия зарядов

где k – коэффициент пропорциональности, зависящий от выбора системы единиц; 

– единичный вектор, направленный вдоль прямой, соединяющей заряды q₁ и q₂.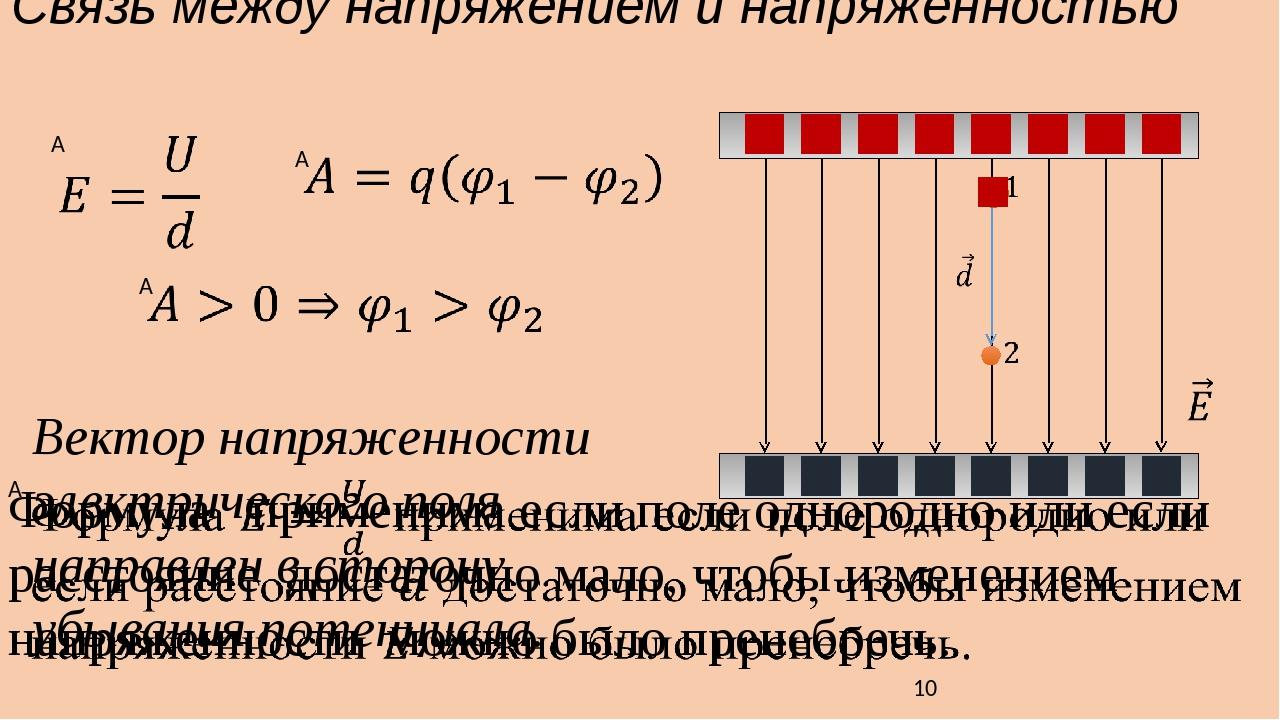

Силу взаимодействия двух зарядов принято называть кулоновской силой в честь ученого-физика Шарля Кулона, обнаружевшего ее существование.

Если объект (система) не обменивается зарядами с окружающей средой, его называют электрически изолированным. В такой системе сумма электрических зарядов (положительных и отрицательных) не меняется со временем, то есть наблюдается закон сохранения заряда.

Большинство тел в природе электрически нейтральны, так как содержат заряды обоих типов в одинаковом количестве. Положительные и отрицательные заряды попарно нейтрализуют действие друг друга. Для перехода тела в заряженное состояние необходимо пространственно перераспределить в нем заряды, сконцентрировав одноименные заряды в одной  области тела. Это возможно сделать, например, при помощи трения или взаимодействия с другим заряженным объектом (рисунок 2).

Рис. 2. Переход незаряженного объекта в заряженное состояние

Электрический заряд порождает в окружающем его пространстве непрерывную материю, называемую электрическим полем. Благодаря электрическому полю заряды имеют возможность  взаимодействовать между собой. В электротехнике электрическое поле характеризуется двумя величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика).

Напряженность электрического поля

Напряженность электрического поля – это векторная физическая количественная характеристика электрического поля. Ее величина показывает силу, которая действует на пробный точечный единичный положительный заряд, помещенный в некоторую точку электрического поля.

Под точечным зарядом понимают упрощенную модель положительного заряда, в которой его формой и размером можно пренебречь.

Вектор напряженности по направлению совпадает с вектором силы , с которой электрическое поле действует на положительный точечный заряд, помещенный в заданную точку поля (рисунок 3).

Рис. 3. Вектор напряженности E , созданной зарядом q, в точке А

Величина напряженности поля в точке А определяется согласно формуле

где r – расстояние от заряда q до точки А, k – коэффициент пропорциональности, зависящий от выбора системы единиц.

Электрическое поле графически изображается линиями напряженности электрического поля, которые условно принято обозначать исходящими из положительно заряженных элементов и входящими в отрицательно заряженные заряды (рисунок 4).

а) изолированные зарядыб) взаимодействующие заряды

Рис. 4. Распределение линий напряженности для изолированных (а) и взаимодействующих (б) зарядов

Потенциал, напряжение

Физическую величину, равную отношению потенциальной энергии W электрического заряда в электростатическом поле к величине самого заряда q, называют потенциалом φ электрического поля

Потенциал – это скалярная величина, которая показывает, какую работу способно затратить поле, чтобы переместить единичный пробный положительный заряд в бесконечно удалённую точку. Единицей измерения электрического потенциала является вольт, [В].

При этом важно отметить, что работа сил электростатического поля при перемещении заряда из одной точки электрического поля в другую не зависит от формы траектории перемещения, а зависит только от начального и конечного положения заряда, а также от его величины.

Если имеется некоторая система, состоящая из N точечных зарядов, то потенциал ее электрического поля φ будет равен алгебраической сумме потенциалов полей каждого входящего в него заряда, то есть

Напряжение электрического поля – это разность потенциалов между двумя точками этого поля (рисунок 5).
Напряжение (U) — это работа (А) совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.

U = A/q  [Дж/Кл] или [В]

Рис. 5. Графическая интерпретация напряжения электрического поля

Напряжение является относительной величиной, то есть всегда определяется относительно некоторого уровня. Нулевой уровень выбирается произвольно и не влияет на итоговое значение напряжения, так как соответствует разности потенциалов в двух точках (то есть изменению потенциальной энергии). Для простоты расчетов в качестве нулевого уровня в большинстве случаев принимают потенциал заземленного проводника или земли.
Как уже было отмечено ранее электрическое напряжение – это разность потенциалов двух точек, следовательно его значение определяется по формуле

В системе СИ за единицу измерения напряжения принимается вольт, [В]. Физически величина напряжения, равная 1 вольту, соответствует работе 1 джоуль при перемещении заряда в 1 кулон.

#1. Физическая величина измеряемая в кулонах?

Напряжение

Электрический заряд

Потенциал

Электрический заряд обозначается через q и в Международной системе единиц (СИ) измеряется в Кулонах, [Кл].

#2. Какие пары электрических зарядов будут притягиваться к друг другу?

Два отрицательных заряда

Два положительных заряда

Один отрицательный заряд, а другой положительный

Одноименные заряды отталкиваются, а разноименные – притягиваются.

#3. … — это работа совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.

Напряжение

Сопротивление

Потенциал

Завершить

Отлично!

Попытайтесь снова(

20.08.2020

ТОЭ

Электрические цепи постоянного тока,ТОЭ

Натяжение струн: уравнение, размеры и расчет

Сила натяжения — это сила, развиваемая в веревке, струне или кабеле при растяжении под действием приложенной силы.

Сила, возникающая при приложении нагрузки к концам объекта, обычно к его поперечному сечению. Его также можно назвать тянущей силой, напряжением или напряжением.

Этот тип силы проявляется только при контакте между кабелем и объектом. Натяжение также позволяет передавать силу на относительно большие расстояния.

Натяжение при отсутствии ускорения

Предположим, у нас есть тело массой (m) на нити, как показано ниже. Сила тяжести тянет ее вниз, что составляет ее вес:

Натяжение струны

Чтобы струна не разгонялась вниз из-за своей массы, ее нужно тянуть обратно вверх с равной силой. Это то, что мы называем напряжением. Если он не ускоряется, мы можем сказать, что T = mg.

Напряжение при ускорении

Когда у нас есть напряжение в объекте, который ускоряется вверх, т.е. в лифте, поднимающем людей на верхние этажи здания, напряжение не может быть таким же, как вес груза — оно обязательно будет больше. Итак, откуда берется дополнение? Напряжение = усилие для балансировки + дополнительная сила для ускорения. Математически это моделируется следующим образом:

T = mg + ma

T = m (g + a).

Другой сценарий, когда лифт спускается вниз. Натяжение не будет равно 0, что приведет к свободному падению. Он будет немного меньше веса предмета. Итак, если выразить это уравнение словами, напряжение = сила, необходимая для баланса, — сила сбрасывается. Математически это будет

Т = мг — мА

Т = м (г — а).

Примеры работы

Давайте посмотрим на пару примеров работы.

Когда частицы высвобождаются из состояния покоя на приведенной ниже диаграмме, каково натяжение удерживающей их струны?

Пример натяжения струны

Ответ:

В такой ситуации упадет частица с наибольшей массой, а поднимется частица с наименьшей массой. Возьмем частицу массой 2 кг за частицу a, а частицу массой 5 ​​кг за частицу b.

Чтобы уточнить вес каждой частицы, мы должны умножить ее массу на силу тяжести.

Вес a = 2 г

Вес b = 5 г

Теперь вы можете смоделировать уравнение для ускорения и напряжения каждой частицы.

T -2g = 2a [Частица a] [Уравнение 1]

5g -T = 5a [Частица b] [Уравнение 2]

Теперь вы решаете это одновременно. Добавьте оба уравнения, чтобы исключить переменную T.

3г = 7а

Если взять 9.8мс-2газ

a=4,2 мс-2

Вы можете подставить ускорение в любое из уравнений, чтобы получить напряжение.

Подставьте ускорение в уравнение 1.

T-2g=2×4,2

T — 19,6 = 8,4

T=28N 20-килограммовый груз, подвешенный сбоку стола над шкивом, соединяющим обе частицы, показан ниже. Эти частицы удерживались на месте все это время, и теперь они высвобождаются. Что будет дальше? Чему равны ускорение и натяжение струны?

Натяжение струны с одной частицей на гладком столе

Ответ: Дополним диаграмму, чтобы увидеть, с чем мы работаем.

Натяжение нити с одной частицей на гладком столе

Примем частицу массой 2 кг за частицу А.

А частицу массой 20 кг за частицу В.

Теперь разложим частицу А по горизонтали.

T = ma [уравнение 1]

Разделение частицы B по вертикали

mg -T = ma [уравнение 2]

Подставляем в них числа:

T = 2a [Уравнение 1]

20g — T = 20a [Уравнение 2]

Теперь мы можем сложить оба уравнения, чтобы исключить напряжения.

20g = 22a

a=9811

a=8,9 мс-2

Теперь разложите ускорение в любом из уравнений. Мы бы сделали первое.

T=2×9811

T=17.8N

Натяжение под углом

Мы можем рассчитать натяжение веревки, прикрепленной к грузу под углом. Давайте возьмем пример, чтобы увидеть, как это делается.

Найдите натяжение каждой части струны на диаграмме ниже.

Растяжение под углом

Ответ: нам нужно будет составить два уравнения из всей диаграммы – одно для вертикальных сил, а другое для горизонтальных. Итак, что мы собираемся сделать, так это разделить натяжение обеих струн на их соответствующие вертикальную и горизонтальную составляющие.

Натяжение под углом

T1cos20+T2cos30=50 [Уравнение 1] [Вертикально]

T1sin20=T2sin30 [Уравнение 2] [Горизонтально]

Так как у нас есть два уравнения и два неизвестных, мы собираемся использовать процедуру одновременного уравнения, чтобы сделать это путем замены.

Теперь перестроим второе уравнение и подставим его в первое уравнение.

role=»math»>

T1=T2sin30°sin20°

(0.5T20.342)cos20°+T2cos30°=50

(0.5T20.342)0.94+0.866T2= 50

1.374T2+ 0,866T2=50

2,24T2=50

T2=22,32N

Теперь, когда у нас есть значение T2, мы можем подставить его в любое из уравнений. Воспользуемся вторым.

T1sin20=22,32sin30

T1=11,160,342

T1=32,63N

Натяжение в струнах – ключевые выводы

• веревка, струна или трос, натянутые под приложенным сила.
• При отсутствии ускорения напряжение равно весу частицы.
• Натяжение также можно назвать тянущей силой, напряжением или натяжением.
• Этот тип силы проявляется только при контакте между кабелем и объектом.
• При наличии ускорения натяжение равно силе, необходимой для равновесия, плюс дополнительная сила, необходимая для ускорения.

Напряжение: значение, примеры, силы и физика

Напряжение — это не просто чувство, которое вы испытываете перед экзаменом. Что касается физики, напряжение — это тип силы. Сила натяжения действует аналогично другим приложенным силам, например, если вы должны тянуть коробку по полу. Однако вместо того, чтобы тянуть коробку руками, вы будете тянуть коробку веревкой, шнуром, цепью или подобным предметом, чтобы это считалось натяжением. Поскольку напряжение похоже на приложенную силу, для него нет конкретного уравнения или формулы. Примером натяжения является ситуация, когда собака тянет поводок, пока вы берете ее на прогулку, — поводок тянет вас вперед с силой натяжения.

Определение напряжения

Напряжение убивает меня! Что такое напряжение? Натяжение — это тип контактной силы, возникающей при использовании веревки или шнура.

В физике мы определяем натяжение как силу, возникающую, когда веревка, шнур или подобный предмет натягивает объект. На противоположных сторонах веревки действуют две силы, создающие натяжение.

Натяжение представляет собой тянущую силу (поскольку вы не можете толкать веревкой) и действует в направлении веревки. Мы считаем напряжение a контактная сила , так как веревка должна коснуться объекта, чтобы оказать на него силу.

Натяжение в физике

Следует отметить, что натянутая веревка прикладывает одинаковую силу к каждому прикрепленному объекту. Например, когда мы упомянули прогулку с собакой, мы описали, как собака, дергающая за поводок, приложит к вам силу натяжения. Если бы нас интересовали только силы, действующие на вас, это все, что нас интересовало бы. Но что, если бы мы также захотели узнать силы, действующие на собаку? Мы заметим, что, когда собака тянет поводок, есть сила, которая удерживает или тянет ее обратно. Сила натяжения, тянущая вас вперед, такая же (имеет ту же величину), что и сила натяжения, удерживающая его назад. Как показано ниже, мы можем нанести на поводок две стрелки, чтобы показать эти две силы.

Силы натяжения

Натяжение в результате межатомных электрических сил. Межатомные электрические силы являются причиной всех контактных сил. Для натяжения веревка состоит из множества атомов и молекул, связанных вместе. По мере того как веревка становится натянутой под действием силы, одна из связей между атомами растягивается все дальше друг от друга на микроскопическом уровне. Атомы хотят оставаться рядом в своем естественном состоянии, поэтому электрические силы, удерживающие их вместе, возрастают. Все эти крошечные силы складываются вместе, чтобы создать одну силу натяжения. Этот принцип делает стрелки на рис. 1 более понятными: если собака и человек тянут поводок наружу, силы, удерживающие поводок вместе, направлены на поводок.

Уравнение натяжения

Для силы натяжения не существует специального уравнения, в отличие от сил трения и упругости. Вместо этого нам нужно использовать диаграмму свободного тела и Второй закон движения Ньютона , чтобы решить напряженность.

Нахождение натяжения с помощью диаграммы свободного тела и второго закона Ньютона

Диаграммы свободного тела помогают визуализировать силы, действующие на объект. Для ящика, тянущегося по полу веревкой, как показано на рисунке ниже,

Рис. 2 – Веревка, тянущая коробку

мы добавили бы стрелки для всех сил, действующих на коробку.

Рис. 3 — Здесь представлены все силы, действующие на коробку.

Эта цифра включает все силы, которые могут действовать в данной ситуации, включая трение \(F_\text{f} \), гравитацию \(F_g\), нормальное \(F_\text{N} \) и напряжение \(Т\).

Помните: всегда отводите стрелки силы натяжения от объекта. Напряжение — это сила притяжения, поэтому сила всегда будет направлена ​​наружу.

Второй закон движения Ньютона утверждает, что ускорение объекта зависит от силы, действующей на объект, и массы объекта

Следующее уравнение:

$$\sum \vec F =m\vec a \mathrm{,}$$

является результатом второго закона Ньютона.

Это уравнение применимо к каждому направлению, поэтому обычно мы хотим включить одно для направления \(y\) и одно для направления \(x\). В нашем примере на рисунках выше нет никакого напряжения, действующего в направлении \(y\), поэтому для определения напряжения мы можем сосредоточиться на направлении \(x\), где у нас есть сила трения, действующая влево и напряжение, действующее вправо. Выбирая право быть положительным, наше результирующее уравнение выглядит так:

$$-F_\text{f} + T =ma\mathrm{.}$$

Затем мы можем переставить для решения натяжения:

$$T=ma+F_\text{f} \mathrm{ . }$$

Если коробка находится на поверхности без трения, сила трения равна нулю, поэтому натяжение будет равно произведению массы коробки на ускорение коробки.

Примеры натяжения

В задачах по физике вы можете увидеть множество реальных сценариев, связанных с натяжением, таких как:

• Автомобили, буксирующие прицепы
• Перетягивание каната
• Шкивы и канаты
• Тренажерный зал

Это может показаться очень разными сценариями, но для решения каждого из них вы будете использовать один и тот же метод. Ниже приведены некоторые проблемы, с которыми вы можете столкнуться, и способы их решения.

Веревка между двумя объектами

Теперь давайте все перемешаем и сделаем пример с двумя объектами, соединенными веревкой.

Рис. 4 – Веревка между двумя объектами.

На приведенном выше рисунке показана веревка между двумя ящиками и одним ящиком, тянущим 2 вправо. Как мы упоминали в случае с собачьим поводком, натяжение, действующее на коробку 1, такое же, как и на коробку 2, поскольку это та же самая веревка. Поэтому на рисунке мы обозначили их одинаково \(T_1 \).

В любой задаче мы можем выбрать, какой объект или группу объектов анализировать на диаграмме свободного тела. Допустим, мы хотели найти \(T_1\) и \(T_2\). Мы могли бы начать с просмотра поля 1, потому что это более простая сторона, и мы ищем только одно неизвестное. На следующем рисунке показана диаграмма свободного тела для ящика 1:

Рис. 5 — Диаграмма свободного тела ящика 1.

Поскольку натяжение действует только в направлении \(x\), мы можем пренебречь действующими силами в \(y\)-направлении. Выбрав положительное значение, уравнение второго закона Ньютона будет выглядеть так:

$$-F_{\text{f}1} +T_1 = m_1 a\mathrm{.}$$

Затем мы можем переставить переменные для решения \(T_1 \)

$$T_1 = m_1 a + F_{\text{f}1}\mathrm{;}$$

, чтобы найти \(T_2 \), мы могли посмотреть силы только на поле 2, показанном здесь:

Рис. 6 — Диаграмма свободного тела из поля 2.

Снова игнорируя \(y\)-направление, уравнение для \(x\)-направления будет следующим:

$$-T_1 — F_{\text{f}2} + T_2 = m_2 a\mathrm{. }$$

Поскольку мы знаем, что \(T_1 \) одинаково для каждого блока, мы можем взять \(T_1 \), который мы узнали из блока 1, и применить его к блоку 2 путем замены

$$-(m_1 a + F_{\text{f}1}) — F_{\text{f}2} +T_2 = m_2 a$$

и тогда мы можем найти \(T_2 \),

$$T_2 = (m_2 + m_1 )a ​​+ F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$

Однако, если нам не нужно известно \(T_1 \), мы всегда можем смотреть на оба ящика вместе, как если бы они были одним целым. Ниже мы можем увидеть, как выглядит диаграмма свободного тела, когда вы группируете два ящика:

Рис. 7 — Диаграмма свободного тела обоих ящиков вместе.

Если мы напишем уравнение второго закона Ньютона для направления \(x\), мы получим

$$-(F_{\text{f}1} + F_{\text{f}2})+T_2 = (m_1 +m_2 )a$$

и может переставить его, чтобы найти \(T_2 \ ),

$$T_2 = (m_1 + m_2 )a + F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$

Мы можем видеть, что это дает тот же результат, что и при рассмотрении квадратов по отдельности, а затем составлении уравнений вместе. Любой метод работает для поиска \(T_2 \) (вы можете решить, какой из них проще, и использовать любой из них), но иногда переменную, которую вам нужно найти, можно найти, только сосредоточившись на одном конкретном объекте.

Тяга под углом

Теперь давайте сделаем пример со всеми любимыми: углы.

Рис. 8 — Натяжение каната под углом.

На рисунке выше веревка тянется за ящик под углом, а не вдоль горизонтальной поверхности. В результате коробка скользит по поверхности горизонтально. Чтобы найти натяжение, мы использовали бы суперпозицию сил , чтобы разделить угловую силу на часть силы, которая действует в направлении \(x\), и часть силы, которая действует в направлении \(y\). )-направление.

Рис. 9 — Диаграмма свободного тела с разделением натяжения на компоненты \(x\) и \(y\).

Это показано красным на рисунке выше на диаграмме свободного тела. Тогда мы можем написать отдельное уравнение для направления \(x\) и направления \(y\) в соответствии с диаграммой свободного тела.

\(T_x = T\cos{\theta}\) и \(T_y = T\sin{\theta}\).

В этом примере у нас теперь есть некоторое напряжение, действующее в направлении \(y\), поэтому мы не хотим игнорировать гравитационную и нормальную силы, как мы делали в примерах выше. Так как коробка не ускоряется в направлении \(y\), сумма сил в направлении \(y\) равна нулю

$$F_\text{N} + T\sin{\theta} -F_g =0\mathrm{,}$$

и перестановка для нахождения \(T\) дает

$$T=\frac{ F_g — F_\text{N} }{\sin{\theta}}\\\mathrm{.}$$

Направление \(x\) похоже на то, что мы сделали выше, но только с \(x\) составляющая угловой силы натяжения:

$$-F_\text{f} + T\cos{\theta} = ma\mathrm{.}$$

Затем переставляем, чтобы найти \( T\):

$$T=\frac{ma+F_\text{f}}{\cos{\theta}}\\\mathrm{.}$$

Оба этих результата дадут вам одно и то же значение для \(T\), поэтому в зависимости от того, какую информацию вы получили, вы можете либо сосредоточиться только на \(x\)-направлении, только на \(y\)-направлении, либо на обоих.

Свободно висящий объект

Когда объект висит на веревке, как показано ниже,

Рис. 10. Объект, висящий на веревке

Единственными силами, действующими на него, являются гравитационная сила, тянущая его вниз, и сила натяжения удерживая его.

Это показано на диаграмме свободного тела ниже.

Рис. 11. Схема свободного тела объекта, подвешенного на веревке

Полученное уравнение будет выглядеть следующим образом:

$$T-F_g =ma\mathrm{.}$$

Если мы перегруппируем, чтобы найти \(T\) и подставим \(mg\) вместо гравитационной силы, мы получим

$$T=ma +mg\mathrm{.}$$

Если объект не ускоряется , напряжение и гравитационная сила были бы равны и противоположны, поэтому \(T=mg\).

Натяжение за наклонную поверхность

Когда к ящику на наклонной поверхности прикладывается натяжение, мы используем ту же стратегию, что и при натяжении веревки под углом.

Рис. 12 – Натяжение объекта на склоне

Сначала начните с диаграммы свободного тела.

Рис. 13 — Схема натяжения свободного тела на наклонной поверхности

При работе с наклонной поверхностью помните, что нормальная сила всегда действует перпендикулярно поверхности, а сила тяжести (вес) всегда действует прямо вниз .

Вместо того, чтобы разбивать силу натяжения на компоненты \(x\) и \(y\), мы хотим разбить гравитационную силу на компоненты. Если мы наклоним нашу систему координат, чтобы она соответствовала углу поверхности, как показано ниже, мы увидим, что натяжение действует в новом направлении \(x\), а нормальная сила действует в новом направлении \(y\)- направление. Гравитационная сила — единственная сила под углом, так что мы разделили бы ее на компоненты, следующие новым направлениям \(x\) и \(y\), показанным ниже красным.

Рис. 14 — Диаграмма свободного тела с новой системой координат и гравитационной силой, разделенной на компоненты \(x\) и \(y\)

Тогда мы применим второй закон Ньютона в каждом направлении, как и в любой другой задаче.

Подвешивание на двух веревках

Когда объект подвешен на нескольких веревках, натяжение неравномерно распределяется по веревкам, если только они не находятся под одинаковыми углами.

Рис. 15. Объект, подвешенный на двух веревках

В этом примере мы подставим действительные числа, чтобы найти \(T_1 \) и \(T_2 \). 92}=0\mathrm{.}$$

Мы можем решить эти два уравнения и два неизвестных алгебраически любым удобным для нас способом. В этом примере мы решим первое уравнение для \(T_1 \) и заменим его вторым. Решение для \(T_1 \) дает

$$\begin{align*} \frac{1}{\sqrt{2}} T_1 &= \frac{1}{2} T_2 \\ T_1 &= \frac{ \sqrt{2}}{2} T_2 \mathrm{,} \\ \end{align*}$$

и подстановка этого во второе уравнение для нахождения \(T_2 \) дает

$$\begin{align *} \frac{\sqrt{2}}{2} T_2 \times \frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2} T_2 — 147,15\,\mathrm{ N} &= 0 \\ \frac{1+\sqrt{3}}{2} T_2 &= 147,15\,\mathrm{N} \\ T_2 &= 107,72\,\mathrm{N.} \\ \end {выравнивание*}$$

Затем подстановка \(T_2 \) обратно в первое уравнение для решения для \(T_1 \) дает нам окончательный ответ

$$\begin{align*} T_1 &= 107,72\,\mathrm{N} \ раз \frac{\sqrt{2}}{2} \\ T_1 &= 76,17\,\mathrm{N. } \\ \end{align*}$$

Шкив, наклон и подвешенный объект

Пример На изображении ниже сочетается многое из того, что мы обсуждали в каждом из приведенных выше примеров.

Рис. 17. Наклон, блок и подвешенный объект

На следующем рисунке показано, как будут выглядеть силы, действующие на каждый объект, с учетом того, что сила трения может действовать в противоположном направлении в зависимости от того, как движется система. .

Рис. 18. Силы, показанные для сценария выше

Ниже приведены советы, которые мы узнали в каждой из приведенных выше задач, которые также применимы к этой задаче:

• Мы можем смотреть на один объект отдельно и выполнять отдельные диаграмма тела и уравнения второго закона Ньютона.
• Веревка оказывает одинаковое натяжение на каждый объект.
• Мы можем наклонить нашу систему координат. У нас даже может быть своя система координат для каждого объекта, если мы будем анализировать силы, воздействующие на каждый объект в отдельности.