Напряжение на сопротивлении формула. Закон Ома: расчет напряжения, тока и сопротивления в электрических цепях

Как рассчитать напряжение в электрической цепи. Как найти силу тока через резистор. Как определить сопротивление участка цепи. Формулы и примеры расчетов по закону Ома.

Закон Ома: основная формула для расчета электрических цепей

Закон Ома — один из фундаментальных законов электротехники, устанавливающий связь между напряжением, током и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году и с тех пор широко используется для расчетов электрических цепей.

Основная формула закона Ома выглядит следующим образом:

U = I * R

где:

• U — напряжение на участке цепи (измеряется в вольтах, В)
• I — сила тока в цепи (измеряется в амперах, А)
• R — сопротивление участка цепи (измеряется в омах, Ом)

Эта простая формула позволяет рассчитать любую из трех величин, если известны две другие. Рассмотрим, как применять закон Ома на практике.

Расчет напряжения по закону Ома

Чтобы найти напряжение на участке цепи, нужно умножить силу тока на сопротивление:

U = I * R

Например, если через резистор сопротивлением 100 Ом протекает ток 0,5 А, напряжение на нем составит:

U = 0,5 А * 100 Ом = 50 В

Таким образом, зная силу тока и сопротивление, мы можем легко рассчитать падение напряжения на любом участке цепи.

Нахождение силы тока по закону Ома

Для расчета силы тока используется следующая формула:

I = U / R

То есть нужно разделить напряжение на сопротивление участка цепи.

Например, если к резистору сопротивлением 200 Ом приложено напряжение 12 В, сила тока через него составит:

I = 12 В / 200 Ом = 0,06 А

Эта формула позволяет определить ток в любой части электрической схемы при известных значениях напряжения и сопротивления.

Определение сопротивления по закону Ома

Сопротивление участка цепи можно найти, разделив напряжение на силу тока:

R = U / I

Например, если на участке цепи напряжение равно 9 В, а сила тока 0,3 А, сопротивление составит:

R = 9 В / 0,3 А = 30 Ом

Эта формула особенно полезна для определения неизвестного сопротивления в цепи по измеренным значениям тока и напряжения.

Применение закона Ома для расчета сложных цепей

В более сложных электрических схемах закон Ома применяется для каждого отдельного участка цепи. При этом учитываются следующие правила:

• При последовательном соединении резисторов их сопротивления складываются
• При параллельном соединении складываются обратные величины сопротивлений
• Общее напряжение в цепи равно сумме напряжений на отдельных участках
• Сила тока одинакова во всех последовательно соединенных элементах

Используя эти принципы и формулу закона Ома, можно рассчитать параметры даже очень сложных электрических схем.

Ограничения применения закона Ома

Важно помнить, что закон Ома справедлив не для всех проводников и электрических цепей. Он не применим в следующих случаях:

• Для нелинейных элементов (например, полупроводниковых диодов)
• При очень высоких напряжениях и токах
• Для сверхпроводников
• В цепях переменного тока высокой частоты

В этих ситуациях для расчетов используются более сложные формулы и методы.

Практическое значение закона Ома

Закон Ома имеет огромное практическое значение в электротехнике и электронике. Он позволяет:

• Рассчитывать параметры электрических цепей
• Подбирать компоненты с нужными характеристиками
• Определять режимы работы электроприборов
• Находить неисправности в электрических схемах
• Проектировать системы электроснабжения

Понимание и умение применять закон Ома необходимо всем специалистам, работающим с электричеством.

Примеры решения задач с использованием закона Ома

Рассмотрим несколько типовых задач на применение закона Ома:

Задача 1

К резистору сопротивлением 300 Ом подключен источник напряжения 12 В. Определить силу тока через резистор.

Решение:

I = U / R = 12 В / 300 Ом = 0,04 А

Задача 2

Через лампу течет ток 0,5 А при напряжении 220 В. Найти сопротивление лампы.

Решение:

R = U / I = 220 В / 0,5 А = 440 Ом

Задача 3

Определить напряжение на резисторе сопротивлением 1 кОм, если сила тока через него 5 мА.

Решение:

U = I * R = 0,005 А * 1000 Ом = 5 В

Решение подобных задач помогает лучше понять применение закона Ома на практике.

Заключение

Закон Ома — фундаментальный закон электротехники, устанавливающий связь между напряжением, током и сопротивлением в электрических цепях. Его понимание и умение применять необходимо для расчетов и анализа электрических схем. Несмотря на кажущуюся простоту, закон Ома лежит в основе работы всех электрических устройств и систем.

Распространённые ошибки при термоэлектрических расчётах

При моделировании различных электротехнических приборов важную роль играет правильный расчёт электромагнитного нагрева материалов, электропроводность и теплопроводность которых нелинейно зависят от температуры. При моделировании таких нелинейностей даже у опытных инженеров могут возникать некоторые трудности и неожиданные результаты расчетов при комплексных сочетаниях нелинейных свойств материалов, граничных условий и геометрии. Давайте на простом примере разберём, почему это происходит.

Закон Ома и резистивный нагрев

Одним из первых физических законов, с которым сталкиваемся и который используем мы как инженеры, является закон Ома: Ток, протекающий через устройство равен приложенному напряжению (разности потенциалов), делённому на электрическое сопротивление или I = V/R_e, где R_e — электрическое сопротивление, которое является функцией от геометрии и электропроводности материала.

Далее мы узнаём о рассеиваемой мощности, которая равна произведению приложенного напряжения и тока, или Q = IV, что можно также записать, как Q = I²R_e или Q = V²/R_e. Немного позже мы сталкиваемся с такими свойствами, как теплопроводность и эквивалентное термическое сопротивление устройства, R_t, которые позволяют нам рассчитать повышение температуры устройства (относительно условий окружающей среды) по формуле ΔT = QR_t.

Теперь мы можем определить абсолютное значение температуры устройства по формуле T = T_ {ambient} + QR_t. С этого момента мы и начнём наше обсуждение. Рассмотрим полностью дискретную модель. Да, пример в данной статье настолько прост, что нам даже не придётся использовать программное обеспечение COMSOL Multiphysics® для этой части. Итак, у нас есть модель с сосредоточенными параметрами, электрическое сопротивление которого равно R_e = 1 Ω, а тепловое сопротивление — R_t = 1 K/W. 2 R_e R_t.

Температуру окружающей среды примем равной 300 K или 27°C, что является примерной комнатной температурой. Теперь давайте рассчитаем температуру нашего устройства, как функцию от напряжения (от 0 до 10 В) и тока (от 0 до 10 А), как показано на рисунке ниже. Неудивительно, что мы видим квадратичную зависимость.

Зависимость температуры устройства от приложенного напряжения (слева) и протекающего тока (справа) при постоянных свойствах материала.

Можно предположить, что возможно использовать кривую для расчёта более широкого диапазона рабочих параметров. Поставим задачу нагреть устройство до критической температуры, при которой материал начнёт плавиться и испаряться. Предположим, что он начнёт испаряться при температуре 700 K (427°C). Основываясь на графиках выше и проведя простые математические вычисления можно рассчитать, что максимальное напряжение будет равно 20 В, а ток — 20 А, однако это совершенно неправильно!

Учет нелинейных свойств материала для сосредоточенной модели

На данном этапе вы можете заметить, что допущена ошибка: Электрическое сопротивление непостоянно и зависит от температуры. e_0)) R_t

Эти уравнения уже немного сложнее (первое — квадратичное уравнение относительно T), но их ещё можно решить вручную. Графики зависимости температуры от приложенного напряжения и тока показаны ниже.

Зависимости температуры устройства от приложенного напряжения (слева) и протекающего тока (справа) для случая зависимости электрического сопротивления от температуры.

Для варианта с напряжением мы видим, что при увеличении температуры, сопротивление также возрастает. Так как в этом случае сопротивление в уравнении для температуры находится в знаменателе, с его увеличением прирост температуры будет уменьшаться: мы видим, что график температуры лежит ниже, чем для случая с постоянным удельным сопротивлением. Если рассматривать вариант с постоянным током, то зависящее от температуры сопротивление будет в числителе.

По мере увеличения тока резистивный нагрев будет, наоборот, больше, чем в первом случае. На данном этапе мы опять-таки можем вычислить максимальное рабочее напряжение и ток, однако, вы, вероятно, уже видите вторую ошибку, которую мы допустили: необходимо также учитывать температурную зависимость теплового сопротивления. t_0 = 300 K), можно построить зависимости температуры устройства, как показано ниже.

Зависимости температуры устройства от приложенного напряжения (слева) и протекающего тока (справа) для случая зависимости электрического и термического сопротивлений от температуры.

Заметим, что для варианта с током температура возрастает асимптотически. Поскольку электрическое и тепловое сопротивление увеличиваются с повышением температуры, температура устройства возрастает очень резко по мере увеличения тока. При повышении температуры до бесконечности, задача становится нерешаемой. На самом деле, это полностью ожидаемо. Так работает предохранитель в вашем автомобиле. Если решать данную задачу в COMSOL Multiphysics, то можно использовать исследование во временной области (введя термальную массу как функцию от от плотности материала и теплоемкости), с помощью которого можно рассчитать время, в течение которого произойдет отказ устройства.

Для варианта с напряжением всё намного проще. Здесь мы также видим вполне предсказуемое поведение системы. С увеличением сопротивления температура растёт быстрее, чем в предыдущем случае. Однако заметьте, что относительно самого первого случая с постоянным сопротивлением, температура всё же ниже. Иногда это может запутать, но просто отметьте для себя, что одна из нелинейностей приводит к уменьшению температуры, а другая — к увеличению. В целом, если составлять более комплексную модель (например, которую можно сделать и рассчитать в COMSOL Multiphysics), то сложно предугадать, какая из нелинейностей будет преобладать.

Какую ещё ошибку можно допустить на этом этапе? В данном случае мы использовали положительный температурный коэффициент теплового сопротивления. Это справедливо для большинства металлов, однако для изоляторов, к примеру для стекла, этот коэффициент будет противоположным. Обычно термическое сопротивление всего устройства в основном зависит как раз от изоляторов, а не от электропроводящих доменов. Кроме того, при расчёте термического сопротивления устройства необходимо учитывать естественное охлаждение. То есть термического сопротивление также будет зависеть от эффектов свободной конвекции (которая возрастает с разницей температур) и излучения (которое пропорционально четвёртой степени разницы температур). Теперь давайте закончим рассмотрение нашей относительно простой задачи и изменим знак температурного коэффициента, α_t = 1/400 K, а затем также сравним два варианта — с питающим напряжением (от 0 до 100 В) и протекающим током (от 0 до 100 А).

Зависимости температуры устройства от приложенного напряжения (розовым) и протекающего тока (голубым) при отрицательном температурном коэффициенте термического сопротивления.

Мы видим, что результаты теперь совершенно другие. Обратите внимание, что в обоих случаях при низких значениях сопротивления кривые возрастают квадратично, а при увеличении сопротивления они уже имеют менее резкий характер, так как термическое сопротивление уменьшается.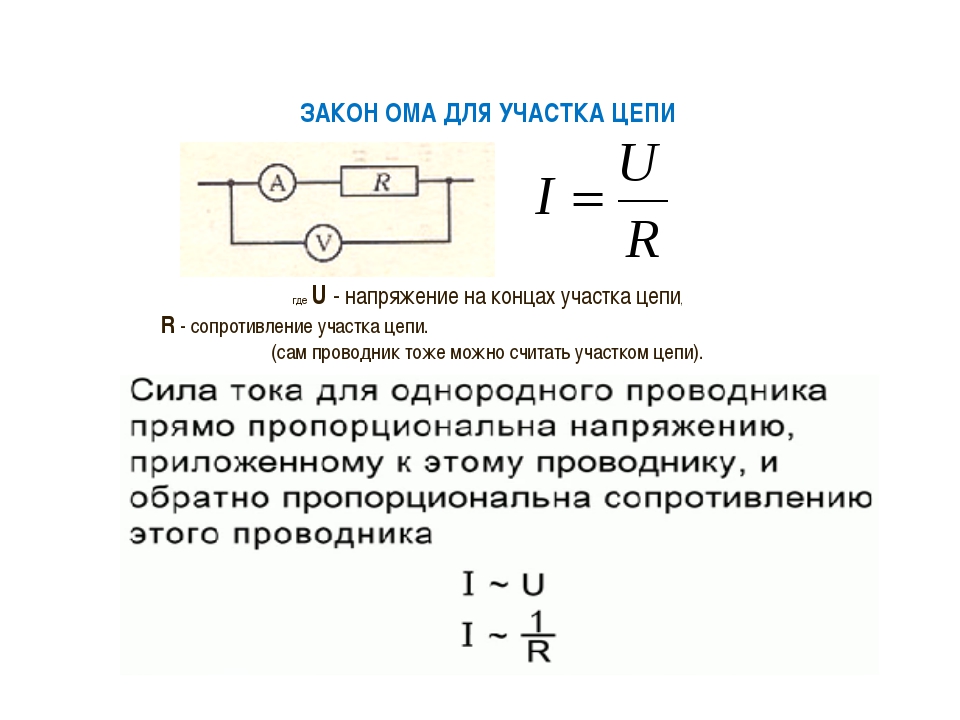 Тангенс угла наклона всегда положителен, но его величина постепенно уменьшается. В случае с током, кривая начинает асимптотически приближаться к значению T = 700 K, а в варианте с напряжением это значение меньше.

Это достаточно важный результат, и он позволяет обратить внимание на ещё одну распространённую ошибку. Нелинейные модели материалов, которые мы здесь используем для электрического и термического сопротивлений, являются приближёнными. Они становятся неэффективными при значениях температур около 700 К. Если мы знаем, что устройство будет работать как раз в этом режиме, то нужно найти более сложную материальную модель. Несмотря на то, что существующие модели позволяли получить какой-то результат, всегда стоит проверять адекватность расчёта на действующей рабочей температуре. Конечно, если наши условия эксплуатации далеки от таких температур, можно воспользоваться линеаризованной моделью резистивности (одной из встроенных материальных моделей в COMSOL Multiphysics). Тогда наша модель будет корректной.

Подводя некоторые итоги, мы видим, что температура имеет очень сложную зависимость от питающего напряжения и тока. При рассмотрении нелинейных материалов температура может быть выше или ниже, чем при постоянных свойствах, угол наклона температурной кривой может быть как довольно резким, так и плавным, в зависимости от условий работы.

Запутали ли вас результаты в последнем варианте ещё больше? Что, если мы вернёмся к выражению для сопротивления и изменим один из коэффициентов? У некоторых материалов отрицательный знак температурных коэффициентов для электрического и термического сопротивлений. Что, если бы мы использовали более комплексные нелинейности? Вы все также будете пытаться предсказать ожидаемую температуру на основании сосредоточенной модели, или вы бы скорее положились на полноценный детальный расчёт?

Выводы о распространённых ошибках при электротермических расчётах

Как насчёт случая реального устройства? В нём будет несколько материалов, различные зависимости электро- и теплопроводностей как функции температуры, а также и сложная геометрия. Какой решатель при моделировании вы бы выбрали: стационарный или временной, чтобы узнать, сколько времени потребуется для повышения температуры? Скорее всего, в модели также будут нелинейные граничные условия такие, как условие излучения и свободная конвекция, которые неправильно будет аппроксимировать только одним приближённым тепловым сопротивлением. Что же в таком случае можно ожидать? Да практически всё! И как же рассчитывать такие сложные задачи? Конечно же с помощью COMSOL Multiphysics!

Следующий шаг

Узнайте, как COMSOL Multiphysics может помочь вам в мультифизическом моделировании при решении поставленных задач. Не стесняйтесь написать нам и задать все интересующие вопросы!

Связаться с COMSOL

Формула тока через сопротивление и напряжение

Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести 2-мя методами: 1-ый метод заключается в использовании формулы закона Ома, а 2-ой вариант расчета предполагает познание геометрических размеров проводника и удельного сопротивления вещества, из которого он изготовлен.

Почему проводник “сопротивляется”?

Напряжение U, поданное на концы проводника, делает снутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем электрический ток цепи.

В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, потому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).

Таким макаром появляется сопротивление протеканию (нарастанию) тока.

Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.

Расчет сопротивления при помощи закона Ома

Германский физик Георг Ом в 1826 г. нашел, что отношение напряжения U между концами железного проводника, являющегося участком электрической цепи, к силе тока I есть величина неизменная:

Данную величину стали именовать электрическим сопротивлением.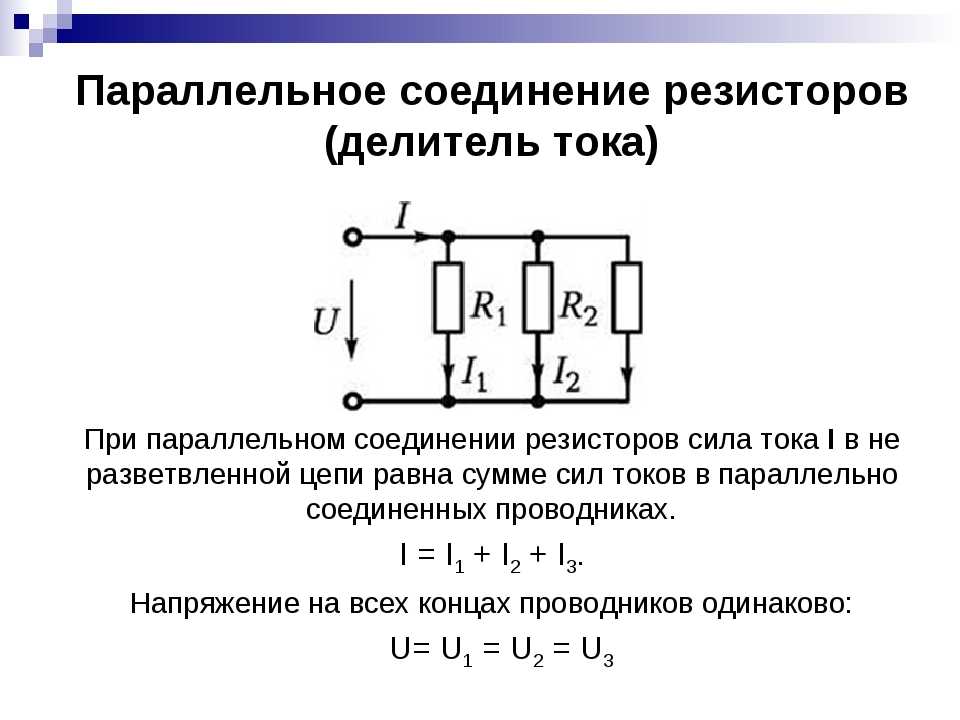 Пользуясь этой формулой, можно экспериментально найти величину неведомого сопротивления.

Рис. 2. Схема измерения напряжения и тока для определения сопротивления участка цепи.

Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Дальше, применяя формулу (1), рассчитывается значение R.

Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:

Расчет при помощи удельного сопротивления

Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого следует знать дополнительную информацию о проводнике.

Рис. 3. Проводник с поперечным сечением S и длиной L, через который течет ток I.

Георг Ом и другие исследователи опытным методом обусловили, что сопротивление проводника прямо пропорционально длине проводника L и назад пропорционально площади поперечного сечения проводника S.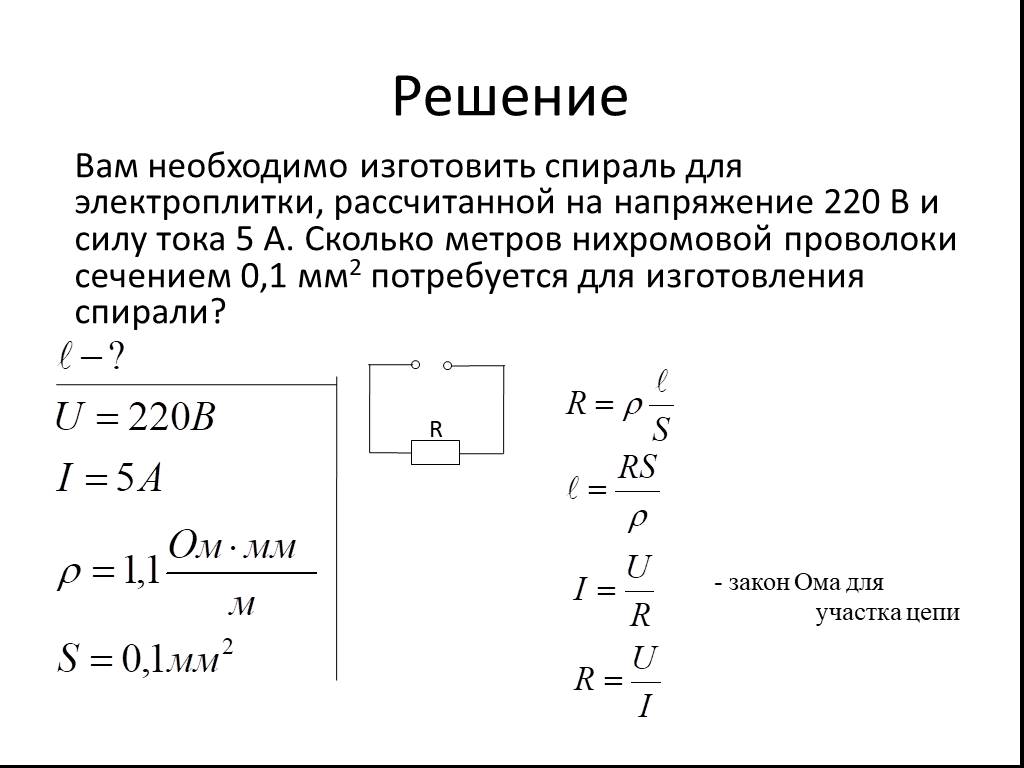 2\over м>$. Этим разъясняется внедрение такового достаточно дорогого металла для пайки в особенности принципиальных радиодеталей (микросхем, процессоров, электронных плат), которые должны как можно меньше греться в процессе работы.

Что мы узнали?

Итак, мы узнали, что расчет сопротивления проводника можно произвести 2-мя методами. 1-ый расчет проводится при помощи формулы закона Ома после измерения величин напряжения и тока. Для второго расчета нужна информация о геометрических размерах проводника и его удельном сопротивлении.

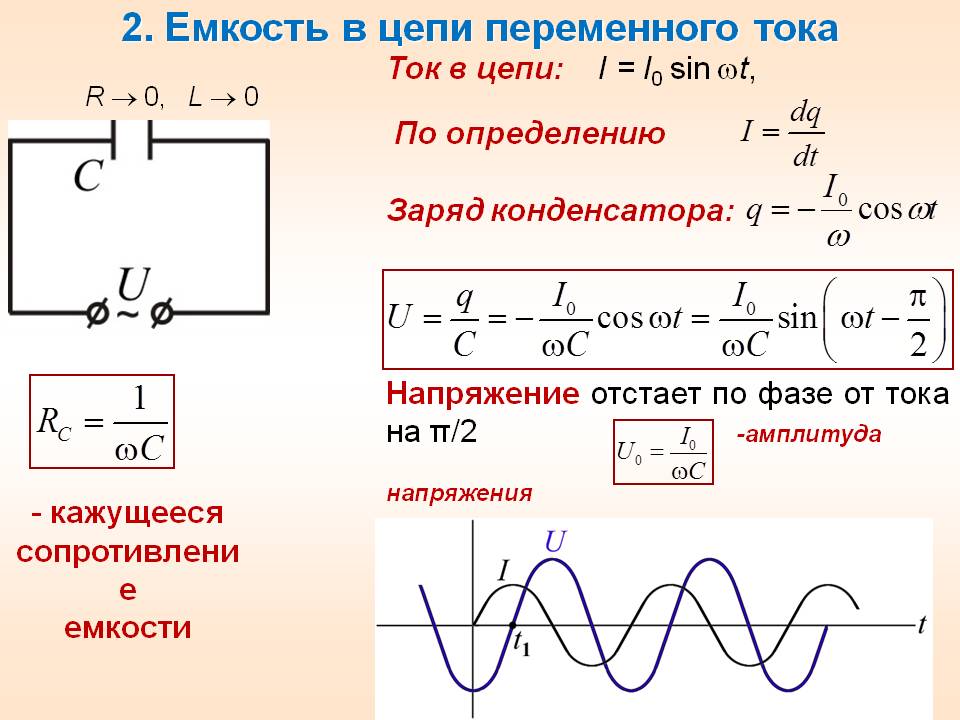
В прошлых статьях мы узнали, что всякое сопротивление, поглощающее энергию, именуется активным, а сопротивление, не поглощающее энергии, безваттным либо реактивным. Не считая того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.

Но есть цепи, где сопротивление не является чисто активным либо чисто реактивным. Другими словами цепи, где совместно с активным сопротивлением включены в цепь, как емкости, так и индуктивности.

Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам нужно для более полного осознания закона Ома для переменного тока

На рисунке 1 представлены варианты электрических цепей и их систематизация зависимо от того какие элементы (активные либо реактивные) включены в цепь.

Набросок 1. Систематизация цепей переменного тока.

Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами гласили, и оно зависит соответственно от общей емкости и индуктивности цепи.

Разглядим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

В любом сечении цепи, изображенной на рисунке 2,а, секундные значения тока должны быть одинаковыми, так как в неприятном случае наблюдались бы скопления и разрежения электронов в каких-то точках цепи. Другими словами, фазы тока по всей длине цепи должны быть одинаковыми. Не считая того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (набросок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) смещены друг относительно друга на угол в 90°.

Набросок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.

Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.

Из геометрии понятно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно приравниваться силе тока, умноженной на сопротивление.

Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

(1)

Извлекая квадратный корень из обеих частей этого равенства, получим,

(2)

Таким макаром, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений

Полное сопротивление можно отыскивать не только лишь методом вычисления, но и методом построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено методом измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Очевидно, измерения катетов и гипотенузы должны выполняться в одном и том же масштабе. Так, к примеру, если мы договорились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу см, укладывающихся на гипотенузе.

Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит внутри себя оба эти вида сопротивлений. Потому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, другими словами он будет больше 0°, но меньше 90°. К которому из этих 2-ух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и напротив, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.

В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление таковой цепи можно найти с помощью треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Набросок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений .

Разница между обоими вариантами состоит только в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.

Для данного варианта:

(3)

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), поначалу определяется реактивное сопротивление этой цепи, а потом уже полное сопротивление цепи.

Набросок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений .

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления обратны друг дружке по собственному нраву, то общее реактивное сопротивление цепи будет равно их разности, т. е.

(4)

Общее реактивное сопротивление цепи может иметь индуктивный либо емкостный нрав, зависимо от того, какое из этих 2-ух сопротивлений (XL либо XC преобладает).

После того как мы по формуле (4) обусловили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

(5)

(6)

Метод построения треугольника сопротивлений для этого варианта изображен на рис. 4 б.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

Для того дабы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), необходимо поначалу вычислить проводимость каждой из параллельных веток, позже найти полную проводимость всей цепи между точками А и В и потом вычислить полное сопротивление цепи между этими точками.

Набросок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных частей. а) — параллельное соединение R и L; б) — параллельное соединение R и C .

Проводимость активной ветки, как понятно, равна 1/R, аналогично проводимость индуктивной ветки равна 1/ωL , а полная проводимость равна 1/Z

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

(7)

Приводя к общему знаменателю подкоренное выражение, получим:

(8)

(9)

Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.

Нахождение полного сопротивления для этого варианта может быть произведено и геометрическим методом. Для этого необходимо выстроить в соответственном масштабе треугольник сопротивлений, и потом произведение длин катетов поделить на длину гипотенузы.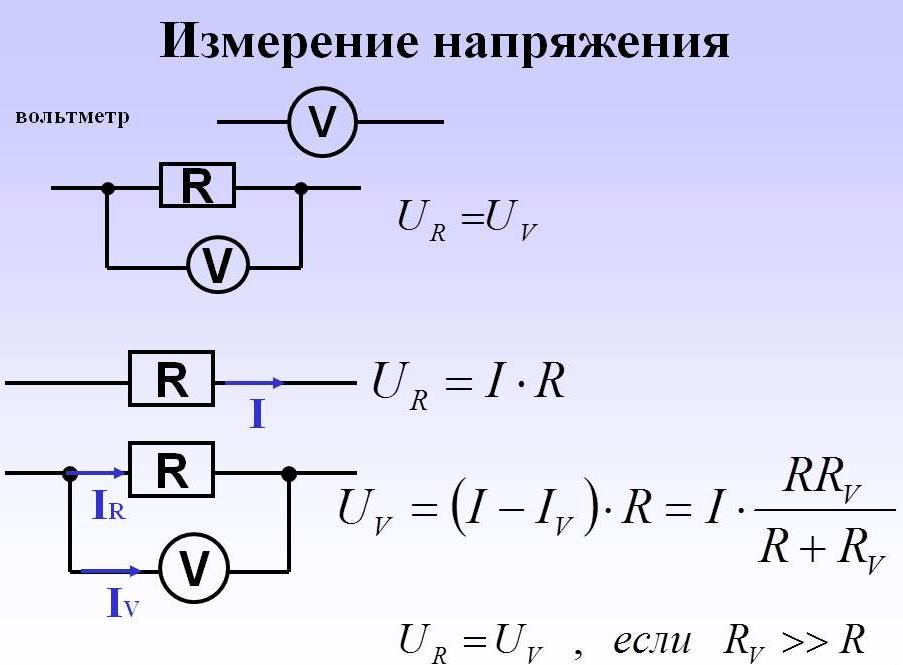 Приобретенный итог и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:

(10)

Полное сопротивление может быть найдено также и в данном случае методом построения треугольника сопротивлений.

В радиотехнике более нередко встречается случай па¬раллельного соединения индуктивности и емкости, к примеру колебательный контур для опции приемников и передатчиков. Так как катушка индуктивности всегда обладает не считая индуктивного к тому же активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветки активное сопротивление (рис 7).

Набросок 6. Эквивалентная схема колебательного контура.

Формула полного сопротивления для этого варианта будет:

(11)

Так как обычно активное сопротивление катушки (R) бывает сильно мало по сопоставлению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

(12)

В колебательном контуре обычно подбирают величины L и С таким макаром, дабы индуктивное сопротивление приравнивалось емкостному, т. е. дабы соблюдалось условие

(13)

При соблюдении этого условия полное сопротивление колебательного контура будет равно:

(14)

где L—индуктивность катушки в Гн;

С—емкость конденсатора в Ф;

R—активное сопротивление катушки в Ом.

Приглянулась СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В Соц СЕТЯХ!

ЗАКОН ОМА (сопротивление и падение напряжения)

ЗАКОН ОМА

Существует простая зависимость между током, протекающим по проводящему пути, и разностью потенциалов между концами пути. По мере увеличения разности потенциалов ток увеличивается , см. схему ниже. Два значения пропорциональны. То есть удвоение разности потенциалов удваивает ток. Утроенная разность потенциалов утроит ток и так далее. Это пропорциональное соотношение между разностью потенциалов и током называется законом Ома в честь Георга Ома. Он был немецким ученым, открывшим эту взаимосвязь в начале 1800-х годов.

Закон Ома обычно выражается в математической форме. Уравнение записывается следующим образом:

E = I x R

где E=разность потенциалов между концами проводника

I=ток через проводник

R=константа пропорциональности между E и I значение R называется сопротивлением проводника. он измеряется в единицах, называемых олмами. Один Ом определяется как сопротивление проводника, по которому течет ток силой 1 А, когда разность потенциалов между его концами составляет 1 В.

Греческая буква Ω (омега) используется в качестве символа для обозначения единицы измерения Ом. Например, 40 Ом означает сопротивление 40 Ом. Когда вы пишете большие или маленькие значения сопротивления, вы можете использовать префиксы для упрощения записи. В таблице показано несколько примеров использования общих префиксов.

Вы можете использовать закон Ома для вычисления третьего значения в уравнении, если вам известны любые два значения. Например, предположим, что вы знаете, что по проводнику течет ток силой 0,50 А, когда разность потенциалов между его концами равна 25 В. Какой будет сила тока, если вы увеличите разность потенциалов до 35 В?

Чтобы ответить на этот вопрос, вы можете использовать закон Ома в два этапа. Сначала вы вычисляете сопротивление проводника, используя данные тока и разности потенциалов. Затем вы используете это значение сопротивления для расчета тока при увеличении разности потенциалов до 35 В. Эти расчеты показаны на схеме.

Обратите внимание на приведенную выше схему, что единицы измерения включены в расчеты. Вы должны делать то же самое, когда решаете проблемы. Уравнение является физическим уравнением. Буквы обозначают физические величины, а не только числа.

Сопротивление и падение напряжения

Разность потенциалов от одного конца проводящего пути до другого зависит от того, к чему подключены эти концы. Но разность потенциалов между другими парами точек лишь частично зависит от того, с чем соединены концы пути. Это также зависит от сопротивления между точками по сравнению с общим сопротивлением.

Пример поможет вам понять этот момент. Предположим, токопроводящий путь состоит из трех участков, каждый из которых имеет разное сопротивление. Эти секции соединены последовательно, то есть встык, см. схему ниже. Весь ток в пути проходит через каждый резистор.

Предположим, что три секции имеют общее сопротивление 100 Ом. Предположим далее, что разность потенциалов между концами пути равна 100 В. Используя закон Ома, можно рассчитать, что сила тока в цепи равна 1А.

Если вы измерите разность потенциалов от одного конца пути до различных точек между участками, вы обнаружите, что разность потенциалов меньше 100 В. Если ваш измерительный прибор охватывает только один участок, разность потенциалов будет еще меньше. И если он не охватывает ни одного участка, разность потенциалов равна нулю.

Вы можете думать об этом сокращении как об уменьшении разности потенциалов по мере того, как вы проходите все меньше и меньше всего пути. Общее название этого уменьшения разности потенциалов на пути — падение напряжения .

Вы можете использовать закон Ома, чтобы понять, почему разность потенциалов уменьшается, когда вы измеряете ее только на части пути. Через каждый резистор проходит такой же ток, как и по всему пути. Следовательно, по закону Ома разность потенциалов на каждом участке равна произведению этого тока на сопротивление участка.

Например, разность потенциалов на участке А в приведенной выше цепи составляет 50 В, поскольку ток равен 1 А (1 А x 50 Ом = 50 В). Если вычислить разность потенциалов на всех трех участках и сложить вместе три результата, общая сумма будет равна разности потенциалов на всем пути.

Падение напряжения пропорционально величине сопротивления в измеряемом диапазоне. Если половина полного сопротивления включена в пролет, падение напряжения равно разности потенциалов на всем пути. Если включить 80% полного сопротивления, падение напряжения составит 80% разности потенциалов на всем пути.

Калькулятор закона Ома

Закон Ома — это фундаментальный принцип в области электричества и электроники, который формирует основу для понимания того, как ведут себя электрические цепи. Калькулятор закона Ома — это инструмент, который поможет вам понять этот принцип, позволяя рассчитать взаимосвязь между электрическим током, напряжением и сопротивлением в цепи. С помощью калькулятора вы можете ввести любые два из трех значений (напряжение, сопротивление или ток) и быстро определить третье неизвестное значение. Это делает его ценным инструментом для инженеров-электриков, техников и энтузиастов-любителей, которым необходимо понимать поведение электрической цепи.

Независимо от того, работаете ли вы со сложной электрической системой или просто пытаетесь устранить неполадки в цепи, калькулятор закона Ома — это важный инструмент, который поможет вам понять, как работают электрические цепи. Благодаря удобному интерфейсу и простым вычислениям он предоставляет доступный способ визуализации взаимосвязей между напряжением, током и сопротивлением в цепи. Являетесь ли вы опытным профессионалом или только начинаете, калькулятор закона Ома станет незаменимым инструментом для всех, кто работает с электрическими цепями.

Калькулятор закона Ома Напряжение (В):

Сопротивление (Ом):

Ток (А):

© 2018-2023 electricmag.com

РЕШЕНО: Рассчитайте следующее, используя формулу для тока и напряжения. 1. Рассчитайте напряжение в следующих цепях: a. Ток = 2А, сопротивление = 10 Ом б. Ток = 5А, сопротивление = 2 Ом c. Ток = 100А, сопротивление = 2,3 Ом

Вопрос

Пошаговый ответ

Рассчитайте следующее, используя формулу для тока и напряжения. 1. Рассчитайте напряжение в следующих цепях: a. Ток = 2А, сопротивление = 10 Ом б. Текущая…

Выполните следующие расчеты, используя формулу для тока и напряжения. 1. Рассчитайте напряжение в следующих цепях: a. Ток = 2А, сопротивление = 10 Ом б. Ток = 5А, сопротивление = 2 Ом c. Ток = 100 А, сопротивление = 2,3 Ом — 2. Рассчитайте ток в следующих цепях: а. Напряжение = 10В. сопротивление = 2 Ом = 2 — b. Напряжение = 120 В, сопротивление = 40 Ом c. Напряжение = 230В, сопротивление = 5 Ом

---

Видео Ответ:

Решено проверенным экспертом

Вопрос о наилучшем совпадении:

Рассчитайте следующее, используя формулу для тока и напряжения. 1. Рассчитайте напряжение в следующих цепях: a. Ток = 2А, сопротивление = 10 Ом б. Ток = 5А, сопротивление = 2 Ом c. Ток = 100 А, сопротивление = 2,3 Ом — 2. Рассчитайте ток в следующих цепях: а. Напряжение = 10В. сопротивление = 2 Ом = 2 — b. Напряжение = 120 В, сопротивление = 40 Ом c. Напряжение = 230 В, сопротивление = 5 Ом

Рекомендуемые видеоролики

Стенограмма

Я Итак, вопрос в том, что я думаю, что так что же еще больше в том, что я все еще в том, что такое постоянное, что мы выпускаем, мы будем делать высоко в нашем, где мы в напряжении, я занавес, и наш агент зарегистрирован . Хорошо, поэтому я должен рассчитать значения, а затем они дают это в первой части, вы можете дополнить знания в следующей, скажем, пицце. Так что в вопросах, которые я и собираюсь поставить на 10 баллов, ладно, тогда мы умножим на наш, что означает умножить на 10, так что это будет по-другому. Хорошо, а на рынке видно, что если я равен пяти годам, а Р. равен двум годам, то какова будет стоимость, умноженная на искусство, тогда это пять умножить на два.