Что такое основные логические операции. Как построить таблицу истинности. Какие законы логики существуют. Как упростить логические выражения. На эти и другие вопросы вы найдете ответы в нашей статье.
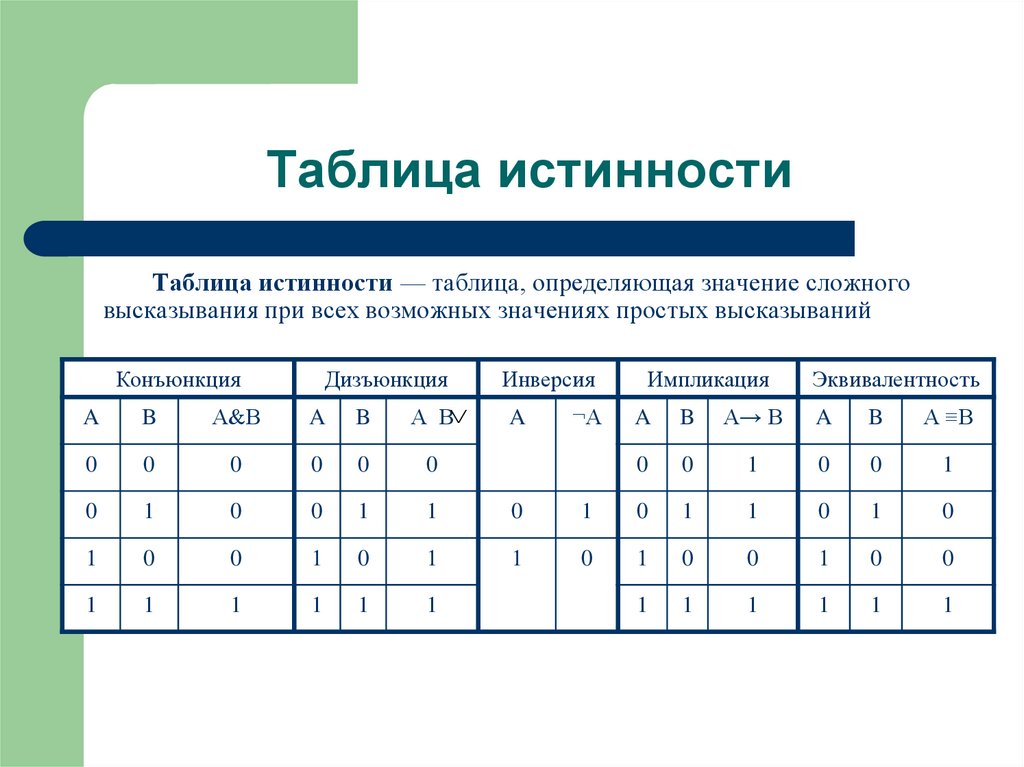
Основные логические операции и их таблицы истинности
Логические операции являются фундаментальными понятиями в математической логике и информатике. Они позволяют комбинировать простые высказывания для получения более сложных логических выражений. Рассмотрим основные логические операции и их таблицы истинности:
Отрицание (НЕ)
Отрицание меняет значение высказывания на противоположное. Обозначается символом ¬ или ~.
| A | ¬A |
|---|---|
| 0 | 1 |
| 1 | 0 |
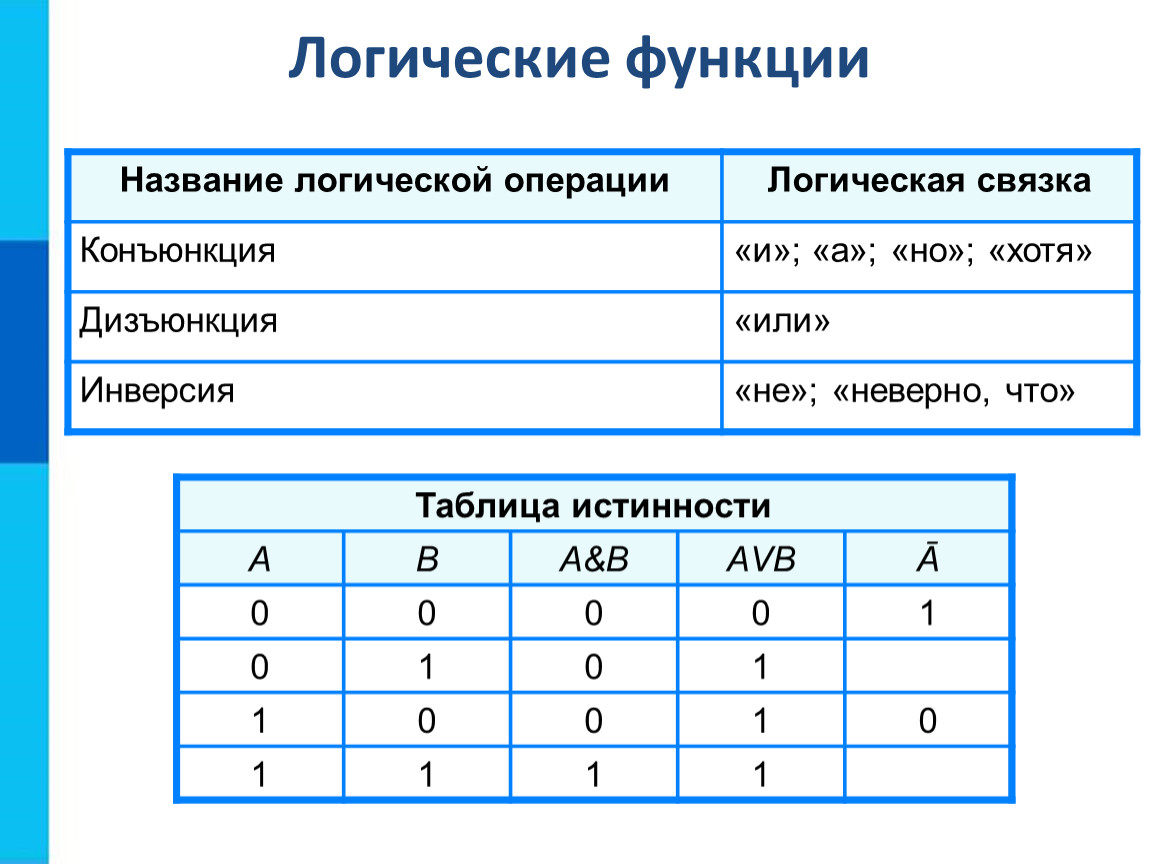
Конъюнкция (И)
Конъюнкция истинна только когда оба высказывания истинны. Обозначается символом ∧ или &.
| A | B | A ∧ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | |
| 1 | 1 | 1 |
Дизъюнкция (ИЛИ)
Дизъюнкция истинна, если хотя бы одно из высказываний истинно. Обозначается символом ∨ или |.
| A | B | A ∨ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
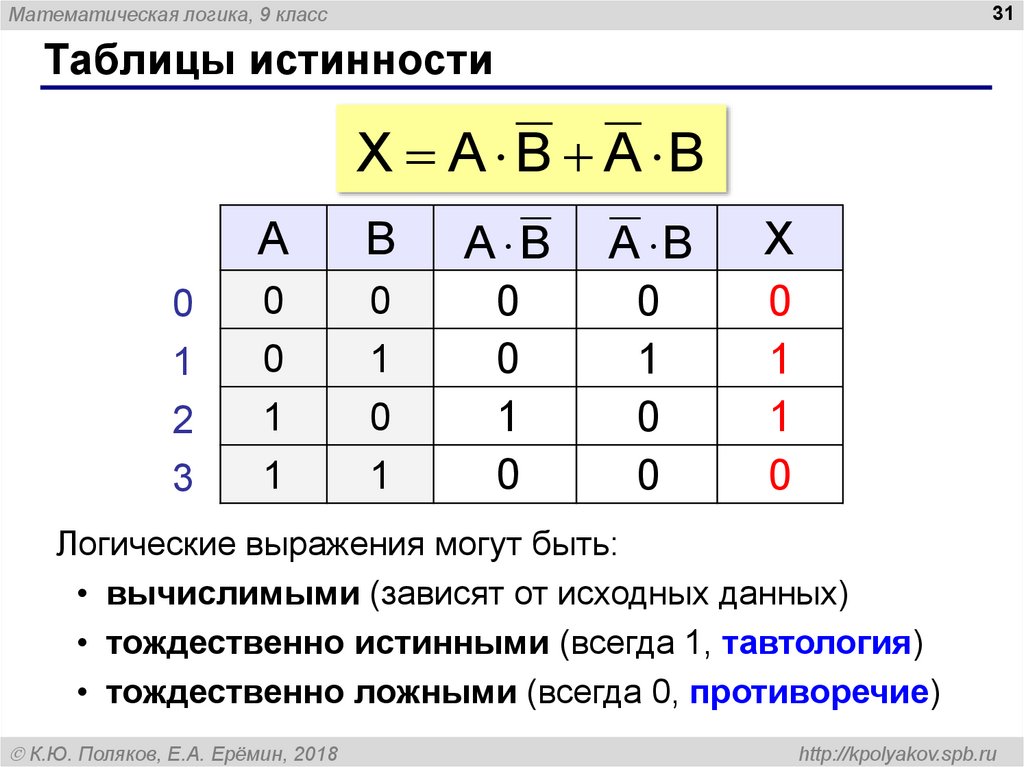
Построение таблиц истинности для сложных выражений
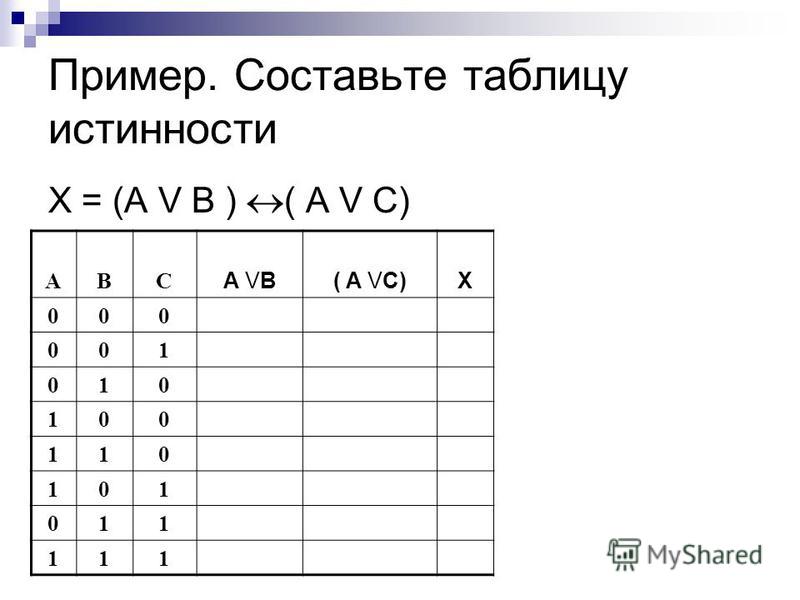
Таблица истинности для сложного логического выражения строится путем последовательного применения операций согласно их приоритету. Рассмотрим пример построения таблицы истинности для выражения (A ∨ B) ∧ ¬C:
| A | B | C | A ∨ B | ¬C | (A ∨ B) ∧ ¬C |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Законы логики и их применение
Существует ряд законов логики, которые позволяют упрощать и преобразовывать логические выражения. Рассмотрим некоторые из них:
Законы де Моргана
- ¬(A ∧ B) = ¬A ∨ ¬B
- ¬(A ∨ B) = ¬A ∧ ¬B
Эти законы позволяют «вносить» отрицание внутрь скобок, меняя при этом операцию И на ИЛИ и наоборот.
Закон двойного отрицания
¬¬A = A
Двойное отрицание высказывания равносильно самому высказыванию.
Законы идемпотентности
- A ∧ A = A
- A ∨ A = A
Конъюнкция или дизъюнкция высказывания с самим собой не меняет его значения.
Упрощение логических выражений
Упрощение логических выражений позволяет сделать их более компактными и легкими для анализа. Рассмотрим пример упрощения выражения:
(A ∧ B) ∨ (A ∧ ¬B) ∨ (¬A ∧ B)
- Применим закон дистрибутивности: A ∧ (B ∨ ¬B) ∨ (¬A ∧ B)
- B ∨ ¬B — это тавтология, равная 1: A ∨ (¬A ∧ B)
- Снова применим закон дистрибутивности: (A ∨ ¬A) ∧ (A ∨ B)
- A ∨ ¬A — это тавтология: 1 ∧ (A ∨ B)
- Окончательный результат: A ∨ B
Таким образом, сложное выражение было упрощено до простой дизъюнкции.
Логические операции в программировании
Логические операции широко используются в программировании для управления потоком выполнения программы и обработки данных. Рассмотрим пример использования логических операций в Python:
def check_eligibility(age, income):
if age >
= 18 and (income > 30000 or age > 65):
return "Eligible"
else:
return "Not eligible"
print(check_eligibility(25, 35000)) # Выведет: Eligible
print(check_eligibility(70, 20000)) # Выведет: Eligible
print(check_eligibility(17, 50000)) # Выведет: Not eligible
В этом примере используются операции AND (и) и OR (или) для проверки соответствия условиям.
Применение логических операций в цифровых схемах
Логические операции лежат в основе работы цифровых схем. Рассмотрим пример простой цифровой схемы, реализующей функцию (A ∧ B) ∨ C:
«` «`В этой схеме используются логические элементы AND и OR для реализации заданной функции. Входы A и B подаются на элемент AND, результат которого затем комбинируется с входом C через элемент OR.
Логические операции в базах данных
В базах данных логические операции часто используются в запросах для фильтрации и комбинирования данных. Рассмотрим пример SQL-запроса с использованием логических операций:
SELECT *
FROM employees
WHERE (department = 'Sales' AND salary >
50000)
OR (department = 'IT' AND experience > 5);
Этот запрос выбирает сотрудников отдела продаж с зарплатой выше 50000 или сотрудников IT-отдела с опытом работы более 5 лет.
Логические парадоксы и их значение
Логические парадоксы — это утверждения, которые кажутся противоречивыми или нелогичными, но на самом деле могут быть истинными. Они часто используются для иллюстрации ограничений формальной логики и языка. Рассмотрим известный парадокс лжеца:
«Это утверждение ложно.»
Если это утверждение истинно, то оно должно быть ложным. Но если оно ложно, то оно должно быть истинным. Этот парадокс демонстрирует, что не все утверждения могут быть однозначно классифицированы как истинные или ложные.
Изучение логических парадоксов важно для развития критического мышления и понимания границ формальной логики. Они также играют роль в развитии теории множеств и оснований математики.
Заключение и перспективы развития логики
Логические операции и законы логики являются фундаментальными концепциями, которые находят применение во многих областях — от математики и информатики до философии и повседневных рассуждений. С развитием искусственного интеллекта и машинного обучения значение логики только возрастает.
Современные направления развития логики включают:
- Нечеткую логику, которая позволяет работать с неопределенностью и частичной истинностью
- Квантовую логику, учитывающую принципы квантовой механики
- Временную логику, используемую для анализа систем, изменяющихся во времени
Эти новые области логики открывают новые возможности для моделирования сложных систем и решения задач, которые трудно решить в рамках классической логики.
отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция, законы де Моргана, тавтология, таблицы истинности
- Отрицание
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Законы де Моргана
- Алгоритм доказательства эквивалентности высказываний с помощью таблиц истинности
- Тавтология
- Примеры
п.1. Отрицание
Отрицанием высказывания A называется новое высказывание «не A», принимающее значение «истина», если A ложно, и значение «ложь», если A истинно.
Обозначение отрицания \(\overline{A}\) читается «не A».
Если записать эту операцию с помощью таблицы истинности, где 0 обозначает «ложь», а 1 – «истина», получаем:
A
\(\overline{A}\)
Закон отрицания отрицания. Двойное отрицание \(\overline{\overline{A}}=A\) истинно только в том случае, если истинно исходное высказывание A.
Правило отрицания высказываний с кванторами: $$ \mathrm{ \overline{(\forall x)A(x)}=(\exists x)\overline{A(x)},\ \ \overline{(\exists x)A(x)}=(\forall x)\overline{A(x)} } $$
Расшифровка первого правила: высказывание «неверно, что для любого x выполняется A(x)» совпадает с высказыванием «найдётся x, для которого A(x) не выполняется». 2-1\geq 0} & \\ \mathrm{x\gt\frac12} & \end{array}\right. \Leftrightarrow x\leq -1 \cup x\gt\frac12 $$
2-1\geq 0} & \\ \mathrm{x\gt\frac12} & \end{array}\right. \Leftrightarrow x\leq -1 \cup x\gt\frac12 $$
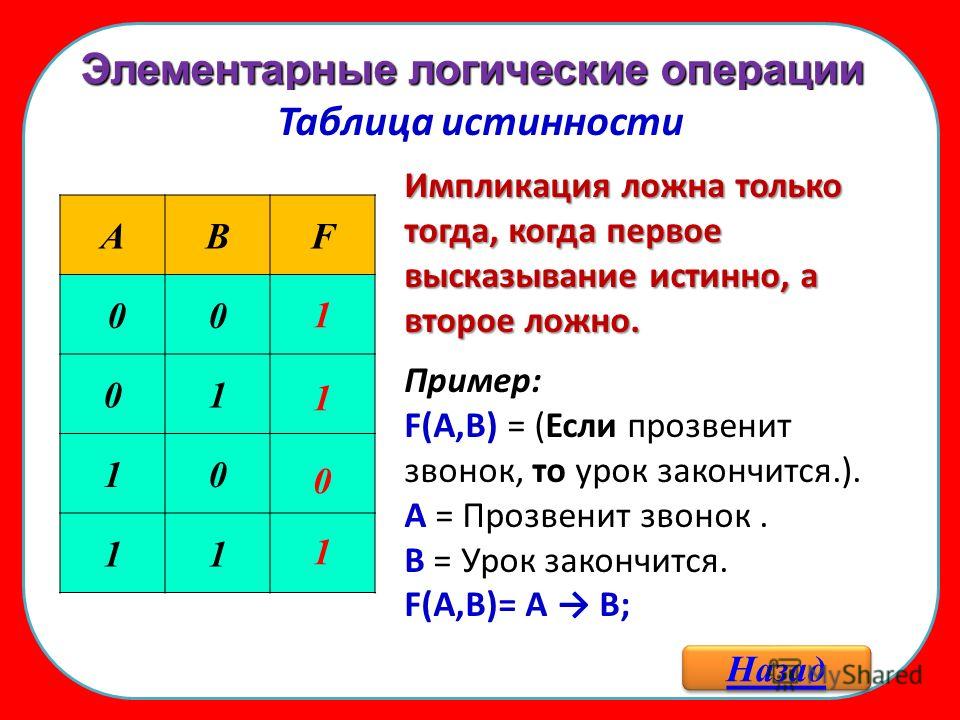
п.4. Импликация
Импликация двух высказываний – это высказывание, которое будет ложным, если первое высказывание истинно, а второе ложно; а во всех остальных случаях – будет истинным.
Обозначение импликации A → B, читается «если A, то B».
Высказывание A называют «посылкой», а высказывание B – «заключением».
Значение импликации зависит от порядка высказываний.
Таблица истинности:
A
B
A → B
п.5. Эквиваленция
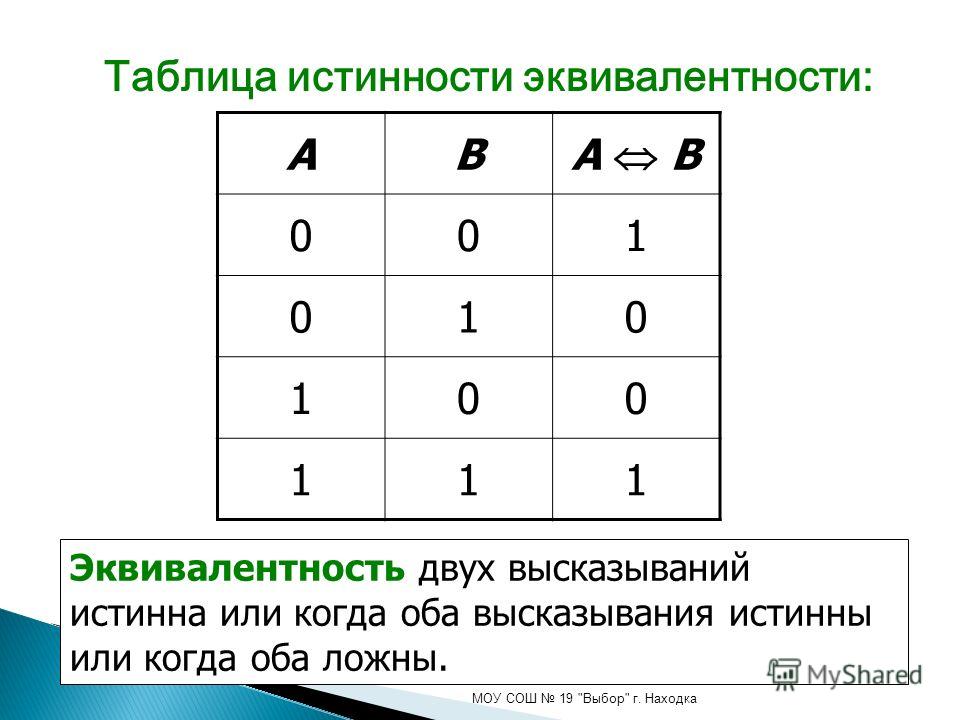
Эквиваленция двух высказываний – это высказывание, которое будет истинным только при совпадении истинности обоих высказываний; а при несовпадении – будет ложным.
Обозначение эквиваленции A ↔ B, читается «A то же самое, что B» или «A эквивалентно B».
Таблица истинности:
A
B
A ↔ B
п.
 6. Законы де Моргана
6. Законы де Моргана Отрицание конъюнкции эквивалентно дизъюнкции отрицаний: \(\mathrm{\overline{A\wedge B}=\overline{A}\vee\overline{B}}\)
Докажем эквивалентность с помощью таблиц истинности:
|
A B A ∧ B \(\mathrm{\overline{A\wedge B}}\) |
A B \(\mathrm{\overline{A}}\) \(\mathrm{\overline{B}}\) \(\mathrm{\overline{A}\vee\overline{B}}\) |
Мы видим, что итоговые столбцы слева и справа полностью совпадают.
Значит, высказывания эквивалентны.
Отрицание дизъюнкции эквивалентно конъюнкции отрицаний: \(\mathrm{\overline{A\vee B}=\overline{A}\wedge\overline{B}}\)
Докажем эквивалентность с помощью таблиц истинности:
|
A B A ∨ B \(\mathrm{\overline{A\vee B}}\) |
A B \(\mathrm{\overline{A}}\) \(\mathrm{\overline{B}}\) \(\mathrm{\overline{A}\wedge\overline{B}}\) |
Высказывания слева и справа эквивалентны.
Высказывания называются эквивалентными (равносильными), если соответствующие значения каждого из них совпадают в таблице истинности.
п.7. Алгоритм доказательства эквивалентности высказываний с помощью таблиц истинности
На входе: две формулы алгебры высказываний, соединенные отношением эквивалентности «=».
Шаг 1. Построить таблицу истинности для формулы слева от знака «=».
Шаг 2. Построить таблицу истинности для формулы справа от знака «=».
Шаг 3. Сравнить итоговые столбцы двух таблиц. Если столбцы полностью совпадают, формулы эквивалентны.
Например:
Докажем следующее свойство:
Отрицание импликации эквивалентно конъюнкции посылки и отрицания заключения: $$ \mathrm{ \overline{A\rightarrow B}=A \wedge\overline{B} } $$
|
A B A → B \(\mathrm{\overline{A\rightarrow B}}\) |
A B \(\mathrm{\overline{B}}\) \(\mathrm{A\wedge\overline{B}}\) |
Столбцы совпадают. Значит, формулы эквивалентны.
Значит, формулы эквивалентны.
Что и требовалось доказать.
п.8. Тавтология
Тавтологией (или законом логики) называется формула, принимающая значение истины при любых значениях переменных.
Таблица истинности для тавтологии даёт итоговый столбец, заполненный только единицами.
Например: \(\mathrm{A \vee \overline{A}}\)
A
\(\mathrm{\overline{A}}\)
\(\mathrm{A\vee\overline{A}}\)
«Быть иль не быть» — это тавтология.
п.9. Примеры
Пример 1. Для формулы P(x, y)=(∃x∀y)(A(x,y)∧B(x,y))
сформулируйте предложения A и B, при которых:
а) формула всегда истинна; б) формула всегда ложна.
a) A(x,y): квадрат числа x больше y
B(x,y): куб числа x больше y
Пусть x = |y + 1|. Тогда x2 = (y + 1)2 > y – истинно ∀y
x3 = |y + 1|3 > y – ∀y
Таким образом, мы нашли x, при котором A(x,y) ∧ B(x,y) = 1 для любого y, т. е.
е.
P(x,y) = 1.
б) A(x,y): x больше y
B(x,y): x меньше y
A(x,y)∧B(x,y) = 0 – ложно для любого y, т.к. не существует x, который одновременно был бы больше и меньше y.
P(x,y) = 0.
Пример 2. Составьте таблицу истинности для формулы \(P=(\overline{A}\rightarrow B)\vee (A\rightarrow \overline{B})\).
Является ли данная формула тавтологией?
A
B
\(\mathrm{\overline{A}}\)
\(\mathrm{\overline{B}}\)
\(\mathrm{\overline{A}\rightarrow B}\)
\(\mathrm{A\rightarrow \overline{B}}\)
P
0
0
1
1
0
1
1
0
1
1
0
1
1
1
1
0
0
1
1
1
1
1
1
0
0
1
0
1
Это – тавтология.
Пример 3*. Составьте таблицу истинности для формулы
P = (A → B) ∧ (B → C) → (A → C)
Является ли данная формула тавтологией?
A
B
C
A → B
B → C
A → C
(A → B)
∧
(B → C)
P
0
0
0
1
1
1
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
1
1
1
1
1
1
1
Это – тавтология.
Создание выражений
Для каждой выходной переменной окно Комбинационный анализ поддерживает две структуры — соответствующую колонку таблицы истинности и логическое выражение — указывающее, как каждый выход связан со своими входами. Вы можете редактировать и таблицу истинности и выражение; одно будет автоматически менять другое по мере необходимости, чтобы они соответствовали друг другу.
Как мы увидим на следующей странице, логические выражения особенно полезны, потому что окно Комбинационный анализ будет использовать их, когда мы укажем ему построить схему, соответствующую текущему состоянию.
Вы можете просматривать и редактировать выражения, используя две последние вкладки: Выражение и Минимизация.
Вкладка Выражение
Вкладка Выражение позволяет вам просматривать и редактировать текущее выражение, связанное с каждой выходной переменной. Вы можете выбрать выходное выражение, которое вы хотите просматривать и изменять, с помощью списка «Выход:» наверху вкладки.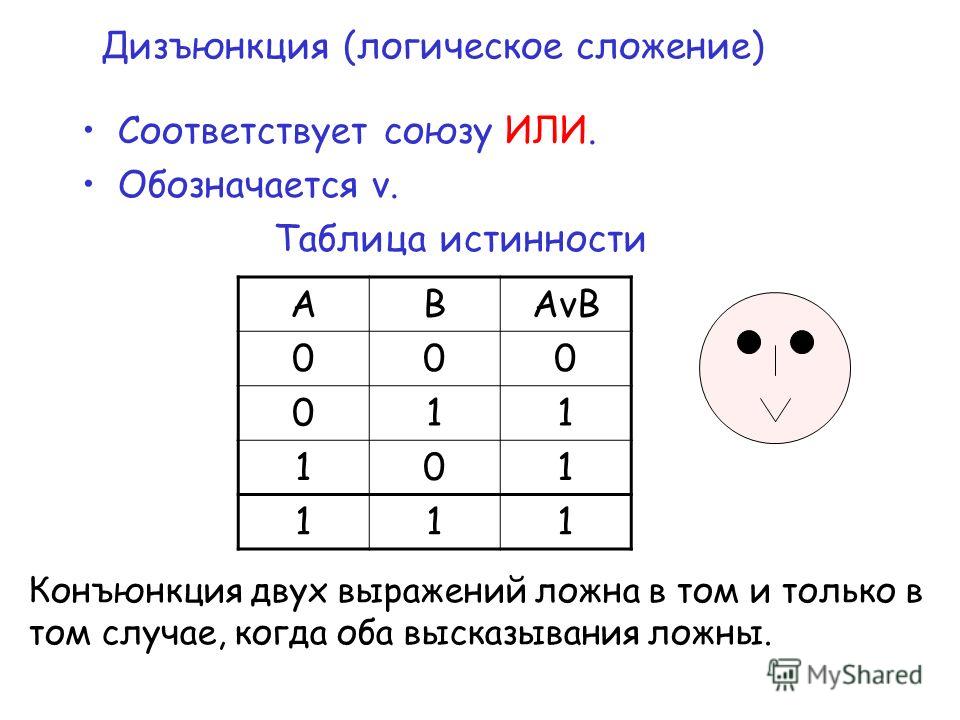
Чуть ниже списка появится выражение, отформатированное в довольно общепринятых обозначениях, где ИЛИ представляется в виде сложения, И — как умножение, а НЕ обозначается чертой над той частью, для которой вычисляется НЕ.
Текстовое поле ниже отображает ту же информацию в виде ASCII последовательности. Здесь НЕ представляется как тильда (‘~’).
Вы можете изменить выражение в текстовом поле и нажать кнопку Ввести, чтобы изменения вступили в силу; это также обновит таблицу истинности для соответствия. Кнопка Очистить очищает текстовое поле, а кнопка Вернуть меняет поле обратно к представлению текущего выражения.
Обратите внимание, что отредактированные вами выражения будут потеряны, если вы измените таблицу истинности.
В дополнение к умножению и сложению, обозначающим И и ИЛИ, выражение, которое вы набираете, может содержать любой из логических операторов C/Java, а также просто английские слова сами по себе.
| высший приоритет | ~ ! ‘ | НЕ |
|---|---|---|
| (отсутствие символа) & && AND | И | |
| ^ XOR | Исключающее ИЛИ | |
| низший приоритет | + | || OR | ИЛИ |
Все нижеприведённые примеры — допустимые представления одного и того же выражения. Кроме того, можно смешивать операторы.
Кроме того, можно смешивать операторы.
| a’ (b + c) |
| !a && (b || c) |
| NOT a AND (b OR c) |
Вообще-то, скобки в последовательностях AND’ов (или OR’ов или XOR’ов) не имеют значения. (В частности, когда Logisim создаёт соответствующую схему, он будет игнорировать такие скобки.)
Вкладка Минимизация
Последняя вкладка отображает минимизированное выражение, соответствующее столбцу таблицы истинности. Вы можете выбрать, для какого выхода вы хотите просматривать минимизированное выражение с помощью списка сверху, и можете указать, какое выражение вы хотите получить — сумму произведений или произведение сумм, с помощью списка снизу.
Если входов четыре или меньше, то ниже списка появится карта Карно, соответствующая выходной переменной. Вы можете щёлкать на карте Карно для изменения соответствующих значений таблицы истинности. Карта Карно будет также показывать выбранные в данный момент для минимизированного выражения термы в виде сплошных полупрозрачных скругленных прямоугольников.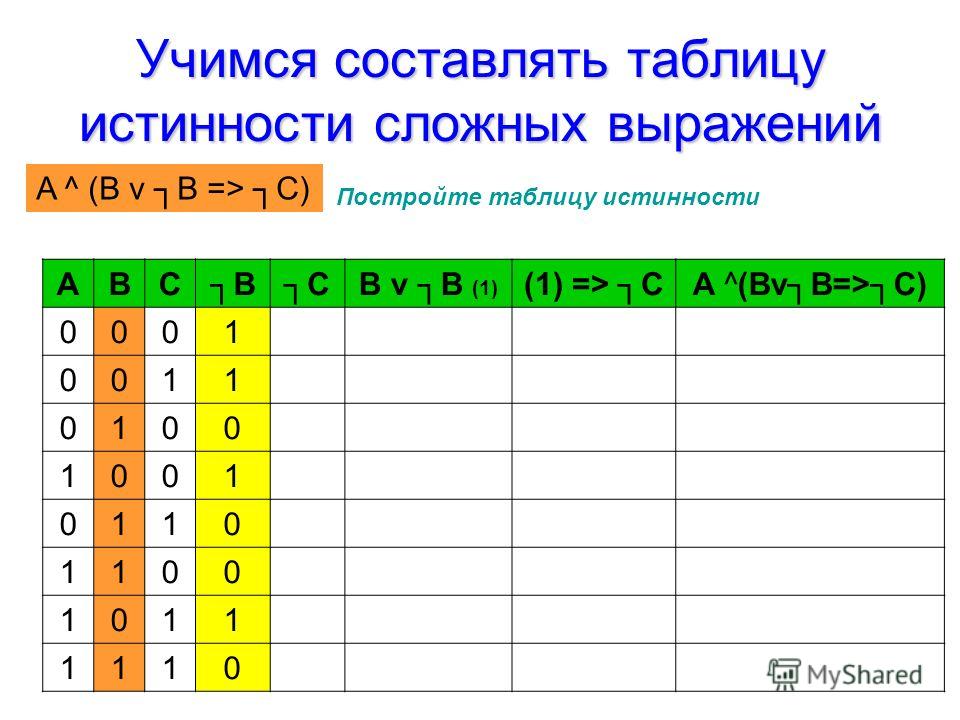
Ниже — само минимизированное выражение, отформатированное так же, как во вкладке Выражение. Если выходов более четырёх, то карта Карно не появится, но минимизированное выражение всё равно будет вычислено. (Logisim использует метод Куайна — Мак-Класки для вычисления минимизированного выражения. Он эквивалентен карте Карно, но применим к любому числу входных переменных.)
Кнопка Установить как выражение позволяет вам выбрать минимизированное выражение как выражение, соответствующее переменной. Это, как правило, не нужно, поскольку изменения в таблице истинности приводят к использованию минимизированного выражения для изменённого столбца; но если вы введете выражение через вкладку Выражение, то это может быть удобно, чтобы перейти к соответствующему минимизированному выражению.
Далее: Создание схемы.
Раздел 1.1
Раздел 1.1Логическая форма и логическая Эквивалентность | Определения | Сложный Заявления | Таблицы истинности
Логический Форма и логическая эквивалентность
Содержание инструкции не совпадает с логической формой. Например,
рассмотрим 2 следующих утверждения:
Например,
рассмотрим 2 следующих утверждения:
Если Салли проснется поздно или опоздает на автобус, она опоздает на работу. Поэтому, если Салли приходит на работу вовремя, она не проснулся поздно и не опоздал на автобус.
Если x действительное число такое, что x < -2 или x > 2, то х 2 > 4. Следовательно, если х 2 < 4, то х > -2 и х < 2.
Логический анализ не помогает определить достоинства аргумента. Вместо это помогает проанализировать форму аргумента, чтобы определить, верна ли вывод следует из истинности предыдущих утверждений. В то время содержание двух приведенных выше утверждений различно, их логическая форма похожий.
Пусть p обозначает утверждения «Салли просыпается поздно».
и «x — действительное число, такое что x < -2».
Пусть q обозначает утверждения «Салли опаздывает на автобус».
и «x — действительное число, такое что x > -2».
Пусть r обозначает утверждения «Салли опаздывает на работу».
и «х 2 > 4».
Тогда общая форма для обоих приведенных выше аргументов:
| Практические упражнения |
| ОПРЕДЕЛЕНИЕ |
|
| Аргумент: | последовательность утверждений, направленных на демонстрацию правды высказывания или утверждения. |
| Выписка: | предложение, которое либо истинно, либо ложно, но не оба. Его еще называют предложением. |
| Отрицание: | если стр — переменная оператора, отрицание
p — это «не p », обозначаемое ~ p .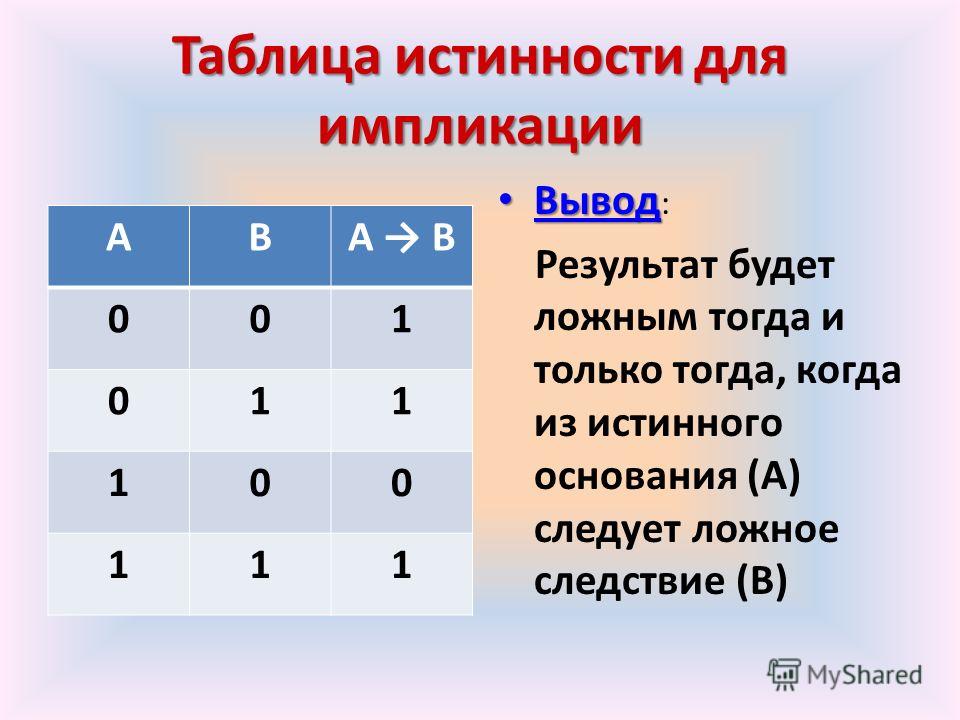 Если р
верно, то ~ p ложно. Если р
верно, то ~ p ложно. |
| Соединение: | , если p и q являются переменными оператора, соединение p и q равно « p и q «, обозначен pq . Конъюнкция истинна только тогда, когда истинны обе переменные. Если 1 или обе переменные ложные, pq является ложным. |
| Разъединение: | , если p и q являются переменными оператора, дизъюнкция p и q есть « p или q «, обозначен pq . Дизъюнкция истинна, если истинны одна или обе переменные. pq ложно, только если обе переменные ложны. |
| Тавтология: | Форма утверждения, которая всегда верна. Правда делает
не полагаться на значения отдельных утверждений, заменяемых
переменные оператора, а на логическую структуру самого оператора.
(т. е. вы получите пятерку в этом классе или нет). Правда делает
не полагаться на значения отдельных утверждений, заменяемых
переменные оператора, а на логическую структуру самого оператора.
(т. е. вы получите пятерку в этом классе или нет). |
| Противоречие: | Форма выписки, которая всегда ложна. Как тавтология, ложность заключается не в отдельных переменных высказываниях, а в логическая структура самого высказывания. (т. е. я всегда лгу). |
Составные операторы
использовать символы (логический И), (логическое ИЛИ), и ~ (НЕ) для построения сложных логических утверждений из более простых.
Пусть p = «Жарко» и пусть q = «Солнечно» Тогда утверждение «Не жарко, но солнечно». можно написать символически как:
| ~ р д |
| Практические упражнения |
Однако утверждения должны иметь четко определенные значения истинности — они должны быть либо истинными, либо ложными.
 Истинность утверждения может быть выражена
на Таблица истинности . А
таблица истинности для данного утверждения отображает результирующие значения истинности для различных
комбинации значений истинности для переменных. Истина о соединении
утверждение может быть логически выведено с использованием известных значений истинности для различных
части высказывания.
Истинность утверждения может быть выражена
на Таблица истинности . А
таблица истинности для данного утверждения отображает результирующие значения истинности для различных
комбинации значений истинности для переменных. Истина о соединении
утверждение может быть логически выведено с использованием известных значений истинности для различных
части высказывания.
| Таблица истинности для ~п | Таблица истинности для pq | Таблица истинности для pq | |||||
| р | ~р | р | q | шт. |
р | q | шт. |
| Т | Ф | Т | Т | Т | Т | Т | Т |
| Ф | Т | Т | Ф | Ф | Т | Ф | Т |
| Ф | Т | Ф | Ф | Т | Т | ||
| Ф | Ф | Ф | Ф | Ф | Ф | ||
| Практические упражнения |
Логическая эквивалентность:
Две инструкции логически эквивалентны
тогда и только тогда, когда их результирующие формы логически эквивалентны, когда идентичны
переменные операторов используются для представления операторов компонентов.
Две формы операторов логически эквивалентны тогда и только тогда, когда их результирующие таблицы истинности идентичны для каждого варианта переменных утверждения.
| р | q | pq | qp |
| Т | Т | Т | Т |
| Т | Ф | Ф | Ф |
| Ф | Т | Ф | Ф |
| Ф | Ф | Ф | Ф |
Другие логически эквивалентные операторы включают:
| (стр. д) ~(р q) р xor д | эксклюзивный или |
| р ~(~п) | Двойное отрицание |
Чтобы проверить логическую эквивалентность двух операторов, создайте таблицу истинности, которая включает каждую переменную для оценки, а затем проверить чтобы увидеть, эквивалентны ли результирующие значения истинности двух утверждений.
Законы Де Моргана
Отрицание конъюнкции (логическое И) двух операторов
логически эквивалентна дизъюнкции (логическому ИЛИ) каждого оператора
отрицание. Звучит как полный рот, но это означает, что «не
(A и B)» логически эквивалентно «не
А или не В» .
Звучит как полный рот, но это означает, что «не
(A и B)» логически эквивалентно «не
А или не В» .
Аналогично, отрицание дизъюнкции двух утверждений логически эквивалентна конъюнкции отрицания каждого утверждения. Помещать просто, «не (A или B)» логически эквивалентно «не А и не Б» . Символически это можно записать как
.| ~(pq) ~ р ~q | . . . и . . . | ~(пк) ~ р ~q |
Эти два оператора логически эквивалентны (нажмите здесь для определения), и это можно проверить с помощью таблицы истинности.
Таблица логических Эквиваленты:
Следующая таблица может помочь сократить составные операторы до более простые формы. Учитывая переменные оператора p, q, и r , тавтология t и противоречие c, следующие правил логики:
| Коммутативный | р qq р | р д д р |
| Ассоциативный | (стр. р) рп
(q
р)
р) рп
(q
р) |
(стр. р) рп (q р) |
| Распределительный | р (q г) (р р) (р р) | р (q г) (р р) (р г) |
| Идентификация | р тп | р кп |
| Отрицание | р ~пт | ~шт. |
| Двойное отрицание | ~(~р)р | |
| Идемпотент | р стр | стр стр |
| Законы Де Моргана | ~(pq)~p ~q | ~(pq)~p ~q |
| Универсальный переплет | р тт | р копия |
| Поглощение | р (р д)р | р (р к)р |
| Отрицания t и c | ~тк | ~ |
Логические эквивалентности можно использовать для упрощения форм выписок, для подтверждения
или опровергнуть эквивалентность, чтобы создать эффективный и логически правильный компьютер
программ или для помощи в разработке цифровых логических схем.
Чтобы упростить эквивалентность, начните с одной стороны уравнения и попытайтесь заменить его части эквивалентными выражениями. Продолжайте делать это, пока вы добились желаемой формы заявления.
| Практические упражнения |
логика — Можно ли использовать И, ИЛИ и НЕ для представления любой таблицы истинности?
Да, любая функция истинности, независимо от ее сложности и количества входных данных, может быть выражена с помощью $\land$, $\lor$ и $\neg$.
Мы можем доказать это напрямую, сгенерировав конъюнкцию для каждой строки, где функция оценивается как истина, а затем дизъюнкцией всех этих конъюнкций, и секундное размышление прояснит, что результирующее выражение фиксирует функцию истинности (если нет строки, в которой функция оценивается как $T$, тогда просто используйте выражение $P \land \neg P$)
Например, предположим, что у нас есть функция истинности, условия истинности которой даны в следующей таблице:
\begin{массив}{ccc|c} P&Q&R&f(P,Q,R)\\ \hline Т&Т&Т&Ф\\ Т&Т&Ф&Т\\ Т&Ф&Т&Ф\\ Т&Ф&Ф&Т\\ Ф&Т&Т&Т\\ Ф&Т&Ф&Ф\\ Ф&Ф&Т&Ф\\ Ж&Ж&Ж&Ж\\ \конец{массив}
Эта функция верна в строках 2, 4 и 5, поэтому мы генерируем термины $P \land Q \land \neg R$, $P \land \neg Q \land \neg R$ и $\ neg P \land Q \land R$ соответственно. Разделение их дает нам:
Разделение их дает нам:
$$(P \land Q \land \neg R) \lor (P \land \neg Q \land \neg R) \lor (\neg P \land Q \land R)$$
Говорят, что эта формула находится в дизъюнктивной нормальной форме (DNF): это обобщенная дизъюнкция, где каждая дизъюнкция является обобщенной конъюнкцией литералов, а литерал является либо атомарной переменной, либо ее отрицанием.
Теперь, я думаю, из этого примера должно быть ясно, что вы можете сделать это для любой функции истинности . То есть любую функцию можно представить с помощью формулы ДНФ, создав дизъюнкцию для каждой строки, где функция оценивается как $T$. Например, если в строке есть строка, в которой $P$ — True, $Q$ — True, а $R$ — false, скажем, сгенерируйте выражение $P \land Q \lor \neg R$. Когда у вас есть выражение для всех этих строк, соедините их все вместе, чтобы получить окончательное выражение. И если нет строки, в которой функция оценивается как $T$, то просто используйте выражение $P \land \neg P$, что — это в ДНФ (его можно рассматривать как обобщенную дизъюнктуру только с одной дизъюнкцией. .. которая является конъюнкцией литералов).
.. которая является конъюнкцией литералов).
Таким образом, для любой функции истинности существует выражение ДНФ, которое фиксирует эту функцию, а ДНФ использует только $\neg, \land и \lor$
Просто для полноты, я также хочу отметить, что есть так называемая конъюнктивная нормальная форма (CNF): это обобщенная конъюнкция, где каждая конъюнкция является обобщенной дизъюнкцией литералов.
Можем ли мы найти эквивалент этой функции в КНФ? Да. Есть два способа сделать это. Во-первых, мы можем взять существующее выражение ДНФ и преобразовать его в выражение, находящееся в КНФ, используя Распределение $lor$ по $\land$. В этом случае это будет довольно объемная формула, начинающаяся с:
$(P \lor P \lor \neg P) \land (P \lor P \lor Q) \land (P \lor P \lor R) \land (P \lor \neg Q \lor \neg P) \land (P \lor \neg Q \lor Q) \land (P \lor \neg Q \lor R) \land (P \lor \ neg R \lor \neg P) \land …$
(посмотрите, что я здесь делаю? Я систематически нахожу все комбинации выбора одного литерала из каждого из трех дизъюнктов. . это работает как FOIL, если вы знакомы с этим)
. это работает как FOIL, если вы знакомы с этим)
Однако другой способ сделать это — пойти вернуться к исходной таблице истинности и сосредоточиться на случаях, когда функция оценивается как False, а не как True. То есть функция False ровно тогда, когда:
$$(P \land Q \land R) \lor (P \land \neg Q \land R) \lor (\neg P \land Q \land \neg R ) \lor (\neg P \land \neg Q \land R) \lor (\neg P \land \neg Q \land \neg R)$$
равно True, и это означает, что функция верна точно тогда, когда:
$$\neg [(P \land Q \land R) \lor (P \land \neg Q \land R) \lor (\neg P \land Q \land \neg R) \lor (\neg P \land \neg Q \land R) \lor (\neg P \land \neg Q \land \neg R)]$$
верно. Согласно ДеМоргану, это эквивалентно:
$$(\neg P \lor \neg Q \lor \neg R) \land (\neg P \lor Q \lor \neg R) \land (P \lor \neg Q \lor R) \land (P \lor Q \lor \neg R) \land (P \lor Q \lor R)$$
и , что выражение находится в CNF, т.е. в Layer-Form.
Опять же, я думаю, из этого примера должно быть ясно, что вы можете сделать это для любой функции истинности .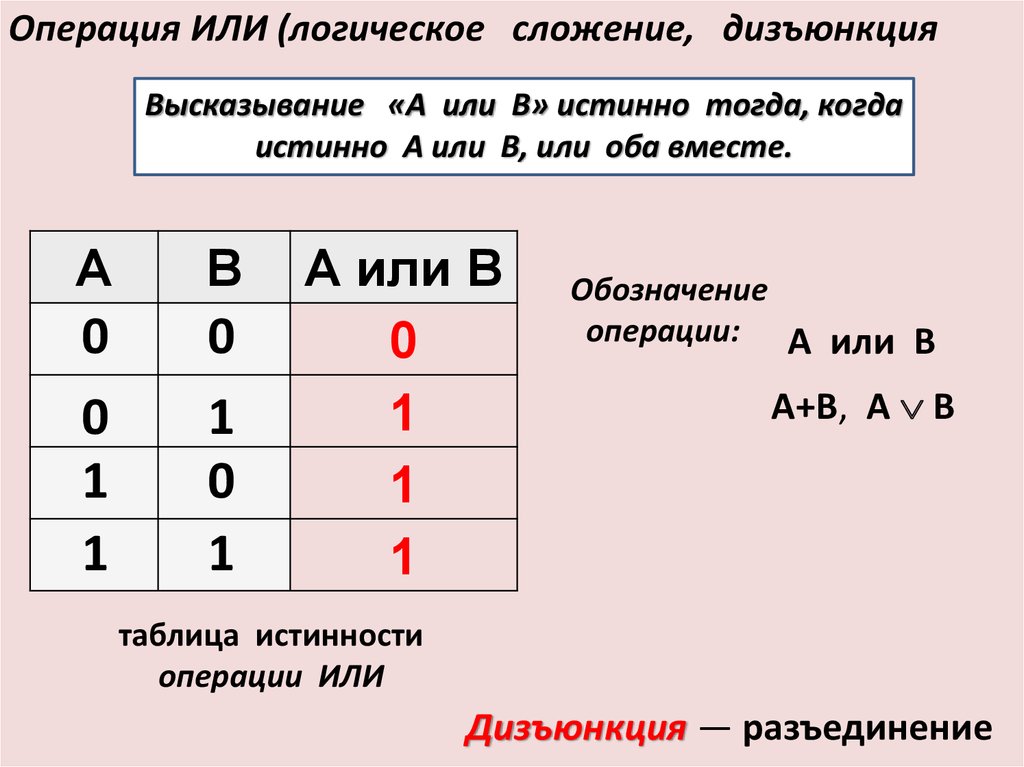 То есть любую функцию можно представить с помощью формулы CNF, создав дизъюнкцию для каждой строки, где функция оценивается как $F$. Например, если это строка, в которой $P$ равно True, $Q$ равно True, а $R$ равно false, скажем, сгенерируйте выражение $\neg P \lor \neg Q \lor R$ (для этого является отрицанием $P \land Q \land \neg R$). Когда у вас есть выражение для всех этих строк, соедините их все вместе, чтобы получить окончательное выражение. Если нет строки, в которой функция оценивается как $F$, то просто используйте выражение $P \lor \neg P$), которое — это в ДНФ (его можно рассматривать как обобщенную конъюнкцию только с одним конъюнктом… который является дизъюнктом литералов).
То есть любую функцию можно представить с помощью формулы CNF, создав дизъюнкцию для каждой строки, где функция оценивается как $F$. Например, если это строка, в которой $P$ равно True, $Q$ равно True, а $R$ равно false, скажем, сгенерируйте выражение $\neg P \lor \neg Q \lor R$ (для этого является отрицанием $P \land Q \land \neg R$). Когда у вас есть выражение для всех этих строк, соедините их все вместе, чтобы получить окончательное выражение. Если нет строки, в которой функция оценивается как $F$, то просто используйте выражение $P \lor \neg P$), которое — это в ДНФ (его можно рассматривать как обобщенную конъюнкцию только с одним конъюнктом… который является дизъюнктом литералов).
Мы также можем привести доказательство на основе выразительной полноты $NAND$. Поскольку $P \ NAND \ Q \Leftrightarrow \neg (P \land Q)$, мы можем просто взять любое выражение, составленное только из $NAND$, которое фиксирует некоторую функцию истинности $f$, и изменить любое из этих $ NAND$, с $\neg$ и $\land$, и результат будет эквивалентен оригиналу и, таким образом, также захватит $f$.

 и qp
имеют одинаковые значения истинности, поэтому они равны логически эквивалентен.
и qp
имеют одинаковые значения истинности, поэтому они равны логически эквивалентен. 