Закон ома переменного тока. Закон Ома для переменного тока: формулы, примеры расчета, особенности применения

Как применяется закон Ома в цепях переменного тока. Какие формулы используются для расчета тока, напряжения и мощности. Чем отличается от закона Ома для постоянного тока. На что нужно обращать внимание при расчетах.

Особенности закона Ома для переменного тока

Закон Ома для переменного тока имеет ряд существенных отличий от классического закона Ома для постоянного тока:

• Учитывается не только активное сопротивление цепи, но и реактивное сопротивление (индуктивное и емкостное)
• Вместо обычного сопротивления R используется полное сопротивление цепи Z
• Ток и напряжение могут быть сдвинуты по фазе друг относительно друга
• Для расчетов используются действующие (среднеквадратичные) значения тока и напряжения

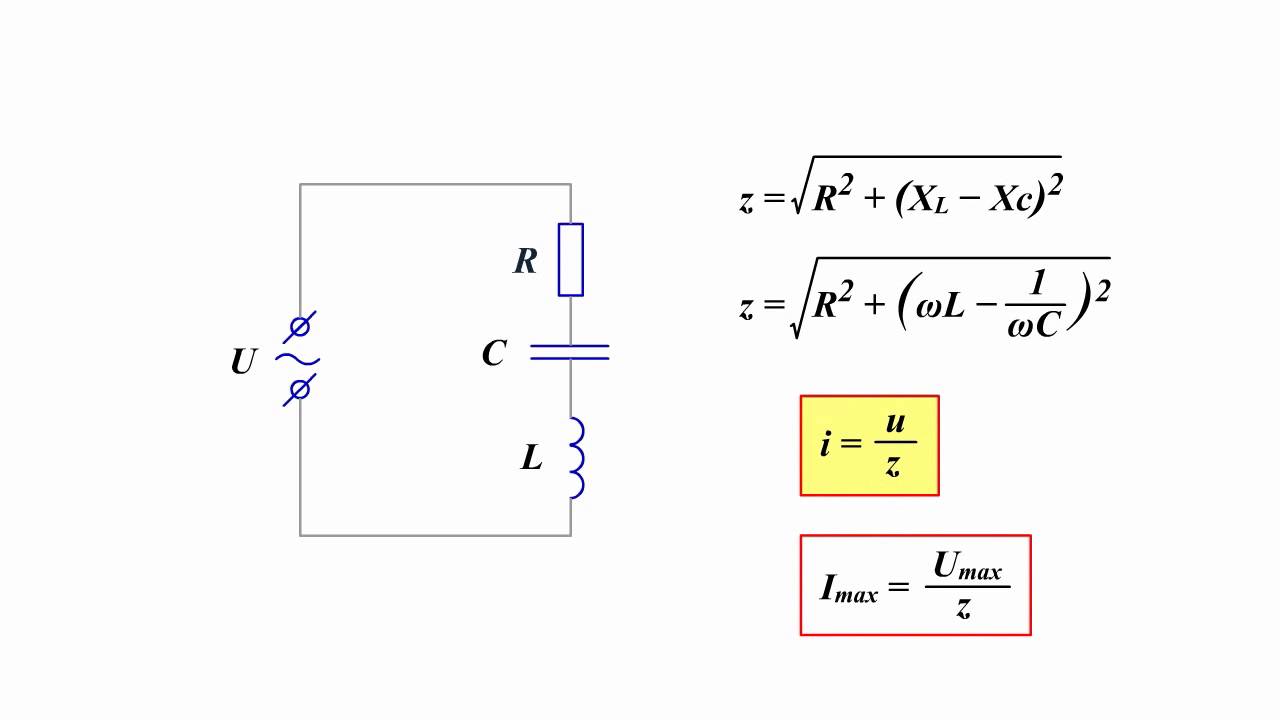
Основная формула закона Ома для переменного тока выглядит следующим образом:

I = U / Z

где:

• I — действующее значение силы тока
• U — действующее значение напряжения
• Z — полное сопротивление цепи

Формулы для расчета полного сопротивления цепи

Полное сопротивление цепи переменного тока Z рассчитывается по формуле:

Z = √(R² + X²)

где:

• R — активное сопротивление
• X — реактивное сопротивление

Реактивное сопротивление X в свою очередь складывается из индуктивного XL и емкостного XC сопротивлений:

X = XL — XC

Индуктивное сопротивление: XL = ωL = 2πfL

Емкостное сопротивление: XC = 1 / (ωC) = 1 / (2πfC)

где:

• ω — угловая частота
• f — частота переменного тока
• L — индуктивность
• C — емкость

Расчет мощности в цепи переменного тока

В цепи переменного тока различают три вида мощности:

• Активная мощность P = U * I * cosφ
• Реактивная мощность Q = U * I * sinφ
• Полная мощность S = U * I = √(P² + Q²)

где φ — угол сдвига фаз между током и напряжением.

Коэффициент мощности cosφ показывает, какая часть полной мощности преобразуется в активную:

cosφ = P / S

Пример расчета цепи переменного тока

Рассмотрим пример применения закона Ома для расчета параметров простой цепи переменного тока.

Дано: напряжение U = 220 В, частота f = 50 Гц, активное сопротивление R = 100 Ом, индуктивность L = 0.1 Гн.

Требуется определить: силу тока I, полное сопротивление Z, угол сдвига фаз φ, активную P, реактивную Q и полную S мощности.

Решение:

1. Рассчитаем индуктивное сопротивление: XL = 2πfL = 2 * 3.14 * 50 * 0.1 = 31.4 Ом
2. Полное сопротивление цепи: Z = √(R² + XL²) = √(100² + 31.4²) = 104.7 Ом
3. Сила тока по закону Ома: I = U / Z = 220 / 104.7 = 2.1 А
4. Угол сдвига фаз: φ = arctg(XL / R) = arctg(31.4 / 100) = 17.4°
5. Активная мощность: P = U * I * cosφ = 220 * 2.1 * cos17.4° = 440 Вт
6. Реактивная мощность: Q = U * I * sinφ = 220 * 2.1 * sin17.4° = 138 вар
7. Полная мощность: S = U * I = 220 * 2.1 = 462 ВА

Особенности применения закона Ома для переменного тока

При использовании закона Ома для расчета цепей переменного тока важно учитывать следующие особенности:

• Необходимо использовать действующие (среднеквадратичные) значения тока и напряжения
• Учитывать фазовые сдвиги между током и напряжением
• Принимать во внимание частотную зависимость реактивных сопротивлений
• Использовать комплексные числа для расчетов в векторной форме
• Применять правила сложения векторных величин

При правильном учете этих факторов закон Ома позволяет выполнять точные расчеты параметров цепей переменного тока любой сложности.

Применение закона Ома в трехфазных цепях

В трехфазных цепях закон Ома применяется отдельно для каждой фазы. При этом учитываются следующие особенности:

• Используются линейные и фазные значения напряжений
• Учитываются схемы соединения «звездой» и «треугольником»
• Рассчитываются фазные и линейные токи
• Определяется мощность для каждой фазы и всей трехфазной системы

Для симметричной трехфазной системы справедливы следующие соотношения:

• При соединении «звездой»: Uл = √3 * Uф, Iл = Iф
• При соединении «треугольником»: Uл = Uф, Iл = √3 * Iф

где Uл и Iл — линейные напряжение и ток, Uф и Iф — фазные напряжение и ток.

Ограничения применения закона Ома для переменного тока

Закон Ома для переменного тока имеет некоторые ограничения применения:

• Справедлив только для линейных цепей
• Не учитывает нелинейные искажения формы сигнала
• Применим только для установившихся режимов
• Не описывает переходные процессы в цепях
• Требует уточнения для сверхвысоких частот

В этих случаях для точных расчетов могут потребоваться более сложные методы анализа электрических цепей.

Заключение

Закон Ома является фундаментальным законом электротехники, который успешно применяется и для цепей переменного тока. Правильное использование формул и учет особенностей переменного тока позволяет выполнять точные расчеты параметров электрических цепей. Понимание принципов применения закона Ома для переменного тока необходимо для эффективного проектирования и эксплуатации электротехнических устройств и систем.

Электротехника

Электротехника

Ломоносов В. Ю. и др. Электротехника/В. Ю. Ломоносов, К. М. Поливанов, О. П. Михайлов. — М.: Энергоатомиздат, 1990. — 400 с. Приводятся основные понятия об элементах электрической цепи, методах расчета простых цепей постоянного и переменного тока. Дается общее описание физических процессов, происходящих в электрическом и магнитном полях. Излагается принцип действия полупроводниковых приборов, электрических машин и аппаратов, электроизмерительных приборов. Приводятся сведения о применении электронных вычислительных устройств в электротехнике. Для читателей, интересующихся основами электротехники и электроники. Оглавление ПРЕДИСЛОВИЕ ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА 1.6. МОЩНОСТЬ 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ 1.20. ЗАКОНЫ КИРХГОФА ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ 2. 4. МАГНИТНАЯ ИНДУКЦИЯ 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ 2.9. ПРАВИЛО ЛЕНЦА 2.10. МАГНИТНЫЙ ПОТОК 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ 2.13. ВЗАИМНАЯ ИНДУКДИЯ 2.14. САМОИНДУКЦИЯ 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ 3. 9. НАМАГНИЧЕННОСТЬ ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА) 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ) 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК? 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА 5.4. СИНУСОИДА 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА 6.7. РЕЗОНАНС ТОКОВ 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК 7.1. ТРЕХФАЗНАЯ СИСТЕМА 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ 9.7. КЛЮЧИ 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН 10. 2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА 10.3. КОЛЛЕКТОР 10.4. ЯКОРНЫЕ ОБМОТКИ 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА 11.2. РАБОТА ТРАНСФОРМАТОРА 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ 11.1. АВТОТРАНСФОРМАТОРЫ ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА 12.4. РАБОТА СИНХРОННЫХ МАШИН 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ 13. 3. ЭЛЕКТРОМАГНИТЫ 13.4. КОНТАКТОРЫ 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ 14.4. СХЕМЫ ТОРМОЖЕНИЯ 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ 15.10. ЦИФРОВЫЕ ПРИБОРЫ 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ

1.

6 Электричество

1.6.1. Терминология и основные определения.

Переменный ток, используемый в том числе для питания осветительных приборов и электродвигателей, в процессе синусоидальных колебаний периодически изменяет свою силу и направление. Сила тока возрастает от нуля до максимального значения, затем падает до нуля, изменяет направление, возрастает до максимального значения в противоположном направлении и снова становится равной нулю. Так ток совершает периодические колебания. Период Т — время в секундах, за которое ток проходит все значения. Частота показывает количество полных циклов, совершенных за секунду.

Говоря о токе или напряжении, обычно имеют в виду среднеквадратичное значение. Для синусоидального тока величина среднеквадратичного значения тока и соответственно напряжения будет равна:

Напряжение ниже 50 В называется сверхнизким. Напряжение ниже 1000 В называется низким. Напряжение свыше 1000 В называется высоким. Стандартными напряжениями переменного тока с частотой 50 Гц являются напряжения 230/300 В и 400/690 В.

1.6.2. Закон Ома для переменного тока.

Протекающий по обмотке переменный ток создает магнитный поток. Этот магнитный поток точно так же, как и ток, изменяет свою силу и направление. При изменении магнитного потока по закону индукции в обмотке создается ЭДС (электродвижущая сила). Направление ЭДС противоположно полярности подаваемого напряжения. Это явление называется самоиндукцией. Самоиндукция в цепи переменного тока частично проявляется в сдвиге по фазе между током и напряжением и частично — в падении индуктивного напряжения. Сопротивление цепи перемен- ного тока становится значительно выше рассчитанного или измеренного сопротивления этой же цепи постоянному току. Сдвиг по фазе между током и напряжением обозначается углом . Индук- тивное сопротивление (реактивное) обозначается Х, активное сопротивление — R, кажущееся сопротивление цепи или проводника — Z. Полное сопротивление (импеданс) вычисляется по формуле:

Закон Ома для цепи переменного тока:

1.

6.3. Трехфазная система

Трехфазный переменный ток вырабатывается генератором с тремя отдельными обмотками. Все значения синусоидального напряжения сдвинуты по фазе относительно друг друга на 120°. Трехфазная сеть обеспечивает подключение различных устройств. Однофазное устройство можно подключить между фазой и нулем. Трехфазные устройства можно подключать двумя спосо- бами: звездой (Y) и треугольником  . При подключении звездой на выводы устройства подается фазовое напряжение. При подключении треугольником на выводы устройства подается линейное напряжение.

1.6.4. Мощность.

Активная мощность Р представляет собой полезную мощность, которую можно использовать для выполнения работы. Реактивная мощность Q — «бесполезная» мощность, которую нельзя использовать для выполнения работы. Кажущаяся мощность S — мощность, которую нужно потреблять из сети для получения необходимой активной мощности. Соотношение между активной, реактивной и кажущейся мощностью обычно наглядно изображают как треугольник мощностей.

1.6.5. Электродвигатель

Наиболее распространенными двигателями являются трехфазные асинхронные двигатели с короткозамкнутым ротором. Двигатели этого типа используются во всех отраслях промышленности. Бесшумные и надежные электродвигатели — часть большинства систем, в том числе компрессоров. Любой электродвигатель состоит из двух основных частей: неподвижного статора и вращающегося ротора. Статор формирует вращающееся магнитное поле, а ротор преобразует энергию этого поля в механическое движение. Статор подключается к питающей трехфазной сети. Ток в обмотках статора создает вращающееся магнитное поле, которое индуцирует ток в роторе, создавая тем самым в роторе магнитное поле. При взаимодействии магнитных полей статора и ротора возникает вращающий момент, который заставляет ротор вращаться.

1.6.5.1. Скорость вращения

Если бы вал двигателя вращался с той же скоростью, что и магнитное поле, индуцируемый в роторе ток равнялся бы нулю. Однако это невозможно, например из-за потерь в подшипниках, кроме того, скорость вращения ротора на 1–5 % ниже синхронной скорости магнитного поля (это явление называется проскальзыванием). Синхронная скорость вычисляется по формуле:

1.6.5.2. Коэффициент полезного действия

Преобразование энергии в электродвигателе не обходится без потерь. Кроме всего прочего к этим потерям относятся потери на активное сопротивление, на вентиляцию, намагничивание и трение. Формула, применяемая для расчета кпд:

Мощность Р2 указывается на паспортной табличке двигателя.

1.6.5.3. Класс изоляции

В соответствии со стандартом IEC 85 (Международной электротехнической комиссии) все изоляционные материалы для обмоток электродвигателя подразделяются на классы изоляции. Каждый класс обозначается буквой, характеризующей верхний предел температуры в зоне использования изоляции. При превышении этого предела на 10°С, продолжительность срока службы изоляции становится вдвое короче.

1.6.5.4. Классы защиты

В соответствии со стандартом IEC 34-45 классы защиты указывают степень защиты электродвигателя от прикосновения и попадания воды. Класс защиты обозначается буквами IP и двумя цифрами. Первая — показывает степень защиты при прикосновении и от попадания твердых предметов. Вторая цифра показывает степень защиты от воды. Например, IP23 означает что: (2) — устройство защищено от попадания твердых предметов размером более 12 мм; (3) — устройство защищено от брызг воды, направленных под углом до 60° к вертикали. IP54 означает: (5) — защита от пыли; (4) — защита от воды, разбрызгиваемой в любом направлении. IP55 означает: (5) — защита от пыли;(5) — защита от струи воды, направляемой под низким давлением в любом направлении.

1.6.5.5. Способы охлаждения

Согласно стандарту IEC 34-45, указывается способ охлаждения двигателя. Он обозначается буквами IC и двумя цифрами. Например, IC 01 означает: свободная циркуляция, собственная вентиляция; IC 41 означает: система охлаждения с водяной рубашкой, собственная вентиляция.

1.6.5.6. Способ монтажа

Способ монтажа указывает, согласно стандарту IEC 34-7, способ установки двигателя. Для этого используются буквы IM и четыре цифры. Например, IM 1001 означает: два подшипника, вал со свободным концом, корпус статора без опор, большой фланец с гладкими отверстиями для крепления.

1.6.5.7. Подключение звездой (Y) и треугольником

Δ

Трехфазный электродвигатель можно подключать двумя способами: звездой (Y) или треугольником Δ . Фазные обмотки в трехфазном двигателе обозначаются буквами U, V и W (U1-U2, V1-V2, W1-W2). При подключении звездой (Y) концы фазных обмоток соединены вместе и образуют нулевую точку. Схема подключения обмоток выглядит как звезда (Y). На обмотки подается фазовое напряжение (фазовое напряжение = линейное напряжение/3, например, 400 В = 690/3). Ток Ih, текущий к нулевой точке, равен фазовому току, и соответственно по обмоткам течет фазовый ток If = Ih. При подключении треугольником (Δ) начало каждой обмотки соединяется с концом другой обмотки. Соединенные таким образом обмотки образуют треугольник. На обмотки подается линейное напряжение. Протекающий через двигатель ток Ih представляет собой линейный ток, который разветвляется по обмоткам; по обмоткам течет фазовый ток Ih/3= If . Один и тот же электродвигатель можно подключать звездой к сети напряжением 690 В или треугольником к сети напряжением 400 В. В обоих случаях на обмотки будет подаваться напряже- ние 400 В. Ток, протекающий через двигатель, при подключении звездой на 690 В будет меньше, чем при подключении треугольником на 400 В. Отношение токов будет равняться 3.

На табличке двигателя указано, например, 690/400 В. Это означает, что подключение звездой предназначено для большего напряжения, а подключение треугольником — для меньшего. На плате может также указываться ток. Меньшее значение соответствует подключению обмоток двигателя звездой, а большее — подключению треугольником.

1.6.5.8. Вращающий момент

Вращающий момент электродвигателя является выражением способности ротора вращаться. У каждого двигателя есть свой максимальный вращающий момент. Если нагрузка превышает этот вращающий момент, у ротора не хватит мощности для вращения. С нормальной нагрузкой двигатель работает с моментом, который значительно меньше максимального. Однако в период пуска нагрузка значительно выше. Обычно характеристика двигателя представляется в виде кривой вращающего момента.

С нами работают и оказали доверие

Закон

Ом для переменного тока. Закон

Ом для переменного тока.

Пользовательский поиск

Полное сопротивление Переменный ток Мощность в Цепи переменного тока
ЗАКОН ОМА ДЛЯ ПЕРЕМЕННОГО ТОКА В общем случае закон Ома нельзя применить к цепям переменного тока, поскольку он не учитывать реактивное сопротивление, которое всегда присутствует в таких цепях. Тем не менее, по модификация закона Ома, учитывающая влияние реактивного сопротивления. получить общий закон, применимый к цепям переменного тока. Поскольку импеданс Z, представляет собой объединенное противостояние всех реактивных сопротивлений и сопротивлений, этот общий закон для переменного тока, Это общее изменение применяется к переменному току, протекающему в любой цепи, и любое из значений может быть найдено из уравнения, если известны остальные. Например, предположим, что последовательная цепь содержит катушку индуктивности с сопротивлением 5 Ом и Индуктивное сопротивление 25 Ом последовательно с конденсатором, имеющим емкостное сопротивление 15 Ом. реактивное сопротивление. Если напряжение 50 вольт, то какой ток? Эту схему можно изобразить как показано на рис. 4-8. Рис. 4-8. — Цепь серии LC. Теперь предположим, что цепь содержит катушку индуктивности с сопротивлением 5 Ом и сопротивлением 15 Ом. индуктивное сопротивление последовательно с конденсатором, имеющим емкостное сопротивление 10 Ом. Если ток 5 ампер, какое напряжение? Q.18 Какие формулы закона Ома используются в цепи переменного тока для определения напряжения и текущий?

Заявление о конфиденциальности — Информация об авторских правах. — Свяжитесь с нами

Integrated Publishing, Inc. — Малый бизнес, принадлежащий ветеранам-инвалидам (SDVOSB)

Импеданс и обобщенный закон Ома

Импеданс и обобщенный закон Ома

Следующий: Системы первого порядка Уровень выше: Глава 3: Цепь переменного тока Предыдущий: Факторное представление синусоидального сигнала

Полное сопротивление основных компонентов

Во временной области соотношение между синусоидальным током через и синусоидальное напряжение на конденсаторе или индуктор описывается дифференциальным уравнением. Однако, в частотной области, где эти синусоидальные переменные представлены в виде комплексных экспонент, а такие компоненты, как поскольку R, C и L представлены своими импедансы , тогда соотношение между синусоидальным напряжением и током можно описать алгебраическим уравнением.

В частности, мы представляем синусоидальное напряжение и ток как проекция соответствующего вектора в комплексе плоскость, вращающаяся против часовой стрелки относительно действительной оси:

(33)

и определите импеданс 90 118 90 119 компонента (R, C и L) как отношение напряжения и тока, связанного с компонент как в комплексной экспоненциальной форме:

Полное сопротивление

(34)

Это обобщенная версия закона Ома для цепей переменного тока.

• Резистор:

  (35)

  Импеданс резистора — это отношение векторных представлений напряжения и тока. Поскольку ток через и напряжение через резистор всегда находится в фазе, т. е. имеем

  (36)

  Величина и фаза тока и напряжения связаны соотношением:

  (37)

  Резистор не вносит фазового сдвига между напряжением и током, т. е. они находятся в фазе.
• Конденсатор:

  (38)

  Импеданс конденсатора — это отношение векторных представлений напряжения и тока:

  (39)

  Величина и фаза тока и напряжения связаны соотношением:

  (40)

  Фазовый сдвиг, вносимый конденсатором, равен , т. е. напряжение отстает от тока на , или ток опережает напряжение на («ICE»).
• Катушка индуктивности:

  (41)

  Импеданс индуктора — это отношение векторных представлений напряжения и тока:

  (42)

  Величина и фаза тока и напряжения связаны соотношением:

  (43)

  Фазовый сдвиг, вносимый катушкой индуктивности, равен , т. е. напряжение опережает ток на («ELI»).

Один из способов запомнить фазу между напряжением и током связанный с конденсатором и катушкой индуктивности, это «ELI the ICE man». Кроме того, рассмотрим два крайних случая:

• Когда , а на конденсаторе ноль проводимость из-за изоляции между двумя его пластинами (разомкнутая цепь), а поскольку нет изменения потока в катушке индуктивности и сопротивления катушки в идеале равен нулю.
• Когда , и конденсатор становится высокопроводящим и как самоиндуцированный напряжение в катушке всегда действует против любого изменения на входе (закон Ленца).

В цепи постоянного тока каждый резистор измеряется либо его сопротивлением или его проводимость. В цепи переменного тока каждый компонент (конденсатор, индуктора или резистора) измеряется его импедансом , из которых действительная и мнимая части — соответственно сопротивление и реактивное сопротивление , или его допуска , действительные и мнимые части которых равны соответственно проводимость и проводимость, как показано ниже:

• Полное сопротивление

  Как комплексная переменная импеданс может быть записан в любом Декартова или полярная форма:

  (44)

  • Действительная часть импеданса называется сопротивлением .
  • Мнимая часть импеданса называется реактивным сопротивлением .
  Импеданс, сопротивление и реактивное сопротивление измеряются в одних и тех же единицах. Ом ().

  Величина и фазовый угол:

  (45)

  Импедансы связанный с и оба являются чисто мнимыми, т. е. оба являются реактивными, что указывает на то, что эти компоненты являются реактивными и не потребляют энергии.
• Вход

  Обратная величина импеданса называется адмиттансом :

  (46)

  • Действительная часть проводимости называется проводимостью :

    (47)

  • Мнимая часть проводимости называется проводимостью :

    (48)

  Адмиттивность, проводимость и реактивная проводимость измеряются одним и тем же единица Сименс ().

  Величина и фаза комплексной проводимости

  (49)

(50)

Импеданс и проводимость являются комплексными переменными. действительные части и всегда положительны, а мнимые частей и может быть как положительным, так и отрицательным. Поэтому и может находиться только в 1-м или 4-м квадрантах комплексной плоскости.

В частности, проводимости трех типов элементов R, L и С

(51)

Закон Ома также может быть выражен в терминах допуска, а также импеданс. Иногда при анализе цепей удобнее использовать адмитанс вместо импеданса.

• Параллельные компоненты:

  (52)

• Компоненты в серии:

  (53)

Обобщенный закон Ома и законы Кирхгофа

В общем, все методы, такие как закон Ома и законы Кирхгофа, используемые для постоянного тока цепи, состоящие из резисторов, можно обобщить до цепей переменного тока, состоящих конденсаторов, катушек индуктивности, а также резисторов, представленных их импедансы. Кроме того, если предположить, что все напряжения и токи в цепи синусоидами одной частоты, их можно представить в виде сложных фазоры.

Закон Ома можно обобщить следующим образом:

(54)

и законы Кирхгофа теперь можно сформулировать как:

• Действующее законодательство (KCL): Векторная сумма токов в узел равен нулю .
• Закон о напряжении (KVL): Векторная сумма напряжений вокруг контура равен нулю .

Решение цепи переменного тока векторным методом

Если только стационарные решения ДУ, описывающего цепь переменного тока, интерес, метод фазора может быть использован для решения задачи алгебраически без решения ДЭ. В частности, все синусоидальные переменные представлены как вектора с точки зрения их амплитуд и фаз, и все компоненты в цепи (L и C, а также R) представлены их импедансами, так что все законы (закон Ома, ККЛ и КВЛ, делители тока и напряжения, параллельные и последовательных комбинаций компонентов) и методы (петлевой ток и узел методы напряжения, теоремы Тевенина и Нортона и т. д.), обсуждаемые для постоянного тока можно применить схему.

Операции над синусоидальными переменными на основе тригонометрических тождеств вообще длинные и нудные. Метод фазора может преобразовать такие синусоидальные переменные в векторы в комплексной плоскости и тем самым упростить операции.

Вот повторение сложной арифметики.

Пример 1:

Решите схему ниже. Напряжение от генератора равно .

Заданное напряжение может быть выражено в векторной форме как

(55)

Сначала найдите импедансы и проводимости компонентов и две ветви. Как , мы получаем

Затем найдите все токи в векторной форме:

Проверять:

Пример 2:

ток течет по цепи, состоящей из резистора , конденсатор , и индуктор соединены последовательно. Найдите результирующее напряжение на всех три элемента.

• Выразить вектором: .
• Найдите импеданс для каждого элемента ( ):

  (56)

• Найти полное сопротивление:

  (57)

• Найдите напряжение на всех трех элементах:

  (58)

  (59)

В качестве альтернативы мы можем найти напряжение на каждом из элементов:

или во временной области:

Складывая , , и , получаем общее напряжение что то же самое, что мы получили выше:

(62)

Пример 3:

В схеме ниже, с некоторым неизвестным пиковым значением, , и . Среднеквадратичное значение поперек составляет 10 В. Это также известно, что и находятся в фазе.

• Найти .