Что такое непрерывные и дискретные сигналы. Как классифицируются электрические сигналы. В чем основные различия между аналоговыми и цифровыми сигналами. Какие преобразования необходимы для обработки сигналов в цифровых системах.
Понятие сигнала и его роль в передаче информации
Сигнал представляет собой изменение физического состояния объекта, несущее информацию. В контексте электротехники и электроники под сигналом обычно понимают изменения электрического тока или напряжения. Сигналы играют ключевую роль в передаче и обработке информации в различных технических системах.
Основные функции сигналов:
- Представление информации в форме, пригодной для передачи по каналам связи
- Кодирование данных для обработки в информационных системах
- Управление различными процессами и устройствами
- Измерение и регистрация физических величин
Для эффективной работы с сигналами важно понимать их классификацию и особенности различных типов сигналов. Одним из ключевых признаков классификации является непрерывность или дискретность сигнала.

Классификация сигналов по характеру изменения во времени
По характеру изменения во времени сигналы можно разделить на две большие группы:
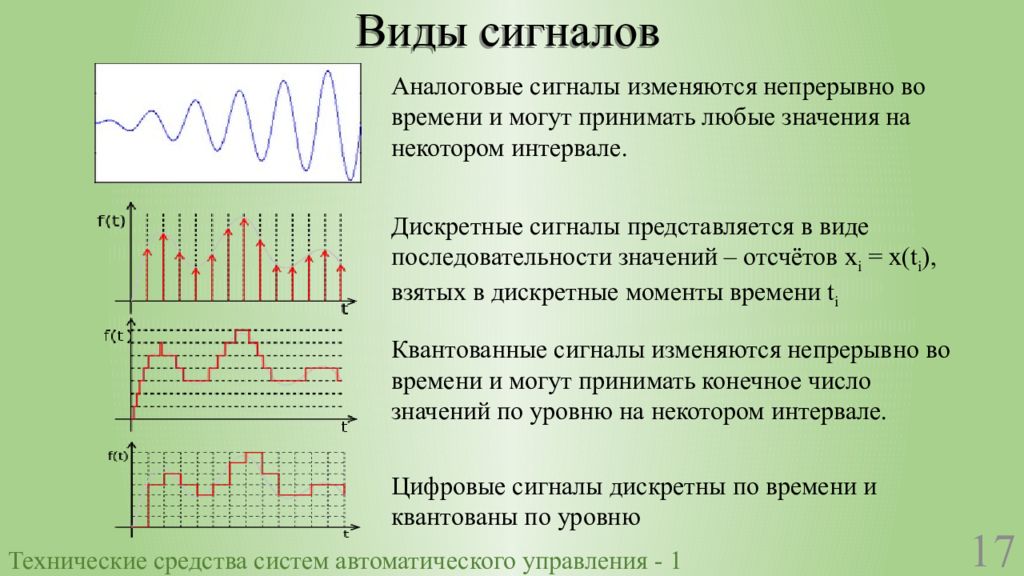
- Непрерывные (аналоговые) сигналы
- Дискретные сигналы
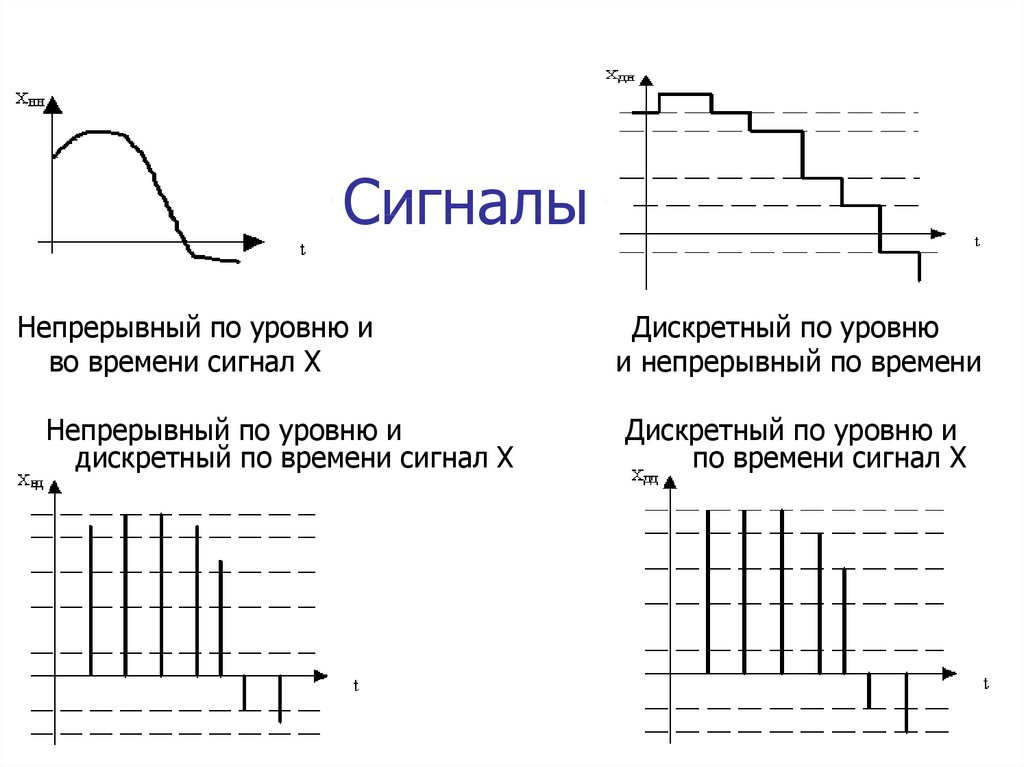
Чем отличаются эти типы сигналов? Непрерывный сигнал характеризуется плавным изменением значений без разрывов. Его можно описать непрерывной математической функцией. Дискретный сигнал, напротив, имеет разрывы и принимает значения только в определенные моменты времени.
Особенности непрерывных сигналов
Ключевые свойства непрерывных сигналов:
- Плавное изменение значений без скачков
- Бесконечное множество значений в любом интервале времени
- Описываются непрерывными функциями
- Характерны для большинства природных процессов
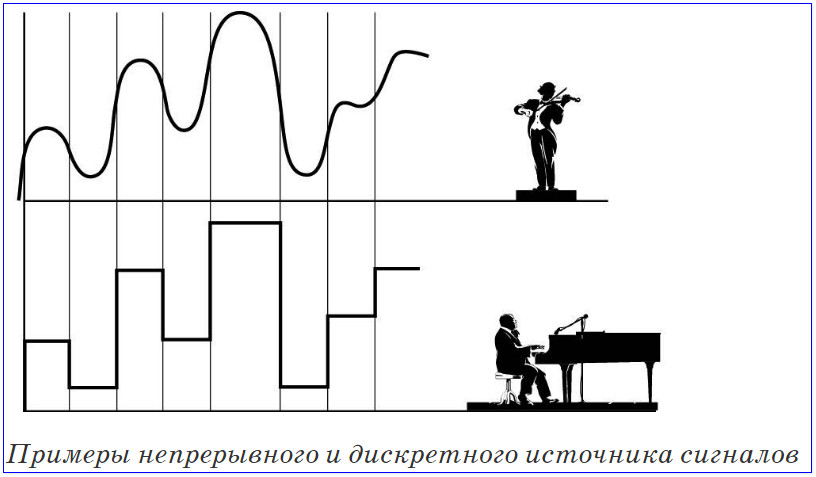
Примерами непрерывных сигналов могут служить изменение температуры воздуха, колебания мембраны микрофона, синусоидальное напряжение.
Характеристики дискретных сигналов
Основные особенности дискретных сигналов:
- Значения определены только в дискретные моменты времени
- Между отсчетами имеются разрывы
- Описываются последовательностями чисел
- Удобны для обработки в цифровых системах
Примеры дискретных сигналов: последовательность импульсов, цифровой звуковой сигнал, отсчеты температуры, снимаемые датчиком с заданной периодичностью.
Основные различия между непрерывными и дискретными сигналами
Рассмотрим ключевые отличия непрерывных и дискретных сигналов:
- Характер изменения во времени:
- Непрерывные — плавное изменение без разрывов
- Дискретные — скачкообразное изменение в отдельные моменты времени
- Математическое описание:
- Непрерывные — непрерывные функции
- Дискретные — числовые последовательности
- Спектральный состав:
- Непрерывные — непрерывный спектр частот
- Дискретные — дискретный линейчатый спектр
- Обработка сигналов:
- Непрерывные — аналоговая обработка
- Дискретные — цифровая обработка
Понимание этих различий важно для правильного выбора методов анализа и обработки сигналов в конкретных приложениях.
Преобразование непрерывных сигналов в дискретные
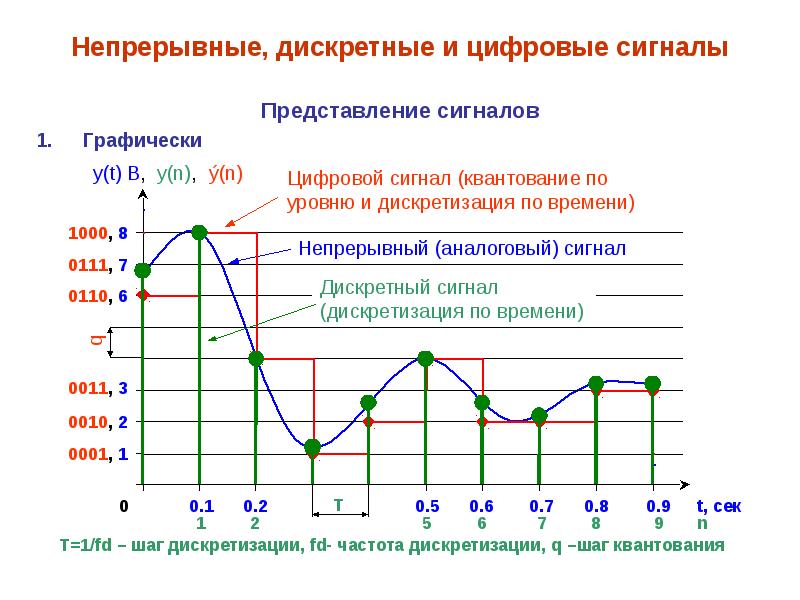
Для обработки непрерывных сигналов в цифровых системах необходимо преобразовать их в дискретную форму. Этот процесс включает два основных этапа:
- Дискретизация по времени
- Квантование по уровню
Дискретизация по времени
Дискретизация по времени заключается в замене непрерывного сигнала последовательностью его мгновенных значений, взятых через равные промежутки времени. Основные характеристики процесса дискретизации:
- Период дискретизации T — интервал между соседними отсчетами
- Частота дискретизации F = 1/T — число отсчетов в единицу времени
- Теорема Котельникова — для точного восстановления сигнала частота дискретизации должна минимум вдвое превышать максимальную частоту в спектре сигнала
Квантование по уровню
Квантование по уровню — это округление значений отсчетов до ближайших допустимых уровней. Основные параметры квантования:
- Шаг квантования — расстояние между соседними уровнями
- Число уровней квантования — определяет разрядность цифрового представления
- Ошибка квантования — разность между исходным и квантованным значением
В результате этих преобразований непрерывный сигнал превращается в цифровой, удобный для обработки в ЭВМ.
Применение непрерывных и дискретных сигналов в современных системах
Непрерывные и дискретные сигналы широко используются в различных областях техники:
Области применения непрерывных сигналов:
- Измерительная техника (аналоговые датчики и приборы)
- Аудиотехника (микрофоны, громкоговорители)
- Аналоговые системы управления
Применение дискретных сигналов:
- Цифровые системы связи (сотовая связь, цифровое ТВ)
- Компьютерная техника и цифровая электроника
- Цифровая обработка сигналов (фильтрация, сжатие данных)
- Системы автоматического управления
Несмотря на широкое распространение цифровых технологий, аналоговые и дискретные сигналы часто используются совместно в современных системах.
Преимущества и недостатки непрерывных и дискретных сигналов
Каждый тип сигналов имеет свои достоинства и ограничения. Рассмотрим основные из них.
Преимущества непрерывных сигналов:
- Высокая точность представления исходного физического процесса
- Отсутствие искажений, связанных с дискретизацией
- Простота генерации и обработки в аналоговых устройствах
Недостатки непрерывных сигналов:
- Подверженность шумам и помехам при передаче
- Сложность точного воспроизведения
- Ограниченные возможности сложной обработки
Преимущества дискретных сигналов:
- Высокая помехоустойчивость
- Возможность сложной математической обработки
- Простота хранения, копирования и передачи без искажений
Недостатки дискретных сигналов:
- Потеря информации при дискретизации и квантовании
- Ограничения по частоте дискретизации
- Необходимость аналого-цифрового преобразования
Выбор между непрерывными и дискретными сигналами зависит от конкретной задачи и требований к системе.
Методы анализа непрерывных и дискретных сигналов
Для исследования свойств сигналов применяются различные методы анализа. Некоторые из них применимы как к непрерывным, так и к дискретным сигналам, другие специфичны для определенного типа.
Методы анализа непрерывных сигналов:
- Преобразование Фурье
- Преобразование Лапласа
- Корреляционный анализ
- Спектральный анализ
Методы анализа дискретных сигналов:
- Дискретное преобразование Фурье (ДПФ)
- Z-преобразование
- Дискретная свертка
- Цифровая фильтрация
Выбор метода анализа зависит от характера сигнала и целей исследования. Часто для полного анализа применяется комбинация различных методов.
Заключение
Понимание особенностей непрерывных и дискретных сигналов критически важно для разработки и эксплуатации современных электронных систем. Каждый тип сигналов имеет свои преимущества и области применения. Развитие цифровых технологий привело к широкому распространению дискретных сигналов, однако непрерывные сигналы по-прежнему играют важную роль во многих приложениях.
Ключевые выводы:
- Непрерывные сигналы точно отражают физические процессы, но чувствительны к помехам
- Дискретные сигналы удобны для цифровой обработки и передачи, но требуют преобразования
- Выбор типа сигнала зависит от конкретной задачи и требований системы
- Во многих современных системах непрерывные и дискретные сигналы используются совместно
- Методы анализа сигналов позволяют изучить их свойства и оптимизировать обработку
Глубокое понимание теории сигналов и систем необходимо для создания эффективных систем обработки информации и управления. Это динамично развивающаяся область, играющая ключевую роль в развитии современных технологий.
26 вопросов и ответов. Теория электрических цепей. Курс лекций
Комплексная спектральная плотность непрерывного сигнала (в дальнейшем для краткости будем говорить: спектр сигнала) вычисляется по формуле прямого преобразования Фурье
. (3)
Сигнал может быть восстановлен по спектру с помощью обратного преобразования Фурье, или интеграла Фурье
. (4)
В соответствии с принципом неопределенности сигнал, имеющий ограниченную протяженность во времени, обладает неограниченным по полосе спектром (рис. 9, а). И наоборот, сигнал с ограниченным спектром имеет бесконечную протяженность во времени (рис. 10, а). Как следует из этих рисунков, непрерывный сигнал, и ограниченной и бесконечной протяженности во времени, имеет сплошной спектр.
Если сигнал является периодическим, то спектр его – дискретный, т.е. теперь вместо используют отсчеты . Эта ситуация показана на рис. 9, б. Период сигнала равен длительности сигнала . Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае . Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник периодического сигнала и отсчетами спектральной плотности непрерывного сигнала:
9, б. Период сигнала равен длительности сигнала . Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае . Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник периодического сигнала и отсчетами спектральной плотности непрерывного сигнала:
Рис. 9
Рис. 10
.
Спектр периодического сигнала вычисляется по формуле
. (5)
Сигнал можно восстановить по его дискретному спектру, воспользовавшись формулой
. (6)
В соответствии с принципом дуальности можно сказать: если периодическим является спектр, то дискретным будет сигнал (рис. 10, б). Обозначая период повторения спектра , получим интервал дискретизации сигнала .
Обозначая период повторения спектра , получим интервал дискретизации сигнала .
Формулы прямого и обратного преобразований Фурье для дискретных сигналов имеют вид
; (7)
. (8)
В формулах (7) и (8) использовано обозначение .
Пример 4.1. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета .
Воспользуемся формулой (7), в которую подставим значения заданного сигнала
.
Пример 4.2. Рассчитаем спектр экспоненциальной дискретной функции , n³ 0.
График дискретной функции приведен на рис. 11, а ее отсчеты можно записать в виде последовательности {1; 0,5; 0,25; 0,125; 0,0625; …}.
Рис. 11
Рис. 12
Спектр дискретной экспоненты рассчитаем по формуле (7)
где для суммирования ряда использована формула
.
Получим выражение для расчета спектра амплитуд , используя формулу Эйлера .
.
Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать .
График спектра амплитуд экспоненциальной дискретной функции приведен на рисунке 12.
Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом .
Самоконтроль
1. Как рассчитывается спектр непериодического (и периодического) непрерывного сигнала?
2. Как восстановить непрерывный сигнал по его спектру (сплошному и дискретному)?
3. Сформулируйте принцип неопределенности.
4. Как рассчитывается спектр дискретного сигнала?
5. Какой спектр у дискретного сигнала: сплошной или дискретный, периодический или непериодический?
6. Как рассчитывается дискретный сигнал, если известен его спектр?
Как рассчитывается дискретный сигнал, если известен его спектр?
7. Найдите спектр дискретного сигнала, состоящего из одного отсчета .
8. Найдите значения спектра дискретного сигнала, заданного двумя отсчетами , на частотах и .
НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕ СИГНАЛЫ. ЦИФРОВЫЕ СИГНАЛЫ — Студопедия
Поделись
Информацией для человека является любой объективно существующий факт, свершившееся событие, на основании которого он может делать те или иные выводы. Способов представления информации бесконечно много. Информация может представляться рисунком, звуком, светом, цветом и т. д. В рамках данного курса мы будем говорить об информации, которая представляется электрическими сигналами.
Сигналом называют изменение физического состояния объекта, несущее информацию. Пользуясь понятием сигнал мы, в большинстве случаев, будем иметь в виду изменения тока или напряжения.
При создании систем измерения и обработки сигналов необходимо ориентироваться в большом многообразии форм представления сигналов, знать особенности каждой из них, уметь правильно их описывать.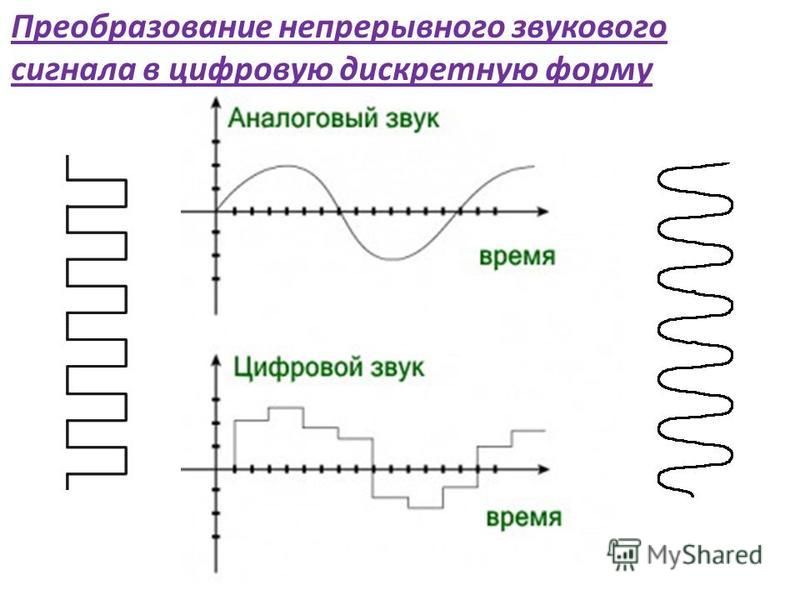 В этом помогает классификация сигналов.
В этом помогает классификация сигналов.
В дальнейшем для нас, прежде всего, будут важны классификационные признаки, позволяющие выделять аналоговые и импульсные сигналы. Аналоговым (непрерывным) сигналом называют сигнал, если функция, описывающая его, не имеет разрывов. Импульсными сигналами называют сигналы, если функция, описывающая его, имеет разрывы.
В окружающем нас мире фактически все сигналы представлены аналоговыми. Температура в печи, давление в трубопроводе и т. п. – все эти величины не могут изменяться скачком (бесконечно быстро), т. е. это аналоговые сигналы (если конечно не рассматривать аварийные ситуации, например, взрыв того же трубопровода). Имея дело изначально с такими сигналами, человек научился делать датчики, преобразующие аналоговые величины в электрический сигнал и устройства, работающие с такими сигналами.
В определенный исторический момент человек создал электронную цифровую вычислительную машину (ЭВМ). Главной ее особенностью по сравнению с аналоговой техникой является универсальность – чтобы выполнять какую-то новую задачу в вычислительной машине нужно менять программу, а не аппаратные средства. Уже только это качество привело к желанию использовать вычислительную технику в системах обработки сигналов и управлении. Но тут же, встал вопрос о том, как осуществлять ввод в ЭВМ информацию о том, как себя ведет непрерывный аналоговый сигнал.
Уже только это качество привело к желанию использовать вычислительную технику в системах обработки сигналов и управлении. Но тут же, встал вопрос о том, как осуществлять ввод в ЭВМ информацию о том, как себя ведет непрерывный аналоговый сигнал.
Для ответа на этот вопрос, прежде всего, попробуем увидеть главное существенное отличие в организации работы аналоговых и цифровых систем обработки сигналов. Очевидны два факта.
Аналоговое устройство преобразует входной сигнал непрерывно. Любые изменения входного сигнала в любой момент времени будут приводить тут же к соответствующим изменениям сигнала на выходе.
В какой бы форме не вводилась в ЭВМ информация о сигнале, обработка будет вестись программно и, поэтому на обработку любого нового значения будет тратиться время, равное времени выполнения этой программы. Пока идет время выполнения программы, обрабатывающей одно значение сигнала, нет смысла вводить новое значение. Новое значение сигнала будет обрабатываться только тогда, когда закончится обработка предыдущего. Иными словами, ЭВМ работает лишь с отдельными отсчетами (выборками) исходного аналогового сигнала, отстоящими друг от друга на время, равное как минимум времени выполнения программы обработки отсчета.
Иными словами, ЭВМ работает лишь с отдельными отсчетами (выборками) исходного аналогового сигнала, отстоящими друг от друга на время, равное как минимум времени выполнения программы обработки отсчета.
Исходя отсюда и рассмотрим, каким преобразованиям должен быть подвержен входной аналоговый сигнал, чтобы с ним могла производиться цифровая (программная) обработка в ЭВМ.
Как видно из наших рассуждений, сигнал, который может воспринимать ЭВМ, является импульсным, причем он представлен ограниченным набором значений. Сигналы, которые могут принимать лишь конечное число значений относят к дискретным, а процесс приведения непрерывного сигнала к дискретному называют дискретизацией.
Условия проведения дискретизации могут быть различными. Прежде всего, говорят о дискретизации по времени и о дискретизации по амплитуде (по уровню).
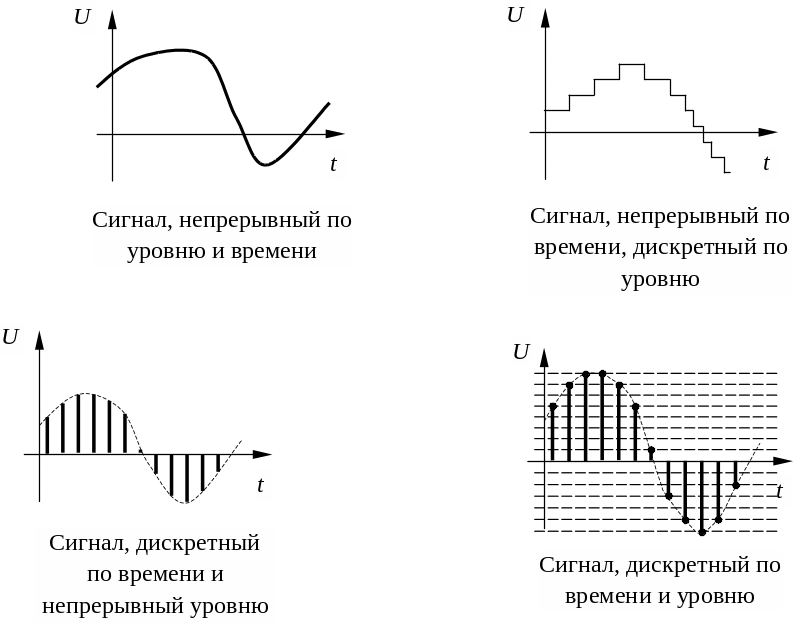
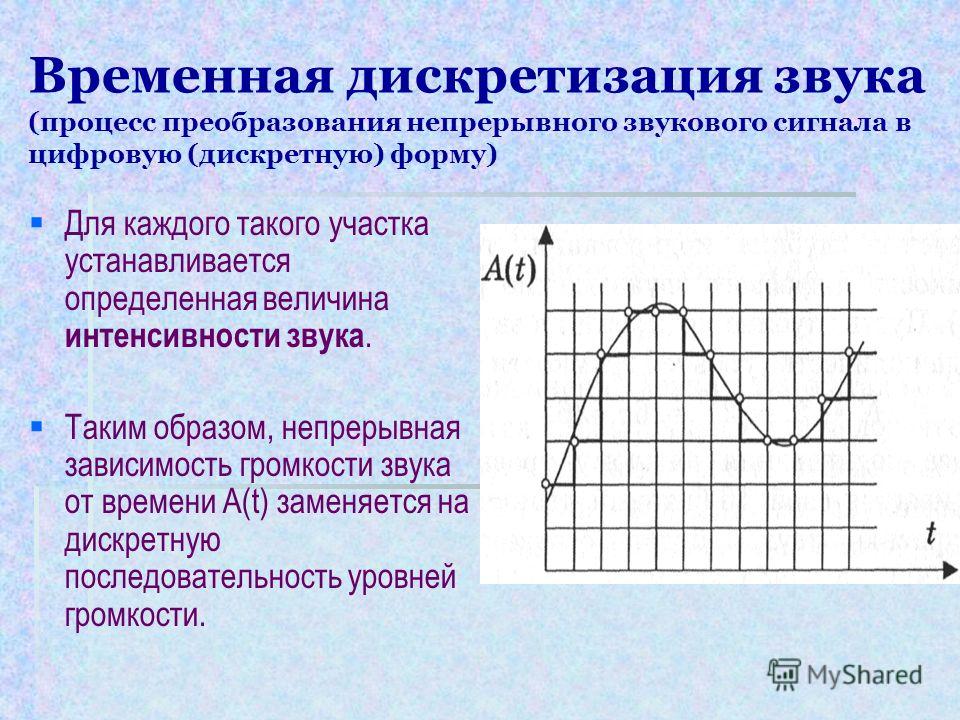
При дискретизации непрерывного сигнала х(t) по времени сигнал представляется его отдельными амплитудными значениями xД(t), взятыми в отдельные моменты времени (рис. ). Полученный сигнал дискретен по времени, но непрерывен по амплитуде, т. к. в пределах динамического диапазона непрерывного сигнала его временные отсчеты по амплитуде могут быть сколь угодно близки друг к другу.
). Полученный сигнал дискретен по времени, но непрерывен по амплитуде, т. к. в пределах динамического диапазона непрерывного сигнала его временные отсчеты по амплитуде могут быть сколь угодно близки друг к другу.
Если дискретизация осуществляется через равные промежутки времени, то дискретизация называется равномерной, в противном случае – неравномерной. При равномерной дискретизации отсчеты берутся с периодом, называемым периодом дискретизации Тд (рис.). Величина обратная периоду дискретизации называется частотой дискретизации FД, или частотой взятия отсчетов. При неравномерной дискретизации шаг ее проведения «подстраивается» под скорость изменения сигнала, увеличиваясь на гладких, мало информативных участках. Несмотря на то, что при этом уменьшается количество несущих информацию о сигнале отсчетов, появляется потребность в хранении значений интервалов дискретизации между каждой парой отсчетов. Поэтому, неравномерная дискретизация на практике фактически не применяется.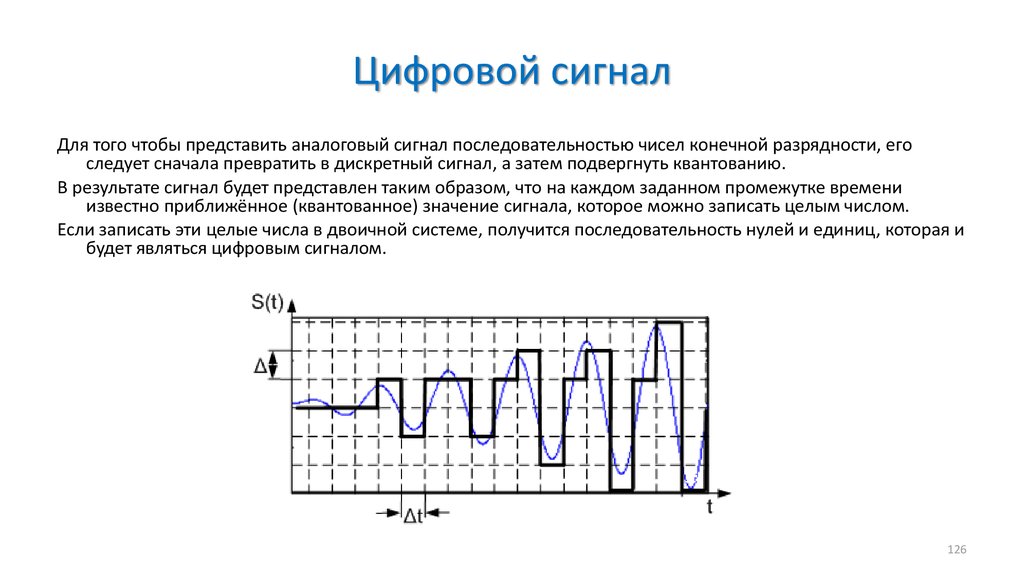
При представлении сигнала х(t) в дискретной форме возникает ошибка дискретизации. При равномерной дискретизации по времени она зависит только от скорости изменения сигнала – чем больше скорости изменения сигнала, тем она больше.
Рис. Дискретизация непрерывного сигнала х(t) по времени.
Случай равномерной дискретизации по времени эквивалентен амплитудно-импульсной модуляции непрерывного сигнала последовательностью импульсов с постоянной амплитудой, что иллюстрируется на рис..
Р и с. 1. Амплитудно-импульсная модуляция непрерывного сигнала
последовательностью импульсов
При дискретизации непрерывного сигнала х(t) по амплитуде сигнал представляется значениями, которые принадлежат конечному множеству заранее определенных значений. Величину, на которую могут отличаться соседние значения этого множества, называют шагом дискретизации. В простейшем случае соседние значения отличаются друг от друга на постоянную величину. Постоянный шаг дискретизации по амплитуде называют квантом дискретизации h. При этом дискретизированный по амплитуде сигнал как бы складывается из набора квантов. Это определило другое название для процесса дискретизации по амплитуде с постоянным шагом – квантование сигнала.
При этом дискретизированный по амплитуде сигнал как бы складывается из набора квантов. Это определило другое название для процесса дискретизации по амплитуде с постоянным шагом – квантование сигнала.
Дискретизированный по амплитуде сигнал отличается от исходного непрерывного сигнала х(t). Разность между значениями исходного и дискретного по уровню сигналами образует ошибку квантования (рис.). При квантовании сигнала такая ошибка не превышает величину кванта дискретизации h. Погрешность квантования является методической погрешностью.
Рис. Дискретизация непрерывного сигнала х(t) по амплитуде.
Можно получить сигнал, дискретный одновременно и по времени и по амплитуде (рис.), осуществив дискретизацию по уровню сигнала, дискретного по времени. Если при этом пронумеровать каждый уровень дискретизации, то такой сигнал можно представить последовательностью цифр, отражающих номера уровней, которые последовательно принимает сигнал. Именно поэтому сигнал дискретизированный одновременно и по времени и по амплитуде называют цифровым.
Рис. Дискретизация непрерывного сигнала х(t) по времени и амплитуде.
С точки зрения преобразования сигналов структурная схема получения цифрового сигнала представляется так как показано на рис. . Непрерывный аналоговый сигнал х(t) от источника информации поступает на дискретизатор, в котором преобразуется в дискретные по времени отсчеты. В квантующем устройстве осуществляется квантование временных отсчетов сигнала по амплитуде. Этот преобразователь определяет количество целых квантов, образующих очередной отсчет, и представляет это значение в двоичном коде.
Рис. Структурная схема устройства получения цифрового сигнала
Периодические сигналы в непрерывном и дискретном времени
спросил
Изменено 2 года, 1 месяц назад
Просмотрено 918 раз
$\begingroup$
Есть ли периодический сигнал в непрерывном времени, но не в дискретном?
Меня уже давно преследует это сомнение.
Все ли периодические сигналы CT являются периодическими в DT?
Если да, то почему синусоидальная волна является периодическим сигналом? Он периодичен только с интервалами в пи радиан, что является иррациональным числом, а не целым числом.
Но для того, чтобы сигнал DT был периодическим, разве сигнал не должен быть периодическим через дискретные интервалы времени?
- дискретные сигналы
- непрерывные сигналы
- периодические
$\endgroup$
2
$\begingroup$
Периодический непрерывный сигнал удовлетворяет условию $x(t)=x(t+T_0)$ для всех $t$. Период $T_0$ не обязательно должен быть рациональным числом. Периодический дискретный сигнал удовлетворяет условию $x[n]=x[n+N]$ для всех целых чисел $n$. Период $N$ является целым числом.
Если вы сэмплируете периодический непрерывный сигнал, вы не обязательно получите периодическую последовательность. Например, выборка периодического сигнала $x(t)=\sin(\omega_0t)$ приводит к последовательности $x_d[n]=x(nT)=\sin(\omega_0Tn)$, которая является периодической, только если $\omega_0T =2\pi k/l$ с целыми числами $k$ и $l$.
Например, выборка периодического сигнала $x(t)=\sin(\omega_0t)$ приводит к последовательности $x_d[n]=x(nT)=\sin(\omega_0Tn)$, которая является периодической, только если $\omega_0T =2\pi k/l$ с целыми числами $k$ и $l$.
В общем случае выборка $T_0$-периодической функции непрерывного времени с интервалом выборки $T$ приводит к периодической последовательности, только если
$$kT_0=lT,\qquad k,l\in\mathbb{Z}$
$доволен.
$\endgroup$
$\begingroup$
Ответ Мэтта Л. правильный, но стоит помнить, что дискретные периодические последовательности не существуют в нашем реальном мире. Основываясь на традиционном определении периодичности, для того чтобы дискретная последовательность была периодической, она должна быть бесконечной по длине. И мы физически не можем иметь последовательности бесконечной длины в нашем реальном мире. Периодические последовательности подобны идеальному кругу, одной из линий Евклида, имеющей бесконечную длину, но нулевую толщину, и единорогам. О них интересно думать, но их не существует в действительности.
О них интересно думать, но их не существует в действительности.
Вместо использования фразы «периодические последовательности» мы должны обсудить «дискретные последовательности, значения выборки которых повторяются в течение конечного числа выборок». У меня нет хорошего (или умного) названия для таких последовательностей конечной длины.
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Непрерывные и дискретные сигналы и системы
- Идентификатор корпуса: 117945339
@inproceedings{Soliman1990ContinuousAD,
title={Непрерывные и дискретные сигналы и системы},
автор = {Самир С. Солиман и Мандьям Д. Шринат},
год = {1990}
} - С. Солиман, М. Шринат
- Опубликовано в 1990 г.
- Математика
1. Представление сигналов. Непрерывное время против сигналов дискретного времени. Периодические и апериодические сигналы. Энергетические и силовые сигналы. Преобразования независимой переменной. Элементарные сигналы. Другие типы сигналов. 2. Непрерывно-временные системы. Классификация систем с непрерывным временем. Линейные стационарные системы. Свойства линейных стационарных систем. Системы, описываемые дифференциальными уравнениями. Представления переменных состояния.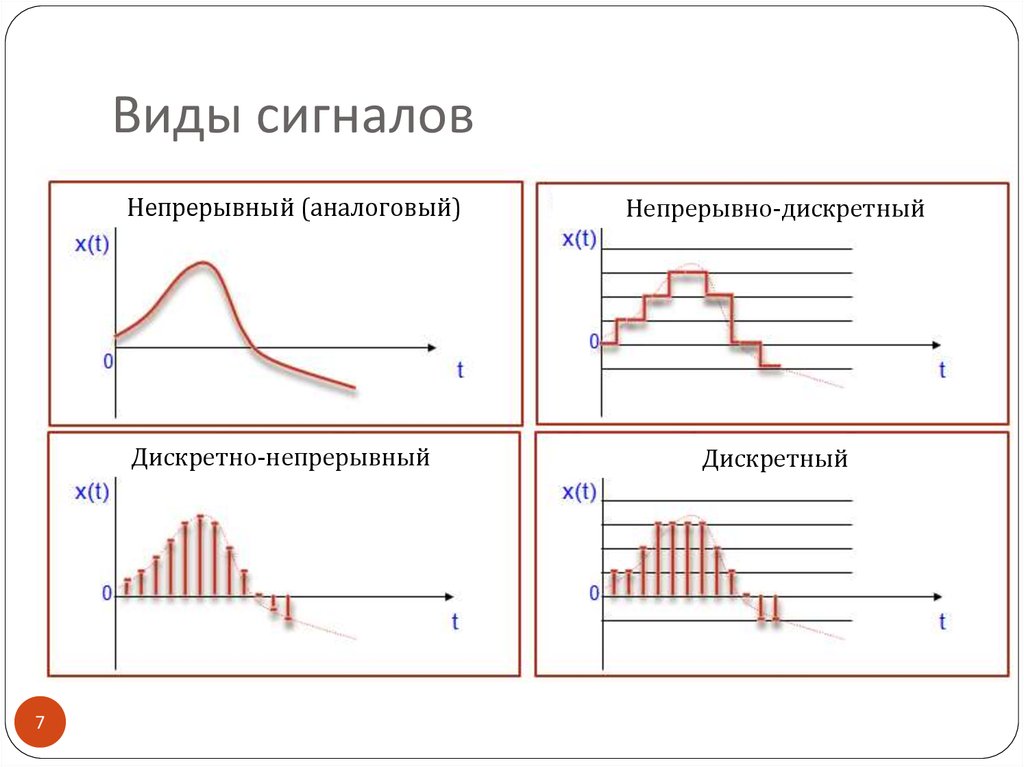 3. Ряды Фурье. Ортогональные представления сигналов…
3. Ряды Фурье. Ортогональные представления сигналов…
Дискретно-временной анализ линейных и нелинейных систем с использованием симуляторов аналоговых цепей
- T. Engel, M. Jackson
-
Информатика
- 1999
Метод обучения концепциям и навыкам анализа дискретных во времени систем студенты-инженеры, и результаты показывают, что элемент задержки и дискретизатор являются стабильными и точными компонентами, полезными при моделировании широкого спектра линейных и нелинейных систем с дискретным временем.
Анализ Фурье для процессов с непрерывным временем
- С. Девасахаям
-
Математика
- 2000
Любая периодическая функция с частотой f 0 , т. 2T 0, 3T 0 , 4T 0 и т. д. Таким образом, набор периодических функций… она обычно представлена в учебниках, где каждый класс сигналов разрабатывается отдельно, в отличие от подхода этой книги, Единой Теории Сигналов.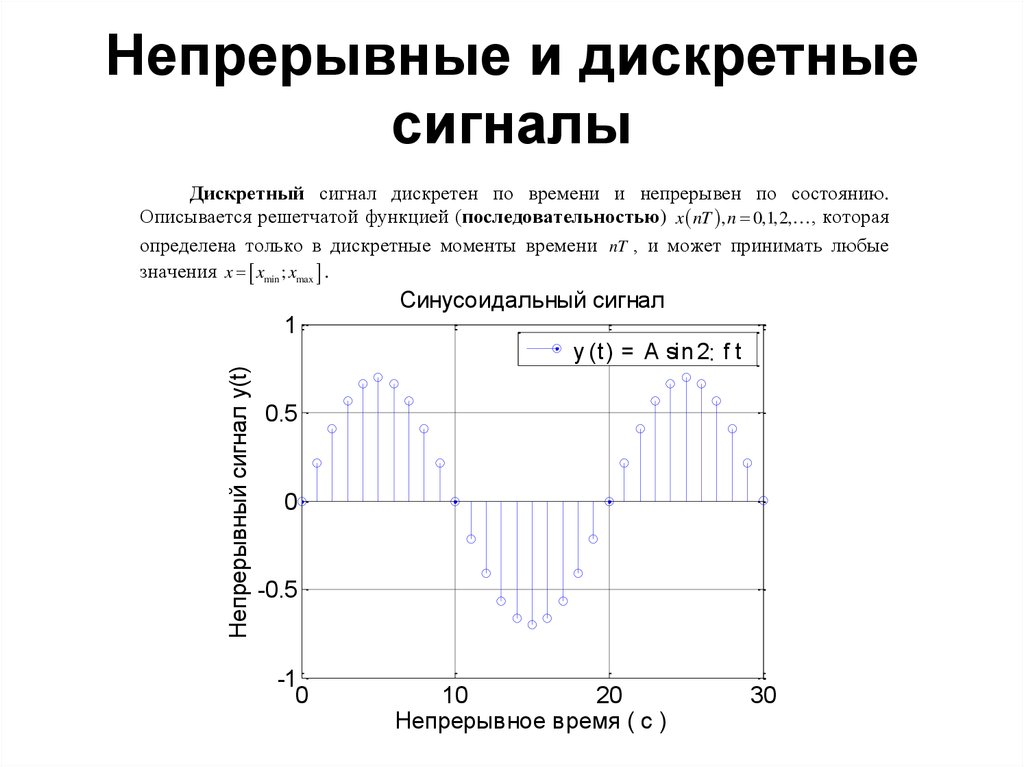
Трансформированный сигналом габора с применением к ЭЭГ-анализу
- Дж. Торрео, Сильвия М. С. Виктер, Жуао Л. Фернандес
-
Компьютерная наука
- 2013
А параметры задаются преобразованием Фурье анализируемого сигнала, что позволяет точно обнаруживать временные и частотные события даже в ситуациях, когда традиционные подходы Габора и S-преобразования, как правило, не работают.
DiffEq: Симулятор системы дискретного времени на основе MATLAB [Проверка себя]
Представлен симулятор системы дискретного времени на основе MATLAB (DiffEq). Этот инструмент исследует линейные разностные уравнения с постоянными коэффициентами, которые представляют линейные инвариантные во времени конечномерные…
Нейронный подход к частотно-временному разложению сигнала
- D. Grabowski, J. Walczak
-
Информатика
ICAISC
9002 - 2004
Статья содержит формализацию задачи частотно-временной декомпозиции сигналов с помощью нейронных сетей в виде оптимизационной задачи с последующим предложением рекуррентной нейронной сети, которая может быть использована для ее решения.