Что такое символическая логика и чем она отличается от традиционной. Как развивалась символическая логика исторически. Какие основные разделы и направления существуют в современной символической логике. Где применяется символическая логика в наши дни.
Что такое символическая логика
Символическая логика — это раздел формальной логики, в котором для исследования логических выводов используются специальные символические языки и математические методы. Основные особенности символической логики:
- Использование формализованных искусственных языков вместо естественного языка
- Применение математических методов и специального аппарата символов
- Исследование мышления с помощью логических исчислений
- Высокая точность формулировок
- Возможность изучения сложных логических объектов
Символическая логика считается следующим этапом развития формальной логики после традиционной логики, разрабатывавшейся в рамках философии. Она позволила преодолеть ограничения естественного языка и существенно расширить возможности логического анализа.
История развития символической логики
Элементы символического подхода в логике начали применяться еще в античности. Аристотель использовал буквенные обозначения для записи логических форм. Однако полноценное развитие символической логики началось только в XVII-XIX веках:
- 1666 г. — Готфрид Лейбниц предложил идею универсального логического исчисления
- 1847 г. — Джордж Буль разработал алгебру логики
- 1879 г. — Готлоб Фреге создал первую формализованную систему логики предикатов
- 1910-1913 гг. — Бертран Рассел и Альфред Уайтхед опубликовали фундаментальный труд «Principia Mathematica»
В XX веке символическая логика активно развивалась, сформировались ее основные разделы и направления. Она нашла широкое применение в математике, информатике и других науках.
Основные разделы символической логики
Современная символическая логика включает несколько основных разделов:
Пропозициональная логика
Изучает логические связи между высказываниями, абстрагируясь от их внутренней структуры. Оперирует логическими связками «и», «или», «если…, то» и др.
Логика предикатов
Анализирует внутреннюю структуру высказываний, выделяя субъекты, предикаты, кванторы. Позволяет формализовать более сложные логические рассуждения.
Модальная логика
Исследует высказывания с модальностями типа «необходимо», «возможно», «случайно» и др. Включает временную, эпистемическую и другие модальные логики.
Интуиционистская логика
Основана на конструктивном подходе в математике. Отвергает закон исключенного третьего, требует конструктивных доказательств.
Применение символической логики
Символическая логика находит широкое применение во многих областях:
- Основания математики
- Теоретическая информатика
- Искусственный интеллект
- Проектирование компьютерных схем
- Анализ естественных и формальных языков
- Формализация научных теорий
Методы символической логики активно используются при разработке систем автоматического доказательства теорем, верификации программ, создании экспертных систем и во многих других приложениях.
Преимущества символической логики
Использование формализованных языков и математических методов дает символической логике ряд важных преимуществ по сравнению с традиционной логикой:
- Высокая точность и строгость рассуждений
- Возможность анализа сложных логических структур
- Автоматизация логического вывода
- Выявление скрытых допущений и ошибок в рассуждениях
- Построение формальных моделей рассуждений
Ключевые понятия символической логики
Основными понятиями, с которыми работает символическая логика, являются:
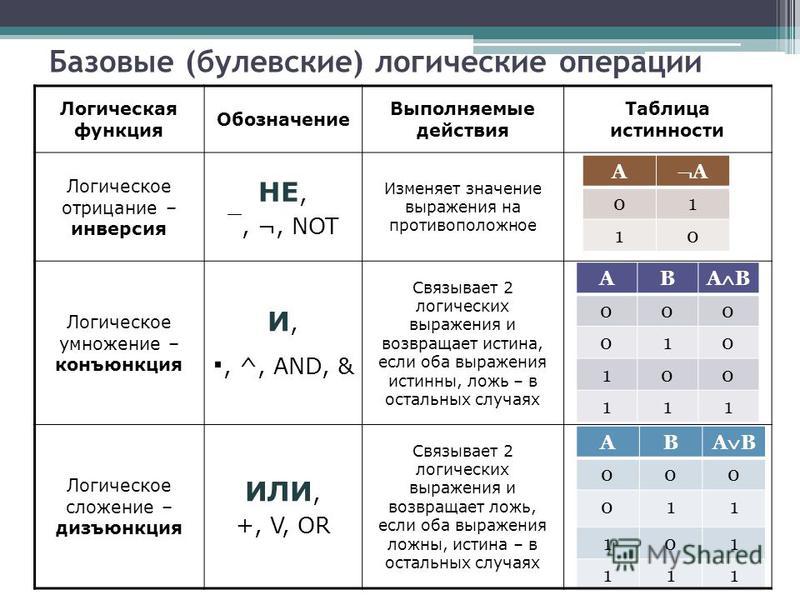
- Высказывания — утверждения, которые могут быть истинными или ложными
- Логические связки — операции над высказываниями (конъюнкция, дизъюнкция и др.)
- Предикаты — функции, принимающие значения «истина» или «ложь»
- Кванторы — операторы общности и существования
- Формулы — символические выражения, построенные по определенным правилам
- Аксиомы — исходные положения теории
- Правила вывода — способы получения новых формул из имеющихся
Оперируя этими понятиями, символическая логика строит формальные теории и исследует их свойства.
Символическая логика и компьютерные науки
Символическая логика сыграла важную роль в становлении и развитии компьютерных наук:
- Булева алгебра легла в основу проектирования цифровых схем
- Логика предикатов используется в языках логического программирования
- Теория доказательств применяется при верификации программ
- Модальные логики используются в системах искусственного интеллекта
Методы символической логики широко применяются при разработке языков программирования, баз данных, экспертных систем и других компьютерных технологий.
Критика и ограничения символической логики
Несмотря на большие успехи, символическая логика имеет ряд ограничений:
- Сложность формализации многих видов рассуждений
- Проблемы с моделированием неточных и неполных рассуждений
- Трудности формализации контекстно-зависимых рассуждений
- Ограниченность в описании динамических процессов
Поэтому наряду с символической логикой развиваются и другие подходы, такие как нечеткая логика, вероятностная логика, немонотонные логики и др.
Перспективы развития символической логики
Основные направления дальнейшего развития символической логики:
- Разработка новых логических формализмов
- Интеграция с другими математическими теориями
- Создание эффективных методов автоматического доказательства
- Применение в новых областях науки и техники
- Развитие междисциплинарных направлений на стыке с когнитивными науками
Символическая логика остается активно развивающейся областью, имеющей большой потенциал для решения сложных теоретических и прикладных задач.
Физика двоичной логики / Хабр
Вопрос «Как работает компьютер?» чрезвычайно многогранен и ответ на него зависит от выбранного уровня абстракции. Рассказ о компьютере может строиться вокруг прикладного ПО, операционной системы или архитектуры. Эта статья — попытка дать ответ на этот вопрос с точки зрения нижних уровней абстракции: логических схем и принципа их работы.
О системах счисления
Система счисления — это метод записи чисел. В повседневной жизни мы используем арабскую систему счисления, а именно десятичную позиционную. По мнению историков, арабские цифры появились в Индии ориентировочно до 5 века нашей эры. В Европу они пришли в начале второго тысячелетия из арабских стран, собственно, поэтому и принято называть привычные нам цифры арабскими. В России арабская система счисления появилась в 14-15 веке, а к 18 веку и вовсе вытеснила отечественную разработку под названием цифирь.
Причины использования арабской системы довольно тривиальны. Человеку попросту проще оперировать с ней, чем с другими непозиционными системами.
Так сложилось, что в компьютеростроении десятичная система показывает себя не с лучшей стороны. На её основе сложно проектировать вычислительные устройства, как с точки зрения технологической сложности самого вычисления, так и с точки зрения работоспособности устройства под действием факторов окружающей среды, например, помех.
Двоичная система счисления минимизирует эти сложности, хотя есть примеры ЭВМ и на других системах, например, ЭВМ «Сетунь» на троичной логике.
Цифровая абстракция
Как правило, физические величины изменяются непрерывно. В противовес им, цифровое представление информации дискретно и строго определенно. В компьютере, построенном на двоичной логике, для абстракции нулей и единиц используется напряжение: высокое значение величины — это логическая единица, а низкое — логический ноль.
Для реализации логических схем отлично подходит алгебра логики, поскольку оперирует величинами с двумя значениями — правда или ложь, единица или ноль. Собственно, как и двоичный компьютер. Однако стоит понимать, что алгебра логики — это абстракция логических выражений и связанных с ними операций, а не двоичной системы счислений. Речь о том, как именно двоичная система счисления и её математический аппарат реализуются с помощью алгебры логики пойдет в следующем разделе.
Логические выражения
Алгебра логики — это раздел математики над логическими выражениями. Под логическими выражениями подразумеваются суждения, высказывания, предложения и т.п., истинность которых можно определить однозначно — правда или ложь. Разумеется, не любое высказывание является логическим. Например, выражение «в декабре 31 день» является логическим, потому что однозначно истинно, а выражение «новая матрица — сомнительное кинопроизведение» не является логическим, поскольку отражает субъективную позицию и содержит неопределенную характеристику «сомнительное», хотя спорить с данным тезисом довольно сложно, если и вообще возможно.
Логические связки
Разобравшись непосредственно с логическими выражениями, определим операции над ними. Под операциями над логическими выражениями принято подразумевать логические связки. Типичными примерами логических связок являются «и», «или», «если …, то» и т.п., позволяющие составлять из логических выражений новые. Например, «Столица России — Москва и столица США — Вашингтон». Это высказывание является истинным, поскольку его составные также являются истинными.
Математический язык
В рамках данной части будут введены основные логические операции и их обозначения, аксиомы алгебры логики и её законы.
Логические операции
| Название операции | Обозначение | Речевой оборот |
| Инверсия (отрицание, логическое НЕ) | ¬A; A̅; | Не A; Неверно, что A; |
| Дизъюнкция (логическое ИЛИ) | A V B; A + B; | А или В или оба вместе; |
| Конъюнкция (логическое И) | A Λ B; A & B; A · B; | A и B вместе; |
| Импликация (следование) | A → B; | если A, то B; |
| Эквивалентность (тождество) | A↔B; A≡B; | A эквивалентно/равносильно B; |
| Стрелка Пирса (ИЛИ-НЕ) | A↓B; | Ни A, ни B; |
| Штрих Шеффера (И-НЕ) | A|B; | Неверно, что A и B; |
| Сложение по модулю 2 (строгая дизъюнкция, XOR) | A⊕ B; | Либо A, либо B; |
Символами A и B обозначены условные логические высказывания.
На логические операции распространяется определенный порядок выполнения:
- Инверсия;
- Конъюнкция и штрих Шеффера;
- Дизъюнкция и стрелка Пирса;
- Импликация и сложение по модулю 2;
- Эквивалентность;
Однако как такового, общего стандарта нет. Поэтому, во избежание путаницы, желательно использовать скобки, принцип работы которых аналогичен обычным.
Аксиомы
Свойства и законы
Булевы функции
Булева функция — это брат-близнец функций из алгебры. Только вместо чисел в качестве переменных в ней логические высказывания.
Предположим, у нас есть такая простецкая функция:
«Если A истинно, то B тоже истинно«, где А и В — это некие логические высказывания.
На математическом языке эта функция имеет такой вид:
Для иллюстрации зависимости между функцией и её аргументами в школьной алгебре обычно используются графики.
В случае с булевой функцией применяются таблицы истинности.
Таблица истинности — это таблица, описывающая логическую функцию. В ней значения аргументов сопоставляются со значениями функциями. Для нашей функции таблица истинности будет следующей:
| A | B | F(A.B) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
На булевы функции распространяются законы и правила алгебры логики. Применим их для упрощения булевой функции f(A, B, C):
С таким видом этой функции работать проще. В том числе проще и составить таблицу истинности:
| A | B | C | F(A, B,C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Базис
В алгебре логики функцию, реализующую одну и ту же таблицу истинности, можно реализовать с помощью разных операций.
Базис — это набор операций, позволяющий построить любые, сколь угодно сложные функции. Например, наиболее распространенным является базис {И, ИЛИ, НЕ}. Базисы особенно полезны при построении логических схем.
Логические схемы
Логические схемы необходимы для реализации функций алгебры логики в цифровом устройстве. Для составления логических схем используются логические вентили (элементарные логические схемы), реализующие логические операции. Упомянутые базисы позволяют сократить перечень логических вентилей, хотя и стремление к полной минимизации этого перечня путем использования наименьших базисов не совсем практично. Мы рассмотрим логические вентили упомянутого базиса {И, ИЛИ, НЕ}
Логические вентиль И
У логического вентиля И два входа (А, В) и один выход (Z). Вентиль можно описать логической функцией Z=F(A,B)=A & B и таблицей истинности:
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический вентиль ИЛИ
У логического вентиля ИЛИ, как и у вентиля И, два входа и один выход.
Его описывает функция Z=F(A,B)=A v B и таблица истинности:
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логический вентиль НЕ
Логический вентиль НЕ имеет только один вход и один выход. На выход поступает инвертированное значение А. Функция вентиля НЕ: Q=F(A)=¬A
Обозначения по ГОСТ и другим стандартам
Сумматор
В качестве примера логической схемы, реализующей математическую операцию, рассмотрим многоразрядный двоичный сумматор. Складывать мы будем два двоичных числа. Для построения многоразрядного двоичного сумматора нам понадобится одноразрядный сумматор. Начнем с него.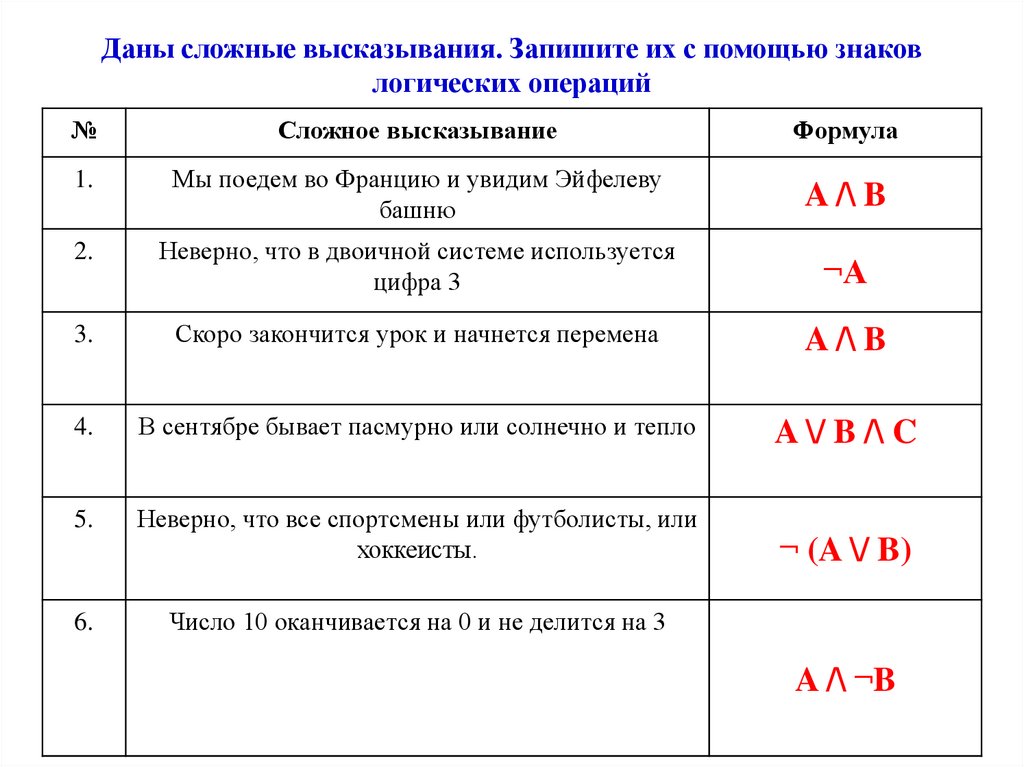
Разберемся с чем мы будем оперировать: две двоичных цифры. При сложении чисел нам, так или иначе, придется работать с переносом. Например, при сложении двух единиц в двоичной системе счисления мы получим 10:
В случае с одноразрядным сумматором на выход будут поступать две величины: перенос (в данном случае 1) и текущий разряд (0). Пока что мы проигнорируем перенос и составим таблицу истинности для разряда:
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Имея таблицу истинности, мы можем составить для неё булеву функцию:
Запомним эту функцию.
Добавим в наш сумматор перенос: как с предыдущего разряда (еще один вход), как и для следующего (ещё один выход).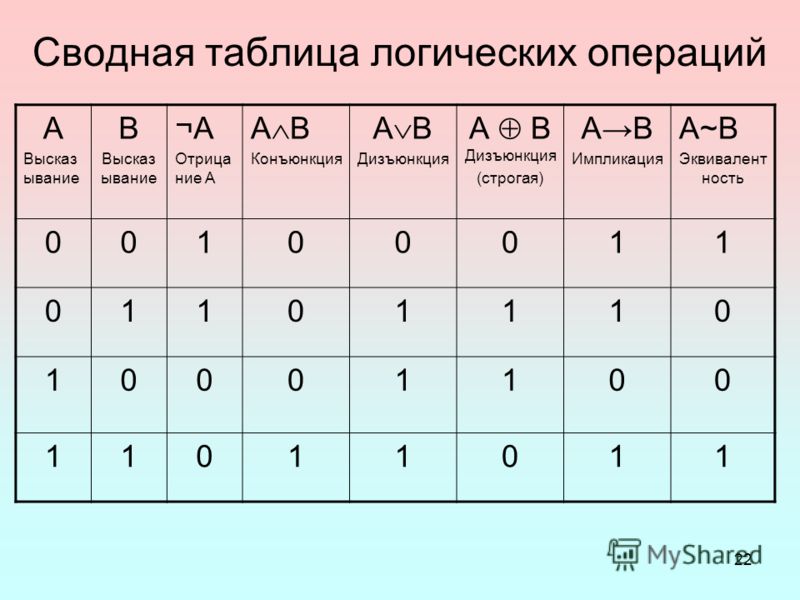
Таблица истинности для сумматора с переносом:
| A | B | P вход | S | P выход |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Теперь необходимо составить две булевы функции: для переноса и новую для разряда.
Чисто математически перенос для разряда — это ещё одно слагаемое в сумме. У нас уже есть функция для суммы, воспользуемся ей:
Нам необязательно раскрывать и упрощать эту функцию. Для построения логической схемы такой формы будет достаточно. Определимся с функцией для переноса.
Перенос равен единице в том случае, если из трех входных величин как минимум две равны единицы. Исходя из этого, можно составить вот такую функцию:
На основе двух имеющихся булевых функций для разряда и переноса мы можем составить логическую схему нашего одноразрядного сумматора. Не будем сразу бросаться в бой и начнем со схем поменьше.
Обозначение будет использовано в следующих схемах. Теперь составим схему для функции переноса:
Имея две логические схемы мы можем составить из них одноразрядный двоичный сумматор:
Если несколько одноразрядных сумматоров соединить последовательно, то получится многоразрядный сумматор:
Физика логического уровня
Итак, мы рассмотрели базовые концепции логического уровня: вентили и булеву алгебру.
Из простейших логических элементов, как из кирпичиков Лего, строятся более сложные устройства (сумматор, шифратор, мультиплексоры, триггеры и другие), из них — еще более нетривиальные схемы и так далее, пока не получится цифровая схема с необходимой логикой. Теперь опустимся на уровень ниже и выясним, какие физические процессы заставляют все это добро работать на практике.
Физические принципы
Физически логические элементы могут быть самыми разнообразными: механическими, электромеханическими, электронными, оптическими и т.д. Некоторые умудряются конструировать схемы на основе жидкости или газов, как в этом видео:
Конечно, сегодня практичность таких «компьютеров» весьма сомнительна. Но когда-то транзисторов и полупроводниковой промышленности не существовало, и инженеры-первопроходцы выкручивались как могли. Например, в Z1 Конрада Цузе, одной из первых программируемых вычислительных машин, логические элементы были реализованы в виде набора металлических пластин, снабженных хитрыми вырезами.
Логический вентиль AND в Z1, реализованный с помощью металлических пластин. Более подробное описание устройства Z1 тут.
Конечно же, такие механизмы часто заедали и искажали результат, делая Z1 почти бесполезной на практике. В Z2-Z4 Цузе заменил пластины на электромагнитные реле и даже просил у правительства Третьего Рейха денег на полностью электронные компоненты, но ему отказали.
Первые полностью электронные компьютеры были ламповыми (в прямом и переносном смысле слова), так как логические элементы в них реализовывались с помощью электровакуумных ламп. Радиолампа — это электронный прибор, выполненный в виде запаянной стеклянной колбы с электродами, из которой откачан воздух. Работа радиолампы основывается на явлении термоэлектронной эмиссии: в диоде (простейшей радиолампе) отрицательно заряженные электроны покидают разогретый электрод (катод) и под действием разности потенциалов притягиваются к другому электроду (аноду).
В обратном направлении заряд не передается, так как холодный анод не производит эмиссии, а заряженных ионов в колбе нет (потому что в ней вакуум). При изменении полярности включения диода в цепь, электроны с разогретого электрода будут тут же притягиваться к нему обратно под действием положительного потенциала.
Радиолампа (двойной триод)
Если добавить между двумя электродами третий электрод (сетку), то получится триод. Изначально триоды предназначались для усиления сигналов, так как ток через триод повторяет изменение потенциала на сетке и может быть намного сильнее. Однако нам интересней другое свойство: при подаче отрицательного потенциала на сетку, она начнет отталкивать электроны, не позволяя им достичь анода. С помощью такого эффекта управления можно реализовывать простейшие логические схемы. Например, возьмем два триода и соединим анод каждого с сеткой другого. Получиться устройство под названием триггер, которое может находиться в одном из двух устойчивых состояний (ток идет либо через первый триод, либо через второй), что позволяет хранить один бит информации.
Другие схемы соединения триодов позволяют строить логические вентили.
Схема триггера на двух ламповых триодах. Через один из триодов идет ток (триод открыт), благодаря этому на сетке второго возникает потенциал, не позволяющий току идти через второй триод (триод закрыт). Если кратковременно подать отрицательный потенциал на сетку открытого триод, то ток прекратится, поэтому второй триод откроется и закроет первый, тем самым перейдя во второе устойчивое состояние.
Хоть устройства на лампах работают быстрее механических и электромеханических, радиолампа остается крайне ненадежным прибором. Колба может потерять герметичность, спираль нагрева со временем перегорает, а сама лампа потребляет много энергии и имеет внушительные габариты. Если учитывать что первые ЭВМ состояли из тысяч ламп, обслуживание лампового монстра превращалось в головную боль для инженеров.
В 1947 Уильям Шокли, Джон Бардин и Уолтер Браттейн создали усилитель нового типа, состоявший из германиевой пластины и полоски золотой фольги.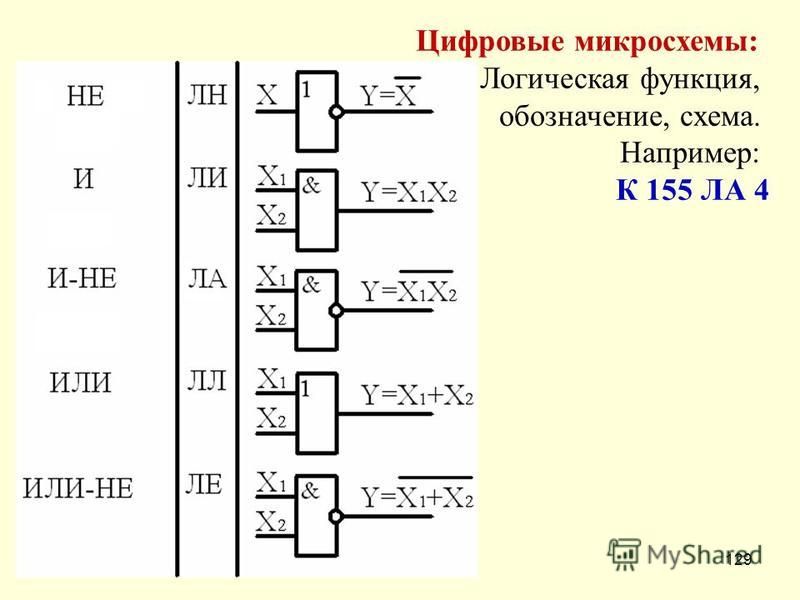
Спустя несколько лет им присудили Нобелевскую премию по физике. Этим изобретением был транзистор — устройство, полностью изменившее индустрию вычислительной техники.
Копия первого в мире работающего транзистора.
Транзистор
С концептуальной точки зрения транзистор очень похож на радиолампу-триод. Это переключатель с двумя положениями «включить» и «выключить», управляемый с помощью подачи напряжения или тока. Однако в сравнении с вакуумными лампами транзисторы имеют ряд преимуществ: они миниатюрны, потребляют значительно меньше электроэнергии и крайне редко выходят из строя (относительно тех же ламп). Благодаря изобретению транзистора компоненты логических элементов перешли из разряда «расходных материалов» в разряд «постоянных узлов конструкции».
Существуют два основных типа транзисторов — биполярные транзисторы и МОП-транзисторы (металл-оксид-полупроводник-транзистор или полевой транзистор).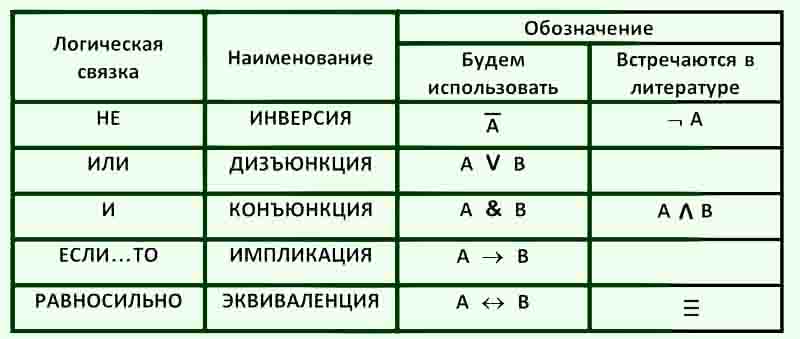
Различаются они тем, что первый управляется током, а второй — электрическим полем (отсюда и название «полевой»). В сфере производства цифровых интегральных схем полевые транзисторы практически полностью вытеснили биполярные.
Сегодня, после нескольких десятилетий развития полупроводниковых технологий, инженеры способны «упаковать» около одного миллиарда МОП-транзисторов на квадратном сантиметре кристалла кремния (с себестоимостью транзистора менее десяти микроцентов).
Полупроводники
Выше мы говорили о «полупроводниковых технологиях». Что такое полупроводник? Некоторые могут подумать, что полупроводники проводят электрический ток в два раза хуже обычных проводников (таких, как медь, золото или серебро). Это не так! МОП-транзисторы изготавливаются из кремния, элемента 14-й группы (4-й по устаревшей классификации, далее будем придерживаться именно ей). Благодаря 4 электронам, атом кремния может образовывать связи с 4 соседними атомами, формируя кристаллическую решетку.
Кремний — так себе проводник (точнее плохой, так как все электроны заняты в ковалентных связях), однако при добавлении в него небольшого количества другого вещества (легировании) его проводимость может улучшиться. Если добавить атом 5 группы (примесь n-типа), то в нем останется один свободный электрон, который легко «гуляет» внутри кристаллической решетки. А если добавить элемент 3 атомной группы (примесь p-типа), то в атоме примеси будет отсутствовать один электрон (дырка). Дырка может перемещаться в кристаллической решетки подобно электрону, причем она будет вести себя как положительно заряженная частица. Отсюда и название «полупроводник» — с помощью концентрации примесей можно управлять проводимостью кремния.
Кристаллическая решетка атомов кремния. В качестве примеси n-типа (центр) использован мышьяк (атом, потерявший электрон, становится положительным ионом), в качестве примеси p-типа (справа) использован бор (при перемещении дырки атом бора получает дополнительный электрон и становится отрицательным ионом).
n-МОП и p-МОП транзисторы
Полевой МОП-транзистор можно представить в виде «сэндвича» из нескольких слоев. Верхний слой называется затвором. Он наложен на слой изолятора — диоксида кремния (SiO2, иногда его называют просто оксидом). Этот слой в свою очередь располагается над кремниевой пластиной, называемой подложкой. Сегодня в качестве металла затвора используется поликристаллический кремний, поскольку он не плавится в ходе высокотемпературной обработки кристалла. Слои металл-оксид-полупроводника образуют конденсатор, в котором тонкий слой оксида (диэлектрик) изолирует металлическую пластину от полупроводниковой.
Существуют два вида полевых МОП-транзисторов: n-МОП и p-МОП. В транзисторах n-типа, называемых n-МОП, области, где расположены полупроводниковые примеси n-типа – в свою очередь называемые истоком и стоком – находятся рядом с затвором, причем вся эта структура размещается на подложке p-типа. В транзисторах же p-МОП и исток, и сток – это области p-типа, размещенные на подложке n-типа.
Полевой МОП-транзистор ведет себя как переключатель, управляемый приложенным к нему напряжением. В таком транзисторе напряжение перехода создает электрическое поле, включающее или отключающее линию связи между источником и стоком.
Диод — соединение p-полупроводника (катода) и n-полупроводника (анода). Когда напряжение на аноде превышает напряжение на катоде, ток идет (от анода к катоду). В обратном случае ток не течет. На рисунке представлена схема работы n-МОП транзистора. Когда напряжение на затворе равно 0 В, канал движения тока между истоком и стоком закрыт (транзистор выключен). Когда напряжение на затворе равно напряжению питания (Vdd), это создает электрическое поле между затвором и подложкой, в результате в зону между истоком и стоком под слоем окисла формируется избыток электронов. При достаточно высоком напряжении на нижней границе затвора накапливается настолько много электронов, что область с полупроводником p-типа превращается в область с полупроводником n-типа.
Такая область называется каналом. В этот момент в транзисторе образуется область проводимости от источника n-типа, через каналы n-типа к стоку n-типа, и через этот канал электроны могут беспрепятственно перемещаться от истока к стоку. Транзистор включен. p-МОП-транзисторы работают ровно наоборот.
К сожалению, полевые МОП-транзисторы плохо работают в роли переключателя. n-МОП-транзисторы хорошо передают логический 0 и плохо логическую единицу. p-МОП — наоборот. Поэтому для создания хороших логических вентилей, хотелось бы иметь оба транзистора на одном кристалле. Однако для n-МОП- и p-МОП-транзисторов требуются разные типы подложек. Для размещения двух типов транзисторов на одном кристалле применяется комплементарный МОП (КМОП). В настоящее время КМОП-процесс используется для изготовления подавляющего большинства транзисторов и микросхем.
Логические вентили на КМОП-транзисторах
Для подробного описания построения всевозможных логических вентилей здесь просто не хватит места.
Поэтому в качестве примера возьмем простейшие логические элементы и рассмотрим их реализацию на КМОП-транзисторах. Вентиль НЕ:
n-МОП-транзистор N1 включен между землей GND и выходным контактом Y. В свою очередь, p-МОП транзистор P1 включен между напряжением питания VDD и выходным контактом Y. Напряжение на входном контакте А управляет переходами обоих транзисторов.
Если напряжение на А соответствует логическому нулю, то транзистор N1 выключен, а транзистор P1 включен. При этом, напряжение на контакте Y равно напряжению питания, а не земли, что соответствует логической единице. В этом случае говорят, что Y «подтянут» к единице. Включенный транзистор P1 хорошо передает логическую единицу (равную напряжению питания), то есть напряжение на контакте Y очень близко к VDD. Если же напряжение на контакте А равно логической единице, то транзистор N1 включен, а транзистор P1 выключен, и напряжение на контакте Y равно напряжению земли, что соответствует логическому нулю.
В этом случае говорят, что Y «подтянут» к нулю. Включенный транзистор N1 хорошо передает логический ноль, то есть напряжение на контакте Y очень близко к GND. Получается, что если A=1, то Y=0, а если A=0, то Y=1. Это соответствует таблице истинности для логического вентиля НЕ.
Схемы вентилей И-НЕ и ИЛИ-НЕ с двумя входами:
Вентиль И-НЕ
n-МОП-транзисторы N1 и N2 соединены последовательно. Причем, чтобы замкнуть выходной контакт на землю GND – то есть понизить логический уровень, оба этих транзистора должны быть включены. В то время как p-МОП-транзисторы P1 и P2 соединены
параллельно, и только один из них должен быть включен, чтобы соединить выходной контакт с напряжением питания – то есть повысить логический уровень.
Вентиль ИЛИ-НЕ
В этом случае все ровно наоборот. n-МОП транзисторы соединены параллельно, а p-МОП последовательно.
Заключение
В этой статье мы затронули только самые основы логического цифрового уровня и физики его работы.
Возможно эта обширная и сложная область вас заинтересовала. В таком случае можем порекомендовать следующую литературу:
Computer Systems: A Programmer’s Perspective
The Elements of Computing Systems (Nand2Tetris)
Digital Design and Computer Architecture
|
Символическая логика — это раздел формальной логики (см. Логика формальная), в котором логические выводы исследуются посредством логических исчислений на основе строгого символического языка. Термин «символическая логика» впервые применил для обозначения нового этапа в развитии логики (см. Логика) английский логик Дж. Венн, опубликовавший в 1881 году под таким названием книгу. Наряду с термином «символическая логика» в настоящее время широко используется также термин «математическая логика» (см. Логика математическая). Хотя эти два термина часто отождествляются, термин «символическая логика» гораздо шире термина «математическая логика», подразумевающего изучение только тех типов логических рассуждений, которыми пользуются математики. Принято считать, что символическая логика — следующая, после традиционной логики, ступень в развитии формальной логики, применяющая математические методы и специальный аппарат символов, и исследующая мышление с помощью исчислений. Они позволяют избежать двусмысленной и логической неясности естественного языка, которым пользовалась при описании правильного мышления традиционная логика, развивавшаяся в рамках философии (см. Философия). Новые методы дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Многие проблемы, исследуемые в символической логике, вообще невозможно было сформулировать с использованием только традиционных методов. Применение в логике математических методов становится возможным тогда, когда суждения формулируются на некотором точном (формализованном) языке. Такие точные языки имеют две составляющие: синтаксис и семантику. Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Уже в Античности (в частности Аристотелем) широко применялись буквенные обозначения для переменных. Идея построения универсального языка для всей математики, для формализации на базе такого языка математических доказательств и вообще любых рассуждений выдвигалась в XVII веке Г. В. Лейбницем. Однако только к середине XIX века стало очевидным, что существующая логическая парадигма, а именно аристотелевская силлогистика, уже не отвечает требованиям развития науки того времени. С одной стороны, значительные успехи абстрактной алгебры в особенности в теории групп позволили перенести алгебраические методы на другие области науки. Это с успехом проделала английская школа, основоположником которой можно считать А. де Моргана, который в 1847 году опубликовал книгу «Formal Logic; or The Calculus of Inference, Necessary and Probable». С другой стороны, возникновение и развитие символической логики связано с работами Г. Фреге и Ч. С. Пирса. После того, как Фреге в 1879 и Пирс в 1885 году ввели в язык алгебры логики предикаты, предметные переменные и кванторы, возникла реальная возможность построения системы логики в виде логического исчисления, что и было сделано Фреге, который по праву считается основателем символической логики в её современном понимании. Пытаясь реализовать идеи Лейбница, Фреге в «Begriffsschrift» (лучшая книга по символической логике XIX века) изобрёл символическую запись для строгих рассуждений. Хотя его нотация сейчас совсем не используется (например, формулы рисовали в виде двумерного дерева), Фреге в действительности впервые построил исчисление предикатов. Исчисление предикатов есть формальная система, состоящая из двух частей: символического языка и логики предикатов. Кроме этого для исчисления предикатов Фреге даёт строгое определение понятия «доказательство», которое является общепринятым и по сей день. Основы современной логической символики были разработаны итальянским математиком Дж. Пеано, чьи интересы, как и Фреге, концентрировались вокруг оснований математики и развития формально-логического языка. Его широко известный труд «Formulaire de mathématiques», опубликованный (в соавторстве) в 1894–1908 годах, был нацелен на развитие математики в её целостности, исходя из некоторых фундаментальных постулатов. Логическая запись Пеано была принята, хотя и частично модифицирована, А. Н. Уайтхедом и Б. Расселом в их широко известной трёхтомной работе «Principia Mathematica» (1910–1913), а затем воспринята Д. Гилбертом. Таким образом, был введён в употребление символический язык, где появляются логические знаки:
Создание такого искусственного языка и с его помощью таких объектов, как логические исчисления, строго формализующие различные теории в виде некоторого конечного списка аксиом и правил вывода, означало, что в науке XIX века возникла потребность в символической логике. Основным стимулом развития символической логики в начале XX века была проблема оснований математики. К. Вейерштрасс, Р. Дедекинд и Г. Кантор показали, что в качестве фундамента всей классической математики может рассматриваться арифметика целых чисел. Дедикинд и Пеано аксиоматизировали арифметику, а Фреге дал определение натурального числа как множества всех равномощных множеств. Таким образом, вся математика сводилась к теории множеств. Однако в 1902 году математический мир был потрясён простотой и глубиной парадокса, обнаруженного Расселом в первом томе «Оснований арифметики» (Grundgesetze der Arithmetik) Фреге (основной закон V). Ответом на этот и на другие парадоксы теории множеств стало возникновение четырёх направлений в основаниях математики:
Как отмечает Э. Мендельсон: «Какой бы мы, однако, не избрали подход к проблеме парадоксов, следует сперва исследовать язык логики и математики, чтобы разобраться в том, какие в ней могут быть употреблены символы, как из этих символов составляются термы, формулы, утверждения и доказательства, что может и что не может быть доказано, если исходить из тех или иных аксиом и правил вывода. В этом состоит одна из задач математической логики» (Мендельсон Э. Развитие и применение мощного технического аппарата самой логики в первую очередь относится к программе Гилберта (начиная с 1904), где была поставлена главная задача: найти строгое основание для математики посредством доказательства её непротиворечивости, то есть доказательства того факта, что в ней недоказуема никакая формула вида A вместе с формулой ~А. Для этого потребовалось развить теорию доказательств, после чего, считал Гилберт, используя только финитные методы, можно будет доказать непротиворечивость теории множеств и самой теории действительных чисел и таким образом решить проблему оснований математики. Однако результат К. Гёделя о неполноте арифметики (1931) убедительно показал, что программа Гилберта невыполнима. Эта теорема утверждает, что если теория S, содержащая арифметику, непротиворечива, то доказательство непротиворечивости теории не может быть проведено средствами самой теории S, то есть всякое такое доказательство обязательно должно использовать невыразимые в теории S идеи и методы (вторая теорема о неполноте). Обширным полем деятельности для современной символической логики является теория рекурсии, которая в первую очередь имеет дело с проблемой разрешимости: доказуема или нет формула A из некоторого множества посылок. Эти исследования привели к теориям вычислимости, к созданию компьютерных программ автоматического поиска доказательств. Решение проблемы разрешимости послужило основным стимулом для создания теории алгоритмов. Формулировка тезиса Чёрча–Тьюринга, утверждающего, что понятие общерекурсивной функции является уточнением интуитивного понятия алгоритма, стало наиболее важным достижением символической логики. Только после уточнения понятия алгоритма выяснилось, что в хорошо известных разделах математики существуют алгоритмически неразрешимые проблемы. И наконец, важное место в современной символической логике занимает теория моделей, которая изучает фундаментальные связи между синтаксическими свойствами множеств предложений формального языка, с одной стороны, и семантическими свойствами их моделей, с другой; и вообще, изучаются соотношения между моделями и теориями, а также преобразование моделей. Совершенно очевидно, что те впечатляющие результаты, которые были получены средствами символической логики, и в первую очередь в области оснований математики, привели к некоторому гипостазированию функции и предмета самой этой логики. Так, в предисловии к «Handbook of Mathematical Logic» (1977) Дж. Барвайс пишет: «Математическая логика традиционно подразделяется на четыре раздела: теория моделей, теория множеств, теория рекурсии и теория доказательств». В свою очередь в «Encyclopedia Britanica» (CD–1998), уже применительно к символической логике, четыре указанных раздела названы «четырьмя главными областями исследования». Особенное свойство символической логики заключается в том, что она является рефлексивной наукой. Это означает, что она применяет свои методы и логические средства для анализа и понимания своей собственной структуры. |
|
|
|
|
Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет.
Им открыты названные в его честь законы де Моргана, разработана теория отношений и в 1838 определено понятие математической индукции. Однако наибольшую известность получили работы Дж. Буля. В 1847 году он публикует брошюру «Mathematical Analaysis of Logic», а в 1854 — свой главный труд по логике «An Investigation into the Laws of Thought, on which are Founded the Mathematical Theories of Logic and Probabilities». Как и де Морган, Дж. Буль был одним из тех математиков из Кембриджа, которые признали чисто абстрактную природу алгебры. Они заметили, что простейшие операции над множествами подчиняются законам коммутативности, ассоциативности и дистрибутивности. Оставалось только провести аналогию между объединением и сложением, пересечением и умножением, пустым классом и нулём, универсальным классом и единицей. Работы Буля 1847 и 1854 годов можно считать началом алгебры логики (см. Алгебра логики ), первоначальный этап развития которой был завершён Э. Шрёдером в трёхтомной монографии «Vorlesungugen uber die Algebra der Logik» (1890–1905).
Просмотр дорожек в виде нотной записи в Logic Pro
Редактор партитуры отображает области MIDI на дорожках программного инструмента (и внешнего MIDI-инструмента) в виде нотной записи, включая ноты, паузы, тональность и тактовый размер, а также знаки ключа. Столбчатые линии показывают разделение между тактами. Промежутки между областями заполняются для отображения непрерывного нотоносца. Если дорожка содержит программные инструменты Apple Loops, нотация отображается для каждой итерации лупа, но редактировать можно только исходную область лупа.
Редактор партитур имеет три представления, оптимизированные для различных видов работы:
Линейное представление: Показывает одну дорожку виртуального инструмента в непрерывном, горизонтально прокручиваемом представлении. Линейный вид — это стандартный вид для редактирования партитуры.
Вид с переносом: Показывает одну или несколько дорожек в виде сводного листа с переносом строк.
Просмотр страницы: Показывает полную оценку на следующих страницах. В представлении страницы отображается максимально возможное количество страниц (в зависимости от размера окна редактора партитуры и текущего уровня масштабирования).
Вы можете работать над макетом партитуры и распечатать полную партитуру в режиме просмотра страницы.
Вы также можете перемещаться по уровням отображения, чтобы просмотреть MIDI-регион, дорожку, несколько дорожек в папке или все дорожки в проекте.
Примечание: Поскольку Редактор партитур отображает содержимое регионов MIDI, любые ноты MIDI, расположенные за пределами региона (например, в Редакторе рояля), не отображаются в Редакторе партитур.
Просмотрите дорожку в Редакторе партитур
Выполните одно из следующих действий:
Измените вид Редактора партитур
Выполните одно из следующих действий:
Вы также можете изменить вид с помощью команд меню Вид > Режим просмотра в строке меню Редактора партитур.
Перемещение по уровням отображения партитуры
Чтобы показать одну дорожку: Дважды щелкните нотоносец этой дорожки (или выберите дорожку в области дорожек).
Чтобы перейти к следующему более высокому уровню отображения: Нажмите кнопку «Уровень отображения» в строке меню Редактора партитуры.
Чтобы отобразить все дорожки виртуальных инструментов в проекте: Дважды щелкните фон Редактора партитур.
При просмотре партитуры в линейном представлении в инспекторе редактора партитуры слева от дисплея партитуры появляются следующие элементы управления (когда во всплывающем меню «Вид партитуры» выбран пункт «Показать локальный инспектор»):
Всплывающее меню «Вставить»: Выберите значение ноты для вставки.
Всплывающее меню Time Quantize (с кнопками Strength и Swing): Квантизировать размер нот.
Всплывающее меню Scale Quantize (с кнопками Strength и Swing): Транспонировать ноты в другую тональность.
Скорость: Измените значение скорости выбранных нот.
Кроме того, всплывающее меню «Сетка» появляется в строке меню «Редактор партитур», так что вы можете установить визуальное квантование нот в Редакторе партитур.
Подготовка сеанса Logic Pro для записи
You are here: Home / How-to / Подготовка сеанса Logic Pro для нотации
Logic ProАкроним, сокращенный от организации прав на публикацию, такой как ASCAP, BMI, SESAC X стал предпочтительной платформой для многих профессиональных композиторов и продюсеров, создающих мокапы или мастер1. Интеллектуальная собственность, состоящая из звукозаписи 2. Процесс оптимизации микса путем дальнейшей обработки сигнала для корректировки присутствия, тембра, громкости и тона записи своей работы.
При создании партий Отдельные музыкальные произведения, каждое из которых предназначено для исполнения одним музыкантом или частью ансамбля. и партитураПисьменное представление музыкального произведения, включая обозначения всех частей ансамбля. если живое выступление с группой или оркестром является последующей возможностью для проекта, то вам необходимо с самого начала подумать о настройке сеанса Logic, чтобы сделать расшифровку менее затратной.
Raw midiПротокол для передачи музыкальной информации, такой как ноты и управляющие сигналы, между электронными музыкальными инструментами и компьютерами. из сеанса Logic может быть хуже, чем полное отсутствие миди для вашего аранжировщика или оркестратора.
Миди без щелчкаВы можете подумать, что миди автоматически снизит стоимость, но обычно это не так. Это может занять очень много времени, чтобы отредактировать импортированный миди в обычной системе обозначений, используемой для записи музыки. (что игроки могут легко понять и прочитать), что делать это «на слух» в программе записи обычно быстрее и дешевле.
Этого не должно быть, если ваш сеанс настроен и отредактирован с учетом нотации.
Быстрый просмотр ваших треков с помощью вкладки Editor>Score (изображение) может дать вам предварительный просмотр того, что транскрибатор увидит после импорта вашего миди. К счастью, это же представление может дать предварительный просмотр изменений. Джазовое сокращение для Chord Changes; последовательность аккордов, которую вы делаете из списка ниже, предоставляя при этом некоторые инструменты, необходимые для повышения удобства использования вашего миди.
Нотация может быть дорогостоящей
В любой момент существуют способы сократить расходы при создании сеанса Logic для максимального увеличения потенциала последующего потока. Вот список вещей, которые следует учитывать, с практическими предложениями, чтобы максимизировать эффективность вашего рабочего процесса.
- Обязательно трек с кликом, вводя миди в сессию с использованием всех виртуальных инструментов (кроме вокала).
- Если возможно, также введите миди-версию вокальной партии в вашу сессию
- Обязательно установите темп. Скорость, с которой исполняется музыкальное произведение, часто указывается в ударах в минуту., время и тональность. Группа звуков или тональность, вокруг которой сосредоточено музыкальное произведение. подписи в Logic для каждой дорожки.
- Установка тактового размераСимвол, написанный в начале музыкального произведения и указывающий количество долей в каждом такте и тип ноты, на которую приходится одна доля. с использованием Signature части Global Tracks
- Установка темпа с помощью Global Tracks Секция темпа
- Установка тональности Набор символов, написанных в начале музыкального произведения, обозначающих тональность, в которой оно должно быть сыграно. в редакторе партитур, перетащив нужную клавишу на партитуру из поля Part в Track Inspector
- Установка тактового размераСимвол, написанный в начале музыкального произведения и указывающий количество долей в каждом такте и тип ноты, на которую приходится одна доля.
- Global Tracks , чтобы получить желаемое звучание
- Если вы не использовали щелчок, используйте Tempo Mapping в Global Tracks , чтобы назначить линию barA, которая разделяет такты в нотах. строки
Длительность и артикуляция
Длительность, которая звучит прямо на рабочей станции DAWDigital Audio. Некоторые из них: Ableton Live, FL Studio, Logic Pro X, Cubase, Pro Tools, Studio One, Reason, Reaper, Digital Performer, Bitwig Studio, Samplitude Pro X, GarageBand (Mac), Cakewalk by BandLab, Presonus Studio One, Tracktion Waveform. будут выглядеть «неправильно» на нотах. Хотя даже самую короткую продолжительность можно передать с помощью нот и пауз, миди, выходящие из Logic, обычно приводят к тому, что в нотной музыке появляется много пауз, что делает ее загроможденной и затрудняет чтение. Мы решаем эту проблему в транскрипции. Процесс записи музыкального произведения по мере его исполнения либо на слух, либо по записи. написав коротко звучащую ноту, символ, используемый для обозначения определенной высоты тона и длительности в виде более длинной ноты с знаком артикуляции.
Чтобы учесть эту разницу между выводом Logic и потребностями расшифровщика, первое, что нужно сделать, — это сохранить копию сеанса Logic, чтобы сохранить исходную работу. Затем просмотрите партии в Logic и отредактируйте продолжительность миди, чтобы перенести сустейн на следующую долю или подразделение. Инструмент Logic Midi Transform>Quantize Durations — немного громоздкий, но удобный способ сделать это, и он начинает работать быстро, когда вы знакомитесь с работой инструмента.
Миди, экспортированные из программного обеспечения для нотной записи, обычно имеют длительность, которая будет правильно воспроизводиться в DAW, потому что они разработали свой миди-интерпретатор для правильной интерпретации знаков артикуляции и включения скорректированных длительностей в экспортированные миди. Если нотация является частью последующей картины проекта, уже один этот факт делает более рентабельным начало проекта в программном обеспечении для нотации.
- При записи треков обязательно используйте квантование входного сигнала. Установите минимальную продолжительность в Inspector>Region>Quantize [раскрывающийся список значений нот]
- Использование педали сустейна при вводе нот может негативно повлиять на удобство использования вашего миди. Перед отправкой файлов в нотную запись выполните одно из следующих действий:
- Избегайте использования педали сустейна, вместо этого удерживайте клавиши в течение нужной длительности ноты во время ввода Педаль до длины ноты, знает, что это может привести к нежелательным результатам.
- Удалить данные педали сустейна и исправить длительность вручную
- Избегайте использования педали сустейна, вместо этого удерживайте клавиши в течение нужной длительности ноты во время ввода Педаль до длины ноты, знает, что это может привести к нежелательным результатам.
- Разделить пианино на 2 трека, один для правой руки и один для левой:
- Открыть вкладку окно
- В Инспекторе регионов установите Стиль на Фортепиано 1/3
- Перетащите инструмент Voice Separation (в списке инструментов редактора) между нотами, чтобы создать динамическую точку разделения, посылая ноты левой руки к нижнему штату
- В области Треки выберите Правка > Отдельные MIDI-события > По каналу событий, , чтобы создать еще один миди-трек в сеансе.
Если вы сделаете все это для подготовки своего миди, ваши затраты значительно снизятся после того, как ваш расшифровщик откроет экспортированный миди в Finale.
См. соответствующую статью о подготовке файлов Finale для использования в Logic Pro 9.
