Общее сопротивление формула: Общее сопротивление: как найти, формулы, расчет

Общее сопротивление электрической цепи, чему оно равно и как найти по формуле. « ЭлектроХобби

Как известно во всем нужна своя мера, которая позволяет делать точные системы, устройства, механизмы, схемы. Мера множественная, имеет свои конкретные величины. В сфере электротехники основными величинами являются напряжение, ток, сопротивление, мощность, частота (для переменного и импульсного тока). Величины между собой связаны определенными формулами. Самой важной формулой, наиболее используемой электриками, электронщиками является закон Ома ( I = U/R, то есть — сила тока равна напряжению деленному на сопротивление). Зная любые две величины из этой формулы всегда можно найти третью.

От сопротивления электрической цепи зависит силы тока при наличии определенного напряжения. Если меняется сопротивление в цепях схемы, то и меняться режимы ее работы в отдельных ее участках или во всей цепи. Знание величины сопротивления могут помочь выявить неисправность, узнать (вычислить из формулы) другие электрические величины в схеме, зависящие от этого сопротивления.

Теперь давайте посмотрим от чего зависит общее сопротивление электрической цепи. Общее — это сумма частных. Любая электрическая цепь и схема содержит в себе электрические компоненты, которые обладают внутренним сопротивлением. Даже обычный конденсатор (две пластины проводника, разделенные диэлектриком, что позволяет накапливать электрический заряд между этими пластинами, не пропуская постоянный ток), который, казалось бы, по сути своей его не должен иметь (точнее оно бесконечно большое) обладает реактивным сопротивлением.

Самая простая электрическая цепь состоит из источника питания и нагрузки. К примеру это будет обычная батарейка и маленькая лампочка накаливания. И батарейка и лампочка имеют свои сопротивления, которые суммируются, что определяет силу тока, текущему по этой простейшей цепи (при определенной величине напряжения). Допустим к нашей цепи мы добавим еще один элемент нагрузки (вторую такую же лампочку). Ее можно подключить к этой простейшей цепи двумя способами либо параллельно первой лампочки, либо же последовательно ей

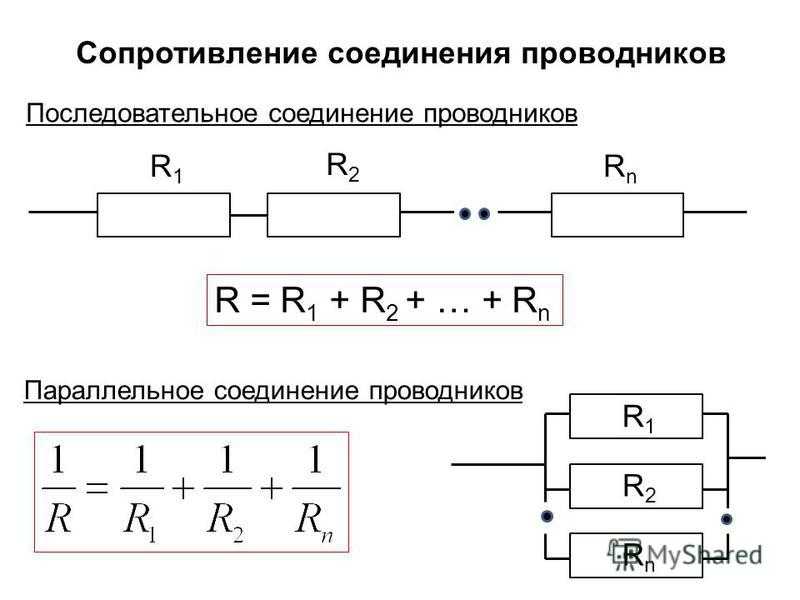
При последовательном подключении сопротивление будет суммироваться:

При параллельном подключении общее сопротивление можно найти по таким формулам:

То есть, большинство схем будут иметь в себе либо параллельное подключение сопротивлений, либо последовательное или же смешанное. В случае сложной электрической цепи определение общего электрического сопротивления происходит по частям (группам), состоящим, опять же, из параллельных и последовательных подключений элементов, обладающими сопротивлением. Правильнее начинать с той части цепи, схемы, которая имеет наибольшую удаленность от двух конечных выводов, рассматриваемых как контакты общего сопротивления. На рисунке ниже приведен пример последовательности вычисления общего сопротивления сложной цепи, схемы.

Но ведь существуют электрические цепи, в которых общее сопротивление может постоянно меняться, к примеру схема стабилизированного регулятора частоты вращения постоянного электродвигателя, подключенная к самому двигателю. При изменении нагрузки на валу двигателя будет меняться его внутреннее сопротивление, следовательно меняться будет и режимы работы схемы (поддерживающая нужную частоту вращения вала). В таких цепях электрическое сопротивление является динамическим, изменяющемся. Можно лишь рассчитать усредненное сопротивление, которое не будет абсолютно точным.

Помимо этого, как было подмечено ранее, существует еще реактивное сопротивление, которое бывает у индуктивных и емкостных элементов цепи. Оно явно себя проявляет в схемах, что работают с переменным, импульсным током. Если в цепях постоянного тока конденсатор (стоящий последовательно) не будет проводить через себя ток, то в цепи переменного тока будет все иначе. Причем его реактивное сопротивление будет зависеть от частоты (при одной и той же емкости). Вот формулы для нахождения реактивного емкостного и индуктивного сопротивления:

P.S. общее сопротивление можно находить и через использование закона Ома, который гласит, что сопротивление равно напряжение деленное на силу тока. Следовательно, берем мультиметр, измеряем ток и напряжение в том месте цепи, где хотим узнать сопротивление. Воспользовавшись формулой Ома находим (определяем) электрическое сопротивление нужного участка цепи. Напомню, что при использовании закона ома нужно применять основные единицы измерения — ток в амперах, напряжение в вольтах, а сопротивление в омах.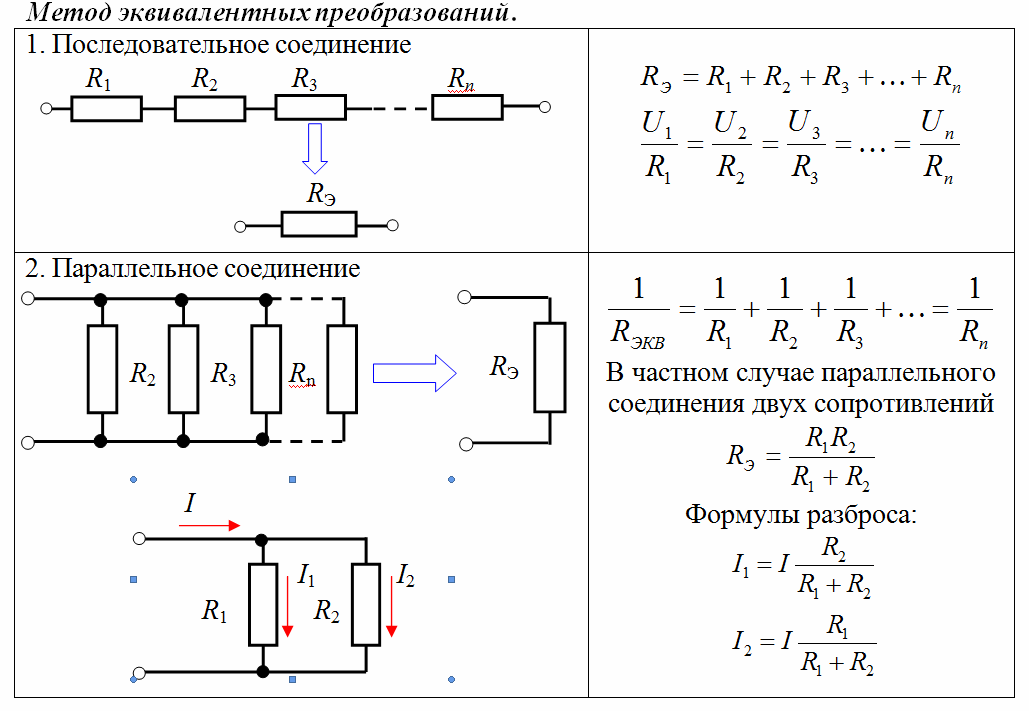

параллельная, последовательная и комбинированная цепь

Решая задачи в области электроники и электрики, приходится сталкиваться с различными вычислениями. Чаще всего они связаны с упрощением электрических схем. Для этого используется метод эквивалента, когда часть цепи заменяется на один элемент с характеристиками, аналогичными ей. Но чтобы это сделать, необходимо знать, как посчитать сопротивление участка цепи и какие виды соединений бывают.

• Определение величины
  • Сопротивление радиоэлемента
  • Удельный параметр вещества
• Эквивалентная схема
• Расчёт импеданса
• Браузерный онлайн-калькулятор
• Практическое применение
  • Простое соединение
  • Комбинированный контур

Определение величины

Ток — это упорядоченное движение носителей заряда под действием электрического поля. Способность вещества проводить ток называют электропроводимостью. Чем больше носителей частиц имеет материал, тем большей проводимостью он обладает.

В зависимости от этой характеристики все вещества разделяют на три вида:

1. Проводники. Характеризуются хорошей электропроводностью. К ним относят металлы и их сплавы, а также электролиты.
2. Диэлектрики. Вещества, практически не проводящие электрический ток. В основном это газы, каучук, минеральные масла, пластмассы.
3. Полупроводники. Материалы, обладающие двумя видами проводимости одновременно — дырочной и электронной. Это вещества, имеющие ковалентную связь: кремний, германий, селен.

Величина, обратная электропроводимости, называется электрическим сопротивлением. То есть это физическая величина, препятствующая прохождению тока. Кроме способности любого материала ограничивать количество проходящих через него зарядов, существует специальный радиоэлемент, ограничивающий силу тока — резистор.

Таким образом, существует два понятия сопротивления: радиоэлемент и физическая величина.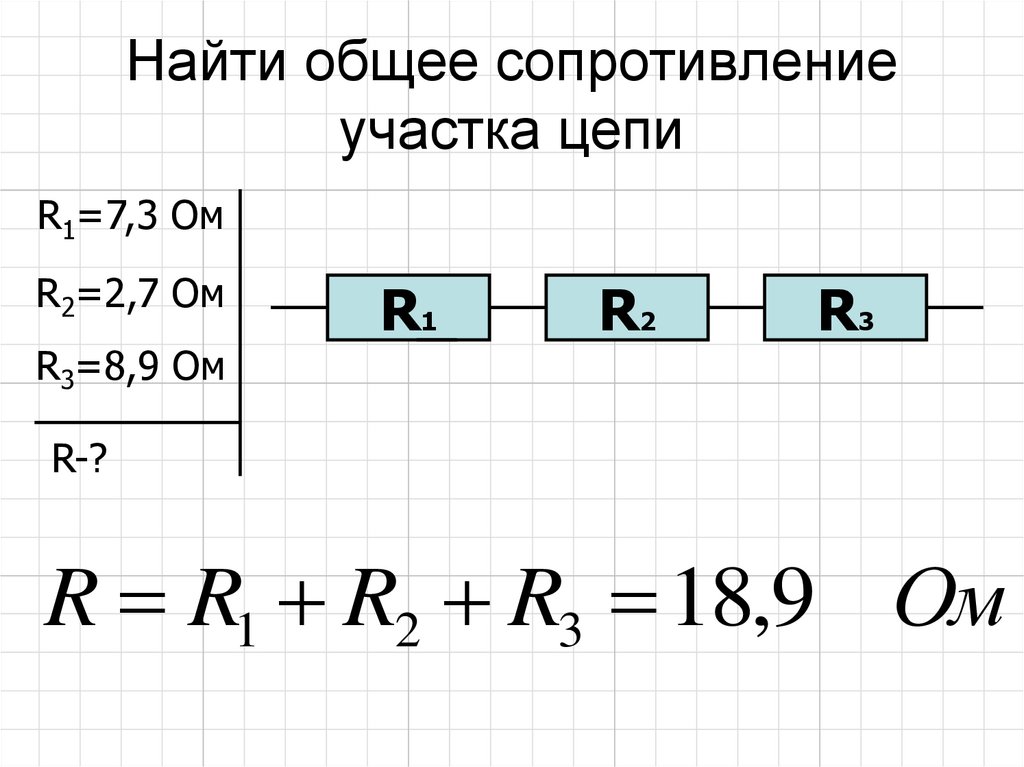

Сопротивление радиоэлемента

Термин «резистор» произошёл от латинского слова resisto — «сопротивляемость». Все резисторы делятся на постоянные и переменные. Последние позволяют изменять своё сопротивление. На схемах и в литературе такая радиодеталь подписывается латинской буквой R. Единицей измерения считается Ом. Графически резистор обозначается в виде прямоугольника с двумя выводами от середины краёв. Кроме номинального сопротивления, он характеризуется рассеиваемой мощностью и классом точности.

По своей сути это пассивный радиоэлемент, преобразующий часть электрической энергии в тепловую. Тем самым он ограничивает ток, линейно преобразовывая его силу в напряжение и наоборот. Главный параметр, описывающий сопротивление, находится согласно закону Ома для участка цепи по следующей формуле:

R = U/I, где:

• R — электрическое сопротивление, Ом.
• U — разность потенциалов приложенная к элементу, В.
• I — сила тока, преходящая через резистор, А.

Но тут следует отметить, что этот закон справедлив только для резистивных цепей. То есть для тех, при расчёте которых ёмкостью и индуктивностью пренебрегают. Если же эту формулу применить к реактивным элементам, то для катушки индуктивности сопротивление будет равным нулю, а для конденсатора — бесконечным. Но это верно для постоянного тока и напряжения.

При переменных величинах напряжение на индуктивности не будет равно нулю, как и ток, проходящий через конденсатор. Такие случаи сопротивлением уже не описываются, поскольку оно предполагает постоянные значения тока и напряжения.

Удельный параметр вещества

Чтобы различать понятие и элемент, было введено название удельное электрическое сопротивление. Обозначается оно греческим символом ρ. В Международной системе единиц эта величина измеряется в Омах, умноженных на метр. Зависит она исключительно от свойства материала.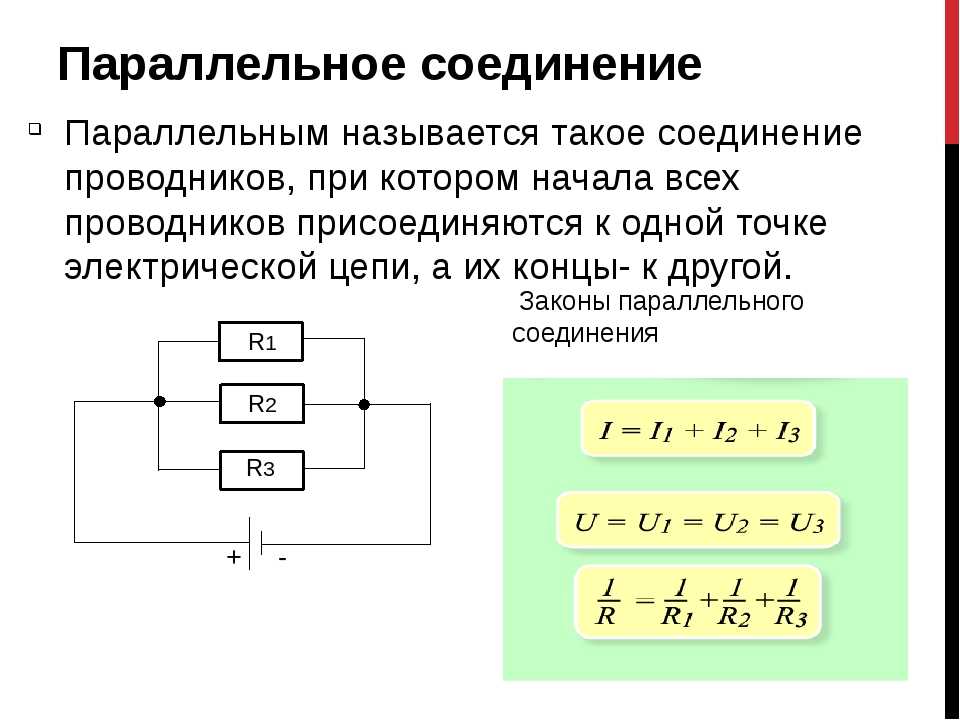

Для расчёта электрического сопротивления однородного вещества используется формула: R = ρ* l/S, где:

• l — длина проводника, м;
• S — площадь поперечного сечения, м².

Поэтому в физическом смысле удельное сопротивление материала — это величина, обратная удельной проводимости, представляющая собой сопротивление однородного проводника единичной длины и площади поперечного сечения. А значит, она численно равна импедансу участка электрической цепи, выполненному из вещества длиною один метр и площадью поперечного сечения один метр квадратный.

Для каждого вещества удельное сопротивление известно и является справочной величиной. Например, для меди — 0,01724 Ом*мм²/м, алюминия — 0,0262 Ом*мм²/м, висмута — 1,2 Ом*мм²/м, нихром — 1,05 Ом*мм²/м. Эти данные получены при температуре t = 20 °C, так как материалы обладают свойством изменять свою удельную характеристику при изменениях температуры. Так, проводимость металлов увеличивается при снижении температуры, а полупроводников — уменьшается.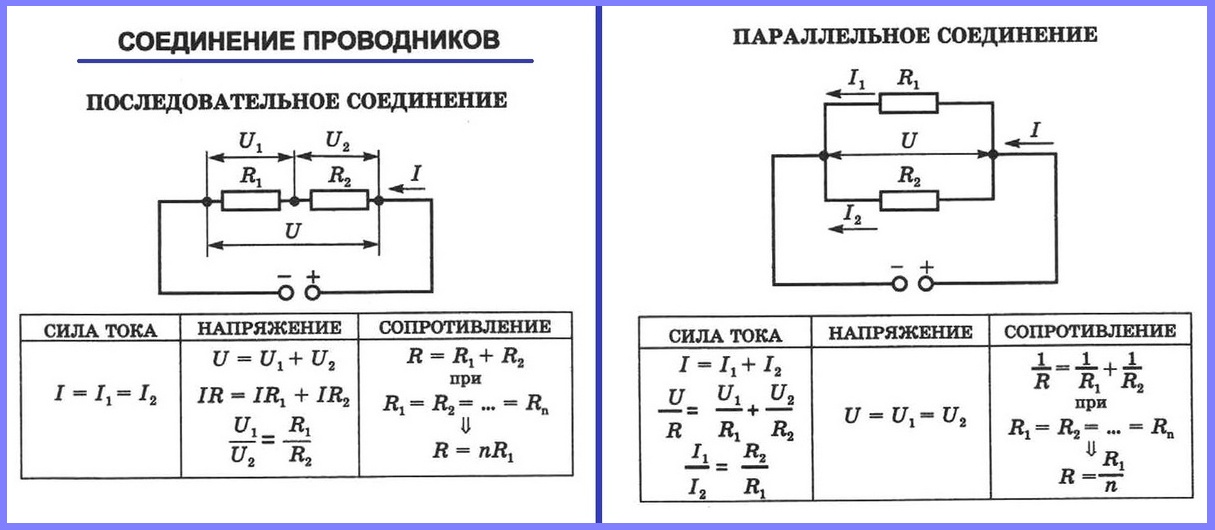

Эквивалентная схема

При расчётах сопротивления электрических цепей широко используется понятие «эквивалентная схема замещения». Её назначение — упростить сложную схему до вида, состоящую из минимума элементов. Иными словами, каждый сложный радиоэлемент можно представить в виде соответствующих ему эквивалентных простых радиодеталей: резистор, ёмкость, индуктивность, источники тока и напряжения. Это позволяет не только математически описать любую схему, но и рассчитать её параметры.

При этом обычно радиоэлементы идеализируются, то есть их паразитные параметры не учитываются. Так и для подсчёта сопротивления цепи каждый компонент представляется как идеальный резистор. После чего схема перерисовывается, и в результате на ней остаются только подключённые разными способами друг к другу резисторы.

Существует два вида подключения:

• последовательное;
• параллельное.

Основными элементами электрической цепи являются узел, ветвь и контур.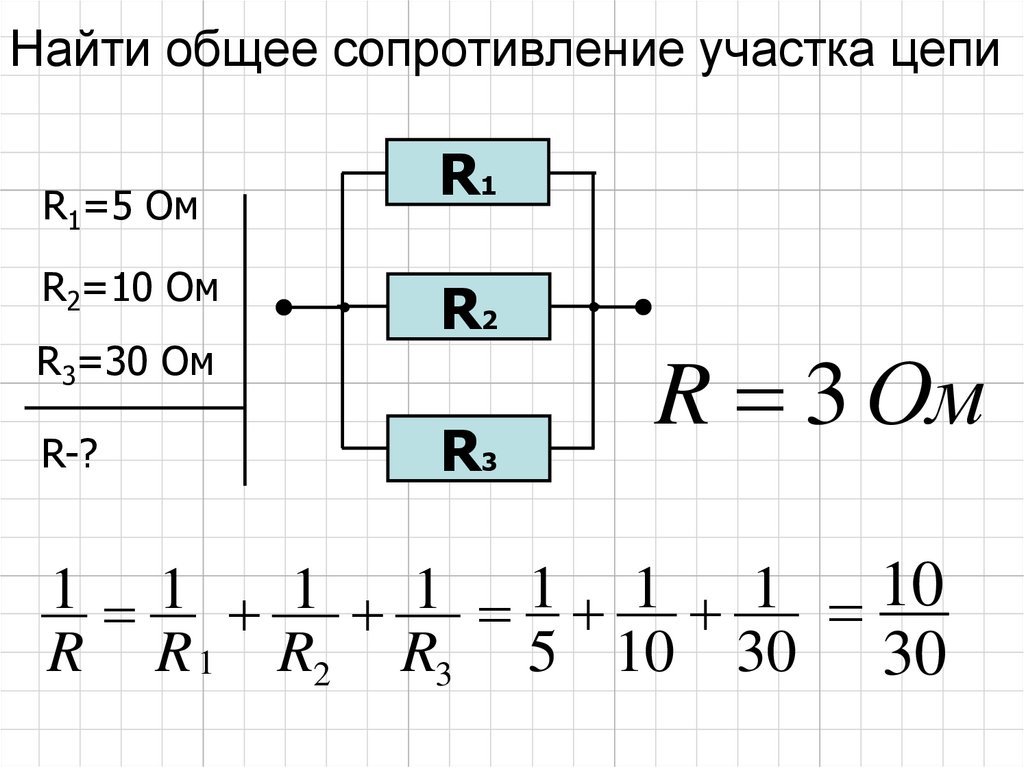 Узел — это место соединения двух и более ветвей. Ветвь — это последовательный участок цепи между двумя узлами, а контур — любая замкнутая цепь. Последовательное соединение состоит из элементов, при котором все компоненты цепи связаны так, что участок цепи, образованный из них, не имеет ни одного узла. А при параллельном соединении все компоненты электрической цепи контактируют между собой в двух узлах. При этом эти узлы напрямую не связаны.

Расчёт импеданса

Методы вычисления общего сопротивления зависят от способа соединения резисторов. При расчётах общего импеданса за основу берутся законы Кирхгофа.

Так, первый его закон гласит: сумма токов в узле равна нулю. Или, если его перефразировать, значение тока, втекающего в узел, равно сумме токов, вытекающих из этого узла. Второй закон связан с электродвижущей силой, и его формулировка звучит так: сумма разности потенциалов в контуре равна сумме падений разности потенциалов на каждом резисторе в цепи.

При последовательном соединении все элементы располагаются друг за другом без ответвлений.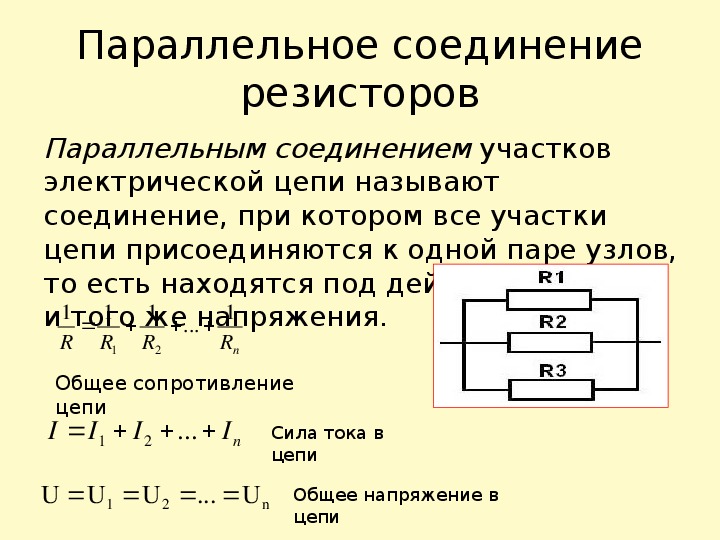

Так как согласно правилу Кирхгофа в любом месте ветви сила тока одинаковая I = I1 = In, то падение напряжения на первом элементе: U1 = I*R1, а на n: Un = I*Rn, где:

• In — сила тока, протекающая через резистор, А.
• Un — значение падения напряжения на резисторе, В.
• Rn — величина сопротивления элемента, Ом.

Общая разность потенциалов равна сумме всех напряжений, поэтому можно записать: U = U1+…+Un = I*(R1+…+Rn) = IRo.

В результате формула для расчёта сопротивления цепи в этом случае будет выглядеть следующим образом:

Ro = R1 +…+ Rn, где:

• Ro — общее сопротивление ветви.
• R1 — значение импеданса первого элемента.
• Rn — величина сопротивления n-го элемента.

Если цепь параллельная то это значит, что на этом участке несколько ветвей расходятся, а после опять соединяются. Получается, что сила тока в каждой ветви будет своя, а величина напряжения одинакова. Поэтому Uo = U1=…= Un, а Io = I1+…+In.

Используя закон Ома, можно записать:

Uo/Ro = U1/R1+…+Un/Rn, или

1/Ro = 1/R1+…1/Rn.

В итоге эквивалентное сопротивление при параллельном соединении рассчитывается как произведение значений резисторов, делённое на сумму их произведений. Для двух резисторов формулу для нахождения общего сопротивления можно записать в виде: Ro = (R1*R2) / (R1+R2).

Браузерный онлайн-калькулятор

Если элементов в цепи немного, то, упрощая схему, довольно легко посчитать, используя формулы для параллельного и последовательного включения резисторов, общий импеданс цепи. Но если в схеме много элементов, да ещё она такая, что содержит и то, и другое соединение (комбинированная), проще воспользоваться браузерными онлайн-калькуляторами.

В их основе используются всё те же формулы для расчёта эквивалентного резистора, но все вычисления происходят автоматически. Существует огромное количество предложений таких калькуляторов. Но при этом все они работают одинаково. Онлайн-расчёт представляет собой программный код, в котором заложен алгоритм вычисления. Потребителю необходимо только в специальных ячейках указать, какой вид соединения используется, сколько элементов в контуре и сопротивления резисторов. Далее надо нажать кнопку «Рассчитать» и через считанные секунды получить ответ.

Необходимо отметить, что, если даже это в программе не указано, все значения вводятся только в Международной системе единиц, сила тока — ампер, напряжение — вольт, сопротивление — Ом. Тогда и ответ получится в Омах.

Бонусом является и то, что многие такие программы сразу рассчитывают и мощность элемента. Для этого используется формула: P = U²/Ro = I²*Ro, Вт.

Практическое применение

Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.

Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.

Простое соединение

Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.

R3 = 1 кОм = 1000 Ом.

Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.

Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:

1/Ro = 1/R1 + 1/R2 +1/R3.

Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).

Подставив исходные данные в эту формулу, получим:

Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.

Комбинированный контур

Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.

Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:

Rp = (R3*R4)/(R3+R4).

Rp = (10*3)/ (10+3) = 2,3 Ом.

Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:

Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.

Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:

I = U/R = 5/2,3 = 2,2 A.

P = I*U = 2,2*5= 11 Вт.

Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.

Расчет общего сопротивления — физика для старших классов

Все ресурсы по физике для старших классов

6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Справка по физике для старших классов » Электричество и магнетизм » Электрические схемы » Резисторы » Расчет полного сопротивления

Десять резисторов, каждый с сопротивлением, соединены последовательно. Каково их эквивалентное сопротивление?

Возможные ответы:

Правильный ответ:

Пояснение:

Для резисторов, соединенных последовательно, эквивалентное сопротивление представляет собой сумму отдельных сопротивлений.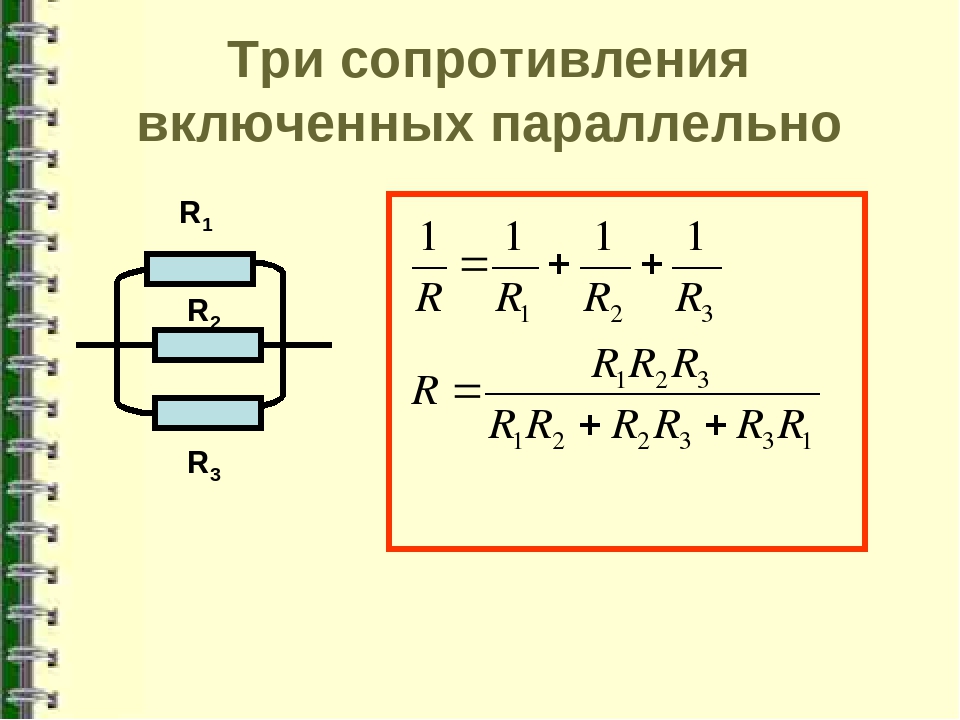

Поскольку все резисторы в этой задаче равны, мы можем упростить с помощью умножения.

Сообщить об ошибке

Десять резисторов, каждый с сопротивлением, установлены параллельно. Чему равно сопротивление?

Возможные ответы:

Правильный ответ:

Объяснение:

Для резисторов, соединенных параллельно, эквивалентное сопротивление можно найти, суммируя обратные величины отдельных сопротивлений, а затем вычисляя обратную величину результирующей суммы.

Поскольку все резисторы в этой задаче равны, мы можем упростить путем умножения.

Сообщить об ошибке

Двенадцать резисторов одинакового сопротивления включены последовательно. Если общее сопротивление , каково сопротивление каждого резистора?

Возможные ответы:

Правильный ответ:

Пояснение:

Общее сопротивление последовательно соединенных резисторов равно сумме сопротивлений отдельных резисторов.

В данном случае мы знаем общее сопротивление и количество резисторов, и нам говорят, что все резисторы одинаковой силы. Это означает, что мы можем упростить эту задачу, используя умножение.

Мы можем использовать общее сопротивление для определения индивидуального значения.

Сообщить об ошибке

Три резистора соединены последовательно. Они имеют , и сопротивление соответственно. Каково общее сопротивление?

Возможные ответы:

Правильный ответ:

Пояснение:

При последовательной работе общее сопротивление равно сумме отдельных сопротивлений.

Используйте данные значения для каждого отдельного резистора, чтобы найти общее сопротивление.

Сообщить об ошибке

Шесть резисторов расположены последовательно. Их сопротивления равны , , , , , и . Каково их общее сопротивление?

Возможные ответы:

Правильный ответ:

Пояснение:

При последовательной работе общее сопротивление равно сумме отдельных сопротивлений.

Используйте данные значения для каждого отдельного резистора, чтобы найти общее сопротивление.

Сообщить об ошибке

Три резистора включены в параллельную цепь. Они имеют сопротивления , и , соответственно. Каково их общее сопротивление?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для параллельных резисторов:

Используя заданные индивидуальные сопротивления, мы можем найти общее сопротивление цепи.

Сообщить об ошибке

Два последовательно соединенных резистора имеют сопротивление и сопротивление соответственно. Каково общее сопротивление?

Возможные ответы:

Правильный ответ:

Пояснение:

Для последовательно соединенных резисторов общее сопротивление равно сумме сопротивлений каждого из них.

Мы можем использовать индивидуальные сопротивления из вопроса, чтобы найти общее сопротивление.

Сообщить об ошибке

Каково общее сопротивление последовательной цепи с резисторами , , и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Для последовательной цепи формула для полного сопротивления:

Нам даны значения каждого сопротивления, что позволяет нам суммировать их, чтобы найти общее сопротивление в цепи.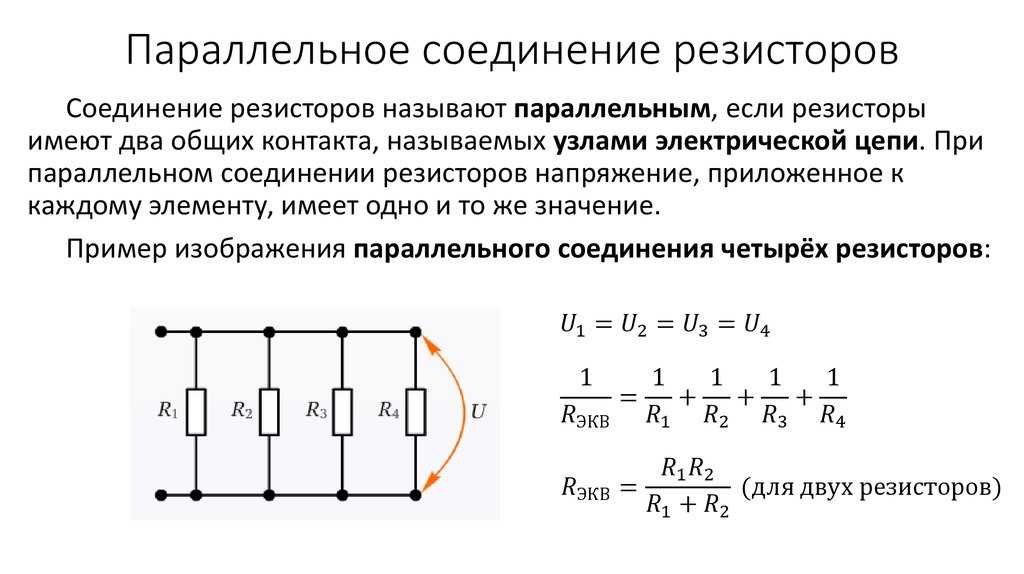

Сообщить об ошибке

Каково общее сопротивление параллельной цепи с резисторами , , и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для параллельного сопротивления:

Нам даны значения для каждого отдельного резистора, что позволяет нам найти общее сопротивление.

Сообщить об ошибке

Рассчитать сопротивление медного провода с площадью поперечного сечения и длиной .

Возможные ответы:

Правильный ответ:

Пояснение:

Сопротивление провода определяется следующим уравнением:

Нам известны удельное сопротивление (), площадь поперечного сечения и длина. Используя эти значения, мы можем найти сопротивление.

Сначала переведите площадь поперечного сечения в квадратные метры.

Для решения используйте уравнение сопротивления.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все ресурсы по физике для старших классов

6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept

Расчет полного сопротивления

Упражнения, в которых вычисляется полное сопротивление электрических цепей. В некоторых упражнениях применяется соотношение между сопротивлением R[Ом] и проводимостью G[S] → G=1/R. При анализе электрических цепей постоянного тока часто возникает необходимость расчета их полного сопротивления, которое видно с клемм источника питания. Знание значения полного сопротивления необходимо для расчета значения тока, протекающего через цепь.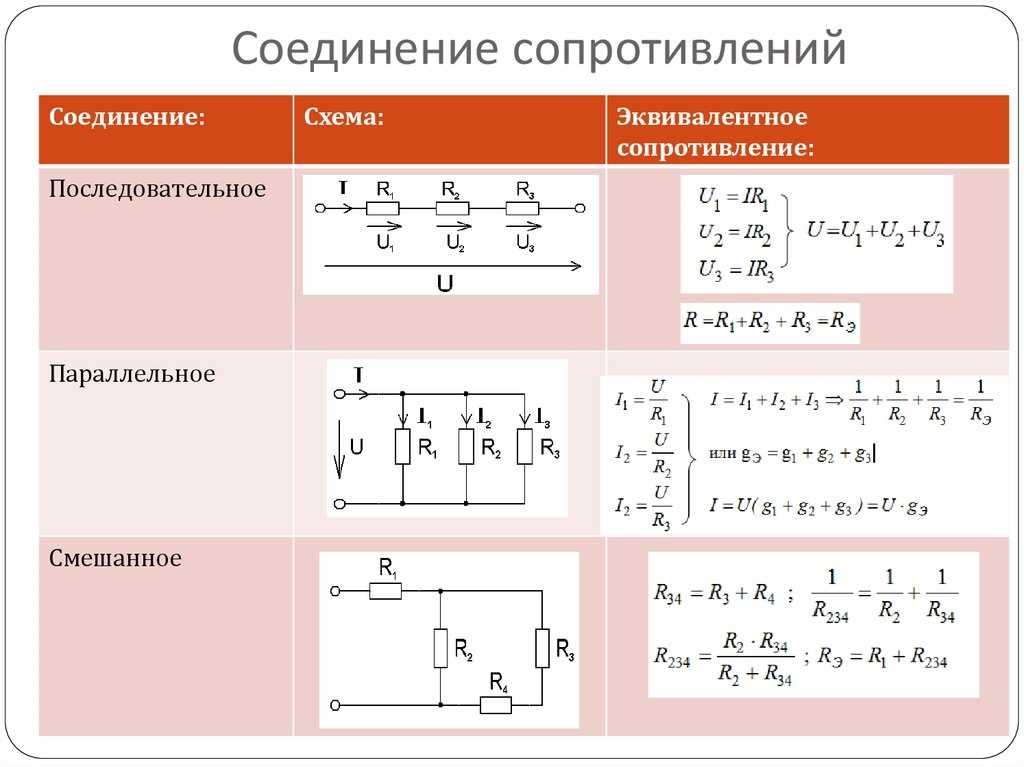 Значение основного тока, протекающего по цепи, можно рассчитать с помощью Закон Ома → I=U/R.

Общее сопротивление – пример 1

Расчет полного сопротивления для конкретной электрической цепи. Электрическая цепь в примере имеет смешанные соединения между резисторами. Суммарное сопротивление видно с клемм питания, клеммы помечены метками А и В. Электрическая схема содержит в своей топологии три резистора. Некоторые соединения между резисторами специфичны. Узлы с одинаковым электрическим потенциалом будут отмечены. Как известно, между узлами с одинаковым электрическим потенциалом ток не течет.

Общее сопротивление – пример 1

Общее сопротивление – пример 2

Расчет полного сопротивления для конкретной электрической цепи. Схема построена на восьми резисторах. Электрическая цепь в примере имеет смешанные соединения между резисторами. Общее сопротивление видно с клемм питания. При расчете полного сопротивления используется соотношение между сопротивлением R[Ом] и проводимостью G[S] → G=1/R. Некоторые соединения между резисторами специфичны. Узлы с одинаковым электрическим потенциалом будут отмечены. Как известно, между узлами с одинаковым электрическим потенциалом ток не течет. Величину электрического потенциала в конкретных узлах обозначают формулой для Делитель напряжения .

Общее сопротивление – пример 2

Общее сопротивление – пример 3

Электрическая цепь построена особым образом, потому что резисторы образуют букву Н. Они выглядят как Н-мост. Обозначение полного сопротивления этой цепи довольно сложно. Можно представить, что его боковые ответвления создают делители напряжения. Если эти делители напряжения равны, то через резистор R3 не будет протекать ток. В этой конкретной ситуации мы можем опустить резистор R3 при расчете общего сопротивления и рассматривать цепь как обрыв вместо резистора R3. Вы можете загрузить симуляцию в pspice и расчет в Excel, чтобы изучить поведение схемы.

Общее сопротивление – пример 3

Общее сопротивление – пример 4

Электрическая цепь построена на пяти резисторах.