Общее сопротивление параллельной резистивной цепи: Расчет сопротивления для параллельного соединения

Физическая формула расчета (определения) эквивалентного сопротивления в цепи

Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.

Метод свёртывания цепи

Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.

Последовательное соединение элементов

В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.

При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.

Последовательное подключение приборов

Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:

I = U/R.

Из вышестоящего выражения получаем значение R:

R = U/I (1).

Поскольку при последовательном соединении:

• I = I1 = I2 =…= IN (2),
• U = U1 + U2 +…+ UN (3),

формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:

• Rэкв = (U1 + U2 + …+ UN)/I,
• Rэкв = R1 + R2 + … + RN (4).

Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:

Rобщ = N·R (5).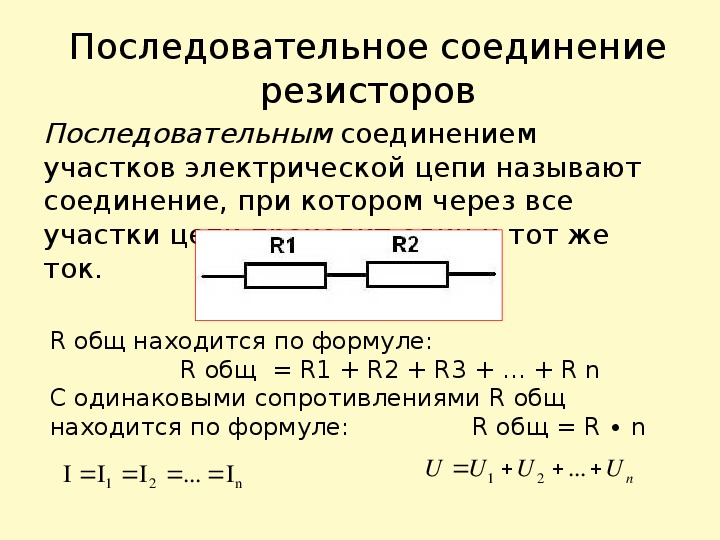

Параллельное соединение

При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.

Параллельное соединение

Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.

В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.

Если имеются N резистивных устройств, подключенных таким образом, то:

I = I1 + I2  + … + IN (6),

U = U1 = U2 = … = UN (7).

Из выражений (1), (6) и (7) имеем:

• Rобщ = U/(I1 + I2 + …+ IN),
• 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).

Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:

Rобщ = R · R / N·R = R / N (9).

Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.

Расчёт при смешанном соединении устройств

В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.

При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.

Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:

• R1 = 1Ом,
• R2 = 2Ом,
• R3 = 3Ом,
• R4 = 6Ом,
• R5 = 9Ом,
• R6 = 18Ом,
• R7 = 2,8Ом,
• U = 32В.

Электрическая схема

Из закона Ома имеем: 

I = U/R,

где R – суммарное сопротивление всех приборов.

Его будем находить, воспользовавшись методом сворачивания цепи.

Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:

R2,3= R2·R3 / (R2+R3).

R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:

1/R4,5,6 = 1/R4+1/R5+1/R6.

Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.

Эквивалентная схема

Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.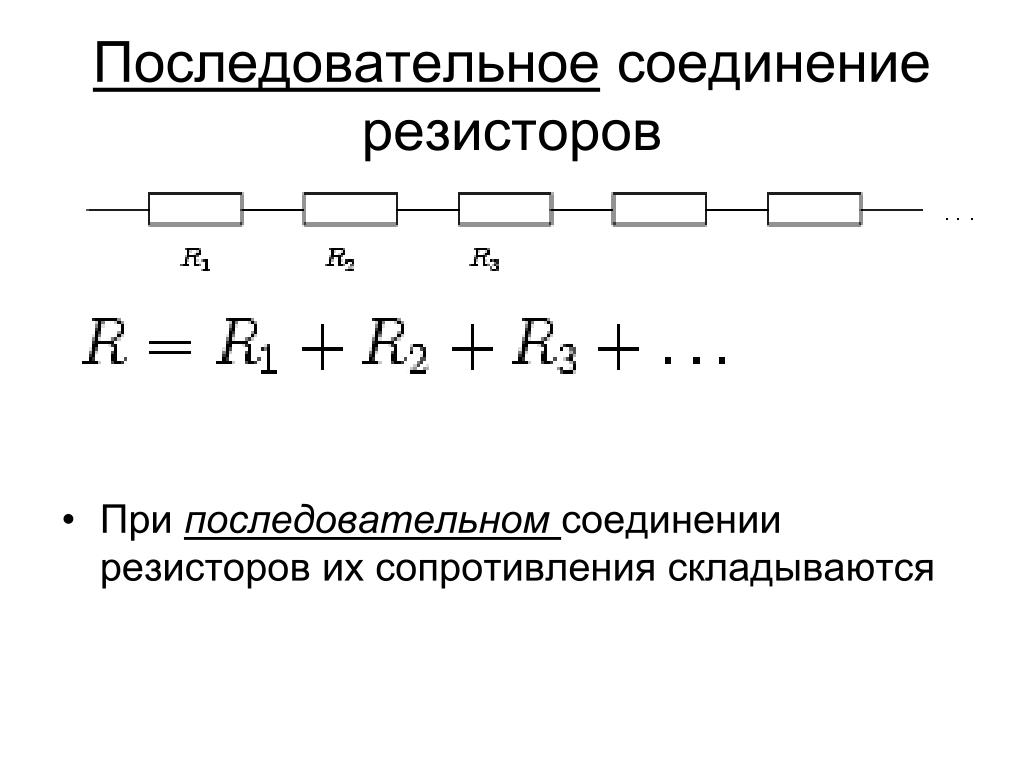

Rобщ может быть найдено по формуле:

Rобщ = R1 + R2,3 + R4,5,6 + R7.

Подставляем числовые значения и рассчитываем R для определённых участков:

• R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
• 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
• R4,5,6 = 3Ом,
• Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.

Теперь, после того, как нашли Rэкв, можно вычислять значение I:

I = 32В / 8Ом = 4А.

После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.

Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:

I1 = I2,3 = I4,5,6 = I7 = I = 4А.

На участке R2,3 напряжение находим по формуле:

• U2,3 = I2,3·R2,3,
• U2,3 = 4А·1,2Ом = 4,8В.

Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:

• I2 = U2 / R2,
• I2 = 4,8В / 2Ом = 2,4А,
• I3 = U3 / R3,
• I3 = 4,8В / 3Ом = 1,6А.

Проверяем правильность решения:

• I2,3 = I2 + I3,
• I2,3 = 2,4А + 1,6А = 4А.

На участке R4,5,б напряжение также находим, исходя из закона Ома:

• U4,5,6 = I4,5,6·R4,5,6,
• U4,5,6 = 4А·3Ом = 12В.

Так как R4, R5, Rб подключены параллельно друг к другу, то:

U4,5,6 = U4 = U5 = U6 = 12В.

Вычисляем I4, I5, I6:

• I4 = U4 / R4,
• I4 = 12В / 6Ом = 2А,
• I5 = U5 / R5,
• I5 = 12В / 9Ом » 1,3А,
• I6 = U6 / R6,
• I5 = 12В / 18Ом » 0,7А.

Проверяем правильность решения:

I4,5,6 = 2А + 1,3А + 0,7А = 4А.

Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.

Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.

Видео

Оцените статью:

Лабораторная работа по исследованию свойств параллельного и последовательного соединения резисторов беспаечным способом



В работе исследованы свойства и физические законы соединения резисторов без пайки. При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.

Ключевые слова: резисторы, макетная плата, соединение без пайки, параллельное и последовательное соединение, токи, напряжение и сопротивления при соединения резисторов.

The paper studies the properties and physical laws of connecting resistors without soldering. When building layouts, soldering installation can be completely, abandoned or reduced to a minimum. As experience has shown, the practical use of layout boards can significantly save time and material costs.

Keyword: resistors, layout Board, connection without soldering, parallel and serial connection, currents, voltage and resistance when connecting resistors.

В современном высшем учебном заведении перед каждым преподавателем стоит цель по развитию научно-исследовательских навыков студентов. Один из задач являетсямотивации студента и совершенствование научно-исследовательских навыков в формулировке исследовательского вопроса во время лабораторной работы на уроках физики. В данной работе исследованы свойства и физические законы соединения резисторов без пайки. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты. [1,2].

Цель работы: опытным путем изучить законы протекания тока через последовательно и параллельно соединение резисторовспомощью беспаечное соединение и определить формулы сопротивлений таких участков. Резисторы примениется в электронных приборах и робототехнике. [3].

Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т. д. Рассмотрим физические законы соединения резисторов. Перечень оборудования показаны на рис.1,2,3.

Перечень оборудования

Рис. 1. Резистор и провода

Рис. 2. Мультиметр

Рис. 3. Макетная плата

Последовательно соединенных резисторов

Сопротивление впоследовательной цепи. Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений.

R_общ = R₁+R₂+R₂+ •••+R_n(1)

Если последовательно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, умножив сопротивление одного резистора на количество резисторов.

R_общ = nR₁ (2)

Пример последовательного соединения двух резисторов показан на рис. 4.

Общее сопротивление для двух резисторов.

R_общ=R₁+R₂ (3)

R_общ = 25 Ом+35 Ом=60 Ом (4)

Рис. 4. Последовательное соединение двух резисторов

Величина тока впоследовательной цепи

Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени в любой точке цепи, будет одинаковым. Следовательно, во всех точках последовательной цепи величина тока одинакова.

Поэтому при последовательном соединении, для измерения тока достаточно включать один амперметр на любом участке цепи.

В качестве примера, можно привести цепь последовательного соединения двух резисторов, который показан на рис.5.

I=I₁=I₂=0,2A

Рис. 5. Величина тока в последовательнойцепи

Распределение напряжения впоследовательной цепи

Напряжение источника тока, приложенное, к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. Напряжение, приложенное, к каждому из этих резисторов определяется по формуле:

U=IR (5)

Так как ток в последовательной цепи везде одинаков, значит, действительно напряжение на ее участках зависит от сопротивления, чем больше сопротивление, тем большее напряжение приложено к данному участку. Сумма напряжений на участках последовательной цепи равна напряжению источника тока.

U_общ=U₁+ U₂+ U₃+ ••• +U_n(6)

Пример, распределение напряжения в последовательной цепи соединения двух резисторов показан на рис.6.

U_общ=U₁+ U₂(7)

12В=5В+7В

Параллельное соединение сопротивлений

Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.

Рис.

6. Распределение напряжения в последовательной цепи

Сопротивлениев параллельной цепи

Общее сопротивление параллельно включенных сопротивлений определяется по формуле:

(8)

Если параллельно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, если сопротивление одного резистора разделить на количество резисторов.

Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. Пример, если параллельно включено только два резистора (рис.7), то их общее сопротивление можно определить по формуле:

(10)

Рис. 7. Параллельное соединение двух резисторов

Распределение тока впараллельной цепи

В цепи с параллельным соединением, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.

Это значит, что чем больше сопротивление, тем меньше по нему пойдет ток.

(11)

Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I₁, I₂, утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду, утекающему от нее:

I=I₁+ I₂+ I₃ +••• +I_n(12)

Следовательно, величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.

Пример, распределение тока в параллельной цепи соединения двух резисторов показан на рис. 8.

I=I₁+ I₂

Рис. 8.

Распределение тока в параллельной цепи

Величина напряжения впараллельных цепях

Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.

Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.

U=U₁=U2=U₃=•••=U_n (13)

Содержание хода работы ипоследовательность действий

Техническое задание

1) Собрать электрическую цепь в макетную плату (рис.9.)

2) Снять показания приборов и записать их в таблицу.

3) Произвести расчеты.

4) Ответить на контрольные вопросы.

5) Сделать вывод.

Порядок выполнения работы

1) Собрать схему в макетную плату (Рис. 9.).

2) Установить на схеме величины R1=1 кОм + N, R2=2 кОм + N, R3=3 кОм + N и R4=4 кОм+ N, где N — номер студента по журналу (мощность резисторов более 1 Вт).

3) Включить источник и установить напряжение U=5В, 9В, 12В, 15В.

4) Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между точками:

А иВ; Ви С; Аи С; Dи Е.

Запишите эти показания в таблицу 1, 2.

Рис. 9. Схема исследования: а) последовательное соединение, б) параллельное соединение

5) Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными.

6) Измерьте с помощью мультиметра (в режиме измерения постоянного тока) токи, текущие через каждое сопротивление. Запишите показания прибора в таблицу 1.

7) Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок.

8) Измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении. Запишите показания прибора в таблицу 2.

9) Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе.

10) Отключить схему.

Таблица 1

Рассчитанные иизмеренные параметры для последовательного соединения резисторов: Аи В; Ви С; Аи С.

№вар.	Установлено		Рассчитано			Измёренные параметры
	R1	R2	А— В	В— С	А— С	I	U	U1	U2
	кОм	кОм	кОм	кОм	кОм	А	В	В	В

Таблица 2

Рассчитанные иизмеренные параметры для параллельного соединения резисторов: Dи Е.

№вар.	Установлено		Рассчитано			Измерённые параметры
	R3	R4	D иЕ			U	I	I1	I2
	кОм	кОм	кОм			В	А	А	А

Содержание отчета

а) название и цель работы;

б) схемы экспериментов и таблицы полученных экспериментальных данных;

в) результаты расчётов:

г) выводы по работе.

Контрольные вопросы

1) Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ.

2) Как по вольтамперной характеристике определить величину сопротивления цепи?

3) Как по показаниям мультиметра можно определить величину сопротивления участка электрической цепи и потребляемая мощность?

4) Нарисуйте схемы последовательное и параллельное соединение двух резисторов.

5) Объясните физические законы соединения резисторов.

Выводы

В работе исследованы свойства и физические законы параллельного и последовательного соединения резисторов бес применения пайки.

При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.

Литература:

1. А. Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
2. Л. Г. Белиовская, Белиовский Н. А. Роботизированные лабораторныее работы по физики, Пропедевтетический курс физика. -М.:ДМК Пресс.2016.-164С.
3. Википедия [Электронный ресурс]. http://ru.wikipedia.org/wiki/Processing.

Основные термины (генерируются автоматически): общее сопротивление, резистор, сопротивление, последовательная цепь, последовательное соединение, соединение резисторов, величина тока, ком, макетная плата, параллельная цепь, параллельное соединение.

Схемные соединения в резисторах — CoderLessons.com

Резистор при подключении в цепи, это соединение может быть последовательным или параллельным. Давайте теперь узнаем, что произойдет с суммарными значениями тока, напряжения и сопротивления, если они будут соединены последовательно, а также при параллельном соединении.

Резисторы в серии

Давайте посмотрим, что происходит, когда несколько последовательно соединенных резисторов. Рассмотрим три резистора с разными значениями, как показано на рисунке ниже.

сопротивление

Общее сопротивление цепи, имеющей последовательные резисторы, равно сумме отдельных сопротивлений. Это означает, что на приведенном выше рисунке три резистора имеют значения 1 кОм, 5 кОм и 9 кОм соответственно.

Общее значение сопротивления резисторной сети составляет —

R=R1 +R2 +R3

Это означает, что 1 + 5 + 9 = 15 кОм — это полное сопротивление.

Где R ₁ — это сопротивление 1- ^го резистора, R ₂ — это сопротивление 2- ^го резистора, а R ₃ — это сопротивление 3- ^го резистора в вышеуказанной сети резисторов.

вольтаж

Общее напряжение, которое появляется в сети последовательных резисторов, является суммой падений напряжения на каждом отдельном сопротивлении. На рисунке выше у нас есть три разных резистора, которые имеют три разных значения падения напряжения на каждой ступени.

Общее напряжение, которое появляется на цепи —

V=V1 +V2 +V3

Это означает, что полное напряжение равно 1v + 5v + 9v = 15v.

Где V ₁ — падение напряжения 1- ^го резистора, V ₂ — падение напряжения 2- ^го резистора, а V ₃ — падение напряжения 3- ^го резистора в вышеуказанной сети резисторов.

Текущий

Общее количество тока, протекающего через набор последовательно включенных резисторов, одинаково во всех точках сети резисторов. Следовательно, ток равен 5А при измерении на входе или в любой точке между резисторами или даже на выходе.

Ток через сеть —

I=I1=I2=I3

Это означает, что ток во всех точках составляет 5А.

Где I ₁ — ток через 1- ^й резистор, I ₂ — ток через 2- ^й резистор, а I ₃ — ток через 3- ^й резистор в вышеупомянутой сети резисторов.

Резисторы параллельно

Давайте посмотрим, что происходит, когда несколько резисторов подключены параллельно. Рассмотрим три резистора с разными значениями, как показано на рисунке ниже.

сопротивление

Общее сопротивление цепи, имеющей параллельные резисторы, рассчитывается иначе, чем метод последовательных резисторных сетей. Здесь обратное (1 / R) значение отдельных сопротивлений складывается с обратной величиной алгебраической суммы, чтобы получить общее значение сопротивления.

Общее значение сопротивления резисторной сети составляет —

 гидроразрыва1R,= гидроразрыва1R1 + гидроразрыва1R2 + гидроразрыва1R3

Где R ₁ — это сопротивление 1- ^го резистора, R ₂ — это сопротивление 2- ^го резистора, а R ₃ — это сопротивление 3- ^го резистора в вышеуказанной сети резисторов.

Например, если рассматриваются значения сопротивления из предыдущего примера, это означает, что R ₁ = ₁ кОм, R ₂ = 5 кОм и R ₃ = 9 кОм. Общее сопротивление параллельной резисторной сети составит —

 гидроразрыва1R,= гидроразрыва11 + гидроразрыва15 + гидроразрыва19

= гидроразрыва45 +9 +545= гидроразрыва5945

R= гидроразрыва4559=0.762K Omega=76,2 Omega

Из метода расчета параллельного сопротивления мы можем вывести простое уравнение для двухрезисторной параллельной сети. Это —

R= гидроразрываR1 разR2R1 +R2 

вольтаж

Общее напряжение, которое появляется в сети параллельных резисторов, совпадает с падением напряжения на каждом отдельном сопротивлении.

Напряжение, которое появляется на цепи —

V=V1=V2=V3

Где V ₁ — падение напряжения 1- ^го резистора, V ₂ — падение напряжения 2- ^го резистора, а V ₃ — падение напряжения 3- ^го резистора в вышеуказанной сети резисторов. Следовательно, напряжение одинаково во всех точках параллельной сети резисторов.

Текущий

Общее количество тока, поступающего в параллельную резистивную сеть, представляет собой сумму всех отдельных токов, протекающих во всех параллельных ветвях. Значение сопротивления каждой ветви определяет значение тока, протекающего через нее. Общий ток через сеть

I=I1 +I2 +I3

Где I ₁ — ток через 1- ^й резистор, I ₂ — ток через 2- ^й резистор, а I ₃ — ток через 3- ^й резистор в вышеупомянутой сети резисторов. Следовательно, сумма отдельных токов в разных ветвях позволяет получить суммарный ток в параллельной резистивной сети.

Резистор особенно используется в качестве нагрузки на выходе многих цепей. Если резистивная нагрузка вообще не используется, перед нагрузкой устанавливается резистор. Резистор обычно является основным компонентом в любой цепи.

Параллельное включение резисторов. Как рассчитать сложные схемы соединения резисторов. Способы соединения проводников

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Резисторы представляют собой пассивные электронные компоненты, основным параметром которых является сопротивление, также называемое электрическим сопротивлением, отсюда и другой называемый резистор. Сопротивление — это параметр, полностью не зависящий от напряжения.

Согласно «старой школе» резисторы были отмечены «сломанной» ветвью схемы, символизирующей избыток на проводнике. В настоящее время представление идеальных резисторов в схемах замещения использует тот же символ, что и в случае идеального однооборотного элемента, описываемого импедансом. Это связано с тем, что резистор является самым элементарным электронным компонентом, а определение импеданса идеального резистора на основе резистора сводится к определению сопротивления резистора, которое рассматривается в конце раздела под названием «Импеданс».

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

Согласно обобщенному закону Ома, сопротивление определяется. Если вы измеряете напряжение и ток, протекающие в резистивный контур, черный ящик, тогда закон Ома может быть заменен одним резистором. Внутренняя структура такого черного ящика не должна играть абсолютно никакой роли, он может содержать любое количество резисторов, свободно взаимосвязанных — замена их одним резистором всегда возможна.

Резисторы-резисторы, соединенные последовательно в данной ветви цепи, равны сумме их сопротивлений. При последовательном подключении резисторов через ветвь, согласно первому закону Кирхгофа, течет ток, т.е. каждый из параллельных подключенных резисторов будет равномерно течь для каждого тока.

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

После преобразования мы получаем. Разделите две стороны током, который мы получаем. Для двух резисторов этот шаблон имеет вид. При параллельном соединении резисторов напряжение на них равно, равно. Согласно закону Кирхгофа сумма течений, протекающих из «верхнего» узла, равна влиянию, которое выражает зависимость. Разделите с обеих сторон напряжение.

Резисторы, отмеченные цветовым кодом. Резисторы чаще всего встречаются в виде дискретных элементов, продаваемых отдельно или в «ленте» с бумажной связью. Резисторы имеют форму небольшого корпуса, напоминающего поперечное сечение принципиальной схемы замены, из которой выводятся два провода, чтобы они могли быть включены в схему.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Резисторы с различными сопротивлениями доступны. Из-за их часто небольших размеров и цилиндрических характеристик, препятствующих описательному процессу, был принят общий стандарт для описания резисторов, чтобы избежать ошибок внедрения. Маркировка выполняется с помощью системы цветового кодирования, показанной в таблице ниже. Коды обычно считываются с самых экстремальных полос — чаще всего первые две полосы определяют сопротивление, третий множитель и следующий допуск, а иногда и температурный коэффициент сопротивления.

Дополнительная информация приведена ниже таблицы. Полосы обычно три, четыре или шесть, если есть 3 полосы — тогда все три являются сопротивлением, а допуск равен ± 20%, если есть 4 полосы — тогда первые три означают сопротивление, а четвертый — толерантность, если их шесть, значит, мы имеем работа с прецизионным резистором, а первые три обозначают номера сопротивлений, четвертый — множитель, пятый — допуск, шестой — коэффициент сопротивления температуры. Публикуется для обеспечения согласованности материала и самого быстрого доступа.

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Информация о сопротивлении резистора кодируется в цвете. В Интернете вы можете найти несколько калькуляторов, которые позволяют конвертировать из слайдов в сленг и наоборот. Ниже графика показаны 4 наиболее популярных значения сопротивления: 100 Ом, 220 Ом, 4, 7 кОм, 10 кОм. Золотая полоса справа указывает на сопротивление резистора ± 5%.

Другие любители — 10% серебра и 2% красные. Цветовые коды наиболее часто используемых значений резисторов. Обратите внимание, что, комбинируя резисторы, мы можем получить другие отсутствующие значения. Резистивное сопротивление резисторов, соединенных параллельно, равно инверсии обратной суммы единичных сопротивлений. Диоды не должны соединяться параллельно друг с другом — в этом случае каждый должен иметь свой собственный резистор. Диоды можно подключать последовательно и параллельно-параллельно, но вам нужно выбрать правильные резисторы.

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:

Стол со стандартными значениями должен быть достаточным. Таблица: Значения резисторов для отдельных светодиодов. Ток, протекающий через диод: 20 мА. Подробные способы расчета и объединения можно найти в Интернете. Хотя энергосберегающие технологии в электронике становятся все более популярными, маловероятно, что механические охлаждающие устройства когда-либо будут полностью оставлены. В настоящее время, помимо жидкостных систем охлаждения, вентиляторы чаще всего используются в корпусах. В статье представлены основные способы их классификации, оценки производительности в отношении требований конкретного приложения и элементов дизайна, на которые вы должны обратить внимание.

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Центробежные вентиляторы разделены на величину угла выхода лопастей для вентиляторов с изогнутыми передними и задними лезвиями. Вентиляторы в основном разделены в зависимости от направления потока воздушного потока относительно оси вентилятора, выделяя в этом отношении три группы: осевые, радиальные и диагональные. При охлаждении электронных устройств используются вентиляторы первого типа, в которых поток воздуха протекает в осевом направлении.

В применениях этого типа вентилятор, характерная особенность которого представляет собой лопасти ротора в виде пропеллера, чаще всего размещается в корпусе вместе с электродвигателем, встроенным в ступицу ротора. Такая компактная конструкция с монтажными отверстиями на фланце вентилятора позволяет устанавливать даже в ограниченных пространственных условиях. Однако проблема с компактным дизайном — это распорки, соединяющие корпус двигателя с фланцем.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Они обеспечивают стабильность, но в то же время препятствуют потоку воздуха. Во время работы лопасти ротора подметают стойки, вызывая скачки давления в их окрестностях. Это один из основных источников шума, создаваемых осевыми вентиляторами. Поэтому на этапе проектирования этого устройства форму и количество распорок тщательно анализируют на предмет их влияния на поток воздуха через вентилятор.

Устройство в одном корпусе вентилятора. Наиболее распространенными являются осевые вентиляторы со спирально изогнутыми распорками. На практике соблюдаются некоторые основные правила относительно их установки. Один из них касается разрыва между лезвиями и стойками — чем они крупнее, тем меньше шума. Значительно большое количество лезвий и прокладок. Чем меньше стойки, тем меньше шума, особенно при высоких скоростях вращения ротора.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

В свою очередь, чем больше лезвий, тем больше поток воздуха, но в то же время лезвия чаще сметают стойки, что создает больше шума. Также важно, чтобы стойки располагались на выходной стороне воздуха от вентилятора, что оправдано характеристиками потока. Воздушный поток у входа вентилятора является ламинарным потоком, а на выходе вентилятора поток изменяет свой характер на турбулентный.

Когда на пути ламинарного потока возникает препятствие, слышится определенная частота, слышится как свисток. С другой стороны, когда турбулентный поток сталкивается с препятствием, появляются звуки разных частот, что делает шум менее раздражающим для людей.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

Центробежные и диагональные вентиляторы

В дополнение к осевым вентиляторам при охлаждении электронных компонентов используются, хотя и реже, радиальные вентиляторы. В этом типе устройства вход воздуха находится в осевом направлении, а выход в направлении, перпендикулярном оси вентилятора. Их характерной особенностью является ротор, напоминающий водяное колесо. Наиболее часто встречается структура, в которой двигатель находится в области всасывания вентилятора. В определенной степени он ограничивает поток воздуха, но в то же время он допускает компактный дизайн.

2. Делитель токов.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.

Третий тип — вентиляторы с смешанным потоком. диагональ, которая, хотя с точки зрения внешнего вида, более похожа на осевые вентиляторы, благодаря принципу работы представляет собой промежуточную конструкцию между осевыми и радиальными вентиляторами: входное отверстие для воздуха находится в осевом направлении на выходе, но выход по диагонали. В результате вентиляторы смешанного потока создают более высокое давление при тех же размерах и рабочих скоростях, что и осевые вентиляторы, а под этим углом образуются радиальные вентиляторы.

Схема замены устройства на рис. Резисторы соответствуют сопротивлению потока отдельных компонентов устройства. Производительность вентилятора описывает его характеристическую кривую, которая представляет объемный расход перекачиваемого газа, в зависимости от увеличения давления, создаваемого вентилятором. Основываясь на этой характеристике, можно сравнивать разные типы вентиляторов, но на практике ее чаще всего используют для оценки производительности вентилятора в соответствии с требованиями конкретного приложения.

Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

В этом случае характеристики вентилятора анализируются вместе с кривой, которая показывает падение давления в охлаждаемом устройстве в зависимости от количества проходящего через него воздуха. Чтобы определить характеристики устройства, сначала определите текущее сопротивление потока. Точные расчеты сопротивления потоку обычно используют специализированное программное обеспечение, которое использует сложные модели и численные методы.

Однако на практике также используются упрощенные методы. Один из них будет рассмотрен на примере устройства, в котором монтируется один вентилятор и вентиляционная решетка. Он состоит из пяти параллельных монтажных плат с компонентами и блоком питания, заключенных в отдельный корпус с отверстиями на передней и задней панелях. На рисунке 3 показана схема замены рассматриваемого устройства. Отдельные компоненты и компоненты корпуса показаны на нем в виде резисторов с определенным сопротивлением потоку.

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Определение характеристик устройства

Характеристики системы вентиляции: охлажденное устройство — вентилятор. Соответствующие формулы используются для определения значений сопротивлений, в которых предполагается, что сопротивление зависит от площади поперечного сечения препятствия, а в случае вентиляционной решетки — от площади поверхности, через которую протекает поток воздуха. Следующий шаг — рассчитать общее сопротивление всей системы.

Для этой цели используются аналоги, применяемые при замене последовательного сопротивления и параллельных электрических сопротивлений. Затем эту характеристику следует разместить на общем графике с характеристиками вентилятора. Тогда в точке пересечения двух кривых определяется точка действия вентилятора. В нем описывается фактическая производительность конкретного вентилятора в этой установке, то есть количество воздуха, которое вентилятор может охлаждать при охлаждении устройства.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Параллельное соединение резисторов, а также последовательное

Вывод формул для определения общего сопротивления. Практические примеры последовательного, параллельного и смешанного соединения резисторов.

Определение эквивалентного сопротивления

При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.

Последовательное соединение[править | править код]

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I = I 1 = I 2 = ⋯ = I n {displaystyle Imathrm {=} I_{1}=I_{2}=cdots =I_{n}} (так как сила тока определяется количеством электронов, проходящих через поперечное сечение проводника, и если в цепи нет узлов, то все электроны в ней будут течь по одному проводнику).

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: U = U 1 + U 2 + ⋯ + U n {displaystyle Umathrm {=} U_{1}+U_{2}+cdots +U_{n}} .

Резисторы[править | править код]

R = R 1 + R 2 + ⋯ + R n {displaystyle R=R_{1}+R_{2}+cdots +R_{n}}

Катушка индуктивности[править | править код]

L = L 1 + L 2 + ⋯ + L n {displaystyle L=L_{1}+L_{2}+cdots +L_{n}}

Электрический конденсатор[править | править код]

1 C = 1 C 1 + 1 C 2 + ⋯ + 1 C n {displaystyle {frac {1}{C}}={frac {1}{C_{1}}}+{frac {1}{C_{2}}}+cdots +{frac {1}{C_{n}}}} .

Мемристоры[править | править код]

M = M 1 + M 2 + ⋯ + M n {displaystyle M=M_{1}+M_{2}+cdots +M_{n}}

Выключатели[править | править код]

Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (См.также Логическая операция И).

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

1. С правого края – правый.
2. С левого края – левый.

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Формула сопротивления

Формула ёмкостного сопротивления выводится следующим образом:

• Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
• Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.

Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление.

Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Последовательное соединение элементов

Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.

Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.

Последовательное включение резисторов

В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:

I = U/R.

Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:

R = U/I.

Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.

Проходящий по цепи ток везде одинаковый:

I = I1= I2= … = In.

Прикладываемое напряжение является суммой напряжений на каждом резисторе:

U = U1 + U2+ … + Un.

Следовательно, рассчитать можно общее:

Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.

Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.

Как по вах определить сопротивление цепи

В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями.

В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения. Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат. Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока. Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 5.1), а полупроводниковые диоды — несимметричные характеристики (рис. 5.2).

Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики (рис. 5.3)

.

Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока.

Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики (рис. 5.4).

.

При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются. Статическое и динамическое сопротивления линейного элемента одинаковы и не зависят от тока или напряжения.

5.2. Графический метод расчета нелинейных цепей постоянного тока

Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения. Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.5). ВАХ 1 и ВАХ 2 приведены на рис. 5.6.

К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2:

(5.1)

По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3).

При параллельном соединении двух нелинейных элементов (рис. 5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3. (аг = ав + аб)

Далее задаваясь произвольным значением напряжения больше и меньше U’, можно построить ВАХ всей цепи (кривая 3). Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I1 и I2 в отдельных ветвях с учетом масштаба тока mI.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Как правильно рассчитать сопротивление

Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где

• U – падение напряжение на конкретном резистивном элементе;
• I – ток, протекающий через него.

При последовательном соединении

Для двух элементов считаем Rобщ = R1+R2.

Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.

При параллельном соединении

Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).

Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле

Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).

Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.

Последовательное соединение сопротивлений в цепи постоянного тока. Последовательное и параллельное соединения проводников

Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)

где R эк = R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи

U = U 1 + U 2 +U 3 (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U 1: U 2: U 3 = R 1: R 2: R 3 (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)

Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :

G эк = G 1 + G 2 +G 3 (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .

Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии

Пример последовательного подключения приемников энергии.

В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления

Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.

Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями

где R – эквивалентное последовательное сопротивление.

Применение последовательного соединения

Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр

Делитель напряжения (слева) и потенциометр (справа).

В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.

Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.

Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже

Пример параллельного соединения приемников энергии.

Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви

Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений

Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.

Смешанное соединение приемников энергии

Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии

Пример смешанного соединения приемников энергии.

В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид

В результате получили цепь из двух последовательных приемников энергии R 12 R 345 эквивалентное сопротивление и ток, протекающий через них, составит

Тогда падение напряжения по участкам составит

Тогда токи, протекающие через каждый приемник энергии, составят

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

Изображение первого закона Кирхгофа.

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением

В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур

Схема, иллюстрирующая второй закон Кирхгофа.

Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид

Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.

Теория это хорошо, но без практического применения это просто слова.

Ток в цепи протекает по проводникам к нагрузке от источника. Чаще всего в качестве таких элементов используют медь. Цепь может иметь несколько электрических приемников. Их сопротивления разнятся. В схеме электроприборов проводники могут иметь параллельное или последовательное соединение. Встречаются также смешанные его типы. Отличие каждого из них следует знать перед выбором структуры электроцепи.

Проводники и элементы цепи

Ток идет через проводники. Он следует от источника к нагрузке. При этом проводник обязан легко высвобождать электроны.

Проводник, имеющий сопротивление, называется резистором. Напряжение этого элемента — это разность потенциалов между концами резистора, которое согласовывается с направлением протекания питания.

Последовательное и параллельное соединение проводников характеризуется одним общим принципом. Ток течет в цепи от плюса (его называют источником) к минусу, где потенциал становится все меньшим, убывает. На электрических схемах сопротивление проводов считается равным нулю, так как оно пренебрежительно мало.

Поэтому, просчитывая последовательное или параллельное соединение, прибегают к идеализации. Это упрощает их изучение. В реальных цепях потенциал постепенно уменьшается при передвижении по проводу и элементам, имеющим параллельное или последовательное соединение.

Последовательное соединение проводников

При наличии последовательного сочетания проводников сопротивления включаются одно за другим. При таком положении сила тока во всех элементах цепи одинакова. Последовательно соединенные проводники создают на участке напряжение, которое равно их сумме на всех элементах.

Заряды не имеют возможности накапливаться в узлах цепи. Это бы привело к изменению напряжения электрического поля и силы тока.

При наличии постоянного напряжения ток будет зависеть от сопротивления цепи. Поэтому при последовательном соединении сопротивление будет меняться из-за перемены одной нагрузки.

Последовательное соединение проводников имеет недостаток. При поломке одного из элементов схемы будет прервана работа всех остальных ее составляющих. Например, как в гирлянде. Если в ней перегорит одна лампочка, все изделие не будет работать.

Если проводники были подсоединены в цепи последовательно, их сопротивление в каждой точке будет одинаковым. Сопротивление в сумме всех элементов схемы будет равняться сумме уменьшения напряжений на участках цепи.

Это может подтвердить опыт. Последовательное соединение сопротивлений подсчитывается при помощи приборов и математической проверки. Например, берутся три постоянных сопротивления известной величины. Их последовательно соединяют и подключают к питанию в 60 В.

После этого подсчитывают предполагаемые показатели приборов, если замкнуть цепь. По закону Ома находится ток в цепи, что позволит определить падение напряжения на всех ее участках. После этого суммируются полученные результаты и получается общая величина снижения сопротивления во внешней цепи. Последовательное соединение сопротивлений можно подтвердить примерно. Если не брать во внимание внутреннее сопротивление, создающееся источником энергии, то падение напряжения будет меньше, чем сумма сопротивлений. По приборам можно убедиться, что равенство приблизительно соблюдается.

Параллельное соединение проводников

При последовательном и параллельном соединении проводников в цепи применяют резисторы. Параллельное соединение проводников представляет собой систему, в которой одни концы всех резисторов сходятся в один общий узел, а другие — в другой узел. В этих местах схемы сходятся более двух проводников.

При таком соединении к элементам прикладывается одинаковое напряжение. Параллельные участки цепи называются ветвями. Они проходят между двумя узлами. Параллельное и последовательное соединение имеют свои свойства.

Если в электросхеме есть ветви, то напряжение на каждой из них будет одинаковым. Оно равняется напряжению на неразветвленном участке. В этом месте сила тока будет рассчитываться как сумма ее в каждой ветви.

Величина, равная сумме показателей, обратных сопротивлениям разветвлений, будет обратна и сопротивлению участка параллельного соединения.

Параллельное соединение сопротивлений

Параллельное и последовательное соединение отличаются расчетом сопротивлений ее элементов. При параллельном соединении ток разветвляется. Это увеличивает проводимость цепи (уменьшает общее сопротивление), которая будет равна сумме проводимости ветвей.

Если несколько резисторов, имеющих одинаковую величину, соединены параллельно, то суммарное сопротивление цепи будет меньше одного резистора во столько раз, сколько их включено в схему.

Последовательное и параллельное соединение проводников имеют ряд особенностей. В параллельном подключении ток обратно пропорционален сопротивлению. Токи в резисторах не зависят друг от друга. Поэтому выключение одного из них не отразится на работе остальных. Поэтому множество электроприборов имеют именно этот тип соединения элементов цепи.

Смешанное

Параллельное и последовательное соединение проводников может комбинироваться в одной и той же схеме. Например, элементы, подключенные между собой параллельно, могут быть соединены последовательно с другим резистором или их группой. Это смешанное соединение. Общее сопротивление цепей вычисляется путем отдельного суммирования значений для параллельно подключенного блока и для последовательного соединения.

Причем сначала вычисляются эквивалентные сопротивления последовательно подключенных элементов, а потом уже рассчитывается общее сопротивление параллельных участков цепи. Последовательное соединение в вычислениях является приоритетнее. Такие типы электросхем довольно часто встречаются в различных приборах и оборудовании.

Ознакомившись с видами соединения элементов цепи, можно понять принцип организации схем различных электрических приборов. Параллельное и последовательное соединение обладают рядом особенностей расчета и функционирования всей системы. Зная их, можно правильно применять каждый из представленных видов для подключения элементов электрических цепей.

Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.

Gif?x15027″ alt=»Общий вид»>

Общий вид

Особенности включения

Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.

Для такого включения типичны следующие особенности:

• Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
• Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.

В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.

Расчёт

Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).

Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:

I= U/R (одного из резисторов).

После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.

Типичные подключения

Пример №1

Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).

Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.

Из неё следует:

16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.

Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.

Пример №2

В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.

Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.

Gif?x15027″ alt=»Пример»>

В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:

1/R = 1/200+1/220+1/470 = 0,0117;

R=1/0,0117 = 85,67Ом.

В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.

Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.

Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.

Расчёт комбинированных схем

Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.

Gif?x15027″ alt=»Смешанная схема»>

Смешанная схема

Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.

Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

\(~I = I_1 = I_2 .\)

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A → 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам Μ и N напряжение U .n R_i .\)

Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

\(~U = U_1 = U_2 .n \frac{1}{R_i} .\)

Если сопротивления всех n параллельно соединенных резисторов одинаковы и равны R 1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .

Сопротивление цепи, состоящей из n одинаковых параллельно соединенных резисторов, в n раз меньше сопротивления каждого из них.

При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 257-259.

Как найти эквивалентное сопротивление цепи формула

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R_экв, и вся схема представляется в виде схемы на рис. 1.3, где R=R_экв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.

Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

,

и по вышеприведенным формулам рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃, т.е. ,

откуда следует, что

.

В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением

.

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

Отсюда следует, что

,

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R. Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно:

.

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно

.

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R₁₂, R₁₃, R₂₄, R₃₄ включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

Рис. 1.12

Рис. 1.13

В мостовой схеме сопротивления R₁₃, R₁₂, R₂₃ и R₂₄, R₃₄, R₂₃ соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R₂₄ R₃₄ R₂₃ звездой R₂ R₃ R₄ (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

; ; .

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

; ; .

После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)

.

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R_экв, и вся схема представляется в виде схемы на рис. 1.3, где R=R_экв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.

Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

,

и по вышеприведенным формулам рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃, т.е. ,

откуда следует, что

.

В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением

.

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

Отсюда следует, что

,

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R. Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно:

.

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно

.

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R₁₂, R₁₃, R₂₄, R₃₄ включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

Рис. 1.12

Рис. 1.13

В мостовой схеме сопротивления R₁₃, R₁₂, R₂₃ и R₂₄, R₃₄, R₂₃ соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R₂₄ R₃₄ R₂₃ звездой R₂ R₃ R₄ (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

; ; .

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

; ; .

После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)

.

Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).

Определение эквивалентного сопротивления

При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.

Последовательное соединение элементов

Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.

Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.

В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:

Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:

Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.

Проходящий по цепи ток везде одинаковый:

Прикладываемое напряжение является суммой напряжений на каждом резисторе:

Следовательно, рассчитать можно общее:

Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.

Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.

Параллельное соединение

Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.

Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:

• общий ток: I = I1 + I2 + … + In;
• общее напряжение: U = U1 = U2 = … = Un;
• Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.

Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.

Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.

Расчёт при смешанном соединении устройств

Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.

Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.

Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.

Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.

Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.

Физические формулы и примеры вычислений

Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:

• параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
• последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.

У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.

Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:

• R1 = 1 Ом;
• R2 = 2 Ом;
• R3 = 3 Ом;
• R4 = 6 Ом;
• R5 = 9 Ом;
• R6 = 18 Ом;
• R7 = 2Ом;
• R8 = 2Ом;
• R9 = 8 Ом;
• R10 = 4 Ом.

Напряжение, поданное на схему:

Требуется рассчитать токи на всех резистивных элементах.

Для расчётов применяется закон Ома:

I = U/R, подставляя вместо R эквивалентное сопротивление.

Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.

Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.

На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:

• АВ – участок, имеющий две параллельных ветви;
• ВС – отрезок, вмещающий в себя последовательное сопряжение;
• CD – отрезок схемы с расположением трёх параллельных цепочек.

Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.

Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.

Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:

• Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
• Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
• Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.

Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.

Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:

• Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
• Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
• 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.

В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.

Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:

Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.

Далее, используя закон Ома, находят ток в последнем последовательном участке:

I = U/ Rэкв. = 24/56,83 = 0,42 А.

Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:

• UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
• UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
• UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.

Следующим шагом станет определение токов на параллельных отрезках AB и CD:

• I1 = UAB/R1 = 0,35/1 = 0,35 А;
• I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
• I3 = UCD/R6 = 0,17/18 = 0,009 А;
• I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
• I7 = UCD/R10 = 0,17/4 = 0,04 А.

Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.

U9 = R9*I6 = 8*0,02 = 0,16 В.

Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.

U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.

После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:

• I4 = U7,8/R7 = 1/2 = 0,5 A;
• I5 = U7,8/R8 = 1/2 = 0,5 A.

Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.

Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.

Видео

Цепи резисторов серии

и параллельные

Электронные компоненты подключаются разными способами. Две простейшие формы подключения — последовательное и параллельное. соединения.

Если компоненты соединены последовательно в цепи, то цепь называется последовательной. Если резисторы соединены последовательно в цепи, тогда цепь говорят, что это цепь последовательного резистора.

Если компоненты соединены в цепи параллельно, то цепь называется параллельной. Если резисторы соединены параллельно в цепи, тогда цепь называется параллельной схемой резистора.

Резистор серии

цепь

А Схема последовательного резистора — это электронная схема, в которой все резисторы подключаются друг за другом по одному и тому же пути так что одинаковый ток течет через все и каждый резистор.

полное сопротивление такой схемы получается простым суммируя значения сопротивлений отдельных резисторов.

R _T = ₁ + ₂ + ₃ + ₄ рандов …… ..и т. Д.

Для Например, если пять резисторов соединены последовательно. Тогда полное сопротивление цепи равно:

R _T = ₁ + ₂ + ₃ + ₄ рандов + Р ₅

Все ток, протекающий через первый резистор, не имеет другого путь идти.Следовательно, он также должен пройти через второй резистор, третий резистор, четвертый резистор и т. д.

Пример:

А Схема последовательного резистора показана на рисунке ниже. Этот схема состоит из пяти резисторов, которые включены в последовательный и источник постоянного напряжения.

Если Значения пяти резисторов равны: R ₁ = 4 Ом, R ₂ = 4 Ом, R ₃ = 2 Ом, R ₄ = 2 Ом, R ₅ = 3 Ом и батарея постоянного тока = 15 В, тогда

Общее сопротивление составляет R _T = ₁ + ₂ + ₃ + ₄ рандов + R ₅ = 4 + 4 + 2 + 2 + 3 = 15 Ом.

Вспомните формулу закона Ома, V = I R

Зная любые две переменные в выше уравнения, мы можем легко найти оставшиеся неизвестные Переменная.

Нам известно значение полного сопротивления, т.е. R _T = 15 Ом и значение напряжения I.e. V = 15 В

Теперь нужно найти оставшееся неизвестное текущее значение I.

Текущий текущий через каждый резистор будет 1 А.

Напряжение на каждый резистор в последовательной цепи отличается. Если все резисторы в последовательной цепи имеют одинаковое значение сопротивления тогда напряжение через каждый резистор такой же. С другой стороны, если каждый резистор имеет другое значение сопротивления, то напряжение на каждом резисторе различается.

Напряжение на резистор (R ₁ ) составляет В ₁ = I × R ₁ = 1 × 4 = 4 В

Напряжение на резистор (R ₂ ) составляет В ₂ = I × R ₂ = 1 × 4 = 4 В

Напряжение на резистор (R ₃ ) составляет В ₃ = I × R ₃ = 1 × 2 = 2 В

Напряжение на резистор (R ₄ ) составляет В ₄ = I × R ₄ = 1 × 2 = 2 В

Напряжение на резистор (R ₅ ) составляет В ₅ = I × R ₅ = 1 × 3 = 3 В

Суммарное напряжение в последовательная цепь равна сумме всех отдельных напряжения в сумме

И.е. В _Т = В ₁ + V ₂ + V ₃ + V ₄ + ………. + V _N

В нашей схеме общее напряжение равно сумме разностей потенциалов по R _1, , _{R 2 , R 3 , 4 и 5 .}

Т.е. В _Т = В ₁ + В ₂ + В ₃ + В ₄ + В ₅ = 4 + 4 + 2 + 2 + 3 = 15 В.

Параллельный схема резистора

А Схема параллельного резистора — это электронная схема, в которой все резисторы соединены бок о бок в разных пути, чтобы один и тот же ток не проходил через каждый резистор. Параллельная схема показывает несколько путей к электрический ток течет.

ток в параллельной цепи прерывается, с некоторым током течет вдоль каждой параллельной ветви и повторно комбинируется, когда ветви снова встречаются.Следовательно, электрический ток через каждый резистор будет другим. Однако напряжение на каждый резистор такой же.

полное сопротивление параллельной цепи резистора получается как сложение обратных величин (1 / R) значений сопротивления отдельные резисторы, а затем взяв обратную величину общее.

Для Например, если три резистора подключены параллельно.потом полное сопротивление цепи

Пример:

А Схема параллельного резистора показана на рисунке ниже. Этот схема состоит из трех резисторов, которые включены в параллельный и источник постоянного напряжения.

Если Значения трех резисторов равны: R ₁ = 8 Ом, R ₂ = 8 Ом, R ₃ = 4 Ом и батарея постоянного тока = 14 В, затем

общее сопротивление

Суммарный ток по контуру —

Как напряжение на каждом резисторе одинаково параллельно схема, мы можем использовать Ом закон чтобы найти ток отдельной ветви следующим образом.

ток через резистор (R ₁ ) _{is I 1 = V / R 1 = 14/8 = 1,75 А}

ток через резистор (R ₂ ) _{is I 2 = V / R 2 = 14/8 = 1,75 А}

ток через резистор (R ₃ ) _{is I 3 = V / R 3 = 14/4 = 3.5 А}

Тогда общая ток равен сумме токов отдельных ветвей

Т.е. Я _Т = Я ₁ + I ₂ + I ₃ = 1,75 + 1,75 + 3,5 = 7 А

Характеристики параллельной цепи

Обновлено 28 декабря 2020 г.

Автор: S.Hussain Ather

В электрических цепях элементы цепи могут быть расположены последовательно или параллельно. В последовательных цепях элементы соединяются с помощью одной и той же ветви, которая пропускает электрический ток через каждую из них один за другим. В параллельных цепях элементы имеют свои отдельные ответвления. В этих цепях ток может проходить по разным путям.

Поскольку ток может проходить по разным путям в параллельной цепи, ток не является постоянным во всей параллельной цепи.Вместо этого для ветвей, которые соединены параллельно друг с другом, падение напряжения или потенциала на каждой ветви является постоянным. Это связано с тем, что ток распределяется по каждой ветви в количестве, обратно пропорциональном сопротивлению каждой ветви. Это приводит к тому, что ток становится наибольшим там, где сопротивление наименьшее, и наоборот.

Эти качества позволяют параллельным цепям пропускать заряд по двум или более путям, что делает его стандартным кандидатом в домах и электрических устройствах через стабильную и эффективную систему питания.Он позволяет электричеству течь через другие части цепи, когда какая-либо часть повреждена или сломана, и они могут распределять мощность равномерно по разным зданиям. Эти характеристики можно продемонстрировать с помощью диаграммы и примера параллельной цепи.

Схема параллельной цепи

••• Syed Hussain Ather

На схеме параллельной цепи вы можете определить поток электрического тока, создав потоки электрического тока от положительного конца батареи к отрицательному.Положительный конец обозначен плюсом на источнике напряжения, а отрицательный -.

По мере прохождения тока по ветвям параллельной цепи помните, что весь ток, входящий в один узел или точку в цепи, должен равняться всему току, выходящему или выходящему из этой точки. Также имейте в виду, что падение напряжения вокруг любого замкнутого контура в цепи должно равняться нулю. Эти два утверждения являются законами цепей Кирхгофа .

Характеристики параллельной цепи

В параллельных цепях используются ответвления, которые позволяют току проходить по разным маршрутам через цепь.Ток проходит от положительного конца батареи или источника напряжения к отрицательному. Напряжение остается постоянным по всей цепи, в то время как ток изменяется в зависимости от сопротивления каждой ветви.

Примеры параллельных цепей

Чтобы найти полное сопротивление резисторов, установленных параллельно друг другу, используйте формулу

\ frac {1} {R_ {total}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + … + \ frac {1} {R_n}

, в котором сопротивление каждого резистора суммируется в правой части уравнения.На приведенной выше диаграмме общее сопротивление в Ом (Ом) можно рассчитать следующим образом:

1. 1 / R _всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
2. 1 / R _всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
3. 1 / R _всего = 14/30 Ом
   
4. R _всего = 15/7 Ом или около 2,14 Ом

Обратите внимание, что вы можете «перевернуть» обе стороны уравнения с шага 3 на шаг 4 только тогда, когда есть только один член с обеих сторон уравнения (в данном случае 1 / R _всего слева и 14/30 Ом справа).

После того, как вы рассчитали сопротивление, ток и напряжение, можно рассчитать по закону Ома V = I / R , в котором V — напряжение, измеренное в вольтах, I — ток, измеренный в амперах. , а R — сопротивление в Ом. В параллельных цепях сумма токов, протекающих по каждому пути, является полным током от источника. Ток на каждом резисторе в цепи можно рассчитать, умножив напряжение на сопротивление резистора.Напряжение остается постоянным по всей цепи, поэтому напряжение является напряжением батареи или источника напряжения.

Параллельная и последовательная цепь

••• Syed Hussain Ather

В последовательных цепях ток постоянен на всем протяжении, падение напряжения зависит от сопротивления каждого резистора, а общее сопротивление складывается из каждого отдельного резистора. В параллельных цепях напряжение постоянно, ток зависит от каждого резистора, а величина, обратная величине общего сопротивления, является суммой величин, обратных величине каждого отдельного резистора.

Конденсаторы и катушки индуктивности могут использоваться для изменения заряда в последовательной и параллельной цепях с течением времени. В последовательной цепи общая емкость , цепи (заданная переменной C ), потенциал конденсатора накапливать заряд с течением времени, является обратной суммой обратных величин каждой отдельной емкости, и общая индуктивность ( I ), мощность индукторов, выделяющих заряд с течением времени, является суммой каждой индуктивности. Напротив, в параллельной цепи общая емкость является суммой каждого отдельного конденсатора, а величина, обратная величине полной индуктивности, является суммой обратных величин каждой индивидуальной индуктивности.

Последовательные и параллельные цепи также имеют разные функции. В последовательной цепи, если одна часть сломана, ток вообще не будет течь по цепи. В параллельной цепи открытие отдельной ветви останавливает только ток в этой ветви. Остальные ветви будут продолжать работать, потому что у тока есть несколько путей, которые он может пройти по цепи.

Последовательно-параллельная цепь

••• Syed Hussain Ather

Цепи, у которых есть оба разветвленных элемента, которые также соединены таким образом, что ток течет в одном направлении между этими ветвями, как последовательные, так и параллельные.В этих случаях вы можете применять правила как для последовательного, так и для параллельного подключения, в зависимости от схемы. В приведенном выше примере R1 и R2 параллельны друг другу, чтобы сформировать R5 , а также R3 и R4 , чтобы сформировать R6 . Их можно суммировать параллельно следующим образом:

1. 1 / R5 = 1/1 Ом + 1/5 Ом
2. 1 / R5 = 5/5 Ом + 1/5 Ом
3. 1 / R5 = 6/5 Ом
   
4. R5 = 5/6 Ом или около 0,83 Ом

1. 1 / R6 = 1/7 Ом + 1/2 Ом
2. 1 / R6 = 2/14 Ом + 7/14 Ом
3. 1 / R6 = 9/14 Ом
   
4. R6 = 14/9 Ом или около 1.56 Ом

••• Syed Hussain Ather

Схема может быть упрощена для создания схемы, показанной непосредственно выше, с R5 и R6 . Эти два резистора могут быть добавлены просто, как если бы цепь была последовательной.

R_ {total} = 5/6 \ Omega + 14/9 \ Omega = 2.38 \ Omega

При напряжении 20 В в качестве напряжения закон Ома определяет, что общий ток равен В / R , или 20 В / (43/18 Ом) = 360/43 А или около 8.37 A. Используя этот общий ток, вы также можете определить падение напряжения на R5 и R6, используя закон Ома ( В = I / R ).

V_5 = \ frac {360} {43} \ times 5/6 = 6.98 \ text {V}

V_5 = \ frac {360} {43} \ times 14/9 = 13.02 \ text {V}

Наконец, эти падения напряжения для R5 и R6 можно разделить обратно на исходные параллельные цепи для расчета тока R1 и R2 для R5 и R2 и R3 для R6 с использованием закона Ома.

I1 = (1800/258 В) / 1 Ом = 1800/258 A или около т 6,98 А.

I2 = (1800/258 В) /5 Ом = 1500/43 А или около т 34,88 А.

I3 = ( 680/129 В ) / 7 Ом = 4760/129 A или около 36,90 A .

I3 = ( 680/129 V ) / 2 Ом = 1360/129 A или около 10.54 А.

Последовательные и параллельные резисторы

Введение

Цепи постоянного тока (DC) характеризуются величинами тока, напряжения и сопротивления. Ток — это скорость потока заряда. Единица СИ — ампер (А). Условно направление тока — это направление потока заряда, хотя в металлических проводниках ток возникает из-за потока отрицательного заряда (электронов) в противоположном направлении. Из-за сохранения заряда ток одинаков во всех точках однопетлевой цепи.В точке ветвления в цепи, где проводящий путь разделяется на два или более, общий ток в точке ветвления равен полному току из этой точки. Обычно ток течет от положительной клеммы батареи или источника питания к отрицательной клемме. Для поддержания тока в цепи должен быть полностью проводящий путь. Напряжение — это мера разности электрических потенциалов между двумя точками в цепи. Единица СИ — вольт (В). Поскольку электрическая сила является консервативной, сумма напряжений увеличивается и уменьшается вокруг любого замкнутого контура, она равна нулю.Сопротивление — это свойство элемента схемы (проводника) препятствовать прохождению тока. Сопротивление определяется где В, — напряжение на элементе схемы, а I — ток, протекающий через него. Если R постоянный, одинаковый для всех V , то элемент схемы подчиняется закону Ома. Единицей измерения сопротивления в системе СИ является ом (Ом). Сопротивление резистивного элемента цепи изменяется в зависимости от температуры. Два резистора R ₁ и R ₂ соединены последовательно, если весь ток, который проходит через R ₁ , также проходит через R ₂ .Следовательно, для двух последовательно соединенных резисторов ток с I ₁ по R ₁ такой же, как ток с I ₂ по R ₂ , и этот ток такой же, как у ток, I , который входит в последовательную сеть:

I = I ₁ = I ₂ .

Общее напряжение В в последовательной сети представляет собой сумму напряжений В ₁ и В ₂ на каждом резисторе.То есть

V = V ₁ + V ₂ .

Эквивалентное сопротивление, R _с , R ₁ и R ₂ последовательно определяется выражением Два резистора R ₁ и R ₂ соединены параллельно, если напряжения В, ₁ и В ₂ на каждом из них одинаковы и равны напряжению, В , через параллельную сеть.То есть

V = V ₁ = V ₂ .

Токи I ₁ и I ₂ через каждый из резисторов складываются, чтобы получить общий ток, I , текущий в сеть и из нее:

I = I ₁ + I ₂ .

Эквивалентное сопротивление R _p из R ₁ и R ₂ параллельно определяется выражением Это также можно записать как Амперметры используются для измерения тока.Амперметр подключается последовательно к цепи, так что весь измеряемый ток течет через амперметр. Следовательно, амперметры должны иметь очень маленькое сопротивление, чтобы не изменять ток в цепи. Вольтметры используются для измерения напряжений. Вольтметр подключается параллельно в двух точках, между которыми должна быть измерена разность потенциалов. Следовательно, вольтметр должен иметь большое сопротивление, чтобы через него проходил очень небольшой ток.

Цель

В этой лаборатории мы будем измерять и анализировать токи и напряжения для цепей, содержащих один резистор, а также для двух последовательно включенных резисторов и двух параллельно.

Аппарат

• Источник питания постоянного тока 0-40 вольт
• Лампочка на 12 вольт и розетка
• Резисторы 150 и 700 Ом
• Цифровой мультиметр

Процедура

Распечатайте лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.

Измерение напряжения

1

Блок питания является источником разности потенциалов (напряжения).Найдите источник питания постоянного тока за столом. Нажмите кнопку POWER ON / OFF в положение ON. Затем нажмите кнопку RANGE в положение IN (0,85 A). Это устанавливает источник питания в диапазоне 0-35 В / 0-0,85 А. Поверните ручку регулировки напряжения и тока ADJUST против часовой стрелки. Затем установите максимальный выходной ток для этого эксперимента, нажав кнопку CC Set и, удерживая ее, поверните ручку регулировки тока ADJUST по часовой стрелке до тех пор, пока на дисплее AMPS не появится 0.30 A. Отпустите кнопку CC Set . Не перемещайте ручку текущей настройки ( CC Set ) в любой момент во время эксперимента.

2

Мультиметр — это измерительное устройство, которое используется для измерения разности напряжений, электрических токов и электрических сопротивлений. Он также может измерять другие электрические свойства. См. Рис. 1. В верхней части измерителя находится ЖК-дисплей (жидкокристаллический дисплей), в середине — переключатель функций / диапазона (диск), а внизу — четыре входных разъема.

Примечание. Измеритель особенно чувствителен (и склонен к перегоранию предохранителя) при использовании входного разъема 200 мА (см. I в обозначении на Рисунке 1).

Ключ для рисунка 1:

• А

  3-1 / 2-разрядный ЖК-дисплей с сигнализаторами.

• В

  Кнопка ВКЛ / ВЫКЛ: включает и выключает питание измерителя.

• С

  Кнопка HI / LO: выбирает высокий или низкий уровень запуска для измерения частоты.

• D

  Кнопка MAX: выбирает функцию удержания максимального показания.

• E

  Кнопка DC / AC: выбирает напряжение постоянного или переменного тока.

• Ф

  Переключатель функции / диапазона: выбирает желаемую функцию и диапазон.

• G

  Входной разъем V Ω: входной разъем для напряжения, сопротивления, проверки диодов, целостности цепи, частоты и логики.

• H

  Входной разъем COM: входной разъем заземления.

• Я

  Входной разъем 200 мА: входной разъем для тока до 200 мА, L _x (индуктивность), C _x (емкость).

• Дж

  Входной разъем на 10 А: входной разъем для тока до 10 А.

Для измерения заданного количества циферблат должен находиться в соответствующем положении и должны использоваться соответствующие два входных разъема.Таким образом, при повороте шкалы для перехода от одного типа измерения к другому (например, от разности напряжений к электрическому току) вам, возможно, также придется изменить входные разъемы. При перегрузке предохранитель может перегореть.

Осторожно:
Для защиты счетчик гудит при перегрузке; если он гудит, немедленно отсоедините провода счетчика!

Чтобы защитить измеритель от перегрузки при измерении неизвестного напряжения или тока, сначала необходимо установить измеритель на максимальную шкалу для этой функции.Если показания недостаточно велики, чтобы дать по крайней мере три значащих цифры, шкалу следует переключить (если возможно) на такую, которая позволяет проводить точное измерение.

3

Чтобы включить мультиметр, нажимайте верхнюю левую кнопку на измерителе, пока на его циферблате не появится дисплей. Чтобы настроить мультиметр на измерение постоянного напряжения, В, , переключите верхнюю правую кнопку на постоянный ток. Убедитесь, что на дисплее глюкометра отображается постоянный ток. Поверните переключатель функций / диапазонов в положение напряжения (В) и установите значение 20.Теперь измеритель настроен на считывание напряжений до 20 вольт постоянного тока. Подключите банан к банановым выводам к общему разъему (COM) и к разъему напряжения (V).

4

Подключите выводы мультиметра к клеммам + и — источника питания. См. Рисунок 2. На блоке питания поверните ручку регулировки напряжения ADJUST по часовой стрелке, пока на дисплее вольт не отобразится 5,0 вольт. Сравните показания напряжения на мультиметре и на измерителе блока питания. Эти два показания могут не совпадать.Ожидается, что мультиметр будет точнее.

Ток и напряжение для одиночного резистора

1

Уменьшите напряжение блока питания (против часовой стрелки) до нуля вольт. Подключите блок питания к резистору на печатной плате с маркировкой 700 Ом. (Не перенастраивайте и не изменяйте настройку тока на источнике питания.) Мы будем использовать мультиметр для измерения постоянного тока через резистор 700 Ом в зависимости от приложенного напряжения. Для этого мы должны соединить мультиметр серии с резистором, чтобы одинаковый ток проходил через оба. Так как предохранитель легко перегорит, когда мультиметр настроен на текущую настройку, внимательно следуйте инструкциям. Установите шкалу мультиметра на шкалу тока 20 мА и подключите банановые штекеры к гнездам COM и мА на измерителе.

Осторожно:
Не повышайте напряжение на блоке питания, пока ТА не проверит вашу цепь.

2

После того, как ваш ТА даст добро, установите источник питания на 1 В и запишите в Таблицу 1 ток через резистор, как показано на мультиметре.Повторите то же самое с источником питания, установленным на 2, 3, 4 и 5 вольт.

3

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Инструкции по построению графиков в Excel см. В приложении к интерактивному руководству лаборатории. Если вы получите ожидаемые результаты, данные будут располагаться близко к прямой линии, проходящей через начало координат. Используйте Excel, чтобы найти наклон прямой линии, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.

4

Используйте закон Ома и наклон графика, чтобы рассчитать сопротивление резистора R в единицах Ом (Ом). Запишите свой результат.

Ток и напряжение для лампочки

1

УСТАНОВИТЕ НАПРЯЖЕНИЕ ПИТАНИЯ НА НУЛЬ, но не выключайте питание. Не изменяйте настройку тока на источнике питания ( CC Set ). Мы будем использовать мультиметр для измерения постоянного тока через лампочку в зависимости от приложенного напряжения.Для этого мы должны соединить мультиметр серии с лампочкой, чтобы через оба проходил одинаковый ток. Так как предохранитель легко перегорит, когда мультиметр настроен на текущую настройку, внимательно следуйте инструкциям.

2

Установите шкалу мультиметра на шкалу постоянного тока 10 А. Используйте входные гнезда COM и 10 A. Подключите схему, как показано на рисунке 3.

Осторожно:
Не повышайте напряжение на блоке питания, пока ТА не проверит вашу цепь.

3

После того, как ваш ТА даст добро, установите напряжение источника питания на 2 вольта. В таблице 2 запишите текущее показание мультиметра. Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.

4

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Ожидается, что ваши данные не будут приближаться к прямой. Определите и вычислите R для каждого набора значений V и I в таблице 2 и запишите в третий столбец таблицы 2.Увеличивается ли R , уменьшается или остается таким же, как ток I через лампочку увеличивается?

Два последовательно подключенных резистора

1

Подключите на печатной плате два резистора с маркировкой 150 Ом и 700 Ом, как показано на рисунке 4. Говорят, что они подключены последовательно, потому что весь ток, проходящий через один, также проходит через другой. Убедитесь, что напряжение источника питания установлено на ноль. Подключите источник питания к комбинации последовательных резисторов, как показано на рисунке 4.Установите блок питания на 5 вольт. Установите шкалу мультиметра на диапазон 20 В и используйте гнезда COM и V. С помощью мультиметра измерьте и запишите разности потенциалов (напряжение) В ₁₅₀ и В ₇₀₀ на каждом резисторе и напряжение В на комбинации из двух резисторов.

2

Когда вы закончите эти измерения, установите напряжение источника питания на ноль и отключите мультиметр от цепи.Что из следующего лучше отражает ваши результаты?

• •

  В = В ₁₅₀ + В ₇₀₀

• •

  В = В ₁₅₀ = В ₇₀₀

3

Когда напряжение источника питания установлено на ноль, подключите мультиметр последовательно с резисторами, как показано на рисунке 5. Установите мультиметр на диапазон постоянного тока 200 мА и подключите выводы мультиметра к правильным гнездам.

Осторожно:
Перед тем, как продолжить, попросите инструктора лаборатории проверить правильность настройки: предохранитель может перегореть, если измеритель не подключен к нужным точкам в цепи.

Получив добро от ТА, включите источник питания и установите его на 5 вольт. Измерьте ток в проводе между двумя резисторами, проводе между резистором 700 Ом и источником питания и проводе между резистором 150 Ом и источником питания.Убедитесь, что эти три тока равны.

4

Продолжая схему, показанную на рисунке 5, установите напряжение источника питания на 2 вольта. В таблице 3 запишите текущие показания мультиметра. Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.

5

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Используйте Excel, чтобы найти наклон прямой линии, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.

6

Используйте закон Ома и наклон графика, чтобы рассчитать эквивалентное сопротивление R _с двух последовательно соединенных резисторов в единицах Ом (Ом). Запишите свой результат.

Два параллельных резистора

1

Подключите на печатной плате два резистора с маркировкой 150 Ом и 700 Ом, как показано на Рисунке 6a. Они считаются параллельными, поскольку напряжение на каждом резисторе равно напряжению источника питания, а резисторы обеспечивают параллельные пути для прохождения тока.

2

Убедитесь, что напряжение источника питания установлено на ноль. Подключите источник питания к комбинации параллельных резисторов, как показано на рисунке 6b. Установите блок питания на 5 вольт. С помощью мультиметра измерьте и запишите токи I ₁₅₀ и I ₇₀₀ , протекающие через каждый резистор, и общий ток, I , протекающий через источник питания.

3

Когда вы закончите эти измерения, установите напряжение источника питания на ноль и отключите мультиметр от цепи.

4

Что из следующего лучше отражает ваши результаты?

• •

  Я = Я ₁₅₀ + Я ₇₀₀

• •

  Я = Я ₁₅₀ = Я ₇₀₀

5

Продолжите параллельную сеть резисторов. Когда напряжение источника питания установлено на ноль, подключите мультиметр для измерения полного тока, I , протекающего через источник питания.Установите мультиметр на диапазон постоянного тока 200 мА.

Осторожно:
Перед тем, как продолжить, попросите инструктора лаборатории проверить правильность настройки: предохранитель может перегореть, если измеритель не подключен к нужным точкам в цепи.

Получив добро от ТА, включите источник питания и установите его на 2 вольта.

6

В таблице 4 запишите текущее показание мультиметра.Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.

7

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Используйте Excel, чтобы найти наклон прямой линии, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.

8

Используйте закон Ома и наклон графика, чтобы рассчитать эквивалентное сопротивление R _p двух параллельно включенных резисторов в единицах Ом (Ом). Запишите свой результат.

Авторские права © 2012-2013 Advanced Instructional Systems Inc. и | Кредиты

параллельных резисторов

Обзор

Резисторы в цепи могут быть подключены последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.

Параллельные резисторы

Сопротивления параллельны, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением.Таким образом, к каждому резистору приложено полное напряжение источника.

Параллельные резисторы

Параллельное соединение резисторов.

Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения. Это верно для схем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.

Закон Ома и параллельные резисторы

Каждый резистор в цепи имеет полное напряжение. Согласно закону Ома токи, протекающие через отдельные резисторы, равны $ I_1 = \ frac {V} {R_1} $, $ I_2 = \ frac {V} {R_2} $ и $ I_3 = \ frac {V} {R_3 } $. Сохранение заряда подразумевает, что полный ток является суммой этих токов:

Резисторы параллельные

Три резистора, подключенных параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление.

$ I = I_1 + I_2 + I_3. $

Подстановка выражений для отдельных токов дает:

$ I = \ frac {V} {R_1} + \ frac {V} {R_2} + \ frac {V} {R_3} $

или

$ I = V (\ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3}) $

Это означает, что полное сопротивление в параллельной цепи равно сумме инверсии каждого отдельного сопротивления. Следовательно, для каждой цепи с числом $ n $ или параллельно подключенными резисторами

$ R_ {n \; (parallel)} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3}… + \ frac {1} {R_n}. $

Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.

Каждый резистор, включенный параллельно, имеет одинаковое полное напряжение источника, приложенного к нему, но делит общий ток между ними. Примером может служить соединение двух лампочек в параллельную цепь с 1.Аккумулятор 5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, поскольку она по существу обеспечивает полную энергию обеими лампочками. В последовательной цепи батарея будет работать столько же, сколько и с одной лампочкой, только тогда яркость будет разделена между лампочками.

резисторов, включенных параллельно | Формула эквивалентного сопротивления

Введение

Два резистора считаются подключенными параллельно, если оба вывода резистора подключены к каждому соответствующему выводу другого резистора. В сети параллельных резисторов ток может проходить по нескольким путям, в отличие от сети с последовательными резисторами, поскольку существует несколько путей для прохождения тока. Следовательно, параллельные резистивные цепи являются делителями тока.

Параллельные резисторы

Если два или более резистора подключены параллельно, то разность потенциалов на каждом резисторе одинакова.При параллельном соединении резисторы подключаются к одним и тем же узлам. Это можно определить по наличию более чем одного пути прохождения тока. Например, приведенная ниже схема представляет собой параллельное соединение резисторов. Разность потенциалов на резисторе R1 такая же, как и на резисторе R2, который равен потенциалу питания V _AB .

Если V _AB — это подаваемый потенциал, то

V _R1 = V _R2 = V _AB

В следующей схеме резисторы R1, R2 и R3 подключены параллельно комбинация.

Здесь потенциал питания составляет V _AB между точками A и B. Поскольку резисторы R1, R2 и R3 соединены параллельно, разность потенциалов на каждом резисторе такая же, как и у источника питания. Следовательно, V _AB = V _R1 = V _R2 = V _R3 .

Где

В _R1 — потенциал на резисторе R1.

В _R2 — это потенциал на резисторе R2.

В _R3 — потенциал на резисторе R3.

Но ток, протекающий через эти три резистора, разный. Если I — это ток, покидающий узел A, то он имеет три пути, чтобы достичь узла B. Ток, протекающий через каждый резистор, зависит от его сопротивления. Следовательно, в случае параллельных резистивных цепей ток во всех резисторах неодинаков. Если I1 — это ток, протекающий через резистор R1, I2 — это ток, протекающий через резистор R2, а I3 — это ток, протекающий через резистор R3, тогда токи I, I1, I2 и I3 могут быть связаны с помощью закона тока Кирхгофа. .Согласно текущему закону Кирхгофа, «сумма токов, входящих в узел, равна сумме токов, выходящих из узла».

Отсюда

I = I1 + I2 + I3.

Формула эквивалентного сопротивления

Любое количество резисторов, включенных в параллельную комбинацию, может быть заменено одним резистором с сопротивлением, равным эквивалентному сопротивлению резисторов параллельной комбинации.

Было установлено, что напряжение на каждом резисторе в параллельной комбинации одинаково, а общий ток равен сумме отдельных токов.Рассмотрим следующую схему.

Здесь I = I1 + I2 + I3

I1 = V / R1

I2 = V / R2

I3 = V / R3

Если R _T — полное сопротивление цепи, то

I = V / R _T

Следовательно, V / R _T = V / R ₁ + V / R ₂ + V / R ₃

1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R ₃

Если R _eq является эквивалентным сопротивлением цепи, то оно рассчитывается путем сложения обратных значений отдельных сопротивлений (1 / R).Обратная величина этой алгебраической суммы даст эквивалентное сопротивление. Уравнение эквивалентного сопротивления R _eq показано ниже для параллельной резистивной цепи из n резисторов.

(1 / R _экв. ) = (1 / R1) + (1 / R2) + (1 / R3) + ……… + (1 / Rn)

Из приведенного выше уравнения можно сделать вывод, что эквивалентное сопротивление резисторов, соединенных параллельно, всегда меньше, чем сопротивление самого маленького резистора.

Если два резистора подключены параллельно, то эквивалентное сопротивление равно

(1 / R _eq ) = (1 / R1) + (1 / R2)

R _EQ = R ₁ * R ₁ / (R ₁ + R ₂ )

Если два резистора равного сопротивления R соединены параллельно, то эквивалентное сопротивление комбинации будет R / 2.

Аналогично, если три резистора равного сопротивления R соединены в параллельном соединении, тогда эквивалентное сопротивление комбинации будет R / 3.

Параллельное соединение резисторов дает значение проводимости. Проводимость — это величина, обратная сопротивлению. Обычно он обозначается символом G. Единицы проводимости — Сименс, представленные символом S. Ранее единицами проводимости были Mho (℧), что означает обратное написание Ом, а символ — перевернутое представление Ω.

Несмотря на то, что резисторы параллельно подключены между двумя узлами, представление этого подключения может иметь любую из следующих форм.

Все вышеупомянутые комбинации представляют собой параллельные резистивные схемы, и все правила параллельных резисторов применимы и к вышеупомянутым комбинациям.

Расчет тока

Ток в каждой ветви параллельной резистивной цепи отличается от другой. Поскольку напряжение на каждом резисторе одинаково, ток, протекающий через каждый резистор, зависит от сопротивления этого резистора.Следовательно, если значение сопротивления в одной ветви отличается от другой, тогда ток в этих ветвях будет другим. Величину этого тока можно определить с помощью закона Ома.

Рассмотрим параллельную сеть из двух резисторов с напряжением питания V между двумя точками A и B.

Пусть I будет полным током в следующей цепи.

Пусть ток, протекающий через резистор R ₁ , равен I _R1 , а ток, протекающий через резистор R ₂ , равен I _R2 .

Тогда, согласно закону Кирхгофа, «полный ток, входящий в цепь, равен току на выходе из цепи».

Если I _T — это общий ток, то

I _T = I _R1 + I _R2

Поскольку падение напряжения на каждом резисторе одинаково

I _R1 = V / R ₁

И I _R2 = V / R ₂

Если рассматривать параллельную резистивную цепь, состоящую из n резисторов, то общий ток в цепи равен

I _Всего = I _R1 + Я _R2 +….+ I _Rn

Если последовательные резистивные цепи называются цепями делителя напряжения, то аналогично параллельные резистивные цепи называются цепями делителя тока.

Если рассматривается параллельная резистивная цепь из n резисторов с разным сопротивлением, то можно иметь n разных путей для прохождения тока и n разных значений тока через эти пути. Резисторы в параллельной комбинации можно менять местами, не влияя на общий ток и эквивалентное сопротивление.

Пример параллельного подключения резисторов

1. Рассмотрим следующую схему, в которой четыре резистора R1, R2, R3 и R4 подключены параллельно.

Значения сопротивления каждого резистора:

R1 = 10 Ом

R2 = 20 Ом

R3 = 30 Ом

R4 = 40 Ом

Напряжение питания V = 24 В

Общий ток в схеме можно рассчитать двумя способами.

Первый метод — вычислить отдельные токи, протекающие через каждый резистор.

Если I1 — это ток, протекающий через резистор R1, то согласно закону Ома

I1 = V / R ₁ = 24/10 = 2,4 A

Аналогично, если I2 — это ток, протекающий через резистор R2, то согласно по закону Ома

I2 = V / R ₂ = 24/20 = 1,2 A

Если I3 — это ток, протекающий через резистор R3, то по закону Ома

I3 = V / R ₃ = 24 / 30 = 0,8 А

И если I4 — это ток, протекающий через резистор R4, то по закону Ома

I4 = V / R ₄ = 24/40 = 0.6 A

Если I _ИТОГО — это полный ток в цепи, то согласно закону Кирхгофа

I _ИТОГО = I1 + I2 + I3 + I4 = 2,4 + 1,2 + 0,8 + 0,6 = 5A

Второй метод расчета тока — это определение эквивалентного сопротивления цепи.

Эквивалентное сопротивление цепи составляет

1 / R _EQ = (1 / R ₁ ) + (1 / R ₂ ) + (1 / R ₃ ) + (1 / R ₄ )

1 / R _EQ = (1/10) + (1/20) + (1/30) + (1/40)

R _EQ = 1/2.083 = 4,8 Ом

Этот единственный резистор можно использовать для замены всех резисторов в параллельной комбинации.

∴ I _ИТОГО = V / R _EQ = 24 / 4,8 = 5 А.

Рассмотрим следующую схему, в которой три резистора R1, R2 и R3 соединены параллельно.

Ток, протекающий через R1, равен I1 = 6A

Ток, протекающий через R2, равен I2 = 4A

Ток, протекающий через R3, равен I3 = 2A

В параллельных резистивных цепях напряжение на каждом резисторе одинаковое и равно напряжению питания.

Здесь напряжение питания V = 12 В.

Если V1 — это напряжение на резисторе R1, V2 — это напряжение на резисторе R2, а V3 — это напряжение на резисторе R3, тогда

V = V1 = V2 = V3 = 12 В

Тогда по закону Ома

R1 = V ₁ / I ₁

R1 = 12/6

R1 = 2 Ом

R2 = V ₂ / I ₂

R2 = 12/4

R2 = 3 Ом

R3 = V ₃ / I ₃

R3 = 12/2

R3 = 6 Ом

Применения

Концепция резисторов в parallel используется при анализе мостовой схемы Уитстона.Параллельно соединенные резисторы действуют как цепь делителя тока. Эта текущая концепция делителя используется в таких приложениях, как аналого-цифровые преобразователи и цифро-аналоговые преобразователи.

параллельных резисторов — видео по физике от Brightstorm

Параллельно подключенные резисторы состоят из двух отдельных независимых цепей, так что, когда ток достигает резистора, ток может выбирать, через что проходить. Большинство домов подключены параллельно, поэтому, в отличие от резисторов, подключенных последовательно, не все приборы в наших домах должны быть включены, чтобы работала хотя бы одна.Добавление резисторов параллельно снижает общее сопротивление. Наименьший ток пройдет через самый большой резистор. Чтобы записать все резисторы как один резистор, используйте уравнение 1 / (эффективное сопротивление) = 1 / (резистор 1) + 1 / (резистор 2). Эффективное сопротивление меньше, чем у любого из двух отдельных резисторов.

Итак, давайте поговорим о резисторных цепях, соединенных параллельно.Итак, во-первых, что означает параллель? Параллельность означает, что есть выбор, это означает, что в цепи есть ответвление, и может ли ток идти в том или ином направлении. Параллельно сеть резисторов выглядит так. Течение входит, и тогда у него есть выбор, он проходит между теми же двумя точками, но есть 2 разные дороги, по которым он может идти. Итак, в основном параллельные сети состоят из 2 отдельных цепей, независимых друг от друга. Итак, параллельная разность потенциалов одинакова, поэтому разность потенциалов между этими двумя точками одинакова, потому что это одни и те же две точки.Это были всего лишь 2 разные ветви, которые прошли. Ток будет добавляться, поэтому мы бы сказали, что i1 плюс i2 равно общему току i. i1 плюс i2 хорошо, как всегда, что мы хотели бы сделать, так это рассматривать эту параллельную сеть как один эффективный резистор. Итак, я хочу, чтобы разность потенциалов была такой же, очевидно, ток, идущий здесь в мой эффективный резистор, будет равен i, и поэтому мы собираемся записать ток как дельта v над потенциалом. Разница делится на сопротивление с нашим обязательным знаком минус.Таким образом, минус разность потенциалов по r параллели будет равна минус разности потенциалов по r1 минус разность потенциалов по r2.

Теперь разность потенциалов такая же, это означает, что она будет сокращаться вместе со знаком минус, и это дает нам формулу для добавления резисторов параллельно. 1 по r параллели равно 1 по r1 плюс 1 по r2. Таким образом, добавление резисторов параллельно сложнее, чем их добавление последовательно. Когда я добавляю их последовательно, я просто добавляю, когда я добавляю их параллельно, мы говорим, что обратные суммы складываются.Таким образом, 1 по эффективному сопротивлению равняется 1 по r1 и 1 по r2. Очень, очень, соблазнительно, но абсолютно неверно пытаться перевернуть это вверх дном и сказать, что это просто означает, что r parallel равно r1 плюс r2, что неверно. Теперь одна вещь, которую мы можем думать о параллельных цепях, как будто вы пытаетесь добраться из точки a в точку b. Если есть только одна дорога, это будет раздражать, любой, кто хочет перейти из пункта А в пункт Б, должен пойти по этой дороге.

Если я добавлю параллельно, это будет похоже на строительство новой дороги, которая также идет от точки a к точке b, и это действительно уменьшит трафик.Так что важно помнить о параллельности, и она сразу же скажет нам, что вы не можете просто добавить. Когда я добавляю резисторы параллельно, я уменьшаю общее сопротивление прямо сейчас, так как эта параллельная сеть будет работать, у меня есть 5 ампер, и у меня есть 2 резистора на 15 Ом и 10 Ом. Разница потенциалов такая же, вы можете думать об этом как о точке b 2 разных дорогах, думайте о резисторах как о светофоре. Чем больше сопротивление, тем больше светофоров на этом пути и тем меньше машин поедет туда.Таким образом, наименьший ток будет проходить через наибольший резистор в параллельной комбинации. Итак, как мы собираемся определить, сколько тока проходит через 15 и сколько тока проходит через 10? На самом деле это действительно просто, сначала мы собираемся добавить эти два резистора параллельно. Теперь помните, что сложение параллельно — это немного сложно, поэтому мы скажем, что 1 по r параллельному равно 1 по 15 плюс 1 по 10.

Хорошо, теперь, как в средней школе, нам нужно пересечь умножение.Так что будет 10 плюс 15 больше 150, хорошо. 10 плюс 15 — это 25 на 150, и если мы сделаем это осторожно, мы можем отменить. Это дает нам одну шестую. 1 по r параллели — это 1 по 6, это означает, что r параллель равняется 6, хорошо. Обратите внимание, что наше эффективное сопротивление меньше, чем любое из двух сопротивлений, которые мы сложили вместе, меньше, чем любое из них, хорошо. И на самом деле это число всегда будет лежать между этим, деленным на 2, и этим, деленным на 2, 5, 7 с половиной, 6. Хорошо, это всегда будет работать таким образом. Хорошо, теперь, когда у нас есть эффективное сопротивление, как мы собираемся определять ток через каждого из этих парней? Что ж, мы собираемся использовать идею о том, что разность потенциалов должна быть одинаковой параллельно всегда, всегда, всегда.Так в чем же разница потенциалов? Ну, разность потенциалов должна быть 5 умноженная на 6, потому что эта сеть на самом деле имеет только 6 Ом и 5 ампер. Ну, 5 умножить на 6 равно 30, так что это означает, что разность потенциалов должна быть 30.

Хорошо, чтобы сделать разность потенциалов 30 вольт на резисторе 15 Ом, 2 ампера, потому что 2 умножить на 15 равно 30, как насчет того, внизу, я хочу 30 вольт на нем, так сколько ампер мне нужно? 3 ампера, и, конечно же, это следует нашему предыдущему решению, что текущие добавленные 5 ампер идут во 2 и 1 ветви, 3 — в другую.Хорошо, еще один способ думать о параллельных цепях — это дома, это способ подключения домов, потому что я не хочу, чтобы мне было необходимо включать телевизор, чтобы посудомоечная машина работала правильно, поэтому мы подключаем эти 2 схемы отдельно. Каждая розетка в вашем доме — это отдельная параллельная ветвь одной и той же цепи, поэтому мы заставляем жилье работать. Хорошо, это параллельные схемы резисторов.

Как рассчитать полное сопротивление параллельной цепи?

Как рассчитать полное сопротивление параллельной цепи?

Эффективное сопротивление резисторов, подключенных параллельно

1. В параллельной цепи есть три важных характеристики:
   (a) Разность потенциалов одинакова на каждом резисторе.
   (b) Ток, который проходит через каждый резистор, обратно пропорционален сопротивлению резистора.
   (c) Полный ток в цепи равен сумме токов, проходящих через резисторы в ее параллельных ветвях.
   
2. Когда два или более сопротивления подключены между двумя общими точками так, что к каждой из них приложена одинаковая разность потенциалов, они считаются подключенными параллельно.
   Когда такая комбинация сопротивлений подключена к батарее, все сопротивления имеют одинаковую разность потенциалов на концах.
3. Вывод математического выражения параллельной комбинации:
   Пусть, V будет разностью потенциалов между двумя общими точками A и B. Затем из закона Ома
   Ток, проходящий через R ₁ , I ₁ = V / R ₁ … (i)
   Ток, протекающий через R ₂ , I ₂ = V / R ₂ … (ii)
   Ток, протекающий через R ₃ , I ₃ = V / R ₃ … (iii)
4. Если R — эквивалентное сопротивление, то по закону Ома полный ток, протекающий по цепи, определяется выражением
   I = V / R… (iv)
   и I = I ₁ + I ₂ + I ₃ … (v)
5. Подставляя значения I, I ₁ , I ₂ и I ₃ в уравнение.(v),
   \ (\ frac {\ text {V}} {\ text {R}} = \ frac {\ text {V}} {{{\ text {R}} _ {\ text {1}} }} + \ frac {\ text {V}} {{{\ text {R}} _ {\ text {2}}}} + \ frac {\ text {V}} {{{\ text {R}} _ {\ text {3}}}} \ text {} …… .. \ text {(vi)} \)
6. Отменяя общий термин V, получаем
   \ (\ frac {\ text {1}} {\ text {R}} = \ frac {\ text {1}} {{{\ text {R}} _ {\ текст {1}}}} + \ frac {\ text {1}} {{{\ text {R}} _ {2}}} + \ frac {\ text {1}} {{{\ text {R} } _ {3}}} \)
   Эквивалентное сопротивление параллельной комбинации сопротивлений меньше, чем каждое из всех отдельных сопротивлений.
7. Эквивалентная схема показана на рисунке.

Важные результаты о параллельной комбинации:

1. Полный ток в цепи равен сумме протекающих по ней токов.
2. В параллельной комбинации резисторов напряжение (или разность потенциалов) на каждом резисторе одинаково и равно приложенному напряжению, то есть V ₁ = V ₂ = V ₃ = V
3. Ток, протекающий через каждый резистор, обратно пропорционален его сопротивлению, поэтому чем выше сопротивление резистора, тем меньше ток, протекающий через него.