Общий эмиттер. Схемы включения биполярного транзистора с общим эмиттером: особенности и применение

Какие преимущества имеет схема с общим эмиттером. Как рассчитать коэффициент усиления и входное сопротивление. Какое влияние оказывает эмиттерная стабилизация. Как работает усилитель на биполярном транзисторе с общим эмиттером.

Принцип работы схемы с общим эмиттером

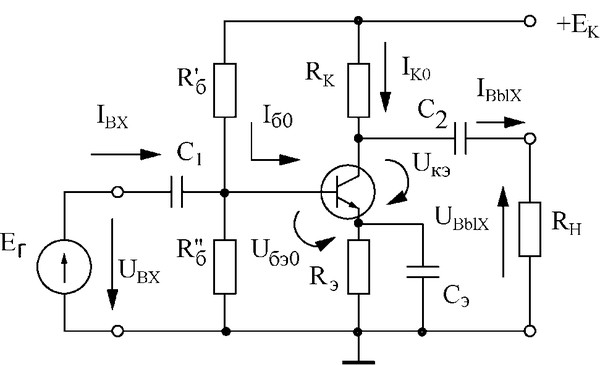
Схема с общим эмиттером (ОЭ) является одной из базовых конфигураций включения биполярного транзистора. В этой схеме эмиттер транзистора подключается к общей шине (земле), а входной сигнал подается на базу. Выходной сигнал снимается с коллектора.

Основные особенности схемы с ОЭ:

• Обеспечивает усиление как по току, так и по напряжению
• Имеет инверсию фазы выходного сигнала относительно входного
• Обладает средним входным сопротивлением (единицы-десятки кОм)
• Имеет относительно высокий коэффициент усиления по напряжению

Благодаря этим свойствам, схема с ОЭ широко применяется в усилителях напряжения и тока.

Расчет коэффициента усиления

Коэффициент усиления по напряжению для схемы с ОЭ можно рассчитать по формуле:

K_U = -R_C / (r_e + R_E)

Где:

• R_C — сопротивление в цепи коллектора
• r_e — дифференциальное сопротивление эмиттерного перехода
• R_E — сопротивление в цепи эмиттера

Знак минус указывает на инверсию фазы выходного сигнала. Типичные значения коэффициента усиления для схемы с ОЭ составляют 10-100.

Входное сопротивление схемы

Входное сопротивление схемы с общим эмиттером определяется выражением:

R_вх = (β + 1)(r_e + R_E)

Где β — коэффициент усиления транзистора по току.

Типичные значения входного сопротивления составляют единицы-десятки кОм. Это больше, чем у схемы с общей базой, но меньше, чем у схемы с общим коллектором.

Влияние эмиттерной стабилизации

Введение резистора R_E в цепь эмиттера (эмиттерная стабилизация) позволяет улучшить температурную стабильность схемы и уменьшить нелинейные искажения. Однако это приводит к снижению коэффициента усиления.

Для сохранения высокого усиления по переменному току применяют шунтирование R_E конденсатором большой емкости. В этом случае:

• По постоянному току действует полное значение R_E, обеспечивая стабилизацию
• По переменному току R_E шунтируется, что дает высокое усиление

Такой подход позволяет достичь компромисса между стабильностью и усилением.

Частотные свойства усилителя с ОЭ

Частотный диапазон усилителя с общим эмиттером ограничен следующими факторами:

• На низких частотах — разделительными и блокировочными конденсаторами
• На высоких частотах — барьерной емкостью коллекторного перехода и эффектом Миллера

Для расширения полосы пропускания применяют различные методы частотной коррекции, например, введение индуктивности в коллекторную цепь.

Практическое применение схемы с ОЭ

Благодаря своим характеристикам, схема с общим эмиттером широко используется в различных электронных устройствах:

• Усилители звуковых частот
• Усилители промежуточной частоты в радиоприемниках
• Импульсные усилители
• Генераторы сигналов
• Преобразователи импеданса

Схема с ОЭ является базовой для построения многокаскадных усилителей и других сложных схем на биполярных транзисторах.

Преимущества и недостатки схемы с ОЭ

Основные достоинства схемы с общим эмиттером:

• Высокий коэффициент усиления по напряжению и току
• Относительно большое входное сопротивление
• Простота реализации
• Универсальность применения

К недостаткам можно отнести:

• Инверсию фазы выходного сигнала
• Зависимость параметров от температуры
• Относительно узкую полосу пропускания
• Возможность самовозбуждения при высоком усилении

Правильный выбор режима работы и применение цепей стабилизации позволяют минимизировать влияние этих недостатков.

Расчет элементов схемы с ОЭ

При проектировании усилителя с общим эмиттером необходимо рассчитать следующие основные элементы:

1. Резисторы делителя напряжения для задания рабочей точки
2. Сопротивление в цепи эмиттера для температурной стабилизации
3. Сопротивление в цепи коллектора для получения требуемого усиления
4. Емкости разделительных и блокировочных конденсаторов

Расчет начинают с выбора рабочей точки транзистора, исходя из требуемых характеристик усилителя. Затем определяют номиналы остальных элементов схемы.

Особенности работы усилителя на биполярном транзисторе

При работе усилителя с общим эмиттером на биполярном транзисторе следует учитывать ряд особенностей:

• Нелинейность вольт-амперных характеристик транзистора приводит к появлению искажений
• Существует зависимость параметров схемы от температуры
• Разброс параметров транзисторов требует индивидуальной настройки каждого экземпляра схемы
• При высоких частотах проявляются эффекты, связанные с барьерными емкостями транзистора

Учет этих факторов позволяет создавать надежные и эффективные усилители на биполярных транзисторах по схеме с общим эмиттером.

Общий эмиттер

Е_см обеспечивает закрытое состояние транзистора.

Когда транзистор работает как ключ, он находится в режиме I и III, пробегая режим усиления (II)

В точке А транзистор находится в режиме отсечки ключ разомкнут.

В точке В, транзистор VT – открыт и насыщен (О(Н)).

Передаточная характеристика

• зависимость

По методу двух узлов найдем

Для того, чтобы биполярный транзистор вошел в режим насыщения, необходимо выполнение токового критерия:

Помехоустойчивость ключа – инвертора

Под помехоустойчивостью понимается то напряжение фиктивного источника, которое включается между выходом ключа и входом такого же ключа, являющегося нагрузкой, при котором схема нагрузки функционирует нормально.

VT₁ – закрыт, VT₂ – открыт (насыщен)

VT₁ – открыт (насыщен)

Схема замещения транзистора в режиме отсечки

В режиме отсечки транзистор можно заменить источником тока = , это соответствует разомкнутому состоянию ключа. Режим отсечки обеспечивается напряжением или осуществляемая за счет для кремниевых транзисторов.

Схема замещения транзистора в режиме насыщения

В режиме насыщения транзистор можно заменить двумя источниками напряжения между базой и эммитером, и между коллектором и эммитером. Режим насыщения обеспечивается токовым критерием:

Расчет элементов связи в транзисторных ключах

Первый случай

VT₁ – открыт (насыщен) , VT₂ – закрыт

1) Ge

2) Si

R₁ ограничивает входной ток

Второй случай

VT₁ – закрыт, VT₂ – открыт(насыщен)

(*) (**)

Определим R₁:

Нагрузочная способность ключа-инвертора

Один ключ нагружен на n ключей

V T₁ – закрыт, VT₂ – о(н)

VT₃ — о(н)

…………

………… в режиме насыщения

…………

VT_(n+1)— о(н)

i_вых = ni_вх 

i_вых =

i_вх =

i_б

i_б=i_вх — i_см

— условие, при котором все транзисторы нагрузки будут входить

в режим насыщения

1. Если VT₁ закрыт и ненагружен (n=0) => I_k0

2. n=1, I_k0,i_вх1 уменьшается

Если n ключей, то I

k0,i_вх,…,i_вхn

С увеличением n нагрузки, логическая “1” уменьшается могут быть сбои, т.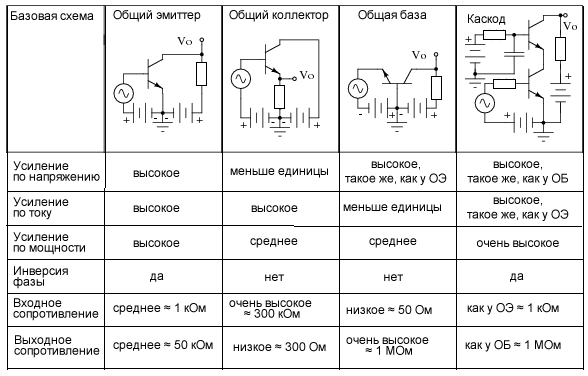 к. нагрузочные параметры могут не войти в режим насыщения.

Ключ на биполярном кремниевом транзисторе с непосредственной связью

1. VT₁ — о(н), VT₂ – з

U_вых1=U_вх2=0.2 В<U_{отсечки} (т.к. кремниевый)=0.6 В

U⁰=0.2 В

2. VT₁ — з, VT₂ — о(н)

U_вх2=U_бн2=U_вых1=0.7 В

U¹=0.7 В — мало (малый перепад между логической “1” и логическим “0”.

1. VT₁-о(н), VT₂-з

U_вых1=U_кэн=0,2 В

U_вых1= U_д+U_бэ2

U_бэ2= U_вых1-U_д

= 0.2-0.6= -0.4 В < U_отс VT₂— надежно закрыт

2. VT₁ — з, VT₂ — о(н)

Эта схема позволяет увеличить разницу перепадов между логической «1” и логическим «0».

Возрастает помехоустойчивость схемы.

IGBT; транзистор/транзистор,общий эмиттер; IGBT x6; SP6P производства MICROCHIP TECHNOLOGY APTGL120TDU120TPG

• Топология

  термистор NTC

• Тип модуля

  IGBT

• Конструкция диода

  общий эмиттер

• Обратное напряжение макс.

  1,2кВ

• Корпус

  SP6P

• Ток коллектора в импульсе

  200А

• Топология

  IGBT x6

• Конструкция диода

  транзистор/транзистор

• Ток коллектора

  120А

• Технология

  Trench

• Механический монтаж

  винтами

• Электрический монтаж

  Press-in PCB

• Технология

  Field Stop

• Напряжение затвор — эмиттер

  ±20В

• Производитель

  MICROCHIP TECHNOLOGY

• Вес

  250g

Бесплатная доставка
заказов от 5000 ₽

Доставим прямо в руки или в ближайший пункт выдачи

NPN Коэффициент усиления усилителя с общим эмиттером

NPN Коэффициент усиления усилителя с общим эмиттером

Глядя на поведение постоянного тока almlifier и следуя соглашению, что строчные буквы представляют изменения в соответствующих количествах: Прирост , что для маленьких r E можно приблизить к Добавить конденсатор байпаса Усилитель с общим эмиттером NPN	Index Концепции электроники
Гиперфизика****Электричество и магнетизм R Шейка	Назад

Глядя на поведение постоянного тока almlifier и следуя соглашению, что строчные буквы представляют изменения в соответствующих количествах: Прирост , но для изменений сигнала переменного тока, для которых C E является эффективным байпасом, усиление равно Снять байпас конденсатор Числовой пример NPN Усилитель с общим эмиттером	Индекс Концепции электроники
Гиперфизика*****Электричество и магнетизм R Ступица	Назад

При наличии шунтирующего конденсатора коэффициент усиления по напряжению определяется сопротивлением коллектора R C и эффективным сопротивлением транзистора r E . Это эффективное сопротивление равно , где R BE — прямое сопротивление диода база-эмиттер. Удалить байпас конденсатор Выражения NPN Усилитель с общим эмиттером	Индекс Концепции электроники
Гиперфизика****Электричество и магнетизм R Ступица	Вернуться назад

7.3: Усилитель с общим эмиттером — Engineering LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25426

• Джеймс М. Фиоре
• Муниципальный колледж Mohawk Valley

Конфигурация с общим эмиттером находит широкое применение в качестве усилителя напряжения общего назначения. Мы начнем с базовой схемы смещения постоянного тока, а затем добавим несколько других компонентов. Например, см. рисунок \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\): Усилитель с общим эмиттером, использующий эмиттерное смещение с двумя источниками питания.

Этот усилитель основан на эмиттерной схеме смещения с двумя источниками питания. Заметными изменениями являются включение напряжения входного сигнала \(V_{in}\) и нагрузки \(R_L\). Чтобы эти компоненты не изменяли смещение, мы изолируем вход и нагрузку с помощью разделительных конденсаторов \(C_{in}\) и \(C_{out}\). Эти конденсаторы будут действовать как размыкатели для постоянного тока, создавая желаемую изоляцию. Что касается сигнала переменного тока, емкости будут выбраны так, чтобы их реактивные сопротивления были намного меньше, чем окружающие резисторы на частоте входа. Следовательно, конденсаторы будут замыкаться и пропускать сигнал переменного тока через усилитель.

Окончательная переделка касается эмиттерного резистора. Единственный резистор сети смещения заменяется парой резисторов \(R_E\) и \(R_{SW}\) вместе с шунтирующим конденсатором \(C_E\). Для постоянного тока конденсатор открыт, а эффективное сопротивление смещения эмиттера равно \(R_E + R_{SW}\). Для переменного тока конденсатор будет идеально вести себя как короткое замыкание, поэтому сопротивление эмиттера переменного тока упадет до всего лишь \(R_{SW}\). Этот резистор называется резистором заболачивания или эмиттерного вырождения. Он используется в основном для управления коэффициентом усиления по напряжению усилителя.

Мы можем использовать нашу модель транзистора переменного тока вместе с теоремой о суперпозиции, чтобы получить эквивалентную цепь переменного тока усилителя, как показано на рисунке \(\PageIndex{2}\).

Рисунок \(\PageIndex{2}\): Эквивалент переменного тока усилителя с общим эмиттером.

Во-первых, мы замкнули все конденсаторы. Во-вторых, мы заменили источники постоянного тока их идеальным внутренним сопротивлением (короткое замыкание), которое помещает эти точки на землю переменного тока. В-третьих, мы заменили транзистор на модель. Наконец, мы объединили и/или переименовали сопротивления там, где это необходимо. Поскольку это цепь переменного тока, мы используем обозначение сопротивления в нижнем регистре \(r\), чтобы избежать путаницы с сопротивлением постоянному току (которое записывается в верхнем регистре). Таким образом, \(r_E\) представляет собой сопротивление переменному току от эмиттера до земли переменного тока. Это соответствует \(R_{SW}\) на исходной схеме. Точно так же \(r_C\) представляет собой полное сопротивление от коллектора до земли переменного тока. В исходной схеме это соответствует \(R_C\) параллельно \(R_L\). Если бы эта схема была разгружена, то \(r_C\) было бы просто равно \(R_C\). Наконец, \(r_B\) соответствует \(R_B\), но при смещении делителя напряжения оно будет равно \(R_1\) параллельно \(R_2\). 9{\circ}\). В некоторых приложениях это может быть серьезной проблемой, в других — не так сильно. Если это проблема, ее можно решить, используя второй инвертирующий усилитель последовательно с первым (инвертируя инверсию).

Второе, что мы видим, это то, что коэффициент усиления немного больше, чем отношение сопротивления коллектора к сопротивлению эмиттера. Вот здесь-то и вступает в действие разделение эмиттерного резистора на две части. В уравнении \(r_E\) — это заглушающий резистор \(R_{SW}\). Чем больше заглушающий резистор, тем ниже коэффициент усиления. Максимальный выигрыш будет достигнут, когда \(R_{SW} = 0\). То есть когда эмиттер полностью зашунтирован. Обратной стороной этого является то, что усиление теперь будет полностью зависеть от \(r’_e\). Это увеличит искажения. Причина в том, что \(R_{SW}\), будучи намного больше, эффективно «заглушает» изменение \(r’_e\) и уменьшает искажения. Чем больше \(R_{SW}\) относительно \(r’_e\), тем больше снижение искажений, но за счет снижения усиления. Вот почему заглушающий резистор также называют резистором дегенерации эмиттера: он ухудшает коэффициент усиления по напряжению.

7.3.2: Входной импеданс

Входной импеданс, \(Z_{in}\), определяется как отношение \(v_{in}\) к \(i_{in}\). На рисунке 7.2.2 это равно \(r_B\) параллельно с импедансом, смотрящим на базовый терминал, \(Z_{in(base)}\). Используя закон Ома, находим

\[Z_{in(основание)} = \frac{v_B}{i_B} \\ Z_{in(основание)} = \frac{i_C (r’_e+r_E )}{i_B} \\ Z_{in(база)} = \frac{i_C (r’_e+r_E)}{i_C / \beta} \\ Z_{i n(база)} = \beta (r’_e+r_E) \label{ 7.5} \]

Поэтому

\[Z_{in} = r_B || Z_{in(base)} \label{7.6} \]

Мы видим, что и шунтирующий резистор, и \(\beta\) играют роль в настройке входного импеданса. Большие значения \(R_{SW}\) и \(\beta\) приводят к большему входному импедансу. Подводя итог, мы обнаруживаем, что в то время как заглушение снижает коэффициент усиления по напряжению, оно уменьшает искажения и увеличивает входной импеданс, последние два параметра обычно желательны для усилителя напряжения. Незаболоченный усилитель будет иметь наибольшее усиление, но будет страдать от наихудших искажений и низкого входного импеданса. Это классический компромисс «качество против количества»: большой выигрыш в низком качестве против скромного прироста в высоком качестве ¹ .

7.3.3: Выходной импеданс

Выходной импеданс, \(Z_{out}\), определяется как внутренний импеданс эквивалентного источника, который управляет нагрузкой. Если мы расположимся на нагрузке и посмотрим на усилитель, показанный на рис. 7.2.1, то \(C_{out}\) идеально закорочен, а \(V_{CC}\) находится на земле переменного тока. Это оставляет нам \(R_C\) параллельно с транзистором. Транзистор моделируется как источник тока, и его идеальное внутреннее сопротивление приближается к бесконечности. В действительности эффективное значение \(r’_C\), вероятно, находится в районе 100 кОм (\Омега\) или около того, в зависимости от тока смещения. Эта параллельная комбинация включает выходной импеданс источника тока. Мы моделируем эту схему как усилитель напряжения, поэтому для корректности мы преобразовали бы источник тока с параллельным внутренним сопротивлением в источник напряжения с последовательным внутренним сопротивлением. Однако эти значения сопротивления идентичны, и мы получаем

\[Z_{out} = r’_C || R_C \nonumber \]

Во многих схемах \(R_C\) значительно меньше, чем \(r’_C\), поэтому

\[Z_{out} \ приблизительно R_C \label{7.7} \]

Пример \(\PageIndex{1}\)

Определите входное и выходное сопротивление усилителя, показанного на рисунке \(\PageIndex{3}\). Также вычислите коэффициент усиления по напряжению. Предположим \(\бета = 150\).

Рисунок \(\PageIndex{3}\): Схема для примера \(\PageIndex{1}\).

Во-первых, самое простое. Мы можем определить выходное сопротивление путем осмотра. Он примерно равен \(R_C\), или 22 k\(\Omega\).

Чтобы найти \(Z_{in}\) и \(A_v\), нам нужно определить \(r’_e\). Чтобы получить \(r’_e\), нам нужно найти \(I_C\). Используя KVL вокруг петли база-эмиттер, если мы аппроксимируем базовое напряжение постоянного тока близким к нулю, тогда все питание эмиттера падает на сопротивление эмиттера постоянного тока, за исключением \(V_{BE}\).

\[I_C = \frac{∣V_{EE}∣−V_{BE}}{R_E+R_{SW}} \nonumber \]

\[I_C = \frac{5 V−0,7 V}{8,2 k \Omega +1,8 k \Omega} \nonumber \]

\[I_C = 0,43 мА \nonumber \]

\[r’_e = \frac{26mV}{I_C} \nonumber \]

\[r’_e = \frac{26mV}{0,43 мА} \nonumber \]

\[r’_e = 60,5 \Omega \nonumber \]

\[Z_{in-base} = \beta (r’_e+r_E ) \nonumber \]

\[Z_{in-base} = 150(60.5 \Omega +1.8k \ Omega ) \nonnumber \]

\[Z_{in-base} = 279 k \Omega \nonnumber \]

Это значение параллельно с резистором смещения базы создает входной импеданс.

\[Z_{in} = R_B || Z_{in(base)} \nonumber \]

\[Z_{in} = 15k \Омега || 279 k \Omega \nonumber \]

\[Z_{i n} = 14.2k \Omega \nonumber \]

Первый способ.

\[r_C = R_C || R_L \nonumber \]

\[r_C = 22 k \Omega || 33 k \Omega \nonumber \]

\[r_C = 13. 2 k \Omega \nonumber \]

\[A_v =− \frac{r_C}{r’_e+r_E} \nonumber \]

\[A_v =− \frac{13,2 k \Omega}{ 60,5 \Omega +1,8 k \Omega} \nonumber \]

\[A_v =−7,1 \nonumber \]

А теперь способ второй; сначала ненагруженное усиление, затем эффект делителя и, наконец, композитное усиление.

\[A_{v (без нагрузки)} =- \frac{r_C}{r’_e+r_E} \nonumber \]

\[A_{v (без нагрузки)} =- \frac{22 k \Omega} {60,5 \Omega +1,8 k \Omega} \nonnumber \]

\[A_{v (без нагрузки)} = −11,82 \nonnumber \]

\[A_{divider} = \frac{R_L}{R_L+R_C } \номер \]

\[A_{делитель} = \frac{33 k \Omega}{33k \Omega +22k \Omega} \nonumber \]

\[A_{divider} = 0,6 \nonumber \]

\[A_v = A_{v (без нагрузки)} \times A_{делитель} \nonnumber \]

\[A_v =−11,82 \times 0,6 \nonumber \]

\[A_v =−7.1 \nonnumber \]

Повторим предыдущий пример, используя ту же схему, но с одним изменением: эмиттерный резистор будет полностью зашунтирован. Это покажет влияние заболачивания на коэффициент усиления по напряжению и входной импеданс.

Пример \(\PageIndex{2}\)

Определите усиление по напряжению и входное сопротивление усилителя, показанного на рисунке \(\PageIndex{4}\). Предположим \(\бета = 150\).

Рисунок \(\PageIndex{4}\): Схема для примера \(\PageIndex{2}\).

Эквивалент постоянного тока этой схемы идентичен схеме, показанной на рисунке \(\PageIndex{3}\). В обоих случаях сопротивление эмиттера по постоянному току равно 10 кОм (\Омега\). Следовательно, \(I_C\) и \(r’_e\) неизменны. Шунтирующий конденсатор закорачивает все это значение для эквивалента переменного тока, потому что нет шунтирующего резистора. Следовательно, \(r_E\) = 0. Мы можем просто использовать 0 вместо \(r_E\) в ранее выведенных уравнениях.

Начнем с входного импеданса.

\[Z_{in-base} = \beta (r’_e+r_E ) \nonnumber \]

\[Z_{in-base} = 150(60,5 \Omega +0) \nonnumber \]

\[Z_{in-base} = 9075 \Omega \nonnumber \]

Это значение значительно меньше, чем значение, полученное из заболоченной схемы. Продолжая,

\[Z_{in} = R_B || Z_{in(base)} \nonumber \]

\[Z_{in} = 15k \Omega ∣∣ 9075 \Omega \nonnumber \]

\[Z_{i n} = 5654 \Omega \nonumber \]

\[A_v =− \frac{r_C}{r’_e+r_E} \nonumber \]

\[A_v =− \frac{13,2 k \Omega}{60,5 \Omega +0 } \nonumber \]

\[A_v =−218,2 \nonnumber \]

Конечным результатом является входное сопротивление менее половины заболоченного корпуса и коэффициент усиления по напряжению более чем в 30 раз больше. Чего эти расчеты не показывают, так это увеличения искажения, которое будет вызвано этим изменением. Подробнее об этом чуть позже.

Давайте рассмотрим немного другое: PNP-усилитель со смещением делителя напряжения.

Пример \(\PageIndex{3}\)

Определите входное сопротивление и коэффициент усиления по напряжению для схемы, показанной на рисунке \(\PageIndex{5}\). Также определите \(v_{нагрузка}\), если \(v_{in}\) = пиковое значение 20 мВ. Предположим \(\бета = 100\).

Рисунок \(\PageIndex{5}\): Схема для примера \(\PageIndex{3}\).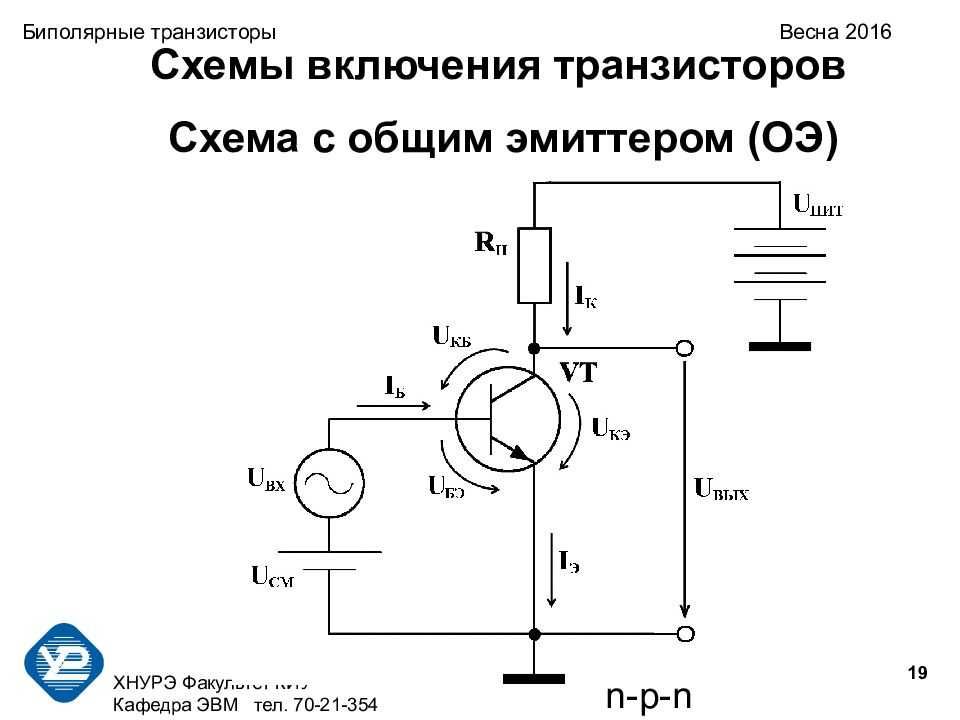

Сначала нам нужно определить \(r’_e\), что означает, что нам нужно найти ток коллектора. Если предположить слабонагруженный делитель, то базовое напряжение будет примерно 15 вольт, а эмиттерное будет выше на 0,7 вольта, или 15,7 вольта. Это оставляет 20 вольт — 15,7 вольт или 4,3 вольта на эквивалентном сопротивлении эмиттера постоянного тока. Это 4,1 кОм\(\Омега\) + 200\(\Омега\), или 4,3 кОм\(\Омега\), что дает 1 мА для \(I_C\). Это даст \(r’_e\) = 26 \(\Omega \).

\[Z_{in(база)} = \beta (r’_e+r_E ) \без номера \]

\[Z_{in(база)} = 100(26 \Omega +200 \Omega ) \без номера \ ]

\[Z_{in(base)} = 22,6 k \Omega \nonnumber \]

Это значение параллельно резисторам смещения делителя напряжения, создающим входное сопротивление.

\[Z_{in} = R_1 || Р_2 || Z_{in(base )} \nonumber \]

\[Z_{in} = 15k \Omega || 5k \ Омега || 22,6 k \Omega \nonumber \]

\[Z_{i n} = 3,22 k \Omega \nonumber \]

\[A_v =− \frac{r_C}{r’_e+r_E} \nonumber \]

\[A_v =− \frac{7. 5k \Omega || 10 k \Omega}{26 \Omega +200 \Omega} \nonumber \]

\[A_v =−19 \nonumber \]

Нам также необходимо учесть влияние импеданса источника 600 \( \Omega \) . Это создаст делитель напряжения с входным сопротивлением.

\[A_{делитель} = \frac{Z_{in}}{Z_{in}+Z_{источник}} \nonumber \]

\[A_{divider} = \frac{3,22 k \Omega}{ 3,22 к \Омега +600 \Омега} \номер\]

\[A_{делитель} = 0,843 \нечисло \]

\[A_{v (система)} = A_v \times A_{делитель} \нечисло \]

\[A_{v (система)} =- 19 \times 0.843 \number \]

\[A_{v (system)} =−16 \nonnumber \]

Наконец, мы подошли к напряжению нагрузки.

\[V_{нагрузка} = A_{v (система)} \times V_{in} \nonumber \]

\[V_{нагрузка} =−16 \times 20 мВ \nonumber \]

\[V_ {нагрузка} = 320 мВ \text{ пиковое, инвертированное} \nonumber \]

Если бы мы проверили схему на рисунке \(\PageIndex{5}\) с помощью осциллографа с прямой связью, мы увидели бы наложение переменного тока и компоненты постоянного тока. Другими словами, мы увидим, что сигнал переменного тока накладывается на смещение постоянного тока. В некоторых случаях сигнал переменного тока будет слишком мал, чтобы его можно было заметить, по сравнению с частью постоянного тока. В правильном масштабе он может быть не толще самого следа. Чтобы измерить его точно, нам пришлось бы подключить осциллограф по переменному току.

Напряжения на источнике и нагрузке будут только переменными, поскольку разделительные конденсаторы блокируют постоянный ток. В базе у нас было бы 15 вольт постоянного тока с сигналом переменного тока поверх него. Переменный ток будет равен входному напряжению 20 мВ, умноженному на делитель входного импеданса/импеданса источника, равный 0,843 или 16,86 мВ. Учитывая, что \(I_C\) составляет 1 мА, падение постоянного тока на \(R_C\) должно быть 7,5 вольт. Это, конечно, \(V_C\). Следовательно, на коллекторе мы увидим инвертированный сигнал 320 мВ на 7,5 вольт постоянного тока.

Компьютерное моделирование

Чтобы получить некоторое представление о проблеме заболачивания и искажения, мы рассмотрим более сложное моделирование схемы. Это повторит примеры \(\PageIndex{1}\) и \(\PageIndex{2}\) в том смысле, что мы будем моделировать две схемы с одинаковыми эквивалентами постоянного тока. Единственное изменение схемы будет состоять в том, что одна версия будет иметь полностью зашунтированный эмиттер, а другая версия будет использовать шунтирующий резистор. Чтобы сравнение было честным, мы увеличим напряжение входного сигнала усилителя с низким коэффициентом усиления, чтобы обе версии имели одинаковое напряжение нагрузки. Таким образом, мы гарантируем, что они оба используют одинаковый процент кривой соединения.

Незаболоченная схема показана на рисунке \(\PageIndex{6}\). Здесь используется прямое смещение эмиттера с двумя источниками питания.

Рисунок \(\PageIndex{6}\): Незаболоченный усилитель CE в симуляторе.

Быстрая приблизительная оценка дает \(I_C \приблизительно 2\) мА, что дает \(r’_e \приблизительно 13 \Омега\). Нагрузка будет около 3к\(\Омега\), что дает прирост в младших 200-х.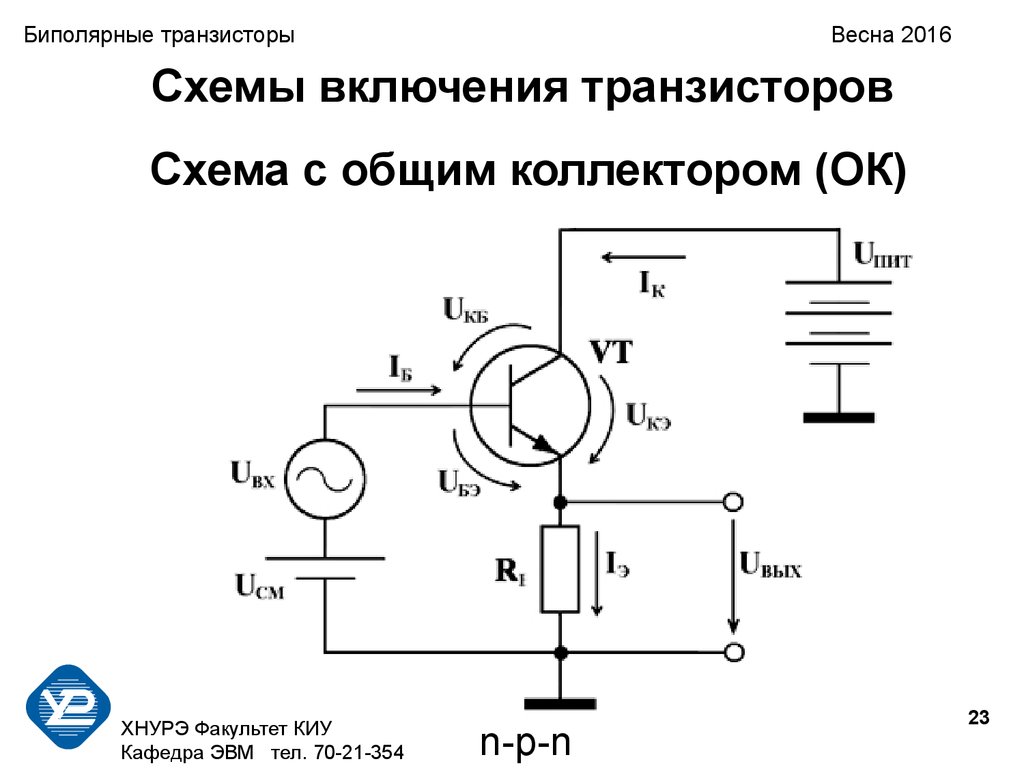 Таким образом, мы ожидаем, что напряжение нагрузки будет около 2 вольт.

График анализа переходных процессов показан на рисунке \(\PageIndex{7}\). Показаны несколько следов.

Рисунок \(\PageIndex{7}\): Незаболоченный усилитель CE, анализ переходных процессов.

При таком масштабе сигнал переменного тока на входе (узел 4, фиолетовый) и на базе (узел 2, бирюзовый) не виден. Как и ожидалось, мы видим небольшое отрицательное значение постоянного тока на базе и на эмиттере, около -0,7 В постоянного тока. Смещение постоянного тока на коллекторе, как и ожидалось, составляет около 8 вольт. Наконец, напряжение нагрузки (узел 5, синий) составляет около 2 вольт.

То, что может быть не видно сразу на графике напряжения нагрузки, так это некоторое искажение асимметрии формы волны. Это можно количественно оценить с помощью моделирования THD, результаты которого показаны на рисунке \(\PageIndex{8}\). Коэффициент нелинейных искажений составляет почти 8%. Не так хорошо, как хотелось бы.

Рисунок \(\PageIndex{8}\): Усилитель CE без заболачивания, анализ THD.

Для второго прохода схема модифицируется для включения шунтирующего резистора, как показано на рисунке \(\PageIndex{9}\). Первоначальный эмиттерный резистор на 4,7 кОм (\Омега\) был разделен на 4,5 кОм (\Омега\) и 200 Ом (\Омега\) заглушающий резистор. Смещение в этой схеме идентично первой, поэтому \(r’_e\) не изменяется. Это снизит наше ожидаемое усиление примерно до 13, уменьшившись в 15 раз. Входной сигнал увеличивается в 15 раз для компенсации, так что наше напряжение нагрузки по-прежнему будет около 2 вольт.

Рисунок \(\PageIndex{9}\): Залитый усилитель CE в симуляторе

Еще раз проведем анализ переходных процессов. Результаты показаны на рисунке \(\PageIndex{10}\). В данном случае мы поступили немного иначе. Увеличив масштаб, мы теперь можем подтвердить инверсию сигнала. Входной сигнал — это фиолетовая кривая в узле 4. Мы также можем видеть этот сигнал в основании, опираясь на небольшое отрицательное напряжение смещения постоянного тока (голубая дорожка, узел 2).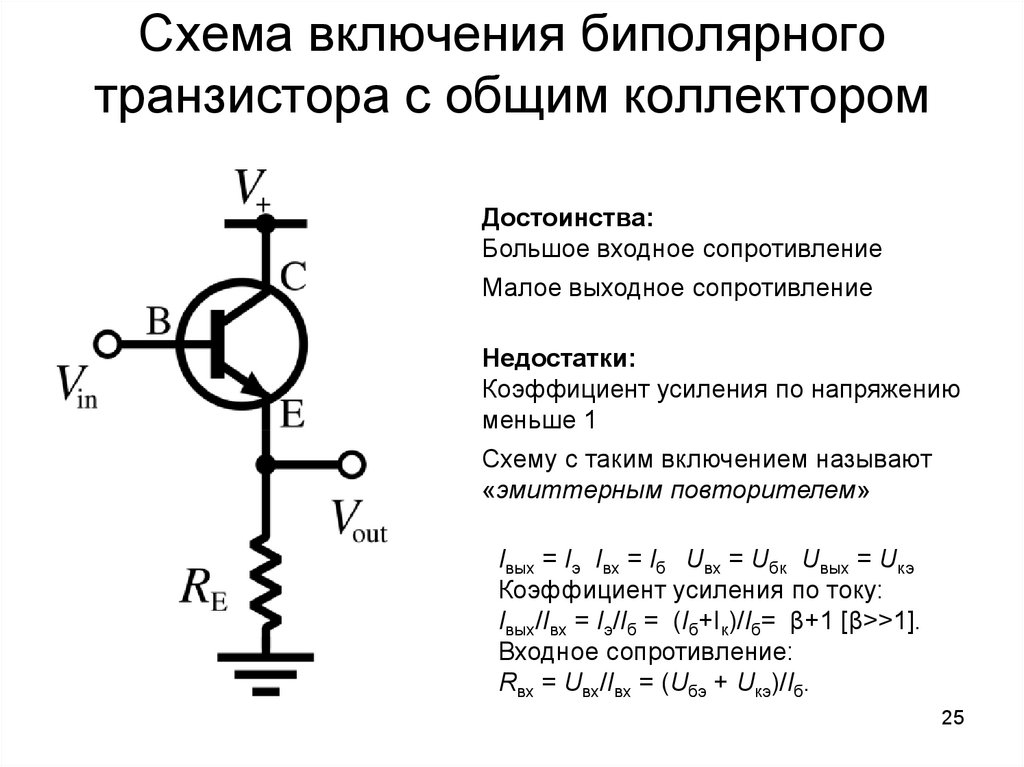 Смещение постоянного тока составляет около -0,1 вольта. Глядя на эмиттер, мы видим ожидаемое падение напряжения база-эмиттер на 0,7 В постоянного тока ниже этого значения, или около -0,8 В постоянного тока. Обратите внимание, что на эмиттере вообще нет сигнала переменного тока. Это ожидается, так как конденсатор обхода эмиттера принудительно подключает эту точку к заземлению переменного тока.

Напряжение нагрузки — это синяя кривая, узел 5. Хотя большая его часть не видна при таком масштабе, ясно, что это инвертированная форма волны по сравнению с входным сигналом.

Рисунок \(\PageIndex{10}\): Заболоченный усилитель CE, анализ переходных процессов.

А как насчет искажения напряжения нагрузки? Моделирование THD выполняется на заболоченном усилителе, результаты показаны на рисунке \(\PageIndex{11}\). Коэффициент нелинейных искажений теперь ниже 0,6 %, что является значительным улучшением, даже если это не аудиофильское качество. Интересно, что в соотношении уменьшение искажений примерно равно уменьшению усиления.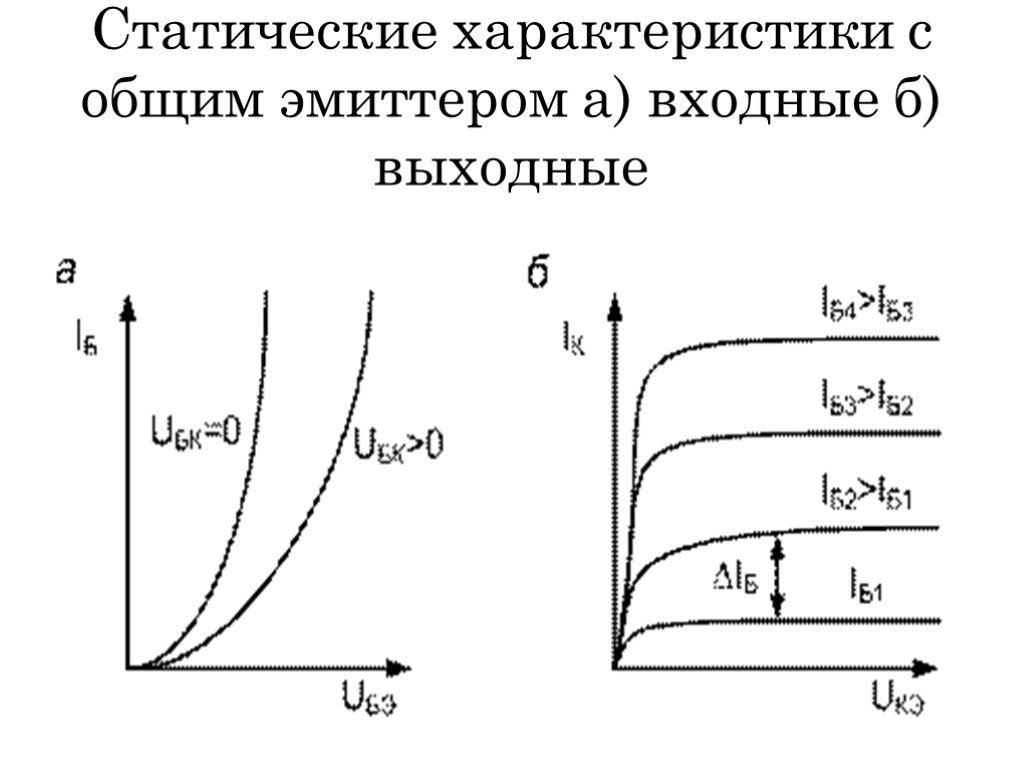 Чем больше вы отдаете, тем больше получаете.

Рисунок \(\PageIndex{11}\): Заболоченный усилитель CE, анализ THD.

Наконец, изменение качества сигнала можно легко увидеть, отобразив одновременно оба напряжения нагрузки, как показано на рисунке \(\PageIndex{12}\). Незаболоченный выход (синий) демонстрирует характерную асимметрию. Обратите внимание, что положительный пик не совсем достигает 2 вольт, а отрицательный пик превышает -2 вольта. Положительный пик также уширен и сглажен, а отрицательный пик более острый. Напротив, заболоченный выходной сигнал (красный) имеет практически идентичные положительные и отрицательные пиковые значения без видимых изменений формы на них. Сравните эту симуляцию с обсуждением искажения формы волны из главы 6. ​​В частности, сравните рисунок \(\PageIndex{12}\) с рисунком 6.3.4.

Рисунок \(\PageIndex{12}\): Заболоченные и не заболоченные усилители CE, анализ переходных процессов.

7.3.4: Байпас источника питания и развязка

В предыдущем анализе мы исходили из идеального поведения источников питания постоянного тока. Во-первых, мы предположили, что они представляют собой идеальное заземление по переменному току, а во-вторых, что в них нет пульсаций или шума. В действительности это может быть не так, и неидеальное поведение может привести к ряду проблем, снижающих качество усиленного выходного сигнала, включая гул и колебания.

Для решения первой проблемы можно использовать обходные конденсаторы блока питания. Эти конденсаторы обычно имеют скромные размеры, возможно, 1 мкФ или около того, хотя они могут быть и намного больше, особенно в усилителях с высокой выходной мощностью. Блокировочные конденсаторы источника питания расположены физически близко к активным устройствам. Такое расположение сводит к минимуму резистивное и индуктивное воздействие дорожек и проводки печатной платы источника питания, которые могут привести к тому, что источник питания не будет надежно заземлен по переменному току.

Вторая проблема связана с шумом и пульсациями источника питания, которые проникают во входной сигнал и становятся частью выходного сигнала. Классическим примером этого являются усилители, в которых используется смещение делителя напряжения, такое как показано на рисунке \(\PageIndex{5}\). Делитель не только создает необходимый потенциал постоянного тока на базовой клемме, но также компенсирует любые шумы или пульсации, которые могут влиять на напряжение постоянного тока. Это особенно неприятно, потому что этот нежелательный сигнал подается на базу, где он будет усиливаться.

Очевидным решением этой проблемы является создание очень высококачественного регулируемого источника постоянного тока, но это не всегда практично, учитывая ограничения по стоимости. Относительно простое решение состоит в том, чтобы отделить нежелательные компоненты переменного тока через сеть \(RC\), как показано на рисунке \(\PageIndex{13}\).

Рисунок \(\PageIndex{13}\): Делитель напряжения с развязкой.

Конденсатор \(C_D\) используется для создания заземления переменного тока на стыке делителя, таким образом шунтируя любой шум или пульсации на землю. К сожалению, это также приведет к короткому замыканию входного сигнала, поэтому для предотвращения этого добавляется \(R_3\). \(R_3\) параллельно \(Z_{in(base)}\) для создания входного импеданса.

Каталожные номера

¹ Возникает очевидный вопрос: «Как добиться одновременно высокого усиления и низкого уровня искажений?» Одним из решений является использование нескольких каскадов с низким коэффициентом усиления в каскаде.

² «шутки» — настоящее слово? Это если мы все согласимся, что это так. Кроме того, если бы это было воображаемое слово, мы бы написали его «\(j\) funsies».

---

Эта страница под названием 7.3: Усилитель с общим эмиттером распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.