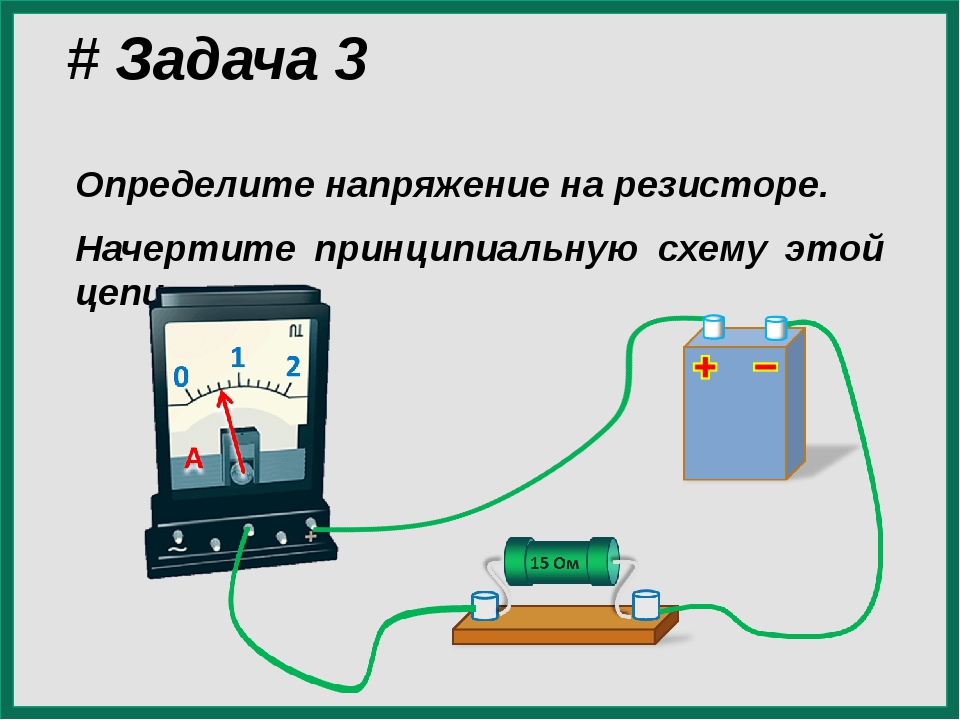
Падение напряжения на резисторе. Расчет падения напряжения на резисторе: формулы и примеры — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать падение напряжения на резисторе. Какие формулы используются для расчета. Как зависит падение напряжения от силы тока и сопротивления. Примеры расчетов для простых электрических цепей.

Содержание

Что такое падение напряжения на резисторе

Падение напряжения на резисторе — это разность потенциалов между его выводами при протекании через него электрического тока. Оно возникает из-за того, что резистор оказывает сопротивление движению электронов.

Основные характеристики падения напряжения на резисторе:

Измеряется в вольтах (В)
Зависит от силы тока и сопротивления резистора
Всегда направлено против движения тока
Приводит к выделению тепла на резисторе

Формулы для расчета падения напряжения

Для расчета падения напряжения на резисторе используются следующие формулы:

U = I * R, где:
- U — падение напряжения (В)
- I — сила тока (А)
- R — сопротивление резистора (Ом)
U = P / I, где:
- P — мощность, выделяемая на резисторе (Вт)
U = √(P * R)

Наиболее часто используется первая формула, основанная на законе Ома. Она позволяет легко рассчитать падение напряжения, зная ток и сопротивление.

От чего зависит падение напряжения

Падение напряжения на резисторе зависит от следующих факторов:

Сила тока — чем больше ток, тем больше падение напряжения
Сопротивление резистора — чем выше сопротивление, тем больше падение напряжения
Мощность, рассеиваемая на резисторе
Температура резистора — при нагреве сопротивление и падение напряжения увеличиваются

Как видно из формулы U = I * R, падение напряжения прямо пропорционально силе тока и сопротивлению. Удвоение любого из этих параметров приведет к удвоению падения напряжения.

Примеры расчета падения напряжения

Рассмотрим несколько примеров расчета падения напряжения на резисторах в простых электрических цепях.

Пример 1: Простая цепь с одним резистором

Дано: резистор 100 Ом подключен к источнику 12 В.

Найти: падение напряжения на резисторе.

Решение:

Найдем ток в цепи по закону Ома: I = U / R = 12 В / 100 Ом = 0.12 А
Рассчитаем падение напряжения: U = I * R = 0.12 А * 100 Ом = 12 В

Ответ: падение напряжения на резисторе равно 12 В, то есть всему приложенному напряжению.

Пример 2: Цепь с двумя последовательными резисторами

Дано: два резистора 100 Ом и 200 Ом подключены последовательно к источнику 12 В.

Найти: падение напряжения на каждом резисторе.

Решение:

Найдем общее сопротивление: R = 100 Ом + 200 Ом = 300 Ом
Рассчитаем ток: I = 12 В / 300 Ом = 0.04 А
Падение напряжения на первом резисторе: U1 = 0.04 А * 100 Ом = 4 В
Падение напряжения на втором резисторе: U2 = 0.04 А * 200 Ом = 8 В

Ответ: падение напряжения на первом резисторе 4 В, на втором — 8 В.

Практическое применение расчетов падения напряжения

Расчет падения напряжения на резисторах имеет важное практическое значение в электронике:

Позволяет определить напряжение на элементах схемы
Используется при проектировании делителей напряжения
Помогает рассчитать мощность, выделяемую на резисторах
Необходим для подбора номиналов резисторов в схемах
Применяется при расчете цепей питания и защиты

Правильный расчет падения напряжения позволяет обеспечить корректную работу электронных устройств и избежать выхода компонентов из строя из-за перегрузки.

Измерение падения напряжения на практике

Для измерения падения напряжения на резисторе используется вольтметр. Порядок измерения:

Подключите щупы вольтметра параллельно резистору

Установите предел измерения больше ожидаемого значения
Включите питание схемы
Считайте показания вольтметра

При измерении важно соблюдать правила техники безопасности и не превышать допустимые напряжения для прибора. Для точных измерений рекомендуется использовать цифровые мультиметры.

Особенности падения напряжения в цепях переменного тока

В цепях переменного тока падение напряжения на резисторе имеет некоторые особенности:

Значение падения напряжения меняется во времени
Используются действующие (среднеквадратичные) значения напряжения и тока
Необходимо учитывать реактивное сопротивление элементов
Возникает сдвиг фаз между током и напряжением

Расчет падения напряжения в цепях переменного тока более сложен и требует применения векторных диаграмм и комплексных чисел.

Заключение

Расчет падения напряжения на резисторе — важная задача при анализе и проектировании электрических цепей. Зная основные формулы и принципы, можно легко определить напряжение на элементах схемы. Это позволяет правильно подобрать компоненты и обеспечить надежную работу электронных устройств.

Падение напряжения — NikiWiki

Согласно Закону Ома на учатске цепи, обладающем сопротивлением R через который протекает ток I возникает падение напряжение:

Падение напряжения

U = I*R

Таким образом, в цепи на каждом сопротивлении падение напряжение будет пропорционально протекающему в цепи току и сопротивлению каждого из резисторов, соответственно R₁ и R₂

ΔU₁ = I * R₁
ΔU₂ = I * R₂

При этом, мощность, выделяемая на участке цепи будет равна

P = U * I

А на каждом из резисторов выделяемая мощность будет равна:

P₁ = I * ΔU₁
P₂ = I * ΔU₂

Все это имеет смысл в применении к резисторам, применяемым для измерения тока в цепи по падению напряжения. Так, из формул выше следует, что ток, протекающий через резистор можно соотнести с падением напряжения на этом резисторе как:

I = ΔU₁ / R₁

Если взять, к примеру, токоизмерительный резистор сопротивлением 1 Ом и измерить на нем напряжение, которое будет равно, скажем 1 В, то протекающий в цепи ток будет равен 1 А.

Однако, такое сопротивление и, как следствие, выделяемая мощность на резисторе, чреваты боком. Мощность будет равна 1 Вт, что значительно снизит КПД любой схемы рас рассчитанной на сбережение энергии источника.

Именно по этой причине токоизмерительные резисторы стараются делать максимально малого сопротивления, но такого, чтобы была возможность измерить падение напряжения на нем с достаточной точностью. Без дополнительного усиления измеряемого сигнала и, соответственно дополнительных погрешностей и элементов.

Например. Известная схема, построенная на компараторе LM398 с гистерезисом 30мв стабильно работает лишь при падении напряжения больше 0.1 вольта и меньше 0.2В (стабильный результат, хотя, можно и больше). Исходя из этого, если схема рассчитывается для питания светодиода, потребляющего 1А, то, R = U / I? т.е. 0.1 или 0.2 Ома. А выделяемая на резисторе мощность при этом будет 0.1 или 0.2 Вт. Что тоже не мало, но значительно эффективнее.

Таким образом на каждом из резисторов выделится энергия пропорциональная падению напряжения и

Падение напряжения — Voltage drop

Падение напряжения — это уменьшение электрического потенциала на пути тока, протекающего в электрической цепи . Падения напряжения на внутреннем сопротивлении источника, на проводниках , на контактах и на разъемах нежелательны, поскольку часть подаваемой энергии рассеивается. Падение напряжения на электрической нагрузке пропорционально мощности, доступной для преобразования в этой нагрузке в какой-либо другой полезный вид энергии.

Например, электрический обогреватель может иметь сопротивление десять Ом , а провода, которые его питают, могут иметь сопротивление 0,2 Ом, что составляет около 2% от общего сопротивления цепи. Это означает, что примерно 2% подаваемого напряжения теряется в самом проводе. Чрезмерное падение напряжения может привести к неудовлетворительной работе обогревателя и перегреву проводов и соединений.

Национальные и местные электротехнические нормы и правила могут устанавливать рекомендации по максимально допустимому падению напряжения в электропроводке для обеспечения эффективности распределения и правильной работы электрического оборудования. Максимально допустимое падение напряжения варьируется от страны к стране.

В электронной конструкции и передаче энергии используются различные методы для компенсации эффекта падения напряжения в длинных цепях или там, где необходимо точно поддерживать уровни напряжения. Самый простой способ уменьшить падение напряжения — увеличить диаметр проводника между источником и нагрузкой, что снизит общее сопротивление. В системах распределения электроэнергии заданное количество мощности может передаваться с меньшим падением напряжения, если используется более высокое напряжение. Более сложные методы используют активные элементы для компенсации чрезмерного падения напряжения.

Падение напряжения в цепях постоянного тока: сопротивление

Рассмотрим постоянного тока цепи с девятью вольт постоянного тока источника; три резистора по 67 Ом , 100 Ом и 470 Ом; и лампочка — все подключены последовательно . Источник постоянного тока, проводники (провода), резисторы и лампочка ( нагрузка ) имеют сопротивление ; все в той или иной степени используют и рассеивают подаваемую энергию.

Их физические характеристики определяют, сколько энергии. Например, сопротивление проводника постоянному току зависит от длины, площади поперечного сечения, типа материала и температуры.

Если измерить напряжение между источником постоянного тока и первым резистором (67 Ом), потенциал напряжения на первом резисторе будет немного меньше девяти вольт. Ток проходит по проводнику (проводу) от источника постоянного тока к первому резистору; при этом часть подаваемой энергии «теряется» (недоступна для нагрузки) из-за сопротивления проводника. Падение напряжения существует как в питающем, так и в обратном проводах цепи. Если измеряется падение напряжения на каждом резисторе, результат измерения будет значительным. Это представляет собой энергию, используемую резистором. Чем больше резистор, тем больше энергии используется этим резистором и тем больше падение напряжения на этом резисторе.

Для проверки падения напряжения можно использовать закон Ома . В цепи постоянного тока напряжение равно току, умноженному на сопротивление.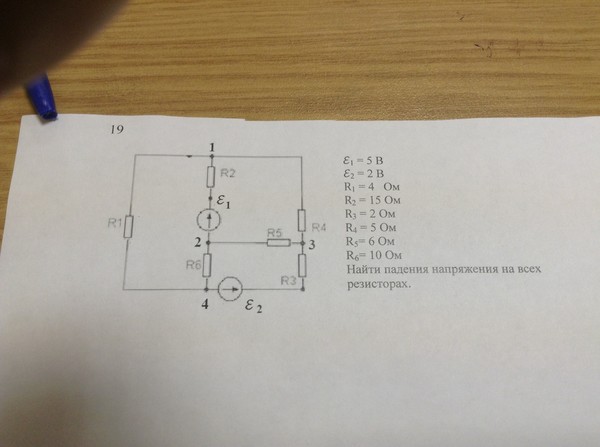 V = I R . Кроме того, законы Кирхгофа для цепей гласят, что в любой цепи постоянного тока сумма падений напряжения на каждом компоненте цепи равна напряжению питания.

Падение напряжения в цепях переменного тока: полное сопротивление

В цепях переменного тока противодействие протеканию тока происходит из-за сопротивления, как и в цепях постоянного тока. Однако цепи переменного тока также включают в себя второй вид сопротивления протеканию тока: реактивное сопротивление . Сумма противодействий току от сопротивления и реактивного сопротивления называется импедансом .

Электрический импеданс обычно представлен переменной Z и измеряется в омах на определенной частоте. Электрический импеданс вычисляется как векторная сумма электрического сопротивления , емкостного реактивного сопротивления и индуктивного реактивного сопротивления .

Величина импеданса в цепи переменного тока зависит от частоты переменного тока и магнитной проницаемости электрических проводников и электрически изолированных элементов (включая окружающие элементы), которая зависит от их размера и расстояния.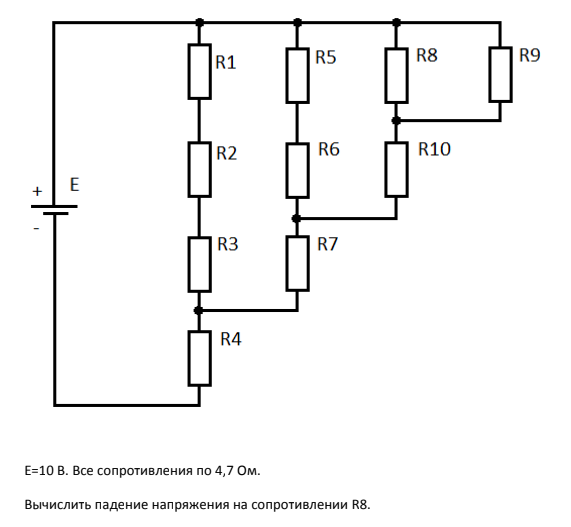

По аналогии с законом Ома для постоянного тока цепей, электрический импеданс может быть выражена формулой E = I Z . Таким образом, падение напряжения в цепи переменного тока является произведением силы тока и полного сопротивления цепи.

Смотрите также

Ссылки

Электротехнические принципы для электротехники (Джим Дженнессон) 5-е издание

внешние ссылки

Какое напряжение после резистора. Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Есть другой способ снижения напряжения на нагрузке, но только для цепей постоянного тока. Про смотри здесь.

Вместо дополнительного резистора используют цепочку из последовательно включенных, в прямом направлении, диодов.

Весь смысл состоит в том, что при протекании тока через диод на нем падает «прямое напряжение» равное, в зависимости от типа диода, мощности и тока протекающего через него — от 0,5 до 1,2 Волта.

На германиевом диоде падает напряжение 0,5 — 0,7 В, на кремниевом от 0,6 до 1,2 Вольта. Исходя из того, на сколько вольт нужно понизить напряжение на нагрузке, включают соответствующее количество диодов.

Чтобы понизить напряжение на 6 В необходимо приблизительно включить: 6 В: 1,0 = 6 штук кремниевых диодов, 6 В: 0,6 = 10 штук германиевых диодов. Наиболее популярны и доступны кремниевые диоды.

Выше приведенная схема с диодами, более громоздка в исполнении, чем с простым резистором. Но, выходное напряжение, в схеме с диодами, более стабильно и слабо зависит от нагрузки. В чем разница между этими двумя способами снижения выходного напряжения?

На Рис 1 — добавочное сопротивление — резистор (проволочное сопротивление), Рис 2 — добавочное сопротивление — диод.

У резистора (проволочного сопротивления) линейная зависимость между током, проходящем через него и падением напряжения на нем. Во сколько раз увеличится ток, во столько же раз увеличится и падение напряжения на резисторе.

Из примера 1: если мы к лампочке подключим параллельно еще одну, то ток в цепи увеличится, с учетом общего сопротивления двух лампочек до 0,66 А. Падение напряжения на добавочном резисторе будет: 12 Ом *0,66 А = 7,92 В. На лампочках останется: 12 В — 7,92 В = 4,08 В. Они будут гореть в пол накала.

Совсем другая картина будет если вместо резистора будет цепочка диодов.

Зависимость между током протекающем через диод и падающем на нем напряжении нелинейная. Ток может увеличиться в несколько раз, падение напряжения на диоде увеличится всего на несколько десятых вольта.

Т.е. чем больше ток диода, тем (сравнительно с резистором) меньше увеличивается его сопротивление. Падение напряжения на диодах мало зависит от тока в цепи.

Диоды в такой цепи выполняют роль стабилизатора напряжения. Диоды необходимо подбирать по максимальному току в цепи. Максимально допустимый ток диодов должен быть больше, чем ток в рассчитываемой цепи.

Падения напряжения на некоторых диодах при токе 0,5 А даны в таблице.

В цепях переменного тока, в качестве добавочного сопротивления можно использовать конденсатор, индуктивность, динистор или тиристор (с добавлением схемы управления).

Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.

Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в (имеется в виду глобальная классификация). Их всего два вида. Первый — это напряжение который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид — это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.

На практике это выглядит следующим образом. Например, если взять обычную вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания — проводники — нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на которым обладает лампа.

Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:

где R — активное сопротивление цепи или ее элемента, измеряется в Омах; U — электрическое напряжение, в Вольтах; и, наконец, I — ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа — вышеуказанная формула.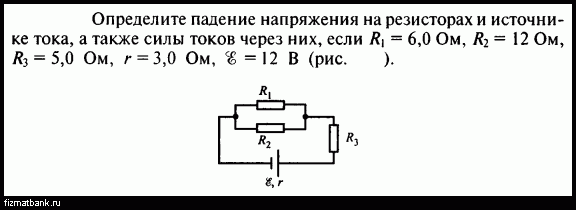

Электрическая энергия — это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны. Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения. Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.

Падение напряжения на резисторе зависит от его и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.

Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На приходится дополнительно учитывать реактивную составляющую.

Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС — E.

Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:

R = (R1*R2) / (R1+R2)

Определяем сопротивление всей цепи через сумму R4 = R+R3.

Рассчитываем ток:

Остается узнать значение падение напряжения на выбраном элементе:

Здесь множитель «R5» может быть любым R — от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.

Итак, резистор … Базовый элемент построения электрической цепи.

Работа резистора заключается в ограничении тока , протекающего по цепи. НЕ в превращении тока в тепло, а именно в ограничении тока . То есть, без резистора по цепи течет большой ток , встроили резистор – ток уменьшился. В этом заключается его работа, совершая которую данный элемент электрической цепи выделяет тепло.

Пример с лампочкой

Рассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток , проходящий через цепь. И Резистор . Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток , например, 0,75А. Лампочка горит ярко. Встроили в цепь резистор — у тока появился труднопреодолимый барьер, протекающий по цепи ток снизился до 0,2А. Лампочка горит менее ярко. Стоит отметить, что яркость, с которой горит лампочка, зависит так же и от напряжения на ней. Чем выше напряжение — тем ярче.

Кроме того, на резисторе происходит падение напряжения . Барьер не только задерживает ток , но и «съедает» часть напряжения, приложенного источником питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт. На всякий случай амперметр, два вольтметра про запас, лампочку и резистор . Включаем цепь без резистора (слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр(снизу на схеме справа) показывает 5В. На лампочку остались остальные 12В-5В=7В. Вольтметр на лампочке показал 7В.

Разумеется, оба примера являются абстрактными, неточными в плане чисел и рассчитаны на объяснение сути процесса, происходящего в резисторе .

Основная характеристика резистора — сопротивление . Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление , тем больший ток он способен ограничить, тем больше тепла он выделяет, тем больше напряжения падает на нем.

Основной закон всего электричества. Связывает между собой Напряжение(V), Силу тока (I) и Сопротивление(R).

Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте используем Закон Ома для нашей цепи с резистором и лампочкой, рассмотренной выше, и рассчитаем сопротивление резистора , при котором ток от источника питания на 12В ограничится до 0,2. При этом считаем сопротивление лампочки равным 0.

V=I*R => R=V/I => R= 12В / 0,2А => R=60Ом

Итак. Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи , будет составлять 0,2А.

Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении схем для реальных устройств.

Мощность электрического тока на каком-либо участке цепи равна произведению силы тока, протекающую по этому участку на напряжение на этом участке цепи. P=I*U. Единица измерения 1Вт.

При протекании тока через резистор совершается работа по ограничению электрического тока . При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающую среду. Но если резистор будет совершать слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.

Характеристика мощности резистора — это максимальная мощность тока, которую он способен выдержать и не перегреться.

Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток , проходящий по цепи(а значит и через резистор ), равный 0,2А. Падение напряжения на резисторе равно 5В (не 12В, не 7В, а именно 5 — те самые 5, которые вольтметр показывает на резисторе ). Это значит, что мощность тока через резистор равна P=I*V=0,2А*5В=1Вт. Делаем вывод: резистор для нашей цепи должен иметь максимальную мощность не менее(а лучше более) 1Вт. Иначе он перегреется и выйдет из строя.

Соединение резисторов

Резисторы в цепях электрического тока имеют последовательное и параллельное соединение .

При последовательном соединении общее сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:

При параллельном соединении общее сопротивление резисторов рассчитывается по формуле:

Остались вопросы? Напишите комментарий.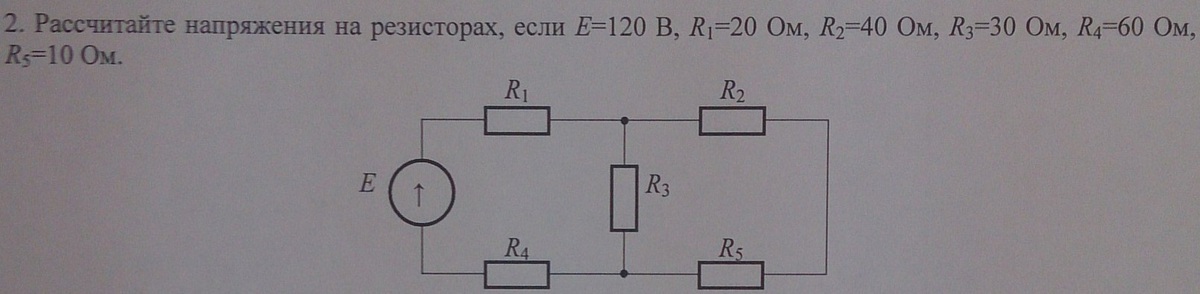 Мы ответим и поможем разобраться =)

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.

Пример 1

Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r = 0,5 Ом. Сопротивления резисторов R 1 = 20 и R 2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей .

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2

Общий ток цепи, содержащей два соединенных параллельно резистора R 1 =70 Ом и R 2 =90 Ом, равен 500 мА.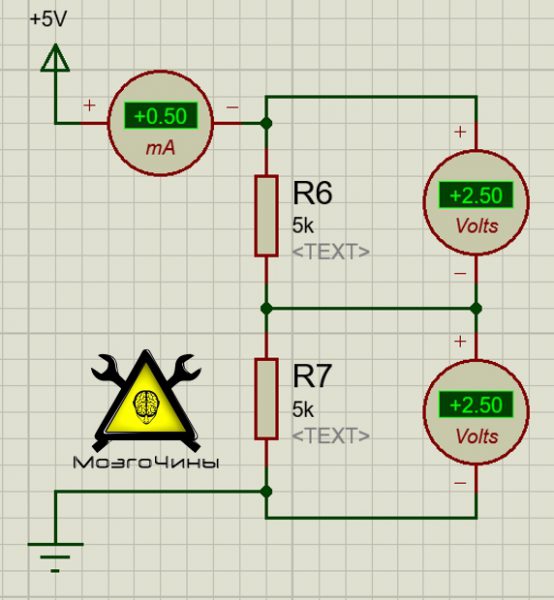 Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока . Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.

Токи в резисторах

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала

Вычислить падение напряжения на резисторе. Падение напряжения

В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.

Представление об электричестве

Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.

Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору.
Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда:
— Сколько тока втекает в узел, столько из него и вытекает
— Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы.
— Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь.
— Электрический ток будет увеличиваться при уменьшении сопротивления, как и скорость потока воды будет увеличиваться с уменьшением сопротивления клапана.

Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.

Резистор

Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах . Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания. Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего. Некоторые датчики основаны на том, что сопротивление варьируется в зависимости от освещённости, температуры или механического воздействия, об этом подробно написано в конце статьи.

Закон Ома

Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе. Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи.

Последовательное и параллельное соединение резисторов

Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:

В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой:

В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:

Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет.
Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути
электрическому току, снижая общее сопротивление цепи.

Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R 3 =R 1 +R 2

В интернете есть удобные он-лайн калькуляторы для расчета и соединения резисторов.

Токоограничивающий резистор

Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их работы, давайте сначала разберём простую схему, где лампа непосредственно подключена к 9В батареи. Лампа, как и любое другое устройство, которое потребляет электроэнергию для выполнения определенной задачи (например, светоизлучение) имеет внутреннее сопротивление, которое определяет его текущее потребление. Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.

Теперь, когда лампа будет рассматриваться как резистор, мы можем использовать закон Ома для расчета тока, проходящего через него. Закон Ома гласит, что ток, проходящий через резистор равен разности напряжений на нем, поделенное на сопротивление резистора: I=V/R или точнее так:
I=(V 1 -V 2)/R
где (V 1 -V 2) является разностью напряжений до и после резистора.

Теперь обратите внимание на рисунок выше, где добавлен токоограничительный резистор. Он будет ограничивать ток идущий к лампе, как это следует из названия. Вы можете контролировать, количество тока протекающего через лампу, просто выбрав правильное значение R1. Большой резистор будет сильно снижать ток, а небольшой резистор менее сильно (так же, как в нашей аналогии с водой).

Математически это запишется так:

Из формулы следует, что ток уменьшится, если значение R1 увеличится. Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.

Вы можете воспользоваться он-лайн калькулятором для .

Резисторы как делитель напряжения

Как следует из названия, резисторы могут быть использованы в качестве делителя напряжения, другими словами, они могут быть использованы для уменьшения напряжения путем деления его. Формула:

Если оба резистора имеют одинаковое значение (R 1 =R 2 =R), то формулу можно записать так:

Другой распространенный тип делителя, когда один резистор подключен к земле (0В), как показано на рисунке 6B.
Заменив Vb на 0 в формуле 6А, получаем:

Узловой анализ

Теперь, когда вы начинаете работать с электронными схемами, важно уметь их анализировать и рассчитывать все необходимые напряжения, токи и сопротивления. Есть много способов для изучения электронных схем, и одним из наиболее распространенных методов является узловой, где вы просто применяете набор правил, и рассчитываете шаг за шагом все необходимые переменные.

Упрощенные правила узлового анализа

Определение узла

Узел – это любая точка соединения в цепи. Точки, которые связаны друг с другом, без других компонентов между ними рассматриваются как единый узел. Таким образом, бесконечное число проводников в одну точку считаются одним узлом. Все точки, которые сгруппированы в один узел, имеют одинаковые напряжения.

Определение ветви

Ветвь представляет собой набор из 1 и более компонентов, соединенных последовательно, и все компоненты, которые подсоединены последовательно к этой цепи, рассматриваются как одна ветвь.

Все напряжения обычно измеряются относительно земли напряжение на которой всегда равно 0 вольт.

Ток всегда течет от узла с более высоким напряжением на узел с более низким.

Напряжение на узле может быть высчитано из напряжения около узла, с помощью формулы:
V 1 -V 2 =I 1 *(R 1)
Перенесем:
V 2 =V 1 -(I 1 *R 1)
Где V 2 является искомым напряжением, V 1 является опорным напряжением, которое известно, I 1 ток, протекающий от узла 1 к узлу 2 и R 1 представляет собой сопротивление между 2 узлами.

Точно так же, как и в законе Ома, ток ответвления можно определить, если напряжение 2х соседних узлах и сопротивление известно:
I 1 =(V 1 -V 2)/R 1

Текущий входящий ток узла равен текущему выходящему току, таким образом, это можно записать так: I 1 + I 3 =I 2

Важно, чтобы вы были в состоянии понимать смысл этих простых формул.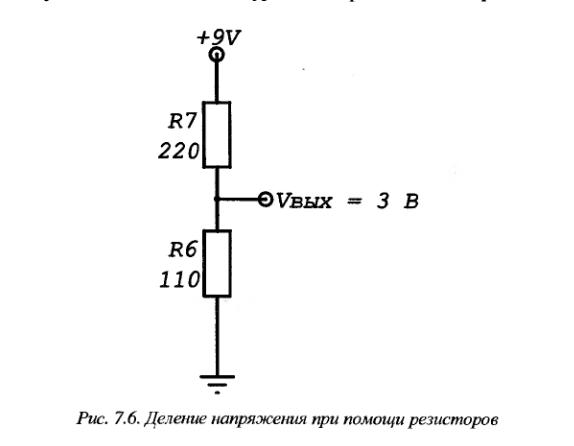 Например, на рисунке выше, ток протекает от V1 до V2, и, следовательно, напряжение V2 должно быть меньше, чем V1.
Используя соответствующие правила в нужный момент, вы сможете быстро и легко проанализировать схему и понять её. Это умение достигается практикой и опытом.

Расчет необходимой мощности резистора

При покупке резистора вам могут задать вопрос: «Резисторы какой мощности вы хотите?» или могут просто дать 0.25Вт резисторы, поскольку они являются наиболее популярными.
Пока вы работаете с сопротивлением больше 220 Ом, и ваш блок питания обеспечивает 9В или меньше, можно работать с 0.125Вт или 0.25Вт резисторами. Но если напряжение более 10В или значение сопротивления менее 220 Ом, вы должны рассчитать мощность резистора, или он может сгореть и испортить прибор. Чтобы вычислить необходимую мощность резистора, вы должны знать напряжение через резистор (V) и ток, протекающий через него (I):
P=I*V
где ток измеряется в амперах (А), напряжение в вольтах (В) и Р — рассеиваемая мощность в ваттах (Вт)

На фото предоставлены резисторы различной мощности, в основном они отличаются размером.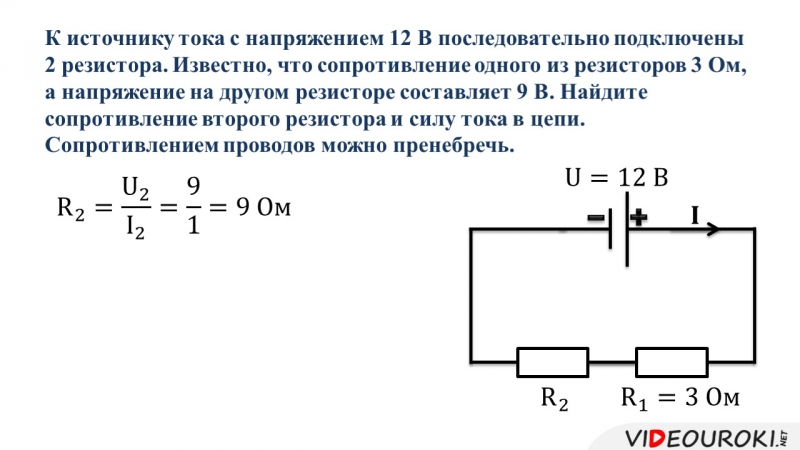

Разновидности резисторов

Резисторы могут быть разными, начиная от простых переменных резисторов (потенциометров) до реагирующих на температуру, свет и давление. Некоторые из них будут обсуждаться в этом разделе.

Переменный резистор (потенциометр)

На рисунке выше показано схематическое изображение переменного резистора. Он часто упоминается как потенциометр, потому что он может быть использован в качестве делителя напряжения.

Они различаются по размеру и форме, но все работают одинаково. Выводы справа и слева эквивалентны фиксированной точке (например, Va и Vb на рисунке выше слева), а средний вывод является подвижной частью потенциометра, а также используется для изменения соотношения сопротивления на левом и правом выводах. Следовательно, потенциометр относится к делителям напряжения, которым можно выставить любое напряжение от Va к Vb.
Кроме того, переменный резистор может быть использован как тока ограничивающий путем соединения выводов Vout и Vb, как на рисунке выше (справа). Представьте себе, как ток будет течь через сопротивление от левого вывода к правому, пока не достигнет подвижной части, и пойдет по ней, при этом, на вторую часть пойдет очень мало тока. Таким образом, вы можете использовать потенциометр для регулировки тока любых электронных компонентов, например лампы.

LDR (светочувствительные резисторы) и термисторы

Есть много датчиков основанных на резисторах, которые реагируют на свет, температуру или давление. Большинство из них включаются как часть делителя напряжения, которое изменяется в зависимости от сопротивления резисторов, изменяющегося под воздействием внешних факторов.

Фоторезистор (LDR)

Как вы можете видеть на рисунке 11A, фоторезисторы различаются по размеру, но все они являются резисторами, сопротивление которых уменьшается под воздействием света и увеличивается в темноте. К сожалению, фоторезисторы достаточно медленно реагируют на изменение уровня освещённости, имеют достаточно низкую точность, но очень просты в использовании и популярны. Как правило, сопротивление фоторезисторов может варьироваться от 50 Ом при солнце, до более чем 10МОм в абсолютной темноте.

Как мы уже говорили, изменение сопротивления изменяет напряжение с делителя. Выходное напряжение можно рассчитать по формуле:

Если предположить, что сопротивление LDR изменяется от 10 МОм до 50 Ом, то V out будет соответственно от 0.005В до 4.975В.

Термистор похож на фоторезистор, тем не менее, термисторы имею гораздо больше типов, чем фоторезисторы, например, термистор может быть либо с отрицательным температурным коэффициентом (NTC), сопротивление которого уменьшается с повышением температуры, или положительным температурным коэффициентом (PTC), сопротивление которого будет увеличиваться с повышением температуры. Сейчас термисторы реагируют на изменение параметров среды очень быстро и точно.

Про определение номинала резистора используя цветовую маркировку можно почитать .

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.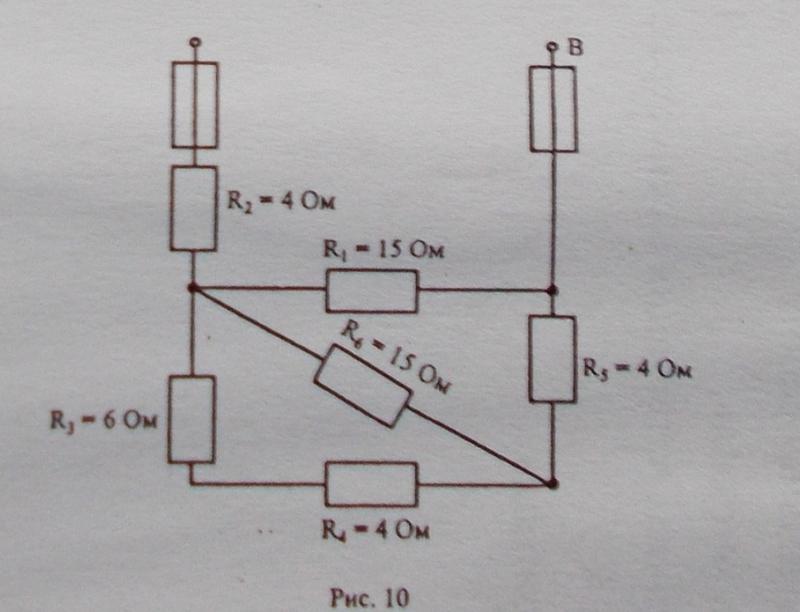

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на .

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн

Примечание: десятичные значения вводите через точку

Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Каждый уважающий себя радио-мастер обязан знать формулы для расчета различных электрических величин. Ведь при ремонте электронных устройств или сборке электронных самоделок очень часто приходится проводить подобные расчеты. Не зная таких формул очень сложно и трудоемко, а порой и невозможно справиться с подобного рода задачей!

Первое, что нужно усвоить – ВСЕ ВЕЛЕЧИНЫ В ФОРМУЛАХ УКАЗЫВАЮТЬСЯ В АМПЕРАХ, ВОЛЬТАХ, ОМАХ, МЕТРАХ И КИЛОГЕРЦАХ.

Закон Ома.

Известный из школьного курса физики ЗАКОН ОМА. На нем строится большинство расчетов в радиоэлектронике. Закон Ома выражается в трех формулах:

Где: I – сила тока (А), U – напряжение (В), R– сопротивление, имеющееся в цепи (Ом).

Теперь рассмотрим на практике применение формул в радиолюбительских расчетах.

Сопротивление гасящего резистора рассчитывают по формуле: R= U /I

Где: U – излишек напряжения, который необходимо погасить (В), I – ток потребляемый цепью или устройством (А).

Расчет мощности гасящего резистора проводят по формуле: P=I 2 R

Где I – ток потребляемый цепью или устройством (А), R– сопротивление резистора (Ом).

Напряжение падения на сопротивлении можно рассчитать по формуле: U пад =RI

Где R– сопротивление гасящего резистора (Ом), I– ток потребляемый устройством или цепью (А).

Где P– мощность устройства (Вт), U– напряжение питания устройства (В).

Где I– ток потребляемый устройством (А), U– напряжение питания устройства (В).

Где ƒ-частота в килогерцах ƛ- длинна волны в метрах.

Где ƛ- длинна волны в метрах, ƒ – частота в килогерцах.

Рассчитать номинальную выходную мощность звуковоспроизводящего устройства (усилитель, проигрыватель и т.п.) можно по формуле: P=U 2 вых. / R ном .

Где U 2 – напряжение звуковой частоты на нагрузке, R– номинальное сопротивление нагрузки.

И в завершении еще несколько формул. По этим формулам, ведут расчет сопротивления и емкости резисторов и конденсаторов в тех случаях, когда возникает необходимость в параллельном или последовательном их соединении.

Расчет соединенных параллельно двух резисторов производят по формуле: R=R 1 R 2 /(R 1 +R 2)

Где R 1 и R 2 — сопротивление первого и второго резистора соответственно (Ом).

Расчет сопротивления включенных параллельно более чем двух резисторов проводят по формуле: 1/R=1/R 1 +1/R 2 +1/R n…

Где R 1 , R 2 , R n … — сопротивление первого, второго и последующих резисторов соответственно (Ом).

Расчет емкости соединенных параллельно нескольких конденсаторов проводят по формуле: C=C 1 + C 2 +C n …

Где C 1 , C 2 и C n – емкость первого, второго и последующих конденсаторов соответственно (мФ).

Расчет емкости двух соединенных последовательно конденсаторов проводят по формуле: C=C 1 C 2 /C 1 +C 2

Где C 1 и C 2 – емкость первого и второго конденсаторов соответственно (мФ).

Расчет емкости включенных последовательно более чем двух конденсаторов проводят по формуле :

Пример 1

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Пример 2

Токи в резисторах

Закон Кирхгофа для напряжения электрической цепи

Главная страница » Закон Кирхгофа для напряжения электрической цепи

Второй закон Кирхгофа демонстрирует сохранение энергии по кругу замкнутого контура. Рассмотрим эту концепцию с теоретической точки зрения, чтобы иметь представление о Законе Кирхгофа. Этот закон также является важным опорным потенциалом для инженеров, занимающихся построением электронных схем разной сложности.

СОДЕРЖИМОЕ ПУБЛИКАЦИИ :

Алгебраическая сумма разностей потенциалов

Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю.

Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:

ΣV = 0

Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура.

Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.

Следовательно, любое падение напряжения по кругу контура теоретически равно потенциалу любых источников напряжения, встречающихся на этом пути.

Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой.

ЭЛЕКТРИЧЕСКАЯ

Эффект Второго закона Кирхгофа для одиночного элемента замкнутого контура электрической цепи

Для лучшего понимания закона Кирхгофа по напряжению, логично рассмотреть эффект падения напряжения на одном элементе контура, например, на резисторе.

Одиночный контурный элемент — резистор

Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы.

Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).

Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R).

Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.

Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору.

Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус.

Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.

Одиночный контур электрической цепи

Второй закон Кирхгофа утверждает — алгебраическая сумма разностей потенциалов любого замкнутого контура равна нулю.

ЭЛЕКТРОННАЯ

Демонстрационная схема действия Второго закона Кирхгофа для замкнутого контура с двумя резисторами и одним источником ЭДС

Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одного контура. Соответственно, одинаковый ток протекает через каждый из резисторов.

Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2, дают напряжение по Второму закону Кирхгофа:

V = I * Rs

где: Rs = R1 + R2.

Очевидно: применение Второго закона Кирхгофа к одиночному замкнутому контуру даёт формулу эквивалентного или полного сопротивления для последовательной цепи. Допустимо расширить эту формулу, чтобы найти значения падений потенциалов по кругу контура:

I = V / Rs

Vr1 = V * (R1 / R1 + R2)

Vr2 = V * (R2 / R1 + R2)

Пример #1 расчёта с применением закона Кирхгофа

Есть три резистора номинальным сопротивлением 10, 20, 30 Ом, соответственно. Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.

РЕЗИСТОРНЫЙ

Пример экспериментальной схемы для демонстрации эффекта закона Кирхгофа

Требуется рассчитать:

общее сопротивление,
ток цепи,
ток через каждый резистор,
падение напряжения на каждом резисторе.

Рассчитаем общее сопротивление:

Ro = R1 + R2 + R3 = 10Ω + 20Ω + 30Ω = 60Ω

Ток цепи:

I = V / Ro = 12 / 60 = 0,2A (200 мА)

Ток через каждый резистор:

I * R1 = I * R2 = I * R3 = 0,2A (200 мА)

Падение потенциала на каждом из резисторов:

VR1 = I * R1 = 0.2 * 10 = 2В

VR2 = I * R2 = 0.2 * 20 = 4В

VR3 = I * R3 = 0.2 * 30 = 6В

Таким образом, Второй закон Кирхгофа справедлив, учитывая что индивидуальные падения напряжения, отмеченные по кругу замкнутого контура, в итоге составляют сумму напряжений.

Вывод

Теория второго закона Кирхгофа, также известного как закон сохранения потенциала, особенно полезна для работы с последовательными схемами. Последовательные схемы действуют как делители потенциала, а цепь делителя потенциала — это важный узел многих электрических (электронных) схем.

При помощи информации: Electronics-Tutorials

Как рассчитать падение напряжения на резисторах?

Автор Александр На чтение 3 мин. Просмотров 47 Опубликовано 15.12.2020 Обновлено 16.12.2020

Простая электрическая цепь состоит из источника питания, проводников и сопротивлений. На практике же электроцепи редко бывают простыми и включают в себя несколько различных ответвлений и повторных соединений.

В больших масштабах в роли сопротивлений может выступать бытовая техника, осветительные приборы и другие потребители. Давайте разберемся, что происходит с током и напряжением на каждом таком потребителе или резисторе с точки зрения электротехники.

Основы электротехники

Закон Ома гласит, что напряжение равно силе тока умноженной на сопротивление. Это может относиться к цепи в целом, участку цепи или к конкретному резистору. Самая распространенная форма этого закона записывается:

U=IR

Два типа схем в электротехнике

Последовательная цепь

Здесь ток протекает по одному проводнику. Независимо от того, какие сопротивления встречаются на его пути, просто суммируйте их, чтобы получить общее сопротивление цепи в целом:

R_о = R₁ + R₂ + … + R_N (последовательная цепь)

Последовательная цепь

Параллельная цепь

В этом случае проводник разветвляется на два или более других проводника, на каждом из которых имеется своё сопротивление. В этом случае полное сопротивление определяется как:

1/R_о = 1/R₁ + 1/R₂ + … + 1/R _N (параллельная цепь)

Параллельная цепь

Если взглянуть на эту формулу, можно сделать вывод, что добавляя сопротивления одинаковой величины, вы уменьшаете сопротивление цепи в целом. Согласно закону Ома это фактически увеличивает ток!

Если это кажется нелогичным, представьте себе поток автомобилей, которые выезжают с парковки через один шлагбаум и тот же самый поток который выезжает со стоянки, которая имеет несколько выездов. Несколько выездов явно увеличит поток покидающих стоянку машин.

Падение напряжения в последовательной цепи

Если вы хотите найти падение напряжения на отдельных резисторах в цепи, выполните следующие действия:

Рассчитайте общее сопротивление, сложив отдельные значения R.
Рассчитайте ток в цепи, который одинаков для каждого резистора, поскольку в цепи только один проводник.
Рассчитайте падение напряжения на каждом резисторе, используя закон Ома.

Пример: источник питания 24 В и три резистора подключены последовательно, где R₁ = 4 Ом, R₂ = 2 Ом и R₃ = 6 Ом. Чему равно падение напряжения на каждом резисторе?

Схема для решения задачи на последовательно подключенное сопротивление

Сначала рассчитаем общее сопротивление: 4 + 2 + 6 = 12 Ом.
Далее рассчитываем ток: 24 В / 12 Ом = 2 А
Теперь используем ток, чтобы вычислить падение напряжения на каждом резисторе. Используя Закон Ома (U = IR) для каждого резистора, получим значения R₁, R₂ и R₃ равными 8 В, 4 В и 12 В соответственно.

Падение напряжения в параллельной цепи

Пример: источник питания 24 В и три резистора подключены параллельно, где R₁ = 4 Ом, R₂ = 2 Ом и R₃ = 6 Ом, как и в предыдущей схеме. Чему будет равно падение напряжения на каждом резисторе?

Схема для решения задачи на паралельно подключенное сопротивление

В этом случае все проще: независимо от значения сопротивления падение напряжения на каждом резисторе одинаково. Это означает, что падение напряжения на каждом из них — это просто общее напряжение цепи, деленное на количество резисторов в цепи, или 24 В / 3 = 8 В.

Применяя эти несложные правила вы сможете рассчитать падение напряжения даже в сложной цепи, достаточно лишь разделить её на простые участки.

Делитель напряжения — Основы электроники

Делитель напряжения это цепь или схема соединения резисторов, применяемая для получения разных напряжений от одного источника питания.

Рассмотрим цепь из двух последовательно соединенных резисторов с разными сопротивлениями (рис. 1).

Рисунок 1. Последовательная цепь есть простейший делитель напряжения.

Согласно закону Ома если приложить к такой цепи напряжение, то падение напряжения на этих резисторах будет тоже разным.

U_R1=I*R1;

U_R2=I*R2.

Схема, изображенная на рисунке 1, и есть простейший делитель напряжения на резисторах. Обычно делитель напряжения изображают, как это показано на рисунке 2.

Рисунок 2. Классическая схема делителя напряжения.

Для примера разберем простейший делитель напряжения, изображенный на рисунке 2. В нем R1 = 2 кОм, R2 = 1 кОм и напряжение источника питания, оно же и есть входное напряжения делителя Uвх = 30 вольт. Напряжение в точке А равно полному напряжению источника, т. е. 30 вольт. Напряжение Uвых, то есть в точке В равно напряжению на R2. Определим напряжение Uвых.

Общий ток в цепи равен:

(1)

Для нашего примера I=30 В/ (1 кОм + 2 кОм) = 0,01 А = 10 мА.

Напряжение на R2 будет равно:

(2)

Для нашего примера UR2 = 0,01 А*1000 Ом = 10 В.

Выходное напряжение можно вычислить вторым способом, подставив в выражение (2) значение тока (1), тогда получим:

(3)

U_R2 = 30 В*1 кОм/(1 кОм + 2 кОм) = 10 В.

Второй способ применим для любого делителя напряжения, состоящего из двух и более резисторов, включенных последовательно. Напряжение в любой точке схемы можно вычислить с помощью калькулятора за один прием, минуя вычисление тока.

Делитель напряжения из двух последовательно включенных резисторов с равными сопротивлениями

Если делитель напряжения состоит из двух одинаковых резисторов, то приложенное напряжение делится на них пополам.

Uвых = Uвх/2

Делитель напряжения из трех последовательно включенных резисторов с равными сопротивлениями

На рисунке 3 изображен делитель напряжения, состоящий из трех одинаковых резисторов сопротивлением в 1 кОм каждый. Вычислим напряжение в точках А и В относительно точки Е.

Рисунок 3. Делитель напряжения из трех резисторов.

Общее сопротивление R= R1+R2+R3 = 1 кОм + 1 кОм + 1 кОм = 3 кОм

Напряжение в точке А относительно точки Е будет равно:

Тгда Ua-e =30 В/(1 кОм + 1 кОм + 1 кОм)*1 кОм = 10 В.

Напряжение в точке В относительно точки Е будет равно:

Тгда Ub-e =30 В/(1 кОм + 1 кОм + 1 кОм)*(1 кОм + 1 кОм) = 20 В.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Как на резисторах, конденсаторах и индуктивностях делить напряжение

Электрическое напряжение между точками A и B электрической цепи или электрического поля — физическая величина, обеспечивающая работу одинакового электрического поля (включающего сторонние поля) ), совершенной при переносе единичного пробного электрического заряда из точки A в точку B.

Для достижения фиксированного значения напряжения, равного доле от исходного значения, в электрических цепях применяют делители напряжения.Делители напряжения могут состоять из двух или более элементов, которые могут служить резисторами либо реактивными сопротивлениями (конденсаторы или катушки индуктивности).

В простейшем виде делитель напряжения представляется парой участков электрической цепи, соединенных друг с другом, которые называются плечами делителя. Верхним плечом называется тот участок, который расположен между точкой положительного напряжения и выбранной точкой соединения участков, а нижним плечом — участок между точкой соединения (выбранной точкой, нулевой точкой) и общим проводом.

Делители напряжения на резисторах

Конечно, делители напряжения как в цепях постоянного тока, так и в цепях переменного тока. Делители на резисторах подходят и для тех, и для других цепей, однако используются они только в цепях низкого напряжения. Для питания устройств делители напряжения на резисторах не применяют.

В простейшем виде резистивный делитель напряжения всего из пары резисторов, соединенных последовательно.Делимое напряжение на делитель, в результате на каждый резисторе падает определенная доля этого напряжения, пропорциональная номиналу резистора. Сумма падений напряжений напряжению напряжению подаваемому на делитель.

Согласно закону Ома для участка электрической цепи, на каждом резисторе падение напряжения будет прямо пропорционально току и величине сопротивления резистора. А согласно первому правилу Кирхгофа, ток через эту цепь будет везде один и тот же.Так, на каждый резистор придутся падения напряжения:

И напряжение на концах участка цепи будет равно:

А ток в цепи делителя составит:

Теперь если подставить выражение для тока в формулы для падений напряжений на резисторах, то получим формулы для нахождения величин напряжений на каждом из резисторов делителя:

Используя делитель напряжения на резисторах для тех или других целей, важно понимать, что присоединенная к одному из плеч делителя нагрузка, будь то измерительный прибор или что-нибудь другое, должно иметь собственное сопротивление большее, чем общее сопротивление резисторов, образующих делитель. В силе сопротивления сопротивление должно быть рассмотрено как параллельный плечу резистор, входящий в состав делителя.

Пример: есть источник постоянного напряжения 5 вольт, необходимо подобрать к нему резисторы для делителя напряжения, чтобы снимать с делителя измерительный сигнал величиной в 2 вольта. Допустимая рассеиваемая на делителе мощность не должна превышать 0,02 Вт.

Решение: Пусть максимальная мощность, рассеиваемая на делителе, равна 0,02 Вт, тогда минимальное общее сопротивление делителя при 5 вольтах найдем из закона Ома, оно получится равно 1250 Ом.Пусть 1,47 кОм — выбранное общее сопротивление делителя, тогда 2 вольта упадет на 588 омах. Выберем постоянный резистор на 470 Ом и переменный на 1 кОм. Установим на переменном резисторе значение в 588 Ом.

Делители напряжения на резисторах широко применяются сегодня в электронных схемах. На этих схемах значения величин резисторов для делителей выбираются из параметров активных элементов. Как правило, делители используются в цепях цепях схем, в цепях обратной связи преобразователей напряжения и т. д. Минус таких решений заключается в том, что резисторы рассеивают на себе мощность в виде тепла, однако целесообразность оправдывает эти малые потери энергии.

Делители на напряжения конденсаторах

В цепях переменного тока, в высоковольтных схемах, применяют делители напряжения на конденсаторах. Здесь используется реактивный характер сопротивления конденсаторов в цепях переменного тока. Величина реактивного сопротивления конденсатора в цепи переменного тока зависит от электроемкости конденсатора и от частоты напряжения.Вот формула для нахождения этого сопротивления:

Формула свидетельствует о том, что чем больше электроемкость конденсатора — тем его реактивное (емкостное) сопротивление меньше и чем выше частота — тем так же меньше реактивное сопротивление. Такие делители используются в измерительных схемах цепей переменного тока, падения напряжений на плечах считаются аналогично случаю с постоянными активными сопротивлениями (резисторами, см.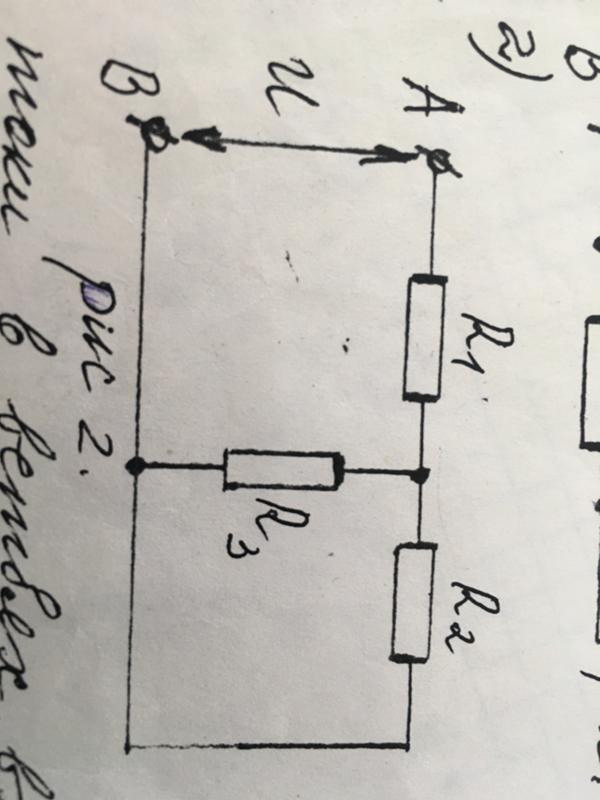 Выше).

Количество конденсаторов, используемых в делителях, состоит в том, что рассеивание энергии в форме тепла получается минимальным, и зависит только от качества диэлектрика.

Делитель на индуктивностях

Индуктивный делитель напряжения — еще один вид делителей, применяемых в измерительной электронике переменного тока, особенно в низковольтных схемах, работающих на высоких частотах. Сопротивление катушек для переменного тока высокой частоты носит преимущественно реактивный (индуктивный) характер, оно находится по формуле:

Формула свидетельствует о том, что чем больше индуктивность и чем выше частота — тем выше сопротивление катушки переменному току.Здесь важно понимать, что провод катушки имеет активное сопротивление, поэтому мощность, рассеиваемая в виде тепла, свой делителю на индуктивностях, значительно выше, чем у делителей на конденсаторах.

В любительской электронике делители напряжения часто используются при подключении аналоговых датчиков к модулям Ардуино.

Ранее ЭлектроВести писали, что немецкие инженеры разработали полевой транзистор на основе оксида галлия с пробивным напряжением 1,8 кВ и рекордной добротностью — 155 МВт на квадратный сантиметр.Такие показатели приближают элемент к теоретическому лимиту оксида галлия.

По материалам: electrik.info.

Полярность падения напряжения

Радиоэлектроника
Схемотехника
Основы электроники и схемотехники
Том 1 — Цепи постоянного тока

Книги / руководства / серии статей
Основы электроники и схемотехники. Том 1. Цепи постоянного тока

Добавлено 24 октября 2020 в 21:29

Сохранить или поделиться

При использовании традиционного обозначения протекания тока мы можем отследить направление тока в цепи, начав с положительного (+) вывода и перейдя к отрицательному (-) выводу батареи, единственного источника напряжения в заданной цепи. Отсюда мы можем увидеть, что ток течет по часовой стрелке, от точки 1 к 2, к 3, к 4, к 5, к 6 и снова обратно к 1 (рисунок 1).

Когда ток встречает сопротивление 5 Ом, на концах резистора происходит падение напряжения. Полярность этого напряжения положительная (+) в точке 3 относительно точки 4. В соответствии с направлением тока мы можем отметить полярность падения напряжения на символами плюс и минус; на какой бы вывод резистора ток ни вход , он будет положителен по отношению к выводу резистора, из которого ток выходит :

Рисунок 1 — Полярность падения напряжения на резисторе

Мы могли бы сделать нашу таблицу напряжений немного более полной, отметив полярность напряжения для каждой пары точек в этой цепи:

  Между точками 1 (+) и 4 (-) = 10 вольт
Между точками 2 (+) и 4 (-) = 10 вольт
Между точками 3 (+) и 4 (-) = 10 вольт
Между точками 1 (+) и 5 (-) = 10 вольт
Между точками 2 (+) и 5 (-) = 10 вольт
Между точками 3 (+) и 5 (-) = 10 вольт
Между точками 1 (+) и 6 (-) = 10 вольт
Между точками 2 (+) и 6 (-) = 10 вольт
Между точками 3 (+) и 6 (-) = 10 вольт

Хотя документировать полярность напряжения в этой цепи может показаться немного глупым, это важная концепция, которую нужно освоить. Это будет критически важно при анализе более сложных схем, включающих несколько резисторов и / или источников напряжения.

Полярность не имеет ничего общего с законом Ома

Следует понимать, что полярность не имеет ничего общего с законом Ома: в уравнении закона Ома никогда не должно входить отрицательное напряжение, ток или сопротивление! Есть и другие математические принципы электричества, которые учитывают полярность с помощью знаков (+ или -), но это не закон Ома.

Резюме

Полярность падения напряжения на любом резистивном компоненте определяется направлением тока через него: плюс на входе и минус на выходе.

Оригинал статьи:

Падение напряжения — NikiWiki

Согласно Закону Ома на учатске цепи, обладающим сопротивлением R через который протекает ток I возникает падение напряжения:

Падение напряжения

 U = I * R

Таким образом, в цепи на каждом сопротивлении напряжение будет соответствовать протекающему в цепи току и сопротивлению каждого из резисторов, соответственно R ₁ и R ₂

 ΔU ₁ = I * R ₁
ΔU ₂ = I * R ₂

При этом, мощность, выделяемая на участке цепи будет равна

 P = U * I

А на каждом из резисторов выделяемая мощность будет равна:

 P ₁ = I * ΔU ₁
Р ₂ = I * ΔU ₂

 I = ΔU ₁ / R ₁

Если взять, к примеру, токоизмерительный резистор сопротивление 1 Ом и измерить на нем напряжение, которое будет равно, скажем 1 В, то протекающий в цепи ток будет равен 1 А.

Однако, такое сопротивление и, как следствие, выделяемая мощность на резисторе, чреваты боком. Мощность будет равна 1 Вт, что значительно снизит КПД любой схемы рассчитанной на сбережение энергии источника.

Именно по этой причине токоизмерительные резисторы стараются делать максимально малого сопротивления, но с такой возможностью измерить падение напряжения на нем с достаточной точностью. Без дополнительного усиления измеряемого сигнала и соответственно дополнительных погрешностей и элементов.

Например. Известная схема, построенная на компараторе LM398 с гистерезисом 30мв стабильно работает лишь при падении напряжения больше 0,1 вольта и меньше 0,2В (стабильный результат, хотя, можно и больше). Если схема рассчитывается для питания светодиода, потребляющего 1А, то, R = U / I? т.е. 0,1 или 0,2 Ома. А выделяемая на резисторе мощность при этом будет 0,1 или 0,2 Вт. Что тоже не мало, но значительно эффективнее.

Таким образом на каждом из резисторов выделится энергия пропорциональная падению напряжения и

Как рассчитать падение напряжения на резисторах?

Автор Александр На чтение 3 мин. Просмотров 48 Опубликовано 15.12.2020 Обновлено 16.12.2020

Простая электрическая цепь из источников питания, проводников и сопротив. На практике же электроцепи редко бывают простыми и включают в себя несколько различных ответвлений и повторных соединений.

В больших масштабах в роли сопротивлений может выступать бытовая техника, осветительные приборы и другие пользователи. Давайте разберемся, что происходит с током и напряжением на каждом таком потребителе или резисторе с точки зрения электротехники.

Основы электротехники

Закон Ома гласит, что напряжение равно силе тока умноженной на сопротивление.Это может относиться к цепи в целом, участку цепи или к конкретному резистору. Самая распространенная форма этого закона записывается:

U = IR

Два типа в схематехнике

Последовательная цепь

R _о = R ₁ + R ₂ +… + R _N ( последовательная цепь)

Последовательная цепь

Параллельная цепь

В этом случае проводник разветвляется на два или более других проводника, на каждом из которых имеется свое сопротивление.В этом случае полное сопротивление определяется как:

1 / R _о = 1 / R ₁ + 1 / R ₂ +… + 1 / R _N (параллельная цепь)

Параллельная цепь

, что добавляя сопротивление одинаковой величины, вы уменьшаете сопротивление цепи в целом. Согласно закону Ома это преобразование ток!

Если это кажется нелогичным, представьте себе поток автомобилей, которые выезжают с парковки через один шлагбаум и тот же самый поток, который выезжает со стоянки, который имеет несколько выездов.Несколько выездов явно увели поток покидающих стоянку машин.

Падение напряжения в последовательной цепи

Если вы хотите найти падение напряжения на отдельных резисторах в цепи, выполните следующие действия:

Рассчитайте общее сопротивление, сложив отдельные значения R.
Рассчитайте ток в цепи, который одинаков для каждого резистора, поскольку в цепи только один проводник.
Рассчитайте падение напряжения на каждом резисторе, используя закон Ома.

Пример : источник питания 24 В и три резистора соединены последовательно, где R ₁ = 4 Ом, R ₂ = 2 Ом и R ₃ = 6 Ом. Чему равно падения напряжения на каждом резисторе?

Схема для решения задачи на последовательное сопротивление

Сначала рассчитаем общее сопротивление: 4 + 2 + 6 = 12 Ом.
Далее рассчитываем ток: 24 В / 12 Ом = 2 А
Теперь используем ток, чтобы вычислить падение напряжения на каждом резисторе.Используя Закон Ома (U = IR) для каждого резистора, получим значения R ₁, R ₂ и R ₃ равными 8 В, 4 В и 12 В соответственно.

Падение напряжения в параллельной цепи

Пример : источник 24 В и три резистора подключены параллельно, где R ₁ = 4 Ом, R ₂ = 2 Ом и R ₃ = 6 Ом, как и в предыдущей схеме. Чему будет падение напряжения на каждом резисторе?

Схема для решения задачи на паралельно подключенное сопротивление

В этом случае все проще: независимо от значения сопротивления падение напряжения на каждом резисторе одинаково.Это означает, что падение напряжения на каждом из них — это просто общее напряжение цепи, деленное на количество резисторов в цепи, или 24 В / 3 = 8 В.

Применяя эти простые методы падения напряжения даже в сложной цепи, достаточно лишь разделить ее на простые участки.

Делитель напряжения: теория и принцип действия

Делитель напряжения позволяет получить меньшее напряжение из большего напряжения может быть как постоянным, так и переменным.

Рис. 1. Схема напряжения простейшего делителя

Пршая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для другой величины падения напряжений на резисторах делителя определяется по формулам

U _R1 = I * R1; U _R2 = I * R2 (1)

где U _R1, U _R2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи.В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.

Сумма падений напряжений U _R1, U _R2 на резисторах равно напряжению источника питания. Ток в цепи будет равен напряжению источника питания, делённому на величину сопротивлений резисторов R1 и R2:

I = U _пит / (R1 + R2) (2)

Рассмотрим практическую схему делителя постоянного напряжения (рис.2)

Рис.2. Делитель постоянного напряжения.

Ток, протекающий в этой схеме, согласно формуле (2) будет равен

I = 10 / (10000 + 40000) = 0,0002 А = 0,2 мА.

Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:

U _R1 = 0,0002 * 10000 = 2 В;
U _R2 = 0,0002 * 40000 = 8 В.

Если из формулы (1) вывести ток:

I = U _R1 / R1 (3)

И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:

U _R1 / R1 = U _пит / (R1 + R2)

Откуда

U _R1 = U _пит * R1 / (R1 + R2) (4)

Подставляя значения и сопротивлений в формулу (4), получим значение напряжения на резисторе R1:

U _R1 = 10 * 10000 / (10000 + 40000) = 2 В,

и на резисторе R2:

U _R2 = 10 * 40000 / (10000 + 40000) = 8 В.

Делитель напряжения с реактивными элементами в цепи переменного тока

В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис. 3).

Рис.3. Ёмкостный делитель напряжения в цепи переменного тока.

Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:

R _c = 1 / (2 * π * f * C)

Здесь R _c — реактивное сопротивление конденсатора;
π — число Пи = 3,14159 …;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.

То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и соответственно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью. Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:

U _С1 = U _пит * С2 / (С1 + С2) (5)

U _С1 = 10 * 40 * 10 ^-9 / (10 * 10 ^-9 + 40 * 10 ^-9) = 8 В,
U _С2 = 10 * 10 * 10 ^{— 9} / (10 * 10 ^-9 + 40 * 10 ^-9) = 2 В.

Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.

Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.

реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:

R _L = 2 * π * f * L

Здесь R _c — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159. ..;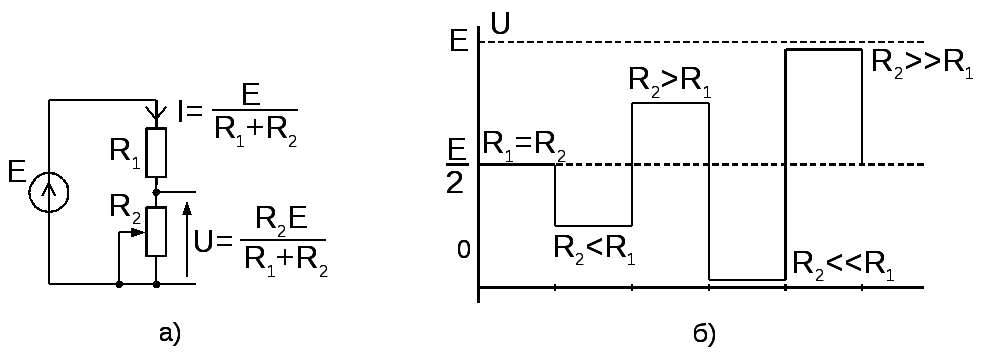
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.

То, как и формула для расчёта индуктивного делителя напряжения будет точно такое же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут отображаться индуктивности:

U _L1 = U _пит * L1 / (L1 + L2) (6)

Подставив в эту формулу параметры элементов из рисунка 4, получим:

U _L1 = 10 * 10 * 10 ^-6 / (10 * 10 ^-6 + 40 * 10 ^-6) = 2 В,
U _L2 = 10 * 40 * 10 ^{— 6} / (10 * 10 ^-6 + 40 * 10 ^-6) = 8 В.

В заключении следует отметить, что во всех расчётах нагрузки была принята равная бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем собственные сопротивлений.

Азъ и буки радиоэлектроники. Пассивные компоненты. — Гитарная передача

Предисловие.

Смыслить в электронике, но обладать прямыми руками и старанием, можно практически ничего не смыслить в электронике.Тем не менее, надобность в простейших знаниях приходит сама, когда электроника становится увлечением. Где же узнать самую необходимую информацию? Её приходится собирать по крупинкам: из учебников и статей, от единомышленников и учителей. Одна из этих крупинок сейчас перед вами. Здесь собрана необходимая информация о пассивных радиокомпонентах, и немножечко сверху. Пусть эта статья даст вам необходимый задел, и до многих других вещей вы додумаетесь сами.

Резистор.

Без резисторов нам никак.Резисторы есть в каждом устройстве, и их много. Резистор обладает электрическим сопротивлением, то есть затрудняет прохождение тока по цепи. Зачем он нужен? Чтобы понять это, для начала нужно выучить Закон Ома, основу электроники.

Закон Ома гласит:

Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна электрическому сопротивлению этого участка.

То есть, всё более чем логично.Прикладываем большее напряжение к резистору, и он начинает течь больший ток. Чем сильнее резистор сопротивляется току, тем сильнее ток через него протечёт. Представьте резистор как водопроводный кран — чем больший напор создаётся станцией, тем быстрее потечёт вода через приоткрытый кран. Закроете кран (сопротивление равно бесконечности) — и вода не течёт.

Кстати, можно очень быстро запомнить этот закон. Вот вам хитрая треугольная диаграмма. Нужно закрыть искомую элемент и два других символа дадут формулу для вычислений.Спасибо Википедии.

Теперь нужно понять, что такое падение напряжения.

Если через резистор течёт ток, то на его концах присутствует определенное напряжение. Посмотрите на эту схему:

Три одинаковых резистора по одному Ому, соединенным соединенным. Сопротивление всей цепочки равно сумме сопротивлений этих резисторов, то есть 3 Ома. Напряжение, приложенное к ней — 3 В. Как следует из закона Ома, через этот участок цепи течёт ток в 1 Ампер.Теперь разобьём этот участок на два: первый участок с первым резистором, и второй со вторым и третьим резистором. Как мы помним, через цепь течёт ток 1 А. Он будет одинаковым по всей цепи. Выразим из закона Ома напряжение:

U = I * R

Подставим в формулу сопротивления первого участка и ток, и получим, что напряжение на его концах равно 1 В. Если подставим второе сопротивление участка, получим 2 В. Эти числа равны падению на этих участках. То есть на первом участке падает 1 В, и второму «остаётся» только два.И наоборот, на втором участке падает 2 В, первому остаётся 1 В. А какое падение напряжения на каждом из резисторов? Правильно, 1 В. Обратите внимание, в сумме всегда получится 3 В. И для каждого из этих участков выполнится отношение:

Вот вам и первое применение — делитель напряжения. Посмотрите на схему. На ней появилась «земля». Грубо говоря, это точка отсчёта в схеме. Все напряжения на схеме указываются именно относительно этой точки.

Подадим на вход схемы напряжение.Пусть его уровень равен U. Через резисторы в «землю» течёт ток. Напряжение же на выходе этой цепочки, есть напряжение падения на R2, равно:

Подставьте туда значения по 1 Ом, и получите, что напряжение ослабляется в 2 раза.

Хочу заметить, что делитель — это частный случай сумматора напряжений с одним «входом». Кроме того, делитель напряжения лежит в основе усилительных каскадов и частотных фильтров. При этом один или оба резистора заменяются на транзисторы, конденсаторы, индуктивности и т.д. Но об этом позже.

Как сопротивление сопротивлению цепочки резисторов — я уже говорил. Нужно просто сложить сопротивление резисторов.

При параллельном соединении другой подход:

Резисторы имеют всего 2 параметра — сопротивление и мощность. Имеется в виду предельная мощность, которая может выделяться на системе управления током резистора, не причиняя ему вреда.

Конденсатор.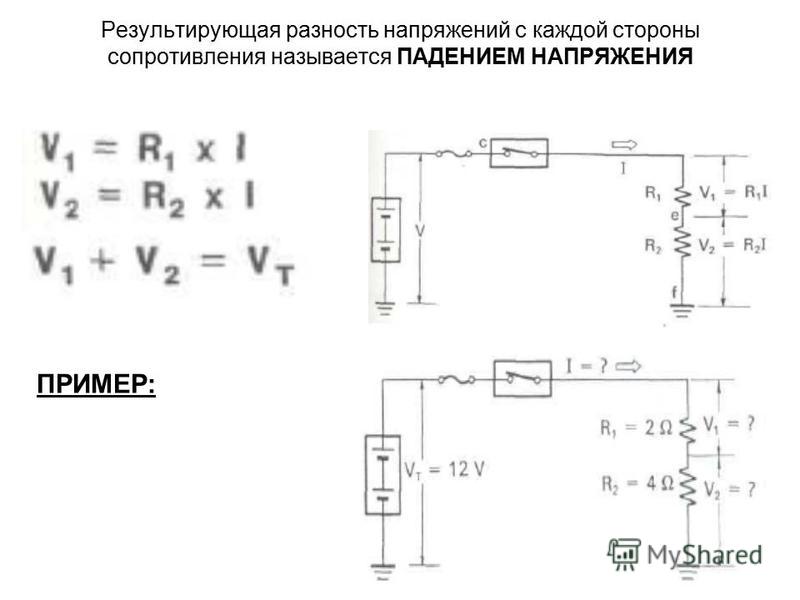

Конденсатор — второе по опыту устройства.Он состоит из двух электродов и диэлектрика между ними. Обладает ёмкостью (С), измеряемой в Фарадах. Упрощённо принцип действия можно представить так. На каждой обкладке имеется запас электронов. Если приложить к обкладкам разность потенциалов, то с одной обкладкой часть электронов уйдёт, на другой же обкладке появится избыток электронов. То есть первая зарядится положительно, а вторая отрицательно. Между обкладками появится электростатическое поле, в виде которого и хранится энергия. Стоит замкнуть обкладки проводника, и избыток электронов устремится на положительно заряженную обкладку.

Как следует из конструкции, конденсатор не может проводить постоянный ток, ведь он по сути является разрывом в цепи. Зато он прекрасно проводит переменное напряжение. И чем выше частота, тем меньшее сопротивление он оказывает. Это сопротивление называется реактивным и посчитать его можно по следующей формуле:

Подставим конденсатор в делитель напряжения вместо одного из резисторов.

При высокая частота, реактивное сопротивление конденсатора значительно ослабляет уровень сигнала.Зато низкие частоты пропускаются почти без изменений. Это фильтр низких частот (ФНЧ). Частный его случай используется для фильтрации питания. При этом, ёмкость велика, сопротивление сопротивление очень мало или он вообще отсутствует. Пульсация питания при этом уходят прямиком в землю.

Изменим конструкцию:

Теперь фильтр пропустит высокие частоты, и отфильтрует низкие. Это фильтр высоких частот (ФВЧ). Частный его случай — разделительный конденсатор: ёмкость конденсатора мала, сопротивление сопротивление наоборот велико.Очень часто сопротивление сопротивления входному сопротивлению следующего каскада. Этот каскад срезает только самые низкие частоты, не несущие полезной информации (инфразвук), и избавляет от постоянной составляющей. Хотя, иногда он используется одновременно и для среза басов, например, передним ограничительным каскадом. Постоянная составляющая на выходе цепочки будет напряжением в точке, к которой подключен резистор, в данном случае ноль (напряжение «земли»).

Частота среза этих фильтров считается по формуле:

Если поймать этот принцип, то сможете разобраться в работе практически любого темброблока.Нужно лишь знать три вещи:

формулу реактивного сопротивления конденсатора X _C;
конденсаторы заменяются резисторами сопротивлением X _C;
закон Ома.

Кроме того, существует много разновидностей фильтров — Т-мост, двойной Т-мост, мост Вина и т.д. Все эти фильтры пассивными, поскольку не имеют в составе активных компонентов.

В то время, как сопротивление резисторов, мы чаще в килоомах, ёмкость чаще измеряется в нанофарадах.Ёмкость в один Фарад воистину, и на практике вы с ними не столкнётесь.

Конструкции конденсаторов различны. Самая простая — когда электроды делаются из полосок фольги, между полосками прокладывается диэлектрик, и все это сворачивается в плотный рулет. В качестве диэлектрика используется бумага (металлобумажные конденсаторы) или плёнка из разных сортов пластика (плёночные). Последние пользуются почётом и уважением за низкие искажения и часто используются в аудиотехнике.

Керамические конденсаторы имеют многослойную конструкцию.В них чередуются тонкие керамические пластинки и пластинки диэлектриков. Они могут как очень малую (единицы пикофарад), так и иметь очень большую ёмкость, на настоящий момент рекордсмен — 100 микрофарад в корпусе примерно 3х5х1 мм. К сожалению, такие конденсаторы часто микрофонят и искажают сигнал. Рекомендуются к применению в цифровой электронике, но не в аудио сфере, кроме некоторых случаев. Например, они неплохо фильтруют высокочастотные помехи, и ими можно шунтировать электролитический конденсатор, фильтрующий питание.

Если нужна высокая ёмкость, то применяются электролитические конденсаторы .

В электролитических конденсаторах два электрода, изготовленные из фольги, погружены в проводящую жидкость, электролит. Роль диэлектрика работает тончайший оксидный слой на одном из электродов. Именно его толщина позволяет достичь высокой ёмкости. К сожалению, пара метал-оксид является полупроводником, и пропускает ток в одном направлении. Поэтому электролитические конденсаторы полярны, за исключением специальных моделей.Есть также танталовые электролитические конденсаторы. В них покрыт оксидной плёнкой пористый танталовый электрод, имеющий большую площадь поверхности при скромных размерах. Поры заполнены вторым электродом. Кстати, электролитические конденсаторы являются самыми ненадежными элементами, уступая лишь соединительным разъемам и потенциометрам. Наиболее частая причина поломки компьютерной техники — как раз надувшийся конденсатор.

Это те конденсаторы, с которой происходит столкновение со звуковым оборудованием.В действительности их гораздо больше. Рекомендую прочитать полезную статью по данной теме.

Конденсаторы обладают двумя характеристиками: ёмкость и напряжение пробоя. При этом напряжении пробивается слой диэлектрика, конденсатор выходит из строя. Это может повлечь за собой печальные последствия. Например, если в ламповом преампе пробивается один из проходных конденсаторов, на сетку одной из ламп сразу поступает значительно возможно, напрямую с анода предыдущей. Формируется очень громкий хлопок, усилитель или динамик могут быть повреждены, не говоря уже о ваших ушах.Если пробивается входной разделительный конденсатор, высокое напряжение поступает в обратном направлении — в гитару или любимую Край Бэби за двести. Наконец, высоковольтные электролитические конденсаторы просто эффектно взрываются, уничтожая лампы, поблизости пальцы, глаза, оказавшиеся. При первом включении усилителей, использующих высокое напряжение, рекомендуется держаться от них подальше.

Индуктивность.

Она же катушка индуктивности или дроссель. Используется редко, поэтому она является полной противоположностью конденсатора.Катушка пропускает низкие частоты, но повышает высокие частотыам. Единица измерения индуктивности — Генри. Формула реактивного сопротивления:

Как видите, это лишь перевернутая формула реактивного сопротивления конденсатора.

Индуктивности применяются в основном для фильтрации питания. Очень редко, но все встречается в темброблоках. Наиболее известное применение — в качестве одного из элементов квакушек, например Dunlop Cry Baby.

На сегодня это всё.Надеюсь, мои единомышленники разовьют тему дальше.

Всем успехов!

Какое напряжение после резистора. Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Есть другой способ снижения на нагрузке, но только для цепей постоянного тока. Про смотри здесь.

Вместо дополнительного резистора используйте цепочку из последовательно включенных, в прямом направлении, диодов.

Весь смысл состоит в том, что при протекании тока через него падает «прямое напряжение» равное, в зависимости от типа диода, мощности и тока протекающего через него — от 0,5 до 1,2 Волта.

На германиевом диоде напряжение напряжение 0,5 — 0,7 В, на кремниевом от 0,6 до 1,2 Вольта. Исходя из того, на сколько вольт нужно понизить напряжение на нагрузке, включая соответствующее количество диодов.

понизить напряжение на 6 В необходимо включить: 6 В: 1,0 = 6 штук кремниевых диодов, 6 В: 0,6 = 10 штук германиевых диодов. Наиболее популярны и доступны кремниевые диоды.

Выше приведенная схема с диодами, более громоздка в исполнении, чем с простым резистором.Но, выходное напряжение, в схеме с диодами, более стабильно и слабо зависит от нагрузки. В чем разница между этими двумя способами снижения выходного напряжения?

У резистора (проволочного сопротивления) линейная зависимость между током, проходящем через него и падением напряжения на нем. Во сколько раз увеличится ток, во сколько же раз увеличится и падение напряжения на резисторе.

В примере 1: если мы к лампочке подключим еще одну, то ток в цепи увеличится, с учетом общего сопротивления двух лампочек до 0,66 А. Падение напряжения на добавочном резисторе будет: 12 Ом * 0,66 А = 7,92 В. На лампочках останется: 12 В — 7,92 В = 4,08 В. Они будут гореть в пол накала.

Совсем другая картина будет если вместо резистора будет цепочка диодов.

Зависимость между током протекающего через диод и падающее на нем напряжении нелинейная.Может увеличиться в несколько раз, падение напряжения на диоде увеличится всего на несколько десятых вольта.

Т.е. чем больше ток диода, тем (сравнительно с резистором) меньше его сопротивление. Падение напряжения на диодах мало зависит от тока в цепи.

Диоды в такой цепи выполняет роль стабилизатора напряжения. Диоды необходимо подбирать по максимальному току в цепи. Максимально допустимый ток диодов должен быть больше, чем ток в рассчитываемой цепи.

Падения напряжения на некоторых диодах при токе 0,5 А даны в таблице.

Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить / выключить) многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом деле, физический смысл происходящих процессов, доступен для понимания даже со школьными знаниями физики.

Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие напряжения бывают в (имеется в виду глобальная классификация). Их всего два вида. Первый — это который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид напряжения — это именно падение. Может быть рассмотрено как в отношении всего контура, так и взятого взятого элемента.

На практике это выглядит следующим образом. Например, если взять обычную вкрутить ее в патрон, то провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания — проводники — нагрузка) составляет 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на имеющей лампа.

Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его так выглядит:

где R — активное сопротивление цепи или ее элемента, измеряется в Омах; U — электрическое напряжение, в Вольтах; и, наконец, I — ток в Амперах. Как видно, все три величины непосредственно связаны между собой.Поэтому, зная любые две, можно довольно просто вычислить третью. В каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа — вышеуказанная формула.

Электрическая энергия — это фактически движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль обладает высоким сопротивлением. Эта энергия потока частиц снижается.Как видно из формулы, с уменьшением тока уменьшение и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения. Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементх в конце схемы.

Падение напряжения на резисторе зависит от его и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемой цепи включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.

Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельных сопротивлений на величину усложняется. На эту систему следует реактивную составляющую.

Рассмотрим пример с параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС — E.

Приводим параллельные ветки к одному из них.Для этой ситуации используется формула:

R = (R1 * R2) / (R1 + R2)

Определение сопротивления всей цепи через сумму R4 = R + R3.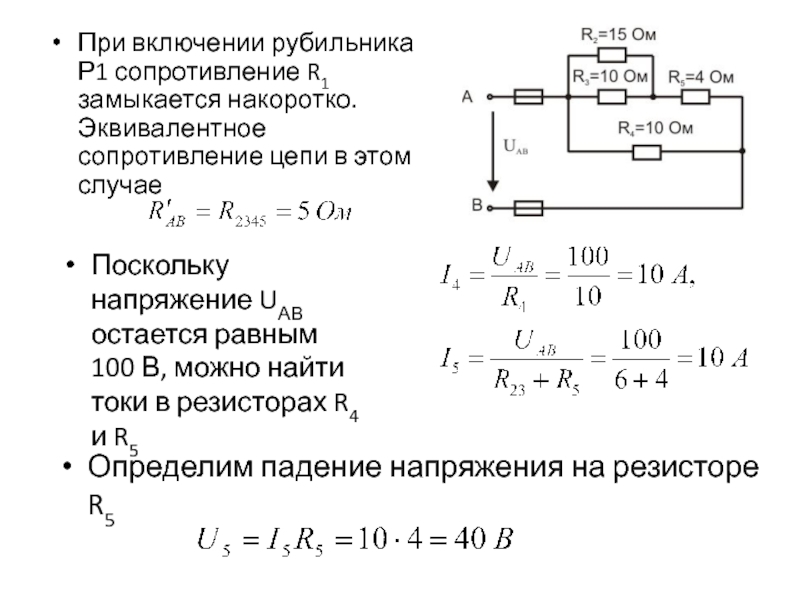

Рассчитываем ток:

Остается узнать значение падения напряжения на выбранном элементе:

Здесь множитель «R5» может быть любым R — от 1 до 4, в зависимости от того, какой именно элемент схемы нужноать.

Итак, резистор … Базовый элемент построения электрической цепи.

Работа резистора заключается в ограничении тока , протекающего по цепи.НЕ в превращении тока в тепло, а именно в ограничении тока . То есть, без резистора по цепи течет большой ток , встроили резистор — ток уменьшился. В этом его работа, совершая данный элемент электрической цепи выделяет тепло.

Пример с лампочкой

Рассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток , проходящий через цепь.И Резистор . Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток , например, 0,75А. Лампочка горит ярко. Встроили в цепь резистор — у тока появился труднопреодолимый барьер, протекающий по цепи ток снизился до 0,2А. Лампочка горит менее ярко. Стоит отметить, что яркость, с которой горит лампочка, зависит так же и от напряжения на ней. Чем выше напряжение — тем ярче.

Кроме того, на резистор происходит падение напряжения .Барьер не только задерживает ток , но и «съедает» часть напряжения, приложенного устройства питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт. На всякий случай амперметр, два вольтметра про запас, лампочку и резистор . Включаем без цепи резистор (слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр (снизу на схеме справа) показывает 5В. На лампочку остались остальные 12В-5В = 7В.Вольтметр на лампочке показал 7В.

Основная характеристика резистор — сопротивление . Единица измерения сопротивления — Ом (Ом, Ом). Чем больше сопротивление , тем больший ток он способен ограничить, тем больше тепла он выделяется, тем больше падает на нем.

Основной закон всего электричества. Связывает между собой Напряжение (В), Силу тока (I) и Сопротивление (R).

Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте использовать Закон Ома для нашей цепи с резистором и лампочкой, рассмотренной выше, и рассчитаем сопротивление резистора , при котором ток от источника питания на 12В ограничивается до 0,2.При этом рассматриваем сопротивление лампочки равным 0.

В = I * R => R = V / I => R = 12В / 0,2А => R = 60Ом

Итак. Если встроить в цепь питания и лампочкой, сопротивление равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи , будет составлять 0,2А.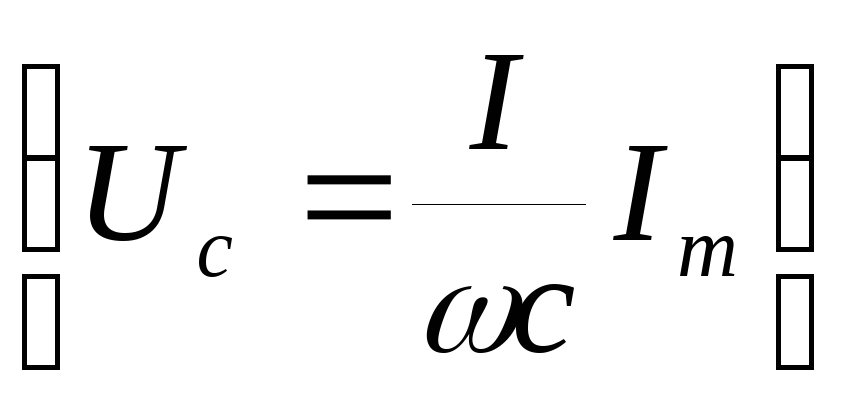

Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении реальных устройств.

При протекании тока через резистор совершается работа по ограничению электрического тока . При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающей среде. Но если резистор будет производить слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в этом результате казуса, зависит от твоего личного коэффициента удачи.

Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток , проходящий по цепи (а значит и через резистор ), равный 0,2А. Падение напряжения на резисторе равно 5В (не 12В, не 7В, а именно 5 — те самые 5, которые вольтметр показывает на резисторе ). Это значит, что мощность тока через резистор равна P = I * V = 0,2А * 5В = 1Вт.Делаем вывод: резистор для нашей цепи должен иметь максимальную мощность не менее (а лучше более) 1Вт. Иначе он перегреется и выйдет из строя.

Соединение резисторов

Резисторы в цепях электрического тока последовательное и параллельное соединение .

При последовательном соединении общего сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:

При параллельном соединении общее сопротивление резисторов 901 рассчитывается по формуле:

Остались вопросы? Напишите комментарий. Мы ответим и поможем разобраться =)
В электротехнике принято считать, что простая цепь — это цепь, которая сводится к цепи с одним и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением соединения цепи, сложным звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением г = 0,5 Ом.Сопротивления резисторов R 1 = 20 и R 2 = 32 Ом. Определить ток в цепи и на резисторах.
Так как резисторы подключены последовательно их, эквивалентное сопротивление будет равно сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.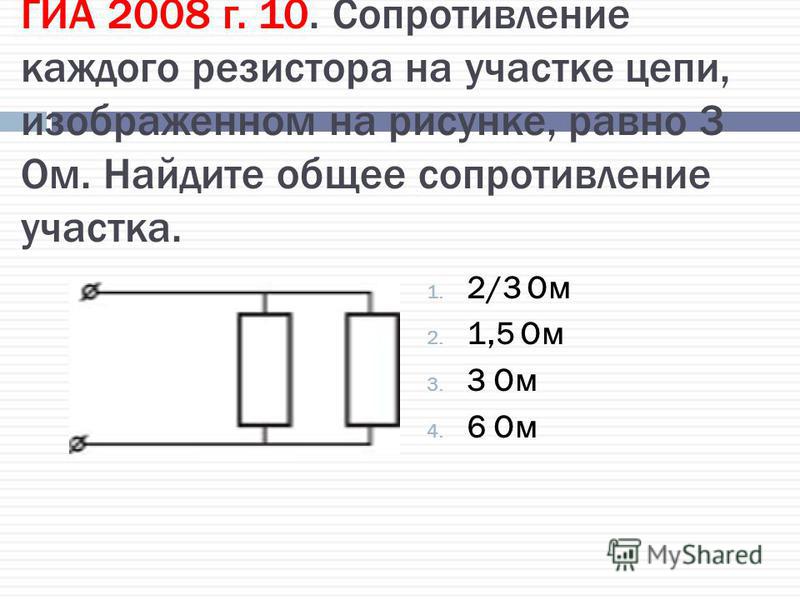
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Проверить правильность решения можно использовать методы. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более совершенный способ проверки является баланс мощностей.
В цепи должен быть полученной энергии.
Мощность источника источника напряжения ЭДС на ток, мощность полученная приемником как падение напряжения на ток.
9 усиление проверки балансом сил в том, что не нужно составлять сложные громоздкие уравнения на основании Кирхгофа, достаточно знать ЭДС, и токи в цепи.
Пример 2
Общий ток цепи. р 1 = 70 Ом и р 2 = 90 Ом, равен 500 мА.Определить токи в каждом из резисторов.

Два соединенных резистора ничто, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, требуется лишь общий ток и резистор сопротивления.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно соответствующей сумме токов сходящихся, в узле равна нулю.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того, чтобы его найти, нужно сначала
.

Что такое падение напряжения на резисторе

Формулы для расчета падения напряжения

От чего зависит падение напряжения

Примеры расчета падения напряжения

Пример 1: Простая цепь с одним резистором

Пример 2: Цепь с двумя последовательными резисторами

Практическое применение расчетов падения напряжения

Измерение падения напряжения на практике

Особенности падения напряжения в цепях переменного тока

Заключение

Падение напряжения — NikiWiki

Падение напряжения — Voltage drop

Падение напряжения в цепях постоянного тока: сопротивление

Падение напряжения в цепях переменного тока: полное сопротивление

Смотрите также

Ссылки

внешние ссылки

Какое напряжение после резистора. Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Пример с лампочкой

Соединение резисторов

Пример 1

Пример 2

Вычислить падение напряжения на резисторе. Падение напряжения

Схема делителя напряжения на резисторах

Расчет делителя напряжения на резисторах

Формула делителя напряжения

Делитель напряжения — калькулятор онлайн

Применение делителя напряжения на резисторах

Потенциометры

Резистивные датчики

Пример работы делителя напряжения на фоторезисторе.<img src='/800/600/https/upload.metrologu.ru/forum/monthly_2017_12/223.png.1263da1ad599da07d6b851fd0f7203a3.png' style='float: right;' />

Пример 1

Пример 2

Закон Кирхгофа для напряжения электрической цепи

Алгебраическая сумма разностей потенциалов

Одиночный контурный элемент — резистор

Одиночный контур электрической цепи

Пример #1 расчёта с применением закона Кирхгофа

Вывод

Как рассчитать падение напряжения на резисторах?

Основы электротехники

Два типа схем в электротехнике

Последовательная цепь

Параллельная цепь

Падение напряжения в последовательной цепи

Падение напряжения в параллельной цепи

Делитель напряжения — Основы электроники

Делитель напряжения из двух последовательно включенных резисторов с равными сопротивлениями

Делитель напряжения из трех последовательно включенных резисторов с равными сопротивлениями

Похожие материалы:

Добавить комментарий

Как на резисторах, конденсаторах и индуктивностях делить напряжение

Полярность падения напряжения

Полярность не имеет ничего общего с законом Ома

Резюме

Теги

Падение напряжения — NikiWiki

Как рассчитать падение напряжения на резисторах?

Основы электротехники

Два типа в схематехнике

Последовательная цепь

Параллельная цепь

Падение напряжения в последовательной цепи

Падение напряжения в параллельной цепи

Делитель напряжения: теория и принцип действия

Делитель напряжения с реактивными элементами в цепи переменного тока

НАЗАД

Азъ и буки радиоэлектроники.<img src='/800/600/https/electroinfo.net/wp-content/uploads/2019/11/rconnectsequencevoltage.png' style='float: right;' /> Пассивные компоненты. — Гитарная передача

Предисловие.

Резистор.

Конденсатор.<img src='/800/600/http/images.myshared.ru/19/1195442/slide_4.jpg' style='float: right;' />

Индуктивность.

Какое напряжение после резистора. Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Пример с лампочкой

Соединение резисторов

Пример 1

Пример 2

Похожие записи

Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании

Новорожденный какает слизью: причины появления слизи в кале грудничка

Пример работы делителя напряжения на фоторезисторе.

Азъ и буки радиоэлектроники. Пассивные компоненты. — Гитарная передача

Конденсатор.