Параллельное соединение активного индуктивного и емкостного сопротивления. Резонанс токов в параллельной RLC-цепи: особенности и применение

Что такое резонанс токов в параллельной RLC-цепи. Как рассчитать резонансную частоту. Какие условия необходимы для возникновения резонанса токов. Какие особенности имеет резонанс токов в параллельной цепи. Где применяется резонанс токов на практике.

Что такое резонанс токов в параллельной RLC-цепи

Резонанс токов — это явление, возникающее в параллельной RLC-цепи при определенной частоте переменного тока, когда индуктивный и емкостной токи становятся равными по величине и противоположными по фазе. При этом полный ток в неразветвленной части цепи оказывается минимальным и равным активному току.

Основные характеристики резонанса токов:

• Индуктивный и емкостной токи компенсируют друг друга
• Полный ток минимален и равен активному току
• Полное сопротивление цепи максимально
• Напряжение и ток совпадают по фазе

Расчет резонансной частоты параллельной RLC-цепи

Резонансная частота параллельной RLC-цепи рассчитывается по формуле:

f_рез = 1 / (2π√LC)

где:

• f_рез — резонансная частота, Гц
• L — индуктивность, Гн
• C — емкость, Ф

При этой частоте индуктивное и емкостное сопротивления становятся равными:

X_L = X_C = ωL = 1 / (ωC)

Условия возникновения резонанса токов

Для возникновения резонанса токов в параллельной RLC-цепи необходимо выполнение следующих условий:

1. Наличие в цепи параллельно соединенных индуктивности, емкости и активного сопротивления
2. Частота переменного тока должна быть равна резонансной частоте цепи
3. Индуктивное и емкостное сопротивления должны быть равны по величине

При соблюдении этих условий в цепи возникает резонанс токов, характеризующийся минимальным полным током.

Особенности резонанса токов в параллельной цепи

Резонанс токов в параллельной RLC-цепи имеет ряд характерных особенностей:

• Токи в индуктивной и емкостной ветвях могут во много раз превышать ток в неразветвленной части цепи
• Полное сопротивление цепи максимально
• Напряжение и ток совпадают по фазе
• Коэффициент мощности равен единице
• Реактивная мощность равна нулю

Эти особенности определяют области практического применения резонанса токов.

Применение резонанса токов на практике

Резонанс токов в параллельных RLC-цепях находит применение в следующих областях:

• Радиотехника — для настройки колебательных контуров приемников и передатчиков
• Электроэнергетика — для компенсации реактивной мощности
• Измерительная техника — в резонансных измерителях частоты
• Электроакустика — в фильтрах и эквалайзерах
• Силовая электроника — в импульсных источниках питания

Везде используется способность резонансной цепи выделять сигналы определенной частоты и подавлять остальные.

Как рассчитать параметры параллельной RLC-цепи при резонансе

При расчете параллельной RLC-цепи в режиме резонанса токов используются следующие формулы:

1. Резонансная частота: f_рез = 1 / (2π√LC)
2. Полное сопротивление: Z = R(1 + Q²), где Q = ωL/R — добротность контура
3. Ток в неразветвленной части: I = U/Z
4. Токи в ветвях: I_L = I_C = IQ

Эти соотношения позволяют рассчитать все параметры цепи при резонансе токов.

Влияние добротности контура на резонанс токов

Добротность колебательного контура оказывает существенное влияние на характеристики резонанса токов:

• Чем выше добротность, тем острее выражен резонанс
• При высокой добротности токи в ветвях могут многократно превышать ток в неразветвленной части
• Полоса пропускания контура обратно пропорциональна добротности
• Потери энергии в контуре снижаются с ростом добротности

Поэтому на практике стремятся обеспечить максимально возможную добротность контура.

Способы настройки параллельного контура в резонанс

Существует несколько способов настройки параллельного колебательного контура в резонанс:

1. Изменение частоты источника питания
2. Подстройка емкости переменным конденсатором
3. Изменение индуктивности катушки с переменным сердечником
4. Использование подстроечных катушек индуктивности
5. Применение варикапов для электронной подстройки емкости

Выбор конкретного способа зависит от требуемого диапазона перестройки и условий эксплуатации устройства.

Заключение

Резонанс токов в параллельных RLC-цепях является важным физическим явлением, широко используемым в электротехнике и электронике. Понимание его особенностей позволяет эффективно применять резонансные цепи в различных устройствах. Правильный расчет параметров и настройка резонансного контура обеспечивают оптимальные характеристики радиотехнических и энергетических систем.

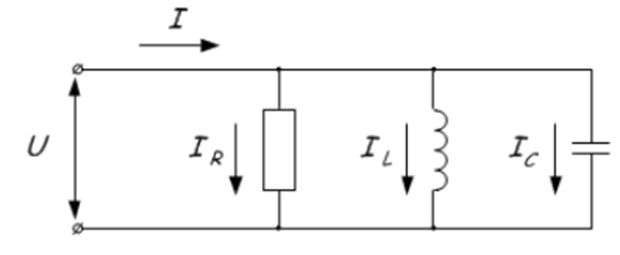
Параллельное соединение активного, индуктивного и емкостного сопротивлений в цепи синусоидального тока. Резонанс токов

Рассмотрим электрическую цепь синусоидального тока, содержащую две параллельно включенные ветви: одна содержит активно-индуктивное сопротивление, другая — активно-емкостное (рис. 32).

Кцепи подключен источник синусоидального напряжения, изменяющегося по закону:.

По I закону Кирхгофа для мгновенных значений токов: , а для комплексов -Разделим обе части последнего уравнения на одно и то же напряжение

,

где — полная проводимость.,- активная проводимость,

— реактивная проводимость.

.

Если известны параметры цепи, то проводимости:

.

Построим векторную диаграмму токов.

Пусть вектор приложенного напряжения совпадает с положительным направлением оси действительных чисел, т.е. (рис. 33). Токотстает отна угол, токопережаетна

Угол сдвига фаз между током в неразветвленном участке цепи и напряжением на концах этого участка определяется следующим образом:.

Проекции вектора тока в неразветвленной части цепи на оси действительных и мнимых чисел: . Действующее значение этого тока.

Есливектор тока отстает от вектора напряжения, цепь носит активно-индуктивный характер.

Если вектор тока опережает вектор напряжения, цепь носит активно-емкостный характер.

Если — цепь носит активный характер, в цепи наблюдается резонанс токов (рис. 34). При этом,,,.

Выводы:

1. — полная проводимость минимальна.

2. Ток в неразветвленной части цепи минимален

3. Если тоСледовательно,то есть токи в ветвях значительно больше, чем ток в неразветвленной части цепи. Применяется в радиотехнике.

Мощность цепи синусоидального тока

Под мгновенной мощностью (мощностью в данный момент времени) понимается произведение мгновенных значений тока и напряжения:

Если илитои в рассматриваемый участок цепи поступает энергия.

Если или, тои участок отдает энергию.

Однако среднее значение мощности за период всегда положительное, т. к. на участке всегда есть необратимые преобразования энергии.

Средняя за период мощность называется активной и определяется следующим образом:

Мощность реактивных элементов в среднем за период равна 0, но в течение четверти периода она положительна, что физически означает накопление энергии в магнитном поле катушки или в электрическом поле конденсатора, а в течении следующей четверти – отрицательна, что соответствует расходу энергии.

Таким образом, имеет место процесс колебания энергии, но необратимых преобразований энергии нет.

Мощность колебаний энергии называют реактивной:

— (вольт-ампер реактивный).

Кроме активной и реактивной мощностей цепь синусоидального тока характеризуется и полной мощностью Это максимально возможная мощность при заданных напряжениии токе

.

Связь между различными мощностями: ,.

В комплексной форме полная мощность определяется следующим образом:

где сопряженный ток;;

Расчет однофазных цепей синусоидального тока символическим методом

Суть метода: если в цепи переменного тока токи, напряжения, сопротивления записаны в комплексной форме, то для этих цепей справедливы законы и методы расчета цепей постоянного тока.

Порядок расчета:

1. Записать в комплексной форме сопротивления всех ветвей.

2. Задать направление на комплексной плоскости известного тока или напряжения; представить в комплексной форме этот ток или напряжение.

3. Любым способом определить комплексы остальных токов и напряжений.

4. Правильность решения проверить, составив уравнения баланса активной и реактивной мощностей.

5. Смоделировать данную электрическую цепь средствами моделирующего пакета ElectronicsWorkbench, определить показания приборов, сравнить полученные результаты с расчетными, сделать выводы.

§54. Последовательное соединение активного сопротивления, индуктивности и емкости

В общем случае в цепях переменного тока обычно имеются все виды сопротивлений: активное, индуктивное и емкостное. Например, электрические двигатели переменного тока могут быть представлены эквивалентной схемой, состоящей из индуктивного сопротивления имеющихся в нем катушек и активного сопротивления образующих эти катушки проводов. Воздушные линии элек-

Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)

тропередачи или кабельные линии обычно представляют в виде совокупности активного, индуктивного и емкостного сопротивлений. Активное сопротивление обусловлено сопротивлением электрических проводов, индуктивное — индуктивностью линии, а емкостное — емкостью, возникающей между отдельными проводами, между проводами и землей или же между отдельными жилами кабеля и между жилами кабеля и его оболочкой.

Расчет электрических цепей переменного тока существенно отличается от расчета цепей постоянного тока, так как при переменном токе в активном, индуктивном и емкостном сопротивлениях имеют место различные сдвиги фаз между токами и напряжениями.

Ток, напряжение и полное сопротивление. При последовательном включении в цепь переменного тока активного R, индуктивного X_L и емкостного Х_с сопротивлений (рис. 192, а) к ним приложены напряжения: активное u_a=iR, индуктивное u_L = iX_L и емкостное u_c=iX_c. Мгновенное значение напряжения и, приложенного к данной цепи, согласно второму закону Кирхгофа равно алгебраической сумме напряжений:

u = u_a + u_L + u_c

Но для действующих значений эта формула неприменима, так как между всеми указанными напряжениями имеется сдвиг по фазе (амплитудные значения этих напряжений не совпадают по

Рис. 193. Треугольник со противлении

времени). Чтобы учесть сдвиг по фазе между напряжениями u_а, u_L и u_c. осуществляют сложение их векторов:

? = ?_a + ?_L + ?_C

Для этого строят векторную диаграмму, на которой откладывают в определенном масштабе векторы тока ? и напряжений ?_a, ?_L, ?_C. Из этих напряжений первое совпадает по фазе с током, второе опережает его на 90°. Векторная диаграмма (рис. 192,б) построена для цепи, в которой индуктивное сопротивление X_L больше емкостного X_c (вектор ?_L, больше вектора ?_C.), а рис. 192, в — для цепи, в которой X_L меньше Хс (вектор ?_L, меньше вектора ?_C). Вектор напряжения U является замыкающим — он сдвинут по фазе относительно вектора тока ? на некоторый угол ?. Напряжение U (действующее значение) может быть определено из треугольника ЛВС по теореме Пифагора:

U = ?(U²_a + (U_L – U_c)²)

Таким образом, из-за наличия угла сдвига фаз ? напряжение U всегда меньше алгебраической суммы U_a + U_L + U_C. Разность U_L – U_C = U_p называется реактивной составляющей напряжения.

Рассмотрим, как изменяются ток и напряжение в последовательной цепи переменного тока.

В цепи, содержащей все три вида сопротивления, ток i и напряжение и оказываются сдвинутыми по фазе на некоторый угол ср (рис. 192, г), при этом 0<?<90°.

Полное сопротивление и угол сдвига фаз. Если подставить в формулу (71) значения U_a = IR; U_L = l?L и U_C=I/(?C), то будем иметь: U = ?((IR)²+ [I?L-I/ (?С) ]²), откуда получаем формулу закона Ома для последовательной цепи переменного тока:

I = U / (? (R²+ [?L-1 / (?С) ]²) ) = U / Z (72)

где Z = ? (R²+ [?L-1 / (?С) ]²) = ? (R²+ (X_L – X_c)²)

Величину Z называют полным сопротивлением цепи, оно измеряется в омах. Разность ?L — l/(?C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи

Z = ? (R²+ X²)

Соотношение между активным, реактивным и полным сопротивлениями цепи переменного тока можно также получить по теореме Пифагора из треугольника сопротивлений (рис.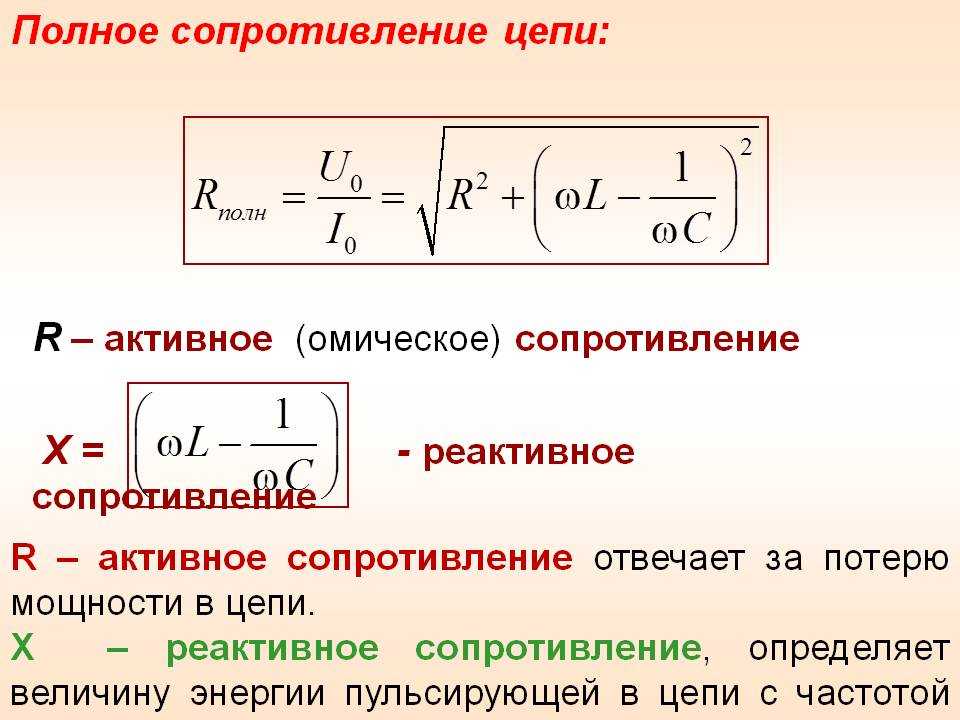 193). Треугольник сопротивлений А’В’С’ можно получить из треугольника напряжений ABC (см. рис. 192,б), если разделить все его стороны на ток I.

Угол сдвига фаз ? определяется соотношением между отдельными сопротивлениями, включенными в данную цепь. Из треугольника А’В’С (см. рис. 193) имеем:

sin ? = X / Z; cos? = R / Z; tg? = X / R

Например, если активное сопротивление R значительно больше реактивного сопротивления X, угол ? сравнительно небольшой. Если в цепи имеется большое индуктивное или большое емкостное сопротивление, то угол сдвига фаз ? возрастает и приближается к 90°. При этом, если индуктивное сопротивление больше емкостного, напряжение и опережает ток i на угол ?; если же емкостное сопротивление больше индуктивного, то напряжение и отстает от тока i на угол ?.

Резистивно-индуктивные параллельные цепи

---

---

ЦЕЛИ

• обсудить работу параллельной цепи, содержащей сопротивление и индуктивность.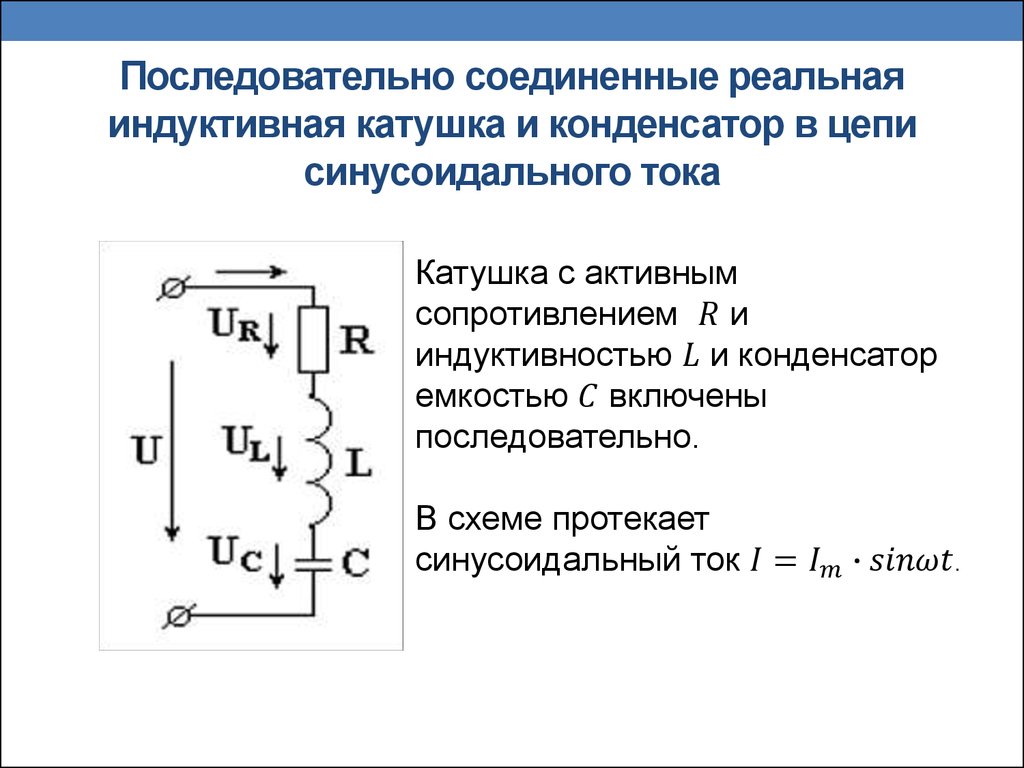

• вычислить значения цепи R-L параллельной цепи.

• подключите параллельную цепь R-L и измерьте значения цепи с помощью теста инструменты.

РЕЗИСТИВНО-ИНДУКТИВНОЕ ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ УСЛОВИЯ

• угол тета (θ u) — разность фазового угла между напряжением и током в цепи, содержащей реактивный компонент, такой как катушка индуктивности или конденсатор
• полная мощность (ВА) — значение, полученное путем умножения приложенного напряжение на общий ток цепи переменного тока. Полная мощность измеряется в вольт-амперах (ВА) и не следует путать с реальной мощностью, измеренной в ваттах
• ток, протекающий через индуктор (IL) — количество протекающего тока через дроссель
• ток, протекающий через резистор (IR) — количество протекающего тока через резистор
• коэффициент мощности (PF) — отношение активной мощности к кажущейся реактивной мощности. мощность Вар
• полный ток (IT) — полный ток, протекающий в электрической цепи; в параллельной цепи R-L это определяется векторным сложением резистивный ток и индуктивный ток
• полное сопротивление (Z) — общее ограничение тока в цепи переменного тока
• истинная мощность (P) — количество преобразуемой электрической энергии. в какую-либо другую форму энергии, такую ​​как тепловая или кинетическая; также известный как ватт
• ватт — реальная мощность в цепи; указывает количество эл. энергия, преобразованная в другую форму

—————-

В этом разделе обсуждаются цепи, содержащие сопротивление и индуктивность, соединенные параллельно друг другу.

Математические расчеты будут использоваться, чтобы показать взаимосвязь текущих и напряжения на всей цепи, и отношения тока через разные ветви цепи.

РЕЗИСТИВНО-ИНДУКТИВНЫЕ ПАРАЛЛЕЛЬНЫЕ ЦЕПИ

Цепь, содержащая резистор и катушку индуктивности, соединенные параллельно показан на фиг.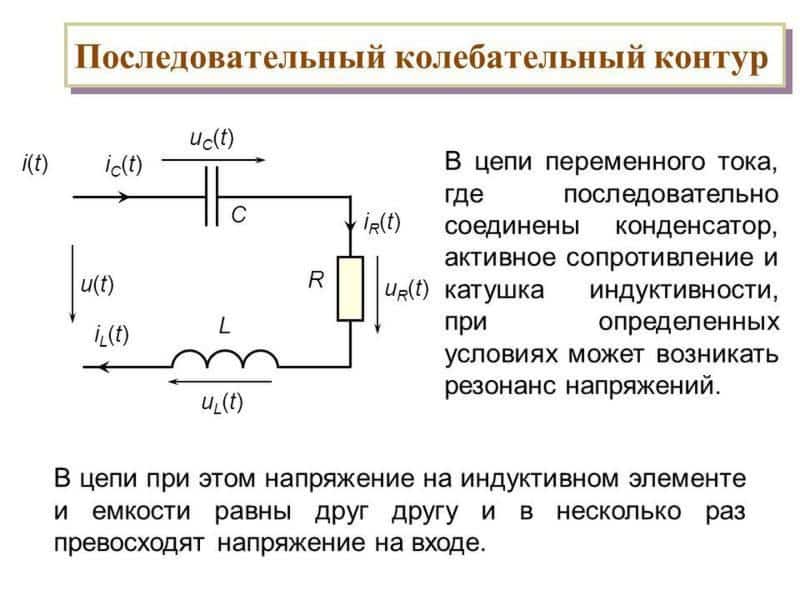 1.

Поскольку напряжение, подаваемое на любое параллельное устройство, должно быть одинаковым, напряжение, подаваемое на резистор и катушку индуктивности, должно быть синфазным и иметь такое же значение. Ток, протекающий через индуктор, будет находиться под углом 90° от фаза с напряжением, и ток, протекающий через резистор, будет быть в фазе с напряжением (РИС. 2). Эта конфигурация производит разность фаз 90° между током, протекающим через чисто индуктивный нагрузка и чисто резистивная нагрузка (фиг. 3).

РИС. 1 Резистивно-индуктивная параллельная цепь.

РИС. 2 Соотношение напряжения и тока в R-L параллельной цепи.

РИС. 3 Резистивные и индуктивные токи не совпадают по фазе на 90° с друг друга в R-L параллельной цепи.

Величина фазового сдвига между полным током цепи и напряжение определяется отношением величины сопротивления к величине индуктивности. Коэффициент мощности цепи по-прежнему определяется соотношением кажущейся мощности к истинной мощности.

ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ЦЕПИ

В схеме, показанной на РИС. 4, подключено сопротивление 15 Ом параллельно с индуктивным сопротивлением 20 Ом. Цепь подключена на напряжение 240 В переменного тока и частоту 60 Гц.

В этом примере задачи будут вычислены следующие значения схемы:

IR — протекание тока через резистор

P — ватт (истинная мощность)

IL — протекание тока через дроссель

ВАР — реактивная мощность

IT — общий ток цепи

Z — полное сопротивление цепи

ВА — полная мощность

PF — коэффициент мощности

θ u — угол отклонения напряжения и тока друг от друга по фазе:

РЕЗИСТИВНЫЙ ТОК

В любой параллельной цепи напряжение одинаково на всех компонентах в цепи. Таким образом, 240 В подается как на резистор, так и на индуктор.

Поскольку величина напряжения, подаваемого на резистор, известна, величина тока через резистор (IR) можно рассчитать с помощью формула:

I _Р = Э/Р

I _R = 240/15

I _R = 16 А

РИС. 4 Типичная параллельная цепь R-L.

ВАТТ

Истинная мощность (P) или ватты может быть рассчитана с использованием любого из ватт. формулы и значения чистого сопротивления.

Количество реальной мощности в этой цепи будет вычислено по формуле

P = E _R x I _R

Р = 240 х 16

P = 3840 Вт

ИНДУКТИВНЫЙ ТОК

Поскольку известно напряжение, подаваемое на катушку индуктивности, протекающий ток можно найти, разделив напряжение на индуктивное сопротивление. Количество тока через индуктор (IL) будет вычисляться по формуле

I _L = E/X _L

I _L = 240/20

I _L = 12 А

ВАРС

Количество реактивной мощности, ВАр, будет рассчитываться по формуле

ВАр = E _L x I _L

ВАР = 240 x 12

ВАР = 2880

ИНДУКТИВНОСТЬ

Частота и индуктивное сопротивление известны, поэтому индуктивность катушки можно найти по формуле

л = Х _л 2пФ

Д = 20/377

Д = 0,053Н

ОБЩИЙ ТОК

РИС. 5 Соотношение резистивного, индуктивного и полного тока в R-L параллельная цепь.

РИС. 6 Построение графика полного тока методом параллелограмма.

Полный ток (IT), протекающий по цепи, можно рассчитать, добавив ток течет через резистор и катушку индуктивности. Поскольку эти два токи 90° не совпадают по фазе друг с другом, сложение векторов будет использовал. Если бы эти текущие значения были нанесены на график, они образовали бы прямоугольный треугольник. аналогичный показанному на фиг. 5. Обратите внимание, что ток течет через резистор и катушка индуктивности образуют стороны прямоугольного треугольника, а сумма ток это гипотенуза. Следовательно, теорему Пифагора можно использовать чтобы сложить эти токи вместе.

Метод параллелограмма для построения графика полного тока показан на РИС. 6.

ИМПЕДАНС

Теперь, когда общий ток и общее напряжение известны, общий импеданс (Z) можно рассчитать, заменив R на Z в омах. формула закона.

Общее сопротивление цепи можно рассчитать по формуле

Значение импеданса также можно найти, если суммарный ток и напряжение не известны. В параллельной цепи величина, обратная полному сопротивлению равно сумме обратных величин каждого резистора. Это же правило могут быть изменены, чтобы разрешить использование аналогичной формулы в параллели R-L. схема. Поскольку сопротивление и индуктивное сопротивление равны 90° вне фазы друг с другом, сложение векторов должно использоваться, когда обратные добавлен. Исходная формула:

Эта формула утверждает, что квадрат обратной величины импеданса равен сумме квадратов обратных величин сопротивления и индуктивное реактивное сопротивление. Чтобы удалить квадрат из обратной величины импеданса, возьми квадратный корень из обеих частей уравнения.

Обратите внимание, что формулу теперь можно использовать для нахождения обратной величины импеданс, а не импеданс. Изменить формулу так, чтобы она была равна к импедансу, возьмите обратную величину обеих частей уравнения.

Теперь в формулу можно подставлять числовые значения для определения импеданса. цепи.

Другая формула, по которой можно определить импеданс сопротивления а индуктивное сопротивление, соединенное параллельно, составляет

Подстановка одинаковых значений сопротивления и индуктивного сопротивления в эта формула даст тот же ответ.

ПОЛНАЯ МОЩНОСТЬ

Полная мощность (ВА) может быть рассчитана путем умножения напряжения цепи по общему течению. Соотношение вольт-ампер, ватт и реактивной мощности то же самое для параллельной цепи R-L, что и для последовательной цепи R-L, потому что мощность добавляется в цепи любого типа. Поскольку истинная мощность и реактивная мощность 90 ° не совпадают по фазе друг с другом, они образуют прямоугольный треугольник с кажущейся мощностью в качестве гипотенузы (РИС. 7).

ВА = ET x IT

ВА = 240 х 20

ВА = 4800

КОЭФФИЦИЕНТ МОЩНОСТИ

РИС. 7 Соотношение полной мощности (вольт-ампер), истинной мощности (ватт), и реактивная мощность (вар) в параллельной цепи R-L.

Коэффициент мощности (PF) в параллельной цепи R-L представляет собой отношение кажущейся мощность до истинной мощности, как это было в цепи серии R-L.

Существуют некоторые различия в формулах, используемых для расчета коэффициента мощности. в параллельной цепи, как всегда. В цепи серии R-L коэффициент мощности можно вычислить, разделив падение напряжения на резисторе на общее или приложенное напряжение. В параллельной цепи напряжение равно одинаковые, а токи разные. Таким образом, можно рассчитать коэффициент мощности. путем разделения тока, протекающего через резистивные части цепи по полному току цепи.

ПФ = ИК/ИТ

Другая формула, которая меняется, включает сопротивление и импеданс. Параллельно цепи, полное сопротивление цепи будет меньше, чем сопротивление. Следовательно, если коэффициент мощности должен быть рассчитан с использованием импеданса и сопротивления, импеданс надо разделить на сопротивление.

ПФ = З/Р

Коэффициент мощности цепи в этом примере будет вычисляться по формуле

УГОЛ ТЕТА

Косинус угла тета (θ u) равен коэффициенту мощности.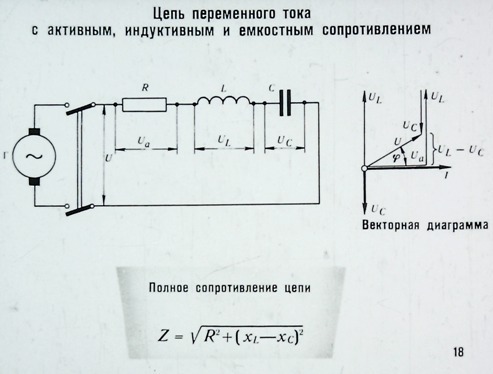

COSθ u = 0,80

θ u = 36,87°

Векторная диаграмма с использованием полной мощности, активной мощности и реактивной мощности. показан на фиг. 8.

Обратите внимание, что угол тета — это угол, создаваемый кажущейся мощностью и истинная власть. Соотношение тока и напряжения для этой цепи показан на фиг. 9. Схема со всеми значениями показана на фиг. 10.

РИС. 8 Угол тета.

РИС. 9 Ток не совпадает по фазе с напряжением на 36,87°.

РИС. 10 Все значения найдены.

ОБЗОР

• Напряжение, подаваемое на компоненты в параллельной цепи, должно быть одинаковый.

• Ток, протекающий через резистивные части цепи, будет фаза с напряжением.

• Ток, протекающий через индуктивные части цепи, будет отставать от напряжение на 90°.

• Общий ток в параллельной цепи равен сумме отдельных токи. Необходимо использовать сложение векторов, потому что ток через резистивные части цепи не совпадают по фазе на 90° с текущим током через индуктивные части.

• Полное сопротивление R-L параллельной цепи можно вычислить с помощью вектора Кроме того, чтобы добавить обратные величины сопротивления и индуктивного реактивного сопротивления.

• Полная мощность, действительная мощность и реактивная мощность суммируются в цепи любого типа. Однако необходимо использовать сложение векторов, поскольку истинная мощность и реактивная мощность 90° не совпадают по фазе друг с другом.

ВИКТОРИНА

1. Сколько градусов при параллельном соединении катушки индуктивности и резистора не совпадают по фазе ток, протекающий через резистор, и ток течь через индуктор?

2. Катушка индуктивности и резистор подключены параллельно к сети 120 В, 60 Гц. линия. Резистор имеет сопротивление 50 Ом, а катушка индуктивности имеет индуктивность 0,2 Гн. Каков общий ток, протекающий по цепи?

3. Каков импеданс рассматриваемой цепи 2?

4. Каков коэффициент мощности рассматриваемой цепи 2?

5. На сколько градусов не совпадают по фазе рассматриваемые ток и напряжение 2?

6. В схеме, показанной на фиг. 1, через резистор протекает ток 6,5 А, а через индуктор течет ток 8 А. Какова общая ток в этой цепи?

7. Резистор и катушка индуктивности соединены параллельно. Резистор имеет сопротивление 24 Ом, а индуктивное сопротивление катушки индуктивности 20 Ом. Каково сопротивление этой цепи?

8. Параллельная цепь R-L, показанная на фиг. 1 имеет кажущуюся мощность 325 ВА. Коэффициент мощности схемы составляет 66%. В чем истинная сила этого схема?

9. Параллельная цепь R-L, показанная на РИС. 1 имеет кажущуюся мощность 465 ВА и реальной мощностью 320 Вт. Что такое реактивная мощность?

10. На сколько градусов не совпадают по фазе суммарный ток и напряжение в вопрос 9?

ПРАКТИЧЕСКИЕ ЗАДАЧИ

Обратитесь к схеме, показанной на РИС. 1.

Используйте формулы переменного тока в резистивно-индуктивной параллели. Раздел «Схемы» приложения.

1. Предположим, что схема, показанная на РИС. 1 подключен к 60-Гц линия и имеет общий ток 34,553 А. Катушка индуктивности имеет индуктивность 0,02122 Гн, а резистор имеет сопротивление 14 Ом.

ET ER EL IT 34.553 IR IL Z R14 XL VA P VARSL PF θ u L 0,02122

2. Предположим, что ток, протекающий через резистор IR, равен 15 А; в ток через индуктор IL равен 36 А; и схема имеет полная мощность 10 803 ВА. Частота переменного напряжения 60 Гц.

ET ER EL IT IR 15 IL 36 Z R XL VA 10,803 P VARSL PF θ u L

3. Предположим, что схема на РИС. 1 имеет кажущуюся мощность 144 ВА и реальная мощность 115,2 Вт. Катушка индуктивности имеет индуктивность 0,15915. Н, а частота 60 Гц.

ET ER EL IT IR IL Z R XL VA 144 P 115.2 VARSL PF θ u L 0,15915

4. Предположим, что схема на РИС.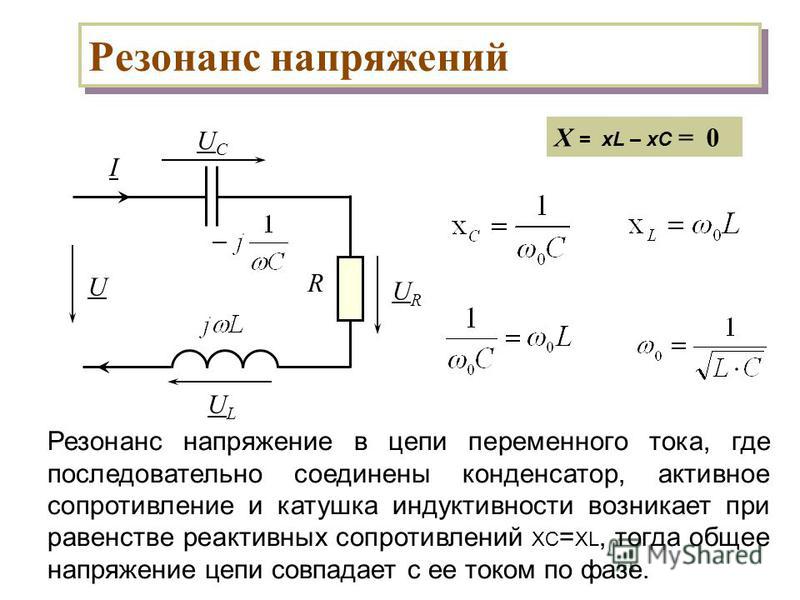 1 имеет коэффициент мощности 78%, полная мощность 374,817 ВА, частота 400 Гц. Индуктор имеет индуктивность 0,0382 Гн

ET ER EL IT IR IL Z R XL VA 374.817 P VARSL PF 78% θ u L 0,0382

РЕАЛЬНЫЕ ПРИМЕНЕНИЯ

1. Лампа накаливания мощностью 500 Вт подключена параллельно с индуктивной нагрузка. Токоизмерительные клещи показывают общий ток цепи 7 А.

Чему равна индуктивность нагрузки, включенной параллельно с лампой накаливания? огни? Предположим, напряжение 120 В при 60 Гц.

2. Вы работаете над бытовым тепловым насосом. Тепловой насос подключен к сети 240 В, 60 Гц. Компрессор потребляет ток 34 А, когда операционная. Компрессор имеет коэффициент мощности 70%. Запасная полоса тепловая мощность 10кВт. Вам нужно знать сумму общего текущего потребления это произойдет, если обогрев полосы будет включаться во время работы компрессора.

Параллельная цепь RLC (коэффициент мощности, активная и реактивная мощность)

Что касается параллельной цепи RLC, в этой статье поясняется приведенная ниже информация.

• Коэффициент мощности \({\cos}{\theta}\) параллельной цепи RLC
• Активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\) Параллельная цепь RLC

На рисунке выше показана параллельная цепь RLC с резистором \(R\), катушкой индуктивности \(L\) и конденсатором \(C\), соединенными параллельно.

Например, параметры параллельной цепи RLC следующие.

• Напряжение питания: \({\dot{V}}=100{\;}{\mathrm{[V]}}\)
• Частота напряжения питания: \(f=60{\;}{ \mathrm{[Гц]}}\)
• Значение сопротивления резистора: \(R=50{\;}{\mathrm{[{\Omega}]}}\)
• Индуктивность индуктора: \(L= 66,4{\;}{\mathrm{[мГн]}}\)
• Емкость конденсатора: \(C=53{\;}{\mathrm{[мкФ]}}\)

Коэффициент мощности \( {\cos}{\theta}\), активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\) параллельной цепи RLC могут быть получены с помощью следующей процедуры (шаги 1 к 4).

Процедура

• Рассчитайте величину \(Z\) импеданса параллельной цепи RLC
• Рассчитайте величину \(I\) тока, протекающего в параллельной цепи RLC
• Рассчитайте коэффициент мощности \( {\cos}{\theta}\) параллельной цепи RLC
• Расчет активной мощности \(P\), реактивной мощности \(Q\) и полной мощности \(S\) параллельной цепи RLC

Теперь мы опишем каждую процедуру по очереди.

Дополнение

В цепи переменного тока существует три типа мощности: активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\).

• Активная мощность \(P\)
  • Это мощность, потребляемая резистором \(R\), также называемая потребляемой мощностью. Единица измерения [Вт].
• Реактивная мощность \(Q\)
  • Это мощность, которая не потребляется резистором \(R\). Мощность, которую индуктор или конденсатор накапливает или выделяет, называется реактивной мощностью. Единица измерения [вар].
• Полная мощность \(S\)
  • Мощность представляет собой сумму активной мощности \(P\) и реактивной мощности \(Q\). Единица измерения [ВА].

Расчет величины \(Z\) импеданса параллельной цепи RLC

Импеданс \({\dot{Z}}_R\) резистора \(R\), импеданс \( {\ dot {Z}} _L \) катушки индуктивности \ (L \), а полное сопротивление \ ({\ dot {Z}} _C \) конденсатора \ (C \) можно выразить следующими уравнениями: соответственно.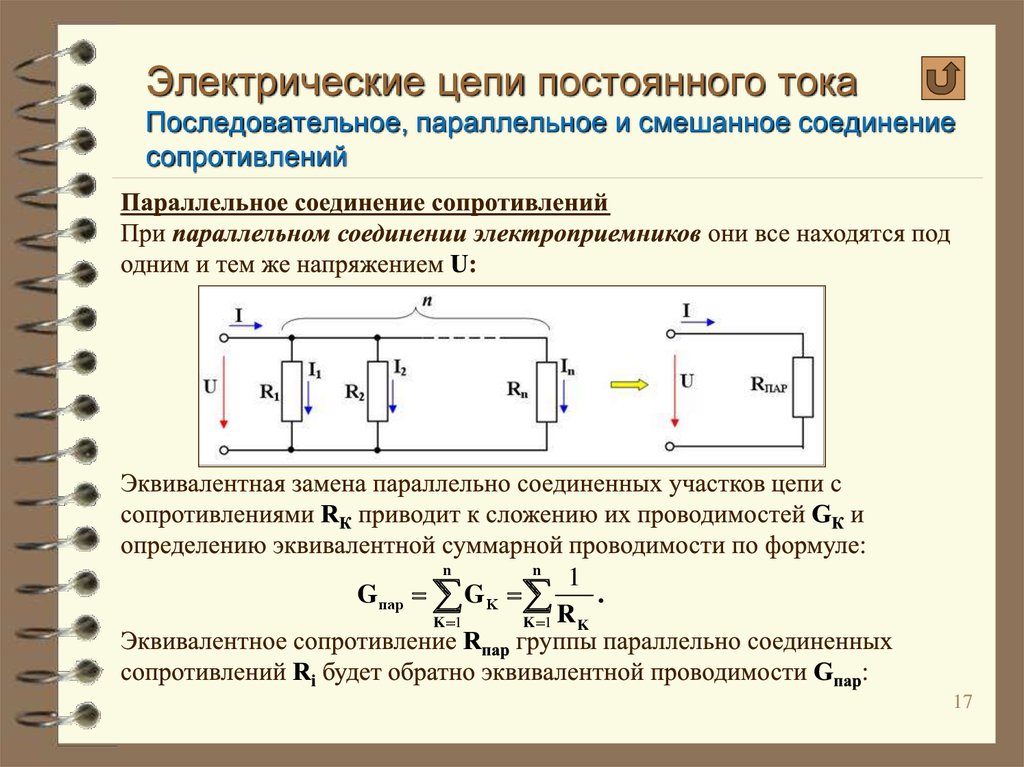

\begin{eqnarray}
{\ dot {Z} _R} & = & R \ tag {1} \\
\\
{\ dot {Z} _L} & = & jX_L = j {\ omega} L \ tag {2} \\
\ \
{\dot{Z}_C}&=&-jX_C=-j\frac{1}{{\omega}C}\tag{3}
\end{eqnarray}

, где \({\omega }\) — угловая частота, равная \(2{\pi}f\), а \(X_L\) называется индуктивным сопротивлением, которое представляет собой резистивную составляющую индуктора \(L\) и \(X_C \) называется емкостным реактивным сопротивлением, которое представляет собой резистивную составляющую конденсатора \(С\).

Индуктивное сопротивление \(X_L\) и емкостное сопротивление \(X_C\) можно получить с помощью следующих уравнений. 9{-6}}{\;}{\приблизительно}{\;}50{\;}{\mathrm{[{\Omega}]}}\tag{5}
\end{eqnarray}

Здесь составное реактивное сопротивление \(X\) катушки индуктивности \(L\) и конденсатора \(C\) можно получить по следующему уравнению.

\begin{eqnarray}
X&=&\left|\frac{1}{\displaystyle\frac{1}{X_L}-\displaystyle\frac{1}{X_C}}\right|=\left|\ frac {1} {\ displaystyle \ frac {1} {25} — \ displaystyle \ frac {1} {50}} \ right | = 50 {\;} {\ mathrm {[{\ Omega}]}} \ tag {6}
\end{eqnarray}

Сумма обратных величин каждого импеданса является обратной величиной импеданса \({\dot{Z}}\) параллельной цепи RLC. Поэтому его можно выразить следующим уравнением.

\begin{eqnarray}
\frac{1}{{\dot{Z}}}&=&\frac{1}{{\dot{Z}_R}}+\frac{1}{{\dot {Z}_L}}+\frac{1}{{\dot{Z}_C}}\\
\\
&=&\frac{1}{R}+\frac{1}{jX_L}+\ frac{1}{-jX_C}\\
\\
&=&\frac{1}{R}-j\frac{1}{X_L}+j\frac{1}{X_C}\\
\\
&=&\frac{1}{R}+j\left(\frac{1}{X_C}-\frac{1}{X_L}\right)\tag{7}
\end{eqnarray}

Из уравнения (7) путем замены знаменателя и числителя получается следующее уравнение:

\begin{eqnarray}
{\dot{Z}}&=&\frac{1}{\displaystyle\frac{1}{{\dot{Z}_R}}+\displaystyle\frac{1}{{ \dot{Z}_L}}+\displaystyle\frac{1}{{\dot{Z}_C}}}\\
\\
&=&\frac{1}{\displaystyle\frac{1}{ R}+j\left(\frac{1}{X_C}-\frac{1}{X_L}\right)}\tag{8}
\end{eqnarray}

Величина \(Z\) импеданс параллельной цепи RLC представляет собой абсолютное значение импеданса \({\dot{Z}}\) в уравнении (8).

\begin{eqnarray}
Z=|{\dot{Z}}|&=&\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+ \left(\displaystyle\frac{1}{X_C}-\displaystyle\frac{1}{X_L}\right)^2}}\\ 92}}\\
\\
&=&25\sqrt{2}{\;}{\mathrm{[{\Omega}]}}\tag{9}
\end{eqnarray}

Связанная статья

Расчет величины \(I\) тока, протекающего в параллельной цепи RLC

Величина \(V\) напряжения питания представляет собой следующую величину.

\begin{eqnarray}
V=|{\dot{V}}|=|100|=100{\;}{\mathrm{[V]}}\tag{10}
\end{eqnarray}

Из уравнений (9) и (10) величина \(I\) тока, протекающего в параллельной цепи RLC, может быть получена по следующему уравнению

\begin{eqnarray}
I=\frac{V}{Z}=\frac{100}{25\sqrt{2}}=2\sqrt{2}{\;}{\mathrm{[A] }}\tag{11}
\end{eqnarray}

Поскольку это параллельная цепь, «величина \(V_R\) напряжения на резисторе \(R\)», «величина \(V_L\ ) напряжения на катушке индуктивности \(L\)», а «величина \(V_C\) напряжения на конденсаторе \(C\)» равна «величине \(V\) напряжения питания «, и справедлива следующая формула.

\begin{eqnarray}
V=V_R=V_L=V_C=100{\;}{\mathrm{[V]}}\tag{12}
\end{eqnarray}

Следовательно, «величина \(I_R\) протекающего тока через резистор \(R\)», «величина \(I_L\) тока, протекающего через индуктор \(L\)», и «величина \(I_C\) тока, протекающего через конденсатор \( С\)» можно получить по следующей формуле.

\begin{eqnarray}
I_R&=&\frac{V_R}{R}=\frac{100}{50}=2{\;}{\mathrm{[A]}}\tag{13}\\
\\
I_L&=&\frac{V_L}{X_L}=\frac{100}{25}=4{\;}{\mathrm{[A]}}\tag{14}\\
\\
I_C&=&\frac{V_C}{X_C}=\frac{100}{50}=2{\;}{\mathrm{[A]}}\tag{15}
\end{eqnarray}

Величина \(I_X\) тока, протекающего в составном реактивном сопротивлении \(X\), может быть получена из следующего уравнения

\begin{eqnarray}
I_X=\frac{V}{X}=\frac {100}{50}=2{\;}{\mathrm{[A]}}\tag{16}
\end{eqnarray}

Как видно из уравнения (16), величина \(I_X\ ) тока, протекающего в составном реактивном сопротивлении \(X\), представляет собой разность (\(|I_L-I_C|\)) между «величиной \(I_L\) тока, протекающего в дросселе \(L\)» и «величина \(I_C\) тока, протекающего в конденсаторе \(C\)».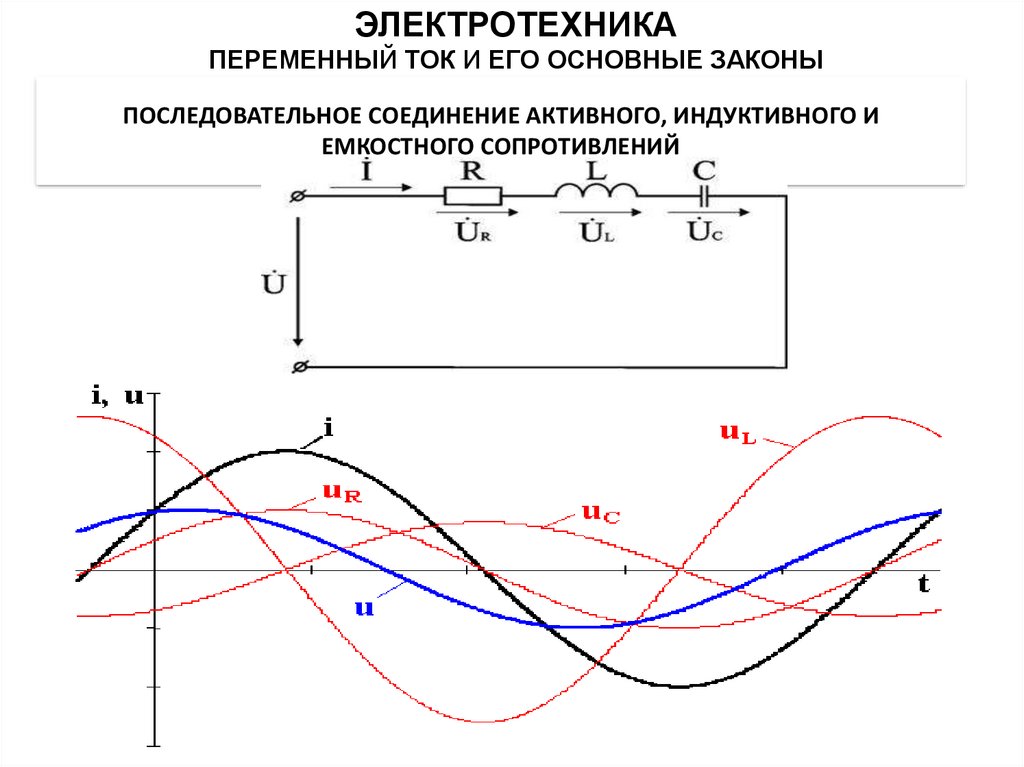

Рассчитайте коэффициент мощности \({\cos}{\theta}\) параллельной цепи RLC

Коэффициент мощности \({\cos}{\theta}\) параллельной цепи RLC представляет собой отношение величины импеданса \(Z\) к сопротивлению \(R\) и может быть получено с помощью следующего уравнения

\begin{eqnarray}
{\cos}{\theta}=\frac{Z}{R}=\ frac{25\sqrt{2}}{50}=\frac{1}{\sqrt{2}}\tag{17}
\end{eqnarray}

Supplement

Коэффициент мощности \({\cos }{\theta}\) параллельной цепи RLC также можно получить отношением «величины \(I_R\) тока, протекающего через резистор \(R\)» к «величине \(I\) тока, протекающего по параллельной цепи RLC». Можно рассчитать следующее уравнение, равное уравнению (17).

\begin{eqnarray}
{\cos}{\theta}=\frac{I_R}{I}=\frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2 }}\tag{18}
\end{eqnarray}

Расчет активной мощности \(P\), реактивной мощности \(Q\) и полной мощности \(S\) параллельной цепи RLC

Путем нахождения «величина \(V\) напряжения источника питания», «величина \(I\) тока, протекающего в параллельной цепи RLC», и «коэффициент мощности \({\cos}{\theta}\ ) параллельной цепи RLC» можно рассчитать активную мощность \(P\), реактивную мощность \(Q\) и полную мощность \(S\). 2{\;}{\cdot}{\;}25\sqrt{2}=200\sqrt{2}{ \;}{\mathrm{[VA]}}\tag{20}\\ 92}{25\sqrt{2}}=200\sqrt{2}{\;}{\mathrm{[VA]}}\tag{21}
\end{eqnarray}

[Параллельная цепь RLC] Расчет активная мощность \(P\)

Активная мощность \(P\) может быть получена из следующего уравнения

\begin{eqnarray}
P=VI{\cos}{\theta}=100{\;}{ \cdot}{\;}2\sqrt{2}{\;}{\cdot}{\;}\frac{1}{\sqrt{2}}=200{\;}{\mathrm{[W] }}\tag{22}
\end{eqnarray}

Другое решение

Поскольку эффективная мощность \(P\) — это мощность, потребляемая резистором \(R\), ее также можно получить с помощью следующего уравнение. Результаты расчета показывают, что он равен уравнению (22). 92}{50}=200{\;}{\mathrm{[var]}}\tag{27}
\end{eqnarray}

Коэффициент мощности \({\cos}{\theta}\) Параллельная цепь RLC также может быть получена по отношению «активной мощности \(P\)» к «полной мощности \(S\)». Расчет дает следующее уравнение, равное уравнениям (17) и (18).

\begin{eqnarray}
{\cos}{\theta}=\frac{P}{S}=\frac{200}{200\sqrt{2}}=\frac{1}{\sqrt{2 }}\tag{28}
\end{eqnarray}

Резюме

В этой статье приводится следующая информация о «параллельной цепи RLC».