Как рассчитать эквивалентное сопротивление при последовательном и параллельном соединении. Какие формулы используются для вычисления токов и напряжений. Чем отличаются последовательные и параллельные цепи на практике.
Основные понятия последовательного и параллельного соединения
Последовательное и параллельное соединение проводников — это два основных способа соединения элементов электрической цепи. Понимание принципов работы этих соединений крайне важно для анализа и расчета электрических схем.
Последовательное соединение
При последовательном соединении элементы цепи соединяются друг за другом, образуя единую цепочку. Основные свойства последовательного соединения:
- Ток через все элементы одинаков
- Напряжение распределяется между элементами
- Общее сопротивление равно сумме сопротивлений всех элементов
Параллельное соединение
При параллельном соединении элементы подключаются к одним и тем же точкам цепи. Ключевые особенности:
- Напряжение на всех элементах одинаково
- Ток распределяется между элементами
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений элементов
Формулы для расчета последовательного соединения
Рассмотрим основные формулы, используемые при анализе последовательных цепей:
Эквивалентное сопротивление
Формула для расчета общего сопротивления последовательной цепи:
Rэкв = R1 + R2 + … + Rn
где Rэкв — эквивалентное сопротивление, R1, R2, …, Rn — сопротивления отдельных элементов.
Ток в цепи
Ток в последовательной цепи одинаков для всех элементов и рассчитывается по закону Ома:
I = U / Rэкв
где I — ток, U — общее напряжение, Rэкв — эквивалентное сопротивление цепи.
Падение напряжения
Падение напряжения на каждом элементе рассчитывается по формуле:
Ui = I * Ri
где Ui — напряжение на i-том элементе, I — ток в цепи, Ri — сопротивление i-того элемента.
Формулы для расчета параллельного соединения
Теперь рассмотрим ключевые формулы для анализа параллельных цепей:
Эквивалентное сопротивление
Формула для расчета общего сопротивления параллельной цепи:
1/Rэкв = 1/R1 + 1/R2 + … + 1/Rn
где Rэкв — эквивалентное сопротивление, R1, R2, …, Rn — сопротивления отдельных элементов.
Общий ток
Общий ток в параллельной цепи равен сумме токов через все ветви:
Iобщ = I1 + I2 + … + In
где Iобщ — общий ток, I1, I2, …, In — токи через отдельные ветви.
Ток в отдельной ветви
Ii = U / Ri
где Ii — ток через i-тую ветвь, U — напряжение (одинаковое для всех ветвей), Ri — сопротивление i-той ветви.
Практическое применение последовательных и параллельных соединений
В реальных электрических схемах последовательные и параллельные соединения встречаются повсеместно. Рассмотрим некоторые примеры их практического применения:
Последовательное соединение
- Гирлянды на новогодней елке — классический пример последовательного соединения ламп
- Предохранители и выключатели в электрических цепях часто включаются последовательно с нагрузкой
- Резисторы для ограничения тока (например, в схемах светодиодов) включаются последовательно
Параллельное соединение
- Бытовые электроприборы в домашней сети подключаются параллельно
- Аккумуляторы в батареях часто соединяются параллельно для увеличения емкости
- Светодиоды в светильниках нередко соединяются параллельно для увеличения яркости
Расчет комбинированных цепей
В реальных схемах часто встречаются комбинации последовательных и параллельных соединений. Рассмотрим алгоритм расчета такой цепи:
- Разбить схему на группы последовательно и параллельно соединенных элементов
- Рассчитать эквивалентное сопротивление для каждой группы
- Заменить группы их эквивалентными сопротивлениями
- Повторять шаги 1-3, пока не останется одно эквивалентное сопротивление
- Рассчитать общий ток цепи
- Последовательно определить токи и напряжения на всех элементах, двигаясь от общего к частному
Преимущества и недостатки различных типов соединений
Каждый тип соединения имеет свои плюсы и минусы. Рассмотрим их подробнее:
Последовательное соединение
Преимущества:
- Простота подключения
- Возможность легко изменять общее сопротивление цепи
- Удобно для создания делителей напряжения
Недостатки:
- При выходе из строя одного элемента перестает работать вся цепь
- Общий ток ограничен самым «слабым» элементом
- Сложность подбора элементов с нужными параметрами для равномерного распределения напряжения
Параллельное соединение
Преимущества:
- Возможность подключения большого количества потребителей
- Выход из строя одного элемента не нарушает работу остальных
- Легко наращивать мощность системы добавлением параллельных ветвей
Недостатки:
- Сложность обеспечения равномерной нагрузки на все ветви
- Риск перегрузки источника питания при добавлении слишком большого числа параллельных ветвей
- Необходимость использования проводов большего сечения для питающих линий
Методы анализа сложных электрических цепей
При анализе сложных цепей, содержащих множество элементов и комбинации различных соединений, используются специальные методы:
Метод контурных токов
Этот метод основан на составлении уравнений для токов, протекающих по замкнутым контурам цепи. Основные шаги:
- Выбрать независимые контуры в схеме
- Задать направления контурных токов
- Составить уравнения по второму закону Кирхгофа для каждого контура
- Решить полученную систему уравнений
Метод узловых потенциалов
Этот метод использует уравнения для потенциалов узлов схемы. Алгоритм:
- Выбрать узел с нулевым потенциалом
- Составить уравнения по первому закону Кирхгофа для остальных узлов
- Выразить токи через разности потенциалов и проводимости ветвей
- Решить полученную систему уравнений относительно потенциалов узлов
Метод наложения
Этот метод применяется для линейных цепей с несколькими источниками. Суть метода:
- Рассмотреть действие каждого источника по отдельности, заменив остальные их внутренними сопротивлениями
- Рассчитать частичные токи от каждого источника
- Найти реальные токи и напряжения суммированием частичных
Применение теории цепей в современных технологиях
Знание принципов работы электрических цепей критически важно для развития современных технологий. Рассмотрим несколько примеров:
Электроника и микроэлектроника
В современных электронных устройствах используются сложные интегральные схемы, содержащие миллионы транзисторов и других элементов. Анализ таких схем требует глубокого понимания теории цепей и использования специализированного программного обеспечения.
Силовая электроника
При проектировании систем электропитания, преобразователей напряжения и частоты, систем управления электродвигателями активно применяются знания о последовательных и параллельных соединениях, а также методы анализа сложных цепей.
Возобновляемая энергетика
В системах солнечной и ветровой энергетики важную роль играет правильное соединение генерирующих элементов и аккумуляторов. Здесь широко применяются как последовательные, так и параллельные соединения для достижения нужных параметров напряжения и мощности.
Телекоммуникации
В сфере телекоммуникаций теория цепей применяется при проектировании антенн, усилителей, фильтров и других элементов систем связи. Особенно важно понимание принципов работы высокочастотных цепей.
Заключение
Понимание принципов последовательного и параллельного соединения проводников, а также методов анализа сложных электрических цепей является фундаментальным для всех, кто работает в области электротехники и электроники. Эти знания позволяют проектировать эффективные и надежные электрические системы, оптимизировать их работу и находить неисправности. В современном мире, где электронные устройства окружают нас повсюду, важность этих знаний только возрастает.
Примеры параллельных цепей серии
— Простой анализ — Wira Electrical
Изучив последовательные и параллельные схемы, мы узнаем о примерах последовательно-параллельных цепей, схем с комбинацией последовательной и параллельной цепей.
В реальных приложениях мы чаще всего находим последовательно-параллельную цепь вместо последовательной или параллельной цепи. Мы можем найти чисто последовательную или параллельную схему, но в нашей жизни в основном это будет комбинация последовательной и параллельной цепи, или мы называем их последовательно-параллельными цепями.
Не волнуйтесь, это не сильно отличается от последовательной или параллельной цепи. Нам нужно только использовать другой подход, чтобы решить эту схему.
Мы должны решить схему для каждой группы параллельных резисторов, чтобы сделать полностью последовательную цепь, а затем решить ее. Просто так.
Или мы можем сделать это быстрее, если разложим все последовательные резисторы на эквивалентные последовательные сопротивления.
Затем разложите все параллельные резисторы на эквивалентные параллельные сопротивления. Последним шагом является преобразование этих эквивалентных сопротивлений в эквивалентное общее сопротивление.
Со следующего пункта и до самого конца мы узнаем все о том, как работает последовательно-параллельная схема.
Анализ последовательно-параллельной цепиРассмотрим простую последовательно-параллельную цепь ниже.
В приведенной выше схеме мы видим, что у нас есть источник напряжения с 4 резисторами R 1 , R 2 , R 3 и R 4 в последовательно-параллельной комбинации. Резисторы R 1 и R 4 соединены последовательно, а резисторы R 2 и R 3 соединены параллельно.
Перед вычислением общего тока, протекающего в цепи, мы должны найти эквивалентное сопротивление этих четырех резисторов.
Мы будем использовать эту схему для решения одного из комбинированных примеров последовательной и параллельной цепей.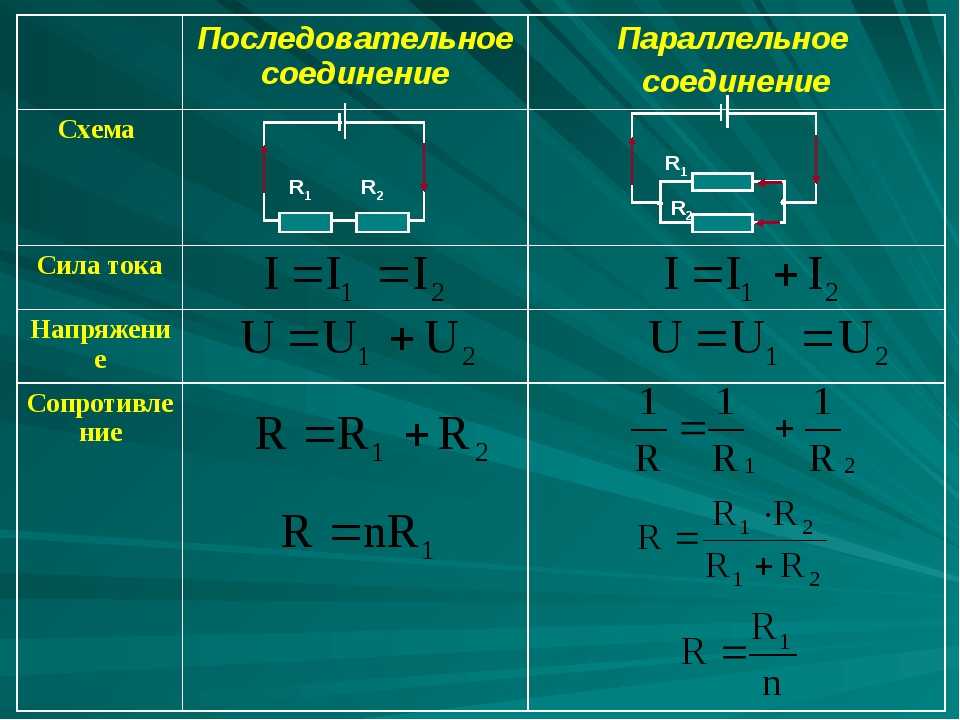
Мы можем использовать два разных подхода, чтобы найти общее сопротивление в этой цепи.
Первый метод , мы решим последовательные резисторы, чтобы получить эквивалентный последовательный резистор (R S ) и параллельные резисторы, чтобы получить эквивалентный параллельный резистор (R P ) отдельно. После этого мы решим эквивалентный резистор (R eq ) для R S и R P , соединенных последовательно.
Найдите эквивалентный серийный резистор, R S :
Найдите эквивалентный параллельный резистор, R P :
Найти эквивалент
, если шаги выше еще длинные. мы можем использовать другой подход.
Второй метод , мы составляем одно уравнение, состоящее из всех резисторов сразу. Мы пишем их в порядке от положительной полярности к отрицательной полярности. Таким образом, мы решим схему за один раз.
Наконец, мы можем записать формулу последовательно-параллельной цепи из приведенной выше схемы.
Теперь приступим к анализу последовательно-параллельной цепи. Это будет отличаться от простого примера выше, потому что мы будем анализировать цепь на ее эквивалентное сопротивление, падение напряжения, протекающий ток и многое другое.
Обратите внимание на схему ниже.
Здесь у нас есть один резистор последовательно с источником напряжения и пара параллельных резисторов.
Серийное параллельное эквивалентное сопротивлениеПрежде всего, мы должны найти эквивалентное сопротивление цепи. Мы будем использовать второй метод, одно уравнение, состоящее из последовательно включенных резисторов.
Таким образом, общий ток, протекающий в цепи, равен
9Падение напряжения в параллельной цепи серии 0015
Теперь приступим к расчету падения напряжения для каждого резистора.
Имейте в виду, что:
- Падение напряжения при последовательном соединении имеет разные значения на каждом резисторе.
- Падение напряжения при параллельном соединении имеет одинаковые значения на каждом резисторе.
Падение напряжения на R 1 (V R1 ) равно
Падение напряжения на R 2 и R 3 эквивалентны падению напряжения на эквивалентном параллельном резисторе (R P ) R 2 и R 3 .
Таким образом, мы также доказываем закон Кирхгофа о напряжении, согласно которому алгебраическая сумма падения напряжения в замкнутой цепи равна нулю.
Тогда падение напряжения на R 2 и R 3 равно 4 В.0103
Далее мы рассчитаем ток, протекающий в цепи.
Имейте в виду, что:
- Ток при последовательном соединении будет иметь постоянное значение через каждый элемент.
- Ток при параллельном соединении будет иметь разные значения в зависимости от сопротивления в каждой ветви.
Поскольку R 1 включен последовательно с источником напряжения, ток (I 1 ) через него равен общему току,
Теперь нам нужно выполнить некоторые математические действия, чтобы определить ток через R 2 и R 3 .
Из приведенного выше результата падение напряжения на параллельном резисторе составляет 4 В, поэтому мы будем использовать его вместе с законом Ома для определения его тока.
для I 2 ,
для I 3 ,
Общий ток, поступающий в ветви R 2 , а R 3 — I = 2a, и он разделен на 4// 3 А через левую ветвь и 2/3А через правую ветвь.
Ток, выходящий из ветви, равен
. Это доказывает закон Кирхгофа о токах, который гласит, что ток, входящий в узел, равен току, выходящему из узла. Или, другими словами, алгебраическая сумма токов, входящих и исходящих из узла, равна нулю.
Последовательно-параллельное разомкнутое соединениеТеперь попробуем сделать разомкнутое соединение в последовательно-параллельной цепи. Мы будем использовать ту же схему, что и выше, но мы дадим разомкнутую клемму последовательно с R 9.0023 1 .
Открытый вывод имеет бесконечное сопротивление.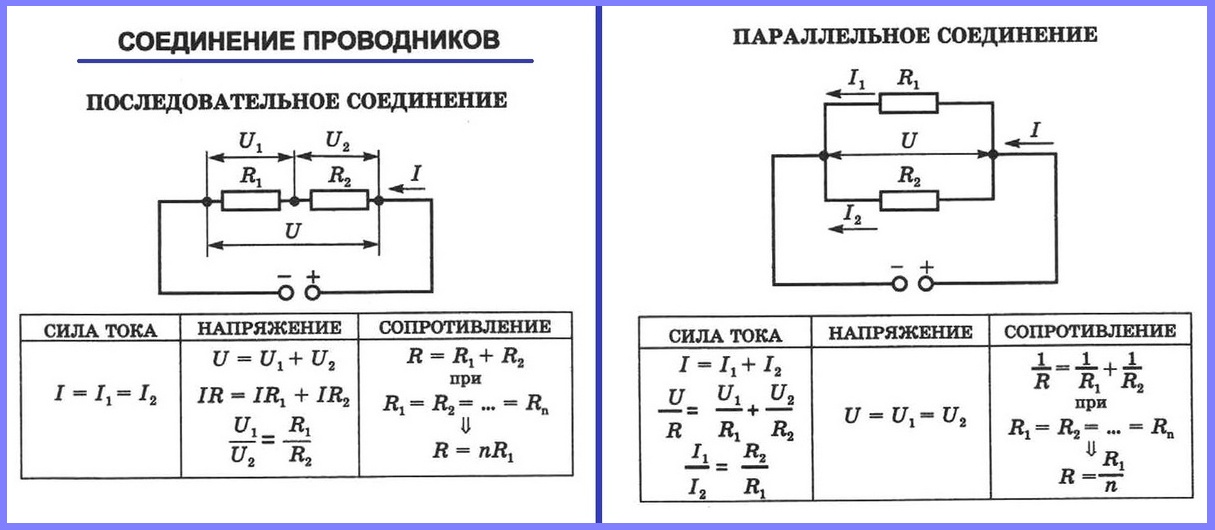
Поскольку он соединен последовательно, то эквивалентное полное сопротивление в цепи бесконечно. Таким образом, общий ток (I) равен нулю, и мы не получим никакого падения напряжения, поскольку в остальной части цепи ток не течет.
Затем мы подключаем открытый терминал параллельно с R 2 и R 3 , как показано ниже.
Поскольку через него не будет протекать ток, его можно игнорировать. Для него падение напряжения будет равно падению напряжения на R 2 и R 3 , так как они параллельны.
Серийное параллельное короткое замыканиеВ отличие от разомкнутой цепи, в большинстве случаев короткое замыкание может повредить цепь и все, что к ней подключено. Сначала делаем короткое замыкание параллельно R1.
Возможно, вы знаете, что электрический ток, скорее всего, выберет путь с наименьшим сопротивлением или импедансом. Таким образом, чем меньше сопротивление, тем больше ток проходит через него.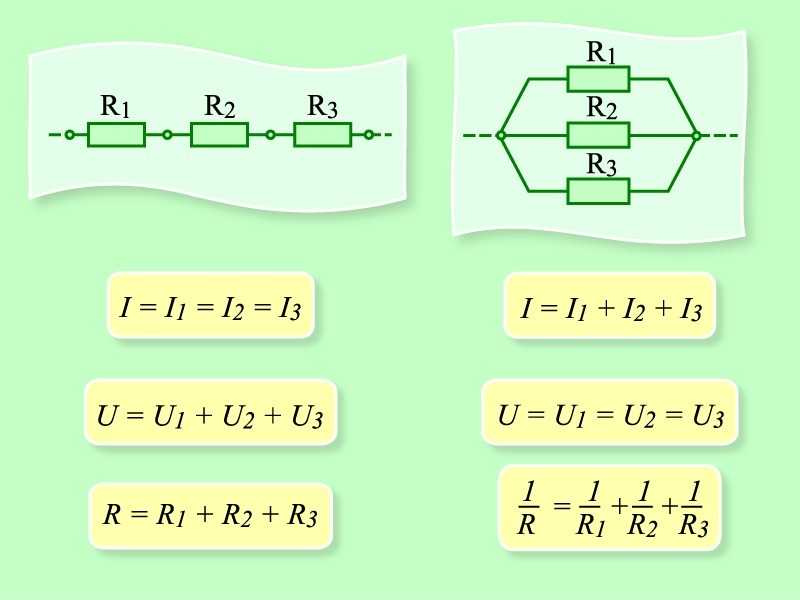
В идеальном состоянии короткое замыкание имеет нулевое сопротивление, поэтому ток, протекающий в ответвлении с нулевым сопротивлением, максимален (бесконечен).
Расчет эквивалентного сопротивления (Rs) для R1 и короткого замыкания параллельно,
Мы можем перерисовать схему в
Поскольку Rs имеет нулевое сопротивление, мы можем заменить его одножильным проводом. Расчет перерисованной схемы такой же простой, как и раньше.
А что если подключить КЗ параллельно R2 и R3?
Эквивалентное сопротивление параллельных резисторов (Rp) равно нулю.
Короткая история мы можем перерисовать схему ниже.
Примеры расчетов последовательных параллельных цепейДавайте выполним несколько упражнений, чтобы лучше понять.
1. Изучите приведенную ниже схему и найдите эквивалентные сопротивления, падения напряжения и токи.
Мы можем рассчитать эквивалентное сопротивление в одном уравнении, но мы будем рассчитывать каждое параллельное соединение отдельно, потому что нам нужны их соответствующие значения для расчета падения напряжения и тока.
Эквивалентное сопротивление для первых параллельных резисторов:
Эквивалентное сопротивление для вторых параллельных резисторов:
Суммарное эквивалентное сопротивление:
Полный ток в цепи:
2
302 можно перерисовать схему на
Падение напряжения на R P1 равно
Падение напряжения на R P2 равно
Это доказывает, что
Далее мы рассчитаем токи через каждый резистор.
For I 1 ,
For I 2 ,
For I 3 ,
For I 4 ,
This proves that
2. Изучите приведенную ниже схему и определите эквивалентное сопротивление, падение напряжения и ток.
Эквивалентное сопротивление параллельных резисторов
Общее эквивалентное сопротивление в цепи
Суммарный ток в цепи
Падение напряжения на
параллельных резисторов
) равно Падение напряжения на R 3 равно
Ток, протекающий через R 1 равен
3
20002 Ток, протекающий через R 2 , равен Ток, протекающий через R 3 , равен
. последовательно-параллельные схемы в нашей жизни», они уже рядом с вами. Самый распространенный ответ, который вы найдете, это электрические розетки в вашем доме. Когда вы выключаете лампу, отсоединяете электронное устройство от розетки или ваша розетка ни к чему не подключена, они не будут мешать другим розеткам. Ваше электронное устройство по-прежнему будет работать нормально и безопасно.
Для последовательной цепи одним из примеров из реальной жизни является гирлянда на рождественской елке. Этот набор световых последовательностей соединен последовательно. Другая последовательная цепь — это соединение между источником питания, выключателем и лампочкой. Они соединены последовательно, чтобы вы могли включать или выключать их с помощью переключателя.
Серия, параллельные и комбинированные | MVWautotechniek.nl
Темы:
- Последовательные и параллельные схемы в целом
- Последовательное соединение на практике 9
Параллельное соединение: расчет парциальных токов цепи в целом:
На этой странице мы рассмотрим последовательные цепи, параллельные цепи и комбинированные цепи, которые используются в автомобильной технике. Для этого необходимы знания основ электроники. Последовательное соединение:
На следующей схеме показана цепь с 12-вольтовой батареей, предохранителем (F), закрытым выключателем (S) и двумя лампами (L1 и L2). Минусовой провод лампы L1 соединяется с плюсовым проводом лампы L2. Мы называем это последовательной схемой.
Ток через обе лампы одинаков. Напряжение распределяется. Так как в примере использовались две лампы одинаковой мощности, то напряжение аккумулятора 12 вольт делится на 6 вольт на лампу. По этой причине лампы в автомобильной технике не ставятся последовательно. Кроме того, в случае неисправности одной лампы вся цепь будет разорвана, так что другая лампа больше не будет гореть.
Параллельное соединение:
В автомобильной технике мы почти всегда имеем дело с параллельными цепями. На следующей схеме показана схема, в которой лампы L1 и L2 имеют свои собственные положительный и заземляющий провода. Напряжение на каждом потребителе равно напряжению батареи; это можно увидеть при измерении вольт. В этом примере используются те же лампы, что и при последовательном соединении; здесь, однако, они горят ярче, потому что лампы теперь получают больше напряжения и тока.
Еще одним свойством параллельной цепи является то, что неисправность одной лампы не влияет на работу другой лампы.
Последовательное соединение на практике:
Как было сказано в предыдущем разделе, в автомобильной технике почти всегда приходится иметь дело с потребителями, подключенными параллельно. Ведь мы хотим, чтобы потребители работали как можно больше по напряжению и току, и как можно меньше рисков возникновения неисправностей при выходе из строя одного из потребителей.
На практике встречаются потребители, которые размещаются последовательно для выполнения своей задачи. В качестве примера возьмем двигатель внутреннего вентилятора / отопителя. Чтобы иметь возможность регулировать скорость вращения вентилятора, в заземляющее соединение между электродвигателем и точкой заземления последовательно включен резистор.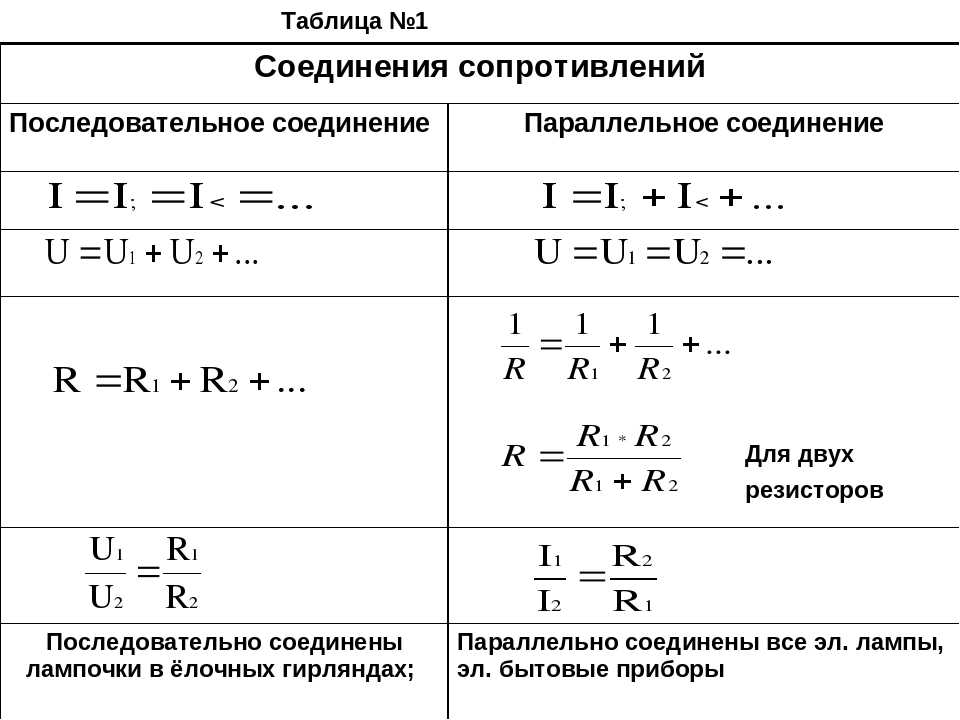 Мы также называем это последовательным резистором.
При последовательном соединении одного или нескольких резисторов потери увеличиваются, а напряжение на электродвигателе уменьшается.
Подробнее об этом читайте на странице: Балластный резистор вентилятора салона.
Возможно также наличие нежелательного последовательного соединения; например, контактное сопротивление в положительном или заземленном соединении с падением напряжения в результате (см. стр. «измерение мультиметром»).
сопротивление Высокое сопротивление приводит к низкому току, другими словами: сопротивление определяет ток Подаваемое напряжение равно напряжению источника (Ub или напряжению батареи)
В примере потребители (R1 и R2) соединены последовательно. Минус R1 соединяется с плюсом R2. Ток через резисторы одинаков. Чтобы рассчитать ток и, наконец, парциальные напряжения, используя закон Ома, мы можем начать с расчета замещающего сопротивления. Значения сопротивлений следующие:
- R1 = 15
- R2 = 10
Для расчета замещающего сопротивления в схеме заменяем резисторы R1 и R2 на Rв.
В последовательной цепи мы можем суммировать значения сопротивления. Формула и разработка показаны ниже.
Результат расчета показывает нам, что замещающее сопротивление равно 25 Ом. В следующих примерах мы можем продолжить расчет с Rv.
Последовательное соединение: расчет тока и парциальных напряжений:
В этом разделе мы вычисляем полный ток и парциальные напряжения на резисторах R1 и R2. Для начала нам нужно исходное напряжение (Ub). В данном примере расчета это напряжение составляет 14 вольт.
Зная напряжение источника (Ub) и замещающее сопротивление (Rv), мы можем рассчитать полный ток (I). Мы определяем I по закону Ома:
Ток в последовательной цепи одинаков через все резисторы. Зеленая стрелка на рисунке указывает направление потока. Сила тока 560 миллиампер.
Теперь, когда ток известен, мы можем рассчитать парциальные напряжения. Мы используем это, чтобы определить, какое напряжение «потребляет» каждый резистор.
- Напряжение (U) на резисторе R1 обозначается как: UR1. Используя закон Ома, мы умножаем ток на значение сопротивления. Напряжение на резисторе 8,4 вольта.
- Рассчитываем UR2 с тем же током, но теперь со значением сопротивления R2; это напряжение 5,6 вольт.
Для проверки можно сложить парциальные напряжения и сравнить их с напряжением источника. Складываем UR1 и UR2 вместе: это 14 вольт. Это равно напряжению источника. Если вы получите другой ответ, небольшое отклонение может быть связано с промежуточным округлением или ошибкой в расчете.
Параллельное соединение: расчет сопротивления замены:
В этом примере R1 и R2 соединены параллельно. Теперь минус одного потребителя уже не связан с плюсом другого. Напряжение на резисторах теперь равно напряжению батареи. Ток распределяется по резисторам. При равных значениях сопротивления общий ток (Iобщий, сокращенно It) делится на два. Чтобы рассчитать It, мы должны сначала определить замещающее сопротивление.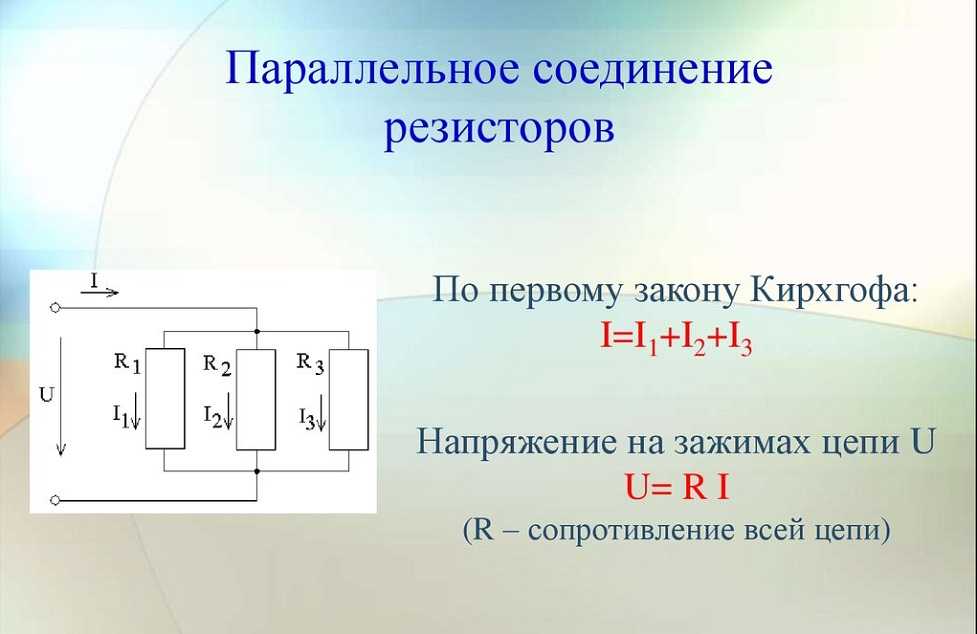 Снова заменяем R1 и R2 одним резистором, называемым Rv. Тогда мы получим ту же ситуацию, что и в примере с последовательным соединением. Значения сопротивления:
- R1 = 10
- R2 = 20
В параллельной цепи мы не можем суммировать значения сопротивления. Общая формула:
Заполняем значения сопротивлений R1 и R2:
Способ 1: Вычисляем результат десятой и двадцатой и складываем значения вместе.
Способ 2: Другой способ заключается в расчете замещающего сопротивления в дробной форме. Снова заполняем значения R1 и R2 в уравнении. Под дефисами (знаменателями) стоят неравные числа; мы не можем сложить знаменатели вместе. Вот почему мы сначала делаем их одинаковыми. В данном примере это просто: десятая часть дважды вписывается в двадцатую, поэтому умножаем десятую целиком на 2. Получаем две двадцатые. В пропорции это то же самое, что одна десятая. С одинаковыми знаменателями мы можем сложить дробь: получится третий-двадцатый.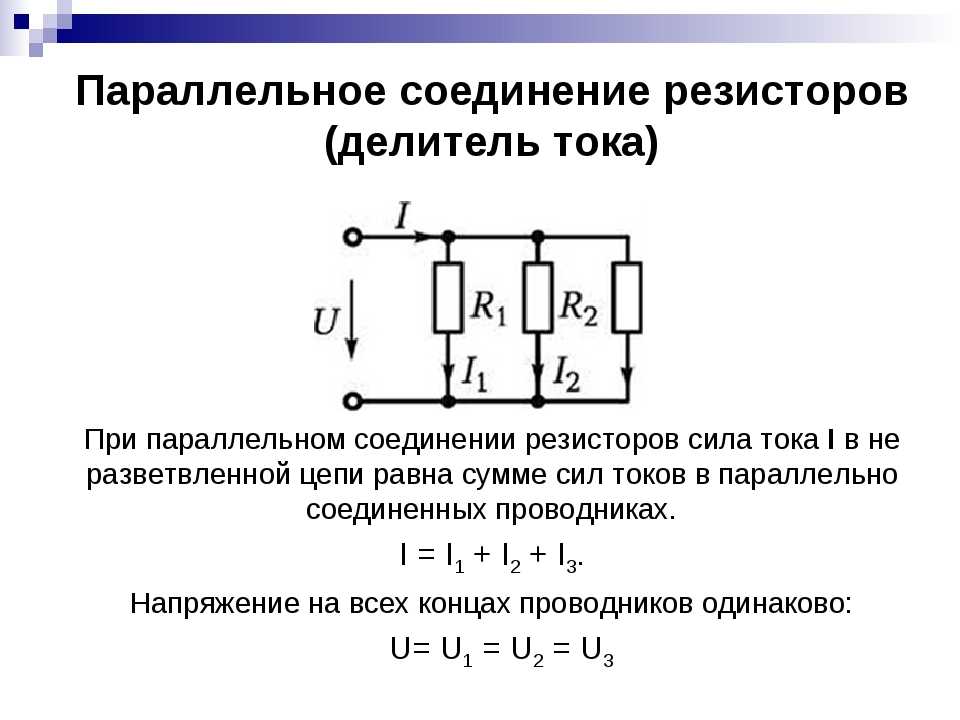 Чтобы рассчитать замещающее сопротивление, нам нужно перевернуть дробь: 1/RV становится RV/1 (тогда мы можем вычеркнуть /1), а третья-двадцатая становится 20, деленной на 3. Результат 6,67 Ом равен результату пути 1.
Параллельное соединение: расчет частичных токов:
Мы можем рассчитать общий ток (It), разделив Ub и Rv друг на друга:
Ток Itotaal разделится на I1 и I2. Через R1 протекает другой ток, чем через R2. В узле частичные токи снова собираются вместе, и он снова течет к минусу батареи.
В параллельной цепи применяется следующее: напряжение на каждом потребителе равно напряжению источника:
Поэтому в формулах UR1 и UR2 мы вводим то же значение, что и напряжение батареи: в данном случае 14 вольт. Делим напряжение на значения сопротивления и получаем парциальные токи. Через резистор R1,4 протекает ток 1 ампер, через R700 — 2 мА.
Когда мы суммируем два частичных тока вместе, мы снова получаем общий ток 2,1 Ампер.
Комбинированная цепь:
В комбинированной цепи мы имеем дело с последовательной и параллельной цепями в одной цепи.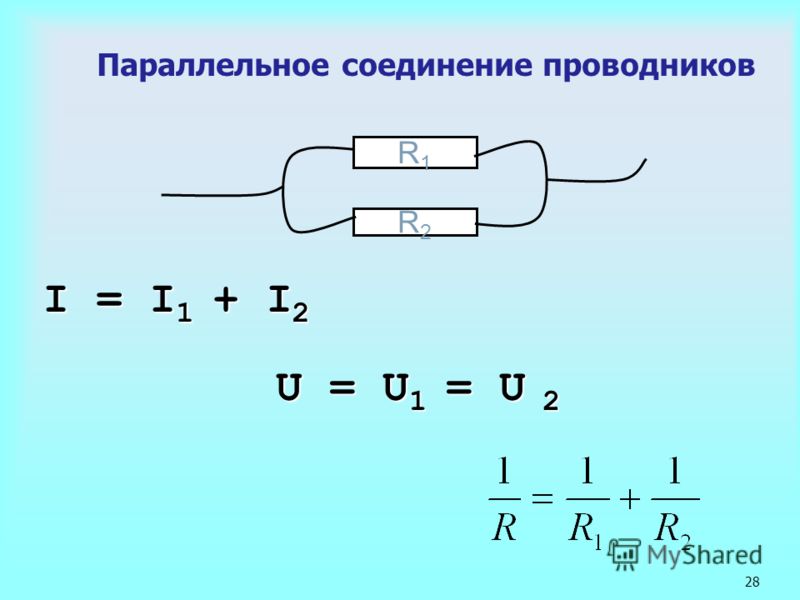 На рисунке мы видим, что резистор R1 включен последовательно с параллельно включенными резисторами R2 и R3. На практике мы могли бы найти это с плохим плюсовым проводом на две лампы: R1 в этом случае — контактное сопротивление, R2 и R3 — лампы.
Рассчитаем токи и напряжения исходя из следующих данных:
- Ub = 12 вольт;
- R1 = 0,5
- R2 = 15
- R3 = 15
Из параллельной цепи мы знаем, что напряжение на резисторах равно напряжению источника. Поскольку теперь мы имеем дело с комбинированной схемой, это больше не применимо; часть занимает R1. Однако напряжения на R2 и R3 равны друг другу.
Для наглядности разделим расчеты на 5 шагов.
1. Определить Rv параллельной цепи:
Заменим R2 и R3 на Rv и для удобства вычислим Rv в дробной форме.
Теперь имеется последовательное соединение: R1 остается, конечно, 0,5, а Rv теперь равно 7,5
2. Определите Rv последовательного соединения:
На шаге 1 определяется заменяющее сопротивление R2 и R3. Заменяющий резистор был включен последовательно с резистором R1.
На этом шаге мы складываем значения сопротивления R1 и Rv вместе, чтобы снова рассчитать замещающее сопротивление, на этот раз для последовательного соединения. Мы называем этот сменный резистор: Rv’ (с акцентом), потому что это «второй» Rv в цепи.
3. Рассчитайте Itotal:
Суммарный ток равен 1,5 А и протекает через резистор R1 и сменный резистор Rv’.
4. Расчет парциальных напряжений:
Поэтапно строим схему обратно; мы соединяем R1 и Rv последовательно, чтобы вычислить парциальные напряжения UR1 и URv с полными значениями тока и сопротивления.
В качестве проверки: суммированные парциальные напряжения соответствуют напряжению источника: (UR1 + URv = Ub), поэтому до сих пор не было допущено ошибок в расчетах.
5. Расчет потоков:
Мы снова заполним график. В шаге 4 мы определили, что напряжение на резисторе R1 составляет 0,75 вольта. Напряжение на сменном резисторе Rv составляет 11,25 вольт.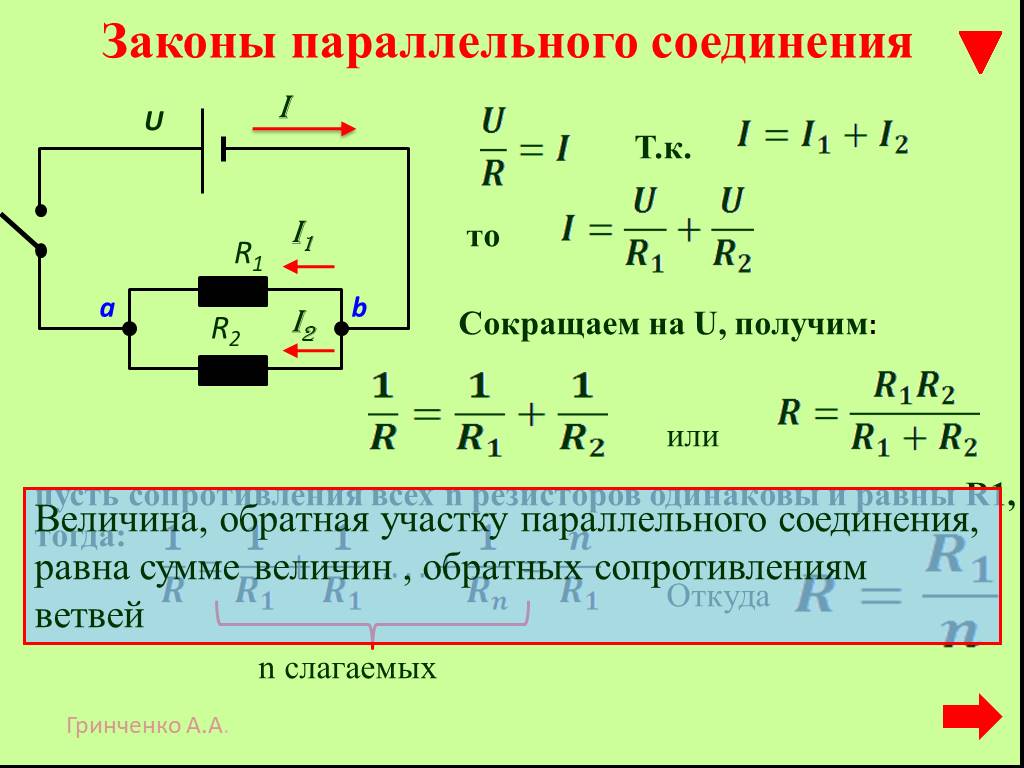 Поскольку в параллельной цепи напряжение на потребителях одинаковое, мы знаем, что напряжение на резисторах R2 и R3 равно 11,25 вольт.
Результаты расчетов показывают, что полный ток протекает через R1, а затем ток делится между R2 и R3. При неодинаковых значениях сопротивления эти токи отличаются друг от друга.
Упражнение с комбинированной схемой:
В этом разделе вы можете самостоятельно попрактиковаться в расчетах комбинированной схемы. Чтобы облегчить себе задачу, вы можете выполнить шаги с 1 по 5 из предыдущего абзаца. Дополните пошаговый план шагом 6, чтобы рассчитать парциальные напряжения R4 и R5.
Приведено:
- UB = 10 вольт
- R1 = 1
- R2 = 10
- R3 = 4
- R4 = 5
- R5 = 15
9
555555559 9000 9000 9000 9000 9000 9000 9000 9000 9000 29000 9000 29000 9000 29000 9000 29000 9000 29000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 29012 9000 29012 9000 R5 = 15 : R5 = 15 : R5 = 4 .
Ток, протекающий через R 3 , равен
.
последовательно-параллельные схемы в нашей жизни», они уже рядом с вами. Самый распространенный ответ, который вы найдете, это электрические розетки в вашем доме.Когда вы выключаете лампу, отсоединяете электронное устройство от розетки или ваша розетка ни к чему не подключена, они не будут мешать другим розеткам. Ваше электронное устройство по-прежнему будет работать нормально и безопасно.
Для последовательной цепи одним из примеров из реальной жизни является гирлянда на рождественской елке. Этот набор световых последовательностей соединен последовательно. Другая последовательная цепь — это соединение между источником питания, выключателем и лампочкой. Они соединены последовательно, чтобы вы могли включать или выключать их с помощью переключателя.
Серия, параллельные и комбинированные | MVWautotechniek.nl
Темы:
- Последовательные и параллельные схемы в целом
- Последовательное соединение на практике 9
На этой странице мы рассмотрим последовательные цепи, параллельные цепи и комбинированные цепи, которые используются в автомобильной технике.
Для этого необходимы знания основ электроники. Последовательное соединение:
На следующей схеме показана цепь с 12-вольтовой батареей, предохранителем (F), закрытым выключателем (S) и двумя лампами (L1 и L2). Минусовой провод лампы L1 соединяется с плюсовым проводом лампы L2. Мы называем это последовательной схемой.
Ток через обе лампы одинаков. Напряжение распределяется. Так как в примере использовались две лампы одинаковой мощности, то напряжение аккумулятора 12 вольт делится на 6 вольт на лампу. По этой причине лампы в автомобильной технике не ставятся последовательно. Кроме того, в случае неисправности одной лампы вся цепь будет разорвана, так что другая лампа больше не будет гореть.
Параллельное соединение:
В автомобильной технике мы почти всегда имеем дело с параллельными цепями. На следующей схеме показана схема, в которой лампы L1 и L2 имеют свои собственные положительный и заземляющий провода. Напряжение на каждом потребителе равно напряжению батареи; это можно увидеть при измерении вольт.
В этом примере используются те же лампы, что и при последовательном соединении; здесь, однако, они горят ярче, потому что лампы теперь получают больше напряжения и тока.
Еще одним свойством параллельной цепи является то, что неисправность одной лампы не влияет на работу другой лампы.
Последовательное соединение на практике:
Как было сказано в предыдущем разделе, в автомобильной технике почти всегда приходится иметь дело с потребителями, подключенными параллельно. Ведь мы хотим, чтобы потребители работали как можно больше по напряжению и току, и как можно меньше рисков возникновения неисправностей при выходе из строя одного из потребителей.
На практике встречаются потребители, которые размещаются последовательно для выполнения своей задачи. В качестве примера возьмем двигатель внутреннего вентилятора / отопителя. Чтобы иметь возможность регулировать скорость вращения вентилятора, в заземляющее соединение между электродвигателем и точкой заземления последовательно включен резистор.
Мы также называем это последовательным резистором.
При последовательном соединении одного или нескольких резисторов потери увеличиваются, а напряжение на электродвигателе уменьшается.
Подробнее об этом читайте на странице: Балластный резистор вентилятора салона.
Возможно также наличие нежелательного последовательного соединения; например, контактное сопротивление в положительном или заземленном соединении с падением напряжения в результате (см. стр. «измерение мультиметром»).
сопротивление Высокое сопротивление приводит к низкому току, другими словами: сопротивление определяет ток Подаваемое напряжение равно напряжению источника (Ub или напряжению батареи)
В примере потребители (R1 и R2) соединены последовательно. Минус R1 соединяется с плюсом R2. Ток через резисторы одинаков. Чтобы рассчитать ток и, наконец, парциальные напряжения, используя закон Ома, мы можем начать с расчета замещающего сопротивления. Значения сопротивлений следующие:
- R1 = 15
- R2 = 10
Для расчета замещающего сопротивления в схеме заменяем резисторы R1 и R2 на Rв.
В последовательной цепи мы можем суммировать значения сопротивления. Формула и разработка показаны ниже.
Результат расчета показывает нам, что замещающее сопротивление равно 25 Ом. В следующих примерах мы можем продолжить расчет с Rv.
Последовательное соединение: расчет тока и парциальных напряжений:
В этом разделе мы вычисляем полный ток и парциальные напряжения на резисторах R1 и R2. Для начала нам нужно исходное напряжение (Ub). В данном примере расчета это напряжение составляет 14 вольт.
Зная напряжение источника (Ub) и замещающее сопротивление (Rv), мы можем рассчитать полный ток (I). Мы определяем I по закону Ома:
Ток в последовательной цепи одинаков через все резисторы. Зеленая стрелка на рисунке указывает направление потока. Сила тока 560 миллиампер.
Теперь, когда ток известен, мы можем рассчитать парциальные напряжения. Мы используем это, чтобы определить, какое напряжение «потребляет» каждый резистор.
- Напряжение (U) на резисторе R1 обозначается как: UR1. Используя закон Ома, мы умножаем ток на значение сопротивления. Напряжение на резисторе 8,4 вольта.
- Рассчитываем UR2 с тем же током, но теперь со значением сопротивления R2; это напряжение 5,6 вольт.
Для проверки можно сложить парциальные напряжения и сравнить их с напряжением источника. Складываем UR1 и UR2 вместе: это 14 вольт. Это равно напряжению источника. Если вы получите другой ответ, небольшое отклонение может быть связано с промежуточным округлением или ошибкой в расчете.
Параллельное соединение: расчет сопротивления замены:
В этом примере R1 и R2 соединены параллельно. Теперь минус одного потребителя уже не связан с плюсом другого. Напряжение на резисторах теперь равно напряжению батареи. Ток распределяется по резисторам. При равных значениях сопротивления общий ток (Iобщий, сокращенно It) делится на два. Чтобы рассчитать It, мы должны сначала определить замещающее сопротивление.
Снова заменяем R1 и R2 одним резистором, называемым Rv. Тогда мы получим ту же ситуацию, что и в примере с последовательным соединением. Значения сопротивления:
- R1 = 10
- R2 = 20
В параллельной цепи мы не можем суммировать значения сопротивления. Общая формула:
Заполняем значения сопротивлений R1 и R2:
Способ 1: Вычисляем результат десятой и двадцатой и складываем значения вместе.
Способ 2: Другой способ заключается в расчете замещающего сопротивления в дробной форме. Снова заполняем значения R1 и R2 в уравнении. Под дефисами (знаменателями) стоят неравные числа; мы не можем сложить знаменатели вместе. Вот почему мы сначала делаем их одинаковыми. В данном примере это просто: десятая часть дважды вписывается в двадцатую, поэтому умножаем десятую целиком на 2. Получаем две двадцатые. В пропорции это то же самое, что одна десятая. С одинаковыми знаменателями мы можем сложить дробь: получится третий-двадцатый.
Чтобы рассчитать замещающее сопротивление, нам нужно перевернуть дробь: 1/RV становится RV/1 (тогда мы можем вычеркнуть /1), а третья-двадцатая становится 20, деленной на 3. Результат 6,67 Ом равен результату пути 1.
Параллельное соединение: расчет частичных токов:
Мы можем рассчитать общий ток (It), разделив Ub и Rv друг на друга:
Ток Itotaal разделится на I1 и I2. Через R1 протекает другой ток, чем через R2. В узле частичные токи снова собираются вместе, и он снова течет к минусу батареи.
В параллельной цепи применяется следующее: напряжение на каждом потребителе равно напряжению источника:
Поэтому в формулах UR1 и UR2 мы вводим то же значение, что и напряжение батареи: в данном случае 14 вольт. Делим напряжение на значения сопротивления и получаем парциальные токи. Через резистор R1,4 протекает ток 1 ампер, через R700 — 2 мА.
Когда мы суммируем два частичных тока вместе, мы снова получаем общий ток 2,1 Ампер.
Комбинированная цепь:
В комбинированной цепи мы имеем дело с последовательной и параллельной цепями в одной цепи.
На рисунке мы видим, что резистор R1 включен последовательно с параллельно включенными резисторами R2 и R3. На практике мы могли бы найти это с плохим плюсовым проводом на две лампы: R1 в этом случае — контактное сопротивление, R2 и R3 — лампы.
Рассчитаем токи и напряжения исходя из следующих данных:
- Ub = 12 вольт;
- R1 = 0,5
- R2 = 15
- R3 = 15
Из параллельной цепи мы знаем, что напряжение на резисторах равно напряжению источника. Поскольку теперь мы имеем дело с комбинированной схемой, это больше не применимо; часть занимает R1. Однако напряжения на R2 и R3 равны друг другу.
Для наглядности разделим расчеты на 5 шагов.
1. Определить Rv параллельной цепи:
Заменим R2 и R3 на Rv и для удобства вычислим Rv в дробной форме.
Теперь имеется последовательное соединение: R1 остается, конечно, 0,5, а Rv теперь равно 7,5
2. Определите Rv последовательного соединения:
На шаге 1 определяется заменяющее сопротивление R2 и R3.
Заменяющий резистор был включен последовательно с резистором R1.
На этом шаге мы складываем значения сопротивления R1 и Rv вместе, чтобы снова рассчитать замещающее сопротивление, на этот раз для последовательного соединения. Мы называем этот сменный резистор: Rv’ (с акцентом), потому что это «второй» Rv в цепи.
3. Рассчитайте Itotal:
Суммарный ток равен 1,5 А и протекает через резистор R1 и сменный резистор Rv’.
4. Расчет парциальных напряжений:
Поэтапно строим схему обратно; мы соединяем R1 и Rv последовательно, чтобы вычислить парциальные напряжения UR1 и URv с полными значениями тока и сопротивления.
В качестве проверки: суммированные парциальные напряжения соответствуют напряжению источника: (UR1 + URv = Ub), поэтому до сих пор не было допущено ошибок в расчетах.
5. Расчет потоков:
Мы снова заполним график. В шаге 4 мы определили, что напряжение на резисторе R1 составляет 0,75 вольта. Напряжение на сменном резисторе Rv составляет 11,25 вольт.
Поскольку в параллельной цепи напряжение на потребителях одинаковое, мы знаем, что напряжение на резисторах R2 и R3 равно 11,25 вольт.
Результаты расчетов показывают, что полный ток протекает через R1, а затем ток делится между R2 и R3. При неодинаковых значениях сопротивления эти токи отличаются друг от друга.
Упражнение с комбинированной схемой:
В этом разделе вы можете самостоятельно попрактиковаться в расчетах комбинированной схемы. Чтобы облегчить себе задачу, вы можете выполнить шаги с 1 по 5 из предыдущего абзаца. Дополните пошаговый план шагом 6, чтобы рассчитать парциальные напряжения R4 и R5.
Приведено:
- UB = 10 вольт
- R1 = 1
- R2 = 10
- R3 = 4
- R4 = 5
- R5 = 15 9
