Что такое эффект Холла и как он возникает. Как измеряется напряжение Холла. Какую информацию можно получить с помощью эффекта Холла. Где применяется эффект Холла на практике. Почему эффект Холла важен для понимания свойств проводников.
Что такое эффект Холла
Эффект Холла — это возникновение поперечной разности потенциалов (напряжения Холла) в проводнике с током, помещенном в магнитное поле, перпендикулярное току. Этот эффект был открыт Эдвином Холлом в 1879 году.
Физическая причина эффекта Холла заключается в следующем:
- На движущиеся в магнитном поле носители заряда действует сила Лоренца, отклоняющая их к краю проводника
- Это приводит к накоплению заряда на краях и возникновению поперечного электрического поля
- Когда электрическая сила уравновешивает магнитную, устанавливается стационарное состояние с постоянным напряжением между краями
Расчет напряжения Холла
Напряжение Холла V_H можно рассчитать по формуле:
V_H = (I * B * d) / (n * e * A)
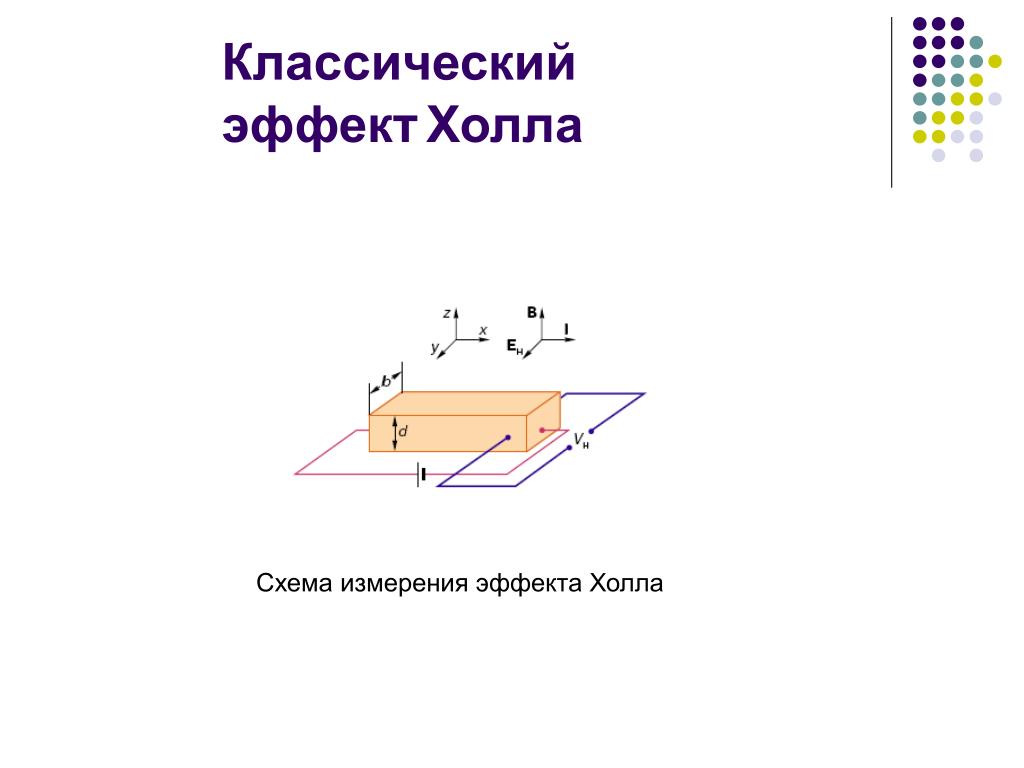
Где:
- I — сила тока
- B — магнитная индукция
- d — толщина образца
- n — концентрация носителей заряда
- e — заряд электрона
- A — площадь поперечного сечения образца
Информация, получаемая из эффекта Холла
С помощью измерений эффекта Холла можно определить:
- Знак носителей заряда (электроны или дырки)
- Концентрацию носителей заряда
- Подвижность носителей заряда
- Величину магнитного поля
Применение эффекта Холла
Эффект Холла нашел широкое применение в различных областях:
- Датчики Холла для измерения магнитного поля
- Измерение силы тока бесконтактным способом
- Изучение свойств полупроводников
- Определение подвижности носителей заряда
- Измерение скорости потока жидкости и газа
Особенности эффекта Холла в различных материалах
Эффект Холла проявляется по-разному в различных проводящих и полупроводниковых материалах:
- В большинстве металлов носителями являются электроны, напряжение Холла отрицательно
- В некоторых металлах (Be, Zn) и полупроводниках p-типа носители — дырки, напряжение Холла положительно
- В полупроводниках эффект Холла сильнее из-за меньшей концентрации носителей
- В сверхпроводниках наблюдается квантовый эффект Холла
Квантовый эффект Холла
При низких температурах и сильных магнитных полях в двумерных электронных системах наблюдается квантовый эффект Холла:

- Холловское сопротивление квантуется, принимая дискретные значения
- Наблюдаются плато на зависимости сопротивления от магнитного поля
- Квантовый эффект Холла позволяет с высокой точностью определять фундаментальные константы
Историческое значение эффекта Холла
- Впервые экспериментально подтвердило существование носителей заряда в металлах
- Позволило определить знак носителей заряда (электроны)
- Стимулировало развитие электронной теории металлов
- Заложило основы для изучения электронных свойств твердых тел
Современные исследования эффекта Холла
В настоящее время исследования эффекта Холла продолжаются в различных направлениях:
- Изучение аномального эффекта Холла в ферромагнетиках
- Исследование спинового эффекта Холла
- Наблюдение квантового эффекта Холла в графене
- Разработка новых материалов с улучшенными характеристиками эффекта Холла
Практическое применение датчиков Холла
Датчики на основе эффекта Холла широко используются в различных устройствах:

- Измерение скорости вращения в автомобильных двигателях
- Бесконтактные переключатели и кнопки
- Позиционирование в жестких дисках компьютеров
- Измерение тока в электрических сетях
- Детектирование приближения в мобильных устройствах
Эффект Холла в полупроводниках
В полупроводниковых материалах эффект Холла имеет ряд особенностей:
- Сильная зависимость от температуры и освещения
- Возможность изменения знака носителей при легировании
- Используется для определения концентрации и подвижности носителей
- Позволяет исследовать примесные уровни в полупроводниках
Заключение
Эффект Холла остается важным инструментом исследования свойств проводящих материалов и источником новых физических явлений. Его практическое применение в датчиках и измерительных устройствах делает этот эффект неотъемлемой частью современных технологий.
что это такое, формулы, применение
В этой статье вы узнаете, что такое эффект Холла и как он применяется на практике. Вы также узнаете, как вывести напряжение Холла, и получите практический пример расчета. Наконец, мы рассмотрим другие варианты эффекта Холла, такие как квантовый эффект Холла.
Простое объяснение
Эффект Холла был продемонстрирован Эдвином Холлом в 1879 году. Как вы, возможно, уже знаете, сила Лоренца действует на движущийся заряд в магнитном поле.
Эффект Холла — это возникновение в электрическом проводнике разности потенциалов на краях образца (напряжения Холла) помещённом в поперечное магнитное поле, при протекании тока, перпендикулярному полю.
Википедия
Это создает электрическое напряжение, которое падает как в направлении протекания электрического тока, так и в направлении магнитного поля на проводнике и называется напряжением Холла.
Физическое объяснение эффекта Холла
Если приложить напряжение к электрическому проводнику, называемому здесь образцом, потечет электрический ток. Электроны движутся по проводнику со средней скоростью v, также называемой скоростью дрейфа. Если держать образец в стационарном магнитном поле, то на электроны действует сила Лоренца. Это вызывает отклонение электронов перпендикулярно движению. Это вызывает избыток электронов на стороне отклонения и соответствующий недостаток электронов на противоположной стороне.
Электроны движутся по проводнику со средней скоростью v, также называемой скоростью дрейфа. Если держать образец в стационарном магнитном поле, то на электроны действует сила Лоренца. Это вызывает отклонение электронов перпендикулярно движению. Это вызывает избыток электронов на стороне отклонения и соответствующий недостаток электронов на противоположной стороне.
Вы можете представить себе это разделение зарядов как сходное с разделением зарядов в конденсаторе. Поскольку положительно и отрицательно заряженные стороны теперь находятся напротив друг друга, создается электрическое поле. Это электрическое поле оказывает на электроны силу, противоположную силе Лоренца. Если эти две силы компенсируют друг друга в одинаковой степени, то усиление разделения зарядов заканчивается.
Как и в случае с конденсатором, здесь можно отводить напряжение. Это электрическое напряжение называется напряжением Холла. Это напряжение Холла линейно возрастает с увеличением магнитного поля и антипропорционально плотности носителей заряда. Это объясняется тем, что неизменная сила тока при меньшем числе носителей заряда может быть достигнута только за счет большей скорости отдельных носителей заряда. Более сильная сила Лоренца действует на более быстрые носители заряда, что увеличивает напряжение Холла.
Это объясняется тем, что неизменная сила тока при меньшем числе носителей заряда может быть достигнута только за счет большей скорости отдельных носителей заряда. Более сильная сила Лоренца действует на более быстрые носители заряда, что увеличивает напряжение Холла.
Вычисление напряжения Холла
Для того чтобы понять вывод напряжения Холла, необходимо базовое понимание векторного исчисления.
Здесь вы можете увидеть набросок расчета напряжения Холла. Он действителен только для одного типа носителей заряда, например, для металлических образцов.
Сила Лоренца, действующая на проводник в магнитном поле, задается следующим образом:
Где, сила Лоренца F, q — электрический заряд, v — скорость и магнитное поле B. В эффекте Холла возникает электрическое поле E, которое нейтрализует отклоняющую силу магнитного поля. Поэтому:
Для упрощения зададим систему координат так, чтобы носители заряда двигались в направлении x, а магнитное поле действовало в направлении z.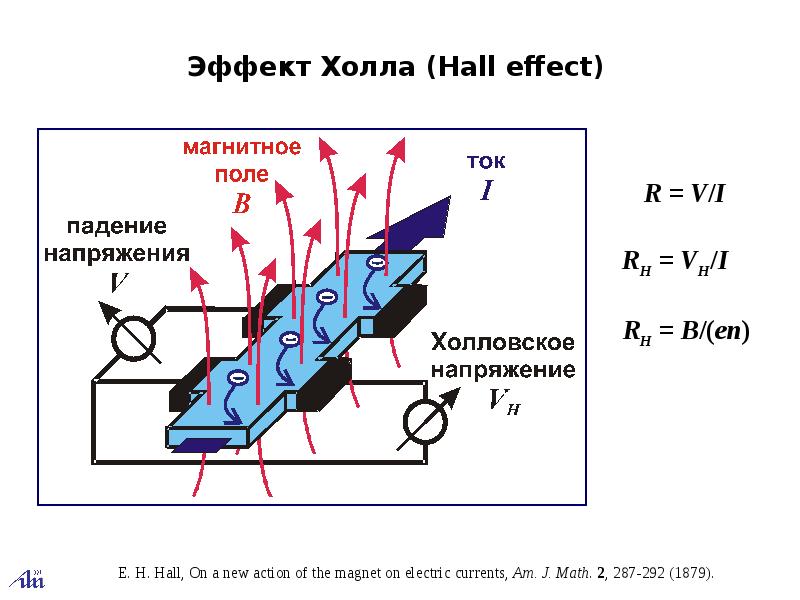 Это дает v = ( vx, 0, 0 ) и B = ( 0, 0, Bz ). После деления на q получается y-компонента:
Это дает v = ( vx, 0, 0 ) и B = ( 0, 0, Bz ). После деления на q получается y-компонента:
Ey — vxBz = 0
Плотность тока J в проводнике выражается через J = n*q*v, при плотности носителей заряда n. Если преобразовать это уравнение в vx и подставить его в вышеприведенное уравнение, то получится:
Ey = jx * Bz * ( 1 / n * q ) = AH * jx * Bz.
Мы определили коэффициента Холла AH, которая характеризует силу эффекта Холла.
Поскольку вы уже знаете, что можно рассматривать разделение зарядов аналогично разделению в конденсаторе, то для упрощения можно использовать следующее обозначение:
Ey = UH / b
Плотность тока в этом случае может быть выражена через jx = I / b*d, где I — сила тока, b — ширина проводника и d — толщина проводника. Подставляя оба выражения, получаем для напряжения Холла следующее выражение:
UH = AH * ( I * Bz / d )
Расчёт коэффициента Холла
В качестве примера представьте медную пластину (ширина b = 18 мм, толщина d = 0,001 м). Она вносится в магнитное поле с плотностью магнитного потока B = 1,2 Тл. Если через пластину протекает электрический ток I = 15 А, то можно измерить напряжение Холла UH = — 1,02 * 10-6 В .
Она вносится в магнитное поле с плотностью магнитного потока B = 1,2 Тл. Если через пластину протекает электрический ток I = 15 А, то можно измерить напряжение Холла UH = — 1,02 * 10-6 В .
Если взять приведенную выше формулу и преобразовать ее в AH, то получится: AH = UH * d / I * B .
Подставляя значения, можно вычислить коэффициент Холла, то есть: AH = — 1,02 * 10-6 * 0,001 / 15 * 1,2 = — 5,7 * 10-11 мм3 / Кл
По их отрицательному знаку видно, что это электроны, а не дырки или положительные заряды.
Применение эффекта Холла
Эффект Холла используется в нескольких областях. В электронике, например, он используется для так называемых датчиков Холла. Они используются для измерения магнитных полей. Для этого известен коэффициент Холла конкретного материала, задается необходимый электрический ток и, таким образом, вычисляется напряжение Холла. С помощью приведенной выше формулы датчик Холла может рассчитать магнитное поле.
С помощью приведенной выше формулы датчик Холла может рассчитать магнитное поле.
Кроме того, эффект Холла также используется для расчета плотности носителей заряда. Для этого измеряется коэффициент Холла и уравнение преобразуется соответствующим образом.
Квантовый эффект Холла.
В квантовом эффекте Холла электрический ток не может произвольно изменяться при низких температурах и сильных магнитных полях в двумерных системах путем изменения напряженности магнитного поля. Вместо этого он изменяется ступенчато.
Существуют и другие известные эффекты Холла. Например, спин-эффект Холла, планарный эффект Холла, тепловой эффект Холла и эффект Нернста.
Список использованной литературы
- Ashcroft Neil W., Mermin N. David. Solid state physics : [англ.]. — New York : Saunders College Publishing, 1976. — ISBN 0-03-083993-9.
- Введение в физику плазмы и управляемый синтез, Том 1, Физика плазмы, второе издание, 1984, Фрэнсис Ф. Чен
- Абрикосов А.
 А. Основы теории металлов. — Москва: «Наука», главная редакция физико-математической литературы, 1987. — 520 с. — ISBN нет, ББК 22.37, УДК 539.21 (075.8).
А. Основы теории металлов. — Москва: «Наука», главная редакция физико-математической литературы, 1987. — 520 с. — ISBN нет, ББК 22.37, УДК 539.21 (075.8).
Эффект Холла
a
b
Рисунок
1.6. — Схема эксперимента
Холла: a – геометрия
опыта; b – поле Холла
в стационарном режиме (при
установившейся дрейфовой
скорости v). Индукция
магнитного поля направлена
перпендикулярно плоскости
чертежа, к наблюдателю.
Схема
эксперимента Холла изображена на рис.
1.6. Имея дело с немагнитными и слабомагнитными
материалами можно считать магнитным
полем величину H, поскольку разница
между H и B в этом случае чрезвычайно
мала. К проводнику, расположенному вдоль
оси , приложено электрическое поле , вызывающее электрический ток .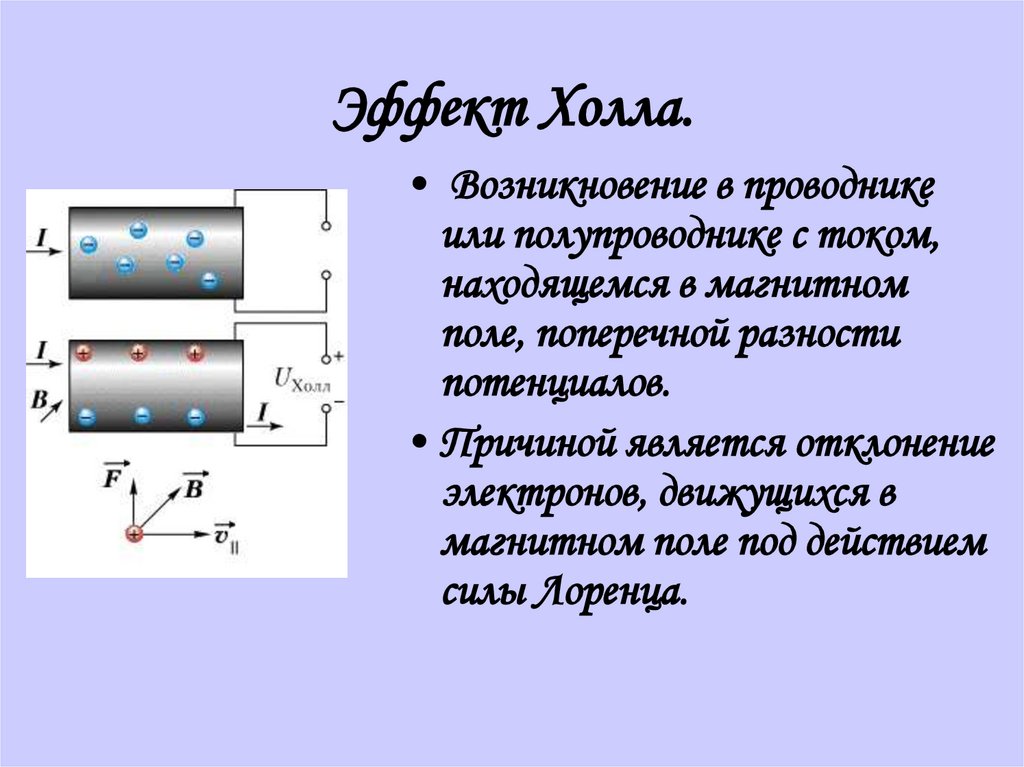 Помимо того, имеется магнитное поле , параллельное оси . В результате появляется сила
Лоренца:
Помимо того, имеется магнитное поле , параллельное оси . В результате появляется сила
Лоренца:
отклоняющая
электроны в отрицательном
Две величины
представляют здесь интерес. Одна из
них — это отношение поля вдоль проводника
Ех к плотности тока
j
 (2.32)
(2.32)
Холл обнаружил, что эта величина (магнетосопротивление) не зависит от поля. Другой характеристикой является величина поперечного поля Еу. Поскольку такое поле уравновешивает силу Лоренца, можно полагать, что оно должно быть пропорциональным как приложенному полю Н, так и току в проводнике. Поэтому величину, называемую коэффициентом Холла, определяют как:
Следует
обратить внимание на то, что, поскольку
поле Холла направлено против оси
у (рис. 1.6), коэффициент RH
должен быть отрицательным. С другой стороны,
если бы заряд носителей был положительным,
знак их X — компоненты скорости был
бы обратным и сила Лоренца осталась бы
неизменной. В результате поле Холла имело
бы направление, противоположное тому,
которое оно имеет при отрицательно заряженных
носителях. Этот вывод очень важен, поскольку
он означает, что измерения поля Холла
позволяют определить знак носителей
заряда. Экспериментальные данные, впервые
полученные Холлом, находились в согласии
со знаком заряда электрона, определенным
позднее Томсоном. Одна из замечательных
особенностей эффекта Холла заключается,
однако, в том, что в некоторых металлах
коэффициент Холла положителен, и поэтому
носители в них должны, видимо, иметь заряд,
противоположный заряду электрона.
В результате поле Холла имело
бы направление, противоположное тому,
которое оно имеет при отрицательно заряженных
носителях. Этот вывод очень важен, поскольку
он означает, что измерения поля Холла
позволяют определить знак носителей
заряда. Экспериментальные данные, впервые
полученные Холлом, находились в согласии
со знаком заряда электрона, определенным
позднее Томсоном. Одна из замечательных
особенностей эффекта Холла заключается,
однако, в том, что в некоторых металлах
коэффициент Холла положителен, и поэтому
носители в них должны, видимо, иметь заряд,
противоположный заряду электрона.
Чтобы рассчитать коэффициент Холла, определим в начале плотности тока jx и jy в случае, когда имеется электрическое поле с произвольными компонентами Ех и Еу, а также магнитное поле Н, направленное вдоль оси z. На каждый электрон, движущийся с дрейфовой скоростью действуют электрическое и магнитное поля, следовательно действует (не зависящая от пространственных координат) сила:
 34)
34)
поэтому уравнение движения электронов для импульса в расчете на один электрон будет выглядеть так:
где второй член в правой части введён, чтобы учесть электрическое сопротивление; — импульс электрона; — время между последовательными соударениями (время свободного пробега).
Следует иметь в виду, что сила Лоренца не одинакова для всех электронов, поскольку она зависит от скорости электрона v. Поэтому силу f из уравнения (2.4) нужно считать средней силой в расчете на один электрон. Поскольку, однако, зависимость этой силы от того, на какой электрон она действует, содержится лишь в члене, линейном по скорости электрона, среднее значение силы получается просто путем замены этой скорости на среднюю скорость :

Для геометрии опыта, представленном на (рис. 1.6), представим в записи по компонентам:
где используются обозначения для циклотронной частоты обращения электронов по спиральным орбитам в магнитном поле:
В стационарном
состоянии ток и дрейфовая
скорость не зависит от времени и
поэтому (2.37) имеет вид:
 39)
39)
Запишем закон Ома по компонентам:
где — статическая удельная электропроводность.
Умножив обе части равенств (2.39) на и учитывая (2.40) получим:
Учтём геометрию опыта (рис. 1.6): , и нет тока в направлении Y, , в результате (2.41) примет вид:
 42)
42)
Поле , существующее благодаря действию силы Лоренца, и получило название поля Холла:
где введена постоянная Холла:
Коэффициент Холла не зависит ни от каких параметров металла, кроме плотности носителей. Выше мы уже вычисляли n, предполагая, что валентные электроны атома в металле превращаются в электроны проводимости. Измерение коэффициента Холла дает прямой способ проверки справедливости такого предположения .
При выводе
уравнения для ЭДС Холла сделан
ряд допущений, связанных с тем, что
полная скорость электронов принимается
раной дрейфовой скорости, т. е. не учитывается
скорость хаотического теплового движение
электронов и их распределение по скоростям.
Поэтому более строгое выражение для постоянной
Холла, имеет вид: , где A – постоянная, зависящая
от механизма рассеяния носителей заряда.
При рассеянии электронов на акустических,
оптических колебаниях решётки, на ионах
примеси величина A соответственно
принимает значения: 1,17; 1,11; 1,93.
е. не учитывается
скорость хаотического теплового движение
электронов и их распределение по скоростям.
Поэтому более строгое выражение для постоянной
Холла, имеет вид: , где A – постоянная, зависящая
от механизма рассеяния носителей заряда.
При рассеянии электронов на акустических,
оптических колебаниях решётки, на ионах
примеси величина A соответственно
принимает значения: 1,17; 1,11; 1,93.
При попытках
определить плотность электронов
n, используя результаты измерений
коэффициентов Холла, возникает трудность,
связанная с тем, что в действительности
в противоречие с формулой (2.44) эти коэффициенты
обычно зависят от магнитного поля. Кроме
того, они зависят от температуры и от
того, насколько тщательно приготовлен
образец. Это кажется довольно странным,
поскольку время релаксации, которое может
сильно зависеть от температуры и состояния
образца, в (2.44) не фигурирует. Тем не менее,
при самых низких температурах для очень
чистых, тщательно приготовленных образцов
в чрезвычайно сильных полях измеряемые
значения постоянной Холла, по-видимому,
действительно стремятся к некоторому
пределу .
Отрицательное значение соответствует электронам. Вообще, знак константы Холла зависит от типа носителей зарядов и, например, в дырочном полупроводнике . Важным следствием формулы (2.44) является возможность экспериментального определения концентрации заряженных частиц с помощью эффекта Холла и в металлах, и в полупроводниках.
Коэффициенты
Холла для некоторых металлов
приведены в таблице №2.
| Металл | Металл | ||||
| Эксперимент | Расчёт | Эксперимент | Расчёт | ||
| Li | -1.70 | -1.33 | Cu | -0.54 | -0.74 |
| Na | -2.34 | -2.3 | Ag | -0. 90 90 |
-1.07 |
| K | -4.45 | -4.45 | Au | -0.72 | -1.06 |
| Rb | -5.04 | -5.4 | |||
Таблица №2. Экспериментальные и вычисленные значения константы Холла.
Расчёт по формуле (2.44) в предположении, что число электронов равно числу атомов .
Применение
константы Холла для расчёта
электрофизических свойств твёрдых
тел показало ошибочность теории
Друде для некоторых металлов.
Теоретический результат Друде подтверждает
экспериментальное наблюдение Холл, не
обнаружившего зависимости сопротивления
от поля. Действительно, при (как это имеет место в стационарном
состоянии, когда поле Холла уже установилось)
первое из уравнений (2.41) сводится к уравнению , то есть проводимость имеет такую
же величину, как и в нулевом магнитном
поле. Однако, как показали более точные
эксперименты на многих металлах, в действительности
сопротивление обнаруживает зависимость
от магнитного поля, в ряде случаев очень
сильную. Объяснение того, почему теория
Друде оказывается применимой для одних
металлов, а для других возникают такие
разительные расхождения, должна дать
квантовая теория твердого тела (Ашкрофт).
Объяснение того, почему теория
Друде оказывается применимой для одних
металлов, а для других возникают такие
разительные расхождения, должна дать
квантовая теория твердого тела (Ашкрофт).
Фактически
формула (2.44) справедлива для произвольной
сферы в — пространстве, заполненной носителями.
Теория эффекта Холла и других гальваномагнитных
явлений основывается очевидно, на существенном
использовании теоремы Блоха и на описании
электронных состояний в пространстве
обратной решётки. В неупорядоченной системе,
когда компоненты вектора уже не есть хорошие квантовые числа,
выводы, полученные с помощью кинетического
уравнения, сразу же попадают под сомнение.
Фактически, однако, пока ещё нет точной
теории, с помощью которой можно заменить
можно заменить простую формулу (2.44). Последняя
формула дает вполне удовлетворительное
согласие с опытными данными для жидких
металлов, несмотря на то что длина свободного
пробега электрона оказывается там порядка
межатомного расстояния. Неясно, однако,
можно ли наблюдать эффект Холла в предельном
случае прыжковой проводимости по локализованным
состояниям .
Неясно, однако,
можно ли наблюдать эффект Холла в предельном
случае прыжковой проводимости по локализованным
состояниям .
Для характеристики
напряженности магнитного поля удобно
использовать безразмерную величину , играющую в теории важную роль. Когда
величина мала, из уравнений (2.41) следует, что
ток j почти параллелен Е, как это
было бы в отсутствие магнитного поля.
В общем случае ток j направлен к
Е под углом (называемым углом Холла). Из уравнений
(2.41) следует, что . Величина , называемая циклотронной частотой,
представляет собой просто круговую частоту
вращения свободного электрона в магнитном
поле H. Произведение мало, если электроны между столкновениями
могут проделать лишь малую часть оборота,
и велико, если они могут совершить много
оборотов. Иначе говоря, когда , магнитное поле лишь слегка деформирует
орбиты электронов, а когда величина сравнима с единицей и больше, то влияние
магнитного поля на орбиты электронов
становится преобладающим. Для численной
оценки циклотронной частоты удобна формула:
Для численной
оценки циклотронной частоты удобна формула:
Калькулятор коэффициента Холла
Создано Miłosz Panfil, PhD
Отзыв от Małgorzata Koperska, MD и Adena Benn
Последнее обновление: 18 ноября 2022 г.
Содержание:- Что такое эффект Холла?
- Формула коэффициента Холла
- Калькулятор коэффициента Холла
С помощью калькулятора коэффициента Холла вы можете легко вычислить коэффициент Холла. Коэффициент Холла раскрывает природу носителей заряда в проводниках. Если вам интересно, что такое эффект Холла и что такое формула коэффициента Холла, вы можете узнать все это из текста ниже.
Что такое эффект Холла?
Если мы приложим к проводу разность потенциалов, по нему потечет электрический ток. Носители заряда, ответственные за электрический ток, будут двигаться по прямым линиям, ускоряемым электрическим полем, пока не столкнутся друг с другом. Подробнее об этом можно узнать в нашем калькуляторе ускорения в электрическом поле.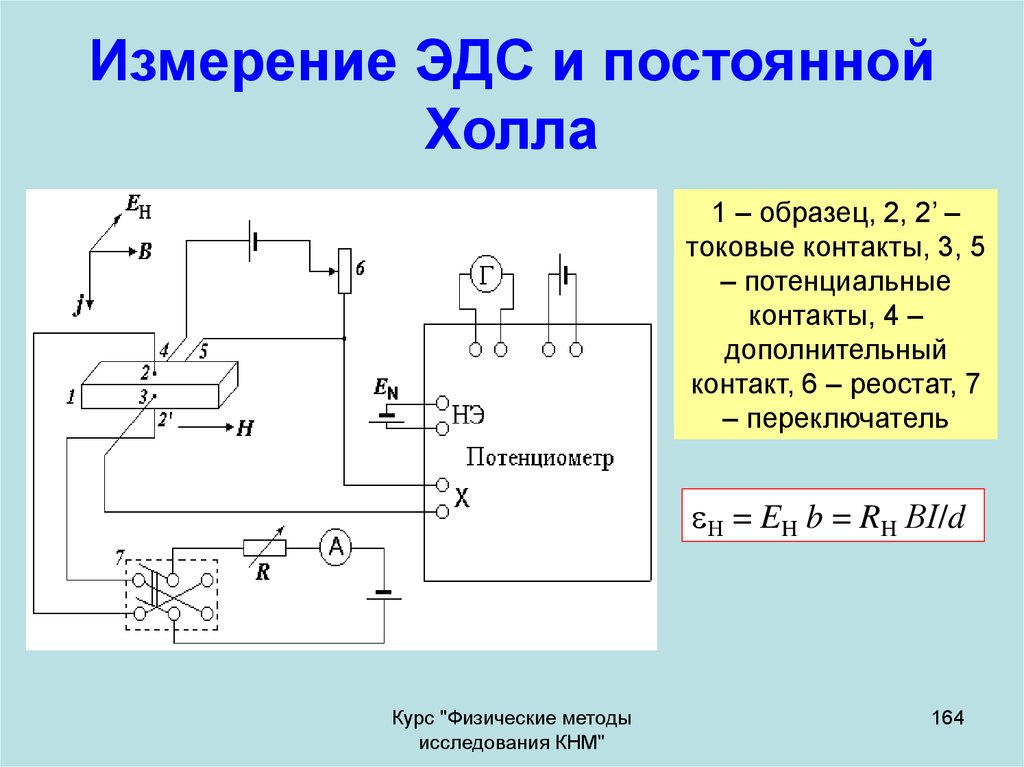 После столкновения они снова ускорятся, в результате чего появится эффективная скорость, называемая скоростью дрейфа, направленная вдоль провода.
После столкновения они снова ускорятся, в результате чего появится эффективная скорость, называемая скоростью дрейфа, направленная вдоль провода.
Вместо тонкой проволоки можно представить плоский, похожий на сэндвич кусок проводника. Теперь, помимо применения разницы напряжений, мы также поместим ее в магнитное поле. Магнитное поле направлено перпендикулярно плоскому проводнику. Из-за силы Лоренца траектории носителей заряда искривляются, что приводит к скоплению носителей заряда на одной стороне проводника . Это накопление приводит к разнице напряжений В на на проводнике. Возникновение разности потенциалов из-за магнитного поля является эффектом Холла.
Чтобы узнать больше о силе Лоренца, посетите наш Калькулятор силы Лоренца.
Формула коэффициента Холла
Формула коэффициента Холла количественно определяет силу эффекта Холла. Коэффициент Холла определяется как
RH = V × t / (I × B) ,
, где
-
RH [м³/C]— коэффициент Холла, -
В [В]— наблюдаемая разность напряжений, -
t [м]— толщина жилы, -
I [A]— ток, проходящий через проводник, -
B [T]— магнитное поле.
Коэффициент Холла показывает природу носителей заряда, их концентрацию в проводнике и их заряд. Формула:
RH = - 1/(n × q) ,
где
-
n [1/м³]— концентрация носителей, -
q [C]— плата одного перевозчика.
Эффект Холла важен тем, что позволяет выяснить знак носителей заряда . Например, с помощью эффекта Холла мы можем продемонстрировать, что в некоторых полупроводниках ток переносится положительно заряженными дырками, а не электронами.
Хотите узнать о концентрации электронов в собственных полупроводниках? Посетите наш калькулятор концентрации внутренних носителей.
Калькулятор коэффициента Холла
Калькулятор коэффициента Холла позволяет быстро вычислить коэффициент Холла. Вы также можете получить другие величины из формулы коэффициента Холла, если знаете коэффициент Холла. Например, эффект Холла иногда используется для измерения магнитного поля. Измерить разность напряжений просто
Измерить разность напряжений просто В с вольтметром и ток I с амперметром. Зная коэффициент Холла, мы можем легко найти магнитное поле.
Например, коэффициент Холла меди равен RH = 0,133 мм³/C . Скажем, у нас есть медная пластина толщиной t = 0,02 мм . Если пропустить через него ток I = 10 А и наблюдать разность напряжений В = 0,05 мВ , то получится, что магнитное поле равно В = 0,7519 Тл .
Miłosz Panfil, PhD
Напряжение
Толщина
Curance
Магнитное поле
Коэффициент зала
мм/C
Проверьте 40 Расчеты Электромагнетизма. подробнее
11.7: Эффект Холла — Физика LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4419
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Объяснить сценарий, в котором магнитное и электрическое поля пересекаются и их силы уравновешивают друг друга, когда заряженная частица движется через переключатель скорости
- Сравните движение носителей заряда в проводящем материале и объясните, как это связано с эффектом Холла
В 1879 г. Э.Х. Холл разработал эксперимент, который можно использовать для определения знака преобладающих носителей заряда в проводящем материале. С исторической точки зрения этот эксперимент был первым, кто продемонстрировал, что носители заряда в большинстве металлов отрицательны.
Э.Х. Холл разработал эксперимент, который можно использовать для определения знака преобладающих носителей заряда в проводящем материале. С исторической точки зрения этот эксперимент был первым, кто продемонстрировал, что носители заряда в большинстве металлов отрицательны.
Посетите этот веб-сайт, чтобы найти дополнительную информацию об эффекте Холла.
Мы исследуем эффект Холла , изучая движение свободных электронов вдоль металлической полосы шириной l в постоянном магнитном поле (рис. \(\PageIndex{1}\)). Электроны движутся слева направо, поэтому магнитная сила, которую они испытывают, толкает их к нижнему краю полоски. Это оставляет избыток положительного заряда на верхнем краю полоски, что приводит к возникновению электрического поля E , направленного сверху вниз. Концентрация заряда на обоих краях увеличивается до тех пор, пока электрическая сила, действующая на электроны в одном направлении, не уравновесится магнитной силой, действующей на них в противоположном направлении.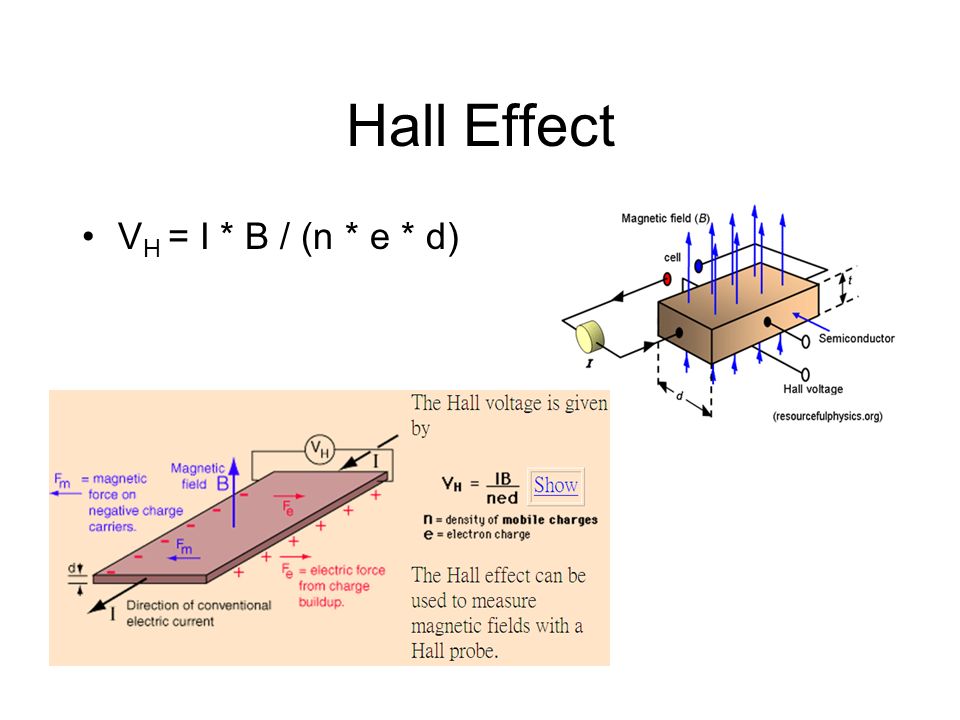 Равновесие достигается, когда:
Равновесие достигается, когда:
\[eE = ev_d B \label{11.24}\]
, где e — величина заряда электрона, \(v_d) — дрейфовая скорость электронов, а E — величина электрического поля, создаваемого отделенным зарядом. Решение этого для скорости дрейфа дает
\[v_d = \frac{E}{B}. \метка{11.25}\]
Рисунок \(\PageIndex{1}\): В эффекте Холла возникает разность потенциалов между верхним и нижним краями металлической полосы, когда движущиеся носители заряда отклоняются магнитным полем. а) эффект Холла для отрицательных носителей заряда; (б) Эффект Холла для положительных носителей заряда. Сценарий, в котором электрическое и магнитное поля перпендикулярны друг другу, называется ситуацией пересечения полей. Если эти поля воздействуют на заряженную частицу равными и противоположными силами со скоростью, равной силам, эти частицы могут пройти через устройство, называемое селектором скорости , без отклонения. Эта скорость представлена в уравнении \ref{11.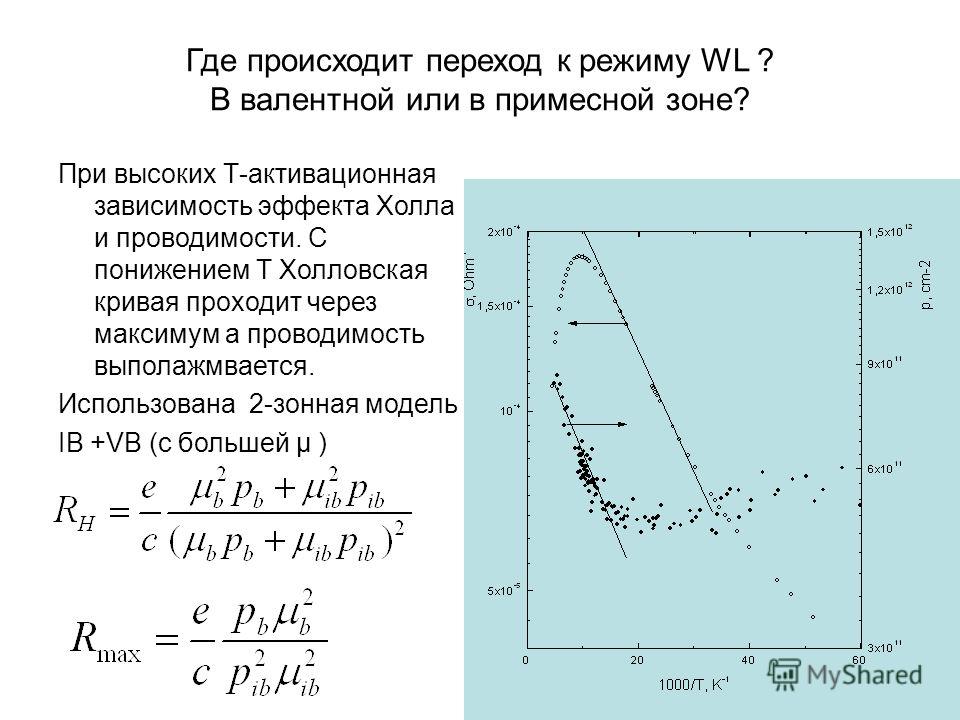 26}. Любая другая скорость заряженной частицы, посланной в те же поля, будет отклонена магнитной или электрической силой.
26}. Любая другая скорость заряженной частицы, посланной в те же поля, будет отклонена магнитной или электрической силой.
Возвращаясь к эффекту Холла, если ток в полосе равен I , то из тока и сопротивления мы знаем, что
\[I = nev_dA \label{11.26}\]
, где n — количество носителей заряда в объеме, а A — площадь поперечного сечения полосы. Объединение уравнений для \(v_d\) и I приводит к
\[I = ne\left(\frac{E}{B}\right)A. \метка{11.27}\]
Поле E связано с разностью потенциалов V между краями полосы по
\[E = \frac{V}{l}. \метка{11.28}\]
Величина \(V\) называется потенциалом Холла и может быть измерена вольтметром. Наконец, объединение уравнений для I и E дает нам
\[V = \dfrac{IBl}{neA} \label{hallV}\]
, где верхний край полосы на рисунке \(\PageIndex{1}\) положителен по отношению к нижнему краю.
Мы также можем объединить уравнение \ref{11.24} и уравнение \ref{11.28}, чтобы получить выражение для напряжения Холла через магнитное поле:
\[V = Blv_d.\]
Что делать, если носители заряда положительны, как на рисунке \(\PageIndex{1}\)? Для того же тока I величина V по-прежнему определяется уравнением \ref{hallV}. Однако верхний край теперь отрицателен по отношению к нижнему краю. Поэтому, просто измерив знак В , мы можем определить знак большинства носителей заряда в металле.
Измерения потенциала Холла показывают, что электроны являются доминирующими носителями заряда в большинстве металлов. Однако потенциалы Холла показывают, что для некоторых металлов, таких как вольфрам, бериллий и многие полупроводники, большинство носителей заряда положительны. Оказывается, проводимость за счет положительного заряда вызвана миграцией недостающих электронных узлов (называемых дырками) на ионах. Проводимость через дырки изучается позже в физике конденсированного состояния.
Эффект Холла можно использовать для измерения магнитных полей. Если материал с известной плотностью носителей заряда n поместить в магнитное поле и измерить В , то поле можно определить по уравнению \ref{11.29}. В исследовательских лабораториях, где поля электромагнитов, используемых для точных измерений, должны быть чрезвычайно устойчивыми, «зонд Холла» обычно используется как часть электронной схемы, регулирующей поле.
Пример \(\PageIndex{1}\): Переключатель скорости 93 \, N/C\) соответственно. а) Какова должна быть скорость электронного луча, чтобы он прошел через скрещенные поля без отклонения? Если электрическое поле выключено, (б) каково ускорение электронного луча и (в) каков радиус кругового движения в результате?
Стратегия
Электронный пучок не отклоняется ни магнитным, ни электрическим полем, если эти силы уравновешены. На основе этих уравновешенных сил мы вычисляем скорость луча. Без электрического поля во втором законе Ньютона для нахождения ускорения используется только магнитная сила.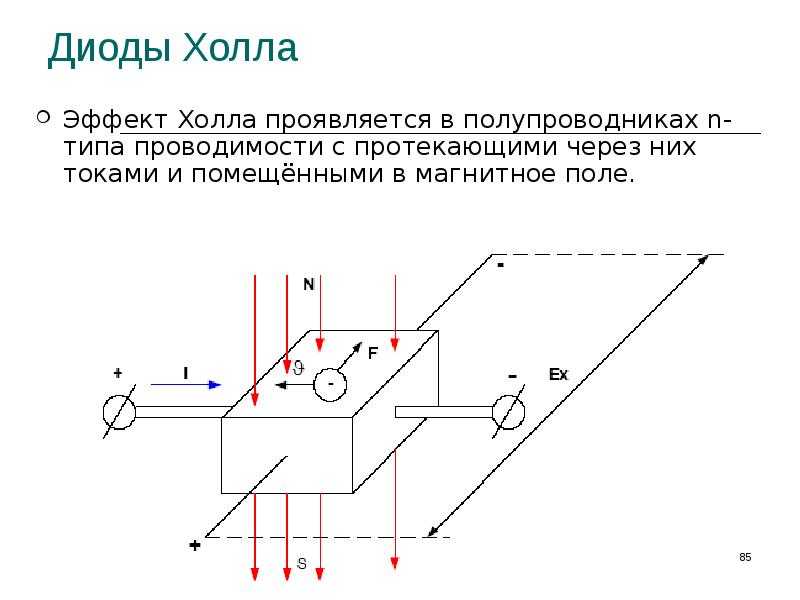 Наконец, радиус пути основан на результирующем круговом движении под действием магнитной силы. 9{-3} м.\]
Наконец, радиус пути основан на результирующем круговом движении под действием магнитной силы. 9{-3} м.\]
Значение
Если бы скорость электронов в пучке была больше или меньше скорости, указанной в ответе в части (а), эти электроны имели бы более сильную результирующую силу, создаваемую либо магнитным, либо электрическим полем. Следовательно, только те электроны с этой конкретной скоростью смогут пройти.
Потенциал Холла в серебряной ленте
На рисунке \(\PageIndex{2}\) показана серебряная лента с поперечным сечением 1,0 см на 0,20 см. По ленте течет ток 100 А слева направо, и она находится в однородном магнитном поле величиной 1,5 Тл. Используя значение плотности \(n = 5,9{28}\) электронов на кубический метр для серебра, найти потенциал Холла между краями ленты.
Рисунок \(\PageIndex{2}\): Показано нахождение потенциала Холла в серебряной ленте в магнитном поле.Стратегия
Поскольку большинство носителей заряда представляют собой электроны, полярность напряжения Холла указана на рисунке. Значение напряжения Холла рассчитывается с использованием уравнения \ref{hallV}.
Значение напряжения Холла рассчитывается с использованием уравнения \ref{hallV}.
Решение
При расчете напряжения Холла нам необходимо знать ток через материал, магнитное поле, длину, количество носителей заряда и площадь. Поскольку все они даны, напряжение Холла рассчитывается как: 9{28}\) электронов на кубический метр шириной 2,0 см и толщиной 0,10 см. Чему равно магнитное поле, если I = 50 А и потенциал Холла равен
- \(4,0 мкВ\) и
- \(6.0\, \мкВ\)?
- Ответить на
-
1,1 Т
- Ответ b
-
1,6 т
Эта страница под названием 11.7: Эффект Холла распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа ООР или издатель
- ОпенСтакс
- Показать оглавление
- нет
-
- Метки
-
- Эффект Холла
- источник@https://openstax.


