Параллельное соединение конденсатора. Параллельное соединение конденсаторов: формулы, расчеты и применение

Как работает параллельное соединение конденсаторов. Какие формулы используются для расчета общей емкости. Где применяются параллельные цепи конденсаторов. Как рассчитать напряжение и заряд на конденсаторах.

Принцип работы параллельного соединения конденсаторов

При параллельном соединении конденсаторов:

• Все конденсаторы подключены к одному источнику напряжения
• Напряжение на всех конденсаторах одинаково и равно напряжению источника
• Общий заряд равен сумме зарядов на отдельных конденсаторах
• Общая емкость увеличивается и равна сумме емкостей отдельных конденсаторов

Почему напряжение на всех конденсаторах одинаково? Это связано с тем, что они подключены к одним и тем же точкам цепи, поэтому разность потенциалов между их обкладками одинакова.

Формула для расчета общей емкости параллельно соединенных конденсаторов

Общая емкость параллельно соединенных конденсаторов рассчитывается по формуле:

C = C1 + C2 + C3 + … + Cn

Где C — общая емкость, C1, C2, C3, …, Cn — емкости отдельных конденсаторов.

Эта формула вытекает из того, что общий заряд равен сумме зарядов на отдельных конденсаторах:

Q = Q1 + Q2 + Q3 + … + Qn

А так как Q = CV, то:

CV = C1V + C2V + C3V + … + CnV

Откуда и получается формула для общей емкости.

Расчет напряжения и заряда на конденсаторах в параллельной цепи

При параллельном соединении:

• Напряжение на всех конденсаторах одинаково и равно напряжению источника: U = U1 = U2 = U3 = … = Un
• Заряд на каждом конденсаторе рассчитывается по формуле: Q = CU
• Общий заряд равен сумме зарядов: Q = Q1 + Q2 + Q3 + … + Qn

Зная емкости конденсаторов и напряжение источника, можно легко рассчитать заряд на каждом конденсаторе и общий заряд цепи.

Преимущества параллельного соединения конденсаторов

Параллельное соединение конденсаторов имеет ряд преимуществ:

• Увеличение общей емкости цепи
• Возможность получить нестандартное значение емкости
• Увеличение максимального рабочего напряжения
• Снижение эквивалентного последовательного сопротивления (ESR)
• Повышение надежности — при выходе из строя одного конденсатора цепь продолжит работать

За счет этих преимуществ параллельное соединение широко применяется на практике.

Области применения параллельного соединения конденсаторов

Параллельное соединение конденсаторов используется во многих областях электроники и электротехники:

• Фильтрация пульсаций в блоках питания
• Сглаживание выходного напряжения в импульсных преобразователях
• Накопление энергии в фотовспышках
• Создание емкостных делителей напряжения
• Компенсация реактивной мощности в электрических сетях
• Формирование колебательных контуров в радиотехнике

В каждом конкретном применении параллельное соединение позволяет оптимальным образом подобрать нужную емкость и рабочее напряжение.

Особенности расчета реальных параллельных цепей конденсаторов

При расчете реальных параллельных цепей конденсаторов нужно учитывать ряд факторов:

• Допуски на номинальные значения емкостей
• Паразитные индуктивности и сопротивления выводов
• Токи утечки конденсаторов
• Температурную зависимость емкости
• Старение диэлектрика и изменение параметров со временем

Все эти факторы могут влиять на реальную емкость цепи. Поэтому при проектировании обычно закладывают некоторый запас по емкости.

Сравнение параллельного и последовательного соединения конденсаторов

Параллельное и последовательное соединение конденсаторов имеют ряд отличий:

Параметр	Параллельное соединение	Последовательное соединение
Общая емкость	Увеличивается	Уменьшается
Напряжение на конденсаторах	Одинаковое	Разное
Заряд на конденсаторах	Разный	Одинаковый
Максимальное рабочее напряжение	Не изменяется	Увеличивается

Выбор типа соединения зависит от конкретной задачи и требуемых параметров цепи.

Практические примеры расчета параллельных цепей конденсаторов

Рассмотрим несколько практических примеров расчета параллельных цепей конденсаторов:

Пример 1

Дано: три конденсатора с емкостями C1 = 10 мкФ, C2 = 22 мкФ, C3 = 47 мкФ соединены параллельно. Найти: общую емкость цепи.

Решение: C = C1 + C2 + C3 = 10 + 22 + 47 = 79 мкФ

Пример 2

Дано: два конденсатора C1 = 100 нФ и C2 = 220 нФ соединены параллельно и подключены к источнику напряжения 12 В. Найти: заряд на каждом конденсаторе и общий заряд цепи.

Решение: Q1 = C1 * U = 100 нФ * 12 В = 1200 нКл Q2 = C2 * U = 220 нФ * 12 В = 2640 нКл Q = Q1 + Q2 = 1200 + 2640 = 3840 нКл

Такие расчеты позволяют правильно спроектировать параллельную цепь конденсаторов для конкретного применения.

Параллельное соединение конденсаторов – общая емкость, заряд, формула кратко

4.6

Средняя оценка: 4.6

Всего получено оценок: 71.

4.6

Средняя оценка: 4.6

Всего получено оценок: 71.

Компоненты электрической цепи могут быть соединены различными способами, чаще всего используется параллельное и последовательное соединение. Рассмотрим работу параллельно соединенных конденсаторов.

Виды соединений в электрической цепи

Любая электрическая цепь состоит из одного или нескольких источников тока и одного или нескольких потребителей. Все эти компоненты связаны между собой проводниками.

Как бы ни сложна была электрическая цепь, в ней всегда можно выделить узлы и звенья:

• узел — это точка, в которой сходятся три и более проводника;
• звено — это участок цепи между двумя соседними узлами.

Каждое звено может быть простым проводником, может состоять из одного потребителя, а может содержать несколько потребителей, соединенных «цепочкой», один за другим. Такое соединение потребителей называется последовательным.

Если несколько звеньев подключаются к одним и тем же двум узлам, такое соединение называется параллельным.

Если три и более звена соединяются так, что некоторые звенья будут соединены параллельно, а некоторые — последовательно, то такое соединение называется смешанным.

Рис. 1. Виды соединений в электрической цепи.

Параллельное соединение конденсаторов

При параллельном соединении к двум выводам звена подключается каждый из соединенных конденсаторов. Получается, что при подключении к внешней цепи электрический ток будет поступать сразу на все конденсаторы. Произведем расчет емкости такой батареи конденсаторов.

Напомним, что емкость конденсатора показывает, насколько легко сообщить конденсатору заряд, и равна отношению заряда к напряжению на обкладках:

$$C={q\over U}$$

Если сообщить батарее конденсаторов некоторый заряд, то по закону сохранения этот заряд может лишь распределиться между конденсаторами, однако суммарно он останется прежним:

$$q_{общ}=q_1+q_2+…+q_n$$

При параллельном соединении конденсаторов напряжение на каждом из них будет одинаково.

Действительно, если на каком-то из конденсаторов напряжение было бы больше, то заряд из этого конденсатора сразу же перешел бы к другому, тем самым уменьшив напряжение на первом и увеличив на втором.

Таким образом, общая емкость батареи конденсаторов равна:

$$C_{общ}={q_1+q_2+…+q_n\over U}={q_1\over U}+{q_2\over U}+…+{q_n\over U}$$

Каждый компонент полученной суммы равен отношению заряда на одном из конденсаторов к напряжению на нем, а это — емкость данного конденсатора. Заменяя каждую дробь на соответствующую емкость, получаем формулу для определения общей емкости параллельно соединенных конденсаторов:

$$C_{общ}=C_1+C_2+…+Cn$$

При параллельном соединении конденсаторов общая емкость батареи равна сумме емкостей отдельных элементов.

Рис. 2. Параллельное соединение конденсаторов.

Использование параллельного соединения конденсаторов

Казалось бы, смысла в параллельном соединении конденсаторов нет. Зачем брать два конденсатора, если можно взять один, большей емкости?

Основная причина состоит в том, что выпускаемые номиналы конденсаторов имеют не любые значения. Например, конденсаторы емкостью 7 мкФ не выпускаются. Однако выпускаются конденсаторы емкостью 6,8 мкФ и 0,2 мкФ. Соединив их параллельно, можно получить требуемые 7 мкФ.

Рис. 3. Стандартные ряды номиналов радиодеталей.

Существует еще одна причина использования параллельного соединения конденсаторов — их неидеальность. Например, у больших конденсаторов имеется заметная на высоких частотах паразитная индуктивность. Из-за этого высокочастотная составляющая сигнала, которая в идеале должна легко проходить через большую емкость конденсатора, не проходит через него. Поэтому в этом случае параллельно конденсатору большой емкости ставится еще один, малой емкости, но имеющий очень малую паразитную индуктивность, которой можно пренебречь. В результате высокочастотная составляющая будет проходить через него.

Что мы узнали?

Общая емкость конденсаторов при параллельном соединении равна сумме емкостей отдельных конденсаторов. Такое соединение используется чаще всего для того, чтобы получить номиналы, не выпускающиеся промышленностью.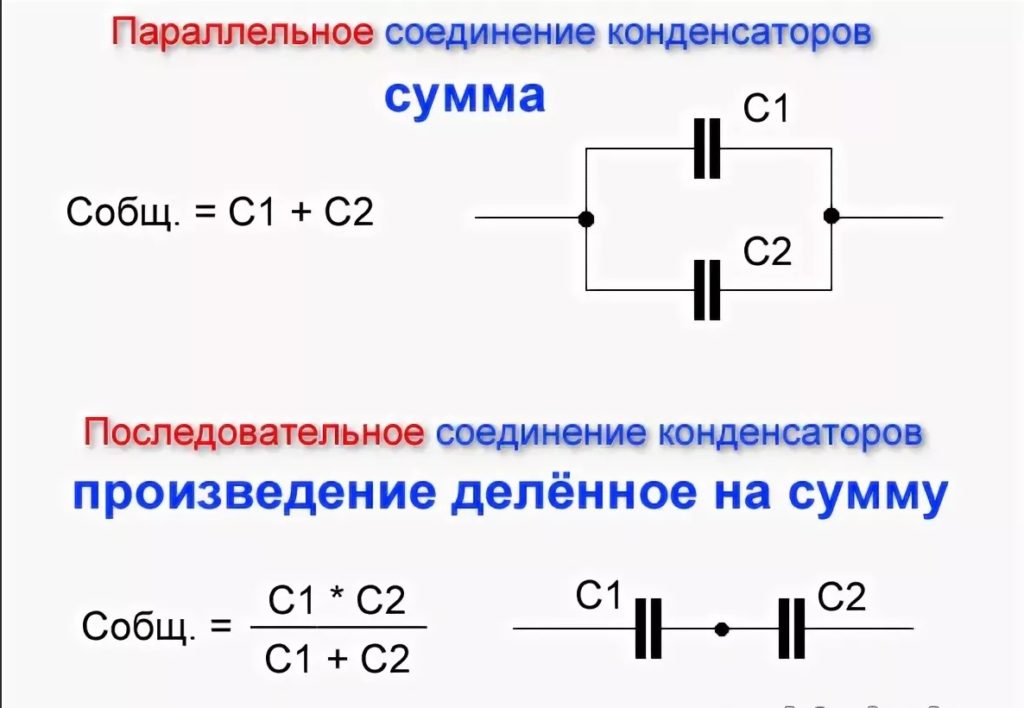

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 71.

---

А какая ваша оценка?

Параллельное и последовательное соединение конденсаторов (формулы, законы для вычисления емкости и напряжения)

Содержание

1. Отличия параллельного и последовательного соединения конденсаторов
2. Смешанное подключение
3. Общая емкость и распределение напряжений между элементами при разных типах включения
4. Примеры подключений

Электрические схемы могут содержать элементы, основным параметром которых является емкость. Чаще всего это конденсаторы (также в этом качестве используются, например, варикапы, ионисторы и т.п.). Такие элементы можно соединять параллельно или последовательно и получать участки схемы с иными параметрами.

Отличия параллельного и последовательного соединения конденсаторов

При параллельном (parallel) подключении обкладки конденсаторов соединяются в одной точке, а противоположные – в другой. К этим точкам подключается источник напряжения. Наглядно продемонстрировать такую схему можно на примере полярных приборов (например, электролитических конденсаторов), когда все положительные электроды соединяются между собой и подключаются к плюсу питания.

Отрицательные обкладки также соединяются в один узел, на который подается минус питающего напряжения. У неполярных элементов нет разделения на положительные и отрицательные электроды, они соединяются произвольным образом, но по тому же принципу (в этом случае на батарею можно подавать и двухполярное напряжение). Каждый конденсатор подключен непосредственно к источнику питания, поэтому напряжение на каждой банке одинаково.

Параллельное включение элементов.

При последовательном (serial) соединении одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

Батарея из последовательно соединенных ячеек.

Смешанное подключение

Также существует смешанное соединение элементов, когда часть ячеек включена параллельно, часть последовательно. Такие схемы несколько сложнее для анализа.

Батарея из смешанно соединенных конденсаторов.

Общая емкость и распределение напряжений между элементами при разных типах включения

Емкость конденсаторов зависит, в том числе, и от площади обкладок. Если однотипные элементы соединить параллельно, это можно рассматривать как суммирование всех площадей обкладок, что означает сложение емкостей банок, входящих в батарею. Очевидно, что это же правило действует и для разнотипных элементов. Аналитическим путем к этому можно прийти в результате следующих рассуждений:

• очевидно, что при таком подключении на каждом элементе напряжения будут равны (U₁=U₂=U);
• запасенные заряды всех пластин суммируются (q=q₁+q₂);
• тогда общая емкость равна С=U*q=U*(q₁+q₂)=U*q₁+U*q₂=C1+C2.

Напряжение и заряды при параллельном включении элементов.

Эта же формула действует при параллельном соединении n конденсаторов:

С=С₁+С₂+..+C_n.

Последовательное соединение емкостей.

Если соединить в последовательную цепь, например, три конденсатора различной емкости и полностью их зарядить до напряжения U, то выяснится, что:

• заряды –q1 и q2, -q2 и q3 равны между собой, так как обкладки с этими зарядами электрически соединены;
• заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по абсолютной величине, но противоположны по знаку.

Конденсаторы в таком включении получают равный заряд q, но при разной емкости получится, что напряжения на каждом элементе равны:

• U₁=q/ C₁;
• U₂=q/ C₂;
• U₃= q/ C₃.

Напряжения распределяются пропорционально емкостям (при равных параметрах на каждой банке падает одинаковое сопротивление).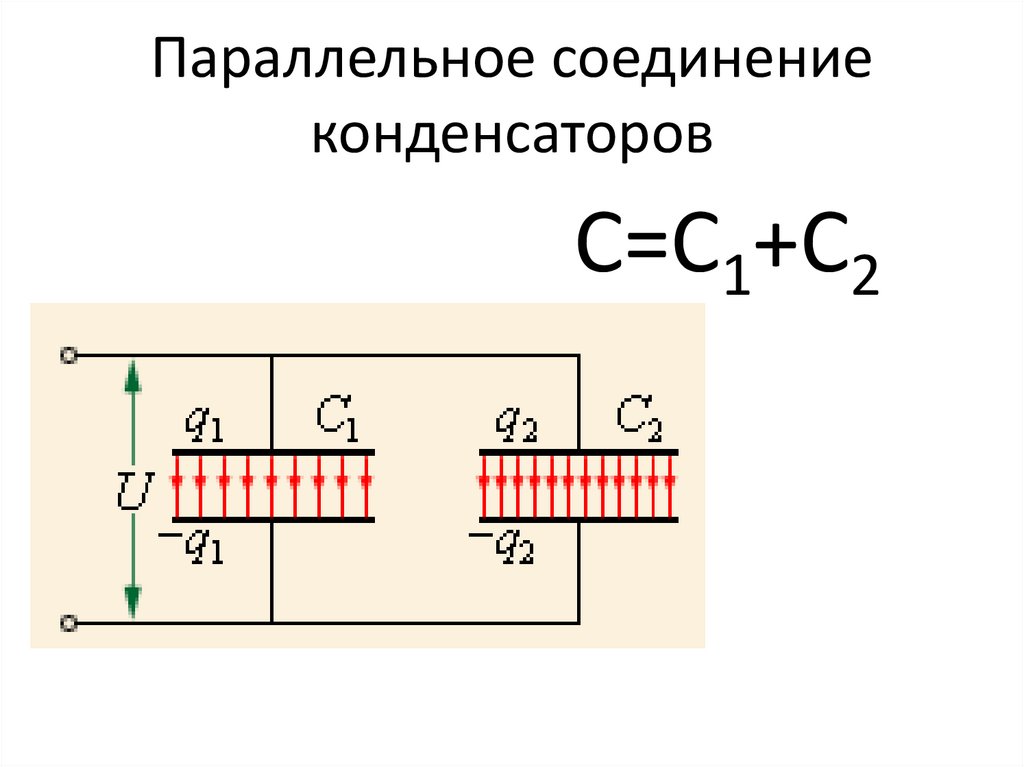 А общая емкость равна С=q/(U₁+U₂+U₃), отсюда 1/С=( U₁+U₂+U₃)/q=1/С₁+1/С₂+1/С₃.

Для n элементов, подключенных в последовательную цепь:

1/С=1/С₁+1/С₂+..+1/С_n.

Формула выглядит громоздко, но для цепи из двух элементов можно пользоваться приведенным видом С= С₁* С₂/( С₁+ С₂).

Для предварительного анализа схем, состоящих из емкостных элементов, подключенных различными способами, надо запомнить несколько законов:

• при параллельном соединении емкости складываются, суммарная емкость всегда больше, чем у элемента с самым большим значением емкости;
• напряжения при параллельном соединении одинаковы на каждом элементе цепи;
• при последовательном соединении итоговая емкость будет меньше наименьшего значения емкости любого элемента;
• напряжения на последовательно включенных звеньях распределяются пропорционально емкости.

Анализ и расчет схем со смешанным подключением элементов надо начинать с приведения цепи к единому виду, где конденсаторы будут включены либо только последовательно, либо только в параллель.

Преобразование к последовательному виду.

Так, схема на рисунке содержит три элемента, два из которых включены в параллель, и один последовательно. Удобно С1 и С3 заменить одним эквивалентным звеном С – при этом останутся только последовательные звенья. Остается выполнить расчет схемы, а потом вернуться к изначальной цепи.

Преобразование к последовательному виду.

Рекомендуем видео-урок по физике.

Примеры подключений

Параллельное соединение применяется в тех случаях, когда надо увеличить итоговую емкость. По экономическим или компоновочным причинам использование одного элемента с необходимыми параметрами может быть невозможно или нерационально. Поэтому собирают батарею из конденсаторов так, чтобы сумма емкостей давала необходимое значение. Такая схема применяется, например, для фильтров блоков питания в целях увеличения емкости сглаживающего фильтра.

Другой вариант параллельного включения – когда емкость надо точно настраивать по месту, а подстроечного конденсатора с необходимыми пределами или нет в наличии, или не существует. Тогда параллельно конденсатору постоянной емкости включают подстроечный элемент. После монтажа устройства во время настройки устанавливается точное значение.

Параллельно включенный прибор с постоянными параметрами и подстроечник.

Последовательное включение нескольких элементов дает увеличение рабочего напряжения цепочки, но уменьшает общую емкость. К тому же купить приборы на высокое напряжение (до нескольких киловольт) несложно, поэтому последовательные цепи в целях достижения необходимых параметров применяются нечасто.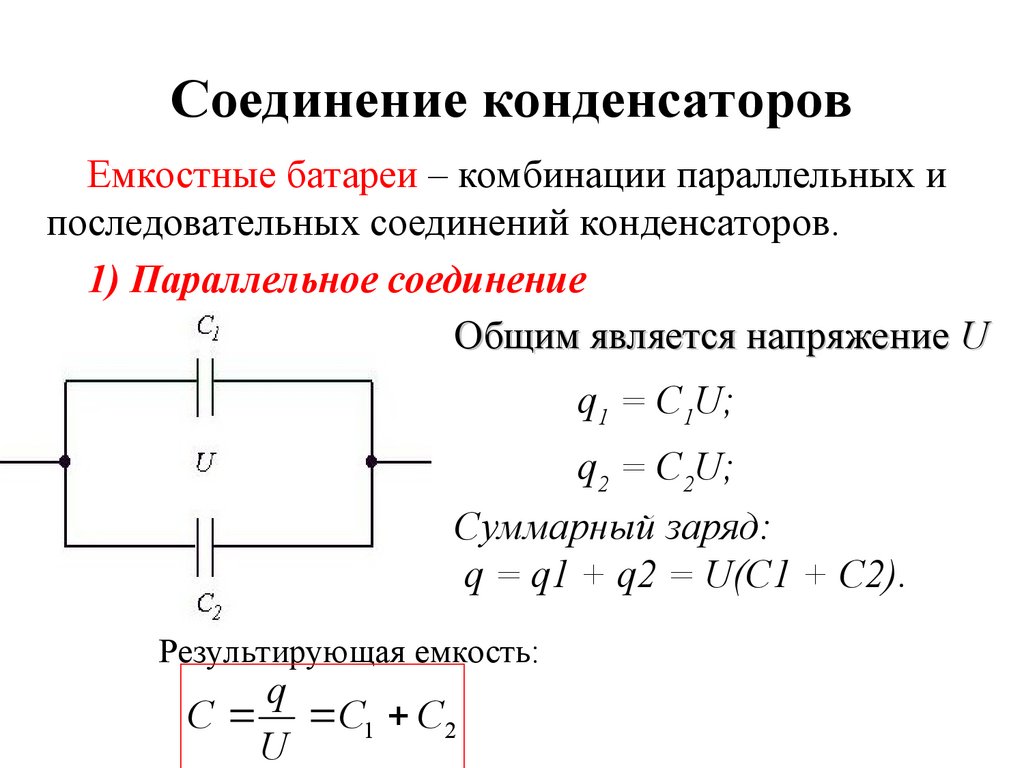 Обычно такое включение используется в емкостных делителях напряжения. В отличие от резистивных компонентов, через реактивные элементы не протекает активный ток, поэтому не надо решать задачу отвода тепла. Такие делители можно применять, к примеру, в индикаторах наличия высокого напряжения. Несколько киловольт на входе подбором номиналов банок делятся так, что напряжение на нижнем элементе безопасно для индикаторной лампы.

Индикатор высокого напряжения.

Также такой делитель можно найти в схемах импульсных источников питания с полумостовой схемой. Таким способом образуется средняя точка с потенциалом, равным половине питания.

Фрагмент схемы блока питания с фильтром-делителем и выравнивающими резисторами.

 

Еще один пример применения последовательного соединения элементов – в умножителях напряжения. В них нагрузочная способность источника питания зависит от емкости, поэтому в умножителях также применяются оксидные конденсаторы.

Последовательная батарея для умножителя.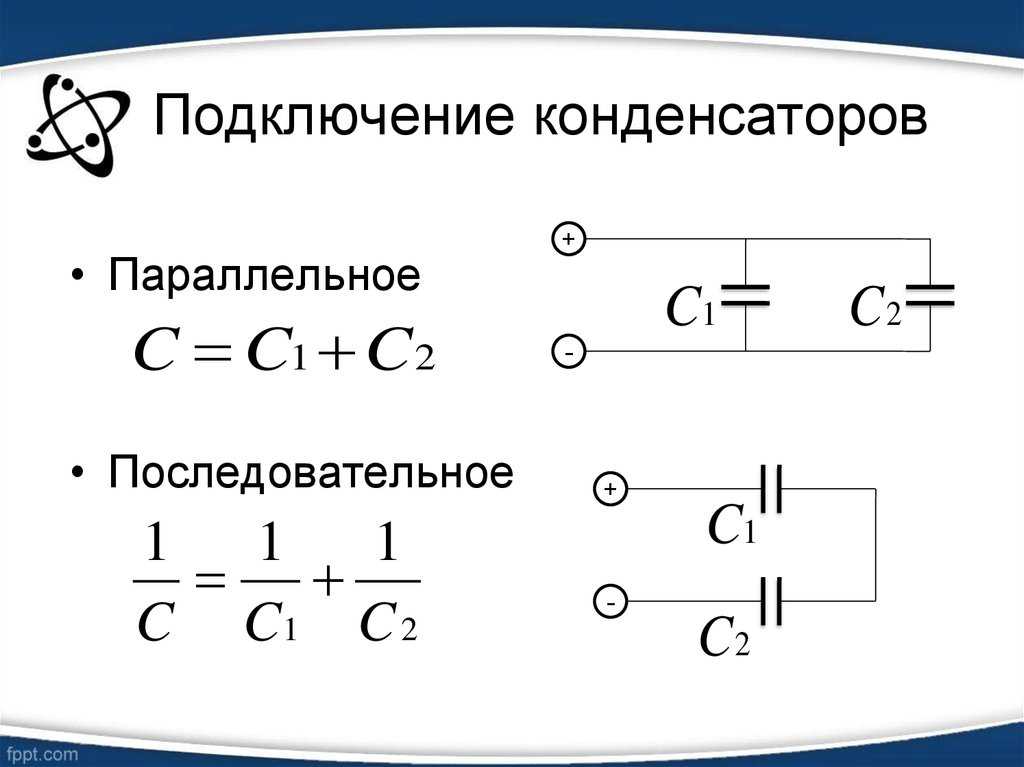

Смешанное включение встречается гораздо реже. Один из примеров такой схемы – колебательный контур с переменной частотой настройки. Его резонанс зависит, в том числе, от емкости конденсатора, и перестройка по частоте зависит от пределов изменения емкости. Ряд конденсаторов переменной емкости, выпускаемый промышленностью, довольно ограничен, поэтому для достижения необходимых границ параллельно и последовательно с КПЕ включают «растягивающие» конденсаторы.

КПЕ с «растягивающими» элементами.

Если имеется конденсатор с пределами изменения характеристик от 10 до 430 пФ, при подключении добавочных конденсаторов пределы изменения емкости получаются:

С1, пФ	С2, пФ	Новые пределы изменения, пФ
15	40	15..36
25	100	25..82

Знание свойств соединения емкостных элементов позволяет быстро анализировать процессы, происходящие в электрических схемах. Также понимание, как изменяются характеристики цепи при различных видах подключения, позволяет комбинировать имеющиеся элементы, создавая участки схем с новыми параметрами.

4.2 Конденсаторы, включенные последовательно и параллельно. Введение в электричество, магнетизм и схемы

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Объясните, как определить эквивалентную емкость конденсаторов при последовательном и параллельном соединении
• Вычислите разность потенциалов на пластинах и заряд на пластинах для конденсатора в сети и определите чистую емкость сети конденсаторов

Несколько конденсаторов можно соединить вместе для использования в различных приложениях. Несколько соединений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Конденсаторы могут быть расположены в двух простых и распространенных типах соединений, известных как ряд и параллельно , для которых мы можем легко рассчитать общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серийная комбинация конденсаторов

На рисунке 4.2.1 показана последовательная комбинация трех конденсаторов, расположенных в ряд внутри цепи. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 4.1.1. При подключении этой последовательной комбинации к батарее с напряжением

В каждый из конденсаторов приобретает одинаковый заряд. Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен  , а заряд на пластине, подключенной к отрицательной клемме, равен . Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала на одном конденсаторе может отличаться от падения потенциала на другом конденсаторе, поскольку, как правило, конденсаторы могут иметь разную емкость. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентная емкость ) меньше, чем наименьшая из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательном соединении: То есть все конденсаторы в последовательном соединении имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд в последовательной цепи снимается с пластины первого конденсатора (обозначается как ), он должен быть помещен на пластину второго конденсатора (обозначается как ) и так далее.

(рис. 4.2.1)  

Рисунок 4.2.1  (a) Три конденсатора соединены последовательно. Величина заряда на каждой пластине равна . (b) Цепочка конденсаторов в (а) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей в (а), а заряд на его пластинах равен .

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах.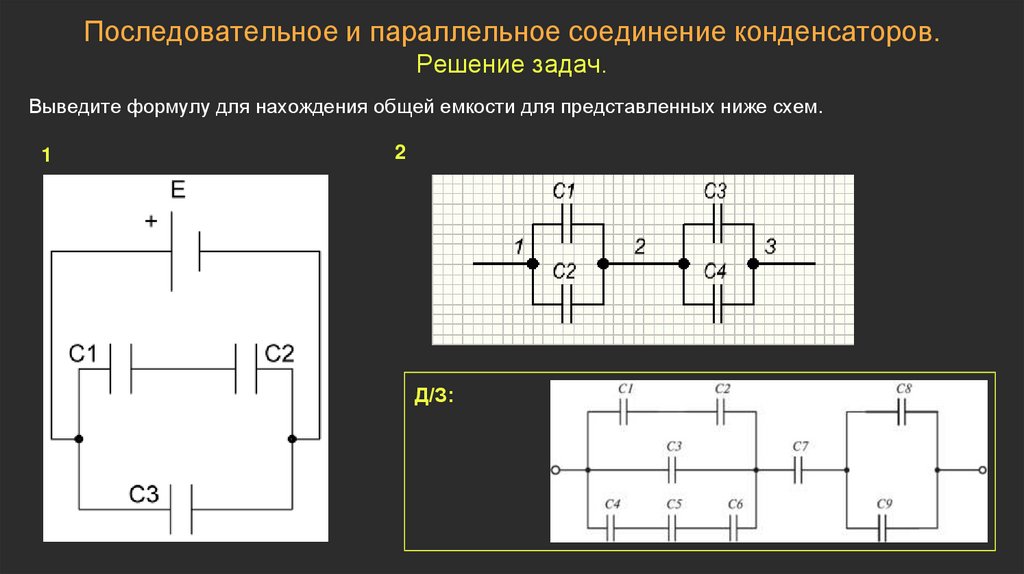 Потенциалы на конденсаторах , , и равны соответственно , , и,. Эти потенциалы должны суммироваться с напряжением батареи, что дает следующий баланс потенциалов:

   

Потенциал измеряется на эквивалентном конденсаторе, который удерживает заряд и имеет эквивалентную емкость. Вводя выражения для , и , получаем

   

Отменяя заряд , получаем выражение, содержащее эквивалентную емкость, , трех последовательно соединенных конденсаторов:

   

Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.

СЕРИЯ

КОМБИНАЦИЯ

---

Для конденсаторов, соединенных в комбинацию серии , обратная величина эквивалентной емкости представляет собой сумму обратных величин отдельных емкостей:

(4.2.1)

ПРИМЕР 4.2.1

---

Эквивалентная емкость последовательной сети

Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны , , и .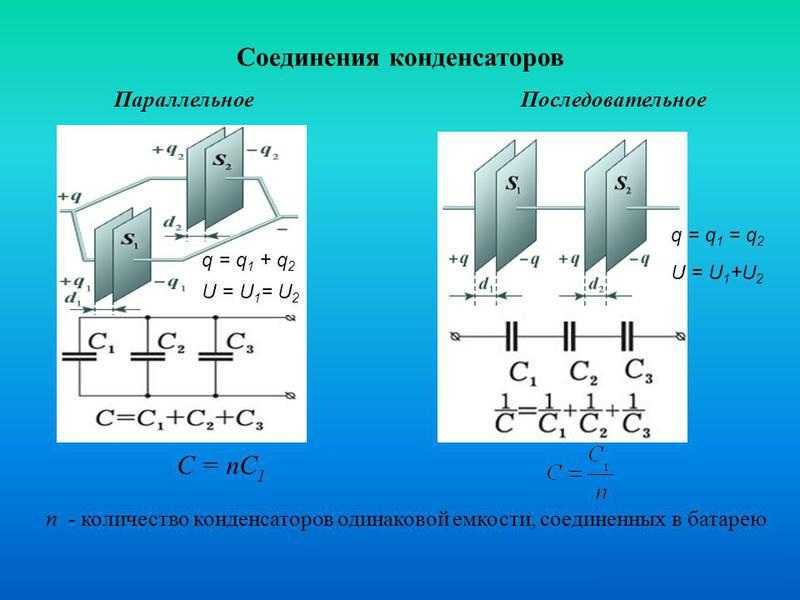

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.1 с тремя членами.

Решение

Мы вводим данные емкости в уравнение 4.2.1:

   

Теперь инвертируем этот результат и получаем .

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше, чем наименьшая отдельная емкость в сети.

Параллельная комбинация конденсаторов

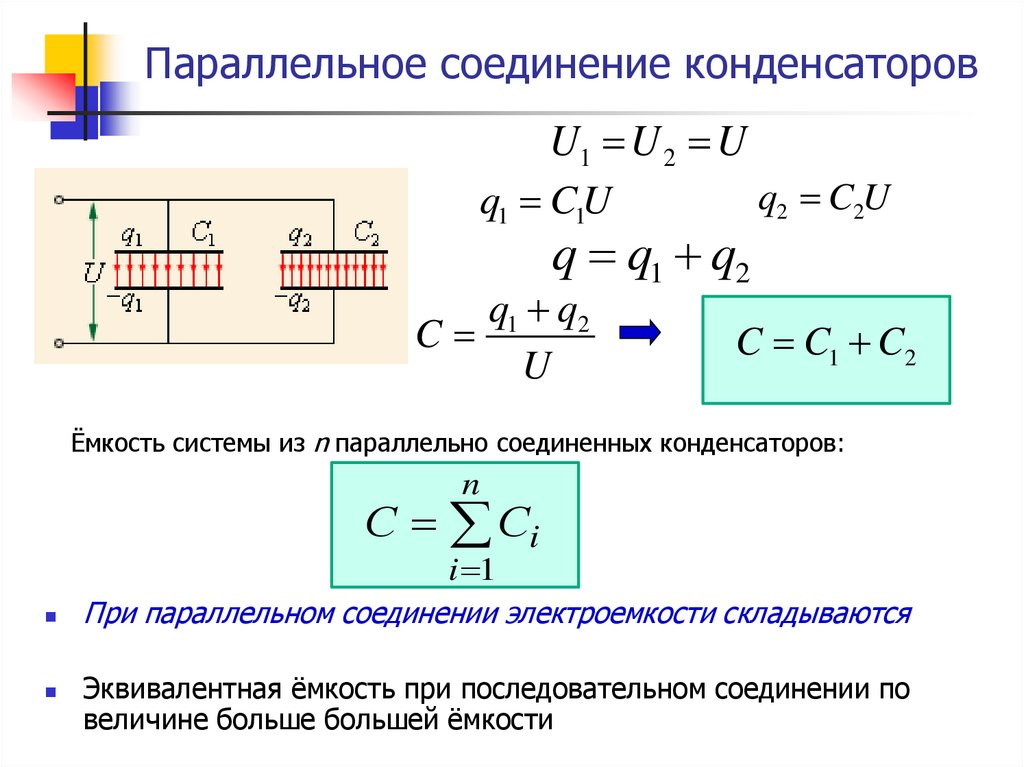
Параллельная комбинация трех конденсаторов, в которой одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на Рисунке 4.2.2(а). Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение на пластинах . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость параллельной сети, заметим, что общий заряд, хранящийся в сети, представляет собой сумму всех отдельных зарядов:

   

В левой части этого уравнения мы используем соотношение , которое справедливо для всей сети. В правой части уравнения мы используем отношения , и  для трех конденсаторов в сети. Таким образом, мы получаем

   

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

   

Это выражение легко обобщается на любое количество конденсаторов, соединенных параллельно в сети.

ПАРАЛЛЕЛЬНАЯ КОМБИНАЦИЯ

---

Для конденсаторов, соединенных в параллельную комбинацию , эквивалентная (чистая) емкость представляет собой сумму всех отдельных емкостей в сети,

(4.2.2)  

(рис. 4.2.2)  

Рисунок 4.2.2  (a) Три конденсатора соединены параллельно. Каждый конденсатор подключен непосредственно к аккумулятору. б) Заряд эквивалентного конденсатора равен сумме зарядов отдельных конденсаторов.

ПРИМЕР 4.2.2

---

Эквивалентная емкость параллельной сети

Найдите общую емкость трех параллельно соединенных конденсаторов, если их индивидуальные емкости равны , , и .

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.2 с тремя членами.

Решение

Ввод заданных емкостей в уравнение 4.2.2 дает

   

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Сети конденсаторов обычно представляют собой некоторую комбинацию последовательных и параллельных соединений, как показано на Рисунке 4.2.3. Чтобы найти чистую емкость таких комбинаций, мы идентифицируем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

(рис. 4.2.3)  

Рисунок 4.2.3  (a) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. б) и расположены последовательно; их эквивалентная емкость . (c) Эквивалентная емкость подключена параллельно к . Таким образом, эквивалентная емкость всей сети представляет собой сумму  и .

ПРИМЕР 4.2.3

---

Эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рис. 4.2.3. Предположим, что емкости известны с точностью до трех знаков после запятой (, , ). Округлите ответ до трех знаков после запятой.

Стратегия

Сначала мы определяем, какие конденсаторы соединены последовательно, а какие — параллельно. Конденсаторы  и  соединены последовательно. Их комбинация, обозначенная , параллельна .

Решение

Поскольку и  соединены последовательно, их эквивалентная емкость получается с помощью уравнения 4.2.1:

   

Емкость подключена параллельно с третьей емкостью, поэтому мы используем уравнение 4.2.2, чтобы найти эквивалентную емкость всей сети:

   

ПРИМЕР 4.

2.4

---

Сеть конденсаторов

Определите чистую емкость комбинации конденсаторов, показанной на рисунке 4.2.4, когда емкости равны , , . Когда на комбинации сохраняется разность потенциалов, найти заряд и напряжение на каждом конденсаторе.

(рис. 4.2.4)  

Рисунок 4.2.4  (a) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.

Стратегия

Сначала мы вычисляем чистую емкость  параллельного соединения и . Тогда  является чистой емкостью последовательного соединения  и . Мы используем соотношение , чтобы найти заряды , , и , и напряжения , , и , на конденсаторах , , и , соответственно.

Решение

Эквивалентная емкость для  и  составляет

   

Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,

   

Рассмотрим эквивалентную комбинацию из двух конденсаторов на Рисунке 4.2.4(b). Так как конденсаторы соединены последовательно, заряд у них одинаковый. Кроме того, конденсаторы имеют общую разность потенциалов, поэтому

   

Теперь разность потенциалов на конденсаторе равна

.

   

Поскольку конденсаторы и соединены параллельно, они имеют одинаковую разность потенциалов:

   

Следовательно, заряды этих двух конденсаторов соответственно равны

   

   

Значение

Как и ожидалось, чистая плата за параллельную комбинацию  и  составляет .

ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 4.5

---

Определите чистую емкость каждой сети конденсаторов, показанной ниже. Предположим, что , , , . Найдите заряд каждого конденсатора, предполагая, что в каждой сети есть разность потенциалов.

Цитаты Кандела

Контент по лицензии CC, конкретное указание авторства

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/7a0f9770-1c44-4acd-9920-1cd9a99f2a1e@8. 1. Лицензия : CC BY: Attribution

Понимание конденсаторов в параллельных соединениях

В предыдущем разделе мы подробно рассмотрели введение конденсаторов, сегодня мы обсудим параллельные конденсаторы. Вы поймете пример, формулу, расчет и применение параллельных конденсаторов. Помните, мы говорили, что конденсаторы — это компоненты, которые хранят электрическую энергию в электрическом поле. Мы также узнали, что разные конденсаторы имеют свое номинальное напряжение, то есть способность накапливать заряд. так что давайте углубимся в то, что привело нас сюда.

Электрические устройства могут быть спроектированы с максимально возможным количеством конденсаторов. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор с общей емкостью. Что ж, величина требуемой емкости будет определять количество конденсаторов и способ их подключения. Два простых и распространенных типа соединений называются последовательными и параллельными соединениями.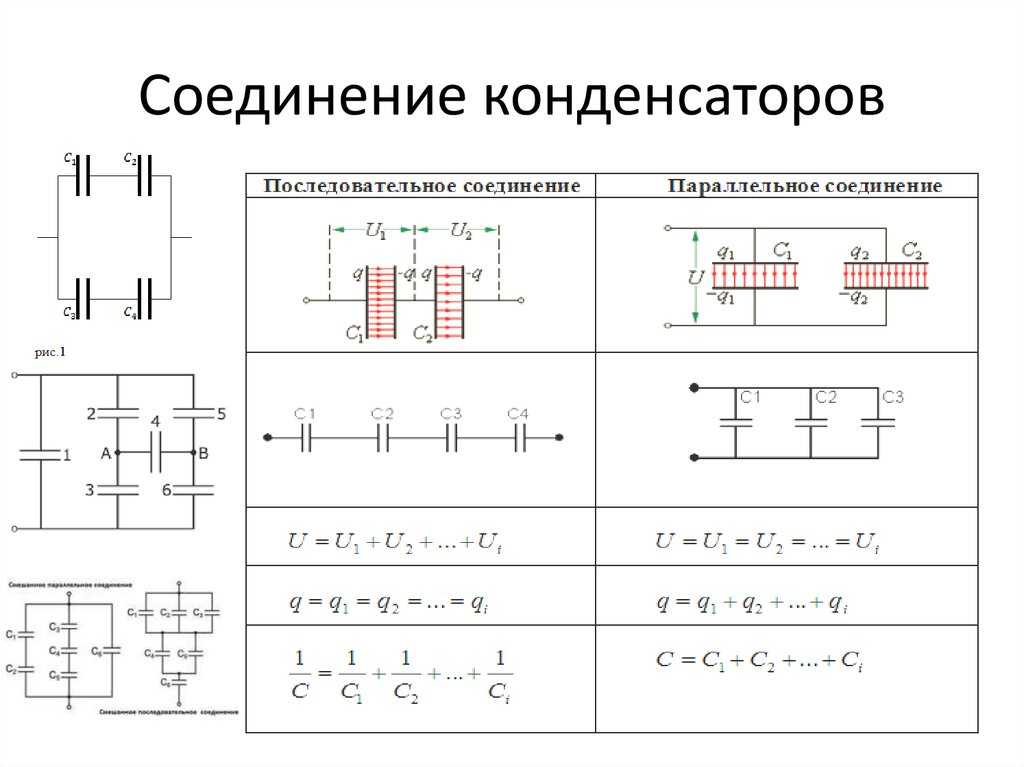 С помощью этих соединений мы можем легко рассчитать общую емкость. Хотя более сложные соединения могут включать комбинации последовательного и параллельного.

Принцип работы конденсатора — Анимация…

Включите JavaScript

Принцип работы конденсатора — Анимация — Учебники — Объяснение

Подробнее: Номинальное напряжение конденсатора

Содержание

• 6 1

. Напряжение Vc, подключенное ко всем параллельно соединенным конденсаторам, одинаково. Таким образом, конденсаторы, включенные параллельно, имеют общую подачу напряжения на них. например,

В _C1  = В _C2  = В _C3  = В _AB  = 12 В

Все конденсаторы с параллельным соединением имеют одинаковое напряжение на них, например, В 9 2909 6 В _{0 1 0270 = … В н . где от V 1 до V n представляют собой напряжение на каждом соответствующем конденсаторе. Это напряжение равно напряжению, приложенному к параллельному соединению конденсатора через входные провода. Хотя количество заряда, хранящегося в каждом конденсаторе, неодинаково. Кроме того, это зависит от емкости каждого конденсатора в соответствии с приведенной ниже формулой:}

Q _n = C _n . V _n

Где Q _n — количество заряда, накопленного на конденсаторе, C _n — емкость конденсатора, а V _n — напряжение, подаваемое на весь блок параллельного соединения. Блок конденсатора хранит общий заряд конденсатора, который представлен Q и делится между всеми конденсаторами в цепи. Это можно представить как:

Q = Q ₁ + Q ₂ + … + Q _n

Подробнее: Типы конденсаторов

Приведенное выше уравнение параллельного конденсатора используется для определения эквивалентной емкости при параллельном соединении нескольких конденсаторов:

C _eq =  =  =    +    + … +

Где C _eq — эквивалентная емкость при параллельном соединении конденсаторов, V — напряжение, подаваемое на конденсаторы по входным проводам, а Q _{1 9От 0270 до Q n — заряды, хранящиеся в каждом соответствующем конденсаторе.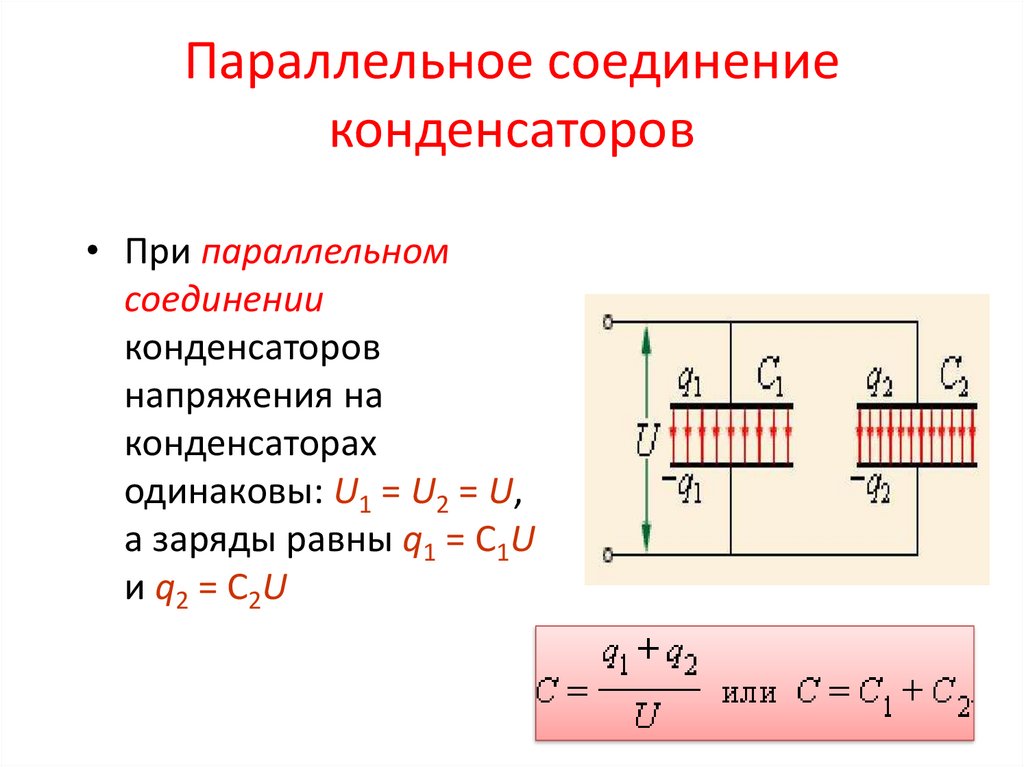 Вот почему у нас есть следующее уравнение:}

C _eq = C ₁ + C ₂ + …. + C _n

Приведенное выше уравнение означает, что эквивалентная емкость параллельного соединения конденсаторов равна сумме емкостей отдельных конденсаторов. Что ж, конденсаторы, включенные параллельно, можно рассматривать как один конденсатор, а его пластины равны сумме площадей пластин отдельных конденсаторов.

Подробнее: Понимание заряда в конденсаторе

Расчет параллельного конденсатора

С объяснением приведенного выше уравнения параллельного соединения конденсатора. В этом разделе вы узнаете, как рассчитать емкость конденсаторов при параллельном соединении. Имейте в виду, что значения отличаются от значений уравнения. Следующая схема показывает, что конденсаторы C1, C2 и C3 подключены в параллельную ветвь между точками A и B, как показано на рисунке ниже:

Помните, что общая или эквивалентная емкость C _eq в цепи равна сумме всех отдельных конденсаторов, сложенных вместе, когда конденсаторы соединены параллельно. Это связано с тем, что верхняя пластина конденсатора C ₁ соединена с верхней пластиной C ₂ , которая соединена с пластиной C _3, и так далее.

Это также относится к нижним пластинам конденсаторов, в результате чего три набора пластин соприкасаются друг с другом. Они равны одной большой одиночной пластине, что увеличивает эффективную площадь пластины в м ² .

Поскольку емкость C связана с площадью пластины (C = E(A/d), значение емкости комбинации также будет увеличиваться. Затем общая емкость конденсатора, подключенного параллельно, рассчитывается путем суммирования площади пластины. . Другими словами, общая емкость равна сумме всех отдельных емкостей, соединенных параллельно. Таким же образом мы получаем общее сопротивление последовательных резисторов.0016

Присоединяйтесь к нашей рассылке новостей

Примеры параллельного подключения конденсаторов

Возьмем значения трех конденсаторов, чтобы мы могли рассчитать общую эквивалентную емкость цепи C _T .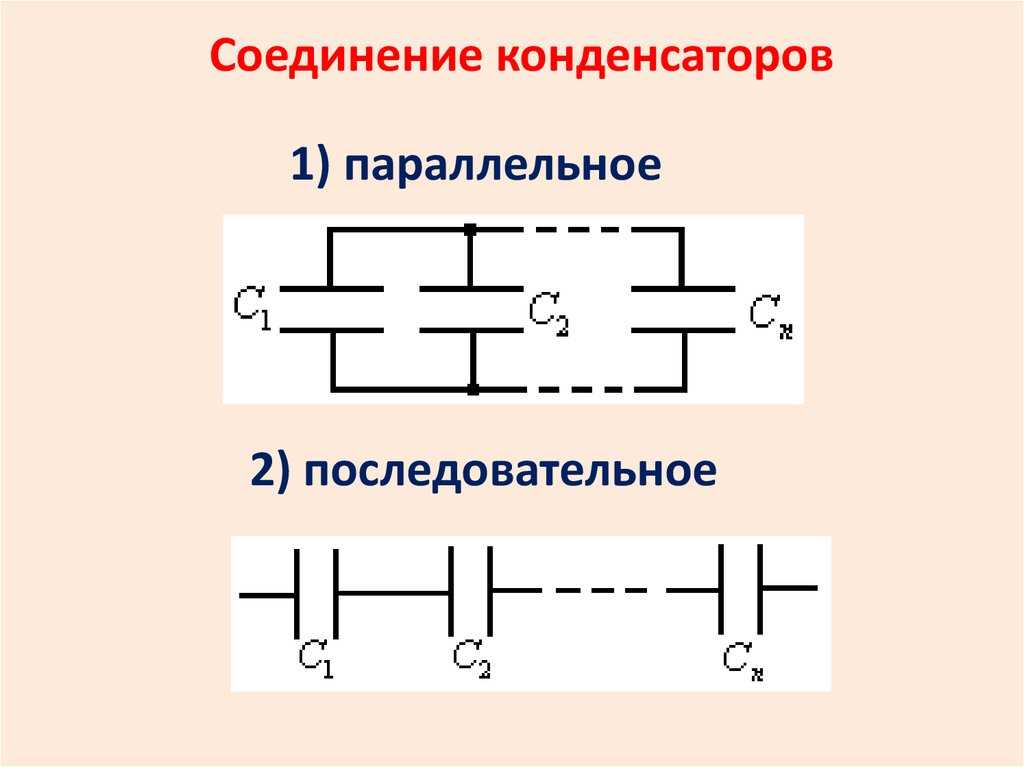 Тогда мы можем сказать:

C1 = C1 + C2 + C3 = 0,1 мкФ + 0,2 мкФ + 0,3 мкФ = 0,6 мкФ

Вы должны знать общую емкость (C _T ) любых двух или более конденсаторов, соединенных в параллельное будет БОЛЬШЕ, чем значение самого большого конденсатора в цепи. Это потому, что все значения суммируются. Итак, в приведенном выше примере C _T = 0,6 мкФ, тогда как конденсатор большей емкости в цепи равен 0,3 мкФ.

 Пример 2 конденсаторов, включенных параллельно

Рассчитайте емкость в микрофарадах (мкФ) следующих конденсаторов при параллельном соединении:

• Два конденсатора емкостью 47 нФ каждый
• параллельно конденсатору 1 мкФ

Подробнее: Значения емкости в цепях переменного тока

Решение

1. Суммарная емкость,

C _T = C ₁ + C ₂ = 47 нФ + 47 нФ = 94 нФ или 0,094 мкФ

---

00 7

С _Т = С ₁ + C ₂ = 470 нФ + 1 мкФ

Итак, C _T = 470 нФ + 1000 нФ = 1470 нФ или 1,47 мкФ

Следовательно, общая или эквивалентная емкость CT электрической цепи, содержащей два или более конденсаторов, включенных параллельно, равна сумма всех отдельных емкостей, сложенных вместе по мере увеличения эффективной площади пластин.

Посмотрите видео ниже, чтобы увидеть работу конденсаторов при параллельном соединении:

Области применения

При параллельном соединении нескольких конденсаторов в цепи может храниться больше энергии, поскольку общая или эквивалентная емкость представляет собой сумму индивидуальных емкостей всех конденсаторов. конденсаторы. Ниже приведены области применения этого эффекта емкости:

Подробнее: Цветовой код конденсатора

Источники питания постоянного тока:

Источники питания постоянного тока часто используются для правильной фильтрации выходного сигнала и устранения пульсаций переменного тока. В этом методе есть возможность использовать конденсаторы меньшего размера, которые имеют лучшие характеристики пульсаций, получая при этом более высокие значения емкости.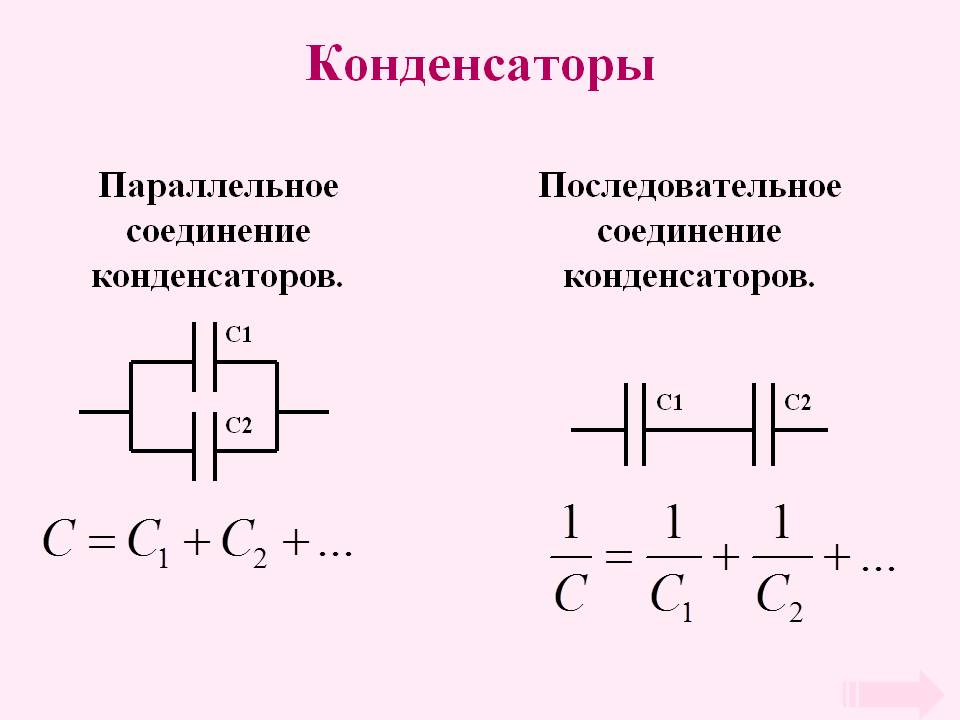

Более высокие значения емкости:

В некоторых приложениях требуются значения емкости, которые намного выше, чем у имеющихся в продаже конденсаторов, в таких ситуациях используются конденсаторные батареи. Одним из хороших примеров является использование батареи конденсаторов для коррекции коэффициента мощности с индуктивными нагрузками. Кроме того, эти банки могут использоваться в приложениях для хранения энергии, таких как автомобильная промышленность, KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи и гибридные автомобили.

Импульсная нагрузка:

Батареи конденсаторов предназначены для достижения очень высоких значений емкости. Так, соединив параллельно несколько суперконденсаторов, можно получить емкости в несколько десятков килофарад. Между тем, ультраконденсаторы способны достигать значений емкости более 2000 фарад.

Конструктивные ограничения:

При параллельном соединении конденсаторов следует знать, что максимальное номинальное напряжение при параллельном соединении конденсаторов равно наименьшему номинальному напряжению всех конденсаторов, используемых в системе.