Параллельное соединение сопротивлений расчет. Параллельное соединение резисторов: расчет, формулы и примеры — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать общее сопротивление при параллельном соединении резисторов. Какие формулы используются для вычислений. Какие особенности имеет параллельное подключение резисторов. На что следует обратить внимание при расчетах.

Содержание

Что такое параллельное соединение резисторов

Параллельное соединение резисторов — это способ подключения, при котором все резисторы подсоединены к одной паре узлов электрической цепи. При этом напряжение на всех резисторах одинаково, а общий ток разветвляется между ними.

Основные особенности параллельного соединения:

Напряжение на всех резисторах одинаково и равно напряжению источника
Общий ток разветвляется между резисторами
Общее сопротивление всегда меньше сопротивления любого из параллельно соединенных резисторов

Формулы для расчета параллельного соединения

Для расчета общего сопротивления при параллельном соединении используются следующие формулы:

1. Общая формула для n резисторов:

1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn

где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных резисторов.

2. Формула для двух параллельных резисторов:

R = (R1 * R2) / (R1 + R2)

3. Формула для n одинаковых параллельных резисторов:

R = R1 / n

где R1 — сопротивление одного резистора, n — количество резисторов.

Пример расчета параллельного соединения

Рассмотрим пример расчета общего сопротивления для трех параллельно соединенных резисторов:

R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом

Используем общую формулу:

1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183

R = 1 / 0.183 = 5.46 Ом

Таким образом, общее сопротивление трех параллельно соединенных резисторов составляет 5.46 Ом.

Особенности параллельного соединения резисторов

При параллельном соединении резисторов следует учитывать следующие особенности:

Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи

Чем больше параллельно соединенных резисторов, тем меньше общее сопротивление
Параллельное соединение позволяет увеличить максимальную мощность рассеивания
При выходе из строя одного резистора, остальные продолжают работать

Применение параллельного соединения резисторов

Параллельное соединение резисторов применяется в следующих случаях:

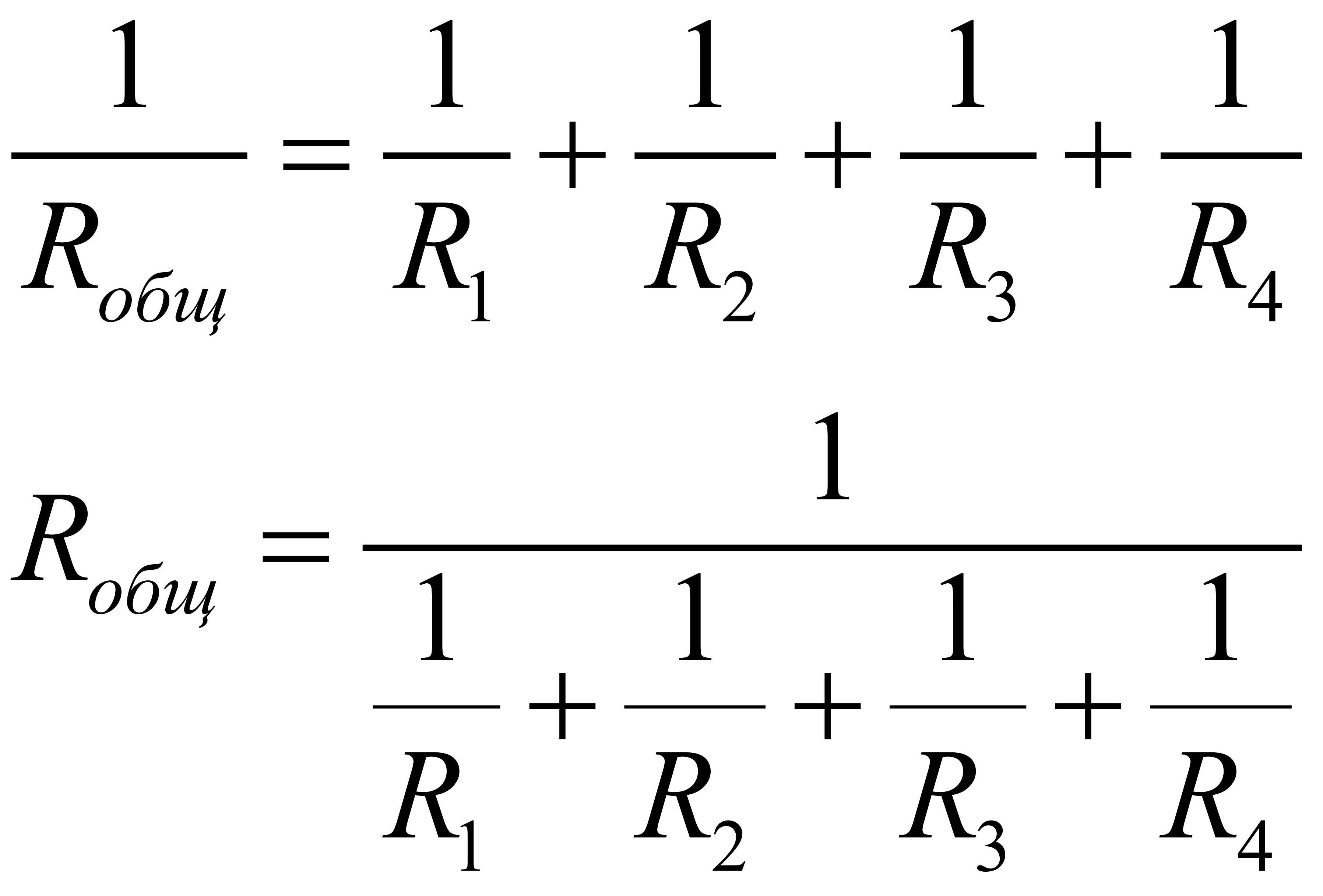
Для получения нестандартного номинала сопротивления
Для увеличения мощности рассеивания
В делителях тока
Для создания шунтов в измерительных приборах
В цепях с параллельными нагрузками

На что обратить внимание при расчетах

При расчете параллельного соединения резисторов важно учитывать следующие моменты:

Правильно определить схему соединения резисторов
Использовать корректную формулу в зависимости от количества резисторов
Учитывать единицы измерения (Ом, кОм, МОм)
Проверять полученный результат на корректность
При большом количестве резисторов использовать калькулятор

Онлайн-калькуляторы для расчета

Для упрощения расчетов параллельного соединения резисторов можно воспользоваться онлайн-калькуляторами. Они позволяют быстро вычислить общее сопротивление при любом количестве параллельно соединенных резисторов.

Преимущества использования калькуляторов:

Экономия времени на расчетах
Исключение ошибок при вычислениях
Возможность быстро просчитать разные варианты
Удобный интерфейс ввода данных

Сравнение с последовательным соединением

В отличие от параллельного, при последовательном соединении резисторов:

Общее сопротивление равно сумме сопротивлений всех резисторов
Ток через все резисторы одинаковый
Напряжение распределяется между резисторами

Общее сопротивление всегда больше сопротивления любого из резисторов

Выбор типа соединения зависит от конкретной задачи и требуемых параметров цепи.

Практические примеры использования

Рассмотрим несколько практических примеров использования параллельного соединения резисторов:

Увеличение мощности нагрузки. Например, для создания мощного нагревательного элемента несколько резисторов соединяются параллельно.
Получение нестандартного номинала. Если нужно получить сопротивление 6.8 кОм, можно параллельно соединить резисторы 10 кОм и 20 кОм.
Создание шунта для амперметра. Параллельное включение резистора позволяет расширить диапазон измерения тока.
Светодиодное освещение. Светодиоды часто соединяются параллельно для увеличения яркости.

Заключение

Параллельное соединение резисторов — важный способ построения электрических цепей. Правильный расчет общего сопротивления при таком соединении позволяет получить нужные параметры схемы. Важно учитывать особенности параллельного соединения и использовать соответствующие формулы для вычислений.

Основные моменты, которые следует запомнить:

Общее сопротивление всегда меньше сопротивления любого из резисторов
Напряжение на всех резисторах одинаково
Ток разветвляется между резисторами
Для расчетов используются специальные формулы
При сложных схемах удобно пользоваться онлайн-калькуляторами

Понимание принципов параллельного соединения резисторов необходимо для грамотного проектирования и анализа электрических цепей.

Смешанное соединение резисторов. Расчет смешанного соединения

26 Ноя 2018г | Раздел: Радио и Электрика начинающим

Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.

В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.

Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.

И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.

Расчет смешанного соединения резисторов.

Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.

Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.

Разберем схему смешанного соединения из семи резисторов:

Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:

Вычисляем их общее сопротивление используя формулу параллельного соединения:

Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.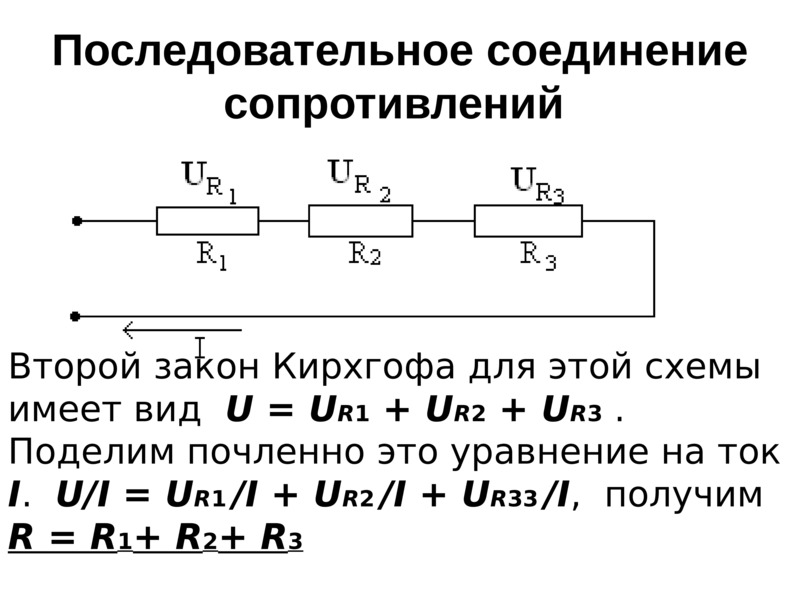

Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:

Вычисляем их общее сопротивление используя формулу

последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):

Схема уменьшилась еще на один элемент и приняла вид:

Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:

Вычисляем их общее сопротивление:

Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.

Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:

Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.

Удачи!

Поделиться с друзьями:

Еще интересно почитать:

Последовательное и параллельное соединение

Вывод формул для определения общего сопротивления. Практические примеры последовательного, параллельного и смешанного соединения резисторов.

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

С правого края – правый.
С левого края – левый.

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов.

При параллельном соединении напряжения на проводниках равны:

U_1 = U_2 = U

А для токов справедливо следующее выражение:

I = I_1 + I_2

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

I_1 = frac{U_1}{R_1} = frac{U}{R_1}

I_2 = frac{U_2}{R_2} = frac{U}{R_2}

Подставим эти выражения в формулу общего тока:

I = frac{U}{R_1} + frac{U}{R_2} = Umedspace (frac{1}{R1} + frac{1}{R2})

А по закону Ома ток:

I = frac{U}{R_0}

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2}

Данную формулу можно записать и несколько иначе:

R_0 = frac{R_1R_2}{R_1 + R_2}

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2} + frac{1}{R_3} + frac{1}{R_4} + frac{1}{R_5} + frac{1}{R_6}

Отличие параллельного и последовательного соединения

Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым. Однако, при одном и том же напряжении, сила тока в контурах будет разной. Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.

В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение. Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.

Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.

Примеры использования[править | править код]

Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
Делитель напряжения
Балласт
Шунт

Типичные подключения

Любой вариант соединений можно разделить на элементарные составляющие по рассмотренной выше методике. На следующем рисунке представлены типичные подключения вместе с основными формулами для расчетов.

Последовательное, параллельное и смешанное соединения

См. также[править | править код]

Теория электрических цепей
Измерительный мост
Делитель напряжения
Делитель тока
Электрический импеданс
Закон Ома
Законы Кирхгофа

Параллельное соединение трех и более сопротивлений, вычислить общее сопротивление по формуле (1)

Ведите в ячейки сопротивления в (Омах)

Параллельное соединение сопротивлений	стр. 608

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

( 1 оценка, среднее 5 из 5 )

Расчет сопротивления параллельного соединения. Расчет сопротивления при параллельном соединении. Смешанное соединение проводников

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Постоянные.
Переменные.

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

Последовательное.
Параллельное.
Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную.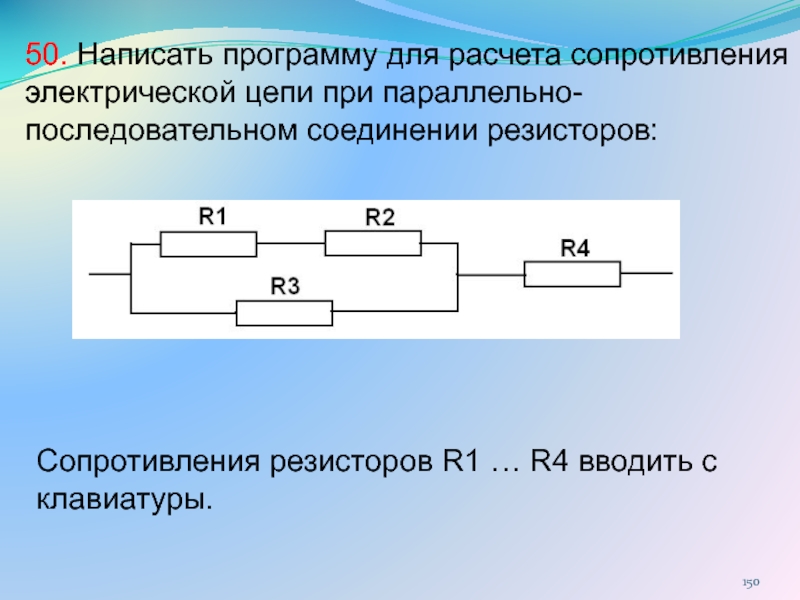 А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.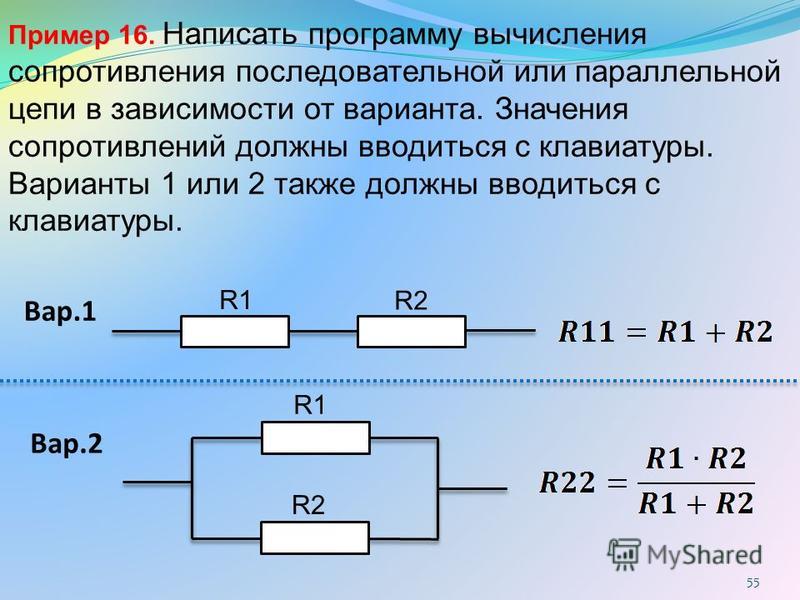

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

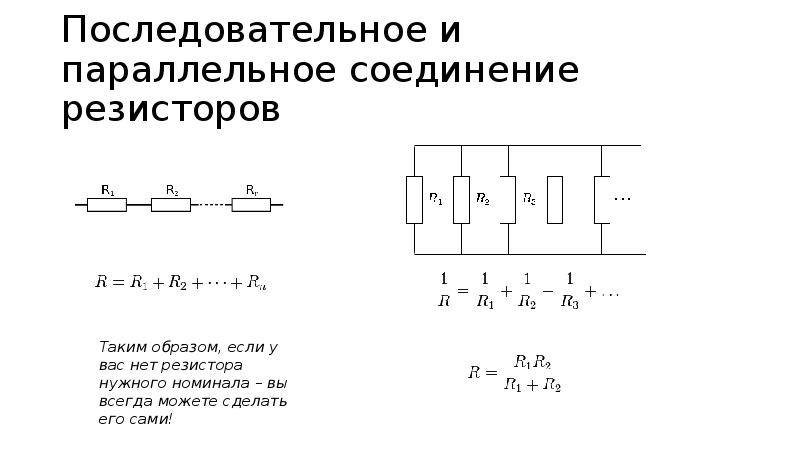
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

R(общ) – суммарное сопротивление;
R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

R(общ) – суммарное значение сопротивления;
R – номинал резистора, подсоединенного по параллельной схеме;
n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчета

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Заключение

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I — ток, S — сечение.

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Расчет смешанного соединения резисторов

Расчет смешанного соединения резисторов.

Разберем схему смешанного соединения из семи резисторов:

Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:

Вычисляем их общее сопротивление используя формулу параллельного соединения:

Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):

Схема уменьшилась еще на один элемент и приняла вид:

Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:

Вычисляем их общее сопротивление:

Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!

В Московском государственном университете имени Ломоносова осуществляется проект по созданию демонстраторов 50-кубитных квантовых компьютеров к 2021 году. Основой для них послужат нейтральные атомы и интегральные оптические схемы. Над чем сейчас работают ученые?

В начале этого года по данной программе был успешно выполнен контрольный эксперимент по созданию ловушек для массивов нейтральных холодных атомов. Он проводился на базе лаборатории квантовых оптических технологий физического факультета МГУ. В будущем квантовом компьютере в этих ловушках будут фиксироваться атомы, находящиеся в состоянии хаотического движения. В квантовых компьютерах такие атомы являются носителями информации.
Стоит заметить, что квантовые компьютеры в отличие от классических вычислительных машин оперируют не битами, а кубитами, которые могут находится не только в состояниях «1» и «0», но и их суперпозиции. При разработке квантовых вычислительных устройств ученые стараются ввести кубиты в состояние квантовой запутанности. Суть явления заключается в том, что изменение одного кубита всегда влияет на состояние связанных с ним соседей. Благодаря этому квантовые компьютеры потенциально способны демонстрировать высокую производительность в вычислениях.
Важной вехой для квантовых технологий считается достижение так называемого квантового превосходства (то есть способности производить вычисления быстрее классических систем). Главной проблемой на текущем этапе развития квантовых технологий является возникновение в процессе работы большого количество ошибок, нуждающихся в коррекции, – сообщают российские исследователи.

Электрические цепи, в которых одна часть сопротивлений соединена последовательно, а другая параллельно, называются цепями со смешанным соединением сопротивлений.

Общих расчетных формул для таких цепей нет, так как число их разновидностей не ограничено.

Чаще всего расчет подобных схем начинается с определения эквивалентного сопротивления всей цепи, а затем определяются величины токов и падение напряжения на отдельных участках.

Для определения эквивалентного сопротивления цепи со смешанным соединением потребителей, питающихся от одного источника тока, необходимо прежде всего разбить эту цепь на отдельные участки, состоящие из последовательного и параллельно соединенных сопротивлений. Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.

Рассмотрим метод решения задач на смешанное соединение сопротивлений на конкретном примере.

На рисунке представлена схема смешанного соединения сопротивлений. Ее можно разбить на три участка:

участок АВ – с двумя параллельно соединенными ветвями;

участок ВС – с последовательно соединенными сопротивлениями;

участок СD – с тремя параллельными ветвями.

Кроме того, нижняя ветвь участка АВ представляет в свою очередь цепь, состоящую из двух последовательно соединенных сопротивлений R₂ и R₃.

Центральная ветвь участка СD представляет собой смешанное соединение сопротивлений.

Расчет данной сложной цепи надо начинать с определения R_экв для нижней ветви участка АВ и центральной ветви участка СD.

Теперь мы можем упростить первоначальную схему. Она будет иметь следующий вид

Определим эквивалентные сопротивления каждого из участков:

После этих вычислений можно продолжить упрощение схемы

Полученная упрощенная схема, состоящая в данном случае из трех последовательно соединенных сопротивлений, называется по отношению к реальной эквивалентной схемой.

Определим R_экв всей цепи как сумму трех последних сопротивлений

Зная напряжение источника тока, применяя формулу закона Ома, определим ток в не разветвленном участке смешанной цепи

Определив величину тока, найдем падение напряжения на участках эквивалентной схемы АВ, ВС, CD:

Теперь можно определить токи в параллельных ветвях участков АВ и СD

Остается определить величину токов, протекающих через сопротивления R₇ и R_8. Для этого надо сначала определить падение напряжения на сопротивлениях R₇ и R_8.

Определим падение напряжения на сопротивлении R₉:

Падение напряжения на сопротивлении R_7,8 определится как разность U_CD и U:

Теперь определим величины токов, протекающих через сопротивления R₇ и R₈:

Величина тока. протекающего через сопротивления R₄ и R₅, равна I – току в неразветвленном участке цепи.

Итак, при решении задач на смешанное соединение сопротивлений необходимо, постепенно упрощая схему, определить эквивалентное сопротивление всей цепи, а затем. восстанавливая постепенно реальную схему. вычислить падение напряжения и токи в отдельных ветвях.

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

Проводники (все металлы, ионизированный газ и электролитические растворы).
Полупроводники (Si, Ge, GaAs, InP и InSb).
Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

Температура окружающей среды и материала.
Электрические величины.
Геометрические свойства вещества.
Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
Визуально определить форму материала.
Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

Номинал резистора в 16 Ом подойдет.
Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

Ток не изменяется на участке цепи.
Общее напряжение равно сумме падений напряжений на каждом резисторе.
Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

I = I1 = I2 = 0,5 (А).
Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Напряжение при параллельном соединении двух резисторов. Формула для расчета параллельного соединения сопротивлений. Мощность при паралл ельном соединение

Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление Rобщ

o Цепь разбивают на участки с только пареллельным или только последовательным соединением. o Вычисляют общее сопротивление для каждого отдельного участка.

o Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

o Если резисторы соединяются последоватеьно — складывать.

o Если резисторы соединяются параллельно — использовать условное обозначение «||». o Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1.

Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)

Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :

G эк = G 1 + G 2 +G 3 (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Эквивалентные преобразования электрических схем.

Определение последовательного соединения элементов

Последовательное соединение элементов электрической цепи — это такое соединение, когда вывод одного элемента подключен к выводу другого элемента. В этом месте подключения нет узлов. Следующий элемент так же подключен к выводу другого элемента и т.д…

На рисунке ниже показано последовательное подключение четырех сопротивлений.

Формулы для расчета эквивалентного сопротивления при последовательном подключении элементов

При последовательном подключении сопротивлений их эквивалентное сопротивление равно сумме сопротивлений.

R экв =ΣR i =R1 + R2 + R3 +…+Rn

При последовательном соединении индуктивностей их эквивалентное сопротивление равно сумме индуктивностей (без учета взаимной индуктивности).

L экв =ΣL i =L1 + L2 + L3 +…+Ln

При последовательном подключении емкостей обратная величина от эквивалентной емкости равна сумме обратных величин емкостей.

1/С экв =Σ(1/C i)=1/С1+1/С2+1/С3+…+1/Cn

Свойства последовательного соединения элементов

При последовательном подключении элементов через них протекает одинаковый ток.

Согласно закону Ома и второму закону Кирхгофа экивалентное (суммарное) напряжение на участке последовательно соединенных сопротивлений равно сумме напряжений на каждом элементе. U общ = U1+U2+U3+U4 = I·(R1+R2+R3+R4). На данном принципе построены простейшие делители напряжения.

Определение параллельного соединения

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

Формула для расчета параллельного соединения сопротивлений

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

Смешанное соединение . Это сочетание последовательного и параллельного соединения элементов.

Эквивалентное сопротивление для последовательно-параллельного соединения элементов:

R экв = R 1 +R 2 R 3 / (R 2 +R 3)

Сложное соединение . Это соединение, имеющее три и более узлов. В сложных цепях встречаются соединения сопротивлений в виде звезды и треугольника.

Формулы преобразования треугольника сопротивлений в эквивалентную трехлучевую звезду имеют вид:

Формулы обратного преобразования ветвей трехлучевой звезды в эквивалентный треугольник:

РЕЖИМЫ РАБОТЫ ИСТОЧНИКОВ ПИТАНИЯ

Различают четыре режима работы источников питания. Е

Режим холостого хода . В режиме холостого хода концы источника разомкнуты: (R х = ∞).

Этот режим используют для измерения ЭДС источника. Параметры режима холостого хода: I х = 0; R х = ∞; U х = E; (U х =E-Ir; r= 0; U х = E)

Режим короткого замыкания . В режиме короткого замыкания концы источника соединены накоротко: (R к = 0).

Номинальный режим . Это режим работы источника питания при номинальных значениях тока и напряжения. Номинальные значения тока и напряжения приводятся в паспорте источника питания.

Согласованный режим . Это режим работы источника питания с максимальной мощностью Р=Р mах. Такое возможно при условии, когда R вн =R вш. Формула мощности для согласованного режима:

P max = I 2 R = E 2 / 4R.

Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.

Определения

Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:

Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.

На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.

Использование параллельного и последовательного соединения проводников

Термины, применяемые к электрическим цепям

Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.

Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.

Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:

Внешняя часть цепи, где заряды движутся, увлекаемые полем.
Внутренняя часть цепи, где заряды движутся против напряженности.

Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:

Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.

Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.

При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.

Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников

Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:

Посчитать сопротивления элементов при последовательном и параллельном соединении

Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:

При последовательном включении суммируются сопротивления, при параллельном — проводимости:
1. Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
2. Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
3. Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.

Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.

У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.

Пример решения уравнений Кирхгофа

Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:

Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.

Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.

Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).

Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.

Рис 1

Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:

U = U1 + U2 + U3

где

U1 = IR1 U2 = IR2 и U3 = IR3

или

IR = IR1 + IR2 + IR3

Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .

Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3

Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.

Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).

Рис. 2. Пример последовательного соединения трех сопротивлений

Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.

Найдем ток в цепи : 60 / 80 = 0 ,75 А

Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.

Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.

Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.

Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.

Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.

Рис 3. Параллельное соединение сопротивлений

Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.

Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.

Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.

Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).

Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).

Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим

Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .

Рассмотрим теперь, каково будет соотношение между токами в ветвях.

Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления.

Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.

Это дает нам право написать, что U = U1 = U2 ,

где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .

Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U1 = U2, то и I1R1 = I2R2 .

Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.

Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.

Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.

Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:

I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА

I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА

Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА

Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.

Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).

Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.

Рис. 4

Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.

Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.

Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.

Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.

По закону разветвленной цепи: I = I1 + I2

Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2

Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2

Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )

Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2

Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.

На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.

Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.

Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.

Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?

Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.

Чтобы убедиться в этом, рассмотрим следующий пример.

Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).

Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями

Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60

Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.

Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.

Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.

Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А

Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.

Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.

I = U / R = 12 / 6 = 2 А

Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.

В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.

На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.

Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.

Какие есть способы соединения приемников электрической энергии

Приемник электрической энергии — устройство, в котором происходит преобразование электрической энергии в другой вид энергии для ее использования.

При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.

В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.

Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.

Последовательное соединение

Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.

Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.

Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:

Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.

Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.

Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.

Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.

В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.

К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.

Параллельное соединение

Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.

Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.

Здесь I – ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.

Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:

Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.

Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.

Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.

Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.

Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.

В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.

Сравнение последовательных и параллельных цепей

Смешанное соединение

Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:

Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.

Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.

Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда электролитических конденсаторов в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.

Ранее ЭлектроВести писали, что львовянка Оксана Денис подключила свою квартиру к солнечным панелям и ветроэнергетическим установкам.

По материалам: electrik.info.

Расчет параллельных резисторов. Соединение резисторов

Расчет сопротивления

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

R(общ)=R1*R2/R1+R2.

R(общ) – суммарное сопротивление;
R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчета

R(общ) – суммарное значение сопротивления;
R – номинал резистора, подсоединенного по параллельной схеме;
n – число подключенных узлов.

Пример расчета

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Важные нюансы

Заключение

В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного подключения сопротивлений. Параллельное соединение одинаковых сопротивлений — это наглядный пример подключения люстры с n-ым количеством ламп и с одинаковым сопротивлением для каждой лампы \рис.1\.

Если допустим в люстре состоящей из нескольких ламп \с одинаковым сопротивлением\ перегорела одна лампа и была произведена замена на лампочку другой мощности, — в этом случае, подключение люстры будет выглядеть как параллельное подключение с разным сопротивлением.

Какие еще можно привести примеры из практики — при параллельном подключении сопротивлений? Допустим, Вы подключили в своей квартире через удлинитель три бытовых электроприбора:

электроплиту;
стиральную машину;
телевизор.

Характер такого подключения примет значение как для параллельного подключения сопротивлений , разных по величине. То-есть, для каждого электроприбора, сопротивление имеет свое значение.

Расчет сопротивления при параллельном соединении

Как уже упоминалось, расчеты сопротивлений при параллельном соединении проводятся:

с одинаковым сопротивлением;
с разным сопротивлением,

а также, проводятся расчеты сопротивлений для смешанных соединений резисторов, при последовательном и параллельном соединениях \для одной цепи\. Расчет сопротивления для смешанных соединений резисторов, больше подходит к различным блок-схемам:

аудиотехники;
видеотехники.

К этой теме, расчеты для смешанных соединений, отношения не имеют.

Параллельное соединение одинаковых сопротивлений

Представим параллельное подключение, к примеру, трех сопротивлений \рис.2\ равных по величине, где R1=R2=R3=36 Ом \сопротивление лампы накаливания мощностью на 95 Вт\. К двум узловым точкам \А, В\ подключено напряжение 220 В. Нужно вычислить общее сопротивление всех трех ламп.

Для расчета общего сопротивления \Rобщ.\, нам необходимо 36 Ом разделить на количество сопротивлений. Решение простое, Rобщ.=12 Ом. То-есть, формула для расчета подобных вычислений выглядит как:

Rобщ. = R /n

Параллельное соединение разных сопротивлений

Допустим, возьмем выборочно три резистора, сопротивлением:

R1=20 Ом;
R2=40 Ом;
R3=10 Ом.

Нужно определить общее сопротивление резисторов при параллельном соединении. Для данного расчета воспользуемся формулой:

1/Rобщ.=1/R1+1/R2+1/R3.

Подставляем значения в формулу:

1/Rобщ. = 1/20+1/40+1/10=7/40=0,18

получаем: Rобщ.=1/0,18=5,5 Ом.

Сопротивление проводника

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

и нагрев проводника

δ = I/S, I — ток, S — сечение.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Виды проводников

Расчёт проводов на нагрев

Расчёт проводников на потерю напряжения

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Виды соединений

Постоянные.
Переменные.

Последовательное.
Параллельное.
Смешанное.

Последовательное соединение проводников

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Смешанное соединение проводников

Калькулятор параллельного и последовательного сопротивления

Параллельный и последовательный

Сопротивление

Параллельное сопротивление	XXXX Ом
Сопротивление серии	XXXX Ом

Рассчитать Прозрачный
⚠️ Сообщить о проблеме

Сопротивление — это электрический элемент, который не позволяет легко протекать через него току. В нашей повседневной жизни сопротивление используется во многих электрических цепях и устройствах.Внутри этих электрических устройств сопротивления расположены в различных конфигурациях.

Вы также должны были наблюдать, выполняя соединения на макетной плате в своей лаборатории электроники, как резисторы подключаются по-разному. В зависимости от способа соединения их концов различают два основных типа цепей сопротивления:

Параллельные схемы

По мере продвижения в этом посте мы поймем работу, сравнение, вычисления и различия между этими последовательными цепями и параллельными цепями.

Цепи серии

Два или более резистора считаются подключенными последовательно, если ток, протекающий через них, одинаков. Другими словами, ток, исходящий от источника, или общий ток не будут разветвляться по какому-либо другому пути, а будут двигаться только по одному прямому пути.

Когда сопротивления соединены последовательно, общее сопротивление цепи является суммой всех сопротивлений цепи.

На следующей принципиальной схеме показаны три последовательно соединенных сопротивления R ₁, R ₂ и R ₃.Чистое сопротивление этой последовательной цепи составляет _{R нетто} = ₁ R ₂ + ₃ R.

Как правило, если «n» сопротивлений соединены последовательно, общее сопротивление составляет R _{, нетто} = R ₁ + R ₂ +…. Р _н.

Например, если в цепи есть три последовательно подключенных резистора по 10 Ом, и источник напряжения 30 В, то ток, протекающий в цепи и через каждый из них, определяется выражением I = V / R = 10/30 = 0. .33 А.

Параллельные цепи

Два или более резистора считаются подключенными параллельно, если они соединены головками на одной стороне и выводами на другой стороне цепи. В параллельной цепи ток, исходящий от источника, или общий ток будет ветвиться в месте соединения, где головки сопротивлений встречаются, а затем течет в разном количестве в каждом резисторе, а затем снова объединяется в точке встречи хвостов резисторы и течет к источнику.

При параллельном соединении сопротивлений сопротивление цепи, обратное сопротивлению цепи, является суммой значений, обратных сопротивлению всех сопротивлений цепи.

На следующей принципиальной схеме показаны три параллельно включенных сопротивления R ₁, R ₂ и R ₃. Общее сопротивление этой параллельной цепи составляет 1 / R _net = 1 / R = 1 / R ₁ + 1 / R ₂ + 1 / R ₃.

Как правило, если «n» сопротивлений подключены параллельно, общее сопротивление составляет:

1 / R _net = 1 / R = 1 / R + 1 / R ₂ + 1 / R ₃ +….+ 1 / R _n

Например, если три резистора 4 Ом, 8 Ом и 8 Ом подключены параллельно в цепи с питанием 10 В, то общее сопротивление цепи определяется как: 1 / Rnet = 1/4 + 1/8 + 1/8 = ½ или Rnet = 2 Ом

Тогда ток, протекающий по цепи, равен V / I = 10/2 = 5 ампер.

Если вы хотите рассчитать ток в каждом резисторе, вы можете использовать закон Ома:

Ток через резистор 4 Ом I ₁ = 10/4 = 2.5 А

Ток через резистор 8 Ом I ₁ = 10/8 = 1,25 A

Ток через резистор 4 Ом I ₁ = 10/8 = 1,25 A

Обратите внимание: если вы сложите отдельные токи через каждый резистор, вы получите общий ток, протекающий в цепи.

Комбинация последовательных и параллельных резисторов

Если вы найдете схему, в которой резисторы включены последовательно и параллельно, то вам нужно решить комбинацию резисторов шаг за шагом, учитывая, находятся ли они последовательно или параллельно с соседними, а затем прийти к окончательному сопротивлению цепи.

Баллы о последовательном и параллельном соединении резисторов:

Эффективное сопротивление последовательной цепи всегда больше, чем у каждого резистора в цепи.
Эффективное сопротивление параллельной цепи всегда меньше, чем сопротивление каждого резистора в цепи.
Ток в каждом из последовательно соединенных резисторов одинаков, а напряжение на каждом параллельном резисторе одинаково.
В цепи последовательных резисторов, если одно сопротивление повреждается, вся цепь разрывается и ведет себя как разомкнутая цепь.
В схеме параллельных резисторов, если один резистор поврежден, ток продолжает течь в других резисторах, и схема будет продолжать работать, но с другим значением сопротивления цепи.

Как вам помогает калькулятор последовательного и параллельного сопротивления CalculatorHut?

В нашей повседневной жизни мы сталкиваемся с последовательным и параллельным сочетанием резисторов во многих местах. Например, для цепей освещения мы используем параллельное соединение, а для приборов, которые работают непосредственно от сети, дается последовательное соединение.

CalculatorHut, универсальный центр научных и ненаучных онлайн-калькуляторов, предлагает бесплатный онлайн-калькулятор последовательного и параллельного сопротивления, который решит все ваши потребности в онлайн-калькуляторе бесплатно. Вы можете рассчитать до десяти резисторов, которые подключены последовательно или параллельно, с помощью этого удобного онлайн-калькулятора последовательного и параллельного сопротивления. Это очень удобный инструмент для студентов, который помогает им проверить правильность расчетов сопротивления.

CalculatorHut также предлагает широкий выбор из более 100 калькуляторов по различным темам — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, физические калькуляторы, химические калькуляторы, математические калькуляторы и многие другие бесплатные онлайн-калькуляторы для научных расчетов.

Наши читатели также могут получить бесплатный виджет любого калькулятора из нашего широкого спектра калькуляторов для встраивания в качестве виджетов на свои веб-сайты. Для этого они могут написать нам по адресу [адрес электронной почты]

Мы пропустили какой-нибудь бесплатный онлайн-калькулятор? Пожалуйста, дайте нам знать.Мы будем более чем счастливы удовлетворить ваши потребности в бесплатном онлайн-калькуляторе бесплатно и всегда!

Вот еще одна фантастическая новость! Вы можете бесплатно носить с собой в кармане наш широкий ассортимент онлайн-калькуляторов. Да! Бесплатное приложение CalculatorHut — ваш друг, который упрощает и упрощает любые вычисления! Удачных расчетов!

Изучение основ последовательного и параллельного сопротивления [Краткое руководство]

Привет, надеюсь, у тебя хорошая жизнь. В этом посте я поделюсь с вами своими знаниями о последовательном и параллельном сопротивлении.Я поделюсь самыми основными моментами, которым я бы хотел, чтобы кто-нибудь научил меня, когда я изучал основы электроники.

При разработке электронной схемы резистор, вероятно, является наиболее важным и часто встречающимся компонентом. Почти все портативные схемы содержат очень сложные комбинации резисторов.

Следовательно, очень полезно иметь набор правил для определения эквивалентных сопротивлений для некоторых общих и общих схем резистивных элементов. И оказалось, что такие простые правила представляют собой комбинации параллельных серий.

Прежде всего, позвольте мне прояснить основную путаницу. Последовательно-параллельные комбинации аналогичны последовательным и параллельным цепям, но состоят только из резисторных элементов. Фактически, большинство пунктов, которые вы здесь изучите, также применимы к любой последовательной и параллельной схеме.

Таким образом, последовательные и параллельные цепи являются общими терминами, а последовательно-параллельное сопротивление — это конкретные цепи, в которых используются только резисторы.

Сопротивление серии

Резисторы любого размера подключены таким образом, чтобы через каждый из них протекал одинаковый ток.Эквивалентное сопротивление таких подключенных резисторов известно как последовательное сопротивление.

В последовательно соединенных сопротивлениях / резисторах есть только один путь для прохождения электрического тока. Все резисторы соединены в ряд как звенья цепи. При обрыве одного из звеньев цепи вся цепь становится бесполезной. То же самое и с последовательными резисторами, когда один резистор перегорает, вся цепь перестает работать.

Рис. 1 Блок-схема последовательного сопротивления (Программное обеспечение: NI Multisim Educational Edition)

Ток остается неизменным в любом узле в цепи последовательного сопротивления.Практически это можно доказать, применив мультиметр и схему на макетной плате. Или просто смоделировав схему (рис. 1) в любом программном обеспечении для моделирования, как я сделал это в NI Multisim.

Как найти полное последовательное сопротивление?

Все резисторы, включенные последовательно, добавлены для получения эквивалентного последовательного сопротивления. Общая формула приведена ниже:

Чтобы найти эквивалентное последовательное сопротивление, удалите из цепи любой источник напряжения, а затем просуммируйте значения каждого резистора, присутствующего в цепи.Возьмем, к примеру, приведенную выше схему (рисунок: 1).

Сопротивление серии

может быть подключено к источнику тока. Те же шаги выполняются и для текущего источника. Удалите источник тока и просуммируйте значения резисторов. Пример приведен ниже:

Математический расчет:

Схема может иметь любую форму. Но резисторы нужно подключать как звенья цепи. Следующая схема является последовательно соединенной.

Вы можете это доказать?

Можете ли вы найти эквивалентное последовательное сопротивление? (Ответ: 378КОм)

Следует помнить, что последовательно соединенные резисторы имеют только один общий узел друг с другом.Это очень важный момент, который нужно понять. Позже в этом посте я поделюсь примером схемы с комбинацией последовательной и параллельной комбинаций.

Тогда это будет немного запутать. Так что обратите на это пристальное внимание, потому что этот момент поможет нам идентифицировать последовательную комбинацию резисторов в сложной цепи.

Параллельное сопротивление

Резисторы любого размера подключены таким образом, чтобы на каждом резисторе было одинаковое напряжение.Эквивалентное сопротивление таких подключенных резисторов известно как параллельное сопротивление.

Или параллельное сопротивление можно определить как резисторы , подключенные параллельно, если узлы на обоих концах резисторов одинаковы. В параллельно подключенных резисторах (параллельное сопротивление) есть разные пути для прохождения электрического тока. Величина протекающего тока зависит от номиналов резисторов.

Параллельно подключенные резисторы

При параллельном подключении эквивалентное сопротивление всегда меньше, чем у наименьшего отдельного резистора.Например, эквивалентное сопротивление вышеупомянутой цепи всегда будет меньше 1 кОм. И напряжение на каждом резисторе составляет 12 В, поскольку все резисторы подключены к тем же узлам, что и резисторы 12 В.

Я говорил о резисторах , включенных параллельно, если узлы на обоих концах резисторов одинаковые. , позвольте мне показать общие узлы в приведенной выше схеме.

Как найти полное параллельное сопротивление?

В параллельно соединенных резисторах эквивалентное сопротивление равно сумме обратных значений каждого резистора.Общая формула эквивалентного параллельного сопротивления приведена ниже:

Найдем значение полного сопротивления для указанной выше цепи.

Удалите источник напряжения и затем введите значения резисторов в приведенную выше общую формулу.

Ответ — меньше самого маленького отдельного резистора.

Приведем еще один пример:

Подскажите, как вообще эта схема параллельна?

Конечно, это параллельно включенная цепь.

Это соответствует критерию, резисторы включены параллельно, если узлы на обоих концах резисторов одинаковы.

Форма смутила нас, правда? Но все же это резистивная цепь, включенная параллельно. Дело в том, что я говорю. Неважно, какую форму может иметь схема, вы должны знать базовую концепцию того, как идентифицировать параллельные резисторы в сложной схеме.

Мы можем перерисовать приведенную выше схему в чистом виде, как показано ниже:

Быстрый трюк, чтобы найти эквивалентное параллельное сопротивление

Когда все параллельно подключенные резисторы имеют одинаковые значения, эквивалентное параллельное сопротивление можно найти, просто разделив одно и то же значение на общее количество резисторов.Общая формула может быть записана так:

Давайте применим этот быстрый трюк на вышеупомянутой схеме.

Было бы хорошо, если бы вы потратили некоторое время, чтобы доказать это, используя общую формулу для параллельного сопротивления. Будет интересно увидеть, что оба метода дадут одинаковый ответ.

Различия между последовательным и параллельным сопротивлением

Я не знаю, сколько всего различий между указанными сопротивлениями. Ниже приведены различия, которые я узнал со временем.

1. При последовательном сопротивлении один и тот же ток протекает через каждый резистор, в то время как при параллельном сопротивлении каждый резистор имеет одинаковое напряжение на нем.

2. В последовательном сопротивлении полное напряжение равно падению напряжения на каждом резисторе. См. Следующую схему:

Общее приложенное напряжение составляет 12 В (аккумуляторный источник), что означает, что общая сумма напряжений на каждом резисторе должна быть равна 12 В.

Попробуем решить указанную выше схему вручную.

Резисторы включены последовательно. Общее последовательное эквивалентное сопротивление можно найти, используя общую формулу для последовательного сопротивления.

Используя закон Ома, полный ток можно определить следующим образом:

Мы рассчитали полный ток. Чтобы найти падение напряжения на каждом резисторе, умножьте общий ток на номинал резистора (закон Ома).

Мы получили те же значения, которые были получены при моделировании Multisim. Суммирование всех рассчитанных напряжений закончится на 12 В.Вы можете доказать это, добавив их самостоятельно с помощью калькулятора.

3. При параллельном сопротивлении полный ток равен сумме токов, протекающих через каждый резистор.

Общий ток (22,0 мА) равен сумме токов, протекающих от каждого резистора. Вы можете доказать это, сложив их вместе с помощью калькулятора. Не путайте с отрицательным знаком. Игнорируй это.

4. В последовательном сопротивлении, если один резистор не работает должным образом, остальная часть цепи также не работает.Параллельно выход из строя одного резистора не влияет на всю схему.

5. Падение напряжения в последовательном сопротивлении пропорционально размеру резистора. В то время как при параллельном подключении количество тока, протекающего в каждом резисторе, зависит от размера резистора. Увеличение размера резистора увеличивает падение напряжения, а также ток.

Зачем вообще нужны эти комбинации?

Есть очень важные применения последовательных и параллельных комбинаций.Прямо сейчас я делюсь тем, что знаю, и буду обновлять по мере того, как узнаю об этом больше.

Я работал над схемой, и мне понадобился резистор 2 кОм, которого у меня не было в то время. Я много искал в своей маленькой лаборатории, но все тщетно. Затем я собрал два резистора 1 кОм, чтобы получился резистор 2 кОм. Я сделал это, поставив последовательно два резистора 1кОм.

Я думаю, вы поняли. Последовательное и параллельное соединение могут быть очень полезны, если у вас нет с собой резистора точного номинала. Это также может быть полезно, если вы разрабатываете схему и вам нужен резистор, которого нет на ближайшем рынке.Вы можете получить желаемое значение резистора, играя с последовательными и параллельными комбинациями резисторов.

Эти комбинации также находят применение в конструкции вольтметра и амперметра соответственно.

Последовательное сопротивление используется в качестве ограничителя тока в цепях. Его можно использовать как делитель напряжения для светодиодной схемы. Возможно, вы видели, что у каждого светодиода есть резистор, включенный последовательно. Задача резистора — ограничить ток, протекающий через светодиод.

Пример

Давайте рассмотрим пример, чтобы еще больше прояснить нашу концепцию последовательного параллельного соединения.Схема в примере имеет смешанные параллельные и последовательные комбинации. Поэтому, пожалуйста, обращайте пристальное внимание и старайтесь решать на каждом этапе.

Я рекомендую захватить с собой блокнот, калькулятор и хорошую ручку. И давай попробуем решить со мной.

Сводка

Резисторы подключены таким образом, что через каждый резистор протекает одинаковый ток, тогда эквивалентное сопротивление резисторов называется последовательным сопротивлением.
Последовательный ток остается неизменным независимо от размеров резисторов.А это возможно только тогда, когда резисторы соединены как звенья цепи.
В параллельно соединенных резисторах напряжение на каждом резисторе остается неизменным независимо от номинала каждого резистора.

Надеюсь, этот пост был вам полезен. Вот что я знаю о последовательном и параллельном сопротивлении. И я буду продолжать обновлять этот пост по мере того, как узнаю что-то новое по упомянутой теме.

Большое спасибо за чтение и хорошей жизни.

Прочие полезные сообщения

Калькулятор параллельного / последовательного резистора

| Детали с усилением

Используйте этот калькулятор для определения общего сопротивления сети.Этот калькулятор может давать результаты для последовательного, параллельного и любого их сочетания. Схема создается автоматически по мере добавления резисторов в сеть в качестве наглядного пособия.

Сложные резистивные схемы часто можно упростить до одного резистора эквивалентного номинала. В процессе упрощения используются два уравнения: резисторы в последовательном уравнении и резисторы в параллельном уравнении.

Резисторы серии

Резисторы включены последовательно, когда они соединены в одну линию.Текущий ток является общим для всех резисторов в этой цепи. Это связано с тем, что ток, протекающий через первый резистор, проходит по одному пути через каждый из следующих резисторов в цепи. Общее сопротивление должно равняться сумме номиналов каждого резистора, используемого в цепи.

$$ R _ {\ text {Equiv}} = R_1 + R_2 + R_3 + \ ldots R_n $$

Мы можем рассматривать всю эту цепочку резисторов как один резистор со значением ~ R _ {\ text {Equiv}} ~.

Параллельные резисторы

Резисторы включены параллельно, если они используют одни и те же два узла.Падение напряжения на каждом резисторе в этой конфигурации обычное. Теперь ток имеет несколько путей и может не быть одинаковым для каждого резистора. Общее сопротивление резисторов, подключенных параллельно, является суммой, обратной величине каждого используемого резистора.

$$ \ frac {1} {R _ {\ text {Equiv}}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + \ ldots \ frac { 1} {R_n} $$

Мы можем рассматривать эти параллельные резисторы как один резистор со значением ~ R _ {\ text {Equiv}} ~

Обратите внимание, что информация, представленная в этой статье, предназначена только для справочных целей.Amplified Parts не делает никаких заявлений, обещаний или гарантий относительно точности, полноты или адекватности содержания этой статьи и прямо отказывается от ответственности за ошибки или упущения со стороны автора. В отношении содержания данной статьи не дается никаких гарантий, подразумеваемых, выраженных или установленных законом, включая, помимо прочего, гарантии ненарушения прав третьих лиц, права собственности, товарной пригодности или пригодности для определенной цели. или его ссылки на другие ресурсы.

21.1 Последовательные и параллельные резисторы — College Physics

Сводка

Нарисуйте схему с резисторами, включенными параллельно и последовательно.
Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
Контраст — способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.

Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела для потока заряда называется сопротивлением . Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.

Рисунок 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.

Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, и попадает в Землю, то $ latex \ boldsymbol {R_1} $ на рисунке 1 (a) может быть сопротивлением вала отвертки, $ latex \ boldsymbol {R_2} $ сопротивление его ручки, $ latex \ boldsymbol {R_3} $ сопротивление тела человека и $ latex \ boldsymbol {R_4} $ сопротивление его обуви.

На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы стать недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением. прибор, уменьшающий рабочий ток.)

Рисунок 2. Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).

Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на Рисунке 2.

Согласно закону Ома , падение напряжения $ latex \ boldsymbol {V} $ на резисторе при протекании через него тока рассчитывается с использованием уравнения $ latex \ boldsymbol {V = IR} $, где $ latex \ boldsymbol {I} $ — ток в амперах (A), а $ latex \ boldsymbol {R} $ — сопротивление в омах $ latex \ boldsymbol {(\ Omega)} $.Другой способ представить это: $ latex \ boldsymbol {V} $ — это напряжение, необходимое для протекания тока $ latex \ boldsymbol {I} $ через сопротивление $ latex \ boldsymbol {R} $.

Таким образом, падение напряжения на $ latex \ boldsymbol {R_1} $ составляет $ latex \ boldsymbol {V_1 = IR_1} $, на $ latex \ boldsymbol {R_2} $ — $ latex \ boldsymbol {V_2 = IR_2} $, и что через $ latex \ boldsymbol {R_3} $ стоит $ latex \ boldsymbol {V_3 = IR_3} $. Сумма этих напряжений равна выходному напряжению источника; то есть

$ латекс \ boldsymbol {V = V_1 + V_2 + V_3}.$

Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия описывается уравнением $ latex \ boldsymbol {PE = qV} $, где $ latex \ boldsymbol {q} $ — электрический заряд, а $ latex \ boldsymbol {V} $ — напряжение. Таким образом, энергия, подводимая источником, равна $ latex \ boldsymbol {qV} $, а энергия, рассеиваемая резисторами, равна

$ латекс \ boldsymbol {qV_1 + qV_2 + qV_3}. $

Connections: законы сохранения

Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые гласят, что общий заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, $ latex \ boldsymbol {qV = qV_1 + qV_2 + qV_3} $. Плата $ latex \ boldsymbol {q} $ отменяется, в результате чего получается $ latex \ boldsymbol {V = V_1 + V_2 + V_3} $, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)

Теперь подстановка значений отдельных напряжений дает

$ латекс \ boldsymbol {V = IR_1 + IR_2 + IR_3 = I (R_1 + R_2 + R_3)}. $

Обратите внимание, что для эквивалентного сопротивления одиночной серии $ latex \ boldsymbol {R_s} $ мы имеем

$ латекс \ boldsymbol {V = IR_s}. $

Это означает, что полное или эквивалентное последовательное сопротивление $ latex \ boldsymbol {R_s} $ трех резисторов равно

$ латекс \ boldsymbol {R_s = R_1 + R_2 + R_3} $.

Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление $ latex \ boldsymbol {R_s} $ последовательного соединения составляет

$ латекс \ boldsymbol {R_s = R_1 + R_2 + R_3 + \ dots} $

как предлагается.Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.

Пример 1: Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

Предположим, что выходное напряжение батареи на рисунке 2 равно $ latex \ boldsymbol {12.0 \; \ textbf {V}} $, а сопротивление равно $ latex \ boldsymbol {R_1 = 1.00 \; \ Omega} $, $ latex \ boldsymbol {R_2 = 6.00 \; \ Omega} $ и $ latex \ boldsymbol {R_3 = 13.0 \; \ Omega} $. а) Каково полное сопротивление? (б) Найдите ток. (c) Вычислите падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:

$ latex \ begin {array} {r @ {{} = {}} l} \ boldsymbol {R_s} & \ boldsymbol {R_1 + R_2 + R_3} \\ [1em] & \ boldsymbol {1.00 \; \ Omega + 6.00 \; \ Omega + 13.0 \; \ Omega} \\ [1em] & \ boldsymbol {20.0 \; \ Omega}. \ end {array}

долларов

Стратегия и решение для (b)

Ток определяется по закону Ома $ latex \ boldsymbol {V = IR} $. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:

$ latex \ boldsymbol {I =} $ latex \ boldsymbol {=} $ latex \ boldsymbol {= 0.600 \; \ textbf {A}}. $

Стратегия и решение для (c)

Напряжение — или падение $ latex \ boldsymbol {IR} $ — в резисторе определяется законом Ома.Ввод значения тока и значения первого сопротивления дает

$ латекс \ boldsymbol {V_1 = IR_1 = (0,600 \; \ textbf {A}) (1,0 \; \ Omega) = 0,600 \; \ textbf {V}}. $

Аналогично

$ латекс \ boldsymbol {V_2 = IR_2 = (0.600 \; \ textbf {A}) (6.0 \; \ Omega) = 3.60 \; \ textbf {V}}

$ латекс \ boldsymbol {V_3 = IR_3 = (0.600 \; \ textbf {A}) (13.0 \; \ Omega) = 7.80 \; \ textbf {V}}. $

Обсуждение для (c)

Три капли $ latex \ boldsymbol {IR} $ добавляют к $ latex \ boldsymbol {12.0 \; \ textbf {V}} $, прогноз:

$ латекс \ boldsymbol {V_1 + V_2 + V_3 = (0,600 + 3,60 + 7,80) \; \ textbf {V} = 12,0 \; \ textbf {V}}. 2 R_1 = (0.2} {R}} $, где $ latex \ boldsymbol {V} $ — это падение напряжения на резисторе (а не полное напряжение источника). Получатся те же значения.

Стратегия и решение для (e)

Самый простой способ рассчитать выходную мощность источника — использовать $ latex \ boldsymbol {P = IV} $, где $ latex \ boldsymbol {V} $ — напряжение источника. Это дает

$ латекс \ boldsymbol {P = (0.600 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 7.20 \; \ textbf {W}}. $

Обсуждение для (e)

Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть

$ латекс \ boldsymbol {P_1 + P_2 + P_3 = (0,360 + 2,16 + 4,68) \; \ textbf {W} = 7.20 \; \ textbf {W}}. $

Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.

Основные характеристики резисторов серии

Сопротивления серии добавляют: $ latex \ boldsymbol {R_s = R_1 + R_2 + R_3 + \ dots} $.
Одинаковый ток течет через каждый резистор последовательно.
Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.

На рисунке 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.

Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)

Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (предоставлено Дмитрием Г., Wikimedia Commons)

Чтобы найти выражение для эквивалентного параллельного сопротивления $ latex \ boldsymbol {R _ {\ textbf {p}}} $, давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны $ latex \ boldsymbol {I_1 = \ frac {V} {R_1}} $, $ latex \ boldsymbol {I_2 = \ frac {V} { R_2}} $ и $ latex \ boldsymbol {I_3 = \ frac {V} {R_3}} $. Сохранение заряда подразумевает, что полный ток $ latex \ boldsymbol {I} $, производимый источником, является суммой этих токов:

$ латекс \ boldsymbol {I = I_1 + I_2 + I_3}. $

Подстановка выражений для отдельных токов дает

Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает

$ латекс \ boldsymbol {I =} $ латекс \ boldsymbol {= V} $

Члены в скобках в последних двух уравнениях должны быть равны.Обобщая на любое количество резисторов, общее сопротивление $ latex \ boldsymbol {R_p} $ параллельного соединения связано с отдельными сопротивлениями соотношением

$ latex \ boldsymbol {=} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+ \ cdots} $

Это соотношение приводит к общему сопротивлению $ latex \ boldsymbol {R_p} $, которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.

Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

Пусть выходное напряжение батареи и сопротивления в параллельном соединении на рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: $ latex \ boldsymbol {V = 12.0 \; \ textbf {V}} $, $ latex \ boldsymbol { R_1 = 1.00 \; \ Omega} $, $ latex \ boldsymbol {R_2 = 6.00 \; \ Omega} $ и $ latex \ boldsymbol {R_3 = 13.0 \; \ Omega} $. а) Каково полное сопротивление? (б) Найдите полный ток.(c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает

Таким образом,

(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)

Мы должны перевернуть это, чтобы найти полное сопротивление $ latex \ boldsymbol {R_p} $. Это дает

$ latex \ boldsymbol {R_p =} $ latex \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. $

Общее сопротивление с правильным количеством значащих цифр составляет $ latex \ boldsymbol {R_p = 0.804 \; \ Omega} $

Обсуждение для (а)

$ latex \ boldsymbol {R_p} $, как и предполагалось, меньше минимального индивидуального сопротивления.

Стратегия и решение для (b)

Полный ток можно найти из закона Ома, заменив полное сопротивление $ latex \ boldsymbol {R_p} $.Это дает

$ latex \ boldsymbol {I =} $ latex \ boldsymbol {=} $ latex \ boldsymbol {= 14.92 \; \ textbf {A}} $

Обсуждение для (б)

Текущее значение $ latex \ boldsymbol {I} $ для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.

Стратегия и решение для (c)

Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение.Таким образом,

$ latex \ boldsymbol {I_1 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 12.0 \; \ textbf {A}}. $

Аналогично

$ latex \ boldsymbol {I_2 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 2.00 \; \ textbf {A}} $

$ latex \ boldsymbol {I_3 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 0.92 \; \ textbf {A}}. $

Обсуждение для (c)

Полный ток складывается из отдельных токов:

$ латекс \ boldsymbol {I_1 + I_2 + I_3 = 14.2} {R}} $, так как каждый резистор получает полное напряжение. Таким образом,

$ latex \ boldsymbol {P_1 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 144 \; \ textbf {W}}. $

Аналогично

$ latex \ boldsymbol {P_2 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 24.0 \; \ textbf {W}} $

$ latex \ boldsymbol {P_3 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 11.1 \; \ textbf {W}}. $

Обсуждение для (d)

Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.

Стратегия и решение для (e)

Общую мощность также можно рассчитать несколькими способами. Выбирая $ latex \ boldsymbol {P = IV} $ и вводя полный ток, получаем

$ латекс \ boldsymbol {P = IV = (14.92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. $

Обсуждение для (e)

Суммарная мощность, рассеиваемая резисторами, также 179 Вт:

$ латекс \ boldsymbol {P_1 + P_2 + P_3 = 144 \; \ textbf {W} + 24.0 \; \ textbf {W} + 11.1 \; \ textbf {W} = 179 \; \ textbf {W}}. $

Это соответствует закону сохранения энергии.

Общее обсуждение

Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.

Основные характеристики параллельных резисторов

Параллельное сопротивление определяется из $ latex \ boldsymbol {\ frac {1} {R_p} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + \ cdots } $, и оно меньше любого отдельного сопротивления в комбинации.
Каждый резистор, включенный параллельно, имеет то же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
Параллельные резисторы не получают суммарный ток каждый; они делят это.

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Комбинации последовательного и параллельного соединения можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 4. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее уменьшаются, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.

Рисунок 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части.Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.

Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 5, также является наиболее поучительной, поскольку она используется во многих приложениях. Например, $ latex \ boldsymbol {R_1} $ может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $ могут быть стартером и светом салона.Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.

Пример 3: Расчет сопротивления, $ latex \ boldsymbol {IR} $, падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей

На рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — сочетание последовательного и параллельного. Мы можем рассматривать $ latex \ boldsymbol {R_1} $ как сопротивление проводов, ведущих к $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $.(а) Найдите полное сопротивление. (б) Что такое падение $ latex \ boldsymbol {IR} $ в $ latex \ boldsymbol {R_1} $? (c) Найдите текущий $ latex \ boldsymbol {I_2} $ через $ latex \ boldsymbol {R_2} $. (d) Какую мощность рассеивает $ latex \ boldsymbol {R_2} $?

Рисунок 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация идет последовательно с R ₁ .

Стратегия и решение для (а)

Чтобы найти полное сопротивление, отметим, что $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $ находятся параллельно, и их комбинация $ latex \ boldsymbol {R_p} $ находится последовательно с $ latex \ boldsymbol { R_1} $. Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет

$ латекс \ boldsymbol {R _ {\ textbf {tot}} = R_1 + R_p}. $

Сначала мы находим $ latex \ boldsymbol {R_p} $, используя уравнение для параллельных резисторов и вводя известные значения:

Инвертирование дает

$ latex \ boldsymbol {R_p =} $ latex \ boldsymbol {\ Omega = 4.11 \; \ Omega}. $

Итак, общее сопротивление составляет

$ латекс \ boldsymbol {R _ {\ textbf {tot}} = R_1 + R_p = 1.00 \; \ Omega + 4.11 \; \ Omega = 5.11 \; \ Omega}. $

Обсуждение для (а)

Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной ($ latex \ boldsymbol {20.0 \; \ Omega} $ и $ latex \ boldsymbol {0.804 \; \ Omega} $, соответственно), найденными для тех же резисторы в двух предыдущих примерах.

Стратегия и решение для (b)

Чтобы найти падение $ latex \ boldsymbol {IR} $ в $ latex \ boldsymbol {R_1} $, отметим, что полный текущий $ latex \ boldsymbol {I} $ течет через $ latex \ boldsymbol {R_1} $.Таким образом, его падение $ latex \ boldsymbol {IR} $ составляет

$ латекс \ boldsymbol {V_1 = IR_1}. $

Мы должны найти $ latex \ boldsymbol {I} $, прежде чем сможем вычислить $ latex \ boldsymbol {V_1} $. Полный ток $ latex \ boldsymbol {I} $ находится с помощью закона Ома для схемы. То есть

$ latex \ boldsymbol {I =} $ latex \ boldsymbol {=} $ latex \ boldsymbol {= 2.35 \; \ textbf {A}}. $

Вводя это в выражение выше, мы получаем

$ латекс \ boldsymbol {V_1 = IR_1 = (2.35 \; \ textbf {A}) (1.00 \; \ Omega) = 2.35 \; \ textbf {V}}. $

Обсуждение для (б)

Напряжение, приложенное к $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $, меньше общего напряжения на величину $ latex \ boldsymbol {V_1} $. Большое сопротивление провода может существенно повлиять на работу устройств, представленных $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $.

Стратегия и решение для (c)

Чтобы найти ток через $ latex \ boldsymbol {R_2} $, мы должны сначала найти приложенное к нему напряжение.Мы называем это напряжение $ latex \ boldsymbol {V _ {\ textbf {p}}} $, потому что оно применяется к параллельной комбинации резисторов. Напряжение, приложенное как к $ latex \ boldsymbol {R_2} $, так и к $ latex \ boldsymbol {R_3} $, уменьшается на сумму $ latex \ boldsymbol {V_1} $, и поэтому оно составляет

$ латекс \ boldsymbol {V_p = V — V_1 = 12.0 \; \ textbf {V} — 2.35 \; \ textbf {V} = 9.65 \; \ textbf {V}}. $

Теперь текущий $ latex \ boldsymbol {I_2} $ через сопротивление $ latex \ boldsymbol {R_2} $ находится по закону Ома:

$ latex \ boldsymbol {I_2 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 1.2 (6.00 \; \ Omega) = 15.5 \; \ textbf {W}}. $

Обсуждение для (d)

Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.

Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, падение $ latex \ boldsymbol {IR} $ в проводах также может быть значительным.

Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

Что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное $ latex \ boldsymbol {R_3} $, имеет очень низкое сопротивление, поэтому при его включении течет большой ток.Этот повышенный ток вызывает большее падение $ latex \ boldsymbol {IR} $ в проводах, представленных $ latex \ boldsymbol {R_1} $, что снижает напряжение на лампочке (которое составляет $ latex \ boldsymbol {R_2} $), что потом заметно тускнеет.

Рисунок 6. Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.

Проверьте свое понимание

1: Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.

Стратегии решения проблем для последовательных и параллельных резисторов

Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении $ latex \ boldsymbol {R_p} $ необходимо с осторожностью относиться к обратному значению.
Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.

Общее сопротивление электрической цепи с последовательно включенными резисторами является суммой отдельных сопротивлений: $ latex \ boldsymbol {R_s = R_1 + R_2 + R_3 + \ cdots} $
Каждый резистор в последовательной цепи имеет одинаковое количество тока, протекающего через него.
Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различается, и их общая сумма складывается с входом источника питания.
Общее сопротивление электрической цепи с резисторами, подключенными параллельно, меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле: $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+ \; \ cdots} $
Каждый резистор в параллельной цепи имеет одинаковое полное напряжение источника.
Ток, протекающий через каждый резистор в параллельной цепи, различается в зависимости от сопротивления.
Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного соединения, оно может быть уменьшено до одного эквивалентного сопротивления, идентифицируя его различные части как последовательные или параллельные, уменьшая каждую до своего эквивалента и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление. .

Концептуальные вопросы

1: Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и чрезвычайно большое в разомкнутом, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.

Рис. 7. Переключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

2: Какое напряжение на разомкнутом переключателе на рисунке 7?

3: Напряжение на разомкнутом переключателе, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?

4: Почему мощность, рассеиваемая замкнутым переключателем, как на рисунке 7, мала?

5: Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампа горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)

Рис. 8. Ошибка подключения: этот переключатель подключен параллельно устройству, представленному R .(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

6: Зная, что сила удара зависит от величины тока, проходящего через ваше тело, вы бы предпочли быть последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он поражен током? Объяснять.

7: Не потускнели бы ваши фары при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.

8: Некоторые гирлянды праздничных огней подключаются последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?

9: Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.

10: Предположим, вы выполняете физическую лабораторию, которая просит вас вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?

11: Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление. Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор.Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.

12: У некоторых лампочек есть три уровня мощности (не включая ноль), получаемых от нескольких нитей накала, которые индивидуально переключаются и подключаются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности?

Проблемные упражнения

Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.

1: (a) Каково сопротивление десяти последовательно соединенных резисторов $ latex \ boldsymbol {275 — \; \ Omega} $? (б) Параллельно?

2: (a) Каково сопротивление $ латексного \ boldsymbol {1.2 — \; \ Omega} $ подключены $ latex \ boldsymbol {2.50 — \; \ textbf {k} \ Omega} $ и резистор $ latex \ boldsymbol {4.00 — \; \ textbf {k} \ Omega} $ последовательно? (б) Параллельно?

3: Какое наибольшее и наименьшее сопротивление вы можете получить, подключив $ latex \ boldsymbol {36.0 — \; \ Omega} $, $ latex \ boldsymbol {50.0 — \; \ Omega} $ и $ латексный \ boldsymbol {700 — \; \ Omega} $ резистор вместе?

4: Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?

5: Фара автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)

6: (a) Учитывая 48.Аккумулятор 0 В и резисторы $ latex \ boldsymbol {24.0 — \; \ Omega} $ и $ latex \ boldsymbol {96.0 — \; \ Omega} $, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.

7: Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите $ latex \ boldsymbol {I_3} $ двумя разными способами: (a) по известным значениям $ latex \ boldsymbol {I} $ и $ latex \ boldsymbol {I_2} $; (б) используя закон Ома для $ latex \ boldsymbol {R_3} $.В обеих частях явно показано, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.

8: Ссылаясь на рисунок 5: (a) Вычислите $ latex \ boldsymbol {P_3} $ и обратите внимание на его сравнение с $ latex \ boldsymbol {P_3} $, найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.

9: См. Рис. 6, где обсуждается затемнение света при включении тяжелого прибора.9 — \; \ Omega} $ сопротивление. Рис. 9. (а) Какое сопротивление относительно земли 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.

Рис. 9. Линия электропередачи высокого напряжения (240 кВ), несущая 5,00 × 10 ² подвешен на заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает 1.00 × 10 ⁹ Ом по сопротивления каждый.

11: Покажите, что если два резистора $ latex \ boldsymbol {R_1} $ и $ latex \ boldsymbol {R_2} $ объединены, и один из них намного больше другого ($ latex \ boldsymbol {R_1 >> R_2} $) : (a) Их последовательное сопротивление почти равно большему сопротивлению $ latex \ boldsymbol {R_1} $. (б) Их параллельное сопротивление почти равно меньшему сопротивлению $ latex \ boldsymbol {R_2} $.

12: Необоснованные результаты

Два резистора, один из которых имеет сопротивление $ latex \ boldsymbol {145 \; \ Omega} $, подключены параллельно, чтобы получить общее сопротивление $ latex \ boldsymbol {150 \; \ Omega} $.а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

13: необоснованные результаты

Два резистора, один из которых имеет сопротивление $ latex \ boldsymbol {900 \; \ textbf {k} \ Omega} $, соединены последовательно, чтобы обеспечить общее сопротивление $ latex \ boldsymbol {0.500 \; \ textbf {M}. \ Omega} $. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Глоссарий

серии: Последовательность резисторов или других компонентов, включенных в цепь один за другим

резистор: Компонент, обеспечивающий сопротивление току, протекающему по электрической цепи

сопротивление: , вызывая потерю электроэнергии в цепи

Закон Ома: соотношение между током, напряжением и сопротивлением в электрической цепи: $ latex \ boldsymbol {V = IR} $

напряжение: — электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором

Падение напряжения: Потеря электроэнергии при прохождении тока через резистор, провод или другой компонент

текущий: поток заряда через электрическую цепь мимо заданной точки измерения

Закон Джоуля: соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое по формуле: $ latex \ boldsymbol {P_e = IV} $

параллельно: подключение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

Решения

Проверьте свое понимание

1: Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы.В таких случаях правила Кирхгофа, которые будут представлены в главе 21.3 «Правила Кирхгофа», позволят вам проанализировать схему.

Задачи Упражнения

1: (a) $ latex \ boldsymbol {2.75 \; \ textbf {k} \ Omega} $

(б) $ latex \ boldsymbol {27.5 \; \ Omega} $

3: (a) $ latex \ boldsymbol {786 \; \ Omega} $

(б) $ latex \ boldsymbol {20.3 \; \ Omega} $

5: 29,6 Вт

7: (а) 0.74 А

(б) 0,742 А

9: (а) 60,8 Вт

(б) 3,18 кВт

11: (a) $ latex \ begin {array} {c} \ boldsymbol {R_s = R_1 + R_2} \\ [1em] \ boldsymbol {\ Rightarrow R_s \ приблизительно R_1 (R_1 >> R_2)} \ end {array}

долларов США

(b) $ latex \ boldsymbol {=} $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {=} $

так что

$ latex \ boldsymbol {R_p =} $ latex \ boldsymbol {\ приблизительно} $ $ latex \ boldsymbol {= R_2 \; (R_1 >> R_2)}.$

13: (a) $ latex \ boldsymbol {-400 \; \ textbf {k} \ Omega} $

(b) Сопротивление не может быть отрицательным.

(c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.

Вычисление сопротивления параллельно включенного

Калькулятор комбинации параллельных резисторов

Калькулятор параллельного сопротивления, Чтобы использовать его, просто укажите количество параллельных резисторов и значение сопротивления для каждого из них.Вы можете легко рассчитать эквивалентное сопротивление, если используете резисторы. Найти лучшую комбинацию может быть непросто. Этот калькулятор позволяет вводить доступные значения сопротивления и мгновенно вычислять все параллельные комбинации любых двух из них. Заполните значения резисторов в

Калькулятор преобразования Параллельный и последовательный резистор, Рассчитайте общее последовательное и параллельное сопротивление цепи с помощью калькулятора параллельных и последовательных резисторов DigiKey.Рассчитайте общее последовательное и параллельное сопротивление цепи с помощью калькулятора параллельных и последовательных резисторов DigiKey.

Калькулятор параллельных резисторов R1 + R2 = эквивалентный резистор R, Калькулятор комбинации параллельных резисторов. Были ли вы когда-нибудь в ситуации, когда вам нужно создать эквивалентное сопротивление, используя набор параллельных резисторов. Расчет эквивалентного сопротивления (R EQ) параллельно подключенных резисторов вручную может быть утомительным. Этот инструмент был разработан, чтобы помочь вам быстро рассчитать эквивалентное сопротивление, независимо от того, подключены ли у вас два или десять резисторов параллельно.Чтобы использовать его, просто укажите количество параллельных резисторов и значение сопротивления для каждого из них.

Как рассчитать полное сопротивление в последовательно-параллельной цепи

Электрический / Электронный, С легкостью рассчитайте общее сопротивление параллельно включенных резисторов! Последовательные резисторы эквивалентны одному резистору, сопротивление которого является суммой каждого отдельного резистора.Как рассчитать общее сопротивление цепи при r1 = 220 Ом, r2 = 130 Ом, r4 = 100 Ом, r5 = 270 последовательно и r3 = 470 Ом параллельно ? Ответ сообщества Общее сопротивление = 1 / (Все последовательные резисторы сложены вместе) + 1 / (значение параллельного резистора).284 Ом = 1 / (1 / (220 + 130 + 100 + 270) + 1 / (470)).

Резисторы в комбинации последовательно и параллельно, Суммируйте сопротивления последовательно. После того, как вы заменили каждую параллельную секцию одним сопротивлением, ваша диаграмма должна быть одной петлей: последовательностью В цепи, соединенной последовательно, общее сопротивление определяется простым сложением всех значений сопротивлений отдельных резисторов, тогда как в Параллельно это находится путем сложения значений, обратных величине сопротивления, и взятия обратной величины от общего значения.

Полное сопротивление последовательной параллельной цепи постоянного тока, Расчет сопротивления в последовательной, параллельной или последовательной параллельной цепи. Чтобы найти полное сопротивление параллельной цепи, вы должны разделить его на каждый из резисторов. Принимая во внимание, что последовательная цепь — это цепь, которая имеет более одного компонента, но только один путь, по которому течет электричество, и все компоненты соединены между собой. Сопротивление — это мера сопротивления току в электрической цепи. Сопротивление измеряется в омах (Ом) Формула для расчета сопротивления в последовательной цепи.

Последовательное сопротивление

Электрическое / электронное, цепь прямо пропорциональна размеру резистора. Резисторы последовательно. Говорят, что резисторы соединены последовательно, когда они последовательно соединены в одну линию, в результате чего через них протекает общий ток. Отдельные резисторы могут быть соединены вместе либо последовательно, либо параллельно, либо в комбинации последовательного и параллельного соединения, чтобы создать более сложные резистивные цепи, эквивалентное сопротивление которых является математической комбинацией отдельных резисторов, соединенных вместе.

Последовательные резисторы, В последовательной резисторной сети отдельные резисторы складываются вместе, чтобы получить эквивалентное сопротивление (RT) последовательной комбинации. Резисторы в последовательной цепи Справка Метод расчета сопротивления 1 из 3: Последовательное сопротивление. Последовательное сопротивление — это просто подключение «внешней» стороны одного резистора к «входной» стороне. Метод 2 из 3: Параллельное сопротивление. Параллельное сопротивление — это когда «входная» сторона 2 или более резисторов подключена, и Метод 3 из 3: Комбинированные резисторы

в комбинации последовательно и параллельно, Метод расчета эквивалентного сопротивления цепей такой же, как и для любая отдельная последовательная или параллельная цепь, и, надеюсь, теперь мы знаем, что RA включен последовательно с R7, поэтому общее сопротивление будет RA + R7 = 4 + 8 = 12 Ом, как показано.Это значение сопротивления 12 Ом теперь подключено параллельно с R6 и может быть рассчитано как RB. RB включен последовательно с R5, поэтому общее сопротивление будет RB + R5 = 4 + 4 = 8 Ом, как показано.

Последовательные и параллельные резисторы. Проблемы и решения.

Последовательные и параллельные резисторы, Последовательные и параллельные резисторы в электрических цепях, примеры с подробными решениями. Два последовательно включенных резистора сгруппированы как Req1 в эквивалентной схеме ниже, а их сопротивление выражается суммой.Req1 = 100 + 400 = 500 Ом. Два параллельных резистора сгруппированы как Req2 в эквивалентной схеме ниже, а их сопротивление определяется уравнением.

Как решить любую проблему последовательной и параллельной цепи, Как вы анализируете схему с последовательно включенными и параллельными резисторами, сводя в таблицу наши решения Продолжительность: 14:06 Отправлено: 31 марта 2015 г. Проблема № 5 Ниже показано последовательное / параллельное соединение. Рассчитайте общее последовательное / параллельное сопротивление, указанное ниже, если уровень установлен между точками A и B.(Величина R 1 = 7 Ом, R 2 = 2,5 Ом, R 3 = 7,5 Ом, R 4 = 5 Ом, R 5 = 3 Ом и R 6 = 2 Ом) Ответ; (a) если уровень установлен между точками A и B

Как рассчитать последовательные и параллельные резисторы — Kitronik Ltd, Это видео содержит множество примеров и практических задач, включая текущее разделение Продолжительность: 34:18 Размещено: 12 декабря 2017 г. Поэтому важно подключать резисторы последовательно и параллельно. Резистор — это электрический компонент, который обеспечивает сопротивление или ограничивает ток в цепи.Например, мы можем рассматривать ламповый светильник, используемый в нашем доме, в качестве резистора. Следовательно, подключение резисторов последовательно и параллельно имеет важное значение.

Примеры параллельных цепей

Типы цепей, . Если одна из ламп перегорает, ток все еще может течь через остальные лампы и приборы. Sciencing_Icons_Science. Sciencing_Icons_Biology. Биология. Sciencing_Icons_Biology. Биология. Sciencing_Icons_Cells. Ячейки. Sciencing_Icons_Molecular. Молекулярный. Sciencing_Icons_Microorganisms.Микроорганизмы. Sciencing_Icons_Genetics. Генетика.

Простые параллельные схемы | Последовательные и параллельные схемы, Давайте рассмотрим несколько примеров параллельных схем, демонстрирующих эти принципы. Мы начнем с параллельной схемы, состоящей из трех резисторов и одного. Давайте взглянем на несколько примеров параллельных схем, которые демонстрируют эти принципы. Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи: напряжение в параллельных цепях.Первый принцип, который следует понимать в отношении параллельных цепей, заключается в том, что напряжение на всех компонентах цепи одинаково. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, должно быть

Physics Tutorial: Parallel Circuits, В примерах вводится новый символ схемы — буква A заключен в круг. Это символ амперметра — устройства, используемого для измерения тока. Применение определения: Пример Давайте начнем с рассмотрения технического определения параллельной цепи.Два или более электрических компонента считаются подключенными параллельно, если общий электрический ток

Резисторы последовательно и параллельно pdf

[PDF] Сегодняшняя повестка дня: последовательно и параллельно подключенные резисторы. Kirchoff’s Rules., Вы должны уметь использовать правила Кирхгофа для расчета токов и напряжений в компонентах схемы, которые не просто включены последовательно или параллельно. Стр. 2. Сопротивления в законе Ома III — Последовательные и параллельные резисторы Резисторы изготавливаются из множества различных материалов, форм, форм, значений, номинальной мощности и допусков.В то время как некоторые значения резисторов помечены текстом, обычные резисторы имеют цветовую кодировку с полосами для обозначения их омических значений. Цветно-цифровые обозначения приведены в таблице 1.

[PDF] Резисторы в последовательной и параллельной цепях, Ток и напряжение измеряются двумя аналоговыми приборами. Сопротивление определяется по закону Ома — как для двух резисторов по отдельности, так и для серии. Есть два способа подключения резисторов в цепь. Их можно прикрепить либо внутрь.ряд. или в. параллельно. Давайте сначала посмотрим на резисторы серии. Если между двумя последовательными резисторами нет точек ветвления, то они включены последовательно. В . На рис. 1а резисторы R. 1. и R. 2. включены последовательно. В . Рис. 1b, R. 1. и R. 2

[PDF] Сопротивления в последовательном и параллельном соединении, заменен одним резистором со значением R, и такой же ток I будет течь от батареи. Б. Параллельное сопротивление. В лабораторной работе 8 говорится, что резисторы подключаются последовательно и параллельно. Цели • Понять фундаментальное различие между резисторами, подключенными последовательно и параллельно.• Для расчета напряжений и токов в простых схемах, включающих только резисторы, используя правила «добавления» последовательных и параллельных резисторов.

Проблемы параллельной цепи

Как решить параллельную цепь (легко), Учебное пособие по решению параллельных цепей. Не можете получить 0,233? Я снял на это видео. Продолжительность: 10:55 Размещено: 30 января, 2016 Параллельная цепь имеет две или более ветвей, которые ведут от точки A к точке B. Один поток электронов разделяется и проходит через несколько ветвей, а затем снова сливается в один поток на другой стороне.Большинство проблем, связанных с параллельными цепями, требуют от вас определения общего напряжения, сопротивления или тока в цепи (от точки A до точки B).

Практика параллельной схемы, проблема 1, Пожалуйста, оцените это видео, если оно вам показалось полезным. Загрузка автозапуска Когда автовоспроизведение включено, продолжительность: 6:57 Опубликовано: 19 января 2014 г. Есть много типов проблем с параллельными цепями. Одна из распространенных проблем — вычислить полное сопротивление двух параллельно включенных резисторов, также известное как эквивалентное сопротивление.Другая проблема — вычислить ток в параллельной сети резисторов, когда она подключена к источнику питания.

Практический рабочий лист по параллельным цепям постоянного тока с листом ответов, Чтобы научиться математическому анализу цепей, требуется много изучения и практики. Обычно студенты практикуются, работая над множеством типовых задач. В параллельной цепи заряд делится на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой.Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей.

Как решить последовательно-параллельную комбинированную схему

Методы анализа последовательно-параллельных резистивных цепей, Третий тип схемы включает двойное использование последовательного и параллельного соединений в A. Следующие предложения по решению проблем комбинированной схемы: Стратегия для достижения этой цели заключается в следующем: Шаг 1. Оцените, какие резисторы в цепи соединены вместе простым последовательным или простым параллельным соединением.Шаг 2: Изобразите схему заново, заменив каждую из тех комбинаций последовательных или параллельных резисторов, указанных на шаге 1, на Шаг 3:

Как решить комбинированную схему (легко), Учебное пособие по электронике по последовательным и параллельным схемам, При решении любой схемы комбинационного резистора, которая состоит из последовательно соединенных резисторов, Преобразуйте комбинированную схему в строго последовательную цепь, заменив (по вашему мнению) параллельную секцию одним резистором, имеющим значение сопротивления, равное эквивалентному сопротивлению параллельной раздел.Часто и надлежащим образом используйте уравнение закона Ома (ΔV = I • R). Большинство ответов будет определено с использованием этого уравнения.

Последовательно-параллельные комбинированные схемы, Аналогичным образом, если бы вышеуказанная схема была простой параллельной, мы могли бы просто вычислить токи ответвления, сложить токи ответвления, чтобы вычислить общий ток, а затем вычислить общее значение Solve для общего сопротивления. Чтобы найти полное сопротивление RT в цепи, решите его в уравнении 1 / RT = 1 / R 1 + 1 / R 2 + 1 / R 3 +, где каждый R в правой части представляет сопротивление на одной ветви цепи. схема.Например, в схеме есть два параллельно включенных резистора, каждый с сопротивлением 4 Ом. 1 / R T = 1 / 4Ω + 1 / 4Ω → 1 / R T = 1 / 2Ω → R T = 2Ω. Другими словами, две ветви равного сопротивления пройти ровно в два раза легче, чем одну ветвь.

Еще статьи

Последовательность и параллельность

— AP Physics 1

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Параллельно резисторов и конденсаторов

Введение

В этом заключительном разделе мы исследуем частотную характеристику цепей, содержащих резисторы и конденсаторы в параллельных комбинациях.Как и в предыдущем разделе, мы можем использовать анализ постоянного тока параллельных цепей резисторов в качестве отправной точки, а затем учесть фазовое соотношение между током, протекающим через резистор и компоненты конденсатора.

Анализ параллельных цепей RC

Как мы видели ранее, в параллельной цепи у тока есть несколько альтернативных путей, и выбранный маршрут зависит от относительного «сопротивления» каждой ветви. На рисунке ниже показано параллельное соединение одного резистора и конденсатора между точками A и B .

Для расчета полного импеданса (сопротивления) этой цепи мы снова используем емкостное реактивное сопротивление Xc как эквивалентное сопротивление конденсатора. Затем мы используем те же правила, что и для последовательного суммирования резисторов, помня, что теперь мы имеем дело с векторными величинами. Вы помните, что правило для параллельного суммирования резисторов дает

, рассматривая R2 выше как емкостное реактивное сопротивление и немного алгебры комплексных чисел, мы можем показать, что величина импеданса и фазовый угол задаются следующим образом:

Теперь мы рассмотрим реакцию схемы, как указано выше, с емкостным реактивным сопротивлением 50 Ом и сопротивлением 100 Ом.

Z = 100 x 50 / (100 2 + 50 2) ½ = 44.7 °

и угол составляет -63,4 °. Частотная характеристика схемы этого типа показана ниже в виде векторов и боде.

Видно, что фазовый угол изменяется от 0 ° на низких частотах, когда ток почти полностью протекает через плечо резистора, до -90 ° на высоких частотах, когда ток протекает через ветвь, содержащую конденсатор.