Параллельные и последовательные цепи. Параллельное и последовательное соединение проводников: особенности, формулы, применение

Как отличить параллельное соединение от последовательного. Какие формулы применяются для расчета силы тока, напряжения и сопротивления при разных типах соединений. Где используются параллельные и последовательные цепи в быту и технике. Как рассчитать общее сопротивление сложной электрической цепи.

Ключевые отличия параллельного и последовательного соединения проводников

Параллельное и последовательное соединение проводников имеют ряд существенных отличий:

• При последовательном соединении элементы цепи соединяются друг за другом в одну линию, без разветвлений. При параллельном — все элементы подключаются к общим точкам начала и конца.
• В последовательной цепи через все элементы протекает одинаковый ток. В параллельной — ток разветвляется между элементами.
• Напряжение в последовательной цепи распределяется между элементами. В параллельной — одинаково на всех элементах.
• Общее сопротивление последовательной цепи равно сумме сопротивлений элементов. Общее сопротивление параллельной цепи меньше сопротивления любого из элементов.

Формулы для расчета параметров электрических цепей

Для расчета параметров электрических цепей при различных соединениях используются следующие основные формулы:

Последовательное соединение:

• Общий ток: I = I1 = I2 = I3
• Общее напряжение: U = U1 + U2 + U3
• Общее сопротивление: R = R1 + R2 + R3

Параллельное соединение:

• Общий ток: I = I1 + I2 + I3
• Общее напряжение: U = U1 = U2 = U3
• Общее сопротивление: 1/R = 1/R1 + 1/R2 + 1/R3

Эти формулы позволяют рассчитать параметры цепи, зная характеристики отдельных элементов.

Применение последовательных и параллельных цепей в быту и технике

Последовательные и параллельные соединения широко применяются в различных электрических устройствах и системах:

Последовательное соединение:

• Электрические звонки и дверные замки
• Карманные фонарики
• Гирлянды некоторых типов
• Предохранители и автоматические выключатели

Параллельное соединение:

• Домашняя электропроводка
• Системы освещения
• Большинство бытовых электроприборов
• Автомобильные электрические системы

Выбор типа соединения зависит от конкретных требований к работе устройства или системы.

Особенности расчета сложных электрических цепей

В реальных электрических схемах часто встречаются комбинации последовательных и параллельных соединений. Для расчета таких цепей используется метод поэтапного упрощения:

1. Схема разбивается на простые участки с последовательным или параллельным соединением.
2. Каждый участок заменяется эквивалентным сопротивлением по соответствующим формулам.
3. Процесс повторяется, пока вся схема не сведется к одному эквивалентному сопротивлению.
4. Затем производится обратный расчет токов и напряжений на каждом участке.

Этот метод позволяет анализировать сколь угодно сложные схемы, последовательно упрощая их.

Влияние типа соединения на работу электрических устройств

Тип соединения элементов существенно влияет на работу электрических устройств:

• При последовательном соединении выход из строя одного элемента приводит к отключению всей цепи. Это используется в устройствах защиты.
• Параллельное соединение обеспечивает независимую работу элементов. При выходе из строя одного элемента остальные продолжают функционировать.
• Последовательное соединение позволяет получить большее общее напряжение (используется в высоковольтных линиях передачи).
• Параллельное соединение обеспечивает больший общий ток (применяется в мощных источниках питания).

Понимание этих особенностей критически важно при проектировании электрических систем.

Параллельное и последовательное соединение источников тока

Источники тока (батареи, аккумуляторы) также могут соединяться последовательно и параллельно:

• Последовательное соединение увеличивает общее напряжение. Используется, когда требуется напряжение выше, чем может дать один элемент.
• Параллельное соединение увеличивает общий ток и емкость. Применяется для увеличения времени работы устройства.

При соединении источников важно учитывать их характеристики и совместимость.

Особенности соединения конденсаторов

Конденсаторы в электрических цепях также могут соединяться последовательно и параллельно, но их поведение отличается от резисторов:

Последовательное соединение конденсаторов:

• Общая емкость уменьшается: 1/C = 1/C1 + 1/C2 + 1/C3
• Напряжение распределяется между конденсаторами обратно пропорционально их емкостям

Параллельное соединение конденсаторов:

• Общая емкость увеличивается: C = C1 + C2 + C3
• Напряжение на всех конденсаторах одинаково

Эти особенности учитываются при проектировании цепей с конденсаторами.

Как отличить параллельное соединение от последовательного

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми.

Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках.

И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.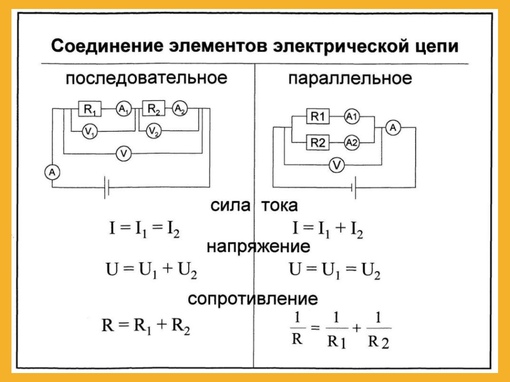

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь.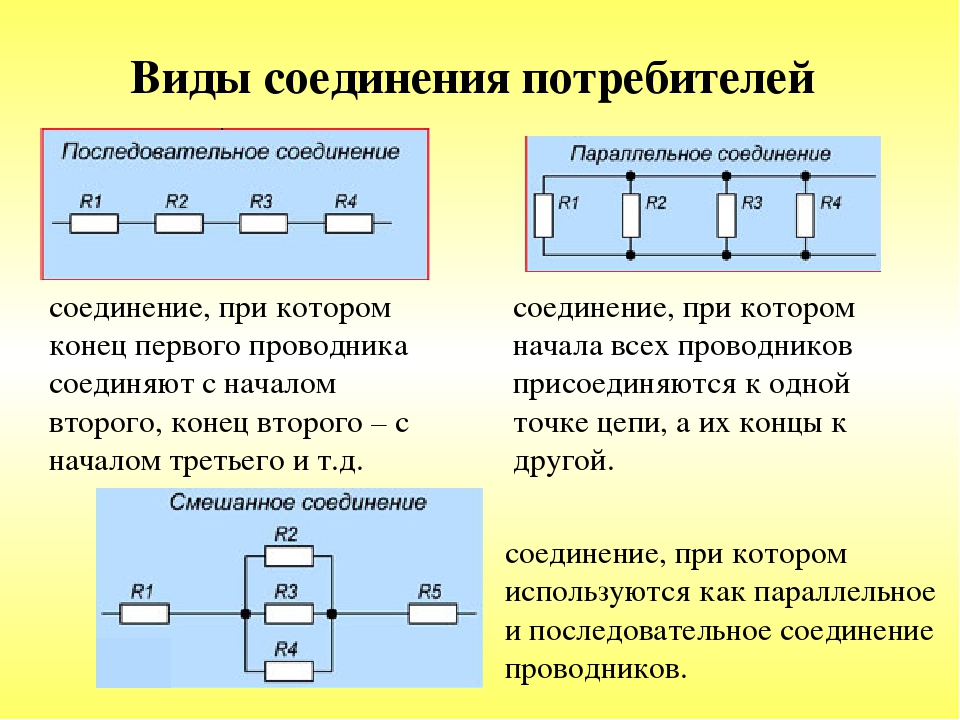 Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой.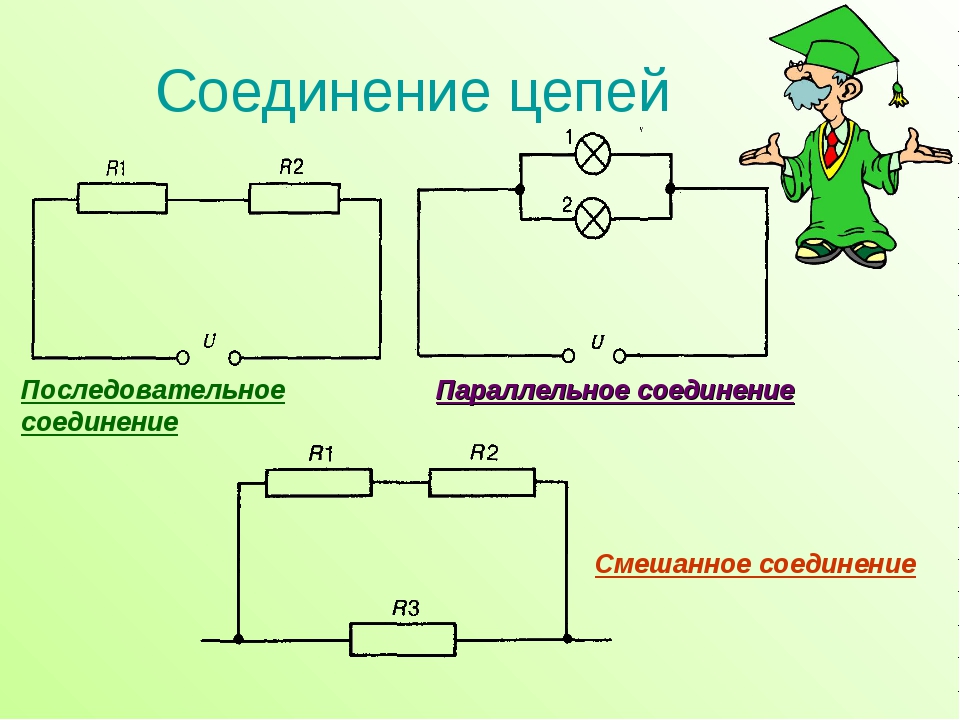 Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В.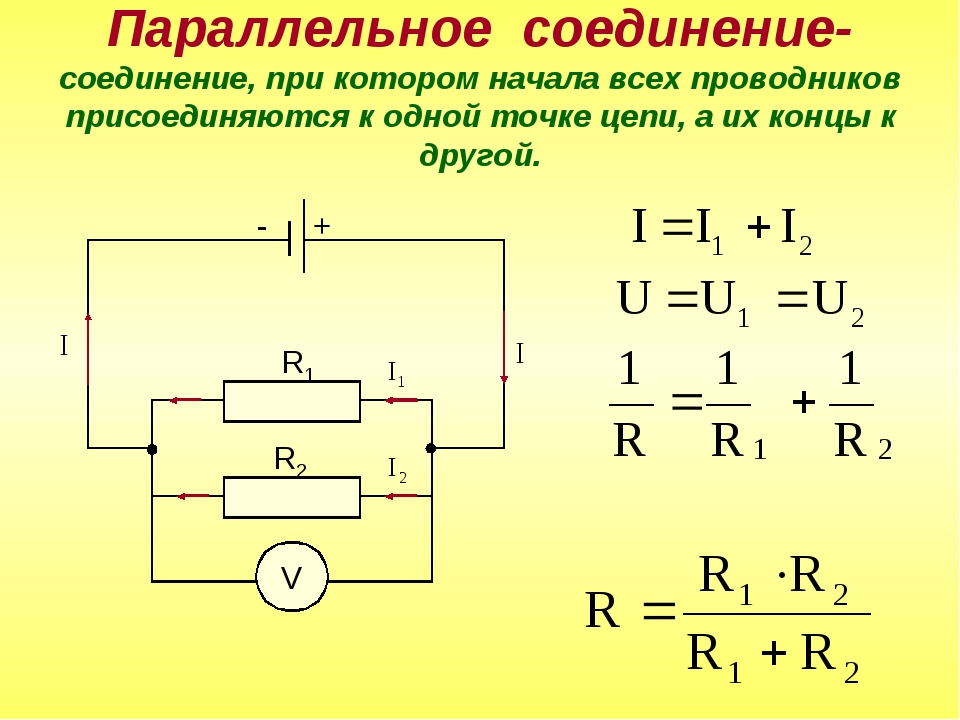 Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

• Первая формула для последовательного вида соединения.
• Далее, для параллельной схемы.
• И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

В физике изучается тема про параллельное и последовательное соединение, причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.

Как различить эти два соединения?

Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов.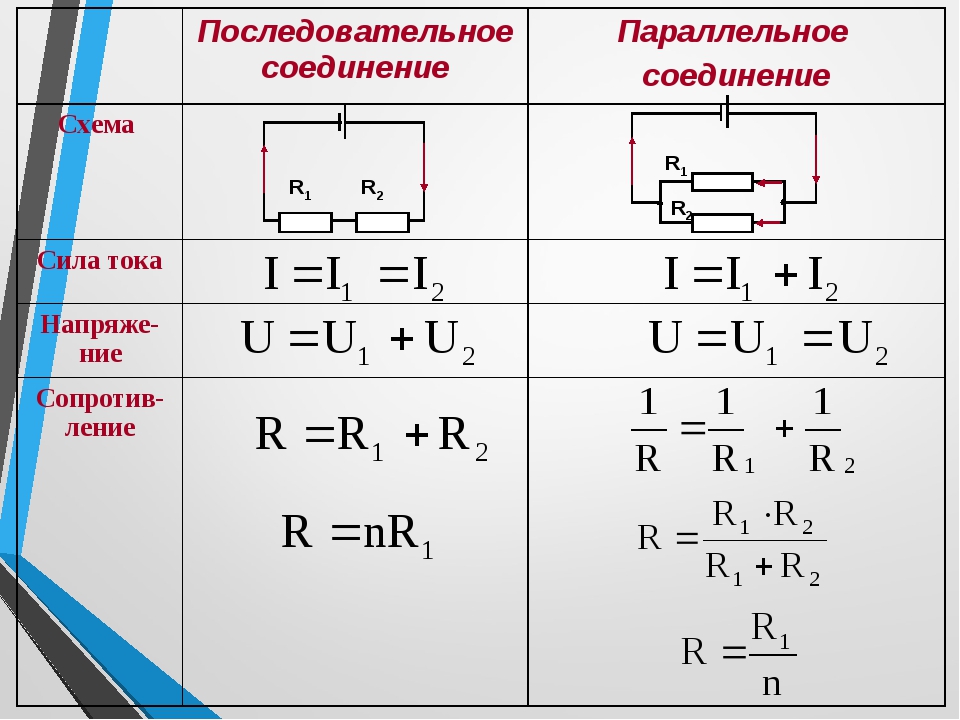 На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.

Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.

Формулы для силы тока

О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.

Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:

Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.

Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:

Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.

Формулы для напряжения

Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе.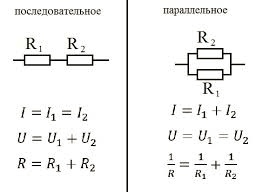 Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.

Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:

Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:

Формулы для электрического сопротивления

Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления.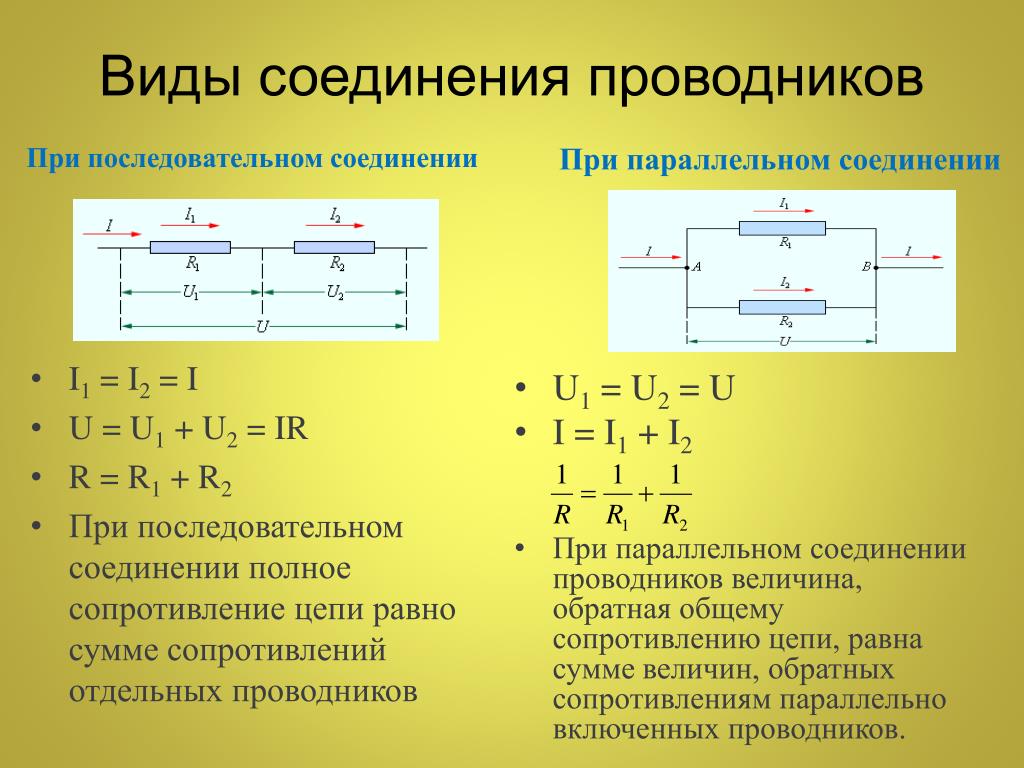 То есть U = I * R, где R — сопротивление.

Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:

• последовательно, значит, нужно равенство для напряжения — I_общ * R_общ = I₁ * R₁ + I₂ * R_2;
• параллельно необходимо пользоваться формулой для силы тока — U_общ / R_общ = U₁ / R₁ + U₂ / R₂ .

Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:

1. R _общ = R ₁ + R ₂ (для последовательного соединения проводников).
2. 1 / R _общ = 1 / R ₁ + 1 / R ₂ (при параллельном соединении).

При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.

Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.

Работа тока

Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.

Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U ₁ + U ₂) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.

Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А ₁ + А ₂.

Мощность тока

При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р ₁ + Р ₂.

То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.

Как влияет соединение проводников на ремонт новогодней гирлянды?

Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее – и гирлянда станет работать.

Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.

Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?

При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:

Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С.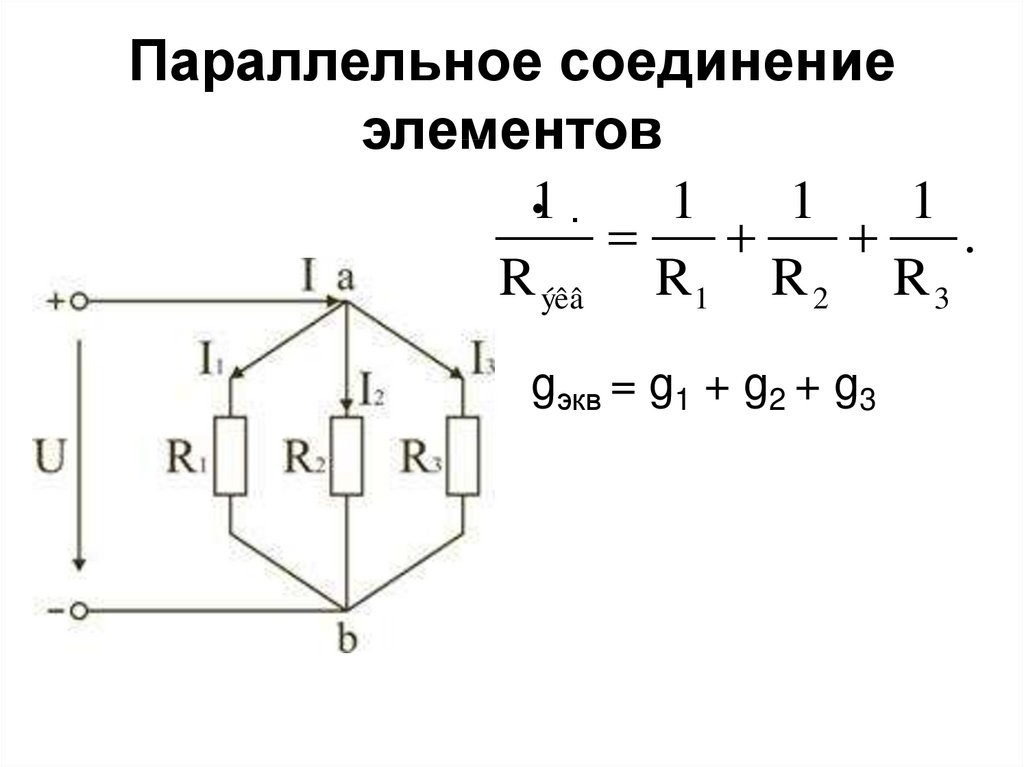 В ней С — емкость конденсатора.

Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:

Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С ₁ + 1 / С ₂.

Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:

С = (q 1 + q 2 ) / U.

То есть эта величина считается, как сумма каждого из использованных в соединении приборов:

Как определить общее сопротивление произвольного соединения проводников?

То есть такого, в котором последовательные участки сменяют параллельные, и наоборот.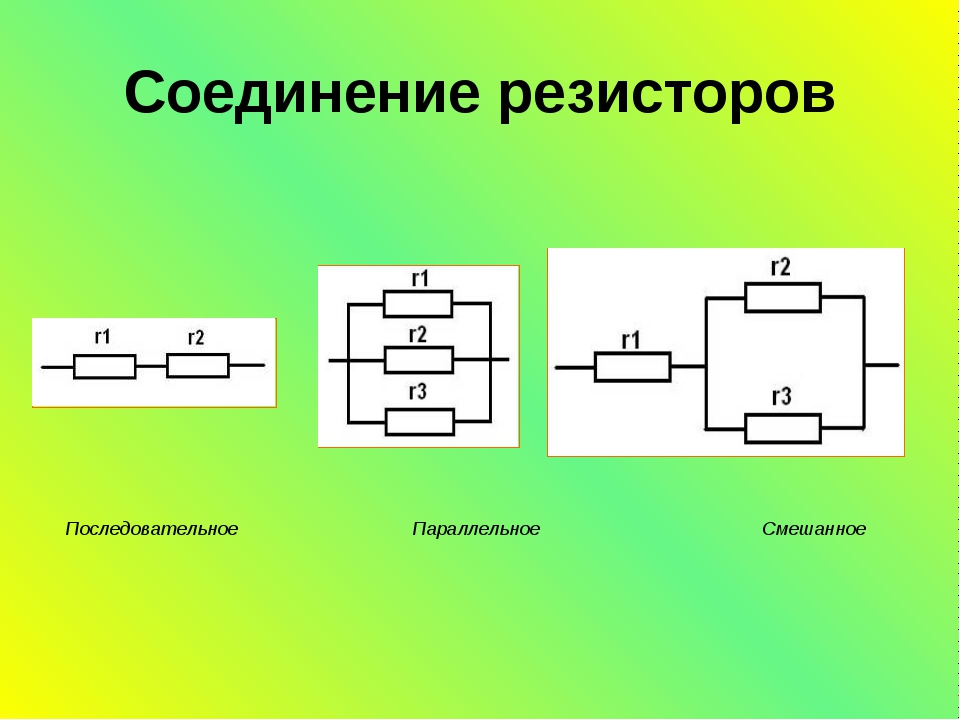 Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.

Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).

Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.

Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.

Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:

• сначала ту, которая приведена для последовательного соединения;
• потом для параллельного;
• и снова для последовательного.

Подобным образом можно развернуть любую, даже очень сложную схему.

Задача на последовательное соединение проводников

Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?

Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.

Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.

Ответ. Сопротивление резистора равно 2,5 Ом.

Задача на соединение конденсаторов, параллельное и последовательное

Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.

Решение. Проще начать с параллельного подключения. В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.

Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.

Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка.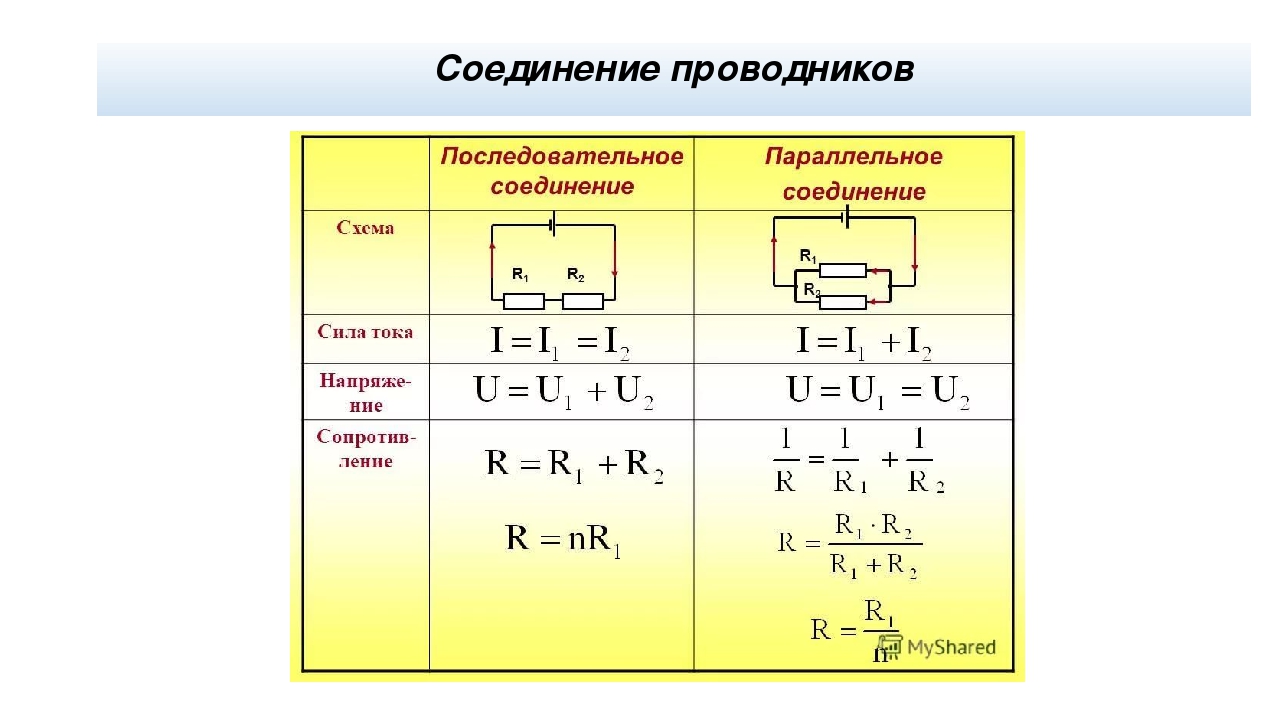 Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях.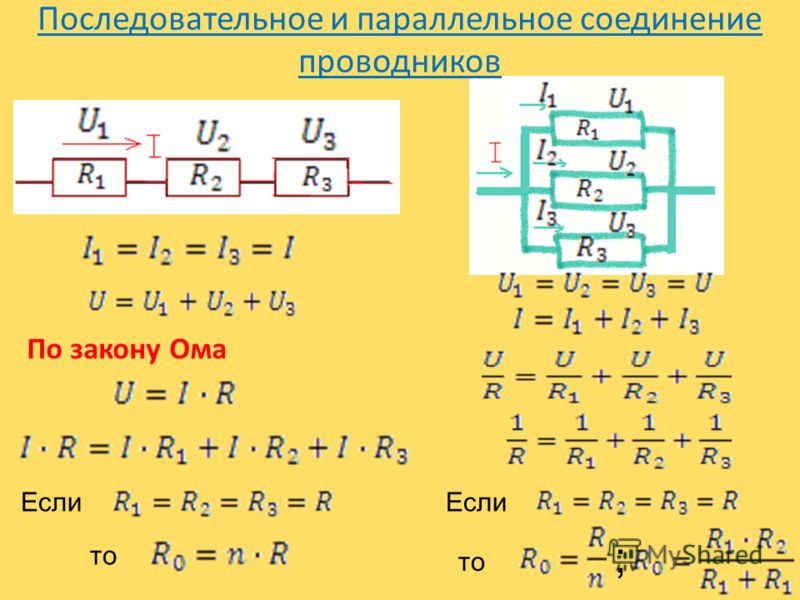 Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов.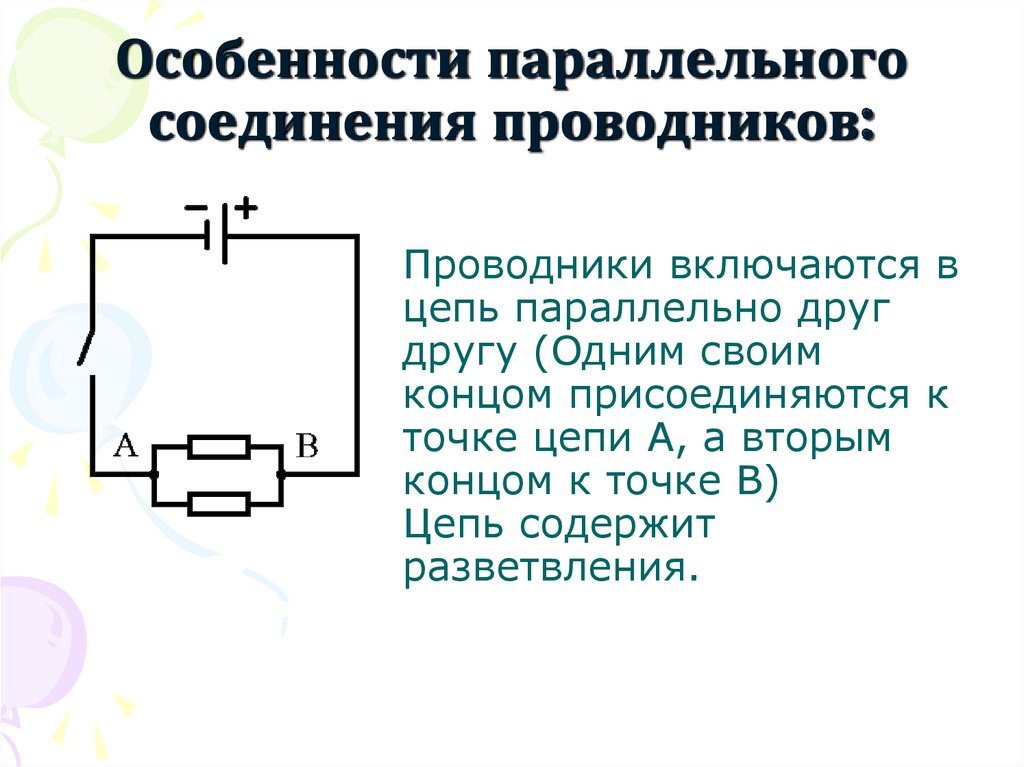 Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

• Первая формула для последовательного вида соединения.
• Далее, для параллельной схемы.
• И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.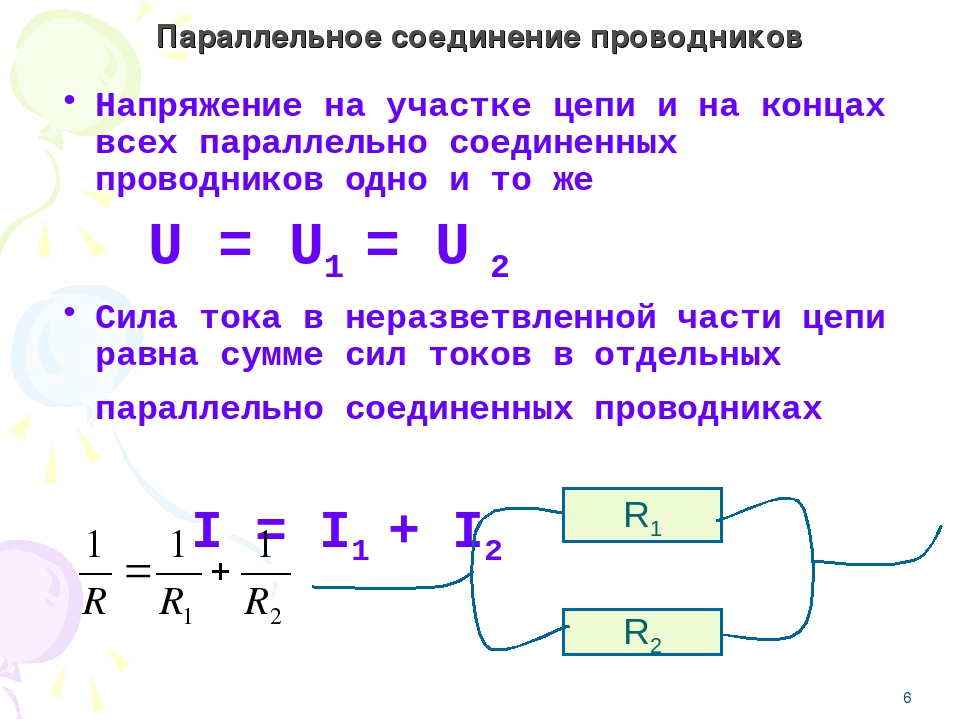

3.2.7 Параллельное соединение проводников. Последовательное соединение проводников

Видеоурок 1: Последовательное соединение проводников

Видеоурок 2: Параллельное соединение проводников

Лекция: Параллельное соединение проводников. Последовательное  соединение проводников

Электрические цепи даже в обыкновенной комнате имеют достаточно сложное строение. Такие цепи называются цепями со смешанным соединением. Однако, несмотря на это, физики привыкли все сложное разбивать на простые элементарные части. Поэтому любое сложное соединение можно разбить на части только с последовательным или параллельным соединением. Прежде, чем убедиться в этом на практике, необходимо знать некоторые основные правила и термины.

Структура и характеристика цепи

В электрической цепи имеется огромное количество различных приборов, а также других составных частей. Однако при рассмотрении любого участка нам необходимо знать величины основных физических величин. Через любую часть цепи проходит определенная сила тока, имеется некоторое значение напряжения, а также всегда есть сопротивление. Именно поэтому участки с сопротивлением обозначаются следующим образом, и называются резисторами:

Напряжением на данном резисторе считают изменение потенциалов на входе и выходе из резистора.  Как известно, в электрической цепи ток направлен от полюса «+» к полюсу «-«, именно поэтому потенциал на входе в резистор всегда больше, чем потенциал на выходе. Вот эта разница и приводит к падению напряжения на данном участке.

При рассмотрении любой цепи в школьном курсе физики пользуются упрощенной схемой — считается, что сопротивление на проводах нулевое и напряжение на них не падает. Но мы знаем, что у каждого вещества, из которого состоит проводник, имеется сопротивление.

Последовательное соединение

При данном виде соединения концы одного участка цепи присоединяются к началу другого участка.

Рассмотрим следующую цепь, где все резисторы соединены последовательно:

1. На каждом участке цепи сила тока одинакова. Из-за того, что не происходит никакого разветвления, при одинаковом поперечном сечении проводников, за одинаковое время проходит одинаковое количество электронов.

 I = const

2. Напряжение во всей цепи равно сумме напряжений на каждом участке. Так как мы знаем, что напряжение — это величина, которая характеризуется работой, необходимой для перемещения заряда, то общая работа равна сумме работ на участках.

3. Для нахождения общего сопротивления, сопротивления всех участков следует сложить.

Все изложенные свойства не зависят от количества участков цепи — их может быть больше двух. В данном случае в формуле увеличится количество слагаемых напряжений и сопротивлений.

Параллельное соединение

При данном соединении начала всех резисторов соединяются в одной точке, а концы — в другой.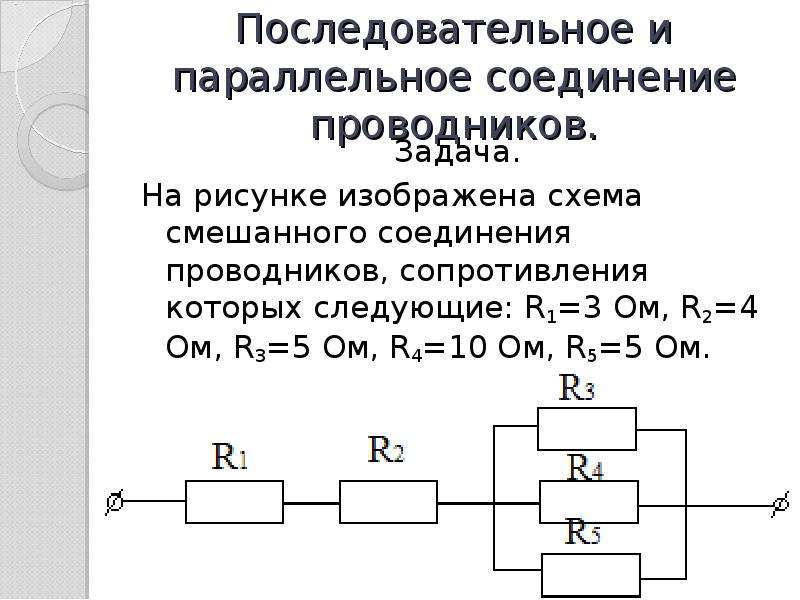

Рассмотрим все свойства параллельного соединения на примере двух параллельно соединенных резисторов. Обратите внимание на схему — на ней указаны две точки, которые названы буквами А и В. Эти точки называются узлами. Именно в данных узлах соединены участки цепи. Каждый участок, разъединенный узлом, называется веткой.

1. На каждой ветке наблюдается одинаковое значение падения напряжения.

 

U = const

2. Как нам известно, ток желает идти по той цепи, где имеется меньшее сопротивление, поэтому по каждой ветви будет проходить различная величина силы тока, в зависимости от сопротивления. Поэтому сила тока во всей цепи равна сумме сил тока на ветвях.

3. Для нахождения сопротивления всей цепи следует воспользоваться следующей формулой:

Сокращая на U, получим:

Если из данного соотношения вывести прямую формулу для нахождения общего сопротивление, то получим:

Если рассматриваемая цепь состоит из бесконечного количества резисторов с одинаковым сопротивлением, то для нахождения общего сопротивления следует значение одного сопротивления разделить на количество резисторов в цепи:

Отсюда можно сделать вывод: при параллельном соединении общее значение сопротивления уменьшается.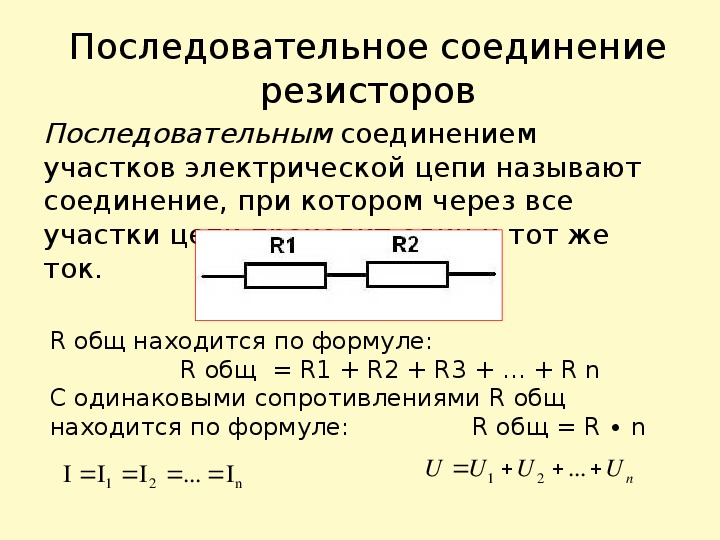

Последовательное и параллельное соединение светодиодов

При конструировании различных электронных устройств часто возникает необходимость в последовательном, параллельном или комбинированном включении элементов. Не стали исключением и светодиоды. Учитывая их небольшие размеры, а также с целью повышения яркости, в одном корпусе осветительного прибора можно разместить несколько LED-чипов.

Как правильно собрать электрическую цепь, чтобы надёжность схемы была на высоком уровне? Что нужно знать о светодиодах, соединяя их параллельно или последовательно?

Параллельное соединение

Необходимость в параллельном включении возникает в случае, когда напряжения источника питания недостаточно для запитки нескольких последовательно соединённых светодиодов. Теоретически, в самом простом варианте можно было бы отдельно объединить все аноды и все катоды излучающих диодов. После чего подключить их к источнику напряжения с соблюдением полярности.

Но такая схема не работоспособна, так как дифференциальное сопротивление открытого светодиода чрезмерно мало, что провоцирует режим короткого замыкания. В результате все светодиоды в цепи единожды вспыхнут и навсегда погаснут.

Но как говорят: «Правило без исключений не бывает». В китайских игрушках и зажигалках с подсветкой можно увидеть, что светодиоды запитаны прямо от батареек без каких-либо промежуточных элементов. Почему они не перегорают? Дело в том, что ток в цепи ограничен внутренним сопротивлением круглых батареек типа AG1. Их мощности недостаточно, чтобы нанести вред светодиоду.

Ограничить резкое нарастание тока в нагрузке можно с помощью резистора. О том, как это грамотно сделать с одним светодиодом, подробно написано в данной статье. Для цепи из нескольких параллельно подключенных LED с одним резистором схема примет следующий вид.

Но и этот вариант не пригоден для конструирования осветительных устройств с высокой надёжностью. Почему? Ответ на этот вопрос кроется в особенностях строения полупроводников. В процессе производства полупроводниковых элементов невозможно получить два абсолютно одинаковых прибора. Даже у светодиодов из одной партии будет разное дифференциальное (внутреннее) сопротивление, от которого зависит величина прямого напряжения. Это касается не только светодиодов, но и других полупроводников. Среди  диодов, транзисторов и тиристоров тоже не найти двух приборов с равными электрическими параметрами.

Из второй схемы видно, что резистор R1 ограничивает только суммарный ток цепи, который затем распределяется по ветвям со светодиодами в зависимости от их сопротивления. По закону Ома светодиод с наименьшим сопротивлением p-n-перехода получит наибольшую порцию тока. И скорее всего он будет больше номинального значения, что ускорит деградацию кристалла. Работа светодиода в режиме перегрузки по току рано или поздно приведёт к выходу из строя на обрыв. Оставшиеся в работе светодиоды распределят между собой ток сгоревшего элемента, что также приведёт к резкой потере яркости.

Как и в первом варианте, китайцы не стесняются конструировать светильники на базе «полурабочих» схем. Схему с одним резистором часто можно встретить в дешёвых фонариках и маломощных светильниках на пальчиковых батарейках. А чтобы светодиоды проработали хотя бы год, сопротивление резистора умышленно завышают, как бы, исключая возможные перегрузки.

Ниже приведен единственно верный вариант параллельного включения светодиодов.

Здесь последовательно с каждым светодиодом подключен ограничительный резистор. Такое схемотехническое решение позволяет выровнять токи в каждой отдельной ветви, не позволяя им превышать рабочее значение.

Подключать светодиоды через резистор рекомендуется только от стабилизированного источника постоянного напряжения.

Пример расчета

Для закрепления теоретических знаний параллельное соединение светодиодов рассмотрим на конкретном примере.

В схеме включены два светодиода: слаботочный красный и мощный одноваттный белый, которые для удобства можно запитать от разных выключателей.

Дано:

• источник напряжения U = +5 В;
• LED1 – красного свечения с U_LED1 = 1,8 В и I_LED1 = 0,02 А;
• LED2 – белого свечения с U_LED2 = 3,2 В и I_LED2 = 0,35 А.

Требуется рассчитать параметры и выбрать резисторы R1 и R2.

При параллельном включении к обеим ветвям (R1-LED1 и R2- LED2) прикладывается одинаковое напряжение, равное 5 В. Сопротивление каждого резистора определим по формуле:

Округляем полученное значение R2 до ближайшего большего значения из стандартного ряда E24 – 5,1 Ом. Подставив его обратно в формулу, находим реальный ток во второй ветви: С учетом возможного отклонения сопротивления выбранного резистора, которое для ряда Е24 может достигать 5%, ток 0,33 А является оптимальным. Снижение рабочего тока примерно на 4% сильно не повлияет на яркость, но позволит светодиоду работать без перегрузок.

Мощность, которую должны рассеивать резисторы, определим с учетом пересчёта тока LED2 по формуле:

Резистор R1 подойдёт любой как планарный, так и с выводами сопротивлением 160 Ом и мощностью 0,125 Вт. Корпус резистора R2 должен эффективно отводить тепло в течение длительной работы светильника. Поэтому его выбираем с двойным запасом по мощности, а именно: 5,1 Ом – 1 Вт.

Последовательное соединение

В последовательном включении светодиодов нужно соблюдать правило: «Напряжение источника питания должно быть больше суммы падений напряжений на светодиодах».

Остаток напряжения в неравенстве гасится одним единственным резистором R, правильное включение которого показано на схеме. Все светодиоды подключаются поочередно от анода к катоду. Сопротивление резистора задаёт ток цепи. Это значит, что соединять последовательно можно светодиоды только с одинаковым рабочим током.

Пример расчета

Расчет сопротивления и мощности резистора проведём на примере включения трёх белых светодиодов из серии Cree XM-L, для которых характерным является ток I_LED = 0,7 А и прямое напряжение U_LED = 2,9 В. Взяв за основу цветовую температуру и требуемую яркость, можно последовательно подключать светодиоды из разных групп в пределах серии XM-L. Например, один Cree XM-L-T6 с ТС=5000°K и два Cree XM-L-T2 с ТС=2600°K, которые в итоге дадут мощный поток нейтрального света.

Питание на схему поступает от блока стабилизированного напряжения U = +12 В. Сопротивление резистора находим по закону Ома: Ближайший стандартный номинал – 4,7 Ом, при котором ток теоретически будет равен 0,702 А. Это не критично, но следует быть уверенным, что сопротивление резистора не изменится под влиянием температуры во время работы. Поэтому устанавливать нужно либо прецизионный резистор с допуском менее 1%, либо последовательно с R1 = 4,7 Ом запаять ещё одно сопротивление 0,1-0,2 Ом такой же мощности.

Найдём мощность резистора:

По аналогии с расчётами для первой схемы устанавливать нужно резистор примерно с двойным запасом по мощности, то есть один на 5 Вт. Можно его заменить на два штуки по 2 Вт, но тогда придётся пересчитать сопротивление.

Два важных момента

В момент первого включения желательно измерить мультиметром ток в цепи и падение напряжения на каждом светодиоде. Если полученные данные будут отличаться от расчётных, то нужно пересчитать сопротивление резистора. Иначе, ток в схеме может оказаться слишком заниженным (с потерей яркости) или завышенным (с перегревом чипа светодиода).

Как в последовательном, так и в параллельном включении светодиодов нельзя делать расчеты, ссылаясь исключительно на способность источника питания обеспечить нужный ток или напряжение. Важны оба этих параметра, произведение которых даёт мощность. Мощность блока питания всегда должна быть больше мощности потребления, чтобы гарантировать стабильную и продолжительную работу всего устройства.

Последовательное, параллельное и смешанное соединения резисторов (приемников электрической энергии)

Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определен­ное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Разли­чают следующие способы соединения резисторов (приемников элек­трической энергии): последовательное, параллельное и смешанное.

Последовательное соединение.При последовательном соединении нескольких резисторов конец первого резистора соединяют с нача­лом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток /.

Последовательное соединение приемников поясняет рис. 25, а. Заменяя лампы резисторами с сопротивлениями /?ь /?₂ и Яз, полу­чим схему, показанную на рис. 25, б.

Если принять, что в источнике /?о = 0, то для трех последо­вательно соединенных резисторов согласно второму закону Кирх­гофа можно написать:

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.

Следовательно, напряжение V на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.

Из указанных формул следует также, что напряжения распре­деляются между последовательно соединенными резисторами про­порционально их сопротивлениям:

т. е. чем больше сопротивление какого-либо приемника в последо­вательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, напри­мер п, резисторов с одинаковым сопротивлением /?|, эквивалентное сопротивление цепи У?_эк будет в п раз больше сопротивления /?1, т. е. /?_зк = «/?1. Напряжение V\ на каждом резисторе в этом случае в п раз меньше общего напряжения V:

 

Последовательно могут соединяться любые приемники, в частно­сти электрические двигатели. На электровозах постоянного тока в начальный период разгона поезда тяговые двигатели включены последовательно. Этим достигается уменьшение напряжения, при­ходящегося на каждый двигатель.

При последовательном соединении приемников изменение со­противления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в осталь­ных приемниках прекращается ток. Поэтому последовательное сое­динение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напря­жение в электрической сети, от которой питаются вагоны метро­политена, составляет 825 В, номинальное же напряжение электри­ческих ламп, применяемых в этих вагонах, 55 В. Поэтому в ваго­нах метрополитена электрические лампы включают последо­вательно по 15 ламп в каждой цепи.

 

Параллельное соединение. При параллельном соединении не­скольких приемников они включаются между двумя точками элек­трической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

лампы резисторами с сопротивлениями , получим схему, показанную на рис. 26, б.

При пьраллелыюм соединении ко всем резисторам приложено одинаковое напряжение II. Поэтому согласно закону Ома:

Ток в неразветвленной части цепи согласно первому закону КирХГОфа

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

Вводя в формулу вместо значений соответствующие проводимости О_эк, Оь Ог и 0₃, получим: эквивалентная проводимость параллельной цепи равна сумме про-водимостей параллельно соединенных резисторов:

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи уве­личивается, а результирующее сопротивление уменьшается.

Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях. В этом отношении имеет место полная аналогия между рас­пределением токов по отдельным ветвям и распределением потоков воды по трубам.

Приведенные формулы дают возможность определить эквива­лентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результи­рующее сопротивление цепи

при трех параллельно включенных резисторах

При параллельном соединении нескольких, например п, рези­сторов с одинаковым сопротивлением Лл результирующее сопро­тивление цепи /?_эк будет в п раз меньше сопротивления Я\, т. е. Проходящий по каждой ветви ток /1 в этом случае будет в п раз меньше общего тока /:

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно полу­чило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы пр»и определенном (номинальном) напряжении, всегда включают параллельно.

На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на парал­лельное.

Читайте также:

 

Лабораторная работа №2 — Исследование электрических цепей при последовательном и параллельном соединении резисторов

Лабораторная работа 2

Тема: Исследование электрических цепей при последовательном и

параллельном соединении резисторов

Цель: Проверка основных закономерностей в цепях последовательного и параллельного соединения резисторов.

Студент должен

знать:

— основные закономерности в цепях с последовательным и параллельным соединением

резисторов;

— законы Ома;

— законы Кирхгофа;

уметь:

— рассчитывать параметры цепей при последовательном и параллельном соединении

резисторов;

— применять законы Ома, Кирхгофа.

Теоретическое обоснование

Соединение резисторов. Законы Кирхгофа позволяют анализировать и рассчитывать

электрические цепи с одним источником при различных соединениях резисторов.

Последовательным соединением участков электрической цепи называют соединение,

при котором через все участки цепи проходит один и тот же ток (см. рисунок 1.1).

Напряжение на каждом последовательно включенном участке пропорционально

величине сопротивления этого участка.

При последовательном соединении потребителей с сопротивлениями и напряжение на их зажимах равно:

Рисунок 1.1 — Последовательное соединение резисторов

Воспользовавшись вторым законом Кирхгофа для рассматриваемой цепи (рисунок 1.1), можно записать:

или

Откуда

т. е. общее (эквивалентное) сопротивление последовательно потребителей равно сумме сопротивлений этих потребителей.

Ток в цепи последовательно включенных потребителей (рисунок 1.1) определяется

выражением:

Из этого выражения следует, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а, следовательно, и режим работы (напряжение)

всех последовательно включенных потребителей (резисторов).

Характерно, что при последовательном соединении потребителей на большем сопротивлении тратится большая мощность:

Параллельным соединением участков электрической цепи называют соединение, при

котором все участки цепи присоединяются к одной паре узлов, т. е. находятся под

действием одного и того же напряжения (см. рисунок 1.2). Токи параллельно

включенных участков обратно пропорциональны сопротивлениям этих участков. При

параллельном соединении потребителей с сопротивлениями токи

потребителей равны:

Воспользовавшись первым законом Кирхгофа для рассматриваемой цепи, можно

определить ток в неразветвленной части цепи:

или

Рисунок 1.2 — Параллельное соединение резисторов

Т. е. обратная величина общего (эквивалентного) сопротивления (R) параллельно

включенных потребителей равна сумме обратных величин сопротивлений этих

потребителей.

Величина, обратная сопротивлению, определяет проводимость потребителя (g).

Общая (эквивалентная) проводимость цепи при параллельном соединении потребителей

определяется выражением:

Если параллельно включены п одинаковых потребителей с cпротивлением

каждое, то эквивалентное сопротивление этих потребителей .

Если параллельно включены два потребителя с сопротивлениями и , то общее

(эквивалентное) их сопротивление по (9):

Изменение сопротивления какого-либо из параллельно соединенных потребителей не

влияет на режим работы (напряжение) всех потребителей, включая изменяемый.

Поэтому параллельное соединение потребителей нашло широкое практическое

применение.

При параллельном соединении потребителей на большем сопротивлении тратится

меньшая мощность:

Ход работы

1 Исследование цепи при последовательном соединении резисторов

1. 1. Собрать электрическую схему (рисунок 1.3) и дать проверить ее преподавателю.

   2. Включить блок питания БП — 15. Установить напряжение цепи 20 В.

   3. Выключатель SA включить. С помощью амперметра измерить ток в цепи, с помощью вольтметра — падения напряжений на отдельных ее участках для двух положений движков реостатов. Результаты измерений занести в таблицу 1.1.

На рисунке 1.3, 1.4 приведены электрические схемы опытов. При сборке электрических цепей по приведенным схемам используется следующее оборудование:

G1, G2 — источники постоянного напряжения БП — 15;

РА — амперметр;

PU — вольтметр;

R1 — реостат на 1 кОм;

R2 — реостат на 220 Ом;

R3 — реостат на 220 Ом;

SA — выключатель.

Рисунок 1.3 — Схема для исследования цепи с последовательным соединением

резисторов

Таблица 1.1 — Результаты исследования цепи с последовательным соединением резисторов

1. 4. По результатам исследования цепи с последовательным соединением резисторов рассчитать напряжение на зажимах цепи

Результаты вычислений занести в таблицу 1.1. Сравнив результат с заданным напряжением

.

1. 5. Вычислить величину эквивалентного сопротивления цепи, воспользовавшись законом Ома

Результаты вычислений нести в таблицу 1.1.

1. 6. Определить сопротивления , воспользовавшись законом Ома для участка электрической цепи.

   7. Определить эквивалентное сопротивление цепи по свойствам последовательного соединения резисторов. Сравнить с результатом, полученным в п.1.5.

   8. По закону Ома для всей цепи вычислить ток . Сравнить с измеренным значением.

   9. Вычислить отношения падений напряжений и отношения соответствующих сопротивлений и сделать вывод о распределении напряжений при последовательном соединении резисторов.

2. Исследование цепи при параллельном соединении резисторов

1. Собрать электрическую схему (рисунок 1.4) и дать проверить ее преподавателю.

2. Включить блок питания БП — 15. Установить напряжение цепи 20 В.

3. Выключатель SA включить. С помощью амперметров измерить общий ток и токи ветвей, с помощью вольтметра — падения напряжений на отдельных ее участках цепи двух положений движков реостатов. Результаты измерений занести в таблицу 1.2.

Рисунок 1.4 — Схема для исследования цепи с параллельным соединением резисторов

Таблица 1.2 — Результаты исследования цепи с параллельным соединением резисторов

опыта

2. 4. Вычислить эквивалентное сопротивление цепи, воспользовавшись законом Ома для всей цепи

Результаты вычислений занести в таблицу 1.2.

2. 4. Определить общий ток в цепи по свойствам параллельного соединения резисторов.

Сравнить с измеренным значением тока.

2. 4. Вычислить сопротивления резисторов по закону Ома для участка цепи.

   5. Определить проводимости элементов и эквивалентную проводимость цепи по формуле

2. 4. Вычислить эквивалентную проводимость цепи по свойству параллельного соединения резисторов. Сравнить с результатом в п.2.7.

   5. Вычислить отношения для двух опытов. Сделать вывод о распределении токов при параллельном соединении резисторов. Проверить справедливость первого закона Кирхгофа.

Контрольные вопросы

1. Как изменится ток в цепи при увеличении последовательно включенных резисторов?

2. Как изменится мощность цепи, если увеличить количество последовательно соединенных резисторов?

3. Чем объяснить равенство отношений и при любом изменении режима работы в последовательной цепи?

4. Перечислите свойства последовательного соединения резисторов.

5. Как изменится ток в цепи при увеличении числа параллельно включенных резисторов?

6. Как зависит величина потребляемой мощности от количества параллельно включенных резисторов?

7. Как изменится ток в цепи, если закоротить .

а) при последовательном соединении резисторов;

б) при параллельном соединении резисторов.

8. Чем объяснить равенство отношений RI/R2, и I2/I1 при любом изменении режима работы в параллельной цепи?

9. Перечислите свойства параллельного соединения резисторов.

Содержание отчета

1. Номер, тема и цель работы.

2. Схема опыта рисунок 1.3, 1.4.

3. Ход работы.

4. Результаты измерений и вычислений.

5. Сделать вывод.

6. Ответы на контрольные вопросы письменно.

Литература

1. А.К. Славинский, И.С. Туревский — Электротехника с основами электроники, 2013.-с. 40

2. Лоторейчук, Е.А.- Теоритические основы электротехники: 2014. –с. 24, 25

Серия

и параллельные схемы — скачать видео на ppt онлайн

Презентация на тему: «Последовательные и параллельные схемы» — стенограмма презентации:

1 Серия и параллельные схемы

2 Последовательные схемы Описывает два или более компонентов в цепи, которые обеспечивают единственный путь для тока.

3 Факты о последовательных схемах
Чем больше лампочек вы добавляете, тем меньше яркость света, потому что ток распределяется по всем из них. Если одна лампочка перегорела, она разрывает цепь и ничего не загорается. Ток одинаков в каждой. резистор Падение напряжения меняется в зависимости от силы резистора

4 Чтобы определить ток, протекающий через каждый резистор….
Нам нужно найти эквивалентное сопротивление

5 Эквивалентное сопротивление: последовательные цепи
Req = R1 + R2 +…. + Rn 3 кОм + 10 кОм + 5 кОм = 18 кОм Req = 18 кОм

6 Параллельные цепи Описывает два или более компонентов схемы, которые обеспечивают отдельные токопроводящие пути, поскольку компоненты соединены через общие точки или соединения.

7 Факты о параллельных цепях
Каждая лампочка получает весь ток — не имеет значения, сколько лампочек вы добавляете Напряжение одинаково на всех резисторах Общий ток в батарее равен сумме токов, проходящих через каждый резистор

8 Чтобы найти эквивалентное сопротивление в параллельной цепи
1 / Req = 1 / R1 + 1 / R2 +… + 1 / Rn 1 / Req = 1 / 10Ω + 1 / 2Ω + 1/1 Ω 1 / Req = 0 .1 Ом + 0,5 Ом + 1 Ом = 1,6 Ом Req = 1 / 1,6 Ом

Параллельные и последовательные цепи

• Ресурс исследования
• Исследовать
  • Искусство и гуманитарные науки
  • Бизнес
  • Инженерная технология
  • Иностранный язык
  • История
  • Математика
  • Наука
  • Социальная наука

  Лучшие подкатегории

  • Продвинутая математика
  • Алгебра
  • Базовая математика
  • Исчисление
  • Геометрия
  • Линейная алгебра
  • Предалгебра
  • Предварительный расчет
  • Статистика и вероятность
  • Тригонометрия
  • другое →

  Лучшие подкатегории

  • Астрономия
  • Астрофизика
  • Биология
  • Химия
  • Науки о Земле
  • Наука об окружающей среде
  • Здравоохранение
  • Физика
  • другое →

  Лучшие подкатегории

  • Антропология
  • Закон
  • Политология
  • Психология
  • Социология
  • другое →

  Лучшие подкатегории

  • Бухгалтерский учет
  • Экономика
  • Финансы
  • Менеджмент
  • другое →

  Лучшие подкатегории

  • Аэрокосмическая техника
  • Биоинженерия
  • Химическая инженерия
  • Ci

Импеданс R и C параллельно Калькулятор

[1] 2020/11/19 22:30 — / 60 лет или старше / Другое / Не совсем /

Цель использования

разработка емкостной навигационной системы

[2] 2020/08/27 09:11 Мужской / 20-летний уровень / Высшая школа / Университет / аспирант / Очень /

Цель использования

Проверка домашнего задания

[3] 2020/08/22 22:25 Мужчина / Уровень 50 лет / Учитель / Исследователь / Полезно /

Цель использования

При обратном, т.е.е. известны различные значения угла и импеданса, каковы значения сопротивления и емкости?

Комментарий / запрос

При инверсии, т.е. известны разные значения угла и импеданса, каковы значения сопротивления и емкости?

[4] 2020/04/17 00:06 Мужчина / Уровень 20 лет / Инженер / Очень /

Цель использования

Сравните результаты с индивидуальной конструкцией анализатора импеданса.

[5] 2020/04/13 06:49 Женский / 50-летний уровень / Высшая школа / Университет / аспирант / Очень /

Цель использования

Убедитесь, что я правильно рассчитываю полное сопротивление для параллельная цепь переменного тока для класса электроники.

[6] 2020/03/14 09:14 Мужчина / Уровень 40 лет / Инженер / Очень /

Цель использования

Определение значений R, C для желаемого гистерезиса, используемого с ОУ (Horowitz & Hill стр. 134-5)

[7] 2019/12/13 05:07 Мужчина / Уровень 30 лет / Инженер / Очень /

Цель использования

bangin ur mom

[8] 2019/10/04 01:42 Мужской / Уровень 20 лет / Средняя школа / Университет / Аспирант / Очень /

Цель использования

Проверь мою интуицию в задаче домашнего задания

[9] 2019/09 / 10 05:36 Мужчина / 60 лет и старше / Учитель / Исследователь / Очень /

Цель использования

Проверка прибора Fluke RCL, чтобы убедиться, что он все еще функционирует нормально

действительно оценил вашу точную программу

[10] 2018/03/21 16:15 Женщина / Уровень 30 лет / Инженер / — /

Цель o f используйте регулятор вентилятора

Комментарий / запрос

предоставьте мне принципиальную схему с номинальными характеристиками конденсаторного регулятора вентилятора

Серия

и параллельные схемы — Скачать PDF бесплатно

Студенческое исследование: схемы

Имя: Дата: Изучение учащимися: Схемы Словарь: амперметр, цепь, ток, омметр, закон Ома, параллельная цепь, сопротивление, резистор, последовательная цепь, напряжение Вопросы предварительных знаний (выполните следующие

Дополнительная информация

Последовательные и параллельные схемы

Постоянный ток (DC) Постоянный ток (DC) — это однонаправленный поток электрического заряда.Термин DC используется для обозначения энергосистем, которые используют постоянное (не меняющееся со временем) среднее (среднее)

. Дополнительная информация

Глава 13: Электрические схемы

Глава 13: Электрические цепи 1. Бытовая цепь, рассчитанная на 120 Вольт, защищена предохранителем на 15 Ампер. Какое максимальное количество лампочек мощностью 100 Вт может одновременно гореть параллельно?

Дополнительная информация

Книга по физике народа

Большие идеи: название «электрический ток» происходит от явления, которое возникает, когда электрическое поле движется по проводу со скоростью, близкой к скорости света.Напряжение — это плотность электрической энергии (энергия

Дополнительная информация

Учебник 12 Решения

Решения PHYS000 Tutorial 2 Tutorial 2 Solutions. Два резистора номиналом 00 Ом и 200 Ом последовательно подключены к источнику питания 6,0 В постоянного тока. (а) Нарисуйте принципиальную схему. 6 В 00 Ом 200 Ом (б) Всего

Дополнительная информация

Параллельные цепи постоянного тока

Параллельные цепи постоянного тока Этот рабочий лист и все связанные файлы находятся под лицензией Creative Commons Attribution License, версия 1.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/1.0/,

. Дополнительная информация

Лампочки в параллельных цепях

Лампочки в параллельных цепях В прошлом упражнении мы проанализировали несколько различных последовательных цепей. В последовательной цепи есть только один полный путь для прохождения заряда. Вот базовый

Дополнительная информация

Расчет схемы трансформатора

Расчеты схемы трансформатора. Эта таблица и все связанные файлы находятся под лицензией Creative Commons Attribution License, версия 1.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/1.0/,

. Дополнительная информация

Резисторы последовательно и параллельно

Последовательные и параллельные резисторы Bởi: OpenStaxCollege Большинство схем имеет более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела для потока заряда

Дополнительная информация

Глава 19.Электрические схемы

Глава 9 Электрические цепи Последовательная проводка Существует много цепей, в которых к источнику напряжения подключено более одного устройства. Последовательная проводка означает, что устройства подключены таким образом, что

Дополнительная информация

ГЛАВА 28 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

ГЛАВА 8 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ 1. Нарисуйте принципиальную схему цепи, которая включает в себя резистор R 1, подключенный к положительной клемме батареи, пару параллельных резисторов R и R, подключенных к

. Дополнительная информация

Закон Ома.Джордж Саймон Ом

Закон Ома Джордж Саймон Ом Закон, регулирующий самые простые и многие сложные электрические явления, известен как закон Ома. Это самый важный закон в электричестве. В 1827 году немецкий слесарь и математик

Дополнительная информация

Закон ОМ и СОПРОТИВЛЕНИЕ

ЗАКОН ОМА И СОПРОТИВЛЕНИЕ Сопротивление — один из основных принципов закона Ома, и его можно найти практически в любом устройстве, используемом для проведения электричества.Георг Симон Ом был немецким физиком, который провел

Дополнительная информация

Лабораторная работа 3 — Цепи постоянного тока и закон Ома

Лабораторная работа 3 — Цепи постоянного тока и закон Ома L3-1 Имя Дата Партнеры Лаборатория 3 — Цепи постоянного тока и закон Ома ЦЕЛИ Научиться применять концепцию разности потенциалов (напряжения) для объяснения действия батареи в

Дополнительная информация

Глава 7 Цепи постоянного тока

Глава 7 Цепи постоянного тока 7.Введение … 7-7. Электродвижущая сила … 7-3 7.3 Последовательные и параллельные резисторы … 7-5 7.4 Правила схемы Кирхгофа … 7-7 7.5 Измерения напряжения-тока … 7-9

Дополнительная информация

Теория электрических цепей

Задачи изучения теории электрических цепей: 1. Ознакомиться с основными электрическими понятиями напряжения, силы тока и сопротивления. 2. Просмотрите компоненты базовой автомобильной электрической цепи.3. Введите

Дополнительная информация

Резисторы последовательно и параллельно

Модуль OpenStax-CNX: m42356 1 Последовательные и параллельные резисторы OpenStax College Эта работа произведена OpenStax-CNX и находится под лицензией Creative Commons Attribution License 3.0 Аннотация Нарисуйте схему

Дополнительная информация

Цепи трехфазного переменного тока

Цепи трехфазного переменного тока Этот рабочий лист и все связанные файлы находятся под лицензией Creative Commons Attribution License, версия 1.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/1.0/,

. Дополнительная информация

Решения на вопросы о лампах

Решения на вопросы о лампах Примечание. Мы сделали несколько основных схем с лампами, на самом деле, три основных, о которых я могу вспомнить. Я суммировал наши результаты ниже. Для сдачи выпускного экзамена вы должны понимать

. Дополнительная информация

Закон Ома и схемы

2.Электропроводность, изоляторы и сопротивление A. Электропроводник — это материал, который позволяет электронам легко проходить через него. Металлы в целом хорошие проводники. Почему? Свойство проводимости

Дополнительная информация

Eisflisfræði 2, vor 2007 г.

[Просмотр задания] [Печать] Eðlisfræði 2, vor 2007 30. Назначение индуктивности должно быть произведено в 2:00 утра в среду, 14 марта 2007 г. Кредит за проблемы, представленные с опозданием, уменьшится до 0% после того, как крайний срок достигнет

. Дополнительная информация

Энергия, работа и сила

Энергия, работа и мощность Этот рабочий лист и все связанные файлы находятся под лицензией Creative Commons Attribution License, версия 1.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/1.0/,

. Дополнительная информация

Эксперимент 3, закон Ома

Эксперимент № 3, Закон Ома 1 Цель Физика 182 — Лето 2013 г. — Эксперимент № 3 1 Для исследования характеристик напряжения, -, углеродного резистора при комнатной температуре и температуре жидкого азота,

Дополнительная информация

ТЕКУЩЕЕ ЭЛЕКТРИЧЕСТВО — I

ТЕКУЩИЙ ЛИСТ — 1.электрический ток 2. Обычный ток 3. Дрейф электронов и ток 4. Плотность тока 5. Закон Ома 6. Сопротивление, удельное сопротивление, проводимость и проводимость 7. Температура

Дополнительная информация

Раздел B: Электричество

Раздел B: Электроэнергия Мы используем электрическую сеть, поставляемую электростанциями, для всех видов бытовой техники в наших домах, поэтому очень важно знать, как ее использовать безопасно.В этой главе вы узнаете

Дополнительная информация

Падение напряжения (однофазное)

Падение напряжения (однофазное) Чтобы найти: Чтобы найти формулу падения напряжения: 2 x K x L x I V.D. = ——————- C.M. Переменные: C.M. = Площадь круговой мельницы (глава 9, таблица 8) для определения процента падения напряжения

Дополнительная информация

Разница в электрическом потенциале

Название: Разница электрических потенциалов Прочтите из Урока 1 главы «Текущее электричество» в Физическом классе: http: // www.Physicsclassroom.com/class/circuits/u9l1a.html http://www.physicsclassroom.com/class/circuits/u9l1b.html

Дополнительная информация

Последовательные и параллельные схемы

Последовательные и параллельные цепи Последовательные цепи постоянного тока Последовательная цепь — это цепь, в которой компоненты соединены в линию, один за другим, как железнодорожные вагоны на одной дороге. Есть

Дополнительная информация

% PDF-1.4 % 17298 0 объект > endobj xref 17298 201 0000000016 00000 н. 0000004400 00000 н. 0000004671 00000 п. 0000004825 00000 н. 0000004880 00000 н. 0000004940 00000 н. 0000004998 00000 н. 0000005056 00000 н. 0000005212 00000 н. 0000008620 00000 н. 0000024375 00000 п. 0000024558 00000 п. 0000024631 00000 п. 0000024787 00000 п. 0000024907 00000 п. 0000025086 00000 п. 0000025277 00000 п. 0000025341 00000 п. 0000025516 00000 п. 0000025580 00000 п. 0000025643 00000 п. 0000025820 00000 н. 0000026013 00000 п. 0000026157 00000 п. 0000026362 00000 п. 0000026530 00000 п. 0000026674 00000 п. 0000026878 00000 п. 0000027048 00000 п. 0000027237 00000 п. 0000027448 00000 н. 0000027616 00000 н. 0000027806 00000 п. 0000028015 00000 п. 0000028184 00000 п. 0000028353 00000 п. 0000028569 00000 п. 0000028737 00000 п. 0000028888 00000 п. 0000029098 00000 н. 0000029275 00000 п. 0000029391 00000 п. 0000029598 00000 п. 0000029766 00000 п. 0000029910 00000 н. 0000030136 00000 п. 0000030304 00000 п. 0000030449 00000 п. 0000030625 00000 п. 0000030757 00000 п. 0000030871 00000 п. 0000030977 00000 п. 0000031157 00000 п. 0000031336 00000 п. 0000031458 00000 п. 0000031599 00000 н. 0000031732 00000 п. 0000031851 00000 п. 0000031964 00000 п. 0000032140 00000 п. 0000032272 00000 п. 0000032429 00000 п. 0000032534 00000 п. 0000032712 00000 п. 0000032890 00000 п. 0000033012 00000 п. 0000033152 00000 п. 0000033285 00000 п. 0000033404 00000 п. 0000033518 00000 п. 0000033696 00000 п. 0000033876 00000 п. 0000034038 00000 п. 0000034144 00000 п. 0000034265 00000 п. 0000034407 00000 п. 0000034540 00000 п. 0000034658 00000 п. 0000034773 00000 п. 0000034983 00000 п. 0000035161 00000 п. 0000035346 00000 п. 0000035471 00000 п. 0000035587 00000 п. 0000035721 00000 п. 0000035887 00000 п. 0000036059 00000 п. 0000036216 00000 п. 0000036334 00000 п. 0000036448 00000 н. 0000036587 00000 п. 0000036774 00000 п. 0000036873 00000 п. 0000036975 00000 п. 0000037153 00000 п. 0000037357 00000 п. 0000037467 00000 п. 0000037585 00000 п. 0000037755 00000 п. 0000037865 00000 п. 0000037979 00000 п. 0000038110 00000 п. 0000038292 00000 п. 0000038473 00000 п. 0000038601 00000 п. 0000038720 00000 п. 0000038834 00000 п. 0000039010 00000 п. 0000039132 00000 п. 0000039310 00000 п. 0000039432 00000 п. 0000039550 00000 п. 0000039729 00000 п. 0000039907 00000 н. 0000040001 00000 п. 0000040122 00000 п. 0000040266 00000 п. 0000040400 00000 н. 0000040526 00000 п. 0000040645 00000 п. 0000040758 00000 п. 0000040943 00000 п. 0000041065 00000 п. 0000041242 00000 п. 0000041365 00000 п. 0000041483 00000 п. 0000041661 00000 п. 0000041789 00000 п. 0000041924 00000 п. 0000042076 00000 п. 0000042210 00000 п. 0000042351 00000 п. 0000042490 00000 п. 0000042626 00000 п. 0000042747 00000 н. 0000042863 00000 п. 0000042997 00000 п. 0000043118 00000 п. 0000043232 00000 п. 0000043389 00000 п. 0000043526 00000 п. 0000043711 00000 п. 0000043890 00000 п. 0000044069 00000 п. 0000044165 00000 п. 0000044285 00000 п. 0000044415 00000 п. 0000044550 00000 п. 0000044677 00000 п. 0000044809 00000 п. 0000044940 00000 п. 0000045053 00000 п. 0000045236 00000 п. 0000045381 00000 п. 0000045556 00000 п. 0000045689 00000 п. 0000045851 00000 п. 0000045956 00000 п. 0000046134 00000 п. 0000046255 00000 п. 0000046398 00000 п. 0000046531 00000 п. 0000046650 00000 п. 0000046763 00000 п. 0000046825 00000 п. 0000046972 00000 п. 0000047168 00000 п. 0000047338 00000 п. 0000047481 00000 п. 0000047647 00000 п. 0000047811 00000 п. 0000047986 00000 п. 0000048118 00000 п. 0000048280 00000 п. 0000048386 00000 п. 0000048564 00000 н. 0000048679 00000 н. 0000048820 00000 н. 0000048953 00000 п. 0000049093 00000 п. 0000049230 00000 п. 0000049349 00000 п. 0000049462 00000 п. 0000049524 00000 п. 0000049644 00000 п. 0000049799 00000 п. 0000052205 00000 п. 0000052691 00000 п. 0000052891 00000 п. 0000053121 00000 п. 0000053415 00000 п. 0000053706 00000 п. 0000054189 00000 п. 0000054502 00000 п. 0000054915 00000 п. 0000054994 00000 п. 0000057634 00000 п. 0000061239 00000 п. 0000061381 00000 п. 0000008665 00000 н. 0000024349 00000 п. трейлер ] >> startxref 0 %% EOF 17299 0 объектов > endobj 17300 0 объект a_

Регистры

• Изучив этот раздел, вы должны уметь:
• Общие сведения о работе регистров цифрового параллельного ввода / вывода (PIPO).
• Опишите действие последовательных и параллельных регистров сдвига.
• • Последовательный вход / последовательный выход (SISO).
• • Последовательный вход / параллельный выход (SIPO).
• • Параллельный вход / последовательный выход PISO.
• Понять работу реверсивных регистров сдвига.
• Распознавать общие особенности, используемые в ИС сдвиговых регистров.
• Используйте программное обеспечение для анализа работы регистров сдвига.

Регистры параллельного входа и выхода (PIPO)

Рис.5.7.1 Регистр

для параллельного входа и выхода (PIPO)

Электронный регистр — это форма памяти, которая использует серию триггеров для хранения отдельных битов двоичного слова, например байта (8 бит) данных. Длина сохраненного двоичного слова зависит от количества триггеров, составляющих регистр. Простой 4-битный регистр показан на рис. 5.7.1 и состоит из четырех триггеров типа D, совместно использующих общий тактовый вход, обеспечивая синхронную работу, гарантирующую, что все биты сохраняются в одно и то же время.

Двоичное слово, которое нужно сохранить, подается на четыре входа D и запоминается триггерами на переднем фронте следующего тактового импульса (CK). Сохраненные данные затем могут быть считаны с выходов Q в любое время, пока поддерживается питание, или пока изменение данных на входах D не будет сохранено с помощью следующего тактового импульса, который перезаписывает предыдущие данные.

Различные типы регистров обычно классифицируются по используемому способу хранения и считывания; поэтому эта базовая форма регистра классифицируется как регистр «параллельный вход / параллельный выход» (PIPO).

регистров сдвига.

Регистры сдвига

имеют структуру, аналогичную регистру PIPO, но имеют дополнительную возможность сдвигать сохраненное двоичное слово влево или вправо, по одному биту за раз. Это делает их чрезвычайно полезными для многих приложений. Они используются для обработки последовательных данных и преобразования их в параллельную форму или обратно в последовательную форму, и поэтому являются важным компонентом в системах связи. Регистры сдвига также важны в арифметических схемах, где двоичные числа могут быть сдвинуты вправо (и, таким образом, делятся на два) или влево (умножаются на два) как часть вычисления.Регистры сдвига могут использоваться для задержки передачи данных в определенной точке цепи. Поскольку данные сдвигаются по одному биту от входа к выходу, величина задержки будет зависеть от количества триггеров в регистре и частоты тактовых импульсов, управляющих сдвиговым регистром. Поскольку ряд последовательных битов данных сохраняется, когда они поступают на вход, а затем восстанавливаются из выхода через некоторое время, это действие также можно описать как последовательную память или как цифровую линию задержки.

Рис. 5.7.2 Регистр сдвига последовательного входа / выхода (SISO)

Простой регистр хранения, показанный на рис. 5.7.1, можно преобразовать в регистр сдвига, подключив выход одного триггера к входу следующего, как показано на рис. 5.7.2. Основой схем регистров сдвига является триггер D-типа, но синхронизированный SR или JK-триггер также могут быть преобразованы в D-типы путем включения инвертора между S и R или между J и K. во всех случаях вход часов находится в синхронном режиме.

Последовательный вход сдвигового регистра на рис. 5.7.2 — это вход D первого триггера, а последовательный выход — это выход Q последнего триггера в цепочке. Логическое состояние на последовательном входе появляется на выходе, количество тактовых импульсов (равное количеству триггеров) позже.

Рис. 5.7.3 Временная диаграмма и таблица состояний для работы SISO

Режимы работы регистра сдвига.

SISO

Таблица состояний и временная диаграмма, иллюстрирующие работу рис.5.7.2 показан на рис. 5.7.3, где временная диаграмма показывает временную зависимость между импульсами CK и изменениями на выходах Q схемы. Можно видеть, что если последовательный вход переходит с 0 на 1 непосредственно перед импульсом CK 1, выход Q триггера FF0 станет высоким на переднем фронте импульса CK 1. На переднем фронте следующего тактового импульса логика 1 будет передан в FF1 и так далее, пока не достигнет FF3, и последовательный вывод.

То же действие можно проиллюстрировать таблицей состояний, которая вместо отображения данных синхронизации показывает состояния четырех выходов Q после каждого тактового импульса.После каждого импульса CK еще один выход триггера устанавливается на 1, пока после 4 импульсов столбец 4 не покажет, что все выходы Q, включая последовательный выход, находятся на логической 1. Эта форма работы называется «последовательный вход / последовательный выход». ‘или SISO.

SIPO

Рис. 5.7.4 Регистр сдвига последовательного входа / параллельного выхода (SISO / SIPO)

На рис. 5.7.4 сдвиговый регистр модифицирован для включения дополнительных Q выходов от каждого триггера, что позволяет регистру вводить последовательные данные и выводить их как в последовательной, так и в параллельной форме.Таким образом, регистр теперь можно было назвать регистром «Последовательный вход / последовательный выход и последовательный вход / параллельный выход» (SISO / SIPO). Этот формат является основой для преобразования последовательных данных в параллельные.

PISO

Рис. 5.7.5 Регистр сдвига с несколькими режимами (SISO, SIPO, PISO, PIPO)

Если также используется выход Q и дополнительные входы предварительной установки (PR) и очистки (CLR), доступные на многих триггерах, регистр сдвига можно было бы сделать еще более универсальным.

Рис.5.7.5 показывает сдвиговый регистр, модифицированный для обеспечения возможности загрузки в него 4-битного параллельного числа, которое затем может быть сдвинуто вправо, чтобы появиться на последовательном выходе по одному биту за раз. Поскольку регистр ‘Parallel In / Serial Out’ или PISO также имеет последовательный вход, он также может использоваться как регистр SISO, и если бы были включены дополнительные выходы из каждого Q-выхода, регистр также имел бы последовательный вход / параллельный выход (SIPO) операция.

Загрузка параллельных данных

Если на входе LOAD установлен логический 0, линия управления LOAD, подключенная к четырем парам вентилей И-НЕ, связанных с четырьмя триггерами, будет иметь логическую 1, и все четыре пары вентилей И-НЕ будут активированы.Следовательно, логическая 1, появляющаяся на любом из входов D, будет инвертирована вентилем НЕ, подключенным к входу D, делая входы на левый вентиль И-НЕ соответствующей пары вентилей, логической 1 и логического 0. Это вызовет логику. 1, который будет применяться к входу CLR триггера.

Правый логический элемент И-НЕ пары будет иметь оба входа на логической 1 из-за логической 1 на линии НАГРУЗКИ и логической 1 на входе D, и поэтому будет выводить логический 0 (правила логического элемента И-НЕ) на вход PR триггер, устанавливающий выход Q на логическую 1.

Если вход D имеет логический 0, левый вентиль пары вентилей И-НЕ будет выводить логический 0, а правый вентиль И-НЕ будет выдавать логическую 1, заставляя вход CLR очищать выход Q соответствующего триггера до логика 0.

Обратите внимание, что поскольку в этой конструкции используются триггеры JK, вентиль НЕ подключен между J и K первого триггера цепи, чтобы триггер JK имитировал тип D. Остальные триггеры сдвигового регистра имеют J и K, подключенные к предыдущим выходам Q и Q, поэтому они также будут в противоположных логических состояниях.

4-битный реверсивный регистр сдвига.

Сдвиговый регистр на рис. 5.7.5 может работать как:

• Регистр параллельного ввода / вывода. (PIPO)
• Регистр последовательного ввода / вывода. (SISO)
• Регистр последовательного ввода / вывода. (SIPO)
• Регистр параллельного ввода / вывода. (PISO)

Однако рис. 5.7.5 может сдвигать данные только в одном направлении, т.е. слева направо. Чтобы быть действительно универсальным, может быть преимуществом возможность сдвигать данные в обоих направлениях и в любом из четырех рабочих режимов регистра сдвига.На рис. 5.7.6 это достигается за счет добавления схемы управления данными.

Рис. 5.7.6 4-битный реверсивный регистр сдвига PIPO / PISO / SISO / SIPO

Схема стробирования в нижней части рисунка 5.7.6 (элементы G1 — G13) точно такая же, как описанная выше на рисунке 5.7.5, и эти ворота управляют загрузкой параллельных данных.

Шлюзы от G14 до G28 на рис. 5.7.6 управляют направлением потока данных через регистр. Триггеры JK используют вентили инвертора от G29 до G32, чтобы гарантировать, что J и K находятся в противоположных логических состояниях, поэтому триггеры имитируют работу типа D, а J используется в качестве входных данных.Также обратите внимание, что часы подключены в привычном синхронном режиме.

Операция.

В любом из режимов, предполагающих последовательную работу, данные могут быть сдвинуты влево или вправо путем применения подходящего логического уровня на входе управления сдвигом (R / L).

С логической 1 на этом входе регистр находится в режиме сдвига вправо, и данные принимаются на вход «Последовательный в R» для сдвига вправо путем применения последовательных тактовых импульсов, появляющихся как параллельные данные, изменяющиеся с каждым тактовым импульсом. , на выходах Q триггера.После четырех тактовых импульсов данные начинают появляться в последовательной форме на выходе Q ₃ , который также является выходом «Serial Out R».

Логическая 1 на управлении переключением (R / L) включает вентили G18, 20, 22 и 24, но поскольку логическая 1 инвертируется G27, вентили G19, 21, 23 и 25 отключены.

Последовательные данные (например, логическая 1) идут слева направо следующим образом; логическая 1, появляющаяся на входе G26, инвертируется и проходит через G18, который повторно инвертирует ее в логическую 1, и, поскольку G19 отключен, его выход также должен быть на логической 1.Оба входа логического элемента И G14 имеют логическую единицу и, следовательно, его выход (правила логического элемента И) являются входом J логической схемы FF0 1.

По прибытии тактового импульса логическая 1, входящая в FF0, появится на выходе Q ₀ . Его инверсия (логический 0) также появится на выходе Q FF0. Этот логический 0 формирует вход для следующего устройства мультиплексора, вентилей G20, 21 и 15. Когда G20 включен (и G21 отключен), логический 0 становится логической 1 на выходе G15 и, таким образом, подается на вход J FF1.Этот метод используется для передачи данных каждому триггеру в цепочке.

Для достижения операции сдвига влево регулятор сдвига (R / L) установлен на логический 0 и, таким образом, включает вентили G19, 21, 23 и 25, блокируя вентили G18, 20, 22 и 24. Таким образом, выход Q FF3 подключен через G23 и G16 на вход D FF2, выход Q FF2 подключен к входу J FF1 через G21 и G15 (помните, что G24 отключен, поэтому FF3 изолирован от этого пути). Наконец, выход Q FF1 подключен через G19 и G14 к входу J FF0, выход Q ₀ которого также является выходом «Serial Out L».Возможность сдвига данных в любом направлении вместе с возможностями параллельного ввода и вывода делают этот регистр очень универсальным устройством.

Обычно ИС сдвигового регистра соединяются каскадом, используя последовательный выход одного регистра для подключения к последовательному входу следующего регистра в цепочке.