Как перевести десятичное число в двоичное на Python. Какие встроенные функции можно использовать для конвертации. Как реализовать перевод без использования готовых функций. Какие есть особенности и нюансы при работе с системами счисления в Python.
Введение в системы счисления и двоичный код
Системы счисления играют важную роль в компьютерных науках и программировании. Двоичная система, использующая только цифры 0 и 1, является фундаментальной для работы компьютеров. Однако людям привычнее работать с десятичной системой. Поэтому задача перевода чисел между этими системами счисления часто возникает на практике.
Почему двоичная система так важна для компьютеров? Двоичный код легко представить с помощью электрических сигналов — наличие тока соответствует 1, отсутствие — 0. Это позволяет эффективно хранить и обрабатывать информацию на физическом уровне.
Встроенные функции Python для перевода в двоичную систему
Python предоставляет удобные встроенные функции для работы с разными системами счисления:
bin()— переводит целое число в строку с двоичным представлениемformat()— форматирует число в двоичном виде"{:b}".format()— еще один способ получить двоичное представление
Рассмотрим примеры использования этих функций:
«`python # Использование bin() print(bin(10)) # 0b1010 # Использование format() print(format(10, ‘b’)) # 1010 # Использование строкового метода format print(«{:b}».format(10)) # 1010 # Удаление префикса ‘0b’ при использовании bin() print(bin(10)[2:]) # 1010 «`Как видим, функция bin() добавляет префикс ‘0b’ к результату. Если он не нужен, его можно легко удалить, взяв срез строки начиная с 3-го символа.
Реализация алгоритма перевода без встроенных функций
Хотя встроенные функции очень удобны, полезно понимать сам алгоритм перевода. Реализуем его на Python без использования готовых решений:
«`python def decimal_to_binary(decimal_num): if decimal_num == 0: return «0» binary = «» while decimal_num > 0: binary = str(decimal_num % 2) + binary decimal_num //= 2 return binary # Пример использования print(decimal_to_binary(10)) # 1010 print(decimal_to_binary(255)) # 11111111 «`Этот алгоритм работает следующим образом:
- Проверяем особый случай — если число равно 0, сразу возвращаем «0»
- Инициализируем пустую строку для хранения результата
- В цикле делим число на 2, каждый раз добавляя остаток от деления (0 или 1) в начало результирующей строки
- Продолжаем, пока от числа что-то остается
Оптимизация алгоритма с использованием рекурсии
Тот же алгоритм можно реализовать рекурсивно, что может быть более элегантным решением для некоторых задач:
«`python def decimal_to_binary_recursive(decimal_num): if decimal_num == 0: return «0» elif decimal_num == 1: return «1» else: return decimal_to_binary_recursive(decimal_num // 2) + str(decimal_num % 2) # Пример использования print(decimal_to_binary_recursive(10)) # 1010 print(decimal_to_binary_recursive(255)) # 11111111 «`Обработка отрицательных чисел и чисел с плавающей точкой
До сих пор мы рассматривали только положительные целые числа. Но как быть с отрицательными числами и числами с плавающей точкой?
Для отрицательных чисел можно использовать представление в дополнительном коде:
«`python def decimal_to_binary_signed(decimal_num): if decimal_num >= 0: return bin(decimal_num)[2:].zfill(8) else: return bin(256 + decimal_num)[2:] # Пример использования print(decimal_to_binary_signed(5)) # 00000101 print(decimal_to_binary_signed(-5)) # 11111011 «` Для чисел с плавающей точкой ситуация сложнее, так как нужно учитывать отдельно целую и дробную части: «`python def decimal_to_binary_float(decimal_num, precision=5): integer_part = int(decimal_num) fractional_part = abs(decimal_num — integer_part) integer_binary = bin(integer_part)[2:] fractional_binary = «» for _ in range(precision): fractional_part *= 2 bit = int(fractional_part) fractional_binary += str(bit) fractional_part -= bit return f»{integer_binary}.{fractional_binary}» # Пример использования print(decimal_to_binary_float(3.14)) # 11.00100 print(decimal_to_binary_float(-0.5)) # -0.10000 «`Производительность и оптимизация
При работе с большими числами или при необходимости выполнять много преобразований, важно учитывать производительность. Встроенные функции Python обычно оптимизированы и работают быстрее пользовательских реализаций.
Если вам нужна максимальная производительность, рассмотрите использование специализированных библиотек или расширений на C, таких как NumPy:
«`python import numpy as np def fast_decimal_to_binary(decimal_num): return np.binary_repr(decimal_num) # Пример использования print(fast_decimal_to_binary(10)) # 1010 print(fast_decimal_to_binary(-5)) # -101 «`Применение двоичного представления в реальных задачах
Понимание двоичного представления чисел полезно во многих областях программирования и компьютерных наук. Вот несколько примеров применения:
- Работа с битовыми операциями для оптимизации кода
- Анализ и отладка низкоуровневых проблем
- Реализация алгоритмов сжатия данных
- Работа с сетевыми протоколами и форматами данных
Рассмотрим пример использования двоичного представления для решения задачи:
«`python def count_set_bits(n): return bin(n).count(‘1’) def find_num_with_most_set_bits(numbers): return max(numbers, key=count_set_bits) # Пример использования numbers = [7, 8, 15, 16, 31] result = find_num_with_most_set_bits(numbers) print(f»Число с наибольшим количеством единиц в двоичном представлении: {result}») # Выведет: Число с наибольшим количеством единиц в двоичном представлении: 31 «` В этом примере мы используем двоичное представление для подсчета количества установленных битов (единиц) в числе, а затем находим число с максимальным количеством таких битов.
Заключение и дальнейшие направления изучения
Мы рассмотрели различные способы перевода десятичных чисел в двоичные на Python — от использования встроенных функций до реализации собственных алгоритмов. Понимание этих концепций открывает путь к более глубокому изучению компьютерных систем и алгоритмов.
Для дальнейшего изучения темы рекомендуется ознакомиться со следующими областями:
- Другие системы счисления (восьмеричная, шестнадцатеричная)
- Битовые операции и их применение
- Представление чисел с плавающей точкой в компьютерных системах
- Алгоритмы быстрого возведения в степень с использованием двоичного представления
Помните, что глубокое понимание систем счисления и двоичного представления чисел — важный навык для любого программиста, особенно при работе с низкоуровневыми системами или оптимизацией производительности.
Как перевести десятичное число в двоичное на python?
Хочу написать алгоритм по переводу числа из десятичной сс в двоичную, но столкнулся с проблемой — код ниже заходит в бесконечный цикл. Если помните, нужно делить число на 2. Весь алгоритм писать не нужно, опишите проблему и её решение кода ниже
a = int(input())
x = []
integer = []
result = []
x = list(str(a))[::-1]
while True:
if a != 1 and a != 0:
if a % 2 == 0:
result.append(0)
a = a / 2
elif a % 2 == 1:
result.append(1)
a = a / 2
else:
False
- python
2
вы просто написали много ненужного кода
a = int(input())
result = []
while a:
result.append(a % 2)
a //= 2
result.reverse()
print(result)
0
код ниже заходит в бесконечный цикл
else:
False
Данный код не завершает цикл, а просто вызывает значение False.
Чтобы завершить цикл нужно либо использовать оператор break, либо в условии использовать переменную и заменить её значение на False для прекращения работы цикла.
1 способ завершения цикла **
a = True
while a: # пока a is True
if False:
pass
else:
a = False
2 способ
While True:
If False:
pass # пропустить
else:
break # завершение цикла
Также a = a / 2 будет возвращать дробное значение и условие a == 1 или a == 0 никогда не выполнится.
Вот работающий код:
a = int(input())
x = []
integer = []
result = []
x = list(str(a))[::-1]
while True:
if a != 0:
if a % 2 == 0:
result.append(0)
a = a // 2
elif a % 2:
result.append(1)
a = a // 2
else:
result.reverse()
print(result)
break
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почтуОтправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Python как написать функцию перевода из k-ичной системы в десятичную?
int в CPython не хранится в десятичной системе:
>>> import sys >>> sys.int_info sys.int_info(bits_per_digit=30, sizeof_digit=4)
int_info
sys.int_info(bits_per_digit=30, sizeof_digit=4)
print(some_number) вызывает str(int) функцию, которая и преобразует int в строку, содержащую десятичные цифры (это не бесплатная операция—она может занимать долгое время для больших чисел).
Будем считать, что задача в вопросе: преобразовать строку kstr, содержащую натуральное число в к-ичной системе исчисления в Python int объект.
Если нельзя использовать int(kstr, base) напрямую (основание больше 36, цифры нестандартные, то легко в цикле собрать из отдельных цифр соответствующее число. К примеру, аналог 1003 = 910:
>>> from functools import reduce
>>> reduce(lambda n, d: n * 3 + d, map("012".index, "100"))
9
>>> int("100", 3)
9
Если цифры abc, а не 012 то есть для baa3 = 910:
>>> reduce(lambda n, d: n * 3 + d, map("abc". index, "baa"))
9
index, "baa"))
9
Вот более подробно о том как reduce() функция последовательность цифр в число превращает (для основания 10).
Можно написать функцию, которая автоматически генерирует функцию преобразования (converter) по заданным цифрам системы счисления:
from functools import reduce
def make_converter_int_from_base_k(digits):
"""Return int(kstr, len(digits)) analog for any digits."""
if not digits:
raise ValueError('no digits')
k = len(digits)
basek2digit = {d:i for i, d in enumerate(digits)}.__getitem__
def converter(kstr):
if not (set(kstr) <= set(digits)) or not kstr:
raise ValueError('invalid literal for int with digits {digits!r}: {kstr!r}')
return reduce(lambda number, digit: number*k + digit, map(basek2digit, kstr))
return converter
Пример:
>>> base3 = make_converter_int_from_base_k('abc')
>>> base3('c')
2
>>> base3('ba')
3
>>> base3('baa')
9
Пример из Википедия как число, представляющее Man в ASCII, можно в основание 64 преобразовать (507121410 = 4d616e16 = TWFu64):
>>> import base64 >>> import string >>> int.
Если известны ограничения на вводимые числа, то можно попробовать угадать систему счисления по самому числу, не задавая digits явно.
При преобразовании между некоторыми парами систем исчисления, иногда достаточно только строковых замен без промежуточного преобразования в int. К примеру из 16-ной в 2-ную (hex2bin()), из 2-ной в 8-ную (bin2oct()).
Стоит заметить, что int в CPython не хранится в десятичной системе (sys.int_info). print вызывает str(int) функцию, которая и преобразует int в строку, содержащую десятичные цифры (это не бесплатная операция—она может занимать долгое время для больших чисел).
Программа Python для преобразования десятичных чисел в двоичные
Улучшить статью
Сохранить статью
Нравится Статья
- Уровень сложности: Easy
- Последнее обновление: 30 декабря 2022 г.
Улучшить статью
Сохранить статью
Нравится Статья
При вводе десятичного числа задача состоит в том, чтобы написать программу Python для преобразования данного десятичного числа в эквивалентное двоичное число.
Примеры:
Ввод: 7 Выход: 111 Вход: 10 Вывод: 1010
Метод №1: Рекурсивное решение
DecimalToBinary(num):
если число >= 1:
DecimalToBinary (число // 2)
print num % 2 Ниже приведена реализация приведенного выше рекурсивного решения:0051
if num > = 1 :
DecimalToBinary(num / / 2 )
Печать (NUM % 2 , END = '')
, если __Name__
= '__main__' :
dec_val = 24
DecimalToBinary( dec_val)
Вывод
011000
Метод №2: Десятичное преобразование в двоичное с использованием встроенной функции
Python3
|
) Выход
1000 10010 111
Способ №3: Без встроенной функции
Python3
|
Output
1000 10010 111
Быстрый метод ниндзя: Однострочный код для преобразования десятичного числа в двоичное с вводом пользователем0051 ( 4785 )[ 2 :])
Output
1001010110001
or
Python3
|
0051 Выход
1001031 10 1010 101011001Использование оператора побитового сдвига >>.
0051
0049 
Это наиболее широко используемая система нумерации. Каждая цифра в этой системе имеет место и десятичную точку. С другой стороны, в двоичной системе используются целые числа по основанию два в диапазоне от 0 до 1. Это самая простая система, поскольку она состоит из двух цифр: 0 и 1. В результате она является обычной для экспертов в области компьютерного программирования или других связанные инженерные области, чтобы преобразовать десятичный код в двоичный.
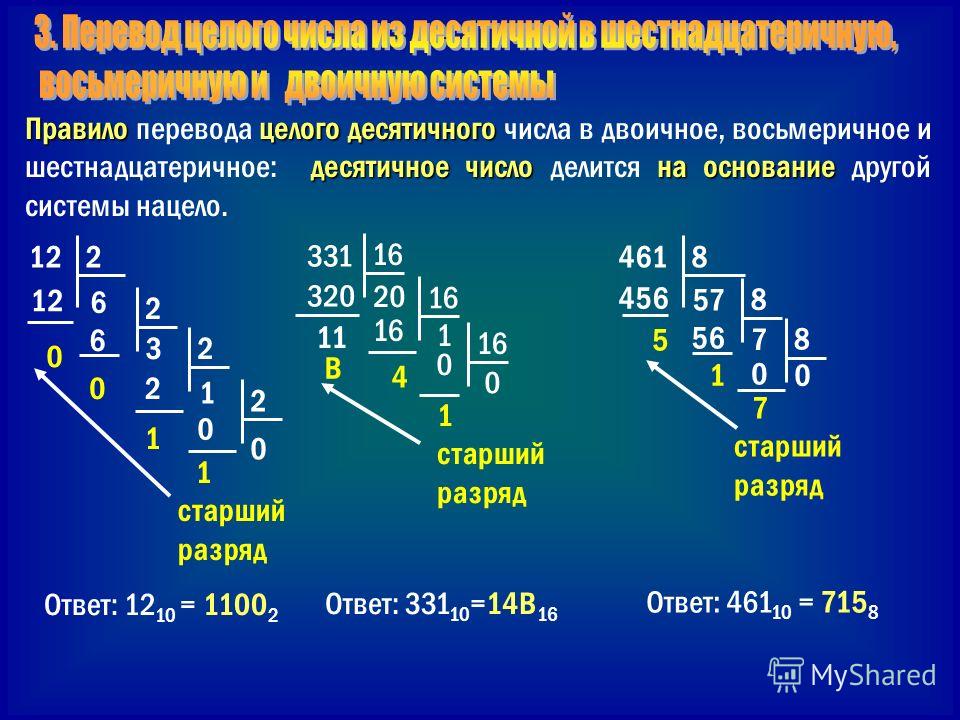
Самый простой метод преобразования десятичных чисел в их двоичный эквивалент — это деление на 2.
