Перевод в децибелы. Преобразование децибелов в разы и обратно: полное руководство

Как перевести децибелы в разы. Как рассчитать отношение величин в децибелах. Когда используется коэффициент 10, а когда 20 перед логарифмом. Примеры расчетов и калькулятор для конвертации дБ.

Что такое децибел и зачем он нужен

Децибел (дБ) — это логарифмическая единица, используемая для выражения отношения двух величин. Основные преимущества использования децибелов:

• Возможность работать с очень большими и очень маленькими числами в компактном виде
• Удобство сложения и вычитания вместо умножения и деления
• Наглядность при сравнении величин разного порядка

Децибелы широко применяются в акустике, радиотехнике, связи и других областях для оценки усиления, ослабления, мощности сигналов и т.д.

Формулы перевода децибелов в разы и обратно

Для перевода отношения величин в децибелы используются следующие формулы:

• Для энергетических величин (мощность, энергия):
  дБ = 10 * log10(P2/P1)
• Для амплитудных величин (напряжение, ток, давление):
  дБ = 20 * log10(A2/A1)

Для обратного перевода из децибелов в разы:

• Для энергетических величин:
  P2/P1 = 10^(дБ/10)
• Для амплитудных величин:
  A2/A1 = 10^(дБ/20)

Когда использовать коэффициент 10, а когда 20?

Выбор коэффициента 10 или 20 перед логарифмом зависит от типа сравниваемых величин:

• Коэффициент 10 используется для энергетических величин (мощность, энергия, интенсивность)
• Коэффициент 20 применяется для амплитудных величин (напряжение, ток, звуковое давление)

Это связано с тем, что энергетические величины пропорциональны квадрату амплитудных. Например, мощность P пропорциональна квадрату напряжения U: P ~ U^2.

Примеры расчетов перевода децибелов в разы

Рассмотрим несколько примеров перевода децибелов в разы и обратно:

Пример 1: Перевод 3 дБ в разы для мощности

Используем формулу для энергетических величин:

P2/P1 = 10^(3/10) = 10^0.3 ≈ 2

Таким образом, 3 дБ соответствует увеличению мощности в 2 раза.

Пример 2: Перевод 6 дБ в разы для напряжения

Для амплитудных величин используем формулу с коэффициентом 20:

U2/U1 = 10^(6/20) = 10^0.3 ≈ 2

6 дБ соответствует увеличению напряжения в 2 раза.

Пример 3: Перевод отношения мощностей 100 в децибелы

дБ = 10 * log10(100) = 10 * 2 = 20 дБ

Увеличение мощности в 100 раз соответствует 20 дБ.

Калькулятор для конвертации децибелов в разы

Для удобства расчетов можно использовать онлайн-калькуляторы. Вот простой пример такого калькулятора:

«` import React, { useState } from ‘react’; import { Card, CardContent, CardHeader } from ‘@/components/ui/card’; const DBCalculator = () => { const [db, setDb] = useState(»); const [ratio, setRatio] = useState(»); const calculateRatio = () => { const dbValue = parseFloat(db); if (!isNaN(dbValue)) { setRatio((Math.pow(10, dbValue / 10)).toFixed(4)); } else { setRatio(»); } }; const calculateDb = () => { const ratioValue = parseFloat(ratio); if (!isNaN(ratioValue) && ratioValue > 0) { setDb((10 * Math.log10(ratioValue)).toFixed(2)); } else { setDb(»); } }; return (

Калькулятор дБ — разы

дБ: setDb(e.target.value)} className=»w-full p-2 border rounded» /> Рассчитать разы

Разы: setRatio(e.target.value)} className=»w-full p-2 border rounded» />

Рассчитать дБ

); }; export default DBCalculator; «`

Этот калькулятор позволяет быстро конвертировать значения между децибелами и разами для энергетических величин (мощность, энергия).

Практическое применение децибелов в различных областях

Децибелы широко используются в различных технических областях. Вот несколько примеров их практического применения:

Акустика и аудиотехника

• Измерение уровня звукового давления (SPL)
• Оценка усиления или ослабления звуковых сигналов
• Расчет звукоизоляции помещений

Радиотехника и связь

• Расчет бюджета радиолинии
• Оценка усиления антенн
• Измерение мощности сигналов

Оптика

• Измерение затухания в оптоволоконных линиях
• Оценка мощности лазерного излучения

Типичные значения децибелов в повседневной жизни

Для лучшего понимания масштаба децибелов, рассмотрим некоторые типичные значения уровня звука в повседневной жизни:

• 0 дБ — порог слышимости
• 20-30 дБ — шепот, тихая комната
• 50-60 дБ — обычный разговор
• 70-80 дБ — шумная улица, крик
• 90-100 дБ — шум метро, громкая музыка
• 120 дБ — болевой порог
• 140 дБ — взлет реактивного самолета

Особенности использования децибелов в различных системах измерения

Помимо обычных децибелов (дБ), существуют различные производные единицы, используемые в специфических областях:

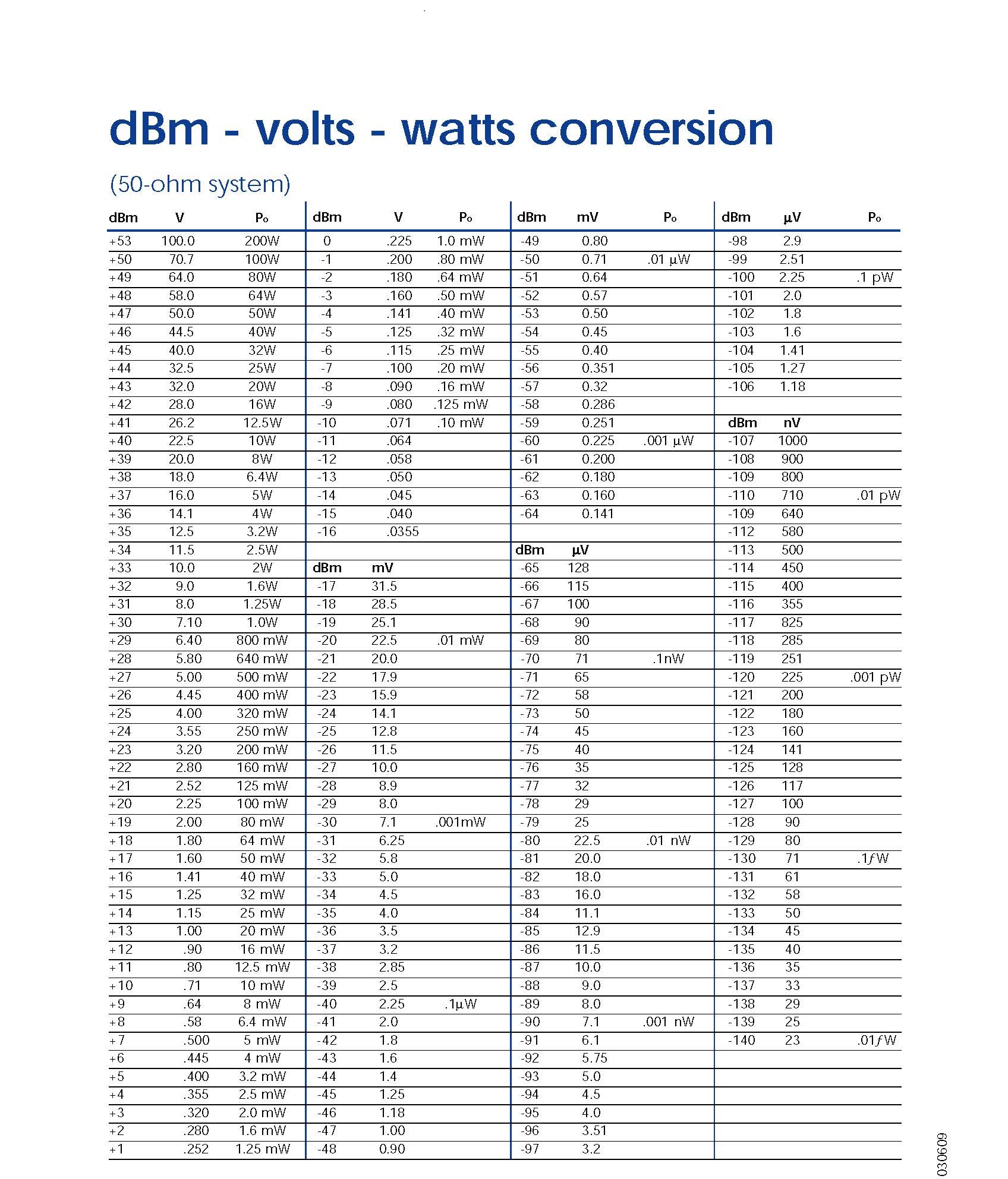
• дБм (dBm) — мощность относительно 1 милливатта
• дБВт (dBW) — мощность относительно 1 ватта
• дБи (dBi) — усиление антенны относительно изотропного излучателя
• дБ SPL — уровень звукового давления относительно порога слышимости

Каждая из этих единиц имеет свою область применения и особенности использования.

Как правильно складывать и вычитать децибелы

Одно из главных преимуществ использования децибелов — возможность складывать и вычитать значения вместо умножения и деления. Однако есть некоторые нюансы:

• Простое сложение и вычитание децибелов корректно только для некоррелированных сигналов
• При сложении одинаковых уровней результат увеличивается на 3 дБ
• Для точных расчетов при сложении близких уровней используются специальные таблицы или формулы

Пример: сложение двух сигналов с уровнями 10 дБ и 13 дБ

1. Переводим в разы: 10 дБ = 10, 13 дБ ≈ 20
2. Складываем: 10 + 20 = 30
3. Переводим обратно в дБ: 10 * log10(30) ≈ 14.8 дБ

Таким образом, результат сложения 10 дБ и 13 дБ равен примерно 14.8 дБ, а не 23 дБ, как могло показаться при прямом сложении.

Таблица перевода дБм в мВт

GSM-Репитеры.РУ » Таблица перевода дБм в мВт

Стандартная единица измерения мощности — Ватт (Вт), а также его кратные и дольные единицы, в том числе милливатты (мВт). Однако для расчета мощности сотового сигнала обычно используется абсолютная логарифмическая единица — децибел-милливатт (дБм).

Чтобы быстро пересчитать дБм в мВт (или мВт в дБм), вы можете воспользоваться нижеприведенным калькулятором. Для наиболее ходовых значений мы составили отдельную таблицу. Если же вы хотите узнать, что такое децибел-милливатты, во второй части статьи приведена теоретическая справка!

Мощность в мВт	Результат в дБм
Мощность в дБм	Результат в мВт

Таблица для перевода дБм в мВт / мВт в дБм

дБм	Вт	дБм	Вт	дБм	Вт
0	1,0 мВт	16	40 мВт	32	1,6 Вт
1	1,3 мВт	17	50 мВт	33	2,0 Вт
2	1,6 мВт	18	63 мВт	34	2,5 Вт
3	2,0 мВт	19	79 мВт	35	3,2 Вт
4	2,5 мВт	20	100 мВт	36	4,0 Вт
5	3,2 мВт	21	126 мВт	37	5,0 Вт
6	4 мВт	22	158 мВт	38	6,3 Вт
7	5 мВт	23	200 мВт	39	8,0 Вт
8	6 мВт	24	250 мВт	40	10 Вт
9	8 мВт	25	316 мВт	41	13 Вт
10	10 мВт	26	398 мВт	42	16 Вт
11	13 мВт	27	500 мВт	43	20 Вт
12	16 мВт	28	630 мВт	44	25 Вт
13	20 мВт	29	800 мВт	45	32 Вт
14	25 мВт	30	1,0 Вт	46	40 Вт
15	32 мВт	31	1,3 Вт	47	50 Вт

Что такое децибелы и для чего они используются?

Децибел (дБ, dB) — это логарифмическая единица, которая широко применяется в физике для выражения отношений величин. Децибелы показывают, во сколько раз одно значение больше (или меньше) другого. Вместо того, чтобы считать в «разах», считают в децибелах — это удобнее.

В основе децибела лежит десятичный логарифм. Рост значения на 3 дБ означает увеличение в 2 раза, что делает запись в децибелах простой и наглядной для сравнения. Децибелы можно складывать и вычитать, а их численное выражение всегда компактнее, чем полная запись «в разах». Например, коэффициент усиления 65 дБ = 3 160 000 раз, а усиление 80 дБ = 100 000 000 раз.

Перевод «раз» в децибелы для энергетических величин (в том числе мощности) осуществляется по формуле:

10log₁₀(P1/P2) = дБ,

где P1 и P2 — сравниваемые значения.

Чтобы перевести децибелы в разы, достаточно воспользоваться формулой:

10^{(n / 10)} = m,

где n — значение в децибелах, m — отношение в «разах».

Из этого следует, что сам по себе децибел — единица относительная (безразмерная), с ее помощью можно сравнить совершенно любые величины. При этом значение в децибелах может быть как положительным (увеличение в разы), так и отрицательным (уменьшение в разы).

Эта особенность децибелов используется, чтобы в компактной форме выражать большие или малые значения мощности и других величин. Для этого их сравнивают с определенным эталонным значением («нулевым уровнем»).

Что такое децибел-милливатт (дБм)? Зачем нужны дБм?

Приняв за «нулевой уровень» эталонное значение и сравнивая с ним конкретное значение, можно существенно упростить запись и оперировать небольшими, удобными для восприятия числами.

Чаще всего подобная запись используется для единиц мощности — милливаттов. Взяв за опорный уровень значение 1 мВт, получаем новую единицу — децибел-милливатт (дБм).

дБм (dBm) указывает, во сколько раз данное значение мощности больше (или меньше) мощности 1 мВт. Значение в децибел-милливаттах может быть как положительным (при мощности >1 мВт), так и отрицательным (при мощности <1 мВт).

0 дБм = 1 мВт

10log₁₀(мВт) = дБм

10^{(дБм / 10)} = мВт

На первый взгляд использование децибел-милливаттов может показаться излишне сложным, однако на практике применение этой единицы упрощает работу с большими и малыми значениями. Децибел-милливаты и децибелы можно складывать и вычитать, выполняя простые арифметические операции, а запись и численные выражения занимают намного меньше места и времени.

Приведем простой пример. Допустим, исходный сигнал мощностью 17 дБм при распространении в свободном пространстве «затух» на 80 дБ. Тогда:

20 дБм − 80 дБ = -60 дБм

Для классической записи в «разах» подобная запись выглядела бы следующим образом:

100 мВт / 100 000 000 раз = 0,000001 мВт

Очевидно, запись в относительных единицах гораздо удобнее и практичнее, чем полная запись в «разах».

Другие логарифмические единицы: дБи, дБн

Помимо дБм, применяются и другие аналогичные единицы:

• дБи (dBi) — изотропный децибел. Единица выражает коэффициент усиления измеряемой антенны по сравнению с идеальной изотропной антенной, излучающей энергию равномерно во всех направлениях. Коэффициент усиления изотропной антенны принят за 0 дБи.
• дБик (dBic) — децибел по отношению к изотропной антенне с круговой поляризацией. Используется для измерения коэффициента усиления антенн с круговой поляризацией (например, GPS/ГЛОНАСС).
• дБн (dBc) — децибел относительно несущей. При помощи этой единицы измеряется мощность шумов, интермодуляционных искажений и прочих помех (по сравнению с мощностью несущего сигнала).

Как измерить мощность сигнала в дБм?

Для точного определения мощности ВЧ-сигнала используются специальные приборы — измерители мощности. К сожалению, высокая цена ограничивает сферу применения этих устройств крупными предприятиями и научными организациями. Для решения бытовых задач существуют гораздо более доступные решения. Например, узнать уровень сотового сигнала оператора в дБм можно при помощи недорогого набора для настройки 4G-антенны!

 

Перевод из дБ в ПВЭ и эквивалентную площадь. | Страница 2

epoch5

Профессионал

• 15.02.2023

• #21

astrut написал(а):

В одной перед логарифмами 10, а в другой 20…Еще одна загадка

Нажмите для раскрытия…

Колян2 написал(а):

Тоже мне загадка. ..Пишут-пишут…Взять всё да и поделить на всех!

Нажмите для раскрытия…

Точно! Единая формула — перед логарифмом 15!

 

astrut

Дефектоскопист всея Руси

• 15.02.2023

• #22

epoch5 написал(а):

Точно! Единая формула — перед логарифмом 15!

Нажмите для раскрытия…

Это по-браЦки

 

Антошка

Мастер дефектоскопии

• 02.2023″ data-time-string=»10:50″ title=»15.02.2023 в 10:50″ itemprop=»datePublished»>15.02.2023

• #23

Вроде не пятница, а тем зафлудили. (

 

dea135

Дефектоскопист всея Руси

• 15.02.2023

• #24

epoch5 написал(а):

Точно! Единая формула — перед логарифмом 15!

Нажмите для раскрытия…

я не против, но предлагаю обдумать вопрос и не продешевить. понимаете, волатильность, таргетирование и пр.
поэтому на обсуждение выносится идея привязки к курсу «корзины» валют.

 

Kaktus_SPb

Дефектоскопист всея Руси

• 15.02.2023

• #25

Alex249 написал(а):

А разве площадь прапорциональна амплитуде сигнала, не квадрату амплитуды?

Нажмите для раскрытия…

Возьмите любой букварь
Там найдите формулу акустического тракта для диска (отверстия с плоским дном, плоскодонки)
Там увидите, что отношение амплитуд сигналов (Р/Р0 или А/А0 или U/U0) пропорционально площади диска (S)
Также в любом букваре можно почитать про децибелы
P. S. Пользоваться формулами акустического тракта можно с кучей допущений….

 

astrut

Дефектоскопист всея Руси

• 15.02.2023

• #26

Kaktus_SPb написал(а):

Также в любом букваре можно почитать про децибелы

Нажмите для раскрытия…

Но интрига про 10 перед логарифмом вместо 20 осталась.
Ну чё, примем по-браЦки 15, али

dea135 написал(а):

привязки к курсу «корзины» валют

Нажмите для раскрытия…

 

ilia

Свой

• 15.02.2023

• #27

Alex249 написал(а):

Например у меня есть индикация на 80% ПВЭ от плоскондонного отверстия площадью 10 кв. мм. И вторая индикация скажем на 70% ПВЭ. Как найти эквивалентную площадь от второй индикации?

Нажмите для раскрытия. ..

20 log (А0/А1)=20 log (Sэкв 0/Sэкв 1)​

 

Kaktus_SPb

Дефектоскопист всея Руси

• 15.02.2023

• #28

ilia написал(а):

20 log (А0/А1)=20 log (Sэкв 0/Sэкв 1)​

Нажмите для раскрытия…

А логарифм по какому основанию?

 

ilia

Свой

• 02.2023″ data-time-string=»14:54″ title=»15.02.2023 в 14:54″ itemprop=»datePublished»>15.02.2023

• #29

Kaktus_SPb написал(а):

А логарифм по какому основанию?

Нажмите для раскрытия…

Ну можно без логорифмов. С логорифмом наглядней ,для меня лично. И формулу легче уже готовую вставить сюда

 

Kaktus_SPb

Дефектоскопист всея Руси

• 15.02.2023

• #30

ilia написал(а):

Ну можно без логорифмов. С логорифмом наглядней ,для меня лично.

Нажмите для раскрытия…

Логарифм — это показатель степени…..
в которую надо возвести число а (основание) , чтобы получить число b…
Чаще всего используют десятичные Lg(основание 10) и натуральный Ln(основание число Непера, экспонента и т.п.) логарифмы….
Если Вы возьмете 20*Log10 (2) или чаще встречаем 20*Lg (2), то получите примерно 6
А если 20*Ln(2) ?
А если 20*Log3(2) ?
P.S. Можно и с логарифмами, только надо понимать что подставлять
Вот у Вас один сигнал 24 дБ, а другой 12 дБ и во сколько раз отличаются эквивалентные площади….?

 

Последнее редактирование: 02.2023 в 15:29″ itemprop=»dateModified»>15.02.2023

ilia

Свой

• 15.02.2023

• #31

Kaktus_SPb написал(а):

Вот у Вас один сигнал 24 дБ, а другой 12 дБ и во сколько раз отличаются эквивалентные площади….?

Нажмите для раскрытия…

В два раза

 

Kaktus_SPb

Дефектоскопист всея Руси

• 02.2023″ data-time-string=»15:38″ title=»15.02.2023 в 15:38″ itemprop=»datePublished»>15.02.2023

• #32

ilia написал(а):

В два раза

Нажмите для раскрытия…

А правильный ответ в 4…..

 

ilia

Свой

• 15.02.2023

• #33

Kaktus_SPb написал(а):

А правильный ответ в 4. ….

Нажмите для раскрытия…

Согласен

Kaktus_SPb написал(а):

А правильный ответ в 4…..

Нажмите для раскрытия…

Согласен, это ж дБ. Не сообразил. Одна амплитуда больше другой в 4 раза. Тут надо по экрану в процентах
или пересчитывать

 

Колян2

Дефектоскопист всея Руси

• 15.02.2023

• #34

astrut написал(а):

Поровну, по-честному, по совести, по справедливости, по трудовому вкладу, али еще как?

Нажмите для раскрытия. ..

Предлагаю по-хорошему или по-семейному-30/70!

 

astrut

Дефектоскопист всея Руси

• 15.02.2023

• #35

ilia написал(а):

Согласен, это ж дБ. Не сообразил.

Нажмите для раскрытия…

А чего это, там же деци(Белл), а перед логарифмом почему-то 20 обычно стоит. Но иногда 10. Опять загадка
Маленькая подсказка здесь

Kaktus_SPb написал(а):

Логарифм — это показатель степени. ….

Нажмите для раскрытия…

Дальше подсказывать не буду.
ЗЫ. Из своего опыта. Большинство студентов, сдав высшую математику на 2-м, к 5 курсу с большим трудом вспоминает, что такое логарифмы

 

astrut

Дефектоскопист всея Руси

• 15.02.2023

• #36

Колян2 написал(а):

Предлагаю по-хорошему или по-семейному-30/70!

Нажмите для раскрытия…

А может, по УСН? там всего 6% отдвавть. ..

 

ilia

Свой

• 16.02.2023

• #37

astrut написал(а):

А чего это, там же деци(Белл), а перед логарифмом почему-то 20 обычно стоит. Но иногда 10. Опять загадка
Маленькая подсказка здесь

Дальше подсказывать не буду.
ЗЫ. Из своего опыта. Большинство студентов, сдав высшую математику на 2-м, к 5 курсу с большим трудом вспоминает, что такое логарифмы

Нажмите для раскрытия…

при r≥3N (но применяют и при r≥N) и прочих соответствующих условиях
🥱

 

Kaktus_SPb

Дефектоскопист всея Руси

• 02.2023″ data-time-string=»07:34″ title=»16.02.2023 в 07:34″ itemprop=»datePublished»>16.02.2023

• #38

ilia написал(а):

Посмотреть вложение 45890
при r≥3N (но применяют и при r≥N) и прочих соответствующих условиях
🥱

Нажмите для раскрытия…

Это если по экрану усиление линейное

 

dea135

Дефектоскопист всея Руси

• 16.02.2023

• #39

astrut написал(а):

ЗЫ. Из своего опыта. Большинство студентов, сдав высшую математику на 2-м, к 5 курсу с большим трудом вспоминает, что такое логарифмы

Нажмите для раскрытия…

сложный вопрос, это надо основы акустики знать как соотносятся интенсивности, давления и напряжения. не подсказываю.

 

astrut

Дефектоскопист всея Руси

• 17.02.2023

• #40

dea135 написал(а):

сложный вопрос, это надо основы акустики знать как соотносятся интенсивности, давления и напряжения. не подсказываю.

Нажмите для раскрытия…

А я чуть-чуть подскажу. В этом ультразвуке всё очень запутано. Начинаешь курить темы про коэффициенты отражения и пропускания (прозрачности), там тоже по две формулы

 

Калькулятор

дБ плюс объяснение. Преобразовать дБ в ватты или ватты в дБ

Дом

Индекс информации VSAT Калькулятор бюджета спутниковой связи Калькулятор диапазона SETI Калькулятор секунд, минут, часов, дней

Пояснение и описание LNB Бюджет радиосвязи линии прямой видимости — в одну сторону — один переход Как измерить EbNo и калькулятор EbNo Расчет шума антенной системы

дБ великолепны и забавны и позволяют много рассчитывать радио и уровень сигнала Полегче. Прочтите здесь объяснение плюс удобный калькулятор, который конвертирует значения дБ в ватты и наоборот.

В радиосвязи у вас есть много предметов (усилители, аттенюаторы, сигнальные разветвители и объединители, кабели с потерями и т. д.), которые либо увеличивают, либо уменьшают уровень сигнала. Чтобы определить конечный результат для сигнала, проходящего через цепочки таких устройств вы используете усиление дБ или затухание дБ каждого устройства и просто сложите все значения дБ вместе.

Калькулятор дБ Преобразование дБ в отношение.. Введите значение дБ здесь Здесь выводится соотношение Калькулятор дБ Коэффициент преобразования в дБ Введите значение коэффициента здесь Выход здесь дБ

На этом примере показано использование дБ. Читайте медленно и постарайтесь понять, потому что если вы поймете этот пример dB весь бизнес станет намного легче понять. Задача расчета дБ : Каков уровень выходной мощности в следующая ситуация и не будет ли перегружен выходной усилитель передатчика ?. Для справки обратите внимание на информационную таблицу справа Уровень мощности входного сигнала = 1 мВт или -30 дБВт (или 0 дБм) Устройства в серии: Двухтранзисторный усилитель: усиление 16 дБ (в сорок раз повышение уровня, х40) Регулируемый аттенюатор диапазона 20 дБ, изначально настроенный вами наполовину в Настройка 10 дБ: ослабление 10 дБ (уменьшение в 10 раз) Длинный коаксиальный кабель: затухание потерь 3 дБ (уменьшение вдвое уровень) Мощный 10-ваттный усилитель: усиление=30 дБ (увеличение уровня сигнала на коэффициент в 1000 раз. Обратите внимание на 3 нуля = 30 дБ) Расчет:    Выход = -30 + 16 -10 — 3 + 30  = 3 дБВт = 2 Вт Комментарий: Это должно работать, но учтите, что если аттенюатор должен быть установлен на минимальное значение ослабления (0 дБ) система попытается выдать +13 дБВт или 20 Вт. Это не приемлемо с 10-ваттным усилителем, так как он сильно искажает сигнал и может повредить усилитель. Это также будет создавать помехи для других людей на соседних частотах. В приведенном выше случае я бы добавьте дополнительный аттенюатор на 3 дБ (также называемый аттенюатором на 3 дБ) где-то вдоль или в конец кабеля. Это будет означать, что установка 0 дБ на Аттенюатор вызовет выходную мощность 10 Вт и, таким образом, просто насытит усилитель звука. Это позволяет избежать риска случайного вмешательства в работу других людей. и повреждение дорогого усилителя мощности. Формулы: Чтобы преобразовать отношение в дБ, выполните log, а затем умножьте на 10. Пример: отношение   = 1234 крата. Лог(1234) = 3,09. Десять раз 3,09 = 30,9 дБ Чтобы преобразовать дБ в соотношение, разделите на 10, а затем сделайте десять с x, например 10 x Пример: дБ = +12,5 дБ. Разделите +12,5 на 10 = +1,25. Соотношение Do 10 1,25 = 17,8.

дБ и отношения Значение дБ раз по +30 дБ 1000 +20 дБ 100 16 дБ 40 13 дБ 20 10 дБ 10 9 дБ 8 8 дБ 6,31 7 дБ 5.01 6 дБ 4 5 дБ 3,16 4 дБ 2,51 3 дБ 2 2 дБ 1,58 1 дБ 1,26 0 дБ 1 -3 дБ 0,5 -10 дБ 0,1 -20 дБ 0,01 -30 дБ 0,001 -40 дБ 0,0001 дБВт и Вт Вт Шкала дБВт Вт +30 дБВт 1000 Вт +20 дБВт 100 Вт +10 дБВт 10 Вт 0 дБВт 1 Вт -10 дБВт 0,1 Вт -30 дБВт 0,001 Вт -30 дБВт 0 дБм дБм и милливатт мВт Шкала дБм милливатт +30 дБм 1000 мВт  0 дБм 1 мВт -10 дБм 0,1 мВт

Определение: дБВт означает дБ относительно 1 ватта, поэтому 0 дБВт = 1 ватт, -3 дБВт = половина ватт.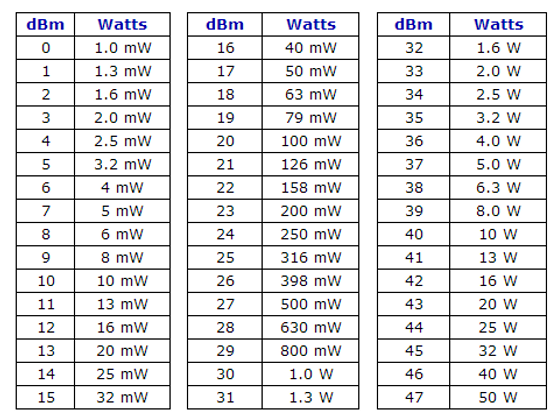 +3 дБВт = 2 Вт и т. д.
Определение: дБм означает дБ относительно 1 милливатт, поэтому 0 дБм = 1 милливатт (один тысячная часть 1 Вт или 0,001 Вт). Также равно -30 дБВт.
Определение: дБи означает усиление антенны по отношению к теоретической эталонной антенне с изотропная, всенаправленная, сферическая диаграмма направленности.
Определение: дБд означает усиление антенны относительно эталонной антенны с дипольная диаграмма направленности. Эталонная антенна может быть настоящим диполем. антенна.

Интересные факты:

Спутниковый луч нисходящего канала с э.и.и.м. 50 дБВт означает, что он выглядит как 100 000 ваттный передатчик, подключенный к всенаправленной спутниковой антенне. Ты можно получить тот же эффект, используя спутниковый передатчик мощностью 100 Вт (+20 дБВт). подключен к направленной антенне нисходящего канала с небольшим лучом покрытия диаметром, с коэффициентом усиления 30 дБи, и вы находитесь на земле в центре принадлежащий диаграмма покрытия спутникового луча.

92 или 0,0000000000012589 ватт на квадратный метр на высоте спутника. Итак, если у вас есть прием антенну на спутнике с эффективной площадью сбора 1 кв. мощность сигнала, поступающего в спутниковый ресивер, составляет -119 дБВт.

---

---

Возможны ошибки; любые проблемы или комментарии, пожалуйста, напишите мне по электронной почте [email protected] Эта страница калькулятора дБ защищена авторским правом (c) 2006 Satellite Signals Ltd, все права защищены Страница начата 26 декабря 2006 г., последние изменения внесены 9 марта 2022 г.

Преобразование и интерпретация децибелов | Unboxing Tomorrow

Радиочастотные аттенюаторы, подобные этим, имеют маркировку в децибелах.

Децибелы (дБ) являются важной единицей для работы с электронными сигналами. И хотя их свойства масштабирования и бесконечные варианты, такие как dBi, dBm, dBFS и dBµ, могут показаться неудобными; мы быстро расскажем, как преобразовать децибелы и обратно.

Децибелы впервые были опубликованы в Техническом журнале Bell System в 1929 году. Важно помнить о них то, что они предназначены для сравнения разницы между двумя уровнями мощности .

Сегодня мы в основном будем сравнивать количество энергии, выходящей из системы, с мощностью, которая поступает. Но децибелы также могут сравнивать измерение со стандартизированным эталонным значением. Так, например, когда мы говорим о громкости звука в децибелах, мы описываем, насколько громким этот звук по сравнению с порогом человеческого слуха (который является эталонным значением).

Когда децибелы впервые использовались, их роль заключалась в сравнении мощности сигнала, входящего в стандартный кабель, с мощностью на выходе. Это стало удобным способом выражения потерь сигнала.

Следующее преобразует это отношение в децибелы:

…где P ₁ — входная мощность, а P ₂ — выходная мощность. В других случаях член знаменателя (P ₁ ) будет фиксированным эталонным значением, а член числителя (P ₂ ) будет измерением.

Чтобы сделать обратное (т. е. преобразовать децибелы в коэффициент мощности), начните с числа децибел (x). Затем используйте экспоненциальную формулу, как показано ниже.

Обратите внимание, что эта форма подходит только для питания. Его не следует использовать, например, для нахождения коэффициентов напряжения (подробнее о том, почему, ниже).

Чтобы попрактиковаться в преобразовании, давайте посмотрим на недавний пример из моего радиотеста по отслеживанию суровых погодных условий. Погодные радиостанции, подобные приведенной ниже, рассылают прогнозы и ранние предупреждения об опасных угрозах, таких как торнадо. Обратите внимание на шкалу децибел слева и отношение сигнал/шум (SNR) справа.

Рисунок 1: Представление радиостанции в программном обеспечении Airspy (SDR Sharp)

На рисунке 1 выше радиопередача о погоде изображена в виде сине-белого пика. Основание пика составляет около -65 dbFS (децибел относительно полной шкалы). Пик (показан желтым кружком) очень близок к -22 дБ полной шкалы. Верхний край графика находится на уровне 0 dBFS, что является верхним пределом для радио. И наконец: индикатор SNR справа показывает значение 43 дБ.

Сначала начнем со значения SNR, переведя его из децибел в отношение уровней мощности. Мы будем представлять мощность шума как P ₁ , мощность сигнала как P ₂ и ОСШ (измеряется в децибелах) как x.

Таким образом, когда ОСШ составляет 43 дБ, результатом является безразмерное значение около 19 952. Это говорит нам о том, что мощность принимаемых сигналов в логарифмическом отношении в 19 952 раза больше, чем шум, что весьма неплохо.

Как насчет того, чтобы сделать это в обратном порядке? В приведенном выше расчете мы использовали 10 в качестве основы для нашего показателя степени.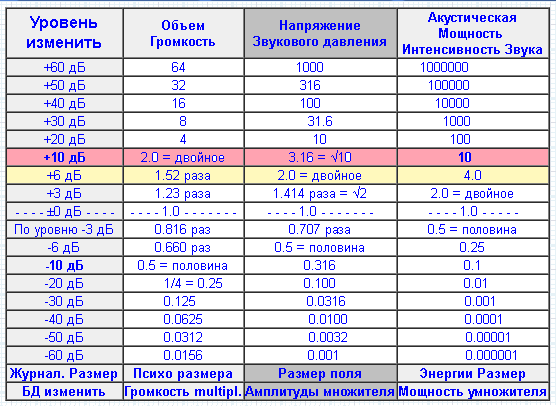 Итак, чтобы обратить этот процесс вспять, мы используем логарифм по основанию 10:9.0007

Ввод P2 / P1 = 19952 дает исходное ОСШ 43 дБ.

Из приведенной ниже таблицы видно, что шкала децибел хорошо работает с нашей десятичной системой счета. Мы также можем сказать, что увеличение на 3 дБ соответствует увеличению мощности примерно в 2 раза; а снижение на 3 дБ соответствует потере примерно ½ мощности. Таблица 1: Перевод децибел по десятилетиям +50 dB 100 000 +40 dB 10 000 +30 dB 1 000 +20 dB 100 +10 dB 10 +0 dB 1 -10 dB 0.1 -20 dB 0.01 -30 dB 0.001 -40 dB 0,000 1 -50 дБ 0,000 01

При выражении прироста напряжения в децибелах вместо прироста мощности все работает немного по-другому. Условные обозначения для преобразования коэффициентов напряжения следующие:

Где |V ₂ | – абсолютное значение выходного напряжения, а |V ₁ | является абсолютным значением входного напряжения. Для краткости мы будем предполагать, что V ₂ /V ₁ всегда положительно с этого момента, и мы будем опускать знаки абсолютного значения…

Table 2: Decibel Scaling for Power vs. Voltage

. 100

Power Decibels (dB)	Voltage Decibels (dB)	Multiplier
+50 dB	+100 dB	100 000
+40 DB	+80 DB	10 000
+30 DB	+60 DB	1000
+208	9000 40008	9000 4000 4000 9000		9000		9000 9000
+10 dB	+20 dB	10
+0 dB	0 dB	1
-10 dB	-20 dB	0.1
-20 dB	-40 dB	0.01
-30 dB	-60 dB	0.001
-40 dB	-80 dB	0.000 1
-50 dB	— 100 дБ	0,000 01

На первый взгляд это может показаться двойным стандартом, когда расчеты мощности в конечном итоге умножаются на 10, а расчеты напряжения умножаются на 20. Но на самом деле двойных стандартов не существует. Отправной точкой все время было 10 ∙ log ₁₀ (A/B)!

Чтобы понять почему: вспомним, что децибелы изначально предназначались для сравнения с (измеряется в ваттах). Напряжение не мощность. Однако мы можем использовать степенной закон для расчета мощности, если известны напряжение (V) и сопротивление (R) (или импеданс)…

Подстановка этого значения в формулу преобразования децибелов дает…

Это можно упростить, используя два логарифмических свойства:

• Правило произведения для логарифмов: log ₁₀ (A*B) = log ₁₀ (A) + log ₁₀ (B)
• Частное правило для логарифмов: log ₁₀ (A/C) = log ₁₀ (A) – log ₁₀ (C)

Это позволяет нам разделить значения напряжения и сопротивления.

Мы используем правило логарифмической экспоненты, чтобы упростить первый логарифм…

• log ₁₀ (A ^B ) = B log ₁₀ (A)

, если R ₁ = R ₂ , то мы можем упростить вещи. ) = 0. Даже если R ₁ и R ₂ неизвестны, мощность по-прежнему пропорциональна V ² , если сопротивление или импеданс постоянны. Таким образом, мы можем аппроксимировать усиление как…

Это объясняет, почему «20» связано с напряжением. Это также относится к другим единицам, таким как электрические поля (измеряемые в вольтах на метр).

Чтобы преобразовать представление напряжения x из децибелов в отношение напряжений, мы используем выражение, подобное предыдущему, только децибелы делятся на 20…

Возникает вопрос: почему бы просто не выразить разницу как P2/P1? Что мы получаем, вводя логарифм?

Вскоре мы рассмотрим это более подробно. Пока отмечу:

• Децибелы могут передать чрезвычайно большие и малые значения всего несколькими цифрами.
• Децибелы отлично подходят для значений, которые приближаются к нулю, но не равны нулю точно.
• Децибелы добавляются к бюджету канала связи.

В особых случаях децибелы могут быть менее обманчивы, чем проценты.

[1]	Д. Лю и Х. К. Робертс, «Физика звука и слуха», в Справочник инженеров-экологов , Бока-Ратон, Флорида, CRC Press, 1997, стр. 452-454 .
[2]	У. Х. Мартин, «Децибел — название единицы передачи», Журнал AIEE, том. 48, нет. 3, с. 223, 1929.
[3]	М. Мардигуян, «Общие сведения об излучаемых помехах», в Controlling Radiated Emissions by Design , 3-е изд., Springer Science + Business Media, 2014, с. 4.

Важное примечание: Эта статья и ее содержание («Информация») принадлежат Unboxing-tomorrow.com и Voxidyne Media LLC. Никакая лицензия не предоставляется для его использования, кроме как для информационных целей.