Что такое петля гистерезиса. Как возникает магнитный гистерезис. Какие виды гистерезиса существуют. Где применяется явление гистерезиса в науке и технике.
Что такое петля гистерезиса и механизм ее возникновения
Петля гистерезиса — это график, отображающий зависимость намагниченности ферромагнитного материала от напряженности внешнего магнитного поля при его циклическом изменении. Гистерезис происходит от греческого слова, означающего «запаздывание» или «отставание».
Механизм возникновения петли гистерезиса связан с особенностями намагничивания и размагничивания ферромагнетиков:
- Изначально в ферромагнетике присутствуют домены с разнонаправленными магнитными моментами, суммарная намагниченность равна нулю.
- При воздействии внешнего поля домены постепенно ориентируются вдоль поля, возникает намагниченность.
- После снятия поля часть доменов сохраняет ориентацию — возникает остаточная намагниченность.
- Для полного размагничивания требуется приложить противоположное поле определенной величины — коэрцитивной силы.
В результате при циклическом изменении поля намагниченность изменяется нелинейно, образуя характерную петлю на графике.

Основные параметры и характеристики петли гистерезиса
Петля гистерезиса характеризуется следующими основными параметрами:
- Остаточная индукция Br — намагниченность, сохраняющаяся после снятия поля.
- Коэрцитивная сила Hc — напряженность размагничивающего поля.
- Индукция насыщения Bs — максимальная намагниченность материала.
- Площадь петли — характеризует потери энергии на перемагничивание.
По форме петли и значениям параметров можно судить о магнитных свойствах материала. Узкая петля характерна для магнитомягких материалов, широкая — для магнитотвердых.
Виды гистерезиса в различных физических системах
Помимо магнитного, выделяют следующие основные виды гистерезиса:
- Сегнетоэлектрический — зависимость поляризации от электрического поля в сегнетоэлектриках.
- Упругий — зависимость деформации от напряжения в упругих материалах.
- Тепловой — зависимость температуры от теплового потока в некоторых системах.
- Адсорбционный — зависимость адсорбции от давления газа.
Во всех случаях наблюдается характерная петлеобразная зависимость выходного параметра от входного при его циклическом изменении.

Применение явления гистерезиса в науке и технике
Гистерезисные свойства материалов находят широкое применение:
- Создание постоянных магнитов на основе магнитотвердых материалов.
- Сердечники трансформаторов и электромагнитов из магнитомягких материалов.
- Носители информации в устройствах магнитной записи.
- Датчики и преобразователи различных физических величин.
- Гистерезисные двигатели и муфты.
- Ферриты в радиотехнике и электронике.
Понимание явления гистерезиса важно для оптимизации характеристик магнитных материалов и устройств на их основе.
Влияние структуры и состава материала на форму петли гистерезиса
Форма и параметры петли гистерезиса существенно зависят от структуры и состава материала:
- Размер зерен и доменов влияет на коэрцитивную силу и остаточную намагниченность.
- Наличие примесей и дефектов расширяет петлю и увеличивает потери на перемагничивание.
- Химический состав определяет намагниченность насыщения.
- Внутренние напряжения искажают форму петли.
Это позволяет использовать анализ петли гистерезиса для контроля структуры и свойств магнитных материалов в металлургии.
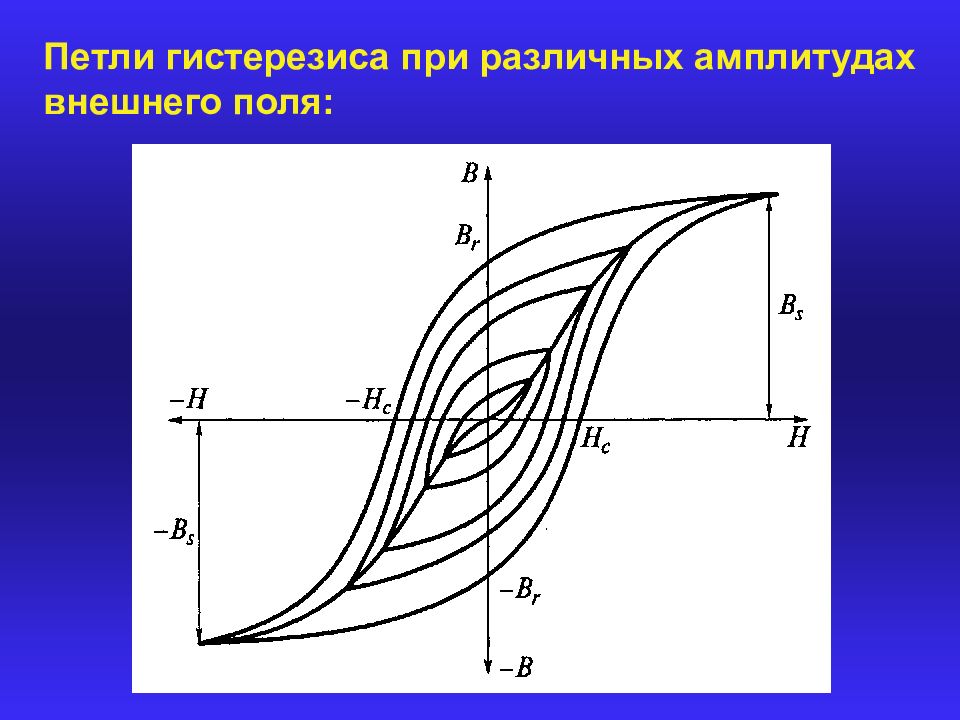
Динамические петли гистерезиса при перемагничивании переменным полем
При перемагничивании материала переменным магнитным полем наблюдаются динамические петли гистерезиса, отличающиеся от статических:
- Петля расширяется из-за дополнительных потерь на вихревые токи.
- Форма петли зависит от частоты перемагничивания.
- При высоких частотах петля вырождается в эллипс.
- Площадь петли характеризует полные магнитные потери.
Анализ динамических петель важен для оценки характеристик магнитных материалов в реальных условиях эксплуатации на переменном токе.
Использование петли гистерезиса в неразрушающем контроле материалов
Анализ параметров петли гистерезиса позволяет проводить неразрушающий контроль ферромагнитных материалов и изделий:
- Оценка структуры и фазового состава сталей и сплавов.
- Контроль механических свойств и термообработки.
- Выявление дефектов и неоднородностей структуры.
- Определение остаточных напряжений.
- Контроль качества постоянных магнитов.
Магнитный структурный анализ на основе измерения петли гистерезиса широко применяется в металлургии и машиностроении.
Гистерезиз и его магнитная петля: механизм возникновения петли гистерезиса
Петля гистерезиса. Подобная зависимость величин характерна для всех видов гистерезиса
Гистере́зис (греч. ὑστέρησις — «отстающий») — свойство систем (обычно физических), которые не сразу следуют приложенным силам. Реакция этих систем зависит от сил, действовавших ранее, то есть системы зависят от собственной истории.
В физике
Наибольший интерес представляют магнитный гистерезис, сегнетоэлектрический гистерезис и упругий гистерезис.
Магнитный гистерезис
Магнитный гистерезис — явление зависимости вектора намагничивания и вектора напряженности магнитного поля в веществе не только от приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется в ферромагнетиках — Fe, Co, Ni и сплавах на их основе. Именно магнитным гистерезисом объясняется существование постоянных магнитов.
Явление магнитного гистерезиса наблюдается не только при изменении поля H по величине и знаку, но также и при его вращении (гистерезис магнитного вращения), что соответствует отставанию (задержке) в изменении направления M с изменением направления H. Гистерезис магнитного вращения возникает также при вращении образца относительно фиксированного направления H.
Гистерезис магнитного вращения возникает также при вращении образца относительно фиксированного направления H.
Теория явления гистерезиса учитывает конкретную магнитную доменную структуру образца и её изменения в ходе намагничивания и перемагничивания.
Эти изменения обусловлены смещением доменных границ и ростом одних доменов за счёт других, а также вращением вектора намагниченности в доменах под действием внешнего магнитного поля.
Всё, что задерживает эти процессы и способствует попаданию магнетиков в метастабильные состояния, может служить причиной магнитного гистерезиса.
Петля гистерезиса для триггера Шмитта имеет прямоугольный вид.
В однодоменных ферромагнитных частицах (в частицах малых размеров, в которых образование доменов энергетически невыгодно) могут идти только процессы вращения M. Этим процессам препятствует магнитная анизотропия различного происхождения (анизотропия самого кристалла, анизотропия формы частиц и анизотропия упругих напряжений).
Благодаря анизотропии, M как бы удерживается некоторым внутренним полем HA (эффективным полем магнитной анизотропии) вдоль одной из осей лёгкого намагничивания, соответствующей минимуму энергии.
Магнитный гистерезис возникает из-за того, что два направления M (по и против) этой оси в магнитоодноосном образце или несколько эквивалентных (по энергии) направлений М в магнитомногоосном образце соответствуют состояниям, отделённым друг от друга потенциальным барьером (пропорциональным HA).
При перемагничивании однодоменных частиц вектор M рядом последовательных необратимых скачков поворачивается в направлении H, Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M коэрцитивная сила . Более универсальным является механизм неоднородного вращения M. Однако наибольшее влияние на Hc он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом Hc может быть существенно меньше эффективного поля анизотропии формы.
При этом Hc может быть существенно меньше эффективного поля анизотропии формы.
В электронике и электротехнике используются устройства, обладающие магнитным — различные магнитные носители информации, или электрическим гистерезисом, например, триггер Шмитта или гистерезисный двигатель.
Сегнетоэлектрический гистерезис
Сегнетоэлектрический гистерезис — неоднозначная петлеобразная зависимость поляризации P сегнетоэлектриков от внешнего электрического поля E при его циклическом изменении.
Сегнетоэлектрические кристаллы обладают в определенном температурном интервале спонтанной (самопроизвольной, то есть возникающей в отсутствие внешнего электрического поля) электрической поляризацией Pc. Направление поляризации может быть изменено электрическим полем.
При этом зависимость P(E) в полярной фазе неоднозначна, значение P при данном E зависит от предистории, то есть от того, каким было электрическое поле в предшествующие моменты времени. Основные параметры сегнетоэлектрического гистерезиса:
Основные параметры сегнетоэлектрического гистерезиса:
- остаточная поляризация кристалла Pост, при E = 0
- значение поля EKt(коэрцитивное поле) при котором происходит переполяризация
Упругий гистерезис
В теории упругости явление гистерезиса наблюдается в поведении упругих материалов, которые под воздействием больших давлений способны сохранять деформацию и утрачивать её при воздействии обратного давления (например, вытягивание сжатого стержня). Во многом именно это явление объясняет анизотропию механических характеристик кованых изделий, а также их высокие механические качества.
Различают два вида упругого гистерезиса — динамический и статический.
Динамический гистерезис наблюдают при циклически изменяющихся напряжениях, максимальная амплитуда которых существенно ниже предела упругости. Причиной этого вида гистерезиса является неупругость либо вязкоупругость.
При неупругости, помимо чисто упругой деформации (отвечающей закону Гука), имеется составляющая, которая полностью исчезает при снятии напряжений, но с некоторым запаздыванием, а при вязкоупругости эта составляющая полностью со временем не исчезает.
Как при неупругом, так и вязкоупругом поведении величина ΔU — энергия упругой деформации не зависит от амплитуды деформации и меняется с частотой изменения нагрузки.
Также динамический гистерезис возникает в результате термоупругости, магнитоупругих явлений и изменения положения точечных дефектов и растворённых атомов в кристаллической решётке тела под влиянием приложенных напряжений.
В биологии
Гистерезисные свойства характерны для скелетных мышц млекопитающих.
В почвоведении
Основная гидрофизическая характеристика почвы обладает гистерезисом.
В гидрологии
Зависимость Q=f(H) — связь расходов и уровней воды в реках — имеет петлеобразную форму.
В экономике
Некоторые экономические системы проявляют признаки гистерезиса: например, могут потребоваться значительные усилия, чтобы начать экспорт в какой-либо отрасли, но для его поддержания на постоянном уровне — небольшие.
В теории игр эффект гистерезиса проявляется в том, что небольшие отличия по одному или нескольким параметрам приводят две системы в противоположные стабильные равновесия, например, «хорошее» — доверие, честность и высокое благосостояние; и «плохое» — воровство, недоверие, коррупция и бедность. Несмотря на небольшие первоначальные различия, системы требуют огромных усилий для перехода из одного равновесия в другое.
Несмотря на небольшие первоначальные различия, системы требуют огромных усилий для перехода из одного равновесия в другое.
Эффект гистерезиса — состояние безработицы; достигнув достаточно высокого уровня, она может в определенной мере самовоспроизводиться и удерживаться на нем. Экономические причины гистерезиса (долгосрочной негибкости рынка труда) неоднозначны. Некоторые институциональные факторы ведут к гистерезису.
Например, социальное страхование, особенно страхование по безработице, может через налоговую систему снижать спрос фирм на рабочую силу в официальной экономике. Безработица может вести к потере человеческого капитала и к «помечиванию» тех, кто долгое время остается безработным.
Профсоюзы могут вести переговоры с целью поддерживать благосостояние их настоящих членов, игнорируя интересы аутсайдеров, оказавшихся безработными. Фиксированные издержки, связанные со сменой должности, места работы или отрасли, также могут приводит к гистерезису.
Наконец, возможны трудности при различении реальных и кажущихся явлений гистерезиса, когда конечное состояние системы определяется, ее текущей динамикой или ее начальным состоянием. В первом случае гистерезис отражает наше незнание: добавив недостающие переменные и информацию, можно более полно описать эволюцию изучаемой системы. Др.
В первом случае гистерезис отражает наше незнание: добавив недостающие переменные и информацию, можно более полно описать эволюцию изучаемой системы. Др.
интерпретация явления гистерезиса — простое существование нескольких состояний равновесия, когда невидимые воздействия перемещают экономику из одного состояния равновесия в др.
Математические модели гистерезиса
Появление математических моделей гистерезисных явлений обуславливалось достаточно богатым набором прикладных задач (прежде всего в теории автоматического регулирования), в которых носители гистерезиса нельзя рассматривать изолированно, поскольку они являлись частью некоторой системы.
Создание математической теории гистерезиса относится к 60-м годам XX-го века, когда в Воронежском университете начал работать семинар под руководством М. А. Красносельского, «гистерезисной» тематики.
Позднее, в 1983 году появилась монография [1], в которой различные гистерезисные явления получили формальное описание в рамках теории систем: гистерезисные преобразователи трактовались как операторы, зависящие от своего начального состояния как от параметра, определенные на достаточно богатом функциональном пространстве(напр.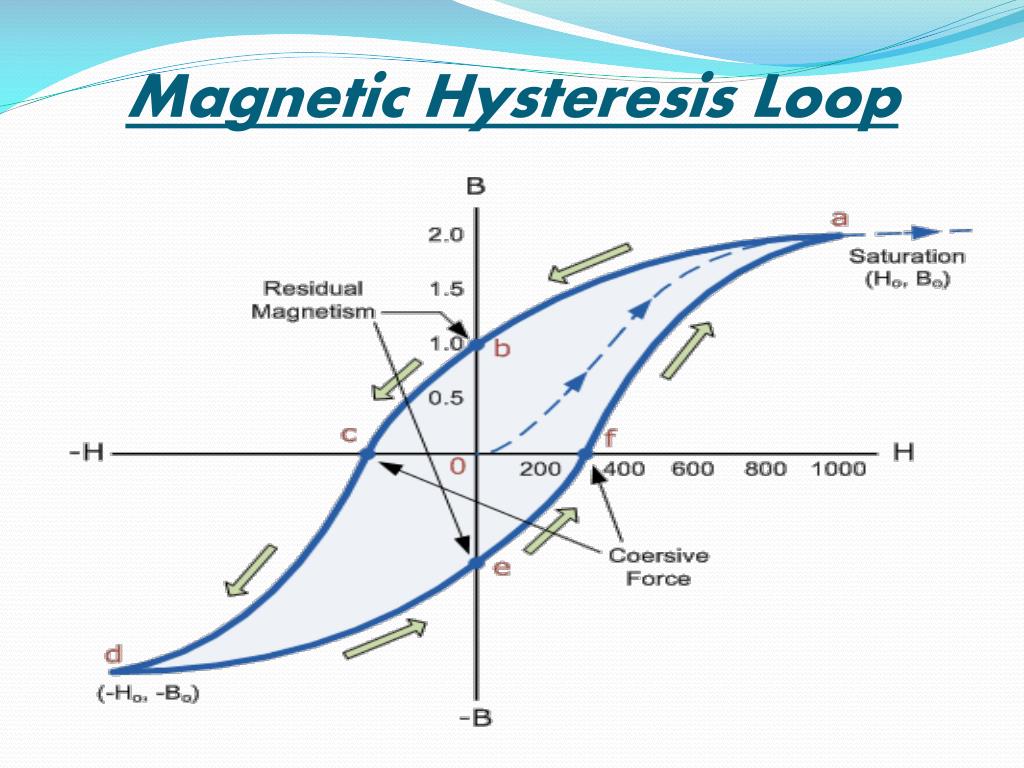 пространстве непрерывных функций), действующие в некоторое функциональное пространство.
пространстве непрерывных функций), действующие в некоторое функциональное пространство.
Свойства
Простое параметрическое описание различных петель гистерезиса можно найти в работе[2]. Замена гармонических функций на прямоугольные, треугольные или трапецеидальные импульсы позволяет получить кусочно-линейные петли гистерезиса, часто встречающиеся в дискретной автоматике.
Литература
См. также
Обменное смещение — как особенность петель гистерезиса.
Wikimedia Foundation. 2010.
Источник: https://dic.academic.ru/dic.nsf/ruwiki/1016749
Петля гистерезиса
Гистерезис происходит от греческого слова, означающего запаздывание или отставание. С данным понятием связана такая физическая величина, как петля гистерезиса, определяющая одну из характеристик тела. Она определенным образом связана также и с физическими величинами, характеризующими внешние условия, такие как магнитное поле.
Общие понятия гистерезиса
Гистерезис можно наблюдать в те моменты, когда какое-либо тело в конкретный период времени будет находиться в зависимости от внешних условий.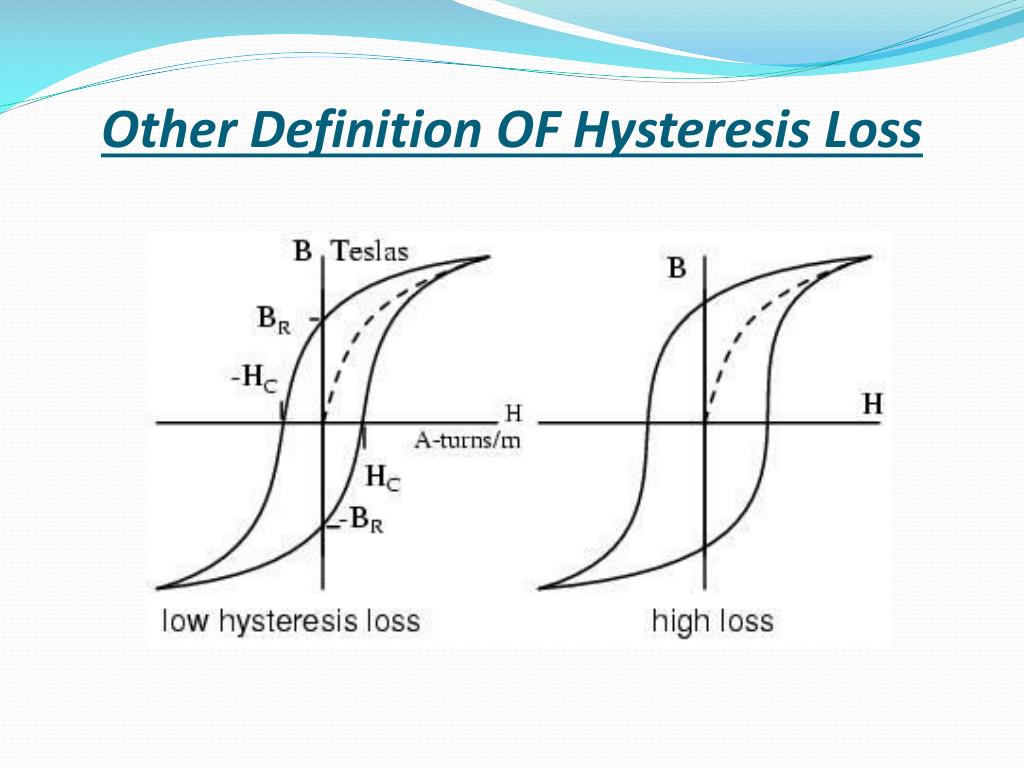 Данное состояние тела рассматривается и в предыдущее время, после чего производится сравнение и выводится определенная зависимость.
Данное состояние тела рассматривается и в предыдущее время, после чего производится сравнение и выводится определенная зависимость.
Механизм возникновения петли гистерезиса
Сам по себе гистерезис представляет собой кривую, отображающую измененный магнитный момент вещества, на которое воздействует периодически изменяющаяся напряженность поля. Когда магнитное поле воздействует на ферромагнетики, то изменение их магнитного момента наступает не сразу, а с определенной задержкой.
В каждом ферромагнетике изначально присутствует самопроизвольная намагниченность. Сам материал включает в свой состав отдельные фрагменты, каждый из которых обладает собственным магнитным моментом. При направленности этих моментов в разные стороны, значение суммарного момента оказывается равным нулю в результате взаимной компенсации.
Если на ферромагнетик оказать воздействие магнитным полем, то все моменты, присутствующие в отдельных фрагментах (доменах) будут развернуты вдоль внешнего поля. В итоге, в материале образуется некоторый общий момент, направленный в одну сторону.
В итоге, в материале образуется некоторый общий момент, направленный в одну сторону.
Если внешнее действие поля прекращается, то домены не все окажутся в изначальном положении. Для этого потребуется воздействие достаточно сильного магнитного поля, предназначенного для разворота доменов. Такому развороту создают препятствия наличие примесей и неоднородность материала.
Поэтому материал имеет некоторую остаточную намагниченность, даже при отключенном внешнем поле.
Для снятия остаточного магнитного момента, необходимо приложение действия поля в противоположном направлении. Напряженность поля должна иметь величину, достаточную, чтобы выполнить полное размагничивание материала. Такая величина известна как коэрцитивная сила. Дальнейшее увеличение магнитного поля приведет к перемагничиванию ферромагнетика в противоположную сторону.
Когда напряженность поля достигает определенного значения, материал становится насыщенным, то есть магнитный момент больше не увеличивается.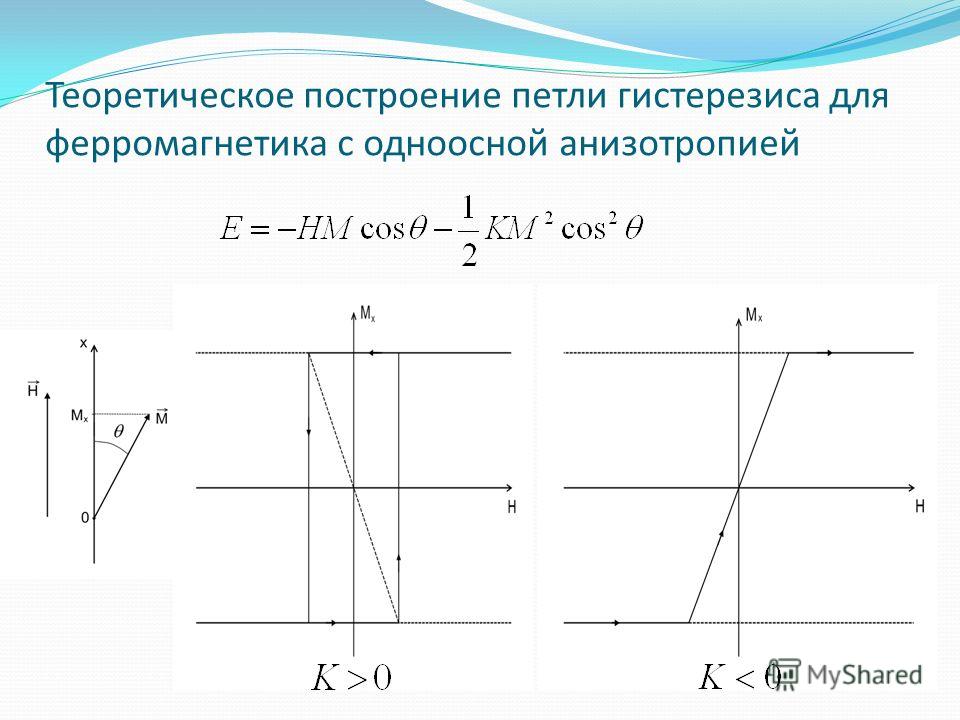 При снятии поля вновь наблюдается наличие остаточного момента, который снова можно убрать. Дальнейшее увеличение поля приводит к попаданию в точку насыщения с противоположным значением.
При снятии поля вновь наблюдается наличие остаточного момента, который снова можно убрать. Дальнейшее увеличение поля приводит к попаданию в точку насыщения с противоположным значением.
Таким образом, на графике появляется петля гистерезиса, начало которой приходится на нулевые значение поля и момента. В дальнейшем, первое же намагничивание выводит начало петли гистерезиса из нуля и весь процесс начинает происходить по графику замкнутой петли.
Источник: https://electric-220.ru/news/petlja_gisterezisa/2016-06-10-974
Что такое петля гистерезиса?
Биологические и физические системы способны мгновенно откликаться на приложенное к ним воздействие. Если рассмотреть это явление на временной оси координат, то становится заметно, что отклик зависит от предыстории системы и ее текущего состояния. График, который наглядно демонстрирует это свойство систем, получил название петли гистерезиса, которая отличается остроугольной формой.
Оригинальная форма петли обусловлена эффектом насыщения и неравномерностью траектории между соседними расстояниями. Эффект гистерезиса имеет кардинальные отличия от инерционности, с которой его часто путают, забывая о том, что монотонное сопротивление существенно отличается от мгновенного сопротивления на воздействие.
Эффект гистерезиса имеет кардинальные отличия от инерционности, с которой его часто путают, забывая о том, что монотонное сопротивление существенно отличается от мгновенного сопротивления на воздействие.
Петля гистерезиса является циклом, в ходе которого часть свойств системы используются независимо от воздействий, а часть – отправляется на повторную проверку.
В физике наиболее часто системы сталкиваются со следующими видами гистерезиса:
- Магнитный – отражает зависимость между векторами напряжения магнитного поля и намагничивания в веществе. Это явление объясняет существование постоянных магнитов.
- Сепнгетоэлектрический – зависимость между поляризацией сегнетоэлектриков и изменения внешнего электрического поля.
- Упругий – зависимость деформации упругих материалов от воздействия высоких давлений. Это явление лежит в основе великолепных механических характеристик изделий из кованого метала.
Упругий гистерезис встречается двух основных видов – статический и динамический. В первом случае петля будет равномерной, во втором – постоянно меняющейся.
В первом случае петля будет равномерной, во втором – постоянно меняющейся.
В электротехнике широко применяются устройства, в основе которых лежат магнитные взаимодействия. Наиболее распространение получили магнитные носители данных. Понимание гистерезиса необходимо для подавления в них шумов, таких как быстрые колебания или дребезжание контактов.
В большинстве электронных приборов наблюдается явление теплового гистерезиса. В процессе работы устройства нагреваются, а после охлаждения ряд характеристик уже не могут принять первоначальные явления.
Так, в процессе нагрева происходит расширение микросхем и печатных плат, полупроводниковых кристаллов. В результате развивается механическое напряжение, воздействие которого на элементы системы сохраняется после остывания. Особенно ярко тепловой гистерезис проявляется в высокоточных источниках опорного напряжения.
Источник: https://Voltiq.ru/wiki/hysteresis-loop/
Магнитный гистерезис
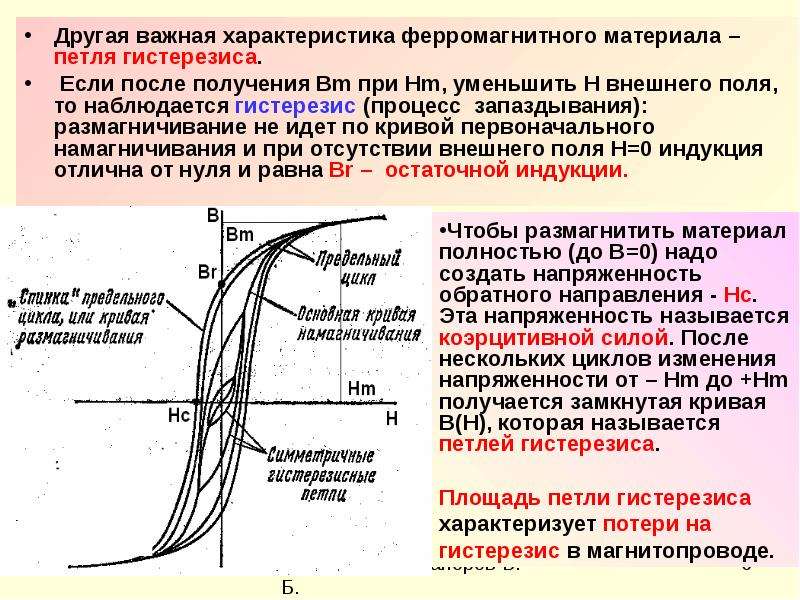
Если предварительно размагниченный образец ферромагнитного материала подвергнуть намагничиванию до состояния технического насыщения, то с увеличением напряженности магнитного поля Н магнитная индукция образца В будет изменяться в соответствии с кривой ОАБ (рисунок 2. 2).
2).
Рисунок 2.2 – Предельная петля магнитного гистерезиса
В точке А при H = Hs магнитная индукция образца достигнет индукции насыщения Bs. При уменьшении напряженности поля Н намагниченность образца уменьшается по кривой БАBr, и при Н = 0 образец будет обладать некоторой индукцией, величина которой будет отлична от нуля.
Эта индукция называется остаточной и обозначается Вr.
Остаточная индукция (остаточная намагниченность) обусловлена тем, что при размагничивании, когда Н = 0, магнитные моменты доменов оказываются ориентированными вдоль оси легкого намагничивания, направление которой близко к направлению внешнего.
Для достижения полного размагничивания образца к нему необходимо приложить противоположное по знаку поле определенной напряженности. Напряженность такого поля называют коэрцитивной силой Нс.
При дальнейшем усилении отрицательного поля магнитная индукция тоже становится отрицательной и в точке A’ при H = –Hs достигает значения индукции технического насыщения (B = –Bs).
После уменьшения отрицательного поля, а затем увеличения положительного поля кривая перемагничивания опишет петлю, называемую предельной петлей магнитного гистерезиса, которая является важной технической характеристикой магнитных материалов.
Таким образом, предельная петля магнитного гистерезиса – это кривая изменения магнитной индукции при изменении внешнего магнитного поля от +Hs до –Hs и обратно. Пользуясь предельной петлей магнитного гистерезиса можно определить основные параметры материала: коэрцитивную силу Нс, индукцию насыщения Bs, остаточную индукцию Br и др.
Такие характеристики материала, как точка Кюри и индукция насыщения, зависят только от химического состава магнитных материалов. Коэрцитивная сил Нс, магнитная проницаемость M и площадь петли гистерезиса являются структурночувствительными.
Чем больше размер зерна (меньше суммарная удельная поверхность зерен) и более совершенна структура кристаллической решетки (меньше дислокаций, внутренних напряжений, примесей и других дефектов), тем меньше Нс и больше M, а материал легче намагничивается и перемагничивается.
По величине коэрцитивной силы магнитные материалы подразделяются на магнитомягкие и магнитотвердые. Материалы, у которых Нс 4 кА/м – к магнитответдым (ГОСТ 19693 – 74).
Для магнитомягких материалов характерно малое значение коэрцитивной силы. У промышленных образцов наименьшая Нс = 0,4 А/м. Поэтому они намагничиваются до индукции технического насыщения при невысоких напряженностях поля. У магнитомягких материалов высокая магнитная проницаемость, малые потери на перемагничивание и узкая петля гистерезиса при высоких значениях магнитной индукции.
Для магнитотвердых материалов характерна широкая петля гистерезиса с большой коэрцитивной силой. У промышленных образцов наибольшая Нс = 800 кА/м. Магнитотвердые материалы намагничиваются при высокой напряженности внешнего магнитного поля, но зато длительное время сохраняют сообщенную энергию.
- ← Раздел 2.1
- Раздел 2.3 →
Источник: https://uas.su/books/newmaterial/22/razdel22. php
php
ПОИСК
| Рис. 4.1. Петля гистерезиса для магнитного материала. |
Карбонильное железо характеризуется специфической кривой первоначального намагничивания, соответствующей формой петли гистерезиса и определенными значениями составляющих магнитных потерь. При этом электромагнитные свойства карбонильного железа в блоке, получаемом металлокерамическим способом из порошка, и в частицах порошка существенно различны. Это в первую очередь объясняется изменением структуры материала при его металлокерамической обработке, а также влиянием на электромагнитные свойства размера частиц. [c.166]
Связь между напряженностью приложенного магнитного поля и магнитной индукцией в образце с упорядоченным магнетизмом, выражается обычно петлей гистерезиса. Петля гистерезиса рис. 4.1) характеризуется максимальной индукцией Вт, остаточной индукцией Вг и коэрцитивной силой Не. Остаточная индукция и коэрцитивная сила магнитного материала зависят от структуры, включений и внутренних напряжений в материале. Максимальная индукция насыщения не чувствительна к структуре и зависит только от химического состава и температуры. [c.94]
Максимальная индукция насыщения не чувствительна к структуре и зависит только от химического состава и температуры. [c.94]
При намагничивании магнитного материала переменным полем петля гистерезиса, характеризующая затраты энергии в течение одного цикла перемагничивания, расширяются (увеличивают свою площадь) как за счет потерь на гистерезис, так и потерь на вихревые токи и дополнительные потери.
Такую петлю называют динамической, а сумму составляющих потерь — полными потерями. Геометрическое место вершин динамических петель гистерезиса называют динамической кривой намагничивания, а отношение индукции к напряженности поля на этой кривой — динамической магнитной проницаемостью [c.
32]
Сложный характер одновременного влияния (часто в противоположных направлениях) различных факторов на магнитные свойства материалов затрудняет их разграничение и определение влияния каждого.
В некоторых простых случаях имеется возможность определить влияние одного или нескольких основных факторов на размеры и форму петли гистерезиса.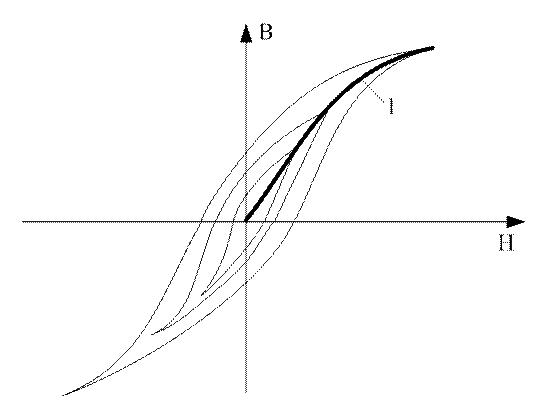
В случае, если этот фактор одновременно и однозначно влияет на другие физические (немагнитные) свойства материала, можно установить [c.165]
Перспективными для использования в многоэлементных преобразователях являются преобразователи магнитных полей на основе кольцевых сердечников из материала с прямоугольной петлей гистерезиса. Достоинством таких преобразователей является наличие у них вентильных свойств, что делает ненужным применение электронных коммутирующих ключей в каждой ячейке матрицы. При этом отсутствует гальваническая связь между отдельными чувствительными элементами, сушественно упрощается конструкция много- [c.144]
СИТ название петли гистерезиса (отставания),Изменение индукции при перемагничивании материала идет термодинамически необратимо за один цикл перемагничивания затрачивается энергия, количество которой пропорционально площади петли гистерезиса. Кроме потерь на гистерезис при действии на материал переменного магнитного поля, в нем появляются вихревые токи, на создание которых потеря энергии тем больше, чем меньше удельное сопротивление материала.
[c.349]
Петли гистерезиса бывают самыми разнообразными по форме. Одним из факторов, влияющих на форму петли, является размер частиц образца, причем увеличение их размера приводит, как правило, к тому, что материал становится более мягким, т. е.
уменьшается поле, необходимое для его перемагничивания (рис. 4.22. и 4.23). Объясняется это тем, что основным процессом при намагничивании очень мелких однодоменных частиц является поворот магнитного момента частицы в сторону поля (рис. 4.
24, А), в то время как намагничивание крупных частиц осуществляется путем смещения доменных стенок, происходящего при меньших полях, чем поворот моментов (рис. 4.24, Б).
Частицы среднего размера обычно бывают разделены на области-домены с разным направлением намагниченности, что уменьшает энергию магнитного поля, создаваемого магнитным моментом частицы. [c.199]
Магнитный вид неразрушающего контроля основан на анализе взаимодействия магнитного поля с контролируемым объектом.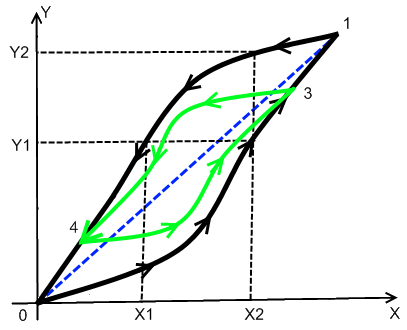 Его, как правило, применяют для контроля объектов из ферромагнитных материалов.
Его, как правило, применяют для контроля объектов из ферромагнитных материалов.
По характеру взаимодействия физического поля с объектом этот вид контроля не дифференцируют во всех случаях используют намагничивание объекта и измеряют параметры, используемые при контроле магнитными методами. Процесс намагничивания и перемагничивания ферромагнитного материала сопровождается гистерезисными явлениями (рис. 1.1).
Свойства, которые требуется контролировать (химический состав, структура, наличие несплошностей и др.), обычно связаны с параметрами процесса намагничивания и петлей гистерезиса. [c.9]
Сложный характер одновременного влияния (часто в противоположных направлениях) различных факторов на магнитные свойства материалов, как правило, не позволяет их разграничить и определить влияние каждого.
Только в некоторых (простых) случаях имеется возможность определить влияние одного или нескольких (основных) факторов на размеры и форму петли гистерезиса.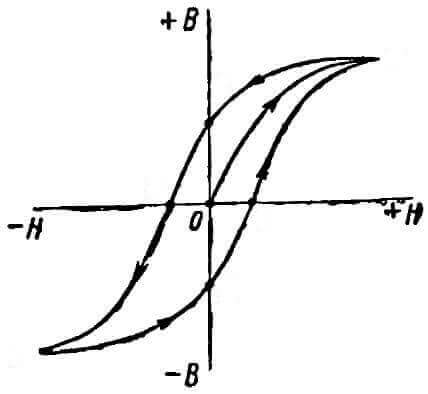
В случае, если этот фактор одновременно и однозначно влияет на другие физические (немагнитные) свойства материала, можно установить связь между ними и использовать магнитные свойства для контроля физических или химических свойств (параметров). [c.361]
МАГНИТОСТРУКТУРНЫЙ АНАЛИЗ — анализ свойств магнитных материалов, основанный на использовании зависимости их магн. характеристик от структуры. К важнейшим магн. характеристикам относятся магнитная восприимчивость, магнитная проницаемость, намагниченность насыщения, коэрцитивная сила. У диамагнитных материалов магн.
восприимчивость X отрицательна, у парамагнитных материалов положительна, вследствие чего диамагнетик выталкивается из неоднородного магн. поля, а парамагнетик втягивается в него. По силе выталкивания или втягивания судят о знаке или абс. величине магн. восприимчивости.
А поскольку при фазовом превращении в твердом состоянии и при плавлении она изменяется скачкообразно, этим обстоятельством пользуются для определения фазового состояния материала. У ферромагнитных материалов магн. восприимчивость — неоднозначная функция магн. поля. Связь между намагниченностью ферромагнетика и напряженностью намагничивающего магн.
У ферромагнитных материалов магн. восприимчивость — неоднозначная функция магн. поля. Связь между намагниченностью ферромагнетика и напряженностью намагничивающего магн.
поля изображается кривой намагничивания и петлей гистерезиса. В процессе намагничивания магн. проницаемость ферромагнетика л = 1 4- [c.749]
Петля магнитного гистерезиса — зависимость магнитной индукции (намагниченности) магнитного материала от напряженности внешнего магнитного поля. [c.410]
Указанные особенности позволяют объяснить изменения магнитных характеристик в зависимости от режимов охлаждения.
Действительно, для феррита из материала 1,3 ВТ незначительное изменение статических параметров петли гистерезиса с изменением температуры начала разрежения соответствует сравнительно мало- Му изменению величины у в пределах однофазной шпинельной структуры.
Вместе с тем импульсная квадратность сердечников иУ 1й]/г), являющаяся более чувствительной характеристикой к изменению дефектности шпинели [189], значительно снижается по [c. 144]
144]
Если образец магнитноупорядоченного материала намагнитить до насыщения, а затем снять намагничивающее поле, то образец будет находиться в так называемом остаточном состоянии, т. е. обладать остаточной индукцией.
Коэрцитивная сила является величиной, наиболее чувствительной к структуре магнитного вещества. Таким образом, по форме петли гистерезиса можно судить об особенностях свойств различных магнитных материалов.
Материалы для эластичных постоянных магнитов (магнитнотвердые резины) должны характеризо- [c.94]
Не и уменьшением остаточной индукции и коэффициента прямоугольности Кп. Образец, отожженный при 300°С, сохраняет исходные магнитные характеристики, чему соответствует неизменное значение постоянной решетки и фазового состава материала.
Отжиг при 400°С и выше приводит к ухудшению статических параметров петли гистерезиса, а на рентгенограммах появляется значительное расширение линий и искажение их формы, свидетельствующее о неоднородности материала.
Последнее может стать результатом окисления, идущего в первую очередь по границам [c.148]
Магнитный гистерезис — явление очень важное. По форме петли все магнитные материалы можно разделить на две большие группы мягкие магнитные материалы и жесткие, или высококоэрцитивные.
Мягкий магнитный материал должен иметь кривую намагничивания с большой проницаемостью (характеризующую кривизну подъема кривой, см. рис. 125), достигаемой в очень слабых полях, и очень узкую петлю гистеризиса с ничтожно малой коэрцитивной силой.
Важнейшее значение мягких магнитных материалов в экономике страны видно, например, из той роли, которую играют в ней трансформаторное и динамное листовое железо.
Жесткий магнитный материал для выполнения своего назначения стабильного источника сильного магнитного поля должен обладать максимально широкой петлей гистерезиса, т. е. максимальными коэрцитивной силой и остаточной индукцией. [c.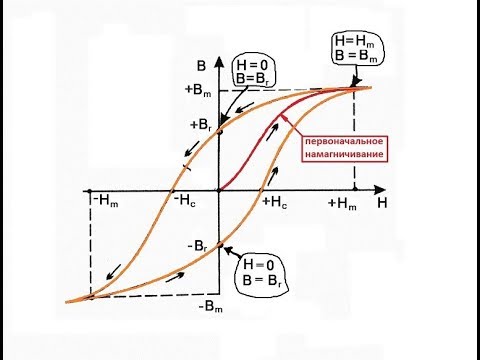 322]
322]
Рассмотрим теперь петлю магнитного гистерезиса (см. ниже) как характеристику магнитного материала, и в первую очередь зависимость формы петли от размера зерен.
Нужно отметить трудоемкость получения петли гистерезиса с помощью сквид-магнитометра, поскольку для изменения намагничивающего поля в сквид-системе требуется отогреть и вновь охладить сверхпроводящий экран при новом значении поля. [c.198]
Известно, что форма и размеры петли гистерезиса зависят от химического состава материала, определяющего кристаллографическую анизотропию, наличие и расположение примесей и атомов легирующих элементов, микро- и макронапряжения, наличие и расположение дислокаций и т. п.
Сложный характер взаимосвязи между указанными факторами затрудняет установить корреляционную связь каждого из них с магнитными свойствами материала. В некоторых случаях можно определить влияние одного или нескольких основных факторов на размеры и форму петли гистерезиса.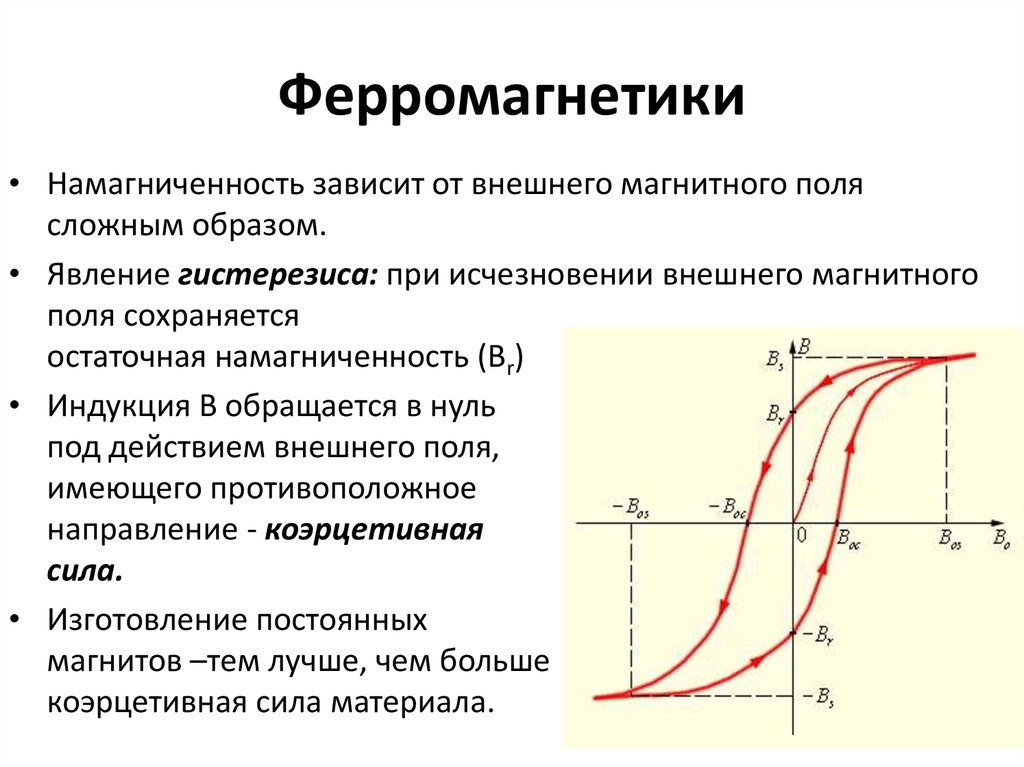 [c.
[c.
72]
В литературе можно найти многочисленные примеры исследования влияния давления на параметры индуктивных элементов. Индуктивность компонентов, содержащих железный порошок в пластиковой матрице, обычно пропорциональна давлению, однако эти изменения не носят постоянного характера.
Единственный описанный в литературе случай существенного остаточного изменения параметров в результате воздействия давления связан со специальным сердечником из материала с ориентированной зеренной структурой и с прямоугольной петлей гистерезиса.
Сведения о влиянии давления на элементы устройств магнитной памяти в литературе найти не удалось, но можно предположить, что такие компоненты будут выходить из строя при однократном повышении давления, поскольку в них используются материалы, аналогичные применяелйлм в ориентированных сердечниках с прямоугольной петлей гистерезиса. [c.482]
Характер наблюдаемых изменений позволяет понять их причину.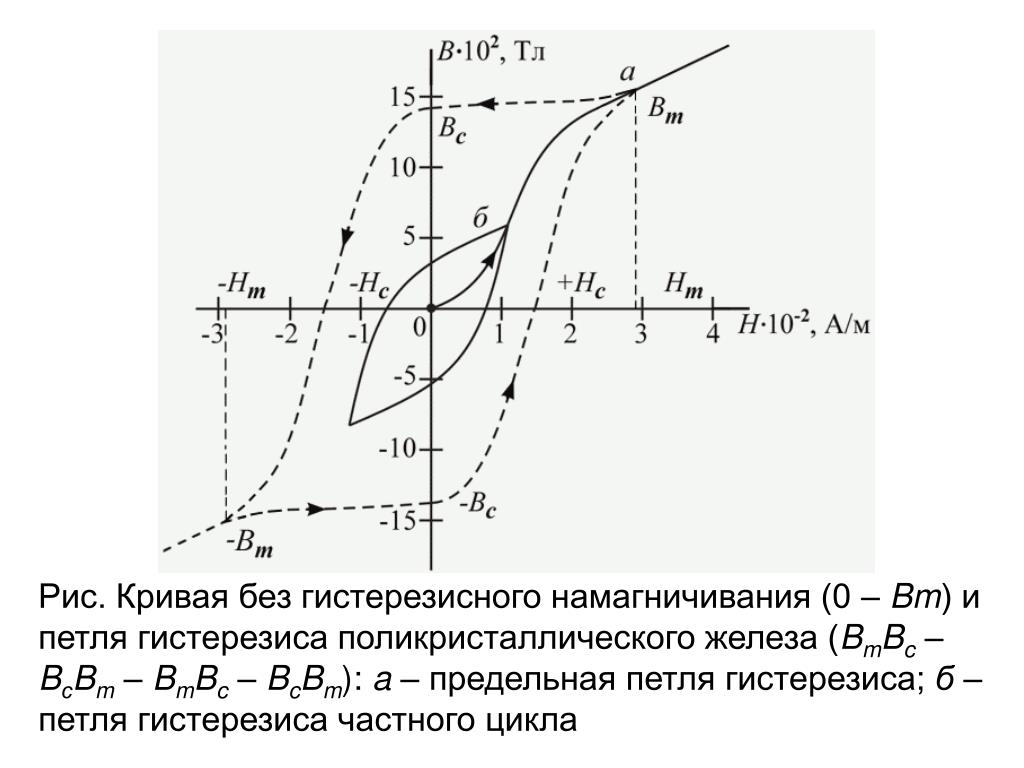 Прежде всего, необходимо обратить внимание на принципиально иной, по сравнению с феррожидкостями, характер зависимости намагниченности суспензий от напряженности поля — наличие гистерезиса.
Прежде всего, необходимо обратить внимание на принципиально иной, по сравнению с феррожидкостями, характер зависимости намагниченности суспензий от напряженности поля — наличие гистерезиса.
Гистерезис — это несовпадение зависимостей свойства (намагниченности) от параметра состояния (напряженности поля), получаемых при увеличении и при уменьшении значения параметра состояния. Гисте-резис намагниченности наглядно представляется в виде петли гистерезиса (рис. 3.73).
Намагничивание суспензии однодоменных частиц магнитно-жесткого материала при напряженности магнитного поля меньшей, чем коэрцитивная сила частиц, возможно только путем механического поворота частиц в магнитном поле достаточно большой напряженности Я.
Она должна быть такой, чтобы крутящий момент [тН], действующий на частицу со стороны магнитного поля, превысил момент [c.665]
В режиме А нарушения сплошности определяют при высоких намагниченностях, когда магнитное состояние материала изделия соответствует индукциям, близким к предельной петле гистерезиса.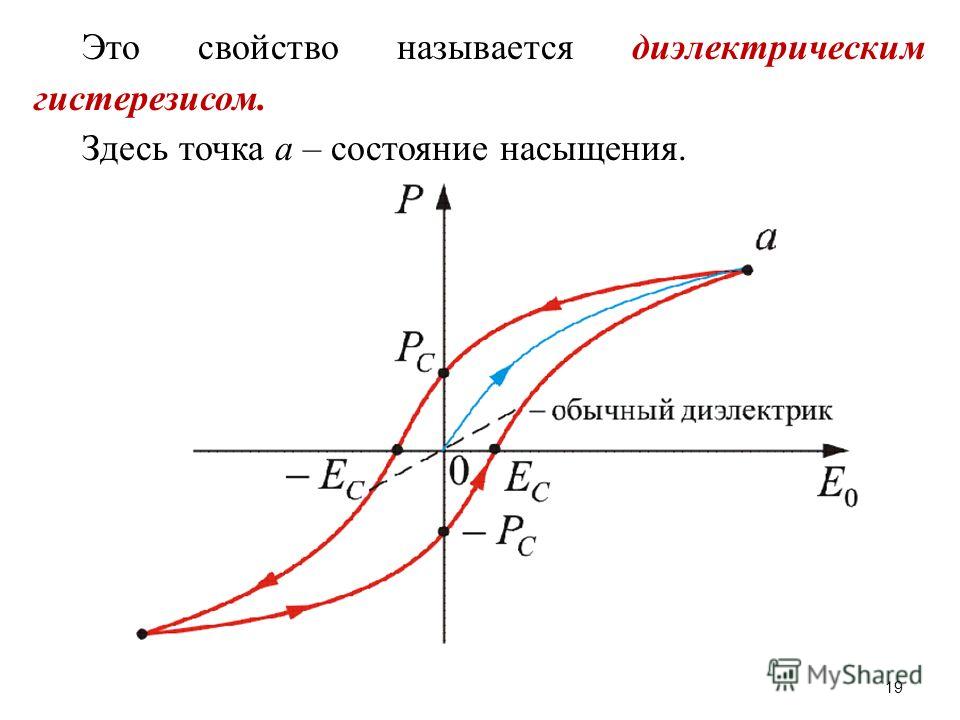
Конструкционные стали относятся, как правило, к группе ферромагнитных материалов с нормальными петлями гистерезиса, у которых отношение остаточной индукции Вг к максимальной 5тах на предельной петле гистерезиса приблизительно постоянно и равно 0,5. .. 0,7.
Для режима А оказалось возможным за критерий выбора расчетной формулы взять значение остаточной индукции. [c.348]
ИНДУКЦИЯ НАСЫЩЕНИЯ (лат. 1пс1ис11о — наведение, возбуждение) — магн. индукция при такой напряженности магн. поля, когда намагниченность материала становится максимальной. Для большинства материалов абс. магн.
насыщение неосуществимо, для остальных — возможно в очень сильных нолях, когда намагниченность насыщения /о не зависит от поля. Магнитные материа.гы, гл. обр. магнитпо-мяг-кие, характеризуются индукцией технического насыщения — магн.
индукцией, при к-рой намагниченность материала достигает значения технического насыщении — состояния, когда векторы намагниченности всех доменов ориентируются в направлении намагничивающего поля с напряженностью Н .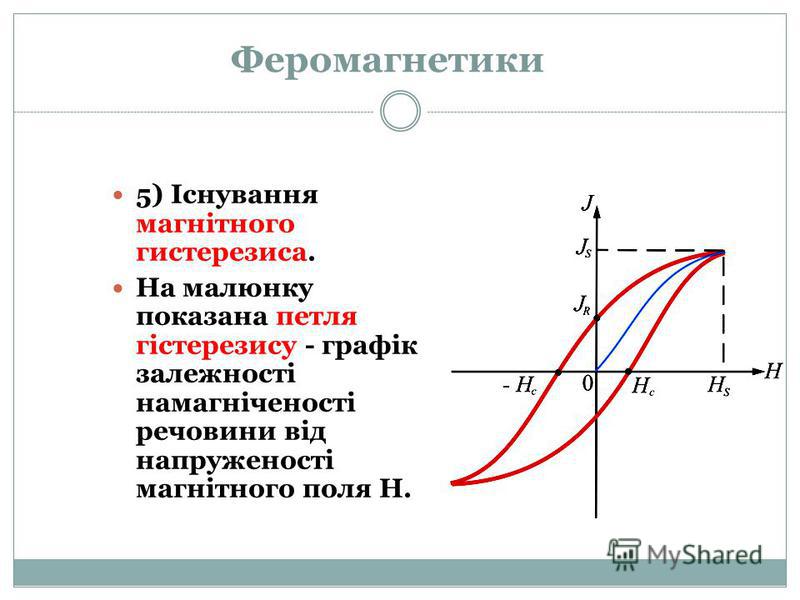 С увеличением наиряженности поля петли гистерезиса остаются одинаковыми. И. н.
С увеличением наиряженности поля петли гистерезиса остаются одинаковыми. И. н.
зависит только от природы ферромагнитных фаз магн. материала и не зависит от технологии мех. обработки. В размагниченном состоянии при т-рах, не превышающих Кюри точку, каждый домен ферромагнетика благодаря действию внутрикристалличе- [c.501]
К сожалению, нельзя использовать ток, проходящий через катушки электромагнита для определения массовых чисел, вследствие эффекта гистерезиса. Чтобы измерять массы в области до 200 массовых единиц с точностью до 0,2 а. е. м.
(10 %), требуется измерение магнитного поля с точностью до 5-10 и специальное приспособление — измеритель масс, который в процессе развертки масс-спектра непрерывно регистрирует развертываемые массы, значения которых оператор наносит на спектр.
В ином случае измеритель должен делать отмэтки на регистрируемом спектре, соответствующие заранее определенной величине отношения массы к заряду регистрируемых ионов.
Для очень точных определений масс предпочтительнее использовать измерение электростатического потенциала, так как необходимо оценивать эффективное магнитное поле на всем пути движения иона, что сложно.
Измерения магнитного поля на небольшом участке недостаточны для оценки этого эффективного поля вследствие неоднородности магнитного материала, обусловливающего разницу в полях на различных участках поверхности магнита.
Положительные ионы в масс-спектрометре проходят через области поля рассеяния, поэтому лучшая характеристика магнитного поля может быть, вероятно, получена в том случае, если измерительное устройство помещено не в области однородного поля около центра полюса, а на участках, подверженных также действию рассеянных полей. Различия отдельных участков поля между полюсами могут изменяться в зависимости от гистерезисиой петли. Эта разница сравнительно невелика и не мешает применению измерителей магнитного поля для определения масс с точностью до 0,1%. [c.57]
[c.57]
В заключение отметим, что собственное атомное разупорядочение существенным образом влияет на магнитные свойства ферритов и это обстоятельство надо учитывать, когда надо получить материал со строго повторяющимися параметрами.
В качестве технологического приема, стабилизирующего магнитную индукцию и квадратность термостабильной петли гистерезиса, иногда рекомендуют дополнительные к основной термообработке отжиги при температурах 700—800°С в течение времени, достаточном для равновесного перераспределения ионов по подрешеткам (продолжительность отжига зависит от природы феррита [2]).
Примером значительного влияния собственно атомного разупорядочения на магнитные свойства является поведение феррита никеля, резко закаленного с высоких температур и обладающего определенной концентрацией ионов N1 + в Л-узлах решетки (при 1300°С в формуле Ре » [Ы1 Ре2111л ]04 д = 0,9955).
Как показали измерения [142], появление N1 + в тетраэдрических узлах шпинельной структуры приводит к изменению анизотропии кристалла и ширины линии ферромагнитного резонанса. [c.116]
[c.116]
Так, например, однополупериодиый магнитный усилитель (рис. Х-1) представляет собой дроссель насыщения ДЯ с рабочей ОР и управляющей ОУ обмотками. Материал сплава, из которого выполнен сердечник дросселя, обладает петлей гистерезиса, форма которой близка к прямоугольной.
В цепь рабочей обмотки, получающей питание от сети переменного тока через трансформатор 1Т, включены выпрямитель ВР и сопротивление нагрузки СН, с которого и снимается импульс отпирающего напряжения. Обмотка управления включена через сопротивление управления СУ в сеть постоянного тока.
СС и Е — сеточные сопротивления и конденсатор СЗН, ЕЗН, ВЗН и ТЗН — сопротивление, емкость, выпрямитель и трансформатор запирающего напряжения. [c.226]
Источник: https://www.chem21.info/info/835559/
Магнитный гистерезис: описание явления, гистерезисная петля
В данной статье мы рассмотрим явление под названием магнитный гистерезис, которое связано со свойствами намагничивания материала, благодаря которому он сначала намагничивается, а затем размагничивается.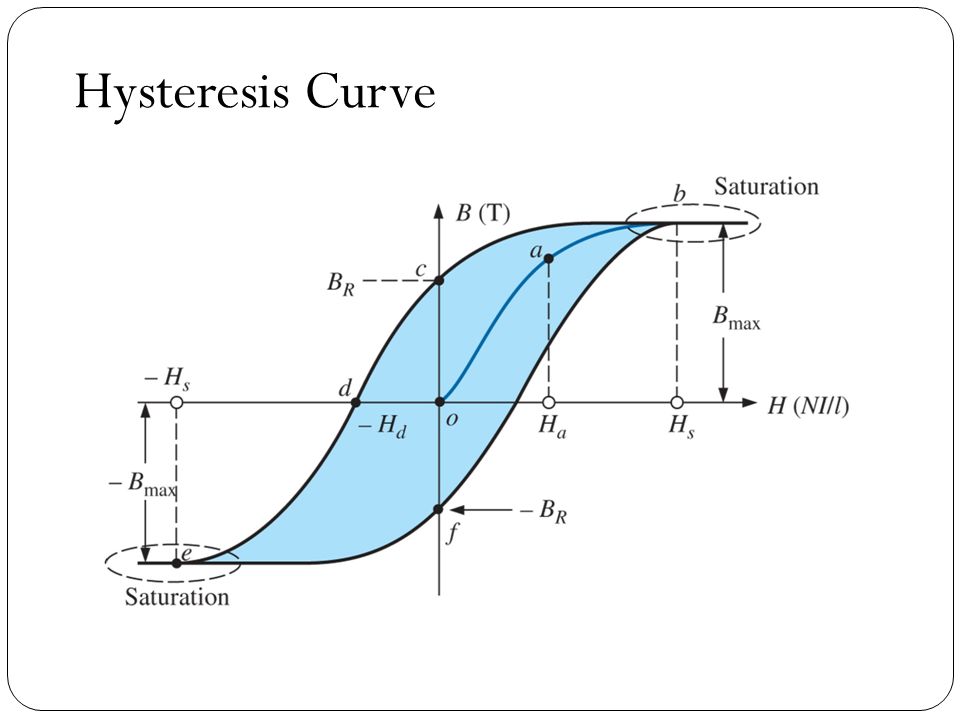 Рассмотрим кривые намагничивания, сохраняемость, а так же магнитную петлю гистерезиса.
Рассмотрим кривые намагничивания, сохраняемость, а так же магнитную петлю гистерезиса.
Описание явления магнитного гистерезиса
Мы знаем, что магнитный поток, создаваемый электромагнитной катушкой, представляет собой величину магнитного поля или силовых линий, создаваемых в данной области, и что его чаще называют «плотностью потока», обозначенным символ B с единицей измерения Тесла, Т.
Мы также знаем из предыдущих уроков, что магнитная сила электромагнита зависит от числа витков катушки, тока, протекающего через катушку, или от типа используемого материала сердечника, и если мы увеличим либо ток, либо число оказывается, мы можем увеличить напряженность магнитного поля H.
Ранее относительная проницаемость, символ µ r, определялась как отношение абсолютной проницаемости µ и проницаемости свободного пространства µ o(вакуум), и это задавалось как постоянная величина.
Однако взаимосвязь между плотностью потока B и напряженностью магнитного поля H может быть определена тем фактом, что относительная проницаемость µ r не является постоянной величиной, а функцией интенсивности магнитного поля, что дает плотность магнитного потока как: B = M H .
Тогда плотность магнитного потока в материале будет увеличена в большей степени в результате его относительной проницаемости для материала по сравнению с плотностью магнитного потока в вакууме, µ o H, а для катушки с воздушной сердцевиной это соотношение определяется как:
Таким образом, для ферромагнитных материалов отношение плотности потока к напряженности поля ( B / H ) не является постоянным, а изменяется в зависимости от плотности потока.
Тем не менее, для катушек с воздушной сердцевиной или любой сердцевины с немагнитной средой, такой как дерево или пластмасса, это отношение можно считать постоянной величиной, и эта постоянная известна как μ o , проницаемость свободного пространства ( μ o = 4.π.10 -7 ч / м ).

Построив значения плотности потока ( B ) против напряженности поля, ( Н ) мы можем произвести набор кривых , называемых Кривые намагничивания, кривые магнитного гистерезиса или более обычно BH кривые для каждого типа основного используемого материала.
Намагниченность или кривая B-H
Набор кривых намагничивания выше, представляет пример взаимосвязи между B и H для сердечников из мягкого железа и стали, но каждый тип материала сердечника будет иметь свой собственный набор кривых магнитного гистерезиса. Вы можете заметить, что плотность потока увеличивается пропорционально напряженности поля до тех пор, пока она не достигнет определенного значения, если оно больше не может становиться почти равным и постоянным, поскольку напряженность поля продолжает увеличиваться.
Это связано с тем, что существует ограничение на количество плотности потока, которое может генерироваться ядром, поскольку все домены в железе идеально выровнены.
Любое дальнейшее увеличение не будет влиять на значение M , и точка на графике, где плотность потока достигает своего предела, называется магнитным насыщением, также известным как насыщение сердечника, и в нашем простом примере выше точки насыщения стальной кривой начинается примерно с 3000 ампер-витков на метр.
Насыщение происходит потому, что, как мы помним из предыдущей статьи по магнетизму, который включал теорию Вебера, случайное расположение структуры молекулы в материале ядра изменяется, когда крошечные молекулярные магниты в материале становятся «выстроенными».
По мере увеличения напряженности магнитного поля ( H ) эти молекулярные магниты становятся все более и более выровненными, пока они не достигнут идеального выравнивания, создавая максимальную плотность потока, и любое увеличение напряженности магнитного поля из-за увеличения электрического тока, протекающего через катушку, будет иметь мало или вообще не будет иметь эффекта.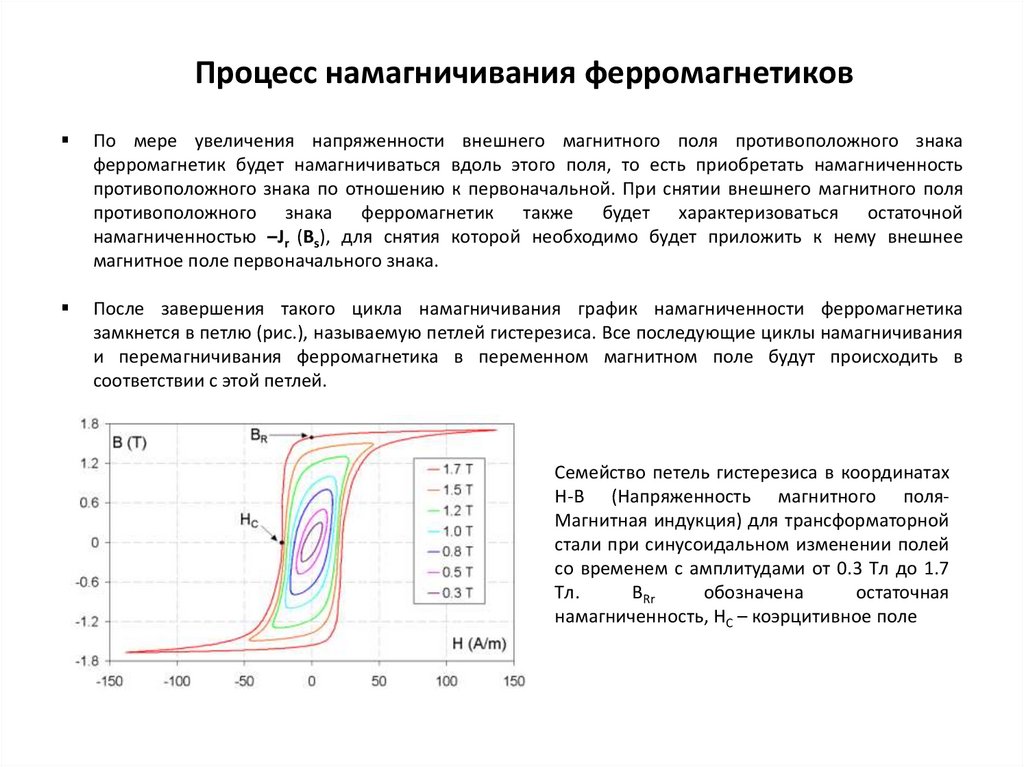
Сохраняемость (способность сохранять остаточный магнетизм)
Предположим, что у нас есть электромагнитная катушка с высокой напряженностью поля из-за тока, протекающего через нее, и что материал ферромагнитного сердечника достиг своей точки насыщения, максимальной плотности потока. Если мы теперь откроем переключатель и удалим ток намагничивания, протекающий через катушку, мы ожидаем, что магнитное поле вокруг катушки исчезнет, когда магнитный поток уменьшится до нуля.
Однако магнитный поток не исчезает полностью, поскольку материал электромагнитного сердечника все еще сохраняет часть своего магнетизма, даже когда ток прекращает течь в катушке.
Эта способность к катушке, чтобы сохранить часть своего магнетизма внутри сердечника после процесса намагничивания остановилось называются сохраняемость или остаточной намагниченности, в то время как величина плотности потока все еще остается в ядре, называется остаточным магнетизмом B R .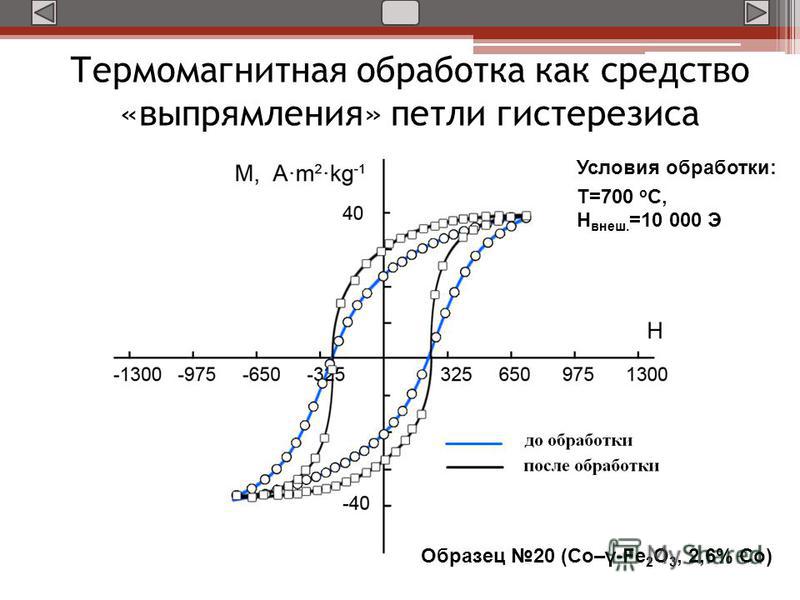
Причиной этого является то, что некоторые из крошечных молекулярных магнитов не возвращаются к совершенно случайному образцу и все же указывают в направлении исходного поля намагничивания, давая им своего рода «память». Некоторые ферромагнитные материалы обладают высокой удельной удерживаемостью (магнитной твердостью), что делает их превосходными для изготовления постоянных магнитов.
В то время как другие ферромагнитные материалы имеют низкую способность удерживать (магнитно-мягкие), что делает их идеальными для использования в электромагнитах, соленоидах или реле.
Один из способов уменьшить эту остаточную плотность потока до нуля — изменить направление тока, протекающего через катушку, путем изменения значения H, напряженности магнитного поля, отрицательной.
Этот эффект называется коэрцитивной силой H C .
Если этот обратный ток увеличивается еще больше, то плотность потока будет также увеличиваться в обратном направлении, пока ферромагнитный сердечник не достигнет насыщения снова, но в обратном направлении от предыдущего. Снижая ток намагничивания I снова до нуля создаст аналогичную величину остаточного магнетизма, но в обратном направлении.
Снижая ток намагничивания I снова до нуля создаст аналогичную величину остаточного магнетизма, но в обратном направлении.
Затем путем постоянного изменения направления тока намагничивания через катушку с положительного направления на отрицательное направление, как в случае с источником переменного тока, можно создать петлю магнитного гистерезиса ферромагнитного сердечника.
Магнитная петля гистерезиса
Магнитная петля гистерезиса выше, показывает поведение ферромагнитного сердечника графически в виде соотношения между B и H является нелинейным. Начиная с немагнитного сердечника, и B, и H будут в нуле, точка 0 на кривой намагничивания.
Если ток намагничивания I увеличивается в положительном направлении до некоторого значения, напряженность магнитного поля H линейно увеличивается с I,и плотность потока B также будет увеличиваться, как показано кривой из точки 0 в точку a, когда она движется к насыщению.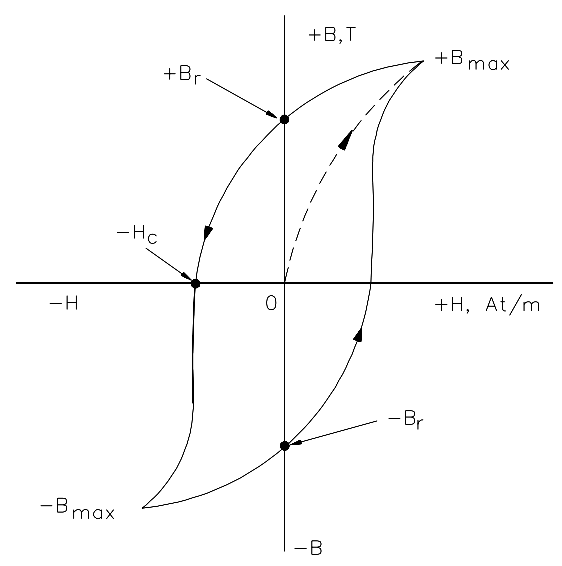
Теперь, если ток намагничивания в катушке уменьшается до нуля, магнитное поле, циркулирующее вокруг сердечника, также уменьшается до нуля. Однако магнитный поток катушек не достигнет нуля из-за остаточного магнетизма, присутствующего в сердечнике, и это показано на кривой от точки а к точке b .
Чтобы уменьшить плотность потока в точке b до нуля, необходимо обратить ток, протекающий через катушку. Сила намагничивания, которая должна применяться для обнуления остаточной плотности потока, называется «Коэрцитивной силой». Эта коэрцитивная сила меняет магнитное поле, перестраивая молекулярные магниты, пока ядро не станет немагнитным в точке с .
Увеличение этого обратного тока вызывает намагничивание сердечника в противоположном направлении, и дальнейшее увеличение этого тока намагничивания приведет к тому, что сердечник достигнет своей точки насыщения, но в противоположном направлении, точки d на кривой.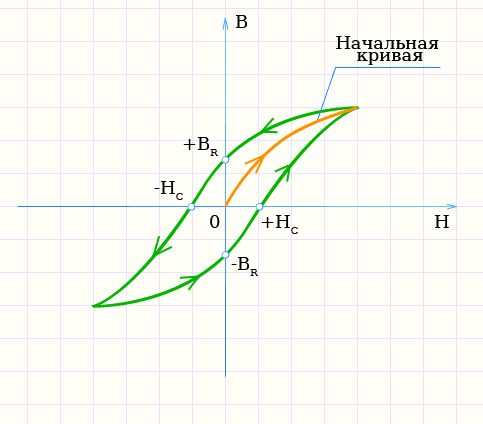
Эта точка симметрична точке b . Если ток намагничивания снова уменьшится до нуля, остаточный намагниченность, присутствующая в сердечнике, будет равна предыдущему значению, но в точке е будет обратной .
Снова изменение направления тока намагничивания, протекающего через катушку на этот раз в положительном направлении, приведет к тому, что магнитный поток достигнет нуля, точка f на кривой, и, как и прежде, дальнейшее увеличение тока намагничивания в положительном направлении приведет к насыщению сердечника в точке а .
Затем кривая B-H следует по пути a-b-c-d-e-f-a, когда ток намагничивания, протекающий через катушку, чередуется между положительным и отрицательным значением, таким как цикл переменного напряжения. Этот путь называется магнитной петлей гистерезиса.
Эффект магнитного гистерезиса показывает, что процесс намагничивания ферромагнитного сердечника и, следовательно, плотность потока зависят от того, на какую часть кривой намагничивается ферромагнитный сердечник, поскольку это зависит от прошлых цепей, придающих сердечнику форму «памяти».
Тогда ферромагнитные материалы имеют память, потому что они остаются намагниченными после того, как внешнее магнитное поле было удалено.
Однако мягкие ферромагнитные материалы, такие как железная или кремниевая сталь, имеют очень узкие петли магнитного гистерезиса, что приводит к очень небольшим количествам остаточного магнетизма, что делает их идеальными для использования в реле, соленоидах и трансформаторах, поскольку они могут легко намагничиваться и размагничиваться.
Поскольку для преодоления этого остаточного магнетизма необходимо применять коэрцитивную силу, необходимо выполнить работу по замыканию петли гистерезиса, чтобы используемая энергия рассеивалась в виде тепла в магнитном материале. Это тепло известно как потеря гистерезиса, величина потери зависит от значения материала коэрцитивной силы.
Добавляя добавки к металлическому железу, такие как кремний, можно получить материалы с очень малой коэрцитивной силой, которые имеют очень узкую петлю гистерезиса. Материалы с узкими петлями гистерезиса легко намагничиваются и размагничиваются и известны как магнитомягкие материалы.
Материалы с узкими петлями гистерезиса легко намагничиваются и размагничиваются и известны как магнитомягкие материалы.
Магнитные петли гистерезиса для мягких и твердых материалов
Магнитный гистерезис приводит к рассеиванию потраченной энергии в виде тепла, причем энергия теряется пропорционально площади петли магнитного гистерезиса. Потери гистерезиса всегда будут проблемой в трансформаторах переменного тока, где ток постоянно меняет направление, и, таким образом, магнитные полюсы в сердечнике будут вызывать потери, потому что они постоянно меняют направление.
Вращающиеся катушки в машинах постоянного тока также будут нести гистерезисные потери, поскольку они попеременно проходят севернее южных магнитных полюсов.
Как указывалось ранее, форма петли гистерезиса зависит от природы используемого железа или стали, и в случае железа, которое подвергается массивным изменениям магнетизма, например, сердечники трансформатора, важно, чтобы петля гистерезиса B-H была как можно меньше.
В следующей статье об электромагнетизме мы рассмотрим закон электромагнитной индукции Фарадея и увидим, что, перемещая проводной проводник в стационарном магнитном поле, можно вызвать электрический ток в проводнике, образующий простой генератор.
Источник: https://meanders.ru/chto-takoe-magnitnyj-gisterezis-krivye-magnitnogo-namagnichivanija.shtml
В каких координатных осях строится петля гистерезиса. Что такое петля гистерезиса
Петля
гистерезиса. При циклическом изменении
напряженности постоянного магнитного
поля от 0 до +Н, от +Н до –Н и снова от –Н
до +Н кривая изменения индукции (кривая
перемагничивания) имеет форму замкнутой
кривой – петли гистерезиса. Для слабых
полей петля имеет вид эллипса. При
увеличении значения напряженности
магнитного поля Н получают серию
заключенных одна в другую петель
гистерезиса. Когда все векторы
намагниченности доменов сориентируются
вдоль направления поля, процесс
намагничивания закончится состоянием
технического насыщения намагниченности
материала.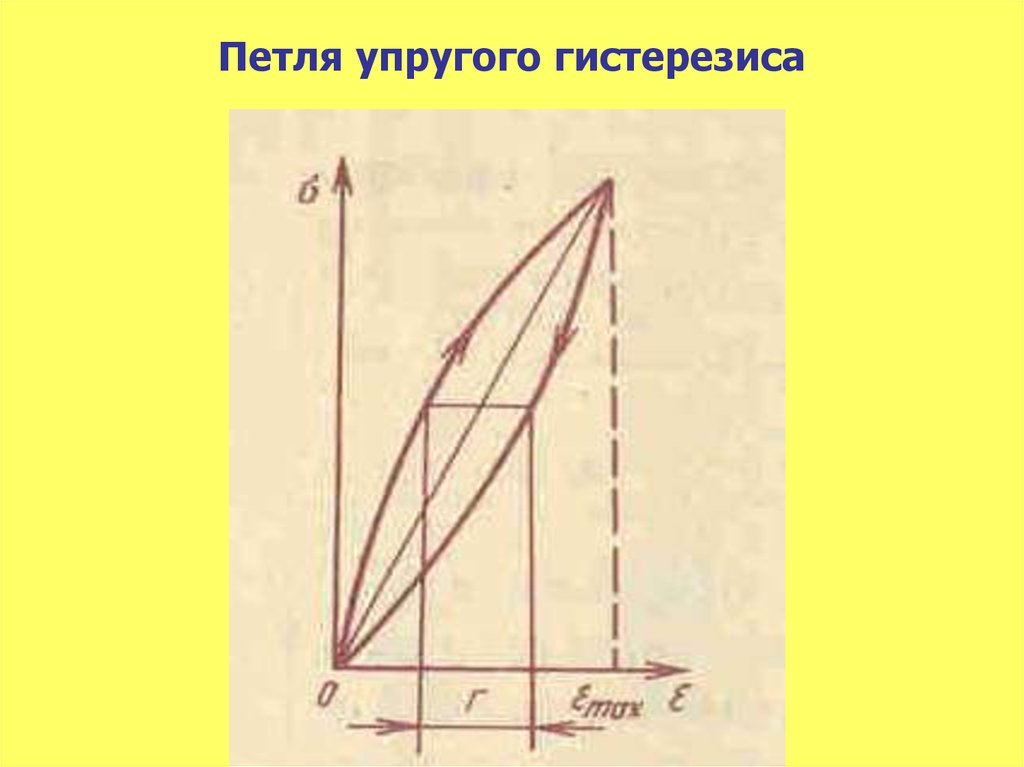 Петлю гистерезиса, полученную
при условии насыщения намагничивания,
называют предельной петлей гистерезиса.
Она характеризуется максимально
достигнутым значением индукции Bs,
называется индукцией насыщения. При
уменьшении напряженности магнитного
поля от +Н до 0 магнитная индукция
сохраняет остаточную индукцию Вс. Чтобы
получить остаточную магнитную индукцию,
равную 0, необходимо приложить
противоположно направленное
размагничивающее поле определенной
напряженности -Нс. Отрицательная
напряженность магнитного поля -Нс
называется коэрцитивной силой материала.
При достижении напряженности магнитного
поля значения –Н, а затем 0 вновь возникает
остаточная индукция –Вс. Если повысить
напряженность магнитного поля до +Нс,
то остаточная магнитная индукция Вс
будет равна 0.
Площадь гистерезисных
петель в промежуточных и предельных
состояниях характеризует рассеивание
электрической энергии в процессе
перемагничивания материала, т.е. потери
на гистерезис. Площадь гистерезисной
петли зависит от свойств материала, его
геометрических размеров и частоты
перемагничивания.
Петлю гистерезиса, полученную
при условии насыщения намагничивания,
называют предельной петлей гистерезиса.
Она характеризуется максимально
достигнутым значением индукции Bs,
называется индукцией насыщения. При
уменьшении напряженности магнитного
поля от +Н до 0 магнитная индукция
сохраняет остаточную индукцию Вс. Чтобы
получить остаточную магнитную индукцию,
равную 0, необходимо приложить
противоположно направленное
размагничивающее поле определенной
напряженности -Нс. Отрицательная
напряженность магнитного поля -Нс
называется коэрцитивной силой материала.
При достижении напряженности магнитного
поля значения –Н, а затем 0 вновь возникает
остаточная индукция –Вс. Если повысить
напряженность магнитного поля до +Нс,
то остаточная магнитная индукция Вс
будет равна 0.
Площадь гистерезисных
петель в промежуточных и предельных
состояниях характеризует рассеивание
электрической энергии в процессе
перемагничивания материала, т.е. потери
на гистерезис. Площадь гистерезисной
петли зависит от свойств материала, его
геометрических размеров и частоты
перемагничивания.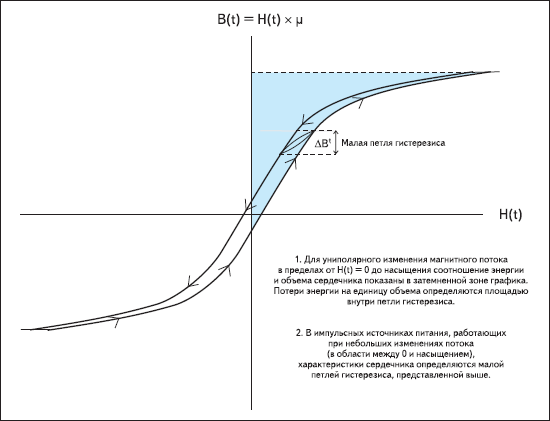 По предельной петле
гистерезиса определяют такие характеристики
магнитных материалов, как индукцию
насыщения Bs, остаточную индукцию Вс,
коэрцитивную силу Нс.
По предельной петле
гистерезиса определяют такие характеристики
магнитных материалов, как индукцию
насыщения Bs, остаточную индукцию Вс,
коэрцитивную силу Нс.
Кривая намагничивания
Кривая
намагничивания. Это важнейшая
характеристика магнитных материалов,
она показывает зависимость намагниченности
или магнитной индукции материала от
напряженности внешнего поля Н. Магнитная
индукция материала Bi измеряется в теслах
(Тл) и связана с намагниченностью.
Основная (коммутационная) кривая
намагничивания представляет собой
геометрическое место вершин петель
гистерезиса, полученных при циклическом
перемагничивании и отражает изменение
магнитной индукции В в зависимости от
напряженности магнитного поля Н, которое
создается в материале при намагничивании.
Напряженность магнитного поля в образце
в виде тороида, когда магнитная цепь
замкнута, равна напряженности внешнего
поля Нв. В разомкнутой магнитной цепи
на концах образца появляются магнитные
полюса, создающие размагничивающее
поле Нр.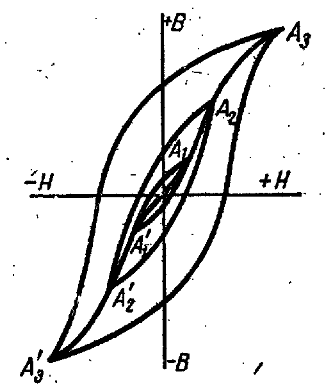 Разница между магнитными
напряженностями внешнего и размагничивающего
полей определяют внутреннюю магнитную
напряженность Hi материала.
Основная
кривая намагничивания имеет ряд
характерных участков, которые можно
условно выделить при намагничивании
монокристалла ферромагнетика. Первый
участок кривой намагничивания
соответствует процессу смещения границ
менее благоприятно ориентированных
доменов. На втором участке происходит
поворот векторов намагниченности
доменов в направлении внешнего магнитного
поля. Третий участок соответствует
парапроцессу, т.е. завершающему этапу
процесса намагничивания, когда сильное
магнитное поле поворачивает в направлении
своего действия не сориентированные
магнитные моменты доменов ферромагнетика.
Разница между магнитными
напряженностями внешнего и размагничивающего
полей определяют внутреннюю магнитную
напряженность Hi материала.
Основная
кривая намагничивания имеет ряд
характерных участков, которые можно
условно выделить при намагничивании
монокристалла ферромагнетика. Первый
участок кривой намагничивания
соответствует процессу смещения границ
менее благоприятно ориентированных
доменов. На втором участке происходит
поворот векторов намагниченности
доменов в направлении внешнего магнитного
поля. Третий участок соответствует
парапроцессу, т.е. завершающему этапу
процесса намагничивания, когда сильное
магнитное поле поворачивает в направлении
своего действия не сориентированные
магнитные моменты доменов ферромагнетика.
Биологические и физические системы способны мгновенно откликаться на приложенное к ним воздействие. Если рассмотреть это явление на временной оси координат, то становится заметно, что отклик зависит от предыстории системы и ее текущего состояния. График, который наглядно демонстрирует это свойство систем, получил название петли гистерезиса, которая отличается остроугольной формой.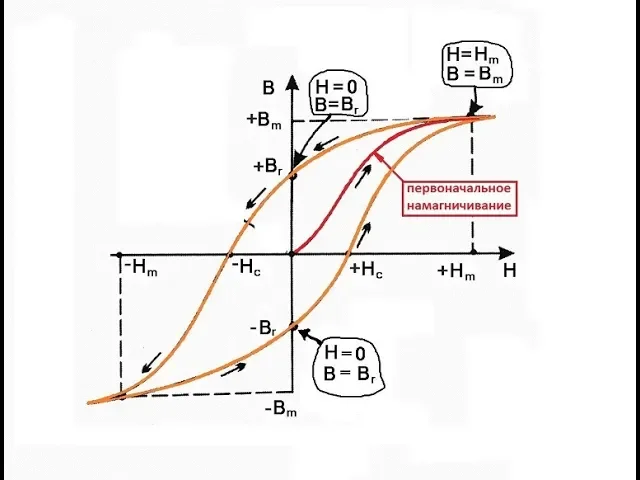
Оригинальная форма петли обусловлена эффектом насыщения и неравномерностью траектории между соседними расстояниями. Эффект гистерезиса имеет кардинальные отличия от инерционности, с которой его часто путают, забывая о том, что монотонное сопротивление существенно отличается от мгновенного сопротивления на воздействие.
Петля гистерезиса является циклом, в ходе которого часть свойств системы используются независимо от воздействий, а часть – отправляется на повторную проверку.
Явление гистерезиса в физике
В физике наиболее часто системы сталкиваются со следующими видами гистерезиса:
- Магнитный – отражает зависимость между векторами напряжения магнитного поля и намагничивания в веществе. Это явление объясняет существование постоянных магнитов.
- Сепнгетоэлектрический – зависимость между поляризацией сегнетоэлектриков и изменения внешнего электрического поля.
- Упругий – зависимость деформации упругих материалов от воздействия высоких давлений.
 Это явление лежит в основе великолепных механических характеристик изделий из кованого метала.
Это явление лежит в основе великолепных механических характеристик изделий из кованого метала.
Упругий гистерезис встречается двух основных видов – статический и динамический. В первом случае петля будет равномерной, во втором – постоянно меняющейся.
Применение гистерезиса в электронике
В электротехнике широко применяются устройства, в основе которых лежат магнитные взаимодействия. Наиболее распространение получили магнитные носители данных. Понимание гистерезиса необходимо для подавления в них шумов, таких как быстрые колебания или дребезжание контактов.
В большинстве электронных приборов наблюдается явление теплового гистерезиса. В процессе работы устройства нагреваются, а после охлаждения ряд характеристик уже не могут принять первоначальные явления.
Так, в процессе нагрева происходит расширение микросхем и печатных плат, полупроводниковых кристаллов. В результате развивается механическое напряжение, воздействие которого на элементы системы сохраняется после остывания. Особенно ярко тепловой гистерезис проявляется в высокоточных источниках опорного напряжения.
Особенно ярко тепловой гистерезис проявляется в высокоточных источниках опорного напряжения.
Гистерезис в общем понятии (от греческого – отстающий) — это свойство определенных физических, биологических и иных систем, которые реагируют на соответствующие воздействия с учетом текущего состояния, а также предыстории.
Гистерезис характерен т.н. «насыщением», и различными траекториями соответствующих графиков, отмечающих состояние системы в данный момент времени. Последние, в итоге, имеют форму остроугольной петли.
Если же рассматривать конкретно электротехнику, то каждый электромагнитный сердечник после окончания воздействия электрического тока в течение некоторого времени сохраняет собственное магнитное поле, называемое остаточным магнетизмом.
Его величина зависит, прежде всего, от свойств материала: у закаленной стали она существенно выше, чем у мягкого железа.
Но, в любом случае, явление остаточного магнетизма всегда присутствует при перемагничивании сердечника, когда необходимо размагнитить его до нуля, а затем изменить полюс на противоположный.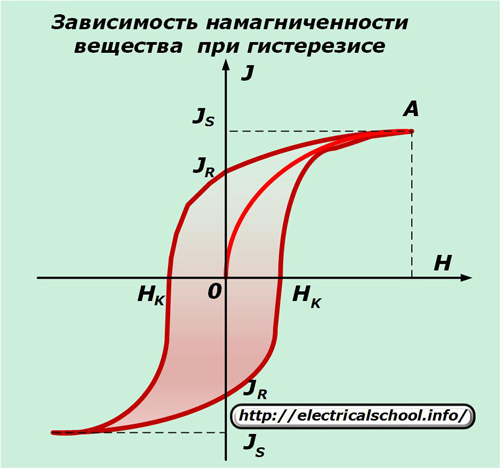
Любое изменение направления тока в обмотке электромагнита предусматривает (из-за наличия вышеуказанных свойств материала) предварительное размагничивание сердечника. Только после этого он может поменять свою полярность — это известный закон физики.
Для перемагничивания в обратном направлении необходим соответствующий магнитный поток.
Другими словами: изменение сердечника не «поспевает» за соответствующими изменениями магнитного потока, которое оперативно создает обмотка.
Вот эта временная задержка намагничивания сердечника от изменений магнитных потоков и получило название в электротехнике как гистерезис.
Каждое перемагничивание сердечника предусматривает избавление от остаточного магнетизма путем воздействия противонаправленным магнитным потоком. На практике это приводит к определенным потерям электроэнергии, которые тратятся на преодоление «неправильной» ориентации молекулярных магнитиков.
Последние проявляются в виде выделения тепла, и представляют так называемые затраты на гистерезис.
Таким образом, стальные сердечники, например, статоров или якорей электродвигателей или генераторов, а также , должны иметь по возможности наименьшую корреляционную силу
. Это позволит снизить гистерезисные потери, повысив в итоге КПД соответствующего электрического агрегата или прибора.
Сам процесс намагничивания определяется соответствующим графиком – так называемой петлей гистерезиса. Она представляет замкнутую кривую, отображающую зависимость скорости намагничивания от изменения динамики напряженности внешнего поля.
Большая площадь петли подразумевает, соответственно, и большие затраты на перемагничивание.
Также практически во всех электронных приборах наблюдается и такое явление, как тепловой гистерезис – невозвращение после прогрева аппаратуры к изначальному состоянию.
В и явление гистерезиса используется в различных магнитных носителях информации (например, триггерах Шмидта), или в специальных гистерезисных электродвигателях.
Широкое распространение этот физический эффект нашел также в различных устройствах, предназначенных для подавления различных шумов (дребезг контактов, быстрые колебания и т. п.) в процессе переключения логических схем.
п.) в процессе переключения логических схем.
В сердечнике любого электромагнита после выключения тока всегда сохраняется часть магнитных свойств, называемая остаточным магнетизмом. Величина остаточного магнетизма зависит от свойств материала сердечника и достигает большего значения у закаленной стали и меньшего у мягкого железа.
Однако, как бы ни было мягко железо, остаточный магнетизм все же будет оказывать известное влияние в том случае, если по условиям работы прибора необходимо перемагничивание его сердечника, т. е. размагничивание до нуля и намагничивание в противоположном направлении.
Действительно, при всяком изменении направления тока в обмотке электромагнита необходимо (благодаря наличию в сердечнике остаточного магнетизма) сначала размагнитить сердечник, и только после этого он может быть намагничен в новом направлении. Для этого потребуется какой-то магнитный поток противоположного направления.
Иначе говоря, изменение намагничивания сердечника (магнитной индукции) всегда отстает от соответствующих изменений магнитного потока (), создаваемого обмоткой.
Это отставание магнитной индукции от напряженности магнитного поля носит название гистерезиса . При каждом новом намагничивании сердечника для уничтожения его остаточного магнетизма приходится действовать на сердечник магнитным потоком противоположного направления.
Практически это будет означать затрату какой-то части электрической энергии на преодоление коэрцитивной силы, затрудняющей поворот молекулярных магнитиков в новое положение. Затраченная на это энергия выделяется в железе в виде тепла и представляет потери на перемагничивание, или, как говорят, потери на гистерезис
.
Исходя из сказанного, железо, подверженное в том или ином приборе непрерывному перемагничиванию (сердечники якорей генераторов и электродвигателей
, сердечники трансформаторов), должно выбираться всегда мягкое, с очень небольшой коэрцитивной силой. Это дает возможность уменьшить потери на гистерезис и тем самым повысить коэффициент полезного действия электрической
машины или прибора.
Петля гистерезиса
Петля гистерезиса
— кривая, изображающая ход зависимости намагничивания от напряженности внешнего поля.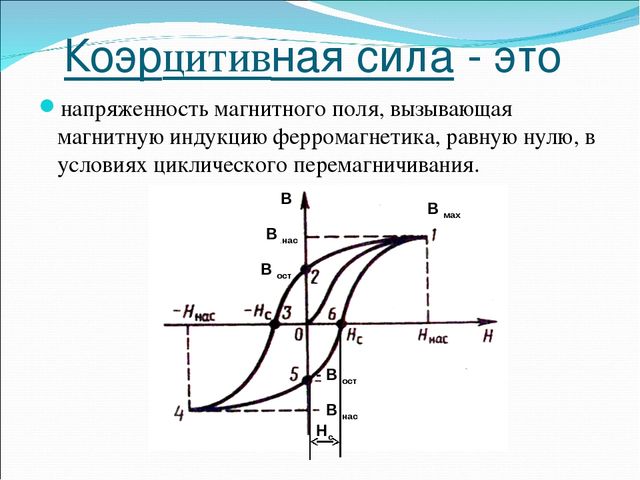 Чем больше площадь петли, тем большую работу на перемагничивание надо затратить.
Чем больше площадь петли, тем большую работу на перемагничивание надо затратить.
Представим себе простой электромагнит с железным сердечником. Проведем его через полный цикл намагничивания, для чего будем менять намагничивающий ток от нуля до величины ОМ в обоях направлениях.
Начальный момент: сила тока равна нулю, железо не намагничено, магнитная индукция В=0.
1-ая часть: намагничивание изменением тока от 0 до величины — + ОМ. Индукция в железе сердечника будет возрастать сначала быстро, затем медленнее. К концу операции, в точке А железо так насыщено магнитными силовыми линиями, что дальнейшее усиление тока (свыше + ОМ) может дать самые незначительные результаты, почему операцию намагничивания можно считать законченной.
Намагничивание до насыщения означает, что имеющиеся в сердечнике молекулярные магниты, находящиеся в начале процесса намагничивания в полном, а затем лишь в частичном беспорядке, почти все расположились теперь стройными рядами, северными полюсами в одну сторону, южными в другую, почему на одном конце сердечника мы имеем теперь северную полярность, на другом — южную.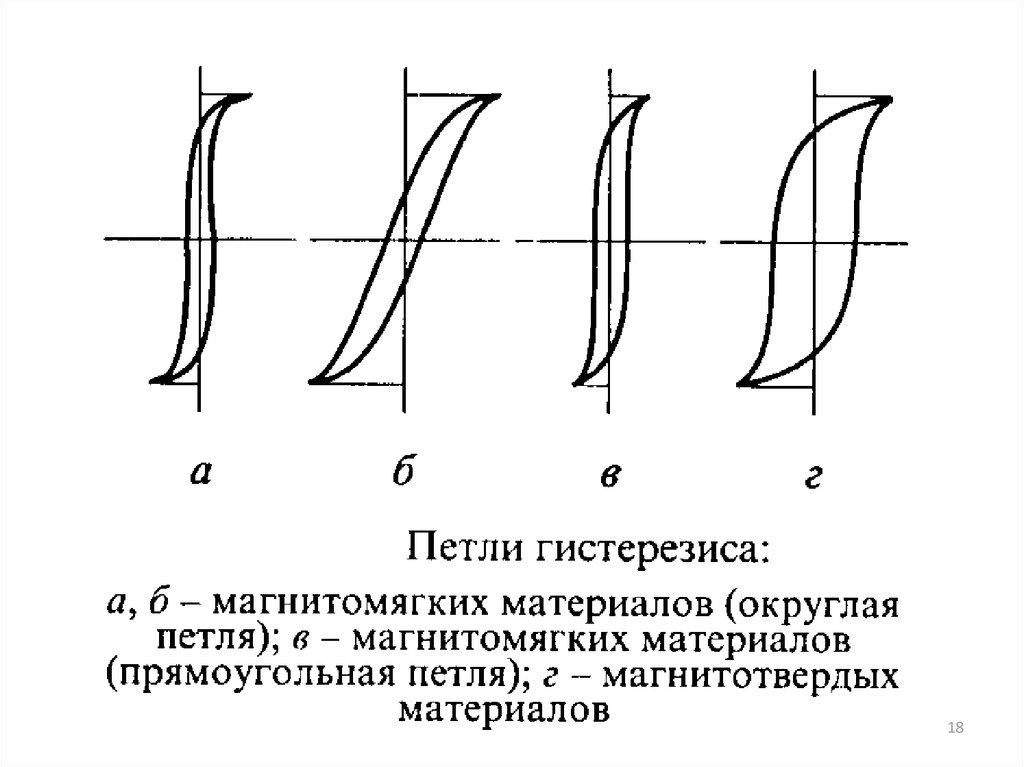
2-я часть: ослабление магнетизма вследствие уменьшения тока от + ОМ до 0 и полное размагничивание при токе — OD. Магнитная индукция, изменяясь по кривой АС, дойдет до значения ОС, в то время как ток уже будет равен нулю. Эту магнитную индукцию называют остаточным магнетизмом, или остаточной магнитной индукцией. Для уничтожения ее, для полного, следовательно, размагничивания, необходимо дать в электромагнит ток обратного направления и довести его до значения, соответствующего на чертеже ординате OD.
3-я часть: намагничивание в обратную сторону путем изменения тока от — OD до — ОМ1. Магнитная индукция, возрастая по кривой DE, дойдет до точки Е, соответствующей моменту насыщении.
4-я часть: ослабление магнетизма постепенным уменьшением тока от — ОМ1, до нуля (остаточный магнетизм OF) и последующее размагничивание путем перемены направления тока и доведения его до величины + ОН.
5-я часть: намагничивание, соответствующее процессу 1-й части, доведение магнитной индукции от нуля до + МА путем изменении тока от + ОН до + ОМ.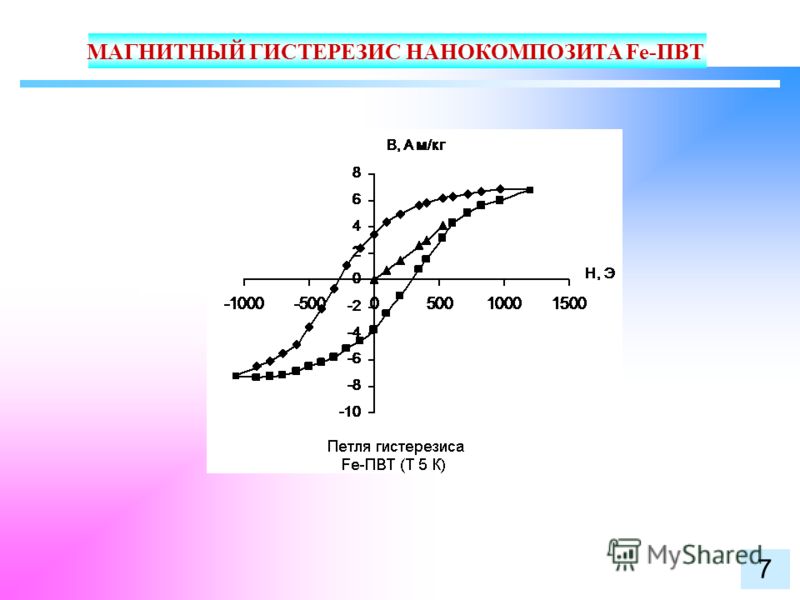
При уменьшении размагничивающего тока до нуля не все элементарные или молекулярные магниты приходят в прежнее беспорядочное состояние, но часть их сохраняет свое положение, соответствующее последнему направлению намагничивания. Это явление запаздывания или задерживания магнетизма и носит название гистерезиса.
Гистерезис
Явление магнитного гистерезиса наблюдается не только при изменении поля H по величине и знаку, но также и при его вращении (гистерезис магнитного вращения), что соответствует отставанию (задержке) в изменении направления M с изменением направления H . Гистерезис магнитного вращения возникает также при вращении образца относительно фиксированного направления H .
Теория явления гистерезиса учитывает конкретную магнитную доменную структуру образца и её изменения в ходе намагничивания и перемагничивания. Эти изменения обусловлены смещением доменных границ и ростом одних доменов за счёт других, а также вращением вектора намагниченности в доменах под действием внешнего магнитного поля.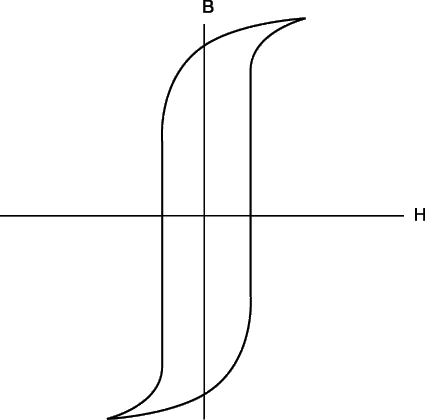 Всё, что задерживает эти процессы и способствует попаданию магнетиков в метастабильные состояния, может служить причиной магнитного гистерезиса.
Всё, что задерживает эти процессы и способствует попаданию магнетиков в метастабильные состояния, может служить причиной магнитного гистерезиса.
В однодоменных ферромагнитных частицах (в частицах малых размеров, в которых образование доменов энергетически невыгодно) могут идти только процессы вращения M
. Этим процессам препятствует магнитная анизотропия различного происхождения (анизотропия самого кристалла, анизотропия формы частиц и анизотропия упругих напряжений). Благодаря анизотропии, M
как-будто удерживается некоторым внутренним полем (эффективным полем магнитной анизотропии) вдоль одной из осей лёгкого намагничивания, соответствующей минимуму энергии. Магнитный гистерезис возникает из-за того, что два направления M
(по и против) этой оси в магнитоодноосном образце или несколько эквивалентных (по энергии) направлений М
в магнитомногоосном образце соответствуют состояниям, отделённым друг от друга потенциальным барьером (пропорциональным ). При перемагничивании однодоменных частиц вектор M
рядом последовательных необратимых скачков поворачивается в направлении H
. Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M
коэрцитивная сила . Более универсальным является механизм неоднородного вращения M
. Однако наибольшее влияние на он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом может быть существенно меньше эффективного поля анизотропии формы.
Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M
коэрцитивная сила . Более универсальным является механизм неоднородного вращения M
. Однако наибольшее влияние на он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом может быть существенно меньше эффективного поля анизотропии формы.
Сегнетоэлектрический гистерезис
— неоднозначная петлеобразная зависимость поляризации P
сегнетоэлектриков от внешнего электрического поля E
при его циклическом изменении. Сегнетоэлектрические кристаллы обладают в определенном температурном интервале спонтанной (самопроизвольной, то есть возникающей в отсутствие внешнего электрического поля) электрической поляризацией P
c . Направление поляризации может быть изменено электрическим полем. При этом зависимость P
(E
) в полярной фазе неоднозначна, значение P
при данном E
зависит от предыстории, то есть от того, каким было электрическое поле в предшествующие моменты времени. Основные параметры сегнетоэлектрического гистерезиса:
Основные параметры сегнетоэлектрического гистерезиса:
- остаточная поляризация кристалла P ост, при E = 0
- значение поля E Kt (коэрцитивное поле) при котором происходит переполяризация
Упругий гистерезис
Гистерезис используется для подавления шумов (быстрых колебаний, дребезга контактов) в момент переключения логических сигналов.
В электронных приборах всех видов наблюдается явление теплового гистерезиса : после нагрева прибора и его последующего охлаждения до начальной температуры его параметры не возвращаются к начальным значениям. Из-за неодинакового теплового расширения кристаллов полупроводников, кристаллодержателей, корпусов микросхем и печатных плат в кристаллах возникают механические напряжения , которые сохраняются и после охлаждения. Явление теплового гистерезиса наиболее заметно в прецизионных , используемых в измерительных аналого-цифровых преобразователях . В современных микросхемах относительный сдвиг опорного напряжения вследствие теплового гистерезиса составляют порядка 10-100 ppm .
В биологии
Гистерезисные свойства характерны для скелетных мышц млекопитающих.
В почвоведении
Одно из них указывает на взаимосвязь приложенных усилий субъектом влияния и достигнутым результатом. Уровень затраченной субъектом просветительской и пропагандистской работы можно соотносить с уровнем «намагниченности» (степенью вовлеченности в новую идею) объекта-носителя общественного мнения, социальную группу, коллектив, социальную общность или общество в целом; при этом может обнаружиться некоторое отставание объекта от субъекта. Переубеждение, в том числе с предполагаемыми деструктивными последствиями, далеко не всегда проходит успешно. Оно зависит от собственных моральных ценностей, обычаев, традиций, характера предыдущего воспитания, от этических норм, доминирующих в обществе и т. д.
Второе обстоятельство связано с тем, что новый этап формирования общественного мнения можно соотносить с историей объекта, его опытом, его оценкой теми, кто ранее выступал объектом формирования общественного мнения.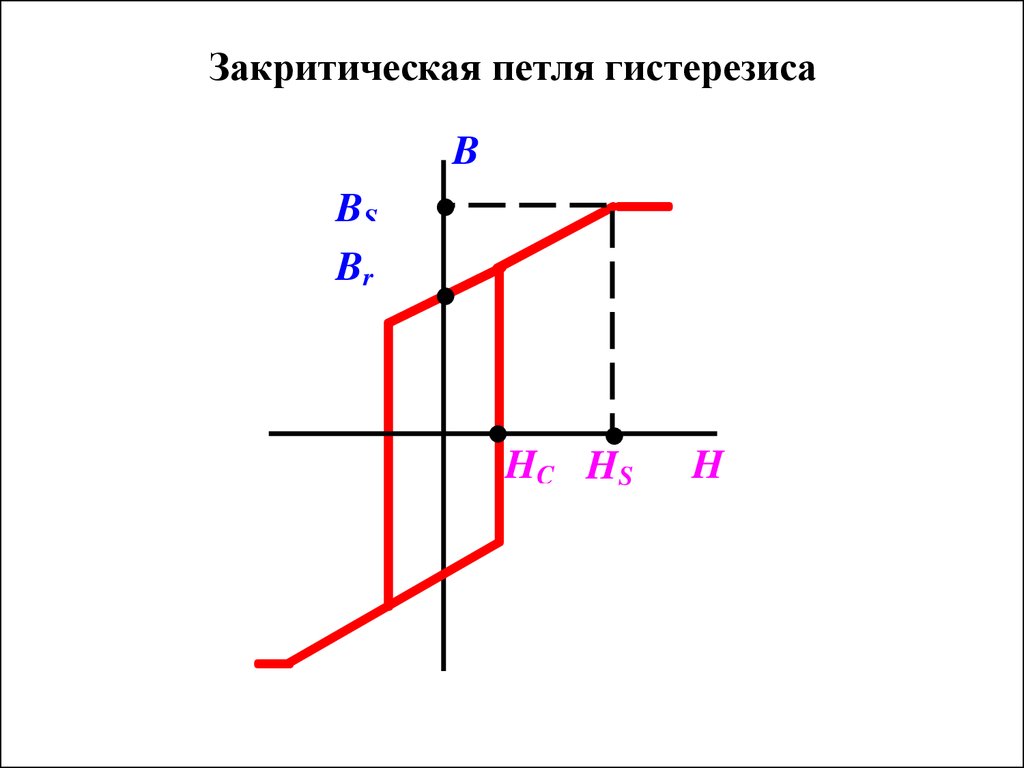 При этом можно обнаружить, что «точка отсчета» времени формирования общественного мнения смещается относительно прежней, что является характеристикой самой системы и ее текущего состояния.
При этом можно обнаружить, что «точка отсчета» времени формирования общественного мнения смещается относительно прежней, что является характеристикой самой системы и ее текущего состояния.
Литература по теме
- Раддай Райхлин Гражданская война, террор и бандитизм. Систематизация социологии и социальная динамика . Раздел «Борьба с толпой»
- Капустин Валерий Сергеевич Введение в теорию социальной самоорганизации . Тема 11. Явление гистерезиса в формировании национальных форм и способов самоорганизации. Современные парадоксы и загадки «начала»
В философии
Математические модели гистерезиса
Появление математических моделей гистерезисных явлений обуславливалось достаточно богатым набором прикладных задач (прежде всего в теории автоматического регулирования), в которых носители гистерезиса нельзя рассматривать изолированно, поскольку они являлись частью некоторой системы. Создание математической теории гистерезиса относится к 60-м годам XX-го века, когда в Воронежском университете начал работать семинар под руководством М. А. Красносельского , «гистерезисной» тематики. Позднее, в 1983 году появилась монография , в которой различные гистерезисные явления получили формальное описание в рамках теории систем: гистерезисные преобразователи трактовались как операторы, зависящие от своего начального состояния как от параметра, определённые на достаточно богатом функциональном пространстве (например, в пространстве непрерывных функций), действующие в некотором функциональном пространстве. Простое параметрическое описание различных петель гистерезиса можно найти в работе (замена в данной модели гармонических функций на прямоугольные, треугольные или трапецеидальные импульсы позволяет также получить кусочно-линейные петли гистерезисы, которые часто встречаются в дискретной автоматике, см. пример на Рис. 2).
А. Красносельского , «гистерезисной» тематики. Позднее, в 1983 году появилась монография , в которой различные гистерезисные явления получили формальное описание в рамках теории систем: гистерезисные преобразователи трактовались как операторы, зависящие от своего начального состояния как от параметра, определённые на достаточно богатом функциональном пространстве (например, в пространстве непрерывных функций), действующие в некотором функциональном пространстве. Простое параметрическое описание различных петель гистерезиса можно найти в работе (замена в данной модели гармонических функций на прямоугольные, треугольные или трапецеидальные импульсы позволяет также получить кусочно-линейные петли гистерезисы, которые часто встречаются в дискретной автоматике, см. пример на Рис. 2).
Литература
Примечания
Wikimedia Foundation . 2010 .
Синонимы :
Смотреть что такое «Гистерезис» в других словарях:
— (от греч.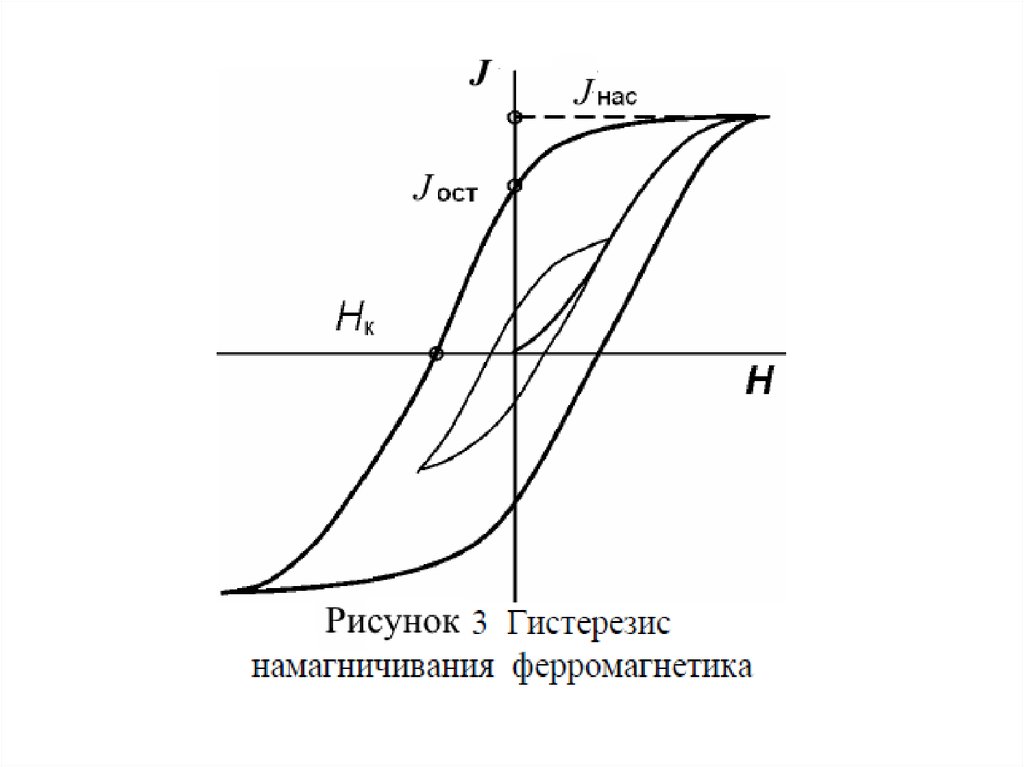 hysteresis отставание) запаздывание изменения физической величины, характеризующей состояние вещества (намагниченности М ферромагнетика, поляризации P сегнетоэлектрика и т. п.), от изменения другой физической величины, определяющей… … Большой Энциклопедический словарь
hysteresis отставание) запаздывание изменения физической величины, характеризующей состояние вещества (намагниченности М ферромагнетика, поляризации P сегнетоэлектрика и т. п.), от изменения другой физической величины, определяющей… … Большой Энциклопедический словарь
Сдвиг, отставание Словарь русских синонимов. гистерезис сущ., кол во синонимов: 2 отставание (10) … Словарь синонимов
ГИСТЕРЕЗИС, явление, характерное для упругих тел; заключается в том, что ДЕФОРМАЦИЯ тела при увеличении НАПРЯЖЕНИЯ меньше, чем при его уменьшении из за задержки эффекта деформации. Когда механическое напряжение удалено полностью, остается… … Научно-технический энциклопедический словарь
— (от греческого hysteresis отставание, запаздывание) 1) Г. в аэродинамике неоднозначность структуры поля течения и, следовательно, аэродинамических характеристик обтекаемого тела при одних и тех же значениях кинематических параметров, но при… … Энциклопедия техники
описание, свойства,области применения.
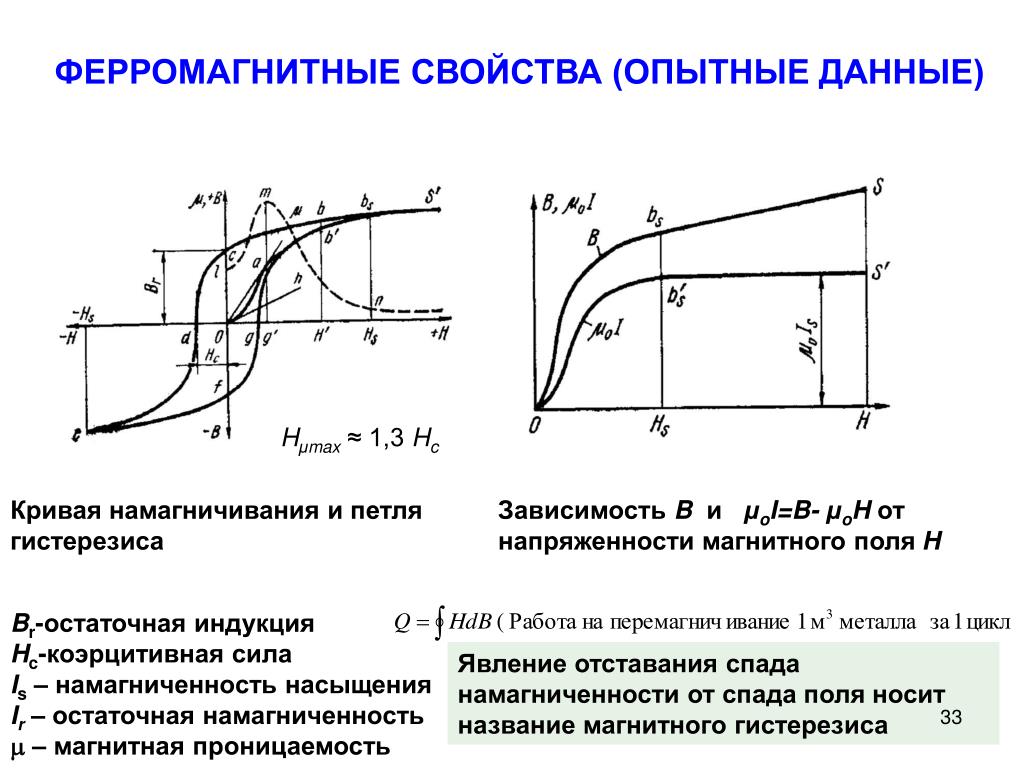 Явление гистерезиса, плюсы и минусы, Эффект гистерезиса.
Явление гистерезиса, плюсы и минусы, Эффект гистерезиса.Содержание:
Что такое гистерезис?
Говоря простым и понятным языком – гистерезис это ответная, запоздалая реакция некой системы на определённый раздражитель (воздействие). При устранении причины, вызвавшей ответную реакцию системы, либо в результате противоположного действия, она полностью или частично возвращается к первоначальному состоянию. Причём для такого явления характерно то, что поведение системы между крайними состояниями не одинаково. То есть: характеристики перехода от первоначального состояния и обратно – сильно отличаются.
Явление гистерезиса наблюдается:
- в физике;
- электротехнике и радиоэлектронике;
- биологии;
- геологии;
- гидрологии;
- экономике;
- социологии.
Гистерезис может иметь как полезное, так и пагубное влияние на происходящие процессы. Это отчётливо просматривается в электротехнике и электронике
Определение понятия
У слова «Гистерезис» греческие корни, оно переводится как запаздывающий или отстающий. Этот термин используется в разных сферах науки и техники. В общем смысле понятие гистерезис отличает различное поведение системы при противоположных воздействиях.
Этот термин используется в разных сферах науки и техники. В общем смысле понятие гистерезис отличает различное поведение системы при противоположных воздействиях.
Это можно сказать и более простыми словами. Допустим есть какая-то система, на которую можно влиять в нескольких направлениях. Если при воздействии на неё в прямом направлении, после прекращения система не возвращается в исходное состояние, а устанавливается в промежуточном — тогда чтобы вернуть в исходное состояние нужно воздействовать уже в другом направлении с какой-то силой. В этом случае система обладает гистерезисом.
Иногда это явление используется в полезных целях, например, для создания элементов, которые срабатывают при определённых пороговых значениях воздействующих сил и для регуляторов. В других случаях гистерезис несёт пагубное влияние, рассмотрим это на практике.
Гистерезис в разных материалах
Гистерезис – это комплексное понятие, характеризующее способность вещества накапливать энергию магнитного поля или другой величины за счет имеющихся магнитных связей между молекулами вещества или особенностей работы системы. Но таким эффектом могут обладать не только сплавы железа, кобальта и никеля. Титанат бария даст несколько иной результат, если его поместить в поле с определенной напряженностью.
Но таким эффектом могут обладать не только сплавы железа, кобальта и никеля. Титанат бария даст несколько иной результат, если его поместить в поле с определенной напряженностью.
Так как он является сегнетоэлектриком, то в нем наблюдается диэлектрический гистерезис. Обратная петля гистерезиса образуется при противоположной полярности подводимого к среде напряжения, а величина противоположного поля, действующего на материал, получило название коэрцитивная сила.
При этом величина поля может предшествовать разным напряженностям, что связано с особенностями фактического состояния диполей – магнитных моментов после прошлого намагничивания. Также на процесс влияют различные примеси, содержащиеся в составе материала. Чем их больше, тем труднее сдвинуть стенки диполей, поэтому остается так называемая остаточная намагниченность.
Виды гистерезистеров в физике
В физике это свойство систем представлено тремя основными разновидностями: магнитным, сегнетоэлектрическим и упругим гистерезисом.
Магнитный гистерезис – явление, которое отражает зависимость вектора напряженности магнитного поля и вектора намагничивания в веществе. Причем как от приложенного внешнего поля, так и от предыстории конкретного образца. Существование постоянных магнитов обуславливается именно этим явлением.
Модель петли представляет собой определенный цикл, который некоторые свойства отправляет на повторную проверку и согласование, а некоторые использует дальше. Избирательный характер зависит от свойств конкретной системы.
Сегнетоэлектрический гистерезис – изменяющаяся зависимость поляризации сегнетоэлектриков от циклического изменения внешнего электрического поля.
Упругий гистерезис – поведение упругих материалов, способных сохранять и утрачивать деформацию под воздействием больших давлений. Это явление обуславливает анизотропию механических характеристик и высокие механические качества кованных изделий.
Магнитный гистерезис
В соответствии с базовым определением, это явление обозначает отставание намагниченности (М) материала от изменяющегося воздействия внешнего поля. Для эксперимента можно собрать схему, в которой ток пропускают через соленоид. Регулируют уровень напряженности (Н) с помощью параллельного переменного резистора. Сердечник – из ферромагнетика.
Для эксперимента можно собрать схему, в которой ток пропускают через соленоид. Регулируют уровень напряженности (Н) с помощью параллельного переменного резистора. Сердечник – из ферромагнетика.
Важно! Представленные зависимости следует рассматривать в комплексе с графиком на первом рисунке.
До начала эксперимента образец обладает нейтральными характеристиками. Намагниченность и напряженность равны нулю, магнитные моменты доменов расположены хаотически. После замыкания цепи и увеличения силы тока увеличивается напряженность. На рисунке показано, как одновременно с этим изменяется направленность моментов. Индукция в образце (B) равна сумме напряженности и намагниченности с корректирующим множителем (μ0):
B = μ0*H + μ0*M.
На определенном уровне показатель μ0*M увеличивается до предельного значения. Последующее изменение напряженности внешнего поля не оказывает на него никакого влияния.
Материалы с магнитными свойствами разделяют на две группы по ширине петли гистерезиса.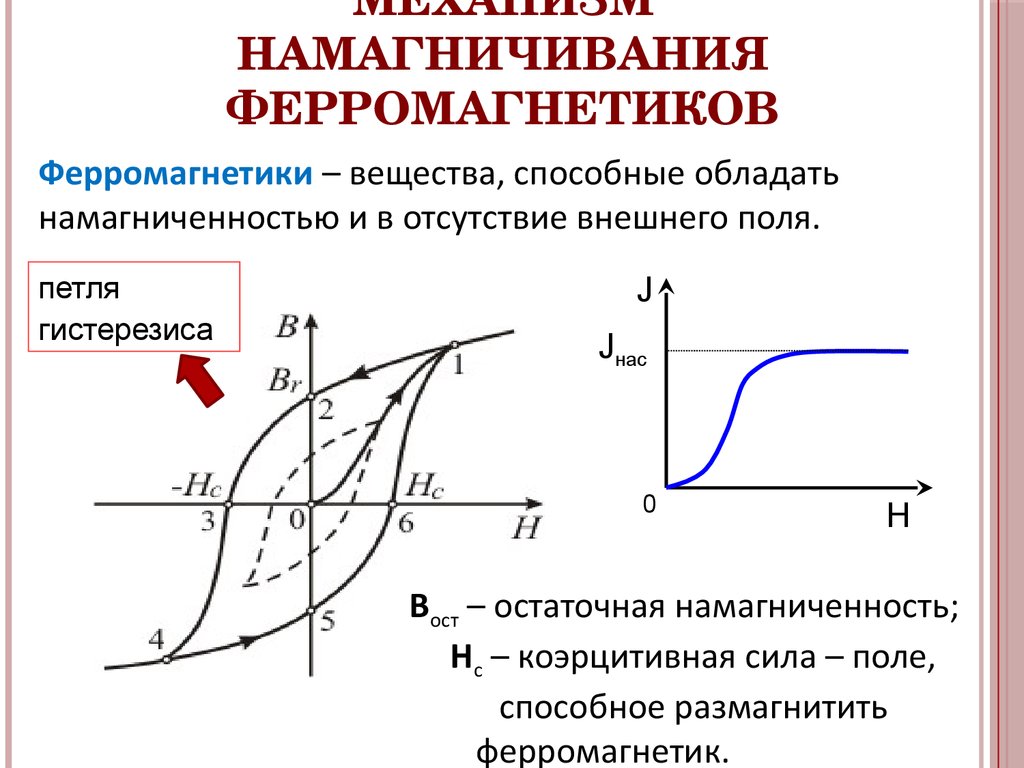 Магнитомягкие (узкий график) отличаются сравнительно небольшой коэрцитивной силой и соответствующими меньшими энергетическими затратами. Такие изделия применяют для изготовления электродвигателей, приводов, трансформаторов напряжения.
Магнитомягкие (узкий график) отличаются сравнительно небольшой коэрцитивной силой и соответствующими меньшими энергетическими затратами. Такие изделия применяют для изготовления электродвигателей, приводов, трансформаторов напряжения.
Магнитомягкие и магнитотвердые материалы
Магнитотвердые отличаются увеличенным временем реакции на воздействие внешним полем. Эти материалы используют для создания микросхем памяти, постоянных магнитов.
Сегнетоэлектрический гистерезис
Причина особой формы графика в этом примере – образование поляризации без приложения сил внешнего поля. Такой эффект наблюдается в определенном температурном диапазоне. Соответствующие материалы называют сегнетоэлектриками.
Сегнетоэлектрики
На первом рисунке показана петля гистерезиса, где отмечены места:
- точкой «а» – состояние насыщения;
- Pc – остаточная поляризованность;
- -Ec– коэрцитивная сила.
На второй части (2) изображено хаотичное (а) и направленное (б) расположение доменов. Ориентацию вдоль линий электростатического поля применяют для создания конденсаторов с изменяемой емкостью.
Ориентацию вдоль линий электростатического поля применяют для создания конденсаторов с изменяемой емкостью.
К сведению. Как и в других веществах, при повышении температуры до уровня точки Кюри намагниченность пропадает.
Упругий гистерезис
Это явление объясняется особыми механическими свойствами отдельных материалов. Они сохраняют созданную достаточно сильным ударным воздействием форму. Типичный пример – изготовление изделий из металла с применением ковки.
Описание явления магнитного гистерезиса
Мы знаем, что магнитный поток, создаваемый электромагнитной катушкой, представляет собой величину магнитного поля или силовых линий, создаваемых в данной области, и что его чаще называют «плотностью потока», обозначенным символ B с единицей измерения Тесла, Т.
Мы также знаем из предыдущих уроков, что магнитная сила электромагнита зависит от числа витков катушки, тока, протекающего через катушку, или от типа используемого материала сердечника, и если мы увеличим либо ток, либо число оказывается, мы можем увеличить напряженность магнитного поля H.
Ранее относительная проницаемость, символ µ r, определялась как отношение абсолютной проницаемости µ и проницаемости свободного пространства µ o(вакуум), и это задавалось как постоянная величина. Однако взаимосвязь между плотностью потока B и напряженностью магнитного поля H может быть определена тем фактом, что относительная проницаемость µ r не является постоянной величиной, а функцией интенсивности магнитного поля, что дает плотность магнитного потока как: B = M H .
Тогда плотность магнитного потока в материале будет увеличена в большей степени в результате его относительной проницаемости для материала по сравнению с плотностью магнитного потока в вакууме, µ o H, а для катушки с воздушной сердцевиной это соотношение определяется как:
Таким образом, для ферромагнитных материалов отношение плотности потока к напряженности поля ( B / H ) не является постоянным, а изменяется в зависимости от плотности потока. Тем не менее, для катушек с воздушной сердцевиной или любой сердцевины с немагнитной средой, такой как дерево или пластмасса, это отношение можно считать постоянной величиной, и эта постоянная известна как μ o , проницаемость свободного пространства ( μ o = 4. π.10 -7 ч / м ).
π.10 -7 ч / м ).
Построив значения плотности потока ( B ) против напряженности поля, ( Н ) мы можем произвести набор кривых , называемых Кривые намагничивания, кривые магнитного гистерезиса или более обычно BH кривые для каждого типа основного используемого материала.
Намагниченность или кривая B-H
Набор кривых намагничивания выше, представляет пример взаимосвязи между B и H для сердечников из мягкого железа и стали, но каждый тип материала сердечника будет иметь свой собственный набор кривых магнитного гистерезиса. Вы можете заметить, что плотность потока увеличивается пропорционально напряженности поля до тех пор, пока она не достигнет определенного значения, если оно больше не может становиться почти равным и постоянным, поскольку напряженность поля продолжает увеличиваться.
Это связано с тем, что существует ограничение на количество плотности потока, которое может генерироваться ядром, поскольку все домены в железе идеально выровнены. Любое дальнейшее увеличение не будет влиять на значение M , и точка на графике, где плотность потока достигает своего предела, называется магнитным насыщением, также известным как насыщение сердечника, и в нашем простом примере выше точки насыщения стальной кривой начинается примерно с 3000 ампер-витков на метр.
Любое дальнейшее увеличение не будет влиять на значение M , и точка на графике, где плотность потока достигает своего предела, называется магнитным насыщением, также известным как насыщение сердечника, и в нашем простом примере выше точки насыщения стальной кривой начинается примерно с 3000 ампер-витков на метр.
Насыщение происходит потому, что, как мы помним из предыдущей статьи по магнетизму, который включал теорию Вебера, случайное расположение структуры молекулы в материале ядра изменяется, когда крошечные молекулярные магниты в материале становятся «выстроенными».
По мере увеличения напряженности магнитного поля ( H ) эти молекулярные магниты становятся все более и более выровненными, пока они не достигнут идеального выравнивания, создавая максимальную плотность потока, и любое увеличение напряженности магнитного поля из-за увеличения электрического тока, протекающего через катушку, будет иметь мало или вообще не будет иметь эффекта.
Предположим, что у нас есть электромагнитная катушка с высокой напряженностью поля из-за тока, протекающего через нее, и что материал ферромагнитного сердечника достиг своей точки насыщения, максимальной плотности потока.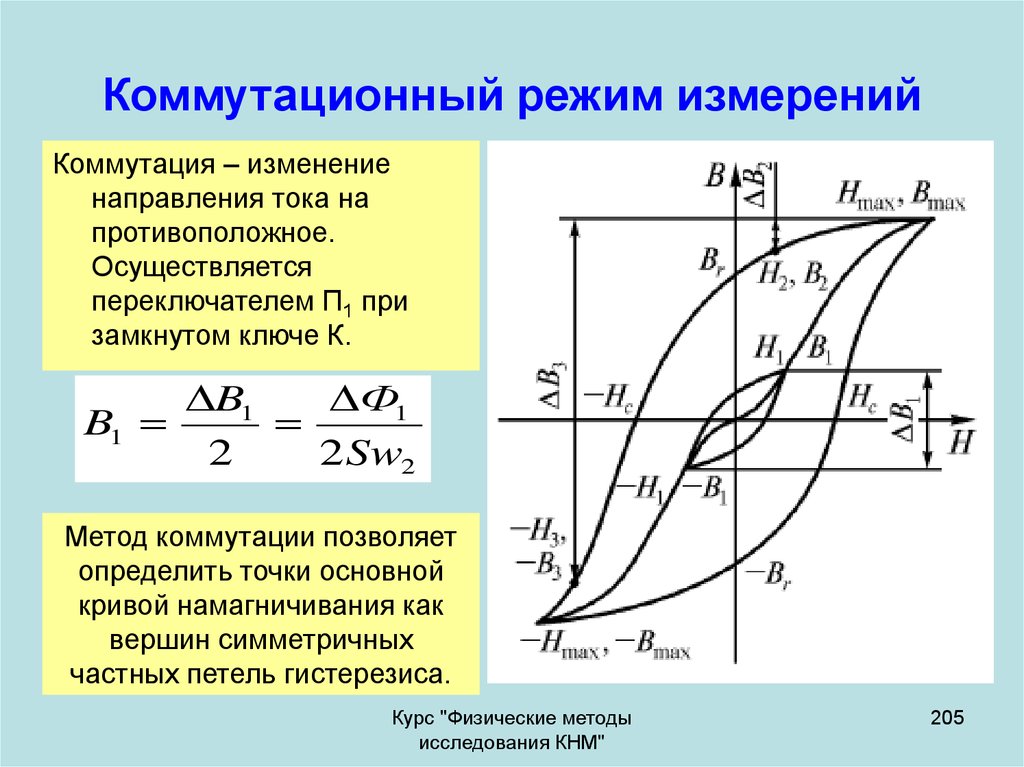 Если мы теперь откроем переключатель и удалим ток намагничивания, протекающий через катушку, мы ожидаем, что магнитное поле вокруг катушки исчезнет, когда магнитный поток уменьшится до нуля.
Если мы теперь откроем переключатель и удалим ток намагничивания, протекающий через катушку, мы ожидаем, что магнитное поле вокруг катушки исчезнет, когда магнитный поток уменьшится до нуля.
Однако магнитный поток не исчезает полностью, поскольку материал электромагнитного сердечника все еще сохраняет часть своего магнетизма, даже когда ток прекращает течь в катушке. Эта способность к катушке, чтобы сохранить часть своего магнетизма внутри сердечника после процесса намагничивания остановилось называются сохраняемость или остаточной намагниченности, в то время как величина плотности потока все еще остается в ядре, называется остаточным магнетизмом B R .
Причиной этого является то, что некоторые из крошечных молекулярных магнитов не возвращаются к совершенно случайному образцу и все же указывают в направлении исходного поля намагничивания, давая им своего рода «память». Некоторые ферромагнитные материалы обладают высокой удельной удерживаемостью (магнитной твердостью), что делает их превосходными для изготовления постоянных магнитов.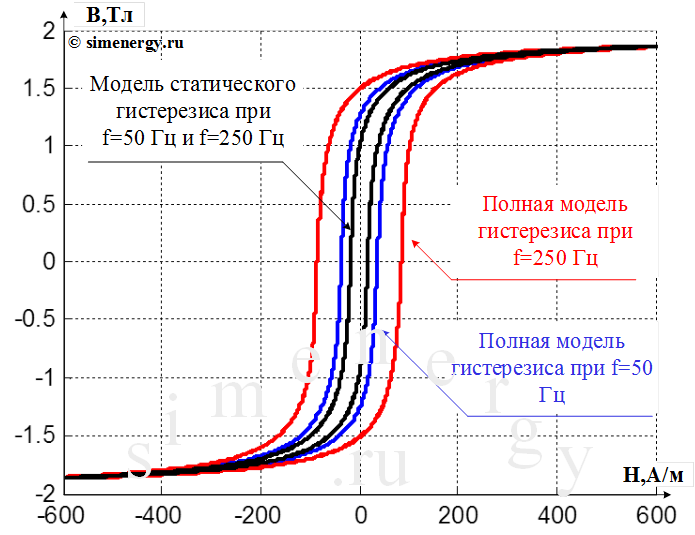
В то время как другие ферромагнитные материалы имеют низкую способность удерживать (магнитно-мягкие), что делает их идеальными для использования в электромагнитах, соленоидах или реле. Один из способов уменьшить эту остаточную плотность потока до нуля — изменить направление тока, протекающего через катушку, путем изменения значения H, напряженности магнитного поля, отрицательной. Этот эффект называется коэрцитивной силой H C .
Если этот обратный ток увеличивается еще больше, то плотность потока будет также увеличиваться в обратном направлении, пока ферромагнитный сердечник не достигнет насыщения снова, но в обратном направлении от предыдущего. Снижая ток намагничивания I снова до нуля создаст аналогичную величину остаточного магнетизма, но в обратном направлении.
Затем путем постоянного изменения направления тока намагничивания через катушку с положительного направления на отрицательное направление, как в случае с источником переменного тока, можно создать петлю магнитного гистерезиса ферромагнитного сердечника.
Гистерезис в электротехнике
Важными характеристиками сердечников электромагнитов и других электрических машин являются параметры намагничивания ферромагнитных материалов, из которых они изготавливаются. Исследовать эти материалы помогают петли ферромагнетиков. В данном случае прослеживается нелинейная зависимость внутренней магнитной индукции от величины внешних магнитных полей.
На процесс намагничивания (перемагничивания) влияет предыдущее состояние ферромагнетика. Кроме того, кривая намагничивания зависит от типа ферромагнитного образца, из которого состоит сердечник.
Если по катушке с сердечником циркулирует переменный ток, то намагничивания образца приводит к отставанию намагничивания. В результате намагничивания сердечника происходит сдвиг фаз в цепи с индуктивной нагрузкой. Ширина петли гистерезиса при этом зависит от гистерезисных свойств ферромагнетиков, применяемых в сердечнике.
Это объясняется тем, что при изменении полярности тока, ферромагнетик какое-то время сохраняет приобретённую ориентацию полюсов. Для переориентации этих полюсов требуется время и дополнительная энергия, которая израсходуется на нагревание вещества, что приводит к гистерезисным потерям. По величине потерь материалы подразделяются на магнитомягкие и магнитотвёрдые (см. рис. 3).
Для переориентации этих полюсов требуется время и дополнительная энергия, которая израсходуется на нагревание вещества, что приводит к гистерезисным потерям. По величине потерь материалы подразделяются на магнитомягкие и магнитотвёрдые (см. рис. 3).
Рис. 3. Классификация магнитных материалов
Магнитный гистерезис в ферромагнетиках отображает зависимость вектора намагничивания от напряженности электрического поля (см. Рис. 3). Но не только изменение поля по знаку вызывает гистерезис. Вращение поля или (что, то же самое) магнитного образца, также сдвигает временные характеристики намагничивания.
Рис. 4. Петли гистерезиса под действием изменения напряжённости поля
Обратите внимание, что на рисунке изображены двойные петли. Такие петли характерны для магнитного гистерезиса.
В однодоменных ферромагнетиках, которые состоят из очень маленьких частиц, образование доменов не поддерживается (не выгодно с точки зрения энергетических затрат). В таких образцах могут происходить только процессы магнитного вращения.
Рис. 5. Механизм возникновения петли магнитного гистерезиса
В электротехнике гистерезисные свойства используются довольно часто:
- в работе электромагнитных реле;
- в конструкциях коммутационных приборов;
- при создании электромоторов и других силовых механизмов.
связанным с магнитными процессами в различных веществах. Он показывает, как себя ведет тот или другой материал в электромагнитном поле, а это тем самым позволяет строить графики зависимости и снимать какие-то показания сред, в которых находятся эти самые материалы. Например, этот эффект используется в работе терморегулятора.
Рассматривая более подробно понятие гистерезиса и эффект с ним связанный, можно заметить такую особенность. Вещество, обладающее такой особенностью, способно переходить в насыщение. То есть, это то состояние, при котором оно больше не способно накапливать в себе энергию. А при рассмотрении процесса на примере ферромагнитных материалов энергия выражается намагниченностью, которая возникает благодаря имеющейся магнитной связи между молекулами вещества.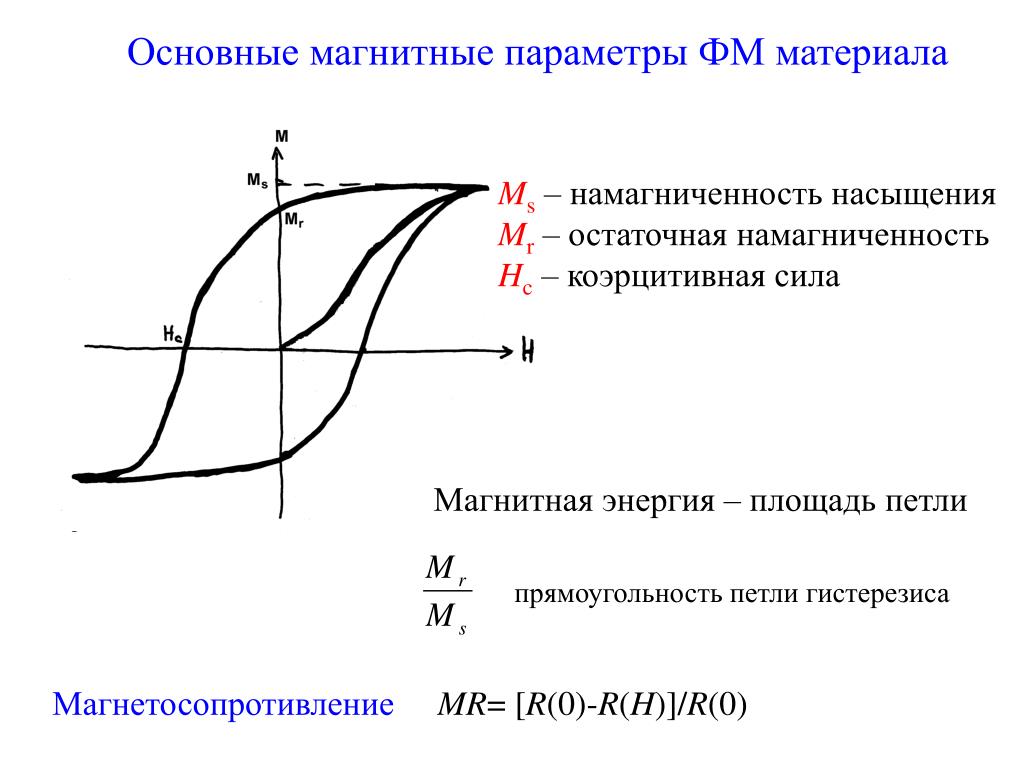 А они создают магнитные моменты – диполи, которые в обычном состоянии направлены хаотически.
А они создают магнитные моменты – диполи, которые в обычном состоянии направлены хаотически.
Намагниченность в данном случае
– это принятие магнитными моментами определенного направления. Если же они направлены хаотически, то ферромагнетик считается размагниченным. Но когда диполи направлены в одну сторону, то материал намагничен. По степени намагниченности сердечника катушки можно судить о величине магнитного поля, создаваемого током, протекающим по ней.
Явления диэлектрического гистерезиса
У диэлектриков отсутствуют свободные заряды. Электроны тесно связаны со своими атомами и не могут перемещаться. Другими словами, у диэлектриков спонтанная поляризация. Такие вещества называются сегнетоэлектриками.
Однако под действием электрического поля заряды в диэлектриках поляризуются, то есть изменяют ориентацию в противоположные стороны. С увеличением напряжённости поля абсолютная величина вектора поляризации возрастает по нелинейному принципу. В определённый момент поляризация достигает насыщённости, что вызывает эффект диэлектрического гистерезиса.
На изменение поляризации уходит часть энергии, в виде диэлектрических потерь.
Другие свойства
Кроме магнитного гистерезиса, также различают гальвономагнитный и магнитострикционный эффекты
. В этих процессах наблюдается изменение электрического сопротивления за счет механической деформации материала. Сегнетоэлектрики под действием деформационных сил способны вырабатывать электрический ток, что объясняется пьезоэлектрическим гистерезисом. Также существует понятие электрооптического и двойного диэлектрического гистерезиса. Последний процесс имеет обычно наибольший интерес, так как сопровождается двойным графиком в зонах, приближающихся к точкам насыщения.
Гистерезис определение относится не только к ферромагнетикам, применяемым в электронике. Такой процесс может происходить и в термодинамике
. Например, при организации отопления от газового или электрического котла. Регулирующим компонентом в системе является терморегулятор. Но только контролируемой величиной является температура воды в системе.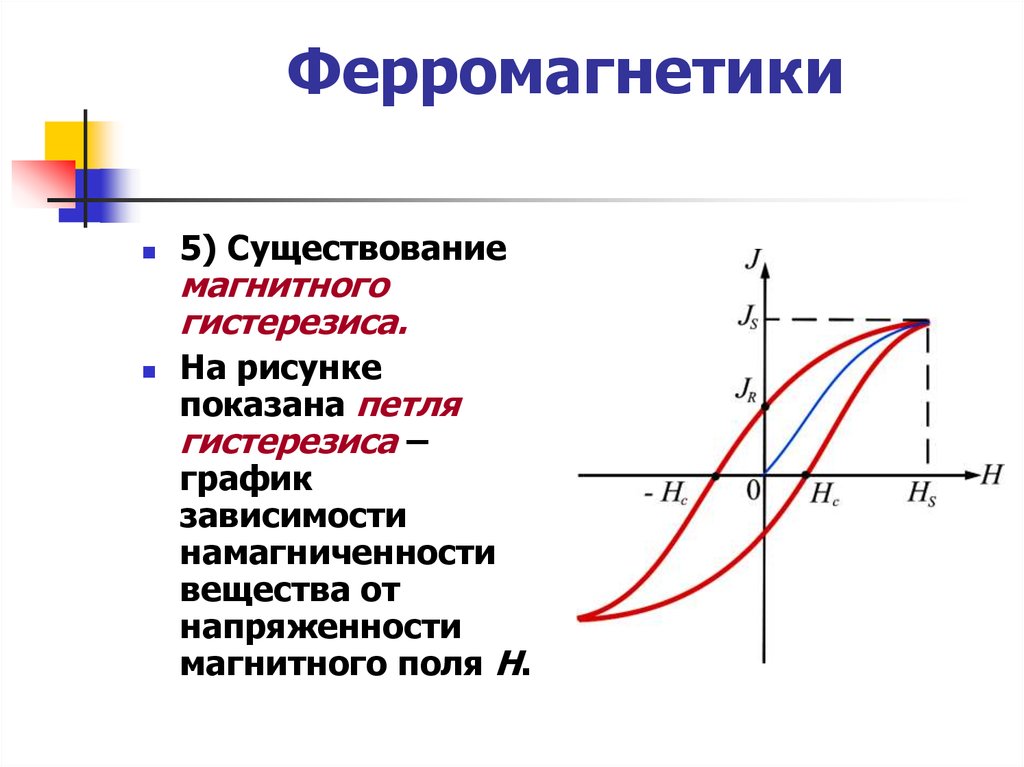
При ее снижении до заданного уровня котел включается, начиная подогрев до заданной величины. После чего выключается и процесс повторяется в цикле. Если снять показания температуры при нагреве и остывании системы при каждом цикле включения и выключения отопления, то получиться график в виде петли гистерезиса, который и получил название гистерезис котла.
В таких системах гистерезис выражается в температуре
. Например, если он составляет 4°С, а температура теплоносителя установлена 18°С, то котел выключится, когда она достигнет значения 22°С. Таким образом, можно настроить любой приемлемый температурный режим в помещениях. А терморегулятор является, по сути, датчиком температуры или термостатом, который включает или выключает отопления при достижении нижнего и верхнего порога, соответственно.
Чтобы лучше понять, что такое магнитный гистерезис, нужно разобраться, где и при каких условиях он возникает.
Физический процесс при гистерезисе
Чтобы подробно понять процесс гистерезиса, необходимо досконально изучить следующие понятия:
- Магнитное поле – это среда, которая создается линиями магнитной индукции, образованными током, протекающим по проводнику или созданные строго направленными магнитными моментами в постоянном магните.
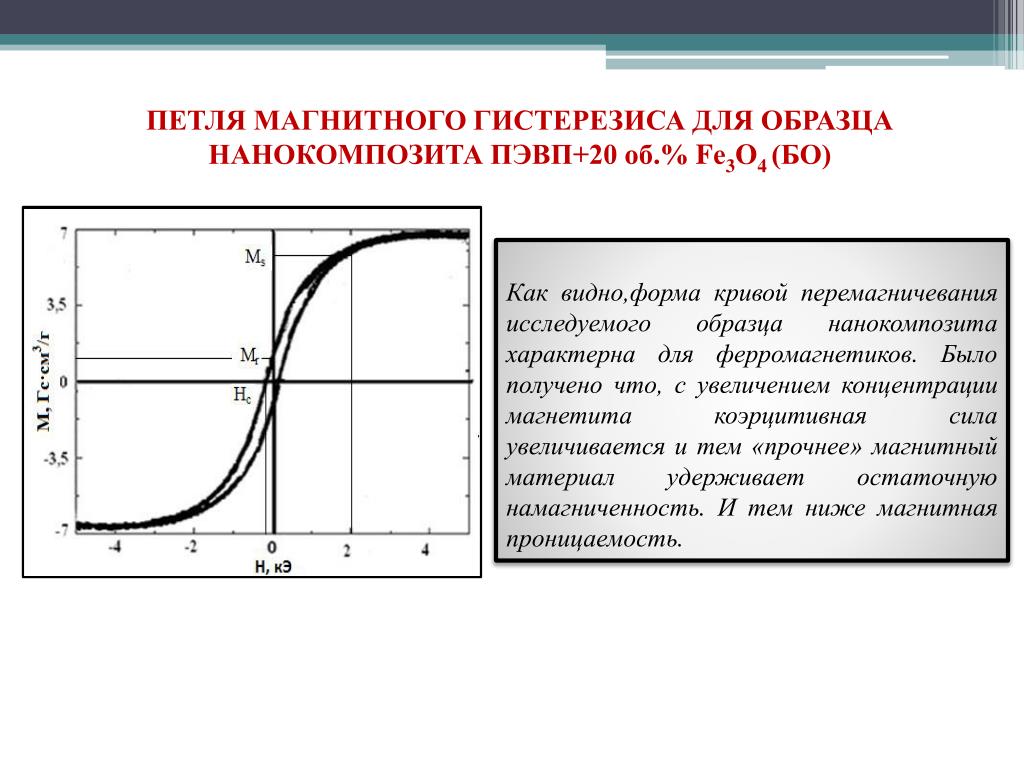
- Вектор магнитной индукции – величина, указывающая направление распространения магнитного поля, обозначается большой буквой В.
- Намагниченность – состояние вещества, при котором в нем еще остались направленные магнитные диполи. В физике и электротехнике обозначается буквой М.
- Напряженность магнитного поля – величина, характеризующая разницу между В и М, обозначается буквой Н.
Что касается материалов, в которых лучше всего наблюдается эффект гистерезиса, то таковыми являются именно ферромагнетики. Это смесь химических элементов, которая способна намагничиваться за счет направленности магнитных диполей, поэтому обычно в составе имеются такие металлы, как:
Читайте также: Сварка меди и виды электродов для этого, преимущества и недостатки разных моделей
- железо;
- кобальт;
- никель;
- соединения на их основе.
Чтобы увидеть гистерезис, на катушку с сердечником из ферромагнетика необходимо подать переменное напряжение.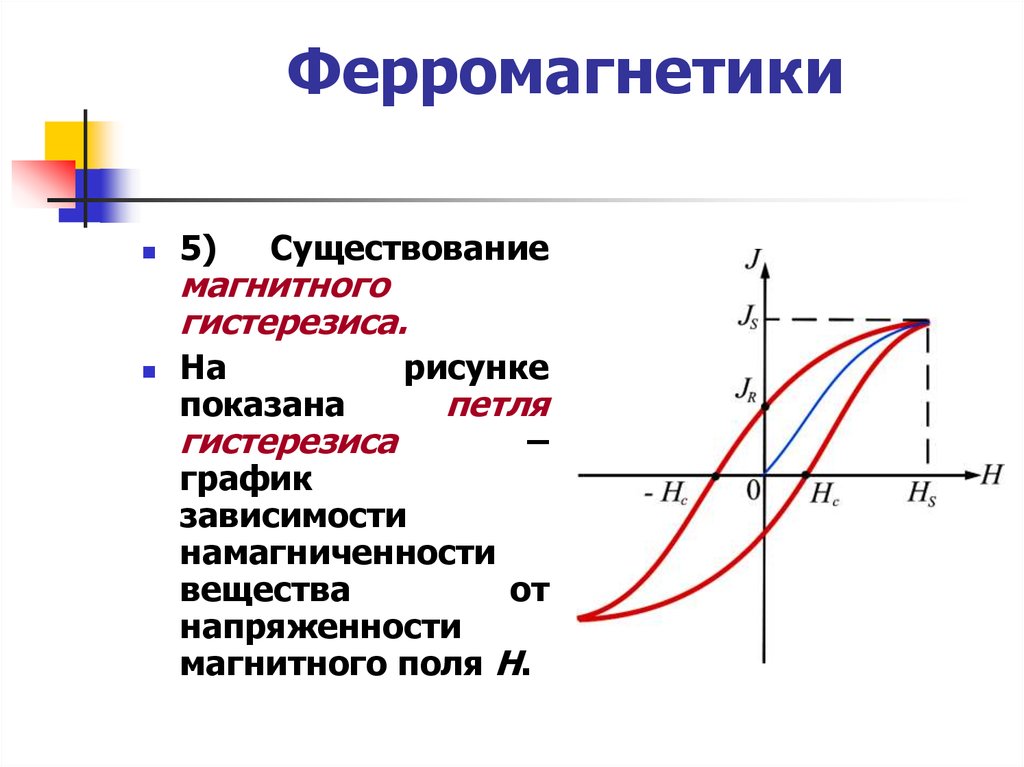 При этом от величины его график намагничивания сильно зависеть не будет, потому как эффект зависит напрямую от свойства самого материала и величины магнитной связи между элементами вещества.
При этом от величины его график намагничивания сильно зависеть не будет, потому как эффект зависит напрямую от свойства самого материала и величины магнитной связи между элементами вещества.
Основополагающим моментом при рассмотрении понятия гистерезиса в электронике является как раз магнитная индукция В, созданная вокруг катушки при подаче напряжения. Она определяется по стандартной формуле, как произведение магнитной диэлектрической проницаемости вещества к сумме напряженности и намагниченности поля.
Чтобы понять общий принцип эффекта гистерезиса, необходимо воспользоваться графиком. На нем видна петля намагничивания из состояния полной размагниченности. Участок можно обозначить цифрами 0-1. При достаточной величине напряжения и длительности воздействия магнитного поля на материал график доходит до крайней своей точки по указанной траектории. Процесс осуществляется не по прямой, а по кривой с определенным изгибом, который характеризует свойства материала.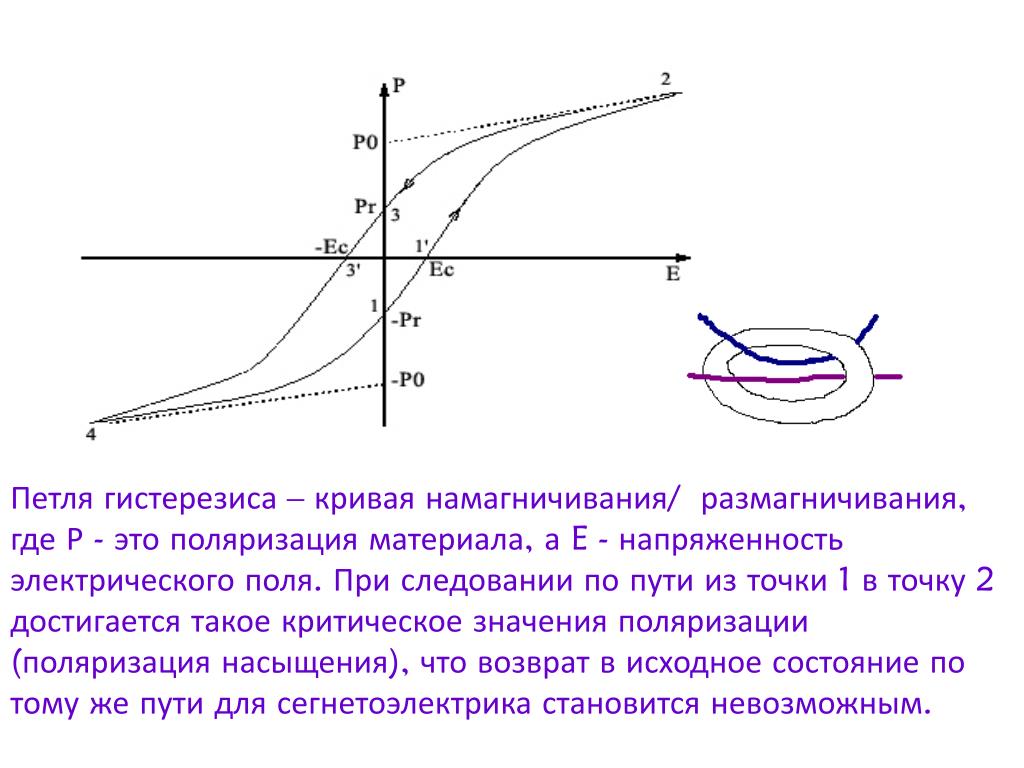 Чем больше в веществе магнитных связей между молекулами, тем быстрее он выходит в насыщение.
Чем больше в веществе магнитных связей между молекулами, тем быстрее он выходит в насыщение.
После снятия напряжения с катушки напряженность магнитного поля падает до нуля. Это участок на графике 1-2. При этом материал за счет направленности магнитных моментов остается намагниченным. Но величина намагниченности несколько ниже, чем при насыщении. Если такой эффект наблюдается в веществе, то оно относится к ферромагнетикам, способным накапливать в себе магнитное поле за счет сильных магнитных связей между молекулами вещества.
Со сменой полярности напряжения, подводимого к катушке, процесс размагничивания продолжается по той же кривой до состояния насыщения. Только в этом случае магнитные моменты диполей будут направлены в обратную сторону. С частотой сети процесс будет периодически повторяться, описывая график, получивший название – петля магнитного гистерезиса.
При многократном намагничивании ферромагнетика меньшей, чем при насыщении напряженностью, то можно получить семейство кривых, из которых можно построить общий график, характеризующий состояние вещества от полного размагниченного до полного намагниченного.
Магнитная петля гистерезиса
Магнитная петля гистерезиса выше, показывает поведение ферромагнитного сердечника графически в виде соотношения между B и H является нелинейным. Начиная с немагнитного сердечника, и B, и H будут в нуле, точка 0 на кривой намагничивания.
Если ток намагничивания I увеличивается в положительном направлении до некоторого значения, напряженность магнитного поля H линейно увеличивается с I,и плотность потока B также будет увеличиваться, как показано кривой из точки 0 в точку a, когда она движется к насыщению.
Теперь, если ток намагничивания в катушке уменьшается до нуля, магнитное поле, циркулирующее вокруг сердечника, также уменьшается до нуля. Однако магнитный поток катушек не достигнет нуля из-за остаточного магнетизма, присутствующего в сердечнике, и это показано на кривой от точки а к точке b .
Чтобы уменьшить плотность потока в точке b до нуля, необходимо обратить ток, протекающий через катушку. Сила намагничивания, которая должна применяться для обнуления остаточной плотности потока, называется «Коэрцитивной силой». Эта коэрцитивная сила меняет магнитное поле, перестраивая молекулярные магниты, пока ядро не станет немагнитным в точке с .
Сила намагничивания, которая должна применяться для обнуления остаточной плотности потока, называется «Коэрцитивной силой». Эта коэрцитивная сила меняет магнитное поле, перестраивая молекулярные магниты, пока ядро не станет немагнитным в точке с .
Увеличение этого обратного тока вызывает намагничивание сердечника в противоположном направлении, и дальнейшее увеличение этого тока намагничивания приведет к тому, что сердечник достигнет своей точки насыщения, но в противоположном направлении, точки d на кривой.
Эта точка симметрична точке b . Если ток намагничивания снова уменьшится до нуля, остаточный намагниченность, присутствующая в сердечнике, будет равна предыдущему значению, но в точке е будет обратной .
Снова изменение направления тока намагничивания, протекающего через катушку на этот раз в положительном направлении, приведет к тому, что магнитный поток достигнет нуля, точка f на кривой, и, как и прежде, дальнейшее увеличение тока намагничивания в положительном направлении приведет к насыщению сердечника в точке а .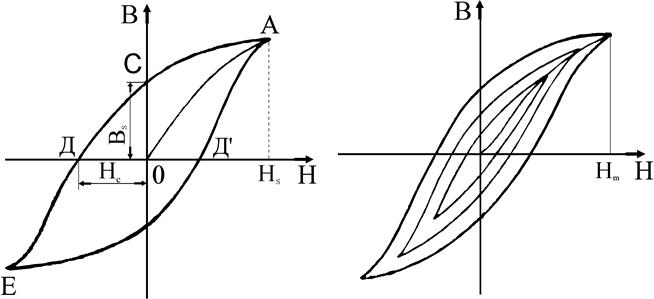
Затем кривая B-H следует по пути a-b-c-d-e-f-a, когда ток намагничивания, протекающий через катушку, чередуется между положительным и отрицательным значением, таким как цикл переменного напряжения. Этот путь называется магнитной петлей гистерезиса.
Эффект магнитного гистерезиса показывает, что процесс намагничивания ферромагнитного сердечника и, следовательно, плотность потока зависят от того, на какую часть кривой намагничивается ферромагнитный сердечник, поскольку это зависит от прошлых цепей, придающих сердечнику форму «памяти». Тогда ферромагнитные материалы имеют память, потому что они остаются намагниченными после того, как внешнее магнитное поле было удалено.
Однако мягкие ферромагнитные материалы, такие как железная или кремниевая сталь, имеют очень узкие петли магнитного гистерезиса, что приводит к очень небольшим количествам остаточного магнетизма, что делает их идеальными для использования в реле, соленоидах и трансформаторах, поскольку они могут легко намагничиваться и размагничиваться.
Поскольку для преодоления этого остаточного магнетизма необходимо применять коэрцитивную силу, необходимо выполнить работу по замыканию петли гистерезиса, чтобы используемая энергия рассеивалась в виде тепла в магнитном материале. Это тепло известно как потеря гистерезиса, величина потери зависит от значения материала коэрцитивной силы.
Добавляя добавки к металлическому железу, такие как кремний, можно получить материалы с очень малой коэрцитивной силой, которые имеют очень узкую петлю гистерезиса. Материалы с узкими петлями гистерезиса легко намагничиваются и размагничиваются и известны как магнитомягкие материалы.
Форма петли
Зависит форма петли от многих параметров – намагниченности, напряженности поля, наличия потерь и т. д. Также немалое влияние оказывает и химический состав ферромагнетика, структурное состояние его, температура, характер и распределение дефектов, наличие обработки (тепловой, термомагнитной, механической). Следовательно, гистерезис ферромагнетиков можно изменять, подвергая материалы механической обработке.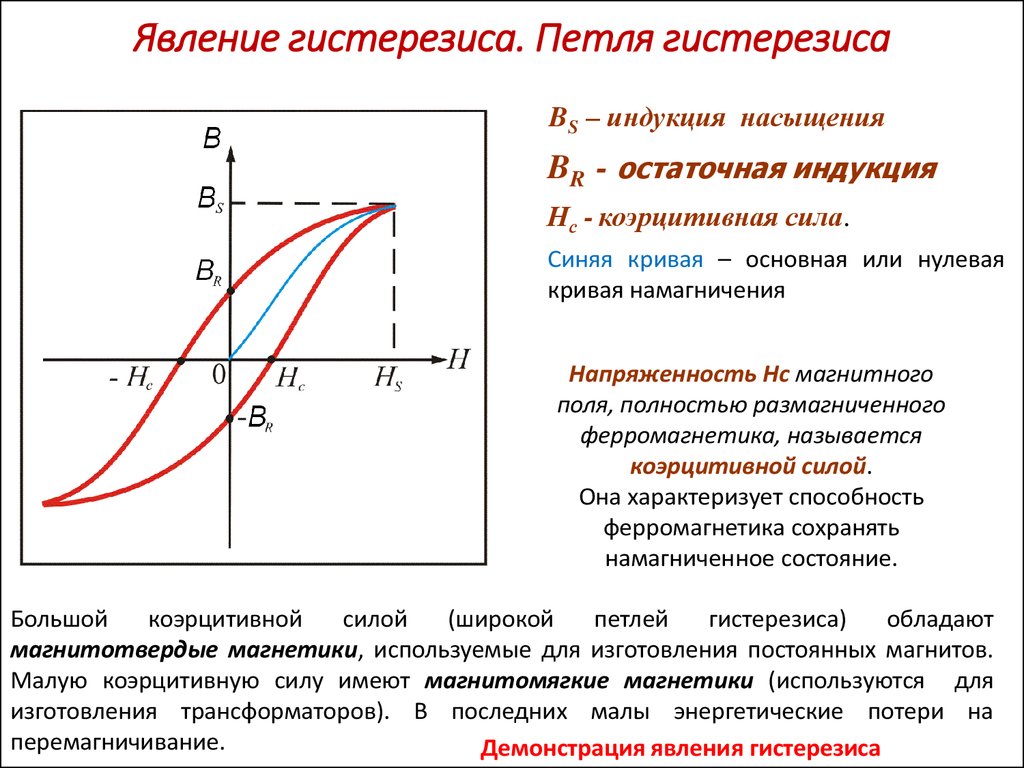 От этого изменяются все характеристики материала.
От этого изменяются все характеристики материала.
На графике зависимости М от Н можно видеть:
- Из нулевого состояния, при котором М=0 и Н=0, с увеличением Н растет и М.
- Когда поле увеличивается, то намагниченность становится практически постоянной и равна значению насыщения.
- При уменьшении Н происходит обратное изменение, но вот когда Н=0, намагниченность М не будет равна нулю. Это изменение можно видеть по кривой размагничивания. И когда Н=0, М принимает значение, равное остаточной намагниченности.
- При увеличении Н в интервале –Нт… +Нт происходит изменение намагниченности вдоль третьей кривой.
- Все три кривые, описывающие процессы, соединяются и образуют своеобразную петлю. Она-то и описывает явление гистерезиса – процессы намагничивания и размагничивания.
Что влияет на петлю гистерезиса?
Гистерезис – это больше внутренний эффект, который не виден на поверхности материала, но он сильно зависит не только от типа самого материала, но и от качества и вида его механической обработки.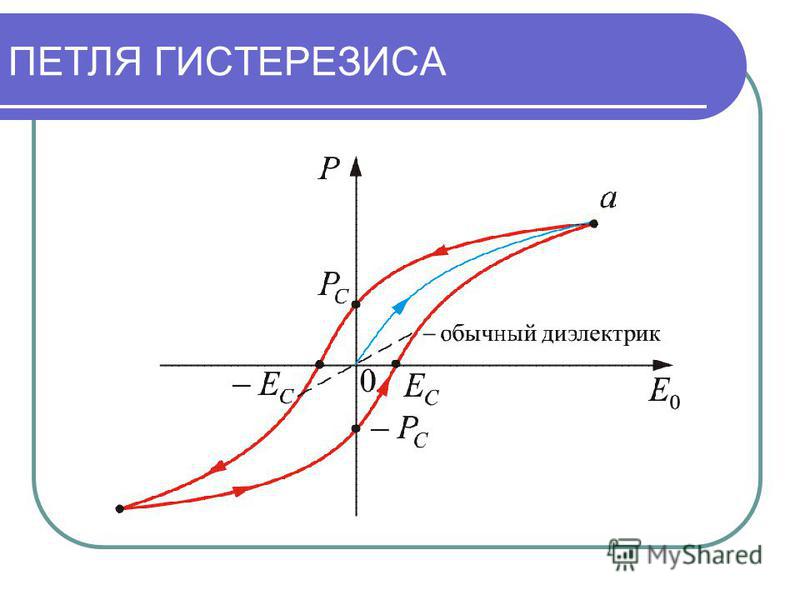 Например, железо переходит в насыщение при напряженности равной 1 э, а сплав магнико достигает своей критической точки только при 580 э. Чем больше дефектов на поверхности материала, тем требуется больше напряженность магнитного поля, чтобы вывести его в насыщение.
Например, железо переходит в насыщение при напряженности равной 1 э, а сплав магнико достигает своей критической точки только при 580 э. Чем больше дефектов на поверхности материала, тем требуется больше напряженность магнитного поля, чтобы вывести его в насыщение.
В результате намагничивания и размагничивания в материале выделяется тепловая энергия, которая равна площади петли гистерезиса. Также к потерям в ферромагнетике можно отнести действие вихревых токов и магнитной вязкости вещества. Это обычно наблюдается при изменении частоты магнитного поля в большую сторону.
В зависимости от характера поведения ферромагнетика в среде с магнитным полем, различают статический и динамический гистерезис. Первый наблюдается при номинальной частоте напряжения, но с ее ростом площадь графика увеличивается, что приводит и к росту потерь.
Для подробного изучения этого процесса нужно проанализировать отдельные участки кривой, обозначающей изменение индукции. Описание основных этапов:
- сначала наблюдается смещение границ между соседними доменами;
- далее ориентация моментов изменяется быстро в направлении силовых линий внешнего поля;
- на этой стадии новое расположение границ становится необратимым;
- этот участок характеризуется ростом отдельных доменов до максимального размера, магнитные моменты располагаются в точном соответствии линиям воздействующего поля;
- завершающий участок показывает отсутствие влияния на магнитные моменты напряженности, созданной соленоидом.
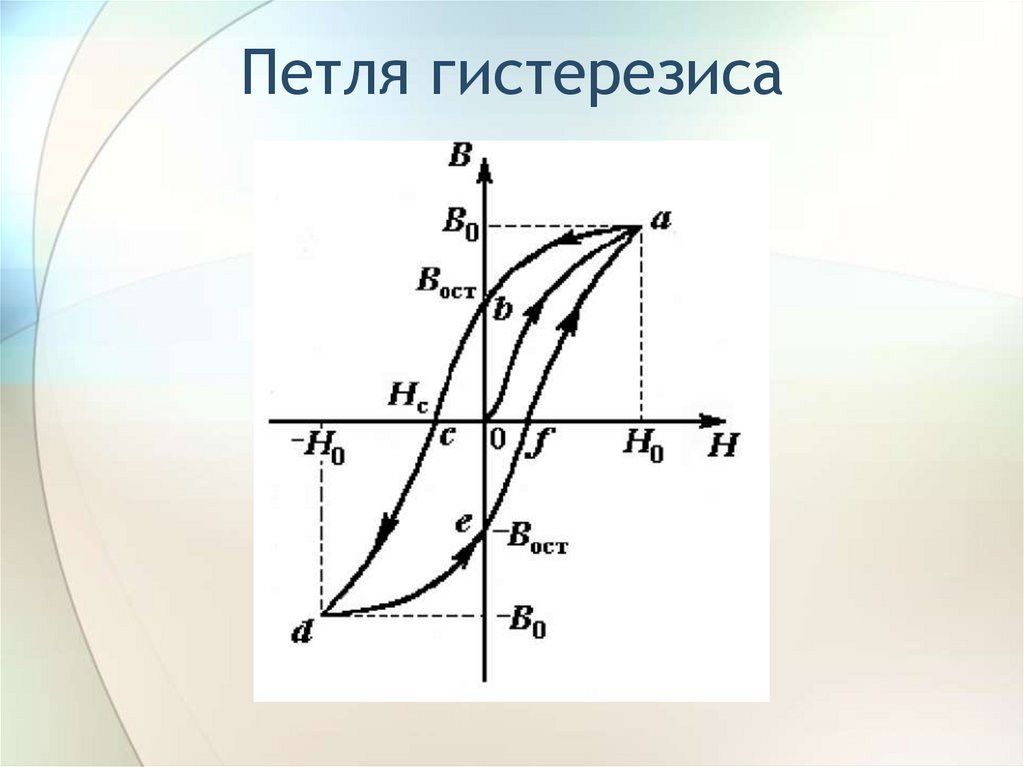
Если уменьшить силовые параметры внешнего поля, образуется петля гистерезиса что это такое показывать можно на первой картинке (по направлению стрелок). Следует обратить внимание, что кривые отличаются. Запаздывание индукции соответствует базовым принципам явления. При нулевой напряженности B≠0. Эту величину называют остаточной индукцией. Данная особенность объясняет понятный процесс создания постоянного магнита. Сердечник сохраняет соответствующие свойства даже после отключения источника питания.
Намагниченность можно убрать повешением температуры до уровня точки Кюри определенного материала. Аналогичный результат получают с помощью соответствующего внешнего силового поля (-Hc). Эта напряженность создает коэрцитивную силу, достаточную для размагничивания сердечника из стали либо другого ферромагнетика. Завершенный полностью цикл называют петлей магнитного гистерезиса.
Теория гистерезиса
Стоит учитывать, что явление магнитного гистерезиса происходит также при вращении поля Н, а не только при его изменении по знаку и величине. Называется это гистерезисом магнитного вращения и соответствует изменению направления намагниченности М с изменением направления поля Н. Возникновение гистерезиса магнитного вращения наблюдается также при вращении исследуемого образца относительно фиксированного поля Н.
Называется это гистерезисом магнитного вращения и соответствует изменению направления намагниченности М с изменением направления поля Н. Возникновение гистерезиса магнитного вращения наблюдается также при вращении исследуемого образца относительно фиксированного поля Н.
Кривая намагничивания характеризует также магнитную структуру домена. Структура изменяется при прохождении процессов намагничивания и перемагничивания. Изменения зависят от того, насколько смещаются границы доменов, от воздействий внешнего магнитного поля. Абсолютно все, что способно задержать все процессы, описанные выше, переводит ферромагнетики в нестабильное состояние и является причиной того, что возникает гистерезис магнитный.
Нужно учесть, что гистерезис зависит от множества параметров. Намагниченность меняется под воздействием внешних факторов – температуры, упругого напряжения, следовательно, возникает гистерезис. При этом появляется гистерезис не только намагниченности, но и всех тех свойств, от которых он зависит. Как можно видеть отсюда, явление гистерезиса можно наблюдать не только при намагничивании материала, но и при других физических процессах, связанных прямо или косвенно с ним.
Как можно видеть отсюда, явление гистерезиса можно наблюдать не только при намагничивании материала, но и при других физических процессах, связанных прямо или косвенно с ним.
Гистерезис в отоплении
Гистерезис определение относится не только к ферромагнетикам, применяемым в электронике. Такой процесс может происходить и в термодинамике. Например, при организации отопления от газового или электрического котла. Регулирующим компонентом в системе является терморегулятор. Но только контролируемой величиной является температура воды в системе.
При ее снижении до заданного уровня котел включается, начиная подогрев до заданной величины. После чего выключается и процесс повторяется в цикле. Если снять показания температуры при нагреве и остывании системы при каждом цикле включения и выключения отопления, то получиться график в виде петли гистерезиса, который и получил название гистерезис котла.
В таких системах гистерезис выражается в температуре. Например, если он составляет 4°С, а температура теплоносителя установлена 18°С, то котел выключится, когда она достигнет значения 22°С. Таким образом, можно настроить любой приемлемый температурный режим в помещениях. А терморегулятор является, по сути, датчиком температуры или термостатом, который включает или выключает отопления при достижении нижнего и верхнего порога, соответственно.
Например, если он составляет 4°С, а температура теплоносителя установлена 18°С, то котел выключится, когда она достигнет значения 22°С. Таким образом, можно настроить любой приемлемый температурный режим в помещениях. А терморегулятор является, по сути, датчиком температуры или термостатом, который включает или выключает отопления при достижении нижнего и верхнего порога, соответственно.
Что такое термореле с регулировкой температуры
Термореле с регулировкой температуры – это электромеханический прибор, предназначенный для контроля температуры в неагрессивной среде. Регулировка температуры посредством устройства происходит благодаря способности реле размыкать и замыкать контакты электрической цепи, в соответствии с изменениями температурного режима.
Это позволяет использовать отопительные приборы только по их фактической необходимости.
Так, например, термореле с внешними теплочувствительными датчиками можно использовать для регулирования работы отопительной системы в зависимости от погодных условий.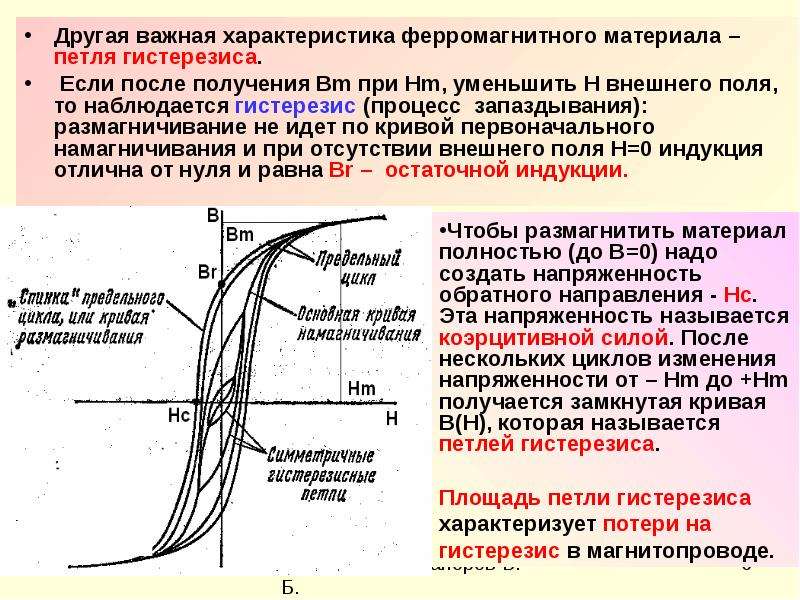 Регулятор будет включать отопительные приборы при понижении температуры на улице ниже заданной.
Регулятор будет включать отопительные приборы при понижении температуры на улице ниже заданной.
Кроме того, термореле можно использовать для:
- Управления оборудованием для нагрева воды в системах автономного отопления и горячего водоснабжения;
- Автономной работы “теплого пола”, водонагревательного котла;
- Автоматизации систем кондиционирования в тепличном хозяйстве;
- В автоматических системах отопления погреба и других складских и подсобных помещений.
Существует несколько видов термореле. В основном, устройства различаются по исполнению. При этом, их устройство остается практически неизменным. К основным конструктивным элементам термореле относят термочувствительный датчик и терморегулятор, подающий сигнал на включение или выключение приборов обогрева и кондиционирования. Информация о фактическом и заданном температурных режимах, обычно, выводится на цифровой дисплей устройства, а светодиодный индикатор сигнализирует о рабочем состоянии реле.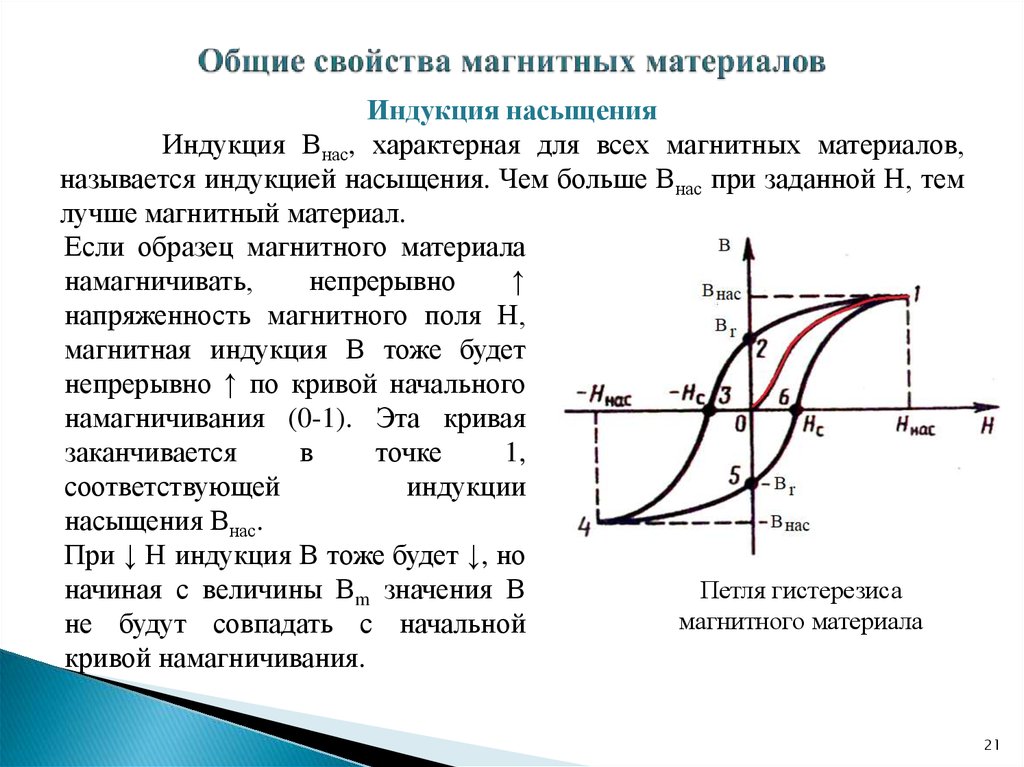
Виды термореле на включение-выключение
Обычный терморегулятор на включение и выключение представляет собой компактный электронный блок, который крепится на стену в подходящем месте и соединяется с контролируемым оборудованием. Самый простой, а поэтому и самый доступный регулятор температуры имеет механическое управление.
Кроме того, все термореле делится на:
- Программируемые устройства контроля. Такие регуляторы подключаются к оборудованию как по проводному, так и по беспроводному принципу. Настройка реле производится через специальную программу или ЖК дисплей. Благодаря программному обеспечению можно настраивать реле на срабатывание в определенное время суток и года.
- Термореле с модулем беспроводного программирования GSM. Такие устройства могут быть как с одним, так и двумя термодатчиками.
- Автономные регуляторы с питанием от аккумуляторов. Такие установки, чаще всего, используют для контроля работы бытовой техники (например, холодильника), инкубаторов.

Для чего нужен гистерезис терморегулятора
Сегодня, большинство устройств по контролю над температурным режимом имеют функции как установки нужной температуры, так и настройки гистерезиса. Что же такое гистерезис терморегулятора? Это величина температуры, при которой сигнал противоположно меняется. Благодаря настройке гистерезиса реле осуществляет включение или выключение подключенного к нему оборудования.
То есть гистерезис – это разница между температурами включения и выключения приборов, обеспечивающих нагревание или охлаждение среды.
Так, например, если гистерезис терморегулятора равен 2 °С, а само устройство выставлено на 25 °С, то при понижении температуры окружающей среды до 23 °С термореле запустит оборудование, контролирующее обогрев комнаты. Такое оборудование может быть представлено электрическим обогревателем или газовым котлом отопления. При этом, чем больше будет гистерезис, тем реже будет запускаться термореле. Это следует учитывать в том случае, если главной целью установки автоматического терморегулятора является экономия электроэнергии.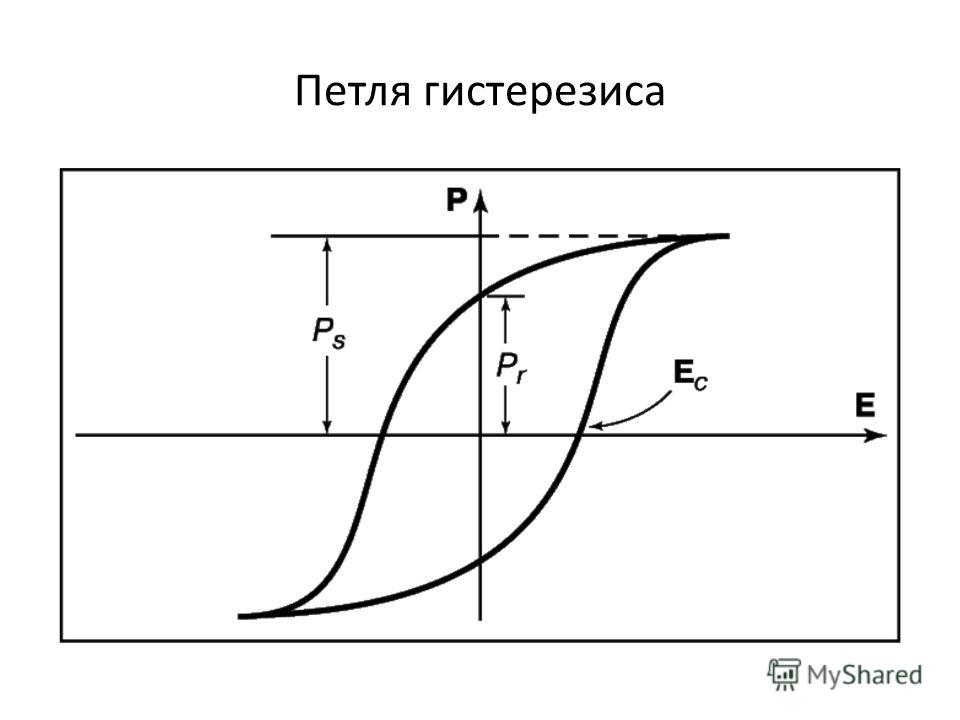
Как изготовить терморегулятор для инкубатора своими руками
Инкубатор – это незаменимая вещь в сельском хозяйстве, которая позволяет выводить птенцов в домашних условиях. Температуру инкубатора можно контролировать с помощью термореле. Термореле для инкубатора можно приобрести, а можно собрать самостоятельно из подручных материалов.
Существует два способа изготовления терморегулятора для инкубатора:
- С использованием стабилитрона, тиристора и 4 диодов мощностью не менее 700 Вт. Регулировка температурного режима выполняться через переменный резистор с сопротивлением в диапазоне от 30 до 50 кОм. Датчиком температуры в данном приборе выступит транзистор, установленный в стеклянной трубке и размещенный на лотке с яйцами.
- С использованием термостата. К корпусу термостата с помощью паяльника нужно будет прикрепить винт и связать его с контактами. Вращение винта будет регулировать температурные показатели.
Наиболее простым и доступным считается второй способ. Независимо от типа термореле, перед закладкой яиц, инкубатор необходимо прогреть, а самодельный терморегулятор настроить.
Независимо от типа термореле, перед закладкой яиц, инкубатор необходимо прогреть, а самодельный терморегулятор настроить.
Настройка гистерезиса
Гистерезис для всех блоков Кситал составляет 1oС.
Это значение оптимально практически для всех применений. В случае особой необходимости его можно изменить.
Нижеприведенные рекомендации не актуальны для старых блоков, которые не реагируют на SMS-команды запроса и изменения констант в энергонезависимой памяти блока.
Возможность изменения именно константы гистерезиса невозможна для прошивок с номером версии ниже, чем
315.210 (как узнать версию прошивки своего блока описано тут).
Когда Вы задаете термостату температуру поддержания, например, +23oС, то при заводских значениях гистерезиса, управляющее реле будет включаться на 22,5oС и отключаться на 23,5oС, поддерживая тем самым температуру 23oС±0,5oС. Это оптимальная настройка для поддержания температуры воздуха.
Необходимо следить, чтобы термодатчик не был размещен вблизи отопителя, поскольку от этого нарушается процесс поддержания температуры в помещении.
Если Вам нужно, чтобы температура поддерживалась в других пределах или управляющее реле более редко включало и выключало бы отопитель, Вы можете подстроить гистерезис выбранного термостата.
Неаккуратным обращением с константами при помощи нижеприведенных команд можно нарушить работоспособность блока.
Все буквы в командах — английские.
«пароль» в командах это актуальный пароль в системе. Значение по умолчанию 00000.
<адрес> в командах это адрес константы половины гистерезиса нужного термостата:
- 03D — адрес константы значения половины гистерезиса для реле №1 в полуградусах
- 03E — адрес константы значения половины гистерезиса для реле №2 в полуградусах
- 03F — адрес константы значения половины гистерезиса для реле №3 в полуградусах
Значения констант по умолчанию равны «01», т. е. половина гистерезиса равна 0,5oС, а полный гистерезис каждого термостата равен 1oС.
е. половина гистерезиса равна 0,5oС, а полный гистерезис каждого термостата равен 1oС.
Вопросы и ответы по терморегуляторам TERNEO
Гистерезис — это разница между температурой включения и выключения нагревателя.
Например: на Вашем терморегуляторе установлено значение температуры 25°С, гистерезис 2°С. При таких настройках терморегулятор будет нагревать помещение и отключит нагреватель при температуре 25°С. При остывании до 23°С снова включится и цикл повторится. Разница в 2°С между этими температурами и будет определять значение гистерезиса терморегулятора.
Варианты использования терморегуляторов TERNEO
Мы представляем в России украинские профессиональные терморегуляторы Тerneo, область применения которых весьма широка: чаще всего в быту терморегуляторы TERNEO (термостаты) применяются при эксплуатации теплых полов или для управления инфракрасными обогревателями, также устанавливаются и в отопительные котлы. Терморегулятор TERNEO может быть важной составляющей сложных промышленных агрегатов и самой разнообразной климатической техники, начиная от бытовых кондиционеров и сушилок и заканчивая специализированным морозильным или нагревательным оборудованием. Купить в России терморегуляторы TERNEO (ТЕРНЕО) можно оформив заявку на нашем сайте.
Купить в России терморегуляторы TERNEO (ТЕРНЕО) можно оформив заявку на нашем сайте.
Термостаты Terneo являются правильным выбором для тех, кто желает получить максимум комфорта, ведь подобные терморегуляторы позволяют легко и быстро устанавливать необходимый режим, который будет поддерживаться в течение заданного времени. Все наши термостаты TERNEO снабжены высококачественными датчиками с высокой чувствительностью, благодаря чему температура в помещении всегда поддерживается с высокой точностью. При этом регулировка и настройка интуитивно понятна, что максимально облегчает задачу по поддержанию определенного микроклимата в помещении.
Различаются терморегуляторы TERNEO и по принципу работы. Термостаты могут быть аналоговыми, цифровыми. У нас вы также можете приобрести программируемые термостаты, которые дают возможность легкого и удобного управления любой системой теплого пола, включая инфракрасную пленку, кабель или нагревательный мат. Термостаты Terneo pro (с кнопочным управлением) иTerneo sen (c сенсорным управлением) позволяют устанавливать температурный режим на всю неделю. При этом эти модели терморегуляторов снабжены двумя температурными датчиками — один для пола и один для воздуха, что дает возможность оборудованию быстро реагировать на изменение условий. Кроме того, «интеллектуальная» система программируемых термостатов сама отключает подогрев в отсутствие людей, что позволяет сократить расход электроэнергии на обогрев до 70 %.
При этом эти модели терморегуляторов снабжены двумя температурными датчиками — один для пола и один для воздуха, что дает возможность оборудованию быстро реагировать на изменение условий. Кроме того, «интеллектуальная» система программируемых термостатов сама отключает подогрев в отсутствие людей, что позволяет сократить расход электроэнергии на обогрев до 70 %.
Использование терморегуляторов при модернизации электрических котлов позволит значительно уменьшить затраты на обогрев. Заменив биметаллический термостат, который имеет большой гистерезис, на терморегулятор terneo rk, с управляемым гистерезисом, КПД системы отопления значительно возрастет. Применив терморегулятор для котла BeeRT с контролем температуры обратки и возможностью управления насосом для прокачки теплоносителя, удастся значительно повысить уровень комфорта в помещениях.
Важной частью современных терморегуляторов для теплых полов, котлов и другого климатического оборудования является датчик температуры, ведь именно он отвечает за надежность срабатывания устройства. В терморегуляторах terneo установлены датчики на основе цифровых микросхем-преобразователей и термисторов, они способны обеспечить высокую точность при изменении температуры, что гарантирует максимально комфортную эксплуатацию.
В терморегуляторах terneo установлены датчики на основе цифровых микросхем-преобразователей и термисторов, они способны обеспечить высокую точность при изменении температуры, что гарантирует максимально комфортную эксплуатацию.
Датчики термостатов Тerneo для теплых полов в зависимости от конфигурации и типа терморегулятора могут измерять как температуру непосредственно пола, так и воздуха в помещении. Датчики Тerneo быстро реагируют на отклонение температуры от заданного значения, поэтому вы можете быть уверены в том, что микроклимат в помещении будет именно таким, какой вам необходим, а пол нагрет точно до нужной температуры. Более того, датчики для терморегуляторов Тerneo оснащены жестким соединительным проводом который обеспечивает удобство монтажа системы теплый пол.
Что касается монтажа, то устанавливать термостаты для инфракрасного обогрева или терморегуляторы для теплых полов можно в монтажной коробке, совмещая их с рамками Unica Schneider Electric, например, для моделей terneo rtp, terneo mex unic, terneo st или terneo vt. Эта серия имеет огромную цветовую гамму, что позволит гармонично вписать наши устройства в любой интерьер.
Эта серия имеет огромную цветовую гамму, что позволит гармонично вписать наши устройства в любой интерьер.
Источники:
- https://www.asutpp.ru/gisterezis.html
- https://ElektroKlub-nn.ru/pravila-montazha/petlej-gisterezisa.html
- https://separett.su/info/gisterezis-regulyatora.html
- https://favourite-svet.ru/elektroprovodka/chto-takoe-gisterezis.html
- https://amperof.ru/teoriya/petlya-gisterezisa.html
- https://meanders.ru.com/chto-takoe-magnitnyj-gisterezis-krivye-magnitnogo-namagnichivanija.shtml
- https://StroiMarket-44.ru/tehspravka/temperaturnyj-gisterezis.html
- https://FB.ru/article/258936/gisterezis-magnitnyiy-opisanie-svoystva-prakticheskoe-primenenie
- https://6watt.ru/elektrooborudovanie/rele-i-datchiki/termorele-s-regulirovkoj-temperatury/
- https://teplobloknn.ru/instrumenty/gisterezis-temperatury.html
Предыдущая
ИнформацияОбзор оптических трансиверов: виды, назначение и принцип работы
7 важных фактов, которые вы должны знать
Содержание:- Введение
- Магнитный гистерезис
- Определение петли гистерезиса
- Гистерезис Значение
- Простая петля гистерезиса
- Петля гистерезиса с разными параметрами
- Объяснение кривой гистерезиса
- Проницаемость свободного пространства
- Интенсивность намагничивания
- Что такое магнитная интенсивность?
- Что такое магнитная восприимчивость?
- Связь между B и H
- Сохраняемость и коэрцитивность в петле гистерезиса
- Остаточный магнетизм
- Коэрцитивная сила
Гистерезис ЗначениеМагнитный гистерезис — обычное явление, если магнитный материал намагничен и завершает один полный цикл намагничивания.
Когда плотность магнитного потока или плотность намагничивания (B) наносится на график зависимости от магнитной напряженности намагничивающего поля (H) для одного полного цикла намагничивания и размагничивания, то полученная в результате петля называется петлей гистерезиса. Кривая петли гистерезиса может быть разной по форме и размеру в зависимости от природы материала.
Кривая гистерезисаПетля гистерезиса, изображающая один полный цикл намагничивания и размагничиванияПетля гистерезиса с разными параметрамиПетля гистерезиса с разными параметрамиЭто произошло от греческого слова «Hysterein», от слова «гистерезис», что означает отставание.
Изображение Фото: Craxd1, Кривая и петля BH, CC BY-SA 3.0Объяснение кривой гистерезиса
- Когда интенсивность намагничивающего поля (H) увеличивается, плотность магнитного потока материала (B) также увеличивается, поскольку все больше и больше доменов выравниваются в направлении внешнего магнитного поля.
 Эта часть показана на приведенном выше рисунке, поскольку мы можем наблюдать от начальной точки до точки «а».
Эта часть показана на приведенном выше рисунке, поскольку мы можем наблюдать от начальной точки до точки «а». - Когда все домены выровнены из-за возрастающего внешнего поля, материал становится магнитно-насыщенным, то есть возникает явление насыщения. Помимо этого, если магнитная напряженность (H) увеличивается, плотность магнитного потока (B) не изменяется, она остается такой же, как мы можем заметить на рисунке, что после достижения точки «a», B становится постоянной.
- Теперь, если магнитная напряженность (H) уменьшается, плотность магнитного потока (B) также уменьшается, но она отстает от магнитной напряженности (H). Следовательно, мы можем заметить на рисунке, что когда магнитная напряженность (H) становится равной нулю в точке «b», плотность магнитного потока (B) не уменьшается до нуля. Значение плотности магнитного потока (B) сохраняется в материале, когда магнитная напряженность (H) равна «0», что считается «удерживающей способностью».
- Кроме того, если направление внешнего магнитного поля меняется на противоположное и величина напряженности магнитного поля (H) увеличивается, материал начинает размагничиваться.
 При наблюдении в точке «c» плотность магнитного потока (B) оказывается равной «0». Это значение напряженности магнитного поля (H), которое необходимо для уменьшения плотности магнитного потока (B) до нуля, называется «коэрцитивностью».
При наблюдении в точке «c» плотность магнитного потока (B) оказывается равной «0». Это значение напряженности магнитного поля (H), которое необходимо для уменьшения плотности магнитного потока (B) до нуля, называется «коэрцитивностью». - Теперь, когда намагничивающее поле, приложенное в обратном направлении, увеличивается дальше, материал снова становится насыщенным, но в противоположном направлении, как показано на диаграмме в точке «d».
- Когда это обратное намагничивающее поле уменьшается, плотность магнитного потока (B) снова отстает от магнитной напряженности (H), и в точке «e» магнитная напряженность (H) становится равной нулю, но плотность магнитного потока (B) не уменьшается до нуля. .
- Опять же, когда текущее направление магнитного поля меняется на противоположное и напряженность магнитного поля (H) снова увеличивается от нуля, цикл повторяется.
Область, ограниченная петлей, представляет собой потерю энергии во время полного цикла намагничивания и размагничивания.
Проницаемость свободного пространства, μo, является постоянным параметром, представленным точным значением 4π x 10-7 Н / м используется для воздуха. Эта постоянная μo появляется в уравнениях Максвелла, которые описывают и связывают электрические и магнитные поля, а также свойства электромагнитный излучение, т. е. помогает связать и определить такие величины, как проницаемость, плотность намагниченности, напряженность магнитного поля и т. д.
Магнитный гистерезис подробно обсуждался в этой статье. но в дополнение к этому, нам нужно прояснить некоторые концепции, связанные с намагничиванием, такие как проницаемость, удерживающая способность в свободном пространстве и в другой среде.
Интенсивность намагничиванияМагнитный материал в магнитном поле создает индуцированный дипольный момент в этом материале, и этот момент на единицу объема распознается как интенсивность намагничивания (I) или плотность намагничивания.
=
где — суммарный индуцированный дипольный момент. Его единица измерения — Am-1
Что такое магнитная интенсивность?Чтобы намагнитить магнитный материал, необходимо приложить магнитное поле. Отношение этого намагничивающего поля к проницаемости свободного пространства известно как напряженность магнитного поля H.
=
где , внешнее магнитное поле также называют плотностью магнитного потока.
Единица магнитной напряженности — Ам.-1 такая же, как у интенсивности намагничивания.
Что такое магнитная восприимчивость?Отношение величины интенсивности намагничивания к величине магнитной напряженности известно как магнитная восприимчивость (). Магнитную восприимчивость можно объяснить как степень легкости, с которой магнитный материал может быть намагничен. Следовательно, материал с более высоким значением магнитной восприимчивости будет легче намагничиваться по сравнению с другими материалами, имеющими меньшее значение магнитной восприимчивости.
= где символы имеют свое обычное значение.
Магнитная восприимчивость — это скалярная величина, не имеющая измерения, следовательно, без единицы измерения.
Что такое магнитная проницаемость?Магнитная проницаемость — это отношение значения чистого магнитного поля внутри материала к значению магнитной напряженности. Здесь чистое магнитное поле внутри материала является векторным сложением приложенного магнитного поля и магнитного поля для намагничивания этого вещества. Магнитную проницаемость можно просто объяснить как меру степени, в которой намагничивающее поле может проникать (проникать) в данный магнитный материал.
=
Магнитная проницаемость — это скалярная величина, единица измерения —
Другой термин, связанный с магнитной проницаемостью, — это относительная проницаемость, которую можно определить как отношение проницаемости среды к проницаемости свободного пространства.
Связь между B и HОбщее магнитное поле B, также называемое плотностью потока, представляет собой сумму силовых линий магнитного поля, созданных внутри заданной области. Обозначается символом B.
Обозначается символом B.
В качестве магнитной напряженности H, которая прямо пропорциональна внешнему магнитному полю, следовательно, можно утверждать, что напряженность магнитного поля или напряженность магнитного поля H может быть увеличена путем увеличения либо величины тока, либо количества витков катушки, в которой материал сохраняется.
Мы знаем, что B = μH или B = H
μr не имеет постоянного значения, а зависит от напряженности поля, поэтому для магнитных материалов отношение плотности потока или общего магнитного поля к напряженности магнитного поля или напряженности магнитного поля известно B / H.
Следовательно, мы получаем нелинейную кривую, когда строим график магнитного потока (B) и магнитной интенсивности (H) по оси X и оси Y соответственно. Но для катушек без материала внутри, то есть магнитный поток не индуцируется внутри какого-либо материала, а индуцируется в вакууме или в случае сердечника из немагнитного материала, такого как дерево, пластик и т. Д.
Д.
Мы можем наблюдать, что плотность магнитного потока для вышеуказанных материалов, то есть железа и стали, становится постоянной с увеличением величины напряженности магнитного поля, и это известно как насыщение, поскольку плотность магнитного потока насыщается для более высоких значений магнитной напряженности. Когда магнитная напряженность мала и, следовательно, приложенная сила магнетизма мала, выравниваются только несколько атомов в материале. С увеличением магнитной напряженности остальные также легко выравниваются.
Однако с увеличением H, поскольку все больший и больший поток скапливается в одной и той же площади поперечного сечения ферромагнитного материала, очень мало атомов доступно внутри этого материала для выравнивания; поэтому, если мы увеличиваем H, магнитный поток (B) больше не увеличивается и, следовательно, становится насыщенным. Как упоминалось ранее, явление насыщения ограничено электромагнитами с железным сердечником.
Как упоминалось ранее, явление насыщения ограничено электромагнитами с железным сердечником.
Удерживающая способность материала — это мера величины магнитного поля, остающегося в материале, когда внешнее намагничивающее поле удалено. Его также можно определить как способность материала сохранять часть своего магнетизма даже после того, как процесс намагничивания был остановлен. Стабильно зависит от характеристик материалов.
После намагничивания магнитного материала некоторые электроны в атомах остаются выровненными в направлении первоначального направления намагничивающего поля и ведут себя как крошечные магниты со своими собственными дипольными моментами и не возвращаются к полностью случайной структуре, как остальные из них. Из-за этого в материалах остается некоторое магнитное поле или общий магнетизм. Ферромагнитные материалы обладают сравнительно высокой удерживающей способностью по сравнению с другими намагничивающими материалами, что делает их идеальными для создания постоянных магнитов.
Остаточный магнетизм — это величина плотности магнитного потока, которая может удерживаться магнитным материалом, и способность удерживать ее известна как удерживающая способность материала.
Коэрцитивная силаКоэрцитивная сила может быть определена как величина силы намагничивания, необходимая для устранения остаточного магнетизма, удерживаемого материалом.
В следующих разделах мы обсудим типы магнитов, постоянных магнитов и электромагнитов в зависимости от свойств и природы материалов.
Дополнительные статьи по электронике нажмите сюда
Вестник Иркутского государственного технического университета
2018 / Том 22, №8 (139) 2018 [ ЭНЕРГЕТИКА ]
ЦЕЛЬ. В условиях постоянного усложнения электроэнергетических систем все более актуальной становится задача обеспечения адекватности функционирования устройства релейной защиты. Для ее решения авторы предлагают использовать детализированные математические модели совокупности измерительных трансформаторов релейной защиты совместно с современными симуляторами электроэнергетических систем. Очень важным является адекватное моделирование измерительных трансформаторов, в частности процесса намагничивания сердечника, поскольку измерительные трансформаторы во многом определяют форму контролируемого сигнала релейной защиты и влияют на ее работу. Однако, ввиду отсутствия точного математического описания характеристики намагничивания сердечника измерительного трансформатора, в настоящее время используются упрощенные модели, не отражающие всех протекающих в сердечнике процессов. Целью работы является разработка математической модели гистерезиса, обладающая высокой точностью воспроизведения процессов перемагничивания сердечника трансформатора. МЕТОДЫ. Основным методом исследования является математическое моделирование процессов перемагничивания ферромагнитного материала. Для проведения исследований использовался программный комплекс MathCAD. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ. В статье представлены фрагменты разработки и исследования математической модели с памятью магнитного гистерезиса, базирующейся на теории Прейзаха, адекватно воспроизводящей как предельные, так и частные петли гистерезиса.
Очень важным является адекватное моделирование измерительных трансформаторов, в частности процесса намагничивания сердечника, поскольку измерительные трансформаторы во многом определяют форму контролируемого сигнала релейной защиты и влияют на ее работу. Однако, ввиду отсутствия точного математического описания характеристики намагничивания сердечника измерительного трансформатора, в настоящее время используются упрощенные модели, не отражающие всех протекающих в сердечнике процессов. Целью работы является разработка математической модели гистерезиса, обладающая высокой точностью воспроизведения процессов перемагничивания сердечника трансформатора. МЕТОДЫ. Основным методом исследования является математическое моделирование процессов перемагничивания ферромагнитного материала. Для проведения исследований использовался программный комплекс MathCAD. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ. В статье представлены фрагменты разработки и исследования математической модели с памятью магнитного гистерезиса, базирующейся на теории Прейзаха, адекватно воспроизводящей как предельные, так и частные петли гистерезиса. ВЫВОДЫ. Анализ существующих математических моделей трансформаторов тока позволил выявить наиболее перспективный подход для описания процесса намагничивания — теория Прейзаха, которая из-за сложности реализации в распространенных программных и программно-аппаратных комплексах не применяется. На основе теории Прейзаха для описания процесса магнитного гистерезиса была разработана математическая модель гистерезиса с памятью состояния вещества и проведены предварительные исследования данной модели, подтвердившие правильность ее работы.
ВЫВОДЫ. Анализ существующих математических моделей трансформаторов тока позволил выявить наиболее перспективный подход для описания процесса намагничивания — теория Прейзаха, которая из-за сложности реализации в распространенных программных и программно-аппаратных комплексах не применяется. На основе теории Прейзаха для описания процесса магнитного гистерезиса была разработана математическая модель гистерезиса с памятью состояния вещества и проведены предварительные исследования данной модели, подтвердившие правильность ее работы.
Ключевые слова:
релейная защита,магнитный гистерезис,инверсная модель гистерезиса,теория Прейзаха,предельная петля гистерезиса,частная петля гистерезиса,relay protection,magnetic hysteresis,inverse hysteresis model,Preisach theory,major hysteresis loop,minor hysteresis loop
Авторы:
- Андреев Михаил Владимирович
- Спица Мария Владимировна
- Киевец Антон Владимирович
Библиографический список:
- Hermann W.
 Dommel. Digital computer solution of electromagnetic transients in single- and multiphase networks // IEEE Transactions on Power Apparatus and Systems. 1969. Vol. 88. No. 4. P. 388-399.
Dommel. Digital computer solution of electromagnetic transients in single- and multiphase networks // IEEE Transactions on Power Apparatus and Systems. 1969. Vol. 88. No. 4. P. 388-399. - Матюк В.Ф., Осипов А.А. Математические модели кривой намагничивания и петель магнитного гистерезиса. Ч. I. Анализ моделей // Неразрушающий контроль и диагностика. 2011. № 2. С. 3-35.
- Deane J.H.B. Modeling the dynamics of nonlinear inductor circuits. IEEE Transactions on Magnetics. 1994. Vol. 30. Issue 5. P. 1-13.
- Наумов В.А, Шевцов В.М. Математические модели трансформатора тока в исследованиях алгоритмов дифференциальных защит // Электрические станции. 2003. № 3. С. 51-56.
- Новаш И.Ф., Румянцев Ю.Ф. Упрощенная модель трехфазной группы трансформаторов тока в системе динамического моделирования // Энергетика. Известия высших учебных заведений и энергетических объединений СНГ. 2015. № 5. С. 23-38.
- Король Е.Г. Анализ методов моделирования петли гистерезиса ферромагнитных материалов // Електротехніка і Електромеханіка.
 2007. № 6. C. 44-47.
2007. № 6. C. 44-47. - Preisach F., Fur Z. Phys. 94, 277 (1935).
- Eichler Ja., Novák M., Košek M. Differences between Preisach Model and Experiment for Soft Ferromagnetic Materials, Effect of Instrument Accuracy // IEEE International Workshop of Electronics, Control, Measurement, Signals and their Application to Mechatronics (ECMSM). 2017.
- Willerich S., Herzog H.-G. Interpretation of an Energy Based Hysteresis Model as a Scalar Preisach Operator // IEEE Conference on Electromagnetic Field Computation (CEFC). 2016. P. 13.
- Tousignant M., Sirois F., Kedous-Lebouc A. Identification of the Preisach Model Parameters Using Only The Major Hysteresis Loop and The Initial Magnetization Curve // IEEE Conference on Electromagnetic Field Computation (CEFC). 2016. P. 11.
- Anooshahpour F., Polushin I.G., Patel R.V. Classical Preisach Model of Hysteretic Behavior in a da Vinci Instrument // IEEE International Conference on Advanced Intelligent Mechatronics (AIM). 2016.
 P. 1392-1397.
P. 1392-1397. - Eichler J., Novák M., Košek M. Experimental-numerical method for identification of weighting function in Preisach model for ferromagnetic materials // International Conference on Applied Electronics (AE). 2016.
- Eichler J., Novák M., Košek M. Implementation of the first order reversal curve method for identification of weight function in Preisach model for ferromagnetics // ELEKTRO. 2016. P. 602-607.
- Zsurzsan T.-G., Andersen M.A.E., Zhe Zhang, Andersen N.A. Preisach model of hysteresis for the Piezoelectric Actuator Drive // IECON 2015 — 41st Annual Conference of the IEEE Industrial Electronics Society. 2015. P. 2788-2793.
- Wawrzała P. Application of a Preisach hysteresis model to the evaluation of PMN-PT ceramics properties // Archives of metallurgy and materials. 2013. Vol. 58.
- Андреев М.В., Боровиков Ю.С., Сулайманов А.О. Средства всережимного моделирования дифференциальных защит трансформаторов в электроэнергетических системах // Известия высших учебных заведений.
 Электромеханика. 2015. № 4. С. 63-67.
Электромеханика. 2015. № 4. С. 63-67. - Андреев М.В., Боровиков Ю.С. Оптимизация уставок дифференциальных защит трансформаторов и автотрансформаторов с помощью их адекватных математических моделей // Современные проблемы науки и образования. 2013. № 3. С. 53.
- Андреев М.В., Рубан Н.Ю., Гордиенко И.С., Боровиков Ю.С., Гусев А.С., Сулайманов А.О. Всережимное математическое моделирование релейной защиты электроэнергетических систем. Томск: Изд-во Томского политехнического университета, 2016. 180 с.
- Суворов А.А., Гусев А.С., Сулайманов А.О., Андреев М.В. Проблема верификации средств моделирования электроэнергетических систем и концепция ее решения // Вестник Ивановского государственного энергетического университета. 2017. № 1. С. 11-23.
- Боровиков Ю.С., Гусев А.С., Андреев М.В., Уфа Р.А. Полигон для отработки решений по построению активно-адаптивных сетей на базе всережимного моделирующего комплекса реального времени // Научные проблемы транспорта Сибири и Дальнего Востока.
 2014. № 4. С. 292-296.
2014. № 4. С. 292-296.
Файлы:
- 10-Андреев_М.В.__Спица_М.В.__Киевец_А.В..pdf (скачать | просмотреть) — скачано 109 раз
|
ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru |
Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Инженерные приемы и понятия/ / Теория автоматического управления (регулирования). ТАУ / / Гистерезис для инженеров. Петля гистерезиса. Прерванные процессы на петле гистерезиса. Смена направления процесса.
| |||||||||||||
|
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. |
||||||||||||||
|
TehTab.ru Реклама, сотрудничество: [email protected] |
Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||
Объяснение петли гистерезиса — База знаний идеальных магнитных решений
Гистерезис означает отставание
Гистерезис основан на греческом слове, которое означает отставание. Итак, магнитный гистерезис — это то, как магнитные свойства материала отстают от силы, создающей эти свойства. Кривая гистерезиса многое говорит нам о реакции материала на магнитное поле, поэтому, если мы знаем, как ее интерпретировать, мы многое узнаем и поймем о реакции материала на магнитное воздействие.
Итак, магнитный гистерезис — это то, как магнитные свойства материала отстают от силы, создающей эти свойства. Кривая гистерезиса многое говорит нам о реакции материала на магнитное поле, поэтому, если мы знаем, как ее интерпретировать, мы многое узнаем и поймем о реакции материала на магнитное воздействие.
Мы наносим гистерезис материала на график, известный как петля гистерезиса. Другой способ выразить это — сказать, что петля гистерезиса показывает взаимосвязь между внешней силой намагничивания и плотностью наведенного магнитного потока.
Что такое кривая BH?
График гистерезиса известен как кривая B-H, где B (плотность потока материала, измеренная в теслах или мегагауссах) отложена по вертикальной оси, а H (внешняя приложенная намагничивающая сила, измеренная в амперах на метр) откладывается по горизонтальной оси. Мы также можем изучить ряд других магнитных концепций и принципов, просто подробно изучив петлю гистерезиса.
Кривая B-H магнитного материала. Следуя буквам от a до g, мы получаем важные магнитные данные о материале, которые помогают нам понять магнитные свойства материала.
Плотность магнитного потока (B) магнитного материала будет увеличиваться — от точки до в начале координат — в присутствии приложенного магнитного поля (H) до тех пор, пока не достигнет максимума, при котором она больше не будет реагировать на увеличение магнитного поля. поле в точке b . Это пункт Положительное насыщение , где любое дальнейшее увеличение внешнего магнитного поля не приведет к дальнейшему увеличению плотности потока материала.
Обнаружение остаточной намагниченности и коэрцитивности в петле гистерезиса
Следующее, что мы делаем, это возвращаемся налево по горизонтальной оси к началу координат. Мы обнаруживаем, что материал высвобождает часть своего магнетизма, и там, где приложенное поле снова достигает нуля (точка c на кривой B-H), материал обнаруживает свою остаточную магнитную силу, которая называется остаточной магнитной силой (также известной как сохраняемость).
Что такое остаточная намагниченность?
Остаточное магнитное поле — это оставшееся магнитное поле в материале после того, как приложенное магнитное поле уменьшится до нуля. Основываясь на необработанном значении остаточной намагниченности и форме кривой, которую мы строим с помощью приложенного магнитного поля, мы можем определить, является ли исследуемый образец магнитно-твердым или магнитомягким материалом.
Теперь, когда мы обращаем приложенное магнитное поле (H) и двигаем его влево, мы видим, что значение B (плотность потока материала) уменьшается до нуля. Сейчас мы находимся в точке d на кривой B-H.
Что такое принудительная сила?
Количество (H), необходимое для перемещения (B) до нулевой линии, дает нам значение коэрцитивной силы материала. Коэрцитивная сила, также известная как коэрцитивная сила, представляет собой сопротивление материала изменениям намагниченности. Магнитомягкие материалы, как правило, имеют низкую коэрцитивную силу, а магнитотвердые материалы имеют высокую коэрцитивную силу. Независимо от магнитной твердости или мягкости материала точка d определяет момент, когда они потеряли свою магнитную силу.
Независимо от магнитной твердости или мягкости материала точка d определяет момент, когда они потеряли свою магнитную силу.
Форма кривой B-H в магнитомягких и твердых материалах
Магнитомягкие материалы имеют тонкую кривую гистерезиса, поэтому они широко используются в приложениях, требующих частого переключения полярности, например, в трансформаторах и обмотки двигателя. Как видно ниже, магнитомягкие материалы имеют низкую остаточную намагниченность и уже потеряли большую часть своего магнитного поля к тому времени, когда они пересекают нулевую линию. Они также имеют крутой отрицательный наклон размагничивания на нулевой линии.
Магнитомягкие материалы — с их низкой коэрцитивной силой — могут часто переключать полярность и иметь относительно небольшие электрические потери. Ширина петли гистерезиса многое говорит нам о потерях. Чем уже кривая, тем меньше потери.
Магнитотвердые материалы имеют очень широкую кривую гистерезиса, что делает их практичными в приложениях, где они воздействуют своим магнитным полем на магнитомягкие материалы. Как видно на рисунке ниже, магнитотвердые материалы обладают высокой остаточной намагниченностью и теряют лишь небольшой процент своего магнитного поля к тому времени, когда они пересекают нулевую линию. Их наклон размагничивания на нулевой линии очень пологий и не круче, пока не уходит далеко влево от нулевой линии. Если бы магнитотвердые материалы часто меняли полярность, потери на гистерезис были бы огромными, поэтому они не используются таким образом.
Как видно на рисунке ниже, магнитотвердые материалы обладают высокой остаточной намагниченностью и теряют лишь небольшой процент своего магнитного поля к тому времени, когда они пересекают нулевую линию. Их наклон размагничивания на нулевой линии очень пологий и не круче, пока не уходит далеко влево от нулевой линии. Если бы магнитотвердые материалы часто меняли полярность, потери на гистерезис были бы огромными, поэтому они не используются таким образом.
Отрицательное Насыщение
Толкая влево по оси B, продолжаем наращивать магнитное поле в обратном направлении до достижения точки e — точки Отрицательного Насыщения. Эта точка точно такая же, как точка b , но в противоположном направлении. Жесткий или мягкий магнитный материал в нашем исследовании теперь намагничен в направлении, противоположном его намагничиванию, в точке b .
Если мы вернемся к точка b из точки e , мы просто повторим то же самое, что и изначально, но в противоположном направлении.
Обращаясь к Рисунку 1, с которого мы начали, мы видим, как мы прошли всю петлю гистерезиса. Но осталось отметить одну вещь. Из-за остаточной намагниченности мы никогда не вернемся к точке а, с которой мы начали, потому что точка а была точкой, в которой материал никогда не подвергался воздействию магнитного поля.
Хотите изучить этот материал более подробно? Очень хороший видеоурок доступен здесь.
Обратные петли гистерезиса в сплаве Fe73,5Cu1Nb3Si13,5B9 с малой коэрцитивной силой размер магнитных материалов, температура и т. д. Двумя важными параметрами, характеризующими петлю гистерезиса, являются остаточная намагниченность
M r и коэрцитивное поле H c соответственно. В норме остаточная намагниченность и коэрцитивное поле сохраняют положительные и отрицательные значения для нисходящей ветви петли гистерезиса. Положительная остаточная намагниченность относится к намагниченности образца после приложения большого магнитного поля. Коэрцитивная сила — это обратное магнитное поле, которое делает значение остаточной намагниченности равным нулю. В отличие от обычной петли гистерезиса с циклом против часовой стрелки, перевернутая петля гистерезиса с отрицательной остаточной намагниченностью имеет цикл по часовой стрелке и наблюдается во многих магнитных системах (Takanashi et al., 19).93; Аарони, 1994; Ошеа и Аль-Шариф, 1994 г.; Окоши и др., 2001; Ву и др., 2001; Ким и др., 2006 г.; Демиртас и др., 2007 г.; Ван Тхо и др., 2008 г.; Зизе и др., 2010 г.; Демирчи и др., 2020 г.; Гизинг и др., 2020 г.; Солдатов и др., 2020; Kumar et al., 2021) за последние десятилетия.
Коэрцитивная сила — это обратное магнитное поле, которое делает значение остаточной намагниченности равным нулю. В отличие от обычной петли гистерезиса с циклом против часовой стрелки, перевернутая петля гистерезиса с отрицательной остаточной намагниченностью имеет цикл по часовой стрелке и наблюдается во многих магнитных системах (Takanashi et al., 19).93; Аарони, 1994; Ошеа и Аль-Шариф, 1994 г.; Окоши и др., 2001; Ву и др., 2001; Ким и др., 2006 г.; Демиртас и др., 2007 г.; Ван Тхо и др., 2008 г.; Зизе и др., 2010 г.; Демирчи и др., 2020 г.; Гизинг и др., 2020 г.; Солдатов и др., 2020; Kumar et al., 2021) за последние десятилетия. В многослойном пленочном материале перевернутые петли гистерезиса наблюдались в многослойных материалах Co/Pt/Gd/Pt Takanashi et al., 1993, которые считали, что источником перевернутой петли гистерезиса является межфазное обменное взаимодействие. Это явление также наблюдалось в мультислоях Co/Mn/Co (Wu et al., 2001) и La 0.7 Sr 0. 3 MnO 3 /SrRuO 3 сверхрешетки с ультратонкими отдельными слоями (Ziese et al., 2010; Song et al., 2013). Кроме того, Эшо сообщил об инвертированных петлях гистерезиса с отрицательной остаточной намагниченностью в напыленном сплаве Gd-Co (Esho, 1976), и было предложено несколько моделей, основанных на эффектах структурной неоднородности (Lutes et al., 1977; Togami, 1978). . Однако сообщалось также об аномальной петле гистерезиса в простых гомогенных системах, таких как соединение пирохлора Nd 9.0085 2 Hf 2 O 7 и наночастиц EuS НЧ (Gu et al., 2014; Opherden et al., 2018), и это объясняется конкуренцией двух анизотропий (Takanashi et al., 1993; Гешев и др., 1998; Валвидарес и др., 2002; Юн Джэ и Лим, 2011). Несмотря на количество предыдущих исследований, физическое происхождение перевернутой петли гистерезиса остается спорным.
3 MnO 3 /SrRuO 3 сверхрешетки с ультратонкими отдельными слоями (Ziese et al., 2010; Song et al., 2013). Кроме того, Эшо сообщил об инвертированных петлях гистерезиса с отрицательной остаточной намагниченностью в напыленном сплаве Gd-Co (Esho, 1976), и было предложено несколько моделей, основанных на эффектах структурной неоднородности (Lutes et al., 1977; Togami, 1978). . Однако сообщалось также об аномальной петле гистерезиса в простых гомогенных системах, таких как соединение пирохлора Nd 9.0085 2 Hf 2 O 7 и наночастиц EuS НЧ (Gu et al., 2014; Opherden et al., 2018), и это объясняется конкуренцией двух анизотропий (Takanashi et al., 1993; Гешев и др., 1998; Валвидарес и др., 2002; Юн Джэ и Лим, 2011). Несмотря на количество предыдущих исследований, физическое происхождение перевернутой петли гистерезиса остается спорным.
Аморфные/нанокристаллические сплавы на основе железа в течение многих лет вызывают значительный интерес, поскольку они обладают превосходной магнитной мягкостью (Fish, 1990). Среди них нанокристаллический сплав Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 с неоднородной структурой, известный как Finemet, является часто изучаемым сплавом благодаря высокой намагниченности насыщения
Среди них нанокристаллический сплав Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 с неоднородной структурой, известный как Finemet, является часто изучаемым сплавом благодаря высокой намагниченности насыщения
5 M M s и низкая коэрцитивная сила H c (Hofmann et al., 1992; Polak et al., 1994; Gorria et al., 1996; Hofmann and Kronmüller, 1996; Barquín et al., 1998). Магнитная мягкость нанокристаллического Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 сплав в основном возникает в результате диспергирования ультрамелких зерен α -Fe(Si) в аморфной матрице, которая снижает эффективную магнитную анизотропию ., 2013).
В этом исследовании мы представляем наблюдение полностью перевернутой петли гистерезиса с отрицательной остаточной намагниченностью в аморфных и нанокристаллических сплавах Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 при комнатной температуре. Сравнивая с результатами кривой намагничивания стандартного образца Pd в тех же условиях, мы находим, что чистые коэрцитивные силы нанокристаллического Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 сплав и стандартный образец Pd практически равны для разных диапазонов поля сканирования. В отличие от предыдущих исследований, мы подтверждаем, что наличие обратной петли гистерезиса в сплавах Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 обусловлено остаточной намагниченностью сверхпроводящего магнита, а не структурной неоднородностью. последствия. Это может внести ясность в полемику о физическом происхождении обратных петель гистерезиса, наблюдаемых в магнетиках с малой коэрцитивной силой.
Сравнивая с результатами кривой намагничивания стандартного образца Pd в тех же условиях, мы находим, что чистые коэрцитивные силы нанокристаллического Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 сплав и стандартный образец Pd практически равны для разных диапазонов поля сканирования. В отличие от предыдущих исследований, мы подтверждаем, что наличие обратной петли гистерезиса в сплавах Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 обусловлено остаточной намагниченностью сверхпроводящего магнита, а не структурной неоднородностью. последствия. Это может внести ясность в полемику о физическом происхождении обратных петель гистерезиса, наблюдаемых в магнетиках с малой коэрцитивной силой.
Экспериментальные методы
Аморфные ленты из сплава Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 были приготовлены методом одиночного медного прялочного колеса. Нанокристаллические сплавы получали термической обработкой аморфных соединений Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 при 813 К в течение 30 мин в вакууме (Fujii 20 et al., 8). выше температуры кристаллизации. Подробности сообщались в другом месте (Ayers et al., 19).98). Идентификацию аморфной и кристаллической фаз измеряли методом дифракции рентгеновских лучей (Cu Kα ) при комнатной температуре. Наблюдение за микроструктурой и электронная дифракция (ED) выбранной области сплавов после закалки и отжига были изучены с использованием просвечивающего электронного микроскопа FEI Talos F200X (TEM). Вибрационный магнитометр (VSM) с системой измерения магнитных свойств 3 (MPMS 3 Quantum Design) использовался для измерения намагниченности (M) в зависимости от приложенного магнитного поля (H) с использованием обычной последовательности для различных диапазонов поля сканирования от ± 0,1 до ± 70 KOe. . Все измерения проводились при 300 К, а нанесенный H находился в плоскости лент.
Нанокристаллические сплавы получали термической обработкой аморфных соединений Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 при 813 К в течение 30 мин в вакууме (Fujii 20 et al., 8). выше температуры кристаллизации. Подробности сообщались в другом месте (Ayers et al., 19).98). Идентификацию аморфной и кристаллической фаз измеряли методом дифракции рентгеновских лучей (Cu Kα ) при комнатной температуре. Наблюдение за микроструктурой и электронная дифракция (ED) выбранной области сплавов после закалки и отжига были изучены с использованием просвечивающего электронного микроскопа FEI Talos F200X (TEM). Вибрационный магнитометр (VSM) с системой измерения магнитных свойств 3 (MPMS 3 Quantum Design) использовался для измерения намагниченности (M) в зависимости от приложенного магнитного поля (H) с использованием обычной последовательности для различных диапазонов поля сканирования от ± 0,1 до ± 70 KOe. . Все измерения проводились при 300 К, а нанесенный H находился в плоскости лент. Образец и магнит размагничивали в колебательном режиме при 350 К перед каждым измерением.
Образец и магнит размагничивали в колебательном режиме при 350 К перед каждым измерением.
Results and Discussions
The phase of Fe 73.5 Cu 1 Nb 3 Si 13.5 B 9 ribbons was identified by X-ray diffraction using a diffractometer with Cu-K α radiation in угловой диапазон 2 θ 25–80 ° при скорости сканирования 0,2 ° / с, как показано на рисунке 1A. На дифрактограмме после закалки образца виден ореол, типичный для аморфных сплавов. Для сравнения, рентгенограмма отожженного образца показывает наличие кристаллического 9Фаза твердого раствора 0083 α -Fe и аморфная остаточная фаза, и никакие другие фазы, кроме α -Fe(Si), не были обнаружены по профилям XRD, что согласуется с предыдущими соответствующими отчетами (Zhang et al., 1998; Горриа и др., 2001; Маджумдар и Ахтар, 2005).
РИСУНОК 1 . (A) Рентгенограммы лент Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 в литом состоянии и после отжига при 813 мин в вакууме в течение 30 км. (B) ПЭМ-микрофотография аморфного Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 ленты. Врезка: соответствующий шаблон быстрого преобразования Фурье (БПФ). (C) – (D) ПЭМ-микрофотографии Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 для лент, отожженных в вакууме 3 при 3 мин. Картина дифракции электронов выбранной области и связанная с ней картина быстрого преобразования Фурье (БПФ) показаны на вставке 9.0019 (С) и (D) соответственно.
(B) ПЭМ-микрофотография аморфного Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 ленты. Врезка: соответствующий шаблон быстрого преобразования Фурье (БПФ). (C) – (D) ПЭМ-микрофотографии Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 для лент, отожженных в вакууме 3 при 3 мин. Картина дифракции электронов выбранной области и связанная с ней картина быстрого преобразования Фурье (БПФ) показаны на вставке 9.0019 (С) и (D) соответственно.
Чтобы дополнительно охарактеризовать морфологию и микроструктуру двух лент, были проведены испытания с помощью просвечивающего электронного микроскопа, и результаты показаны на рис. 1B,D. Наблюдение под трансмиссионным электронным микроскопом ленты Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 после закалки подтвердило, что микроструктура образца очень однородна. Изображение с высоким разрешением TEM (HRTEM) (рис. 1B) показывает однородный материал без кристаллической решетки. Кроме того, нет никаких следов кристаллических отражений в соответствующей картине быстрого преобразования Фурье (БПФ). Эти факторы указывают на то, что лента после закалки является полностью аморфной.
Изображение с высоким разрешением TEM (HRTEM) (рис. 1B) показывает однородный материал без кристаллической решетки. Кроме того, нет никаких следов кристаллических отражений в соответствующей картине быстрого преобразования Фурье (БПФ). Эти факторы указывают на то, что лента после закалки является полностью аморфной.
На рисунках 1C,D показаны изображения микроструктуры ПЭМ отожженного образца Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 при различных увеличениях. Изображение в темном поле (рис. 1C) демонстрирует наличие большого количества наночастиц размером около 20 нм в отожженных образцах. Выбранная картина электронной дифракции показала дифракционные кольца для (1 1 0) и (2 0 0) фазы α -Fe, как показано на вставке к рисунку 1C. Изображение HRTEM отожженных лент продемонстрировало наночастицы размером около 20 нм, внедренные в аморфную матрицу, как показано на рисунке 1D. Картина БПФ, связанная с рисунком 1D, показывает поликристаллическое дифракционное кольцо и диффузное аморфное кольцо. Микроструктуры, идентифицированные с помощью ПЭМ, хорошо согласовывались с результатами рентгеноструктурного анализа.
Микроструктуры, идентифицированные с помощью ПЭМ, хорошо согласовывались с результатами рентгеноструктурного анализа.
Измерения магнитного гистерезиса с использованием следующей процедуры для различных диапазонов поля сканирования H FR от ± 0,1 до ± 70 кЭ были выполнены при 300 К. Для каждого H FR данные были получается в обычной последовательности: 0 →+ H FR →− H FR (нисходящая ветвь) →+ H FR ветвь (окончание 90c FR ветвь) Кроме того, перед каждым измерением магнит размагничивали в режиме колебаний от 7 Тл при 350 К для устранения остаточной намагниченности в образце и магните. На рис. 2 показан ряд нормированных петель намагниченности отожженного Fe 9.0085 73,5 Cu 1 Nb 3 Si 13,5 B 9 , которые увеличены в центральной части для лучшего понимания. Полная петля, измеренная в соответствующих диапазонах поля, показана на дополнительном рисунке S1. На рисунке 2А мы ясно наблюдаем явление перевернутой петли гистерезиса с очевидной отрицательной остаточной намагниченностью для H FR = 3000 Э. Стрелки, приклеенные к кривой, указывают направление переключения магнитного поля. Перевернутая петля гистерезиса с отрицательной остаточной намагниченностью представляет собой петлю по часовой стрелке, что является очевидным отличием от нормальной петли гистерезиса с положительной остаточной намагниченностью и циклом против часовой стрелки. Коэрцитивная сила составляет 12,86 Э и −90,67 Э для нисходящей (HCdes) и восходящей (HCasc) ветвей соответственно. Чистая коэрцитивная сила, определяемая как Hc = HCasc-HCdes, составляет -22,53 Э.
На рисунке 2А мы ясно наблюдаем явление перевернутой петли гистерезиса с очевидной отрицательной остаточной намагниченностью для H FR = 3000 Э. Стрелки, приклеенные к кривой, указывают направление переключения магнитного поля. Перевернутая петля гистерезиса с отрицательной остаточной намагниченностью представляет собой петлю по часовой стрелке, что является очевидным отличием от нормальной петли гистерезиса с положительной остаточной намагниченностью и циклом против часовой стрелки. Коэрцитивная сила составляет 12,86 Э и −90,67 Э для нисходящей (HCdes) и восходящей (HCasc) ветвей соответственно. Чистая коэрцитивная сила, определяемая как Hc = HCasc-HCdes, составляет -22,53 Э.
РИСУНОК 2 . Серия нормированных петель M ( H ), увеличенных вблизи начала координат для различных диапазонов поля сканирования нанокристаллического Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 at стрелки, прикрепленные к кривой, представляют направление развертки поля. (A) Normalized M ( H ) loops for H FR = 3000 Oe of nanocrystalline Fe 73.5 Cu 1 Nb 3 Si 13.5 B 9 sample . Можно отчетливо наблюдать явление перевернутой петли гистерезиса. (B–E) Петли гистерезиса, измеренные при различных диапазонах поля сканирования. При низких полях сканирования обратная петля гистерезиса отсутствует, как показано на (B) , а для более высоких полей сканирования на (C–E) , цикл перевернут.
(A) Normalized M ( H ) loops for H FR = 3000 Oe of nanocrystalline Fe 73.5 Cu 1 Nb 3 Si 13.5 B 9 sample . Можно отчетливо наблюдать явление перевернутой петли гистерезиса. (B–E) Петли гистерезиса, измеренные при различных диапазонах поля сканирования. При низких полях сканирования обратная петля гистерезиса отсутствует, как показано на (B) , а для более высоких полей сканирования на (C–E) , цикл перевернут.
Однако кривая намагничивания не имеет гистерезисного поведения и почти перекрывается для разных H FR при малых полях сканирования (≤500 Э). Между тем, явление инверсии петли гистерезиса отсутствовало, как видно из рисунка 2В. Кроме того, кривые намагничивания в других более высоких диапазонах поля сканирования (≥1000 Э) показаны на рисунке 2C,E. Начинает наблюдаться поведение перевернутой петли гистерезиса, и соответствующие значения коэрцитивной силы, включая HCdes и HCasc, очень малы, когда диапазон поля сканирования составляет 1000 Э, как показано на рисунке 2C. С увеличением диапазона поля сканирования явление перевернутой петли гистерезиса становится яснее, и коэрцитивная сила постепенно увеличивается. Когда поле сканирования превышает 50 кЭ, кривые намагничивания почти перекрываются, а коэрцитивная сила почти постоянна (≈72 Э). Результаты петель гистерезиса для аморфных образцов на основе Fe также показали результаты, аналогичные результатам для нанокристаллических образцов (см. Дополнительный рисунок S2). Это указывало на то, что происхождение перевернутой петли гистерезиса может не возникать из-за структурных неоднородностей в аморфных сплавах, как предполагалось в предыдущих отчетах (Эшо, 19).76; Цудзимото и Сакураи, 1983 г.; Ошеа и Аль-Шариф, 1994 г.; Ян и Сюй, 1996 г.; Гу и др., 2014).
Начинает наблюдаться поведение перевернутой петли гистерезиса, и соответствующие значения коэрцитивной силы, включая HCdes и HCasc, очень малы, когда диапазон поля сканирования составляет 1000 Э, как показано на рисунке 2C. С увеличением диапазона поля сканирования явление перевернутой петли гистерезиса становится яснее, и коэрцитивная сила постепенно увеличивается. Когда поле сканирования превышает 50 кЭ, кривые намагничивания почти перекрываются, а коэрцитивная сила почти постоянна (≈72 Э). Результаты петель гистерезиса для аморфных образцов на основе Fe также показали результаты, аналогичные результатам для нанокристаллических образцов (см. Дополнительный рисунок S2). Это указывало на то, что происхождение перевернутой петли гистерезиса может не возникать из-за структурных неоднородностей в аморфных сплавах, как предполагалось в предыдущих отчетах (Эшо, 19).76; Цудзимото и Сакураи, 1983 г.; Ошеа и Аль-Шариф, 1994 г.; Ян и Сюй, 1996 г.; Гу и др., 2014).
Поскольку стандартный образец Pd является парамагнитным материалом, кривая намагничивания должна представлять собой прямую линию, проходящую через начало координат и не имеющую гистерезиса. Для дальнейшего изучения причины перевернутой петли гистерезиса в наших образцах были также измерены петли гистерезиса стандартного образца Pd, следуя той же процедуре, что и для сплавов Finemet при 300 К. На рис. 3 показаны M ( H ) увеличенные петли вблизи начала координат для различных диапазонов поля сканирования стандартного образца Pd, а полные петли, измеренные в соответствующих диапазонах полей, на вставке. Мы можем ясно видеть, что перевернутая петля гистерезиса отсутствует при малых полях сканирования (≤ 500 Э), как показано на рисунке 3А. В то время как для более высоких диапазонов поля сканирования (≥ 1000 Э) петли инвертируются (см. рисунки 3B, C). Когда H FR = 3000 Э, коэрцитивные силы составляют 11 Э и -11,3 Э для нисходящей (HCdes) и восходящей (HCasc) ветвей соответственно. Чистая коэрцитивная сила Hc составляет −22,3 Э, что очень близко к результатам для нашего образца сплава.
Для дальнейшего изучения причины перевернутой петли гистерезиса в наших образцах были также измерены петли гистерезиса стандартного образца Pd, следуя той же процедуре, что и для сплавов Finemet при 300 К. На рис. 3 показаны M ( H ) увеличенные петли вблизи начала координат для различных диапазонов поля сканирования стандартного образца Pd, а полные петли, измеренные в соответствующих диапазонах полей, на вставке. Мы можем ясно видеть, что перевернутая петля гистерезиса отсутствует при малых полях сканирования (≤ 500 Э), как показано на рисунке 3А. В то время как для более высоких диапазонов поля сканирования (≥ 1000 Э) петли инвертируются (см. рисунки 3B, C). Когда H FR = 3000 Э, коэрцитивные силы составляют 11 Э и -11,3 Э для нисходящей (HCdes) и восходящей (HCasc) ветвей соответственно. Чистая коэрцитивная сила Hc составляет −22,3 Э, что очень близко к результатам для нашего образца сплава.
РИСУНОК 3 . Петли M ( H ), увеличенные вблизи начала координат, для различных диапазонов полей сканирования стандартного образца Pd при 300 К. Стрелки, приклеенные к кривой, обозначают направление развертки поля. На вставке показана полная петля, измеренная в соответствующих диапазонах поля. (A) При малых полях сканирования инвертированная петля гистерезиса отсутствует для стандартного образца Pd. (B,C) M ( H ) петли для более высоких полей сканирования, петля инвертируется.
Петли M ( H ), увеличенные вблизи начала координат, для различных диапазонов полей сканирования стандартного образца Pd при 300 К. Стрелки, приклеенные к кривой, обозначают направление развертки поля. На вставке показана полная петля, измеренная в соответствующих диапазонах поля. (A) При малых полях сканирования инвертированная петля гистерезиса отсутствует для стандартного образца Pd. (B,C) M ( H ) петли для более высоких полей сканирования, петля инвертируется.
Для сравнения, результирующая коэрцитивная сила Hc отожженного образца и стандартного образца Pd построена как функция диапазонов поля сканирования H FR на рисунке 4. Суммарная коэрцитивная сила почти равна нулю, когда диапазон приложенного магнитного поля менее 1000 Э. Однако результирующая коэрцитивная сила быстро увеличивается, когда диапазон магнитного поля превышает 1000 Э, и она почти достигает насыщения при максимальном поле 50 КОэ. H c1 , определяемая как результирующая разница коэрцитивных сил между отожженным образцом и образцом Pd, составляет всего несколько Э.
H c1 , определяемая как результирующая разница коэрцитивных сил между отожженным образцом и образцом Pd, составляет всего несколько Э.
РИСУНОК 4 . Чистая коэрцитивная сила H c и H c1 как функция диапазонов поля сканирования H FR , используемых в измерениях петли гистерезиса.
Поскольку стандартный образец Pd является парамагнитным материалом, отклонение между кривой намагничивания и началом координат может отражать остаточную намагниченность сверхпроводящего магнита, вызванную пиннингом вихря. Из рисунка 3 видно, что когда приложенное магнитное поле превышает 1 кОЭ, а затем магнитное поле удаляется, сверхпроводящий магнит будет иметь отрицательную остаточную намагниченность, и эта отрицательная остаточная намагниченность будет увеличиваться с увеличением приложенного магнитного поля. даже если обработка вибрационным размагничиванием проводится в режиме колебаний от 7T перед каждым измерением. Это указывает на то, что результаты измерения кривой намагничивания могут иметь погрешности для образцов с результирующей коэрцитивной силой менее десятков Э, что не следует игнорировать при приложенном магнитном поле более 1000 Э. Чтобы дополнительно подтвердить наш вывод, мы также выполнили магнитные измерения сплава AlNiCo с большой коэрцитивной силой ~ 1300 Э, используя ту же последовательность, которая намного больше, чем остаточная намагниченность сверхпроводящего магнита после приложения сильного магнитного поля и последующего его удаления. Кривая намагничивания сплава AlNiCo при 300 К представляет собой нормальную петлю гистерезиса с коэрцитивной силой 1 333 Э для H FR = 7 T (более подробную информацию см. Дополнительный рисунок S3). Кроме того, мы отметили, что обменный уклон | H EB | почти равна коэрцитивной силе |HCdes| или |HCasc| для перевернутой петли гистерезиса при той же температуре. Следовательно, ранее сообщавшееся смещение обмена (Maity et al.
Это указывает на то, что результаты измерения кривой намагничивания могут иметь погрешности для образцов с результирующей коэрцитивной силой менее десятков Э, что не следует игнорировать при приложенном магнитном поле более 1000 Э. Чтобы дополнительно подтвердить наш вывод, мы также выполнили магнитные измерения сплава AlNiCo с большой коэрцитивной силой ~ 1300 Э, используя ту же последовательность, которая намного больше, чем остаточная намагниченность сверхпроводящего магнита после приложения сильного магнитного поля и последующего его удаления. Кривая намагничивания сплава AlNiCo при 300 К представляет собой нормальную петлю гистерезиса с коэрцитивной силой 1 333 Э для H FR = 7 T (более подробную информацию см. Дополнительный рисунок S3). Кроме того, мы отметили, что обменный уклон | H EB | почти равна коэрцитивной силе |HCdes| или |HCasc| для перевернутой петли гистерезиса при той же температуре. Следовательно, ранее сообщавшееся смещение обмена (Maity et al. , 2017; Ghising et al., 2020)) также может быть вызвано остаточной намагниченностью сверхпроводящего магнита.
, 2017; Ghising et al., 2020)) также может быть вызвано остаточной намагниченностью сверхпроводящего магнита.
Выводы
Таким образом, инверсия петли гистерезиса наблюдалась в нанокристаллическом Fe 73.5 Cu 1 Nb 3 Si 13.5 B 9 alloy ribbons and amorphous Fe 73.5 Cu 1 Nb 3 Si 13.5 B 9 alloy ribbons at room temperature. Мы доказываем, что явление полностью перевернутой петли гистерезиса вызвано остаточной намагниченностью сверхпроводящего магнита, а не эффектами неоднородности. Подчеркнем, что существуют небольшие различия в остаточной намагниченности для разных устройств MPMS 3. Наши результаты показывают, что результаты кривой намагничивания могут иметь ошибки для образцов с результирующей коэрцитивной силой менее десятков Э, которые нельзя игнорировать, когда приложенное магнитное поле превышает 1000 Э с использованием MPMS 3.
Заявление о доступности данных
Первоначальные материалы, представленные в исследовании, включены в статью/дополнительный материал; дальнейшие запросы можно направлять соответствующему автору.
Вклад авторов
PPS провел эксперименты и написал рукопись; YTW провела анализ данных; BAS задумал данные и написал рукопись.
Финансирование
Это исследование было поддержано Гуандунским крупным проектом фундаментальных и прикладных фундаментальных исследований Китая (грант № 2020B1515120092 и 2019B030302010), Национальный план ключевых исследований и разработок (грант № 2018YFA0703603), Национальный фонд естественных наук Китая (NSFC) (гранты № 51822107, 117 и 61888102), Программа стратегических приоритетных исследований Китайской академии наук наук (грант № XDB30000000) и Пекинской муниципальной комиссии по науке и технологиям (№ Z1 007219006). Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. Все претензии, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций или издателя, редакторов и рецензентов. Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fmats.2021.765427/full#дополнительный материал. Ахарони, А. (1994). Обменная анизотропия в пленках и проблема перевернутых петель гистерезиса. J. Appl. физ. 76, 6977–6979. doi:10.1063/1.358061 Полный текст CrossRef | Google Scholar Аллег С., Картут С., Ибрир М., Аззаза С., Фенинече Н. Э. и Сунол Дж. Дж. (2013). Магнитные, структурные и термические свойства порошков типа Finemet, полученных механическим сплавлением. J. Phys. хим. Сол. 74, 550–557. doi:10.1016/j.jpcs.2012.12.002 Полный текст CrossRef | Google Scholar Айерс, Дж. Д., Харрис, В. Г., Спраг, Дж. А., Элам, В. Т., и Джонс, Х. Полный текст CrossRef | Академия Google Баркин, Л.Ф., Сал, Дж.К.Г., Горриа, П., Гаритаонандия, Дж.С., и Барандиаран, Дж.М. (1998). Кристаллическая структура и магнитное поведение нанокристаллических сплавов Fe-Nb-Cu-Si-B, изученных методом дифракции ситунейтронов. J. Phys. Конденс. Материя 10, 5027–5038. doi:10.1088/0953-8984/10/23/009 CrossRef Full Text | Google Scholar Демирчи Э., Озтюрк М., Пишкин Х. и Акдоган Н. (2020). Зависящие от угла инвертированные петли гистерезиса в обменном смещении [Co/Pt] 5 /IrMn Тонкая пленка. J. Supercond Nov Magn. 33, 721–726. doi:10.1007/s10948-019-05235-0 Полный текст CrossRef | Google Scholar Демиртас С., Хоссу М. Р., Арикан М. CrossRef Полный текст | Google Scholar Эшо С. (1976). Аномальные магнитооптические петли гистерезиса распыленных пленок Gd-Co. япон. Дж. Заявл. физ. 15, 93. doi:10.7567/jjaps.15s1.93 CrossRef Full Text | Google Scholar Fish, GE (1990). Мягкие магнитные материалы. Проц. IEEE 78, 947–972. doi:10.1109/5.56909 Полный текст CrossRef | Google Scholar Фуджи Х., Ярдли В. А., Мацудзаки Т. и Цурэкава С. (2008). Нанокристаллизация Fe 73,5 Si 13,5 B 9 Nb 3 Cu 1 Магнитомягкий сплав из аморфного прекурсора в магнитном поле. Дж. Матер. науч. 43, 3837–3847. doi:10.1007/s10853-007-2220-7 Полный текст CrossRef | Google Scholar Гешев Дж. Полный текст CrossRef | Академия Google Гисинг П., Самантарай Б. и Хоссейн З. (2020). Спиновые неоднородности на границе раздела и обратная петля гистерезиса в La 0,7 Sr 0,3 MnO 3/SrTiO 3. Phys. B 101, 024408. doi:10.1103/physrevb.101.024408 CrossRef Полный текст | Google Scholar Горриа П., Гаритаонандия Дж. С. и Барандиаран Дж. М. (1996). Структурные и магнитные изменения в аморфных сплавах FeNbCuSiB в процессе кристаллизации. J. Phys. Конденс. Материя 8, 5925–5939. doi:10.1088/0953-8984/8/32/012 Полный текст CrossRef | Google Scholar Горриа П., Прида В. М., Техедор М., Эрнандо Б. и Санчес М. Л. (2001). Корреляция между структурой, магнитными свойствами и эффектом MI в процессе нанокристаллизации сплавов типа FINEMET. Полный текст CrossRef | Google Scholar Gu, S., He, W., Zhang, M., Zhuang, T., Jin, Y., EIBidweihy, H., et al. (2014). Физическое обоснование отрицательной остаточной намагниченности гомогенных наночастиц. Scientific Rep. 4, 6267. doi:10.1038/srep06267 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar Хофманн Б. и Кронмюллер Х. (1996). Индуцированная напряжением магнитная анизотропия в нанокристаллическом сплаве FeCuNbSiB. J. Магнетизм Magn. Матер. 152, 91–98. doi:10.1016/0304-8853(95)00447-5 Полный текст CrossRef | Google Scholar Хофманн Б., Райнингер Т. и Кронмюллер Х. (1992). Влияние микроструктуры на процессы намагничивания в нанокристаллическом Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 . Физ. Стат. Сол. (А) 134, 247–261. doi:10.1002/pssa. Полный текст CrossRef | Google Scholar Ким Д., Ким К., Ким К. О., Юн С. С., Нака М., Цунода М. и др. (2006). Характеристики отрицательной коэрцитивной силы в антиферромагнитных связанных жестких/мягких мультислоях. J. Магнетизм Magn. Матер. 304, Е356. doi:10.1016/j.jmmm.2006.01.198 Полный текст CrossRef | Академия Google Кумар Р., Саранги С. Н., Самал Д. и Хоссейн З. (2021). Смещение положительного обмена и обратная петля гистерезиса в Y 3 Fe 5 O 12/Gd 3 Ga 5 O 12. Phys. Rev. B 103, 064421. doi:10.1103/physrevb.103.064421 CrossRef Полный текст | Google Scholar Лутес О., Холмен Дж., Койер Р. и Адланд О. (1977). Инвертированные и смещенные петли в аморфных пленках Gd-Co. IEEE Trans. Магн. 13, 1615–1617. doi:10.1109/tmag.1977.1059654 Полный текст CrossRef | Академия Google Майти, Т., Кепапцоглу, Д., Шмидт, М., Рамассе, К., и Рой, С. (2017). Наблюдение полной инверсии петли гистерезиса в бимодальной магнитной тонкой пленке. CrossRef Полный текст | Google Scholar Маджумдар Б. и Ахтар Д. (2005). Структура и коэрцитивная сила нанокристаллических сплавов Fe-Si-B-Nb-Cu. Бык. Матер. науч. 28, 395–399. doi:10.1007/bf02711225 Полный текст CrossRef | Академия Google Окоси С.-и., Ходзуми Т. и Хашимото К. (2001). Проектирование и изготовление объемного магнита с перевернутой петлей гистерезиса. Физ. Rev. B 64, 132404. doi:10.1103/physrevb.64.132404 CrossRef Full Text | Google Scholar Оферден Л., Билитевски Т., Хорнунг Дж., Херрманнсдорфер Т., Самарцис А., Ислам А. Т. М. Н. и др. (2018). Инвертированный гистерезис и отрицательная остаточная намагниченность в однородном антиферромагнетике. Физ. Ред. B 98, 180403. doi:10.1103/physrevb.98.180403 Полнотекстовая перекрестная ссылка | Google Scholar Ошеа М.Дж. и Альшариф А.Л. (1994). Инвертированный гистерезис в магнитных системах с обменом интерфейсами. CrossRef Full Text | Google Scholar Полак С., Нобель М., Гроссингер Р. и Туртелли Р. С. (1994). Развитие нанокристаллов Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 : Магнетизм и структурный беспорядок. J. Магнетизм Magn. Матер. 134, 6977. doi:10.1016/0304-8853(94)-5 CrossRef Полный текст | Google Scholar Солдатов И., Андрей П. и Шефер Р. (2020). Инвертированный гистерезис, магнитные домены и гистероны. IEEE Magnetics Lett. 11, 2405805. doi:10.1109/lmag.2020.3035136 CrossRef Full Text | Google Scholar Сонг К., Цуй Б., Ю Х.Ю. и Пан Ф. (2013). Полностью перевернутые петли гистерезиса: эффекты неоднородности или экспериментальные артефакты. J. Appl. физ. 114, 183906. doi:10.1063/1.4830011 CrossRef Full Text | Google Scholar Таканаши К., Курокава Х. и Фухимори Х. (1993). Новая петля гистерезиса и непрямая обменная связь в многослойных пленках Co/Pt/Gd/Pt. Полный текст CrossRef | Google Scholar Тогами, Ю. (1978). Стабильность небольших битов, записанных в тонких аморфных пленках GdCo. Заяв. физ. лат. 32, 673–675. doi:10.1063/1.89851 Полный текст CrossRef | Google Scholar Цудзимото Х. и Сакураи Ю. (1983). Температурная зависимость аномальной петли в двухслойной аморфной пленке GdCo. япон. Дж. Заявл. физ. 22, 1845–1850 гг. doi:10.1143/jjap.22.1845 Полный текст CrossRef | Google Scholar Валвидарес С. М., Мартин Дж. И., Альварес-Прадо Л. М., Пейн Д., Ачер О., Суран Г. и др. (2002). Инвертированные петли гистерезиса в отожженных аморфных тонких пленках Co-Nb-zr и Co-Fe-Mo-Si-B. J. Магнетизм Magn. Матер. 242–245, 169–172. doi:10.1016/s0304-8853(01)01195-7 Полный текст CrossRef | Google Scholar Ван Тхо, Л., Ким, К.Г., и Ким, К.О. (2008). Исследование отрицательной коэрцитивной силы при однослойном формировании магнитомягких и магнитотвердых материалов. Полный текст CrossRef | Google Scholar Ву, Ю. З., Донг, Г. С., и Джин, X. Ф. (2001). Отрицательная магнитная остаточная намагниченность в Co/Mn/Co, выращенном на GaAs(001). Физ. Rev. B 64 (5), 214406. doi:10.1103/physrevb.64.214406 CrossRef Полный текст | Google Scholar Ян X. и Сюй Ю. (1996). Отрицательная остаточная намагниченность в магнитных наноструктурах. J. Appl. физ. 79, 6013. doi:10.1063/1.362137 CrossRef Full Text | Google Scholar Юн Джэ, Н., и Лим, С. Х. (2011). Отрицательная остаточная намагниченность в однодоменной частице с двумя одноосными анизотропиями. Заяв. физ. лат. 99, 092503. doi:10.1063/1.3633107 Полный текст перекрестной ссылки | Google Scholar Zhang, X.Y., Zhang, F.X., Zhang, J.W., Yu, W., Zhang, M., Zhao, J.H., et al. (1998). Влияние давлений на процесс кристаллизации аморфного сплава Fe 73,5 Cu 1 Nb 3 Si 13,5 B 9 . Полный текст CrossRef | Google Scholar Ziese, M., Vrejoiu, I., and Hesse, D. (2010). Инвертированный гистерезис и гигантское обменное смещение в сверхрешетках La0,7Sr0,3MnO3/SrRuO3. Заявл. физ. лат. 97, 052504. doi:10.1063/1.3470101 CrossRef Full Text | Google Scholar 1. Bonate PL, Howard DR. Глава 6: Роль доклинической фармакокинетики в лекарствах
разработка. В: Bonate PL, Howard DR, редакторы. Фармакокинетика в разработке лекарств. Арлингтон, Вирджиния: AAPS Press; 2004. с. 146. [Google Scholar] 2. Girard P, Boissel JP. Гистерезис или протерезис по часовой стрелке. Журнал фармакокинетики и биофармацевтики. 1989;17:401–402. [PubMed] [Google Scholar] 3. Шейнер Л.Б., Стански Д.Р., Возех С., Миллер Р.Д., Хэм Дж. Одновременное моделирование фармакокинетики и фармакодинамики:
применение к d-тубокурарину. 4. Remington JP, Gennaro AR. Ремингтон: Наука и практика фармации. 21 изд. Истон, Пенсильвания: Mack Publishing; 2006. [Google Scholar] 5. Campbell DB. Использование кинетико-динамических взаимодействий в оценке
наркотики. Психофармакология (Берл) 1990;100:433–450. [PubMed] [Google Scholar] 6. Квон Ю. Справочник по основным фармакокинетике, фармакодинамике и лекарствам.
метаболизм для промышленных ученых. Нью-Йорк: Kluwer Academic/Plenum Publishers; 2001. [Google Scholar] 7. Бауэр Л.А. Глава 8: Клиническая фармакокинетика и
фармакодинамика. В: Talbert RL, DiPiro JT, Matzke GR, Posey LM, Wells BG, Yee GC, редакторы. Фармакотерапия: патофизиологический подход. Нью-Йорк: Макгроу-Хилл; 2011. [Google Академия] 8. Гупта С.К., Хван С.С., Бенет Л.З., Гамблтон М. Интерпретация и использование данных о воздействии и концентрации
собранные в фармакокинетических и фармакодинамических исследованиях in vivo
исследование. 9. Pedraz JL, Calvo B, Smithers JA, Thompson GA. Фармакокинетико-фармакодинамическое моделирование: белок, зависящий от времени
привязка — альтернативная интерпретация по часовой стрелке и против часовой стрелки
гистерезис. Журнал фармацевтических наук. 1992;81:232–236. [PubMed] [Google Scholar] 10. Мехвар Р. Стереохимические соображения в фармакодинамическом моделировании
хиральные препараты. Журнал фармацевтических наук. 1992; 81: 199–200. [PubMed] [Google Scholar] 11. Miyamoto M, Tsukune T, Hori S, Hayashi T, Natsume H, Sugibayashi K, Morimoto Y. Оценка скорости всасывания альфа-человеческого предсердного натрийуретика
пептид из профиля плазмы и диуретический эффект после интраназального
введение крысам. Биофармацевтика и утилизация лекарств. 2001; 22: 137–146. [PubMed] [Академия Google] 12. Ким Э., Хоус О.Д., Ким Б.Х., Чон Дж.М., Ли Дж.С., Джанг И.Дж., Шин С.Г., Туркхаймер Ф. 13. Song J, Li J, Jin Y, Wang H, Zheng S, Gao J. Фармакокинетико-фармакодинамическая оценка основных
компонент астрагалозид IV на иммуномодулирующее действие Ю-пин-фэн
рецепт. Eur J Европейский журнал метаболизма и фармакокинетики лекарственных средств. 2013 [PubMed] [Академия Google] 14. Jia J, Dong C, Zhang W, Cui Y, Liu J. Оценка фармакокинетических и фармакодинамических взаимосвязей.
для пероральных гранул атенолола пролонгированного действия у крыс. Джей Фарм Биомед Анал. 2011;55:342–348. [PubMed] [Google Scholar] 15. Farenc C, Lefrant JY, Audran M, Bressolle F. Фармакокинетическое-фармакодинамическое моделирование атракурия в
пациентов интенсивной терапии. 16. Ohtani H, Taninaka C, Hanada E, Kotaki H, Sato H, Sawada Y, Iga T. Сравнительный фармакодинамический анализ удлинения интервала Q-T.
индуцируется макролидами кларитромицином, рокситромицином и азитромицином.
крысы. Антимикробные препараты и химиотерапия. 2000;44:2630–2637. [Бесплатная статья PMC] [PubMed] [Google Scholar] 17. Балерио Г.Н., Рубио М.С. Фармакокинетико-фармакодинамическое моделирование антиноцицептивного
Действие баклофена на мышей. Европейский журнал метаболизма и фармакокинетики лекарственных средств. 2002; 27: 163–169. [PubMed] [Google Scholar] 18. Кобаяши Х., Кобаяши С. Взаимосвязь между концентрацией в плазме и антигипертензивным действием.
действие дигидропиридинового антагониста кальция бенидипина на
крысы. Журнал фармации и фармакологии. 1997;49:1200–1204. [PubMed] [Академия Google] 19. Atsumi M, Kawakami J, Sugiyama E, Kotaki H, Sawada Y, Sato H, Yamada Y, Iga T. 20. Yagi N, Kiuchi T, Satoh H, Ishikawa Y, Takada M, Sekikawa H. Биодоступность и диуретический эффект после приема
отсроченные капсулы буметанида у людей. Биол Фарм Бык. 1999;22:275–280. [PubMed] [Google Scholar] 21. Koike Y, Mineshita S, Mizoguchi H, Nomura Y. Фармакокинетика и фармакодинамика буназозина у пациентов
с почечной недостаточностью. Американский журнал терапии. 1999; 6: 83–89. [PubMed] [Google Scholar] 22. Fuchs B, Breithaupt-Grogler K, Belz GG, Roll S, Malerczyk C, Herrmann V, Spahn-Langguth H, Mutschler E. Сравнительная фармакодинамика и фармакокинетика кандесартана
и лозартан у мужчин. Журнал фармации и фармакологии. 2000;52:1075–1083. [PubMed] [Академия Google] 23. 24. Brazzell RK, Khoo KC, Szuna AJ, Sandor D, Aogaichi K, Wills RJ. Фармакокинетика и фармакодинамика внутривенного цибензолина
у обычных добровольцев. Журнал клинической фармакологии. 1985;25:418–423. [PubMed] [Google Scholar] 25. Porchet HC, Piletta P, Dayer P. Фармакокинетико-фармакодинамическое моделирование эффектов
клонидин на болевой порог, артериальное давление и слюноотделение
поток. Европейский журнал клинической фармакологии. 1992; 42: 655–661. [PubMed] [Google Scholar] 26. Фукудо М., Яно И., Масуда С., Окуда М., Инуи К. Различное ингибирующее действие такролимуса и циклоспорина на
активность кальциневринфосфатазы. Журнал фармакологии и экспериментальной терапии. 27. Belldina EB, Huang MY, Schneider JA, Brundage RC, Tracy TS. Стационарная фармакокинетика и фармакодинамика цистеамина
битартрат у детей с нефропатическим цистинозом. Британский журнал клинической фармакологии. 2003; 56: 520–525. [Бесплатная статья PMC] [PubMed] [Google Scholar] 28. Rowley HL, Kulkarni R, Gosden J, Brammer R, Hackett D, Heal DJ. Лисдексамфетамин и d-амфетамин с немедленным высвобождением – различия
в фармакокинетических/фармакодинамических взаимосвязях, выявленных полосатым телом
микродиализ у свободноподвижных крыс с одновременным определением
концентрация препарата в плазме крови и двигательная активность. Нейрофармакология. 2012;63:1064–1074. [PubMed] [Академия Google] 29. Torres-Lopez JE, Lopez-Munoz FJ, Castaneda-Hernandez G, Flores-Murrieta FJ, Granados-Soto V. Фармакокинетико-фармакодинамическое моделирование антиноцицептивного
Влияние диклофенака на крыс. Журнал фармакологии и экспериментальной терапии. 30. Lötsch J, Kettenmann B, Renner B, Drover D, Brune K, Geisslinger G, Kobal G. Популяционная фармакокинетика перорального диклофенака с быстрым высвобождением в
здоровые добровольцы: отношение к фармакодинамике при экспериментальной боли
модель. Фармацевтические исследования. 2000; 17:77–84. [PubMed] [Академия Google] 31. Le Coz F, Funck-Brentano C, Morell T, Ghadanfar MM, Jaillon P. Фармакокинетическое и фармакодинамическое моделирование эффектов
пероральное и внутривенное введение дофетилида на желудочки
реполяризация. Клиническая фармакология и терапия. 1995; 57: 533–542. [PubMed] [Google Scholar] 32. Имбимбо Б.П., Личини М., Скеттино М., Моска А., Онелли Э., Зекка Л., Джустина А. Связь между фармакокинетикой и фармакодинамикой
эптастигмина у молодых здоровых добровольцев. Журнал клинической фармакологии. 1995;35:285–290. [PubMed] [Google Scholar] 33. Kreilgaard M, Smith DG, Brennum LT, Sanchez C. Прогноз клинического ответа на основе
фармакокинетические/фармакодинамические модели обратного захвата 5-гидрокситриптамина
ингибиторы у мышей. 34. Ларссон Р., Карлберг Б.Е., Гелин А., Аберг Дж., Регард К.Г. Острая и устойчивая фармакокинетика и антигипертензивное действие
Эффекты фелодипина у пациентов с нормальной и нарушенной функцией почек
функция. Журнал клинической фармакологии. 1990;30:1020–1030. [PubMed] [Google Scholar] 35. Формелли Ф., Кавадини Э., Лукш Р., Гаравента А., Аппьерто В., Персиани С. Взаимосвязь между фармакокинетикой и фармакодинамикой
снижение уровня фенретинида и ретинола в плазме при нейробластоме
пациенты. Химиотерапия рака и фармакология. 2010;66:993–998. [PubMed] [Google Scholar] 36. Вьяс Ф.И., Пракаш С., Сингх А.Дж. Удлинение интервала QTc фексофенадином у здорового человека
добровольцев и его корреляция с уровнями фексофенадина в плазме: A
демонстрация гистерезиса против часовой стрелки. Индийский журнал фармакологии. 2010; 42:366–369.. [PMC free article] [PubMed] [Google Scholar] 37. 38. Alvan G, Paintaud G, Eckernas SA, Grahnen A. Несоответствие между биодоступностью, оцененной по моче.
восстановление фуросемида и общего диуретического эффекта. Британский журнал клинической фармакологии. 1992; 34:47–52. [Бесплатная статья PMC] [PubMed] [Google Scholar] 39. Yagi N, Kiuchi T, Satoh H, Terashima Y, Kenmotsu H, Sekikawa H, Takada M. Биодоступность и диуретический эффект фуросемида после
введение таблеток и капсул пролонгированного действия человеку
предметы. Биол Фарм Бык. 1996; 19: 616–622. [PubMed] [Google Scholar] 40. Abou-Auda HS. Сравнительная фармакокинетика и фармакодинамика фуросемида
в ближневосточных и азиатских субъектах. Int J Clin Pharmacol Ther. 1998; 36: 275–281. [PubMed] [Google Scholar] 41. Wakelkamp M, Alvan G, Scheinin H, Gabrielsson J. 42. Райт М.Р., Дэвис Н.М., Джамали Ф. Токсикокинетика вызванной индометацином кишечной
крыса. Фармакол рез. 1997; 35: 499–504. [PubMed] [Google Scholar] 43. Huang XH, Li J, Qiu FR, Xie HT, Huang JH, Li JC, Zheng QS. PK-PD моделирование ирбесартана у здоровых взрослых добровольцев из Китая
в нестационарных условиях. Европейский журнал метаболизма и фармакокинетики лекарственных средств. 2006; 31: 259–264. [PubMed] [Академия Google] 44. Моррисон Р.А., Виганд У.В., Янхен Э., Хохманн Д., Бехтольд Х., Мейнерц Т., Фунг Х.Л. Кинетика и динамика изосорбида динитрата после внутривенного,
сублингвальное и чрескожное введение при стенокардии. Клиническая фармакология и терапия. 1983; 33: 747–756. [PubMed] [Google Scholar] 45. Carrara V, Porchet H, Dayer P. Влияние скорости ввода на (+/−)-исрадипин
гемодинамика и зависимость концентрация-эффект у здоровых
волонтеры. 46. Quinney SK, Galinsky RE, Jiyamapa-Serna VA, Chen Y, Hamman MA, Hall SD, Kimura RE. Гидроксиитраконазол, образующийся при первом прохождении через кишечник.
метаболизм итраконазола, контролирует временную динамику печеночного CYP3A
ингибирование и биодоступность итраконазола у крыс. Метаболизм и распределение лекарств: биологическая судьба
химические вещества. 2008;36:1097–1101. [PubMed] [Google Scholar] 47. Икава К., Шиматани Т., Хаято С., Морикава Н., Тадзума С. Фармакокинетические и фармакодинамические свойства лафутидина
после постпрандиального перорального приема у здоровых добровольцев: сравнение с
фамотидин. Биологический и фармацевтический вестник. 2007; 30:1003–1006. [PubMed] [Академия Google] 48. Poder P, Eha J, Sundberg S, Antila S, Heinpalu M, Loogna I, Planken U, Rantanen S, Lehtonen L. Фармакокинетические-фармакодинамические взаимосвязи внутривенных
и пероральный левосимендан у пациентов с тяжелой застойной сердечной недостаточностью
отказ. 49. Сандберг С., Антила С., Шейнин Х., Хайха М., Виртанен М., Лехтонен Л. Комплексная фармакокинетика и фармакодинамика романа
сенсибилизатор кальция левосимендан по оценке систолического времени
интервалы. Международный журнал клинической фармакологии и терапии. 1998;36:629–635. [PubMed] [Google Scholar] 50. Хуан М.Л., Ван Пир А., Вестенборгс Р., Де Костер Р., Хейкантс Дж., Янсен А.А., Зилич З., Вишер Х.В., Йонкман Дж.Х. Фармакокинетика нового нейролептика рисперидона и
реакция пролактина у здоровых людей. Клиническая фармакология и терапия. 1993; 54: 257–268. [PubMed] [Google Scholar] 51. Гупта С.К., Эллинвуд Э.Х., Никайдо А.М., Хизерли Д.Г. Одновременное моделирование фармакокинетических и фармакодинамических
свойства бензодиазепинов. Я: Лоразепам. Журнал фармакокинетики и биофармацевтики. 1990;18:89–102. [PubMed] [Google Scholar] 52. Гринблатт Д. 53. Аптон Р.Н., Хуан Ю.Ф., Мазер Л.Е., Дулетт Д.Дж. Взаимосвязь между миокардиальной кинетикой меперидина
и его влияние на сократительную способность миокарда: модельно-независимый анализ и
оптимальная региональная модель. Журнал фармакологии и экспериментальной терапии. 1999;290:694–701. [PubMed] [Google Scholar] 54. Lee SH, Kwon KI. Фармакокинетико-фармакодинамическое моделирование взаимосвязи
между сахароснижающим эффектом и концентрацией метформина в плазме
волонтеры. Архив фармацевтических исследований. 2004; 27:806–810. [PubMed] [Google Scholar] 55. Шафер С.Л., Варвел Дж.Р., Гронерт Г.А. Сравнение параметрического с полупараметрическим анализом
Зависимость концентрации от эффекта метокурина у собак и
свиньи. 56. Rosenkranz B, Winkelmann BR, Parnham MJ. Клиническая фармакокинетика молсидомина. Клиническая фармакокинетика. 1996; 30: 372–384. [PubMed] [Google Scholar] 57. Hoekman JD, Ho RJ. Усиленный анальгетический ответ после предпочтительной доставки
морфина и фентанила в обонятельный эпителий крыс. Анестезия и обезболивание. 2011;113:641–651. [Бесплатная статья PMC] [PubMed] [Google Scholar] 58. Van Crugten JT, Somogyi AA, Nation RL. Влияние почечной недостаточности, вызванной уранилнитратом, на морфин
расположение и антиноцицептивный ответ у крыс. Клиническая и экспериментальная фармакология и физиология. 2000; 27:74–79. [PubMed] [Google Scholar] 59. Shang GW, Liu DN, Yan LH, Cui XY, Zhang KP, Qi C, Chen J. Разница, связанная с модальностью ноцицептивного стимула в
Фармакокинетико-фармакодинамическое моделирование морфина в
крыса. Фармакол Биохим Поведение. 2006; 85: 464–473. 60. Castaneda-Hernandez G, Favari L, Hoyo-Vadillo C. Взаимосвязь между концентрацией напроксена в плазме и его
противовоспалительный эффект при экспериментальном гепатите. Арцнаймиттель-Форшунг. 1995; 45: 585–589.. [PubMed] [Google Scholar] 61. Нунан П.К., Уильямс Р.Л., Бенет Л.З. Дозозависимая фармакокинетика нитроглицерина после многократного
внутривенные инфузии у здоровых добровольцев. Журнал фармакокинетики и биофармацевтики. 1985; 13: 143–157. [PubMed] [Google Scholar] 62. Lee FW, Salmonson T, Benet LZ. Фармакокинетика и фармакодинамика нитроглицерина и его
Метаболиты динитрата у собак в сознании: внутривенная инфузия
исследования. Журнал фармакокинетики и биофармацевтики. 1993;21:533–550. [PubMed] [Google Scholar] 63. Woodworth JR, Howey DC, Bowsher RR. Установление профилей времени действия для обычного инсулина и инсулина НПХ
с помощью фармакодинамического моделирования. Уход за диабетом. 1994; 17:64–69. [PubMed] [Google Scholar] 64. 65. Chu KM, Hu OY, Shieh SM. Сердечно-сосудистый эффект и одновременный фармакокинетический и
фармакодинамическое моделирование пимобендана у здоровых людей в норме
предметы. Метаболизм и распределение лекарств: биологическая судьба
химические вещества. 1999; 27: 701–709. [PubMed] [Google Scholar] 66. Girard P, Saumet JL, Dubois F, Boissel JP. Фармакодинамическая модель гемодинамических эффектов пинацидила у
нормотензивные добровольцы. Европейский журнал клинической фармакологии. 1993;44:177–182. [PubMed] [Google Scholar] 67. Feng MR, Turluck D, Burleigh J, Lister R, Fan C, Middlebrook A, Taylor C, Su T. Микродиализ мозга и корреляция PK/PD прегабалина в
крысы. 68. Ludbrook GL, Upton RN, Grant C, Gray EC. Концентрации пропофола в мозге и крови после быстрого
внутривенная инъекция овцам и их взаимосвязь с церебральной
последствия. Анестезия и интенсивная терапия. 1996;24:445–452. [PubMed] [Google Scholar] 69. Hermann DJ, Egan TD, Muir KT. Влияние артериовенозной пробы на ремифентанил
фармакокинетика и фармакодинамика. Клиническая фармакология и терапия. 1999; 65: 511–518. [PubMed] [Google Scholar] 70. Lee DY, Lee KU, Kwon JS, Jang IJ, Cho MJ, Shin SG, Woo JI. Фармакокинетико-фармакодинамическое моделирование эффектов рисперидона
на электроэнцефалографии у здоровых добровольцев. Психофармакология. 1999; 144: 272–278. [PubMed] [Академия Google] 71. Хань Д.В., Парк К., Джанг С.Б., Керн С.Э. Моделирование влияния севофлюрана на скорректированное удлинение интервала QT:
фармакодинамический анализ. Анестезиология. 72. Нельсон М.В., Берчоу Р.С., Левитт П.А., Карети Д., Кесари Н., Шлик П., Галлоуэй М.П. Фармакокинетическое и фармакодинамическое моделирование L-дофа плазмы
концентрации и клинические эффекты при болезни Паркинсона после
Синемет. Клиническая нейрофармакология. 1989; 12: 91–97. [PubMed] [Академия Google] 73. Минемацу Т., Отани Х., Ямада Ю., Савада Ю., Сато Х., Ига Т. Количественная взаимосвязь между концентрацией в миокарде
такролимус и удлинение интервала QT у морских свинок:
фармакокинетическая/фармакодинамическая модель, включающая место неблагоприятного
эффект. Журнал фармакокинетики и фармакодинамики. 2001; 28: 533–554. [PubMed] [Google Scholar] 74. Stangier J, Su CA, van Heiningen PN, Meinicke T, van Lier JJ, de Bruin H, Tamminga WJ, Jonkman JH. Ингибирующее действие телмисартана на реакцию артериального давления
к стимуляции ангиотензином II. Журнал сердечно-сосудистой фармакологии. 2001; 38: 672–685. [PubMed] [Академия Google] 75. 76. Upton RN, Huang YF, Grant C, Gray EC, Ludbrook GL. Миокардиальная фармакокинетика тиопентала у овец после
краткосрочное введение: связь с тиопентал-индуцированным снижением
сократимость миокарда. Журнал фармацевтических наук. 1996;85:863–867. [PubMed] [Google Scholar] 77. Бриндли С.Дж., Тейлор Т., Динесс В., Остергаард П.Б., Шассо Л.Ф. Взаимосвязь между фармакокинетикой и фармакодинамикой
тинзапарин (логипарин), низкомолекулярный гепарин, в
собаки. ксенобиотики; судьба чужеродных соединений в биологических
системы. 1993; 23: 575–588. [PubMed] [Google Scholar] 78. Гупта С.К., Эллинвуд Э.Х., Никайдо А.М., Хизерли Д.Г. Одновременное моделирование фармакокинетических и фармакодинамических
свойства бензодиазепинов. 79. Уиллс Р.Дж., Галло-Торрес Х.Е., Бертко Р., Мин Б.Х. Фармакокинетика и антисекреторная активность тримопростила при
Сумчатые собаки Heidenhain. Журнал фармакологии и экспериментальной терапии. 1987; 241: 433–437. [PubMed] [Google Scholar] 80. Райт К.Э., Сиссон Т.Л., Флейшакер Дж.К., Антал Э.Дж. Фармакокинетика и психомоторные характеристики алпразолама:
зависимость концентрация-эффект. Журнал клинической фармакологии. 1997; 37: 321–329. [PubMed] [Академия Google] 81. Барбаной М.Дж., Урбано Г., Антонихоан Р., Баллестер М.Р., Валле М. Развитие различной острой толерантности к ЭЭГ, психомоторной
производительность и субъективная оценка эффектов после двух прерывистых пероральных
дозы алпразолама у здоровых добровольцев. Нейропсихобиология. 2007; 55: 203–212. [PubMed] [Google Scholar] 82. Гупта С.К., Шах Дж., Гуинта Д., Хванг С. Фармакокинетика и фармакодинамика многократных доз OROS и
препараты амитриптилина гидрохлорида с немедленным высвобождением. 83. Harder S, Baas H, Demisch L, Simon E. Взаимосвязь доза-реакция и концентрация-реакция
апоморфин у пациентов с болезнью Паркинсона и в конце дозы
акинезия. Int J Clin Pharmacol Ther. 1998; 36: 355–362. [PubMed] [Google Scholar] 84. Patat A, le Coz F, Dubruc C, Gandon JM, Durrieu G, Cimarosti I, Jezequel S, Curet O, Zieleniuk I, Alllain H, Rosenzweig P. Фармакодинамика и фармакокинетика двух режимы дозирования
бефлоксатон, новый обратимый и селективный ингибитор моноаминоксидазы,
стабильное состояние у здоровых добровольцев. Журнал клинической фармакологии. 1996;36:216–229. [PubMed] [Google Scholar] 85. Эллинвуд Э.Х., Никайдо А., Хизерли Д. Диазепам: предсказание фармакодинамики на основе
фармакокинетика. Психофармакология (Берл) 1984; 83: 297–298. [PubMed] [Google Scholar] 86. Бойд Р.А., Чин С.К., Дон-Педро О., Веротта Д., Шейнер Л.Б., Уильямс Р.Л., Джакомини К.М. Фармакокинетика и фармакодинамика дилтиазема и его
метаболитов у здоровых взрослых после однократного перорального приема. 87. Луков В., Делла Пашоа О. Моделирование ФК/ФД высоких доз дилтиазема — скорость всасывания
зависимость петли гистерезиса. Int J Clin Pharmacol Ther. 1997; 35: 418–425. [PubMed] [Google Scholar] 88. Ito Y, Harada T, Fushimi K, Kagawa Y, Oka H, Nakazawa H, Homma R, Kato Y, Yamada S. Фармакокинетический и фармакодинамический анализ
Ингибирование ацетилхолинэстеразы дистигмина бромидом в
крысы. Препарат Метаб Фармакокинет. 2010; 25: 254–261. [PubMed] [Академия Google] 89. Hammarlund MM, Odlind B, Paalzow LK. Острая толерантность к фуросемидному диурезу у человека.
Фармакокинетико-фармакодинамическое моделирование. Журнал фармакологии и экспериментальной терапии. 1985; 233:447–453. [PubMed] [Google Scholar] 90. Бойко М., Степенский Д., Грюнбаум Б.Ф., Грюнбаум С.Е., Меламед И., Охайон С., Глейзер М., Шапира Ю., Злотник А. Фармакокинетика глутамат-оксалоацетаттрансаминазы и
глутамат-пируваттрансаминаза и их глутаматснижающая активность в крови
у наивных крыс. 91. Kemme MJ, Burggraaf J, Schoemaker RC, Kluft C, Cohen AF. Количественная оценка гепарин-индуцированного высвобождения TFPI: максимальное высвобождение
при низких дозах гепарина. Британский журнал клинической фармакологии. 2002; 54: 627–634. [Бесплатная статья PMC] [PubMed] [Google Scholar] 92. Марино М.Р., Лангенбахер К.М., Форд Н.Ф., Рэймонд Р.Х., Мэннинг Дж., Вестерквист О., Шамблен Е.К., Лассетер К.С. Фармакодинамика и фармакокинетика ирбесартана у пациентов
При легкой и умеренной гипертензии. J Cardiovasc Pharmacol Ther. 1999;4:67–75. [PubMed] [Google Scholar] 93. Аояма Т., Ямамото К., Котаки Х., Савада Ю., Ига Т. Фармакодинамическое моделирование изменения двигательной активности с помощью
метилфенидата у крыс. Фармацевтические исследования. 1997; 14:1601–1606. [PubMed] [Google Scholar] 94. Gehr TW, Sica DA, Brater DC, Wallace HJ, Davis J, Fakhry I. Фармакокинетика и фармакодинамика метолазона при почечной недостаточности. 95. Aymard G, Warot D, Demolis P, Giudicelli JF, Lechat P, Le Guern ME, Alquier C, Diquet B. Сравнительная фармакокинетика и фармакодинамика внутривенных
и пероральный нефопам у здоровых добровольцев. Фармакол Токсикол. 2003; 92: 279–286. [PubMed] [Google Scholar] 96. Kietzmann D, Bouillon T, Hamm C, Schwabe K, Schenk H, Gundert-Remy U, Kettler D. Фармакодинамическое моделирование обезболивающих эффектов пиритрамида
у послеоперационных больных. Acta anaesthesiologica Scandinavica. 1997;41:888–894. [PubMed] [Google Scholar] 97. De Paepe P, Belpaire FM, Rosseel MT, Van Hoey G, Boon PA, Buylaert WA. Влияние гиповолемии на фармакокинетику и
электроэнцефалографический эффект пропофола у крыс. Анестезиология. 2000;93:1482–1490. [PubMed] [Google Scholar] 98. Cox EH, Knibbe CA, Koster VS, Langemeijer MW, Tukker EE, Lange R, Kuks PF, Langemeijer HJ, Lie AHL, Danhof M. 99. Liem-Moolenaar M, de Boer P, Timmers M, Schoemaker RC, van Hasselt JG, Schmidt S, van Gerven JM. Фармакокинетические-фармакодинамические взаимоотношения центральной нервной
системные эффекты скополамина у здоровых людей. Британский журнал клинической фармакологии. 2011;71:886–898. [Бесплатная статья PMC] [PubMed] [Google Scholar] 100. Fox AW, Sullivan BW, Buffini JD, Neicin ML, Nicora R, Hoehler FK, O’Rourke R, Stoltz RR. Снижение лактата в сыворотке дихлорацетатом натрия и человеческим
фармакокинетические-фармакодинамические отношения. Журнал фармакологии и экспериментальной терапии. 1996;279:686–693. [PubMed] [Google Scholar] 101. Kroboth PD, Smith RB, Rault R, Silver MR, Sorkin MI, Puschett JB, Juhl RP. Влияние терминальной стадии почечной недостаточности и гидроксида алюминия на
Кинетика темазепама. 102. Луурила Х., Олккола К.Т. Фармакокинетико-фармакодинамическое моделирование эффектов зопиклона на
центральная нервная система человека. Фармакол Токсикол. 1996; 78: 348–353. [PubMed] [Академия Google] 103. Веротта Д., Бил С.Л., Шейнер Л.Б. Полупараметрический подход к фармакокинетике-фармакодинамике
данные. Am J Physiol. 1989; 256: R1005–R1010. [PubMed] [Google Scholar] 104. Chiou WL. Феномен и обоснование выраженной наркотической зависимости
концентрация на месте забора крови. Влияние на фармакокинетику,
фармакодинамика, токсикология и терапия (Часть I) Клиническая фармакокинетика. 1989; 17: 175–199. [PubMed] [Google Scholar] 105. Chiou WL. Феномен и обоснование выраженной наркотической зависимости
концентрация на месте забора крови. Влияние на фармакокинетику,
фармакодинамика, токсикология и терапия (Часть II) Клиническая фармакокинетика. 1989;17:275–290. [PubMed] [Google Scholar] 106. 107. Chiang CW, Barnett G. Эффект марихуаны и дельта-9-тетрагидроканнабиноловая плазма
уровень. Клиническая фармакология и терапия. 1984; 36: 234–238. [PubMed] [Google Scholar] 108. Thadani U, Fung HL, Darke AC, Parker JO. Пероральный изосорбида динитрат при лечении стенокардии.
Зависимость доза-реакция и продолжительность действия при остром
терапия. Тираж. 1980;62:491–502. [PubMed] [Google Scholar] 109. Bogaert MG, Rosseel MT. Сосудистые эффекты динитратных и мононитратных эфиров
изосорбид, изоманнид и изоидид. Naunyn Schmiedebergs Arch Pharmacol. 1972; 275: 339–342. [PubMed] [Google Scholar] 110. Wendt RL. Системные и коронарные сосудистые эффекты 2- и
5-мононитратные эфиры изосорбида. Журнал фармакологии и экспериментальной терапии. 111. Pleuvry BJ. Гистерезис реакции на лекарство. Анестезия и реаниматология. 2008;9: 372–373. [Google Scholar] 112. Капур С., Симан П. Антипсихотические препараты различаются по скорости их действия.
дофаминовые D2-рецепторы. Последствия для атипичных нейролептиков
действие. J Psychiatry Neurosci. 2000; 25: 161–166. [Бесплатная статья PMC] [PubMed] [Google Scholar] 113. Wienen W, Entzeroth M, van Meel JCA, Stangier J, Busch U, Ebner T, Schmid J, Lehmann H, Matzek K, Kempthorne-Rawson J, Gladigau В., Хауэль Н.Х. Обзор телмисартана: новый ангиотензин длительного действия
Антагонист II-рецепторов. Обзоры сердечно-сосудистых препаратов. 2000; 18: 127–154. [Академия Google] 114. Wienen W, Hauel N, Van Meel JC, Narr B, Ries U, Entzeroth M. Фармакологическая характеристика нового непептида
антагонист рецептора ангиотензина II, BIBR 277. Британский журнал фармакологии. 1993; 110: 245–252. [Бесплатная статья PMC] [PubMed] [Google Scholar] 115. 116. Schambye HT, Hjorth SA, Bergsma DJ, Sathe G, Schwartz TW. Различия между сайтами связывания ангиотензина II и
непептидные антагонисты ангиотензина II типа 1
рецепторы. Proc Natl Acad Sci U S A. 1994; 91:7046–7050. [Бесплатная статья PMC] [PubMed] [Google Scholar] 117. Brunner HR, Nussberger J, Waeber B. Блокада ангиотензина II по сравнению с другими фармакологическими препаратами
методы ингибирования ренин-ангиотензиновой системы. Приложение J Hypertens. 1993;11:С53–С58. [PubMed] [Google Scholar] 118. Delacretaz E, Nussberger J, Biollaz J, Waeber B, Brunner HR. Характеристика антагониста рецептора ангиотензина II
TCV-116 у здоровых добровольцев. Гипертония. 1995; 25:14–21. [PubMed] [Google Scholar] 119. 120. Belz GG, Butzer R, Mang C, Kober S, Mutschler E. Большая степень и продолжительность ингибирующего эффекта
ирбесартан при стимуляции ангиотензином II у мужчин по сравнению с лозартаном и
валсартан. Европейский журнал клинической фармакологии. 1998;54:А8. [Google Scholar] 121. Островски Дж., Швейцер П., Эрбель Р. Труды Первого Европейского конгресса по биофармакологии и
Фармакокинетика. Франция: Клермон-Ферран; 1981. Корреляция фармакокинетических данных с клиническим эффектом
молсидомин; стр. 418–424. [Академия Google] 122. Meinertz T, Brandstatter A, Trenk D, Jahnchen E, Ostrowski J, Gartner W. Связь между фармакокинетикой и фармакодинамикой
молсидомина и его метаболитов у человека. Американский кардиологический журнал. 1985; 109: 644–648. 123. Crevoisier C, Ziegler WH, Eckert M, Heizmann P. Связь между концентрацией в плазме и эффектом мидазолама
после перорального и внутривенного введения. Британский журнал клинической фармакологии. 1983; 16 (Приложение 1): 51S–61S. [Бесплатная статья PMC] [PubMed] [Google Scholar] 124. Hardin TC, Graybill JR, Fetchick R, Woestenborghs R, Rinaldi MG, Kuhn JG. Фармакокинетика итраконазола после приема внутрь
нормальные добровольцы. Антимикробные препараты и химиотерапия. 1988; 32: 1310–1313. [Бесплатная статья PMC] [PubMed] [Google Scholar] 125. Heykants J, Van Peer A, Van de Velde V, Van Rooy P, Meuldermans W, Lavrijsen K, Woestenborghs R, Van Cutsem J, Cauwenbergh G. The Clinical Фармакокинетика итраконазола:
обзор. Микозы. 1989; 32 (Приложение 1): 67–87. [PubMed] [Академия Google] 126. Шин Дж.Х., Чой К.И., Ким Ю.К., Ли М.Г. Дозозависимая фармакокинетика итраконазола после внутривенного введения
или пероральное введение крысам: эффект первого прохождения через кишечник. 127. Yoo SD, Kang E, Jun H, Shin BS, Lee KC, Lee KH. Всасывание, метаболизм первого прохождения и утилизация
итраконазол у крыс. Химико-фармацевтический вестник. 2000; 48: 798–801. [PubMed] [Академия Google] 128. Poirier JM, Cheymol G. Оптимизация терапии итраконазолом с использованием целевого препарата
концентрации. Клиническая фармакокинетика. 1998; 35: 461–473. [PubMed] [Google Scholar] 129. Кнапп С., Уордлоу М.Л., Альберт К., Уотерс Д., Тал Л.Дж. Корреляция между концентрациями физостигмина в плазме и
процент ингибирования ацетилхолинэстеразы с течением времени после контролируемого
высвобождение физостигмина у добровольцев. Метаболизм и распределение лекарств: биологическая судьба
химические вещества. 1991;19: 400–404. [PubMed] [Google Scholar] 130. Moriarty PL, Becker RE. Ингибирование ацетилхолинэстеразы (АХЭ) головного мозга человека и эритроцитов
гептилфизостигмин (HPTL) Методы и результаты экспериментальной и клинической фармакологии. 131. Унни Л.К., Хатт В., Имбимбо Б.П., Беккер Р.Э. Кинетика ингибирования холинэстеразы эптастигмином в
человек. Европейский журнал клинической фармакологии. 1991;41:83–84. [PubMed] [Google Scholar] 132. Бруфани М., Марта М., Помпони М. Антихолинэстеразная активность нового карбамата,
гептилфизостигмин в связи с его применением у пациентов с болезнью Альцгеймера
слабоумие. Евр Дж Биохим. 1986;157:115–120. [PubMed] [Google Scholar] 133. Аутери А., Моска А., Латтуада Н., Луццана М., Зекка Л., Радиче Д., Имбимбо Б.П. Фармакодинамика и фармакокинетика эптастигмина у пожилых людей
предметы. Европейский журнал клинической фармакологии. 1993; 45: 373–376. [PubMed] [Google Scholar] 134. Swift RH, Mant TG, Heald A, Sciberras DG, Imbimbo B, Morrison PJ, Goldberg MR. Совместная встреча Британского фармакологического общества с Северными
Общество. Великобритания: Университет Саутгемптона; 1991. Исследование по изучению безопасности, переносимости и
фармакодинамика однократных возрастающих доз L-693487 (гептил-физостигмин
тартрат) у здоровых пожилых добровольцев. 135. Kaojarern S, Day B, Brater DC. Динамика доставки фуросемида в мочу:
независимая детерминанта общего отклика. Почки международные. 1982; 22: 69–74. [PubMed] [Google Scholar] 136. Пенник М. Абсорбция димезилата лиздексамфетамина и его ферментативных
превращение в d-амфетамин. Нейропсихиатр Dis Treat. 6: 317–327. [Бесплатная статья PMC] [PubMed] [Google Scholar] 137. Biederman J, Boellner SW, Childress A, Lopez FA, Krishnan S, Zhang Y. Димезилат лисдексамфетамина и смешанные соли амфетамина
пролонгированного действия у детей с СДВГ: двойной слепой плацебо-контролируемый
перекрестное аналоговое исследование в классе. Биол психиатрия. 2007; 62: 970–976. [PubMed] [Google Scholar] 138. Wigal SB, Kollins SH, Childress AC, Squires L. 13-часовое школьное лабораторное исследование димезилата лиздексамфетамина.
у детей школьного возраста с дефицитом внимания/гиперактивностью
расстройство. Детская подростковая психиатрия Ment Health. 2009 г. 139. Wigal T, Brams M, Gasior M, Gao J, Squires L, Giblin J. Рандомизированное, двойное слепое, плацебо-контролируемое, перекрестное исследование
Эффективность и безопасность лиздексамфетамина димезилата у взрослых с
Синдром дефицита внимания/гиперактивности: новые результаты с использованием смоделированного
дизайн рабочей среды для взрослых. Поведение Мозг Функц. 6:34. [Бесплатная статья PMC] [PubMed] [Google Scholar] 140. Kalant H, LeBlanc AE, Gibbins RJ. Толерантность и зависимость от некоторых неопиоидных психотропных средств
наркотики. Фармакол Ред. 1971;23:135–191. [PubMed] [Google Scholar] 141. Rosenfeld GC, Burks TF. Толерантность однократной дозы морфина к гипотермии у крыс:
дифференциация острой толерантности от длительной. Журнал фармакологии и экспериментальной терапии. 1977; 202: 654–659. [PubMed] [Google Scholar] 142. Schuttler J, Schwilden H, Stoeckel H. Инфузионные стратегии для исследования фармакокинетики и
фармакодинамика снотворных: на примере этомидата. 143. Джонс Б.М., Вега А. Когнитивные показатели, измеренные на восходящей и нисходящей
часть алкогольной кривой крови. Психофармакология. 1972; 23: 99–114. [PubMed] [Google Scholar] 144. Van Dyke C, Jatlow P, Ungerer J, Barash PG, Byck R. Пероральный кокаин: концентрация в плазме и центральная
последствия. Наука. 1978; 200: 211–213. [PubMed] [Google Scholar] 145. Ellinwood EH, Jr, Heatherly DG, Nikaido AM, Bjornsson TD, Kilts C. Сравнительная фармакокинетика и фармакодинамика лоразепама,
алпразолам и диазепам. Психофармакология (Берл) 1985;86:392–399. [PubMed] [Google Scholar] 146. Kroboth PD, Smith RB, Erb RJ. Толерантность к алпразоламу после внутривенного болюсного и непрерывного
инфузии: психомоторные и ЭЭГ эффекты. Клиническая фармакология и терапия. 1988; 43: 270–277. [PubMed] [Google Scholar] 147. Bertz RJ, Kroboth PD, Kroboth FJ, Reynolds IJ, Salek F, Wright CE, Smith RB. 148. Fleshaker JC, Chambers JH, Peters GR. Оценка развития острой толерантности к
психомоторные эффекты мидазолама после внутривенных инфузий у здоровых
волонтеры. Психофармакология человека: клиническая и экспериментальная. 1995; 10: 97–104. [Google Scholar] 149. Кробот П.Д., Берц Р.Дж., Смит Р.Б. Острая толерантность к триазоламу при непрерывном и ступенчатом
инфузии: оценка константы скорости смещения эффекта. Журнал фармакологии и экспериментальной терапии. 1993;264:1047–1055. [PubMed] [Google Scholar] 150. Бейтсон А.Н. Основные фармакологические механизмы, вовлеченные в действие бензодиазепинов.
толерантность и уход. Текущий фармацевтический дизайн. 2002; 8: 5–21. [PubMed] [Google Scholar] 151. Sieghart W. GABAA-рецепторы: лиганд-управляемые Cl-ионные каналы, модулируемые
множественные сайты связывания лекарств. 152. Холфорд Н. Холфорд NHG и Шейнер Л.Б. «Понимание эффекта дозы».
Взаимосвязь-клиническое применение фармакокинетики-фармакодинамики
Модели». Клин Фармакокин. 1981;6:429–453. Предыстория, AAPS J, 13 (1981) 662–664. [Бесплатная статья PMC] [PubMed] [Google Scholar] 153. Джек М.Л., Колберн В.А., Спирт Н.М., Баутц Г., Занко М., Хорст В.Д., О’Брайен Р.А. Модель фармакокинетического/фармакодинамического/рецепторного связывания для
прогнозировать начало и продолжительность фармакологической активности
бензодиазепины. Прог Нейропсихофармакол Биол Психиатрия. 1983; 7: 629–635. [PubMed] [Google Scholar] 154. Виттенборн младший. Влияние бензодиазепинов на психомоторные
производительность. Британский журнал клинической фармакологии. 1979; 7 (Прил. 1): 61S–67S. [Бесплатная статья PMC] [PubMed] [Google Scholar] 155. Ellinwood EH, Jr, Linnoila M, Easler ME, Molter DW. Профиль острой толерантности к трем седативным
анксиолитики. 156. Экблом М., Хаммарлунд-Уденаес М., Паалзов Л. Моделирование развития толерантности и эффекта рикошета во время
различные внутривенные введения морфина крысам. Журнал фармакологии и экспериментальной терапии. 1993;266:244–252. [PubMed] [Google Scholar] 157. Oosterhuis B, van Boxtel CJ. Кинетика действия лекарств на человека. Терапевтический лекарственный мониторинг. 1988; 10: 121–132. [PubMed] [Google Scholar] 158. Carruthers SG, McCall B, Cordell BA, Wu R. Взаимосвязь между частотой сердечных сокращений и интервалом PR во время
физиологические и фармакологические воздействия. Британский журнал клинической фармакологии. 1987; 23: 259–265. [Бесплатная статья PMC] [PubMed] [Google Scholar] 159. Smith MS, Verghese CP, Shand DG, Pritchett EL. Фармакокинетические и фармакодинамические эффекты
дилтиазем. Ам Джей Кардиол. 1983;51:1369–1374. [PubMed] [Google Scholar] 160. Элленбоген К. 161. Joyal M, Pieper J, Cremer K, Feldman RL, Pepine CJ. Фармакодинамические аспекты внутривенного введения дилтиазема
администрация. Американский кардиологический журнал. 1986; 111: 54–61. [PubMed] [Google Scholar] 162. Fukuhara S, Echizen H, Naito M, Ishikawa S, Toyama M, Nagoshi H, Honda M, Ishizaki T. Межиндивидуальная изменчивость чувствительности
атриовентрикулярного узла к дилтиазему у больных с пароксизмальной
наджелудочковая тахикардия. Журнал клинической фармакологии. 1989;29:102–106. [PubMed] [Google Scholar] 163. Zar JH. Биостатистический анализ. 5-е изд. Pearson: 2010. [Google Scholar] 164. Holford NH, Sheiner LB. Понимание зависимости доза-эффект: клиническое применение
фармакокинетических-фармакодинамических моделей. Клиническая фармакокинетика. 165. Стански Д.Р., Хадсон Р.Дж., Гомер Т.Д., Саидман Л.Дж., Мит Э. Фармакодинамическое моделирование тиопенталовой анестезии. Журнал фармакокинетики и биофармацевтики. 1984;12:223–240. [PubMed] [Google Scholar] 166. Porchet HC, Benowitz NL, Sheiner LB, Copeland JR. Явная толерантность к острому воздействию никотина приводит к
часть кинетики распределения. Джей Клин Инвест. 1987; 80: 1466–1471. [Бесплатная статья PMC] [PubMed] [Google Scholar] 167. Montamat SC, Abernethy DR. N-монодесметилдилтиазем является преобладающим метаболитом
дилтиазем в плазме молодых и пожилых гипертоников. Британский журнал клинической фармакологии. 1987; 24: 185–189.. [Бесплатная статья PMC] [PubMed] [Google Scholar] 168. Goebel KJ, Kolle EU. Высокоэффективная жидкостная хроматография определение
дилтиазем и четыре его метаболита в плазме. Приложение к
фармакокинетика. J Хроматогр. 1985; 345: 355–363. [PubMed] [Google Scholar] 169. 170. Yabana H, Nagao T, Sato M. Сердечно-сосудистые эффекты метаболитов дилтиазема в
собаки. J Cardiovasc Pharmacol. 1985;7:152–157. [PubMed] [Google Scholar] 171. Narita H, Otsuka M, Yabana H, Nagao T. Гипотензивный ответ спонтанно гипертензивных крыс на
центрально вводимый дилтиазем и его метаболиты: в связи с
гипотензивное действие при приеме внутрь. J Фармакобиодин. 1986; 9: 547–553. [PubMed] [Google Scholar] 172. Bromet N, Courte S, Aubert Y, Baune A, Guillandeux J. Фармакокинетическое исследование алмитрина. Преподобный отец Мал Респир. 1980; 8: 145–147. [Академия Google] 173. Кэмпбелл Д.Б., Гордон Б.Х., Ингс Р.М. Фармакодинамические и фармакокинетические взаимодействия алмитрина
бисмезилат. Преподобный Мал Респир. 1985; 2 (Приложение 1): S39–S44. [PubMed] [Google Scholar] 174. 175. McQueen DS, Evrard Y, Gordon BH, Campbell DB. Ганглиогломерулярные нервы влияют на чувствительность сонной артерии кошки
хеморецепторы организма к алмитрину. J Auton Nerv Syst. 1989;27:57–66. [PubMed] [Google Scholar] 176. Янхен Э., Леви Г. Ингибирование элиминации фенилбутазона его метаболитом.
оксифенбутазон. Proc Soc Exp Biol Med. 1972; 141: 963–965. [PubMed] [Google Scholar] 177. Yamamoto I, Ho IK, Loh HH. Антагонистические эффекты от
5-этил-5-(3-гидрокси-1-метилбутил)-барбитуровая кислота на пентобарбитале
наркоза как у наивных, так и у толерантных мышей. Жизнь наук. 1978; 22:1103–1112. [PubMed] [Google Scholar] 178. Ставчанский С.А., Любавский В.К., Костенбаудер Х.Б. Увеличение времени сна гексобарбитала и ингибирование препарата
метаболизируется основным метаболитом дифенилгидантоина. 179. Райт М.Р. Влияние хиральности на фармакодинамические
моделирование. Хиральность. 1994; 6: 467–471. [Google Scholar] 180. Ritschel WA, Hussain A. Обзор корреляции между фармакологическим ответом и действием препарата.
расположение. Методы и результаты экспериментальной и клинической фармакологии. 1984; 6: 627–640. [PubMed] [Google Scholar] 181. Келман А.В., Уайтинг Б. Моделирование реакции на лекарство у отдельных субъектов. Журнал фармакокинетики и биофармацевтики. 1980;8:115–130. [PubMed] [Google Scholar] 182. Gillespie WR, Veng-Pedersen P, Antal EJ, Phillips JP. Системный подход к фармакодинамике. II: глибурид
фармакодинамика и оценка оптимальной доставки лекарств. Журнал фармацевтических наук. 1988; 77: 48–55. [PubMed] [Google Scholar] 183. Zahler R, Wachtel P, Jatlow P, Byck R. Кинетика действия лекарств с помощью анализа распределенных лагов:
приложение к кокаину. Клиническая фармакология и терапия. 184. Ван Россум Дж.М., Бургерс Дж.П. Количественные связи между динамикой и кинетикой
наркотики: системно-динамический подход. Drug Metab Rev. 1984; 15:365–382. [PubMed] [Google Scholar] 185. Colburn WA. Комбинированный фармакокинетический/фармакодинамический (ФК/ФД)
Моделирование. Журнал клинической фармакологии. 1988; 28: 769–771. [PubMed] [Google Scholar] 186. Dahlstrom BE, Paalzow LK, Segre G, Agren AJ. Связь между фармакокинетикой морфина и
обезболивание. Журнал фармакокинетики и биофармацевтики. 1978;6:41–53. [PubMed] [Google Scholar] 187. Холфорд Н. Холфорд NHG и Шейнер Л.Б. «Понимание эффекта дозы».
Взаимосвязь-клиническое применение фармакокинетики-фармакодинамики
Models». Clin Pharmacokin. 1981; 6: 429–453. The Backstory, AAPS J, 13 (2011) 662–664. [Бесплатная статья PMC] [PubMed] [Google Scholar] 188. Holford NH, Sheiner LB. Кинетика фармакологического ответа. Фармакология и терапия. 1982;16:143–166. 189. Fuseau E, Sheiner LB Одновременное моделирование фармакокинетики и фармакодинамики
с непараметрической фармакодинамической моделью. Клиническая фармакология и терапия. 1984;35:733–741. [PubMed] [Google Scholar] 190. Unadkat JD, Bartha F, Sheiner LB. Одновременное моделирование фармакокинетики и фармакодинамики
с непараметрическими кинетическими и динамическими моделями. Клиническая фармакология и терапия. 1986; 40:86–93. [PubMed] [Google Scholar] 191. Сегре Г. Кинетика взаимодействия лекарств и биологических
системы. Фармако наук. 1968; 23: 907–918. [PubMed] [Google Scholar] 192. Галеацци Р.Л., Бенет Л.З., Шейнер Л.Б. Взаимосвязь между фармакокинетикой и фармакодинамикой
прокаинамид. Клиническая фармакология и терапия. 1976;20:278–289. [PubMed] [Google Scholar] 193. Menasse R, Hedwall PR, Kraetz J, Pericin C, Riesterer L, Salllmann A, Ziel R, Jaques R. Фармакологические свойства диклофенака натрия и его
метаболиты. 194. Faigle JW, Bottcher I, Godbillon J, Kriemler HP, Schlumpf E, Schneider W, Schweizer A, Stierlin H, Winkler T. Новый метаболит диклофенака натрия в организме человека
плазма. ксенобиотики; судьба чужеродных соединений в биологических
системы. 1988;18:1191–1197. [PubMed] [Google Scholar] 195. Tonussi CR, Ferreira SH. Механизм обезболивания диклофенаком: прямая блокада
воспалительная сенсибилизация. Европейский журнал фармакологии. 1994; 251:173–179. [PubMed] [Google Scholar] 196. Dayneka NL, Garg V, Jusko WJ. Сравнение четырех основных моделей непрямой фармакодинамической
ответы. Журнал фармакокинетики и биофармацевтики. 1993; 21: 457–478. [Бесплатная статья PMC] [PubMed] [Google Scholar] 197. Garg V, Jusko WJ. Фармакодинамическое моделирование нестероидных противовоспалительных препаратов:
жаропонижающий эффект ибупрофена. Клиническая фармакология и терапия. 1994;55:87–88. [PubMed] [Google Scholar] 198. 199. Porchet HC, Benowitz NL, Sheiner LB. Фармакодинамическая модель толерантности: приложение к
никотин. Журнал фармакологии и экспериментальной терапии. 1988; 244: 231–236. [PubMed] [Google Scholar] 200. Перский А.М., Берри Н.С., Поллак Г.М., Брауэр К.Л. Моделирование сердечно-сосудистых эффектов эфедрина. Британский журнал клинической фармакологии. 2004; 57: 552–562. [Бесплатная статья PMC] [PubMed] [Google Scholar] 201. Мясник С.П., Липтрот Дж., Абуртнотт Г.В. Характеристика индуцированных метилфенидатом и номифензином
Высвобождение дофамина в полосатом теле крысы с использованием мозга in vivo
микродиализ. Нейроски Летт. 1991; 122: 245–248. [PubMed] [Google Scholar] 202. Hurd YL, Ungerstedt U. Нейрохимический профиль ингибиторов захвата дофамина in vivo и
релизеры в хвостатом скорлупе крысы. 203. Gumbleton M, Oie S, Verotta D. Фармакокинетически-фармакодинамическое (PK-PD) моделирование в
нестационарные исследования и артериовенозная концентрация препарата
различия. Британский журнал клинической фармакологии. 1994;38:389–400. [Бесплатная статья PMC] [PubMed] [Google Scholar] 204. Moschitto LJ, Greenblatt DJ. Независимое от концентрации связывание с белками плазмы
бензодиазепины. Дж Фарм Фармакол. 1983; 35: 179–180. [PubMed] [Google Scholar] 205. Fleshaker JC, Phillips JP, Eller MG, Smith RB. Фармакокинетика и фармакодинамика алпразолама после
однократная и многократная пероральная доза пролонгированного действия
формулировка. Журнал клинической фармакологии. 1989; 29: 543–549. [PubMed] [Академия Google] 206. Sunzel M, Paalzow L, Berggren L, Eriksson I. Дыхательные и сердечно-сосудистые эффекты по отношению к плазме
уровни мидазолама и диазепама. Британский журнал клинической фармакологии. 207. Маттила М. Острые и подострые эффекты диазепама на работоспособность человека:
сравнение простой таблетки и капсулы с контролируемым высвобождением. Фармакол Токсикол. 1988; 63: 369–374. [PubMed] [Google Scholar] 208. Baktir G, Fisch HU, Huguenin P, Bircher J. Взаимосвязь концентрации и эффекта триазолама у здоровых
предметы. Клиническая фармакология и терапия. 1983;34:195–201. [PubMed] [Google Scholar] 209. Шульц Р., Рейманн И.В. Практический эффект добровольцев при повторном психометрическом тестировании.
Как обращаться с этой промежуточной переменной в клинической фармакологии
исследования? Методы и результаты экспериментальной и клинической фармакологии. 1988; 10: 657–661. [PubMed] [Google Scholar] 210. Montastruc JL, Rascol O, Senard JM. Текущий статус агонистов дофамина при болезни Паркинсона
управление болезнью. Наркотики. 1993; 46: 384–393. [PubMed] [Академия Google] 211. 212. Эллинвуд Э. Х., мл., Никайдо А. М., Хизерли Д. Г., Бьорнссон Т. Д. Фармакодинамика бензодиазепинов: данные о биофазной скорости
ограничивающие механизмы. Психофармакология (Берл) 1987; 91: 168–174. [PubMed] [Академия Google] 213. Гоа KL, Heel RC. Зопиклон. Обзор его фармакодинамических и фармакокинетических
свойства и терапевтическую эффективность в качестве снотворного. Наркотики. 1986; 32: 48–65. [PubMed] [Google Scholar] 214. Julou L, Bardone MC, Blanchard JC, Garret C, Stutzmann JM. Фармакологические исследования зопиклона. Фармакология. 1983; 27 (Приложение 2): 46–58. [PubMed] [Google Scholar] 215. Elie R, Deschenes JP. Эффективность и переносимость зопиклона при бессоннице у пожилых людей
пациенты. 216. Pecknold J, Wilson R, le Morvan P. Долгосрочная эффективность и отмена зопиклона: сон
лабораторное исследование. Int Clin Psychopharmacol. 5 (Приложение 2): 57–67. [PubMed] [Google Scholar] 217. Paintaud G, Alvan G, Eckernas SA, Wakelkamp M, Grahnen A. Влияние приема пищи на эффект двух контролируемых
выпустить формы фуросемида. Биофармацевтика и утилизация лекарств. 1995; 16: 221–232. [PubMed] [Академия Google] 218. Wakelkamp M, Alvan G, Gabrielsson J, Paintaud G. Фармакодинамическое моделирование толерантности к фуросемиду после многократного
внутривенное введение. Клиническая фармакология и терапия. 1996; 60: 75–88. [PubMed] [Google Scholar] 219. Sjostrom PA, Odlind BG, Beermann BA, Hammarlund-Udenaes M. О механизме острой толерантности к фуросемиду
диурез. Scand J Urol Nephrol. 1988; 22: 133–140. [PubMed] [Google Scholar] 220. de Wardener HE. Идиопатический отек: роль злоупотребления диуретиками. 221. Castaneda-Hernandez G, Caille G, du Souich P. Влияние состава лекарственного средства на эффект концентрации лекарственного средства.
отношения. Клиническая фармакокинетика. 1994; 26: 135–143. [PubMed] [Google Scholar] 222. Kleinbloesem CH, van Brummelen P, Danhof M, Faber H, Urquhart J, Breimer DD. Скорость увеличения концентрации нифедипина в плазме как
основной детерминантой его гемодинамических эффектов в организме человека. Клиническая фармакология и терапия. 1987;41:26–30. [PubMed] [Google Scholar] 223. van Harten J, van Brummelen P, Zeegers RR, Danhof M, Breimer DD. Влияние скорости инфузии на фармакокинетику и
гемодинамические эффекты нисолдипина у мужчин. Британский журнал клинической фармакологии. 1988; 25: 709–717. [Бесплатная статья PMC] [PubMed] [Google Scholar] 224. Elliott HL, Vincent J, Meredith PA, Reid JL. Взаимосвязь между концентрацией празозина в плазме и
альфа-антагонизм у человека: сравнение обычного и контролируемого
(Орос) составы. 225. Fung HL. Фармакокинетические детерминанты действия нитратов. Am J Med. 1984; 76: 22–26. [PubMed] [Google Scholar] 226. Perry PJ, Pfohl BM, Holstad SG. Взаимосвязь между реакцией на антидепрессанты и трициклическими
концентрации антидепрессантов в плазме. Ретроспективный анализ
литературы с использованием логистического регрессионного анализа. Клиническая фармакокинетика. 1987; 13: 381–392. [PubMed] [Google Scholar] 227. Smith RC, Vroulis G, Shvartsburd A, Allen R, Lewis N, Schoolar JC, Chojnacki M, Johnson R. Уровни галоперидола в эритроцитах и плазме и клинический ответ при
шизофрения. Am J Психиатрия. 1982;139:1054–1056. [PubMed] [Google Scholar] 228. Whitehouse S, Cooper RH, Randle PJ. Механизм активации пируватдегидрогеназы
дихлорацетат и другие галогенированные карбоновые кислоты. Биохим Дж. 1974; 141:761–774. [Бесплатная статья PMC] [PubMed] [Google Scholar] 229. 230. Castillo J, Dávalos A, Noya M. Прогрессирование ишемического инсульта и эксайтотоксического
аминокислоты. Ланцет. 1997; 349: 79–83. [PubMed] [Google Scholar] 231. Johnston MV, Trescher WH, Ishida A, Nakajima W. Нейробиология гипоксически-ишемического повреждения в развивающихся
мозг. Педиатрическое исследование. 2001; 49: 735–741. [PubMed] [Google Scholar] 232. Zauner A, Bullock R, Kuta AJ, Woodward J, Young HF. Высвобождение глутамата и мозговой кровоток после тяжелой человеческой головы
рана. Акта нейрохирургическая. Добавка. 1996;67:40–44. [PubMed] [Google Scholar] 233. Gottlieb M, Wang Y, Teichberg VI. Опосредованное кровью удаление спинномозговой жидкости
глутамат. Журнал нейрохимии. 2003; 87: 119–126. 234. Inturrisi CE. Фармакокинетические аспекты исследования анальгетиков
дизайн. В: Макс М.Б., Портеной Р.К., Ласка Э., редакторы. Достижения в области исследований и терапии боли: дизайн клинического обезболивания
испытания. Нью-Йорк: Рэйвен; 1991. стр. 533–558. [Google Scholar] 235. Greenblatt DJ, Ehrenberg BL, Gunderman J, Locniskar A, Scavone JM, Harmatz JS, Shader RI. Фармакокинетическое и электроэнцефалографическое исследование внутривенных
диазепам, мидазолам и плацебо. Клиническая фармакология и терапия. 1989;45:356–365. [PubMed] [Google Scholar] 236. Koopmans R, Dingemanse J, Danhof M, Horsten GP, van Boxtel CJ. Фармакокинетико-фармакодинамическое моделирование эффектов мидазолама на
центральной нервной системы человека. Клиническая фармакология и терапия. 1988; 44:14–22. [PubMed] [Google Scholar] 237. Friedman H, Greenblatt DJ, Peters GR, Metzler CM, Charlton MD, Harmatz JS, Antal EJ, Sanborn EC, Francom SF. Фармакокинетика и фармакодинамика перорального диазепама: влияние
дозы, концентрации в плазме и времени. 238. van Beijsterveldt LE, Geerts RJ, Leysen JE, Megens AA, Van den Eynde HM, Meuldermans WE, Heykants JJ. Региональное распределение рисперидона и его активного вещества в головном мозге
метаболит 9-гидрокси-рисперидон у крыс. Психофармакология (Берл) 1994;114:53–62. [PubMed] [Google Scholar] 239. Holford NH, Coates PE, Guentert TW, Riegelman S, Sheiner LB. Влияние хинидина и его метаболитов на
электрокардиограмма и систолические временные интервалы: концентрация-эффект
отношения. Британский журнал клинической фармакологии. 1981;11:187–195. [Бесплатная статья PMC] [PubMed] [Google Scholar] 240. Terashima A, Nakai M, Hashimoto T, Kawamata T, Taniguchi T, Yasuda M, Maeda K, Tanaka C. Одноканальная активность Ca2+-зависимого K+ канал
модулируется FK506 и рапамицином. Исследование мозга. 1998; 786: 255–258. [PubMed] [Google Scholar] 241. Уайтинг Б., Холфорд Н.Х., Шейнер Л.Б. Количественный анализ влияния концентрации дизопирамида
отношение. 242. Макаллистер Р.Г., младший, Кирстен Э.Б. Фармакология верапамила. IV. Кинетические и динамические эффекты
после однократного внутривенного и перорального введения. Клиническая фармакология и терапия. 1982; 31: 418–426. [PubMed] [Google Scholar] 243. Reiter MJ, Shand DG, Pritchett EL. Сравнение внутривенного и перорального верапамила
дозирование. Клиническая фармакология и терапия. 1982; 32: 711–720. [PubMed] [Google Scholar] 244. Colburn WA. Фармакокинетическое/фармакодинамическое моделирование: что это такое
является! Журнал фармакокинетики и биофармацевтики. 1987;15:545–555. [PubMed] [Google Scholar] 245. Winter CA, Flataker L. Пороги реакции на давление в отечных задних лапах крыс и
реакции на обезболивающие препараты. Журнал фармакологии и экспериментальной терапии. 1965; 150: 165–171. [PubMed] [Google Scholar] 246. Strange C, Vaughan L, Franklin C, Johnson J. 247. Yate PM, Flynn PJ, Arnold RW, Weatherly BC, Simmonds RJ, Dopson T. Клинический опыт и концентрация лауданозина в плазме во время
инфузия атракурия в отделении интенсивной терапии. Британский журнал анестезии. 1987; 59: 211–217. [PubMed] [Google Scholar] 248. Tschida SJ, Hoey LL, Nahum A, Vance-Bryan K. Устойчивость к атракурию у тяжелобольного пациента. Фармакотерапия. 1995; 15: 533–539. [PubMed] [Google Scholar] 249. Parker CJ, Hunter JM. Новая четырехпараметрическая пороговая модель плазменного атракурия
зависимость концентрация-реакция. Британский журнал анестезии. 1992;68:548–554. [PubMed] [Google Scholar] 250. Greenblatt DJ, Ehrenberg BL, Culm KE, Scavone JM, Corbett KE, Friedman HL, Harmatz JS, Shader RI. Кинетика и ЭЭГ-эффекты мидазолама во время и через 1 мин.
1-часовые и 3-часовые внутривенные инфузии. 251. Ludbrook GL, Upton RN, Grant C, Martinez A. Длительное нарушение равновесия между концентрациями крови и мозга.
пропофола при инфузии овцам. Acta anaesthesiologica Scandinavica. 1999;43:206–211. [PubMed] [Google Scholar] 252. Kanto J, Gepts E. Фармакокинетические последствия для клинического применения
пропофол. Клиническая фармакокинетика. 1989; 17: 308–326. [PubMed] [Google Scholar] 253. Bundgaard C., Jorgensen M., Mork A. Интегрированная модель микродиализа крыс для множественных
фармакокинетические/фармакодинамические исследования серотонинергических
агенты. J Pharmacol Toxicol Methods. 2007; 55: 214–223. [PubMed] [Google Scholar] 254. Yassen A, Olofsen E, Dahan A, Danhof M. Фармакокинетико-фармакодинамическое моделирование антиноцицептивного
Эффект бупренорфина и фентанила у крыс: роль уравновешивания рецепторов
кинетика. Журнал фармакологии и экспериментальной терапии. 255. Кляйн Н., Захер Дж., Гейсс-Гранадиа Т., Моссахеб Н., Аттарбаши Т., Ланценбергер Р., Шпинделеггер С., Холик А., Асенбаум С., Дудчак Р., Таушер Дж., Каспер С. Высшее Занятость переносчика серотонина после многократной дозы
введение эсциталопрама по сравнению с циталопрамом: [123I]ADAM SPECT
исследование. Психофармакология (Берл) 2007; 191:333–339. [PubMed] [Google Scholar] 256. Schran HF, Tse FL, Bhuta SI. Фармакокинетика и фармакодинамика бромокриптина при
крыса. Биофармацевтика и утилизация лекарств. 1985;6:301–311. [PubMed] [Google Scholar] 257. Фелан Д.Г., Грейг Н.Х., Рапопорт С.И., Сонкрант Т.Т. Высокоэффективный жидкостный хроматографический анализ бромокриптина в
плазма и мозг крысы. J Хроматогр. 1990; 533: 264–270. [PubMed] [Google Scholar] 258. Huang YF, Upton RN, Rutten AJ, Mather LE. Гемодинамические эффекты внутривенных болюсных доз меперидина
у сознательных овец. Анестезия и обезболивание. 259. Huang YF, Upton RN, Mather LE. Фармакокинетика меперидина в миокарде в сознании
овец. Анестезия и обезболивание. 1994;79:987–992. [PubMed] [Google Scholar] 260. Perola E, Cellai L, Lamba D, Filocamo L, Brufani M. Аналоги физостигмина с длинной цепью как потенциальные лекарства для
Болезнь Альцгеймера: новый взгляд на механизм действия
ингибирование ацетилхолинэстеразы. Биохим Биофиз Акта. 1997; 1343:41–50. [PubMed] [Google Scholar] 261. Grunder G, Fellows C, Janouschek H, Veselinovic T, Boy C, Brocheler A, Kirschbaum KM, Hellmann S, Spreckelmeyer KM, Hiemke C, Rosch F, Schaefer WM, Vernaleken I. Фармакокинетика арипипразола в мозге и плазме у пациентов
с шизофренией: ПЭТ-исследование с [18F]фаллипридом. Am J Психиатрия. 2008;165:988–995. [PubMed] [Google Scholar] 262. Нагашима Р., О’Рейли Р.А., Леви Г. Кинетика фармакологических эффектов у человека: антикоагулянт
действие варфарина. Клиническая фармакология и терапия. 263. Shetty HG, Fennerty AG, Routledge PA. Клинические фармакокинетические аспекты контроля перорального
антикоагулянтная терапия. Клиническая фармакокинетика. 1989; 16: 238–253. [PubMed] [Google Scholar] 264. Fung HL, Sutton SC, Kamiya A. Поглощение кровеносными сосудами и метаболизм органических нитратов в
крыса. Журнал фармакологии и экспериментальной терапии. 1984;228:334–341. [PubMed] [Google Scholar] 265. Sutton SC, Fung HL. Метаболиты снижают плазменный клиренс изосорбида динитрата.
у крыс. Биофармацевтика и утилизация лекарств. 1984; 5: 85–89. [PubMed] [Google Scholar] 266. Blundell JE, Campbell DB, Lesham M, Tozer R. Сравнение динамики аноректического эффекта
фенфлурамин и амфетамин с уровнями наркотиков в крови. Дж Фарм Фармакол. 1975; 27: 187–192. [PubMed] [Google Scholar] 267. Хансен А.Р., Кеннеди К.А., Амбре Дж.Дж., Фишер Л.Дж. Отравление глутетимидом. Метаболит способствует заболеваемости и
смертность. 268. Морино А., Сугияма М. Связь между динамикой фармакологических эффектов и
уровень камазепама и его активных метаболитов в плазме
крысы. J Фармакобиодин. 1985; 8: 597–606. [PubMed] [Google Scholar] 269. Sandouk P, Serrie A, Urtizberea M, Debray M, Got P, Sherrmann JM. Фармакокинетика морфина и оценка боли после
интрацеребровентрикулярное введение у больных с терминальной
рак. Клиническая фармакология и терапия. 1991;49:442–448. [PubMed] [Google Scholar] 270. Экблом М., Гардмарк М., Хаммарлунд-Уденаес М. Оценка несвязанных концентраций морфина в
концентрации микродиализата с использованием нелинейного регрессионного анализа в
vivo и in vitro в стационарных условиях. Жизнь наук. 1992; 51: 449–460. [PubMed] [Google Scholar] 271. Gardmark M, Hammarlund-Udenaes M. Отсроченный антиноцицептивный эффект после морфина-6-глюкуронида
введение крысам — фармакокинетические/фармакодинамические
моделирование. 272. Bouw MR, Gardmark M, Hammarlund-Udenaes M. Фармакокинетическое-фармакодинамическое моделирование транспорта морфина
через гематоэнцефалический барьер как причина антиноцицептивного эффекта
задержка у крыс — исследование микродиализа. Фармацевтические исследования. 2000;17:1220–1227. [PubMed] [Google Scholar] 273. Bouw MR, Xie R, Tunblad K, Hammarlund-Udenaes M. Транспорт через гематоэнцефалический барьер и распределение в головном мозге
морфин-6-глюкуронид в отношении антиноцицептивного эффекта при
крысы — фармакокинетическое/фармакодинамическое моделирование. Британский журнал фармакологии. 2001;134:1796–1804. [Бесплатная статья PMC] [PubMed] [Google Scholar] 274. Мердок Д., Брогден Р.Н. Препараты нифедипина с замедленным высвобождением. оценка их
современные применения и предполагаемые роли в лечении гипертонии,
ишемическая болезнь сердца и заболевания периферических сосудов. Наркотики. 1991; 41: 737–779. 275. Hocht C, Di Verniero C, Opezzo JA, Bramuglia GF, Taira CA. Фармакокинетико-фармакодинамическое (ПК-ФД) моделирование
Сердечно-сосудистые эффекты метопролола у крыс со спонтанной гипертензией:
микродиализное исследование. Naunyn Schmiedebergs Arch Pharmacol. 2006; 373:310–318. [PubMed] [Академия Google] 276. Hocht C, Di Verniero C, Opezzo JA, Taira CA. Фармакокинетические-фармакодинамические свойства метопролола при
хроническая коарктация аорты у крыс. Naunyn Schmiedebergs Arch Pharmacol. 2004; 370:1–8. [PubMed] [Google Scholar] 277. van Steeg TJ, Freijer J, Danhof M, de Lange EC. Фармакокинетико-фармакодинамическое моделирование
S(-)-атенолол у крыс: уменьшение индуцированной изопреналином тахикардии
как непрерывная фармакодинамическая конечная точка. Британский журнал фармакологии. 2007; 151: 356–366. [Бесплатная статья PMC] [PubMed] [Google Scholar] 278. Вакилы М., Хораше Ф., Джамали Ф. Зависимость желудочно-кишечной токсичности от скорости высвобождения
тиапрофеновая кислота: новый фармакокинетико-фармакодинамический
модель. 279. Клифтон Г.Д., Блуэн Р.А., Дилеа С., Шран Х.Ф., Хасселл А.Е., Гонасун Л.М., Фостер Т.С. Фармакокинетика перорального исрадипина в норме
волонтеры. Журнал клинической фармакологии. 1988; 28:36–42. [PubMed] [Google Scholar] 280. Перес-Уризар Дж., Гранадос-Сото В., Флорес-Мурриета Ф.Дж., Кастанеда-Эрнандес Г. Фармакокинетическое-фармакодинамическое моделирование: почему? Арх Мед Рез. 2000;31:539–545. [PubMed] [Google Scholar] 281. Westin UE, Bostrom E, Grasjo J, Hammarlund-Udenaes M, Bjork E. Прямой перенос морфина через нос в мозг после назального введения.
введение крысам. Фармацевтические исследования. 2006; 23: 565–572. [PubMed] [Google Scholar] 282. Westin U, Piras E, Jansson B, Bergstrom U, Dahlin M, Brittebo E, Bjork E. Перенос морфина по обонятельному пути в центральную
нервной системы после назального введения грызунам. Eur J Pharm Sci. 2005; 24: 565–573. [PubMed] [Академия Google] 283. 284. Мандема Дж. В., Венг-Педерсен П., Данхоф М. Оценка уравновешивания плазменного эффекта амобарбитала.
кинетика. Актуальность полиэкспоненциальных функций проводимости. Журнал фармакокинетики и биофармацевтики. 1991;19:617–634. [PubMed] [Google Scholar] 285. Duggan DE, Hooke KF, Noll RM, Kwan KC. Энтерогепатическая циркуляция индометацина и его роль в
раздражение кишечника. Биохимическая фармакология. 1975; 24: 1749–1754. [PubMed] [Google Scholar] 286. Colburn WA. Одновременное фармакокинетическое и фармакодинамическое
моделирование. Журнал фармакокинетики и биофармацевтики. 1981; 9: 367–388. [PubMed] [Google Scholar] 287. Hooper SA, Bowsher RR, Howey DC. 288. Ebling WF, Wada DR, Stanski DR. От кусочного к полному физиологическому фармакокинетическому моделированию:
применительно к расположению тиопентала у крыс. Журнал фармакокинетики и биофармацевтики. 1994; 22: 259–292. [PubMed] [Google Scholar] 289. Kitts JB, Fisher DM, Canfell PC, Spellman MJ, Caldwell JE, Heier T, Fahey MR, Miller RD. Фармакокинетика и фармакодинамика атракурия при
пожилой. Анестезиология. 1990; 72: 272–275. [PubMed] [Академия Google] 290. Донати Ф., Варин Ф., Дюшарм Дж., Гилл С.С., Теоретик Ю., Беван Д.Р. Фармакокинетика и фармакодинамика атракурия, полученного с
образцы артериальной и венозной крови. Клиническая фармакология и терапия. 1991; 49: 515–522. [PubMed] [Google Scholar] 291. 292. Marathe PH, Dwersteg JF, Pavlin EG, Haschke RH, Heimbach DM, Slattery JT. Влияние термического повреждения на фармакокинетику и
Фармакодинамика атракурия у человека. Анестезиология. 1989; 70: 752–755. [PubMed] [Google Scholar] 293. Строуго А., Зуурман Л., Рой С., Пинкьер Дж. Л., ван Гервен Дж. М., Коэн А. Ф., Шумейкер Р. С. Моделирование зависимости концентрация-эффект ТГК на
параметры центральной нервной системы и частота сердечных сокращений — понимание ее
механизмов действия и инструмент для клинических исследований и разработки
каннабиноиды. Дж Психофармакол. 2008; 22: 717–726. [PubMed] [Академия Google] 294. Андерсон Б.Дж., Холфорд Н.Х., Вуллард Г.А., Чан П.Л. Фармакокинетика парацетамола в плазме и спинномозговой жидкости при
дети. 295. Schwartz JB, Verotta D, Sheiner LB. Фармакодинамическое моделирование эффектов верапамила в равновесном состоянии
и нестационарных условиях. Журнал фармакологии и экспериментальной терапии. 1989; 251:1032–1038. [PubMed] [Академия Google] 296. Rumpler MJ, Kandala B, Vickroy TW, Hochhaus G, Sams RA. Фармакокинетика и фармакодинамика гликопирролата после
непрерывная инфузия лошади. J Vet Pharmacol Ther. 2013 [PubMed] [Google Scholar] 297. Sogaard B, Mengel H, Rao N, Larsen F. Фармакокинетика эсциталопрама после перорального и внутривенного введения.
введение однократной и многократной дозы здоровым
предметы. Журнал клинической фармакологии. 2005;45:1400–1406. [PubMed] [Академия Google] 298. Памулапати Ч.Р., Шенвальд Р.Д. Глазная фармакокинетика нового аналога тетрагидрохинолина при
кролик: компартментальный анализ и оценка PK-PD. Журнал фармацевтических наук. 299. Huang YF, Upton RN, Runciman WB. В/в болюсное введение субконвульсивных доз лигнокаина
овца в сознании: взаимосвязь между фармакокинетикой миокарда и
фармакодинамика. Британский журнал анестезии. 1993; 70: 556–561. [PubMed] [Академия Google] 300. Huang YF, Upton RN, Zheng D, McLean C, Gray EC, Grant C. Специфичная для энантиомера кинетика и динамика верапамила после
быстрое внутривенное введение овцам: физиологический анализ и
моделирование. Журнал фармакологии и экспериментальной терапии. 1998; 284:1048–1057. [PubMed] [Google Scholar] 301. Davis NR, Mapleson WW. Физиологическая модель распределения введенных агентов,
с особой ссылкой на петидин. Британский журнал анестезии. 1993; 70: 248–258. [PubMed] [Академия Google] 302. Габриэльссон Дж.Л., Йоханссон П., Бондессон У., Карлссон М., Паалзов Л.К. Анализ петидиновой диспозиции у беременных крыс с помощью
модель физиологического течения. Журнал фармакокинетики и биофармацевтики. 303. Бьоркман С., Вада Д.Р., Стански Д.Р., Эблинг В.Ф. Сравнительная физиологическая фармакокинетика фентанила и
альфентанил у крыс и людей на основе параметрического
модели. Журнал фармакокинетики и биофармацевтики. 1994;22:381–410. [PubMed] [Google Scholar] 304. Krejcie TC, Jacquez JA, Avram MJ, Niemann CU, Shanks CA, Henthorn TK. Использование параллельных функций плотности Эрланга для анализа первого прохода
легочное поглощение нескольких индикаторов у собак. Журнал фармакокинетики и биофармацевтики. 1996; 24: 569–588. [PubMed] [Google Scholar] 305. Робертс М.С., Дональдсон Дж.Д., Роуленд М. Модели печеночной элиминации: сравнение стохастических моделей с
описывать распределения времени пребывания и прогнозировать влияние наркотиков
распределение, гетерогенность ферментов и системная рециркуляция в печени
устранение. Журнал фармакокинетики и биофармацевтики. 1988;16:41–83. [PubMed] [Google Scholar] 306. 307. Ariens EJ. Стереохимия, основа изощренной чепухи в
фармакокинетика и клиническая фармакология. Европейский журнал клинической фармакологии. 1984; 26: 663–668. [PubMed] [Google Scholar] 308. Patat A, le Coz F, Dubruc C, Gandon JM, Durrieu G, Cimarosti I, Jezequel S, Curet O, Zieleniuk I, Allain H, Rosenzweig P. Фармакодинамика и фармакокинетика двух режимы дозирования
бефлоксатон, новый обратимый и селективный ингибитор моноаминоксидазы,
стабильное состояние у здоровых добровольцев. Журнал клинической фармакологии. 1996;36:216–229. [PubMed] [Google Scholar] 309. Jenkins AJ, Keenan RM, Henningfield JE, Cone EJ. Корреляция между фармакологическими эффектами и кокаином в плазме
концентрации после курения администрации. Журнал аналитической токсикологии. 2002; 26: 382–392. [PubMed] [Google Scholar] 310. Evans SM, Cone EJ, Henningfield JE. Артериальные и венозные концентрации кокаина в плазме крови человека:
взаимосвязь с путем введения, сердечно-сосудистыми эффектами и
субъективные эффекты. 311. Mold DR, DeFeo TM, Reele S, Milla G, Limjuco R, Crews T, Choma N, Patel IH. Одновременное моделирование фармакокинетики и
Фармакодинамика мидазолама и диазепама. Клиническая фармакология и терапия. 1995; 58: 35–43. [PubMed] [Google Scholar] 312. Бюрер М., Мэтр П.О., Кревуазье С., Стански Д.Р. Электроэнцефалографические эффекты бензодиазепинов. II.
Фармакодинамическое моделирование электроэнцефалографических эффектов мидазолама
и диазепам. Клиническая фармакология и терапия. 1990;48:555–567. [PubMed] [Google Scholar] 313. Bellissant E, Giudicelli JF. Фармакокинетико-фармакодинамическая модель фантофарона для сердечно-сосудистой и
Влияние на плечевую гемодинамику у здоровых добровольцев. Британский журнал клинической фармакологии. 1999; 48:801–810. [Бесплатная статья PMC] [PubMed] [Google Scholar] 314. Woodworth JR, Howey DC, Bowsher RR. Установление профилей времени действия для обычного инсулина и инсулина НПХ
с помощью фармакодинамического моделирования. 315. Carlucci L, Song KH, Yun HI, Park HJ, Seo KW, Giorgi M. Фармакокинетика и фармакодинамика (PK/PD) или ирбесартан в
Собаки породы бигль после перорального введения в двух дозировках. Польский журнал ветеринарных наук. 2013; 16: 555–561. [PubMed] [Google Scholar] 316. Bellissant E, Giudicelli JF. Фармакокинетико-фармакодинамическая модель периндоприлата региональная
гемодинамические эффекты у здоровых добровольцев и при застойной сердечной недостаточности
пациенты. Журнал клинической фармакологии. 2001; 52: 25–33. [Бесплатная статья PMC] [PubMed] [Google Scholar] 317. Эванс М.А., Шанкс К.А., Браун К.Ф., Триггс Э.Дж. Фармакокинетическое и фармакодинамическое моделирование с
панкуроний. Eur J Clin Pharmacol. 1984; 26: 243–250. [PubMed] [Google Scholar] 318. Takahashi H, Ogata H, Kashiwada K, Ohira M, Someya K. Зависимость дозирования пропранолола от плазмы
концентрация и β-блокаторы. Журнал фармакологии и экспериментальной терапии. 319. Paintaud G, Alvan G, Berninger E, Gustafsson LL, Idrizbegovic E, Karlsson KK, Wakelkamp M. Связь между концентрацией и эффектом слуха, вызванного хинином.
нарушение. Клиническая фармакология и терапия. 1994;55:317–323. [PubMed] [Google Scholar] 320. Koch KM, Liu M, Davis IM, Shaw S, Yin Y. Фармакокинетика и фармакодинамика ранитидина при почечной недостаточности.
нарушение. Европейский журнал клинической фармакологии. 1997; 52: 229–234. [PubMed] [Google Scholar] 321. Шварц Дж. Б., Веротта Д., Шейнер Л. Б. Фармакодинамическое моделирование эффектов верапамила в равновесном состоянии
и нестационарных условиях. Журнал фармакологии и экспериментальной терапии. 1989; 251:1032–1038. [PubMed] [Академия Google] 322. Bellissant E, Giudicelli JF. Фармакокинетическая-фармакодинамическая модель забициприлата
концентрации в плазме к плечевым и бедренным гемодинамическим эффектам в
нормотензивные добровольцы. Британский журнал клинической фармакологии. 323. Buss NE, Renwick G. Изменения артериального давления и симпатические функции у крыс с учетом
циклогексиламин внутривенно. Токсикология и прикладная фармакология. 1992; 115: 211–215. [PubMed] [Академия Google] 324. Эйхельбаум М., Хенгстманн Дж. Х., Рост Х. Д., Брехт Т., Денглер Х. Дж. Фармакокинетика, сердечно-сосудистые и метаболические действия
циклогексиламин у человека. Архивы токсикологии. 1974; 31: 243–264. [PubMed] [Google Scholar] 325. Porchet HC, Benowitz NL, Sheiner LB. Фармакодинамическая модель толерантности: приложение к
Никотин. Журнал фармакологии и экспериментальной терапии. 1988; 244: 231–236. [PubMed] [Google Scholar] 326. Hull CJ, Van Beem HB, McLeod K, Sibbald A, Watson MJ. Фармакодинамическая модель панкурония. Британский журнал анестезии. 1978;50:1113–1123. [PubMed] [Google Scholar] 327. Кахконен С. Пропранолол у больных алкоголизмом. Немецкий журнал психиатрии. 328. Lemmens HJ, Dyck JB, Shafer SL, Stanski DR. Фармакокинетико-фармакодинамическое моделирование при разработке лекарственных средств:
Применение к исследуемому опиоиду трефентанилу. Клиническая фармакология и терапия. 1994; 56: 261–271. [PubMed] [Google Scholar] 329. Jusko WJ, Ko HC, Ebling WF. Конвергенция прямого и непрямого фармакодинамического ответа
модели. Джей Фарм Биофарм. 1995;23:5–8. [PubMed] [Google Scholar] 330. Dayneka NL, Garg V, Jusko WJ. Сравнение четырех основных моделей непрямой фармакодинамической
ответы. J Pharmacokinet Biopharm. 1993; 21: 457–478. [Бесплатная статья PMC] [PubMed] [Google Scholar] 331. Jusko WJ, Ko HC. Модели физиологической непрямой реакции характеризуют различные типы
фармакодинамических эффектов. Клин Фарм Тер. 1994; 56: 406–419. [PubMed] [Google Scholar] 332. Шарма А., Юско В.Дж. Характеристика четырех основных моделей косвенного
фармакодинамические реакции. J Pharmacokinet Biopharm. 333. Sharma A, Jusko WJ. Характеристики моделей непрямой фармакодинамики и
приложения к клиническому лекарственному ответу. Бр Дж Клин Фармакол. 1998; 45: 229–239. [Бесплатная статья PMC] [PubMed] [Google Scholar] 334. Antila S, Kivikko M, Lehtonen L, Eha J, Heikkilä A, Pohjanjousi P, Pentikäinen PJ. Фармакокинетика левосимендана и его циркулирующих метаболитов
у пациентов с сердечной недостаточностью после длительной непрерывной инфузии
левосимендан. Бр Дж Клин Фармакол. 2004; 57: 412–415. [Бесплатная статья PMC] [PubMed] [Google Scholar] 335. Bellisant E, Sebille V, Paintaud G. Методологические вопросы фармакокинетики-фармакодинамики
моделирование. клин. Фармакокин. 1998;35(2):151–165. [PubMed] [Google Scholar] 336. Upton RN, Mold DR. Основные понятия в моделировании населения, имитационном моделировании и
разработка лекарств на основе моделей: Часть 3. Введение в фармакодинамические исследования
Методы моделирования. 337. Yamazaki S, Skaptason J, Romero D, Lee JH, Zou HY, Christensen JG, Koup JR, Smith BJ, Koudriakova T. Фармакокинетико-фармакодинамическое моделирование реакции биомаркеров
и ингибирование роста опухоли перорально доступным ингибитором киназы cmet в
мышиные модели ксенотрансплантата опухоли человека. Метаболизм и распределение лекарств. 2008; 36: 1267–1274. [PubMed] [Академия Google] 338. Groenendaal D, Freijer J, de Mik D, Bouw MR, Danhof M. ECM de Lange, Влияние биофазного распределения и
Взаимодействие Р-гликопротеина при фармакокинетически-фармакодинамическом моделировании
Влияние морфина на ЭЭГ. Британский журнал фармакологии. 2007; 151:713–720. [Бесплатная статья PMC] [PubMed] [Google Scholar] 339. Chen C, Pollack GM. Измененное расположение и антиноцицепция
[D-пеницилламин 2,5 ] Энкефалин в mdr1a-дефицитном гене
Мыши. Журнал фармакологии и экспериментальной терапии. 340. Bellissant E, Chau NP, Thuillez C, Gerbeau C, Richard C, Giudicelli JF. Фармакокинетико-фармакодинамическая модель, относящаяся к плазме спираприлата
концентрации к системным и регионарным гемодинамическим эффектам при застойных
сердечная недостаточность. Журнал сердечно-сосудистой фармакологии. 1997; 30: 253–260. [PubMed] [Google Scholar] Сегнетоэлектрические материалы имеют петлю гистерезиса, как и ферромагнитные материалы. также сохраняют свое состояние поляризации после воздействия электрического поля, что делает их полезными в качестве воспоминаний. Текущий класс сегнетоэлектрических компонентов ограничен памятью от нескольких производителей, но новые области электрооптики и электроники могут использовать преимущества сегнетоэлектриков для создания широкого спектра устройств. Сегнетоэлектрическая память использует для хранения данных ферроэлектрическую петлю гистерезиса. Когда вы думаете о гистерезисе, вы, вероятно, думаете о ферромагнитных компонентах, таких как катушки индуктивности с железным сердечником и ферритовые трансформаторы. Гистерезис также имеет место в триггерах Шмитта, чтобы обеспечить некоторый уровень помехозащищенности, который обеспечивает простое электрическое переключение, когда входное напряжение превышает некоторый заданный порог. Существует еще один класс материалов, демонстрирующих гистерезис и характер переключения: сегнетоэлектрики. Сегнетоэлектрический материал является электрическим аналогом ферромагнитного материала, но физический механизм, управляющий гистерезисом в этих материалах, отличается. Ферромагнетики нашли множество применений, связанных с преобразованием энергии, фильтрацией и изоляцией, но сегнетоэлектрики не получили такого же уровня распространения. Уникальные устройства в электронике могут использовать гистерезис в сегнетоэлектрических материалах, возникающий при взаимодействии электрического поля с веществом. Отличие сегнетоэлектриков от других диэлектриков состоит в том, что сегнетоэлектрики сохраняют свою поляризацию после снятия поля, тогда как другие диэлектрики возвращаются в нейтральное состояние. Кроме того, сегнетоэлектрики могут быть возвращены в нейтральное состояние, если к материалу приложено достаточно сильное противоположно направленное поле. Это похоже на ферромагнетизм тем, что ферромагнетик может сохранять свою намагниченность после воздействия магнитного поля. Эта необходимость преодолеть порог для изменения величины и направления остаточной поляризации означает, что эти материалы демонстрируют гистерезис, как магнит. Сегнетоэлектрическая петля гистерезиса, показывающая полную поляризацию в сегнетоэлектрическом материале. На сегнетоэлектрической петле гистерезиса есть три важных момента: Электрическая коэрцитивность (E C ) : Это электрическое поле, необходимое для переключения поляризации между положительными и отрицательными значениями. Обратите внимание, что положительное поле может индуцировать отрицательную поляризацию, приводя к отрицательной емкости. Остаточная поляризация (P R ) : Величина поляризации, которая остается в материале после удаления электрического поля Поляризация насыщения (P S ) : Это максимальная степень поляризации, которая может быть вызвана в материале при высокой напряженности электрического поля. Обратите внимание, что те же самые точки могут быть извлечены из петли ферромагнитного гистерезиса. Эти важные точки на петле гистерезиса зависят от физического механизма, управляющего поляризационным гистерезисом в сегнетоэлектрических материалах. На макроскопическом уровне падающее электрическое поле создает сдвиг в пространственном распределении связанных зарядов, который количественно определяется как поляризация в уравнениях Максвелла. Структура этих материалов позволяет зафиксировать это изменение в распределении связанного заряда, при этом связанный заряд остается в новом распределении даже после того, как падающее электрическое поле исчезнет. Физические механизмы этого явления на микроскопическом уровне включают миграцию ионов и заполнение состояния ловушки, и это лишь некоторые из них. Математически поляризация в материале является кусочно-нелинейной, в зависимости от того, увеличивается или уменьшается поле. Существует множество применений ферроэлектрических материалов для использования в электронике, от настраиваемых нелинейных компонентов до производства энергии. Некоторые примеры включают: Динамические конденсаторы с большим динамическим диапазоном и чувствительностью, чем варакторы Конденсаторы с отрицательной емкостью Нелинейные волноводы для фотоники Солнечные элементы на основе перовскита, эффективность которых может поддерживаться при падении поля Высокочувствительные пироэлектрические датчики Модуляторы Энергонезависимая память Среди этих потенциальных применений перовскитные солнечные элементы привлекли большое внимание исследователей и могут стать следующими коммерчески доступными сегнетоэлектрическими продуктами. Возможно, самым популярным ферроэлектрическим устройством, доступным в настоящее время, является ферроэлектрическая оперативная память (FRAM). Эти устройства имеют относительно простую структуру, в которой используется ферроэлектрический полупроводник в процессе CMOS. В этом типе устройства ферроэлектрический материал размещается в качестве диэлектрического прокладочного слоя на основании структуры NPN-транзистора. Бит можно сохранить как поляризацию в сегнетоэлектрике. Кроме того, гистерезис в сегнетоэлектрике гарантирует, что бит не будет потерян, если только к словной линии не будет приложено достаточно большое поле, чтобы изменить или сбросить поляризацию. Сегнетоэлектрическая петля гистерезиса, показывающая полную поляризацию в сегнетоэлектрическом материале. Текущая линейка продуктов FRAM обеспечивает только до 8 МБ памяти на модуль, которая распределена по нескольким банкам. Однако остаточная поляризация в этом материале имеет неограниченную способность к циклическому чтению-записи, а остаточная поляризация гарантирует, что материал функционирует как энергонезависимая память. Если процессы сегнетоэлектрических полупроводников будут усовершенствованы, можно будет продавать больше устройств FRAM и других сегнетоэлектрических продуктов. Если вам нужно учесть петлю сегнетоэлектрического гистерезиса в ваших новых проектах, вы можете использовать интерфейсные функции Cadence для создания электрической схемы для вашего проекта, а также вы можете использовать приложения для моделирования в PSpice Simulator для создания сегнетоэлектрические компоненты для моделирования. Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin
Посетить сайт
Больше контента от Cadence PCB Solutions
Загрузка, подождите Ошибка — что-то пошло не так! Хотите последние новости о печатных платах? Спасибо! Точка зрения Крис Лейтон • Physics 3, 79 Измерения петли гистерезиса в технологически важных магнитных материалах выявили поразительные отклонения от некоторых фундаментальных и общепринятых представлений в физике ферромагнетизма. Кредит: адаптировано из A. Berger et al. [14] Авторы и права: адаптировано из A. Berger et al. [14] × Понятие гистерезиса является фундаментальным для физики ферромагнетизма, значительно увеличивая как необычайное богатство отображаемой физики, так и разнообразие применений магнитных материалов. Проще говоря, магнитное состояние ферромагнетика зависит не только от внешнего магнитного поля, испытываемого в какой-то момент времени, но и от поля история , что приводит к двузначным кривым зависимости намагниченности от поля, называемым петлями гистерезиса [1,2]. Описанные выше простые петли гистерезиса намагниченности на самом деле правильнее называть большими петлями гистерезиса, т. е. такими, для которых начальное и конечное поля превышают поле замыкания, где свойство гистерезиса исчезает. Незначительные петли гистерезиса , где максимальные приложенные поля лежат ниже замыкающего поля, также полезны, поскольку они предоставляют дополнительную информацию о микроскопических деталях того, как меняется намагниченность на противоположное, в дополнение к тому, что они больше напоминают цикл рабочего поля в некоторых приложениях. Они также составляют основу для множества более сложных анализов (например, ссылки [6–10]), таких как «ΔH» [8] и кривая обращения первого порядка (FORC) [9].,10] методики, дающие более детальное представление о механизмах гистерезиса. Таким образом, малые петли составляют основную часть арсенала экспериментатора, пытающегося понять механизмы перемагничивания в ферромагнитных материалах. Однако уникальность и повторяемость, которые так хорошо известны для макроскопических больших петель, представляют собой гораздо более тонкую проблему для малых петель гистерезиса. Учитывая эту ситуацию, весьма неожиданно, что в статье Physical Review B Андреаса Бергера, Стефана Манжена, Джеффри МакКорда, Олава Хеллвига и Эрика Фуллертона [14] сообщается об открытии поразительно больших отклонений с этой картинки. Эта группа, состоящая из исследователей из CIC nanoGUNE (Испания), Nancy-Université (Франция), Forschungszentrum Dresden-Rossendorf (Германия), Hitachi Global Storage Technologies (США) и Калифорнийского университета в Сан-Диего (США), наблюдала явление, при котором последовательные второстепенные петли, полученные в идентичных условиях, вместо того, чтобы быть в значительной степени повторяемыми, на самом деле демонстрируют массивное кумулятивное расширение, претерпевая увеличение потерь на гистерезис до 350%. Основное явление показано на рис. 1(а), на котором показана большая петля гистерезиса многослойной тонкой пленки Co/Pt в дополнение к ряду последовательных второстепенных петель, полученных путем циклического изменения поля в пределах ±290Э. Эти многослойные образцы изготавливаются путем последовательного физического осаждения из паровой фазы нескольких ультратонких слоев Co и Pt, процесса, специально разработанного для создания свойства перпендикулярной магнитной анизотропии [2], которое необходимо для работы современных магнитных записывающих сред. Как ясно показано на рис. Ключевое понимание лежащего в основе физического механизма было обеспечено визуализацией магнитных доменов, полученной с использованием магнитооптического эффекта Керра [1,2]. Используя эту технику, авторы смогли отобразить доменную структуру в различных точках вокруг малой петли, повторяя это в течение нескольких последовательных циклов поля. Результаты показывают некоторые поразительные корреляции между паттернами доменов как в разных полях в пределах данной малой петли, так и между последовательными малыми петлями в данном поле. Изображения показывают не только эффект памяти, когда структура доменов воссоздает структуру, полученную во время предыдущего цикла поля, но также, что особенно важно, эффект расширения, когда обратные домены растут в поперечном направлении с последовательным циклом поля, как показано на рис. В дополнение к демонстрации того, что кумулятивный рост малых петель может быть очень большим (что явно имеет важные последствия для других методов анализа, основанных на измерениях малых петель), и выяснению еще одного интересного явления в магнетизме материалов с перпендикулярной магнитной анизотропией. , весьма вероятно, что эта работа будет стимулировать дополнительные исследования в будущем. Хотя визуализация доменов авторов дает глубокое представление о механизме реверсии, физическое понимание процессов, лежащих в основе зарождения таких доменных структур, потребует дальнейших исследований. Крис Лейтон — адъюнкт-профессор кафедры химического машиностроения и материаловедения Миннесотского университета. После докторской степени. по физике конденсированного состояния в Даремском университете (1998) и после получения докторской степени по физике конденсированных сред в Калифорнийском университете в Сан-Диего (1998–2001 гг.), он присоединился к факультету материаловедения в Университете Миннесоты, где в настоящее время занимает кафедру и является президентом Макнайта. Парень. Его исследовательские интересы лежат в основном в области магнетизма, в настоящее время в области сложных оксидов, ферромагнетиков с высокой спиновой поляризацией, спинового транспорта, а также магнитных наноструктур и интерфейсов. Магнетизм Магнетизм Конфликт интересов
Примечание издателя
 Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.
Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем. Дополнительный материал
Ссылки
 Н. (1998). О формировании нанокристаллов в магнитомягком сплаве Fe 73,5 Nb 3 Cu 1 Si 13,5 B 9 . Acta Materialia 46, 1861–1874 гг. doi:10.1016/s1359-6454(97)00436-9
Н. (1998). О формировании нанокристаллов в магнитомягком сплаве Fe 73,5 Nb 3 Cu 1 Si 13,5 B 9 . Acta Materialia 46, 1861–1874 гг. doi:10.1016/s1359-6454(97)00436-9  , Коймен А. Р. и Саламон М. Б. (2007). Настраиваемая отрицательная и положительная коэрцитивность обменных пружин SmCo∕(Co∕Gd), исследованная с помощью СКВИД-магнитометрии. Физ. Rev. B 76, 214430. doi:10.1103/physrevb.76.214430
, Коймен А. Р. и Саламон М. Б. (2007). Настраиваемая отрицательная и положительная коэрцитивность обменных пружин SmCo∕(Co∕Gd), исследованная с помощью СКВИД-магнитометрии. Физ. Rev. B 76, 214430. doi:10.1103/physrevb.76.214430  , Вьегас А.Д.К. и Шмидт Дж.Э. (1998). Отрицательная остаточная намагниченность мелких частиц с конкурирующими кубическими и одноосными анизотропиями. J. Appl. физ. 84, 1488–1492. doi:10.1063/1.368214
, Вьегас А.Д.К. и Шмидт Дж.Э. (1998). Отрицательная остаточная намагниченность мелких частиц с конкурирующими кубическими и одноосными анизотропиями. J. Appl. физ. 84, 1488–1492. doi:10.1063/1.368214  Physica B: Конденсированные вещества 299, 215–224. doi:10.1016/s0921-4526(01)00468-9
Physica B: Конденсированные вещества 299, 215–224. doi:10.1016/s0921-4526(01)00468-9  2211340122
2211340122  Физ. Rev. B 95, 100401. doi:10.1103/physrevb.95.100401
Физ. Rev. B 95, 100401. doi:10.1103/physrevb.95.100401  J. Appl. физ. 75, 6673. doi:10.1063/1.356891
J. Appl. физ. 75, 6673. doi:10.1063/1.356891  Заяв. физ. лат. 63, 1585–1587. doi:10.1063/1.110756
Заяв. физ. лат. 63, 1585–1587. doi:10.1063/1.110756  J. Appl. физ. 103 (3), 07б906. doi:10.1063/1.2830966
J. Appl. физ. 103 (3), 07б906. doi:10.1063/1.2830966  J. Appl. физ. 84, 1918–1923 гг. doi:10.1063/1.368319
J. Appl. физ. 84, 1918–1923 гг. doi:10.1063/1.368319 Понимание загадки петли гистерезиса в фармакокинетике /
Фармакодинамические отношения
 Клиническая фармакология и терапия. 1979; 25: 358–371. [PubMed] [Google Scholar]
Клиническая фармакология и терапия. 1979; 25: 358–371. [PubMed] [Google Scholar]  Фармацевтические исследования. 1993; 10:889–894. [PubMed] [Google Scholar]
Фармацевтические исследования. 1993; 10:889–894. [PubMed] [Google Scholar]  Е., Капур С., Квон Дж.С. Прогнозирование занятости головного мозга по уровням в плазме с помощью ПЭТ:
превосходство сочетания фармакокинетики с фармакодинамикой при
моделирование отношений. Журнал мозгового кровотока и метаболизма : официальный журнал
Международное общество мозгового кровотока и метаболизма. 2012; 32: 759–768. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Е., Капур С., Квон Дж.С. Прогнозирование занятости головного мозга по уровням в плазме с помощью ПЭТ:
превосходство сочетания фармакокинетики с фармакодинамикой при
моделирование отношений. Журнал мозгового кровотока и метаболизма : официальный журнал
Международное общество мозгового кровотока и метаболизма. 2012; 32: 759–768. [Бесплатная статья PMC] [PubMed] [Google Scholar]  Журнал клинической фармакологии. 2001; 41:44–50. [PubMed] [Google Scholar]
Журнал клинической фармакологии. 2001; 41:44–50. [PubMed] [Google Scholar]  Фармакокинетический и фармакодинамический анализы на основе допамина
Оккупация D2-рецепторов бромокриптином, индуцированная бромкриптином
контралатеральные вращения у крыс с односторонним поражением 6-OHDA. Synapse (Нью-Йорк, штат Нью-Йорк) 2003; 50: 110–116. [PubMed] [Google Scholar]
Фармакокинетический и фармакодинамический анализы на основе допамина
Оккупация D2-рецепторов бромокриптином, индуцированная бромкриптином
контралатеральные вращения у крыс с односторонним поражением 6-OHDA. Synapse (Нью-Йорк, штат Нью-Йорк) 2003; 50: 110–116. [PubMed] [Google Scholar]  Malerczyk C, Fuchs B, Belz GG, Roll S, Butzer R, Breithaupt-Grogler K, Herrmann V, Magin SG, Hogemann A, Voith B, Mutschler E. Антагонизм ангиотензина II и радиорецепторная кинетика плазмы
кандесартан у мужчин. Британский журнал клинической фармакологии. 1998; 45: 567–573. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Malerczyk C, Fuchs B, Belz GG, Roll S, Butzer R, Breithaupt-Grogler K, Herrmann V, Magin SG, Hogemann A, Voith B, Mutschler E. Антагонизм ангиотензина II и радиорецепторная кинетика плазмы
кандесартан у мужчин. Британский журнал клинической фармакологии. 1998; 45: 567–573. [Бесплатная статья PMC] [PubMed] [Google Scholar]  2005; 312: 816–825. [PubMed] [Академия Google]
2005; 312: 816–825. [PubMed] [Академия Google]  1997; 282: 685–690. [PubMed] [Google Scholar]
1997; 282: 685–690. [PubMed] [Google Scholar]  Британский журнал фармакологии. 2008; 155: 276–284. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Британский журнал фармакологии. 2008; 155: 276–284. [Бесплатная статья PMC] [PubMed] [Google Scholar]  Davies NM, Jamali F. Влияние лекарственной формы на гастроэнтеропатию флурбипрофена
у крыс: свидетельство смещения места токсичности. Фармацевтические исследования. 1997; 14:1597–1600. [PubMed] [Google Scholar]
Davies NM, Jamali F. Влияние лекарственной формы на гастроэнтеропатию флурбипрофена
у крыс: свидетельство смещения места токсичности. Фармацевтические исследования. 1997; 14:1597–1600. [PubMed] [Google Scholar]  Влияние скорости ввода лекарств на развитие толерантности
к фуросемиду. Британский журнал клинической фармакологии. 1998;46:479–487. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Влияние скорости ввода лекарств на развитие толерантности
к фуросемиду. Британский журнал клинической фармакологии. 1998;46:479–487. [Бесплатная статья PMC] [PubMed] [Google Scholar]  Европейский журнал клинической фармакологии. 1994;46:29–33. [PubMed] [Google Scholar]
Европейский журнал клинической фармакологии. 1994;46:29–33. [PubMed] [Google Scholar]  Международный журнал клинической фармакологии и терапии. 2003; 41: 365–373. [PubMed] [Google Scholar]
Международный журнал клинической фармакологии и терапии. 2003; 41: 365–373. [PubMed] [Google Scholar]  Дж., фон Мольтке Л.Л., Эренберг Б.Л., Харматц Дж.С., Корбетт К.Е., Уоллес Д.В., Шейдер Р.И. Кинетика и динамика лоразепама во время и после непрерывного
внутривенное вливание. Медицина интенсивной терапии. 2000;28:2750–2757. [PubMed] [Google Scholar]
Дж., фон Мольтке Л.Л., Эренберг Б.Л., Харматц Дж.С., Корбетт К.Е., Уоллес Д.В., Шейдер Р.И. Кинетика и динамика лоразепама во время и после непрерывного
внутривенное вливание. Медицина интенсивной терапии. 2000;28:2750–2757. [PubMed] [Google Scholar]  Журнал фармакокинетики и биофармацевтики. 1989;17:291–304. [PubMed] [Google Scholar]
Журнал фармакокинетики и биофармацевтики. 1989;17:291–304. [PubMed] [Google Scholar]  [PubMed] [Google Scholar]
[PubMed] [Google Scholar]  Brockmeier D, Hajdu P, Henke W, Mutschler E, Palm D, Rupp W, Spahn H, Verho MT, Wellstein A. Пенбутолол: фармакокинетика, влияние на тахикардию при физической нагрузке и
ингибирование связывания радиолиганда in vitro. Европейский журнал клинической фармакологии. 1988;35:613–623. [PubMed] [Google Scholar]
Brockmeier D, Hajdu P, Henke W, Mutschler E, Palm D, Rupp W, Spahn H, Verho MT, Wellstein A. Пенбутолол: фармакокинетика, влияние на тахикардию при физической нагрузке и
ингибирование связывания радиолиганда in vitro. Европейский журнал клинической фармакологии. 1988;35:613–623. [PubMed] [Google Scholar]  Европейский журнал метаболизма и фармакокинетики лекарственных средств. 2001; 26: 123–128. [PubMed] [Google Scholar]
Европейский журнал метаболизма и фармакокинетики лекарственных средств. 2001; 26: 123–128. [PubMed] [Google Scholar]  2010; 113:806–811. [PubMed] [Google Scholar]
2010; 113:806–811. [PubMed] [Google Scholar]  Lehr T, Staab A, Tillmann C, Nielsen EO, Trommeshauser D, Schaefer HG, Kloft C. Вклад активного метаболита M1 в фармакологическую
активность тезофензина in vivo: фармакокинетико-фармакодинамическое моделирование
подход. Британский журнал фармакологии. 2008; 153:164–174. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Lehr T, Staab A, Tillmann C, Nielsen EO, Trommeshauser D, Schaefer HG, Kloft C. Вклад активного метаболита M1 в фармакологическую
активность тезофензина in vivo: фармакокинетико-фармакодинамическое моделирование
подход. Британский журнал фармакологии. 2008; 153:164–174. [Бесплатная статья PMC] [PubMed] [Google Scholar]  II. Триазолам. Фармацевтические исследования. 1990;7:570–576. [PubMed] [Google Scholar]
II. Триазолам. Фармацевтические исследования. 1990;7:570–576. [PubMed] [Google Scholar]  Журнал клинической фармакологии. 1998;38:60–67. [PubMed] [Google Scholar]
Журнал клинической фармакологии. 1998;38:60–67. [PubMed] [Google Scholar]  Клиническая фармакология и терапия. 1989; 46: 408–419.. [PubMed] [Google Scholar]
Клиническая фармакология и терапия. 1989; 46: 408–419.. [PubMed] [Google Scholar]  Нейрохим Рез. 2012;37:2198–2205. [PubMed] [Google Scholar]
Нейрохим Рез. 2012;37:2198–2205. [PubMed] [Google Scholar]  трансплантация. Международный журнал клинической фармакологии, терапии и
токсикология. 1991; 29: 116–123. [PubMed] [Академия Google]
трансплантация. Международный журнал клинической фармакологии, терапии и
токсикология. 1991; 29: 116–123. [PubMed] [Академия Google]  Влияние различных внутривенных инъекций на основе жировой эмульсии
препараты по фармакокинетике и фармакодинамике
пропофол. Фармацевтические исследования. 1998;15:442–448. [PubMed] [Google Scholar]
Влияние различных внутривенных инъекций на основе жировой эмульсии
препараты по фармакокинетике и фармакодинамике
пропофол. Фармацевтические исследования. 1998;15:442–448. [PubMed] [Google Scholar]  Клиническая фармакология и терапия. 1985; 37: 453–459. [PubMed] [Google Scholar]
Клиническая фармакология и терапия. 1985; 37: 453–459. [PubMed] [Google Scholar]  Jacobs JR, Nath PA. Модель отсека для описания периферического артериально-венозного препарата
градиенты концентрации с элиминацией препарата из венозной пробы
купе. Журнал фармацевтических наук. 1995; 84: 370–375. [PubMed] [Google Scholar]
Jacobs JR, Nath PA. Модель отсека для описания периферического артериально-венозного препарата
градиенты концентрации с элиминацией препарата из венозной пробы
купе. Журнал фармацевтических наук. 1995; 84: 370–375. [PubMed] [Google Scholar]  1972; 180: 732–742. [PubMed] [Google Scholar]
1972; 180: 732–742. [PubMed] [Google Scholar]  Иноуэ Ю., Накамура Н., Инагами Т. Обзор исследований мутагенеза ангиотензина II типа 1.
рецептор, трехмерная модель рецептора в поисках агониста и
сайт связывания антагониста и гипотеза активации рецептора
механизм. Дж Гипертензия. 1997;15:703–714. [PubMed] [Google Scholar]
Иноуэ Ю., Накамура Н., Инагами Т. Обзор исследований мутагенеза ангиотензина II типа 1.
рецептор, трехмерная модель рецептора в поисках агониста и
сайт связывания антагониста и гипотеза активации рецептора
механизм. Дж Гипертензия. 1997;15:703–714. [PubMed] [Google Scholar]  Ojima M, Inada Y, Shibouta Y, Wada T, Sanada T, Kubo K, Nishikawa K. Candesartan (CV-11974) медленно диссоциирует от ангиотензина.
Рецептор АТ1. Европейский журнал фармакологии. 1997; 319: 137–146. [PubMed] [Академия Google]
Ojima M, Inada Y, Shibouta Y, Wada T, Sanada T, Kubo K, Nishikawa K. Candesartan (CV-11974) медленно диссоциирует от ангиотензина.
Рецептор АТ1. Европейский журнал фармакологии. 1997; 319: 137–146. [PubMed] [Академия Google]  [PubMed] [Google Scholar]
[PubMed] [Google Scholar]  Антимикробные препараты и химиотерапия. 2004; 48: 1756–1762. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Антимикробные препараты и химиотерапия. 2004; 48: 1756–1762. [Бесплатная статья PMC] [PubMed] [Google Scholar]  1992; 14: 615–621. [PubMed] [Google Scholar]
1992; 14: 615–621. [PubMed] [Google Scholar]  [Google Scholar]
[Google Scholar]  ;3:17. [Бесплатная статья PMC] [PubMed] [Google Scholar]
;3:17. [Бесплатная статья PMC] [PubMed] [Google Scholar]  Евр Дж Анаэстезиол. 1985; 2: 133–142. [PubMed] [Академия Google]
Евр Дж Анаэстезиол. 1985; 2: 133–142. [PubMed] [Академия Google]  Алпразолам у молодых и пожилых мужчин: чувствительность и переносимость
психомоторное, седативное и память эффекты. Журнал фармакологии и экспериментальной терапии. 1997;281:1317–1329. [PubMed] [Google Scholar]
Алпразолам у молодых и пожилых мужчин: чувствительность и переносимость
психомоторное, седативное и память эффекты. Журнал фармакологии и экспериментальной терапии. 1997;281:1317–1329. [PubMed] [Google Scholar]  Trends Pharmacol Sci. 1992; 13: 446–450. [PubMed] [Google Scholar]
Trends Pharmacol Sci. 1992; 13: 446–450. [PubMed] [Google Scholar]  Психофармакология (Берл) 1983; 79: 137–141. [PubMed] [Google Scholar]
Психофармакология (Берл) 1983; 79: 137–141. [PubMed] [Google Scholar]  А., Роарк С.Ф., Смит М.С., Маккарти Э.А., Бьорнссон Т.Д., Притчетт Э.Л. Эффекты длительной внутривенной инфузии дилтиазема у здоровых
лиц. Ам Джей Кардиол. 1986; 58: 1055–1060. [PubMed] [Google Scholar]
А., Роарк С.Ф., Смит М.С., Маккарти Э.А., Бьорнссон Т.Д., Притчетт Э.Л. Эффекты длительной внутривенной инфузии дилтиазема у здоровых
лиц. Ам Джей Кардиол. 1986; 58: 1055–1060. [PubMed] [Google Scholar]  1981; 6: 429–453. [PubMed] [Google Scholar]
1981; 6: 429–453. [PubMed] [Google Scholar]  Sugihara J, Sugawara Y, Ando H, Harigaya S, Etoh A, Kohno K. Исследования метаболизма дилтиазема у человека. J Фармакобиодин. 1984; 7: 24–32. [PubMed] [Google Scholar]
Sugihara J, Sugawara Y, Ando H, Harigaya S, Etoh A, Kohno K. Исследования метаболизма дилтиазема у человека. J Фармакобиодин. 1984; 7: 24–32. [PubMed] [Google Scholar]  Ribeiro JA, Pallot D, Gordon BH, Pallot DJ, Mir A, Ings RMJ, Evrard Y, Campbell DB. Хеморецепторы в дыхательной регуляции. Нидерланды: Спрингер; 1987. Кинетика бисмезилата алмитрина и его метаболитов в
Каротидное тело и другие ткани крысы; стр. 394–407. [Google Scholar]
Ribeiro JA, Pallot D, Gordon BH, Pallot DJ, Mir A, Ings RMJ, Evrard Y, Campbell DB. Хеморецепторы в дыхательной регуляции. Нидерланды: Спрингер; 1987. Кинетика бисмезилата алмитрина и его метаболитов в
Каротидное тело и другие ткани крысы; стр. 394–407. [Google Scholar]  Жизнь наук. 1974;14:1535–1539. [PubMed] [Google Scholar]
Жизнь наук. 1974;14:1535–1539. [PubMed] [Google Scholar]  1982; 31: 775–782. [PubMed] [Академия Google]
1982; 31: 775–782. [PubMed] [Академия Google]  [PubMed] [Google Scholar]
[PubMed] [Google Scholar]  Scand J Rheumatol Suppl. 1978: 5–16. [PubMed] [Google Scholar]
Scand J Rheumatol Suppl. 1978: 5–16. [PubMed] [Google Scholar]  Веротта Д., Шейнер Л.Б. Общая концептуальная модель для нестационарного состояния
фармакокинетические/фармакодинамические данные. Журнал фармакокинетики и биофармацевтики. 1995; 23:1–4. [PubMed] [Google Scholar]
Веротта Д., Шейнер Л.Б. Общая концептуальная модель для нестационарного состояния
фармакокинетические/фармакодинамические данные. Журнал фармакокинетики и биофармацевтики. 1995; 23:1–4. [PubMed] [Google Scholar]  Европейский журнал фармакологии. 1989; 166: 251–260. [PubMed] [Google Scholar]
Европейский журнал фармакологии. 1989; 166: 251–260. [PubMed] [Google Scholar]  1988; 25: 561–569. [Бесплатная статья PMC] [PubMed] [Google Scholar]
1988; 25: 561–569. [Бесплатная статья PMC] [PubMed] [Google Scholar]  Hansen JB, Sandset PM, Huseby KR, Huseby NE, Nordoy A. Истощение внутрисосудистых пулов пути тканевого фактора
ингибитор (TFPI) при многократном или длительном внутривенном введении
гепарин у человека. Тромбоз и гемостаз. 1996; 76: 703–709. [PubMed] [Google Scholar]
Hansen JB, Sandset PM, Huseby KR, Huseby NE, Nordoy A. Истощение внутрисосудистых пулов пути тканевого фактора
ингибитор (TFPI) при многократном или длительном внутривенном введении
гепарин у человека. Тромбоз и гемостаз. 1996; 76: 703–709. [PubMed] [Google Scholar]  Фармакология. 1983; 27 (Приложение 2): 179–187. [PubMed] [Google Scholar]
Фармакология. 1983; 27 (Приложение 2): 179–187. [PubMed] [Google Scholar]  Почки международные. 1981;19:881–891. [PubMed] [Google Scholar]
Почки международные. 1981;19:881–891. [PubMed] [Google Scholar]  Клиническая фармакология и терапия. 1988;43:582–587. [PubMed] [Google Scholar]
Клиническая фармакология и терапия. 1988;43:582–587. [PubMed] [Google Scholar]  Castillo J, Dávalos A, Naveiro J, Noya M. Нейровозбудительные аминокислоты и их связь с размером инфаркта
и неврологический дефицит при ишемическом инсульте. Инсульт; журнал мозгового кровообращения. 1996; 27:1060–1065. [PubMed] [Академия Google]
Castillo J, Dávalos A, Naveiro J, Noya M. Нейровозбудительные аминокислоты и их связь с размером инфаркта
и неврологический дефицит при ишемическом инсульте. Инсульт; журнал мозгового кровообращения. 1996; 27:1060–1065. [PubMed] [Академия Google]  [PubMed] [Google Scholar]
[PubMed] [Google Scholar]  Клиническая фармакология и терапия. 1992;52:139–150. [PubMed] [Google Scholar]
Клиническая фармакология и терапия. 1992;52:139–150. [PubMed] [Google Scholar]  Британский журнал клинической фармакологии. 1980; 9: 67–75. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Британский журнал клинической фармакологии. 1980; 9: 67–75. [Бесплатная статья PMC] [PubMed] [Google Scholar]  Сравнение четырех и наилучшей клинической оценки во время
постоянный паралич. Am J Respir Crit Care Med. 1997; 156: 1556–1561. [PubMed] [Академия Google]
Сравнение четырех и наилучшей клинической оценки во время
постоянный паралич. Am J Respir Crit Care Med. 1997; 156: 1556–1561. [PubMed] [Академия Google]  Журнал клинической фармакологии. 2004; 44: 605–611. [PubMed] [Google Scholar]
Журнал клинической фармакологии. 2004; 44: 605–611. [PubMed] [Google Scholar]  2005; 313:1136–1149. [PubMed] [Google Scholar]
2005; 313:1136–1149. [PubMed] [Google Scholar]  1994; 78: 442–449. [PubMed] [Google Scholar]
1994; 78: 442–449. [PubMed] [Google Scholar]  1969; 10: 22–35. [PubMed] [Google Scholar]
1969; 10: 22–35. [PubMed] [Google Scholar]  Медицинский журнал Новой Англии. 1975;292:250–252. [PubMed] [Google Scholar]
Медицинский журнал Новой Англии. 1975;292:250–252. [PubMed] [Google Scholar]  Боль. 1998;74:287–296. [PubMed] [Google Scholar]
Боль. 1998;74:287–296. [PubMed] [Google Scholar]  [PubMed] [Google Scholar]
[PubMed] [Google Scholar]  Фармацевтические исследования. 1999; 16: 123–129. [PubMed] [Google Scholar]
Фармацевтические исследования. 1999; 16: 123–129. [PubMed] [Google Scholar]  Cox EH, Knibbe CA, Koster VS, Langemeijer MW, Tukker EE, Lange R, Kuks PF, Langemeijer HJ, Lie-A-Huen L, Danhof M. Влияние различных внутривенных инъекций на основе жировой эмульсии
препараты по фармакокинетике и фармакодинамике
пропофол. Фармацевтические исследования. 1998; 15: 442–448. [PubMed] [Google Scholar]
Cox EH, Knibbe CA, Koster VS, Langemeijer MW, Tukker EE, Lange R, Kuks PF, Langemeijer HJ, Lie-A-Huen L, Danhof M. Влияние различных внутривенных инъекций на основе жировой эмульсии
препараты по фармакокинетике и фармакодинамике
пропофол. Фармацевтические исследования. 1998; 15: 442–448. [PubMed] [Google Scholar]  Фармакокинетика и фармакодинамика внутривенных регулярных
человеческого инсулина. В: Garzone PD, Colburn WA, Motokoff M, редакторы. Фармакокинетика и фармакодинамика: пептиды, пептиды и
Белки. Цинциннати, Огайо: Книги Харви Уитни; 1991. [Google Scholar]
Фармакокинетика и фармакодинамика внутривенных регулярных
человеческого инсулина. В: Garzone PD, Colburn WA, Motokoff M, редакторы. Фармакокинетика и фармакодинамика: пептиды, пептиды и
Белки. Цинциннати, Огайо: Книги Харви Уитни; 1991. [Google Scholar]  Donati F, Gill SS, Bevan DR, Ducharme J, Theoret Y, Varin F. Фармакокинетика и фармакодинамика атракурия с и
без предшествующего введения суксаметония. Британский журнал анестезии. 1991; 66: 557–561. [PubMed] [Академия Google]
Donati F, Gill SS, Bevan DR, Ducharme J, Theoret Y, Varin F. Фармакокинетика и фармакодинамика атракурия с и
без предшествующего введения суксаметония. Британский журнал анестезии. 1991; 66: 557–561. [PubMed] [Академия Google]  Британский журнал клинической фармакологии. 1998; 46: 237–243. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Британский журнал клинической фармакологии. 1998; 46: 237–243. [Бесплатная статья PMC] [PubMed] [Google Scholar]  101:414–423. [PubMed] [Google Scholar]
101:414–423. [PubMed] [Google Scholar]  1986; 14: 381–395. [PubMed] [Google Scholar]
1986; 14: 381–395. [PubMed] [Google Scholar]  Beek WJ, Muttzall KMK. Транспортные явления. 2-е изд. Wiley, London: 2000. [Google Scholar]
Beek WJ, Muttzall KMK. Транспортные явления. 2-е изд. Wiley, London: 2000. [Google Scholar]  Журнал фармакологии и экспериментальной терапии. 1996;279:1345–1356. [PubMed] [Google Scholar]
Журнал фармакологии и экспериментальной терапии. 1996;279:1345–1356. [PubMed] [Google Scholar]  Уход за диабетом. 1994; 17:64–69. [PubMed] [Академия Google]
Уход за диабетом. 1994; 17:64–69. [PubMed] [Академия Google]  1993; 265: 681–689. [PubMed] [Google Scholar]
1993; 265: 681–689. [PubMed] [Google Scholar]  1998; 46: 383–393. [Бесплатная статья PMC] [PubMed] [Google Scholar]
1998; 46: 383–393. [Бесплатная статья PMC] [PubMed] [Google Scholar]  1999; 2:12–18. [Google Scholar]
1999; 2:12–18. [Google Scholar]  1996;24:611–635. [PubMed] [Google Scholar]
1996;24:611–635. [PubMed] [Google Scholar]  CPT Pharmacometrics Syst Pharmacol. 2014 2 января; 3:e88. [Бесплатная статья PMC] [PubMed] [Google Scholar]
CPT Pharmacometrics Syst Pharmacol. 2014 2 января; 3:e88. [Бесплатная статья PMC] [PubMed] [Google Scholar]  1998;287:545–552. [PubMed] [Google Scholar]
1998;287:545–552. [PubMed] [Google Scholar] Понимание ферроэлектрической петли гистерезиса в электронике
Ключевые выводы

 Вот некоторые из потенциальных применений этого уникального класса материалов и то, как они могут вести себя в ваших схемах.
Вот некоторые из потенциальных применений этого уникального класса материалов и то, как они могут вести себя в ваших схемах. Что такое ферроэлектрическая петля гистерезиса?
 На приведенном ниже графике показана петля сегнетоэлектрического гистерезиса, которая имеет ту же основную структуру, что и петля магнитного гистерезиса. Некоторые важные моменты отмечены на рисунке.
На приведенном ниже графике показана петля сегнетоэлектрического гистерезиса, которая имеет ту же основную структуру, что и петля магнитного гистерезиса. Некоторые важные моменты отмечены на рисунке. Важные моменты сегнетоэлектрической петли гистерезиса

Движущие силы сегнетоэлектричества
 Те же методы, которые используются для моделирования магнитного гистерезиса, также могут быть использованы для моделирования петли сегнетоэлектрического гистерезиса. Это становится важным при использовании сегнетоэлектриков для создания новых компонентов и для моделирования цепей с этими компонентами. Некоторые интересные устройства могут использовать преимущества сегнетоэлектрического гистерезиса в ряде областей.
Те же методы, которые используются для моделирования магнитного гистерезиса, также могут быть использованы для моделирования петли сегнетоэлектрического гистерезиса. Это становится важным при использовании сегнетоэлектриков для создания новых компонентов и для моделирования цепей с этими компонентами. Некоторые интересные устройства могут использовать преимущества сегнетоэлектрического гистерезиса в ряде областей. Applications of Ferroelectric Materials
 Однако петля сегнетоэлектрического гистерезиса в этих устройствах рассматривается как препятствие на пути к успешному преобразованию энергии, поскольку определение эффективности преобразования становится неоднозначным. Динамические конденсаторы и отрицательные конденсаторы также могут быть коммерциализированы, если процессы производства сегнетоэлектрических полупроводников продолжат развиваться.
Однако петля сегнетоэлектрического гистерезиса в этих устройствах рассматривается как препятствие на пути к успешному преобразованию энергии, поскольку определение эффективности преобразования становится неоднозначным. Динамические конденсаторы и отрицательные конденсаторы также могут быть коммерциализированы, если процессы производства сегнетоэлектрических полупроводников продолжат развиваться. 
 После того, как вы спроектировали свои схемы, вы можете запускать стандартные симуляции с вашими сегнетоэлектрическими компонентами и совершенствовать свои сегнетоэлектрические конструкции.
После того, как вы спроектировали свои схемы, вы можете запускать стандартные симуляции с вашими сегнетоэлектрическими компонентами и совершенствовать свои сегнетоэлектрические конструкции.
Подпишитесь на нашу ежемесячную рассылку новостей Значительный рост малых петель гистерезиса
 .. Показать больше
.. Показать больше  Параметры, характеризующие эти петли, наиболее часто используются для описания магнитного отклика ферромагнетика, определяя соответствующий физический режим, наиболее подходящие модели и возможные области применения [1,2]. Эти приложения широко варьируются в зависимости от степени гистерезиса, от почти полностью обратимых «мягких» ферромагнетиков, используемых в сердечниках трансформаторов, до сильно гистерезисных «жестких» постоянных магнитов, используемых в двигателях, проходящих через точно спроектированные материалы, используемые в носителях записи из жестких материалов. Дисковый привод. Хотя петли гистерезиса демонстрируют сложную зависимость от температуры, времени и частоты, широко распространено мнение, что макроскопические петли гистерезиса повторяются для заданного набора внешних условий. Это замечательный результат, учитывая стохастический характер процесса намагничивания и отсутствие повторяемости в микроскопическом масштабе [3–5], вытекающее только из чисто масштаба макроскопического усреднения.
Параметры, характеризующие эти петли, наиболее часто используются для описания магнитного отклика ферромагнетика, определяя соответствующий физический режим, наиболее подходящие модели и возможные области применения [1,2]. Эти приложения широко варьируются в зависимости от степени гистерезиса, от почти полностью обратимых «мягких» ферромагнетиков, используемых в сердечниках трансформаторов, до сильно гистерезисных «жестких» постоянных магнитов, используемых в двигателях, проходящих через точно спроектированные материалы, используемые в носителях записи из жестких материалов. Дисковый привод. Хотя петли гистерезиса демонстрируют сложную зависимость от температуры, времени и частоты, широко распространено мнение, что макроскопические петли гистерезиса повторяются для заданного набора внешних условий. Это замечательный результат, учитывая стохастический характер процесса намагничивания и отсутствие повторяемости в микроскопическом масштабе [3–5], вытекающее только из чисто масштаба макроскопического усреднения.
 Фактически, измерение последовательных малых петель в идентичных экспериментальных условиях может привести к «дрейфу» формы и размера малой петли, часто называемому «рептацией» (например, ссылки [11,12]). Хотя этот и другие подобные эффекты [13] конечны, до сих пор было обнаружено, что они малы, что позволяет предположить, что их, возможно, лучше всего рассматривать как «возмущение» широко распространенной идеи повторяемости макроскопических петель гистерезиса.
Фактически, измерение последовательных малых петель в идентичных экспериментальных условиях может привести к «дрейфу» формы и размера малой петли, часто называемому «рептацией» (например, ссылки [11,12]). Хотя этот и другие подобные эффекты [13] конечны, до сих пор было обнаружено, что они малы, что позволяет предположить, что их, возможно, лучше всего рассматривать как «возмущение» широко распространенной идеи повторяемости макроскопических петель гистерезиса.  Эти результаты были воспроизведены в двух системах материалов и, в сочетании с подробным исследованием магнитной микроскопии, позволили авторам представить объяснение этого поразительного явления с точки зрения последовательного накопления малых доменов зарождения , то есть микроскопических областей перемагничивания, которые действуют как зародыши для последующего макроскопического перемагничивания.
Эти результаты были воспроизведены в двух системах материалов и, в сочетании с подробным исследованием магнитной микроскопии, позволили авторам представить объяснение этого поразительного явления с точки зрения последовательного накопления малых доменов зарождения , то есть микроскопических областей перемагничивания, которые действуют как зародыши для последующего макроскопического перемагничивания.  1, последовательное циклирование поля приводит к резкому увеличению площади малой петли, что является неожиданным отклонением от простых ожиданий. Далее авторы не только показывают, что такое же явление наблюдается в родственных мультислоях Co/Pd, но также представляют подробную информацию о зависимости от количества циклов, а также о максимальном и минимальном полях в малой петле. Возникают два важных наблюдения: (i) этот эффект исчезает для максимальных полей, которые превышают замыкающее поле, показывая, несколько обнадеживающе, что повторяемость петли гистерезиса все еще является допустимой концепцией при достаточно сильном поле, и (ii) существует четкая корреляция между рост второстепенных петель и небольшое, но заметное уменьшение максимальной намагниченности (т. е. получаемой при самых больших положительных полях в каждом цикле). Хотя это не видно на рис. 1 (а), эта максимальная намагниченность уменьшается с последовательным циклированием поля (всего примерно на 1%) в точном соответствии с расширением в области малой петли.
1, последовательное циклирование поля приводит к резкому увеличению площади малой петли, что является неожиданным отклонением от простых ожиданий. Далее авторы не только показывают, что такое же явление наблюдается в родственных мультислоях Co/Pd, но также представляют подробную информацию о зависимости от количества циклов, а также о максимальном и минимальном полях в малой петле. Возникают два важных наблюдения: (i) этот эффект исчезает для максимальных полей, которые превышают замыкающее поле, показывая, несколько обнадеживающе, что повторяемость петли гистерезиса все еще является допустимой концепцией при достаточно сильном поле, и (ii) существует четкая корреляция между рост второстепенных петель и небольшое, но заметное уменьшение максимальной намагниченности (т. е. получаемой при самых больших положительных полях в каждом цикле). Хотя это не видно на рис. 1 (а), эта максимальная намагниченность уменьшается с последовательным циклированием поля (всего примерно на 1%) в точном соответствии с расширением в области малой петли. Этот тонкий эффект указывает на то, что материал , а не , полностью насыщаются в самых больших положительных полях, что дает важный ключ к пониманию механизма кумулятивного роста малых петель.
Этот тонкий эффект указывает на то, что материал , а не , полностью насыщаются в самых больших положительных полях, что дает важный ключ к пониманию механизма кумулятивного роста малых петель.  1 (b). Таким образом, эти данные демонстрируют, что расширение малой петли обусловлено последовательным накоплением небольших доменов зародышеобразования [15], которые, по-видимому, способствуют последующему обращению намагниченности. Интересно, что результирующие структуры доменов [например, рис. 1(b), панели (a1)–(d1)] удивительно похожи на то, что можно было бы ожидать для одного перемагничивания, несмотря на то, что они собраны в течение нескольких последовательных малых перемагничиваний. петли.
1 (b). Таким образом, эти данные демонстрируют, что расширение малой петли обусловлено последовательным накоплением небольших доменов зародышеобразования [15], которые, по-видимому, способствуют последующему обращению намагниченности. Интересно, что результирующие структуры доменов [например, рис. 1(b), панели (a1)–(d1)] удивительно похожи на то, что можно было бы ожидать для одного перемагничивания, несмотря на то, что они собраны в течение нескольких последовательных малых перемагничиваний. петли.  Роль дефектов в этом процессе зарождения и характер взаимодействия доменных стенок с протяженной дефектной структурой остаются открытыми вопросами [16]. Кроме того, еще предстоит выяснить, насколько эти результаты являются общими. В частности, неясно, существуют ли эффекты аналогичной величины в других системах материалов, и если да, то какие факторы способствуют необычному поведению доменов, ответственному за этот эффект.
Роль дефектов в этом процессе зарождения и характер взаимодействия доменных стенок с протяженной дефектной структурой остаются открытыми вопросами [16]. Кроме того, еще предстоит выяснить, насколько эти результаты являются общими. В частности, неясно, существуют ли эффекты аналогичной величины в других системах материалов, и если да, то какие факторы способствуют необычному поведению доменов, ответственному за этот эффект. Ссылки
 Nakamura, IEEE Trans. Магн. 27 , 4975 (1991)
Nakamura, IEEE Trans. Магн. 27 , 4975 (1991)  H. Kronmuller and M. Fahnle, Micromagnetism and the Microstructure of Ferro Magnetic Solids (Cambridge University Press, New York, 2003) [Amazon][WorldCat ]
H. Kronmuller and M. Fahnle, Micromagnetism and the Microstructure of Ferro Magnetic Solids (Cambridge University Press, New York, 2003) [Amazon][WorldCat ] Об авторе
Читать PDF Тематические области
Статьи по теме
Колебание ультрахолодного атомарного газа моделирует спиновую динамику .
 Подробнее »
Подробнее »
Атомная и молекулярная физика
Интерферометрическое исследование молекулярного магнетизма
Интерферометр материи-волны может исследовать магнетизм широкого спектра веществ, от отдельных атомов до очень больших, слабомагнитных молекулы. Подробнее »
Астрофизика
Эксперимент обнаруживает неуловимую нестабильность магнитной жидкости
Магнито-вращательная нестабильность — процесс, который может объяснить динамику астрофизических аккреционных дисков — наконец-то была обнаружена в лаборатории. Подробнее »
Другие статьиПетля гистерезиса — определение, потери энергии, преимущества, примеры вопросов
В системе с магнитным полем возникает гистерезис. Ферромагнитные материалы имеют общую характеристику, называемую гистерезисом. Эффект гистерезиса — это явление, возникающее, когда намагниченность ферромагнитных материалов отстает от магнитного поля. Слово гистерезис означает «отставание». Плотность магнитного потока (B) отстает от напряженности магнитного поля, что приводит к гистерезису (H).
Эффект гистерезиса — это явление, возникающее, когда намагниченность ферромагнитных материалов отстает от магнитного поля. Слово гистерезис означает «отставание». Плотность магнитного потока (B) отстает от напряженности магнитного поля, что приводит к гистерезису (H).
Гистерезис является свойством всех ферромагнитных материалов. Давайте рассмотрим пример, когда ферромагнитный материал помещается в катушку с током, чтобы лучше понять это понятие. Материал становится намагниченным в результате присутствия магнитного поля. Гистерезис известен как процесс размагничивания материала путем изменения направления тока.
Петля гистерезиса
Плотность магнитного потока и напряженность поля намагничивания представлены петлей гистерезиса. Петля создается путем контроля магнитного потока, излучаемого ферромагнитным материалом, при изменении внешнего намагничивающего поля.
На графике будет показана петля гистерезиса, если B измеряется для различных значений H, а результаты представлены в визуальном формате.
- Когда напряженность магнитного поля (H) увеличивается от нуля, плотность магнитного потока (B) увеличивается.
- По мере увеличения магнитного поля значение магнетизма увеличивается, пока не достигнет точки A, известной как точка насыщения, где B остается постоянным.
- С падением величины магнитного поля происходит уменьшение величины магнетизма. Однако, когда B и H оба равны нулю, вещество или материал сохраняет некоторое магнитное поле, известное как сохраняющая способность или остаточный магнетизм.
- При уменьшении магнитного поля в отрицательную сторону магнетизм также уменьшается. Материал полностью размагничен в точке C.
- Коэрцитивная сила — это сила, необходимая для устранения удерживающей способности материала (C).
- Цикл повторяется в противоположном направлении с точкой насыщения D, точкой сохранения E и коэрцитивной силой F.
- Цикл завершается благодаря процессам прямого и противоположного направления, и этот цикл известен как петля гистерезиса.
 .
.
Преимущества петли гистерезиса
- На потерю гистерезиса указывает уменьшение площади петли гистерезиса.
- Релевантность удерживающей способности и коэрцитивной силы обеспечивается петлей гистерезиса для материала. В результате сердце машины облегчает выбор правильного материала для изготовления постоянного магнита.
- График B-H можно использовать для определения остаточного магнетизма, что упрощает выбор материала для электромагнитов.
Сохраняющая способность и коэрцитивность
После того, как внешнее поле намагничивания используется для намагничивания ферромагнитного материала, материал не вернется в состояние нулевой намагниченности, когда внешнее поле намагничивания удаляется.
Сохраняемость – Это количество магнетизма, которое остается после снятия внешнего намагничивающего поля. Это относится к способности материала сохранять определенные магнитные свойства после прекращения воздействия внешней намагничивающей силы. Значение плотности потока в точке B петли гистерезиса является сохраняющей способностью.
Значение плотности потока в точке B петли гистерезиса является сохраняющей способностью.
Коэрцитивная сила – Коэрцитивная сила вещества определяется как величина обратного (-ve H) внешнего намагничивающего поля, необходимая для полного размагничивания вещества. Значение H в точке C петли гистерезиса является коэрцитивной силой.
Потери энергии из-за гистерезиса
- Величайшим примером анализа потерь энергии из-за гистерезиса является трансформатор, поскольку мы знаем, что энергия требуется во всех процессах намагничивания и размагничивания.
- Энергия расширяется во время намагничивания и размагничивания магнитных объектов, и эта расширенная энергия проявляется как тепло. Гистерезисные потери — это термин для этого типа потерь тепла.
- Из-за непрерывного процесса намагничивания и размагничивания в трансформаторах энергия постоянно теряется в виде тепла, что снижает эффективность трансформатора.
- Сердечники из мягкого железа используются в трансформаторах для предотвращения потерь энергии, поскольку потери энергии или потери на гистерезис в мягком железе значительно ниже, чем в других материалах.

Разница между мягкими магнитами и жесткими магнитами
- По сравнению с жесткими магнитами, мягкие магниты легко намагничиваются и размагничиваются.
- Сохраняющая способность мягких магнитов выше, чем у жестких магнитов.
- Твердые магниты имеют коэрцитивную силу выше, чем у мягких магнитов.
- Мягкие магниты теряют меньше энергии, чем жесткие магниты, из-за их небольшой площади поверхности.
- В случае мягких магнитов площадь петли меньше, чем у жестких магнитов.
- Мягкие магниты имеют более высокую магнитную проницаемость, чем жесткие магниты.
- В мягких магнитах значения I и χ высокие, а в твердых магнитах они оба низкие.
- Мягкие магниты — это временные магниты, а жесткие магниты — это постоянные магниты.
- Железоникелевый сплав, ферриты и т. д. являются примерами мягких магнитов, тогда как углеродистая сталь, сталь, вольфрам, хромистая сталь и т. д. являются примерами жестких магнитов.

Намагничивание и размагничивание
Метод проявления магнитных свойств внутри магнитного вещества известен как намагничивание. С помощью электрического тока или мощного магнита можно намагнитить любой магнитный материал.
- Проще говоря, если любое магнитное вещество поместить во внешнее намагничивающее поле, материал станет намагниченным, а если внешнее намагничивающее поле изменить на противоположное, материал размагнитится.
- Когда ферромагнитные материалы помещаются внутрь катушки с током, намагничивающее поле H, создаваемое током, заставляет некоторые или все атомные магнитные диполи материала выровняться с внешним намагничивающим полем, намагничивая материал.
Примеры задач
Задача 1. Какие материалы имеют самую узкую петлю гистерезиса?
Решение:
Узкая петля гистерезиса подразумевает минимальное количество потерянной энергии.
Это происходит из-за его ограниченной площади поверхности, что приводит к более частым реверсам приложенной намагничивающей силы. Эти узкие формы гистерезиса наблюдаются в магнитомягких материалах, используемых в системах, требующих переменных магнитных полей.
Задача 2: Каков цикл гистерезиса материала сердечника трансформатора?
Решение:
Сердечник трансформатора изготовлен из мягкого железа с низкой коэрцитивной силой и высокой сохраняющей способностью. В результате его петля гистерезиса получается высокой и тонкой.
Проблема 3: Что такое потеря гистерезиса?
Решение:
Когда на сердечник трансформатора воздействует переменная сила намагничивания, возникают потери на гистерезис из-за перемагничивания. Когда ядро подвергается воздействию переменного магнитного поля, домены материала меняют ориентацию каждые полпериода.


