Что такое закон Ома и как он применяется для участка цепи и полной цепи. Какие формулы используются для расчета силы тока, напряжения и сопротивления. В каких случаях закон Ома не работает. Как закон Ома помогает объяснить некоторые явления природы.
Закон Ома для участка цепи: основная формула и варианты
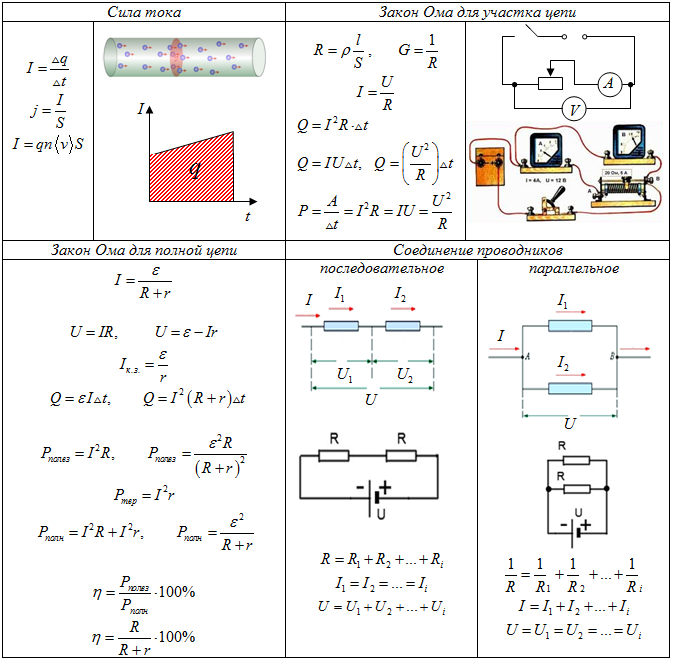
Закон Ома для участка цепи устанавливает связь между силой тока (I), напряжением (U) и сопротивлением (R) проводника:
I = U / R
Из этой базовой формулы можно вывести две другие:
- U = I * R — для расчета напряжения
- R = U / I — для расчета сопротивления
Эти формулы применимы только для участков цепи с одним сопротивлением. Для более сложных цепей используются другие варианты закона Ома.
Закон Ома для полной (замкнутой) цепи
Для полной замкнутой цепи, содержащей источник тока, закон Ома выглядит так:
I = E / (R + r)
Где:
- E — электродвижущая сила (ЭДС) источника
- R — внешнее сопротивление цепи
- r — внутреннее сопротивление источника
Эта формула учитывает как внешнее, так и внутреннее сопротивление цепи.
Закон Ома для неоднородного участка цепи
Для участков цепи, содержащих источник тока (неоднородных), закон Ома принимает вид:
I = (φ1 — φ2 + E) / R
Где φ1 — φ2 — разность потенциалов на концах участка. Знак ЭДС (E) может быть как положительным, так и отрицательным, в зависимости от направления тока источника относительно внешнего тока.
Особенности применения закона Ома для переменного тока
При наличии в цепи емкости или индуктивности, для переменного тока закон Ома записывается как:
I = U / Z
Где Z — полное сопротивление цепи (импеданс), включающее активное и реактивное сопротивления.
В каких случаях закон Ома не работает?
Закон Ома не является фундаментальным законом природы, а лишь эмпирическим соотношением. Он может нарушаться в следующих случаях:
- При очень высоких частотах тока
- В сверхпроводниках при низких температурах
- При сильном нагреве проводника током
- В диэлектриках и проводниках под высоким напряжением
- В полупроводниках и полупроводниковых приборах
- В светодиодах
Элементы и участки цепи, подчиняющиеся закону Ома, называются омическими.

Как закон Ома объясняет некоторые природные явления?
С помощью закона Ома можно объяснить, почему птицы могут безопасно сидеть на высоковольтных проводах. Птица представляет собой проводник с очень малым сопротивлением по сравнению с воздушным промежутком между проводами. Поэтому практически все напряжение приходится на этот промежуток, а не на тело птицы.
Однако если птица коснется одновременно двух проводов или провода и заземленной конструкции, она может погибнуть от удара током. Поэтому в некоторых местах устанавливают специальные защитные приспособления для птиц на линиях электропередач.
Практическое применение закона Ома для обеспечения электробезопасности
Закон Ома позволяет рассчитать безопасные уровни напряжения для человека. Сопротивление тела человека в среднем составляет около 1000 Ом, но может сильно меняться в зависимости от условий:
- Сухая неповрежденная кожа имеет высокое сопротивление
- Влажная кожа или открытые раны резко снижают сопротивление
- Усталость, нервное напряжение, алкогольное опьянение также снижают сопротивление тела
Считается, что для человека безопасно напряжение не более 36 В в нормальных условиях. При работе с более высоким напряжением необходимо использовать средства защиты.

Как рассчитать параметры электрической цепи по закону Ома?
Используя формулы закона Ома, можно рассчитать различные параметры электрической цепи:
- Силу тока при известном напряжении и сопротивлении
- Напряжение при известной силе тока и сопротивлении
- Сопротивление участка цепи при известных токе и напряжении
- Мощность, выделяемую на участке цепи
- Работу электрического тока за определенное время
Для сложных цепей с несколькими резисторами сначала рассчитывают эквивалентное сопротивление, а затем применяют закон Ома для всей цепи.
История открытия закона Ома
Закон Ома был открыт немецким физиком Георгом Омом в 1826 году. Ом экспериментально установил соотношение между силой тока, напряжением и сопротивлением участка цепи. Позднее это соотношение было названо законом Ома в честь ученого.
Открытие закона Ома стало важным этапом в развитии электротехники и позволило проводить точные расчеты электрических цепей. На основе закона Ома были разработаны методы измерения электрических величин и созданы различные электроизмерительные приборы.

Электрический ток. Закон Ома для участка цепи. Виды соединения проводников.
Электрический ток — упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил.Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени.
Пусть цилиндрический проводник имеет поперечное сечение площадью S. За положительное направление в проводнике примем направление слева направо. Заряд каждой частицы будем считать равным q0.
В объеме проводника, ограниченном поперечными сечениями 1 и 2 с расстоянием Δl между ними, содержится общий заряд q = q0nSΔl. Если частицы движутся слева направо со средней скоростью v, то за время Δt = Δl / v все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение 2. Поэтому сила тока равна:
В СИ единицей силы тока является
ампер (А). Эту
единицу устанавливают на основе магнитного взаимодействия токов.
Поэтому сила тока равна:
В СИ единицей силы тока является
ампер (А). Эту
единицу устанавливают на основе магнитного взаимодействия токов.
Измеряют силу тока амперметрами. Принцип устройства этих приборов основан на магнитном действии тока.
Скорость упорядоченного движения электронов в проводнике. Найдем скорость упорядоченного перемещения электронов в металлическом проводнике. Согласно формуле v = I /enS, где е — модуль заряда электрона. Пусть, например, сила тока I = 1 A, а площадь поперечного сечения проводника S = 10-6 м2. Модуль заряда электрона е = 1,6•10-19 Кл. Число электронов в 1 м3 меди равно числу атомов в этом объеме, так как один из валентных электронов каждого атома меди коллективизирован и является свободным. Это число есть n = 8,5•1028 м3. Следовательно,
Очевидно, что скорость упорядоченного перемещения электронов очень мала.
Основная количественная характеристика электрического тока — сила тока. Она определяется электрическим зарядом, переносимым через поперечное сечение проводника за единицу времени. Скорость заряженных частиц (электронов) в проводнике очень мала — около 0,1 мм/с.
Условия существования постоянного электрического тока.
Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.
Источник тока — устройство, в котором
осуществляется преобразование какого-либо вида энергии в энергию электрического
поля. В источнике тока на заряженные частицы в замкнутой цепи действуют
сторонние силы. Причины возникновения сторонних сил в различных источниках тока
различны. Например, в аккумуляторах и гальванических элементах сторонние силы
возникают благодаря протеканию химических реакций, в генераторах электростанций
они возникают при движении проводника в магнитном поле, в фотоэлементах —
при действия света на электроны в металлах и полупроводниках.
Закон Ома для участка цепи.
Немецкий ученый Георг Ом в 1827 г. связал воедино три физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
I=U/R,
где I – сила
тока, U – напряжение, R – сопротивление.
Последовательное и параллельное соединение проводников.
Электрическая цепь включает в себя источника тока и проводники (потребители, резисторы и др), которые могут соединятся последовательно или параллельно.
Смешанное соединение — комбинация параллельного и последовательного соединений.
Решение задач на закон Ома для участка и полной цепи
Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.
Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Формула закона Ома для участка цепи:
Формула закона Ома для полной цепи:
Задача 1
Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.
|
Дано U = 220 В I = 1,2 А |
Решение Согласно закону Ома для участка цепи: |
|
Найти R — ? |
|
|
Ответ: R = 183,3 Ом. |
|
Задача 2
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
|
Дано E = 12 В I = 0,5 А Rл = Rр/2 Rр = 10 Ом |
Решение Найдем экв. сопротивление двух параллельно соединённых резисторов: Сопротивление лампочки: Согласно закону Ома для полной цепи: |
|
Найти r — ? |
|
|
Ответ: r = 14 Ом. |
|
Задача 3
К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.
|
Дано Uобщ = 10 В Rр = 2 Ом Rл = 10 Ом |
Решение Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи: При последовательном соединении ток в цепи общий: Выразим Uл через Uобщ: Найдем Rэкв: Окончательно получим: |
|
Найти Uл — ? |
|
|
Ответ: Uл = 4 В. |
|
Задача 4
Как определить длину мотка медной проволоки, не разматывая его?
Решение:
Для решения данной задачи необходимо воспользоваться формулой:
отсюда длина проволоки
В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.
Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив диаметр проволоки и по формуле Πr2 вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.
Задача 5
Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?
Что произойдет в цепи при перегорании одной лампы?
Решение:
При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I1 и I2 проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.
Закон Ома для полной цепи
1. Источник тока
При прохождении тока в проводнике выделяется некоторое количество теплоты. Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.
Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического поля. Таким участком цепи является источник тока (рис. 59.1).
Таким участком цепи является источник тока (рис. 59.1).
В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.
В химических источниках тока сторонние силы имеют химическую природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.
В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Электродвижущая сила источника тока
В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим Aстор.
Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:
ξ = Aстор/q. (1)
(Это название не совсем удачно, потому что ЭДС – не «сила» в механическом смысле, а энергетическая характеристика источника.)
ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.
2.
 Закон Ома для полной цепи
Закон Ома для полной цепи
Если сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде
Aстор = ξIt. (2)
При этом во внешней цепи сопротивлением R выделяется количество теплоты
Qвнеш = I2Rt, (3)
а внутри источника тока выделяется количество теплоты
Qвнутр = I2rt, (4)
где r – сопротивление источника, которое называют его внутренним сопротивлением.
Из закона сохранения энергии следует, что
Qвнеш + Qвнутр = Aстор. (5)
? 1. Докажите, что из формул (2) – (5) следует:
I = ξ / (R + r). (6)
Это соотношение называют законом Ома для полной цепи.
Сумму сопротивлений R + r называют полным сопротивлением цепи.
? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом.
а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом?
б) Какова максимально возможная сила тока в цепи? При каком сопротивлении внешней цепи это имеет место?
? 3.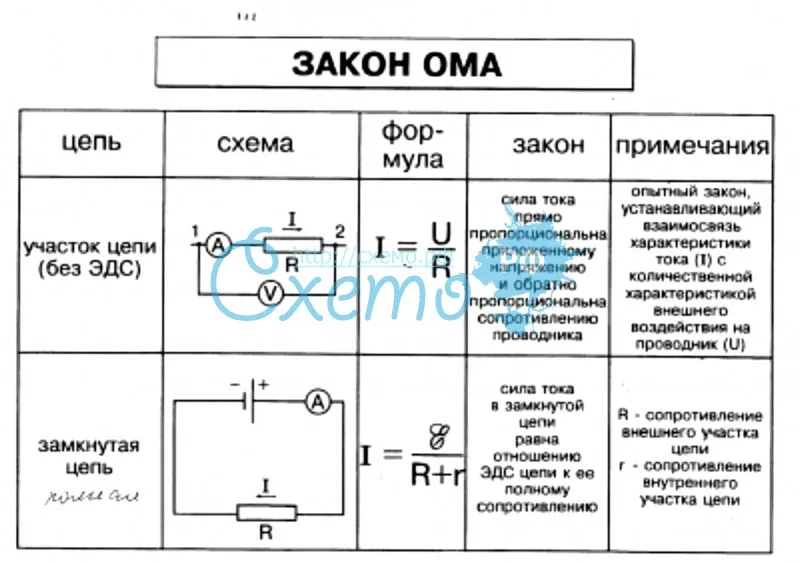 При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
а) Чему равно внутреннее сопротивление источника?
б) Чему равна ЭДС источника?
Напряжение на полюсах источника
Закон Ома для полной цепи можно записать в виде
ξ = IR + Ir. (7)
Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:
IR = U.
Поэтому формулу (7) можно записать в виде
U = ξ – Ir. (8)
Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.
Поставим опыт
Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате. Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.
? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока.
а) Чему равна ЭДС этого источника тока?
б) Чему равна наибольшая сила тока?
в) Чему равно внутреннее сопротивление источника тока?
г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна?
е) Чему равно внешнее сопротивление при I = 1,5 А?
Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.
Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.
? 5. Покажите, что сила тока короткого замыкания выражается формулой
Покажите, что сила тока короткого замыкания выражается формулой
Iка = ξ/r. (9)
Подсказка. Воспользуйтесь законом Ома для полной цепи.
Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.
? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А.
а) Как изменилось полное сопротивление цепи?
б) Чему равно внутреннее сопротивление батарейки?
Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.
? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В.
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным.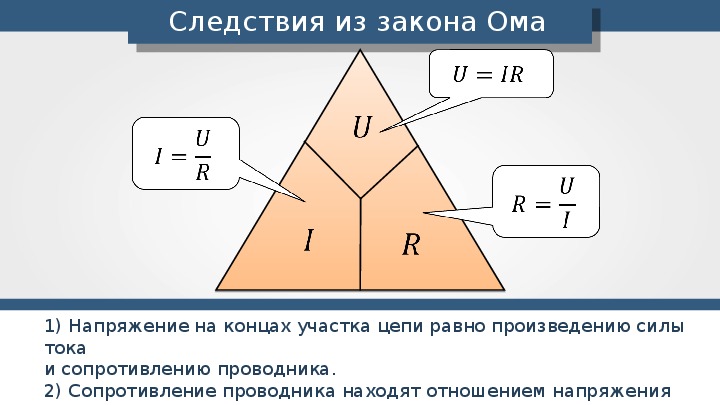
б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.
3. КПД источника тока
Работу тока во внешней цепи называют полезной работой. Обозначим ее Aпол. Используя формулу для работы тока, получаем:
Aпол = I2Rt.
Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I2rt. Поскольку
Aстор = I2Rt + I2rt,
получаем для отношения полезной работы к работе сторонних сил:
η = Aпол / Aстор = (I2Rt) / (I2Rt + I2rt) = R / (R + r).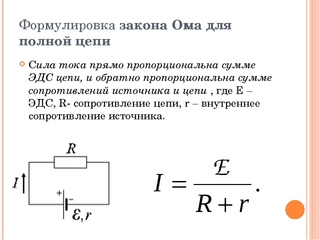
Это отношение, выраженное в процентах, называют КПД источника тока.
? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?
Дополнительные вопросы и задания
9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I. Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.
а) Как сдвинули ползунок реостата между первым и вторым измерениями – влево или вправо?
б) Чему равны ЭДС источника тока и его внутреннее сопротивление?
в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?
10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт.
а) Чему равна ЭДС источника тока?
б) Чему равно внутреннее сопротивление источника тока?
в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?
Законы Ома для участка цепи и для полной цепи
Автор Alexey На чтение 4 мин. Просмотров 3.6k. Опубликовано Обновлено
В 1826 году немецкий ученый Георг Ом совершил открытие и описал
эмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.
В дальнейшем выяснилось, что эти особенности не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством.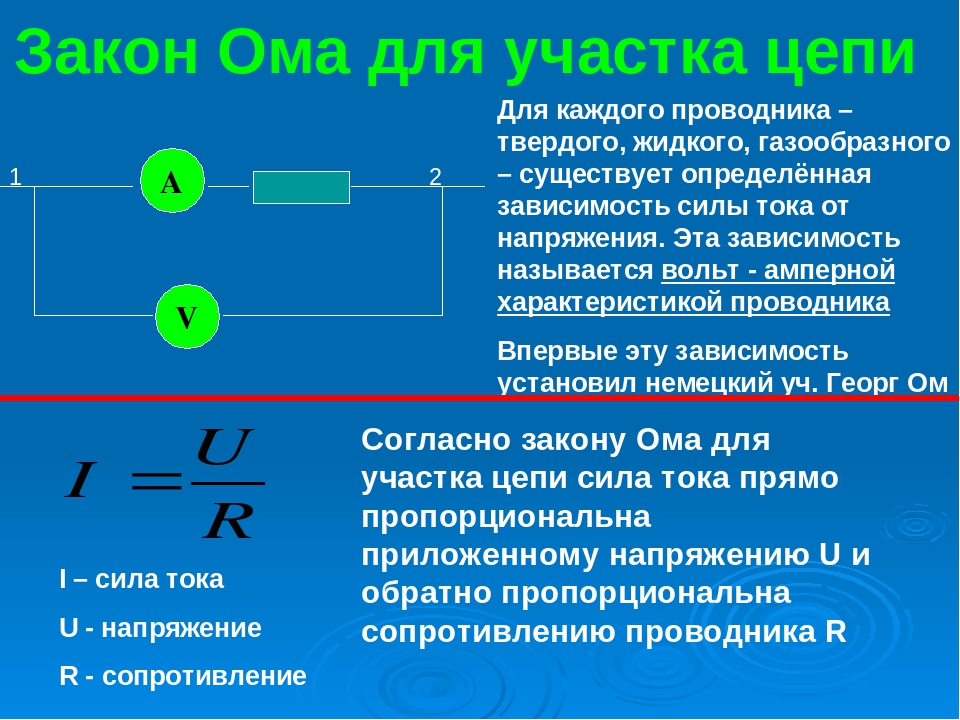 Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока.
Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока.
Закон Ома для участка цепи
Согласно обобщенному закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.
I = U/ R
Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.
Беря во внимание вышеприведенную формулу, есть возможность найти неизвестные значенияUиR, сделав несложные математические операции.
U = I*R
R = U / I
Данные выше формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.
Закон Ома для замкнутой цепи
Сила тока полной цепи равна ЭДС, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Замкнутая сеть имеет одновременно сопротивления внутреннего и внешнего характера. Поэтому формулы отношения будут уже другими.
I = E/ Rвн+r
Где E – электродвижущая сила (ЭДС), R- внешнее сопротивление источника, r-внутреннее сопротивление источника.
Закон Ома для неоднородного участка цепи
Замкнутая электрическая сеть содержит участки линейного и нелинейного характера. Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = f1 – f2 + E/ R
Где f1 – f2 – разница потенциалов на конечных точках рассматриваемого участка сети
R – общее сопротивление нелинейного участка цепи
ЭДС нелинейного участка цепи бывает больше нуля или меньше. Если направление движения тока, идущего из источника с движением тока в электрической сети, совпадают, будет преобладать движение зарядов положительного характера и ЭДС будет положительная. В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
Если направление движения тока, идущего из источника с движением тока в электрической сети, совпадают, будет преобладать движение зарядов положительного характера и ЭДС будет положительная. В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
Закон Ома для переменного тока
При имеющейся в сети емкости или инертности, необходимо учитывать при проводимых вычислениях, что они выдают свое сопротивление, от действия которого ток приобретает переменный характер.
Закон Ома для переменного тока выглядит так:
I = U/ Z
где Z – сопротивление по всей длине электрической сети. Его еще называют импеданс. Импеданс составляют сопротивления активного и реактивного характера.
Закон Ома не является основным научным законом, а лишь эмпирическим отношением, причем в некоторых условиях оно может не соблюдаться:
- Когда сеть обладает высокой частотой, электромагнитное поле меняется с большой скоростью, и при расчетах необходимо учитывать инертность носителей заряда;
- В условиях низкой температуры с веществами, которые обладают сверхпроводимостью;
- Когда проводник сильно нагревается проходящим напряжением, отношение тока к напряжению становится переменным и может не соответствовать общему закону;
- При нахождении под высоким напряжением проводника или диэлектрика;
- В светодиодных лампах;
- В полупроводниках и полупроводниковых приборах.

В свою очередь элементы и проводники, соблюдающие закон Ома, называются омическими.
Закон Ома может дать объяснение некоторым явлениям природы. Например, когда мы видим птиц, сидящих на высоковольтных проводах, у нас возникает вопрос – почему на них не действует электрический ток? Объясняется это довольно просто. Птицы, сидя на проводах, представляют собой своеобразные проводники. Большая часть напряжения приходится на промежутки между птицами, а та доля, что приходится на сами «проводники» не представляет для них опасности.
Но это правило работает лишь при единичном соприкосновении. Если птица заденет клювом или крылом провод или телеграфный столб, она неминуемо погибнет от огромного количества напряжения, которое несут в себе эти участки. Такие случаи происходят повсеместно. Поэтому в целях безопасности в некоторых населенных пунктах установлены специальные приспособления, защищающие птиц от опасного напряжения. На таких насестах птицы находятся в полной безопасности.
Закон Ома также широко применятся на практике. Электричество смертельно опасно для человека при одном лишь касании к оголенному проводу. Но в некоторых случаях сопротивление человеческого тела может быть разным.
Так, например, сухая и неповрежденная кожа обладает большим сопротивлением к воздействию электричества нежели рана или кожа, покрытая потом. В следствие переутомления, нервного напряжения и опьянения, даже при небольшом напряжении тока человек может получить сильный удар током.
В среднем, сопротивление тела человека – 700 Ом, значит, для человека является безопасным напряжение в 35 В. Работая с большим напряжением, специалисты используют специальные средства защиты.
Глава 21. Электрический ток.
 Законы Ома и Джоуля-Ленца
Законы Ома и Джоуля-Ленца
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
| (21.1) |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю.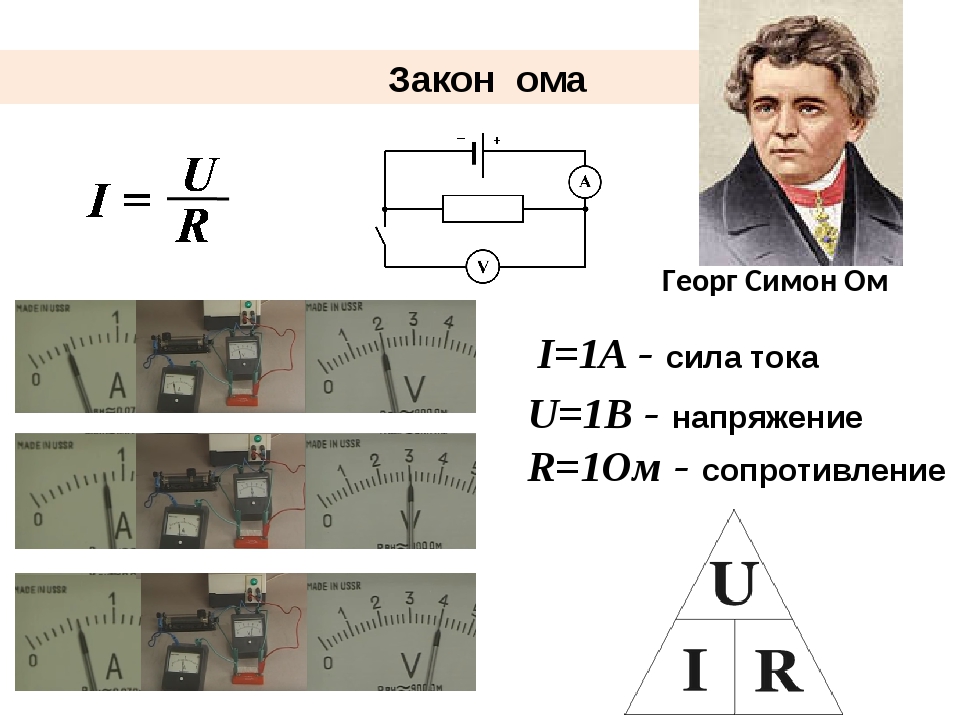 Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
| (21.2) |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
| (21. |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).
Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
| (21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
| (21. |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников
| (21.5) |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
| (21. |
В этом случае сила тока в цепи равна
| (21.7) |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
| (21.8) |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение
Поэтому отношение
| (21.9) |
которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ 3).
Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
Закон ома — формулировка простыми словами, определение,
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
- Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала. 2.
2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
- Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Таблица удельных сопротивлений различных материалов
Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
Алюминий | 0,028 |
Бронза | 0,095 — 0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан ( сплав Ni-Cu + Mn) | 0,5 |
Латунь | 0,025 — 0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин ( сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 |
Олово | 0,12 |
Платина | 0. |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103 — 0,137 |
Титан | 0,6 |
Хромаль | 1,3 — 1,5 |
Цинк | 0,054 |
Чугун | 0,5-1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Не сопротивляйтесь зову сердца и запишите ребенка в современную школу Skysmart. Здесь школьники решают захватывающие задачки по физике и понимают, как это пригодится в жизни.
А еще следят за прогрессом в личном кабинете, задают учителям любые — даже самые неловкие — вопросы и чувствуют себя увереннее на школьных экзаменах и контрольных.2/м]
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
|
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье 😇
Давайте решим несколько задач на Закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Таблица удельных сопротивлений различных материалов
Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
Алюминий | 0,028 |
Бронза | 0,095 — 0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан ( сплав Ni-Cu + Mn) | 0,5 |
Латунь | 0,025 — 0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин ( сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 |
Олово | 0,12 |
Платина | 0.107 |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103 — 0,137 |
Титан | 0,6 |
Хромаль | 1,3 — 1,5 |
Цинк | 0,054 |
Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
- ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
|
Закон Ома для полной цепи I = ε/(R + r) I — сила тока [A] ε — ЭДС [В] R — сопротивление [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
I = ε/(R + r)
Подставим значения:
I = 4/(3+1) = 1 A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
|
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Последовательное соединение | Параллельное соединение |
|
Схема | Резисторы следуют друг за другом | Между резисторами есть два узла Узел — это соединение трех и более проводников |
Сила тока | Сила тока одинакова на всех резисторах I = I1 = I2 | Сила тока, входящего в узел, равна сумме сил токов, выходящих из него I = I1 + I2 |
Напряжение | Общее напряжение цепи складывается из напряжений на каждом резисторе U = U1 + U2 | Напряжение одинаково на всех резисторах U = U1 = U2 |
Сопротивление | Общее сопротивление цепи складывается из сопротивлений каждого резистора R = R1 + R2 | Общее сопротивление для бесконечного количества параллельно соединенных резисторов 1/R = 1/R1 + 1/R2 + … + 1/Rn Общее сопротивление для двух параллельно соединенных резисторов R = (R1 * R2)/R1 + R2 Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов R = R1/n |
|
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала? Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов. Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой. Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного. |
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.
Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом
Ответ: общее сопротивление цепи равно 1 ⅓ Ом
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2.2)/2R = R/2 = 10/2 = 5 Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
I = ε/(R + r)
R + r = ε/I
r = ε/I — R
Подставим значения:
r = 12/0,5 — 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.
Чтобы ребенок научился решать самые сложные задачи и чувствовал себя уверенно на олимпиадах и экзаменах, запишите его на бесплатный вводный урок в Skysmart.
Профессиональные учителя физики не только научат решать задачи и подготовят к экзамену, но и объяснят, как это все устроено: легко, интерактивно и с примерами из реальной жизни современных подростков.
Закон ома для полной цепи
Закон Ома для полной цепи
Решение
1. При разомкнутом ключе К закон Ома для полной цепи записывается следующим образом
. (1)
2. При замыкании ключа сопротивление нагрузки изменится
. (2)
3. Закон Ома в этом случае примет вид
. (3)
4. Отношение токов определится как
. (4)
5. Падение напряжения на клеммах источника при разомкнутом ключе
. (5)
6. Падение напряжения после замыкания ключа
. (6)
7. Отношение напряжений на клеммах источника
. (7)
2.3.2. Батарея замкнутая на сопротивлениеR1 = 10 Ом, даёт ток силой I1 = 3 А; замкнутая на сопротивлениеR2 = 20 Ом, она даёт ток силой I2 = 1,6 А. Определите ЭДС источника и её внутреннее сопротивление r.Решение
1. Запишем дважды уравнение закона Ома для полной цепи
(1)
2. Выразим из первого уравнения системы (1) величину и подставим во второе уравнение
, (2)
3. Разрешим полученное уравнение относительно внутреннего сопротивления источника r
. (3)
4. Значение величины можно получить из любого уравнения системы (1) при подстановки в него r из уравнения (3)
.
2.3.3. Батареи с ЭДС 1 = 20 В, 2 = 30 В и внутренними сопротивлениями соответственно r1 = 4 Ом, r2 = 6 Ом соединены параллельно и согласно. Каковы должны быть параметры и r эквивалентного источника, которым можно заменить соединение?Решение
1. Определим силу тока, протекающего через источники при их совместном включении
. (1)
2. Сила тока, который может быть получен от двух источников при их совместной работе I0 = I1 + I2 = 5 A
3. Общее внутреннее сопротивление
. (2)
4. Определим далее эквивалентную ЭДС
. (3)
Таким образом, эквивалентный источник должен иметь ЭДС = 12 В и внутреннее сопротивление r = 2,4 Ом.
2.3.4. Две батареи с одинаковым внутренним сопротивлением соединены так, что ЭДС образовавшегося источника напряжения равна . ЭДС одной из батарей 3/2. Нарисуйте все возможные схемы соединений. Для каждого варианта соединений определите ЭДС второй батареи.
Решение
1. Один из вариантов включение источников последовательно и встречно, когда ЭДС второго источника равна 2 = 0,5, а 1 = . В этом случае общая ЭДС определится как . Внутренне сопротивление такого включения источников будет равно 2r. 2. Возможно и параллельное согласное включение источников, общее сопротивление которых будет равно r/2. Падение напряжения на источниках будет одинаковым и равным . Сила тока через общую шину определится как. (1)
Сила тока через первый источник
. (2)
Сила тока через второй источник
. (3)
Электродвижущая сила второго источника
. (4)
3. Следующий способ отличается от предыдущего тем, что источники включены встречно. Чтобы получить в результате батарею с ЭДС, равной , необходимо, чтобы у второго элемента ЭДС была равна /2. Как и в предыдущем случае сила тока будет определяться уравнением (1), потому что внутренние сопротивления включены параллельно. Сила тока через первый источник будет определяться как
. (5)Ток через второй источник
. (6)
Электродвижущая сила второго элемента должна составлять
. (7)
2.3.5. Три одинаковые батареи соединены параллельно и подключены к внешнему сопротивлению. Как изменится сила тока через это сопротивление, если полярность одной из батарей поменять на обратную?Решение
1. Отметим сразу что, в связи с идентичностью элементов в обоих случаях их параллельного включения суммарное внутреннее сопротивление будет в три раза меньше, чем у одного источника, при этом при согласном включении сила тока через внешнее сопротивление R определится уравнением
. (1)
2. Проанализируем ситуацию при встречном включении одного из источников тока. Результирующий ток определится как. (2)
3. Отношение сил токов
. (3)
2.3.6. Что покажет вольтметр, если в цепи, изображённой на рисунке, если источники одинаковы, ЭДС каждого из них =1,5 В, внутреннее сопротивление r = 2 Ом? Чему будет равна сила тока в цепи?Решение
1. Будем считать, что вольтметр обладает бесконечно большим сопротивлением, в этом случае сила тока в цепи определится соотношением
. (1)
2. Поскольку все три элемента в данной схеме включения работают в режиме короткого замыкания, и ток I0, по сути является током короткого замыкания, то в указанных на схеме точках разность потенциалов будет равна нулю, т.е. UV =0.
2.3.7. Определите заряд конденсатора С ёмкостью С = 4 мкФ в стационарном режиме, если R1 = R2 = R3 = R= 100 Ом. Источник тока обладает ЭДС = 300 В и нулевым внутренним сопротивлением.Решение
1. Сопротивления R2 и R3 включены параллельно, поэтому их можно представить эквивалентным одним сопротивлением величиной
. (1)2. Определим силу тока в цепи
. (2)
3. Падение напряжения на сопротивлении R1 будет равно разности потенциалов на обкладках конденсатора, который для постоянного тока обладает бесконечным сопротивлением
. (3)
4. Заряд конденсатора определим из уравнения энергии
. (4)
2.3.8. Два вертикально расположенных стержня, имеющие длину L = 1 м и диаметр d = 1 см сопротивление на единицу длины = 110 5 Омм, подсоединены через идеальный амперметр к источнику ЭДС = 1,5 В и внутренним сопротивлением r0 = 0,05 Ом. Полосок касается сопротивление R = 0,1 Ом, которое в поле тяжести g начинает соскальзывать вдоль них из верхней точки вниз без нарушения контакта, как показано на рисунке. В пренебрежении эффектами, связанными с магнитным полем, определить какое значение тока I покажет амперметр через время = 0,5 с после начала движения? Силу трения не учитыватьРешение
1. Запишем кинематические уравнения движения сопротивления, считая, что на него действует только сила тяжести и движение происходит по вертикальной оси с нулевой начальной скоростью
, (1)
и определим расстояние которое пройдёт сопротивление за время
. (2)
2. Определим электрическое сопротивление одного отрезка стержня длиной
. (3)
3. Электрическая схема установки, таким образом представит собой три последовательно включенных внешних сопротивления: R0 = R + 2rи внутреннее сопротивление источника r0. Закон Ома для полной цепи в этом случае запишется так
. (4)
2.3.9. Два гальванических элемента с 1 =1,5 В и 2 = 4,5 В соединены одноимёнными полюсами. Внутреннее сопротивление первого источника r1 в два раза меньше внутреннего сопротивления второго элемента r2, т.е. r2 = 2 r1. Каковы при этом включении элементов будут показания вольтметра?Решение
1. Если считать, что вольтметр обладает бесконечным сопротивлением, то разность электродвижущих сил источников тока будет равна сумме падений напряжения на их внутренних сопротивлениях
. (1)
2. С другой стороны второй элемент является внешней нагрузкой для первого элемента
, (2)
где U показания вольтметра.
3. Выразим из последнего уравнения силу тока в цепи
. (3)
4. Подставим значение силы тока в уравнение (1)
, (4)
откуда
. (5)
2.3.10. Источник тока обладает внутренним сопротивлением r = 1 Ом, ёмкость конденсатора С = 10 мкФ, R1 = 5 Ом, R2 = 10 Ом. До замыкания ключа вольтметр показывает напряжение U1 = 10 В, а после замыкания U2 = 8 В. Определить заряд конденсатора и величину сопротивления R3.Решение
1. При разомкнутом ключе ток в цепи отсутствует, поэтому вольтметр будет демонстрировать величину ЭДС, U1 = = 10 В.
2. Запишем далее уравнение общего сопротивления цепи, считая что конденсатор для постоянного тока в стационарном режиме представляет бесконечное сопротивление
, (1)
с другой стороны
. (2)
3. Определим величину сопротивления R3
. (3)
4. Определим падение напряжения на сопротивлении R3, которое включено параллельно конденсатору
. (4)
5. Заряд, прошедший через конденсатор
. (5)
2.3.11. Идеальный источник тока с = 100 В включен в цепь, состоящую из конденсаторов С3 = С4 = 1 мкФ, С1 = 2 мкФ, С2 =4 мкФ и сопротивления R. Определить падение напряжения на конденсаторах С1 и С2.Решение
1. При подключении схемы к источнику в цепи потечёт ток до момента полной зарядки всех конденсаторов. После того как конденсаторы зарядятся ток прекращается, т.к. электрические ёмкости представляют для постоянного тока разрыв цепи.
2. Все обкладки конденсаторов, соединённые с сопротивлением будут иметь одинаковый потенциал, при этом пары конденсаторов С1 + С3 и С2 + С4 включены с источником тока последовательно.
3. Падение напряжения на конденсаторах определится уравнением
. (1)
4. Заряд конденсаторов определится как
. (2)
5. Выразим из последнего уравнения величину U2, подставим её в уравнение (1) и разрешим его относительно U1
, (3)
, (4)
. (5)
6. Определим далее величину U2 из уравнения (1)
. (6)
2.3.12. Электрическая схема состоит из двух конденсаторов С1 = 2 мкФ и С2 = 4 мкФ и трёх сопротивлений R1 = 200 Ом, R2 = R3 = 100 Ом. В цепь включён идеальный источник тока с = 100 В. Определить падение напряжения на конденсаторах U1, U2 и их заряд Q1, Q2.Решение
1. Падение напряжения U1 на конденсаторе С1 равно разности потенциалов между точками цепи 1 и 3, а напряжение на С2 определяется разностью потенциалов между точками 2 и 4
, . (1)
2. После зарядки конденсаторов цепь будет представлять собой три последовательно соединённых сопротивления
=400 Ом. (2)
3. Определим силу тока в цепи
. (3)
4. Определим величину напряжений U1, U2 которые, как следует из уравнений (1) будут равны сумме падений напряжения на сопротивлениях U1 = UR1 + UR2, U2 = UR3 + UR4
, (4)
, (5)
5. Заряд конденсаторов определим, используя взаимосвязь падения напряжения заряда и ёмкости
(6)
2.3.13. Два последовательно соединённых конденсатора С1 = 2 мкФ и С2 = 4 мкФ замкнуты на источник тока с = 20 В, параллельно которому включено сопротивление R = 20 Ом. Ток короткого замыкания источника IКЗ в три раза превышает рабочий стационарный ток в цепи I. Определить падение напряжения на каждом из конденсаторов.Решение
1. При последовательном соединении конденсаторов через них протекает одинаковый зарядный ток, поэтому заряд на их обкладках будет одинаковым, т.е. Q1 = Q2
. (1)
2. Падение напряжения на конденсаторах можно представить в виде суммы
. (2)
3. Выразим далее величину U2 из уравнения (1) подставим её в уравнение (2) и определим падение напряжения на С1 и С2
, (3)
5. Определим далее внутреннее сопротивление источника тока и величину U0
. (4)
6. Подставим далее величину U0 в уравнения (3)
. (5)
Правила Кирхгофа
2.4.1. Определить силу токов во всех участках цепи, если источники тока обладают ЭДС: 1 = 10 B, 2 = 20 В, их внутренние сопротивления соответственно равны: r1 = 2 Ом, r2 = 3 Ом. Источники нагружены на внешнее сопротивление R = 100 Ом.
Решение
1. Задачу целесообразно решать, используя правила Кирхгофа, которые удобны при расчетах параметров разветвлённых цепей. В общем виде математические выражения правил имеют вид:
. (1)
2. В соответствие с первым правилом алгебраическая сумма сил токов в любом из узлов должна быть равна нулю
. (2)
3. Выделим два замкнутых контура, содержащих источники тока (направление обхода контуров показано пунктиром) и запишем для них второе правило Кирхгофа
. (3)
4. Таким образом, приходим к системе трёх алгебраических уравнений с тремя неизвестными величинами
(4)
5. Выразим из второго и третьего уравнений системы (4) силы тока I1 и I2
, (5)
и подставим эти значения в первое уравнение системы с целью его решения относительно силы тока I
, (6)
, (7)
, (8)
. (9)
6. Определим далее значение сил токов I1 и I2
(10)
7. Знак минус для тока I1 показывает, что направление тока выбрано неправильно, ток будет течь в обратном направлении.
8. Проверим правильность решения путём анализа баланса токов по уравнению (1)
. (11)
2.4.2. Электрическая цепь состоит из резисторов R1 = R2 = 10 Ом и трёх идеальных источников тока, причём 1 = 10 В, 2 = 14 В. При каком значении ЭДС третьего источника 3 ток через сопротивление R3 не потечёт?Решение
1. Выберем направление токов, выделим два контура и запишем уравнения правил Кирхгофа в соответствии с уравнениями (1) предыдущей задачи
(1)
2. Так как по условию задачи I3 = 0, то I1 = I2, уравнения (1) при этом примут вид
(2)
3. Поделим почленно последние уравнения друг на друга и полученное соотношение разрешим относительно 3
,
,
. (3)
2.4.3. Схема состоит из трёх идеальных источников ЭДС, два из которых заданы: 1 = 10 В, 2 = 8 В, и трёх сопротивлений два из которых тоже известны: R1 = 100 Ом, R2 = 80 Ом. Определить при каком значении 3 ток через сопротивление R3 ток течь не будет.Решение
1.Выберем узел схемы для которого запишем уравнение первого правила Кирхгофа
. (1)
2. Выделим два замкнутых контура и совершим их обход в указанных пунктирной линией направлениях по второму правилу Кирхгофа
. (2)
3. По условию задачи I3 =0, поэтому уравнения (1) и (2) можно переписать следующим образом
. (3)
4. Поделим почленно последние два уравнения системы (3) друг на друга
,
. (4)
5. Определим из уравнения (4) значение 3
,
. (5)
2.4.4. Две аккумуляторные батареи (1 = 8 В, r1 = 2 Ом; 2 = 6 В, r2 = 1,5 Ом) включены параллельно и согласно. Параллельно источникам тока подсоединено сопротивление R = 10 Ом. Определить силу тока текущего через сопротивление.Решение
1. Выберем узел, для которого запишем уравнение первого правила Кирхгофа
. (1)
2. Выделим два контура, показанные на схеме пунктирными линиями и составим для них уравнения второго правила Кирхгофа
. (2)
3. Из уравнений (2) выразим токи I1 и I2 и подставим полученные значения в уравнение (1)
, (3)
, (4)
. (5)
4. Определим из уравнения (5) силу тока, протекающего через сопротивление R
, (6)
. (7)
5. Определим далее токи через источники тока
. (8)
Знак «минус» показывает, что направление тока I1 выбрано неверно.
2.4.5. Определить силу тока I3 в резисторе R3 и падение напряжения U3, если: 1 = 4 В, 2 = 3 В, R1 = 2 Ом, R2 = 6 Ом, R3 = 1 Ом. Источники считать идеальными, их внутренним сопротивлением пренебречь.Решение
1. Запишем три уравнения в соответствии с правилами Кирхгофа
. (1)
2. Выразим из первого уравнения системы (1) силу тока I1
, (2)
и подставим полученное значение во второе уравнение
, (3)
. (4)
3. Разрешим третье уравнение системы (1) относительно силы тока I2
. (5)
4. Подставим значение I2 из уравнения (5) в уравнение (4)
. (6)
5. Уравнение (6) содержит одну неизвестную искомую величину I3
. (7)
. (8)
Таким образом, ток через сопротивление R3 равен нулю, это значит, что падение напряжения на этом резисторе тоже равно нулю.
2.4.6. Три источника с ЭДС 1 = 12 В, 2 = 5 В и 3 = 10 В с одинаковым внутренним сопротивлением r = 1 Ом соединены между собой одноимёнными полюсами. Пренебрегая сопротивлением соединительных проводов, определить силы токов, протекающих через источники.
Решение1. Выберем один из узлов и выделим два замкнутых контура, для которых запишем три уравнения первого и второго правила Кирхгофа
. (1)
2. Подставим в последние два уравнения системы (1) заданные числовые значения и сведём её к виду
. (2)
3. Выразим значения сил токов I1 и I3
, (3)
и подставим эти значения в первое уравнение системы (2)
, (4)
следовательно
. (5)
2.4.7. Для заданной цепи определить величины сил токов через резисторы, если известно, что: 1 = 2 = 4 В; 3 = 2 В; R1 = 1 Ом; R2 = 4 Ом; R3 = 2 Ом. Внутренним сопротивлением источников тока и сопротивлением соединительных проводов пренебречь.Решение
1. Запишем для данной цепи уравнения Кирхгофа, рассматривая баланс токов в узле А и баланс напряжений для выбранных контуров
(1)
2. Подставим численные значения заданных по условию задачи величин
(2)
3. Выразим из первого уравнения системы (2) силу тока I3 и подставим это значение в третье уравнение
, (3)
, (4)
. (5)
4. Образуем новую систему алгебраических уравнений из второго уравнения системы (2) и уравнения (5)
. (6)
5. Выразим далее из второго уравнения системы (6) силу ток I1 и подставим в первое уравнение
. (7)
6. Определим остальные две силы тока, воспользовавшись ранее записанными соотношениями между ними
. (8)
. (9)
2.4.8.Определить силы токов, текущих в каждой ветви цепи, если: 1 = 6,5 В, 2 = 3,9 В; R1 = R2 = R3 = R4 = R5 = 10 Ом.Решение
1. Для определения искомых величин токов необходимо составить шесть уравнений: три уравнения баланса токов и три уравнения баланса напряжений. Выберем для баланса токов три узла, а для баланса напряжений выделим три замкнутых контура.
2. Составим уравнения баланса токов для узлов a, b и с
. (1)
3. Для обозначенных на схеме цепи пунктирными линиями замкнутых контуров 1, 2 и 3 составим уравнения баланса напряжений, направление обхода показаны стрелками
. (2)
4. С учётом одинаковой величины всех сопротивлений R = 10 Ом последнюю систему уравнений можно переписать следующим образом
(3)
5. Совместное решение системы алгебраических уравнений (4)
(4)
методом подстановки позволяет прийти к следующим значениям сил токов
(5)
Отрицательные значения сил токов, полученные в результате решения, показывают, что их направление было изначально выбрано неверно и следует поменять на обратное.
2.5. Нелинейные элементы в цепях постоянного тока
2.5.1. Определить величину силы тока через идеальный источник (r = 0, = 10 В) при включении его в схему двумя способами, если R1 = R2 = R3 = R4 = 10 Ом, а диод идеальный, т.е. обладает в прямом направлении нулевым сопротивлением, а в обратном направлении бесконечно большим сопротивлением.
Решение
1. В первом случае (левая схема) диод будет представлять собой бесконечно большое сопротивление, т.е., по сути, разрыв цепи. Во втором случае (правая схема) сопротивление диода будет мало. Таким образом эквивалентные схемы цепей можно преобразовать следующим образом.
2. В случае большого сопротивления цепи резисторы R3 и R4 оказываются включенными последовательно, их общее сопротивление R3,4 = 20 Ом, которое, в свою очередь включено параллельно резистору R2. (1)
3. Определим эквивалентное сопротивление правой цепи
. (2)
4. Сила тока в первом случае включения источника тока
. (3)
5. При открытом диоде, когда он обладает весьма малым сопротивлением схему тоже можно последовательно преобразовать, при этом, (4)
, (5)
. (6)
6. Сила тока при открытом диоде составит
. (7)
2.5.2. Определить силу тока, протекающего через идеальный диод, если он включен в диагональ симметричного моста, составленного из сопротивлений R1 = 10 кОм, R2 = 15 кОм, R3 = 30 кОм R4 = 25 кОм. Мостик подключен к идеальному источнику тока с = 200 B.Решение
1. Предположим, что диод заперт, т.е. между точками а и b бесконечно большое сопротивление. В этом случае общее сопротивление схемы определится уравнением
. (1)
2. Сила тока через источник определится как
. (2)
3. Эквивалентная схема цепи в этом случае может быть представлена в виде последовательного соединения сопротивлений R1,4 и R2,3, которые, в свою очередь, включены параллельно источнику тока, (1)
. (2)
4. Падение напряжения на элементах эквивалентной схемы
, (3)
, (4)
, (5)
. (6)
5. Разность потенциалов между точками включения диода составляет U = 12 В, при такой полярности в узловых точках диод должен быть открыт и должен представлять собой весьма малое сопротивление. Другими словами эквивалентная схема цепи будет представлять собой параллельное включение сопротивлений R1, R2 и R3,R4, которые образуют последовательную цепь. Общее сопротивление цепи в этом случае определится как. (7)
6. Сила тока через источник
. (8)
7. Составим систему уравнений Кирхгофа для баланса токов в узлах a и b, дополнив их двумя уравнениями закона Ома для участка цепи
(9)
8. Подставив в уравнения (5) и (6) заданные значения сопротивлений, преобразуем их к виду
. (10)
9. Подставим значение силы тока I1 из уравнения (10) в уравнение (1) системы (9)
. (11)
10. Сила тока I1 из уравнений (10) определится как
. (12)
11. Далее подставим значение силы тока I2 из уравнения (10) в уравнение (4) системы (9)
. (13)
12. Определим далее силу тока I2, воспользовавшись для этого уравнениями (10)
. (14)
13. Из уравнения (4) системы (9) найдём искомую величину силы тока через диод
. (15)
2.5.3. Фотоэлемент включён в диагональ моста, составленного из четырёх резисторов R1 = 100 кОм, R2 = 400 кОм, R3 = 200 кОм, R4 = 300 кОм. Идеальный источник тока с ЭДС = 1 кВ включен в другую диагональ моста. Определить напряжение на фотоэлементе, если через него течёт ток силой ID = 10 мА. Решение1.Поскольку через фотоэлемент от анода к катоду течёт, заданный по условию задачи ток силой ID = 10 мА, то он открыт и представляет собой малое сопротивление. Эквивалентная схема цепи в этом случае может быть представлена в виде параллельного включения сопротивлений R1, R2, и R3, R4, которые в свою очередь соединены последовательно.
2. Определим эквивалентное сопротивление всей цепи
. (1)
3. Найдём величину силы тока через источник I0
. (2)
4. Составим систему из пяти (по количеству неизвестных величин) алгебраических уравнений на основе первого правила Кирхгофа и условий равенства потенциалов узлов a и b
(3)
5. Запишем уравнения (4), (5) с учётом заданных величин резисторов
. (4)
6. Перепишем уравнение (2) системы (3) с учётом уравнений (4)
. (5)
7. Определим из уравнения (2) системы (3) значение силы тока I1
. (6)
8. Найдём падение напряжений на резисторах R1 и R2
. (7)
. (8)
9. Напряжение на фотоэлементе: .
Согласно закону Ома, напряжение V, ток I и сопротивление R в цепи связаны уравнением V = IR, где единицы измерения — вольты, амперы и омы. Предположим, что напряжение является постоянным и составляет V = 18 В. Рассчитайте среднюю скорость изменения I
.
Исходя из закона Ома,
$$ V = ИК, $$
мы можем выразить ток как функцию напряжения и сопротивления,
$$ I = \ dfrac {V} {R} $$
Средняя скорость изменения интенсивности по отношению к сопротивлению определяется по формуле, приведенной ниже.
$$ \ eta = \ dfrac {\ Delta I} {\ Delta R} = \ dfrac {I (R + \ Delta R) -I (R)} {\ Delta R} $$
Подставляя функцию,
$$ \ begin {align} \ bar {\ eta} & = \ dfrac {V / (R + \ Delta R) -V / R} {\ Delta R} \\ [0,3 см] & = V \ dfrac {R-R- \ Delta R} {R (R + \ Delta R) \ Delta R} \\ [0,3 см] & = — \ dfrac {V \ Delta R} {R (R + \ Delta R) \ Delta R} \\ [0,3 см] & = — \ dfrac {V} {R (R + \ Delta R)} \ end {align} \\ $$
Оценка результата, когда {eq} V = 18 \; \ rm V {/ eq}, а сопротивление изменится с {eq} 8.0 \; \ rm \ Омега {/ eq} к {eq} 8.1 \; \ rm \ Omega {/ eq}, т.е. {eq} R = 8.0 \; \ rm \ Omega {/ eq} и {eq} \ Delta R = 0.1 \; \ rm Omega {/ eq},
$$ \ eta = — \ dfrac {18 \; \ rm V} {8.0 \; \ rm \ Omega \ cdot (8.0 \; \ rm \ Omega +0.1 \; \ rm Omega)} \ приблизительно \ в штучной упаковке {- 0,28 \; \ rm A / \ Omega} $$
Обратите внимание, что скорость изменения выражается в {eq} \ rm A / \ Omega {/ eq} — единицы тока, разделенные на единицы сопротивления. Отрицательная средняя скорость изменения означает, что ток уменьшится в среднем на {eq} 0.2} \ приблизительно \ в штучной упаковке {-0,28 \; \ rm A / \ Omega} $$
Мгновенная скорость изменения интенсивности составляет {eq} 0,28 \; \ rm A / \ Omega {/ экв}. Опять же, знак минус в скорости изменения указывает на уменьшение тока при увеличении сопротивления.
Что такое закон Ома и о чем он нам говорит?
Закон Ома гласит, что электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на нем. Другими словами, постоянная пропорциональность приводит к сопротивлению проводника.Закон Ома гласит, что постоянный ток, протекающий в проводнике, также прямо пропорционален разнице между его концами. Закон Ома сформулирован как V = IR, где V — напряжение, I — ток, а R — сопротивление проводника. Закон Ома представляет собой важнейшее математическое соотношение между напряжением, сопротивлением и током.
Ток
Согласно закону Ома, ток течет по проводнику, как вода течет по реке. По поверхности проводника ток течет от отрицательного к положительному.Электрический ток, содержащийся в цепи, можно рассчитать, разделив напряжение на сопротивление. Ток пропорционален напряжению и обратно пропорционален сопротивлению. Таким образом, увеличение напряжения приведет к увеличению тока. Это может произойти, только если сопротивление остается постоянным. Если сопротивление увеличивается, а напряжение нет, ток будет уменьшаться.
Напряжение
Напряжение можно описать как разность электрических потенциалов между двумя точками в цепи.Вы можете рассчитать напряжение, если известны ток и сопротивление в цепи. Если ток или сопротивление приводят к увеличению в цепи, напряжение автоматически увеличивается.
Сопротивление
Сопротивление определяет, сколько тока будет проходить через компонент. Резисторы можно использовать для управления уровнями тока и напряжения. Высокое сопротивление пропускает только небольшое количество тока. И наоборот, очень низкое сопротивление позволит пропускать большое количество тока.Сопротивление измеряется в Ом.
Мощность
Согласно закону Ома мощность — это количество тока, умноженное на уровень напряжения в данной точке. Мощность измеряется в ваттах или ваттах.
Закон Ом
- Изучив этот раздел, вы должны уметь:
- Опишите закон Ома для металлических проводников:
- • Сопротивление, напряжение и ток.
- Определить:
- Ом, Ампер и Вольт.
Ом, вольт и ампер.
Сопротивление проводника измеряется в Омах, а Ом — это единица измерения, названная в честь немецкого физика Джорджа Симона Ома (1787–1854 гг.), Который первым показал взаимосвязь между сопротивлением, током и напряжением. При этом он разработал свой закон, который показывает взаимосвязь между тремя основными электрическими свойствами сопротивления, напряжения и тока.Он демонстрирует одну из самых важных взаимосвязей в электротехнике и электронной технике.
Закон Ома гласит: «В металлических проводниках при постоянной температуре и нулевом магнитном поле протекающий ток пропорционален напряжению на концах проводника и обратно пропорционален сопротивлению проводника. »
Проще говоря, при условии, что температура постоянна и электрическая цепь не подвержена влиянию магнитных полей, тогда:
• В цепи постоянного сопротивления, чем больше напряжение, приложенное к цепи, тем больше будет протекать ток.
• При постоянном напряжении, чем больше сопротивление цепи, тем меньше ток.
Обратите внимание, что закон Ома гласит: «В металлических проводниках». Это означает, что закон применим для большинства металлических материалов, но не для всех. Например, вольфрам, используемый для накаливания накала лампочек, имеет сопротивление, которое изменяется в зависимости от температуры нити, отсюда в законе Ома ссылка на «при постоянной температуре». В электронике также используются компоненты, которые имеют нелинейную зависимость между тремя электрическими свойствами: напряжением, током и сопротивлением, но их можно описать разными формулами.Для большинства схем или компонентов, которые могут быть описаны законом Ома:
Вместо того, чтобы пытаться запомнить весь закон Ома, три электрических свойства напряжения, тока и сопротивления отдельными буквами:
Сопротивление обозначается буквой R и измеряется в единицах Ом, которые имеют символ Ω (греческая заглавная буква O).
Напряжение обозначается буквой V (или иногда E, сокращением от Electromotive Force) и измеряется в вольтах, которые имеют символ V.
Ток обозначается буквой I (не C, поскольку он используется для обозначения емкости) и измеряется в единицах ампер (часто сокращается до ампер), которые имеют символ A.
Используя буквы V, I и R для выражения отношений, определенных в Законе Ома, дает три простые формулы:
Каждый из них показывает, как найти значение любой из этих величин в цепи, если известны две другие. Например, чтобы найти напряжение V (в вольтах) на резисторе, просто умножьте ток I (в амперах) через резистор на значение резистора R (в омах).
Обратите внимание, что при использовании этих формул значения V I и R, записанные в формулу, должны быть в БАЗОВЫХ ЕДИНИЦАХ, то есть в ВОЛЬТАХ (не в милливольтах) в Омах (не в киломах) и в АМПЕРАХ (не в микроамперах) и т. Д.
Вкратце 15 кОм (килоом) вводится как 15 EXP 03, а 25 мА (миллиампер) вводится как 25 EXP -03 и т. Д. Это проще всего сделать с помощью научного калькулятора.
Как пользоваться калькулятором с инженерными обозначениями, широко используемыми в электронике, объясняется в нашем бесплатном буклете под названием «Подсказки по математике». Загрузите его со страницы загрузки.
Определение Ом, Ампера и Вольт
1 Ом
Может быть определено как «величина сопротивления, которая создает разность потенциалов (p.d.) или напряжение в 1 вольт на нем, когда через него протекает ток в 1 ампер».
1 АМПЕР
Можно определить как «Величина тока, которая при прохождении через сопротивление 1 Ом создает разность потенциалов на сопротивлении в 1 Вольт».
(Хотя доступны более полезные определения ампера)
1 ВОЛЬТ
Может быть определено как «Разность потенциалов (напряжений), возникающая на сопротивлении 1 Ом, через которое протекает ток в 1 Ампер.«
Эти определения относятся к Вольтам, Амперам и Ом в пределах величин, описанных в Законе Ома, но также могут использоваться альтернативные определения с использованием других величин.
ПОПРОБУЙТЕ ПРОСТЫЕ РАСЧЕТЫ, ИСПОЛЬЗУЯ Закон Ома.
% PDF-1.5 % 1 0 obj> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 4 0 obj> поток конечный поток эндобдж xref 0 5 0000000000 65535 ф 0000000016 00000 н. 0000000075 00000 п 0000000120 00000 н. 0000000210 00000 н. трейлер ] >> startxref 3379 %% EOF 1 0 obj> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 5 0 obj null эндобдж 6 0 obj> эндобдж 7 0 obj> эндобдж 8 0 obj> эндобдж 9 0 obj> / Font> / XObject> / ProcSet [/ PDF / Text / ImageB] / ExtGState >>> эндобдж 10 0 obj> эндобдж 11 0 obj> эндобдж 12 0 obj> эндобдж 13 0 obj> эндобдж 14 0 obj> / Ширина 661 / Высота 221 / BitsPerComponent 1 / ImageMask true / Type / XObject / Subtype / Image >> stream & M‚Ck
Какое утверждение верно в соответствии с законом Ома A Текущий класс физики 12 JEE_Main
Подсказка: Мы знаем, что закон Ома гласит, что напряжение на проводнике с током прямо пропорционально току, протекающему в токе.Итак, математическое уравнение закона Ома имеет вид $ V = I \ cdot R $, где $ V $ — напряжение, $ I $ — ток, а $ R $ — сопротивление проводника, которое фиксировано для заданная температура проводника. Теперь мы можем получить ответ, проанализировав все варианты. Используемая формула:
Закон Ома гласит, что $ V = I \ cdot R $, где $ V $ — напряжение, $ I $ — ток, а $ R $ — сопротивление проводника.
Полное пошаговое решение:
Мы знаем, что закон Ома гласит, что напряжение пропорционально току.Следовательно,
$ V = I \ cdot R $,
где $ V $ — напряжение, $ I $ — ток, а $ R $ — сопротивление проводника, которое фиксировано для данной температуры проводника. Теперь, проанализировав по очереди все варианты, указанные в вопросе, мы получим ответ.
Вариант A: Теперь в этом варианте указывается, что ток будет увеличиваться за счет увеличения напряжения в цепи. Теперь, как мы обсуждали выше, согласно закону Ома $ I \ propto V $, это означает, что если ток будет увеличиваться, то одновременно будет увеличиваться и напряжение.
Значит, это правильный вариант.
Вариант B: Теперь в этом варианте указано, что сопротивление будет увеличиваться при увеличении напряжения в цепи. Как обсуждалось выше, сопротивление проводника фиксировано для данной температуры. Значит, сопротивление не увеличится, если мы увеличим напряжение цепи.
Следовательно, этот вариант неверен.
Вариант C: Теперь эта опция указывает, что сопротивление будет увеличиваться за счет увеличения тока в цепи. Как обсуждалось выше, сопротивление проводника фиксировано для данной температуры.Значит, сопротивление не увеличится, если мы увеличим ток в цепи.
Следовательно, этот вариант неверен.
Вариант D. Теперь в этом варианте указывается, что сопротивление и ток будут увеличиваться при увеличении напряжения в цепи. Как обсуждалось выше, ток увеличивается с увеличением напряжения, но сопротивление проводника остается неизменным для данной температуры. Значит, сопротивление не увеличится, если мы увеличим напряжение в цепи.
Следовательно, этот вариант неверен.
Итак, правильный ответ — вариант (А).
Примечание: Мы знаем, что сопротивление постоянно для данной температуры в соответствии с законом Ома. Итак, варианты B, C и D неверны. Теперь, поскольку ток прямо пропорционален напряжению в цепи. Значит, ток будет увеличиваться с увеличением напряжения в цепи.
Что такое закон Ома? | Fluke
Закон Ома — это формула, используемая для расчета взаимосвязи между напряжением, током и сопротивлением в электрической цепи.
Для изучающих электронику закон Ома (E = IR) столь же фундаментально важен, как уравнение относительности Эйнштейна (E = mc²) для физиков.
E = I x R
В тексте это означает, что напряжение = ток x сопротивление , или В = А x Ом , или В = A x Ом .
Названный в честь немецкого физика Георга Ома (1789-1854), закон Ома определяет ключевые величины, действующие в цепях:
| Количество | Закон Ома символ | Единица измерения (аббревиатура) | Роль в схемы | Если вам интересно: |
|---|---|---|---|---|
| Напряжение | E | Вольт (В) | Давление, которое запускает поток электронов | E = электродвижущая сила (старая школа) |
| Ток | I | Ампер, ампер (A) | Скорость потока электронов | I = интенсивность |
| Сопротивление | R | Ом (Ом) | Ингибитор потока | Ом = omega |
Если известны два из этих значений, технические специалисты могут перенастроить закон Ома, чтобы вычислить третье.Просто измените пирамиду следующим образом:
Если вам известны напряжение (E) и ток (I) и вы хотите узнать сопротивление (R), вытяните R в пирамиде и вычислите оставшееся уравнение (см. Первое или дальнее слева, пирамида вверху).
Примечание: Сопротивление нельзя измерить в рабочей цепи, поэтому закон Ома особенно полезен, когда его нужно вычислить. Вместо того, чтобы отключать цепь для измерения сопротивления, технический специалист может определить R, используя вышеуказанный вариант закона Ома.
Теперь, если вы знаете напряжение (E) и сопротивление (R) и хотите знать ток (I), вытяните X-I и вычислите оставшиеся два символа (см. Среднюю пирамиду выше).
И если вы знаете ток (I) и сопротивление (R) и хотите знать напряжение (E), умножьте нижние половины пирамиды (см. Третью или крайнюю правую пирамиду выше).
Попробуйте несколько примеров расчетов на основе простой последовательной схемы, которая включает только один источник напряжения (аккумулятор) и сопротивление (свет).В каждом примере известны два значения. Используйте закон Ома для вычисления третьего.
Пример 1: Напряжение (E) и сопротивление (R) известны.
Какой ток в цепи?
I = E / R = 12 В / 6 Ом = 2 А
Пример 2: Напряжение (E) и ток (I) известны.
Какое сопротивление создает лампа?
R = E / I = 24 В / 6 A = 4 Ом
Пример 3: Ток (I) и сопротивление (R) известны. Какое напряжение?
Какое напряжение в цепи?
E = I x R = (5A) (8Ω) = 40 В
Когда Ом опубликовал свою формулу в 1827 году, его ключевым выводом было то, что величина электрического тока, протекающего по проводнику, прямо пропорциональна приложенному напряжению. в теме.Другими словами, требуется один вольт давления, чтобы протолкнуть один ампер тока через один ом сопротивления.
Что проверять с помощью закона Ома
Закон Ома можно использовать для проверки статических значений компонентов схемы, уровней тока, источников напряжения и падений напряжения. Если, например, измерительный прибор обнаруживает значение тока, превышающее нормальный, это может означать, что сопротивление уменьшилось или что напряжение увеличилось, вызывая ситуацию высокого напряжения. Это может указывать на проблему с питанием или цепью.
В цепях постоянного тока (dc) измерение тока ниже нормального может означать, что напряжение снизилось или сопротивление цепи увеличилось. Возможные причины повышенного сопротивления — плохие или неплотные соединения, коррозия и / или поврежденные компоненты.
Нагрузки в цепи потребляют электрический ток. Нагрузки могут быть любыми компонентами: небольшими электрическими устройствами, компьютерами, бытовой техникой или большим двигателем. На большинстве этих компонентов (нагрузок) есть паспортная табличка или информационная наклейка.На этих паспортных табличках указаны сертификаты безопасности и несколько ссылочных номеров.
Технические специалисты обращаются к заводским табличкам на компонентах, чтобы узнать стандартные значения напряжения и тока. Во время тестирования, если технические специалисты обнаруживают, что обычные значения не регистрируются на их цифровых мультиметрах или токоизмерительных клещах, они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и на основании этого определить, в чем может заключаться проблема.
Основы науки о схемах
Схемы, как и вся материя, состоят из атомов.Атомы состоят из субатомных частиц:
- Протоны (с положительным электрическим зарядом)
- Нейтроны (без заряда)
- Электроны (с отрицательным зарядом)
Атомы остаются связанными силами притяжения между ядром атома и электронами в его внешняя оболочка. Под воздействием напряжения атомы в цепи начинают преобразовываться, и их компоненты проявляют потенциал притяжения, известный как разность потенциалов. Взаимно привлеченные свободные электроны движутся к протонам, создавая поток электронов (ток).Любой материал в цепи, ограничивающий этот поток, считается сопротивлением.
Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.
Сопутствующие статьи
мощность — Соотношение между током, сопротивлением и напряжением согласно закону Ома, закону тепла Джоуля и P = IV
Давайте приведем свои мысли по порядку …
Закон Ома касается линейного (постоянного) сопротивления. Значит, мы не должны допускать потепления. В таком расположении мы начинаем экспериментировать.
Сначала мы подключаем источник напряжения к резистору и начинаем изменять напряжение на нем. В результате пропорционально изменится ток через резистор — Iout = Vin / R. Если мы изменим сопротивление, ток будет пропорционально изменяться обратно — Iout = V / Rin.
Затем мы подключаем источник тока к резистору и начинаем изменять ток через него. Теперь напряжение на резисторе будет пропорционально изменяться — Vout = Iin.R. Если мы изменим сопротивление, напряжение будет пропорционально изменяться — Vout = I.2.Р. Если вы хотите, чтобы оно оставалось постоянным, измените сопротивление в соответствующем направлении. Это означает, что в законе Ома есть две входные переменные — Iout = Vin / Rin и Vout = Iin.Rin, или сопротивление стало «динамическим».
Такие уловки используются для создания нелинейных резисторов, которые поддерживают постоянное напряжение (например, стабилитрон) или постоянный ток (например, транзистор). Это видно по ВАХ диода и выходной характеристике транзистора.
Конечно, мы можем поддерживать постоянную мощность в соответствии с Pout = Vin.Iin. Это означает подключение источника напряжения к источнику тока. Таким образом, источник напряжения будет устанавливать напряжение на источниках, а источник тока будет устанавливать ток через них. Точнее говоря, в этом расположении только один из элементов является источником; другой — нагрузка, реализованная как нелинейный резистор.
Теперь, чтобы сохранить постоянную мощность, при увеличении напряжения мы уменьшаем ток и v.


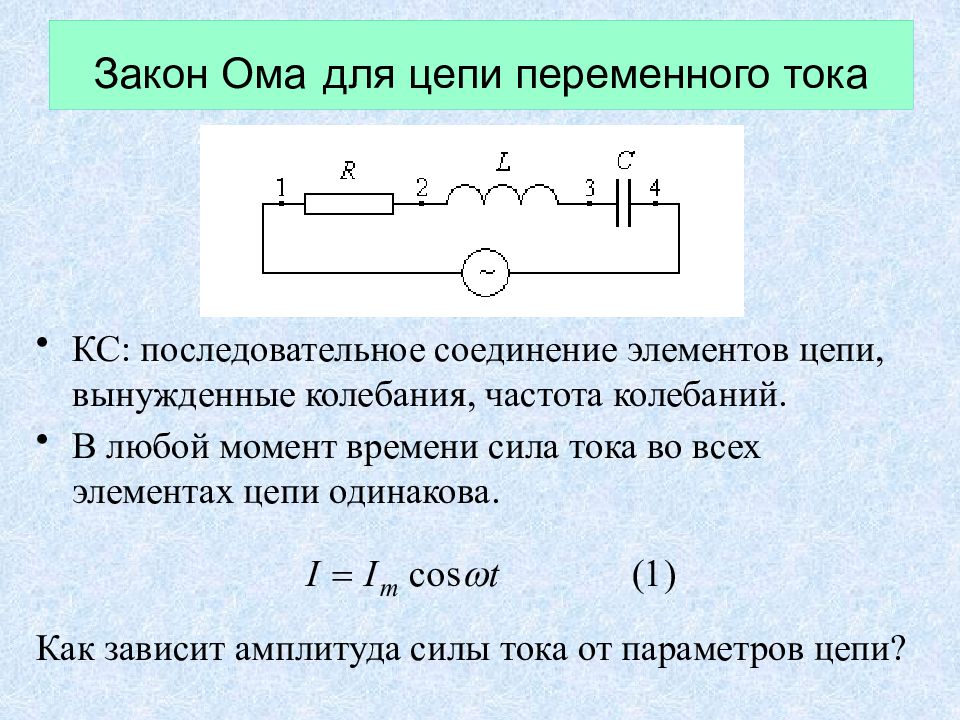 3)
3) 4)
4) 6)
6) 107
107