Что такое порядок фильтра в акустических системах. Как порядок фильтра влияет на качество звучания. Какие существуют типы фильтров и в чем их отличия. Как выбрать оптимальный порядок фильтра для автомобильной акустики.
Что такое порядок фильтра в акустических системах
Порядок фильтра в акустических системах определяет крутизну спада амплитудно-частотной характеристики (АЧХ) за пределами полосы пропускания. Чем выше порядок фильтра, тем быстрее происходит ослабление сигнала вне рабочего диапазона частот.
Основные особенности порядка фильтра:
- Измеряется целым положительным числом (1, 2, 3 и т.д.)
- Определяется количеством реактивных элементов (катушек и конденсаторов) в схеме фильтра
- Влияет на крутизну спада АЧХ — 6 дБ на октаву умножается на порядок фильтра
- Более высокий порядок обеспечивает лучшую фильтрацию, но может вносить фазовые искажения
Как правило, в акустических системах применяются фильтры от 1-го до 4-го порядка. Выбор оптимального порядка зависит от многих факторов и требует компромисса между качеством фильтрации и фазовыми искажениями.
Влияние порядка фильтра на качество звучания
Порядок фильтра оказывает существенное влияние на звучание акустической системы. Рассмотрим основные аспекты:
Фильтрация сигнала
Фильтры более высокого порядка обеспечивают лучшую фильтрацию нежелательных частот:
- Уменьшают нагрузку на динамики вне их рабочего диапазона
- Снижают интермодуляционные искажения
- Позволяют точнее разделить частотные полосы между динамиками
Фазовые искажения
С увеличением порядка фильтра растут фазовые искажения сигнала:
- Могут приводить к размытию стереообраза
- Ухудшают точность воспроизведения импульсных сигналов
- Искажают тембр звучания некоторых инструментов
Групповая задержка
Фильтры высокого порядка вносят неравномерную групповую задержку в разных частотных диапазонах. Это может приводить к искажению формы сложных звуковых сигналов.
Типы фильтров в акустических системах
В акустических системах применяются различные типы фильтров, отличающиеся формой АЧХ и фазовой характеристикой:
Фильтры Баттерворта
- Максимально плоская АЧХ в полосе пропускания
- Умеренная крутизна спада за пределами полосы пропускания
- Хороший компромисс между качеством фильтрации и фазовыми искажениями
Фильтры Бесселя
- Наиболее линейная фазовая характеристика
- Минимальные искажения формы импульсных сигналов
- Пологий спад АЧХ за пределами полосы пропускания
Фильтры Линквица-Райли
- Обеспечивают ровную суммарную АЧХ при акустическом сложении сигналов от разных полос
- Хорошее подавление сигнала вне полосы пропускания
- Синфазность выходных сигналов на частоте раздела
Выбор оптимального порядка фильтра для автомобильной акустики
При выборе порядка фильтра для автомобильной акустической системы следует учитывать несколько факторов:

Частота раздела
На низких частотах раздела (до 200-300 Гц) рекомендуется использовать фильтры более высокого порядка (3-4) для лучшей защиты среднечастотных динамиков от перегрузки басом.
Характеристики динамиков
Для динамиков с широким рабочим диапазоном можно применять фильтры более низкого порядка. Узкополосные излучатели требуют более крутых срезов АЧХ.
Акустическое оформление
В закрытых корпусах допустимо использовать фильтры 1-2 порядка. Для фазоинверторных систем лучше применять фильтры 3-4 порядка во избежание перегрузки динамика на частотах ниже настройки порта.
Качество компонентов
При использовании высококачественных конденсаторов и катушек можно применять фильтры более высокого порядка без существенного ухудшения звучания.
Активная или пассивная фильтрация в автомобильной акустике
В современных автомобильных аудиосистемах часто применяется активная фильтрация сигнала на входе усилителей мощности. Это позволяет:
- Избежать потерь мощности на элементах пассивных фильтров
- Точнее настроить частоты раздела и крутизну спада АЧХ
- Уменьшить нелинейные искажения за счет работы усилителей в оптимальном частотном диапазоне
- Снизить требования к качеству пассивных компонентов фильтров
Однако полностью отказаться от пассивных фильтров обычно не удается. Они необходимы для защиты высокочастотных динамиков от низкочастотных составляющих сигнала.
Практические рекомендации по выбору порядка фильтра
На основе рассмотренной информации можно сформулировать некоторые общие рекомендации по выбору порядка фильтра для автомобильной акустики:
- Для разделения низких и средних частот (до 300-400 Гц) рекомендуется использовать фильтры 3-4 порядка
- В диапазоне 400-2000 Гц оптимальны фильтры 2-3 порядка
- Для высокочастотных динамиков (выше 2-3 кГц) допустимо применение фильтров 1-2 порядка
- При использовании качественных компонентов предпочтительны фильтры Линквица-Райли 4 порядка
- Для бюджетных систем оптимальны фильтры Баттерворта 2-3 порядка
Важно помнить, что универсальных рекомендаций не существует. Оптимальный выбор порядка и типа фильтра зависит от конкретных характеристик используемых динамиков и особенностей их установки в автомобиле.
Заключение
Выбор оптимального порядка фильтра для акустической системы — сложная задача, требующая учета множества факторов. Высокий порядок фильтра обеспечивает лучшую защиту динамиков и более точное разделение частотных полос, но может приводить к фазовым искажениям и ухудшению качества звучания.
В современных автомобильных аудиосистемах все чаще применяется активная фильтрация сигнала, позволяющая более гибко настраивать частотное разделение. Однако полностью отказаться от пассивных фильтров пока не удается.
При выборе порядка фильтра следует ориентироваться на характеристики конкретных динамиков, особенности их установки в автомобиле и качество используемых компонентов. В большинстве случаев оптимальным выбором являются фильтры 2-4 порядка.
Порядок фильтра – 4;
граничные частоты – 100Гц, 18кГц;
коэффициент передачи по напряжению – 1.
Изучение вопроса начнем с рассмотрения общих положений.
Фильтрация
— преобразование сигналов с целью
изменения соотношения между их различными
частотными составляющими. Фильтры
обеспечивают выделение полезной
информации из смеси информационного
сигнала с помехой с требуемыми
показателями. Основная задача выбора
типа фильтра и его расчета заключается
в получении таких параметров, которые
обеспечивают максимальную вероятность
обнаружения информационного сигнала
на фоне помех. Частотно-избирательная
цепь, выполняющая обработку смеси
сигнала и шума некоторым наилучшим
образом, называется оптимальным фильтром.
Критерием оптимальности принято считать
обеспечение максимума отношения
сигнал-шум. Это требование приводит к
выбору такой формы частотного коэффициента
передачи фильтра, которая обеспечивает
максимум отношения сигнал-шум на его
выходе. В задачах линейной фильтрации
предполагается, что наблюдаемый реальный
процесс представляет собой аддитивную
смесь сигнала и помехи.
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (пропускают высокие частоты и задерживают низкие частоты), полосовые
фильтры (пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы) и режекторные фильтры (задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы).Рис. 1. Общее изображение электрического фильтра.
Более точно характеристику частотно-избирательного фильтра можно описать, рассмотрев его передаточную функцию
H(s)=U2(s)/U2(s), (1)
Величины
U1 и U2 представляют собой соответственно
входное и выходное напряжения, как
показано на общем изображении фильтра
на рис. 1.
1.
Для установившейся частоты s=j ( ) передаточную функцию можно переписать в виде
H(j)=H(j)e
где H(j) модуль передаточной функции или амплитудно-частотная характеристика; () фазо-частотная характеристика, а частота (рад/с) связана с частотой f (Гц) соотношением =2f.
Диапазоны
или полосы частот, в которых сигналы
проходят, называются полосами
пропускания и в них значение амплитудно-частотной
характеристики H(j)
относительно велико, а в идеальном
случае постоянно. Диапазоны частот, в
которых сигналы подавляются, образуют
полосы задерживания и в них значение
амплитудно-частотной характеристики
относительно мало, а в идеальном случае
равно нулю. В качестве примера на рис.
2 штриховой линией показана
амплитудно-частотная характеристика
идеального фильтра нижних частот с
единственной полосой пропускания 0<<c и полосой задерживания >c .
Рис. 2. Идеальная и реальная АЧХ фильтра нижних частот.
В
практическом случае полосы пропускания
и задерживания четко не разграничены
и должны быть формально определены.
Исходя из нашего определения, в качестве
полосы пропускания выбирается диапазон
частот, где значение амплитудно-частотной
характеристики превышает некоторое
заранее выбранное число, обозначенное
A1 на рис. 2, а полосу задерживания образует
диапазон частот, в котором амплитудно-частотная
характеристика меньше определенного
значения, например, A Интервал частот, в котором
амплитудно-частотная характеристика
постоянно спадает, переходя от полосы
пропускания к полосе задерживания,
называется переходной областью.
Приведенный на рис. 2 пример имеет полосу
пропускания 0<<c,
полосу задерживания >1 и переходную область c<<1.
Интервал частот, в котором
амплитудно-частотная характеристика
постоянно спадает, переходя от полосы
пропускания к полосе задерживания,
называется переходной областью.
Приведенный на рис. 2 пример имеет полосу
пропускания 0<<c,
полосу задерживания >1 и переходную область c<<1.
Значение АЧХ можно также выразить в децибелах (дБ) следующим образом
=20lgH(j), (3)
и в этом случае характеризует затухание. Например, предположим, что на рис. 2 выбрано A=1, которому соответствует =0. Тогда если
то затухание на частоте c
1=20lg(1/20,5)=10lg2=3 дБ.
В
основном пропускание в полосе пропускания
никогда не превышает 3 дБ. Таким образом,
из приведенного примера следует, что
значение АЧХ в полосе пропускания
составляет по крайней мере 1/20,5=0,707
или 70,7% ее максимального значения.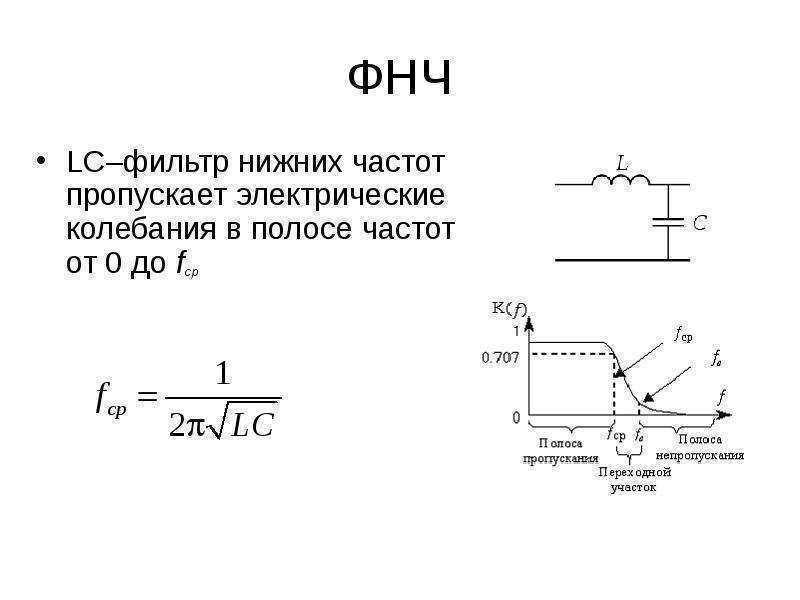 В
этом случае можно также сказать, что в
полосе пропускания амплитудно-частотная
характеристика на 3 дБ ниже или меньше
максимального значения.
В
этом случае можно также сказать, что в
полосе пропускания амплитудно-частотная
характеристика на 3 дБ ниже или меньше
максимального значения.
Для частотно-избирательных фильтров наиболее важной является амплитудно-частотная характеристика, поскольку ее значение на некоторой частоте определяет прохождение сигнала этой частоты или его подавление.
Фильтры
Немногим счастливчикам известно, каким добрым, мягким, домашним, натуральным звуком отличались старые, лучше всего – довоенные, немецкие громкоговорители с легкими бумажными диффузорами большого размера. Однако стремление еще более приблизить звучание к реальности, а именно, достичь равномерности АЧХ в более широкой полосе, создать большие уровни громкости и в то же время по возможности уменьшить габариты АС, привело к постепенному отходу от традиций и принципов, заложенных во время серебряного века электроакустики, и отправиться в погоню за золотым тельцом объективных технических показателей. Какие же объективные недостатки однополосных систем заставили разработчиков искать счастья на ниве частотного разделения? Если кратко (обещали!), то основных причин немного:
Какие же объективные недостатки однополосных систем заставили разработчиков искать счастья на ниве частотного разделения? Если кратко (обещали!), то основных причин немного:
Первое. Диффузор любой головки способен к поршнеобразному движению, то есть к движению как единое целое только в определенном частотном диапазоне. Как только частота достигает определенной величины – на поверхности диффузора появляются упругие волны, способные организовать интерференционную картину. Поршнеобразное движение, на факте которого основаны все расчеты параметров головки, прекращается. Для большинства низкочастотных головок такая частота лежит в районе нескольких сотен герц. Широкополосные и среднечастотные головки могут сохранить характер колебаний диффузора до частот в единицы килогерц, некоторые из них, с композитными и керамическими диффузорами – до 5 – 8 кГц. На более высоких частотах уверенно работают лишь купольные излучатели: среднечастотные обслуживают диапазон от сотен герц до 10 килогерц, и на всем его протяжении купольный диффузор головок пытается двигаться поршнеобразно. У легких тканевых, композитных или металлических куполов ВЧ-головок в звуковом диапазоне частот рассмотренных проблем не возникает.
У легких тканевых, композитных или металлических куполов ВЧ-головок в звуковом диапазоне частот рассмотренных проблем не возникает.
Объективно описанные процессы проявляются в возникновении начиная с некоторой частоты изрезанности АЧХ, в росте нелинейных искажений, интермодуляции, фазовых нарушениях. Главное субъективно оцениваемое последствие – потеря натуральности звучания акустических инструментов, появление в звуке жесткости, иногда призвуков. Следует заметить, что старые добрые головки довоенных приемников болели описанной болезнью по полной программе, – даже легкие бумажные диффузоры не были способны ей сопротивляться. Однако кропотливый труд целых поколений экспериментаторов, варивших секретные бумажные массы, не пропал даром – характер паразитных колебаний старых диффузоров был таким, что последствия их с точки зрения слуха (извините за каламбур) оказывались минимальными.
Второе. Совсем простое. Индуктивность не отменили даже итоги мировой войны. Например, если индуктивность звуковой катушки низкочастотной головки 1 мГн (совсем не много), то на 1 кГц реактивная составляющая импеданса уже равна 6,28 Ом, а на 10 кГц – 62,8 Ом. На этом сопротивлении и упадет все напряжение сигнала, естественно, не вызвав требуемого нам движения диффузора.
На этом сопротивлении и упадет все напряжение сигнала, естественно, не вызвав требуемого нам движения диффузора.
Третье. Все ждут от динамической головки производства сферической звуковой волны. Тогда характеристика направленности создаваемого излучения будет круговой, и перемещающийся в пространстве слушатель не будет ощущать дискомфорта. В машине слушатель не изменяет своего положения (разве что при ДТП), но здесь на характеристики направленности возлагаются еще более ответственные задачи, ведь компоновочные возможности в салоне далеко не безграничны. Сферическую волну порождает точечный излучатель. Иначе: размеры диффузора должны быть заметно меньше длины волны. Как только это условие перестает выполняться, характеристика направленности головки обуживается, что способно породить массу проблем.
Четвертое. На низких частотах, особенно вблизи резонансной частоты, диффузор головки движется с довольно большой скоростью, составляющей единицы процентов от скорости звука. Следовательно, при одновременном воспроизведении и высоких, и низких частот будет наблюдаться доплеровская модуляция колебаний высоких частот низкими, так как часть времени эти частоты будут излучаться движущимся с большой скоростью диффузором на слушателя, а часть времени – от слушателя. Последствия доплеровской модуляции проявляются в крайне неприятной на слух потере чистоты тона, у слушателя пропадает удовольствие от классических фрагментов, основанных на строгих законах музыкальной гармонии.
Следовательно, при одновременном воспроизведении и высоких, и низких частот будет наблюдаться доплеровская модуляция колебаний высоких частот низкими, так как часть времени эти частоты будут излучаться движущимся с большой скоростью диффузором на слушателя, а часть времени – от слушателя. Последствия доплеровской модуляции проявляются в крайне неприятной на слух потере чистоты тона, у слушателя пропадает удовольствие от классических фрагментов, основанных на строгих законах музыкальной гармонии.
Иными словами – как ни сильна ностальгия по хорошему звучанию бумажных раритетов, отлично играть может лишь многополосная система. Эта истина стала очевидной для разработчиков больше полувека назад, и с тех пор разделительные фильтры начали пробивать себе дорогу на рынок.
Мы не будем рассматривать все этапы развития фильтров как полноценного компонента аудиотракта. Заметим лишь, что они прошли сложный путь, в начале которого фильтры выполняли лишь энергетические частотно-разделяющие функции, а сейчас от фильтров требуют комплексного решения вопросов энергоразделения, формирования характеристики направленности АС в целом, компенсации реактивности головки с учетом воздействия акустического оформления и т. п.
п.
Надо сказать, что техническую задачу разработчики решили: АС формируют великолепную АЧХ при оптимальных ФЧХ, характеристиках направленности при использовании совершенно реальных головок. Все математические проблемы, связанные с расчетами, взяли на себя компьютеры, программами для расчета в любительских условиях кишит Интернет. Но сказать, что АС начали от этого играть лучше, чем хорошо, мы не можем. Проблема стара как мир: стремиться надо не к идеальной АЧХ и ФЧХ, а к хорошему звуку, и на пути этого стремления во весь рост встают куда более сложные, нежели трудный расчет, проблемы.
Тем не менее, не поделиться с читателем элементарными основами построения разделительных фильтров было бы неверно. У любого стремления к качеству должна быть отправная точка. Наша точка находится там, где достигаются приемлемые объективно оцениваемые параметры АС, а в их формировании едва ли не главную роль играют разделительные фильтры.
Рис. 1. Простейшие ФНЧ (а) и ФВЧ (б) второго порядка.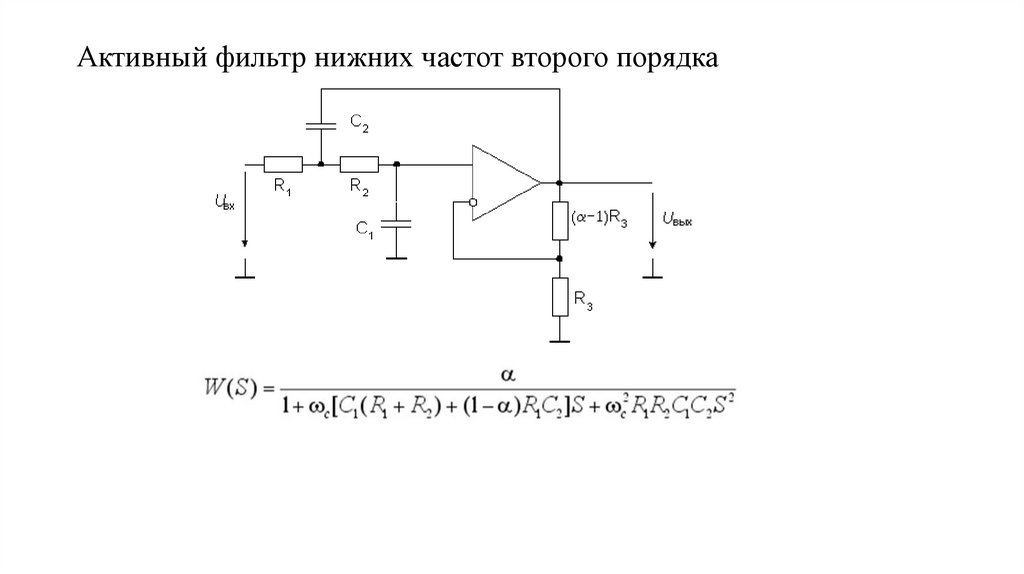 Обычно при расчете фильтров АС считается, что питание фильтра осуществлено от генератора напряжения, а нагрузкой служит омическое сопротивление головки. Более сложные случаи оговариваются особо.
Обычно при расчете фильтров АС считается, что питание фильтра осуществлено от генератора напряжения, а нагрузкой служит омическое сопротивление головки. Более сложные случаи оговариваются особо.
Рис. 2. К понятию всепропускающего разделительного фильтра. Акустическое суммирование сигналов НЧ, СЧ и ВЧ-головок способно создать в точке наблюдения плоскую АЧХ, естественно, при соблюдении некоторых условий. Отметим, что полосовой фильтр, питающий СЧ-головку, может быть выполнен как на полосовых элементах (см. рис.), так и представлять каскадно включенные ФВЧ и ФНЧ.
Рис. 3. Головка только в первом приближении представляет активное сопротивление. Попытка достичь хороших характеристик при работе с реальными головками требует учета их реактивности. На данном рисунке представлены основные реактивные параметры головки вблизи резонансной частоты и простейшая компенсирующая цепь.
Суммирование АЧХ двух фильтров Баттерворта второго порядка (ФНЧ и ФВЧ).
Суммирование АЧХ двух фильтров Баттерворта третьего порядка.
Суммирование АЧХ двух фильтров второго порядка с характеристикой Линквица – Райли.
О фильтрах вообще и о фильтрах в АС в частности
Фильтр – линейная электрическая цепь, обладающая свойством избирательного пропускания сигналов разных частот. Линейная – в том смысле, что подача на нее синусоидального сигнала не приводит к искажению его формы. Понятно, что фильтры нижних частот (ФНЧ) лучше пропускают нижние частоты, фильтры верхних частот (ФВЧ) – верхние. Полосовые фильтры пропускают сигналы, лежащие выше определенной нижней, но ниже определенной верхней частоты. Это – основы. Фильтр характеризуется АЧХ и ФЧХ. Для простейших фильтров они связаны преобразованием Гильберта, проще говоря, зная АЧХ, можно рассчитать и ФЧХ, и наоборот.
Процессы в фильтрах легко описываются линейными дифференциальными уравнениями или их системами, причем по науке именно порядок системы уравнений и принимается за порядок фильтра. А на практике, когда не до уравнений (тем более дифференциальных), порядок, как правило, равен числу индуктивностей и емкостей, из которых сделан фильтр, вместе взятых.
Вне полосы пропускания фильтр вносит затухание, причем далеко от частоты среза это затухание определяется простой зависимостью и равняется 6N децибел на октаву, где N – порядок фильтра. Поясню на примере. Рассмотрим ФНЧ пятого порядка с частотой среза 1 кГц. Для двух частот F1 и F2, если они достаточно далеко отстоят от частоты среза и, скажем, отличаются в 2 раза (на одну октаву), то затухания, вносимые фильтром на этих частотах, будут отличаться в 6 х 5 х 1 = 30 дБ. Вот и весь расчет.
Недалеко от частоты среза характер поведения АЧХ зависит не только от порядка, но и от типа фильтра. Тип фильтра – более сложное понятие, чем порядок. Как фильтр, так и соответствующее дифференциальное уравнение, характеризуется полиномом, так и называемым – характеристическим. Его коэффициенты зависят от номиналов электрических компонентов фильтра. Полиномы бывают разные – Бесселя, Баттерворта, Чебышева, Золотарева – Кауэра и др., по имени исследовавших их еще задолго до появления фильтров, и уж тем более автомобильного аудио, математиков.
Фильтры Бесселя отличаются минимальной крутизной вблизи среза. То есть, формально, отфильтровывают «лишние» частоты довольно лениво. Зато ФЧХ таких фильтров наиболее гладка, и характеристика группового времени запаздывания (ГВЗ) от частоты имеет минимальный перепад, что свидетельствует о возможности минимального искажения формы несинусоидальных процессов.
Фильтр Баттерворта предпочтительнее, но и ФЧХ с ГВЗ имеет похуже. И так далее: чем лучше фильтруем, тем хуже звучим. Одна беда – фильтровать все же приходится!
Теперь о фильтрах в акустике. Главное их отличие от просто фильтров заключается в том, что стоит задача не частотной фильтрации, а частотного разделения. Иными словами, уха слушателя должны достичь составляющие всех частот, но, скажем, составляющие с частотами ниже Fразд. должны воспроизводиться НЧ-головкой, выше – ВЧ-головкой (двухполосная система). АЧХ такой системы в идеале должна быть плоской, в том числе и в зоне частотного разделения. В связи с этим такие разделительные фильтры получили название всепропускающих.
Оказывается, что сделать всепропускающий фильтр из ФНЧ и ФВЧ даже с учетом их полной развязки (суммирование ведь акустическое, а не электрическое) непросто. Так, если применять фильтры Баттерворта четных порядков, то АЧХ получит выброс в 3 дБ на частоте раздела, очень даже заметный на слух. Суть этого явления может быть отслежена на одном из графиков, приведенных в статье. Поэтому применяют либо фильтры Линквица – Райли (похожие на баттервортовские, но с несколько другими номиналами), либо вообще отказываются от фильтров четных порядков и применяют фильтры 3-го порядка.
Еще один путь, ведущий к получению плоской АЧХ, заключается в разнесении частот среза ФВЧ и ФНЧ. Например, частота среза ФНЧ выбирается 900 Гц, а ФВЧ – 1111 Гц. Однако заметим: плоская АЧХ – средство, а не самоцель.
Идеальной ФЧХ любого фильтра, в том числе и разделительного, можно было бы считать нулевую (отсутствие временной задержки) либо линейно нарастающую (постоянная задержка на всех частотах). Среди тех фильтров, которые могут применяться в качестве разделительных, только фильтр 1-го порядка имеет идеальную ФЧХ. Как итог – форма сигнала, прошедшего АС с разделительными фильтрами 1-го порядка, имеет больше шансов остаться неискаженной, чем, скажем, с фильтрами 3-го порядка. Однако понятно, что решение главной задачи – фильтрации и частотного разделения – с фильтрами столь малого порядка затруднительно.
Среди тех фильтров, которые могут применяться в качестве разделительных, только фильтр 1-го порядка имеет идеальную ФЧХ. Как итог – форма сигнала, прошедшего АС с разделительными фильтрами 1-го порядка, имеет больше шансов остаться неискаженной, чем, скажем, с фильтрами 3-го порядка. Однако понятно, что решение главной задачи – фильтрации и частотного разделения – с фильтрами столь малого порядка затруднительно.
ГВЗ – тоже частотная характеристика, представляющая производную ФЧХ по частоте как функцию опять же частоты. Резкие колебания ГВЗ свидетельствуют о возможности разных задержек составляющих реального сигнала, имеющих разные частоты: сигнал исказит свою форму, как говорят акустики, «рассыплется». Барабан будет уже не барабан, пиццикато – не пиццикато. |
Порядок и тип фильтров и что от них зависит
Чем больше порядок фильтра, тем лучше он фильтрует. Как говорили в популярном советском кинофильме, чем мех лучше, тем он дороже. Фильтр не мех, и порядок выбирается исходя из очень многих предпосылок. Не будем углубляться в теорию, приведем несколько примеров.
Фильтр не мех, и порядок выбирается исходя из очень многих предпосылок. Не будем углубляться в теорию, приведем несколько примеров.
Пример 1. Организация раздела «сабвуфер – мидбас». Пусть применена частота раздела, скажем, 100 Гц. Если использован низкий порядок фильтра, то:
– на сабвуферную головку проникают частоты, лежащие существенно выше 100 Гц. Сабвуфер, понятное дело, находится сзади, поэтому он начинает «петь человеческим голосом» и вызывает изъяны в формируемой стереопанораме;
– на мидбасовую головку проникают басы. Это может ее перегрузить в лучшем случае до повышенных искажений, в худшем – до откровенного треска от соударения подвижной системы и магнитопровода. Как правило, мидбас требует при таком раскладе применения фильтров не ниже 2-го порядка, при этом ниже частоты раздела независимо от расположения резонансной частоты СЧ-головки, величина смещения ее диффузора начнет падать;
– ФЧХ и ГВЗ оказываются хорошими, форма сигнала искажается мало.
Если использован высокий порядок фильтра, то:
– рассмотренных только что проблем не возникает;
– однако ФЧХ и ГВЗ оставляют желать лучшего: форма импульсных сигналов страдает. Впрочем, считается, что порядки, вплоть до четвертого включительно, при правильном подходе к расчетам оказываются приемлемыми.
Если применяется повышенная частота раздела НЧ/СЧ, положим, 400 или 800 Гц, то проблема возможной перегрузки СЧ-головки могучим басом отступает на второй план при любых порядках фильтров: все мидбасы доставляются по адресу. Вместе с тем, использование фильтров высоких порядков для организации частотного разделения посередине диапазона основных музыкальных тонов может привести к нарушениям, в первую очередь стереолокализационным, и существенно ухудшить звучание скрипки, вокала, фортепиано.
Пример 2. Организация раздела СЧ/ВЧ. Случай первый: ВЧ-головке отведен участок тонально значимого диапазона – частота раздела выбрана в районе 1800 – 2200 Гц. Здесь применение фильтров низких порядков не препятствует загрузке ВЧ-головки мощными среднечастотными составляющими и, что наиболее опасно, область резонанса ВЧ-головки (1200-1400 Гц) оказывается в недостаточной мере отгорожена фильтром. Это может привести как к исправимым (горб на АЧХ), так и более тяжелым (перегрев катушки ВЧ-головки) последствиям. Вместе с тем, применение в нашем случае фильтров высокого (3-го и выше) порядка означает создание цепи с существенными фазовыми сдвигами в той области, где ухо к ним еще достаточно чувствительно.
Это может привести как к исправимым (горб на АЧХ), так и более тяжелым (перегрев катушки ВЧ-головки) последствиям. Вместе с тем, применение в нашем случае фильтров высокого (3-го и выше) порядка означает создание цепи с существенными фазовыми сдвигами в той области, где ухо к ним еще достаточно чувствительно.
Если частота раздела СЧ/ВЧ выбрана более высокой (4 кГц и выше), проблем практически не возникает, однако такой вариант характерен для трехполосных систем, в которых цветут и пахнут проблемы разделения НЧ/СЧ, обсужденные нами чуть ранее.
В современной аудиотехнике используются фильтры с гладкими АЧХ и малыми колебаниями ФЧХ: Бесселя, Баттерворта, Линквица – Райли. (Не все именитые фильтры обладают этими свойствами. Взгляните, например, на характеристику фильтра Чебышева. Он тоже применяется на практике, только не для акустики. А для нас это – гибель, однозначно.) Таблица дает пример краткого сравнительного анализа случаев использования этих фильтров.
АЧХ фильтров различного порядка (типа Баттерворта). Чем выше порядок, тем решительнее фильтрация частот вне полосы пропускания и тем больше фазовые искажения, вносимые фильтром.
Чем выше порядок, тем решительнее фильтрация частот вне полосы пропускания и тем больше фазовые искажения, вносимые фильтром.
АЧХ фильтров четвертого порядка различного типа с одной и той же частотой среза 1 кГц. Самый «ленивый» с точки зрения разделения частот фильтр Бесселя обеспечивает самую гладкую ФЧХ. А «радикальный» фильтр Чебышева – сами видите.
Железо. Фильтры в автомобиле
Если схема фильтра нарисована, его реализация не вызывает особых проблем – была бы медь, конденсаторы, место и деньги. Однако в ряде случаев все же возникают ситуации, требующие разумного вмешательства разработчика. Сейчас мы их и рассмотрим.
Первое: фильтрация на достаточно низких частотах. Нетрудно показать, что попытка организации раздела в зоне около 100 Гц (не говоря уже о более низких значениях, а там-то как раз и самое место) может потребовать катушек индуктивности в 10 – 20 мГн и конденсаторов в десятки и сотни мкФ. Более того, не исключено, что при попытке компенсировать реактивность звуковой катушки НЧ-головки (есть такой этап в методике расчета реальных фильтров) потребуются еще большие, и существенно, номиналы.
В таком случае разработчики вспоминают о катушках с сердечником из магнитного материала и неполярных электролитических конденсаторах, а потребитель – о том, что вышеперечисленные компоненты заметно портят звук.
Действительно, применение электролитов способно вызвать проблемы как при малых сигналах (нелинейность неполярного конденсатора без смещения), так и при больших (потери). Аналогично обстоят дела с сердечником: на малых и на больших сигналах индуктивность катушки с сердечником существенно разнится. В результате звук приобретает размытый, ватный характер, страдает стереолокализация, ощущаются огрехи в макродинамике. В автомобильной аудиотехнике проблему первого частотного раздела решили уже относительно давно – активной фильтрацией на входе усилителя с отдельными каналами для сабвуфера и всего остального. А вот в заносчивом мире домашнего аудио даже высококлассные АС с разделом НЧ/СЧ в районе 100 Гц несвободны от рассмотренных недостатков.
Второе: фильтрация в тонально значимой зоне 250 – 2500 Гц. Любые упражнения с электрическим сигналом, выполняемые с частотно-зависимыми цепями в этой области, должны проводиться с особой аккуратностью. Ухо оказывается чувствительнее измерительных приборов и ревниво относится к каждой ошибке разработчика.
Любые упражнения с электрическим сигналом, выполняемые с частотно-зависимыми цепями в этой области, должны проводиться с особой аккуратностью. Ухо оказывается чувствительнее измерительных приборов и ревниво относится к каждой ошибке разработчика.
Здесь уже не только наличие сердечника или электролита нежелательно: ухо реагирует даже на характер намотки катушки и на тип диэлектрика в конденсаторе. Проблема усугубляется тем, что разделительный фильтр АС является мощным устройством в том смысле, что через него транслируется вся энергия, предназначенная для питания АС.
Тем не менее, как мне кажется, появление великолепно оформленных, чрезвычайно дорогих разрекламированных пассивных разделительных фильтров для автомобильного аудио вызвано не стремлением к техническому совершенству и хорошему звуку, а попыткой застолбить место в коммерческой нише. Когда не существовало car audio в современном понимании, не было и возможности красиво оформить и продать просто фильтр. Фильтры даже дорогих домашних АС иногда выглядели так, что потребителя спасал от разочарования лишь толстый-толстый слой шоколада, простите, МДФП, скрывающий внутреннюю убогость конструкции.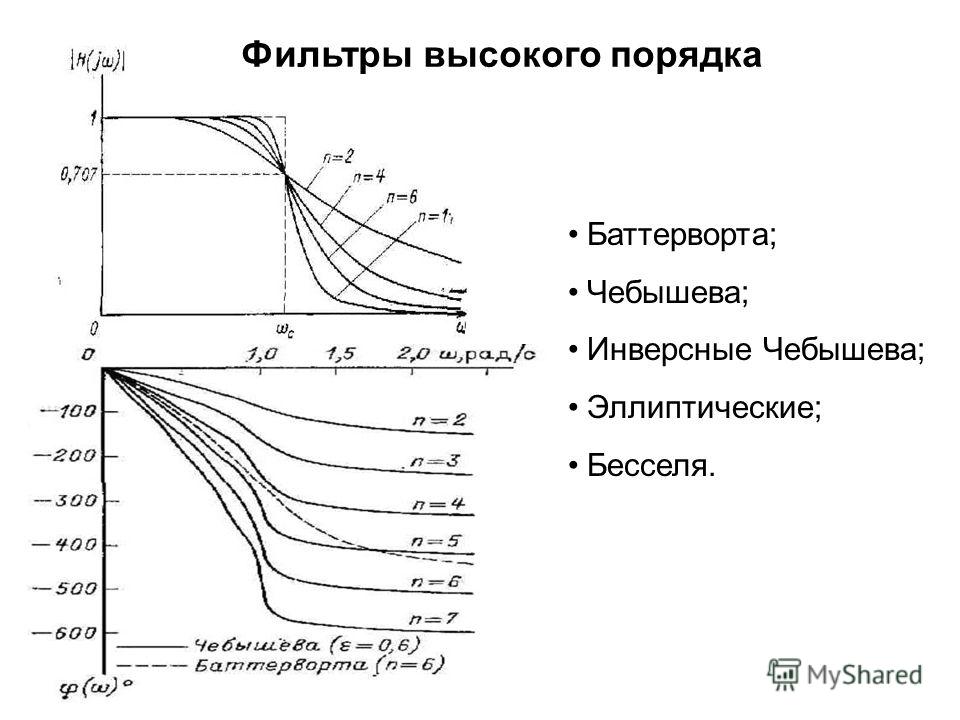 Лозунг «Все на виду», характерный для современной автоаудиотехники, с ее прозрачными крышками фильтров, усилителей и пр., – дань моде и коммерческое ухищрение.
Лозунг «Все на виду», характерный для современной автоаудиотехники, с ее прозрачными крышками фильтров, усилителей и пр., – дань моде и коммерческое ухищрение.
Третье: поливариантность фильтрации в автоаудиотехнике – одна из отличительных черт современных тенденций. Как и в области домашних компьютеров – возможность поиграть, варьируя N процессоров, M материнских плат, L винчестеров и т.д., доставляет невыразимое удовольствие, сравнимое лишь с апельсином (приблизительно), так и в звуке. Истинный автоаудиофил не успокоится, пока вконец не запутается в неисчислимом множестве возможных реализаций полосной фильтрации с применением как активных фильтров (принадлежащих усилителю и прочих), так и пассивных. Что и требуется производителю, а уж тем более продавцу. Нам же остается лишь добавить, что оптимум существует и к нему надо стремиться, естественно, не путем простого бездумного перебора возможных вариантов.
Фильтры и характеристика направленности АС
Мы уже касались направленности, когда сравнивали размеры излучателя с длиной волны. Если система становится многополосной, то неизбежным оказывается пространственное разнесение излучателей различных полос. Следовательно, на частоте раздела мы имеем возможность получить два излучателя, разнесенных в пространстве и работающих на одной и той же частоте. Такая система излучателей будет обладать характеристикой направленности, отличной от круговой, если расстояние между акустическими центрами полосных излучателей окажется сравнимым с длиной волны на частоте раздела. В этом случае на частоте раздела и в прилегающей к ней полосе, тем большей, чем меньший порядок имеют фильтры, сформируется характеристика направленности, не являющаяся круговой, а, скажем, трехлепестковой. Кстати, один из доводов в пользу применения не низких порядков разделительных фильтров. С ними ширина таких «проблемных» частотных полос меньше. Максимум лепестка формируется вдоль линии равных фаз – то есть там, где сигналы каждого из полосных излучателей складываются в фазе. В отсутствие фильтрации главный лепесток будет перпендикулярен линии, соединяющей акустические центры излучателей.
Если система становится многополосной, то неизбежным оказывается пространственное разнесение излучателей различных полос. Следовательно, на частоте раздела мы имеем возможность получить два излучателя, разнесенных в пространстве и работающих на одной и той же частоте. Такая система излучателей будет обладать характеристикой направленности, отличной от круговой, если расстояние между акустическими центрами полосных излучателей окажется сравнимым с длиной волны на частоте раздела. В этом случае на частоте раздела и в прилегающей к ней полосе, тем большей, чем меньший порядок имеют фильтры, сформируется характеристика направленности, не являющаяся круговой, а, скажем, трехлепестковой. Кстати, один из доводов в пользу применения не низких порядков разделительных фильтров. С ними ширина таких «проблемных» частотных полос меньше. Максимум лепестка формируется вдоль линии равных фаз – то есть там, где сигналы каждого из полосных излучателей складываются в фазе. В отсутствие фильтрации главный лепесток будет перпендикулярен линии, соединяющей акустические центры излучателей.
Рис. 4. Пояснение возникновения многолепестковости характеристики направленности АС, в которой на одной частоте работают две разнесенные в пространстве головки. Ситуация (а) характерна для отсутствия разделительных фильтров и для случая использования фильтров четных порядков, ситуация (б) – для нечетных. Для наблюдателей на осях ОА, ОА’ и ОА’’ сигналы головок складываются в фазе.
Теперь представим, что один (например, СЧ-излучатель), питается через ФНЧ, а второй (ВЧ) – через ФВЧ. В этом случае фазы сигналов, излучаемых головками на частоте раздела, не совпадают и, как следствие, линия равных фаз отклоняется от горизонтали. Несложный анализ показывает, что применение фильтров четных порядков не приводит к отклонению, а фильтры нечетных отклоняют все три лепестка (три лепестка получаются в первом критическом случае, когда расстояние между акустическими центрами достигает всего лишь длины волны. При больших расстояниях число лепестков может стать практически любым).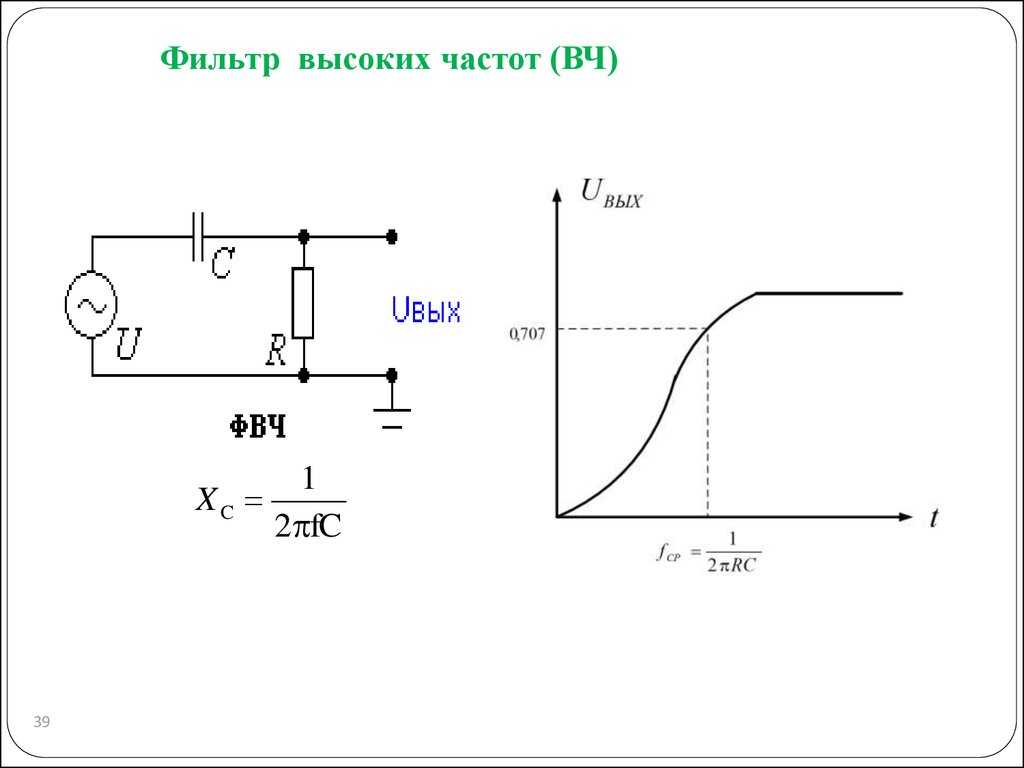
Направление отклонения зависит от порядка фильтра (первый, пятый, девятый и т.д. или третий, седьмой и т.п.) и еще от полярности включения ВЧ-головки. Вопросы переполюсовки и прочие тонкости мы рассмотрим в приложении к статье в других номерах «АЗ», если к тому нас склонит читательская почта.
Известно два случая активного использования такого явления. Первый прост: к нему прибегает фирма Castle в моделях Inversion. В АС этого типа ВЧ-головка располагается под СЧ головкой, что в условиях определенной полярности и при применении фильтров 3-го порядка направляет главный лепесток под углом 30 градусов вниз. Именно там разработчики Castle и надеются отловить уши слушателя, и не напрасно.
Более знаменитый пример дает нам система d’Appolito, где в вертикальной плоскости головки чередуются в определенном порядке: СЧ – ВЧ – СЧ. Каждая из комбинаций СЧ/ВЧ при применении фильтра 3-го порядка обладает трехлепестковой диаграммой, направленной главным лепестком или вверх, или вниз. Понятно, что суммарная диаграмма будет заведомо симметричной в связи с симметрией конфигурации. Более того, нетрудно показать, что она окажется почти круговой. Система d’Appolito – почти столь же эффективный инструмент создания круговых диаграмм на частоте раздела, как и коаксиальная конструкция излучателей, где вообще нет разнесения их акустических центров.
Понятно, что суммарная диаграмма будет заведомо симметричной в связи с симметрией конфигурации. Более того, нетрудно показать, что она окажется почти круговой. Система d’Appolito – почти столь же эффективный инструмент создания круговых диаграмм на частоте раздела, как и коаксиальная конструкция излучателей, где вообще нет разнесения их акустических центров.
Нам же важно запомнить главное: работа полосных излучателей, разнесенных в пространстве, на частоте раздела приводит к многолепестковости характеристики направленности. Это явление вредное, и с ним надо бороться. Фильтры активно вмешиваются в механизм создания лепестков направленности, и этим разработчики могут воспользоваться в своих целях.
Применительно к автомобильной тематике надо иметь в виду следующее: в машине не поставишь домашнюю акустическую систему. Хочешь не хочешь, а приходится размещать головки громкоговорителей в пределах возможного. Понятно, что характеристика направленности в таком случае, особенно с учетом переотражений от стекол, будет непредсказуемой.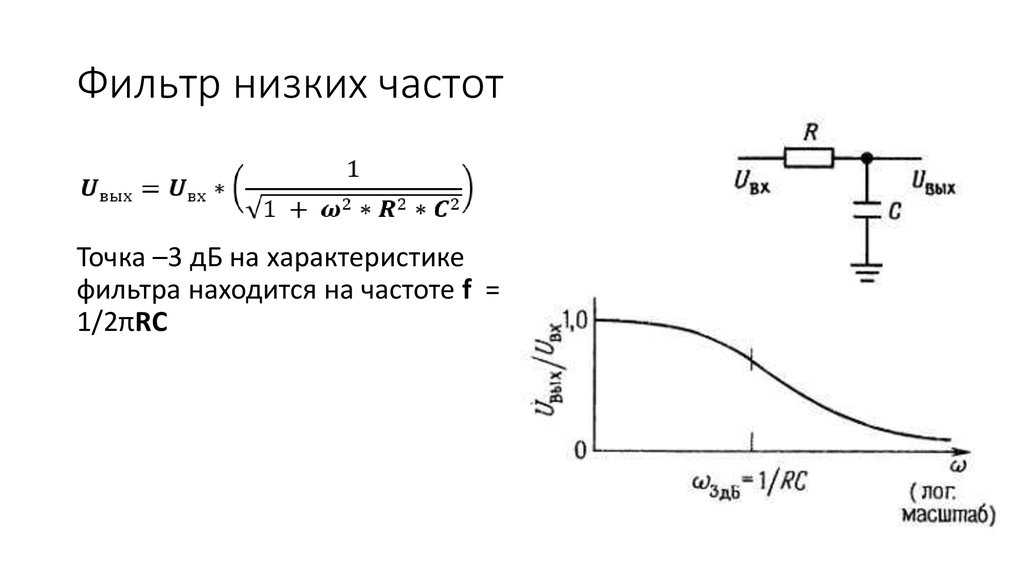 Тем не менее, можно дать несколько рекомендаций, выполнение которых поможет получить в автомобиле звук, напоминающий домашнее аудио. Я знаю, что к этому стремятся многие. Итак:
Тем не менее, можно дать несколько рекомендаций, выполнение которых поможет получить в автомобиле звук, напоминающий домашнее аудио. Я знаю, что к этому стремятся многие. Итак:
Первое. Не надо добиваться использования всех возможностей, предоставляемых кузовом для установки головок. В большинстве случаев злоупотребление тыловыми каналами заметно ухудшает натуральность звука, предназначенного для слушателей на передних сиденьях.
Второе. Сабвуфер в автомобиле требует активной фильтрации на возможно более низкой частоте фильтром возможно более высокого порядка. Головка сабвуфера установлена в автомобиле жестко на конкретном и всегда акустически неудачном месте и ни при каких условиях не должна быть локализована. Попадание на нее составляющих с частотами выше 100 – 200 Гц должно быть значительно ослаблено, а выше 200 Гц – практически исключено. Границу – на замок. Поэтому, если в других областях частотного диапазона фильтры повышенной крутизны это еще бабушка надвое сказала, то здесь, на первом рубеже частотной обороны, 3-й порядок лучше, чем 2-й, а 4-й – лучше, чем 3-й. Всегда.
Всегда.
Третье и достаточно тяжелое для выполнения. Размещение головок в передних дверях – решение общепринятое в автоаудиопрактике. Однако, если отдать таким излучателям диапазон, значимый с точки зрения стереолокализационных характеристик, получение реальной стереопанорамы окажется затруднительным: попробуйте дома разместить небольшие АС слева и справа от себя и к тому же «в ногах»! Разумеется, примеры удачных реализаций при таком расположении акустики есть, но примеры по большей части далеко не безупречные, да и способ, которым их создатели пришли к успеху, как правило, трудновоспроизводим. Потому что остается во многом загадочным результатом многочисленных переотражений звука внутри салона. С точки зрения максимально гарантированного результата оптимальным было бы ограничить полосу дверных динамиков верхней граничной частотой 200 – 250 Гц, чтобы их значение в формировании стереопанорамы было уменьшено до предела. В этом случае к СЧ/ВЧ-излучателям, располагающимся в торпеде или стойках, будет предъявлено требование воспроизводить диапазон от 200 – 250 Гц до самых верхов. Что ж, с этой задачей можно и справиться, найдя для таких АС хотя бы литр объема или подобрав хорошие головки free air. Понятно, что выполнение рассмотренных процедур потребует активной работы инженера с фильтрами, которым и посвящена настоящая статья.
Что ж, с этой задачей можно и справиться, найдя для таких АС хотя бы литр объема или подобрав хорошие головки free air. Понятно, что выполнение рассмотренных процедур потребует активной работы инженера с фильтрами, которым и посвящена настоящая статья.
В следующей части статьи о фильтрах:
– примеры расчета;
– активная фильтрация: «за» и «против»;
– сколько полос надо иметь в домашнем и автомобильном аудио;
– возможен ли возврат к однополосным системам.
Краткая сравнительная характеристика разделительных фильтров акустических систем
Константин НИКИТИН, Журнал «Автозвук»,№ 5, 2001 г.
Сигнал— Как определить порядок фильтра?
спросил
Изменено 4 года, 6 месяцев назад
Просмотрено 23 тысячи раз
\$\начало группы\$
Это мое первое исследование по анализу сигналов. Я очень смущен порядком фильтра.
Я очень смущен порядком фильтра.
Моя проблема в том, как я могу узнать, 4-й ли это порядок, 12-й порядок или 2-й порядок, как написано в книге? Я хотел бы знать процесс, стоящий за этим.
- фильтр
- сигнал
- обработка сигналов
- теория сигналов
\$\конечная группа\$
1
\$\начало группы\$
Порядок n фильтра равен количеству реактивных элементов (если все вносят свой вклад)
Используя линейный наклон (на логарифмической сетке) от точки останова f, будет 6 дБ/октава на порядок n.
n = 4-й порядок имеет наклон 24 дБ/октаву, как и в обоих первых примерах.
Я мог бы подумать, что это похоже на фильтр 10-го порядка Баттерворта -60 дБ/окт и 8-го порядка Чебычева -40 дБ/окт. Здесь присутствует визуальная неоднозначность из-за отсутствия диапазона после разрыва, чтобы оценить крутизну фильтра при обрезании графика около 1 октавы выше. Кроме того, это примеры фильтров с низкой и высокой добротностью, поэтому наклоны точек останова сильно различаются.
Кроме того, это примеры фильтров с низкой и высокой добротностью, поэтому наклоны точек останова сильно различаются.
Так что я согласен, что трудно оценить в цифре 1.12 . Тогда как на рис. 1.11 проще измерить наклон.
Графический метод
Используйте линейку, чтобы пройти через точку пересечения оси Y и подогнать линейный наклон к кривой. Затем измерьте наклон в n кратных -6n дБ/октава или лучше, если возможно -20n дБ/дек.
Это усложняется, когда ось Y недостаточно велика.
Десятка равна 1/10 = 20 log 0,1 = -20 дБ x n порядка.
Октава равна 1/2 = 20 log 0,5 = -6,02 дБ x n порядка.
Итак, из рис. 1.11 фильтр 12-го порядка
Графический метод имеет некоторую неопределенность, но наиболее близок к 12-му порядку.
\$\конечная группа\$
8
\$\начало группы\$
При уменьшении отклика фильтра до его передаточной функции порядок дифференциального уравнения совпадает с порядком фильтра. См. страницу:
См. страницу:
https://www.st-andrews.ac.uk/~www_pa/Scots_Guide/audio/part3/page2.html
Порядок фильтра отражает количество элементов, которые задерживают вашу выборку на единицу, т. е. фильтру первого порядка требуется одна выборка для получения желаемого результата, фильтру второго порядка нужны две выборки и т. д.
Вот некоторые примеры, которые я беру из изображений Google:
Низкочастотный фильтр Баттерворта первого порядка:
Низкочастотный фильтр Баттерворта второго порядка:
Большинство фильтров более высокого порядка состоят из нескольких фильтров 1-го или 2-го порядка. фильтры.
Фильтр нижних частот Баттерворта четвертого порядка:
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Что подразумевается под порядком фильтрации пассивного фильтра?
спросил
Изменено 1 год, 2 месяца назад
Просмотрено 513 раз
\$\начало группы\$
Когда мы говорим о пассивных фильтрах (фильтрах, состоящих только из R, L и C), мы часто изучаем, что 9Порядок фильтра 0043 будет равен общему количеству реактивных компонентов (L и C) в цепи. Это утверждение действительно для всех фильтров (низкочастотных, высокочастотных, полосовых и полосовых)?
Схемы полосового пропускания и полосового останова немного сложны, поэтому мне интересно, применимо ли это утверждение к этим сценариям.
- фильтр
- пассивный фильтр
\$\конечная группа\$
6
\$\начало группы\$
Порядок схемы зависит от полиномиальной степени ее знаменателя. Сама эта степень зависит от количества независимых переменных состояния. Переменные состояния связаны с энергоаккумулирующими элементами, такими как \$C\$ и \$L\$, присутствующими в схеме. Таким образом, их подсчет кажется хорошим способом определить порядок схемы.
Однако в приведенном выше заявлении я использовал термин независимый . Например, это уже не тот случай, когда конденсатор, помещенный напротив идеального источника напряжения, видит, что его напряжение фиксируется самим источником, или когда катушка индуктивности, расположенная последовательно с источником тока, имеет свой ток, определяемый источником. Два параллельно соединенных конденсатора имеют общее напряжение, а две катушки индуктивности, соединенные последовательно, имеют общий ток. Рассмотрим классический пример, описанный в моей книге о методах быстрых аналитических схем или ФАКТАХ:
Рассмотрим классический пример, описанный в моей книге о методах быстрых аналитических схем или ФАКТАХ:
В этом примере переменная состояния конденсатора \$C_2\$ \$x_2\$ однозначно определяется переменными состояния \$x_1\$ и \$x_3\$. В этом так называемом вырожденном корпусе с емкостной петлей, несмотря на наличие 4 конденсаторов, это система 3-го порядка. Добавьте небольшое сопротивление последовательно с \$C_2\$, и вы получите сеть 4-го порядка.
Та же проблема с классическим компенсированным делителем с двумя конденсаторами:
Несмотря на наличие двух конденсаторов, это все еще система 1-го порядка, поскольку обе переменные состояния находятся в цикле, включающем источник входного напряжения, который фиксирует потенциал: когда вы обнуляете источник напряжения для определения полюсов, оба конденсатора соединены параллельно, образуя только один конденсатор, а постоянная времени равна \$\tau=(R_1||R_2)(C_1+C_2)\$
В заключение подсчитайте количество элементов, накапливающих энергию, но всегда проверяйте, что каждая переменная состояния не зависит однозначно от других переменных состояния.

