Что такое последовательное и параллельное соединение резисторов. Как рассчитать общее сопротивление при разных типах соединений. Какие формулы используются для вычислений. Какие особенности у каждого вида соединения.
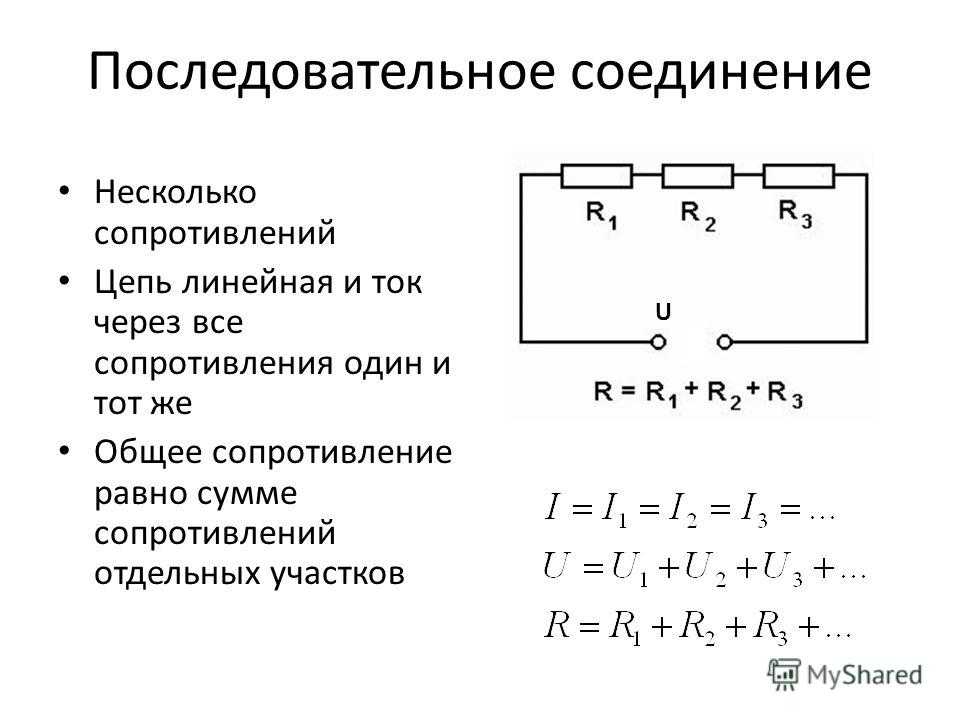
Последовательное соединение резисторов: принцип работы и основные характеристики
Последовательное соединение резисторов представляет собой цепь, в которой конец одного резистора соединен с началом следующего. При таком соединении через все резисторы протекает одинаковый ток.
Каковы основные особенности последовательного соединения?
- Общее сопротивление цепи равно сумме сопротивлений всех резисторов
- Ток во всех участках цепи одинаковый
- Напряжение на резисторах распределяется пропорционально их сопротивлениям
- При выходе из строя одного резистора размыкается вся цепь
Формула для расчета общего сопротивления при последовательном соединении:
R общ = R1 + R2 + R3 + … + Rn
Где R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Параллельное соединение резисторов: принцип и ключевые характеристики
- Напряжение на всех резисторах одинаковое
- Общий ток равен сумме токов через отдельные резисторы
- Общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи
- При выходе из строя одного резистора остальные продолжают работать
Как рассчитать общее сопротивление при параллельном соединении? Для этого используется следующая формула:
1/R общ = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где R1, R2, R3 и т.д. — сопротивления параллельно соединенных резисторов.
Сравнение последовательного и параллельного соединения резисторов
Каковы ключевые различия между последовательным и параллельным соединением резисторов?
| Параметр | Последовательное соединение | Параллельное соединение |
|---|---|---|
| Общее сопротивление | Больше любого из резисторов | Меньше самого маленького резистора |
| Ток | Одинаковый во всех участках | Разный в каждой ветви |
| Напряжение | Разное на каждом резисторе | Одинаковое на всех резисторах |
| Надежность | При обрыве одного элемента вся цепь размыкается | При выходе из строя одного резистора остальные работают |
Примеры расчетов при последовательном соединении резисторов
Рассмотрим несколько примеров вычисления общего сопротивления при последовательном соединении резисторов.
Пример 1
Дано: три резистора с сопротивлениями 100 Ом, 200 Ом и 300 Ом соединены последовательно.
Решение: R общ = R1 + R2 + R3 = 100 Ом + 200 Ом + 300 Ом = 600 Ом
Пример 2
Дано: в цепи последовательно соединены резисторы 50 Ом, 75 Ом, 100 Ом и 125 Ом.
Решение: R общ = 50 Ом + 75 Ом + 100 Ом + 125 Ом = 350 Ом
Как видим, при последовательном соединении общее сопротивление всегда больше сопротивления любого из резисторов в цепи.
Примеры вычислений при параллельном соединении резисторов
Теперь рассмотрим примеры расчета общего сопротивления для параллельно соединенных резисторов.
Пример 1
Дано: два резистора 100 Ом и 200 Ом соединены параллельно.
Решение:
- 1/R общ = 1/R1 + 1/R2 = 1/100 + 1/200 = 0.01 + 0.005 = 0.015
- R общ = 1/0.015 ≈ 66.67 Ом
Пример 2
Дано: параллельно соединены три резистора: 30 Ом, 60 Ом и 120 Ом.
Решение:
- 1/R общ = 1/30 + 1/60 + 1/120 = 0.0333 + 0.0167 + 0.0083 = 0.0583
- R общ = 1/0.0583 ≈ 17.15 Ом
Обратите внимание, что при параллельном соединении общее сопротивление всегда меньше самого маленького сопротивления в цепи.
Применение последовательного и параллельного соединения резисторов
Где на практике используются различные схемы соединения резисторов?
Последовательное соединение
- В делителях напряжения
- Для увеличения общего сопротивления цепи
- В измерительных приборах
- Для ограничения тока в цепи
Параллельное соединение
- Для уменьшения общего сопротивления
- В системах распределения электроэнергии
- Для увеличения мощности в нагрузке
- В схемах защиты от перегрузок
Выбор типа соединения зависит от конкретной задачи и требуемых характеристик электрической цепи.
Смешанное соединение резисторов: особенности и расчеты
Что представляет собой смешанное соединение резисторов? Это комбинация последовательного и параллельного соединения в одной схеме. Такой тип соединения позволяет получить более сложные конфигурации сопротивлений.
Как рассчитать общее сопротивление при смешанном соединении?
- Разбить схему на участки с однотипным соединением
- Рассчитать сопротивление для каждого участка
- Объединить полученные результаты
Пример расчета смешанного соединения:
Дано: R1 = 100 Ом, R2 = 200 Ом, R3 = 300 Ом, R4 = 400 Ом
Решение:
- Найдем R12 (параллельное соединение R1 и R2): 1/R12 = 1/100 + 1/200 = 0.015 R12 = 1/0.015 ≈ 66.67 Ом
- R12 и R3 соединены последовательно: R123 = 66.67 + 300 = 366.67 Ом
- R123 и R4 соединены параллельно: 1/R общ = 1/366.67 + 1/400 = 0.00523 R общ = 1/0.00523 ≈ 191.2 Ом
Таким образом, общее сопротивление схемы составляет около 191.2 Ом.
Влияние температуры на сопротивление резисторов
Как температура влияет на сопротивление резисторов? Для большинства материалов с повышением температуры сопротивление увеличивается. Это связано с увеличением амплитуды колебаний атомов, что затрудняет движение электронов.
Зависимость сопротивления от температуры описывается формулой:
R = R0(1 + α(T — T0))
Где:
- R — сопротивление при температуре T
- R0 — сопротивление при начальной температуре T0
- α — температурный коэффициент сопротивления
Учет температурной зависимости особенно важен при проектировании точных измерительных схем и устройств, работающих в широком диапазоне температур.
Правила выбора резисторов для электрических схем
Как правильно выбрать резисторы для электрической схемы? Вот несколько ключевых факторов, которые следует учитывать:
- Номинальное сопротивление: должно соответствовать расчетному значению
- Мощность: выбирается с запасом относительно расчетной
- Точность: зависит от требований схемы
- Температурный коэффициент: важен для схем, работающих в широком диапазоне температур
- Тип резистора: проволочный, углеродистый, металлопленочный и т.д.
- Габариты: должны соответствовать доступному пространству на плате
Правильный выбор резисторов обеспечивает надежную и эффективную работу электронного устройства.
Калькулятор | ColorAndCode
| LCD1602/2004 — HD44780 | |
Параллельное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Последовательное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Параллельное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Последовательное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
| Реактивное сопротивление конденсатора | |
| Реактивное сопротивление конденсатора (+) | |
| Реактивное сопротивление катушки индуктивности | |
| Реактивное сопротивление катушки индуктивности (+) | |
| Обратное определение при параллельном соединении резисторов и последовательном конденсаторов | |
| Определение индуктивности из частоты и реактивного сопротивления | |
| Определение емкости из частоты и реактивного сопротивления | |
| Проводники | |
| Цилиндрические однослойные катушки | |
| Цилиндрические однослойные катушки (+) | |
Тороидальные катушки на ферритовых кольцах
Дополнительно: — Возможность использовать данные из справочника. | |
| Программирование ДПКД (делитель с переменным коэффициентом деления) | |
Сопротивление резистора для светодиода
Дополнительно: — Возможность использовать данные из справочника; — Вывод номинала в 4-х цветной маркировке для ряда E24 +/- 5 %. | |
| Расчёт схемы на основе NE555 | |
| Расчёт схем на основе LM317, LM338, LM350 | |
| Расчёт схем на основе LM2596 | |
| Расчет катушек на ферритовых кольцах фирмы Amidon |
|
| Расчёт индуктивности квадратной плоской катушки |
|
| Индуктивность прямого провода над проводящей подложкой |
Дополнительный материал в статье:
— Полупроводниковая светотехника № 4 за 2019 год
— Радиолюбитель № 3 за 2010 год
— Компоненты и технологии № 6 за 2010 год
последовательное и параллельное соединение + калькулятор
Резисторы представляют собой элементы с переменным или постоянным сопротивлением.
Содержание
Последовательное соединение
Последовательным называется соединение двух и более резисторов, при котором конец первого элемента соединяется с началом второго и так далее. В результате получается последовательная цепочка, где по всем ее составляющим проходит одинаковый ток. В качестве примера можно взять последовательную цепь, состоящую из трех резисторов R1, R2 и R3. Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.
В этой формуле значение эквивалентного сопротивления последовательной цепи составит сумму сопротивлений всех резисторов, имеющихся в данной цепи: Rэк = R1 + R2 + R3. По закону Ома напряжение при последовательном соединении на отдельных участках будет иметь следующее значение, поскольку E = U: U1=IR1; U2 = IR2, U3 = IRз, то есть U = U1 + U2 +U3. Данные формулы показывают, что в резисторах, последовательно соединенных между собой, напряжения распределяются пропорционально их сопротивлениям. То есть, чем выше сопротивление любого из резисторов, тем больше напряжение, приложенное к нему. В виде формулы — это утверждение будет выглядеть следующим образом: U1 : U2 : U3 = R1 : R2 : R3.
При последовательном соединении сопротивление R1 нескольких резисторов в количестве n, будет одинаковым. Следовательно, значение эквивалентного сопротивления цепи будет в n раз превышать сопротивление каждого из них: Rэк = nR1. Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n.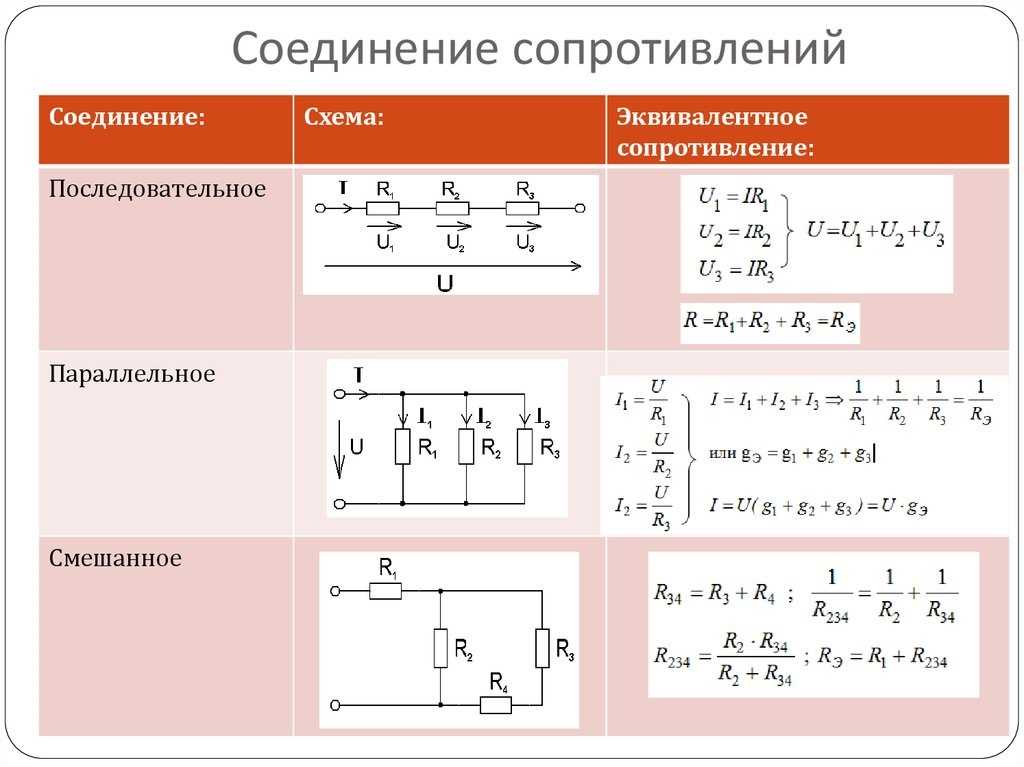
Таким образом, изменение сопротивления любого из резисторов при последовательном соединении, приводит к изменению напряжения на других резисторах, находящихся с ним в одной цепи. Поэтому, если электрическая цепь обрывается или выключается в одной из нагрузок, в других нагрузках также прекращается течение тока. Из-за этого последовательное соединение в электрических схемах используется довольно редко.
Параллельное соединение
Гораздо чаще в электрических цепях применяется параллельное соединение резисторов, отличающихся наличием общих точек, где соединяются начала и концы каждого элемента. Данный вид соединения характеризуется собственными физическими свойствами.
Основными из них являются следующие:
- Каждый из подключенных резисторов, обладает одинаковым напряжением: U = U1 = U2 = U3. То есть, напряжение в параллельном соединении на каждом участке будет одно и то же.
- Общая проводимость резисторов, соединенных параллельно, включает в себя сумму проводимостей каждого отдельного сопротивления, выраженную соотношением: 1/R = 1/R1 + 1/R2 + 1/R3 = R1R2 + R1R3 + R2R3/R1R2R3.
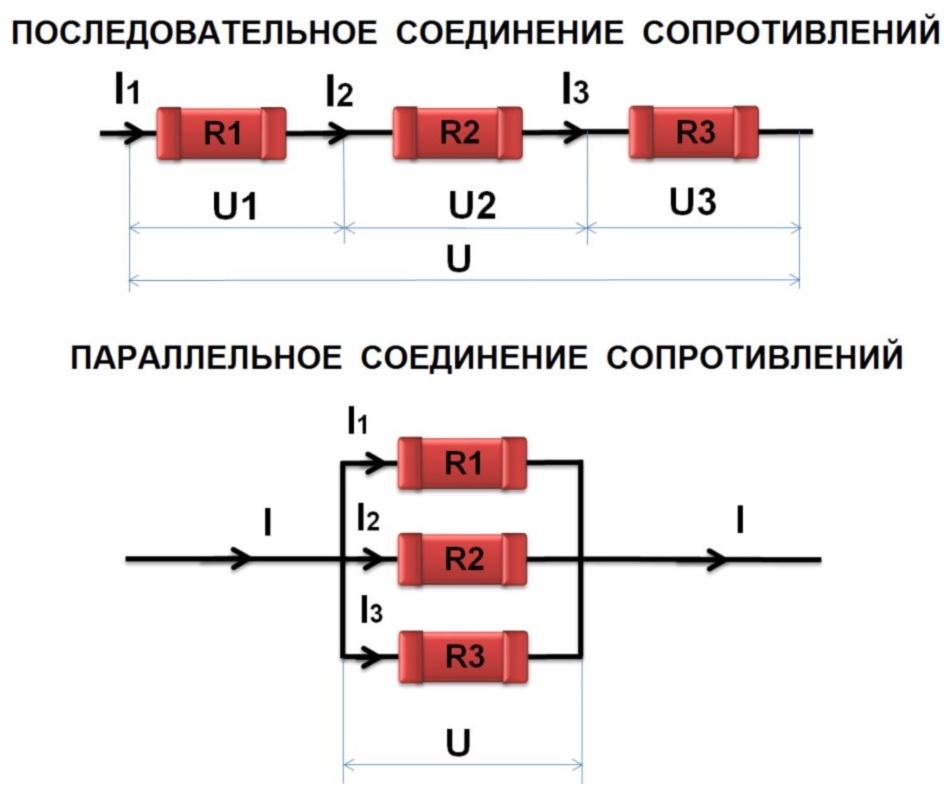Здесь R является эквивалентным или равнодействующим сопротивлением всех трех резисторов. Оно может полностью заменить их, без изменения величины силы тока в цепи. Значение эквивалентного сопротивления можно вычислить путем сложения проводимостей каждого участка. В результате, получится общая проводимость. Обратная ей величина и будет фактически общим сопротивлением. - Существуют и особенности эквивалентной проводимости, когда используется параллельное соединение. Она составляет сумму проводимостей всех отдельно взятых ветвей. В этом случае при параллельном соединении сопротивление эквивалентное будет всегда ниже самого маленького сопротивления, включенного параллельно.
- соотношения касаются не только трех резисторов, соединенных параллельно, но и любого количества сопротивлений, соединенных этим способом. Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.
Здесь R является эквивалентным или равнодействующим сопротивлением всех трех резисторов. Оно может полностью заменить их, без изменения величины силы тока в цепи. Значение эквивалентного сопротивления можно вычислить путем сложения проводимостей каждого участка. В результате, получится общая проводимость. Обратная ей величина и будет фактически общим сопротивлением.
В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.Калькулятор вычисления параллельного соединения резисторов
Смешанное соединение
В радиоэлектронных и электрических схемах широко применяется последовательное, параллельное и смешанное соединение резисторов, наиболее подходящее на том или ином конкретном участке. Первые два соединения были рассмотрены выше, осталось лишь отметить характерные особенности комбинированного варианта.
В смешанных схемах нашли отражение свойства, присущие последовательному и параллельному соединениям. Частично выполняется последовательное подключение резисторов, а другая группа элементов подключается параллельно. Резисторы R1 и R2, изображенные на схеме, включаются последовательно, а резисторы R1, R2 и R3 соединены параллельно.
Последовательное и параллельное соединение проводников» src=»https://www.youtube.com/embed/XvlVPf43lzo?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Калькулятор сопротивления серии: формула, примеры и многое другое!
Вам нужно рассчитать эквивалентное сопротивление нескольких резисторов, включенных последовательно ? Не волнуйтесь, вот утилита, которая позволит вам рассчитать эквивалентное сопротивление до 8 последовательно соединенных резисторов.
Единственное, что вам нужно сделать, это выбрать количество резисторов , расположенных последовательно , и записать значение каждого из них в омах. Когда он у вас есть, нажмите кнопку расчета, и вы получите результат эквивалентного сопротивления в Омах и в кОмах.
Разделы артикулов
- Соединение резисторов последовательно
- Сумма резисторов
Соединение резисторов последовательно
Чтобы идентифицировать последовательное соединение резисторов, нужно просто отметить, что это выход одного резистора.
подключен непосредственно ко входу следующего резистора .
В случае параллельного соединения Входы резисторов соединены вместе, а выходы каждого резистора также связаны с выходами других резисторов.
Имея это в виду, легко определить, является ли соединение последовательным или параллельным . Если вам это нужно, здесь вы можете найти больше информации о параллельном соединении резисторов.
При решении задач или упражнений с последовательными резисторами помните, что в этой конфигурации одинаковая сила или ток протекает через все резисторы . С другой стороны, напряжение будет разным в зависимости от удельного сопротивления каждого из них. Если вам это нужно, здесь у вас есть калькулятор, основанный на цветовых кодах резисторов.
Сумма последовательных резисторов
Для добавления резисторов в серию мы просто должны добавить значение каждого из них, таким образом, получая значение эквивалентного сопротивления, как показано в следующем математическом выражении:
R eq = R 1 + R 2 + .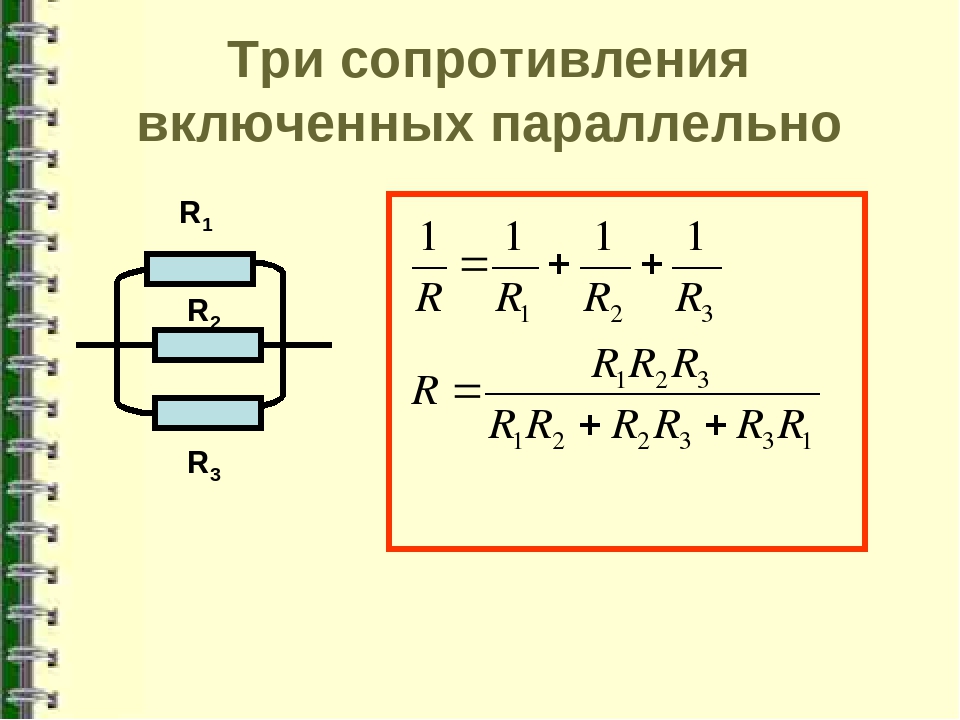
.. + R n
На примере , Предположим, что у нас есть следующий пример, в котором мы последовательно соединили два резистора 100 Ом и 300 Ом, как показано на следующем рисунке:
Применяя формулу, которую мы видели ранее, мы имеем:
R eq = R 1 + R 2 = 100 Ом + 300 Ом = 400 Ом
5 эквивалентное сопротивление при последовательном соединении очень просто.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
- Калькулятор 3 параллельных резисторов
- Калькулятор пикселей на дюйм (PPI)
- Калькулятор последовательного резистора
- Калькулятор закона Ома
- Калькулятор скорости интернет-соединения
- Вычисление реальной емкости 1 мегапикселя 14 фото1 или памяти 900
- Золотые пропорции в веб-дизайне
- Расчет размера телевизора
- Цветовое кодирование резистора
- Преобразователь бит, байт и компьютерных единиц
- Какой у меня IP
- Какое у меня разрешение экрана
- Сколько посетителей вам нужно, чтобы зарабатывать на вашем сайте?
- Делитель напряжения
- 301 Генератор веб-перенаправления
- Генерация безопасного пароля онлайн
- Время зарядки аккумулятора
- Ватт в ампер
Калькулятор параллельного резистора — Как решить сложные параллельные цепи
Вы чувствуете препятствие для расчета эквивалентного или отсутствующего сопротивления параллельной цепи? Перестаньте беспокоиться и начните использовать наш бесплатный калькулятор параллельных резисторов, который делает то же самое.
Да, вы были бы поражены тем фактом, что этот калькулятор позволит вам сравнить сопротивления в электрической цепи, чтобы вычислить общее сопротивление цепи, необходимое для ее бесперебойной работы.
Переходя к делу, давайте продолжим, чтобы узнать больше о сопротивлении цепи.
Держись!
Что такое сопротивление?
«Сопротивление току, протекающему внутри цепи, известно как сопротивление цепи»
Обозначение:
Основной символ, используемый для обозначения резистора:
Параллельный резистор:
«Сопротивление обе клеммы которого подключены к одному и тому же узлу, называется параллельным сопротивлением»9.0004
В электрической сети, содержащей параллельные резисторы, ток всей цепи будет эквивалентен сумме всех токов, протекающих через каждый отдельный резистор. и когда дело доходит до вычисления его значения, бесплатный онлайн-калькулятор параллельного резистора — единственный вариант, который у вас остался.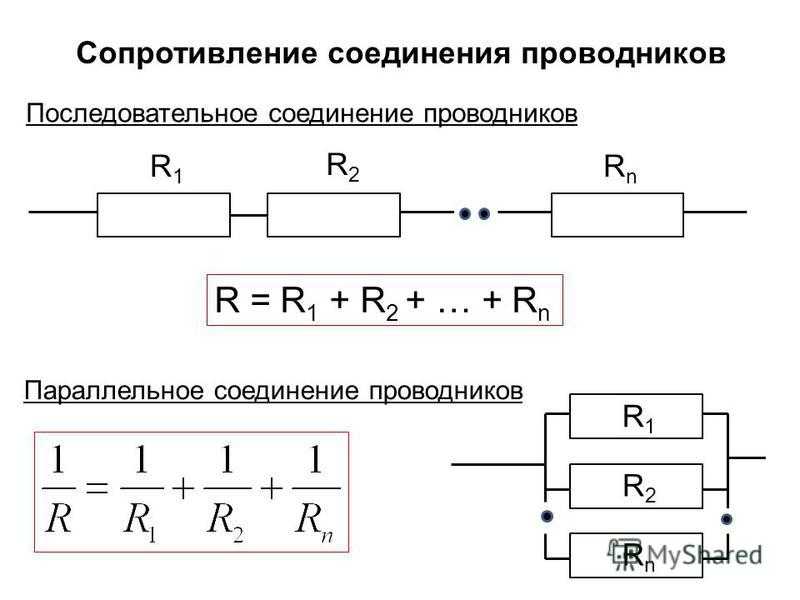
Формула параллельного сопротивления:
В параллельной цепи каждый подключенный резистор имеет определенную разность потенциалов (падение напряжения) на его концах. И это вызывает большое падение напряжения в каждом узле сети электронных схем. Вот почему становится очень важным вычислить, сколько потерь в нем в целом. И это можно рассчитать, только если вы используете следующие параллельные резисторы в параллельной формуле:
$$ R_{eq} = \frac{V}{I_{total}} = \frac{V}{(\frac{V}{R_1} + \frac{V}{R_2} + \frac{V }{R_3} + … + \frac{V}{R_n})} $$
Взяв НОК приведенного выше выражения, его можно привести к простейшему виду:
$$ R_{eq} = \frac{ 1}{(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … + \frac{1}{R_n})} $$
И самое упрощенная запись приведенного выше выражения может быть записана как:
$$ \frac{1}{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
Свободная параллель Калькулятор резисторов также учитывает следующую формулу для расчета эквивалентного сопротивления всей электрической сети.
Как найти сопротивление в параллельной цепи?
Чаще всего при работе со сложными электрическими сетями на ум приходит вопрос «как решать сложные параллельные схемы». Единственный ответ на эту проблему — использовать любую формулу параллельного резистора для этого онлайн-калькулятора параллельного резистора.
Иллюстрация:
Посмотрите на рисунок ниже:
В этой цепи три резистора соединены параллельно, чтобы отклонить путь тока, тем самым уменьшая его потенциал. Предполагая, что к нему подключена идеальная нагрузка, как рассчитать сопротивление в параллельной цепи по заданной схеме?
Решение:
Используя формулу параллельного сопротивления:
$$ \frac{1}{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
$ $ \frac{1}{R_{eq}} = \frac{1}{10 + 2 + 1} $$
$$ \frac{1}{R_{eq}} = \frac{1}{10 } + \frac{1}{2} +\frac{1}{1} $$
$$ \frac{1}{R_{eq}} = 0,1 + 0,5 + 1 $$
$$ \frac {1}{R_{eq}} = 1,6 кОм $$
Какой идентификатор является требуемым ответом, а также может быть проверен с помощью этого калькулятора параллельного сопротивления.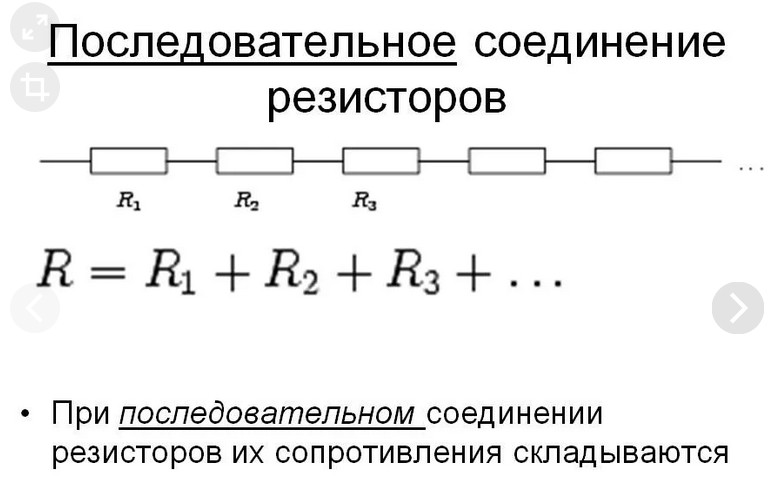
Иллюстрация № 02:
Как найти полное сопротивление в параллельной цепи, в которой следующие резисторы соединены параллельно?
- 25 кОм
- 52 кОм
- 785 кОм
- 65 кОм
Решение:
Используя формулу параллельного соединения резисторов:
$$ \frac{1}{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
$$ \frac{1}{R_{eq}} = \frac{1}{25 + 52 + 785 + 65} $$
$$ \frac{1}{R_{eq}} = \frac{1}{927} $$
$$ \frac{1}{R_{eq}} = 0,001 кОм $$
Как параллельно Калькулятор резисторов работает?
Вам просто нужно выполнить шаги ниже, чтобы рассчитать эквивалентное сопротивление параллельной цепи с помощью нашего онлайн-калькулятора резисторов в параллельной цепи:
Ввод:
- В первом раскрывающемся списке выберите сопротивление, которое вы хотите найти
При выборе эквивалентного сопротивления:
- Добавьте значения сопротивлений в соответствующие поля. Вы также можете добавить до 30 сопротивлений
- После того, как вы закончите, нажмите кнопку расчета
Вы также можете добавить до 30 сопротивленийЕсли выбрать «Отсутствует сопротивление»:
- Введите значение желаемого общего сопротивления и количество сопротивлений, подключенных к цепи
- Теперь нажмите кнопку расчета
Вывод:
Калькулятор параллельных цепей за считанные секунды выполняет следующие вычисления:
- Расчет эквивалентного и недостающего сопротивления в параллельной цепи
Часто задаваемые вопросы:
Что происходит при параллельном подключении резистора?
Добавление дополнительных резисторов в электрическую сеть открывает новые пути для прохождения токов. Вот почему добавление резисторов прямо пропорционально увеличению потока заряда.
Как узнать, параллельны ли два резистора?
Два сопротивления будут считаться соединенными параллельно, если узлы на обоих концах резисторов одинаковы.
В этом случае сопротивления R_1 и R_2 будут параллельны, так что (R_1||R_2) . А если есть еще общее сопротивление R_3 , то оно будет последовательно с параллельным соединением этих двух резисторов.
Параллельное напряжение одинаковое?
Да, при параллельной схеме общее напряжение сети всегда одинаково. Вы можете лучше понять соотношение между напряжением и током любой цепи или отдельного проводника, используя калькулятор закона Ома.
Что такое закон сопротивления?
Закон сопротивления гласит:
«Сопротивление проводника прямо пропорционально длине проводника при сохранении постоянной температуры и физического состояния».
Что называют проводимостью?
Электропроводность — это особое свойство материалов, таких как металлы или неметаллы, благодаря которому электрический ток протекает по электрической сети. Обозначается символом G.
Почему мы предпочитаем параллельное подключение дома?
Параллельные соединения позволяют подавать ток без каких-либо помех для работающих приборов.
