Как построить графики в C# и .NET. Какие библиотеки использовать для создания диаграмм и визуализации данных. Сравнение OxyPlot, LiveCharts, ScottPlot и других инструментов. Примеры кода построения линейных, столбчатых и круговых диаграмм.
Популярные библиотеки для построения графиков в C# и .NET
Для создания графиков и диаграмм в C# и .NET существует множество библиотек и инструментов. Рассмотрим наиболее популярные из них:
- OxyPlot — мощная кроссплатформенная библиотека с открытым исходным кодом
- LiveCharts — современная библиотека с анимированными графиками
- ScottPlot — быстрая и легковесная библиотека для научной визуализации
- ZedGraph — классическая библиотека для Windows Forms
- Microsoft Chart Controls — встроенные в .NET средства для построения диаграмм
OxyPlot — универсальная библиотека для построения графиков
OxyPlot — одна из самых популярных библиотек для построения графиков в .NET. Ее ключевые преимущества:
- Кроссплатформенность — работает на Windows, macOS, Linux
- Поддержка WPF, Windows Forms, UWP, Xamarin
- Широкий набор типов графиков и диаграмм
- Хорошая производительность
- Гибкая настройка внешнего вида
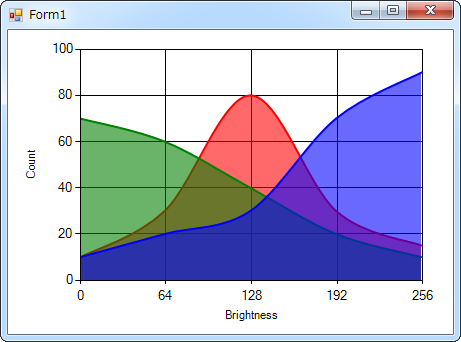
Пример построения линейного графика с помощью OxyPlot:
«`csharp using OxyPlot; using OxyPlot.Series; var model = new PlotModel { Title = «Линейный график» }; var series = new LineSeries(); series.Points.Add(new DataPoint(0, 0)); series.Points.Add(new DataPoint(10, 18)); series.Points.Add(new DataPoint(20, 12)); series.Points.Add(new DataPoint(30, 25)); model.Series.Add(series); // Отобразить график var view = new PlotView { Model = model }; «`LiveCharts — современные анимированные графики
LiveCharts позволяет создавать интерактивные анимированные графики. Основные особенности:
- Плавные анимации при обновлении данных
- Поддержка WPF, Windows Forms, UWP
- Богатые возможности настройки
- Встроенная поддержка тем оформления
Как построить столбчатую диаграмму с LiveCharts:
«`csharp using LiveCharts; using LiveCharts.Wpf; var chart = new CartesianChart(); var columnSeries = new ColumnSeries { Values = new ChartValuesScottPlot — быстрая библиотека для научной визуализации
ScottPlot — относительно новая библиотека, ориентированная на научную визуализацию. Ее преимущества:
- Высокая производительность
- Простой API
- Поддержка большого объема данных
- Специальные типы графиков для научных данных
Как создать круговую диаграмму с помощью ScottPlot:
«`csharp using ScottPlot; var plt = new Plot(400, 300); double[] values = { 778, 43, 283, 76, 184 }; string[] labels = { «C#», «F#», «VB.NET», «C++/CLI», «Other» }; plt.PlotPie(values, labels); plt.Title(«Популярность языков .NET»); // Сохранить график в файл plt.SaveFig(«pie_chart.png»); «`Сравнение производительности библиотек для построения графиков
| Библиотека | Время построения (мс) | Использование памяти (МБ) |
|---|---|---|
| OxyPlot | 120 | 15 |
| LiveCharts | 180 | 22 |
| ScottPlot | 90 | 12 |
Как видим, ScottPlot показывает лучшие результаты по скорости и потреблению памяти. Однако при выборе библиотеки стоит учитывать не только производительность, но и удобство использования, функциональность и соответствие вашим конкретным требованиям.
Советы по оптимизации производительности при построении графиков
Чтобы улучшить производительность при работе с графиками, следуйте этим рекомендациям:
- Ограничивайте количество отображаемых точек данных. Используйте прореживание или агрегацию для больших наборов данных.
- Применяйте виртуализацию данных, чтобы отображать только видимую область графика.
- Используйте аппаратное ускорение, если оно доступно в выбранной библиотеке.
- Оптимизируйте обновление данных, обновляя только изменившиеся части графика.
- Выбирайте подходящий тип графика. Например, для больших объемов данных лучше использовать точечную диаграмму вместо линейного графика.
Интеграция графиков в веб-приложения ASP.NET
Для отображения графиков в веб-приложениях ASP.NET можно использовать несколько подходов:
- Серверный рендеринг с помощью библиотек вроде System.Drawing
- Клиентский рендеринг с использованием JavaScript-библиотек (Chart.js, D3.js)
- Гибридный подход с генерацией данных на сервере и отрисовкой на клиенте
Пример интеграции графика Chart.js в ASP.NET MVC:
 «`csharp
// Контроллер
public class ChartController : Controller
{
public ActionResult Index()
{
return View();
}
public JsonResult GetChartData()
{
var data = new
{
Labels = new[] { «Янв», «Фев», «Мар», «Апр», «Май» },
Datasets = new[]
{
new
{
Label = «Продажи»,
Data = new[] { 65, 59, 80, 81, 56 }
}
}
};
return Json(data, JsonRequestBehavior.AllowGet);
}
}
// Представление (Index.cshtml)
@{
ViewBag.Title = «Chart.js Example»;
}
@section scripts {
}
«`
«`csharp
// Контроллер
public class ChartController : Controller
{
public ActionResult Index()
{
return View();
}
public JsonResult GetChartData()
{
var data = new
{
Labels = new[] { «Янв», «Фев», «Мар», «Апр», «Май» },
Datasets = new[]
{
new
{
Label = «Продажи»,
Data = new[] { 65, 59, 80, 81, 56 }
}
}
};
return Json(data, JsonRequestBehavior.AllowGet);
}
}
// Представление (Index.cshtml)
@{
ViewBag.Title = «Chart.js Example»;
}
@section scripts {
}
«`
Заключение: выбор оптимальной библиотеки для ваших задач
При выборе библиотеки для построения графиков в C# и .NET учитывайте следующие факторы:
- Тип приложения (десктоп, веб, мобильное)
- Требования к производительности
- Необходимые типы графиков и диаграмм
- Возможности настройки внешнего вида
- Простота использования и качество документации
- Активность сообщества и поддержка
Каждая из рассмотренных библиотек имеет свои сильные стороны:
- OxyPlot отлично подходит для кроссплатформенной разработки
- LiveCharts — лучший выбор для создания интерактивных анимированных графиков
- ScottPlot оптимален для научной визуализации и работы с большими объемами данных
- ZedGraph удобен для быстрого создания графиков в Windows Forms приложениях
- Microsoft Chart Controls интегрированы в .NET и не требуют установки дополнительных пакетов
Экспериментируйте с разными библиотеками, чтобы найти оптимальное решение для ваших конкретных задач по визуализации данных в C# и .NET приложениях.
Средства построения графиков для .NET / Хабр
Не так давно пришлось столкнуться с тривиальной задачей — найти решение, которое позволит рендерить рисунки графиков для .NET. Сразу оговорюсь, что меня интересовали только линейные графики. Камнем преткновения, который подтолкнул к переделыванию уже существующего решения (это были графики, встроенные в rdlc отчеты), было быстродействие. В целом, к искомому решению были предъявлены такие требования:
- Необходимо оставить данную оптимизацию незамеченной для конечного пользователя, следовательно, решение должно быть широко настраиваемым, чтобы, в конечном счете, выглядеть так же, как и предшественник.
- Работать быстро (ну понятно, пользователи не любят ждать).
- Желательно, быть бесплатным или с открытым исходным кодом. Покупка не стала бы большой проблемой, найди я отличное платное решение, но начать лучше с open source.
Что было сделано?
Погуглив, выяснилось, что существует достаточно много вариантов для решения данной задачи, и все они достаточно сильно отличаются по многим параметрам (размер сообщества, скорость работы, удобство).
 В процессе выбора решения было опробовано 8 бесплатных вариантов:
В процессе выбора решения было опробовано 8 бесплатных вариантов:- DisLin. Кроссплатформенная библиотека (UNIX, Linux, FreeBSD, OpenVMS, Windows, Mac OSX и MS-DOS). Чрезвычайно мощная, гибкая, действительно стоит того, чтобы написать отдельную статью только о ней. Может быть, немного уступает своим конкурентам по степени читабельности кода (использует классический функциональный подход), но зато, благодаря этому, может быть легко портирована практически на любой язык. Имеет ванильные
- Google Chart Sharp. Обертка над Google Chart API для С#. На хабре уже были статьи о нем, поэтому в двух словах: бесплатный (с ограничением 50000 тыс. вызовов в день), работает очень шустро, присутствуют основные параметры для кастомизации. Среди плюсов: возможность использовать везде, где есть подключение к интернету, независимость от используемого языка / ОС.
 Основной минус — это, естественно, дополнительный round-trip данных по сети (если график Вам нужен ещё на сервере), что замедляет процесс.
Основной минус — это, естественно, дополнительный round-trip данных по сети (если график Вам нужен ещё на сервере), что замедляет процесс. - Microsoft Chart Controls. Нативный функционал от Microsoft, который был представлен общественности в далеком 2008 году. К тому времени уже существовал ряд решений от сторонних разработчиков, но это не помешало Ms Chart Controls быстро завоевать популярность среди разработчиков. И не удивительно, ведь они поставлялись с .NET framework, имели удачную архитектуру, были легко настраиваемыми и привлекательными на вид. По скорости уступают остальным, но, тем не менее, работают тоже вполне прилично.
- NPlot. Ещё одна open source библиотека. Правда, не самая быстрая и популярная — информацию по ней можно найти в Интернете, хотя и не так много, как, например, по Microsoft Chart Controls. Тем не менее, поигравшись с ней, у меня осталось довольно приятное послевкусие.
- OxyPlot. «Живой» кроссплатформенный open source, где можно даже зарепортить баг, на который, скорее всего, отреагируют.
 Доступен также в NuGet. Есть соответствующие контролы для WPF/Silverligth, WinForms, Metro. Плюшки, вроде экспорта напрямую в OpenXml и Pdf. Если Вам необходимо не «минутное» решение и возможность поправить его под себя, это решение для Вас.
Доступен также в NuGet. Есть соответствующие контролы для WPF/Silverligth, WinForms, Metro. Плюшки, вроде экспорта напрямую в OpenXml и Pdf. Если Вам необходимо не «минутное» решение и возможность поправить его под себя, это решение для Вас. - ZedGraph. Также «живой» open source, прямой конкурент для OxyPlot. По количеству поддерживаемых платформ (только Windows) и технологий (только WinForms и ASP .NET) уступает ему, но очень симпатичный и один из самых быстрых. Отличный выбор, если Вам надо «просто красивый график» и больше ничего.
- WebChart. Бесплатный предшественник Microsoft Chart Controls. Насколько я вижу, мертвый с 2004 года. У него чуть более убогий функционал в сравнении с остальными решениями, но, так как он имеет некоторые внешние отличия от остальных, может быть вполне полезен.
- OpenMinded. Беплатный вариант от пользователя OpenMinded. Выглядит красиво. О производительности судить трудно, так как я не нашел возможности рендерить результирующий рисунок иначе как на жесткий диск.
 Но поскольку проэкт открытый, любой желающий может его доделать под себя, уверен — это не проблема.
Но поскольку проэкт открытый, любой желающий может его доделать под себя, уверен — это не проблема.
Ещё в самом начале я решил, что надо собрать как можно больше вариантов в одном месте и протестить их на быстродействие, а уже после этого было очень жалко выбрасывать в корзину проделанную работу. Поэтому было решено оформить эту статейку и выложить то, что получилось, на GitHub. Таким образом, если возникла необходимость, Вы можете настроить каждое решение под себя и сразу же его проверить. Лично мне очень не хватало такой статьи в начале. Может быть, исходники вызовут улыбку у гуру, но новичкам, которые только вникают в .NET и ASP, они однозначно будут очень полезны.
Для сравнения скорости работы берутся дефолтные настройки графика, указывается разрешение выходного рисунка и ему скармливается фиксированное количество точек. Каждое решение прогоняется несколько раз, и в качестве реальной скорости берется среднее. Опять же, это достаточно субъективно, и, если Вы можете предложить более красивый подход, я с интересом выслушаю.

На моем ПК (Intel Core I5 3.10 GHz, 8gb ОЗУ, Windows 7 x64) вышло следующее распределение скорости работы:
| № |
Решение |
Количество итераций |
Суммарное время (сек) |
Среднее время на одну итерацию (сек) |
| 1 |
Dislin charts |
5 |
1.9071907 |
0.38143814 |
| 2 |
Zed Graph |
5 |
2.750275 |
0.550055 |
| 3 |
NPlot |
5 |
3.1833183 |
0.63666366 |
| 4 |
Web Chart Control |
5 |
5.130513 |
1.0261026 |
| 5 |
Microsoft Chart Controls |
5 |
6. 8456845 8456845 |
1.3691369 |
| 6 |
Oxy Plot |
5 |
7.0067006 |
1.40134012 |
| 7 |
Open minded plot |
5 |
8.257 |
1.6514 |
| 8 |
Google Sharp charting |
5 |
9.8049804 |
1.96099608 |
Для различных входных параметров (разрешение изображения, количество точек на графике, параметры ПК, скорость интернета, фаза Луны и т.д.) результаты немного отличаются, поэтому Вы можете протестировать быстродействие у себя.
Я специально не делал глубокое сравнения фич и возможностей кастомизации, так как это довольно субъективная информация, которая сильно зависит от конкретной задачи. При необходимости, каждый желающий может провести полчаса, подебажить, посмотреть архитектуру решений, прикинуть, насколько легко их настроить под конкретные требования.
Если кто-то знает ещё бесплатные решения для графиков под .NET, которые пропущены в статье, — пишите в комментариях, и я постараюсь их добавить.
upd — (добавил решение от OpenMinded)
upd2 — (включил DevExpress в опрос)
Построение графика функции онлайн | umath.ru
- Обязательно писать все знаки умножения
- Десятичные дроби нужно разделять точкой
- Список функций и констант смотрите ниже
Как пользоваться программой:
- Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
- Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
- Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
- Кнопка «·» в центре джойстика переносит начало координат в центр экрана.
- Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
- В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.

Режимы
Обычный. В этом режиме можно строить графики функций, заданных уравнением
Параметрический. Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде
Полярные координаты. Режим позволяет построить график кривой, заданной в полярной системе координат, то есть уравнением где — радиальная координата, а — полярная координата.
Список констант
| Константа | Описание |
|---|---|
pi |
Число =3,14159... |
e |
Число Эйлера =2,71828... |
Список функций
| Функция | Описание |
|---|---|
+ − * / | Сложение, вычитание, умножение, деление |
( ) | Группирующие скобки |
abs() или | | |
Модуль числа. 3 дают 3 дают x в третьей
степени |
sqrt() | Квадратный корень |
sin() | Синус |
cos() | Косинус |
tg() | Тангенс |
ctg() | Котангенс |
arcsin() | Арксинус |
arccos() | Арккосинус |
arctg() | Арктангенс |
arcctg() | Арккотангенс |
ln() | Натуральный логарифм числа |
lg() | Десятичный логарифм числа |
log(a, b) |
Логарифм числа b по основанию a |
exp() |
Степень числа e |
sh() | Гиперболический синус |
ch() | Гиперболический косинус |
th() | Гиперболический тангенс |
cth() | Гиперболический котангенс |
График функции
Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты
этих точек удовлетворяют уравнению .
Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах (например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.
Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.
Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет носить ваше имя ;).
Построение поверхности 3D, заданной уравнением — Контрольная Работа РУ
Введите уравнение
Построим поверхность, заданную уравнением f(x, y, z) = 0, где a < x < b, c < y < d, m < z < n.
Другие калькуляторы
Примеры поверхностей
| Название поверхности | Уравнение |
|---|---|
| Плоскость | z/4 - y/4 - x/5 = 1 |
| Сфера | x^2 + y^2 + z^2 = 1 |
| Эллиптический параболоид | x^2 + y^2 - 7*x + 8*y - 4*z + 11 = 0 |
| Двухсторонний гиперболоид | x^2 + y^2 - z^2 - 2*x - 2*y + 2*z + 2 = 0 |
| Мнимый эллипсоид | 2*x^2 + 4*y^2 + z^2 - 4*x*y - 4*y - 2*z + 5 = 0 |
| Две параллельные плоскости | x^2 + 4*y^2 + 9*z^2 + 4*x*y + 12*y*z + 6*x*z - 4*x - 8*y - 12*z + 3 = 0 |
| Тригонометрические функции | z = sin((x^2 + y^2)^(1/2)) |
Канонический вид кривой и поверхности
Вы можете определить вид кривой и поверхности 2-го порядка онлайн с подробным решением:
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
-
Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
-
Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
-
вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
-
Число «Пи», которое примерно равно ~3.
 14159..
14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- oo
- Символ бесконечности — знак для бесконечности
Построение графиков функций в Excel
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
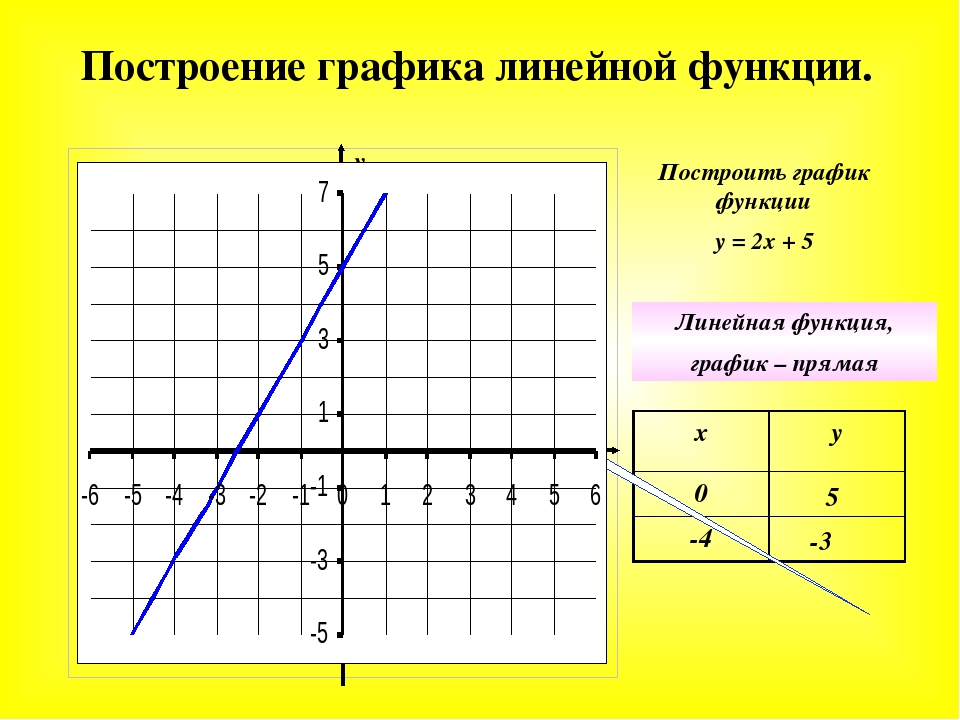
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. 2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
на Ваш сайт.
Оператор |
Описание |
Простейшие математические операции |
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . Знак умножения * — необязателен: выражение 2sin(3x) эквивалентно 2*sin(3*x). Cкобки используются для группирования выражений. |
0.5 |
Десятичные дроби записываются через точку:
|
Элементарные функции |
|
xn |
Возведение в степень: x^n, например, для ввода x2 используется x^2 |
√x |
Квадратный корень: \sqrt(x) или x^(1/2) |
3√x |
Кубический корень: x^(1/3) |
n√x |
Корень n-той степени из x: x^(1/n) |
ln(x) |
Натуральный логарифм (логарифм c основанием e): log(x) |
logax |
Логарифм от x по основанию a: log(x)/log(a) |
lg(x) |
Десятичный логарифм (логарифм по основанию 10): log(x)/log(10) |
ex |
Экспоненциальная функция: exp(x) |
Тригонометрические функции |
|
sin(x) |
Синус от x: sin(x) |
cos(x) |
Косинус от x: cos(x) |
tg(x) |
Тангенс от x: tan(x) |
ctg(x) |
Котангенс от x: 1/tan(x) |
arcsin(x) |
Арксинус от x: arcsin(x) |
arccos(x) |
Арккосинус от x: arccos(x) |
arctan(x) |
Арктангенс от x: arctan(x) |
arcctg(x) |
Арккотангенс от x: \pi/2 — arctan(x) |
Некоторые константы |
|
e |
Число Эйлера e: \e |
π |
Число π: \pi |
построение графиков в c — Stack overflow на русском
Переполнение стека- Около
- Продукты
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Qt Plotting Widget QCustomPlot — Введение
QCustomPlot — это виджет Qt C ++ для построения графиков и визуализации данных.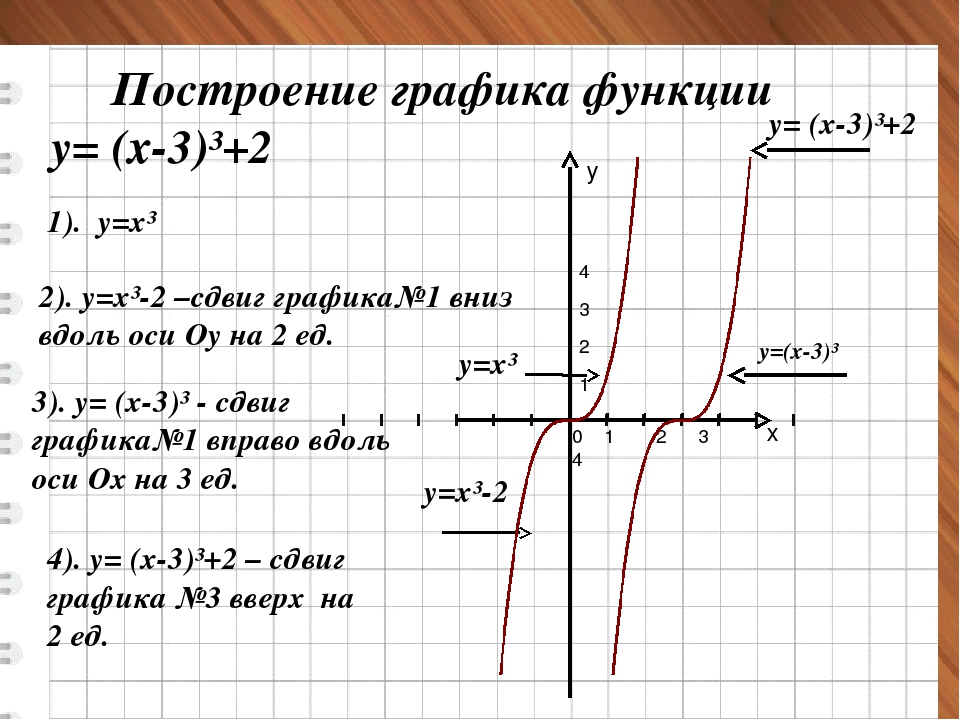 Он не имеет дополнительных зависимостей и хорошо документирован. Эта библиотека для построения графиков предназначена для создания красивых 2D-графиков, графиков и диаграмм качества публикации, а также обеспечивает высокую производительность для приложений визуализации в реальном времени. Чтобы начать работу, ознакомьтесь с руководствами по настройке и основам построения графиков.
Он не имеет дополнительных зависимостей и хорошо документирован. Эта библиотека для построения графиков предназначена для создания красивых 2D-графиков, графиков и диаграмм качества публикации, а также обеспечивает высокую производительность для приложений визуализации в реальном времени. Чтобы начать работу, ознакомьтесь с руководствами по настройке и основам построения графиков.
QCustomPlot может экспортировать в различные форматы, такие как векторизованные файлы PDF и растровые изображения, такие как PNG, JPG и BMP. QCustomPlot — это решение для отображения данных в реальном времени внутри приложения, а также для создания высококачественных графиков для других носителей.
|
Лицензия по умолчанию GPL, не стесняйтесь использовать QCP в бесплатном ПО! |
Свяжитесь с нами, если вам нужна коммерческая лицензия. |
Скриншоты участка
Скриншоты ниже показывают, чего можно достичь с помощью QCustomPlot, всего в нескольких строках. Чтобы просмотреть код, щелкните соответствующее изображение. Все коды также доступны в полном пакете, который можно найти в разделе загрузки.Внутри пакета перейдите к проекту examples / plots / plot-examples.pro.
Чтобы просмотреть код, щелкните соответствующее изображение. Все коды также доступны в полном пакете, который можно найти в разделе загрузки.Внутри пакета перейдите к проекту examples / plots / plot-examples.pro.
Простая функция затухающего синуса с заливкой и ее экспоненциальной огибающей красным цветом
функция sinc с точками данных, соответствующими планками ошибок и доверительным интервалом 2 сигмы
Демонстрация нескольких стилей точек разброса
Демонстрация универсальности QCustomPlot в стилизации сюжета
Двухмерная цветовая карта с цветовой шкалой. Цветовые шкалы можно перетаскивать и масштабировать, как оси
Точки разброса пиксельной карты и многострочная метка оси, а также заголовок графика вверху
Данные, генерируемые в реальном времени, и нижняя ось времени
Несколько стилей графика с разными осями ключ / значение и маркировкой пи-тика на верхней оси
Масштабирование логарифмической оси.Обратите внимание на правильное отображение функции синуса, пересекающей ноль в отрицательной бесконечности.
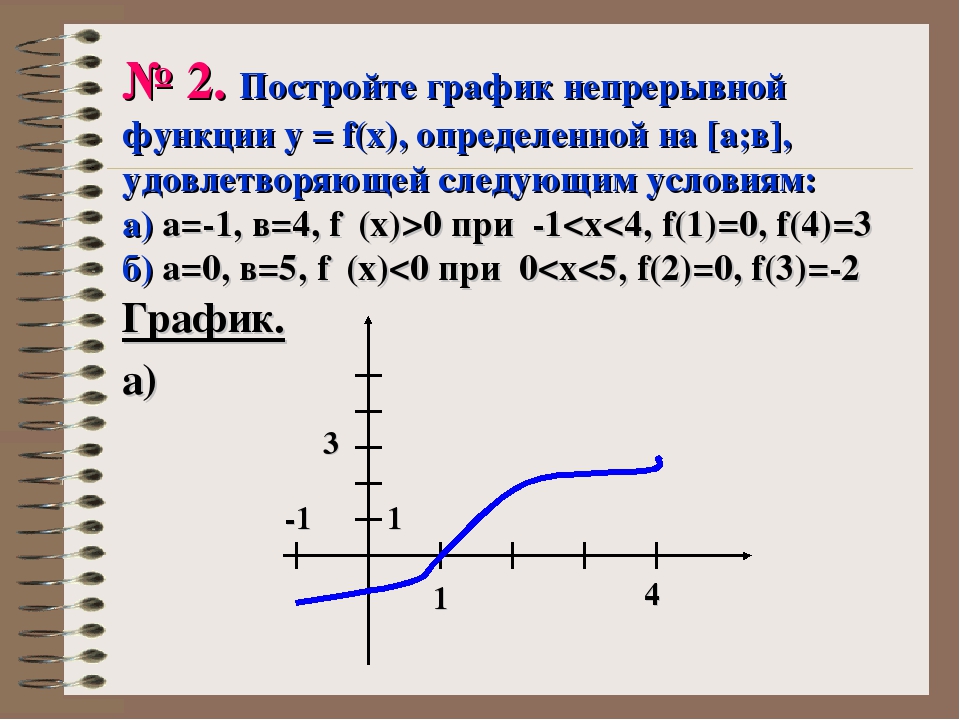
Демонстрация нескольких стилей линий
Случайные прогулки с отметками заполнения и умной даты на нижней оси
Параметрические кривые с полупрозрачной градиентной заливкой
Три гистограммы с накоплением и метками делений по оси X
Статистическая диаграмма с пятью параметрами с выбросами
Пример взаимодействия, показывающий выбор графиков пользователем
Использование таких элементов, как текстовые метки, стрелки и скобки.Это на самом деле анимировано, см. Примеры проекта
QCP поддерживает несколько осей на одной стороне прямоугольника и несколько прямоугольных осей для каждого виджета графика
QCP показывает финансовые и биржевые данные с типичными графиками Candlestick и OHLC
Компонент диаграмм и графиков, Библиотека управления и построения графиков для .NET (C # / VB), Java, C ++, ASP, COM, PHP, Perl, Python, Ruby, ColdFusion
Общие характеристики
Функции, общие для всех языковых редакций ChartDirector
Расширенные типы диаграмм
Пирог, пончик, полоса, линия, сплайн, ступенчатая линия, линия тренда, аппроксимация кривой, межстрочное заполнение, площадь, полоса, разброс, пузырь, плавающий ящик, коробочка-ус, водопад, контур, тепловая карта, поверхность, вектор, финансы, диаграмма Ганта, радар, полярная, роза, пирамида, конус, воронка.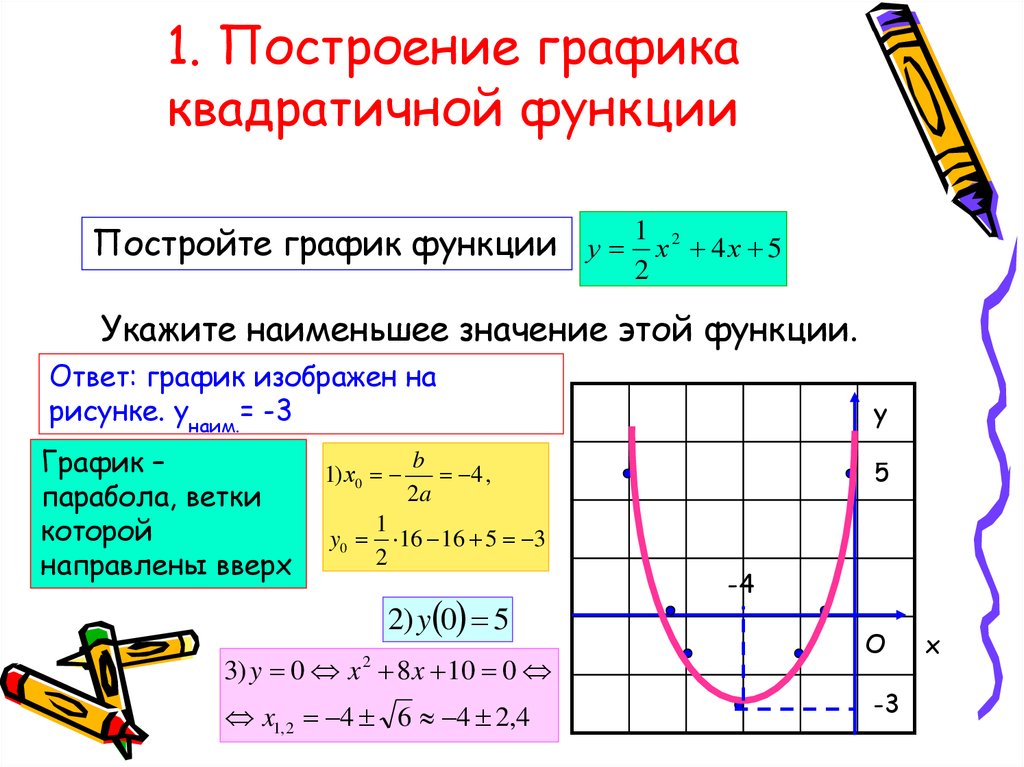 ..
..
Многоуровневая архитектура
Синтезируйте нужные диаграммы с помощью нескольких слоев диаграмм. Используйте слои для построения комбинированных диаграмм, добавляйте специальные символы, метки и подписывать диаграммы, выделять точки данных, добавлять полосы ошибок …Приборы и калибры
Угловые измерители настраиваемого диапазона углов и ориентации — полукруглые, круглые, 120 градусов … Линейные измерители с указателями и полосами по горизонтали и вертикали ориентации.Программируемый курсор трека
Добавьте линии развертки, которые отслеживают мышь или палец, отображая значения данных в легенда, ось или плавающие текстовые поля.Программируемое поведение для максимального гибкость.Интерфейс масштабирования и прокрутки
Масштабирование и прокрутка с помощью перетаскивания мышью, колесика мыши, щелчка или касания или использования Viewport Control для визуализации и выбора диапазона данных. Также поддерживает внешние элементы управления, такие как полосы прокрутки, ползунки и средства выбора даты.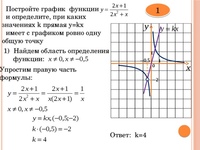
Графики в реальном времени
Постройте диаграммы и графики, которые обновляются в реальном времени с масштабированием и прокруткой, программируемые курсоры треков и снимки.Всплывающие подсказки, детализация и объекты интерактивных диаграмм
Настраиваемые всплывающие подсказки для объектов диаграммы.События мыши и касания для объектов диаграммы для поддержки детализации и настраиваемого взаимодействия с пользователем.Финансовая библиотека с исходным кодом
Включите сложную библиотеку финансовых графиков с 47 техническими индикаторами. Расширяемый и настраиваемый, поставляется с исходным кодом. Также включает Пример программы Interactive Financial Chart.PDF, SVG и вывод изображений
Диаграммы могут быть созданы как векторная графика в PDF и SVG, а растровая графика в PNG, JPG, GIF и BMP.Вывод может быть отправлен прямо в браузеры на лету, сохранен в памяти для обработки или сохраняются в виде файлов.Беспрецедентная настраиваемость
Комплексный объектно-ориентированный API позволяет настраивать каждую деталь диаграммы. Текст и метки
могут быть помечены тегами для включения значков и изображений, а также для установки шрифтов, цветов,
макет, выравнивание, межстрочный интервал, перенос, усечение … Заливка объектов сплошным цветом
а также узоры, градиенты или другие динамические цвета. Неограниченное количество осей XY на графике,
с автоматическим, полуавтоматическим и ручным масштабированием…
Текст и метки
могут быть помечены тегами для включения значков и изображений, а также для установки шрифтов, цветов,
макет, выравнивание, межстрочный интервал, перенос, усечение … Заливка объектов сплошным цветом
а также узоры, градиенты или другие динамические цвета. Неограниченное количество осей XY на графике,
с автоматическим, полуавтоматическим и ручным масштабированием…
Универсальный и универсальный
Идеальный компонент диаграммы и графика в наборе инструментов разработчика для ваших текущих и будущих проектов. Подходит для настольных ПК, Интернета, клиент / сервер, консоли, пакетного, фонового и др. типы приложений. Поддерживает .NET (C #, VB и другие языки интерфейса командной строки), C ++, Java, JSP, ASP, COM, VB, VBScript, VBA, JavaScript, PHP, Perl, Python, Ruby и Холодный синтез. Работает на Windows, Linux, FreeBSD, Solaris, macOS и поддерживает Java. системы.Построение областей принятия решений — mlxtend
Функция для построения областей принятия решений классификаторов в 1 или 2 измерениях.
из mlxtend.plotting import plot_decision_regions
Список литературы
Пример 1 — Области принятия решения в 2D
из mlxtend.plotting import plot_decision_regions
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из sklearn.svm импортировать SVC
# Загрузка некоторых примеров данных
iris = datasets.load_iris ()
X = iris.data [:, [0, 2]]
y = iris.target
# Обучение классификатора
svm = SVC (C = 0,5, ядро = 'линейный')
svm.fit (X, y)
# Построение областей принятия решений
plot_decision_regions (X, y, clf = svm, legend = 2)
# Добавление аннотаций осей
plt.xlabel ('длина чашелистика [см]')
plt.ylabel ('длина лепестка [см]')
plt.title ('SVM на радужке')
plt.show ()
Пример 2 — Области принятия решения в 1D
из mlxtend.plotting import plot_decision_regions
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из sklearn.svm импортировать SVC
# Загрузка некоторых примеров данных
iris = datasets.load_iris ()
X = iris.data [:, 2]
X = X [:, Нет]
y = iris.target
# Обучение классификатора
svm = SVC (C = 0,5, ядро = 'линейный')
svm.fit (X, y)
# Построение областей принятия решений
plot_decision_regions (X, y, clf = svm, legend = 2)
# Добавление аннотаций осей
plt.xlabel ('длина чашелистика [см]')
plt.title ('SVM на радужке')
plt.show ()
Пример 3 — Сетка области принятия решения
из sklearn.linear_model import LogisticRegression
из sklearn.naive_bayes импортировать GaussianNB
из sklearn.ensemble импортировать RandomForestClassifier
из sklearn.svm импортировать SVC
из наборов данных импорта sklearn
импортировать numpy как np
# Инициализация классификаторов
clf1 = логистическая регрессия (random_state = 1,
solver = 'ньютон-cg',
multi_class = 'мультиномиальный')
clf2 = RandomForestClassifier (random_state = 1, n_estimators = 100)
clf3 = GaussianNB ()
clf4 = SVC (гамма = 'авто')
# Загрузка некоторых примеров данных
iris = наборы данных.load_iris ()
X = iris.data [:, [0,2]]
y = iris.target
импортировать matplotlib.pyplot как plt
из mlxtend.plotting import plot_decision_regions
импортировать matplotlib.gridspec как gridspec
импортировать itertools
gs = gridspec.GridSpec (2, 2)
fig = plt.figure (figsize = (10,8))
label = ['Логистическая регрессия', 'Случайный лес', 'Наивный байесовский', 'SVM']
для clf, lab, grd в архиве ([clf1, clf2, clf3, clf4],
этикетки
itertools.product ([0, 1], repeat = 2)):
clf.подходят (X, y)
ax = plt.subplot (gs [grd [0], grd [1]])
fig = plot_decision_regions (X = X, y = y, clf = clf, legend = 2)
plt.title (лаборатория)
plt.show ()
Пример 4 — Выделение контрольных точек данных
из mlxtend.plotting import plot_decision_regions
из mlxtend.preprocessing import shuffle_arrays_unison
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из sklearn.svm импортировать SVC
# Загрузка некоторых примеров данных
iris = datasets.load_iris ()
X, y = радужная оболочка.данные [:, [0,2]], iris.target
X, y = shuffle_arrays_unison (массивы = [X, y], random_seed = 3)
X_train, y_train = X [: 100], y [: 100]
X_test, y_test = X [100:], y [100:]
# Обучение классификатора
svm = SVC (C = 0,5, ядро = 'линейный')
svm.fit (X_train, y_train)
# Построение областей принятия решений
plot_decision_regions (X, y, clf = svm, legend = 2,
X_highlight = X_test)
# Добавление аннотаций осей
plt.xlabel ('длина чашелистника [см]')
plt.ylabel ('длина лепестка [см]')
plt.title ('SVM на радужке')
plt.show ()
Пример 5 — Оценка поведения классификатора при решении нелинейных задач
из sklearn.linear_model импорт LogisticRegression
из sklearn.naive_bayes импортировать GaussianNB
из sklearn.ensemble импортировать RandomForestClassifier
из sklearn.svm импортировать SVC
# Инициализация классификаторов
clf1 = LogisticRegression (random_state = 1, решатель = 'lbfgs')
clf2 = RandomForestClassifier (n_estimators = 100,
random_state = 1)
clf3 = GaussianNB ()
clf4 = SVC (гамма = 'авто')
# Loading Plotting Utilities
импортировать matplotlib.pyplot как plt
импортировать matplotlib.gridspec как gridspec
импортировать itertools
из mlxtend.построение графика импорта plot_decision_regions
импортировать numpy как np
XOR
xx, yy = np.meshgrid (np.linspace (-3, 3, 50),
np.linspace (-3, 3, 50))
rng = np.random.RandomState (0)
X = rng.randn (300, 2)
y = np.array (np.logical_xor (X [:, 0]> 0, X [:, 1]> 0),
dtype = int)
gs = gridspec.GridSpec (2, 2)
fig = plt.figure (figsize = (10,8))
label = ['Логистическая регрессия', 'Случайный лес', 'Наивный байесовский', 'SVM']
для clf, lab, grd в архиве ([clf1, clf2, clf3, clf4],
этикетки
itertools.product ([0, 1], repeat = 2)):
clf.fit (X, y)
ax = plt.subplot (gs [grd [0], grd [1]])
fig = plot_decision_regions (X = X, y = y, clf = clf, legend = 2)
plt.title (лаборатория)
plt.show ()
Полумесяцы
из sklearn.datasets import make_moons
X, y = make_moons (n_samples = 100, random_state = 123)
gs = gridspec.GridSpec (2, 2)
fig = plt.figure (figsize = (10,8))
label = ['Логистическая регрессия', 'Случайный лес', 'Наивный байесовский', 'SVM']
для clf, lab, grd в архиве ([clf1, clf2, clf3, clf4],
этикетки
itertools.product ([0, 1], repeat = 2)):
clf.fit (X, y)
ax = plt.subplot (gs [grd [0], grd [1]])
fig = plot_decision_regions (X = X, y = y, clf = clf, legend = 2)
plt.title (лаборатория)
plt.show ()
Концентрические круги
из sklearn.datasets import make_circles
X, y = make_circles (n_samples = 1000, random_state = 123, noise = 0.1, factor = 0.2)
gs = gridspec.GridSpec (2, 2)
fig = plt.figure (figsize = (10,8))
label = ['Логистическая регрессия', 'Случайный лес', 'Наивный байесовский', 'SVM']
для clf, lab, grd в архиве ([clf1, clf2, clf3, clf4],
этикетки
itertools.product ([0, 1], repeat = 2)):
clf.fit (X, y)
ax = plt.subplot (gs [grd [0], grd [1]])
fig = plot_decision_regions (X = X, y = y, clf = clf, legend = 2)
plt.title (лаборатория)
plt.show ()
Пример 6 — Работа с существующими объектами осей с использованием дополнительных графиков
импортировать matplotlib.pyplot как plt
из mlxtend.plotting import plot_decision_regions
из sklearn.linear_model import LogisticRegression
из sklearn.naive_bayes импортировать GaussianNB
из наборов данных импорта sklearn
импортировать numpy как np
# Загрузка некоторых примеров данных
iris = наборы данных.load_iris ()
X = iris.data [:, 2]
X = X [:, Нет]
y = iris.target
# Инициализация и установка классификаторов
clf1 = логистическая регрессия (random_state = 1,
solver = 'lbfgs',
multi_class = 'мультиномиальный')
clf2 = GaussianNB ()
clf1.fit (X, y)
clf2.fit (X, y)
fig, axes = plt.subplots (1, 2, figsize = (10, 3))
fig = plot_decision_regions (X = X, y = y, clf = clf1, ax = axes [0], legend = 2)
fig = plot_decision_regions (X = X, y = y, clf = clf2, ax = axes [1], legend = 1)
plt.show ()
Пример 7 — Области принятия решения с более чем двумя функциями обучения
из mlxtend.построение графика импорта plot_decision_regions
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из sklearn.svm импортировать SVC
# Загрузка некоторых примеров данных
X, y = datasets.make_blobs (n_samples = 600, n_features = 3,
центры = [[2, 2, -2], [- 2, -2, 2]],
cluster_std = [2, 2], random_state = 2)
# Обучение классификатора
svm = SVC (гамма = 'авто')
svm.fit (X, y)
# Построение областей принятия решений
fig, ax = plt.subplots ()
# Регион принятия решения для функции 3 = 1,5
значение = 1.5
# Постройте обучающую выборку с признаком 3 = 1,5 +/- 0,75
ширина = 0,75
plot_decision_regions (X, y, clf = svm,
filler_feature_values = {2: значение},
filler_feature_ranges = {2: width},
легенда = 2, топор = топор)
ax.set_xlabel ('Функция 1')
ax.set_ylabel ('Функция 2')
ax.set_title ('Характеристика 3 = {}'. формат (значение))
# Добавление аннотаций осей
fig.suptitle ('SVM на make_blobs')
plt.show ()
Пример 8 — Сетка срезов области принятия решения
из mlxtend.построение графика импорта plot_decision_regions
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из sklearn.svm импортировать SVC
# Загрузка некоторых примеров данных
X, y = datasets.make_blobs (n_samples = 500, n_features = 3, center = [[2, 2, -2], [- 2, -2, 2]],
cluster_std = [2, 2], random_state = 2)
# Обучение классификатора
svm = SVC (гамма = 'авто')
svm.fit (X, y)
# Построение областей принятия решений
fig, axarr = plt.subplots (2, 2, figsize = (10,8), sharex = True, sharey = True)
значения = [-4.0, -1.0, 1.0, 4.0]
ширина = 0,75
для значения ax в zip (значения, axarr.flat):
plot_decision_regions (X, y, clf = svm,
filler_feature_values = {2: значение},
filler_feature_ranges = {2: width},
легенда = 2, топор = топор)
ax.set_xlabel ('Функция 1')
ax.set_ylabel ('Функция 2')
ax.set_title ('Характеристика 3 = {}'. формат (значение))
# Добавление аннотаций осей
fig.suptitle ('SVM на make_blobs')
plt.show ()
Пример 9 — Настройка стиля печати
из mlxtend.построение графика импорта plot_decision_regions
из mlxtend.preprocessing import shuffle_arrays_unison
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из sklearn.svm импортировать SVC
# Загрузка некоторых примеров данных
iris = datasets.load_iris ()
X = iris.data [:, [0, 2]]
y = iris.target
X, y = shuffle_arrays_unison (массивы = [X, y], random_seed = 3)
X_train, y_train = X [: 100], y [: 100]
X_test, y_test = X [100:], y [100:]
# Обучение классификатора
svm = SVC (C = 0,5, ядро = 'линейный')
svm.fit (X_train, y_train)
# Укажите аргументы ключевого слова, которые будут переданы базовым функциям построения графика
scatter_kwargs = {'s': 120, 'edgecolor': нет, 'альфа': 0.7}
contourf_kwargs = {'альфа': 0,2}
scatter_highlight_kwargs = {'s': 120, 'label': 'Тестовые данные', 'alpha': 0,7}
# Построение областей принятия решений
plot_decision_regions (X, y, clf = svm, legend = 2,
X_highlight = X_test,
scatter_kwargs = scatter_kwargs,
contourf_kwargs = contourf_kwargs,
scatter_highlight_kwargs = scatter_highlight_kwargs)
# Добавление аннотаций осей
plt.xlabel ('длина чашелистника [см]')
plt.ylabel ('длина лепестка [см]')
plt.title ('SVM на радужке')
plt.show ()
Пример 10 — Предоставление собственных меток легенды
Пользовательские метки легенды могут быть предоставлены путем возврата объекта (ов) оси из функции plot_decision_region и последующего получения дескрипторов и меток легенды. Пользовательские ручки (например, метки) могут быть предоставлены через ax.legend
ax = plot_decision_regions (X, y, clf = svm, legend = 0)
ручки, метки = ax.get_legend_handles_labels ()
топор.легенда (ручки,
['класс 0', 'класс 1', 'класс 2'],
framealpha = 0,3, точки разброса = 1)
Пример показан ниже.
из mlxtend.plotting import plot_decision_regions
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из sklearn.svm импортировать SVC
# Загрузка некоторых примеров данных
iris = datasets.load_iris ()
X = iris.data [:, [0, 2]]
y = iris.target
# Обучение классификатора
svm = SVC (C = 0,5, ядро = 'линейный')
svm.fit (X, y)
# Построение областей принятия решений
ax = plot_decision_regions (X, y, clf = svm, legend = 0)
# Добавление аннотаций осей
plt.xlabel ('длина чашелистика [см]')
plt.ylabel ('длина лепестка [см]')
plt.title ('SVM на радужке')
ручки, метки = ax.get_legend_handles_labels ()
ax.legend (ручки,
['квадрат класса', 'треугольник класса', 'круг класса'],
framealpha = 0,3, точки разброса = 1)
plt.show ()
Пример 11 — Графики с разными коэффициентами масштабирования
из mlxtend.plotting import plot_decision_regions
импортировать matplotlib.pyplot как plt
из наборов данных импорта sklearn
из склеарна.svm import SVC
# Загрузка некоторых примеров данных
iris = datasets.load_iris ()
X = iris.data [:, [0, 2]]
y = iris.target
# Обучение классификатора
svm = SVC (C = 0,5, ядро = 'линейный')
svm.fit (X, y)
SVC (C = 0,5, break_ties = False, cache_size = 200, class_weight = None, coef0 = 0,0,
solution_function_shape = 'ovr', степень = 3, гамма = 'масштаб', ядро = 'линейный',
max_iter = -1, вероятность = False, random_state = None, сжатие = True,
tol = 0,001, verbose = False)
Коэффициент масштабирования по умолчанию
plot_decision_regions (X, y, clf = svm, zoom_factor = 1.)
plt.show ()
Уменьшение
plot_decision_regions (X, y, clf = svm, zoom_factor = 0.1)
plt.show ()
Увеличение
Обратите внимание, что при увеличении масштаба (путем выбора zoom_factor > 1.0) графики по-прежнему создаются так, что все точки данных отображаются на графике.
plot_decision_regions (X, y, clf = svm, zoom_factor = 2.0)
plt.show ()
Обрезка осей
Для дальнейшего увеличения масштаба, что означает, что некоторые обучающие примеры не будут показаны, вы можете просто обрезать оси, как показано ниже:
plot_decision_regions (X, y, clf = svm, zoom_factor = 2.0)
plt.xlim (5, 6)
plt.ylim (2, 5)
plt.show ()
Пример 12 — Использование классификаторов, ожидающих вывода с однократным кодированием (Keras)
Большинство объектов для классификации, которые имитируют API оценки scikit-learn, должны быть совместимы с функцией plot_decision_regions . Однако, если модель классификации (например, типичная модель Кераса) выводит предсказания с однократным кодированием, мы должны использовать дополнительный трюк. То есть для выходных данных с кодировкой onehot нам нужно обернуть модель Keras в класс, который преобразует эти кодированные переменные onehot в целые числа.Такой класс-оболочка может быть таким простым, как:
класс Onehot2Int (объект):
def __init __ (я, модель):
self.model = модель
def предсказывать (self, X):
y_pred = self.model.predict (X)
вернуть np.argmax (y_pred, axis = 1)
В приведенном ниже примере показано, как класс Onehot2Int можно использовать с моделью Keras, которая выводит метки в кодировке onehot:
импортные керасы
из keras.models импорт Последовательный
from keras.layers import Плотный
импортировать matplotlib.pyplot как plt
импортировать numpy как np
из mlxtend.data импорт iris_data
из mlxtend.preprocessing import standardize
из mlxtend.plotting import plot_decision_regions
from keras.utils import to_categorical
X, y = iris_data ()
X = X [:, [2, 3]]
X = стандартизировать (X)
# OneHot кодировка
y_onehot = to_categorical (y)
# Создаем модель
np.random.seed (123)
model = Последовательный ()
model.add (Dense (8, input_shape = (2,), Activation = 'relu', kernel_initializer = 'he_uniform'))
model.add (Dense (4, активация = 'relu', kernel_initializer = 'he_uniform'))
модель.добавить (Плотный (3, активация = 'softmax'))
# Настроить модель и начать обучение
model.compile (loss = "category_crossentropy", optimizer = keras.optimizers.adam (lr = 0,005), metrics = ['precision'])
history = model.fit (X, y_onehot, epochs = 10, batch_size = 5, verbose = 1, validation_split = 0.1)
Использование серверной части TensorFlow.
Обучение на 135 образцах, проверка на 15 образцах
Эпоха 1/10
135/135 [==============================] - 0s 907us / step - потеря: 1.0485 - точность: 0.4593 - val_loss : 1.1127 - val_accuracy: 0.0000e + 00
Эпоха 2/10
135/135 [==============================] - 0 с. 198us / шаг - потеря: 0,8551 - точность: 0,6519 - val_loss : 1.1561 - val_accuracy: 0.0000e + 00
Эпоха 3/10
135/135 [==============================] - 0s 167us / step - потеря: 0,6599 - точность: 0,6889 - val_loss : 1.1097 - val_accuracy: 0.0000e + 00
Эпоха 4/10
135/135 [==============================] - 0s 168us / шаг - потеря: 0,5326 - точность: 0,7185 - val_loss : 1.0635 - val_accuracy: 0.0000e + 00
Эпоха 5/10
135/135 [==============================] - 0s 155us / step - потеря: 0.4369 - точность: 0.8444 - val_loss: 1.0050 - val_accuracy: 0.6667
Эпоха 6/10
135/135 [==============================] - 0s 154us / step - потеря: 0,3777 - точность: 0,8963 - val_loss : 0.9089 - val_accuracy: 0.8000
Эпоха 7/10
135/135 [==============================] - 0s 160us / шаг - потеря: 0,3363 - точность: 0,9407 - val_loss : 0.8491 - val_accuracy: 0.8667
Эпоха 8/10
135/135 [==============================] - 0s 156us / step - потеря: 0,3090 - точность: 0,9259 - val_loss : 0.7793 - val_accuracy: 0.8667
Эпоха 9/10
135/135 [==============================] - 0 с. 165us / шаг - потеря: 0.2795 - точность: 0.9407 - val_loss: 0.7046 - val_accuracy: 0.9333
Эпоха 10/10
135/135 [==============================] - 0s 153us / шаг - потеря: 0,2621 - точность: 0,9556 - val_loss : 0.6322 - val_accuracy: 1.0000
# Wrap keras модель
model_no_ohe = Onehot2Int (модель)
# Граница решения графика
plot_decision_regions (X, y, clf = model_no_ohe)
plt.show ()
plot_decision_regions (X, y, clf, feature_index = None, filler_feature_values = None, filler_feature_ranges = None, ax = None, X_highlight = None, res = None, zoom_factor = 1.oxv <> ‘, colors =’ # 1f77b4, # ff7f0e, # 3ca02c, # d62728, # 9467bd, # 8c564b, # e377c2, # 7f7f7f, # bcbd22, # 17becf ‘, scatter_kwargs = None, contourfone_kwargs = Nighgone_kwargs )
Графическое решение областей классификатора.
Обратите внимание, что эта функция предполагает, что метки классов
помечены последовательно, например, 0, 1, 2, 3, 4 и 5. Если у вас есть класс
метки с целыми метками> 4, вы можете указать дополнительные цвета
и / или маркеры цветов и маркеры аргументов.См. Http://matplotlib.org/examples/color/ named_colors.html для получения дополнительной информации.
Информация.
Параметры
-
X: в виде массива, shape = [n_samples, n_features]Матрица признаков.
-
y: в виде массива, shape = [n_samples]Ярлыки истинного класса.
-
clf: Объект классификатора.Должен иметь метод .predict.
-
feature_index: как массив (по умолчанию: (0,) для 1D, (0, 1) в противном случае)Указатели объектов для использования при построении графиков.Первый индекс в
feature_indexбудет на оси x, второй индекс будет по оси ординат. -
filler_feature_values : dict (по умолчанию: нет)Требуется только для числовых функций> 2. Словарь функций пары индекс-значение для объектов, которые не отображаются.
-
filler_feature_ranges: dict (по умолчанию: нет)Требуется только для числовых функций> 2. Словарь функций пары индекс-значение для объектов, которые не отображаются.Будет использовать диапазоны, предоставленные для выбора обучающих выборок для построения графика.
-
ax: matplotlib.axes.Axes (по умолчанию: нет)Существующий matplotlib Axes. Создает один, если ax = None.
-
X_highlight: в виде массива, shape = [n_samples, n_features] (по умолчанию: None)Массив с точками данных, которые используются для выделения образцов в
X. -
res: float или array-like shape = (2,) (по умолчанию: None)Этот параметр использовался для определения ширины сетки, но он устарел в пользу определение количества точек по рисунку DPI и размеру автоматически для получения оптимальных результатов и эффективности вычислений.Для увеличения разрешения рекомендуется использовать для обеспечения аргумент
dpi через matplotlib, например,plt.figure (dpi = 600) `. -
zoom_factor: float (по умолчанию: 1.0)Управляет масштабом осей x и y графика принятия решений.
-
hide_spines: bool (по умолчанию: True)Скрыть шипы осей, если True.
-
легенда: int (по умолчанию: 1)Целое число, чтобы указать расположение легенды.oxv <> ‘)
Маркеры диаграммы рассеяния.
-
цветов: str (по умолчанию: ‘красный, синий, салатовый, серый, голубой’)Список цветов, разделенных запятыми.
-
scatter_kwargs: dict (по умолчанию: нет)Аргументы ключевого слова для базовой функции разброса matplotlib.
-
contourf_kwargs: dict (по умолчанию: нет)Аргументы ключевого слова для базовой функции contourf matplotlib.
-
scatter_highlight_kwargs: dict (по умолчанию: нет)Аргументы ключевого слова для базовой функции разброса matplotlib.
Возврат
-
ax: объект matplotlib.axes.Axes
Примеры
Примеры использования см. http://rasbt.github.io/mlxtend/user_guide/plotting/plot_decision_regions/
ython
PLOT
PLOTФункция PLOT рисует линейный график векторных аргументов.Если используется один параметр, векторный параметр откладывается по оси ординат в зависимости от номера точки на оси абсцисс. Чтобы построить один вектор как функцию другого, используйте два параметра.
Вместо данных вы также можете ввести уравнение X , используя входной аргумент или свойство EQUATION. В этом случае IDL автоматически сгенерирует независимые данные X и использует ваше уравнение для вычисления зависимых данных Y .
Пример
Следующие строки создают график, показанный выше.
теория = SIN (2.0 * FINDGEN (200) *! PI / 25.0) * EXP (-0.02 * FINDGEN (200))
p = СЮЖЕТ (теория, "r4D-", YTITLE = 'Resistance ($ \ Omega $)', $
TITLE = "Сопротивление цепи", DIM = [450,400], MARGIN = 0,2)
стр. SYM_INCREMENT = 5
p.SYM_COLOR = "синий"
с.SYM_FILLED = 1
стр. SYM_FILL_COLOR = 0
Дополнительные примеры
См. Дополнительные примеры использования функции PLOT в примерах графиков.
Синтаксис
графика = PLOT ( Y , [Формат] [, Ключевые слова = значение ] [, Свойства = значение ])
графика = ГРАФИК (X , Y , [Формат] [, Ключевые слова = значение ] [, Свойства = значение ])
графика = PLOT (Уравнение , [Формат] [, Ключевые слова = значение ] [, Свойства = значение ])
Ключевые слова
Ключевые слова применяются только во время первоначального создания графики.
AXIS_STYLE = значение
/ BUFFER, / CURRENT, / DEVICE, DIMENSIONS = [ width , height ], LAYOUT = array , LOCATION = [ x , y ], MARGIN = скаляр или [ слева , внизу , справа , вверху ], / NO_TOOLBAR, / NODATA, / OVERPLOT, / WIDGETS
Недвижимость
Свойства могут быть заданы как ключевые слова для функции во время создания, а также могут быть получены или изменены с помощью символа «.»обозначение после создания.
сглаживать, aspect_ratio, топоры, background_color, BACKGROUND_TRANSPARENCY, CLIP, COLOR, перекрестие, EQN_SAMPLES, EQN_USERDATA уравнение, FILL_BACKGROUND, FILL_COLOR, FILL_LEVEL, FILL_TRANSPARENCY, FONT_COLOR, font_name, FONT_SIZE, FONT_STYLE, ЗАКРЫТЬ, ГИСТОГРАММА, LineStyle, MAPGRID, MAPPROJECTION, MAP_PROJECTION , MAX_VALUE, MIN_VALUE, ФИО, должность, RGB_TABLE, STAIRSTEP, SYM_COLOR, SYM_FILLED, SYM_FILL_COLOR, SYM_INCREMENT, SYM_OBJECT, SYM_SIZE, SYM_THICK, SYM_TRANSPARENCY, ОБОЗНАЧЕНИЕ, ТОЛСТАЯ, НАЗВАНИЕ, ТРАНСПАРЕНТНОСТЬ, UVALUE, VERT_COLORS, оКНО, WINDOW_TITLE, XRANGE, YRange, Zvalue
Методы
Закрыть
ConvertCoord
CopyWindow
Удалить
Стереть
GenerateCode
GetData
GetValueAtLocation
Карта вперед
Карта обратная
Заказать
Печать
Обновить
Повернуть
Сохранить
Масштаб
Выбрать
SetData
Перевести
Возвращаемое значение
Функция PLOT возвращает ссылку на созданную графику.Используйте возвращенную ссылку, чтобы управлять графикой после создания, изменяя свойства или вызывая методы.
Аргументы
X
Вектор, представляющий значения абсцисс для построения графика. Если X не указан, Y строится как функция номера точки (начиная с нуля). Если указаны оба аргумента, Y отображается как функция от X .
Y
Данные по ординате для построения графика.
Формат
Строка, которая устанавливает свойства формата линии и символа с помощью коротких маркеров для представления значений цвета, символа, стиля линий и толщины. Например, чтобы создать график со сплошной красной линией толщиной 2, используя символ «+» для обозначения точек данных, вы должны использовать следующее:
p = УЧАСТОК (данные, '-r2 +')
Токены в строке формата представляют значения свойств LINESTYLE, COLOR, THICK и SYMBOL.Может присутствовать от одного до четырех жетонов, и жетоны могут быть в любом порядке. Токены чувствительны к регистру. Дополнительные сведения о синтаксисе аргумента Format см. В разделе Форматирование графических символов и линий IDL.
Уравнение
Если первым аргументом является строка, то предполагается, что он представляет либо уравнение X , либо имя функции IDL, которая принимает входной аргумент X . Установка этого аргумента аналогична установке свойства EQUATION.См. УРАВНЕНИЕ для деталей.
Ключевые слова
AXIS_STYLE
Задайте для этого ключевого слова одно из следующих значений:
- 0 — без осей. Уменьшите поля, чтобы изображение почти заполнило окно. Это значение по умолчанию для изображений.
- 1 — Отдельные оси X, Y (и Z, если 3D) расположены на минимальном значении данных. Поля будут скорректированы, чтобы оставить место для осей. Это значение по умолчанию для 3D-графики.
- 2 — Прямоугольные оси — несколько осей, расположенных как на минимальном, так и на максимальном значениях данных. Поля будут скорректированы, чтобы оставить место для осей. Это значение по умолчанию для 2D-графики.
- 3 — Оси в виде перекрестия — расположены в средней точке каждого измерения данных. Поскольку оси находятся посередине, уменьшите поля, чтобы изображение почти заполнило окно. Это значение по умолчанию для полярных графиков.
- 4 — Осей нет, но используются такие же поля, как если бы оси были.Это полезно, если вы хотите позже добавить еще один рисунок, у которого есть оси, и вы хотите, чтобы две визуализации были правильно выровнены.
На осях можно задать следующие свойства:
|
Объект |
Описание |
|
[XYZ] ЦВЕТ |
Строка или вектор RGB, содержащий цвет оси. |
|
[XYZ] СЕТКА |
Строка, целое число или вектор с двумя элементами, задающий стиль линий для отметок. |
|
[XYZ] LOG |
Установите в 1, если ось логарифмическая.Минимальное значение диапазона оси должно быть больше нуля. |
|
[XYZ] MAJOR |
Количество основных делений. Установите -1 для автоматического вычисления, установите 0 для подавления. |
|
[XYZ] MINOR |
Количество второстепенных делений.Установите -1 для автоматического вычисления, установите 0 для подавления. |
|
[XYZ] SUBGRIDSTYLE |
Строка, целое число или вектор из двух элементов, задающий стиль линий для второстепенных делений. По умолчанию для сплошных линий установлено значение 0. Установите значение -1, чтобы заставить второстепенные тики иметь тот же стиль линии, что и основные тики. |
|
[XYZ] SHOWTEXT |
Установите 1 для отображения текстовых меток или 0 для скрытия текстовых меток. |
|
[XYZ] СТИЛЬ |
Стиль диапазона оси. Допустимые значения: (0) Хорошая дальность. По умолчанию для всей графики, кроме изображения, штриховой диаграммы и карты. (1) Установить точный диапазон данных. По умолчанию для изображения, штриховой диаграммы и карты. (2) Разместите оси немного вне допустимого диапазона. (3) Сдвинуть оси немного за пределы точного диапазона данных. ДИАПАЗОН [XYZ] имеет приоритет над этим свойством. |
|
[XYZ] СУБТИКЛЕН |
Отношение длины второстепенного тика к длине основного тика.По умолчанию — 0,5. |
|
[XYZ] TEXT_COLOR |
Строка или вектор RGB, содержащий цвет текста оси. |
|
[XYZ] TEXT_ORIENTATION |
Угол (в градусах) меток меток. |
|
[XYZ] TEXTPOS |
Установите 1, чтобы разместить текст над осью. По умолчанию — 0, ниже оси. |
|
[XYZ] ТОЛЩ. |
Установите значение с плавающей запятой от 0 до 10, чтобы указать толщину линии для отметок.Толщина 0 дает тонкую линию роста волос. По умолчанию 1. |
|
[XYZ] TICKDIR |
Установите значение 1, чтобы отметки были обращены наружу. По умолчанию 0, обращено внутрь. |
|
[XYZ] TICKFONT_NAME |
Строка, содержащая имя шрифта для текста оси. |
|
[XYZ] TICKFONT_SIZE |
Размер текста по оси в пунктах. |
|
[XYZ] TICKFONT_STYLE |
Строка или целое число, содержащее стиль шрифта: обычный (0), полужирный (1), курсив (2) или полужирный курсив (3). |
|
[XYZ] TICKFORMAT |
Строка или массив строк форматов меток. См. Коды форматов для получения дополнительной информации. |
|
[XYZ] TICKINTERVAL |
Интервал между основными делениями. |
|
[XYZ] TICKLAYOUT |
Установите в 1 для подавления отметок; установите значение 2, чтобы нарисовать рамку вокруг меток. |
|
[XYZ] TICKLEN |
Длина каждой основной отметки, нормализованная по ширине или высоте рисунка.Значение по умолчанию рассчитывается автоматически на основе соотношения сторон изображения. |
|
[XYZ] ИМЯ |
Строковый массив, содержащий метки галочки. |
|
[XYZ] БИЛЕТЫ |
Строка, указывающая единицы измерения тиков.Допустимые значения: null (значение по умолчанию, обозначается пустыми кавычками), годы, месяцы, дни, часы, минуты, секунды, время, экспонента для экспоненциальной записи или научная для экспоненциальной записи. Если используются какие-либо единицы времени, то значения деления интерпретируются как значения даты / времени по юлианскому календарю. Если предусмотрено несколько единиц, ось будет нарисована с несколькими уровнями. |
|
[XYZ] TICKVALUES |
Массив местоположений отметок. |
|
[XYZ] НАЗВАНИЕ |
Строка, дающая заголовок оси. |
|
[XYZ] ПРОЗРАЧНОСТЬ |
Целое число от 0 до 100, дающее процент прозрачности. |
Для более подробного объяснения этих свойств см. Функцию AXIS.
Совет: Вы также можете использовать функцию AXIS для вставки дополнительных осей после создания графики.
БУФЕР
Установите для этого ключевого слова значение 1, чтобы направить графику в буфер вне экрана вместо создания окна.
ТОК
Установите это ключевое слово, чтобы создать графику в текущем окне с новым набором осей.Если окна не существует, создается новое окно. Метод SetCurrent в WINDOW может использоваться для установки текущего окна.
Или установите это ключевое слово для существующей ссылки на графику IDL, чтобы сделать это окно текущим окном и направить новую графику в это окно.
Совет: Ключевое слово CURRENT обычно используется с ключевым словом LAYOUT или свойством POSITION для создания окна, которое имеет несколько изображений в разных местах.
Совет: Для графического изображения с теми же осями , что и существующий графический объект, используйте вместо этого ключевое слово OVERPLOT.
УСТРОЙСТВО
Задайте это ключевое слово, если значения указаны в координатах устройства (в пикселях) для ключевых слов MARGIN и POSITION. (Для этих ключевых слов по умолчанию используются нормализованные координаты.)
РАЗМЕРЫ
Задайте для этого ключевого слова двухэлементный вектор формы [ ширина , высота ], чтобы указать размеры окна в пикселях. Если вы не укажете значение для DIMENSIONS, IDL по умолчанию использует значения предпочтений IDL_GR_WIN_HEIGHT и IDL_GR_WIN_WIDTH для платформ Windows или предпочтений IDL_GR_X_HEIGHT и IDL_GR_X_WIDTH для систем X Windows в UNIX.
Совет: Минимальная ширина устанавливается панелью инструментов в окне, обычно около 400 пикселей. Чтобы создать графическое окно меньшего размера, используйте ключевое слово NO_TOOLBAR.
ПЛАН
Задайте для этого ключевого слова трехэлементный вектор [ ncol , nrow , index ], который упорядочивает графику в сетке. Первое измерение ncol — это количество столбцов в сетке, nrow — количество строк, а , индекс — это позиция сетки, в которой нужно разместить графику (начиная с элемента 1).Это ключевое слово игнорируется, если указано OVERPLOT или POSITION.
МЕСТО
Задайте для этого ключевого слова двухэлементный вектор [ X смещение , Y смещение ], задающий смещение экрана окна в пикселях.
МАРЖА
Задайте для этого ключевого слова значения полей текущего изображения в макете, заданном свойством LAYOUT. Используйте скалярное значение, чтобы установить одинаковые поля со всех сторон, или используйте вектор из четырех элементов [ слева , снизу , справа , сверху ], чтобы указать разные поля с каждой стороны.
По умолчанию значения маржи выражаются в нормализованных единицах от 0,0 до 0,5. Если задано ключевое слово DEVICE, значения даются в единицах устройства (пикселях).
Это ключевое слово игнорируется, если указано OVERPLOT или POSITION.
NO_TOOLBAR
По умолчанию в графическом окне есть панель инструментов, содержащая некоторые общие инструменты, такие как «Печать» и «Сохранить». Задайте это ключевое слово, чтобы удалить панель инструментов. Это ключевое слово не действует, если окно уже создано.
Совет: Когда панель инструментов существует, минимальная ширина окна устанавливается равной ширине панели инструментов, обычно около 400 пикселей. Чтобы создать графическое окно меньшего размера, используйте ключевое слово NO_TOOLBAR.
NODATA
Установите для этого ключевого слова значение 1, чтобы создать графику, но без прикрепленных к нему данных. Оси и заголовок (если есть) также создаются и отображаются. Если указано ключевое слово OVERPLOT, диапазоны осей не изменятся.
Примечание: Вы все равно должны предоставить допустимые входные аргументы. Диапазон данных входных аргументов используется для автоматической установки диапазона осей. Свойства [XYZ] RANGE могут использоваться для переопределения этих диапазонов по умолчанию.
ПЕРЕГРУЗКА
Задайте для этого ключевого слова значение 1 (один), чтобы поместить изображение поверх текущего выбранного изображения в текущем окне. Тогда два графических элемента будут иметь один и тот же набор осей. Если текущего окна не существует, то это ключевое слово игнорируется и создается новое окно.
Если у вас есть рисунок в другом окне, которое в данный момент не выбрано, вы также можете установить это ключевое слово для ссылки на этот рисунок для наложения поверх этого рисунка.
Совет: Чтобы в графике имелся новый набор осей , используйте вместо этого ключевое слово CURRENT.
ВИДЖЕТЫ
По умолчанию при запуске из IDL Workbench графическое окно будет использовать собственные виджеты для вашей платформы.Установите это ключевое слово, чтобы вместо этого использовать виджеты IDL для графического окна. Это ключевое слово игнорируется при запуске из командной строки IDL, поскольку в этом случае всегда используются виджеты IDL.
Недвижимость
ANTIALIAS
По умолчанию при рисовании линий используется сглаживание. Установите для этого свойства значение 0, чтобы отключить сглаживание.
ASPECT_RATIO
Значение с плавающей запятой, указывающее отношение измерения Y к измерению X в единицах данных.Если для этого свойства установлено ненулевое значение, соотношение сторон будет сохранено при растяжении или сжатии графики. Значение по умолчанию — 0 для всей графики, кроме изображений, что означает, что соотношение сторон не фиксировано, но может изменяться при растяжении или сжатии графики.
AXES (только получить)
Это свойство извлекает массив, содержащий все объекты AXIS в визуализации. Например, для визуализации сюжета:
p = УЧАСТОК (/ ТЕСТ)
топор = стр.ТОПОРЫ
ax [0] .TITLE = 'Ось X'
ax [1] .TITLE = 'Ось Y'
ax [2] .HIDE = 1
ax [3] .HIDE = 1
См. AXIS для списка доступных свойств.
BACKGROUND_COLOR
Установите для этого свойства строку или вектор RGB, указывающий цвет фона изображения. Значение по умолчанию — [255, 255, 255] (белый). Установите для этого свойства скалярное значение, чтобы удалить цвет фона.
Совет: Чтобы установить цвет фона всего окна, извлеките объект окна с помощью свойства WINDOW и установите BACKGROUND_COLOR для объекта окна.
BACKGROUND_TRANSPARENCY
Задайте для этого свойства целое число от 0 до 100, задающее процентную прозрачность цвета фона. По умолчанию — 100 (полностью прозрачный).
Примечание: Если свойство BACKGROUND_COLOR изменено, и текущая прозрачность фона равна 100, то BACKGROUND_TRANSPARENCY будет автоматически установлен на 0 (непрозрачный), чтобы вы могли видеть новый цвет.
ЗАЖИМ
Установите для этого свойства значение 1, чтобы вырезать части графики, лежащие за пределами диапазона пространства данных, или значение 0, чтобы отключить обрезку. По умолчанию 1.
ЦВЕТ
Задайте для этого свойства строку или вектор RGB, который определяет цвет линии графика.
Примечание: Когда вы извлекаете свойство COLOR, возвращаемое значение всегда будет трехэлементным вектором RGB, независимо от того, как цвет был изначально указан.
ПЕРЕКРЕСТОК (Get Only)
Используйте это свойство, чтобы получить ссылку на изображение перекрестия. Все графические объекты в одном и том же наборе осей имеют одно изображение перекрестия. Для графики Plot по умолчанию отображается перекрестие при получении события Mouse_Down. Для другой графики перекрестие отключено. Свойство STYLE можно использовать для автоматического рисования перекрестия, а свойство LOCATION можно использовать для рисования перекрестия вручную.
Вы можете получить и установить следующие свойства полученного прицела:
|
Объект |
Описание |
|
АНТИАЛИАС |
Установите в 1, чтобы включить сглаживание линий. |
| ЦВЕТ |
Строка или вектор RGB, содержащий цвет. |
| СКРЫТЬ |
Установите 1, чтобы скрыть перекрестие, и 0, чтобы показать. |
|
ИНТЕРПОЛЯЦИЯ |
Установите в 1, чтобы принудительно выполнить интерполяцию между точками данных графика, когда активен протокол SNAP. Для другой графики это свойство игнорируется. По умолчанию — 0. |
|
СТИЛЬ ЛИНИИ |
Целое число или строка, задающая стиль линии.По умолчанию — точка. Дополнительные параметры см. В разделе «Значения стиля линии». |
|
МЕСТО |
Место для рисования прицела. Для графической графики, если включен протокол SNAP, необходимо указать только координату X. В противном случае LOCATION следует установить на двухэлементный вектор [X, Y] для двумерной графики или [X, Y, Z] для трехмерной графики.Если СТИЛЬ в настоящее время «Нет», то установка МЕСТОПОЛОЖЕНИЯ автоматически устанавливает СТИЛЬ на «Ручной». |
| НАИМЕНОВАНИЕ |
Имя изображения. |
| SNAP |
Установите на 1, чтобы привязать перекрестие к ближайшей точке данных графика.Для другой графики это свойство игнорируется. По умолчанию 1. |
| СТИЛЬ |
Целое число или строка, задающая стиль прицела. Возможные значения: |
|
ТОЛЩИНА |
Толщина линий. По умолчанию 1. |
|
ПРОЗРАЧНОСТЬ |
Процент прозрачности линий.По умолчанию — 50. |
| UVALUE |
IDL-переменная любого типа данных. |
Например, используйте свойство CROSSHAIR, чтобы нарисовать перекрестие на изображении:
im = ИЗОБРАЖЕНИЕ (/ ТЕСТ, ПРОЗРАЧНОСТЬ = 50, AXIS_STYLE = 2)
c = им.ПЕРЕКРЕСТОК
c.COLOR = 'красный'
c. ТОЛЩИНА = 2
c.LOCATION = [300, 200]
См. Создание функций для управления событиями мыши для более подробного примера перекрестия.
EQN_SAMPLES
Задайте для этого свойства целое число, дающее количество выборок для использования со свойством EQUATION. Более высокое значение даст более плавный график, но будет медленнее вычисляться. По умолчанию 1000 баллов.Это свойство не действует, если не задано EQUATION.
EQN_USERDATA
Задайте для этого свойства выражение, содержащее данные любого типа. Если EQUATION установлено для функции, а EQN_USERDATA установлено, тогда значение EQN_USERDATA будет передано в качестве второго аргумента функции. Если EQUATION не задано или если EQUATION установлено в выражение X , то это свойство не будет иметь никакого эффекта.
УРАВНЕНИЕ
Задайте для этого свойства строку, содержащую уравнение.Уравнение может быть либо допустимым оператором IDL с переменной с именем « x », либо именем функции, которая принимает единственный аргумент, X . Обратите внимание, что ваш оператор (или функция) IDL должен иметь возможность обрабатывать массив значений X. Другими словами, все значения X передаются в векторе сразу, а не по отдельности. Результатом вычисления уравнения с X должен быть еще один одномерный массив, содержащий данные для построения графика.
- При отображении графика IDL автоматически построит одномерный массив X , охватывающий текущий диапазон осей.
- Начальный диапазон [-10, 10].
- Если EQUATION является выражением, то IDL вызывает функцию EXECUTE один раз с массивом X. Обратите внимание, что при определенных обстоятельствах (таких как виртуальная машина IDL) вы не сможете использовать функцию EXECUTE.
- Если EQUATION — это имя функции, то IDL запускает CALL_FUNCTION один раз с массивом X в качестве входного аргумента. Функция должна возвращать одномерный массив результатов.
- После того, как уравнение оценено, IDL проверяет результат для любых значений NaN, и диапазон X обрезается, чтобы покрыть только допустимую область.
- Уравнение должно быть «одиночным» оператором IDL (знак «&» использовать нельзя). Если вам нужно несколько операторов, вы должны создать функцию, которая принимает один аргумент, X , и поместить весь ваш код в функцию.
- Если вы измените диапазон оси X (либо с помощью мыши для панорамирования, либо с помощью свойства XRANGE), то будет создан новый набор значений X , и IDL снова вызовет ваше уравнение с новыми значениями.
- Вы можете использовать EQN_SAMPLES для управления количеством точек выборки.
- Вы можете использовать EQN_USERDATA для передачи пользовательских данных в вашу функцию.
Пример свойства EQUATION с выражением
Следующий код создаст график с заданным уравнением:
p = PLOT ('SMOOTH (sin (1 / x), 9)', XRANGE = [0,01,0,2], $
/ FILL_BACKGROUND, FILL_LEVEL = 0)
Пример свойства EQUATION с функцией
Чтобы использовать свойство EQUATION с функцией, сначала создайте функцию и сохраните ее в файл с именем ex_plotequation.pro где-то на текущем пути IDL:
FUNCTION ex_plotequation, x
данные = ГЛАДКАЯ (sin (1 / x), 9)
ВОЗВРАТ, данные
КОНЕЦ
Затем запустите следующий код, чтобы использовать уравнение:
p = PLOT ('ex_plotequation', XRANGE = [0,01,0,2], долларов США
/ FILL_BACKGROUND, FILL_LEVEL = 0)
Более подробный пример см. В разделе «Динамические визуализации».
FILL_BACKGROUND
Значение 1 заполняет область под графиком.
FILL_COLOR
Задайте для этого свойства строку или вектор RGB, который определяет цвет залитой области. Значение по умолчанию — [128,128,128] (серый). Это свойство игнорируется, если FILL_BACKGROUND не задано.
FILL_LEVEL
Значение с плавающей запятой, определяющее значение Y для границы области заливки.Это свойство игнорируется, если FILL_BACKGROUND не задано.
FILL_TRANSPARENCY
Целое число от 0 до 100, указывающее процент прозрачности фоновой заливки. Это свойство игнорируется, если FILL_BACKGROUND не задано.
FONT_COLOR
Задайте для этого свойства строку или вектор RGB, который определяет цвет текста заголовка и осей (если они есть). Значение по умолчанию — «черный».
FONT_NAME
Установите это свойство равным строке, определяющей IDL или системный шрифт для заголовка и осей (если есть).Значение по умолчанию — «DejaVuSans».
FONT_SIZE
Установите это свойство равным целому числу, определяющему размер шрифта для заголовка и осей (если они есть). Значение по умолчанию — 9 пунктов для текста оси и 11 пунктов для заголовка.
FONT_STYLE
Задайте для этого свойства целое число или строку, определяющую стиль шрифта для заголовка и осей (если они есть). Допустимые значения:
|
Целое |
Строка |
Результирующий стиль |
|
0 |
«Нормальный» или «рм» |
По умолчанию (римская буква) |
| 1 |
«Полужирный» или «bf» |
Полужирный |
| 2 |
«Курсив» или «оно» |
курсив |
| 3 |
«Полужирный курсив» или «bi» |
Полужирный курсив |
СКРЫТЬ
Установите для этого свойства значение 1, чтобы скрыть графику.Установите HIDE на 0, чтобы показать графику.
ГИСТОГРАММА
Установите для этого свойства значение 1, чтобы соединить каждую точку горизонтальными и вертикальными линиями. Горизонтальные линии начинаются в положении X каждой точки и продолжаются до следующего положения X. Это свойство полезно для отображения информации с дискретными или нелинейными данными, где значения X обычно не являются целочисленными ячейками, а значения Y представляют собой «количество» значений в каждой ячейке. См. Свойство STAIRSTEP для полос по центру.
Совет: Вы также можете использовать функцию ГРАФИК, чтобы создать график с вертикальными или горизонтальными полосами.
СТИЛЬ ЛИНИИ
Задайте для этого свойства целое число или строку, задающую стиль линии для графика.
В следующей таблице перечислены значения индекса, строки и символы, которые можно использовать со свойством LINESTYLE, а также эквивалентные символы и строки, которые можно использовать в строковом аргументе формата .
| Индекс |
ЛИНЕЙНЫЙ СТИЛЬ Недвижимость |
Аргумент формата |
Описание |
|
0 |
‘solid_line’, ‘-‘ (тире) |
‘-‘ (тире) |
сплошная линия |
| 1 |
‘точка’, ‘:’ (двоеточие) |
‘:’ (двоеточие) |
с точками |
| 2 |
‘тире’, ‘-‘ (двойные тире) |
‘-‘ (двойные тире) |
штриховые |
| 3 |
‘dash_dot’, ‘-.’ |
‘-.’ |
тире точка |
| 4 |
‘dash_dot_dot_dot’, ‘-:’ |
‘-:’ |
тире точка точка точка |
| 5 |
‘long_dash’, ‘__’ (два символа подчеркивания) |
‘__’ (двойное подчеркивание) |
длинная черта |
| 6 |
‘none’, » (пробел) |
» (космос) |
без строки |
Примечание: Если вы используете значение LINESTYLE или Format , строка ‘-.’, стиль линий установлен на пунктир, а символ графика не установлен.
Примечание: Вы также можете установить СТИЛЬ ЛИНИИ на двухэлементный вектор [ повтор , битовая маска ], указав образец штриховки. Повторение указывает, сколько раз следует повторить отдельные биты в битовой маске . (То есть, если три последовательных 0 появляются в битовой маске и значение repeat равно 2, то у нарисованной линии шесть последовательных битов будут отключены.) Значение повторения должно быть целым числом от 1 до 255. Битовая маска указывает, какие пиксели отрисовываются, а какие нет по длине линии. Битовая маска должна быть указана как 16-битное шестнадцатеричное значение. Например, LINESTYLE = [2, ‘F0F0’X] описывает пунктирную линию (8 бит включены, 8 бит отключены, 8 бит включены, 8 бит отключены).
MAPGRID (только получить)
Если в настоящее время действует картографическая проекция, это свойство извлекает ссылку на объект MAPGRID.
MAPPROJECTION (Get Only)
Если в настоящий момент действует картографическая проекция, это свойство извлекает ссылку на объект MAPPROJECTION.
КАРТА_ПРОЕКТ
Строка, дающая имя текущей картографической проекции. После создания используйте это свойство, чтобы получить или установить текущую проекцию карты.
MAX_VALUE
Максимальное значение для построения графика. Если это свойство установлено, значения данных, превышающие значение MAX_VALUE, обрабатываются как отсутствующие данные и не отображаются.
Примечание: Значение с плавающей запятой IEEE NaN также обрабатывается как отсутствующие данные.
MIN_VALUE
Минимальное значение для построения графика. Если это свойство установлено, значения данных меньше, чем значение MIN_VALUE, обрабатываются как отсутствующие данные и не отображаются.
Примечание: Значение с плавающей запятой IEEE NaN также рассматривается как отсутствующие данные.
НАЗВАНИЕ
Строка, определяющая имя изображения.Имя можно использовать для извлечения изображения с использованием обозначения массива скобок. Если NAME не задано, то имя по умолчанию выбирается в зависимости от типа графики.
ПОЛОЖЕНИЕ
Установите для этого свойства четырехэлементный вектор, который определяет положение графики в окне. Координаты [X 1 , Y 1 , X 2 , Y 2 ] определяют нижний левый и верхний правый углы изображения. Координаты выражаются в нормированных единицах от 0.От 0 до 1.0. При создании, если задано ключевое слово DEVICE, единицы измерения даются в единицах устройства (пикселях).
Примечание: После создания вы можете установить POSITION на двух- или четырехэлементный вектор. Если предусмотрено два элемента, центр изображения будет перемещен в это положение. Если предоставлено четыре элемента, графика будет переведена и масштабирована в соответствии с положением.
RGB_TABLE
Номер предопределенной таблицы цветов IDL или массива размером 3 x 256 или 256 x 3 байта, содержащего значения цвета, используемые для цветов вершин.Если предоставленные значения не относятся к байтовому типу, они масштабируются до байтового диапазона с помощью BYTSCL. Используйте свойство VERT_COLORS, чтобы указать индексы, которые выбирают цвета из значений, указанных с помощью RGB_TABLE.
ЛЕСТНИЦА
Установите для этого свойства значение 1, чтобы соединить каждую точку горизонтальными и вертикальными линиями. Горизонтальные линии центрируются в каждой точке X. Это свойство полезно для отображения информации с дискретными или нелинейными данными, где значения X обычно являются целыми числами, а значения Y представляют собой «счетчик» в этом местоположении X.См. Свойство HISTOGRAM для полосок, охватывающих значения X.
Совет: Вы также можете использовать функцию ГРАФИК, чтобы создать график с вертикальными или горизонтальными полосами.
SYM_COLOR
Задайте для этого свойства строку или вектор RGB, который определяет цвет символа графика. Если это свойство не установлено, цвет символа будет соответствовать ЦВЕТУ.
SYM_FILLED
Установите для этого свойства значение 1, чтобы заполнить символы.
SYM_FILL_COLOR
Задайте для этого свойства строку или вектор RGB, который определяет цвет заполненной части символа. Если это свойство не установлено, цвет заливки символа будет соответствовать SYM_COLOR.
SYM_INCREMENT
Установите для этого свойства целочисленное значение, определяющее количество вершин графика между символами. Значение по умолчанию — 1, что означает размещение символа на каждой вершине.
SYM_OBJECT
Установите это свойство равным ссылке на объект, которая будет использоваться для графического символа.SYM_OBJECT может быть объектом IDLgrModel или атомарным графическим объектом.
Примечание: При использовании пользовательских графических символов обратите внимание, что свойство SYM_OBJECT имеет приоритет над свойством SYMBOL. Другими словами, если вы устанавливаете пользовательский символ с помощью SYM_OBJECT, а затем пытаетесь изменить этот символ с помощью свойства SYMBOL, IDL игнорирует новое свойство SYMBOL и сохраняет SYM_OBJECT.
SYM_SIZE
Значение с плавающей запятой, определяющее размер графического символа.Значение 1.0 создает символ, который составляет 10% ширины / высоты графика.
SYM_THICK
Значение с плавающей запятой от 1,0 до 10,0, определяющее толщину (в точках) графического символа.
SYM_TRANSPARENCY
Целое число от 0 до 100, указывающее процент прозрачности символов. Значение по умолчанию — 0.
СИМВОЛ
Строка, дающая имя символа.Допустимые значения:
|
«Нет» (по умолчанию) «Плюс» или «+» «Звездочка» или «*» «Точка» или «точка» «Бриллиант» или «Д» «Треугольник» или «ту» «Квадрат» или «з» «X» «Greater_than» или «>» |
«Less_than» или «<" «Треугольник вниз» или «тд» «Треугольник влево» или «tl» «Triangle_right» или «tr» «Три_уп» или «Ту» «Три_даун» или «Тд» «Три-лево» или «Тл» «Три_райт» или «Тр»
|
«Тонкий_алмаз» или «d» «Пентагон» или «П» «Hexagon_1» или «h» «Hexagon_2» или «H» «Vline» или «|» «Hline» или «_» «Звезда» или «S» «Круг» или «о»
|
Обратите внимание, что все имена графических символов чувствительны к регистру.
Примечание: При использовании пользовательских графических символов обратите внимание, что свойство SYM_OBJECT имеет приоритет над свойством SYMBOL. Другими словами, если вы устанавливаете пользовательский символ с помощью SYM_OBJECT, а затем пытаетесь изменить этот символ с помощью свойства SYMBOL, IDL игнорирует новое свойство SYMBOL и сохраняет SYM_OBJECT.
ТОЛЩИНА
Установите для этого свойства значение от 0 до 10, которое определяет толщину линии графика. При толщине 0 на выбранном устройстве отображается тонкая линия роста волос.Значение по умолчанию — 1.
НАЗВАНИЕ
Установите для этого свойства строку, определяющую заголовок. Свойства заголовка можно изменить с помощью FONT_COLOR, FONT_NAME, FONT_SIZE и FONT_STYLE. После создания свойство TITLE можно использовать для извлечения ссылки на текстовый объект заголовка, а свойства TEXT можно использовать для изменения объекта заголовка. Например:
p = PLOT ([0,1], TITLE = 'My Title')
p.title.font_size = 16
Вы можете добавлять греческие буквы и математические символы, используя синтаксис типа TeX, заключенный в пару символов «$».Подробнее см. Добавление математических символов и греческих букв в текстовую строку.
ПРОЗРАЧНОСТЬ
Целое число от 0 до 100, указывающее процент прозрачности линии графика. Значение по умолчанию — 0.
UVALUE
Установите это свойство для переменной IDL любого типа данных.
VERT_COLORS
Вектор индексов в таблице цветов для цвета каждой вершины (точка данных графика).В качестве альтернативы, массив байтов 3 x N , содержащий значения цвета вершины. Если предоставленные значения не относятся к байтовому типу, они масштабируются до байтового диапазона с помощью BYTSCL. Если указаны индексы, но не предоставлены цвета со свойством RGB_TABLE, используется шкала градаций серого по умолчанию. Если предоставляется массив цветов 3 x N , цвета используются напрямую, а значения цвета, предоставленные с помощью RGB_TABLE, игнорируются. Если указанное количество индексов или цветов меньше количества вершин, цвета повторяются циклически.
Примечание. VERT_COLORS может быть массивом триплетов RGB или цветов RGBA.
ОКНО (только Get)
Это свойство извлекает ссылку на объект WINDOW, который содержит графику.
WINDOW_TITLE
Установите это свойство в заголовок окна IDL Graphic. Заголовок отображается в строке заголовка окна.
XRANGE
Двухэлементный вектор, задающий диапазон данных X для построения.По умолчанию отображается весь диапазон данных.
YRANGE
Двухэлементный вектор, задающий диапазон данных Y для построения графика. По умолчанию отображается весь диапазон данных.
ZVALUE
Скалярное значение, которое будет использоваться в качестве координаты z для всего графика. По умолчанию в качестве z-координаты используется 0,0.
История версий
| 8.0 |
Представлен |
| 8,1 |
Добавлены следующие свойства: CROSSHAIR, MAPPROJECTION, MAP_PROJECTION, MAPGRID, UVALUE, WINDOW, [XYZ] SHOWTEXT, [XYZ] STYLE .Свойство THICK было изменено, чтобы принимать значение от 0 до 10 Добавлены следующие методы: Delete, GetData, GetValueAtLocation, MapForward, MapInverse, SetData |
| 8.2 |
Добавлены свойства AXES, BACKGROUND_COLOR, BACKGROUND_TRANSPARENCY, CLIP |
| 8.2.1 |
[XYZ] TICKUNITS принимает показатель степени в качестве значения, добавлено свойство ANTIALIAS, добавлено свойство HISTOGRAM. |
| 8.2,2 |
Измените POSITION с ключевого слова на свойство. Изменено свойство HISTOGRAM, чтобы оно начиналось с каждого значения X, а не с центра каждого значения X. Добавлено свойство STAIRSTEP, чтобы центрировать ячейки по каждому значению X. |
| 8.2.3 |
Добавлена возможность использовать образец пунктирной линии для СТИЛЯ ЛИНИИ. |
| 8,3 |
Добавлен аргумент Equation и свойства EQUATION, EQN_SAMPLES и EQN_USERDATA. |
| 8,6 | Изменены имя и размер шрифта по умолчанию. |
См. Также
! ЦВЕТ, БАРПЛОТ, ERRORPLOT, Форматирование графических символов и линий IDL, ЛЕГЕНДА, PLOT3D, ПОЛЯРПЛОТ, Использование графики IDL
Quick-R: объединение графиков
R позволяет легко объединить несколько графиков в один общий график, используя функцию
par () или layout () .
С помощью функции par () вы можете включить опцию mfrow = c ( nrows , ncols ) для создания матрицы из nrows x ncols графиков, которые заполняются построчно. mfcol = c ( nrows , ncols ) заполняет матрицу по столбцам.
# 4 фигуры, расположенные в 2 строки и 2 столбца
прикрепить (mtcars)
par (mfrow = c (2,2))
plot (wt, mpg, main = "Scatterplot of wt vs.mpg ")
plot (wt, disp, main =" Диаграмма рассеяния wt vs disp ")
hist (wt, main =" Гистограмма wt ")
boxplot (wt, main =" Boxplot of wt ")
нажмите для просмотра
# 3 фигуры, расположенные в 3 ряда и 1 столбец
прикрепить (mtcars)
номинал (mfrow = c (3,1))
hist (wt)
hist (миль на галлон)
hist (disp)
нажмите для просмотра
Макет (), функция имеет вид layout ( mat ) , где
mat — матричный объект, определяющий расположение N фигур для построения.
# Одна фигура в строке 1 и две фигуры в строке 2
attach (mtcars)
layout (matrix (c (1,1,2,3), 2, 2, byrow = TRUE))
hist (wt)
гист (миль на галлон)
гист (дисп)
нажмите для просмотра
Дополнительно вы можете включить параметры widths = и heights = в функцию layout () для более точного управления размером каждой фигуры. Эти параметры имеют вид
widths = вектор значений ширины столбцов
heights = вектор значений высоты строк.
Относительная ширина указывается числовыми значениями. Абсолютная ширина (в сантиметрах) указывается с помощью функции lcm () .
# Одна цифра в строке 1 и две цифры в строке 2
# строка 1 составляет 1/3 высоты строки 2
# столбец 2 составляет 1/4 ширины столбца 1
прикрепить (mtcars)
макет (матрица (c (1,1,2,3), 2, 2, byrow = TRUE),
widths = c (3,1), heights = c (1,2))
hist (wt)
hist (миль на галлон)
hist (disp)
нажмите для просмотра
Подробнее см. Справку (макет) .
Создание расстановки фигур с точным управлением
В следующем примере к диаграмме рассеяния добавляются две ящичные диаграммы, чтобы создать расширенный график.
# Добавить коробчатые диаграммы к диаграмме рассеяния
par (fig = c (0,0.8,0,0.8), new = TRUE)
plot (mtcars $ wt, mtcars $ mpg, xlab = "Car Weight",
ylab = " Миль на галлон ")
номинальной стоимости (fig = c (0,0.8,0.55,1), новое = TRUE)
boxplot (mtcars $ wt, horizontal = TRUE, axes = FALSE)
par (fig = c (0.65,1) , 0,0.8), new = TRUE)
boxplot (mtcars $ mpg, axes = FALSE)
mtext ("Enhanced Scatterplot", side = 3, outer = TRUE, line = -3)
нажмите для просмотра
Чтобы понять этот график, представьте, что вся область графика идет от (0,0) в нижнем левом углу до (1,1) в правом верхнем углу.Формат параметра fig = представляет собой числовой вектор вида c (x1, x2, y1, y2). Первый fig = устанавливает диаграмму рассеяния от 0 до 0,8 по оси x и от 0 до 0,8 по оси y. Верхний прямоугольный график изменяется от 0 до 0,8 по оси x и от 0,55 до 1 по оси y. Я выбрал 0,55, а не 0,8, чтобы верхнее число было приближено к диаграмме рассеяния. График справа изменяется от 0,65 до 1 по оси x и от 0 до 0,8 по оси y. Опять же, я выбрал значение, чтобы приблизить правую коробчатую диаграмму к диаграмме рассеяния.Вы должны поэкспериментировать, чтобы понять это правильно.
fig = запускает новый график, поэтому для добавления к существующему используйте new = TRUE .
Вы можете использовать это, чтобы объединить несколько графиков в любом порядке в один график.
к практике
Попробуйте бесплатную первую главу этого интерактивного курса визуализации данных, в которой рассматривается комбинирование графиков.
.
