Что такое поверхностный эффект в проводниках. Как он проявляется при протекании переменного тока. Какие факторы влияют на глубину проникновения тока. Как учитывать поверхностный эффект на практике. Способы снижения негативного влияния поверхностного эффекта.
Сущность поверхностного эффекта в проводниках
Поверхностный эффект (скин-эффект) — это явление вытеснения переменного электрического тока к поверхности проводника. При этом плотность тока максимальна у поверхности и экспоненциально уменьшается по мере углубления внутрь проводника.
Основные особенности поверхностного эффекта:
- Возникает только при протекании переменного тока
- Приводит к неравномерному распределению тока по сечению проводника
- Вызывает увеличение активного сопротивления проводника
- Усиливается с ростом частоты переменного тока
Причины возникновения поверхностного эффекта
Поверхностный эффект обусловлен следующими физическими процессами:
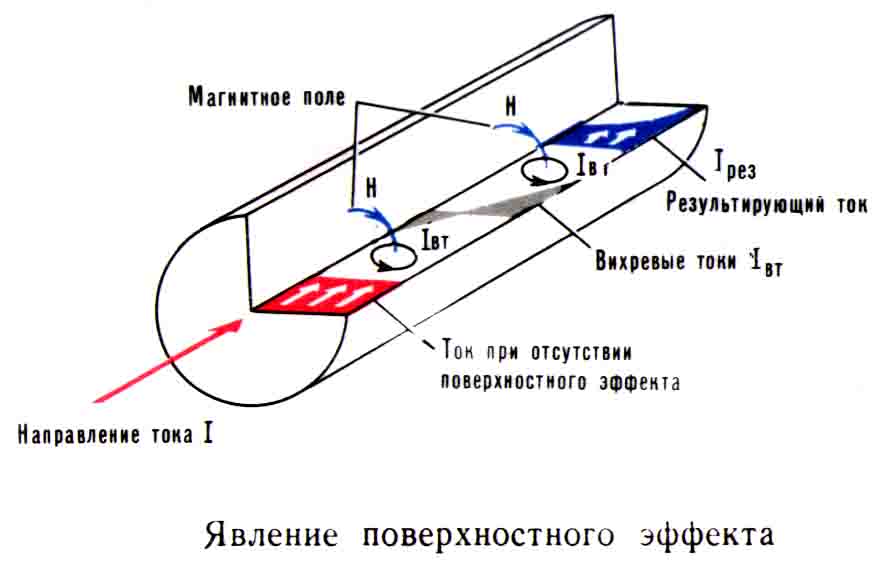
- Переменный ток, протекающий по проводнику, создает переменное магнитное поле вокруг и внутри проводника.
- Изменяющееся магнитное поле индуцирует вихревые токи внутри проводника.
- Вихревые токи создают собственное магнитное поле, препятствующее изменению основного тока.
- В результате ток вытесняется к поверхности проводника.
Какие факторы усиливают поверхностный эффект? Основное влияние оказывают:
- Увеличение частоты переменного тока
- Повышение магнитной проницаемости материала проводника
- Увеличение электропроводности материала
- Рост поперечных размеров проводника
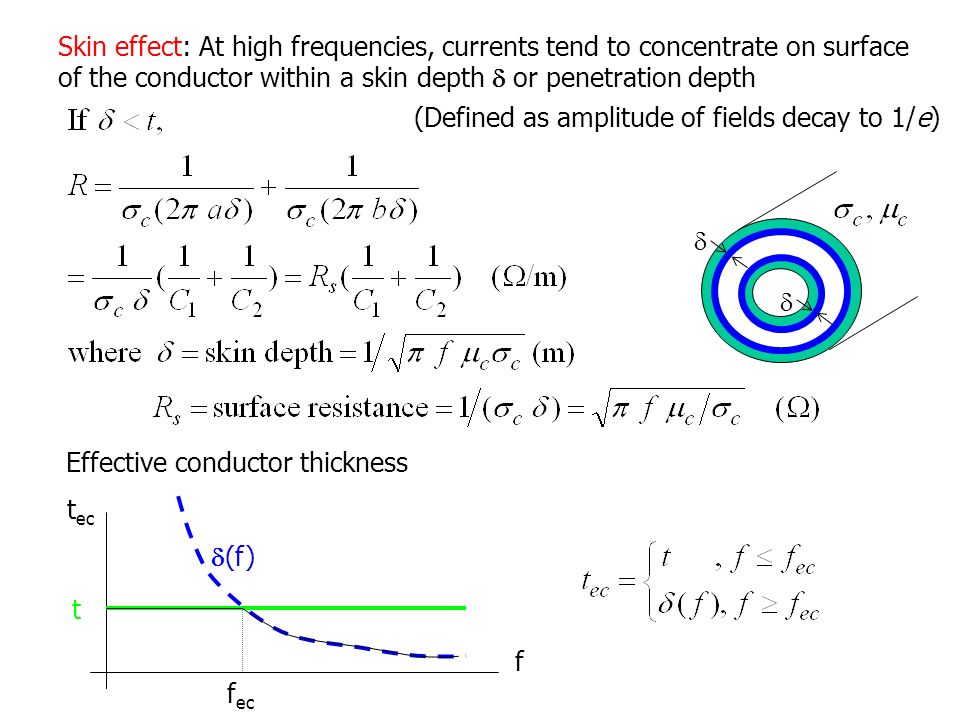
Глубина проникновения тока при поверхностном эффекте
Важной характеристикой поверхностного эффекта является глубина проникновения тока δ. Она показывает, на какой глубине плотность тока уменьшается в e раз (примерно до 37%) по сравнению с поверхностью.
Глубина проникновения определяется по формуле:
δ = √(2ρ / ωμ)
Где:
- ρ — удельное электрическое сопротивление проводника
- ω — угловая частота тока
- μ — абсолютная магнитная проницаемость материала проводника
Из формулы видно, что глубина проникновения уменьшается с ростом частоты, магнитной проницаемости и проводимости материала.
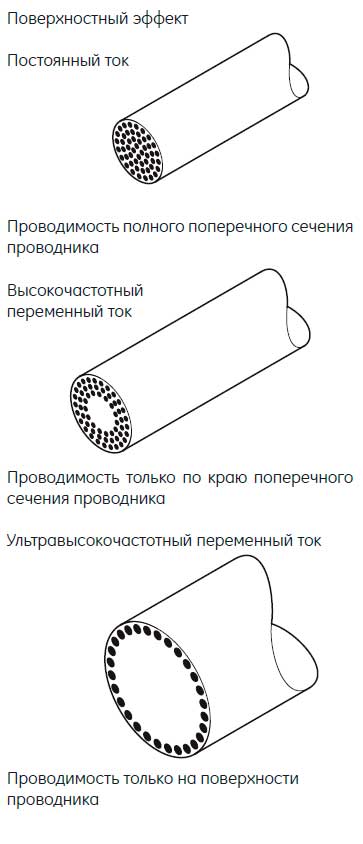
Проявление поверхностного эффекта в различных проводниках
Степень проявления поверхностного эффекта зависит от свойств материала и геометрии проводника:
- В медных проводах на частоте 50 Гц глубина проникновения составляет около 9 мм
- В стальных проводах эффект выражен сильнее из-за высокой магнитной проницаемости
- В тонких проводах и фольге эффект менее заметен
- В массивных шинах и трубах эффект проявляется очень сильно
Как сильно влияет поверхностный эффект на сопротивление проводника? Например, на частоте 1 МГц активное сопротивление медного провода диаметром 1 мм возрастает примерно в 30 раз по сравнению с сопротивлением постоянному току.
Практическое значение поверхностного эффекта
Поверхностный эффект необходимо учитывать во многих областях электротехники и электроники:
- При расчете потерь в линиях электропередачи
- При конструировании высокочастотных трансформаторов и дросселей
- При проектировании антенн и других СВЧ-устройств
- При выборе сечения проводов для высокочастотных цепей
Какие негативные последствия может вызвать поверхностный эффект? Основные проблемы:
- Увеличение активных потерь в проводниках
- Снижение добротности катушек индуктивности
- Уменьшение эффективности экранирования
- Искажение формы импульсных сигналов
Способы снижения влияния поверхностного эффекта
Для уменьшения негативного влияния поверхностного эффекта применяются следующие методы:
- Использование многожильных проводов (литцендрат)
- Применение полых трубчатых проводников
- Уменьшение диаметра одиночных проводников
- Использование материалов с низкой магнитной проницаемостью
- Нанесение на поверхность проводника слоя с высоким сопротивлением
Какой из этих способов наиболее эффективен? Выбор метода зависит от конкретной задачи, но наиболее универсальным является применение многожильных проводов из изолированных тонких жил.
Применение поверхностного эффекта в технике
Несмотря на в основном негативное влияние, поверхностный эффект находит и полезное применение:
- В индукционных нагревателях для поверхностной закалки металлов
- В устройствах для бесконтактного измерения толщины покрытий
- В СВЧ-волноводах для уменьшения потерь
- В специальных типах антенн
Математическое описание поверхностного эффекта
Для точного расчета распределения тока при поверхностном эффекте используются уравнения Максвелла. В простейшем случае плоского проводника плотность тока на глубине x определяется выражением:

J = J₀ * e^(-x/δ)
Где:
- J₀ — плотность тока на поверхности
- x — расстояние от поверхности
- δ — глубина проникновения
Активное сопротивление проводника при поверхностном эффекте можно рассчитать по формуле:
R = R₀ * √(f / f₀)
Здесь R₀ — сопротивление постоянному току, f — частота, f₀ — характеристическая частота проводника.
Заключение
Поверхностный эффект играет важную роль во многих областях электротехники, особенно при работе с высокочастотными токами. Понимание его физической сущности и умение учитывать на практике необходимо для правильного проектирования электрических устройств и систем. При этом в ряде случаев поверхностный эффект можно использовать с пользой для решения технических задач.
Поверхностный эффект в проводниках
Наблюдается, когда по проводу течёт высокочастотная энергия.
Ближе к центру провода наведённое электричество направлено обратно.
Уменьшается плотность тока, и он может быть даже обратным.
Это распределение задаётся уравнением Бестеля. В радиолокаторах ВЧ – колебания передаются по антенне, которая выполнена в виде позолоченной трубки.
Пробой проводящего слоя
– коэффициент динотронного эффекта
Если как минимум , то произойдёт электрический разряд.
Этот критерий называется критерием Тацкссенда.
– коэффициент ионизации (линейный или объёмный)
Закон сохранения полного тока в плазме
Это и есть закон сохранения полного тока в плазме.
Высокоионизированная плотная плазма
Соударение электронов происходит с
электронами и ионами.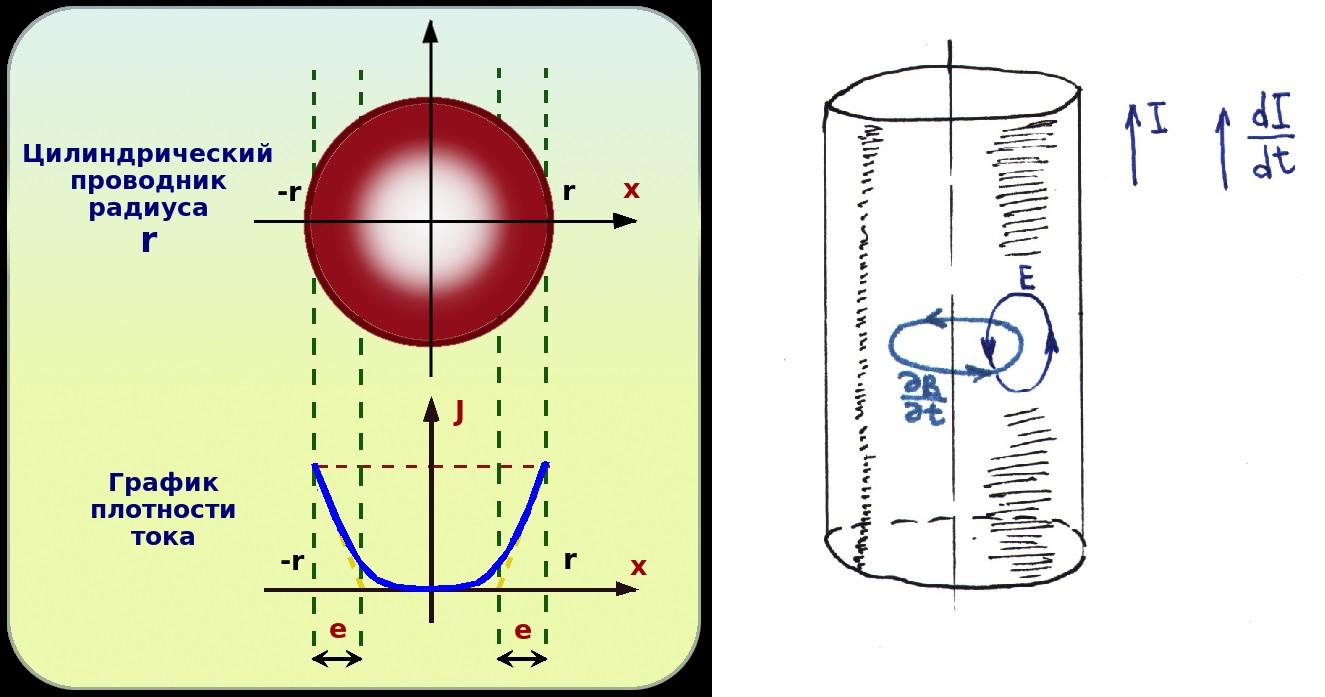 Правда, кулоновские
силы – силы дальнодействия. Специфика
такова, что если кинетическая энергия
электронов превосходит их потенциальную
электрическую энергию, то искажение,
изменение направления движения ионов
и электронов мало.
Правда, кулоновские
силы – силы дальнодействия. Специфика
такова, что если кинетическая энергия
электронов превосходит их потенциальную
электрическую энергию, то искажение,
изменение направления движения ионов
и электронов мало.
(вCGS) Если кинетическая энергия меньше потенциальной, то происходит рассеяние частиц.
Когда– кулоновский радиус
– эффективное сечение рассеянных частиц
Однако, в действительности эффективный радиус рассеянья больше этой величины, из-за того, что кулоновское воздействие происходит не на очень малых расстояниях.
где. Это логарифм эффективного сечения рассеянья.
– радиус Дебая
Для воздуха, когда в единице объёма 1014см-3при температуре 1 эВ (1эВ = 11600К).
Плотная плазма отличается ещё и тем,
что в предыдущем объекте нет термического
равновесия. Более того, там основные
частицы – электроны, и для них нельзя
говорить о температуре. Температура –
мера средней энергии хаотического
кинетического движения частиц. Необходимо
Максвелловское распределение частиц.
В плазме высокого давления такое
распределение возникает вследствие
частных соударений электронов между
собой. Это квазированное состояние.
Поэтому можно говорить об электронной
температуре плазмы, которая, впрочем,
может отличаться от ионной.
Необходимо
Максвелловское распределение частиц.
В плазме высокого давления такое
распределение возникает вследствие
частных соударений электронов между
собой. Это квазированное состояние.
Поэтому можно говорить об электронной
температуре плазмы, которая, впрочем,
может отличаться от ионной.
Как правило, в плазме имеется не одна температура, но в теоретически равновесной плазме говорят об одной температуре. Здесь ионы и электроны имеют одну температуру.
Равновесие плазмы описывается уравнением Саха:
. Формула экспериментальная.
Проводимость плазмы (воздушной, аргонной, азотной):
, с погрешностью до 3%, причём;W= 6,2 эВ
Даже равновесная плазма имеет детальное
равновесие, причём температура несколько
отстаёт от энергии плазмы. Имеются
области с более высокой температурой,
и здесь ионизация происходит более
интенсивно, а когда эти ионы попадают
в области с более низкой температурой,
там происходит рекомбинация, и отдаётся
та энергия, которая была затрачена на
ионизацию. Так устанавливается полное
равновесие в плотной плазме.
Так устанавливается полное
равновесие в плотной плазме.
Излучение плазмы
Плазма излучает в УФ, ИК областях и даже в области рентгеновских лучей. Эти излучения бывают трёх типов:
Дискретные – когда электрон переходит на более низкие уровни
Сплошной спектр рекомбинационного излучения при соударении второго рода между положительными и отрицательными ионами, или положительным ионом и электроном
Тормозное излучение. При торможении электронов возникает рентгеновское излучение.
В некоторых случаях в плазме отсутствуют дискретные излучения. Это происходит, когда плазма состоит из лёгких атомов водорода, дейтерия и т.д.
Тяжёлые атомы всегда дают дискретный спектр, потому, что атомы теряют лишь внешние электроны. Тяжёлые атомы иногда появляются в плазме неконтролируемо и не при термоядерной реакции. Это происходит, когда ионы бомбардируют стенки сосуда.
В плотной плазме происходит рассеянье
света. Кванты света рассеиваются на
атомах и изменяют своё направление.
Кванты света рассеиваются на
атомах и изменяют своё направление.
Если первоначальное излучение не покидает плазму, то такую плазму называют замкнутой.
Рассеянье плазмы происходит по закону Релея.
Циклотронное и синхротронное излучение плазмы
Электроны и ионы плазмы движутся. Движение это происходит как хаотически, так и по силовым линиям поля. Если имеются и магнитные поля (внешние и в самой плазме), то сила Лоренца заставляет заряженные частицы двигаться по окружностям. В результате возникает циклотронное излучение плазмы.
Если скорости заряженных частиц в плазме очень велики, то излучение является релятивистским, оно называется синхротронным.
Наличие — поверхностный эффект — Большая Энциклопедия Нефти и Газа, статья, страница 1
Наличие — поверхностный эффект
Cтраница 1
Наличие поверхностного эффекта ( вытеснение тока из внутренних слоев проводника на его поверхность при увеличении частоты) приводит к увеличению сопротивления R с ростом частоты.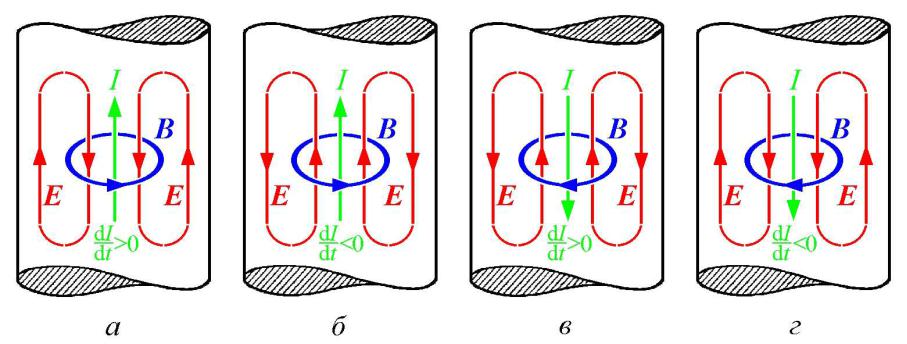
Наличие поверхностного эффекта приводит к тому, что электрический ток на сверхвысоких частотах течет только по поверхности проводников линии. На дециметровых и сантиметровых волнах толщина скин-слоя имеет порядок всего лишь 10 — 3 мм и передача энергии в основном производится электромагнитной волной, распространяющейся в пространстве между проводниками. [2]
Особенности расчета шинопроводов связаны с наличием поверхностного эффекта и эффекта близости. Плотность тока в проводнике большого сечения неодинакова — она больше на поверхности и уменьшается по мере приближения к центру проводника. Это свойство проводника, обусловленное действием электромагнитного поля, называется поверхностным эффектом. Эффект близости проявляется в изменении распределения плотности тока в близко расположенных проводниках. [3]
Одним из явлений, связанных с наличием поверхностных эффектов, является так называемый эффект засыпания. Это явление заключается в том, что на низких частотах запуска триггер перестает срабатывать. Открытые транзисторы, находящиеся в режиме насыщения, перестают закрываться.
[4]
Это явление заключается в том, что на низких частотах запуска триггер перестает срабатывать. Открытые транзисторы, находящиеся в режиме насыщения, перестают закрываться.
[4]
Эта закономерность позволяет легко вычислять сопротивление проводника при наличии явно выраженного поверхностного эффекта. [6]
При переменном токе сопротивление проводов больше их сопротивления при постоянном токе, что объясняется наличием поверхностного эффекта и эффекта близости. Влияние этих двух факторов на сопротивление проводов в осветительных сетях ничтожно, что позволяет при расчетах осветительных сетей принимать активное сопротивление проводов равным их сопротивлению при постоянном токе. [7]
Напряженность внутри проводников при отсутствии поверхностного эффекта изменяется по линейному закону ( рис. 9.3), а при наличии поверхностного эффекта — по экспоненте. [8]
[8]
Поскольку распределение индукции по сечению образца в общем случае неравномерно ( в особенности при измерениях в переменных магнитных полях из-за н
Поверхностный эффект — Энциклопедия по машиностроению XXL
Для упрощения выкладок рассмотрим это уравнение для случая отсутствия фазовых переходов, малых флуктуаций плотностей фаз II отсутствия поверхностных эффектовНеравновесная термодинамика двухфазных сред с неравными давлениями и температурами фаз н поверхностными эффектами. [c.206]
Влияние вязкости, являющейся стабилизирующим фактором, определяется числом Лапласа, показывающим отношение поверхностных эффектов к вязким [c.259]
Существуют также поверхностные эффекты, понижающие скорость массопереноса.
 К ним прежде всего относится появление
[c.8]
К ним прежде всего относится появление
[c.8]Поверхностные эффекты. Капица [42] заметил, что снабженный внутренним нагревателем и термометром металлический блок, свободно подвешенный в Не II, может перегреваться значительно выше температуры окружающей его гелиевой ванны. Он пришел к выводу, что граница между [c.848]
Так как поверхность тела растет пропорционально квадрату размеров этого тела, а объем— пропорционально кубу этих размеров, то для больших тел поверхностными эффектами по сравнению с объемными можно пренебречь. [c.223]Однако если вещество находится в мелкораздробленном состоянии, то такая система обладает развитой поверхностью и поэтому пренебрежение поверхностными эффектами может в этом случае привести в результатах вычислений к существенным погрешностям. [c.151]
Характеристические функции. Характеристические функции системы, т. е. внутренняя энергия и, энергия Гельмгольца Р, энтропия 5 и энергия Гиббса Ф при наличии поверхностного натяжения могут быть представлены в виде суммы двух членов, первый из которых зависит от объемных эффектов и представляет собой известные из гл.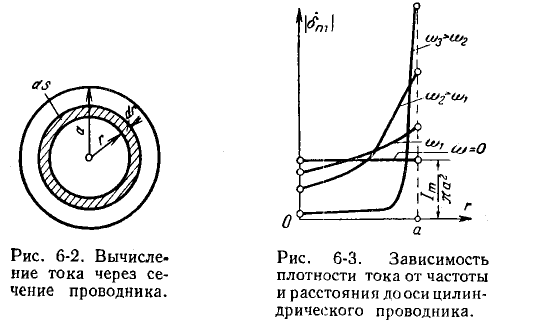 3 выражения для 7, Р, 8, Ф, а второй описывает зависимость характеристических- функцией от поверхностных эффектов (коэффициента поверхностного натяжения и площади О поверхности раздела фаз).
3 выражения для 7, Р, 8, Ф, а второй описывает зависимость характеристических- функцией от поверхностных эффектов (коэффициента поверхностного натяжения и площади О поверхности раздела фаз).
Когда существуют свободные границы (или поверхности раздела между двумя средами), возможны и другие скорости распространения. При этом могут появляться поверхностные волны , при которых движение происходит по существу лишь в тонком слое. Они подобны кругам на гладкой поверхности жидкости, вызываемым брошенным в нее камнем, и тесно связаны с поверхностным эффектом в проводниках, по которым течет переменный ток высокой частоты. Рэлей ), впервые обнаруживший существование поверхностно-волновых решений общих уравнений, заметил Не исключена возможность, что рассмотренные здесь поверхностные волны играют важную роль при землетрясениях и при соударении упругих тел. Распространяясь только в двух направлениях, они должны с удалением от источника приобретать все большее значение . Изучение записей сейсмических волн подтверждает предположение Рэлея.
[c.509]
Изучение записей сейсмических волн подтверждает предположение Рэлея.
[c.509]
Спадание кривой удельной энергии связи при малых А можно объяснить ролью поверхностных эффектов. Нуклоны, находящиеся на поверхности ядра, не полностью используют свои связи, что приводит к возникновению поверхностного натяжения, уменьшающего Ес, 1А на величину, пропорциональную площади поверхности, т. е. А . Роль поверхностных эффектов возрастает при увеличении отношения поверхности к объему, т. е. при переходе к более легким ядрам. [c.41]
Можно получить дифференциальное уравнение кривой фазового равновесия. В отсутствие гравитационных, электрических и поверхностных эффектов справедливо уравнение Максвелла [c.91]
Существование поверхностной энергии означает, что внутренняя энергия термодинамической системы, а следовательно, и все термодинамические функции обусловлены не только объемными эффектами. Необходимо учитывать также поверхностные эффекты (поверхностную энергию на границах системы), т. е. принимать во внимание поверхностное натяжение и обусловленные им капиллярные силы.
[c.225]
Необходимо учитывать также поверхностные эффекты (поверхностную энергию на границах системы), т. е. принимать во внимание поверхностное натяжение и обусловленные им капиллярные силы.
[c.225]
При переменном токе в стали, как магнитном материале, сильно сказывается поверхностный эффект, поэтому активное сопротивление стальных проводников для переменного тока выше, чем для постоянного. Кроме того, при переменном токе в стальных проводниках появляются потери мощности на перемагничивание. [c.21]
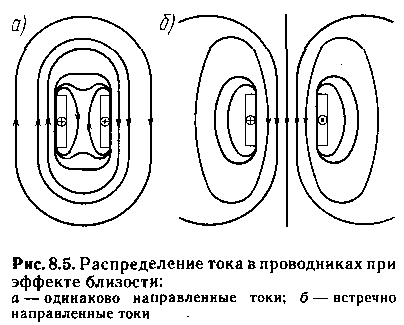
Неравномерное распределение плотности тока и напряженности магнитного поля по сечению проводника носит название поверхностного эффекта. Формы проявления поверхностного эффекта в системе проводников (эффект близости) и в замкнутых контурах (кольцевой эффект) рассмотрены в 4-1 и 4-2, [c.14]
При выводе выражений (1-20), (1-22), (1-23) и (1-26) не делалось никаких предположений о характере зависимости удельного сопротивления и магнитной проницаемости от координаты х. В этом смысле указанные зависимости являются общими, и мы будем ими пользоваться также и при более сложных формах поверхностного эффекта.
[c.16]
В этом смысле указанные зависимости являются общими, и мы будем ими пользоваться также и при более сложных формах поверхностного эффекта.
[c.16]
Таким образом, при резком проявлении поверхностного эффекта КПД индуктора зависит от отношения диаметров индуктора и цилиндра, удельных сопротивлений и магнитных проницаемостей материалов, но не зависит от частоты. Последнее объясняется тем, что и г , и прямо пропор- [c.19]
Поверхностному эффекту в ферромагнитной среде посвящено много работ наиболее точно отражает физическое содержание процесса упомянутая выше работа Л. Р. Неймана, которой мы и будем следовать, введя лишь некоторые упрощения в соответствии с рассматриваемой задачей. [c.24]
Таким образом, при переменной магнитной проницаемости, возрастающей с глубиной, поверхностный эффект проявляется сильнее. [c.32]
Выражение (3-10) соответствует также хорошо известному случаю одностороннего поверхностного эффекта в пластине толщиной лгц, ограниченной с двух сторон непроводящей средой, например воздухом т = —-1 и Уз = 0). [c.39]
[c.39]
Эффект близости проявляется тем сильнее, чем меньше расстояние между проводниками н чем сильнее проявляется поверхностный эффект, т. е. чем больше отношение толщины проводника к глубине проникновения тока. [c.51]
Множители Н и X представляют собой поправки к сопротивлениям, вычисленным при условии резко выраженного поверхностного эффекта [c.61]
Введем глубину активного слоя и по аналогии с глубиной проникновения тока зададим ее такой, чтобы в слое выделялось 86,5% всей энергии, поступающей сквозь поверхность пластины. Тогда при резком проявлении поверхностного эффекта = Аз, а при низких частотах I A , причем формально глубина проникновения тока может быть больше толщины пластины. [c.65]
Затвердевание металлов происходит при падении свободной энергии твердой фазы ниже уровня энергии жидкого состояния. Температура, при которой это имеет место, есть температура затвердевания (или в случае сплава) температура ликвидуса. Затвердевание требует, однако, образования в жидкости центров кристаллизации, механизм возникновения и роста которых весьма сложен. При температурах, лежащих ниже температур затвердевания, но близких к ней, различие в свободных энергиях жидкой и твердой фаз малы, поэтому и силы, приводящие к переходу между ними, невелики. Когда появляется твердый зародыщ, свободная энергия падает в результате перехода в твердую фазу, однако поверхностные силы на границе между фазами приводят к росту свободной энергии. И только когда эффект от образования новой фазы превысит этот поверхностный эффект, маленькая твердая частица сможет расти. Когда это происходит, говорят, что зарождается затвердевание и твердая фаза быстро распространяется в жидкости с выделением скрытого тепла, которое увеличивает температуру до температуры затвердевания. Величина переохлаждения, возможного до образования центров затвердевания, зависит от тепловых свойств конкретного металла.
[c.176]
Затвердевание требует, однако, образования в жидкости центров кристаллизации, механизм возникновения и роста которых весьма сложен. При температурах, лежащих ниже температур затвердевания, но близких к ней, различие в свободных энергиях жидкой и твердой фаз малы, поэтому и силы, приводящие к переходу между ними, невелики. Когда появляется твердый зародыщ, свободная энергия падает в результате перехода в твердую фазу, однако поверхностные силы на границе между фазами приводят к росту свободной энергии. И только когда эффект от образования новой фазы превысит этот поверхностный эффект, маленькая твердая частица сможет расти. Когда это происходит, говорят, что зарождается затвердевание и твердая фаза быстро распространяется в жидкости с выделением скрытого тепла, которое увеличивает температуру до температуры затвердевания. Величина переохлаждения, возможного до образования центров затвердевания, зависит от тепловых свойств конкретного металла.
[c.176]
Каждый дополнительный контакт увеллчивает вариантность на единицу, поскольку добавляется одна внешняя независимая переменная. Так, если система подвержена действию электростатического поля, заметно влияющего на ее свойства, то вариантность будет с+3, если к тому же необходимо учесть энергию граничной поверхности, считая ее принадлежащей системе, то с+4 и т. д. С другой стороны, постоянство некоторых из переменных уменьшает вариантность. При фиксированных массах компонентов, т. е. для закрытых систем, в отсутствие внешних силовых полей и поверхностных эффектов справедливо правило Дюгема общая вариантность равновесия равняется двум вне зависимости от числа компонентов и их распределения внутри системы [3]. Система, изолированная или имеющая с внешней средой-только тепловой контакт, является моновариантной. Вариантность уменьшается также, если есть дополнительные связи между внешними переменными,, так как это эквивалентно уменьшению числа независимых переменных. Например, изменение площади поверхности тела однозначно определяется изменением его объема при однородной (с сохранением формы) деформации тела.
[c.
Так, если система подвержена действию электростатического поля, заметно влияющего на ее свойства, то вариантность будет с+3, если к тому же необходимо учесть энергию граничной поверхности, считая ее принадлежащей системе, то с+4 и т. д. С другой стороны, постоянство некоторых из переменных уменьшает вариантность. При фиксированных массах компонентов, т. е. для закрытых систем, в отсутствие внешних силовых полей и поверхностных эффектов справедливо правило Дюгема общая вариантность равновесия равняется двум вне зависимости от числа компонентов и их распределения внутри системы [3]. Система, изолированная или имеющая с внешней средой-только тепловой контакт, является моновариантной. Вариантность уменьшается также, если есть дополнительные связи между внешними переменными,, так как это эквивалентно уменьшению числа независимых переменных. Например, изменение площади поверхности тела однозначно определяется изменением его объема при однородной (с сохранением формы) деформации тела.
[c. 24]
24]
Оредполагается, что N достаточно велико, чтобы можно было пренебречь поверхностными эффектами. В формуле (2.16) множитель V2 появляется за счет того, что при суммировании производится учет энергии взаимодействия каждой пары частиц дважды. Выражение (2.16) для потенциальной энергии справедливо как для однородных, так и для неоднородных систем. [c.64]
Здесь //j достаточно велико, чтоби перевести образец в нормальное состояние. Поверхностными эффектами, а также дна- или парамагнетизмом нормального состояния мы пренебрегли. Предполагалось также, что переход происходит обратимо. [c.684]
В п. 30 рассмотрена зависимость глубины проникновения от поля, обусловленная как изменением параметра упорядочения п , так и истиннонелинейными членами в теории. В п. 31 обсуждается вопрос о том, как зависят переходы в тонких пленках и других образцах малых размеров от поверхностных эффектов и от изменения параметра упорядочения.
[c. 732]
Однородная система (фаза) в заданном объеме может существовать в некотором интервале температур, имея свободную энергию, большую свободной энергии неоднородной системы из тех же частиц. Такое состояние фазы является метастабильным. С течением времени система перейдет в состояние с минимальным значением свободной энергии, т. е. станет неоднородной. Однако этот переход затрудняется поверхностным эффектом, т. е. тем, что образование в данной фазе объектов малых размеров другой фазы из-за поверхностной свободной энергии этих объектов приводит к увеличению свободной энергии системы и поэтому переход термодинамически невыгоден. Например, начало конденсации пара затруднено по той причине, что при образовании в паре малых (радиуса Л) капель жидкости их поверхностная свободная энергия Л, пропорциональная растет быстрее, чем уменьшается их объемная свободная энергия, пропорциональная Поэтому появление малых капель оказывается термодинамически невыгодным и конденсация задерживается. При больших же каплях, начиная с некоторого Л = У кр, наоборот, объемный член уменьшается быстрее, чем растет поверхнос1Ный, и конденсация становится возможной возникшая в результате флуктуаций такая капля будет расти.
[c.229]
При больших же каплях, начиная с некоторого Л = У кр, наоборот, объемный член уменьшается быстрее, чем растет поверхнос1Ный, и конденсация становится возможной возникшая в результате флуктуаций такая капля будет расти.
[c.229]
Формула Лапласа. В предыдущих разделах предполагалось, что внутренняя энергия термодинамической системы, а следовательно, и все термодинамические потенциалы обусловлены только объемными эффектами поверхностными эффектами (поверхностной энергией, сосредоточенной на поверхности раздела разнородных тел или фаз) пренебрегалось. На самом деле в довольно большом числе случаев оказывается необходиымым учитывать поверхностную энергию на границе раздела каждой из фаз, в частности, принимать во внимание поверхностное натяжение и связанные с ним капиллярные силы. [c.146]
В течение XIX века были сделаны открытия, составляющие основу современной электротехники. Фарадеем был открыт закон электромагнитной индукции, Ленц и Джоуль установили, что прохождение тока по проводнику сопровождается выделением тепла, Максвелл получил основополагающие уравнения электромагнитного поля, носящие его имя, и построил систему современной электродинамики.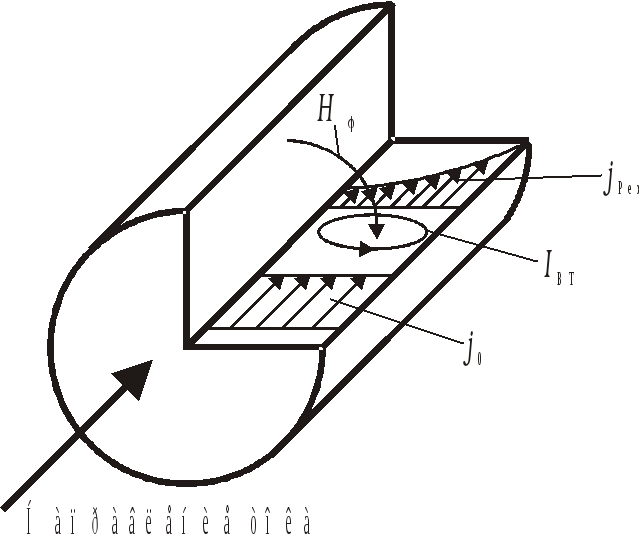 В 80-х годах У. Томсон открыл и исследовал поверхностный эффект, заключающийся в том, что переменный ток вытесняется к поверхности проводника. В 1886 г. русский ученый И. И. Боргман исследовал нагревание стекла в конденсаторе при быстро следующих друг за другом зарядах и разрядах. Таким образом, уже в XIX веке были заложены теоретические основы техники индукционного нагрева.
[c.4]
В 80-х годах У. Томсон открыл и исследовал поверхностный эффект, заключающийся в том, что переменный ток вытесняется к поверхности проводника. В 1886 г. русский ученый И. И. Боргман исследовал нагревание стекла в конденсаторе при быстро следующих друг за другом зарядах и разрядах. Таким образом, уже в XIX веке были заложены теоретические основы техники индукционного нагрева.
[c.4]
I Вследствие более яркого проявления поверхностного эффекта электрические сопротивления и мощность очевидно будут больше, чем вычисленные по формулам для р = onst при том же значении Н .. [c.24]
Активное сопротивление при поверхностном эффекте независимо от характера изменення р и р по сечению всегда может быть представлено в виде [c.48]
Ранее указывалось (см. 1-2), что при ярко выраженном поверхностном эффекте можно считать, что D rja и = ziD xJa, где Го и Хо — сопротивления единичного квадрата, вычисленные по формулам для плоской волны. Повысить точность вычисления и расширить применение этих формул возможно, если учесть, что путь тока короче длины окружности, путем введения так называемого расчетного диаметра D . Если в качестве расчетного диаметра при нагреве внешней поверхности цилиндра взят1з средний диаметр активного слоя
[c.49]
Повысить точность вычисления и расширить применение этих формул возможно, если учесть, что путь тока короче длины окружности, путем введения так называемого расчетного диаметра D . Если в качестве расчетного диаметра при нагреве внешней поверхности цилиндра взят1з средний диаметр активного слоя
[c.49]
Значение 7ср значительно больше кр для одиночного проводника даже при не очень ярко пыражерпгом поверхностном эффекте. Поэтому пы-нолненне многослойных обмоток обычно не рекомендуется, если d/Д > 1. [c.57]
Эффект кожи — Skin effect
«Глубина кожи» перенаправляется сюда. Для получения информации о глубине (слоях) биологической / органической кожи см. Кожа . Распределение тока в цилиндрическом проводнике в поперечном сечении. Для переменного тока плотность тока экспоненциально убывает от поверхности внутрь. Глубина скин-слоя, δ, определяется как глубина, на которой плотность тока составляет всего 1 / е (около 37%) от значения на поверхности; это зависит от частоты тока и электрических и магнитных свойств проводника.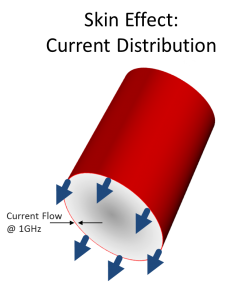 Каждый 3-проводной жгут в этой установке для передачи энергии действует как один провод. Один провод, в котором используется такое же количество металла на километр, будет иметь более высокие потери из-за скин-эффекта.
Каждый 3-проводной жгут в этой установке для передачи энергии действует как один провод. Один провод, в котором используется такое же количество металла на километр, будет иметь более высокие потери из-за скин-эффекта.
Скин-эффект — это тенденция переменного электрического тока (AC) к распределению внутри проводника , так что плотность тока является наибольшей у поверхности проводника и экспоненциально уменьшается с увеличением глубины в проводнике. Электрический ток протекает в основном по «коже» проводника между внешней поверхностью и уровнем, называемым глубиной скин-слоя . Глубина кожи зависит от частоты переменного тока; по мере увеличения частоты электрический ток перемещается к поверхности, что приводит к уменьшению глубины кожи. Скин-эффект уменьшает эффективное сечение проводника и, таким образом, увеличивает его эффективное сопротивление . Скин-эффект вызывается противодействующими вихревыми токами, вызванными изменяющимся магнитным полем, возникающим из-за переменного тока. При 60 Гц в меди глубина скин-слоя составляет около 8,5 мм. На высоких частотах глубина скин-слоя становится намного меньше.
При 60 Гц в меди глубина скин-слоя составляет около 8,5 мм. На высоких частотах глубина скин-слоя становится намного меньше.
Повышенное сопротивление переменному току, вызванное скин-эффектом, можно уменьшить, используя специально сплетенную проволоку . Поскольку внутри большого проводника проходит очень мало тока, можно использовать трубчатые проводники, такие как труба, для снижения веса и стоимости. Скин- эффект имеет практические последствия при анализе и проектировании радиочастотных и микроволновых цепей, линий передачи (или волноводов) и антенн. Это также важно на частотах сети (50–60 Гц) в системах передачи и распределения электроэнергии переменного тока . Это одна из причин, почему для передачи электроэнергии на большие расстояния предпочтение отдается постоянному току высокого напряжения .
Эффект был впервые описан в статье Горация Лэмба в 1883 году для случая сферических проводников и был обобщен на проводники любой формы Оливером Хевисайдом в 1885 году.
Причина
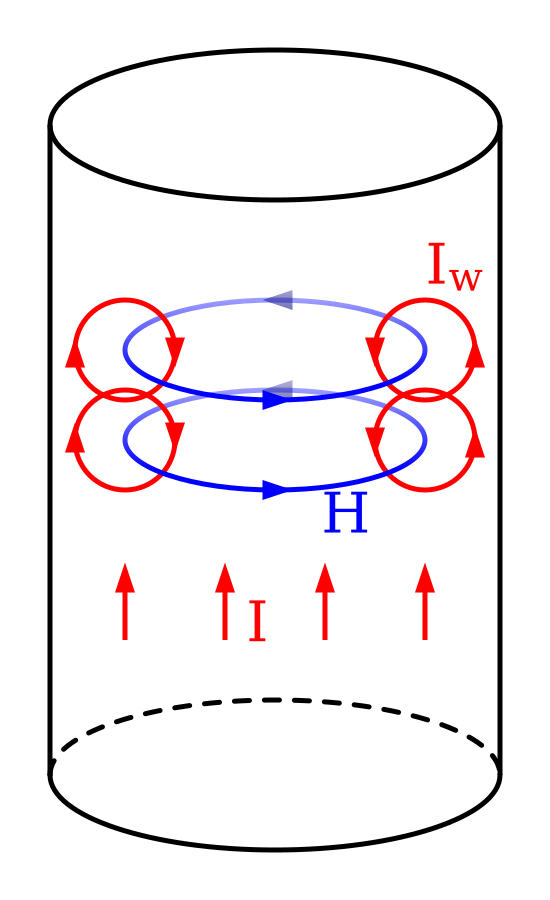
Причина скин-эффекта. Ток I, протекающий по проводнику, индуцирует магнитное поле H. Если ток увеличивается, как на этом рисунке, результирующее увеличение H вызывает циркулирующие вихревые токи I W, которые частично нейтрализуют ток в центре и усиливают его около кожи. Проводники, обычно в форме проводов, могут использоваться для передачи электрической энергии или сигналов с использованием переменного тока, протекающего по этому проводнику. Носители заряда, составляющие этот ток, обычно электроны , приводятся в действие электрическим полем из-за источника электрической энергии. Ток в проводнике создает магнитное поле внутри и вокруг проводника. При изменении силы тока в проводнике изменяется и магнитное поле. Изменение магнитного поля, в свою очередь, создает электрическое поле, которое препятствует изменению силы тока. Это противоположное электрическое поле называется « противоэлектродвижущей силой » (противо-ЭДС).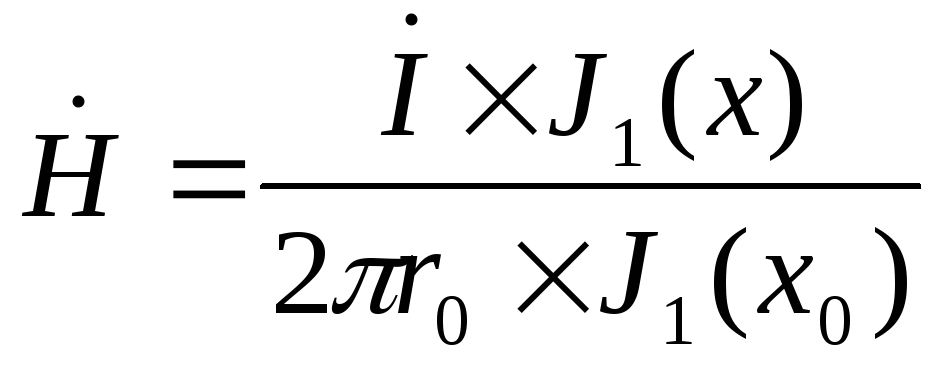 Обратная ЭДС наиболее сильна в центре проводника и вынуждает проводящие электроны выходить за пределы проводника, как показано на схеме справа.
Обратная ЭДС наиболее сильна в центре проводника и вынуждает проводящие электроны выходить за пределы проводника, как показано на схеме справа.
Независимо от движущей силы, плотность тока оказывается наибольшей на поверхности проводника, а его величина уменьшается глубже в проводнике. Это снижение плотности тока известно как скин-эффект, а глубина скин-слоя является мерой глубины, на которой плотность тока падает до 1 / е от своего значения вблизи поверхности. Более 98% тока будет проходить в слое, в 4 раза превышающем глубину скин-слоя от поверхности. Это поведение отличается от поведения постоянного тока, который обычно равномерно распределяется по поперечному сечению провода.
Переменный ток может также индуцироваться в проводнике из-за переменного магнитного поля согласно закону индукции . Электромагнитные волны , падающие на проводнике будет , следовательно , как правило , дают такому ток; это объясняет отражение электромагнитных волн от металлов. {- {(1 + j) d / \ delta}}}
{- {(1 + j) d / \ delta}}}
где называется глубиной скин-слоя . Таким образом, глубина скин-слоя определяется как глубина под поверхностью проводника, на которой плотность тока упала до 1 / е (около 0,37) Дж · с . Мнимая часть показателя степени показывает, что фаза плотности тока задерживается на 1 радиан для каждой глубины проникновения скин-слоя. Одна полная длина волны в проводнике требует 2π глубины скин-слоя, в этот момент плотность тока снижается до e −2π (-54,6 дБ) от его поверхностного значения. Длина волны в проводнике намного короче, чем длина волны в вакууме , или, что то же самое, фазовая скорость в проводнике намного меньше, чем скорость света в вакууме. Например, радиоволна с частотой 1 МГц имеет длину волны в вакууме λ 0 около 300 м, тогда как в меди длина волны сокращается до примерно 0,5 мм с фазовой скоростью только примерно 500 м / с. Вследствие закона Снеллиуса и этой очень маленькой фазовой скорости в проводнике любая волна, попадающая в проводник, даже при скользящем падении, преломляется в основном в направлении, перпендикулярном поверхности проводника. {2}}} + \ rho \ omega \ varepsilon}}}
{2}}} + \ rho \ omega \ varepsilon}}}
где
- ρ {\ displaystyle \ rho} = удельное сопротивление проводника
- ω {\ displaystyle \ omega} = угловая частота тока = , где — частота. 2 π ж {\ displaystyle 2 \ pi f} ж {\ displaystyle f}
- μ {\ displaystyle \ mu} = проницаемость проводника, μ р {\ displaystyle \ mu _ {r}} μ 0 {\ displaystyle \ mu _ {0}}
- μ р {\ displaystyle \ mu _ {r}} = относительная магнитная проницаемость проводника
- μ 0 {\ displaystyle \ mu _ {0}} = проницаемость свободного пространства
- ε {\ displaystyle \ varepsilon} = диэлектрическая проницаемость проводника, ε р {\ displaystyle \ varepsilon _ {r}} ε 0 {\ displaystyle \ varepsilon _ {0}}
- ε р {\ displaystyle \ varepsilon _ {r}} = относительная диэлектрическая проницаемость проводника
- ε 0 {\ displaystyle \ varepsilon _ {0}} = диэлектрическая проницаемость свободного пространства
На частотах намного ниже величина внутри большого радикала близка к единице, и формула обычно имеет вид: 1 / ρ ϵ {\ displaystyle 1 / \ rho \ epsilon}
-
δ знак равно 2 ρ ω μ {\ displaystyle \ delta = {\ sqrt {{2 \ rho} \ over {\ omega \ mu}}}} .
Эта формула действительна на частотах, отличных от сильных атомных или молекулярных резонансов (где будет большая мнимая часть), и на частотах, которые намного ниже как плазменной частоты материала (в зависимости от плотности свободных электронов в материале), так и обратной величины среднее время между столкновениями с участием электронов проводимости. В хороших проводниках, таких как металлы, все эти условия обеспечиваются, по крайней мере, до микроволновых частот, что подтверждает справедливость этой формулы. Например, в случае меди это будет верно для частот намного ниже 10 18 Гц. ϵ {\ displaystyle \ epsilon}
Однако в очень плохих проводниках на достаточно высоких частотах фактор под большим радикалом увеличивается. На частотах, намного превышающих допустимые, можно показать, что глубина скин-слоя вместо того, чтобы продолжать уменьшаться, приближается к асимптотическому значению: 1 / ρ ϵ {\ displaystyle 1 / \ rho \ epsilon}
- δ ≈ 2 ρ ε μ {\ displaystyle \ delta \ приблизительно {2 \ rho} {\ sqrt {\ varepsilon \ over \ mu}}}
Это отклонение от обычной формулы применимо только к материалам с довольно низкой проводимостью и на частотах, где длина волны вакуума не намного больше самой глубины скин-слоя.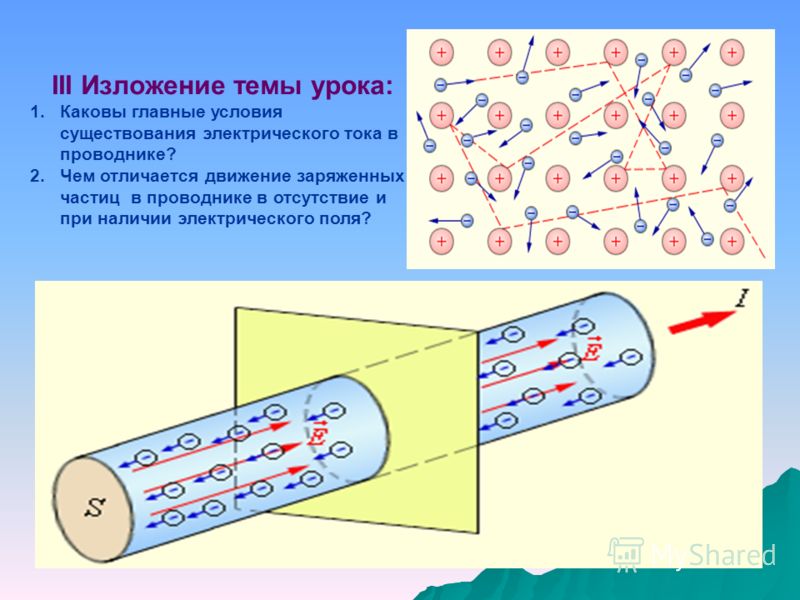 Например, объемный кремний (нелегированный) является плохим проводником и имеет толщину скин-слоя около 40 метров на частоте 100 кГц (λ = 3000 м). Однако, поскольку частота увеличивается до мегагерцового диапазона, его скин-толщина никогда не опускается ниже асимптотического значения 11 метров. Вывод состоит в том, что в плохих твердых проводниках, таких как нелегированный кремний, скин-эффект не нужно учитывать в большинстве практических ситуаций: любой ток равномерно распределяется по поперечному сечению материала независимо от его частоты.
Например, объемный кремний (нелегированный) является плохим проводником и имеет толщину скин-слоя около 40 метров на частоте 100 кГц (λ = 3000 м). Однако, поскольку частота увеличивается до мегагерцового диапазона, его скин-толщина никогда не опускается ниже асимптотического значения 11 метров. Вывод состоит в том, что в плохих твердых проводниках, таких как нелегированный кремний, скин-эффект не нужно учитывать в большинстве практических ситуаций: любой ток равномерно распределяется по поперечному сечению материала независимо от его частоты.
Плотность тока в круглом проводнике
Когда глубина скин-слоя не мала по сравнению с радиусом провода, плотность тока можно описать с помощью функций Бесселя . Плотность тока внутри круглого провода вдали от влияния других полей как функция расстояния от оси определяется выражением:
Плотность тока в круглой проволоке для различной глубины скин-слоя. Числа на каждой кривой представляют собой отношение глубины скин-слоя к радиусу провода.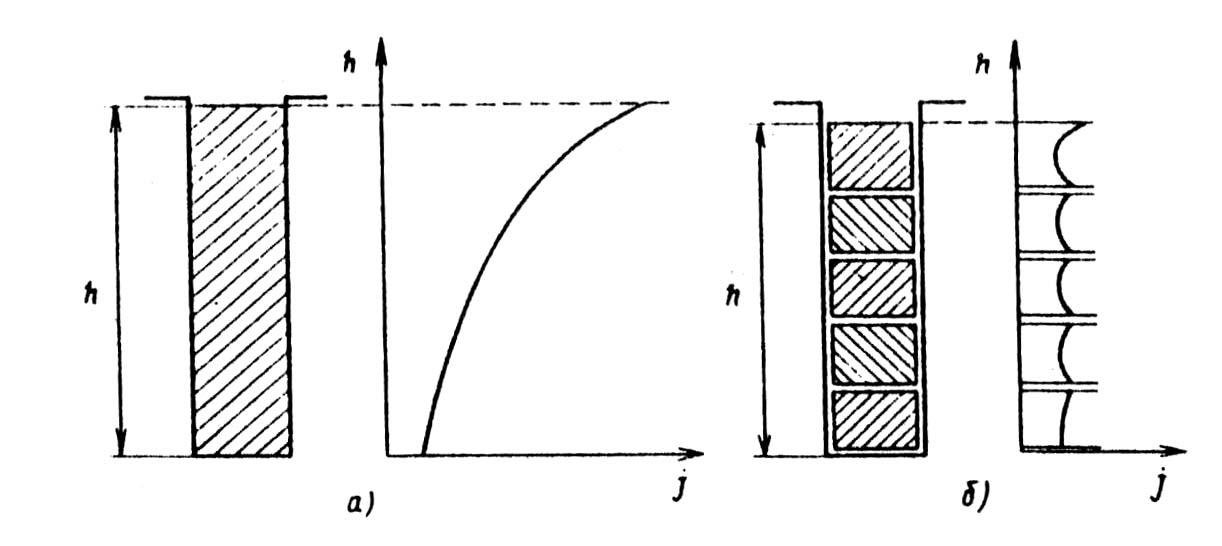 Кривая со знаком бесконечности соответствует случаю нулевой частоты (DC). Все кривые нормированы так, чтобы плотность тока на поверхности была одинаковой. Горизонтальная ось — это положение внутри провода, при этом левый и правый крайние точки являются поверхностью провода. По вертикальной оси отложена относительная плотность тока.
Кривая со знаком бесконечности соответствует случаю нулевой частоты (DC). Все кривые нормированы так, чтобы плотность тока на поверхности была одинаковой. Горизонтальная ось — это положение внутри провода, при этом левый и правый крайние точки являются поверхностью провода. По вертикальной оси отложена относительная плотность тока.
- J р знак равно k я 2 π р J 0 ( k р ) J 1 ( k р ) знак равно J р J 0 ( k р ) J 0 ( k р ) {\ displaystyle \ mathbf {J} _ {r} = {\ frac {k \ mathbf {I}} {2 \ pi R}} {\ frac {J_ {0} (kr)} {J_ {1} (kR )}} = \ mathbf {J} _ {R} {\ frac {J_ {0} (kr)} {J_ {0} (kR)}}}
где
- ω {\ displaystyle \ quad \ omega} = угловая частота тока = 2π × частота
- р знак равно {\ displaystyle \ quad r =} расстояние от оси провода
- р знак равно {\ Displaystyle \ quad R =} радиус проволоки
- J р знак равно {\ Displaystyle \ quad \ mathbf {J} _ {r} =} вектор плотности тока на расстоянии r от оси провода
- J р знак равно {\ Displaystyle \ quad \ mathbf {J} _ {R} =} вектор плотности тока на поверхности провода
- я знак равно {\ Displaystyle \ quad \ mathbf {I} =} полный вектор тока
- J 0 знак равно {\ displaystyle \ quad J_ {0} =} Функция Бесселя первого рода порядка 0
- J 1 знак равно {\ displaystyle \ quad J_ {1} =} Функция Бесселя первого рода, порядок 1
- k знак равно — j ω μ ρ знак равно 1 — j δ {\ displaystyle \ quad к = {\ sqrt {\ frac {-j \ omega \ mu} {\ rho}}} = {\ frac {1-j} {\ delta}}} волновое число в проводнике
-
δ знак равно 2 ρ ω μ {\ displaystyle \ quad \ delta = {\ sqrt {\ frac {2 \ rho} {\ omega \ mu}}}} также называется глубиной кожи.

- ρ {\ Displaystyle \ quad \ rho} = удельное сопротивление проводника
- μ р {\ displaystyle \ quad \ mu _ {r}} = относительная магнитная проницаемость проводника
- μ 0 {\ displaystyle \ quad \ mu _ {0}} = проницаемость свободного пространства = 4π x 10 −7 Гн / м
- μ {\ Displaystyle \ quad \ mu} знак равно μ р {\ displaystyle \ mu _ {r}} μ 0 {\ displaystyle \ mu _ {0}}
Поскольку является комплексным, функции Бесселя также являются комплексными. Амплитуда и фаза плотности тока меняется с глубиной. k {\ displaystyle k}
Импеданс круглого провода
Внутреннее сопротивление на единицу длины отрезка круглой проволоки определяется по формуле:
- Z я п т знак равно k ρ 2 π р J 0 ( k р ) J 1 ( k р ) {\ displaystyle \ mathbf {Z} _ {int} = {\ frac {k \ rho} {2 \ pi R}} {\ frac {J_ {0} (kR)} {J_ {1} (kR)}} } .
Этот импеданс представляет собой сложную величину, соответствующую сопротивлению (действительному) последовательно с реактивным сопротивлением (мнимым) из-за внутренней самоиндукции провода на единицу длины.
Индуктивность
Часть индуктивности провода может быть отнесена к магнитному полю внутри самого провода, которое называется внутренней индуктивностью ; это учитывает индуктивное реактивное сопротивление (мнимую часть импеданса), определяемое приведенной выше формулой. В большинстве случаев это небольшая часть индуктивности провода, которая включает в себя эффект индукции от магнитных полей вне провода, создаваемых током в проводе. В отличие от этой внешней индуктивности, внутренняя индуктивность уменьшается за счет скин-эффекта, то есть на частотах, где глубина скин-слоя больше не велика по сравнению с размером проводника. Эта небольшая составляющая индуктивности приближается к значению (50 нГн / м для немагнитного провода) на низких частотах, независимо от радиуса провода. Его уменьшение с увеличением частоты, когда отношение глубины скин-слоя к радиусу провода становится ниже примерно 1, показано на прилагаемом графике и учитывает уменьшение индуктивности телефонного кабеля с увеличением частоты в таблице ниже . μ 8 π {\ displaystyle {\ frac {\ mu} {8 \ pi}}}
μ 8 π {\ displaystyle {\ frac {\ mu} {8 \ pi}}}
Сопротивление
Однако наиболее важным эффектом скин-эффекта на импеданс одиночного провода является увеличение сопротивления провода и, как следствие, потери . Эффективное сопротивление из-за тока, удерживаемого около поверхности большого проводника (намного более толстого, чем δ ), может быть решено, как если бы ток протекал равномерно через слой толщиной δ на основе удельного сопротивления постоянного тока этого материала. Эффективная площадь поперечного сечения приблизительно равна δ, умноженному на длину окружности проводника. Таким образом, длинный цилиндрический проводник , такие как провод, имеющий диаметр D велик по сравнению с б , имеет сопротивление приблизительно , что из полой трубы с толщиной стенки б проведения постоянного тока. Сопротивление переменного тока провода длиной L и удельным сопротивлением составляет:
ρ {\ displaystyle \ rho}
Эффективная площадь поперечного сечения приблизительно равна δ, умноженному на длину окружности проводника. Таким образом, длинный цилиндрический проводник , такие как провод, имеющий диаметр D велик по сравнению с б , имеет сопротивление приблизительно , что из полой трубы с толщиной стенки б проведения постоянного тока. Сопротивление переменного тока провода длиной L и удельным сопротивлением составляет:
ρ {\ displaystyle \ rho}
- р ≈ L ρ π ( D — δ ) δ ≈ L ρ π D δ {\ displaystyle R \ приблизительно {{L \ rho} \ над {\ pi (D- \ delta) \ delta}} \ приблизительно {{L \ rho} \ over {\ pi D \ delta}}}
Предполагается окончательное приближение выше . D ≫ δ {\ Displaystyle D \ gg \ delta}
Удобная формула (приписываемая Ф.Э. Терману ) для диаметра D W проволоки круглого сечения, сопротивление которой увеличивается на 10% при частоте f :
- D W знак равно 200 м м ж / ЧАС z {\ displaystyle D _ {\ mathrm {W}} = {\ frac {200 ~ \ mathrm {mm}} {\ sqrt {f / \ mathrm {Hz}}}}}
Эта формула увеличения сопротивления переменного тока верна только для изолированного провода. Для соседних проводов, например, в кабеле или катушке, на сопротивление переменного тока также влияет эффект близости , который может вызвать дополнительное увеличение сопротивления переменного тока.
Для соседних проводов, например, в кабеле или катушке, на сопротивление переменного тока также влияет эффект близости , который может вызвать дополнительное увеличение сопротивления переменного тока.
Влияние материала на глубину кожи
В хорошем проводнике толщина скин-слоя пропорциональна корню квадратному из удельного сопротивления. Это означает, что у лучших проводников меньшая глубина скин-слоя. Общее сопротивление лучшего проводника остается ниже даже при меньшей толщине скин-слоя. Однако лучший проводник будет иметь более высокое соотношение между сопротивлением переменного и постоянного тока по сравнению с проводником с более высоким удельным сопротивлением. Например, при 60 Гц медный проводник площадью 2000 м3 (1000 квадратных миллиметров) имеет на 23% большее сопротивление, чем при постоянном токе. Провод такого же размера из алюминия имеет только на 10% большее сопротивление при переменном токе 60 Гц, чем при постоянном токе.
Глубина скин-слоя также изменяется как корень, обратный квадратному из проницаемости проводника. В случае железа его проводимость составляет примерно 1/7 проводимости меди. Однако из-за ферромагнетизма его проницаемость примерно в 10 000 раз больше. Это уменьшает толщину скин-слоя для железа примерно до 1/38 от толщины меди, примерно 220 микрометров при 60 Гц. Таким образом, железная проволока бесполезна для линий электропередачи переменного тока (за исключением добавления механической прочности, служащей сердечником для неферромагнитного проводника, такого как алюминий). Скин-эффект также снижает эффективную толщину пластин в силовых трансформаторах, увеличивая их потери.
В случае железа его проводимость составляет примерно 1/7 проводимости меди. Однако из-за ферромагнетизма его проницаемость примерно в 10 000 раз больше. Это уменьшает толщину скин-слоя для железа примерно до 1/38 от толщины меди, примерно 220 микрометров при 60 Гц. Таким образом, железная проволока бесполезна для линий электропередачи переменного тока (за исключением добавления механической прочности, служащей сердечником для неферромагнитного проводника, такого как алюминий). Скин-эффект также снижает эффективную толщину пластин в силовых трансформаторах, увеличивая их потери.
Стальные прутки хорошо подходят для сварки на постоянном токе (DC), но их невозможно использовать на частотах намного выше 60 Гц. На частоте в несколько килогерц сварочный стержень будет раскаленным докрасна, поскольку ток будет протекать через значительно увеличенное сопротивление переменному току, вызванное скин-эффектом, с относительно небольшой мощностью, остающейся для самой дуги . Для высокочастотной сварки можно использовать только немагнитные стержни.
Для высокочастотной сварки можно использовать только немагнитные стержни.
На 1 мегагерце глубина скин-эффекта во влажной почве составляет около 5,0 м, в морской воде — около 0,25 м.
Смягчение
Тип кабеля, называемый litz wire (от немецкого Litzendraht , плетеный провод), используется для смягчения скин-эффекта на частотах от нескольких килогерц до одного мегагерца. Он состоит из нескольких изолированных жил, сплетенных вместе по тщательно продуманному рисунку, так что общее магнитное поле действует одинаково на все провода и вызывает равное распределение общего тока между ними. Поскольку скин-эффект оказывает незначительное влияние на каждую из тонких жил, пучок не испытывает такого же увеличения сопротивления переменному току, как сплошной проводник той же площади поперечного сечения из-за скин-эффекта.
Литц-проволока часто используется в обмотках высокочастотных трансформаторов для повышения их эффективности за счет уменьшения скин-эффекта и эффекта близости . Силовые трансформаторы большой мощности намотаны многожильными проводниками, конструкция которых аналогична литц-проводам, но с большим поперечным сечением, соответствующим большей глубине скин-слоя на частотах сети. Проводящие нити, состоящие из углеродных нанотрубок , были продемонстрированы как проводники для антенн от средних волн до микроволновых частот. В отличие от стандартных антенных проводников, нанотрубки намного меньше глубины скин-слоя, что позволяет полностью использовать поперечное сечение нити, что приводит к очень легкой антенне.
Силовые трансформаторы большой мощности намотаны многожильными проводниками, конструкция которых аналогична литц-проводам, но с большим поперечным сечением, соответствующим большей глубине скин-слоя на частотах сети. Проводящие нити, состоящие из углеродных нанотрубок , были продемонстрированы как проводники для антенн от средних волн до микроволновых частот. В отличие от стандартных антенных проводников, нанотрубки намного меньше глубины скин-слоя, что позволяет полностью использовать поперечное сечение нити, что приводит к очень легкой антенне.
В высоковольтных и сильноточных воздушных линиях электропередачи часто используется алюминиевый кабель со стальной арматурой ; более высокое сопротивление стального сердечника не имеет значения, поскольку он расположен намного ниже глубины скин-слоя, где практически не протекает переменный ток.
В приложениях, где протекают большие токи (до тысяч ампер), сплошные проводники обычно заменяются трубками, полностью устраняя внутреннюю часть проводника, где протекает слабый ток. Это практически не влияет на сопротивление переменному току, но значительно снижает вес проводника. Высокая прочность при небольшом весе труб существенно увеличивает пролёт. Трубчатые проводники типичны для распределительных устройств электроэнергии, где расстояние между опорными изоляторами может составлять несколько метров. Длинные пролеты обычно имеют физический прогиб, но это не влияет на электрические характеристики. Чтобы избежать потерь, проводимость материала трубки должна быть высокой.
Это практически не влияет на сопротивление переменному току, но значительно снижает вес проводника. Высокая прочность при небольшом весе труб существенно увеличивает пролёт. Трубчатые проводники типичны для распределительных устройств электроэнергии, где расстояние между опорными изоляторами может составлять несколько метров. Длинные пролеты обычно имеют физический прогиб, но это не влияет на электрические характеристики. Чтобы избежать потерь, проводимость материала трубки должна быть высокой.
В ситуациях с большим током, когда проводники (круглые или плоские шины ) могут иметь толщину от 5 до 50 мм, скин-эффект также возникает на острых изгибах, когда металл сжимается внутри изгиба и растягивается за пределами изгиба. Более короткий путь на внутренней поверхности приводит к более низкому сопротивлению, что приводит к концентрации большей части тока вблизи внутренней поверхности изгиба. Это вызывает повышение температуры в этой области по сравнению с прямой (несогнутой) областью того же проводника. Аналогичный скин-эффект возникает в углах прямоугольных проводников (если смотреть в поперечном сечении), где магнитное поле больше сконцентрировано в углах, чем по бокам. Это приводит к превосходным характеристикам (то есть более высокому току при меньшем повышении температуры) от широких тонких проводников (например, «ленточных» проводников), в которых эффективно устраняется влияние углов.
Аналогичный скин-эффект возникает в углах прямоугольных проводников (если смотреть в поперечном сечении), где магнитное поле больше сконцентрировано в углах, чем по бокам. Это приводит к превосходным характеристикам (то есть более высокому току при меньшем повышении температуры) от широких тонких проводников (например, «ленточных» проводников), в которых эффективно устраняется влияние углов.
Отсюда следует, что трансформатор с круглым сердечником будет более эффективным, чем трансформатор аналогичного номинала с квадратным или прямоугольным сердечником из того же материала.
Твердые или трубчатые проводники могут быть серебро — гальваническое воспользоваться более высокой проводимостью Сильвера. Этот метод особенно используется на частотах от ОВЧ до СВЧ, где небольшая толщина скин-слоя требует только очень тонкого слоя серебра, что делает улучшение проводимости очень экономичным. Серебряное покрытие аналогичным образом используется на поверхности волноводов, используемых для передачи микроволн. Это уменьшает затухание распространяющейся волны из-за резистивных потерь, влияющих на сопровождающие вихревые токи; скин-эффект ограничивает такие вихревые токи очень тонким поверхностным слоем волноводной структуры. Сам по себе скин-эффект в этих случаях фактически не борется, но распределение токов вблизи поверхности проводника делает использование драгоценных металлов (имеющих более низкое удельное сопротивление) практичным. Хотя он имеет более низкую проводимость, чем медь и серебро, также используется золочение, потому что в отличие от меди и серебра оно не подвержено коррозии. Тонкий окисленный слой меди или серебра будет иметь низкую проводимость, что приведет к большим потерям мощности, поскольку большая часть тока все еще будет проходить через этот слой.
Это уменьшает затухание распространяющейся волны из-за резистивных потерь, влияющих на сопровождающие вихревые токи; скин-эффект ограничивает такие вихревые токи очень тонким поверхностным слоем волноводной структуры. Сам по себе скин-эффект в этих случаях фактически не борется, но распределение токов вблизи поверхности проводника делает использование драгоценных металлов (имеющих более низкое удельное сопротивление) практичным. Хотя он имеет более низкую проводимость, чем медь и серебро, также используется золочение, потому что в отличие от меди и серебра оно не подвержено коррозии. Тонкий окисленный слой меди или серебра будет иметь низкую проводимость, что приведет к большим потерям мощности, поскольку большая часть тока все еще будет проходить через этот слой.
Недавно было показано, что метод наслоения немагнитных и ферромагнитных материалов толщиной в нанометровом масштабе снижает повышенное сопротивление скин-эффекта для приложений с очень высокой частотой. Рабочая теория заключается в том, что поведение ферромагнитных материалов на высоких частотах приводит к появлению полей и / или токов, противоположных тем, которые генерируются относительно немагнитными материалами, но для проверки точных механизмов требуется дополнительная работа. Как показали эксперименты, это может значительно повысить эффективность проводников, работающих на частотах в десятки ГГц и выше. Это имеет серьезные последствия для связи 5G .
Как показали эксперименты, это может значительно повысить эффективность проводников, работающих на частотах в десятки ГГц и выше. Это имеет серьезные последствия для связи 5G .
Примеры
Зависимость глубины скин-слоя от частоты для некоторых материалов при комнатной температуре, красная вертикальная линия обозначает частоту 50 Гц:Мы можем получить практическую формулу глубины кожи следующим образом:
- δ знак равно 2 ρ ( 2 π ж ) ( μ 0 μ р ) ≈ 503 ρ μ р ж {\ displaystyle \ delta = {\ sqrt {{2 \ rho} \ over {(2 \ pi f) (\ mu _ {0} \ mu _ {r})}}} \ приблизительно 503 \, {\ sqrt { \ frac {\ rho} {\ mu _ {r} f}}}}
где
- δ знак равно {\ displaystyle \ delta =} глубина кожи в метрах
- μ р знак равно {\ displaystyle \ mu _ {r} =} относительная проницаемость среды (для меди, = μ р {\ displaystyle \ mu _ {r}} 1,00 )
- ρ знак равно {\ Displaystyle \ rho =} удельное сопротивление среды в Ом · м, также равное обратной величине ее проводимости: (для меди ρ = ρ знак равно 1 / σ {\ Displaystyle \ rho = 1 / \ sigma} 1,68 × 10 -8 Ом · м )
- ж знак равно {\ displaystyle f =} частота тока в Гц
Золото — хороший проводник с удельным сопротивлением 2,44 × 10 -8 Ом · м и по существу немагнитен: 1, поэтому толщина его скин-слоя на частоте 50 Гц определяется выражением μ р знак равно {\ displaystyle \ mu _ {r} =}
- δ знак равно 503 2,44 ⋅ 10 — 8 1 ⋅ 50 знак равно 11.
 {- 8}} {1 \ cdot 50}}} = 11,1 \, \ mathrm {мм}}
{- 8}} {1 \ cdot 50}}} = 11,1 \, \ mathrm {мм}}
Свинец , напротив, является относительно плохим проводником (среди металлов) с удельным сопротивлением 2,2 × 10 -7 Ом · м , что примерно в 9 раз больше, чем у золота. Глубина его скин-слоя при 50 Гц также составляет около 33 мм, или в несколько раз больше, чем у золота. 9 знак равно 3 {\ displaystyle {\ sqrt {9}} = 3}
Сильно магнитные материалы имеют уменьшенную толщину скин-слоя из-за их большой проницаемости, как было указано выше для случая железа, несмотря на его более низкую проводимость. Практические последствия видят пользователи индукционных плит , когда некоторые типы посуды из нержавеющей стали непригодны для использования, потому что они не ферромагнитны. μ р {\ displaystyle \ mu _ {r}}
На очень высоких частотах толщина скин-слоя для хороших проводников становится крошечной. Например, толщина скин-слоя некоторых распространенных металлов на частоте 10 ГГц (микроволновая область) меньше микрометра :
| Дирижер | Глубина скин-слоя ( мкм ) |
|---|---|
| Алюминий | 0,820 |
| Медь | 0,652 |
| Золото | 0,753 |
| Серебряный | 0,634 |
Таким образом, на микроволновых частотах большая часть тока протекает в очень тонкой области у поверхности. Следовательно, омические потери волноводов на микроволновых частотах зависят только от покрытия поверхности материала. Таким образом, слой серебра толщиной 3 мкм, напыленный на кусок стекла, является отличным проводником на таких частотах.
Следовательно, омические потери волноводов на микроволновых частотах зависят только от покрытия поверхности материала. Таким образом, слой серебра толщиной 3 мкм, напыленный на кусок стекла, является отличным проводником на таких частотах.
В меди можно увидеть, что глубина скин-слоя уменьшается согласно квадратному корню из частоты:
| Частота | Глубина скин-слоя (мкм) |
|---|---|
| 50 Гц | 9220 |
| 60 Гц | 8420 |
| 10 кГц | 652 |
| 100 кГц | 206 |
| 1 МГц | 65,2 |
| 10 МГц | 20,6 |
| 100 МГц | 6.52 |
| 1 ГГц | 2,06 |
В своей работе « Engineering Electromagnetics» Хейт указывает, что на электростанции шина для переменного тока с частотой 60 Гц с радиусом более одной трети дюйма (8 мм) является пустой тратой меди, а на практике шины для сильного переменного тока. редко бывают более полдюйма (12 мм), за исключением механических причин.
редко бывают более полдюйма (12 мм), за исключением механических причин.
Снижение скин-эффекта внутренней индуктивности проводника
См. Схему ниже, на которой показаны внутренние и внешние проводники коаксиального кабеля. Поскольку скин-эффект вызывает протекание тока на высоких частотах в основном по поверхности проводника, можно видеть, что это уменьшит магнитное поле внутри провода, то есть ниже глубины, на которой протекает основная часть тока. Можно показать, что это незначительно повлияет на самоиндукцию самого провода; см. Скиллинг или Хейт для математической обработки этого явления.
Обратите внимание, что индуктивность, рассматриваемая в этом контексте, относится к неизолированному проводнику, а не к индуктивности катушки, используемой в качестве элемента схемы. В индуктивности катушки преобладает взаимная индуктивность между витками катушки, которая увеличивает ее индуктивность пропорционально квадрату количества витков. Однако, когда задействован только один провод, то в дополнение к «внешней индуктивности», связанной с магнитными полями за пределами провода (из-за общего тока в проводе), как показано в белой области рисунка ниже, существует также намного меньшая составляющая «внутренней индуктивности» из-за части магнитного поля внутри самого провода, зеленая область на рисунке B. Эта небольшая составляющая индуктивности уменьшается, когда ток концентрируется к поверхности проводника, что когда глубина скин-слоя не намного больше радиуса провода, как это будет иметь место на более высоких частотах.
Эта небольшая составляющая индуктивности уменьшается, когда ток концентрируется к поверхности проводника, что когда глубина скин-слоя не намного больше радиуса провода, как это будет иметь место на более высоких частотах.
Для одиночной проволоки это уменьшение становится все менее значимым, поскольку проволока становится длиннее по сравнению с ее диаметром, и обычно им пренебрегают. Однако наличие второго проводника в случае линии передачи снижает степень внешнего магнитного поля (и общую самоиндуктивность) независимо от длины провода, так что уменьшение индуктивности из-за скин-эффекта все еще может быть важно, например, в случае телефонной витой пары, описанной ниже, индуктивность проводников существенно уменьшается на более высоких частотах, где становится важным скин-эффект. С другой стороны, когда внешний компонент индуктивности увеличивается из-за геометрии катушки (из-за взаимной индуктивности между витками), значение внутренней составляющей индуктивности еще больше принижается и игнорируется.
Индуктивность на длину коаксиального кабеля
Пусть размеры a , b и c будут радиусом внутреннего проводника, внутреннего радиуса экрана (внешнего проводника) и внешнего радиуса экрана соответственно, как показано в поперечном сечении рисунка A ниже.
Четыре стадии скин-эффекта в коаксиальном кабеле, показывающие влияние на индуктивность. На схемах показано поперечное сечение коаксиального кабеля. Цветовой код: черный = общая изолирующая оболочка, желто-коричневый = проводник, белый = диэлектрик, зеленый = ток, указанный на диаграмме, синий = ток, выходящий из диаграммы, пунктирные черные линии со стрелками = магнитный поток (B). Ширина пунктирных черных линий предназначена для показа относительной силы магнитного поля, интегрированного по окружности с этим радиусом. Четыре ступени, A , B , C и D : обесточены, низкая частота, средняя частота и высокая частота соответственно. Есть три области, которые могут содержать индуцированные магнитные поля: центральный проводник, диэлектрик и внешний проводник.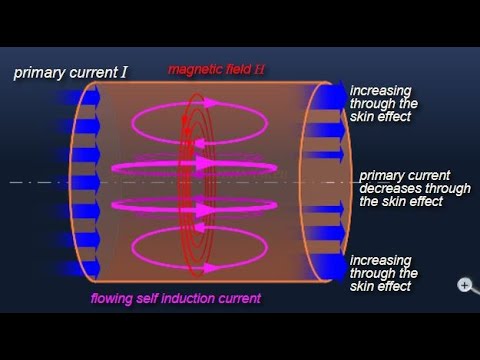 На стадии B ток равномерно покрывает проводники, и во всех трех областях присутствует значительное магнитное поле. По мере увеличения частоты и возникновения скин-эффекта ( C и D ) магнитное поле в диэлектрической области не изменяется, поскольку оно пропорционально полному току, протекающему в центральном проводнике. Однако в C имеется пониженное магнитное поле в более глубоких частях внутреннего проводника и внешних частях экрана (внешний проводник). Таким образом, при одинаковом общем токе в магнитном поле сохраняется меньше энергии, что соответствует уменьшенной индуктивности. На еще более высокой частоте D толщина скин-слоя мала: весь ток ограничивается поверхностью проводников. Единственное магнитное поле находится в областях между проводниками; остается только «внешняя индуктивность».
На стадии B ток равномерно покрывает проводники, и во всех трех областях присутствует значительное магнитное поле. По мере увеличения частоты и возникновения скин-эффекта ( C и D ) магнитное поле в диэлектрической области не изменяется, поскольку оно пропорционально полному току, протекающему в центральном проводнике. Однако в C имеется пониженное магнитное поле в более глубоких частях внутреннего проводника и внешних частях экрана (внешний проводник). Таким образом, при одинаковом общем токе в магнитном поле сохраняется меньше энергии, что соответствует уменьшенной индуктивности. На еще более высокой частоте D толщина скин-слоя мала: весь ток ограничивается поверхностью проводников. Единственное магнитное поле находится в областях между проводниками; остается только «внешняя индуктивность».
Для данного тока полная энергия, запасенная в магнитных полях, должна быть такой же, как вычисленная электрическая энергия, относящаяся к этому току, протекающему через индуктивность коаксиального кабеля; эта энергия пропорциональна измеренной индуктивности кабеля.
Магнитное поле внутри коаксиального кабеля можно разделить на три области, каждая из которых, таким образом, будет вносить вклад в электрическую индуктивность, видимую на отрезке кабеля.
Индуктивность связана с магнитным полем в области с радиусом , в области внутри центрального проводника. L cen {\ Displaystyle L _ {\ текст {cen}} \,} р < а {\ Displaystyle г <а \,}
Индуктивность связана с магнитным полем в области , области между двумя проводниками (содержащими диэлектрик, возможно, воздух). L доб {\ Displaystyle L _ {\ текст {ext}} \,} а < р < б {\ Displaystyle а <г <Ь \,}
Индуктивность связана с магнитным полем в области , области внутри проводника экрана. L шд {\ displaystyle L _ {\ text {shd}} \,} б < р < c {\ Displaystyle б <г <с \,}
Чистая электрическая индуктивность обусловлена всеми тремя составляющими:
- L Всего знак равно L cen + L шд + L доб {\ displaystyle L _ {\ text {total}} = L _ {\ text {cen}} + L _ {\ text {shd}} + L _ {\ text {ext}} \,}
L доб {\ Displaystyle L _ {\ текст {ext}} \,} не изменяется из-за скин-эффекта и определяется часто цитируемой формулой для индуктивности L на длину D коаксиального кабеля:
- L / D знак равно μ 0 2 π пер ( б а ) {\ displaystyle L / D = {\ frac {\ mu _ {0}} {2 \ pi}} \ ln \ left ({\ frac {b} {a}} \ right) \,}
На низких частотах все три индуктивности присутствуют полностью, так что . L ОКРУГ КОЛУМБИЯ знак равно L cen + L шд + L доб {\ displaystyle L _ {\ text {DC}} = L _ {\ text {cen}} + L _ {\ text {shd}} + L _ {\ text {ext}} \,}
L ОКРУГ КОЛУМБИЯ знак равно L cen + L шд + L доб {\ displaystyle L _ {\ text {DC}} = L _ {\ text {cen}} + L _ {\ text {shd}} + L _ {\ text {ext}} \,}
На высоких частотах только диэлектрическая область имеет магнитный поток, так что . L ∞ знак равно L доб {\ Displaystyle L _ {\ infty} = L _ {\ text {ext}} \,}
Большинство обсуждений коаксиальных линий передачи предполагает, что они будут использоваться для радиочастот, поэтому уравнения представлены, соответствующие только последнему случаю.
По мере увеличения скин-эффекта токи концентрируются около внешней стороны внутреннего проводника ( r = a ) и внутри экрана ( r = b ). Поскольку по существу нет тока глубже внутреннего проводника, под поверхностью внутреннего проводника нет магнитного поля. Поскольку ток во внутреннем проводнике уравновешивается противоположным током, протекающим внутри внешнего проводника, в самом внешнем проводнике не остается магнитного поля . Только увеличивает электрическую индуктивность на этих более высоких частотах.
б < р < c {\ Displaystyle б <г <с \,} L доб {\ displaystyle L _ {\ text {ext}}}
Только увеличивает электрическую индуктивность на этих более высоких частотах.
б < р < c {\ Displaystyle б <г <с \,} L доб {\ displaystyle L _ {\ text {ext}}}
Хотя геометрия иная, витая пара, используемая в телефонных линиях, подвергается аналогичному воздействию: на более высоких частотах индуктивность уменьшается более чем на 20%, как видно из следующей таблицы.
Характеристики телефонного кабеля в зависимости от частоты
Типичные данные о параметрах для телефонного кабеля PIC 24 калибра при 21 ° C (70 ° F).
| Частота (Гц) | R (Ом / км) | L (мГн / км) | G (мкСм / км) | C (нФ / км) |
|---|---|---|---|---|
| 1 | 172,24 | 0,6129 | 0,000 | 51,57 |
| 1к | 172,28 | 0,6125 | 0,072 | 51,57 |
| 10 тыс. | 172,70 | 0,6099 | 0,531 | 51,57 |
100 тыс. {b}}} \,} {b}}} \,} Смотрите такжеНотыРекомендации
внешние ссылкиГлубина проникновения тока в металл6 ноября 2018 Явление поверхностного эффекта Постоянный ток в проводнике распределяется равномерно по сечению, переменный ток распределяется по сечению неравномерно в зависимости от частоты тока (рис. 10.6.).
Рис. 10.6. Глубина проникновения тока в металл в зависимости от его частоты: а — постоянный, б, в, г — переменный 50, 10 000, 125 000 Гц соответственно
При пропускании переменного тока наибольшая противоэлектродвижущая сила индуктируется в центре проводника, который охватывается полным магнитным потоком. Чем ближе к поверхности проводника, тем слабее магнитное поле, а, следовательно, меньше противо электродвижущая сила. Свойство тока высокой частоты протекать только по поверхностному слою проводника принято называть поверхностным эффектом, или скин-эффектом. Плотность тока для различных точек сечения проводника будет неодинаковой. Чем выше частота тока, тем больше в центре проводника индуктивное сопротивление и меньше плотность тока. Неравномерное распределение индукционных токов приводит к неравномерному нагреву деталей: поверхностные слои очень быстро нагреваются до высоких температур, а сердцевина или совсем не нагревается или нагревается незначительно, благодаря теплопроводности стали. Для количественной оценки явления поверхностного эффекта введено понятие глубины проникновения тока 8 (дельта). При этом считают, что переменный ток протекает только в поверхностном слое, толщина которого равна глубине проникновения тока, и имеет на этой глубине равномерную плотность. Глубина проникновения тока или толщина слоя определяется по формуле:
где р — удельное электрическое сопротивление, Ом-мм2/м; р — магнитная проницаемость, Гс/Э; f- частота тока, Гц. Следовательно, с увеличением частоты глубина проникновения индукционных токов уменьшается (рис. .103, таблица 10.4.). Если менять частоту тока, то можно в широких пределах изменять глубину проникновения 8, а, следовательно, и толщину слоя, по которому идет ток, вызывающий нагрев поверхности закаливаемой детали. Из приведенных в табл., данных следует, что с повышением температуры нагрева металла глубина проникновения тока растет и достигает наибольшего значения при температуре потери магнитных свойств — точки Кюри. Таблица 10. =1 Гс/Э |
||||
|
50 |
0,5 |
7.0 |
1,0 |
|
|
2500 |
0,067 |
1.0 |
0,13 |
|
|
10000 |
0.034 |
0,5 |
0,07 |
|
|
100000 |
0,011 |
0.16 |
0,022 |
|
|
1 000 000 |
0,0034 |
0,05 |
0,007 |
С ростом температуры нагрева (рис. 10.7.) стальных деталей удельное сопротивление р возрастает и выше 1000°С достигает своего максимального значения.
Рис. 10.7. Кривые изменения магнитной проницаемости и удельного электрического сопротивления стали 45 в зависимости от температуры нагрева
Магнитная проницаемость в интервале 600…700°С почти не зависит от температуры, но при дальнейшем ее повышении резко падает и достигает минимального значения, равного магнитной проницаемости вакуума ( jli =1).
Для практических расчетов глубину проникновения 8 тока в металл вычисляют по упрощенным формулам: для стальных деталей при температуре 15° С:
мм и при температуре 760° С , мм
Где: S- глубина проникновения тока, мм; f- частота тока, Гц.
Для большинства сталей магнитные превращения протекают в интервале критических температур 765-780° С, при которых магнитная проницаемость резко падает и становится равной единице. После потери сталью магнитных свойств с образованием аустенита глубина проникновения тока резко возрастает.
Наибольшее значение глубины проникновения тока называют горячей глубиной проникновения и обозначают ГОр- Приближенно она может быть определена по упрощенной формуле:
Зная зависимость глубины проникновения тока от температуры, процесс индукционного нагрева стали можно представить по следующей схеме.
В первый момент начинается, нагрев стали в тонком поверхностном слое, равном глубине проникновения тока в холодный металл. После потери этим слоем магнитных свойств, глубина проникновения тока возрастает и нагревается слой, расположенный глубже. Повышение температуры в первом нагретом слое замедляется.
После потери магнитных свойств вторым слоем начинает быстро нагреваться третий слой и т.д. Пределом роста глубины проникновения тока является горячая глубина проникновения.
Повышение температуры в слое с горячей глубиной проникновения происходит за счет индуктированных токов, а в более глубоких слоях — в основном за счет теплопроводности.
Этот процесс нагрева объясняет причину быстрого распространения тепла при нагреве ТВЧ, в связи с изменениями магнитных свойств. На рис. 10.5 изображен график индукционного нагрева, из которого видно, что более быстрый нагрев происходит при температурах ниже точки Кюри (769°С). Выше этой критической точки нагрев замедляется в связи с потерей сталью магнитных свойств и фазовыми превращениями.
Существует три основных способа поверхностной индукционной закалки в зависимости от размера, формы детали и некоторых специальных требований нагрева: одновременный, непрерывно последовательный и последовательный (поочередный).
Рис. 10.8. График индукционного нагрева
Неизолированные жесткие проводники
Электрические шины
Неизолированные жесткие проводники — проводники этого вида принято называть шинами. По соображениям экономического порядка применяют исключительно шины из алюминия и его сплавов с различными электрическими и механическими характеристиками. Форму и размеры поперечного сечения шины выбирают в соответствии с рабочим током, учитывая явление поверхностного эффекта, а также требования термической и динамической стойкости при КЗ.
Поверхностный эффект. Как известно, переменный ток вытесняется к поверхности проводника, при этом потери мощности увеличиваются, что равносильно увеличению сопротивления. Отношение активного сопротивления Ra уединенного проводника при переменном токе к сопротивлению R при постоянном токе и той же температуре называют коэффициентом поверхностного эффекта Кп=Ra/R. Он зависит от формы и размеров поперечного сечения проводника, а также от частоты тока.
Рис.1. Коэффициент поверхностного эффекта в шинах прямоугольного сечения
Рис.2. Коэффициент поверхностного эффекта в трубах круглого сечения
На рис.1, рис.2 приведены кривые для определения коэффициента поверхностного эффекта в проводниках прямоугольного и круглого сечения. По оси абсцисс отложена величина √f/R, где f — частота; R — сопротивление проводника длиной 1000 м при постоянном токе. Отношения b/h и t/D приняты в качестве параметров. Как видно из рисунков, по мере увеличения √f/R коэффициент поверхностного эффекта быстро увеличивается. Так как сопротивление R обратно пропорционально сечению S проводника, можно утверждать, что по мере увеличения сечения коэффициент поверхностного эффекта увеличивается. Чем меньше отношение b/h или t/D. тем меньше коэффициент поверхностного эффекта.
Для проводников сплошного сечения он значительно больше, чем для труб того же сечения. Так, например, сечение круглого алюминиевого проводника диаметром 60 мм и сечение алюминиевой трубы диаметром 100 мм при отношении t/D = 0,1 одинаковы и равны 28,3 см2. Следовательно, сопротивление их постоянному току и отношение √f/R также одинаковы (R=0,01225 Ом и √f/R=63,8 Гц1/2/Ом1/2). Однако коэффициент поверхностного эффекта в первом случае равен 1,375, а во втором — 1,025. Следовательно, активное сопротивление трубы с указанными размерами на25 % меньше сопротивления круглого проводника сплошного сечения.
Рис.3. Зависимость активного сопротивления алюминиевых труб от толщины стенки
Зависимость активного сопротивления алюминиевых труб диаметром от 50 до 150 мм от толщины стенки показана на рис.3. По мере увеличения толщины стенки, начиная от очень малого значения, сечение трубы увеличивается, а сопротивление ее быстро уменьшается, пока не достигнет некоторого минимума. При дальнейшем увеличении толщины стенки сечение трубы продолжает увеличиваться, однако ее активное сопротивление не только не уменьшается, но даже несколько увеличивается вследствие быстрого увеличения коэффициента поверхностного эффекта.
Критическая толщина стенки трубы, соответствующая минимуму активного сопротивления, зависит не от диаметра, а только от удельного сопротивления материала и частоты. Для алюминиевых труб круглого сечения при частоте 50 Гц критическая толщина стенки составляет около 20 мм, а для медных труб около 14 мм. Ясно, что применение труб с толщиной стенки, превышающей критическую, нецелесообразно.
Распространенные формы поперечного сечения шин
Рис.4. Распространенные виды шин
Простейшая форма поперечною сечения шины — прямоугольная с отношением сторон b/h от 1/8 до 1/12 (рис.4,а). Это так называемые плоские шины. Они обеспечивают хороший отвод тепла в окружающую среду, поскольку отношение поверхности охлаждения к объему здесь больше, чем в шинах любой другой формы. Момент сопротивления изгибу относительно оси z во много раз больше, чем относительно оси у. Следовательно, при расположении проводников трех фаз в плоскости у-у плоские шины способны противостоять значительным электродинамическим силам при КЗ.
Плоские шины изготовляют с поперечным сечением до 120х10=1200 мм2. Допустимый продолжительный ток таких шин из алюминия при нормированной температуре воздуха 25°С равен 2070 А. При большем рабочем токе можно применить составные проводники из двух или трех полос с зазорами между ними (рис.4,б,в). Допустимый ток при этом увеличится соответственно до 3200 и 4100 А, т.е. далеко не пропорционально числу полос. Это объясняется поверхностным эффектом — вытеснением переменного тока на поверхность составного проводника. Распределение тока между полосами составного проводника неравномерно, потери мощности заметно увеличиваются.
Недостаток составных проводников заключается также в сложности монтажа и недостаточной механической прочности. Последнее объясняется взаимодействием полос при КЗ. Поскольку токи в полосах направлены одинаково, они стремятся сблизиться. Чтобы исключить смыкание полос при КЗ. необходимы дистанционные прокладки между ними с соответствующим креплением. Проводники из трех и четырех полос безусловно нецелесообразны при переменном токе. Ограниченное применение имеют проводники из двух полос.
При больших рабочих токах применяются составные шины из двух корытных проводников (рис.4,г). Здесь также необходимы дистанционные прокладки между корытами.
Наиболее совершенной формой поперечного сечения шины при рабочем токе свыше 2000 А является круглое кольцевое (рис.4,д). При правильно выбранном отношении толщины стенки к диаметру трубы обеспечивается хороший отвод тепла, а также механическая прочность. Момент сопротивления изгибу одинаков в любом направлении. Применение получили трубы с наружным диаметром до 250 мм и толщиной стенки до 12 мм.
Проводников в электростатическом поле. Распределение заряда в проводнике. Связь между напряженностью поля на поверхности проводника и поверхностной плотностью заряда. Емкостные проводники. Конденсаторы. Энергия электростатического поля.
Проводники в электростатическом поле
§ 1 из Распределение заряда в проводнике.
Связь между напряжённостью поля на поверхности проводника и поверхностной плотностью зарядаСвободные заряды в проводнике могут перемещаться под действием сколь угодно малой силы. Следовательно, для уравновешивания зарядов в проводнике должны выполняться следующие условия:
- Напряженность поля внутри проводника должна быть равна нулю, т.к.
- т.е. потенциал внутри проводника должен быть постоянным.
Следовательно, поверхностный заряд проводника в состоянии равновесия является эквипотенциальным.
В состоянии равновесия заряды в любом месте внутри проводника не могут быть избыточными — они распределены по поверхности проводника с плотностью σ.
Рассмотрим замкнутую поверхность в форме цилиндра, генераторы которого перпендикулярны поверхности проводника.На поверхности проводника находятся свободные заряды с поверхностной плотностью σ.
Поскольку внутри проводника нет зарядов, поток через поверхность цилиндра внутри проводника равен нулю. Поток через верхнюю часть цилиндра вне проводника по теореме Гаусса равен
т.е. вектор электрического смещения, равный поверхностной плотности свободных зарядов проводника или
II.Приводя незаряженный проводник к внешнему электростатическому полю, его свободные заряды будут двигаться: положительные — по полю, отрицательные — против поля. Тогда на одной стороне проводника будут накапливаться положительные, а на другой отрицательные заряды. Эти обвинения называются искусственными. Перераспределение зарядов будет до тех пор, пока интенсивность в проводнике станет равной нулю, а интенсивность линии вне проводника будет перпендикулярной к поверхности. Индуцированные заряды появляются на проводнике из-за смещения, т. Е. Представляют собой заряды с поверхностной плотностью и смещены, поэтому это называется вектором электрического смещения.
§ 2 Емкостные проводники.
Конденсаторы
I. Уединенные называют проводниками, вдали от других проводников тел зарядов. Потенциал такого проводника прямо пропорционален заряду на нем.
Из опыта следует, что разные проводники, будучи одинаково заряженными Q 1 = Q 2 , принимают разные потенциалы φ 1 ≠ φ 2 из-за различных форм, размеров и окружающей среды проводник (ε).Следовательно, для изолированного проводника имеем формулу
,
где — емкость , уединенного проводника . Емкость изолированного проводника равна заряду q, дают проводник, изменяющий свой потенциал на 1 вольт.
В системе СИ емкость измеряется в фарадах
Вместимость мяча
- II.Емкость одиночных проводников очень мала. Для практических целей необходимо создание такого устройства, позволяющего хранить большие заряды при небольших размерах и емкостях. Конденсатор — устройство для хранения заряда и электроэнергии. Самый простой конденсатор состоит из двух проводников, разделенных зазором из воздуха или диэлектрика (воздух — это тоже диэлектрик). Проводники называются обкладками конденсатора, и их расположение по отношению друг к другу выбирается таким, чтобы электрическое поле было сосредоточено в зазоре между ними.Под емкостью конденсатора понимается физическая величина C, равная отношению заряда q, накопленного на пластинах, к разности потенциалов между пластинами.
Рассчитайте емкость конденсатора с параллельными пластинами с пластинами площадью S, поверхностную плотность заряда σ, диэлектрическую проницаемость диэлектрика ε между пластинами, расстояние между пластинами d. Напряженность поля
.
Используя соотношение Δ φ и E , находим
–
емкость пластинчатого конденсатора
Для цилиндрического конденсатора:
Для сферического конденсатора:
Поскольку при некоторых значениях напряжения в диэлектрике происходит пробой (электрический разряд через диэлектрический слой), то возникает напряжение пробоя конденсаторов.Напряжение пробоя зависит от формы облицовки, диэлектрических свойств и ее толщины.
III. Емкость при параллельном и последовательном соединении конденсаторов
параллельно
По закону сохранения заряда
б) последовательное соединение
По закону сохранения заряда
§ 3 Энергия электростатического поля
1.Энергия системы фиксированных зарядов
Электростатическое поле потенциальное. Силы, действующие между зарядами — консервативные силы. Система фиксированных зарядов должна обладать потенциальной энергией. Находим потенциальную энергию двух фиксированных зарядов q 1 и q 2 , разделенных расстоянием r друг от друга.
Потенциальная энергия заряда q 2 в поле созданного заряда q 1 , равна
Аналогично потенциальная энергия заряда q 1 в поле, созданном зарядом q 2 , равна
Видно, что Вт 1 = Вт 2 , затем определить потенциальную энергию системы зарядов q 1 и q 2 в Вт , мы можем написать
где φ i — потенциал, генерируемый в точке, где находится заряд q i , все заряды, кроме i-го.
- Энергия изолированного заряженного проводника.
Энергию электрического поля заряженного изолированного проводника можно определить, рассматривая полную работу, совершаемую при перемещении небольших количеств заряда dq из бесконечности к этому проводнику.
Если проводник имеет заряд q , емкость C и потенциал φ , то для переноса заряда d q из бесконечности на проводник работа должна быть затрачена
Для зарядки проводника от потенциала земли до потенциала φ необходимо выполнить работу
Потенциальная энергия, равная работе, которую необходимо совершить, чтобы зарядить проводник
4.Энергия заряженного конденсатора.
Выразим энергию конденсатора через значения, характеризующие конденсатор.
, поскольку поле внутри конденсатора однородно, вы можете ввести объемную плотность энергии (объемная плотность — энергия на единицу объема)
Электростатика проводников
- Дом
- Английский
- Класс 10
- Наука
- Химические реакции
- Кислоты основания и соли
- Металлы и неметаллы
- Углеродные соединения
- Периодическая классификация элементов
- Жизненные процессы
- Контроль и координация в отношении животных и растений
- Репродукция
- Наследственность и эволюция
- Природный феномен
- Отражение света
- Преломление света
- Влияние тока
- Магнитные эффекты тока
- Наука
- Класс 11
- Физика 1
- Физический мир
- Единицы и измерения
- Движение по прямой
- Движение в плоскости
- Законы движения
- Рабочая энергия и мощность
- Гравитация
- Физика 2
- Система частиц и вращательного движения
- Механические свойства твердых тел
- Механические свойства жидкостей
- Тепловые свойства вещества
- Термодинамика
- Кинетическая теория
- Колебания
- Волны
- Физика 1
- Класс 12
- Физика 1
- Электрические заряды и поле
- Электростатический потенциал и емкость
- Текущее электричество
- Движущиеся заряды и магнетизм
- Магнетизм и материя
- Электромагнитная индукция
- Переменный ток (AC)
- Электромагнитные волны
- Физика 2
- Лучевая оптика
- Волновая оптика
- Двойная природа излучения и материи
- Атомов
- Ядра
- Электронные устройства
- Химия 1
- Твердотельный
- Решение
- Электрохимия
- Химическая кинетика
- Химия поверхности
- Изоляция элементов
- p — Элементы блока
- Группа 15 элементов
- Группа 16 элементов
- Группа 17 элементов
- Группа 18 — Благородные газы
- d- и f- элемент блока
- Переходные элементы (d-блок)
- Внутренние переходные элементы (f-блок)
- Химия 2
- Соединения ко-ординации
- Галоалканы и галоарены
- Спирты, фенолы и эфиры
- Альдегиды, кетоны и карбоновые кислоты
- Органические соединения, содержащие азот
- Биомолекулы
- Полимеры
- Химия в повседневной жизни
- Физика 1
- Дополнительные знания
- प्रसिद्द व्यक्तित्व
- पंचतंत्र
- Важные дни
- Вдохновение
- Свяжитесь с нами
- Укажите свой институт
- Логин
- Дом
- Английский
- Класс 10
- Наука
- Химические реакции
- Кислоты основания и соли
- Металлы и неметаллы
- Углеродные соединения
- Периодическая классификация элементов
- Жизненные процессы
- Контроль и координация животных и растений
- Репродукция
- Наследственность и эволюция
- Природный феномен
- Отражение света
- Преломление света
- Влияние тока
- Магнитные эффекты тока
- Наука
- Класс 11
- Физика 1
- Физический мир
- Единицы и измерения
- Движение по прямой
- Движение в плоскости
- Законы движения
- Рабочая энергия и мощность
- Гравитация
- Физика 2
- Система частиц и вращательного движения
- Механические свойства твердых тел
- Механические свойства жидкостей
- Тепловые свойства вещества
- Термодинамика
- Кинетическая теория
- Колебания
- Волны
- Физика 1
- Класс 12
- Физика 1
- Электрические заряды и поле
- Электростатический потенциал и емкость
- Текущее электричество
- Движущиеся заряды и магнетизм
- Магнетизм и материя
- Электромагнитная индукция
- Переменный ток (AC)
- Электромагнитные волны
- Физика 2
- Лучевая оптика
- Волновая оптика
- Двойная природа излучения и материи
- Атомов
- Ядра
- Электронные устройства
- Химия 1
- Твердотельный
- Решение
- Электрохимия
- Химическая кинетика
- Химия поверхности
- Изоляция элементов
- p — Элементы блока
- Группа 15 элементов
- Группа 16 элементов
- Группа 17 элементов
- Группа 18 — Благородные газы
- d- и f- блочный элемент
- Переходные элементы (d-блок)
- Внутренние переходные элементы (f-блок)
- Химия 2
- Соединения ко-ординации
- Галоалканы и галоарены
- Спирты, фенолы и эфиры
- Альдегиды, кетоны и карбоновые кислоты
- Органические соединения, содержащие азот
- Биомолекулы
- Полимеры
- Химия в повседневной жизни
- Физика 1
- Дополнительные знания
- प्रसिद्द व्यक्तित्व
- पंचतंत्र
- Важные дни
- Вдохновение
- Свяжитесь с нами
советов по созданию спецэффектов в After Effects
Узнайте о четырех приемах создания спецэффектов в After Effects.Посмотрите руководство и узнайте, как использовать эти советы без каких-либо плагинов.
Мы уже рассмотрели несколько основных советов по созданию композиций в After Effects, так что теперь давайте изучим некоторые приемы наложения специальных эффектов. Эти советы полезны как для практических, так и для компьютерных эффектов, которые вы добавляете в видеоматериал. Самое приятное то, что вам не нужны сторонние плагины для каких-либо эффектов в After Effects.
Готовы? Давайте начнем!
Создание кадра на зеленом экране
Прежде, чем мы начнем, если вам нужна помощь с вводом кадра зеленого экрана, PremiumBeat поможет вам.В этой статье описан процесс ввода ключей, рекомендованный Adobe. На самом деле я использую его постоянно, даже вместо сторонних плагинов для ввода ключей, которыми я владею.
Обработка кадра зеленого экрана в Adobe.Подбор цвета
Согласование цветов — один из моих любимых эффектов, потому что он имитирует свет сцены, отраженный от элемента, который вы составляете. К тому же это очень просто! В вашей композиции у вас должен быть фоновый материал и элемент, который вы на него накладываете.(Это может быть изображение, видео с зеленого экрана, видео CGI и т. Д.)
Создайте корректирующий слой.Сначала создайте корректирующий слой и поместите его между фоновым материалом и составным элементом. Примените эффект Gaussian Blur к корректирующему слою и установите Blurriness на 100 . Это помогает сгладить цвета, чтобы получить хороший средний цвет.
Примените эффект «Оттенок», удалите корректирующий слой, затем установите меньшее значение «Оттенок».Затем примените эффект Tint к составному элементу. (В моем примере это космический корабль.) Теперь используйте палитру цветов в эффекте «Оттенок» для настроек Map Black to и Map White to . Выберите более темный цвет и более светлый цвет для фонового материала рядом с местом, где будет компоноваться ваш объект.
Теперь удалите корректирующий слой с эффектом «Размытие по Гауссу» и установите для параметра «Оттенок» меньшее значение. Обычно около 10% -15% , но иногда до 50% , если ваш объект находится далеко от неба, как в этом случае.
Вуаля! Конечный продукт.Легкая пленка
Создайте эффект легкого обтекания объекта, чтобы имитировать естественный свет, исходящий от него. Обычно это используется для сцен, где фон очень яркий или переэкспонированный — например, яркое небо или огни позади объекта. В этом примере мы собираемся работать с кадрами зеленого экрана и пластиной с фоновыми материалами.
Имитируйте естественный свет, создавая эффект светового обертывания.Сначала продублируйте фоновый материал и переместите его копию в верхнюю часть композиции.Он будет служить нашим световым слоем после того, как мы применим к нему некоторые эффекты. Примените Gaussian Blur effect и установите Blurriness на 100 .
Затем примените эффект Set Matte и установите Take Matte From Layer для видеоряда зеленого экрана. Также обратите внимание на Invert Matte . Затем примените эффект Channel Blur и установите для Alpha Blurriness значение 50-80 . Наконец, примените второй эффект Set Matte и снова установите Take Matte From Layer для видеоряда зеленого экрана.
Не забудьте настроить прозрачность.В результате должен получиться слой, на котором будет только ваша световая пленка. Установите для слоя режим наложения Screen и настройте параметр Alpha Blurriness , чтобы настроить необходимое количество светового покрытия. Я также рекомендую отрегулировать непрозрачность слоя светового обтекания, если необходимо.
Добавление размытия в движении
После того, как вы настроили видео на зеленом экране, вы можете заметить, что он немного нервный.Это связано с тем, что во время движения по краям объекта исчезает большое количество естественного размытия при движении. Однако мы можем добавить это обратно, используя Pixel Motion Blur в After Effects.
Добавьте размытие в движении обратно в изображение с помощью Pixel Motion Blur.Во-первых, предварительно скомпонует кадра зеленого экрана. Затем примените эффект Pixel Motion Blur . Установите Shutter Samples между 12-16 (или выше) в зависимости от того, насколько быстро движется ваш объект.Вы также можете увеличить настройку Shutter Angle , чтобы добавить еще больше размытия при движении, если это необходимо.
Добавьте еще больше размытия в движении, увеличив значение Shudder Angle .Использование цветного освещения
Вы можете использовать практичное цветное освещение на зеленом экране объекта, чтобы оно соответствовало сцене, в которую он будет добавлен. Вы можете сделать это разными способами. Два из самых простых — использовать цветные гели или цветные огни RGB.
Совместите сцену с фоном, используя цветные гели или цветные огни RGB.Цветные гели — определенно более дешевый вариант, и обычно вы можете купить хороший набор примерно за 20–30 долларов. Самым большим преимуществом для них является то, что вы можете использовать их с более крупными источниками света для получения большого количества цветов.
В качестве альтернативы, очень популярны более мелкие цветные огни RGB, которые позволяют быстро и легко набрать множество различных цветовых комбинаций. Единственный недостаток в том, что они, скорее всего, не будут излучать столько света.
Свет на заднем плане соответствует свету, отраженному от объекта.Другой способ использования цветного освещения — это добавить свет в место, где вы снимаете, где вы собираетесь что-то скомпоновать позже. Например, для красного светящегося шара я добавил свет, обращенный вниз, с красным гелем, чтобы осветить окружающую область красным светом.
Осветите объект во время съемки.Заинтересованы бесплатными треками, которые мы использовали для создания этого видео? Послушайте еще раз:
Узнайте больше советов по созданию видео и найдите БЕСПЛАТНЫЕ элементы видео:
.
.jpg) (1995), Руководство по сигнализации и передаче абонентских шлейфов , IEEE Press, ISBN 978-0-7803-0440-6
(1995), Руководство по сигнализации и передаче абонентских шлейфов , IEEE Press, ISBN 978-0-7803-0440-6
 , ISBN 978-0-471-73277-8
, ISBN 978-0-471-73277-8
 Существование этой силы равноценно появлению в проводнике некоторого добавочного сопротивления, носящего название индуктивного сопротивления цепи. Встречая в центре проводника наибольшее индуктивное сопротивление, ток будет стремиться пройти в направлении наименьшего сопротивления и вытисниться к поверхности проводника.
Существование этой силы равноценно появлению в проводнике некоторого добавочного сопротивления, носящего название индуктивного сопротивления цепи. Встречая в центре проводника наибольшее индуктивное сопротивление, ток будет стремиться пройти в направлении наименьшего сопротивления и вытисниться к поверхности проводника.
