Преобразование звезды в треугольник и треугольника в звезду: подробное руководство

Как выполнить преобразование звезды в треугольник и треугольника в звезду. Какие формулы используются для этих преобразований. Как легко запомнить формулы преобразования звезды и треугольника. Почему эти преобразования важны в электротехнике.

Что такое преобразование звезды и треугольника

Преобразование звезды и треугольника — это метод в электротехнике, позволяющий упростить расчет сложных электрических цепей. Он включает в себя два типа преобразований:

• Преобразование звезды в треугольник (Y-Δ)
• Преобразование треугольника в звезду (Δ-Y)

Эти преобразования позволяют заменить одну конфигурацию резисторов на эквивалентную, не меняя общего сопротивления цепи. Это очень полезно, когда резисторы не соединены просто последовательно или параллельно.

Почему преобразование звезды и треугольника важно

Преобразование звезды и треугольника имеет большое значение в электротехнике по нескольким причинам:

1. Упрощение сложных цепей: Позволяет преобразовать запутанные соединения в более простые эквивалентные схемы.
2. Облегчение расчетов: Упрощенные схемы намного легче анализировать и рассчитывать.
3. Анализ трехфазных систем: Широко применяется при анализе трехфазных электрических систем.
4. Проектирование электрических сетей: Помогает оптимизировать конфигурацию электрических сетей.

Как выполняется преобразование звезды в треугольник? Для этого используются специальные формулы, которые мы рассмотрим далее.

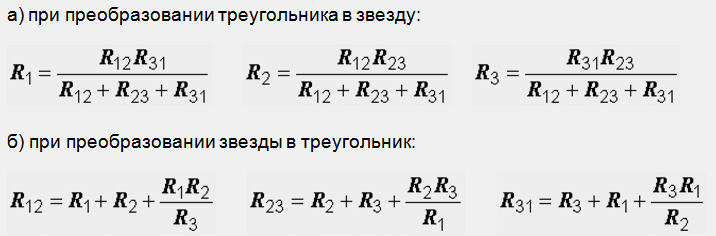
Формулы преобразования звезды в треугольник

При преобразовании звезды в треугольник используются следующие формулы:

• R_ab = R_a + R_b + (R_aR_b)/R_c
• R_bc = R_b + R_c + (R_bR_c)/R_a
• R_ca = R_c + R_a + (R_cR_a)/R_b

Где R

ab, R_bc и R_ca — сопротивления сторон треугольника, а R_a, R_b и R_c — сопротивления лучей звезды.

Как запомнить формулы преобразования звезды в треугольник

Чтобы легко запомнить эти формулы, обратите внимание на следующее:

• Каждое сопротивление треугольника равно сумме двух соответствующих сопротивлений звезды.
• К этой сумме добавляется произведение этих же сопротивлений, деленное на третье сопротивление звезды.
• Индексы в формуле соответствуют узлам схемы.

Как выполняется обратное преобразование — из треугольника в звезду? Давайте рассмотрим соответствующие формулы.

Формулы преобразования треугольника в звезду

При преобразовании треугольника в звезду используются следующие формулы:

• R_a = (R_abR_ca) / (R_ab + R_bc + R_ca)
• R_b = (R_abR_bc) / (R_ab + R_bc + R_ca)
• R_c = (R_bcR _ca) / (R_ab + R_bc + R_ca)

Где R_a, R_b и R_c — сопротивления лучей звезды, а R_ab, R_bc и R_ca — сопротивления сторон треугольника.

Как запомнить формулы преобразования треугольника в звезду

Чтобы легко запомнить эти формулы, обратите внимание на следующую закономерность:

• В числителе — произведение двух сопротивлений треугольника, примыкающих к соответствующему узлу.
• Знаменатель одинаков для всех трех формул — сумма всех сопротивлений треугольника.
• Индексы в формуле соответствуют узлам схемы.

Теперь, когда мы разобрали формулы, давайте рассмотрим практические примеры применения этих преобразований.

Пример преобразования звезды в треугольник

Рассмотрим схему звезды с сопротивлениями R_a = 2 Ом, R_b = 3 Ом, R_c = 4 Ом. Требуется преобразовать ее в эквивалентный треугольник.

Используя формулы преобразования звезды в треугольник, получаем:

• R_ab = 2 + 3 + (2 * 3) / 4 = 6.5 Ом
• R_bc = 3 + 4 + (3 * 4) / 2 = 13 Ом
• R_ca = 4 + 2 + (4 * 2) / 3 = 8.67 Ом

Таким образом, эквивалентная схема треугольника будет иметь сопротивления 6.5 Ом, 13 Ом и 8.67 Ом.

Пример преобразования треугольника в звезду

Теперь рассмотрим обратную задачу. Дана схема треугольника с сопротивлениями R_ab = 6 Ом, R_bc = 8 Ом, R_ca = 12 Ом. Требуется преобразовать ее в эквивалентную звезду.

Используя формулы преобразования треугольника в звезду, получаем:

• R_a = (6 * 12) / (6 + 8 + 12) = 2.77 Ом
• R_b = (6 * 8) / (6 + 8 + 12) = 1.85 Ом
• R_c = (8 * 12) / (6 + 8 + 12) = 3.69 Ом

Таким образом, эквивалентная схема звезды будет иметь сопротивления 2.77 Ом, 1.85 Ом и 3.69 Ом.

Практическое применение преобразований звезды и треугольника

Преобразования звезды и треугольника находят широкое применение в электротехнике и электронике:

• Анализ сложных электрических цепей
• Расчет трехфазных систем
• Проектирование электрических сетей
• Оптимизация схем электронных устройств

Какие преимущества дает использование этих преобразований на практике? Рассмотрим основные из них.

Преимущества использования преобразований звезды и треугольника

Применение преобразований звезды и треугольника предоставляет ряд существенных преимуществ:

1. Упрощение анализа сложных цепей
2. Сокращение времени на расчеты
3. Повышение точности вычислений
4. Облегчение поиска неисправностей в электрических схемах
5. Оптимизация проектирования электрических сетей

Эти преимущества делают преобразования звезды и треугольника незаменимым инструментом для инженеров-электриков и электронщиков.

Ограничения и особенности применения преобразований

Несмотря на свою полезность, преобразования звезды и треугольника имеют некоторые ограничения и особенности применения:

• Применимы только для линейных цепей
• Не учитывают реактивные составляющие сопротивлений
• Могут усложнить анализ при наличии источников тока в преобразуемых участках
• Требуют внимательности при выборе узлов для преобразования

Учет этих особенностей позволяет корректно применять преобразования и получать достоверные результаты.

Заключение

Преобразования звезды в треугольник и треугольника в звезду — мощный инструмент анализа электрических цепей. Они позволяют упростить сложные схемы, сделать расчеты более точными и эффективными. Освоение этих преобразований — важный шаг в изучении электротехники и электроники.

Регулярная практика в применении этих преобразований поможет развить интуитивное понимание поведения электрических цепей и стать более квалифицированным специалистом в области электротехники.

Эквивалентное преобразование треугольника и звезды сопротивлений

    Пусть требуется рассчитать цепь, показанную на рис. 1.12, (а).

 

    Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.

    Треугольник и звезда сопротивлений имеют вид, показанный на рис. 1.13.

    Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.

    Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:

 

 

б) при преобразовании звезды в треугольник:

 

 

Структура приведенных формул проста и легко запоминается.

    Например, сопротивление звезды R₁, присоединенное к узлу 1, получается перемножением сопротивлений R₁₂ и R₃₁ треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.

    При обратном преобразовании сопротивление треугольника R₁₂, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R₁ и R₂, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R₃.

Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В,
R₁ = 20 Ом, R₂ = 30 Ом, R₃ = 5 Ом, R₄ = 20 Ом, R₅ = 50 Ом.

 а) Решение преобразования треугольника в звезду: 

после преобразования треугольника, образованного сопротивлениями R₁, R₂ и R₅, в звезду, получаем схему, показанную на рис. 1.12, б. Обращаем внимание на то, что токи в непреобразованной части схемы (I, I₃ и I₄) остались теми же.

    Сопротивления звезды определяем по сформулированному выше правилу:

Где,общее сопротивление цепи легко находится по последней формуле R_общ = 16,5 Ом.

    Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:

    Токи в параллельных ветвях: 

 

 

где, I₃ = 28 A и I₄ = 12 A соответственно.

Возвращаемся к исходной схеме (рис. 1.12, а):

 

 

где, I₁ = 26 A и I₂ = 14 A соответственно.

  Ток в пятой ветви находим из первого закона Кирхгофа: I₅ = I₁–I₃ = 26–28 = –2 A. Знак (—) минус говорит о том, что действительное направление тока I₅ противоположно указанному на схеме.

    б) Решение  преобразованием звезды в треугольник. 

Преобразуем звезду, образуемую в схеме на рис. 1.12, а сопротивлениями R₁, R₅ и R₃, в эквивалентный треугольник (рис. 1.12, в).

    Определяем сопротивления треугольника:

 

 

Теперь рассчитываем преобразованную цепь.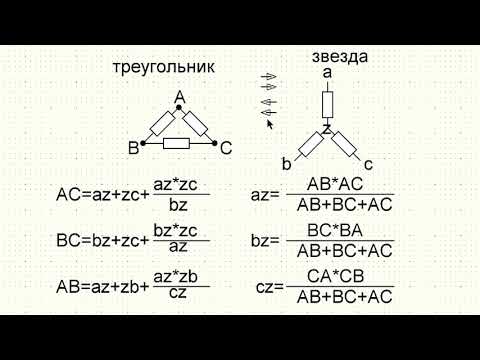

Сначала находим эквивалентные сопротивления участков ac и cd:

Затем определяем общее сопротивление и токи:

Возвращаемся к исходной схеме:

   Для решения в приведенных формулах, вставьте числовые значения параметров цепи и сравните результаты вычислений с полученными выше решения в примере 1.3а.

Подготовка к олимпиаде. Методы расчета резисторных схем постоянного тока. 3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»

          

Методы расчета резисторных схем постоянного тока

3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»

Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.

Подобные преобразования широко известны для случая двух выводов. Так, например, два резистора сопротивлениями R₁ и R₂, включенные последовательно, можно заменить одним резистором сопротивлением R₁ + R₂. Если резисторы включены параллельно, то их можно заменить одним резистором сопротивлением

$\frac{R_1R_2}{R_1 + R_2}$

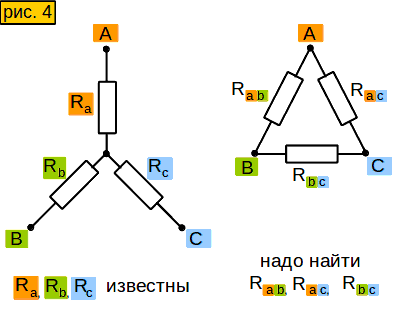
И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения. Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (рис. а) в «треугольник» (рис. б), и наоборот.

Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r₁ соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R₁₃ подключен к точкам 1 и 3. Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек). Так, в «звезде» сопротивление между точками 1 и 2 равно r₁ + r₂, в «треугольнике»

$\frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$,

следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:

$r_1 + r_2 = \frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$.

Аналогично для точек 2 и 3 и для точек 1 и 3:

$r_2 + r_3 = \frac{R_{23}(R_{12} + R_{13})}{R_{12} + R_{13} + R_{23}}$,

$r_1 + r_3 = \frac{R_{13}(R_{12} + R_{23})}{R_{12} + R_{13} + R_{23}}$.

Сложим все эти уравнения и, поделив обе части на 2, получим:

$r_1 + r_2 + r_3 = \frac{R_{12}R_{13} + R_{12}R_{23} + R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.

Вычитая из этого уравнения поочередно предыдущие, получим:

$r_1 = \frac{R_{12}R_{13}}{R_{12} + R_{13} + R_{23}}$,

$r_2 = \frac{R_{12}R_{23}}{R_{12} + R_{13} + R_{23}}$,

$r_3 = \frac{R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.

Эти выражения легко запомнить:

знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:

$r_1 \rightarrow R_{12}R_{13}, r_2 \rightarrow R_{12}R_{23}, r_3 \rightarrow R_{13}R_{23}$.

Аналогично получают и формулы обратного преобразования:

$R_{12} = \frac{r_1r_2 + r_1r_3 + r_2r_3}{r_3}$,

$R_{13} = \frac{r_1r_2 + r_1r_3 + r_2r_3}{r_2}$,

$R_{23} = \frac{r_1r_2 + r_1r_3 + r_2r_3}{r_1}$.

Последние выражения также легко запомнить и проверить:

числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.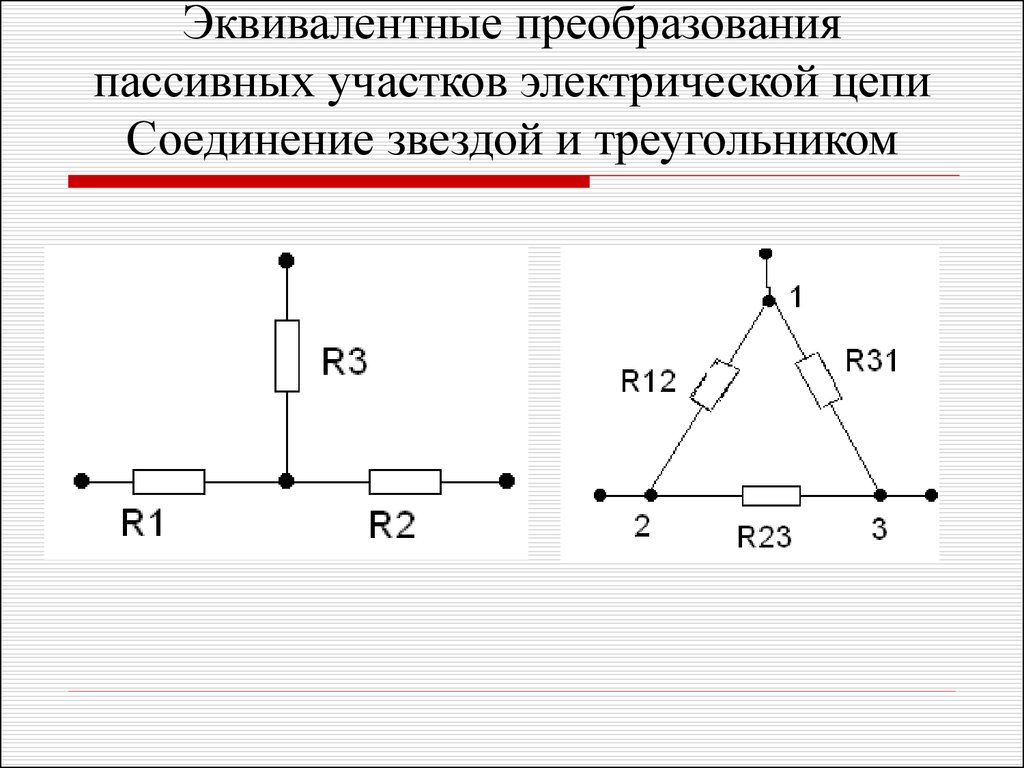

Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.

Задача 27. Определите сопротивление цепи АВ (рис.), если R₁ = R₅ = 1 Ом, R₂ = R₆ = 2 Ом, R₃ = R₇ = 3 Ом, R₄ = R₈ = 4 Ом.

Решение. Преобразуем «треугольники» R₁R₂R₈ и R₄R₅R₆ в эквивалентные «звезды». Схема примет иной вид (рис.).

Сопротивления $r_1, r_2, …, r_6$ найдем по формулам:

$r_1 = \frac{R_1R_8}{R_1 + R_2 + R_8} = \frac{4}{7}$ Ом;

$r_2 = \frac{R_1R_2}{R_1 + R_2 + R_8} = \frac{2}{7}$ Ом;

$r_3 = \frac{R_2R_8}{R_1 + R_2 + R_8} = \frac{8}{7}$ Ом;

$r_4 = \frac{R_4R_6}{R_4 + R_5 + R_6} = \frac{8}{7}$ Ом;

$r_5 = \frac{R_5R_6}{R_4 + R_5 + R_6} = \frac{2}{7}$ Ом;

$r_6 = \frac{R_4R_5}{R_4 + R_5 + R_6} = \frac{4}{7}$ Ом.

Теперь нет никаких препятствий для расчета схемы, которая состоит из последовательно и параллельно соединенных резисторов (рис.). После простых расчетов получим

$R_{AB} = \frac{47}{14}$ Ом

---

1.1. Шаговый (рекуррентный) метод

1.2. Метод преобразования

1.3. Метод равнопотенциальных узлов

1.3.1. Метод исключения «пассивных» участков цепи

1.3.2. Метод объединения равнопотенциальных узлов

1.3.3. Метод разделения узлов

1.3.4. Метод расщепления ветвей

1.4.1 Расчет эквивалентных сопротивлений линейных бесконечных цепей

1.4.2. Расчет эквивалентных сопротивлений плоскостных бесконечных цепей

1.4.3. Расчет эквивалентных сопротивлений объемных бесконечных цепей

2. Расчет цепей по правилам Кирхгофа

3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»

Преобразование звезды/треугольника 1.0 — подробная информация

Преобразование звезды/треугольника 1.0 — подробная информация

0012 Описание: Довольно простая программа для преобразования звезды/треугольника. Также имеет возможности зеркалирования и поворота. Имя файла: delta.zip ID: 4530 1.0 Author: José María Paz Downloaded file size: 2,631 bytes Size on calculator: 5 KB Платформы: 49/50 48   Рейтинг пользователей: Еще нет оценки (вы должны войти в систему, чтобы проголосовать) 9091 Основная категория0012 Science/Electricity Languages:   File date: 2001/03/09 14:56:02 Source code: Not included Скачать Счет: 16 959 История версий: 2001/03/09: Добавлена ​​на сайте Архив. 0012 Дата длина Дата Имя времени ——— —- —- —- 168 03-08-01 17:00 readme.txt 5104 03-08 -01 16:19   delta  ———                   ——-      5272                   2 files Screenshot: User comments: John Kerpal 28-11-2002 11:37:05 Не могли бы вы мне помочь, ребята, я получаю сообщение об ошибке PROMPT: HALT не разрешено при попытке запустить программу. Это происходит и в некоторых других программах. Вы должны войти в систему, чтобы добавить свой комментарий.

Часть архива калькуляторов HP,
Copyright 1997-2022 Eric Rechlin.

Преобразование звезда-треугольник с советами по запоминанию формул

Почему и как мы делаем преобразование звезда в дельта или дельта в звезду

Преобразование звезда и дельта включает в себя преобразование из звезды в дельту или дельты в звезду, и мы делаем это когда наши резисторы не соединены параллельно или последовательно.

Этот метод весьма полезен, но в большинстве случаев учащиеся забывают формулу для быстрого использования, но, в В этом разделе я дам вам наглядный совет, чтобы никогда не забывать об этом, так что давайте начнем.

Способ соединения треугольника и звезды проиллюстрирован ниже в сравнении с последовательностью и последовательностью. параллельное соединение резисторов.

Дельта может быть построена двумя способами: треугольником. форму или форму пирога, в то время как звезда имеет звезда или Т-образная форма, поэтому обязательно обратите внимание на это.

Маленький самородок

Звезду иногда называют звездой, а дельту — буквой Пи.

Преобразование треугольника в звезду не легче работать, за исключением того, что мы преобразуем его в другую форму, а затем решаем, поэтому мы выполнить это преобразование.

Итак, чтобы преобразовать дельту в звезду, это делается следующим образом, хотя формула указана как —

Формула преобразования треугольника в звезду

Как запомнить формулу преобразования треугольника в звезду

Итак, давайте вспомним эту формулу, начав с R ₁ .

Глядя на R ₁ , мы видим, что узел в верхней части R ₁ имеет два резистора. из дельта сети, связаны или привязаны к нему. Итак, в этом случае мы говорим, что есть 2 ноги, влияющие на R ₁ , которые являются R _и и Р _б .

Затем, поскольку дельта является нашим источником преобразования и также соединены последовательно (помните в резисторы, соединенные последовательно, значения складываются и через них протекает одинаковый ток) поэтому, суммируем (R _a + R _b + R _c ), а затем разделить на наш первый результат это R _a и R _b (помните, что нам нужно умножить R _на и R _{b на} , поскольку они влияют на R ₁ ).

Таким образом, преобразование дает R ₁ = (R _a R _b ) / (R _a + R _b + R _c ).

Проделав то же самое для R ₂ , получим Р ₂ = (Р _и Р _c ) / (R _a + R _b + R _c ) а для R ₃ что будет если сделать самому не глядя в ответ.

Если вы получили ответ правильно, это хорошо и по существу видно, это только ножка, привязанная к нашему резистору в фокусе имеет значение, поскольку нижняя часть (R _a + R _b + R _c ) одинакова для R ₁ , R ₂ и R ₃ .

Преобразование или преобразование из звезды в треугольник

Во-первых, в этом преобразовании мы должны найти R _a , R _b и R _c как напротив последнего раздела, где мы должны найти R ₁ , R ₂ и R ₃ .

Формула представлена ​​как

R _a = (R ₁ R ₂ + R ₂ R ₃ + Р ₃ Р ₁ ) / Р ₃ , Р _б = (Р ₁ Р ₂ + Р ₂ Р ₃ + Р ₃ Р ₁ ) / Р ₂ и Р _с = (Р ₁ Р ₂ + Р ₂ Р ₃ + R ₃ R ₁ ) / R ₁

Формула преобразования звезда в треугольник

Как запомнить формулу преобразования звезда в треугольник

А теперь вспомним формулу, воспользовавшись нашей подсказкой. Прежде всего, вы можете видеть, что R _и затронуты по R ₁ и R ₂ . А это Р ₁ и R ₂ также соединены в средней точки друг к другу с R ₃ , поэтому в этом случае мы не можем просто применить то же правило, что и предыдущий мы сделали для преобразования из дельты в звезду.

Но что нам нужно сделать, так это то, что R ₁ и R ₂ привязаны к R _a , а также R ₁ и R ₂ соединены в узле с R ₃ , тогда мы просто умножаем R ₁ R ₂ и затем добавить R ₂ R ₃ и, наконец, добавить R ₃ R ₁ что дает это.

Этот шаг может показаться немного запутанным, но просто повторите его еще раз, пока не добьетесь нужного результата. этого.

Подсказка

Если вы посмотрите на два предыдущих изображения, вы обнаружите, где показан шаблон — это также может помочь вспомнить формулу.

Затем после этого мы делим наш первый результат, который равен (R ₁ R ₂ + R ₂ R ₃ + R ₃ R ₁ ) за ногу, противоположную нашей R _a это R ₃ , или мы можем сказать, что ветвь не связана напрямую с R _a .

Аналогично, R _b = (R ₁ R ₂ + R ₂ R ₃ + R ₃ R ₉₀₂ 1,8 ) /

Примечание

Так как верхняя сторона одинакова для всех случаев, а меняется только нижняя, вспомним нижнюю часть как ножку напротив искомого резистора. И в этом случае R _b и противоположная сторона R ₂ .

Теперь ваша очередь выполнить R _c , а позже проверить свой ответ.

Наконец, давайте попробуем резюмировать все, что мы только что обсудили, решив несколько примеров.

Пример преобразования треугольника в звезду

Пример 1 преобразовать приведенную ниже схему треугольника в эквивалент звезды.