При параллельном соединении резисторов. Параллельное соединение резисторов: принципы, расчеты и применение

Как работает параллельное соединение резисторов. Какие формулы используются для расчета общего сопротивления. Где применяется параллельное соединение на практике. Какие преимущества и недостатки у такого типа соединения.

Что такое параллельное соединение резисторов

При параллельном соединении резисторов все элементы подключаются к одним и тем же двум точкам электрической цепи. Это означает, что напряжение на всех резисторах одинаково и равно напряжению источника питания.

Основные особенности параллельного соединения:

• Напряжение на всех элементах одинаково
• Общий ток делится между параллельными ветвями
• Общее сопротивление всегда меньше сопротивления наименьшего из параллельно соединенных резисторов

Расчет общего сопротивления при параллельном соединении

Для расчета общего сопротивления при параллельном соединении резисторов используется следующая формула:

1/R_общ = 1/R₁ + 1/R₂ + 1/R₃ + … + 1/R_n

Где R_общ

— общее сопротивление, R₁, R₂ и т.д. — сопротивления отдельных резисторов.

Для двух параллельно соединенных резисторов формула упрощается:

R_общ = (R₁ * R₂) / (R₁ + R₂)

Распределение токов в параллельной цепи

При параллельном соединении общий ток I разветвляется на отдельные токи I₁, I₂ и т.д., протекающие через каждый резистор. Сумма этих токов равна общему току:

I = I₁ + I₂ + I₃ + … + I_n

Ток в каждой ветви обратно пропорционален сопротивлению этой ветви. То есть чем меньше сопротивление участка, тем больший ток через него протекает.

Преимущества параллельного соединения резисторов

Параллельное соединение имеет ряд важных преимуществ:

• Позволяет уменьшить общее сопротивление цепи
• Обеспечивает независимую работу параллельно подключенных устройств
• Повышает надежность электрической цепи
• Дает возможность подключать устройства с разным сопротивлением к одному источнику питания

Области применения параллельного соединения

Параллельное соединение широко используется в различных областях электротехники и электроники:

• В бытовых электрических сетях — для подключения различных потребителей к одной линии
• В системах освещения — для независимого управления группами светильников
• В электронных схемах — для создания делителей напряжения и тока
• В измерительной технике — для расширения пределов измерения приборов
• В системах электропитания — для повышения мощности и надежности

Расчет параллельного соединения на практике

Рассмотрим пример расчета параллельного соединения трех резисторов:

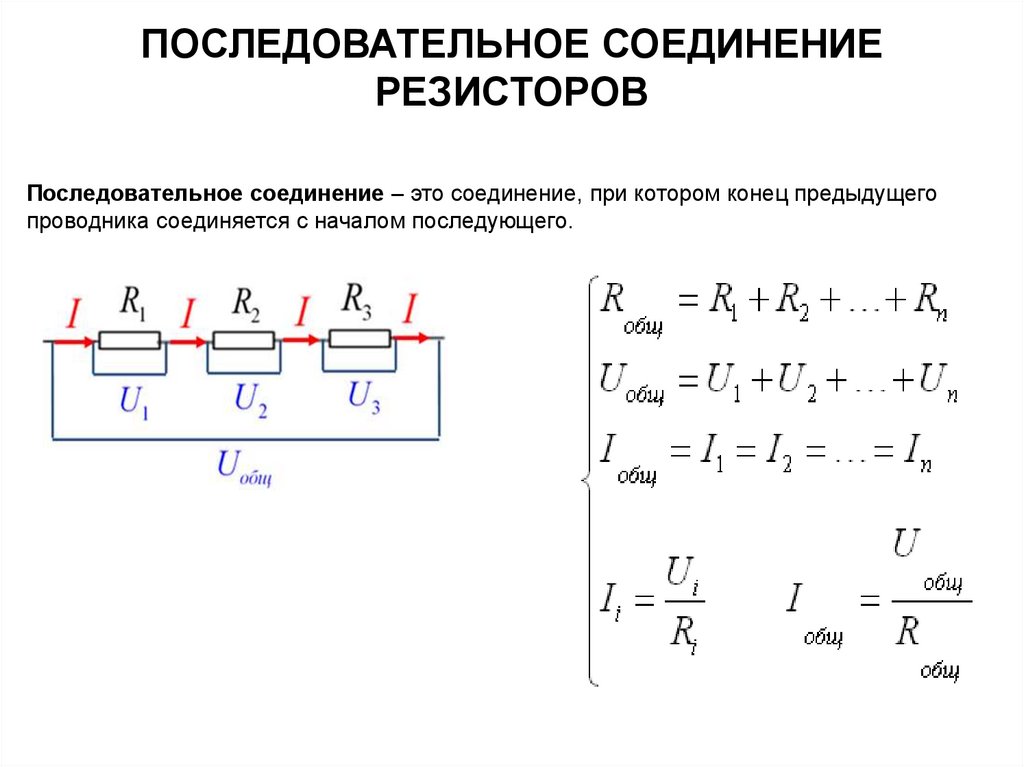
Даны резисторы: R₁ = 10 Ом, R₂ = 20 Ом, R₃ = 30 Ом

Находим общее сопротивление:

1/R_общ = 1/10 + 1/20 + 1/30 = 0,1 + 0,05 + 0,033 = 0,183

R_общ = 1 / 0,183 ≈ 5,46 Ом

Как видим, общее сопротивление оказалось меньше сопротивления наименьшего из резисторов (10 Ом).

Особенности расчета сложных параллельных цепей

При расчете сложных параллельных цепей следует учитывать несколько важных моментов:

• Общее сопротивление всегда меньше сопротивления любого из параллельно включенных элементов
• Чем больше параллельных ветвей, тем меньше общее сопротивление
• Для упрощения расчетов сложные параллельные участки можно заменять их эквивалентным сопротивлением
• В некоторых случаях удобно использовать метод узловых потенциалов

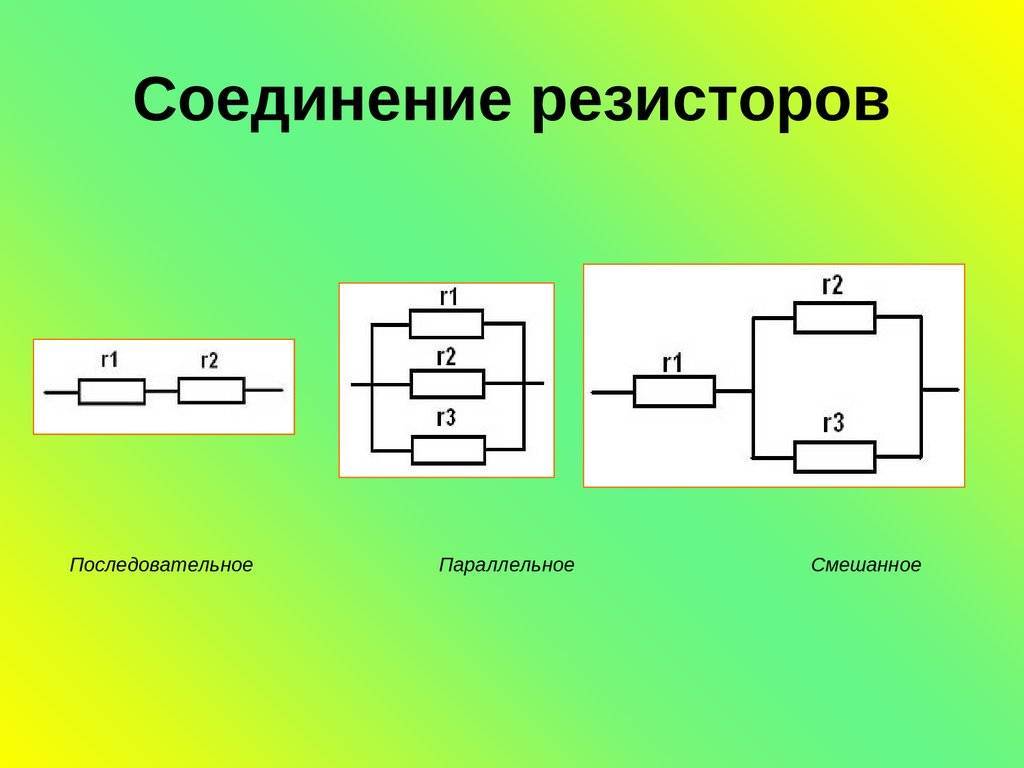
Сравнение параллельного и последовательного соединения

Параллельное и последовательное соединения имеют принципиальные различия:

Параметр	Параллельное соединение	Последовательное соединение
Напряжение	Одинаково на всех элементах	Сумма напряжений на элементах
Ток	Сумма токов через элементы	Одинаков во всех элементах
Общее сопротивление	Меньше наименьшего	Сумма сопротивлений

Параллельное соединение в быту и промышленности

Параллельное соединение широко применяется как в бытовых электрических сетях, так и в промышленных установках:

• В домашней электропроводке все розетки и осветительные приборы подключены параллельно
• В автомобильной электрике большинство потребителей соединены параллельно
• На производстве параллельно подключают мощные электродвигатели и другое оборудование
• В электронике параллельное соединение используется в схемах стабилизаторов, усилителей, фильтров

Проблемы и ограничения параллельного соединения

Несмотря на преимущества, параллельное соединение имеет ряд ограничений:

• Увеличение общего тока в цепи, что требует проводов большего сечения
• Сложность равномерного распределения тока между параллельными ветвями
• Возможность протекания уравнительных токов при неидентичности параллельных элементов
• Необходимость использования защитных устройств в каждой параллельной ветви

Расчет мощности при параллельном соединении

При параллельном соединении общая мощность равна сумме мощностей всех параллельно включенных элементов:

P_общ = P₁ + P₂ + P₃ + … + P_n

Это позволяет легко наращивать мощность системы путем параллельного подключения дополнительных элементов.

Заключение

Параллельное соединение резисторов — важный принцип построения электрических цепей, широко применяемый в различных областях техники. Понимание особенностей параллельного соединения позволяет грамотно проектировать и эксплуатировать электрические и электронные устройства, обеспечивая их эффективную и надежную работу.

Основы электроники

Основы

Основы электроники и схемотехники начинаются с изучения последовательных и параллельных соединений электронных компонентов и их свойств.

Последовательное и параллельное соединение батарей

При последовательном соединении общее напряжение (Вольты) батареи равно сумме напряжений входящих в нее элементов. Получившаяся батарея будет иметь ту же емкость, что и одиночный элемент. При этом через все элементы будет течь одинаковый ток (Амперы), а максимально допустимый ток, который можно получить при разрядке батареи, равен максимальному току, который можно получить от одного элемента.

При параллельном соединении одинаковых элементов общее напряжение батареи (Вольты) будет равно напряжению одного элемента, а общий ток (Амперы) будет равен сумме токов каждого элемента.

Емкость такой батареи равна сумме емкостей входящих в нее элементов.

Резюмируя, можно сказать, что последовательное соединение элементов в батарее увеличивает напряжение (Вольты), а параллельное соединение увеличивает ток (Амперы) и емкость (Амперы/Час).

На практике при создании BEAM-роботов своими руками чаще всего используют последовательно соединенные пальчиковые батареи по 1,5 вольта. Таким образом, три батареи дают 4,5 вольта, а четыре – 6 вольт.

Соединяют батареи как при помощи пайки, используя короткие отрезки проводов, так и применяя специальные отсеки для батарей.

Последовательное и параллельное соединение резисторов

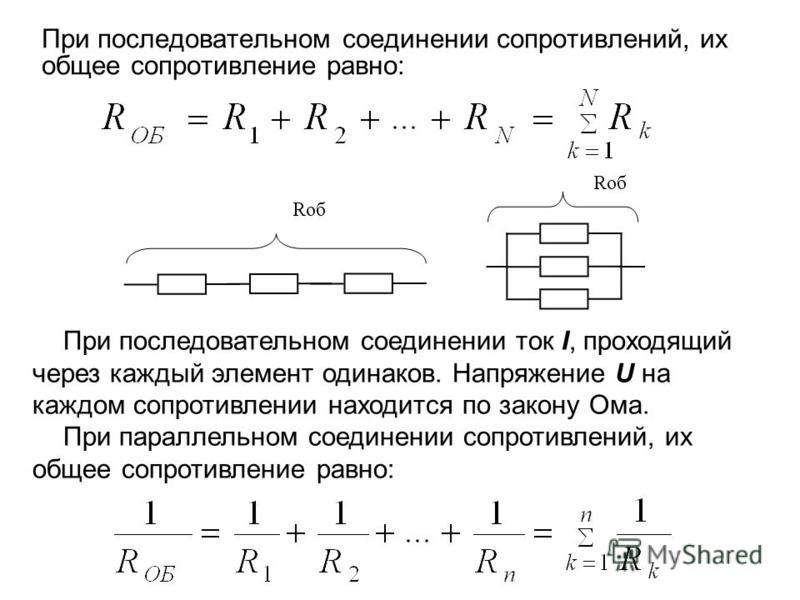
При последовательном соединении общее сопротивление составного резистора будет равно сумме сопротивлений отдельных резисторов.

При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.

При использовании такого соединения резисторов, через каждый резистор потечет свой ток. Сила этого тока для каждого резистора будет обратно пропорциональна его сопротивлению. Таким образом, общая проводимость участка цепи с параллельным соединением резисторов увеличится, а его общее сопротивление наоборот уменьшится.

Для расчета сопротивления двух параллельно соединенных резисторов формула примет следующий вид:

Для трех:

При параллельном соединении двух одинаковых резисторов, их общее сопротивление будет равным половине сопротивления одного из резисторов:

Для N одинаковых резисторов:

Для параллельно подсоединенных резисторов с различным сопротивлением, их общее сопротивление окажется всегда меньше самого маленького из сопротивлений.

Если резисторы на участке цепи соединены между собой частично параллельно, а частично последовательно, то такое соединение называют смешанным. В зависимости от итогового типа соединения, смешанные соединения могут быть параллельного и последовательного типов.

Соединение резисторов

Используя приведеные выше формулы, мы можем, например, из трех резисторов получить сборки с шестью различными сопротивлениями. Рассмотрим это на примере трех резисторов с сопротивлением 1К (1 килоом) каждый.

Соединение конденсаторов

Для параллельного соединения конденсаторов, их общая емкость складывается. При этом допустимое напряжение для всего набора конденсаторов будет равно самому малому значению допустимого напряжения из всего набора.

При последовательном соединении уменьшается общая емкость и увеличивается общее напряжение конденсаторов.

Общее напряжение в данном случае будет равно сумме всех напряжений конденсаторов.

Закон Ома

Для вычисления напряжения, тока и сопротивления в цепи используют самый главный закон в электронике и электротехнике, который был эмпирически открыт в 1826 году Георгом Омом и получил его имя.

Соглано закону Ома для участка цепи, сила тока прямо пропорциональна разности потенциалов (напряжению) на концах участка цепи и обратно пропорциональна сопротивлению этого участка:

Где

I – величина тока, протекающего через участок цепи;
U – величина приложенного напряжения к участку цепи;
R – величина сопротивления рассматриваемого участка цепи.

При помощи второго варианта закона Ома для участка цепи можно вычислить приложенное напряжение к участку цепи, если мы знаем величину тока, протекающего через участок, и сопротивление этого участка.

Третий вариант закона Ома для участка цепи, позволяет вычислить сопротивление участка цепи по известным величинам напряжения и тока.

Используя третий вариант закона Ома можно, например, расчитать сопротивление ограничительного резистора для подключения светодиода к электрической цепи с напряжением, превышающим рабочее напряжение светодиода.

Подключение светодиодов

Предположим, что мы хотим подключить светодиод с рабочим напряжением 2В (2 вольта) и потреблением тока 20mA (20 миллиампер) к электрической батарее с напряжением 6В (6 вольт). Нам необходимо расчитать сопротивление ограничительного резистора. Падение напряжения на резисторе должно составлять 6В — 2В = 4В. Так как сила тока на всех участках цепи одинаковая, значит на нашем резисторе будет столько же ампер, сколько и на светодиоде, а именно 20mA = 0,02A. Используя закон Ома вычислим сопротивление резистора.

Сопротивление ограничительного резистора лучше выбирать с небольшим запасом. В нашем случае оно может быть 220 Ом.

Подключение светодиода

Соединение резисторов — презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Тема урока: «Соединение резисторов»

2. Что такое сопротивление?

Сопротивление проводника
можно характеризовать, как
свойство препятствовать
прохождению тока.

3. Почему обмотку электротехнических устройств выполняется из меди? Почему при расчете сопротивления проводника нужно учитывать

удельное
сопротивление материала проводника?

4. Материалы, с малым удельным сопротивлением

5. Материалы, с большим удельным сопротивлением

6. Задача 1 Сечение проволоки из нихрома 1,5 мм². Из неё изготовили десять спиралей для электронагревательного устройства.

Сопротивление каждой из них равно
150 Ом. Определить длину
проволоки, использованной для этих
спиралей.

7. Дано: S = 1,5 мм² R = 150 Ом = 1 Ом ∙ мм²/м Найти ℓ -? Решение: = RS/ = 150 ∙ 1,5 / 1 = 225 м; для 10 спиралей потребуется 2250

м проволоки.

8. Задача 2 Определите удельное сопротивление провода и материал из которого он изготовлен, если длина провода 69,79 м,

сопротивление 6 Ом и
площадь поперечного сечения
5 мм².

9. Дано: = 69,79 м R = 6 Ом S = 5 мм² _____________ Найти: -? Материал провода? Решение: R = ∙ /S = R∙S/ = 6∙5 /69,79 =0,42

10.

Устройства, обладающие электрическим сопротивлением, называются резисторами.

11. Переменный и постоянный резистор

Переменный
резистор
Постоянный
резистор

12. Реостат

14. Соединение резисторов

Последовательное
Параллельное
Смешанное

15. При последовательном соединении нескольких резисторов с разными сопротивлениями r общ находится по формуле: r общ = r1 + r2 +

r3 + … + r n
С одинаковыми сопротивлениями r общ находится по формуле:
r общ = r ∙ n
Пример:
Дано: R1 = 10 Ом
R2 = 12 Ом
Rобщ = R1+ R2
Rобщ = 10+12= 22 Ом
Вывод: при последовательном соединении R общ
всегда будет больше, чем большее из сопротивлений
включённых в цепь.

16. Недостатки последовательного соединения: 1) выключение одного из приёмников приводит к прекращению работы всех остальных. 2)

все приёмники должны иметь
одинаковое сопротивление (или
мощность), так как иначе создаётся
неравномерное распределение
напряжения на зажимах.
3) нельзя включать последовательно
большое число приёмников, так как
придётся подавать на зажимы большое
напряжение.

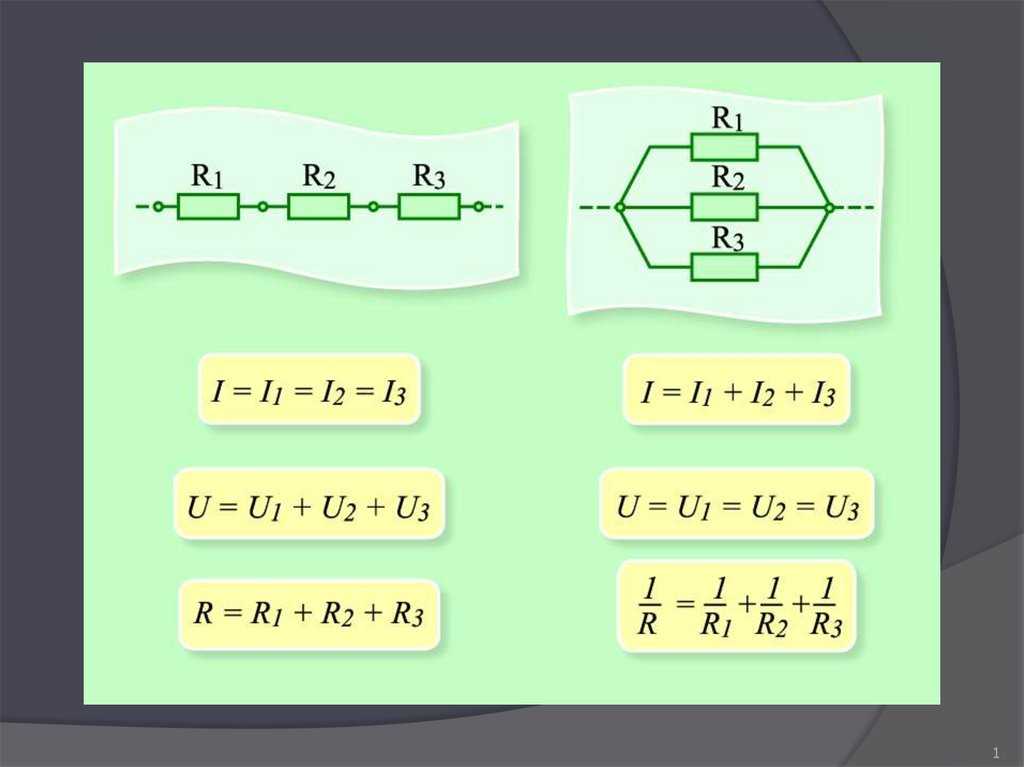
17. При параллельном соединении резисторов с разными сопротивлениями Rобщ находится по формуле: 1/r общ = 1/r1 + 1/r2 + 1/r3 + … +

1/r n
С одинаковыми сопротивлениями находится по формуле:
r общ = r/n
для двух параллельно соединённых находится по формуле:
r общ = r1 ∙ r2 / r1 + r2
Пример:
R1 = 8 Ом
R2 = 4 Ом
R3 = 2 Ом
1/R общ = 1/R1 + 1/R2 + 1/R3R общ = 1/R общ = 1/R1 + 1/R2 + 1/R3R1 + 1/R общ = 1/R1 + 1/R2 + 1/R3R2 + 1/R общ = 1/R1 + 1/R2 + 1/R3R3
1/R общ = 1/R1 + 1/R2 + 1/R3R общ = 1/R общ = 1/R1 + 1/R2 + 1/R38 + 1/R общ = 1/R1 + 1/R2 + 1/R34 + 1/R общ = 1/R1 + 1/R2 + 1/R32 = 1+2+4/R общ = 1/R1 + 1/R2 + 1/R38 = 7/R общ = 1/R1 + 1/R2 + 1/R38 = 8/R общ = 1/R1 + 1/R2 + 1/R37 = 1,14 Ом
Вывод: при параллельном соединении Rобщ будет меньше,
чем величина наименьшего сопротивления включённого в
цепь.

18. Смешанное соединение приёмников электроэнергии. Определение r общ смешанного соединения сводится к постепенному упрощению схемы

путём нахождения общего
сопротивления отдельных ветвей и участков, содержащих чисто
последовательное или чисто параллельное соединения.

19. Дано : R1 = 24 Ом R2 = 36 Ом R3 = 12 Ом R4 = 4 Ом R5 = 60 Ом R6 = 4 Ом Найти Rобщ — ?

21. Составьте соответствие

1 По какой формуле можно
определить Rобщ трёх общ трёх
резисторов соединённых
смешанно
1 Величину сопротивления нельзя
изменять
2 Формула по которой
определяют полное
сопротивление проводника
2 ВЛЭП, обмотки трансформатора,
электродвигателя
3 Единица измерения удельного
сопротивления материала
проводника
3 Rобщ трёх общ = Rобщ трёх 1 + Rобщ трёх 2 ∙ Rобщ трёх 3/Rобщ трёх 2+Rобщ трёх 3
4 Материалы, обладающие
малым удельным
сопротивлением
4 Электронагревательные устройства
5 Материалы, обладающие
большим удельным
сопротивлением
5 Величину сопротивления можно
изменять в определённых пределах
6 В переменных резисторах
6 Ом ∙ мм 2 / м
7 В постоянных резисторах
7 Rобщ трёх = p ∙ l/S

22.

Задание

English     Русский Правила

Параллельные Резисторы — Физика Видео от Brightstorm

Параллельные Резисторы состоят из двух отдельных независимых цепей, поэтому, когда ток достигает резистора, ток может выбрать, через какой из них пройти. Большинство домов подключены параллельно, так что, в отличие от резисторов, соединенных последовательно, не все приборы в наших домах должны быть включены, чтобы работал один. Параллельное добавление резисторов снижает общее сопротивление. Наименьший ток будет проходить через самый большой резистор. Чтобы записать все резисторы как один резистор, используйте уравнение 1/(эффективное сопротивление) = 1/(резистор 1) + 1/(резистор 2). Эффективное сопротивление меньше, чем у любого из двух отдельных резисторов.

резисторов параллельно электрические цепи

Итак, давайте поговорим о резисторных сетях, которые соединены параллельно. Итак, во-первых, что означает параллель? Параллельность означает, что есть выбор, это означает, что в цепи есть ответвление, и может ли ток выбирать направление движения в том или ином направлении. Таким образом, параллельная сеть резисторов выглядит так. Поток приходит, и тогда у него есть выбор, он движется между теми же двумя точками, но есть 2 разных пути, по которым он может идти. Итак, в основном параллельные сети состоят из двух отдельных цепей, которые не зависят друг от друга. Итак, параллельная разность потенциалов одинакова, поэтому разность потенциалов между этими двумя точками одинакова, потому что это одни и те же две точки. Это были просто 2 разные ветки, которые прошли. Ток будет добавляться, поэтому здесь мы бы сказали, что i1 плюс i2 равно общему току i. i1 плюс i2 Хорошо, теперь, как всегда, мы хотели бы рассмотреть эту параллельную сеть как один эффективный резистор. Итак, я хочу, чтобы разность потенциалов была одинаковой, очевидно, что ток, протекающий здесь через мой эффективный резистор, будет равен i, и поэтому мы собираемся записать ток как дельта v над потенциалом r. разница деленная на сопротивление с нашим обязательным знаком минус. Таким образом, это будет минус разность потенциалов на r параллели, равна минус разность потенциалов на r1 минус разность потенциалов на r2.

Теперь разность потенциалов одинакова, а это означает, что она уравновешивается со знаком минус, и это дает нам формулу для параллельного добавления резисторов. 1 над параллелью r равно 1 над r1 плюс 1 над r2. Таким образом, добавить резисторы параллельно сложнее, чем последовательно. Когда я добавляю их последовательно, я просто добавляю, когда я добавляю их параллельно, мы говорим, что обратные величины складываются. Таким образом, 1 на эффективное сопротивление равно 1 на r1 плюс 1 на r2. Теперь очень, очень заманчиво, но абсолютно неправильно пытаться перевернуть это с ног на голову и сказать, что просто означает, что r parallel равно r1 плюс r2, что неверно. Теперь мы можем думать о параллельных цепях как о попытке добраться из точки а в точку б. Если есть только одна дорога, то это будет раздражать, любой, кто хочет добраться из точки а в точку б, должен выбрать эту дорогу.

Если я добавлю параллельно, это будет похоже на строительство новой дороги, которая также ведет из точки а в точку б, и это на самом деле сократит трафик. Так что важно помнить о параллельном, и это сразу скажет нам, что вы не можете просто добавить. Когда я добавляю резисторы параллельно, я уменьшаю общее сопротивление, и теперь так, как будет работать эта параллельная сеть, у меня есть 5 ампер на входе, и у меня есть 2 резистора: 15 Ом и 10 Ом. Разность потенциалов одинакова, вы можете думать об этом как о точке b двух разных дорогах, представьте, что резисторы представляют собой светофоры. Чем больше сопротивление, тем больше светофоров на этом пути, а значит, и меньше машин будет туда ехать. Таким образом, наименьший ток будет проходить через самый большой резистор в параллельной комбинации. Итак, как мы собираемся определить, сколько тока проходит через 15 и сколько тока проходит через 10? На самом деле это очень просто, сначала мы добавим эти 2 резистора параллельно. Теперь помните, что сложение в параллельном режиме немного сложно, поэтому мы скажем, что 1 на r parallel равно 1 на 15 плюс 1 на 10.

Хорошо, теперь, как в средней школе, мы должны скрестить умножение. Так что это будет 10 плюс 15 на 150, хорошо. 10 плюс 15 — это 25 больше 150, и если мы сделаем это осторожно, мы можем отменить. Таким образом, это дает нам одну шестую часть. 1 над r parallel — это 1 над 6, так что это означает, что r parallel равно 6 в порядке. Обратите внимание, что наше эффективное сопротивление меньше, чем любое из двух сопротивлений, которые мы сложили вместе, меньше, чем любое из них в порядке. И в действии это число всегда будет лежать между этим, деленным на 2, и этим, деленным на 2, 5, 7 с половиной, 6, хорошо, это всегда будет работать так. Итак, теперь, когда у нас есть эффективное сопротивление, как мы собираемся определить ток через каждого из этих парней? Что ж, мы воспользуемся идеей, что разность потенциалов должна быть одинаковой при параллельном соединении всегда, всегда, всегда. Так какова разница потенциалов? Ну, разность потенциалов должна быть 5 умножить на 6, потому что эта сеть на самом деле всего лишь 6 Ом, 5 ампер. Итак, 5 умножить на 6 равно 30, значит, разность потенциалов должна быть 30.

Хорошо, чтобы создать разность потенциалов 30 вольт на резисторе 15 Ом, 2 ампера, потому что 2 умножить на 15 равно 30, а здесь, внизу, я хочу 30 вольт на резисторе, так сколько ампер мне нужно? 3 ампера и, конечно же, это следует из нашего предыдущего решения, что добавление тока 5 ампер идет на 2 и 1 ветвь, 3 на другую. Хорошо, еще один способ думать о параллельных цепях — это дома, так дома подключены, потому что я не хочу, чтобы мне было необходимо включать телевизор, чтобы заставить посудомоечную машину работать правильно, поэтому мы подключаем провода эти 2 цепи отдельно. Каждая розетка в вашем доме — это отдельная параллельная ветвь одной и той же цепи, и именно так мы заставляем жилье работать. Хорошо, это параллельные цепи резисторов.

Пример: Параллельное соединение резисторов — Nexus Wiki

Понимание ситуации

В этом примере мы рассмотрим простейший пример параллельной цепи: одна батарея и два резистора, соединенных параллельно.

Два элемента цепи расположены параллельно   означает, что они соединены таким образом, что любой потенциал на вершине одного из них является также потенциалом на вершине другого; точно так же основания двух элементов также имеют одинаковый потенциал. ( одинаковое изменение напряжения )

Давайте посмотрим, как это работает, решив задачу по определению падений потенциала и токов в паре параллельно соединенных резисторов.

Представление примера задачи

Два резистора сопротивлением $R_1$ и $R_2$ подключены друг к другу и к батарее, как показано на схеме(ах) справа. Если на клеммах батареи сохраняется разность напряжений $V_0$, найдите ток и падение напряжения на каждом резисторе. Предположим, что батарея и резисторы идеальны, а соединительные провода не имеют сопротивления.

Решение этой проблемы

Мы нарисовали диаграмму в двух формах: полуреалистичная слева и более стандартная символическая форма справа.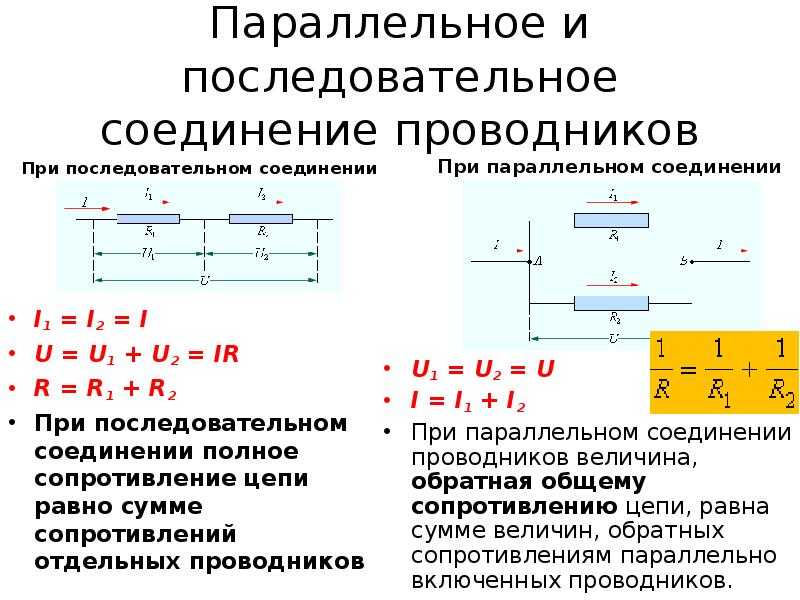

Чтобы ответить на вопросы задачи, у нас есть пять инструментов: принципы Кирхгофа, эвристика нулевого сопротивления и наше определение батареи.

1. Общее количество тока, втекающего в любой объем электрической сети, равно количеству вытекающего. (К1)
2. Падение потенциала на любом отдельном резисторе пропорционально току через резистор. Константой пропорциональности является сопротивление: $ΔV = IR$. (К2)
3. При обходе любого контура в электрической сети потенциал должен вернуться к одному и тому же значению (сумма падений = сумма подъемов). (К3)
4. Элемент (например, провод) с сопротивлением 0 находится под постоянным потенциалом: падения потенциала нет, так как $R = 0$. (эвристика)
5. Аккумулятор — это устройство, поддерживающее фиксированную разность потенциалов на своих клеммах. (Определение батареи)

Чтобы подойти к этой проблеме, давайте сначала поймем, что происходит («расскажем историю проблемы»). Батарея поддерживает разность потенциалов на своих клеммах в соответствии с принципом 5, поэтому она как бы пытается вытолкнуть ток из своего верхнего предела.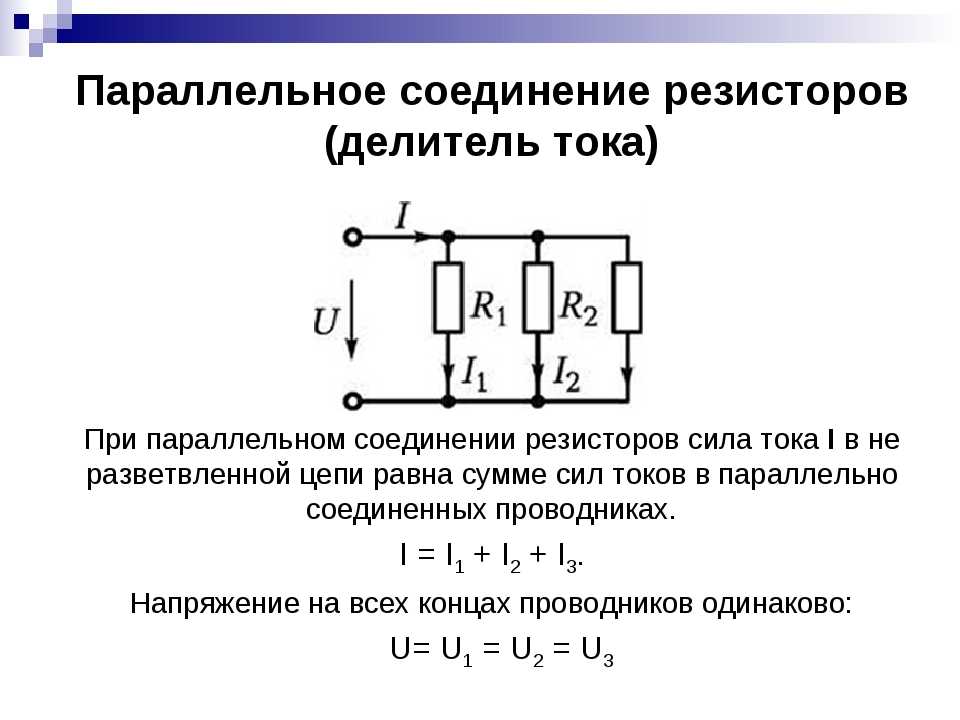 Как только он соединен в петлю, он может создать поток — электрический ток. В устойчивом состоянии (что занимает около наносекунды для установления в такой схеме, которая поместилась бы на столе). Когда ток $I$ бежит по цепи, когда он проходит по проводам, с потенциалом ничего не происходит (он не меняется) по принципу 4. Когда ток достигает узла, соединяющего два резистора, он должен разделиться. Принцип 1 говорит нам, как это сделать. Часть будет проходить через один из резисторов, часть через другой. Мы еще не знаем, сколько, но можно ожидать, что через небольшое сопротивление пройдет больше («следуйте по пути наименьшего сопротивления»). Когда ток проходит через резисторы, он воссоединяется и проходит обратно через батарею. Для токов, протекающих через каждый резистор, существует падение, величина которого регулируется принципом 2.  

Давайте разыграем это подробно с точки зрения символов. Назовите ток через батарею $I$. Достигнув перекрестка, он распадается. Мы не знаем как, но давайте дадим им имена.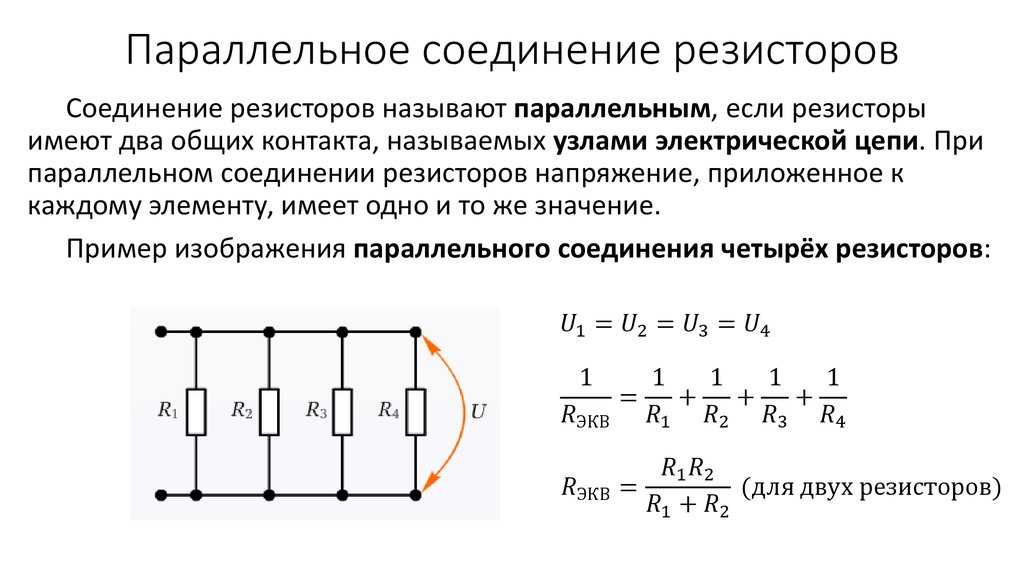 Пусть ток в $R_1$ равен $I_1$, а ток в $R_2$ равен $I_2$. Принцип 1 говорит нам, что

$$I= I_1 + I_2$$

и, следовательно, когда они снова соединятся в нижней части резисторов, мы снова получим $I$   .

Полезным вторым шагом часто является «картирование потенциала». У нас есть только одна батарея, поэтому мы можем выбрать нижний предел батареи как 0 нашего потенциала.

Поскольку батарея поддерживает фиксированную разность потенциалов на своих клеммах, мы знаем верхний предел. Затем мы можем следовать за проводами в обоих направлениях, используя нашу эвристику для определения потенциала (поскольку в проводе без сопротивления нет никаких изменений). Когда мы доберемся до резистора, будет изменение, когда мы пересечем его.

 

В нашем примере с током было легко справиться, поскольку была только одна петля. Здесь это уже не так, поскольку текущий разделяется. Мы увидим, что в этом случае с напряжением действительно легче иметь дело. Если мы проследим за напряжениями вдоль проводов без сопротивления сверху и снизу батареи, мы увидим, что мы знаем напряжения везде. Нет необходимости вводить новое название для неизвестного напряжения.

Что еще мы знаем? Мы использовали принципы 1, 4 и 5 при построении наших диаграмм, и принцип 3 выполняется автоматически. (Вот что принцип 4 делает для нас в сети с одним контуром. Он не всегда будет делать это для нас.) Ясно, что мы должны удовлетворять принципу 2: закону Ома. Поскольку это верно ТОЛЬКО для одного резистора, мы должны применить его один раз для каждого резистора. Это дает следующие два уравнения:

$$V_0 = I_1R_1$$

$$V_0 = I_2R_2$$

В этом случае, поскольку мы знаем $V_0$ и $R_1$ и $R_2$, эти уравнения дают нам токи в резисторах. Поскольку они суммируются, чтобы дать нам $I$ в батарее, мы знаем все токи и все падения напряжения.

$$I = I_1 + I_2 = \frac{V_0}{R_1} + \frac{V_0}{R_2}$$

Осмысление результата

В общем, недостаточно решить проблему; нам нужно посмотреть на наш ответ и убедиться, что он имеет смысл. Здесь это особенно важно, поскольку параллельное подключение резисторов будет компонентом более сложных проблем, которые мы будем анализировать.