Что такое параллельное соединение проводников. Как рассчитывается сила тока при параллельном соединении. Как определить общее сопротивление параллельной цепи. Какие преимущества у параллельного соединения перед последовательным.
Что такое параллельное соединение проводников
Параллельное соединение проводников — это такой способ подключения элементов электрической цепи, при котором все элементы присоединяются к одним и тем же двум точкам цепи. При этом напряжение на всех элементах одинаково и равно напряжению источника тока.
Основные особенности параллельного соединения:
- Напряжение на всех элементах одинаково
- Общий ток равен сумме токов в отдельных ветвях
- Общее сопротивление меньше сопротивления любого из элементов
Расчет силы тока при параллельном соединении
При параллельном соединении общий ток I в неразветвленной части цепи равен сумме токов I1, I2, I3 и т.д. в отдельных параллельных ветвях:
I = I1 + I2 + I3 + …
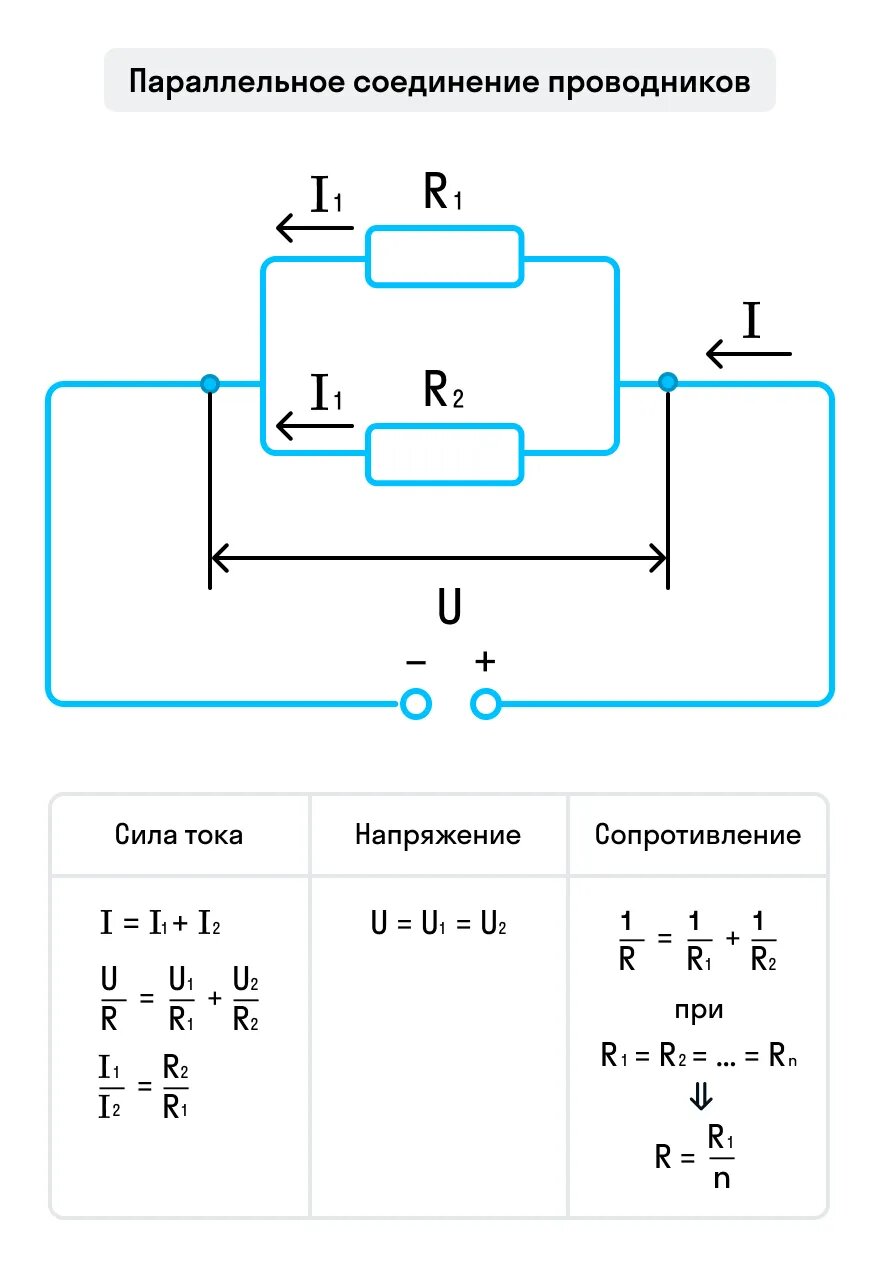
Это следует из закона сохранения электрического заряда — сколько заряда втекает в точку разветвления, столько же должно и вытекать из нее.
Ток в каждой ветви можно рассчитать по закону Ома:
I1 = U / R1, I2 = U / R2 и т.д.
где U — напряжение на параллельном участке, R1, R2 — сопротивления отдельных ветвей.
Определение общего сопротивления параллельной цепи
Общее сопротивление R параллельно соединенных проводников определяется по формуле:
1/R = 1/R1 + 1/R2 + 1/R3 + …
Из этой формулы следует, что общее сопротивление параллельной цепи всегда меньше сопротивления любого из параллельно соединенных элементов. Это объясняется тем, что при параллельном соединении увеличивается площадь поперечного сечения проводника, по которому течет ток.
Преимущества параллельного соединения перед последовательным
Параллельное соединение имеет ряд важных преимуществ перед последовательным:
- Все элементы находятся под одинаковым напряжением
- Выход из строя одного элемента не нарушает работу остальных
- Можно подключать элементы с разными номинальными напряжениями
- Легко наращивать мощность цепи добавлением параллельных ветвей
Именно поэтому параллельное соединение широко применяется в электротехнике, например, в бытовой электропроводке.
Примеры расчета параллельных цепей
Рассмотрим несколько типовых задач на расчет параллельных цепей:
Пример 1. Расчет общего сопротивления
Даны три резистора с сопротивлениями 2 Ом, 3 Ом и 6 Ом, соединенные параллельно. Определить их общее сопротивление.
Решение:
1/R = 1/2 + 1/3 + 1/6 = 0.5 + 0.33 + 0.17 = 1
R = 1 / 1 = 1 Ом
Ответ: общее сопротивление равно 1 Ом.
Пример 2. Расчет токов в ветвях
К источнику напряжения 12 В подключены параллельно три лампочки с сопротивлениями 20 Ом, 30 Ом и 60 Ом. Определить ток в каждой лампочке и общий ток.
Решение:
I1 = 12 В / 20 Ом = 0.6 А I2 = 12 В / 30 Ом = 0.4 А I3 = 12 В / 60 Ом = 0.2 А
Общий ток: I = I1 + I2 + I3 = 0.6 + 0.4 + 0.2 = 1.2 А
Ответ: токи в лампочках 0.6 А, 0.4 А и 0.2 А, общий ток 1.2 А.
Применение параллельного соединения на практике
Параллельное соединение широко используется в различных областях электротехники:
- Бытовая электропроводка — все розетки и приборы подключены параллельно
- Автомобильная электрика — параллельное подключение фар, фонарей и других потребителей
- Солнечные батареи — для увеличения тока панели соединяют параллельно
- Источники питания — для увеличения мощности блоки питания включают параллельно
Параллельное соединение позволяет гибко наращивать мощность систем и обеспечивает их надежность.
Сравнение последовательного и параллельного соединения
Рассмотрим основные отличия последовательного и параллельного соединения:
| Параметр | Последовательное | Параллельное |
|---|---|---|
| Ток | Одинаковый во всех элементах | Разный в ветвях, суммируется |
| Напряжение | Суммируется | Одинаковое на всех элементах |
| Сопротивление | Суммируется | Уменьшается |
| Надежность | Низкая | Высокая |
Как видно, параллельное соединение имеет ряд преимуществ с точки зрения надежности и гибкости.
Ошибки при расчетах параллельных цепей
При расчетах параллельных цепей часто допускают следующие ошибки:
- Суммирование сопротивлений вместо проводимостей
- Деление напряжения на число ветвей
- Игнорирование внутреннего сопротивления источника
- Неправильный учет полярности при параллельном соединении источников
Чтобы избежать ошибок, важно четко понимать физический смысл параллельного соединения и правильно применять законы Ома и Кирхгофа.
Соединение элементов в цепи переменного напряжения и тока
Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Последовательное соединение элементов цепи при переменном напряжении
Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.
Последовательное соединение элементов цепи.
В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах
где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Im – амплитудное значение переменного тока.
Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже
Напряжения и токи при последовательном соединении.
Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде
где R – активное сопротивление,
Х – реактивное сопротивление.
Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.
В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.
При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи.
Для этого продолжим преобразовывать напряжение
где Z – полное сопротивление цепи,
ψ – разность фаз между напряжением и током.
Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
Z – полное сопротивление цепи.
Параллельное соединение элементов цепи при переменном напряжении
Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.
Параллельно соединение элементов цепи.
Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи
IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Um – амплитудное значение переменного тока.
Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже
Напряжение и токи при параллельном соединении.
Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения
где g – активная проводимость, b – реактивная проводимость.
Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.
Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы
Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.
Определим зависимость между напряжением и силой тока в параллельной цепи
где y – полная проводимость,
ψ – разность фаз между напряжением и током в цепи.
Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
y – полная проводимость цепи.
Чему равна мощность в цепи при синусоидальном напряжении?
Мощность является основной энергетической характеристикой, поэтому рассмотрим мощность в цепи переменного напряжения. Мгновенная мощность в цепи будет равна
Как видно из получившегося выражения, мгновенная мощность состоит из постоянной составляющей UIcos(φ) и переменной составляющей UIcos(2ωt – φ), изменяющейся с удвоенной частотой по сравнению с частотой напряжения (тока).
Теперь определим среднее значение мощности за период или активную мощность, которая будет равна
где U – действующее значение переменного напряжения,
I – действующее значение переменного тока,
cos(φ) – коэффициент мощности.
Таким образом, активная мощность в цепи переменного напряжения (тока), равна произведению действующих значений напряжения и тока на коэффициент мощности.
При разработке и проектировании цепей переменного напряжения стараются сделать коэффициент мощности как можно больше, в идеале должен быть равен единице cos(φ) = 1. При небольших значениях данного коэффициента для создания в цепи необходимой мощности Р необходимо повышать величину напряжения U (тока I).
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБЫВАТЬ МОЖНО ЗДЕСЬ
Сила тока и сопротивление при параллельном соединении проводников
Nach oben
Информация
- Контактное лицо
- Условия сотрудничества
- Декларация о конфиденциальности
- Вводные данные
Обслуживание
- Краткий обзор услуг
- Скачать
- Каталоги
- Вебинары и Видео
- Связаться со службой поддержки клиентов
Компания
- О нас
- Качественная политика
- Безопасность в классе
Please note
* Prices subject to VAT.
We only supply companies, institutions and educational facilities. No sales to private individuals.
Please note: To comply with EU regulation 1272/2008 CLP, PHYWE does not sell any chemicals to the general public. We only accept orders from resellers, professional users and research, study and educational institutions.
Пожалуйста, введите имя, под которым должна быть сохранена Ваша корзина.
Сохраненные корзины вы можете найти в разделе My Account.
Название корзины
Параллельная цепь | Основы, уравнения, напряжение, ток
Понимание основ электрических цепей очень важно для студентов, инженеров и электриков. Двумя основными типами электрических цепей являются последовательные цепи и параллельные цепи. Мы можем упростить любую сложную электрическую цепь, используя последовательную, параллельную или их комбинацию.
Итак, в этом руководстве давайте подробнее рассмотрим параллельную цепь, ее характеристики, протекание тока и напряжения в параллельной цепи, а также некоторые важные уравнения.
Краткое описание
Что такое параллельная цепь?
Прежде чем узнать о параллельной схеме, давайте быстро рассмотрим основы электрической цепи. Проще говоря, электрическая цепь представляет собой набор компонентов и устройств, таких как резисторы, конденсаторы, катушки индуктивности, транзисторы, диоды, источники напряжения и/или тока и многие другие, которые соединены с помощью металлических проводников.
В электрической цепи электроны текут от отрицательной клеммы источника питания (обычно источника напряжения) через металлические провода, различные компоненты и, наконец, обратно к положительной клемме источника питания.
Если цепь спроектирована/спланирована таким образом, что электроны могут течь только по одному пути, такая цепь называется последовательной цепью.
Напротив, если в цепи есть несколько путей для движения электронов, то цепь называется параллельной цепью.
На следующем рисунке показана простая иллюстрация последовательных и параллельных цепей с использованием источника напряжения и нескольких лампочек.
Изображение
Правила, связанные с параллельными цепями
В последовательных цепях напряжение пропорционально делится на все компоненты цепи. Но в параллельной цепи на всех параллельных ветвях присутствует одинаковое напряжение, и это напряжение равно напряжению источника.
Например, в следующей параллельной резистивной цепи, если V S является напряжением источника и V 1 , V 2 и V 3 являются соответствующими напряжениями ветвей, то
V S = В 1 = V 2 = V 3
Вступая в ток, в последовательной цепи в цепи течет один ток, а в параллельной — другой.
Ток источника в параллельной цепи делится между параллельными ветвями в зависимости от сопротивления этой ветви.
Если «I S » — это ток источника, а I 1 , I 2 и I 3 — соответствующие токи ветвей в приведенной выше схеме, то
I S = I 1 + I 2 + I 3
Мы можем применить закон Ома на уровне отдельных ветвей для определения тока.
Различные компоненты в параллельной конфигурации
Теперь, когда мы рассмотрели основы параллельной схемы, а также пару важных уравнений, давайте теперь приступим к определению эквивалентных значений различных компонентов параллельной схемы.
Параллельные резисторы
В последовательной резистивной цепи эквивалентное сопротивление всех последовательно соединенных резисторов равно сумме номиналов отдельных резисторов. Но когда мы соединяем кучу резисторов параллельно, эквивалентное сопротивление равно:
1/R Уравнение = 1/R 1 + 1/R 2 + 1/R 3
Конденсаторы в параллельном
Приходят к конденсаторам на параллеле, если C 1 , C 77777777777777 года.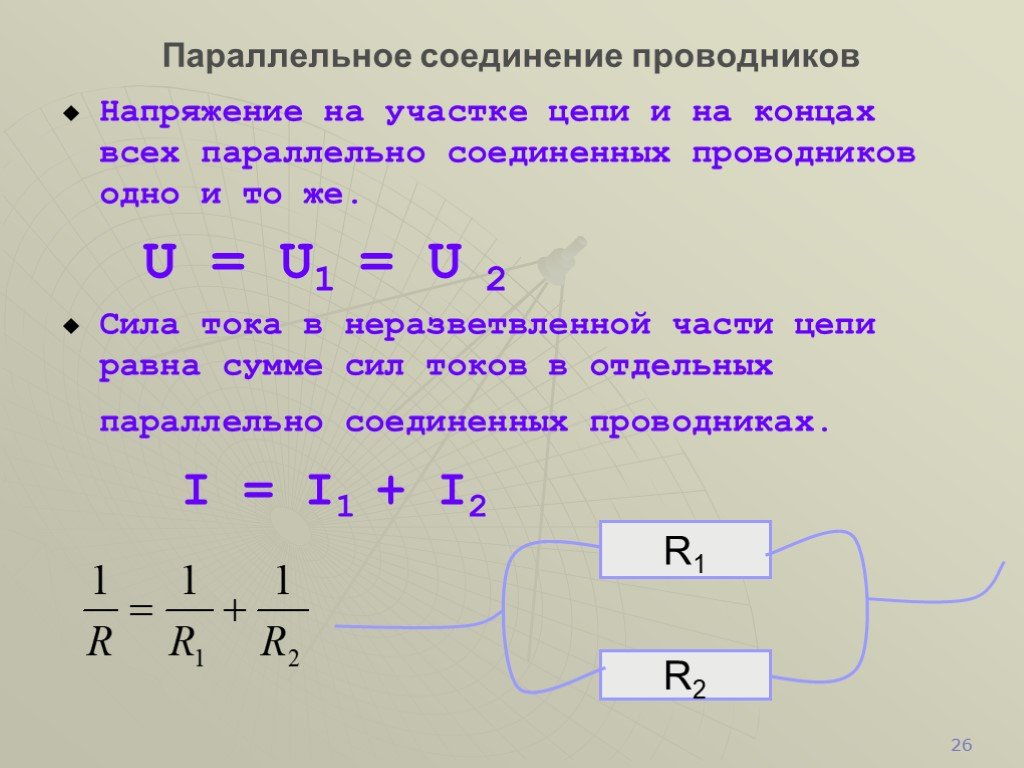
2 и C 3 подключены параллельными, а C Уравнение — эквивалентная емкость, затем
C Уравнение = C 1 + C 2 + C 3 9003
7 Indoor Наконец, у нас есть катушки индуктивности параллельно. Подобно резисторам, соединенным параллельно, когда группа катушек индуктивности соединена параллельно, обратная величина эквивалентной индуктивности равна сумме обратных величин отдельных индуктивностей. Вы можете лучше понять это с помощью следующей формулы.
1/L EQ = 1/L 1 + 1/L 2 + 1/L 3
Заключение
Параллельные цепи являются неотъемлемой частью всех электрических цепей. Мы используем их в нашей повседневной жизни в виде жилой проводки. Итак, понимание основ параллельных цепей, как определить напряжение, ток и сопротивление в параллельной цепи, очень важно.
Параллельные цепи — преимущества, мощность, ток, напряжение и эффективное сопротивление
Введение
В этом уроке мы рассмотрим параллельные цепи.
Мы увидим, почему они так распространены. Мы также рассмотрим напряжение, мощность, ток и эффективное сопротивление.
Преимущество параллельных цепей перед последовательными
Если мы хотим подключить две лампочки к одной и той же батарее, очевидным способом будет их последовательное соединение. Это означает, что обе лампочки находятся на одном и том же проводящем пути от одной клеммы батареи к другой.
Проблема с последовательным подключением двух лампочек заключается в том, что обе лампочки тусклые, и если выключить одну лампочку, то обе гаснут.
Параллельное подключение ламп имеет два преимущества.
- Все они получают полное напряжение батареи, поэтому они все яркие
- Все они находятся в собственной токопроводящей петле, так что вы можете выключить одну лампочку, не затрагивая остальные.
Параллельные цепи в доме
Дома все бытовые приборы соединены параллельно друг с другом. Это означает, что все они получают полное сетевое напряжение, и вы можете включить телевизор, не включая микроволновую печь.
Как это работает?
Электрические кабели в вашем доме состоят из трех проводов. На данный момент мы проигнорируем землю и сосредоточимся только на двух из них: живом и нейтральном. В Европе живой цвет коричневый, а нейтральный синий. В США живой может быть черным, красным или желтым; и нейтральный, как правило, белый или белый с желтыми полосами.
Между фазой и нейтралью имеется напряжение, так как они косвенно связаны с электростанцией. Каждая электрическая розетка в вашем доме подключена к фазе и нейтрали. Металлические контакты вилки обеспечивают электрическое соединение с розеткой. Провод, опять же с токоведущими и нейтральными проводами, соединяет вилку с вашим прибором.
Каждое устройство имеет собственное соединение между фазой и нейтралью, поэтому каждое устройство можно включать отдельно, и на него подается полное напряжение.
Параллельное подключение всегда увеличивает общий ток.
Несмотря на то, что все приборы в вашем доме подключены к одному и тому же напряжению, все они потребляют разные токи.
Электрическая духовка быстро передает энергию, поэтому потребляемый ею ток будет большим. Телевизор передает энергию довольно медленно, поэтому потребляемый им ток будет довольно мал.
Все эти токи должны добавляться в блок питания, поскольку он должен обеспечивать их все одновременно. Чем больше приборов подключено, тем больше потребляемый ток.
Почему ток не «расщепляется» на соединениях в параллельных цепях
Довольно часто говорят, что ток разделяется на соединениях в параллельных цепях, но с этой идеей нужно быть очень осторожным. Часто это может привести к неправильному представлению о постоянном токе.
Первое, что нужно помнить, это то, что заряды не начинаются с аккумулятора, а затем текут по пустым проводам, пока они не дойдут до соединения, а затем нужно решить, что делать. Заряды уже есть везде в цепи, и все они начинают очень медленно течь везде одновременно.
Другая проблема заключается в том, что не существует «потока». Чем больше вещей вы подключаете параллельно, тем больше ток, потребляемый от источника питания.
Один и тот же ток не просто делится по-разному.
Иногда проще думать о компонентах как об активных вещах, требующих тока от источника питания. Если схема устроена так, что иногда эти токи должны протекать по одному проводу, их нужно сложить.
Расчет токов в параллельных цепях
При параллельном подключении ламп на них должно быть одинаковое напряжение. Вы можете относиться к ним так, как если бы они были в своей собственной цепи (что, если вы относитесь к цепи как к смысловой петле, так и есть).
Если лампы разные, то лампочка с меньшим сопротивлением потребляет больший ток и светит ярче. Это просто закон Ома: малое сопротивление означает большой ток.
Вот стратегия:
- рассчитать ток через каждую лампочку, используя закон Ома
- сложите токи, чтобы найти ток, потребляемый от батареи
Вы можете рассчитать ток, используя уравнение закона Ома V = IR. Сначала вам нужно переставить его так, чтобы I = V / R, и помните, что V — это просто напряжение батареи.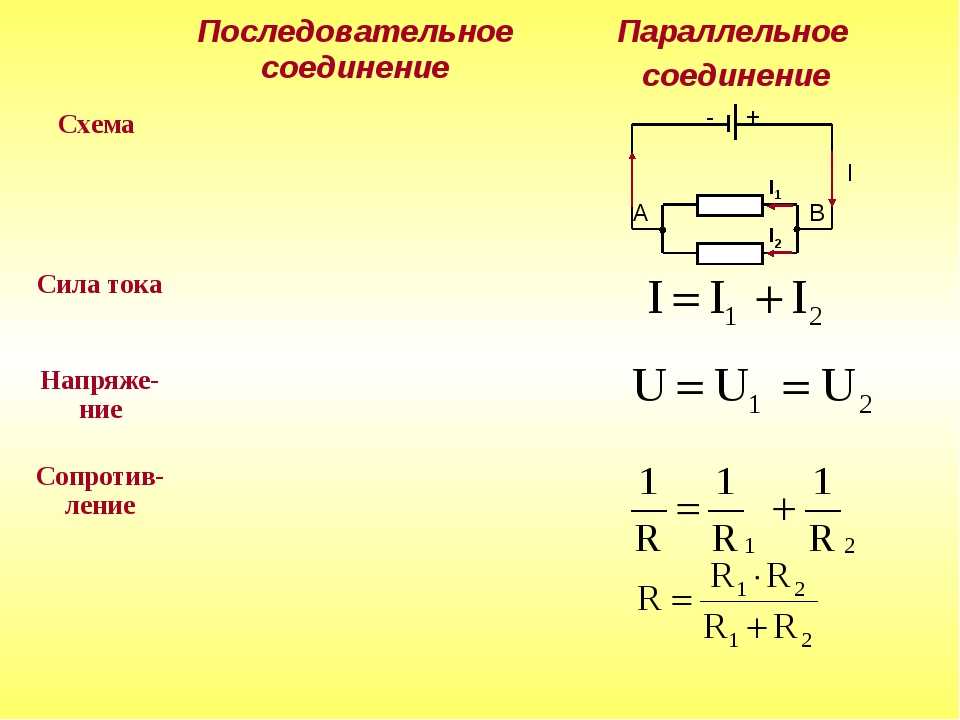
Параллельное соединение всегда снижает эффективное сопротивление.
Батарея с параллельной цепью не «знает», что к ней подключено. Все, что он чувствует, это общее сопротивление (или, если хотите, общий спрос на ток). Сопротивление, которое испытывает батарея, называется эффективным сопротивлением цепи.
По мере того, как вы добавляете все больше и больше компонентов параллельно, ток, потребляемый от источника, становится все больше и больше. Если ток увеличивается, сопротивление должно уменьшаться. Таким образом, добавляя сопротивления, вы фактически уменьшаете эффективное сопротивление, что кажется странным.
Не имеет значения, насколько велико сопротивление, добавление его параллельно всегда снижает эффективное сопротивление. Есть пара аналогий для объяснения этого.
Если у вас есть ванна с отверстием на дне, она будет опорожняться. Если вы добавите еще одно отверстие, каким бы маленьким оно ни было, ванна всегда будет опорожняться быстрее.
Или подумайте об огромной толпе, покидающей спортивный стадион через главные ворота. Если открыть хотя бы маленькую боковую калитку, количество людей, покидающих стадион каждую минуту, увеличивается.
Эмпирические правила расчета эффективного сопротивления параллельных цепей
- Общее сопротивление всегда меньше наименьшего сопротивления (потому что вы всегда можете представить, что сначала строите цепь с наименьшим сопротивлением, а затем эффективное сопротивление продолжает уменьшаться по мере добавления большее сопротивление).
- Два одинаковых резистора имеют эффективное сопротивление, равное половине их значения (поскольку добавление второго сопротивления удваивает ток, поэтому сопротивление уменьшается вдвое).
- Три одинаковых резистора имеют эффективное сопротивление в три раза меньше их номинала и так далее.
- Параллельное очень большое сопротивление и очень маленькое сопротивление имеют эффективное сопротивление, которое немного меньше, чем у малого сопротивления (маленькое сопротивление похоже на большую дыру в ванне, добавление еще одной крошечной дырочки все равно немного увеличивает общую скорость потока).
