Расчет катушки индуктивности без сердечника. Расчет индуктивности катушки на ферритовом сердечнике: полное руководство

Как рассчитать индуктивность катушки на ферритовом сердечнике. От чего зависит индуктивность. Какие факторы влияют на расчет. Пошаговая инструкция расчета с примерами. Советы по выбору сердечника.

Факторы, влияющие на индуктивность катушки с ферритовым сердечником

При расчете индуктивности катушки на ферритовом сердечнике необходимо учитывать следующие основные факторы:

• Геометрические размеры и форма сердечника
• Магнитная проницаемость материала сердечника
• Количество витков обмотки
• Наличие и размер воздушного зазора
• Расположение обмотки на сердечнике

Рассмотрим подробнее, как каждый из этих факторов влияет на индуктивность катушки.

Влияние размеров и формы сердечника на индуктивность

Геометрические параметры сердечника напрямую определяют его магнитные свойства:

• Площадь поперечного сечения — чем она больше, тем выше индуктивность
• Длина средней магнитной линии — чем она меньше, тем выше индуктивность
• Объем сердечника — от него зависит количество магнитной энергии, которую может запасать сердечник

Наиболее распространенные формы ферритовых сердечников:

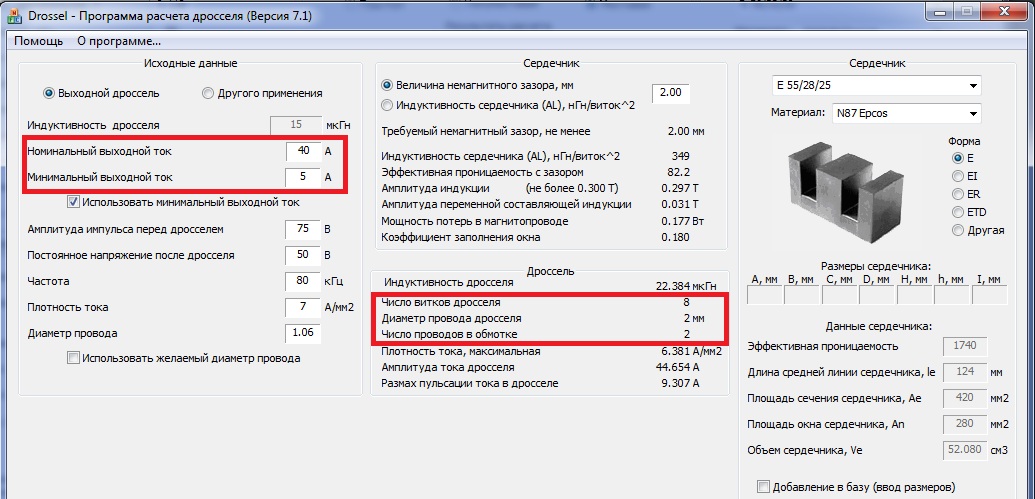
• Кольцевые (тороидальные)
• П-образные и Ш-образные
• Стержневые (цилиндрические)
• Чашечные (горшковые)

Для каждой формы существуют свои методики расчета индуктивности.

Зависимость индуктивности от магнитной проницаемости феррита

Магнитная проницаемость μ характеризует способность материала усиливать магнитное поле. Чем выше μ, тем большую индуктивность можно получить на данном сердечнике.

Основные виды ферритов по магнитной проницаемости:

• Низкопроницаемые (μ = 100-1000)
• Среднепроницаемые (μ = 1000-5000)
• Высокопроницаемые (μ > 5000)

При этом высокопроницаемые ферриты быстрее входят в насыщение при протекании постоянного тока.

Как влияет число витков на индуктивность катушки

Индуктивность катушки пропорциональна квадрату числа витков:

L ~ N²

Где:

• L — индуктивность
• N — число витков

Увеличение числа витков — самый простой способ повысить индуктивность. Однако это приводит к росту активного сопротивления обмотки и ее паразитной емкости.

Влияние воздушного зазора на индуктивность

Введение воздушного зазора в магнитопровод позволяет:

• Снизить эффективную магнитную проницаемость
• Увеличить запас по магнитному насыщению
• Уменьшить зависимость индуктивности от тока подмагничивания

При этом индуктивность уменьшается пропорционально увеличению воздушного зазора.

Как расположение обмотки влияет на индуктивность

Оптимальное расположение обмотки на сердечнике:

• Для кольцевых сердечников — равномерно по всей длине
• Для П- и Ш-образных — на центральном керне
• Для стержневых — в средней части

Отклонение от оптимального расположения приводит к снижению индуктивности.

Пошаговая инструкция расчета индуктивности

Рассмотрим порядок расчета на примере катушки с П-образным ферритовым сердечником:

1. Выбрать тип и размер сердечника исходя из требуемой индуктивности и тока
2. Определить эффективную магнитную проницаемость с учетом воздушного зазора
3. Рассчитать эффективную длину магнитной линии и площадь сечения
4. Вычислить индуктивность одного витка по формуле:

AL = μ0 * μэфф * Sэфф / lэфф

Где:

• AL — индуктивность одного витка
• μ0 — магнитная постоянная
• μэфф — эффективная магнитная проницаемость
• Sэфф — эффективная площадь сечения
• lэфф — эффективная длина магнитной линии

5. Рассчитать необходимое число витков:

N = √(L / AL)

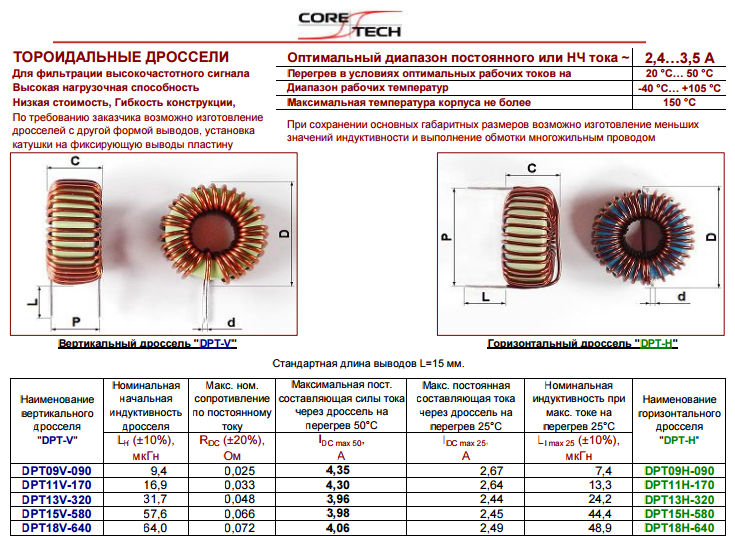
Где L — требуемая индуктивность

6. Проверить запас по насыщению и скорректировать расчет при необходимости

Пример расчета индуктивности катушки

Рассчитаем катушку индуктивностью 1 мГн на токе 2 А.

Исходные данные:

• Сердечник ETD34 из феррита N87
• Воздушный зазор 0.5 мм
• Эффективная площадь Sэфф = 97.1 мм²
• Эффективная длина lэфф = 78.6 мм

Расчет:

1. Эффективная магнитная проницаемость μэфф = 160
2. Индуктивность одного витка: AL = 4π*10⁻⁷ * 160 * 97.1 / 78.6 = 248 нГн
3. Необходимое число витков: N = √(1000000 / 248) = 63.5
4. Округляем до 64 витков

Таким образом, для получения индуктивности 1 мГн потребуется намотать 64 витка на выбранный сердечник.

Рекомендации по выбору ферритового сердечника

При выборе сердечника для катушки индуктивности следует учитывать:

• Требуемую индуктивность и ток
• Рабочую частоту
• Допустимые габариты
• Температурный диапазон
• Стоимость

Основные рекомендации:

• Для импульсных преобразователей оптимальны силовые ферриты с низкими потерями
• Для работы на частотах до 100 кГц подходят марганец-цинковые ферриты
• Для частот выше 100 кГц лучше использовать никель-цинковые ферриты
• При больших токах подмагничивания нужен воздушный зазор
• Для миниатюризации применяют высокопроницаемые ферриты

Как проверить правильность расчета индуктивности

Для проверки расчетов можно использовать:

• Измерение индуктивности готовой катушки с помощью LCR-метра
• Моделирование в специализированных программах
• Расчет по альтернативным методикам и сравнение результатов

При значительном расхождении расчетных и измеренных значений следует проверить:

• Правильность выбора параметров сердечника
• Точность намотки катушки
• Влияние паразитных параметров

Заключение

Расчет индуктивности катушки на ферритовом сердечнике — важный этап проектирования магнитных компонентов. Правильный выбор сердечника и точный расчет позволяют получить требуемые параметры при оптимальных габаритах и стоимости. Использование современных методик и средств автоматизации существенно упрощает процесс проектирования.

Как рассчитать индуктивность катушек с замкнутыми сердечниками?

Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

где ω – количество витков катушки,

R_M – сопротивление магнитной цепи,

μ_а – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

S_M – площадь поперечного сечения сердечника,

l_M – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l_e и эффективная площадь поперечного сечения S_e сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

S_e – эффективная площадь поперечного сечения сердечника,

l_e – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм^-1;

С₂ – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм^-3;

где N – количество разнородных участков сердечника,

l_N – длина N – го участка сердечника,

S_N – площадь N – го участка сердечника.

Тогда величины S_e и l_e определятся из следующих выражений

Кроме индуктивности с помощью постоянных С₁ и С­₂ определяют эффективный объём V_e, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С₁ по следующему выражению

где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Расчёт катушки с тороидальным сердечником

Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.

Тороидальный сердечник.

Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D₁ – внешний диаметр, D₂ – внутренний диаметр, h – высота сердечника.

Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С₁ и С₂, которые составляют

где h_e – эффективная высота сердечника,

D₁ – внешний диаметр сердечника,

D₂ – внутренний диаметр сердечника.

Расчёт эффективной высоты h_e сердечника зависит от конструктивных особенностей.

Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).

Рассмотрим несколько случаев:

а) прямоугольное поперечное сечение с острыми кромками

б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления r_s

в) трапецеидальное поперечное сечение с острыми кромками

г) трапецеидальное поперечное сечение со скруглёнными кромками

Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D₁ = 20 мм, D₂ = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления r_s = 0,5 мм, относительная магнитная проницаемость материала сердечника μ_r = 1000.

Так как рассчитываем только индуктивность, то в расчёте коэффициента С₂ нет необходимости

Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей.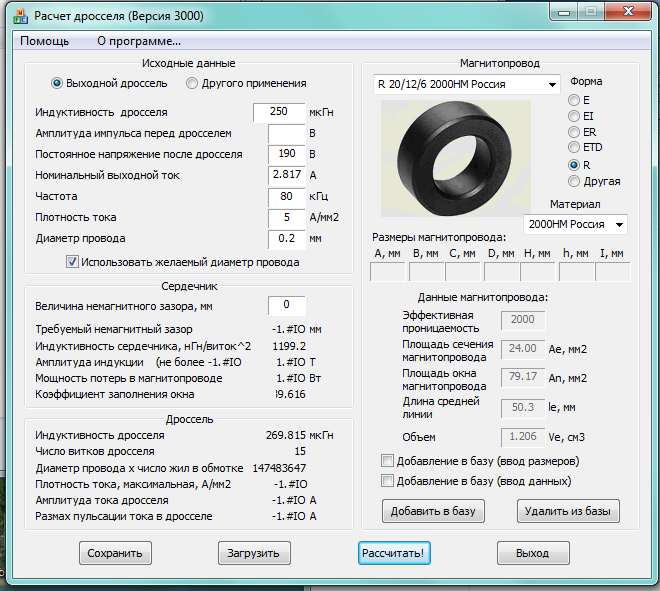 Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

Сечение П-образного прямоугольного сердечника. Данный сердечник состоит из нескольких участков l₁, l₂, l₃, l₄, l₅ имеющих различное сечение S₁, S₂, S₃, S₄, S₅,. Тогда коэффициенты С₁ и С₂ составят

Неизвестные величины можно найти следующим образом

Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μ_r = 1950, количество витков ω = 150.

 

Сердечник Epcos U93/76/16.

Таким образом, расчётные параметры сердечника составят

Таким образом коэффициент С1 и индуктивность L составят

Расчёт катушки с П-образным сердечником круглого сечения

Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.

Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

Сечение П-образного сердечника с круговым сечением.

Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже.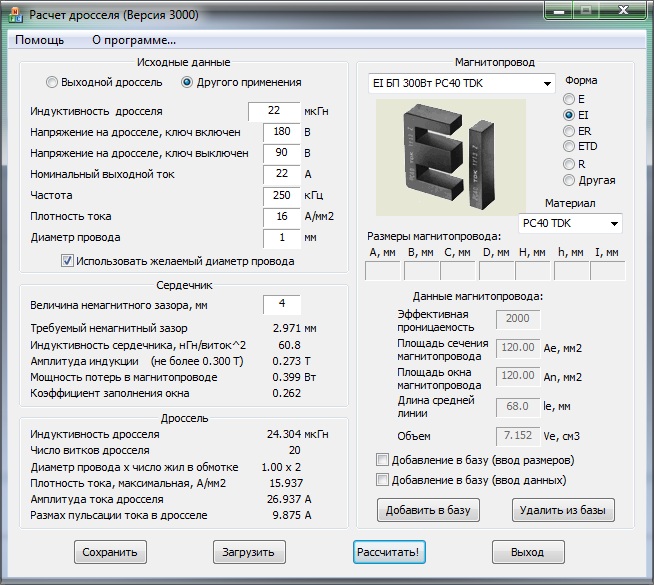 Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь

Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μ_r = 2500), количество витков ω = 60.

Сердечник типа SDMR 40 UY20.

Параметры сердечника для расчёта составят

Таким образом коэффициент С1 и индуктивность L составят

На сегодня всё. Продолжение смотри в следующей статье.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

Как рассчитать индуктивность катушек на разомкнутых сердечниках?

Всем доброго времени суток! В прошлой статье я рассказал о катушках индуктивности на сердечниках с малым магнитным зазором (длина зазора δ меньше любого линейного размера сердечника). Кроме сердечников с малым зазором существует сердечники, имеющие воздушный зазор сопоставимый с линейными размерами самого сердечника. Такие сердечники называются разомкнутыми. Данная статья описывает расчёт и параметры стержневых сердечников, являющихся разомкнутыми.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Факторы, влияющие на индуктивность катушки на разомкнутом сердечнике

В сердечниках с малым воздушным зазором магнитное поле практически всё сосредоточенно в сердечнике, и в воздушном зазоре рассеивание магнитного поля незначительно. Другая картина возникает, если магнитное поле возникает в сердечнике, имеющем воздушный зазор l_з сопоставимый с длиной магнитной силовой линии в сердечнике l_c.

Магнитное поле в разомкнутом сердечнике.

Таким образом, магнитные сопротивления сердечника и воздушного зазора становятся соизмеримыми, что приводит к усложнению расчётных выражений для индуктивности катушек на таких сердечниках. В этом случае расчёт параметров ведут с учётом того, что в разомкнутых сердечниках на торцах сосредотачиваются противоположно ориентированные магнитные частицы, то есть частицы с положительным доменом смещаются в направлении внешнего поля, а отрицательные навстречу ему. В результате возникает размагничивающее поле, противоположное основному. Данное поле характеризуется размагничивающим фактором N или коэффициентом размагничивания. Данный фактор зависит от формы и размеров самого сердечника. Влияние размагничивающего фактора на магнитное поле сердечника описывается следующим выражением

где Н – напряженность магнитного поля в сердечнике,

Н₀ – напряженность внешнего магнитного поля, то есть поля создаваемого катушкой, намотанной на разомкнутый сердечник,

Н_Р – размагничивающее поле сердечника,

N – размагничивающий фактор,

J – вектор намагничивания сердечника.

Точное значение размагничивающего фактора, возможно, рассчитать только для однородно намагниченных тел, например, эллипсоидов вращения, шаров, дисков. Для учёта размагничивающего фактора на магнитные свойства сердечника ввели понятие эффективной магнитной проницаемости сердечника μ_е, которая зависит от магнитной проницаемости вещества сердечника μ_r и размагничивающим фактором N. Значение эффективной магнитной проницаемости сердечника для однородно намагниченных тел определяется следующим выражением

Однако в практике, используются неоднородно намагниченные тела – цилиндры, призмы, поэтому для расчёта эффективной магнитной проницаемости таких сердечников применяются эмпирически выведенные выражения.

Вследствие того, что значение размагничивающего фактора в неоднородно намагничиваемых телах различно по длине, то необходимо учитывать и расположение катушки индуктивности относительно сердечника и длину данной катушки относительно длины сердечника.

Таким образом, индуктивность катушки, выполненной на разомкнутом сердечнике можно определить по следующему выражению

где L₀ – индуктивность катушки без сердечника, расчет смотреть (Часть 1, Часть 2, Часть 3),

μ_е – эквивалентная магнитная проницаемость разомкнутого сердечника,

k– коэффициент зависящий от отношения длины катушки к длине сердечника,

p_l – коэффициент зависящий от расположения катушки относительно середины длины сердечника.

Рассмотри более подробно зависимость индуктивности от различных факторов.

Расчёт размагничивающего фактора

Как я уже говорил, размагничивающий фактор N зависит от размеров сердечника

Катушка индуктивности с разомкнутым сердечником

Для его определения введём коэффициент λ, зависящий от отношения длины сердечника l_c к его диаметру d_c

Тогда в интервале 2 ≤ λ ≤ 50 с точностью 10 % размагничивающий фактор данного сердечника можно определить по следующему выражению

где λ – отношение длины сердечника к диаметру сердечника

Тогда эффективная магнитная проницаемость разомкнутого сердечника можно рассчитать по следующей формуле

где μ_r – относительная магнитная проницаемость вещества сердечника,

l_c – длина сердечника,

d_c – диаметр сердечника.

Как влияет форма сердечника на магнитную проницаемость?

Эмпирическая формула вычисления эквивалентной магнитной проницаемости сердечников предполагает, что сечение сердечника представляет собой круг, но существует большое количество сердечников с не круглым сечением (прямоугольные, трубчатые).

Вычисление эквивалентных диаметров сердечника.

Для упрощения расчётов все сердечники необходимо приводить к эквивалентному круговому сечению согласно следующим выражениям:

для прямоугольного сечения

где с – ширина сердечника,

h – высота сердечника.

для трубчатого сечения

где d_нар – наружный диаметр сердечника,

d_вн – внутренний диаметр сердечника.

Влияние расположение катушки индуктивности относительно сердечника

Довольно часто стержневые сердечники используют для точной настройки индуктивности или подстройки в небольших пределах, также длинные стержневые сердечники используют в магнитных антеннах радиоприёмников на средне- и длинноволновом диапазоне. Их объединяет то, что катушка индуктивности зачастую расположена не на средине сердечника. Ниже представлена катушка индуктивности на разомкнутом сердечнике, используемая в качестве магнитной антенны

Расположение катушки индуктивности на сердечнике в магнитной антенне.

Как я уже говорил, размагничивающий фактор не равномерно распределён по длине разомкнутого сердечника. Его значение увеличивается от середины сердечника к его краям, а магнитная проницаемость, а соответственно уменьшается от центра сердечника к его краям. Чтобы не усложнять выражение для размагничивающего фактора введем корректирующий коэффициент p_l, зависящий от расположения катушки на сердечнике

где х – расстояние от середины сердечника до середины катушки,

l – длина сердечника,

β – коэффициент, зависящий от расположения катушки на сердечнике.

Влияние размеров катушки относительно размеров сердечника

Как я писал выше, размагничивающий фактор неравномерен по длине сердечника, то необходимо учитывать любое различие в относительных размерах катушки индуктивности и сердечника.

Ещё одним существенным фактором при расчёте индуктивности является различие в длине катушки и длине сердечнике. Данное различие можно описать коэффициентом k, зависящем от отношения длины сердечника к длине катушки

где а – длина катушки индуктивности,

l – длина сердечника,

γ – коэффициент, зависящий от отношения длины катушки к длине сердечника.

Пример расчёта индуктивности катушки на разомкнутом сердечнике

В качестве примера рассчитаем катушку индуктивности на разомкнутом сердечнике круглого сечения со следующими параметрами: диаметр сердечника d_c = 6 мм, длина сердечника l_c = 30 мм, катушка состоит из 30 витков провода диаметром d_p = 1 мм, намотанных плотно виток к витку в один ряд, магнитная проницаемость материала сердечника μ_r = 600.

1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит l_k = 30*1 = 30 мм, а диаметр катушки d_k = d_cp = 30,5 мм.

2.Вычислим эффективную магнитную проницаемость сердечника

3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Так как длина катушки совпадает с длинной сердечника и смещение катушки относительно сердечника отсутствует, то поправочные коэффициенты будут равны 1, тогда индуктивность данной катушки составит

В качестве второго примера рассчитаем индуктивность магнитной антенны выполненной на сердечнике из феррита марки 600НН, размерами l_c = 160 мм, d_с = 8 мм, количество витков провода w = 60, диаметр провода d_р = 0,15 мм. Катушка смещена на 30 мм относительно середины сердечника.

1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит l_k = 60*0,15 = 9 мм, а диаметр катушки d_k = d_cp = 8,075 мм.

2.Вычислим эффективную магнитную проницаемость сердечника

3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Коэффициент, учитывающий расположение катушки на сердечнике составит

Коэффициент, учитывающий отношение длины катушки по отношению к длине сердечника составит

4.Рассчитаем индуктивность катушки индуктивности на разомкнутом сердечнике

Данная статья заканчивает цикл расчётов индуктивности катушек с различными конструктивными параметрами.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

Значение AL [Encyclopedia Magnetica]

Содержание

• Значение AL

  • Единицы и уравнения

  • Расчет индуктивности по значению AL и количеству витков

  • Практическое использование

  • Пример технического паспорта

  • См. также

  • Каталожные номера

Стэн Зурек, AL value, Encyclopedia Magnetica, E-Magnetica.pl

A _L ^{, A _L значение , коэффициент AL , коэффициент индуктивности 9 0052 , коэффициент индуктивности , индуктивность на виток , индуктивность на квадратный виток а также удельная индуктивность — значение удельной индуктивности (измеряется с 1 витка), характерное для данного магнитопровода (типа, размера, воздушного зазора и т.п.), часто предоставляемое изготовителем, для простоты расчетов. 9}

A _L =250 нГн/виток 7 А25/ надпись на сердечнике, 3х2 обозначает тип ферритового материала)

Величина A _L обычно используется при проектировании электронных трансформаторов на основе ферритовых сердечников, для которых величина часто указывается в наногенри.

Значение A _L широко используется в отношении магнитопроводов из мягкого феррита.

Название магнитной проводимости физически и математически синонимично значению A _L , но является более общим термином, относящимся к свойству данной магнитной цепи. ^{Постоянная величина является обратной величиной магнитного сопротивления}

→ → → Полезная страница? Поддержите нас! → → →

PayPal

← ← ← Помогите нам с всего за $0,10 в месяц? Давай… ← ← ←

Единицы и уравнения

Математически A _L имеет единицу измерения СИ генри ( H ), но связь с индуктивностью нелинейна, а практическая единица измерения — наногенри на квадратный виток или нГн/виток ² .

Следовательно, для расчета индуктивности 92 $$ (Н)

A _L значение = (nH/t²)(µH/t²)(mH/t²)(H/t²) количество витков Н = (безразмерно)

л = (нГн)(мкГн)(мГн)(Гн)

Примечание: значение AL обычно указывается только в единицах индуктивности, т. е. (nH), без квадратных витков. В этом случае просто выберите соответствующую единицу измерения, например. (нН/т ² ).

---

(См. также калькулятор Значение AL от индуктивности и числа витков ).

Практическое использование

При разработке трансформаторов и катушек индуктивности для импульсных источников питания параметры переключения и уровень мощности определяют значения индуктивности, необходимые для такого компонента.

Следовательно, значение индуктивности известно для следующего шага проектирования. Использование значения A _L позволяет быстро рассчитать необходимое количество витков для данного размера сердечника.

Следует отметить, что значение A _L часто дается в единицах (нГн) или подобных, подразумевая «на квадратный оборот». Важно помнить, что связь между значением A _L и индуктивностью не пропорциональна из-за возведения в квадрат витков.

Значение A _L особенно полезно при проектировании с сердечниками с зазором, например, для катушек индуктивности с зазором или трансформаторов обратного хода. В нормальных условиях воздушный зазор аккумулирует всю энергию и определяет эффективную магнитную проницаемость магнитопровода. 92 ⋅ \mu_0 ⋅ \mu_r ⋅ A}{l} $$ ( H )

где: Н — число витков, мк ₀ — магнитная проницаемость свободного пространства ( Гн/м ), мк _r — относительная проницаемость материала (безразмерная), А — площадь поперечного сечения ( м ² ), l — длина магнитного пути ( м ).

Приведенное выше уравнение можно переписать как: 92 ⋅ x $$ ( H )

где:

$$ x = \frac{\mu_0 ⋅ \mu_r ⋅ A}{l} $$

(W)

И, сравнивая уравнения, можно увидеть, что значение $x = A_L$ и является константой для данного магнитного сердечника с фиксированными параметрами, пока это не влияет на эффективную магнитную проницаемость (например, предотвращается насыщение).

Поэтому, если производитель предоставляет A _L это упрощает расчеты.

Типичное обозначение A _L =160 нГн ±3% означает, что сердечник имеет такой воздушный зазор, что A _L = 160 нГн (на квадратный оборот). Для сердечника ER14,5-3-7 это синоним воздушного зазора 150 мкм.

Жесткий допуск ±3% можно получить для пропорционально больших зазоров. В приведенном выше примере 150 мкм — это относительно большое значение для магнитного пути сердечника, которое составляет 19мм. Это снижает эффективную проницаемость с более чем 1000 до примерно 137 (см. также калькулятор эффективной проницаемости).

Для меньших зазоров влияние сердечника увеличивается, и допуск может достигать ±25%. То же самое относится и к неразрывным жилам.

Пример технического паспорта

Пример листа технических данных со значением A _L .

Файл	Описание
	Спецификация: ER14. 5-3-7, Сердечники Planar ER и аксессуары, Ferroxcube ER14.5-3-7, Сердечники Planar ER и аксессуары, Ferroxcube

См. также

• Проницаемость

• Индуктивность

• Проницаемость

Каталожные номера

---

^{1) , 1) , 1)} Спецификация, ER14.5-3-7, Ferroxcube.pdf

^{2) , 2)} W.G.Hurley, W.H. Вольфле, Трансформаторы и катушки индуктивности для силовой электроники: теория, конструкция и применение, John Wiley & Sons, 2013, ISBN 9781118544662, с. 63

^{3) , 3) , 3)} Конструкция индуктора и обратноходового трансформатора, Texas Instruments Inc., 2001, с. 5–7, {по состоянию на 24 июня 2013 г.}

⁴⁾ Ferrite, Summary, Ferrites, TDK, 2014, 001-01 / 20140308 / ferrite_summary_en.fm, {по состоянию на 2021-09 гг.-12}

⁵⁾ Патент US7117583, T. E. Динан и др., Метод и устройство, использующие затравочный слой с предварительно нанесенным рисунком для создания выровненной катушки для конструкции индуктивной головки, 2006

^{6) , 6)} Венцислав Чеков Валчев, Алекс Ван ден Босше, Катушки индуктивности и трансформаторы для силовой электроники, CRC Press, 2005, ISBN 9781420027280, с. 17

⁷⁾ Симус О’Дрисколл, Питер Мини, Джон Флэннери и Джордж Янг, Проектирование магнитных компонентов для оптимальной работы недорогих преобразователей переменного тока в постоянный, 2010–2011 Семинар по проектированию источников питания, тема 5 , Texas Instruments, {по состоянию на 27 июня 2013 г.}

⁸⁾ T. Brander, A. Gerfer, B. Rall, H. Zenker, Trilogy of Magnetics, Руководство по проектированию фильтров электромагнитных помех, SMPS и RF-схемы, Wurth Elektronik, 2001, ISBN 9783899291575

9000 6 ⁹⁾ Джон Клейтон Роулинз, Основные схемы переменного тока, Newnes, 2000, ISBN 9780750671736, с. 264

Магнитопроводы, Магнитные свойства, Калькуляторы, Счетчик

Конструкция индуктора с магнитными ферритовыми сердечниками

Следующее руководство по проектированию также можно загрузить в формате PDF. По другим вопросам, касающимся конструкции индуктора с ферритовыми сердечниками Magnetics, свяжитесь с нашими инженерами по применению или отправьте запрос на проектирование индуктора по индивидуальному заказу.

Сердечники из феррита E

и сердечники с горшковыми сердечниками обладают такими преимуществами, как низкая стоимость и низкие потери в сердечнике на высоких частотах. Для импульсных стабилизаторов рекомендуются силовые материалы из-за их температурных характеристик и характеристик смещения постоянного тока. Добавляя воздушные зазоры к этим ферритовым формам, можно эффективно использовать сердечники, избегая при этом насыщения.

Эти процедуры выбора сердечника упрощают проектирование катушек индуктивности для импульсных регуляторов. Можно определить наименьший размер сердечника, предполагая коэффициент намотки 50% и пропускную способность провода по току 500 круговых мил на ампер.

Должны быть известны только два параметра проектных приложений: 
(a) Требуемая индуктивность при смещении постоянного тока
(б) постоянный ток

1. Вычислите произведение LI², где: 
L = требуемая индуктивность при смещении постоянного тока (миллигенри)
I = максимальный выходной постоянный ток + 1/2 пульсации переменного тока

2. Найдите значение LI² в таблице выбора ферритовых сердечников ниже.
Следуйте этой координате на пересечении с первой кривой размера сердцевины. Считайте максимальную номинальную индуктивность, A _L , по оси Y. Это представляет собой наименьший размер ядра и максимальный A _L  , при котором можно избежать насыщения.

3. Любая линия размера сердечника, пересекающая координату LI², представляет рабочий сердечник для катушки индуктивности, если значение A _L сердечника меньше максимального значения, полученного на диаграмме.

4. Требуемая индуктивность L, размер сердечника и номинальная индуктивность сердечника (A _L ) известны.
Рассчитайте количество витков, используя 

.

, где L в миллигенри.

5. Пример: Если I _MAX = 8 Ампер; L, требуемая индуктивность = 100 мкГенри
LI² = (0,100 мГн) X (8² Ампер) = 6,4 миллиджоуля

6. Доступно множество ферритовых сердечников, поддерживающих необходимую энергию.
Любой размер сердечника, который пересекает координата LI², может использоваться для значения A _L  , показанного на диаграмме.

7. Некоторые варианты, основанные на значении LI², равном 6,4 миллиджоуля: 
Сердцевина горшка 43622 A _L  = 400      Двойная плита 43622 A _L  = 250 
PQ core 43220 A _L  = 300       E core 44317 A _L  = 250 

8. Для следующих значений AL требуется количество витков: 
A _L  = 400, N = 16       A _L  = 300, N = 19       A _L  = 250, N = 20 
Убедитесь, что выбранный размер провода выдержит ток и подойдет к набору сердечников.