Расчет напряжения после резистора. Расчет напряжения на резисторе: формулы, методы и примеры

Как рассчитать падение напряжения на резисторе. Какие формулы использовать для вычисления напряжения на резисторе. Какие методы применяются для определения напряжения после резистора. Как подобрать номинал резистора для получения нужного напряжения.

Основные формулы для расчета напряжения на резисторе

Для расчета напряжения на резисторе используются следующие основные формулы:

• Закон Ома: U = I * R, где U — напряжение, I — ток, R — сопротивление резистора
• Формула делителя напряжения: Uвых = Uвх * R2 / (R1 + R2)
• Падение напряжения на резисторе: ΔU = I * R

Рассмотрим подробнее применение этих формул на конкретных примерах расчетов.

Расчет напряжения по закону Ома

Закон Ома — основополагающая формула для расчета электрических цепей. Она позволяет вычислить напряжение на резисторе, если известны протекающий через него ток и сопротивление:

U = I * R

Пример: Через резистор 100 Ом протекает ток 0.5 А. Какое напряжение на нем возникнет?

Решение:

U = 0.5 А * 100 Ом = 50 В

Таким образом, напряжение на резисторе составит 50 В.

Формула делителя напряжения

Делитель напряжения — это схема из двух последовательно соединенных резисторов. Формула позволяет рассчитать выходное напряжение:

Uвых = Uвх * R2 / (R1 + R2)

Пример: Входное напряжение 12 В подается на делитель из резисторов 1 кОм и 2 кОм. Какое напряжение будет на втором резисторе?

Решение:

Uвых = 12 В * 2 кОм / (1 кОм + 2 кОм) = 8 В

На втором резисторе будет напряжение 8 В.

Расчет падения напряжения на резисторе

Падение напряжения на резисторе рассчитывается по формуле:

ΔU = I * R

Пример: Ток через резистор 220 Ом составляет 100 мА. Какое падение напряжения на нем возникнет?

Решение:

ΔU = 0.1 А * 220 Ом = 22 В

Падение напряжения на резисторе составит 22 В.

Методы определения напряжения после резистора

Для нахождения напряжения после резистора можно использовать следующие методы:

• Измерение вольтметром
• Расчет по закону Ома
• Применение правил Кирхгофа
• Моделирование в программах схемотехники

Рассмотрим некоторые из этих методов подробнее.

Измерение вольтметром

Самый простой способ определить напряжение после резистора — измерить его мультиметром в режиме вольтметра. Для этого нужно:

1. Установить мультиметр в режим измерения постоянного напряжения
2. Подключить щупы параллельно резистору
3. Считать показания с дисплея

Это даст точное значение напряжения на резисторе.

Расчет по закону Ома

Если известны параметры схемы, напряжение можно рассчитать по закону Ома:

1. Определить ток через резистор
2. Умножить ток на сопротивление резистора
3. Полученное значение будет напряжением на резисторе

Этот метод требует знания параметров цепи, но позволяет произвести расчет без измерений.

Подбор номинала резистора для получения нужного напряжения

При проектировании схем часто требуется подобрать резистор для получения заданного напряжения. Для этого можно использовать следующий алгоритм:

1. Определить требуемое падение напряжения на резисторе
2. Рассчитать ток через резистор
3. По закону Ома найти необходимое сопротивление
4. Выбрать ближайший номинал из стандартного ряда

Пример: Нужно получить напряжение 5 В из источника 12 В. Ток нагрузки 20 мА.

Решение:

1. Падение напряжения на резисторе: 12 В — 5 В = 7 В
2. Ток через резистор: 20 мА
3. Сопротивление: R = U / I = 7 В / 0.02 А = 350 Ом
4. Выбираем ближайший номинал 360 Ом

Таким образом, для получения напряжения 5 В нужен резистор 360 Ом.

Особенности расчета напряжения в цепях переменного тока

При расчете напряжения на резисторах в цепях переменного тока нужно учитывать следующие особенности:

• Используются действующие (среднеквадратичные) значения напряжения и тока
• Учитывается реактивное сопротивление конденсаторов и катушек индуктивности
• Применяется векторное сложение напряжений и токов
• Используются комплексные числа для расчетов

В простейшем случае для резистора в цепи переменного тока можно использовать те же формулы, что и для постоянного тока, но с действующими значениями напряжения и тока.

Влияние температуры на напряжение резистора

Температура оказывает влияние на сопротивление резистора, а значит и на падение напряжения на нем. Основные эффекты:

• С ростом температуры сопротивление металлических проводников увеличивается
• Сопротивление полупроводников при нагреве уменьшается
• Изменение сопротивления приводит к изменению падения напряжения

Для учета температурной зависимости используется температурный коэффициент сопротивления (ТКС). Он показывает, на сколько процентов изменяется сопротивление при изменении температуры на 1°C.

Применение расчетов напряжения на резисторах

Расчеты напряжения на резисторах применяются во многих областях электроники и электротехники:

• Проектирование источников питания
• Разработка усилителей
• Создание делителей напряжения
• Расчет светодиодных схем
• Проектирование измерительных приборов

Точный расчет напряжений позволяет обеспечить корректную работу электронных устройств и избежать выхода компонентов из строя из-за перенапряжения.

Программы для автоматизации расчетов

Для автоматизации расчетов напряжения на резисторах можно использовать различные программы:

• Онлайн-калькуляторы (резистор.рф, circuitlab.com)
• Программы схемотехнического моделирования (LTspice, Multisim)
• Инженерные калькуляторы (SMath Studio, Mathcad)
• Электронные таблицы (Excel, Google Sheets)

Эти инструменты позволяют быстро выполнять сложные расчеты и моделировать работу схем.

Он-лайн калькуляторы для радиолюбителя

Расчет резистора для светодиода

Он-лайн расчет резистора (или резисторов) для неограниченного количества светодиодов. Есть небольшая база светодиодов с заданными параметрами. Рассчитывает номиналы резисторов, цветовую маркировку, рассеиваемую мощность и потребляемый ток.

Перейти

Цветовая маркировка резисторов

Он-лайн калькулятор для расчета сопротивления и допуска резисторов с цветовой маркировкой в виде 4 или 5 колец

Перейти

LM317/LM350/LM338 калькулятор

Он-лайн калькулятор популярного линейного стабилизатора напряжения LM317. Расчет стабилизатора напряжения и тока. Рассчитывает номинал резистора, цветовую маркировку, рассеиваемую мощность и др. параметры.

Перейти

Калькулятор 555 таймера

Он-лайн калькулятор 555-го таймера работающего в режиме астабильного мультивибратора. Расчет как по заданию времени, так и по заданию сопротивлений (можно с учетом стандартных значений)

Перейти

LM2596 калькулятор

Он-лайн калькулятор DC-DC стабилизатора напряжения LM2596 с ограничением тока. Рассчитывает значение сопротивления (с учетом стандартного ряда) для требуемого выходного напряжения.

Перейти

TL431 калькулятор

Он-лайн калькулятор регулируемого стабилитрона TL431 (LM431).

Перейти

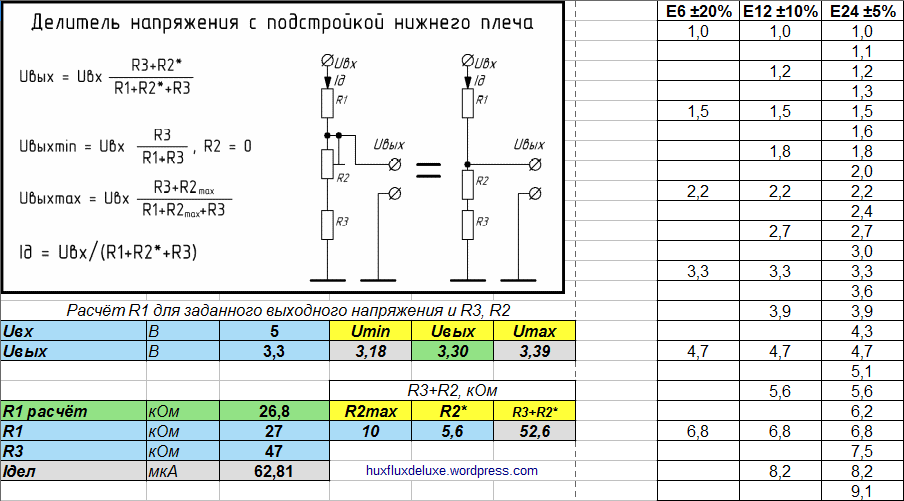
Делитель напряжения

Он-лайн расчет делителя напряжения. Два вида расчета: расчет выходного напряжения или расчет сопротивлений (сопротивления).

Перейти

Калькулятор маркировки на SMD резисторах

Вывод маркировки по указанию сопротивления, а также обратный расчет сопротивления по коду маркировки. Поддержка маркировки с 3-мя и 4-мя цифрами, а также стандарта EIA-96.

Перейти

Расчет диаметра провода для плавких предохранителей

Он-лайн калькулятор для расчета диаметра провода для плавких предохранителей. А также расчет максимального тока по диаметру провода. Шесть видов различных материалов проводников.

Перейти

Расчет сопротивления провода

Он-лайн калькулятор для расчета сопротивления провода. Также предусмотрено нахождение длины провода в зависимости от сопротивления.

Перейти

Закон Ома

Он-лайн калькулятор закона Ома для постоянного тока. Вычисление напряжения, сопротивления или тока. А также расчет мощности.

Перейти

Калькулятор колебательного контура LC

Он-лайн калькулятор LC колебательного контура.

Перейти

Калькулятор однослойной катушки

Расчет однослойных катушек индуктивности. Расчет числа витков и индуктивности.

Перейти

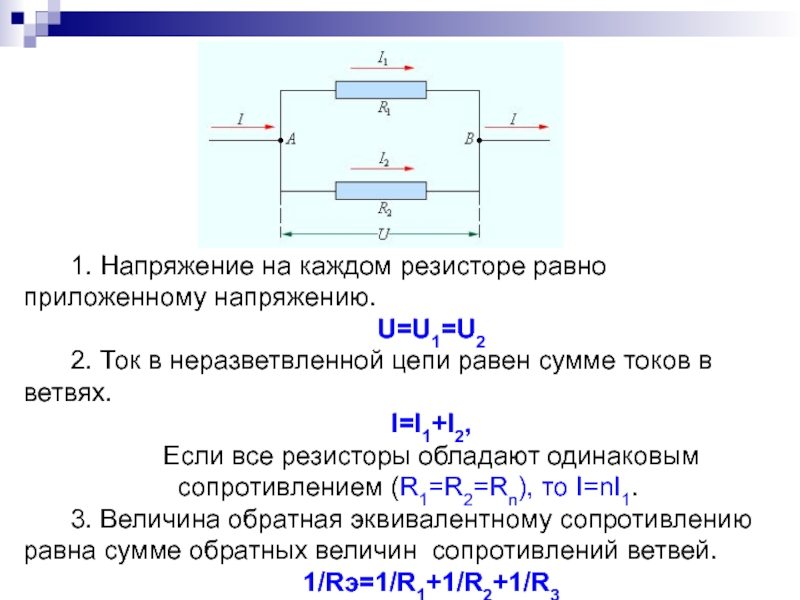
Последовательное соединение резисторов

Он-лайн расчет последовательного соединения резисторов

Перейти

Параллельное соединение резисторов

Он-лайн расчет параллельного соединения резисторов

Перейти

Последовательное соединение конденсаторов

Он-лайн расчет последовательного соединения конденсаторов

Перейти

Параллельное соединение конденсаторов

Он-лайн расчет параллельного соединения конденсаторов

Перейти

Расчет напряжения после резистора

Самым распространённым элементом в электрических схемах является резистор. Эта несложная в изготовлении радиодеталь используется для ограничения проходящего через него тока, а также изменения напряжения. По своей сути она является пассивным элементом, преобразующим электрическую энергию в тепло. Существование электричества было обнаружено ещё в VII веке до н. Учёный Уильям Гилберт, проводя эксперименты с янтарём, обнаружил его способность притягивать другие вещества электростатический заряд.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Калькулятор расчета делителя напряжения
• Primary Menu
• Расчет резисторов для светодиодов
• Делитель напряжения: схема и расчёт
• Резисторы, ток и напряжение
• Электроника для начинающих
• Расчёт сопротивления для понижения напряжения
• Падение напряжения на резисторе

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Урок №41.

Как с помощью резистора уменьшить напряжение?

Калькулятор расчета делителя напряжения

Светодиоды все чаще используются нами в различных сферах. Они представляют собой полупроводниковый прибор, превращающий электрический ток в световое излучение. Для получения света с их помощью, не надо применять специальные дополнительные преобразователи. Достаточно подать на него электрический ток. В этом моменте часто проблемы.

Они чувствительны к большим скачкам тока, которые наблюдаются при включении. Резисторы по праву считаются самыми распространенными радиоэлементами. Главная их характеристика состоит в сопротивлении, в двух словах, они препятствуют протеканию электрического тока. Резисторы считаются пассивными элементами электрической цепи. Они могут быть постоянными, то есть такими сопротивлениями, у которых протекание тока остается неизменным.

Их используют как токоограничительные элементы, делители напряжения, шунты для измерительных приборов, и тому подобное. Основной параметр резистора — это его сопротивление. Измеряемой характеристикой величины сопротивления есть Ом. Для провидения расчета понадобится знать точные параметры светодиода и источника напряжения. Их можно прочитать в паспортных данных, или найти в интернете. По источнику питания нам понадобятся данные выходного напряжения.

Возьмем, к примеру, простейшую схему на рисунке выше. Подставив в формулу значение напряжения и тока, мы получили величину сопротивления. После этого, находим по справочным таблицам, ближайшее стандартное значение. Если нет точного значения, лучше взять с небольшим запасом в большую сторону.

Для расчета на онлайн-калькуляторе понадобятся все те же данные, что и для расчетов в ручном режиме. Принцип работы резистора построен на рассеивании мощности. Номинальной мощностью рассеивания является та мощность, которую резистор может рассеять не повреждаясь. Единица мощности — ватты.

Резисторы, в том числе балластные, используются для поглощения некоторой части напряжения, выравнивают силы тока в различных участках цепи.

Тем самым, они поддерживают стабильность напряжения. Этот принцип используют в резисторах для светодиодов. Светодиоды чувствительны к большим скачкам тока, которые могут возникнуть при их включении, они могут привести их негодность.

Включенный последовательно с ним токоограничивающий резистор, уменьшит ток до приемлемой величины. Светодиоды — это полупроводниковые приборы, при их подключении необходимо соблюдать полярность. При неправильном подключении они работать не будут, и довольно часто выходят со строя. Обычно, ножка катода немного меньше по длине. Часто, катод можно опознать по более толстой ножке внутри прибора.

В любом случае, данные по контактам можно найти в справочной литературе. Диоды также боятся перегрева во время пайки. Для пайки нельзя использовать мощные паяльники, лучше использовать приборы мощностью до Вт. Он отведет часть тепла. Вместо пинцета, можно использовать и другие металлические инструменты. Сам процесс пайки одной ножки не должен превышать секунд. При этом времени, прибор не успеет перегреться. При монтаже светодиода на месте установки, старайтесь, чтобы контакты ближе к корпусу, оставались параллельны, как при выходе из производства.

Изгибайте контакты небольшими радиусами, уступив подальше от корпуса. Собирайте их на твердом плоском материале. Предварительно, подготовьте отверстия для ножек светодиодов с помощью дрели. Подбирая источник питания, следует помнить: чем больше разница рабочего напряжения светодиода и источника питания, тем меньше они будут подвержены влиянию скачков напряжения блока питания.

Не забывайте устанавливать предохранители. Если у вас безвыходные SMD светодиоды, у них вместо ножек для пайки контактные площадки. Эти площадки расположены на нижней части их корпуса. Паяют их маломощными паяльниками не более 15 ВТ. Часто, для этой работы применяют специальное жало. Оно имеет разветвление на рабочем конце. Народные умельцы вместо специального жала наматывают тонкий медный провод на стандартное жало. Оптимальный диаметр такого провода 1 мм. Проверяется он как обычный диод.

Его надо включить в прямом положении, чтобы между анодом и катодом пошло положительное напряжение. Многие современные цифровые приборы имеют встроенную возможность проверки диодов.

Главное при проверке — соблюдать полярность. Найдем падения напряжения на резисторе. Резисторы являются важными элементами электрической цепи, главная их функция — это сопротивление протеканию электрического тока. Этим он способствует стабилизации и ограничении силы тока протекающей по цепи. Его часто используют в качестве балластного резистора, чтобы иметь возможность регулировать напряжение в цепи.

Паяльник перед пайкой надо разогреть до его максимальной температуры. Было бы хорошо, чтобы его температура была в пределах градусов Цельсия. Понравилась статья? Поделиться с друзьями:. Добавить комментарий Отменить ответ.

Все права защищены. Копирование материалов сайта без указания активной ссылки на наш сайт как на источник запрещено. Контакты О сайте Рекламодателям Карта сайта.

Primary Menu

Светодиоды все чаще используются нами в различных сферах. Они представляют собой полупроводниковый прибор, превращающий электрический ток в световое излучение. Для получения света с их помощью, не надо применять специальные дополнительные преобразователи. Достаточно подать на него электрический ток.

Изменение этого напряжения заряжает или разряжает . После расчета и подбора резистора важно соблюдать следующее условие.

Расчет резисторов для светодиодов

Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Калькулятор справочный портал. Избранные сервисы. Кликните, чтобы добавить в избранные сервисы. Калькулятор расчета делителя напряжения поможет вам рассчитать выходное напряжение электрической цепи с резистивным или ёмкостным делителем напряжения, по значениям входного напряжения, сопротивлениям резисторов и емкостям конденсаторов.

Делитель напряжения: схема и расчёт

Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов резисторов, реактивных сопротивлений. Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой — верхнее плечо , между нулевой и минусом — нижнее плечо.

Допустим, вы построили модель игрушечной железной дороги и хотите освещать платформу главного вокзала, но не слишком ярко, чтобы соседи не заметили и не подумали невесть что. Для этого достаточно в схему, составленную выше, дополнительно ввести резистор.

Резисторы, ток и напряжение

Добрый день. Раз общественность просит схем и расчетов я так полагаю и некая наглядность подразумевается, как форма для лучшего восприятия позволю себе дать автору непрошеный совет. Вот особенно если MathCad вам не чужд полезная онлайн штуковина в простонародье Smath Studio , а уж если вы воспользуетесь вот этим замечательным инструментом, то последующие статьи, а может и эта если не лень немного доработать станут весьма внушительнее и интерактивней. Мой совет — почитайте несколько даташитов хороших на драйвера, далеко не у всех достаточное выходное сопротивление, плюс прикиньте мощность и как корпус драйвера сможет её рассеять. Хорошая заметка.

Электроника для начинающих

Иногда возникает задача понизить переменное напряжение сети вольт до некоторого заданного значения, причем применение понижающего трансформатора в таком случае не всегда бывает целесообразным. Скажем, низкочастотный понижающий трансформатор, выполненный традиционно на трансформаторном железе, способный преобразовать мощность Ватт, весит больше килограмма, не говоря о высокой стоимости. Следовательно в некоторых случаях можно применить гасящий резистор, который ограничит ток, однако при этом на самом гасящем резисторе выделится мощность в виде тепла, а это не всегда является приемлемым. Например, если нужно запитать Ваттную лампу только на половину ее наминала, потребовалось бы рассеять мощность в Ватт на гасящем резисторе, а это крайне сомнительное решение. Весьма удобной альтернативой, для данного примера, может служить применение гасящего конденсатора, емкостью около14мкф, такой можно собрать из трех металлопленочных типа К по 4,7мкф, рассчитанных на в, а лучше — на в это позволит получить нужный ток без необходимости рассеивать значительную мощность в виде тепла. Рассмотрим физическую сторону этого решения.

Доброго времени all-audio.proнно у меня вылетает из головы, как определить падение напряжения на резисторе. В очередной раз.

Расчёт сопротивления для понижения напряжения

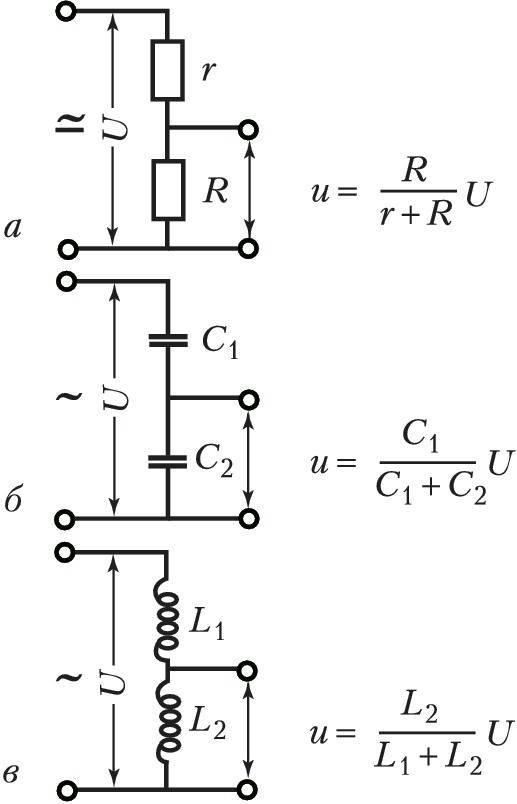
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения voltage divider. Это схема, строящаяся на основе пары резисторов. В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе V out?

Падение напряжения на резисторе

ВИДЕО ПО ТЕМЕ: ⚡️#7 Переменные и подстроечные резисторы. Делители напряжения и тока

Есть другой способ снижения напряжения на нагрузке, но только для цепей постоянного тока. Про смотри здесь. Вместо дополнительного резистора используют цепочку из последовательно включенных, в прямом направлении, диодов. На германиевом диоде падает напряжение 0,5 — 0,7 В, на кремниевом от 0,6 до 1,2 Вольта.

В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него.

Он же емкость — еще один вид пассивных элементов. На схеме обозначен как две одинаковые параллельные черточки. В отличии от резистора, конденсатор это нелинейный элемент. По нашей канализационной аналогии его можно сравнить с резиновым баком. Вначале, когда он пуст, вода резко его заполняет, растягивая стенки. Постепенно, когда стенки растянутся до предела, его сопротивление возрастет настолько, что поток воды остановится. А если убрать внешнее давление, то хлынет обратно.

Многие сталкивались с необходимостью подбора ограничительного резистора для светодиодов, при организации дополнительной подсветки в авто. Предлагаю простую методику расчета номинала и мощности резистора. Ток потребления яркого светодиода равен 10…15 мА или 0,01…0, А.

4.6 Цепи постоянного тока, содержащие резисторы и конденсаторы

Цели обученияRC-схемыРазрядка конденсатораRC-цепи для измерения времени

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Объяснить значение постоянной времени τ и вычислить постоянную времени для данного сопротивления и емкости
• Объясните, почему батарейки в фонарике постепенно разряжаются, а свет со временем тускнеет
• Опишите, что происходит с графиком зависимости напряжения на конденсаторе от времени при его зарядке
• Объясните, как работает схема синхронизации, и перечислите некоторые приложения
• Расчет необходимой скорости стробоскопической вспышки, необходимой для остановки движения объекта на определенной длине

Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:

• 5. C.3.6 Учащийся может определить недостающие значения и направление электрического тока в ветвях цепи как с резисторами, так и с конденсаторами по значениям и направлениям тока в других ветвях цепи путем соответствующего выбора узлов и Применение правила соединения. (СП 1.4, 2.2)
• 5.C.3.7 Учащийся может определять недостающие значения, направление электрического тока, заряд конденсаторов в установившемся режиме и разность потенциалов в цепи с резисторами и конденсаторами по значениям и направлениям тока в других ветвях схема. (СП 1.4, 2.2)

При использовании камеры со вспышкой для зарядки конденсатора, питающего вспышку, требуется несколько секунд. Световая вспышка разряжает конденсатор за доли секунды. Почему зарядка занимает больше времени, чем разрядка? Этот вопрос и ряд других явлений, связанных с зарядкой и разрядкой конденсаторов, обсуждаются в этом модуле.

RC Цепи

Цепь RCRC размера 12{ ital «RC»} {} содержит резистор RR размера 12{R} {} и конденсатор C.C. размер 12{C} {} Конденсатор представляет собой электрический компонент, хранящий электрический заряд.

На рис. 4.41 показана простая схема RCRC размера 12{ ital «RC»} {}, в которой используется источник постоянного напряжения. Конденсатор изначально не заряжен. Как только ключ замыкается, ток течет к и от первоначально незаряженного конденсатора. По мере увеличения заряда на пластинах конденсатора увеличивается сопротивление потоку заряда за счет отталкивания одинаковых зарядов на каждой пластине.

Что касается напряжения, это связано с тем, что напряжение на конденсаторе определяется как Vc=Q/C,Vc=Q/C, размер 12{V rSub { размер 8{c} } =Q/C} {}, где размер QQ 12{Q} {} – это количество заряда, хранящегося на каждой пластине, а размер CC 12{C} {} – это емкость. Это напряжение противодействует батарее, возрастая от нуля до максимальной ЭДС при полной зарядке. Таким образом, ток уменьшается от своего начального значения I0=emfRI0=emfR size 12{I rSub { size 8{0} } = {{«emf»} over {R} } } {} до нуля, когда напряжение на конденсаторе достигает то же значение, что и ЭДС. Когда нет тока, нет падения, поэтому напряжение на конденсаторе должно быть равно ЭДС источника напряжения. Это также можно объяснить вторым правилом Кирхгофа (правилом петли), обсуждаемым в Правилах Кирхгофа, которое гласит, что алгебраическая сумма изменений потенциала вокруг любой замкнутой петли должна быть равна нулю.

Начальный ток равен I0=emfRI0=emfR размер 12{I rSub { размер 8{0} } = {{«ЭДС»} свыше {R} } } {}, поскольку все IRIR размера 12{ ital «IR»} {} падение сопротивления. Следовательно, чем меньше сопротивление, тем быстрее будет заряжаться данный конденсатор. Обратите внимание, что внутреннее сопротивление источника напряжения включено в R, R, размер 12 {R} {}, как и сопротивления конденсатора и соединительных проводов. В приведенном выше сценарии камеры со вспышкой, когда батареи питания камеры начинают изнашиваться, их внутреннее сопротивление возрастает, уменьшая ток и увеличивая время, необходимое для подготовки к следующей вспышке.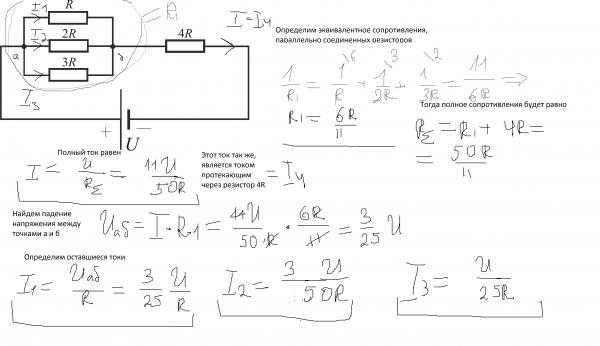

Рис. 4.41 (a) Цепь RCRC размера 12{ ital «RC»} {} с изначально незаряженным конденсатором. Ток течет в указанном направлении (противоположном потоку электронов), как только переключатель замыкается. Взаимное отталкивание одинаковых зарядов в конденсаторе постепенно замедляет поток по мере заряда конденсатора, останавливая ток, когда конденсатор полностью заряжен и Q=C⋅ЭДС. Q=C⋅ЭДС. size 12{Q=C cdot «emf»} {} (b) График зависимости напряжения на конденсаторе от времени при замыкании ключа в момент времени t=0.t=0. size 12{t=0} {} (Обратите внимание, что в двух частях рисунка заглавная буква E означает ЭДС, qq означает заряд, хранящийся в конденсаторе, а ττ – постоянную времени RCRC.)

Напряжение на конденсаторе изначально равно нулю и сначала быстро возрастает, так как начальный ток максимален. На рис. 4.41(b) показан график зависимости напряжения конденсатора от времени (размер tt 12{t} {}), начиная с момента замыкания ключа в момент времени t=0.t=0. size 12{t=0} {} Напряжение приближается к ЭДС асимптотически, поскольку чем ближе оно приближается к ЭДС, тем меньше ток течет. Уравнение зависимости напряжения от времени при зарядке конденсатора CC типоразмера 12{C} {} через резистор R, R, типоразмера 12{R} {}, полученное с помощью вычислений, равно 9.0003

4,77 В=ЭДС(1-e-t/RC) (зарядка),V=ЭДС(1-e-t/RC) (зарядка), размер 12{V=»ЭДС» \( 1 — e rSup { размер 8{ — т/ итал «RC»} } \) } {}

, где ВВ размером 12{В} {} — напряжение на конденсаторе, ЭДС равна ЭДС источника постоянного напряжения, а экспонента e = 2,718… — основание натурального логарифма. Обратите внимание, что единицы измерения RCRC size 12{ ital «RC»} {} — это секунды. Определяем

4,78 τ=RC,τ=RC, размер 12{τ= итал. «RC»} {}

, где ττ size 12{τ} {} (греческая буква tau) называется постоянной времени для цепи RCRC size 12{ ital «RC»} {}. Как отмечалось ранее, малое сопротивление RR размером 12{R}{} позволяет конденсатору заряжаться быстрее. Это разумно, так как больший ток протекает через меньшее сопротивление. Также разумно, что чем меньше конденсатор C,C, размер 12{C} {}, тем меньше времени требуется для его зарядки. Оба фактора содержатся в τ=RC.τ=RC. размер 12{τ= итал. «RC»} {}

Более количественно рассмотрим, что происходит, когда t=τ=RC.t=τ=RC. size 12{t=τ= ital «RC»} {} Тогда напряжение на конденсаторе равно

4,79 В=ЭДС1-e-1=ЭДС1-0,368=0,632⋅ЭДС.V=ЭДС1-e-1=ЭДС1-0,368=0,632⋅ЭДС. size 12{V=»emf» влево (1 — e rSup { size 8{- 1} } right )=»emf» влево (1 — 0 «.» «368» right )=0 «.» «632» cdot «emf»} {}

Это означает, что за время τ=RC,τ=RC, размер 12{τ= ital «RC»} {} напряжение возрастает до 0,632 своего конечного значения. Напряжение вырастет на 0,632 остатка в следующий момент времени τ.τ. size 12{τ} {} Характеристика экспоненциальной функции состоит в том, что конечное значение никогда не достигается, но 0,632 остатка от этого значения достигается каждый раз, τ.τ. size 12{τ} {} Всего за несколько кратных постоянной времени τ,τ, size 12{τ} {} окончательное значение будет почти достигнуто, как показано на графике на рис. 4.41(b).

Разрядка конденсатора

Разрядка конденсатора через резистор происходит аналогичным образом, как показано на рис. 4.42. Первоначально ток I0=V0R,I0=V0R, размер 12{I rSub {размер 8{0} } = {{V rSub {размер 8{0} } } над {R} } } {} управляется начальным напряжение V0V0 габарит 12{V rSub { габарит 8{0} } } {} на конденсаторе. По мере уменьшения напряжения ток и, следовательно, скорость разряда уменьшаются, что подразумевает другую экспоненциальную формулу для В.В. типоразмер 12{V} {} Расчетным путем установлено, что напряжение VV ​​типоразмера 12{V} {} на конденсаторе CC типоразмера 12{C} {}, разряжаемом через резистор RR типоразмера 12{R} {}, равно

4,80 V=V0e-t/RC (разрядка).V=V0e-t/RC (разрядка). size 12{V=`V»» lSub { size 8{0} } `e rSup { size 8{ — t/ ital «RC»} } } {}

Рисунок 4.42 (a) Замыкание ключа разряжает конденсатор CC размера 12{C} {} через резистор R.R размера 12{R} {} Взаимное отталкивание одинаковых зарядов на каждой пластине вызывает ток. (b) График зависимости напряжения на конденсаторе от времени для V=V0V=V0 размера 12{V=V rSub { размера 8{0} } } {} при t=0.t=0. Напряжение уменьшается экспоненциально, падая на фиксированную долю пути до нуля в каждую последующую постоянную времени τ.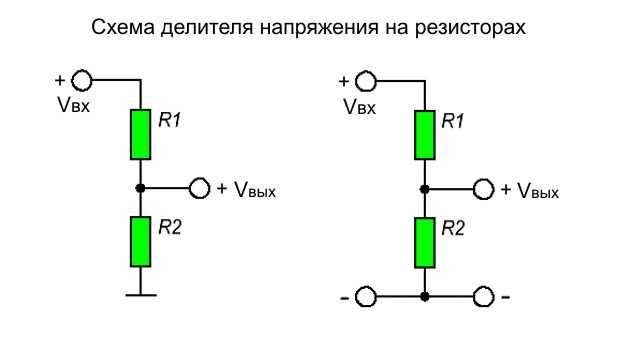 τ. размер 12{τ} {}

График на рис. 4.42(b) является примером такого экспоненциального затухания. Опять же, постоянная времени равна τ=RC.τ=RC. размер 12{τ= ital «RC»} {} Небольшое сопротивление RR размера 12{R} {} позволяет конденсатору разрядиться за короткое время, так как ток больше. Точно так же малой емкости требуется меньше времени для разряда, поскольку сохраняется меньше заряда. В первый интервал времени τ=RCτ=RC size 12{τ= ital «RC»} {} после замыкания ключа напряжение падает до 0,368 от исходного значения, так как V=V0⋅e−1=0,368V0,V =V0⋅e−1=0,368V0. size 12{V=V rSub { size 8{0} } cdot e rSup { size 8{- 1} } =0 «.» «368»V rSub { размер 8{0} } } {}

В течение каждого последующего времени τ,τ размером 12{τ} {} напряжение падает до 0,368 предыдущего значения. При величине 12{τ} {}, кратной τ,τ, напряжение становится очень близким к нулю, как показано на графике на рис. 4.42(b).

Теперь мы можем объяснить, почему фотовспышка в нашем сценарии заряжается гораздо дольше, чем разряжается; сопротивление при зарядке значительно больше, чем при разрядке. Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки. По мере старения батареи увеличивающееся внутреннее сопротивление еще больше замедляет процесс зарядки. (Возможно, вы это заметили.)

Вспыхивающий разряд происходит через ионизированный газ с низким сопротивлением в импульсной трубке и происходит очень быстро. Фотографии со вспышкой, такие как на рис. 4.43, могут запечатлеть краткий момент быстрого движения, потому что продолжительность вспышки может быть меньше микросекунды. Такие вспышки можно сделать чрезвычайно интенсивными.

Во время Великой Отечественной войны проводились ночные разведывательные фотосъемки с воздуха с одной вспышкой, освещавшей более квадратного километра территории противника. Краткость вспышки устранила размытие из-за движения самолета-разведчика. Сегодня важным применением мощных импульсных ламп является накачка энергии в лазер. Короткая интенсивная вспышка может быстро активировать лазер и позволить ему переизлучать энергию в другой форме.

Рис. 4.43 Эта покадровая фотография рыжей колибри ( Selasphorus rufus ), питающейся цветком, была получена с чрезвычайно короткой и интенсивной вспышкой света, вызванной разрядом конденсатора через газ. (Дин Э. Биггинс, Служба рыболовства и дикой природы США)

Пример 4.6 Интегрированная концептуальная задача: расчет размера конденсатора — стробоскопы

Впервые фотосъемка с высокоскоростной вспышкой была предложена Док Эдгертон в 1930-х годах, когда он был профессором электротехники в Массачусетском технологическом институте. Вы могли видеть примеры его работы в удивительных кадрах движущихся колибри, капли молока, разбрызгивающейся на стол, или пули, пронзающей яблоко (см. рис. 4.43). Чтобы остановить движение и сделать эти снимки, нужна мощная вспышка с очень коротким импульсом, как упоминалось ранее в этом модуле.

Предположим, кто-то хочет сфотографировать пулю (двигающуюся со скоростью 5,0×102 м/с5,0×102 м/с), которая проходит сквозь яблоко. Длительность вспышки связана с постоянной времени 12{ итал. «RC»} {} КРКР, τ.τ. размер 12{τ} {} Конденсатор какого размера потребуется в цепи RCRC размера 12{ ital «RC»} {}, чтобы добиться успеха, если сопротивление лампы-вспышки 10,0 Ом10,0 Ом размера 12{«10» %OMEGA } {}? Предположим, что яблоко представляет собой шар диаметром 8,0×10–2м.8,0×10–2м.

Стратегия

Начнем с определения задействованных физических принципов. Этот пример имеет дело со стробоскопом, как обсуждалось выше. На рис. 4.42 показана схема этого пробника. Характерное время ττ размера 12{τ} {} строба задается как τ=RC.τ=RC. размер 12{τ= итал. «RC»} {}

Решение

Мы хотим найти C,C, размер 12{C} {}, но не знаем τ.τ. size 12{τ} {} Мы хотим, чтобы вспышка была включена только тогда, когда пуля пересекает яблоко. Поэтому нам нужно использовать кинематические уравнения, которые описывают взаимосвязь между расстоянием x, x, размером 12{x} {}, скоростью v, v, размером 12{v} {} и временем t. t. размер 12{т} {}

4.81 x=vtort=xvx=vtort=xv size 12{t= {{x} over {v} } } {}

Скорость пули дается как 5.0×102 м/с, 5.0×102 м/с, и расстояние xx размера 12{x} {} составляет 8,0×10–2м.8,0×10–2м. Тогда время прохождения равно

4,82 t=xv=8,0×10–2 м5,0×102 м/с=1,6×10−4 с.t=xv=8,0×10–2 м5,0×102 м/с=1,6× 10−4 с. size 12{t= {{x} over {v} } = {{0 «.» «08»» м»} свыше {«500 м/с»} } =1 «.» 6 раз «10» rSup { size 8{ — 4} } » s»} {}

Устанавливаем это значение для времени пересечения tt size 12{t} {} равным τ.τ. size 12{τ} {} Следовательно,

4,83 C=tR=1,6×10−4 с10,0 Ом=16 мкФ.C=tR=1,6×10−4 с10,0 Ом=16 мкФ. размер 12{C= {{t} над {R} } = { { слева (1 «.» 6´»10″ rSup {размер 8{-4} } справа )} над {«10″} } =»16 » мкФ} {}

Примечание. Емкость CC размера 12{C} {} обычно измеряется в фарадах, Ф,Ф, определяемых как кулоны на вольт. Из уравнения мы видим, что размер CC 12{C} {} также может быть указан в секундах на ом.

Обсуждение

Интервал вспышки 160 мкс160 мкс размером 12{«160» мс} {} (время прохождения пули) относительно легко получить сегодня. Стробоскопы открыли новые миры от науки до развлечений. Информация с изображения яблока и пули была использована в отчете Комиссии Уоррена об убийстве президента Джона Ф. Кеннеди в 1963, чтобы подтвердить, что была выпущена только одна пуля.

RC Цепи синхронизации Нулевые цепи

обычно используются для целей синхронизации. Приземленный пример этого можно найти в вездесущих прерывистых системах стеклоочистителей современных автомобилей. Время между очистками варьируется путем регулировки сопротивления нулевой цепи. Другой пример нулевой схемы можно найти в новых украшениях, костюмах на Хэллоуин и различных игрушках с мигающими огнями на батарейках. См. рис. 4.44 для временной схемы.

Более важным использованием нулевых цепей для целей синхронизации является искусственный кардиостимулятор, используемый для контроля частоты сердечных сокращений. Частота сердечных сокращений в норме контролируется электрическими сигналами, генерируемыми синоатриальным (СА) узлом, который находится на стенке камеры правого предсердия. Это заставляет мышцы сокращаться и перекачивать кровь. Иногда сердечный ритм ненормальный, а сердцебиение слишком высокое или слишком низкое.

Искусственный кардиостимулятор вставляется рядом с сердцем, чтобы подавать электрические сигналы к сердцу, когда это необходимо, с соответствующей постоянной времени. У кардиостимуляторов есть датчики, которые обнаруживают движение тела и дыхание, чтобы увеличить частоту сердечных сокращений во время упражнений, чтобы удовлетворить повышенные потребности организма в крови и кислороде.

Рис. 4.44 (a) Лампа в этой нулевой цепи обычно имеет очень высокое сопротивление, так что батарея заряжает конденсатор, как если бы лампы не было. Когда напряжение достигает порогового значения, через лампу протекает ток, резко уменьшающий ее сопротивление, и конденсатор разряжается через лампу, как будто батареи и зарядного резистора не было. После разряда процесс начинается снова, при этом период вспышки определяется нулевой константой. (b) График зависимости напряжения от времени для этой схемы.

Пример 4.7 Расчет времени:

RC Цепь дефибриллятора сердца

Дефибриллятор сердца используется для реанимации пострадавшего в результате несчастного случая путем разрядки конденсатора через туловище ее тела. Упрощенный вариант схемы показан на рис. 4.42. (a) Какова постоянная времени, если используется нулевой конденсатор, а сопротивление пути через ее тело составляет 1,00×103 Ом?1,00×103 Ом? (b) Если начальное напряжение равно 10,0 кВ, сколько времени потребуется, чтобы снизиться до 5,00×102 В? 5,00×102 В?

Стратегия

Поскольку сопротивление и емкость известны, их просто перемножить, чтобы получить постоянную времени, требуемую в части (a). Чтобы найти время снижения напряжения до 5,00×102 В, 5,00×102 В, мы многократно умножаем начальное напряжение на 0,368, пока не получим напряжение, меньшее или равное 5,00×102 В5,00×102 В. Каждое умножение соответствует времени нулевых секунд.

Решение для (a)

Нулевая постоянная времени определяется уравнением null Ввод заданных значений сопротивления и емкости (и памятование о том, что единицы измерения фарад могут быть выражены как ноль, дает

4,84 null

Решение для (b)

За первые 8,00 мс напряжение (10,0 кВ) снижается до 0,368 от исходного значения. То есть

4,85 null

(Обратите внимание, что мы вносим дополнительную цифру для каждого промежуточного вычисления.) Еще через 8,00 мс мы снова умножаем на 0,368, и напряжение равно

4,86 ​​В′=0,368 В=0,3683,680. × 103 В = 1,354 × 103 Вт = 16,0 мс. V′ = 0,368 В = 0,3683,680 × 103 В = 1,354 × 103 Вт = 16,0 мс.

Аналогично, еще через 8,00 мс напряжение равно

4,87 V′′=0,368 В′=(0,368)(1,354×103 В)=498 В при t=24,0 мс. V′′=0,368 В′=(0,368)(1,354×103 В)=498 В при t=24,0 мс.

Обсуждение

Таким образом, уже через 24,0 мс напряжение падает до 498 В, или 4,98% от исходного значения. Такие короткие промежутки времени полезны при дефибрилляции сердца, поскольку кратковременный, но интенсивный ток вызывает кратковременное, но эффективное сокращение сердца. сердце. Фактическая схема сердечного дефибриллятора немного сложнее, чем схема на рис. 4.42, чтобы компенсировать магнитные и переменные эффекты, которые будут рассмотрены в разделе «Магнетизм».

 

 

Проверьте свое понимание

Когда разность потенциалов на конденсаторе является ЭДС?

Решение

Только когда ток, потребляемый или подаваемый на конденсатор, равен нулю. Конденсаторы, как и батареи, имеют внутреннее сопротивление, поэтому их выходное напряжение не является ЭДС, если только ток не равен нулю. На практике это трудно измерить, поэтому мы ссылаемся на напряжение конденсатора, а не на его ЭДС. Но источник разности потенциалов в конденсаторе фундаментальный, и это ЭДС.

PhET Explorations: Circuit Construction Kit (только DC)

Комплект электроники в вашем компьютере! Создавайте схемы с резисторами, лампочками, батареями и переключателями. Проведите измерения с помощью реалистичного амперметра и вольтметра. Просмотрите схему в виде принципиальной схемы или переключитесь на реалистичный вид.

Рисунок 4.45 Комплект для построения схемы (только для постоянного тока)

• Печать
• Поделиться

Как рассчитать падение напряжения в последовательной цепи: подробные факты —

Автор: Kaushikee Banerjee

В этой статье разъясняется, что такое падение напряжения и как рассчитать падение напряжения в последовательной цепи. Всякий раз, когда напряжение встречает какой-либо резистивный элемент в цепи, значение уменьшается или «падает».

В последовательной цепи имеется несколько сопротивлений или импедансов. Каждый раз, когда через них проходит ток, напряжение уменьшается. Итак, нам нужно знать значение определенного сопротивления и тока, проходящего через него, чтобы вычислить падение напряжения на нем. Падение напряжения — это ток, умноженный на сопротивление.

Что такое падение напряжения?

Предположим, мы соединяем батарею с резистором через провод. Электроны имеют тенденцию течь от отрицательной стороны батареи к положительной. Это похоже на электрический заряд, идущий от положительного к отрицательному выводу.

Когда одна единица заряда сталкивается с резистором, он на некоторое время останавливается. Когда он проходит резистор, приходит другая единица заряда и останавливается. В любой момент времени заряд на конце резистора меньше, чем заряд на начале резистора. Это явление создает «падение потенциала или напряжения».

Подробнее…..Постоянно ли напряжение в последовательной цепи: полная информация и часто задаваемые вопросы

Как рассчитать общее падение напряжения в последовательной цепи?

Полное падение напряжения в последовательной цепи представляет собой сумму всех отдельных падений напряжения, вызванных параметрами импеданса. Кроме того, сумма равна общему напряжению, подаваемому на цепь, или напряжению до любого «падения».

Рассмотрим явления с помощью схемы. В схеме ниже есть два резистора, R ₁ на 100 Ом и R ₂ на 200 Ом, подключенных к источнику питания V 30 вольт. Ток i = V/(R ₁ + R ₂ ) = 30/(100+200) = 0,1 А. Следовательно, напряжение падает на R ₁ = i x R ₁ = 0,1 x 100 = 10 В и на R ₂ = i x R ₂ = 0,1 x 200 = 20 В. 

Как рассчитать падение напряжения в последовательной цепи переменного тока?

Цепи переменного или переменного тока представляют собой электрические цепи с напряжением питания переменного тока.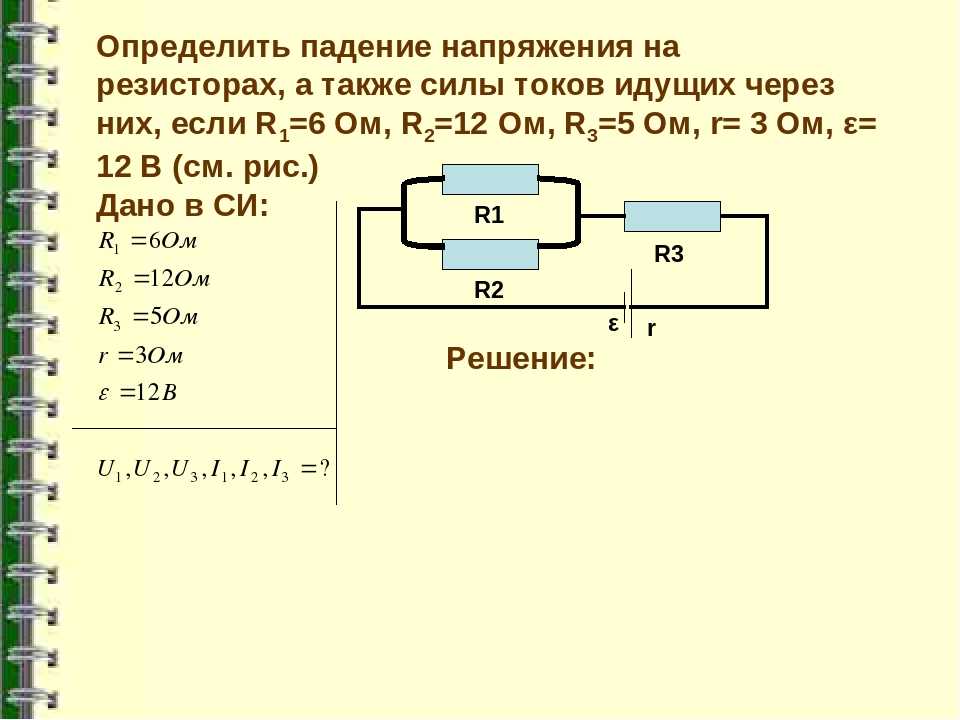 Последовательная цепь переменного тока состоит из любой комбинации резистора, катушки индуктивности и конденсатора, соединенных последовательно.

Точно так же, как и при постоянном токе, мы можем вычислить полное сопротивление последовательной цепи переменного тока, складывая их. Аналогичным образом можно найти и падение напряжения. Падение напряжения на любом элементе последовательной цепи переменного тока равно V = iZ, где Z — полное сопротивление цепи, а i — полный ток, протекающий через нее. «Файл: AC Source-R-C.svg» Pierre5018 лицензируется в соответствии с CC BY-SA 4.0

Подробнее о…..Как рассчитать напряжение в последовательной цепи: подробные факты

Падение напряжения в последовательной цепи RLC:

Цепь RLC является частным случаем цепей переменного тока. Цепь RLC состоит из резисторов, конденсаторов и катушек индуктивности, соединенных последовательно. Давайте разберемся с падением напряжения в последовательной цепи RLC на примере.

Схема состоит из трех компонентов, изображенных ниже: резистор ом, индуктор L Генри и конденсатор C фарад. Ранее мы знали, что падение напряжения на любом из них = импеданс × ток. Итак,

Падение напряжения на резисторе = iR, индуктивности = iXL и конденсаторе = iXC, где XL = 2πfL и XC = 1/2πfC

Q1. Три резистора соединены последовательно со значениями R ₁ = 4 Ом, R ₂ = 5 Ом и R ₃ = 6 Ом. Цепь соединена с источником питания 15 В. Найдите падение напряжения на резисторах.

Для расчета падения потенциала на R ₁ , R ₂ и R ₃ нам сначала нужно получить ток в цепи. Мы знаем, что ток = чистое напряжение/эквивалентное сопротивление

Эквивалентное сопротивление R _eq = R ₁ + R ₂ + R ₃ = 4 + 5 + 6 = 15 Ом

Следовательно, общий ток = 15 В /15 Ом = 1 А

Теперь мы можем использовать закон Ома (V = IR) для каждого резистора и найти падение напряжения на них.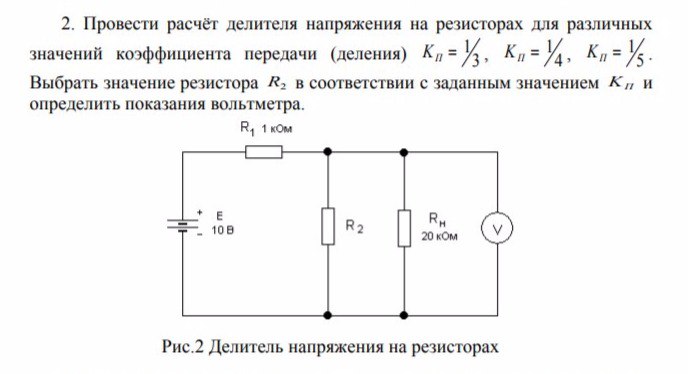 9В ₃ = 1 x 6 = 6 В

Q2. Для приведенной ниже схемы падение напряжения на резисторе 6 Ом составляет 12 В. Найдите другие падения напряжения и рассчитайте общее падение напряжения или напряжение питания.

Мы знаем, что падение напряжения на любом резисторе в последовательной цепи = сопротивление × общий ток

Если в цепи протекает ток i, падение напряжения на резисторе 6 Ом равно 6i.

6i = 12 или i = 2 ампера

Следовательно, падение напряжения на резисторе 2 Ом = 2 x 2 = 4 В

Падение напряжения на резисторе 4 Ом = 2 x 4 = 8 В

Таким образом, чистое напряжение падение напряжения питания = (12 + 4 + 8) = 24 В

Q3. На изображении ниже показана цепь серии RLC со следующими компонентами: Источник питания переменного тока 120 В, 50 Гц , Резистор 100 Ом , Конденсатор 20 мкФ , Катушка индуктивности 420 мГн. Рассчитать падение напряжения на всех трех импедансах.