Как рассчитать общее сопротивление при последовательном и параллельном соединении резисторов. Какие формулы используются для расчета сопротивления в цепях типа «треугольник» и «звезда». Какие методы применяются для анализа сложных электрических схем.
Основные типы соединений резисторов в электрических цепях
В электротехнике существует два основных способа соединения резисторов в электрической цепи:
- Последовательное соединение
- Параллельное соединение
Каждый из этих типов соединений имеет свои особенности и формулы для расчета общего сопротивления. Рассмотрим их подробнее.
Последовательное соединение резисторов
При последовательном соединении резисторы включаются друг за другом, образуя единую цепь. Ток, протекающий через все резисторы, одинаков. Общее сопротивление цепи при последовательном соединении рассчитывается по формуле:
Rобщ = R1 + R2 + R3 + … + Rn
где R1, R2, R3, …, Rn — сопротивления отдельных резисторов.
Параллельное соединение резисторов
При параллельном соединении резисторы подключаются к одним и тем же точкам цепи. Напряжение на всех резисторах одинаково. Общее сопротивление при параллельном соединении рассчитывается по формуле:
1/Rобщ = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Для двух параллельно соединенных резисторов формула упрощается:
Rобщ = (R1 * R2) / (R1 + R2)
Методы расчета сопротивления в сложных электрических цепях
Для анализа сложных электрических схем, содержащих комбинации последовательных и параллельных соединений, а также более сложные конфигурации, применяются различные методы:
- Метод эквивалентных преобразований
- Метод контурных токов
- Метод узловых потенциалов
- Метод наложения
Рассмотрим подробнее некоторые из этих методов.
Метод эквивалентных преобразований
Этот метод заключается в последовательном упрощении схемы путем замены групп резисторов их эквивалентными сопротивлениями. Применяются формулы для последовательного и параллельного соединения. В результате сложная схема сводится к простой цепи с одним эквивалентным сопротивлением.

Метод контурных токов
В основе метода лежит составление уравнений по второму закону Кирхгофа для независимых контуров схемы. Число уравнений равно числу независимых контуров. Решение системы уравнений позволяет найти токи во всех ветвях.
Расчет сопротивления в схемах «треугольник» и «звезда»
Особый интерес представляют схемы соединения резисторов типа «треугольник» и «звезда». Эти конфигурации часто встречаются в сложных электрических цепях.
Схема «треугольник»
В схеме «треугольник» три резистора соединены в замкнутый контур. Общее сопротивление между двумя точками треугольника рассчитывается по формуле:
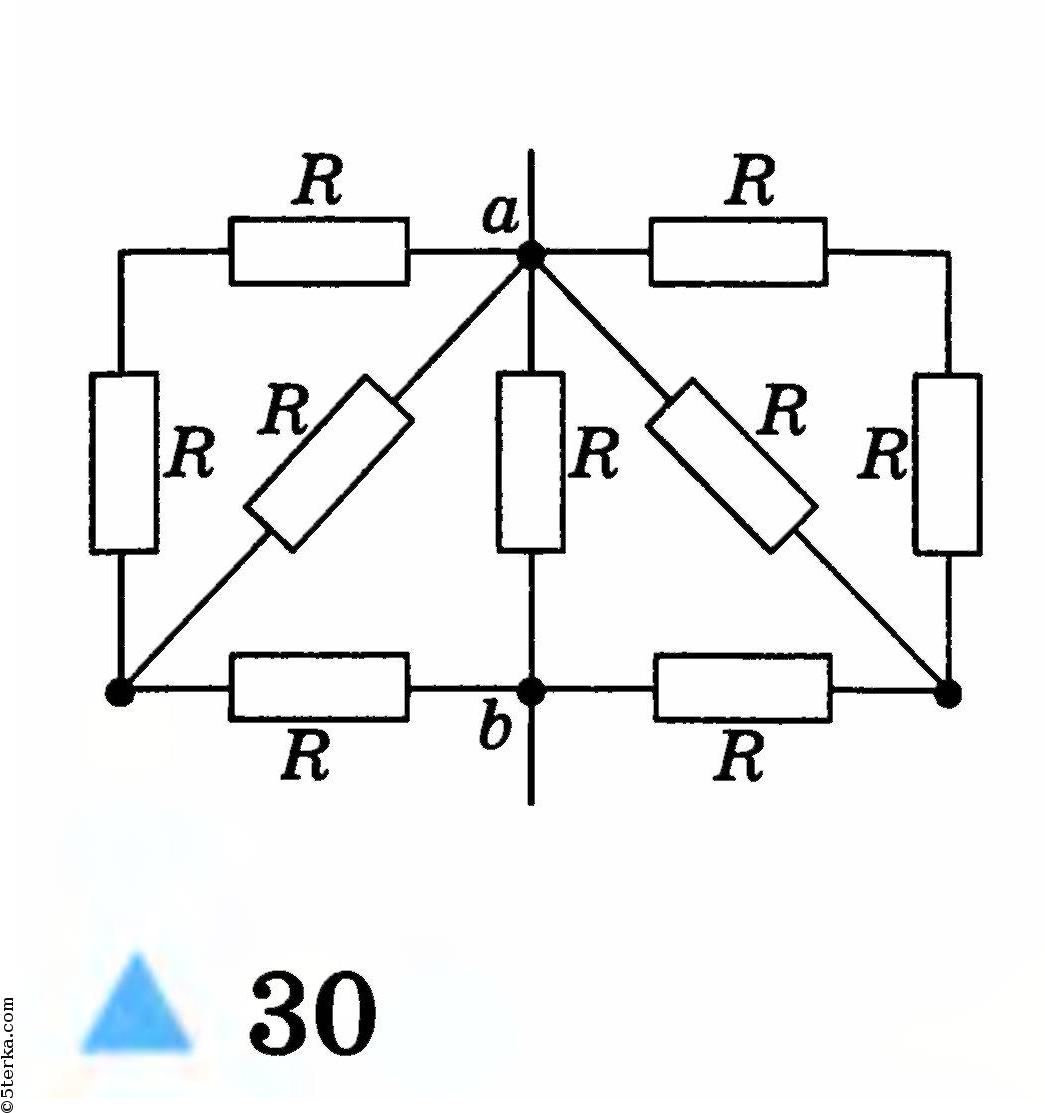
RAB = (RaRb + RbRc + RcRa) / (Rb + Rc)
Схема «звезда»
В схеме «звезда» три резистора соединены общей точкой. Общее сопротивление между двумя лучами звезды равно:
RAB = Ra + Rb + (RaRb) / Rc
где Ra, Rb, Rc — сопротивления лучей звезды, RAB — сопротивление между точками A и B.
Применение формул для расчета сопротивления на практике
Рассмотрим несколько примеров применения изученных формул для расчета общего сопротивления в различных электрических схемах.
Пример 1: Последовательное соединение
Дано: три резистора с сопротивлениями 10 Ом, 20 Ом и 30 Ом соединены последовательно.
Решение:
Rобщ = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Пример 2: Параллельное соединение
Дано: два резистора с сопротивлениями 100 Ом и 200 Ом соединены параллельно.
Решение:
Rобщ = (R1 * R2) / (R1 + R2) = (100 * 200) / (100 + 200) = 66,7 Ом
Особенности расчета сопротивления в цепях постоянного и переменного тока
При расчете сопротивления важно учитывать тип тока в цепи — постоянный или переменный. В цепях переменного тока помимо активного сопротивления необходимо учитывать реактивное сопротивление, создаваемое катушками индуктивности и конденсаторами.
Расчет сопротивления в цепях постоянного тока
В цепях постоянного тока расчет общего сопротивления производится по формулам для последовательного и параллельного соединения резисторов, рассмотренным выше. Индуктивности и емкости в установившемся режиме не оказывают влияния на сопротивление цепи.
Расчет сопротивления в цепях переменного тока
В цепях переменного тока вводится понятие полного сопротивления (импеданса), которое учитывает как активное, так и реактивное сопротивление. Полное сопротивление рассчитывается по формуле:
Z = √(R2 + (XL — XC)2)
где R — активное сопротивление, XL — индуктивное сопротивление, XC — емкостное сопротивление.
Влияние температуры на сопротивление проводников
Температура оказывает существенное влияние на сопротивление проводников. С ростом температуры сопротивление металлических проводников увеличивается. Это явление необходимо учитывать при расчетах электрических цепей.
Зависимость сопротивления от температуры
Зависимость сопротивления от температуры для металлических проводников описывается формулой:
Rt = R0(1 + αt)
где Rt — сопротивление при температуре t, R0 — сопротивление при 0°C, α — температурный коэффициент сопротивления, t — температура в градусах Цельсия.
Заключение
Расчет общего сопротивления является важной задачей при анализе электрических цепей. Знание основных формул и методов позволяет решать как простые, так и сложные задачи. При этом важно учитывать особенности цепей постоянного и переменного тока, а также влияние температуры на сопротивление проводников.
Применение рассмотренных методов расчета сопротивления на практике позволяет проектировать эффективные электрические схемы и оптимизировать работу электронных устройств.
Калькулятор онлайн для параллельного соединения резисторов: общие сведения, формулы расчета
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Видео: Последовательное и параллельное соединение проводников
youtube.com/embed/zBJdO004zfg»>Параллельное соединение: общая информация
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
Какое освещение Вы предпочитаете
ВстроенноеЛюстра
причем :
- R(общ) – суммарное значение сопротивления;
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
R(общ)=R1*R2/R1+R2.
причем:
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
R(общ)=R1n.
причем :
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
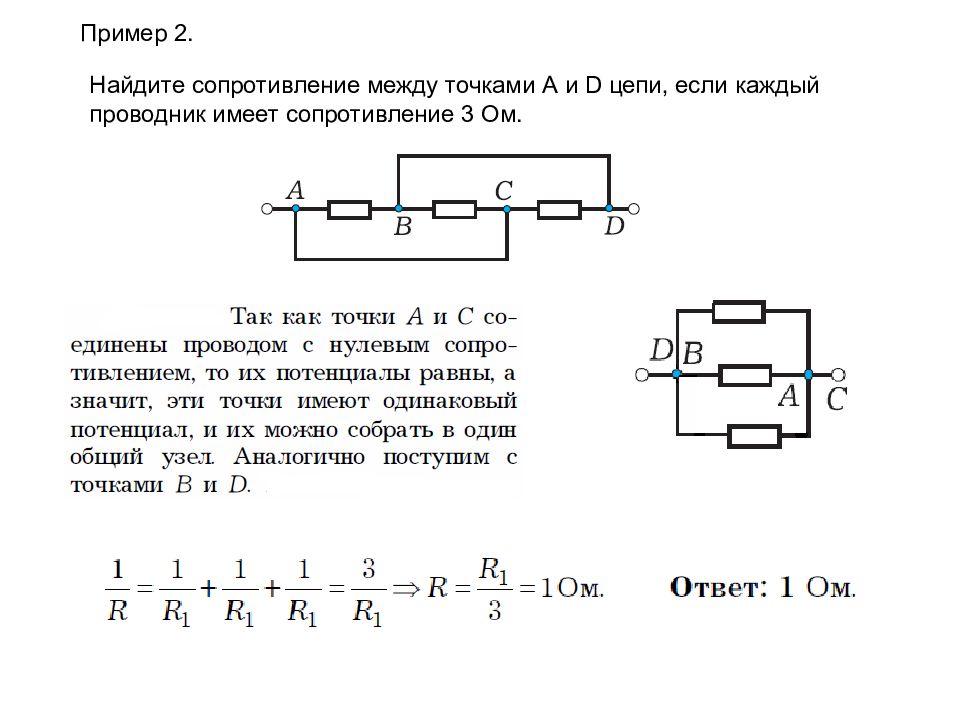
Расчет общего сопротивления цепи при смешанном соединении элементов (решение задач)
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1.
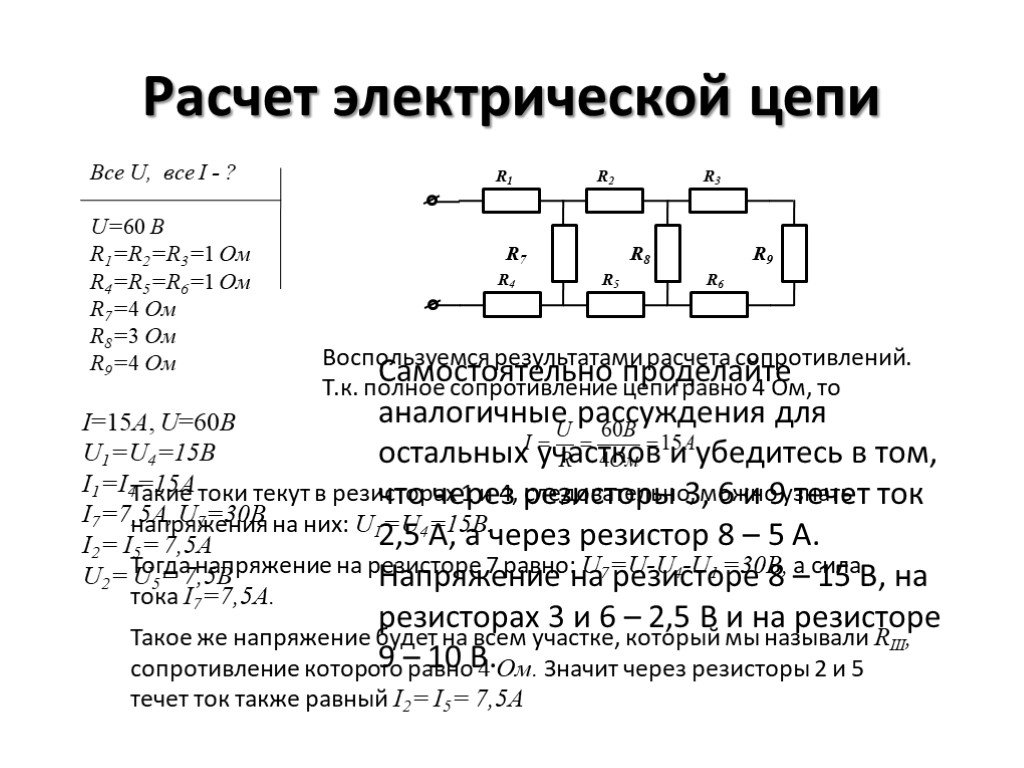 Решение задач по теме:«Расчет общего сопротивления
Решение задач по теме:«Расчет общего сопротивленияцепи при смешанном соединении
элементов»
2. 1 этап
RR
4R
R
R
4R
R
2R
R
Внимательно изучите схему и найдите на
ней участок последовательно
соединенных проводников
3. 1 этап
RR
4R
R
R
4R
R
2R
R
Вспомните правило вычисления
сопротивления при последовательном
соединении.
4. 1 этап
RR
4R
R
Rоб=R+2R+R
4R
R
5. 2 этап
RR
4R
R
Rоб=4R.
4R
R
4R
6. 2 этап
RR
4R
R
4R
4R
R
Полученное сопротивление соединено
параллельно с сопротивлением 4R
7. 2 этап
RR
4R
R
4R
R
Рассчитаем Rоб=R/2
4R
8. 3 этап
RR
4R
R
Rоб= 2R
R
9. 3 этап
RR
4R
R
2R
R
На схеме опять участок из трех
последовательно соединенных
проводников.
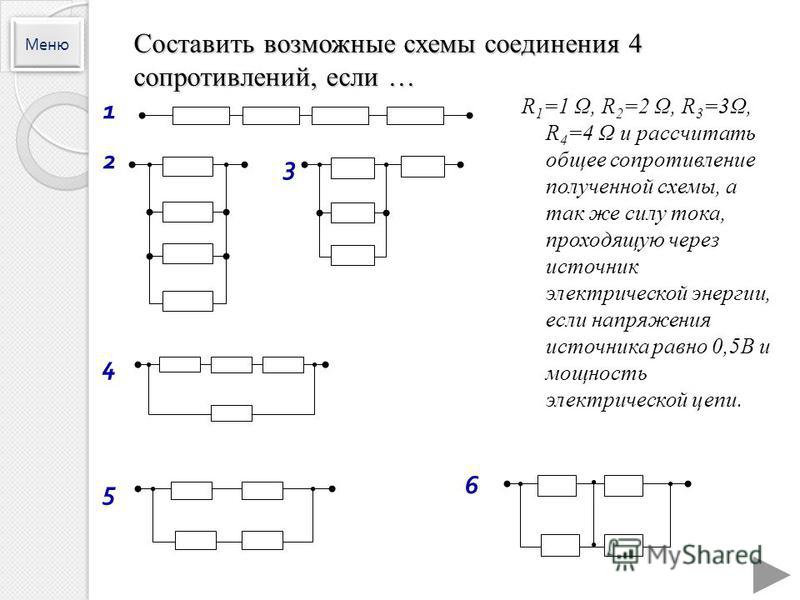
10. 3 этап
RR
4R
R
2R
R
Применим к нему еще раз процедуру
нахождения общего сопротивления.
11. 3 этап
R4R
R
Еще раз вычислим значение общего
сопротивления при последовательном
соединении .Rоб=R+2R+R
12. 3 этап
R4R
R
4R
13. 4 этап
R4R
4R
R
На схеме последовательное соединение
двух проводников одинакового
сопротивления 4R
14. 4 этап
R4R
4R
R
На схеме последовательное соединение
двух проводников одинакового
сопротивления 4R
15. 4 этап
RR
Вычислим общее сопротивление в этом
случае. Rоб=R/2
16. 4 этап
R2R
R
Вычислим общее сопротивление в этом
случае.
17. 5 этап
R2R
R
Теперь схема значительно упростилась. В ней
три последовательно соединенных проводника.
Повторим процедуру вычисления общего
сопротивления в последний раз.
18.
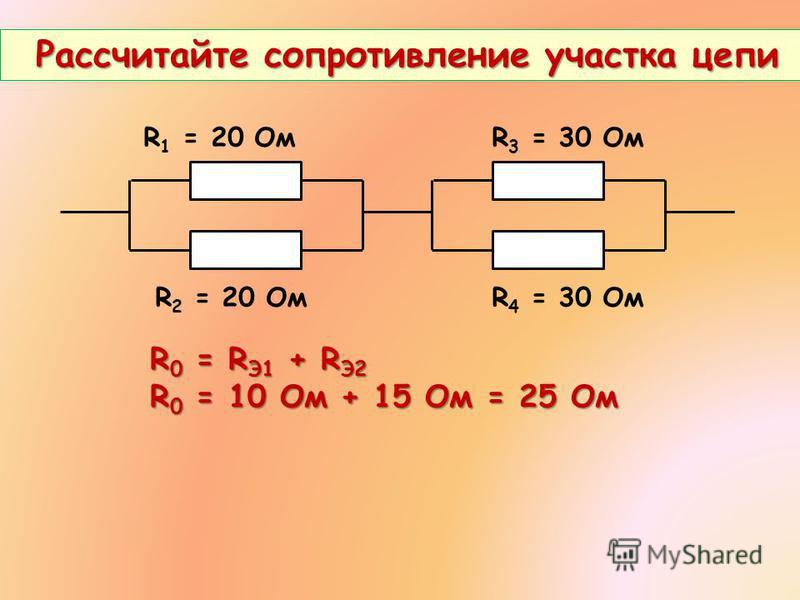 5 этапОбщее сопротивление последовательного
5 этапОбщее сопротивление последовательногосоединения проводников Rоб=R+2R+R
19. 5 этап
4RОбщее сопротивление 4R
20. Задача для закрепления.
Все ли Вам было понятно впредыдущей демонстрации? Если
нет, то повторить ее вновь.
21. Задача для закрепления.
Теперь попробуйте самостоятельнопрокомментировать решение
аналогичной задачи.
22. Задача для закрепления.
4,5 Ом4 Ом
5 Ом
10 Ом
6 Ом
23. Задача для закрепления.
4,5 Ом4 Ом
5 Ом
10 Ом
6 Ом
24. Задача для закрепления.
4,5 Ом4 Ом
5 Ом
10 Ом
6 Ом
25. Задача для закрепления.
4,5 Ом5 Ом
10 Ом
26. Задача для закрепления.
4,5 Ом5 Ом
10 Ом
10 Ом
27. Задача для закрепления.
4,5 Ом5 Ом
10 Ом
10Ом
28. Задача для закрепления.
4,5 Ом5 Ом
10 Ом
10 Ом
29. Задача для закрепления.
4,5 Ом5 Ом
30.
 Задача для закрепления.4,5 Ом
Задача для закрепления.4,5 Ом5 Ом
5 Ом
31. Задача для закрепления.
4,5 Ом5 Ом
5 Ом
32. Задача для закрепления.
4,5 Ом5 Ом
5 Ом
33. Задача для закрепления.
4,5 Ом34. Задача для закрепления.
4,5 Ом2,5 Ом
35. Задача для закрепления.
4,5 Ом2,5 Ом
36. Задача для закрепления.
4,5 Ом2,5 Ом
37. Задача для закрепления.
38. Задача для закрепления.
7 Ом39. Задачи для самостоятельного решения
8 Ом2 Ом
4 Ом
2 Ом
2 Ом
4 Ом
4 Ом
3 Ом
1 вариант
2 вариант
40. Ответы на задачи для самостоятельного решения
1 вариантR=10 Ом
2 вариант
R=7Ом
English Русский Правила
Программное обеспечение— Калькулятор резисторов, чтобы приблизиться к окончательному значению?
Если я ищу в Интернете, я вижу тысячи последовательных или параллельных калькуляторов резисторов, где вы можете ввести «входные» резисторы, и указано выходное сопротивление.
Однако мне интересно, есть ли программа/приложение/веб-сайт, где вы можете установить выходное сопротивление, и оно вычисляет ближайшее значение, используя, например, 1, 2, 3 и 4 резистора в любой последовательно-параллельной комбинации.
Итак. например Я хочу сопротивление 1,5К.
Результат будет примерно таким:
- 1 резистор: 1 K (= 1000R)
- 2 резистора: 1 кОм + 510 (= 1510 Ом)
- 3 резистора: 1 кОм + 470 + 22 (= 1492 Ом)
- 4 резистора: 1 кОм + 470 + 22 + 10 (= 1503 Ом)
Вероятно, есть лучшие решения с использованием параллельных комбинаций, но найти их довольно сложно (методом проб и ошибок).
- резисторы
- программное обеспечение
- веб-сайт
\$\конечная группа\$
9
\$\начало группы\$
После того, как вы привыкли к существующим номиналам резисторов E24/E48, а в некоторых случаях даже к E96 и E192, необходимость в таком приложении/веб-сайте отпадает.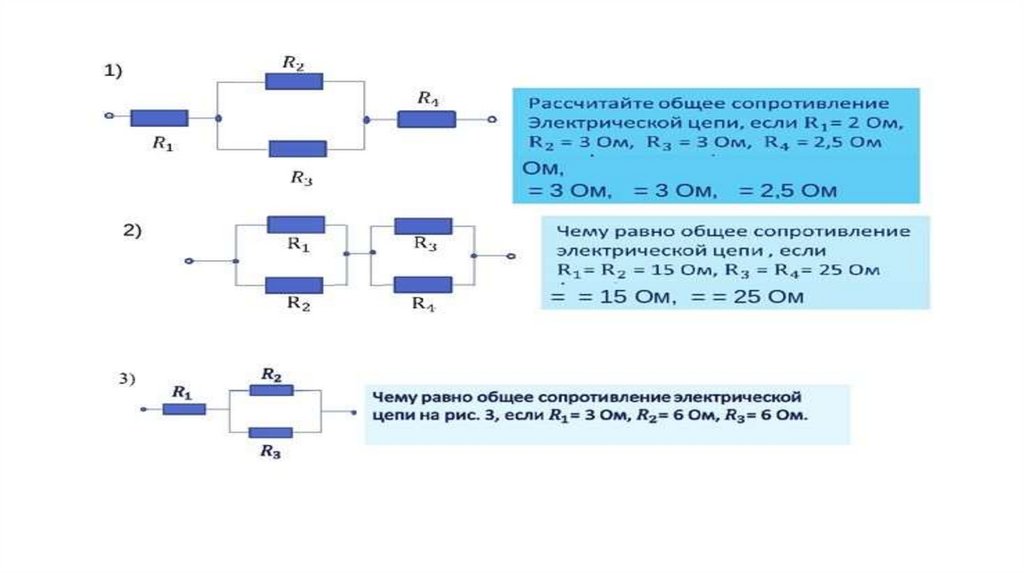 Во-первых, имея немного опыта, вы можете угадать значение двух резисторов, включенных параллельно, но зная, например, что 2 резистора одинакового номинала, включенные параллельно, дают в сумме половину значения каждого.
Во-первых, имея немного опыта, вы можете угадать значение двух резисторов, включенных параллельно, но зная, например, что 2 резистора одинакового номинала, включенные параллельно, дают в сумме половину значения каждого.
В общем, когда вы выбираете резисторы, вы начинаете с серии E24, а затем, в зависимости от требуемого допуска схемы, вы выбираете серию с большим числом значений. В большинстве случаев вы обнаружите, что нет необходимости соединять их параллельно или последовательно, потому что нужное вам значение уже существует или доступные находятся в пределах допуска схемы.
Например, когда дело доходит до установки резисторов для обратной связи регулируемого регулятора напряжения, вы начинаете с произвольного значения для одного, а затем вычисляете второй резистор. Если это значение далеко от существующего, вы меняете первый резистор и снова пересчитываете второй, и так далее, пока не найдете подходящую комбинацию. Я обычно ввожу формулу в excel, а потом играю со значениями, пока не получу то, что хочу.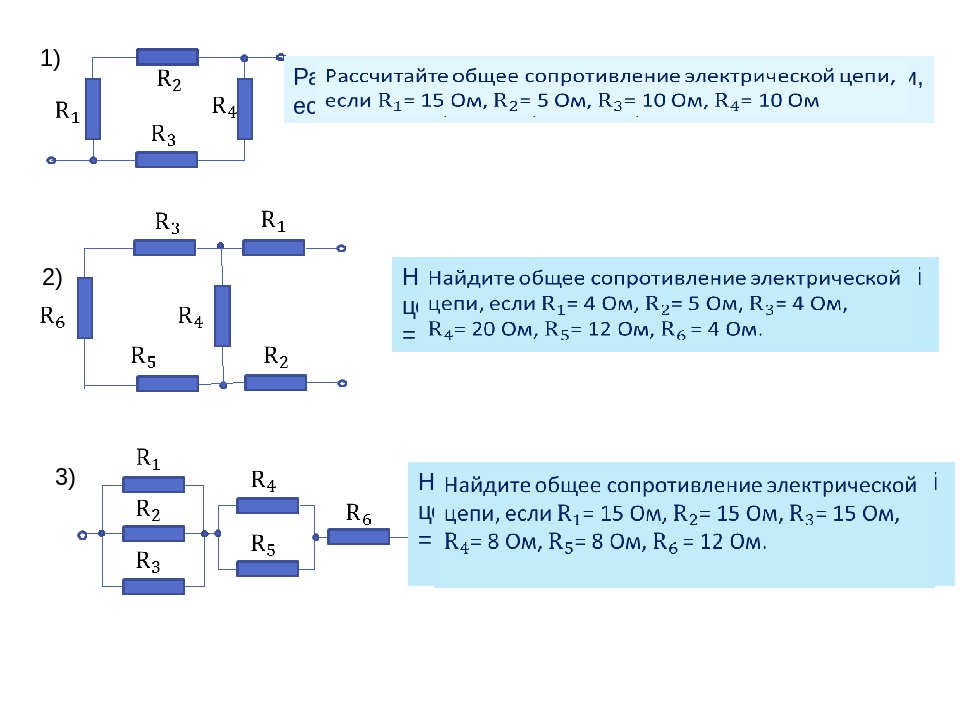 Помните, что пока на выходе стабилизатора стабильно, схема будет работать, даже если вы подаете на нее напряжение на 1% выше/ниже.
Помните, что пока на выходе стабилизатора стабильно, схема будет работать, даже если вы подаете на нее напряжение на 1% выше/ниже.
\$\конечная группа\$
1
\$\начало группы\$
Необходимость найти комбинацию неиндуктивных силовых резисторов с проволочной обмоткой на складе вашего любимого дистрибьютора (или какая-то другая кропотливая задача) может оставить вас с небольшим выбором. В сочетании с ограниченным опытом калькулятор резисторов становится удобным, например этот:
http://kirr.homeunix.org/electronics/resistor-network-finder/
Оставив мой запас пустым и заполнив только «Плюс эти дополнительные значения»:
Я быстро нашел комбинацию резисторов:
Он даже может показать графическое представление сети резисторов:
\$\конечная группа\$
1
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Анализ взаимосвязи между сопротивлениями в цепи треугольника для определения полного сопротивления
1. Введение
Для анализа проблемы электрической цепи, особенно сложной цепи, все, что нам нужно выучить, — это основная формула, называемая законом Ома. Это очень важная вещь, которую нам нужно знать в первую очередь, чтобы помочь нам решить проблемы для электрических цепей. Из этого закона мы выводим еще одну важную формулу для поддержки анализа цепей; Закон напряжения Кирхгофа (KVL), закон тока Кирхгофа (KCL), делитель напряжения и делитель тока. Благодаря этим различным законам производных решение схемы упрощается за счет разработки схемных методов и теорем.
Двумя основными электрическими цепями, известными при анализе цепей, являются цепи сопротивления и Δ – Υ цепи. Эти два типа схем в основном обсуждаются и применяются в этой статье [1, 4, 5, 6, 7] .
2. Обсуждение
2. 1. Базовая теория
1. Базовая теория
Рисунок 1. Цепи сопротивления: (a) последовательная и (b) параллельная
Существуют две общие цепи сопротивления: последовательная и параллельная, как показано на рис. 1. Используя правильную формулу для последовательной и параллельной цепи, в первую очередь мы можем рассчитать общее сопротивление для одиночной или комбинированной формы электрической цепи [1, 4, 5, 6, 7] .
Последовательное сопротивление имеет одинаковое значение тока I и разное значение напряжения V, а параллельное сопротивление имеет разное значение I и одно значение V [1, 2, 6, 7, 8] .
| (1) |
| (2) |
) звезда (Υ). В этом случае мы должны использовать специальную формулу, чтобы получить правильный результат [1, 2, 3] .
Рис. 2. Соединения Δ и Υ
2. Соединения Δ и Υ
Для расчета полного сопротивления электрической цепи с соединением треугольником, в основном цепь необходимо преобразовать из треугольника (Δ) в звезду (Υ) [2, 3, 6, 8] .
| (3) |
3. Цели исследования
В этой статье будет проведен простой анализ применения теории базовой электрической цепи, чтобы выяснить соотношение сопротивлений в схеме треугольника, чтобы решить любые проблемы относится к общему сопротивлению. Использование полученной формулы дает еще одно быстрое и лучшее решение для анализа цепей в отношении сопротивления и концепции Δ – Υ. Надеемся, что это красивое описание теории укрепит наше критическое мышление и вдохновит на поиск хороших решений в мире электроники.
4. Метод исследования
Для такого рода анализа я пытаюсь сравнить несколько форм цепей сопротивления с дельта-моделью, увидеть отношения и применить точный метод и формулу для получения другой формулы уравнений для расчета общего сопротивления.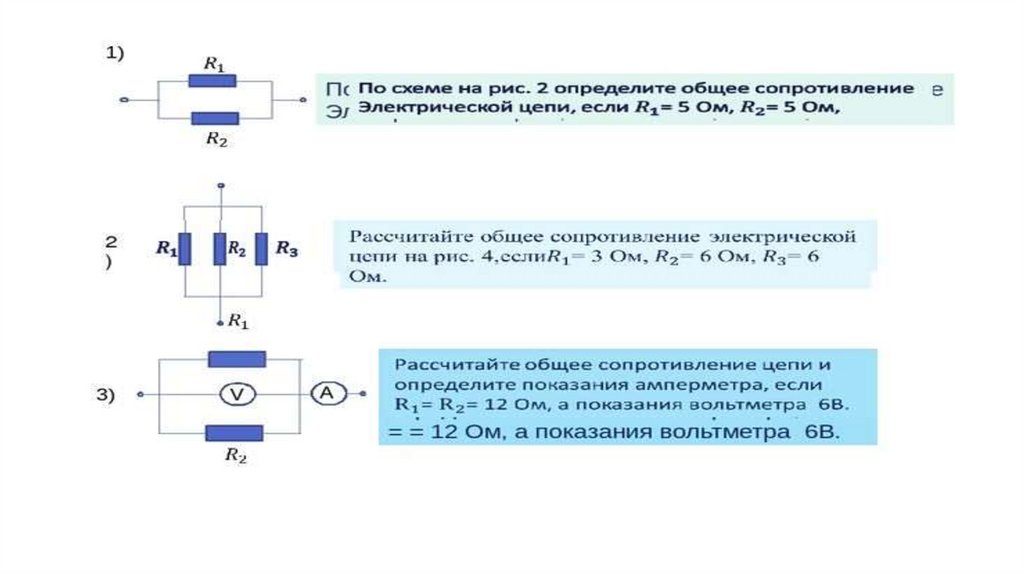
5. Анализ и результаты
Используя эталон сопротивления и формулу Δ – Υ, можно вывести различные уравнения и решить полное сопротивление в задачах электрических цепей, моделируемых в конкретных узлах и ветвях [2, 3, 6, 8] .
Обратите внимание на проблему с электрической цепью на рис. 3. Это особая форма цепи, с которой мы обычно сталкиваемся при решении проблем с цепями сопротивления. Он имеет модель Δ как на верхней, так и на нижней стороне схемы. Чтобы решить схему, мы должны изменить форму Δ на форму Υ, как показано на рисунке 4, а затем выполнить расчет параллельного сопротивления. Поскольку все значения сопротивления одинаковы, мы можем утверждать, что все сопротивления равны R, уравнение 4.
Рисунок 3. Цепи сопротивления, имеющие модель Δ и одинаковые значения сопротивлений
Рисунок 4. форма Δ на верхней стороне изменяется на форму Υ, и все сопротивления, обозначенные буквой R
Используя формулу Δ – Υ, мы получаем результат каждого сопротивления в модели Y следующим образом: формуле, и мы получаем результат в уравнении 5 следующим образом:
| (5) |
Предположим, мы изменим значение двух сопротивлений на (1+R), снова мы получим результат каждого сопротивления в модели Y и рассчитаем общее сопротивление, чтобы получить результат в уравнение 6 выглядит следующим образом:
| (6) |
Рисунок 5. На двух нижних сторонах сопротивлений указано значение (1+R)
На двух нижних сторонах сопротивлений указано значение (1+R)
Вот несколько симуляций, которые были проведены для подтверждения предыдущих результатов расчета. Они показывают ожидаемые значения из текущего анализа, уравнение 6.
Рисунок 6. Моделирование цепей с использованием программного обеспечения электроники Workbench 5.12
Продолжая изменять два сопротивления на (2+R) и (3+R), мы получим «похожий» результат, как описано в следующих уравнениях:
Он следует тем же правилам и шаблону для результата полного сопротивления. Это уникальные отношения, и их можно применять для этой особой формы задач со схемой.
6. Заключение
Из конкретного соотношения сопротивлений, смоделированного в двух соединениях треугольником, можно вывести стандартную и простую формулу для решения связанных проблем для упрощения анализа и расчетов. Величины сопротивлений в данной конкретной электрической цепи формируются по особым закономерностям и определяются соотношением между двумя и тремя величинами сопротивлений в цепи.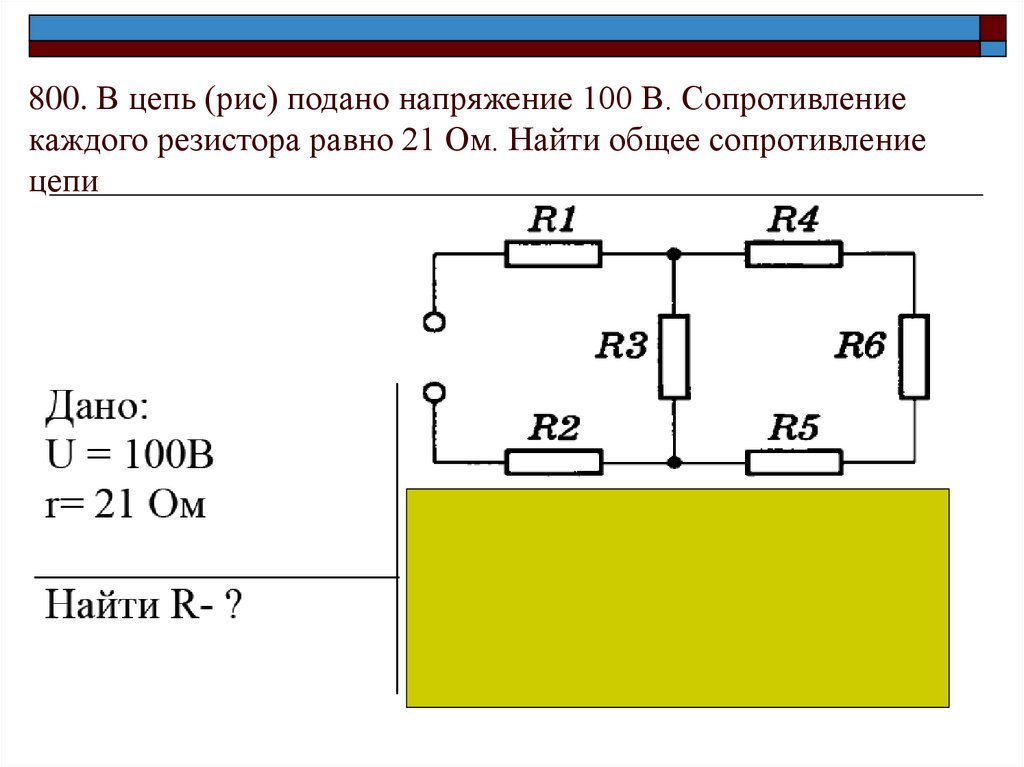 В будущем можно провести предварительный анализ, чтобы узнать больше об этой особой форме цепи и вывести другие формулы с другим соотношением сопротивлений.
В будущем можно провести предварительный анализ, чтобы узнать больше об этой особой форме цепи и вывести другие формулы с другим соотношением сопротивлений.
Ссылки
| [1] | Мальвино, А.П., перевод: Алб. Джоко Сантосо. (2003) Prinsip-prinsip Elektronika Jilid 1, Jakarta: Penerbit Salemba Teknika. | ||
| в статье | |||
| [2] | NAHVI, M. Dan Joseph A. EdmiNister. (2004) Easy Outlines Шаума: Rangkaian Listrik , Джакарта: Penerbit Erlangga. | ||
| В статье | |||
| [3] | Эндар Сугард (1991) Prima EBTA Fisika SMA, Edisi ke-1, Semarang: PT Intan Pariwara. | ||
| в статье | |||
| [4] | William H.
| ||

