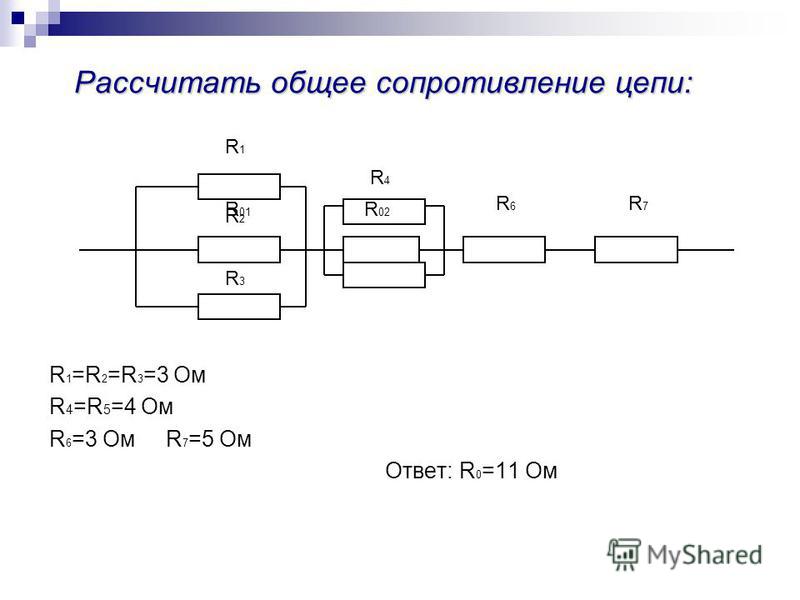
Как рассчитать общее сопротивление цепи при последовательном соединении резисторов. Как определить суммарное сопротивление параллельно подключенных резисторов. Какие формулы используются для вычисления эквивалентного сопротивления смешанных цепей. Какие законы электротехники применяются при расчете сопротивления сложных электрических схем.
Основные принципы расчета сопротивления электрических цепей
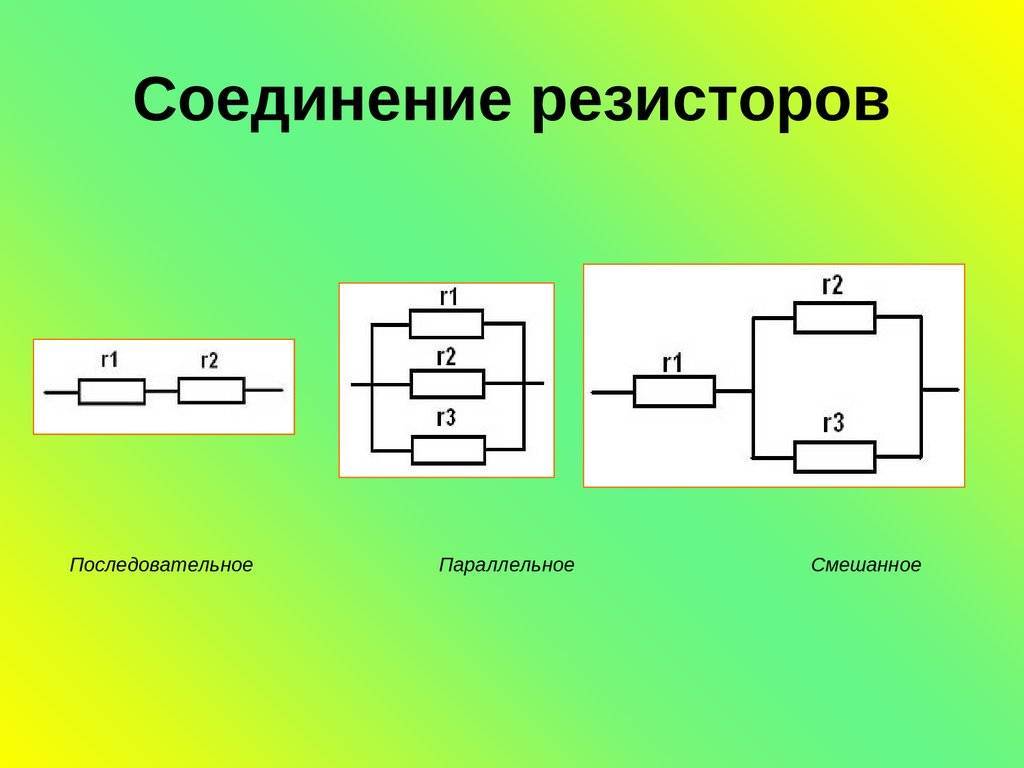
При расчете общего сопротивления электрической цепи необходимо учитывать способ соединения резисторов:
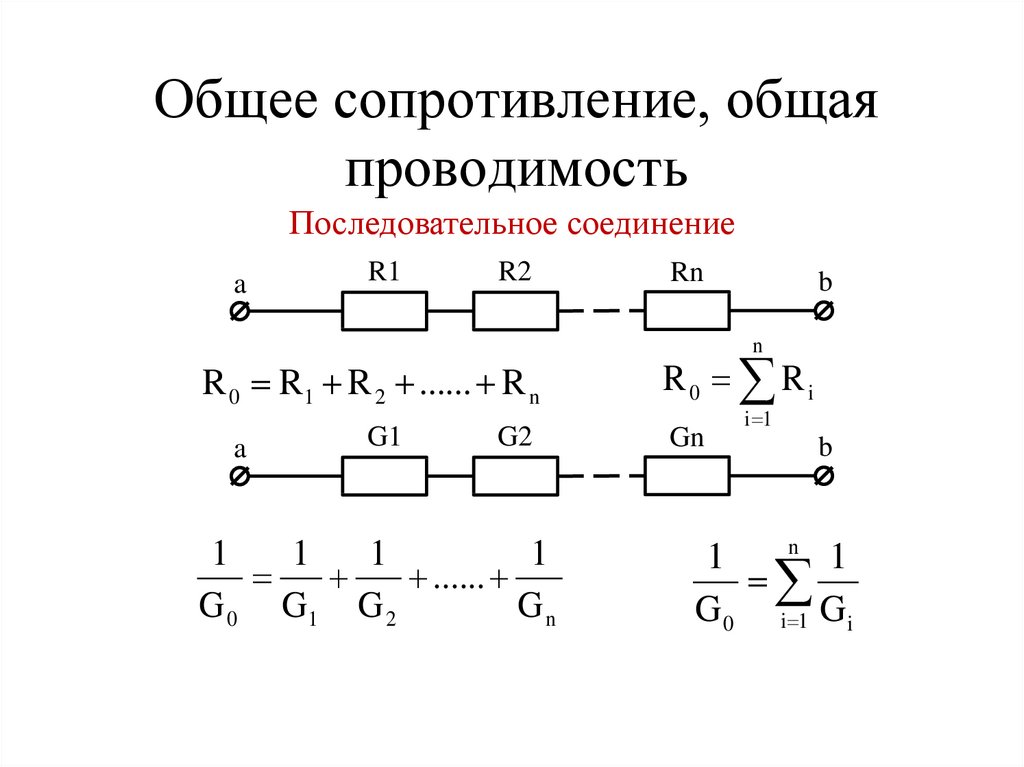
- При последовательном соединении общее сопротивление равно сумме сопротивлений отдельных резисторов
- При параллельном соединении обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных резисторов
- Для смешанных цепей применяется комбинация этих двух принципов
Рассмотрим подробнее каждый из этих случаев.
Расчет сопротивления при последовательном соединении резисторов
При последовательном соединении резисторов общее сопротивление цепи определяется по формуле:

R = R1 + R2 + R3 + … + Rn
Где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных резисторов.
Какие основные свойства последовательного соединения резисторов необходимо учитывать при расчетах?
- Сила тока одинакова во всех элементах цепи
- Общее напряжение равно сумме напряжений на отдельных резисторах
- Общее сопротивление всегда больше сопротивления любого из резисторов
Определение общего сопротивления при параллельном соединении
При параллельном соединении резисторов общее сопротивление цепи рассчитывается по формуле:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных резисторов.
Какие особенности параллельного соединения следует учитывать?
- Напряжение на всех элементах одинаково и равно общему напряжению
- Общий ток равен сумме токов через отдельные резисторы
- Общее сопротивление всегда меньше сопротивления любого из резисторов
Расчет сопротивления в смешанных цепях
Для расчета сопротивления в сложных цепях со смешанным соединением резисторов применяется следующий алгоритм:

- Разбить схему на участки с последовательным и параллельным соединением
- Рассчитать сопротивление для каждого участка по соответствующим формулам
- Заменить рассчитанные участки эквивалентными резисторами
- Повторять шаги 1-3, пока вся схема не будет сведена к одному эквивалентному резистору
Какие сложности могут возникнуть при расчете смешанных цепей?
- Необходимость правильного определения типа соединения на каждом участке
- Возможность ошибки при упрощении схемы
- Трудоемкость расчетов для очень сложных схем
Применение закона Ома для расчета параметров цепи
I = U / R
Где I — сила тока, U — напряжение, R — сопротивление.
Как использовать закон Ома при анализе цепей?
- Определять неизвестные параметры, зная два из трех (I, U, R)
- Проверять правильность расчетов
- Анализировать изменения параметров при изменении схемы
Практические примеры расчета сопротивления цепей
Рассмотрим несколько примеров расчета сопротивления для различных схем соединения резисторов:

Пример 1: Последовательное соединение
Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом
Решение: R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Пример 2: Параллельное соединение
Дано: R1 = 6 Ом, R2 = 3 Ом
Решение: 1/R = 1/R1 + 1/R2 = 1/6 + 1/3 = 1/2
R = 2 Ом
Пример 3: Смешанное соединение
Дано: R1 = 10 Ом, R2 = 20 Ом параллельно, последовательно с R3 = 30 Ом
Решение:
- Рассчитаем R12 (параллельное соединение R1 и R2): 1/R12 = 1/10 + 1/20 = 3/20 R12 = 20/3 Ом
- Общее сопротивление (последовательное R12 и R3): R = R12 + R3 = 20/3 + 30 = 120/3 = 40 Ом
Методы проверки правильности расчетов
Для проверки правильности расчетов сопротивления цепи можно использовать следующие методы:
- Измерение реальной цепи с помощью мультиметра
- Моделирование цепи в специальных программах
- Проверка расчетов с использованием закона Ома
Что нужно учитывать при проверке расчетов?
- Погрешность измерительных приборов
- Возможные отклонения реальных значений сопротивлений от номинальных
- Влияние внешних факторов (температура, влажность) на сопротивление
Влияние температуры на сопротивление проводников
Сопротивление большинства проводников увеличивается с ростом температуры. Это явление описывается формулой:
R = R0(1 + αΔT)
Где R — сопротивление при измененной температуре, R0 — сопротивление при начальной температуре, α — температурный коэффициент сопротивления, ΔT — изменение температуры.
Как учитывать температурную зависимость сопротивления в расчетах?
- Использовать справочные значения температурных коэффициентов
- Проводить измерения при различных температурах
- Учитывать возможный нагрев проводников при прохождении тока
Применение расчетов сопротивления в электротехнике
Расчет общего сопротивления электрических цепей имеет широкое практическое применение:
- Проектирование электрических схем
- Расчет параметров электрических сетей
- Разработка электронных устройств
- Диагностика неисправностей в электрооборудовании
Какие навыки необходимы для успешного применения расчетов на практике?
- Глубокое понимание законов электротехники
- Умение читать и анализировать электрические схемы
- Навыки работы с измерительными приборами
- Знание особенностей реальных компонентов
Расчет сопротивления цепи резисторов
Содержание
- 1 Пример 1
- 2 Пример 2
- 3 Пример 3
- 4 Пример 4
- 5 Пример 5
- 6 Пример 1
- 7 Пример 2
- 8 Пример 3
- 9 Пример 4
- 10 Пример 5
Разделы: Физика
Цели:
- Образовательная: систематизировать и закрепить знания учащихся о различных соединениях проводников, сформировать умения применять законы последовательного и параллельного соединений для расчёта электрических цепей, объединить знания, полученные на уроках физики и математики.
- Развивающая: развить мышление учащихся, активизировать познавательную деятельность через решение задач на расчет электрических цепей, развить умение рассчитывать параметры электрических цепей и совершенствовать полученные на уроке навыки.
- Воспитательная: формирование интереса к изучаемому предмету, продолжить формирование коммуникативных умений.
Тип урока: урок проверки и закрепления новых знаний по физике и математике.
Метод проведения урока: практический
Оборудование:
- Громов С.В. Учебник “Физики-9”;
- план урока;
- методика расчета участка электрической цепи постоянного тока;
- карточки-задания.
Сегодня на уроке мы должны применить полученные ранее знания о законах последовательного и параллельного соединений для расчёта участка электрической цепи, а также определить степень усвоения изученного материала с помощью карточек – заданий.
Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:
1) Какие виды соединений бывают и как они изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
Рассмотрим расчёт участка электрической цепи на примере следующих задач:
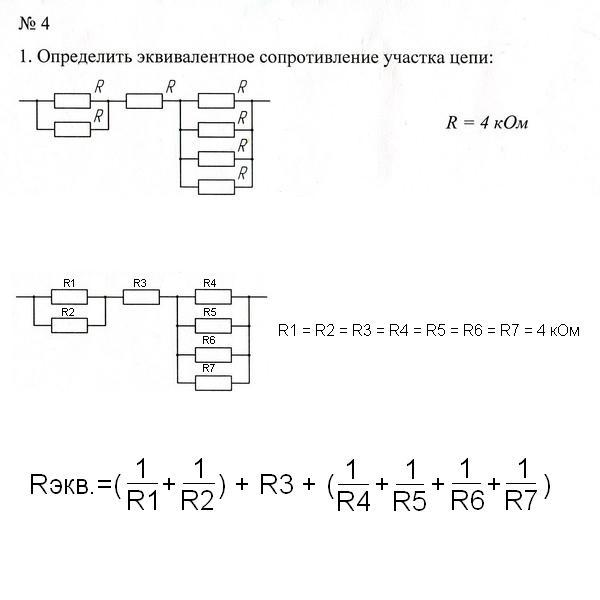
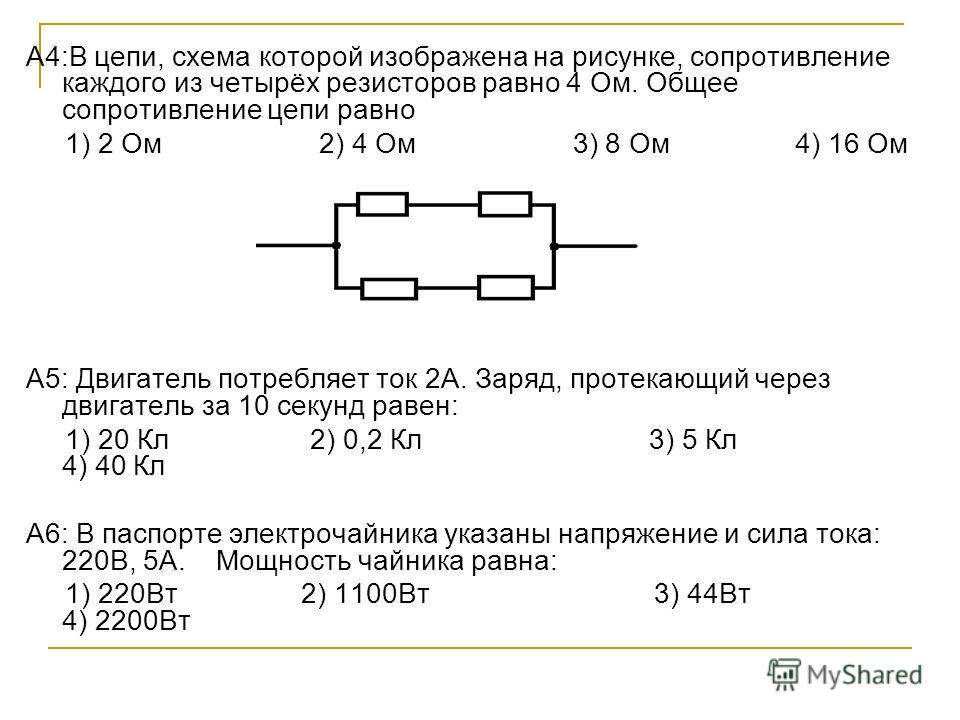
1. Рассчитайте общее электрическое сопротивление участка цепи?
1) Наиболее удалённые от источника элементы – это резисторы R2 и R3.
2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R2 и R3 подключены параллельно, т.к образуют в соединении два узла, следовательно:
Ом
3) Изображаем получившуюся в результате свёртывания резисторы R2 и R3 электрическую схему:
4) Полученные в результате объединения схему с двумя резисторами группируем во второй участок и рассчитываем их общее сопротивление. Так как резисторы R
Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.
2. Рассчитайте общее электрическое сопротивление участка цепи?
1) Резисторы R1 и R2 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
2) Резисторы R3 и R4 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
3) Полученные в результате объединения схему с двумя резисторами группируем в третий участок и рассчитываем их общее сопротивление.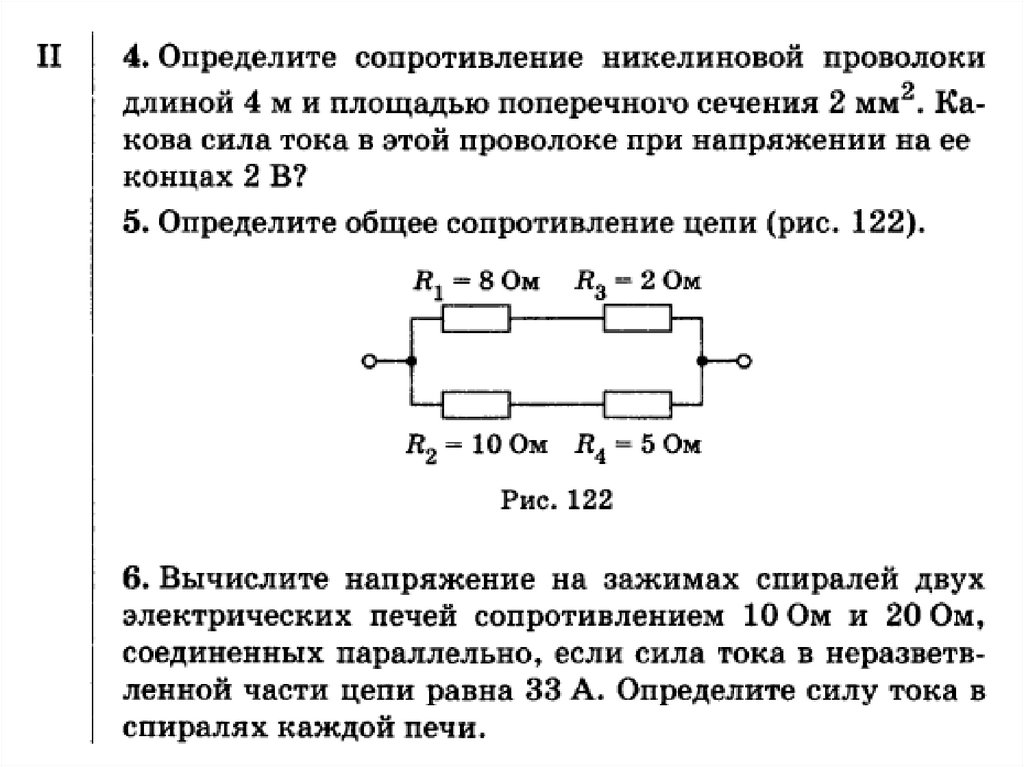 Так как резисторы Rоб.1 и Rоб.2 соединены параллельно, значит:
Так как резисторы Rоб.1 и Rоб.2 соединены параллельно, значит:
Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.
3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:
а) Рассчитайте общее электрическое сопротивление участка цепи?
б) Рассчитайте общее электрическое сопротивление участка цепи?
в) Рассчитайте общее электрическое сопротивление участка цепи?
Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.
Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.
Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.
Допустим, что R1=10 Ом R2=20 Ом, тогда
Пример 2
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1)
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.
Пример 3
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
Пример 5
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.
Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.
Подробнее о видах соединений тут.
Допустим, что R1=10 Ом R2=20 Ом, тогда
Пример 2
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1)
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.
Пример 3
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
Пример 5
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.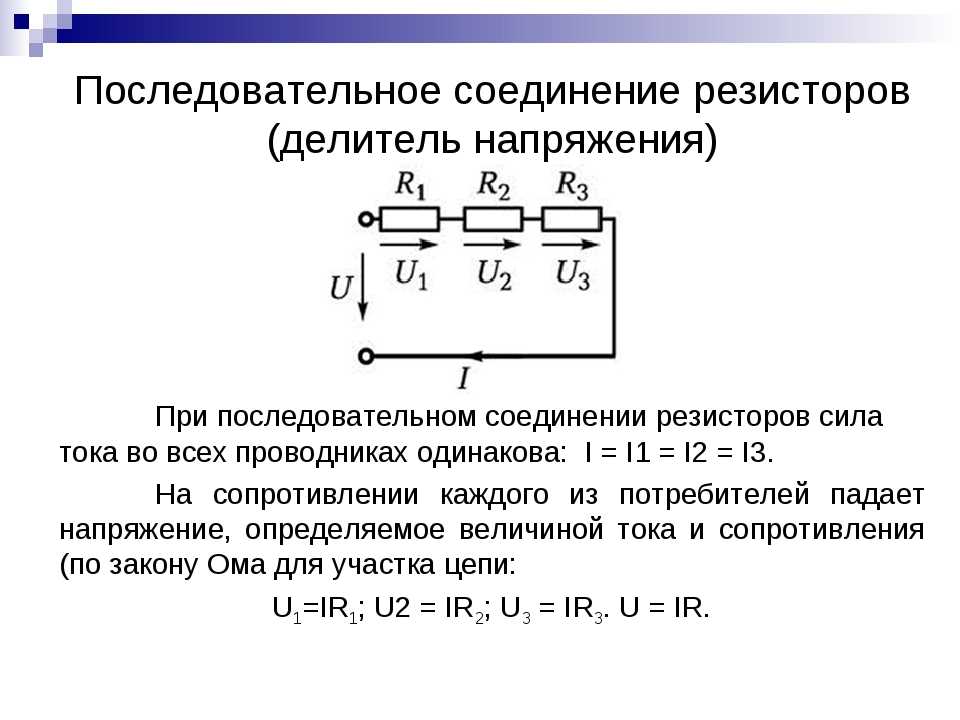
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
5.4 Расчет общего сопротивления сварочного контура
Общее сопротивление сварочного контура рассчитывается по формуле:
, (5.11)
где Rк — сумма активных сопротивлений всех элементов контура и контактов между ними при температуре 100°С; Хк — индуктивное сопротивление контура.
(5.12)
, (5.13)
где Кп – коэффициент поверхностного
эффекта, зависит от формы сечения и от
охлаждения. Кп ≈1.
Кп ≈1.
ρт – удельное электрическое сопротивление при 100 ˚С, ,
α – температурный коэффициент изменения ρ, для меди α = 0,0043 град-1,
l — длина элемента,
S – площадь сечения.
Для меди мкОм∙см
Для бронзы мкОм∙см
Сопротивление электродов мкОм
Сопротивление верхнего хобота мкОм
Сопротивление нижнего хобота мкОм
Сопротивление нижней части крышки мкОм
Сопротивление гибкой шины мкОм
Сопротивление жестких шин мкОм
Полное активное сопротивление контура мкОм
, (5.14)
где S – площадь, охватываемая контуром.
,
мкОм
мкОм
5.5 Расчет вторичного номинального напряжения машины
Вторичное номинальное напряжение рассчитывается по формуле:
U2Н = I2Н
. ZM,
(5.15)
ZM,
(5.15)
где I2Н – номинальный сварочный ток, А;
ZM – полное сопротивление машины, мкОм;
U2Н =25. 103 109 10-6 = 2,725В
Зная I2Н и U2Н можно определить полную мощность машины на номинальной ступени.
РН = I2Н* U2Н, кВА (5.16)
РН = 25 103 2,725= 68,125 кВА
6 Расчет трансформатора
Трансформатор представляет собой
статический электромагнитный аппарат
с двумя (или больше) обмотками,
предназначенный чаще всего для
преобразования переменного тока одного
напряжения в переменный ток другого
напряжения. Преобразование энергии в
трансформаторе осуществляется переменным
магнитным полем. Трансформаторы широко
применяются при передаче электрической
энергии на большие расстояния,
распределении ее между приемниками, а
также в различных выпрямительных,
усилительных, сигнализационных и других
устройствах.
Трансформаторы широко
применяются при передаче электрической
энергии на большие расстояния,
распределении ее между приемниками, а
также в различных выпрямительных,
усилительных, сигнализационных и других
устройствах.
Трансформатор — статическое электромагнитное устройство, имеющее две или более индуктивно связанные обмотки и предназначенное для преобразования посредством электромагнитной индукции одной или нескольких систем переменного тока в одну или несколько других систем переменного тока.
Конструктивные особенности трансформаторов.
Основными частями трансформатора
являются магнитопровод и катушка с
обмотками. Материалом для магнитопровода
трансформаторов служит листовая
электротехническая сталь различных
марок и толщины, горячей прокатки и
холоднокатаная; от содержания кремния,
которое отражено в марке стали, а также
от толщины листа зависят потери мощности
в магнитопроводе от вихревых токов.
Толщину листа применяемой стали выбирают
в зависимости от частоты сети, питающей
трансформатор: с увеличением частоты
толщину листа надо уменьшать. Ленточные
(витые) магнитопроводы изготавливают
из лент рулонной стали; предварительно
лента покрывается изолирующим и
склеивающим составом. Броневые
магнитопроводы собирают из пластин
Ш-образной формы и прямоугольных пластин,
замыкающих Ш-образную пластину. Эти
магнитопроводы имеют один стержень, на
котором располагают все обмотки
трансформатора. Сборка броневого
магнитопровода производится так же,
как и магнитопровода стержневого типа,
описанного выше. Поскольку в броневом
магнитопроводе обмотка размещается на
среднем стержне, магнитный поток
разветвляется на правую и левую части
и, таким образом, в крайних стержнях его
значение будет в 2 раза меньше, чем в
центральном; это позволяет уменьшить
сечение крайних стержней в 2 раза по
сравнению с центральным. собирают из
отдельных штампованных колец, покрытых
изолирующим лаком; сборка производится
с помощью намотки на пакет пластин
ленточной лакоткани. Этот магнитопровод
обладает наилучшими магнитными
свойствами: наименьшее магнитное
сопротивление, минимальные индуктивность
рассеивания и чувствительность к внешним
магнитным полям, однако изготовление
обмоток в данном случае может производиться
только на специальных станках челночного
типа или вручную.
Ленточные
(витые) магнитопроводы изготавливают
из лент рулонной стали; предварительно
лента покрывается изолирующим и
склеивающим составом. Броневые
магнитопроводы собирают из пластин
Ш-образной формы и прямоугольных пластин,
замыкающих Ш-образную пластину. Эти
магнитопроводы имеют один стержень, на
котором располагают все обмотки
трансформатора. Сборка броневого
магнитопровода производится так же,
как и магнитопровода стержневого типа,
описанного выше. Поскольку в броневом
магнитопроводе обмотка размещается на
среднем стержне, магнитный поток
разветвляется на правую и левую части
и, таким образом, в крайних стержнях его
значение будет в 2 раза меньше, чем в
центральном; это позволяет уменьшить
сечение крайних стержней в 2 раза по
сравнению с центральным. собирают из
отдельных штампованных колец, покрытых
изолирующим лаком; сборка производится
с помощью намотки на пакет пластин
ленточной лакоткани. Этот магнитопровод
обладает наилучшими магнитными
свойствами: наименьшее магнитное
сопротивление, минимальные индуктивность
рассеивания и чувствительность к внешним
магнитным полям, однако изготовление
обмоток в данном случае может производиться
только на специальных станках челночного
типа или вручную.
Броневые магнитопроводы с находящимися на них обмотками собирают в узел с помощью шпилек и накладок либо путем запрессовки в скобу.
Расчёт сопротивления электрических цепей с использованием законов последовательного и параллельного соединений
- Волкова Вера Васильевна, учитель математики
- Швейкина Юлия Сергеевна, учитель физики
Разделы: Физика
Цели:
Образовательная: систематизировать и
закрепить знания учащихся о различных
соединениях проводников, сформировать умения
применять законы последовательного и
параллельного соединений для расчёта
электрических цепей, объединить знания,
полученные на уроках физики и математики.

Тип урока: урок проверки и закрепления новых знаний по физике и математике.
Метод проведения урока: практический
Оборудование:
- Громов С.В. Учебник “Физики-9”;
- план урока;
- методика расчета участка электрической цепи постоянного тока;
- карточки-задания.
Приложение 1
Ход урока
Сегодня на уроке мы должны применить
полученные ранее знания о законах
последовательного и параллельного соединений
для расчёта участка электрической цепи, а также
определить степень усвоения изученного
материала с помощью карточек – заданий.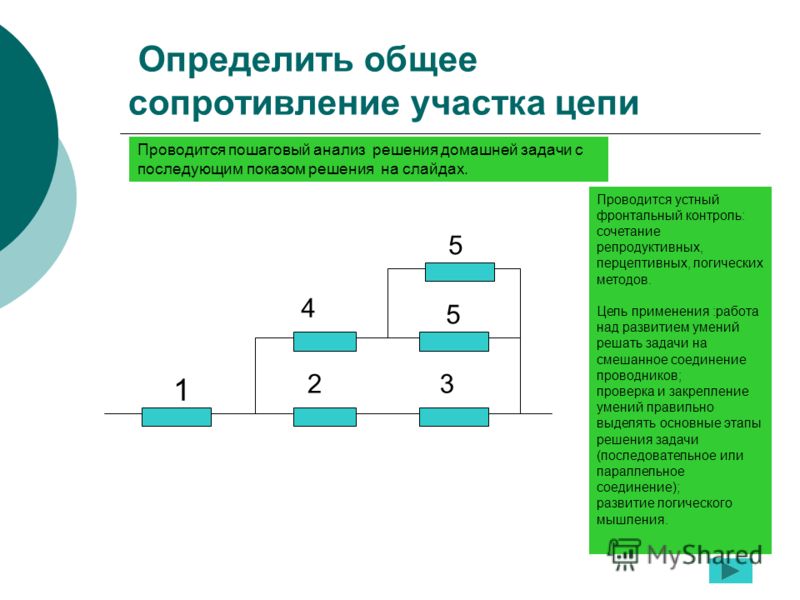
Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:
1) Какие виды соединений бывают и как они
изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
4) Какая отличительная особенность параллельного
соединения?
Рассмотрим расчёт участка электрической цепи на примере следующих задач:
1. Рассчитайте общее электрическое сопротивление участка цепи?
1) Наиболее удалённые от источника элементы – это резисторы R2 и R3.
2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R2 и R3 подключены параллельно, т.к образуют в соединении два узла, следовательно:
Ом
3) Изображаем получившуюся в результате свёртывания резисторы R2 и R3 электрическую схему:
4) Полученные в результате объединения схему с
двумя резисторами группируем во второй участок и
рассчитываем их общее сопротивление. Так как
резисторы R1 и Rоб.1 соединены
последовательно, значит:
Так как
резисторы R1 и Rоб.1 соединены
последовательно, значит:
Rоб = R1 + Rоб.1 = 4 Ом + 2 Ом = 6 Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.
2. Рассчитайте общее электрическое сопротивление участка цепи?
1) Резисторы R1 и R2 соединены между собой последовательно:
Rоб.1 = R1 + R2 = 1 Ом + 2 Ом = 3 Ом
Изобразим полученный электрический участок цепи:
2) Резисторы R3 и R4 соединены между собой последовательно:
Rоб.2 = R3 + R4 = 3 Ом + 4 Ом = 7 Ом
Изобразим полученный электрический участок цепи:
3) Полученные в результате объединения схему с
двумя резисторами группируем в третий участок и
рассчитываем их общее сопротивление.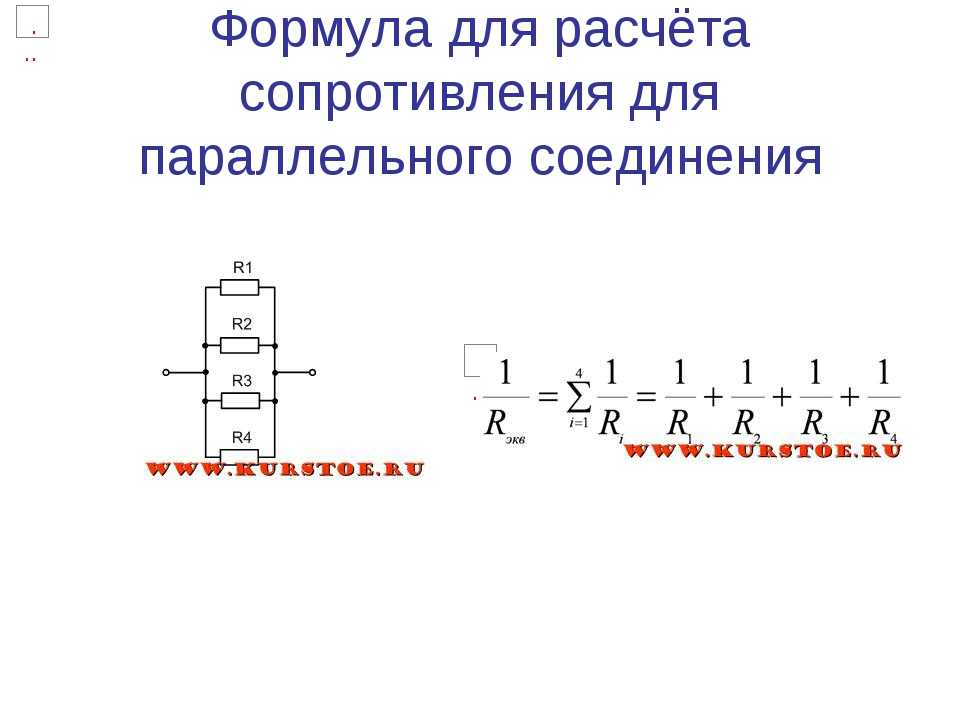 Так как
резисторы Rоб.1 и Rоб.2 соединены
параллельно, значит:
Так как
резисторы Rоб.1 и Rоб.2 соединены
параллельно, значит:
Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.
3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:
а) Рассчитайте общее электрическое сопротивление участка цепи?
б) Рассчитайте общее электрическое сопротивление участка цепи?
в) Рассчитайте общее электрическое сопротивление участка цепи?
Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.
Последовательное соединение резисторов — делитель напряжения — FINDOUT.SU
Поможем в ✍️ написании учебной работы
Имя
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности
Расчет общего сопротивления.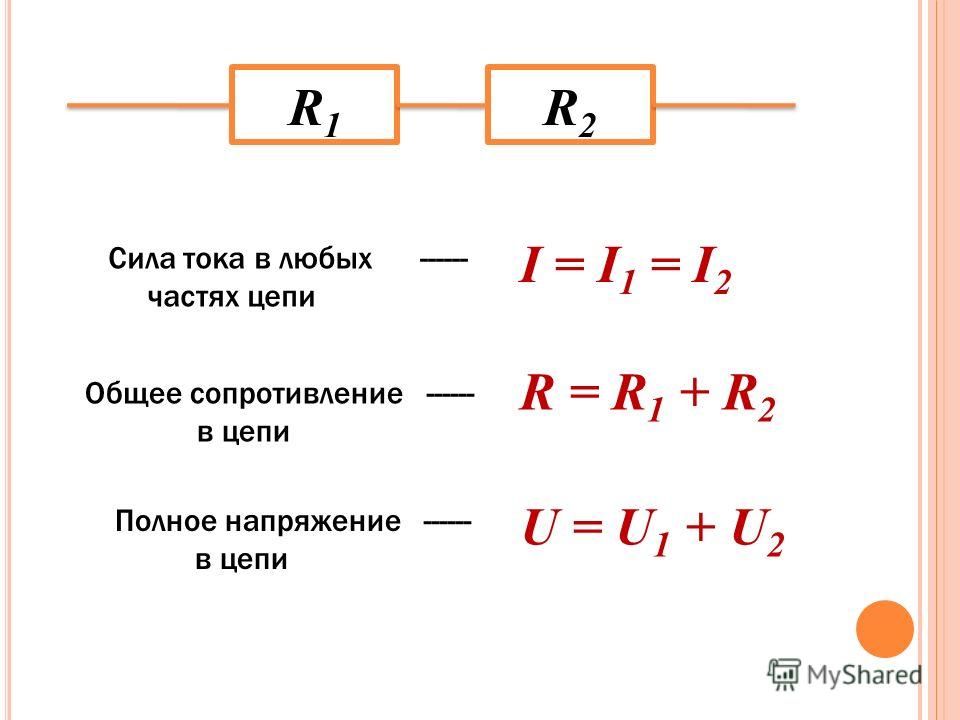
Сведения из теории. Общее сопротивление последовательно соединенных резисторов равно сумме сопротивлений отдельных резисторов. R общ. = R 1 + R 2 + R 3 +……+ Rn . В последовательной цепи по всем резисторам течет один и тот же ток. Падение напряжения на резисторе прямо пропорционально величине сопротивления каждого резистора, поэтому последовательная цепь делит общее напряжение, подаваемое на вход схемы, на напряжения прямо пропорциональные величине каждого отдельного резистора , а сумма падений напряжений на каждом резисторе равна входному напряжению. Суммарное падение напряжение равно U общ.= U 1 + U 2 + U 3 +……+ Un . Можно сказать по другому. Общая работа, проводимая током на всех участках последовательной цепи равна сумме работ на отдельных ее участках, а работа тока на каждом отдельном участке прямо пропорциональна величине его сопротивления.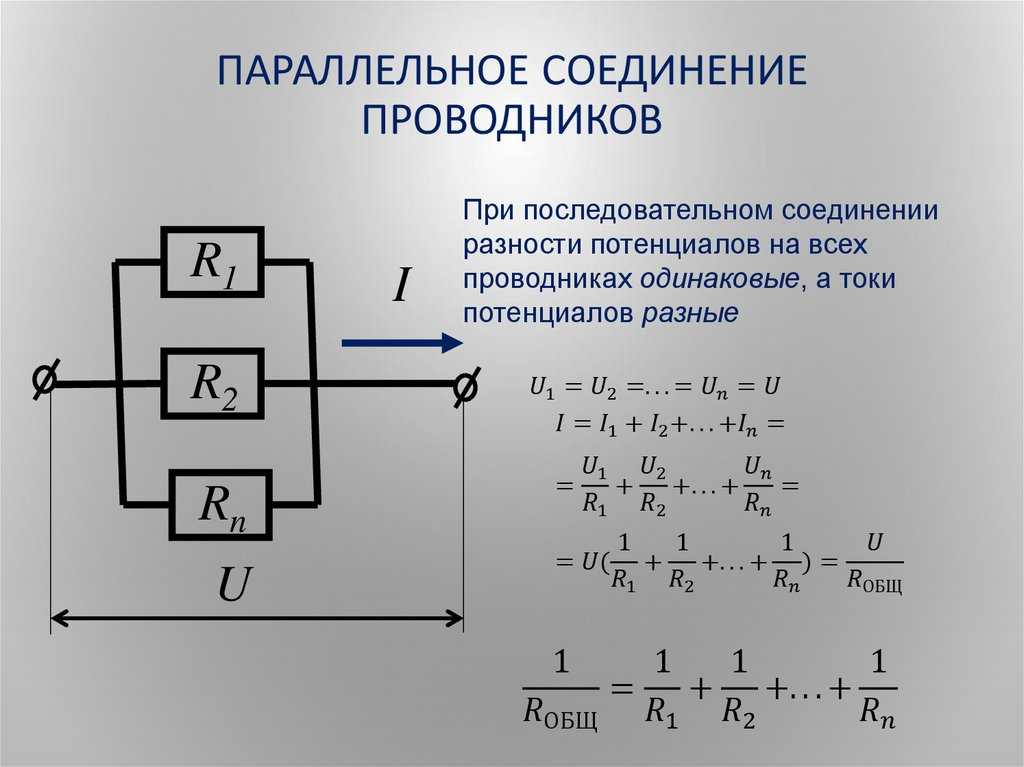
Цель работы: Закрепить навыки работы с мультиметром по измерению сопротивлений и напряжений, свойства последовательной цепи, способ деления напряжения резисторами последовательной цепи, попрактиковаться в соединении деталей методом пайки.
1.Записать тему и зарисовать схему в тетрадку. Выбрать резисторы сопротивлением в пределах 10кОм> R > 10 Ом.
2.Измерить омметром каждый из резисторов и записать его значение в омах в тетрадь.
R1 =… R2 =… R3 =… R4 =… R5 =… R6 =… R7 =…
3.Определить общее сопротивление по формуле
Rвх = R1 + R2 + R3 + R4 + R5 + R6 + R7
4.Собрать схему на макетной плате и измерить общее сопротивление Rизм омметром. Сравнить рассчитанное и измеренное сопротивления.
Rвх = ……………. Rвх изм = …………….
6.Подать напряжение с источника питания (Uобщ), измерить общее напряжение и напряжение на каждом резисторе.
U1 =… U2 =… U3 =… U4 =… U5 =… U6 =… U7 =… U общ изм.= …….
7.Просуммировать измеренные напряжения. Un
U общ = U1 + U2 + U3 + U4 + U5 + U6 + U7
U общ = ……….
| Номер измерения n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| R измеренное | |||||||
| U измеренное |
8. Сравнить рассчитанные значения сопротивлений с измеренными значениями и записать в тетрадь выводы.
Примечание. Жирным шрифтом выделены ключевые слова или термины, курсивом – слова на которые необходимо обратить внимание.
Вопросы:
1. Какая электрическая цепь называется последовательной? Какие цепи бывают?
2. Какая электрическая цепь называется делителем напряжения?
3. Как делится общее напряжение по сопротивлениям, которые включены последовательно? Почему делится именно так, а не иначе?
4. Одинакова ли величина тока проходящего по разным резисторам этой электрической цепи? Почему?
5. Чему равна сумма падений напряжений по всем резисторам этой электрической цепи? Почему?
6. В каких единицах измеряется напряжение?
7. Справедливы ли утверждения:
Падение напряжения на каждом резисторе пропорционально его сопротивлению!
Сила тока по всем резисторам одинакова! Если да, то почему?
Сумма падений напряжений на резисторах равна входному напряжению!
Сумма сопротивлений резисторов равна общему сопротивлению схемы!
Общее напряжение на схеме делится пропорционально сопротивлениям резисторов!
8. Какая пропорция между сопротивлением участка цепи и падением напряжения на нем, прямая или обратная?
Используемое оборудование
1. Вольтметр (Ампервольтомметр) — один.
Вольтметр (Ампервольтомметр) — один.
2. Амперметр (Ампервольтомметр) — один.
3. Омметр (Ампервольтомметр) — один.
4. Калькулятор.
5. Блок питания.
6. Резистор постоянный — 7 штук
7. Соединительные концы.
8. Макетная плата.
9. Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 12
Параллельное соединение. Проводимость. Расчет общего сопротивления.
Сведения из теории. Проводимостью (G) называется свойство материала обратное сопротивлению, то есть свойство материала проводить ток с наименьшим сопротивлением. G = 1/R Проводимость измеряется в Сименсах. Общая проводимость параллельно соединенных резисторов равна сумме проводимостей отдельных резисторов:
Gобщ. = 1/Rобщ. = 1/R1 + 1/R2 + 1/R3 +….+ 1/Rn = G1 + G2 + G3 + ….+ Gn
= 1/Rобщ. = 1/R1 + 1/R2 + 1/R3 +….+ 1/Rn = G1 + G2 + G3 + ….+ Gn
Соединение проводников имеющих три конца (входа и выхода тока) и более называется электрическим узлом. Параллельная цепь содержит два узла соединений.
Цель работы: Закрепить навыки работы с мультиметром по измерению сопротивлений, закрепить правило расчета общего сопротивления в параллельной цепи, попрактиковаться в соединении деталей методом пайки. Закрепить понятие проводимости.
1.Записать тему и зарисовать схему в тетрадку.
Выбрать R > 100 Ом.
2.Измерить омметром каждый из резисторов и записать его значение в омах.
R1 =… R2 =… R3 =…
R4 =… R5 =… R6 =…
R7 =… Rвх =…
3.Определить проводимости каждого из резисторов в Сименсах.
4.Определить общую проводимость в Сименсах.
Gвх(Сим.) = G1 + G2 + G3 + G4 + G5 + G6 + G7
5.Определить общее сопротивление
| Номер измерения n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| G расчетное (Сим) | |||||||
| I измеренное(Ампер) |
7.Измерить токи на каждом резисторе и на входе схемы. Измерить напряжение.
8.Просуммировать токи, проходящие по резисторам, сравнить с общим током. Сравнить Rвх измеренное с расчетным.
9.Записать результаты измерений и свои выводы в тетрадку.
Примечание. Жирным шрифтом выделены ключевые слова или термины, курсивом – слова на которые необходимо обратить внимание.
Жирным шрифтом выделены ключевые слова или термины, курсивом – слова на которые необходимо обратить внимание.
Вопросы:
1. Что называется проводимостью?
2. Объяснить, почему сумма проводимостей по резисторам равна общей проводимости всей цепи? В каких единицах измеряется проводимость?
3. Можно ли утверждать, что общая проводимость по всем ветвям параллельной электрической цепи равна сумме проводимостей каждой из этих цепей?
4. Можно ли утверждать, что сумма токов по всем ветвям параллельной электрической цепи равна общему току на входе этой цепи?
5. Можно ли утверждать что напряжение на всех ветвях параллельной электрической цепи одинаково и равно общему напряжению на входе этой цепи? В каких единицах измеряется напряжение?
6. Что называется электрическим узлом?
7. Какое соединение элементов или электрических цепей называется параллельным?
Используемое оборудование
1. Амперметр (Ампервольтомметр) — один.
2. Омметр (Ампервольтомметр) — один.
3. Калькулятор.
4. Блок питания.
5. Резистор постоянный — 7 штук
6. Соединительные концы.
7. Макетная плата.
8. Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 13
Смешанное соединение резисторов. Определение общего сопротивления.
Сведения из теории. Электрическая цепь, имеющая участки последовательно и параллельно соединенных элементов называется цепью смешанных соединений. Общее сопротивление последовательно соединенных элементов равно сумме сопротивлений отдельных элементов цепи. R общ.= R 1 + R 2 + R 3 +….+ Rn. Общая проводимость параллельно соединенных элементов равно сумме проводимостей отдельных элементов. 1/ R общ.= 1/ R 1 + 1/ R 2 + 1/ R 3 +….+ 1/ Rn Сложное смешанное соединение всегда можно упростить, заменяя участки параллельно и последовательно соединенных элементов на один элемент равный им по сопротивлению. В практике бывает необходимым определить общее сопротивление смешанной цепи или ее элемента расчетом. Для определения общего сопротивления смешанной цепи необходимо разбить ее на участки параллельных и последовательных соединений, определить сопротивление этих участков и подставить в цепь вместо соответствующего участка резистор, с рассчитанным значением сопротивления упрощая этим схему электрической цепи. Соединение проводников в одной точке называется электрическим узлом. Сумма токов в узле равна нулю, потому что, сколько тока приходит в узел столько и уходит.
В практике бывает необходимым определить общее сопротивление смешанной цепи или ее элемента расчетом. Для определения общего сопротивления смешанной цепи необходимо разбить ее на участки параллельных и последовательных соединений, определить сопротивление этих участков и подставить в цепь вместо соответствующего участка резистор, с рассчитанным значением сопротивления упрощая этим схему электрической цепи. Соединение проводников в одной точке называется электрическим узлом. Сумма токов в узле равна нулю, потому что, сколько тока приходит в узел столько и уходит.
Цель работы: Закрепить навыки работы с мультиметром по измерению сопротивлений, закрепить правило расчета общего сопротивления в смешанной цепи, попрактиковаться в соединении деталей методом пайки.
1.Записать тему и зарисовать схему в тетрадку. Подобрать резисторы из условия 10кОм>R> 100 Ом
2. Измерить сопротивления резисторов мультиметром и записать результаты в тетрадку.
Измерить сопротивления резисторов мультиметром и записать результаты в тетрадку.
3.Собрать схему на плате и определить расчетом сопротивление параллельно соединенных резисторов.
Измерить сопротивление Rпар. и сравнить с расчетным.
4.Теперь сопротивления R3 и R2 можно заменить в расчете сопротивлением Rпар. и получится цепь из последовательно соединенных сопротивлений R1 и Rпар.
Тогда Rобщ = R1 + Rпар.
5.Рассчитайте (Rобщ) и измерьте общее сопротивление ( Rобш. изм )цепи и сравните результаты.
6.Запишите результаты измерений и свои выводы в тетрадку.
Примечание. Жирным шрифтом выделены ключевые слова или термины, курсивом – слова на которые необходимо обратить внимание.
Вопросы:
1. Какое соединение элементов электрической цепи называется смешанным?
2. Что называется электрическим узлом?
3. Какое соединение элементов электрической цепи называется последовательным?
4. Какое соединение элементов электрической цепи называется параллельным?
Какое соединение элементов электрической цепи называется параллельным?
5. Можно ли утверждать, что сумма токов в электрическом узле, состоящем из цепи R1, R2 и R3, равна нулю?
6. Можно ли утверждать, что напряжение на входе делится цепочкой R1 и Rпар. пропорционально величине их сопротивлений.
7. Почему результат расчета не точно совпадает с результатом измерений прибором?
8. Что называется электрическим узлом?
9. Каков порядок упрощения схемы электрической цепи?
10. Для чего упрощать схему электрической цепи?
11. Как получилась формула расчета сопротивления двух параллельно соединенных резисторов?
12. Чем похожи правила расчета сопротивления последовательно соединенных резисторов и проводимости параллельно соединенных резисторов?
Используемое оборудование
1. Омметр (Ампервольтомметр) — один. 2. Калькулятор.
3. Резистор постоянный — 3 штуки 4. Соединительные концы.
5. Макетная плата. 6. Паяльник, припой, флюс.
6. Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 14
Мостовое соединение резисторов. Свойства моста.
Сведения из теории. Мостовой схемой называют две параллельных цепи последовательно включенных элементов. Если это резисторы, то схема соединений элементов представляет квадрат, стороны которого составлены из резисторов и называются «плечами» моста. При подключении источника питания в одну из диагоналей этого «квадрата» последовательные соединения резисторов образует два делителя напряжения. Если напряжение в средней точке одного делителя, составленного из двух резисторов (1), равно напряжению в средней точке другого делителя (2), то разность потенциалов (падение напряжения) между этими средними точками равна нулю и ток по цепи, соединяющей эти точки, не пойдет. Вольтметр или амперметр, включенные в эту цепь покажут нулевые значения напряжения или тока. Такое состояние моста, когда разность потенциалов равна нулю, называется равновесным или сбалансированным, и возникает только при условии R1 / R2 = R31 / R32 или R1 x R32 = R2 x R31. Произведения величин сопротивлений противоположных плеч у сбалансированного моста равны. Для изменения сопротивлений плеч вместо двух резисторов делителя можно поставить переменный резистор, который этой схеме состоит как бы из двух резисторов (R31 и R32), которые делят входное напряжение (Uвх.) каждый пропорционально величине своего сопротивления, а сумма этих напряжений на резисторах равна Uвх. Здесь переменный резистор включен как делитель напряжения и изменяет потенциал напряжения на движущемся электроде пропорционально его перемещению, или говорят, что он включен как потенциометр.
Такое состояние моста, когда разность потенциалов равна нулю, называется равновесным или сбалансированным, и возникает только при условии R1 / R2 = R31 / R32 или R1 x R32 = R2 x R31. Произведения величин сопротивлений противоположных плеч у сбалансированного моста равны. Для изменения сопротивлений плеч вместо двух резисторов делителя можно поставить переменный резистор, который этой схеме состоит как бы из двух резисторов (R31 и R32), которые делят входное напряжение (Uвх.) каждый пропорционально величине своего сопротивления, а сумма этих напряжений на резисторах равна Uвх. Здесь переменный резистор включен как делитель напряжения и изменяет потенциал напряжения на движущемся электроде пропорционально его перемещению, или говорят, что он включен как потенциометр.
Цель работы: Закрепить навыки работы с мультиметром по измерению сопротивлений, закрепить знание свойств мостовой схемы. Познакомится с использованием переменного резистора в качестве делителя напряжения (потенциометра), исследовать свойства мостовой схемы. Попрактиковаться в соединении деталей методом пайки.
Познакомится с использованием переменного резистора в качестве делителя напряжения (потенциометра), исследовать свойства мостовой схемы. Попрактиковаться в соединении деталей методом пайки.
1.Записать тему и зарисовать схему в тетрадку. Выбрать R > 100 Ом., а R1/R2 ≤ 10.
R1 =…. Ом.
R2 =…. Ом.
2.Собрать схему и подать входное напряжение U вх. (подключить источник питания).
3.Вращая ручку переменного сопротивления добиться нулевого показания вольтметра включенного в диагональ моста (сбалансировать мост). Измените, напряжение Uвх. и вновь снимите показания вольтметра включенного в диагональ моста.
4.Отключите входное напряжение U вх и измерьте значения сопротивлений R31 =…. Ом. R32 =…. Ом. отключив потенциометр от схемы. На переменном резисторе это сопротивления между подвижным и неподвижным контактом с каждой стороны.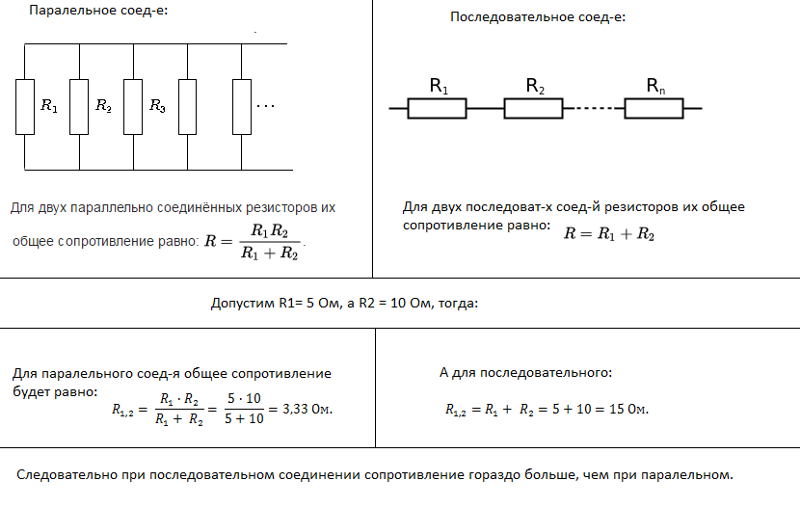
5.Произведите расчет по формулам:
R 31 = ( R 1 x R 32)/ R 2 и R 32 = ( R 2 x R 31)/ R 1 R31 =……… R32 = ……….
R 1 x R 32 = ……… R 2 x R 31 = …………
Сравните полученные результаты.
6.Запишите результаты измерений и расчетов в тетрадь.
Вопросы:
1. Какая схема называется электрическим мостом?
2. Что такое «плечи моста» и «диагональ моста»?
3. Каковы условия равновесия моста?
4. Почему переменное сопротивление в этой схеме можно назвать делителем напряжения?
5. Изменяется ли баланс моста при изменении напряжения питания, почему?
6. Каким будет напряжение в диагонали моста, если все сопротивления резисторов составляющих мост будут равны?
7. В каких единицах измеряется напряжение. Как называется прибор, измеряющий напряжение?
8. Изменится ли баланс моста, если изменить питание схемы с постоянного тока на переменный ток?
9. Может ли сумма падений напряжения на плечах моста превышать напряжение питания?
Может ли сумма падений напряжения на плечах моста превышать напряжение питания?
10. Когда резистор переменного сопротивления называется потенциометром?
Используемое оборудование
1. Вольтметр (Ампервольтомметр) — один.
3. Омметр (Ампервольтомметр) — один.
4. Калькулятор.
5. Блок питания с регулированием выходного напряжения.
6. Резистор постоянный — 2 штуки
7. Резистор переменный — 1 штука
8. Соединительные концы.
9. Макетная плата.
10. Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 15
Свойства конденсатора.
Сведения из. теории: Устройство, предназначенное для накопления электрических зарядов, называется конденсатором. Основные свойства конденсатора заряд и разряд. Заряд конденсатора — накопление электрических зарядов при подключении к источнику питания. Разряд – расход (уравновешивание) количества разноименных зарядов на обкладках при подсоединении к внешней пассивной электрической цепи. Пассивной электрической цепью называется соединение элементов не имеющее источников питания. Конденсатор, в момент разряда, становится источником питания. Физически конденсатор представляет собой два рядом расположенных проводника объединенных в одном корпусе, не имеющих электрического соединения между собой называемых обкладками конденсатора. Способность накапливать заряды оценивается емкостью конденсатора. Емкость — это количество электрических зарядов, отнесенное к напряжению между обкладками конденсатора, измеряется в Фарадах. Емкость конденсатора зависит от площади обкладок конденсатора и расстояния между ними. Характеристиками конденсатора являются емкость и максимальное напряжение между обкладками, до которого его можно заряжать.
Разряд – расход (уравновешивание) количества разноименных зарядов на обкладках при подсоединении к внешней пассивной электрической цепи. Пассивной электрической цепью называется соединение элементов не имеющее источников питания. Конденсатор, в момент разряда, становится источником питания. Физически конденсатор представляет собой два рядом расположенных проводника объединенных в одном корпусе, не имеющих электрического соединения между собой называемых обкладками конденсатора. Способность накапливать заряды оценивается емкостью конденсатора. Емкость — это количество электрических зарядов, отнесенное к напряжению между обкладками конденсатора, измеряется в Фарадах. Емкость конденсатора зависит от площади обкладок конденсатора и расстояния между ними. Характеристиками конденсатора являются емкость и максимальное напряжение между обкладками, до которого его можно заряжать. Такое напряжение называется рабочим. Время заряда и разряда конденсатора зависит только от емкости конденсатора и сопротивления цепи, по которой происходит заряд (разряд) конденсатора, называется постоянной времени заряда (разряда). Постоянная времени разряда идеального конденсатора не зависит от величины напряжения заряда и тока. t = C x R t — в секундах. С — в Фарадах. R — в Омах. Напряжение на емкости измеряется вольтметром, имеющим входное сопротивление и оказывающим им влияние на точность измерения времени. Входным сопротивлением называется внутреннее сопротивление измерительного прибора, измеренное на его входных клеммах.
Такое напряжение называется рабочим. Время заряда и разряда конденсатора зависит только от емкости конденсатора и сопротивления цепи, по которой происходит заряд (разряд) конденсатора, называется постоянной времени заряда (разряда). Постоянная времени разряда идеального конденсатора не зависит от величины напряжения заряда и тока. t = C x R t — в секундах. С — в Фарадах. R — в Омах. Напряжение на емкости измеряется вольтметром, имеющим входное сопротивление и оказывающим им влияние на точность измерения времени. Входным сопротивлением называется внутреннее сопротивление измерительного прибора, измеренное на его входных клеммах.
Цель работы: Проверить, изменяется ли время заряда и разряда о величины поданного напряжения. Закрепить навыки работы с мультиметром по измерению напряжений, усвоить понятия емкости, единицы измерения емкости, постоянной времени заряда (разряда) конденсатора.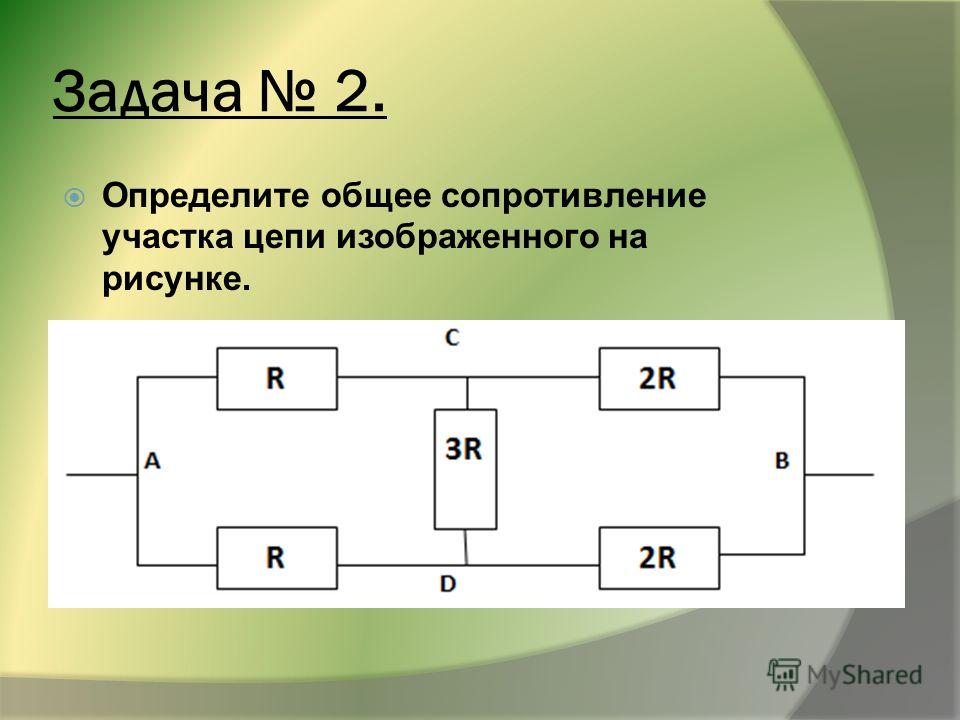 Попрактиковаться в соединения деталей методом пайки.
Попрактиковаться в соединения деталей методом пайки.
1. Выбрать напряжение и источник питания для заряда конденсатора. U вход. должно быть меньше рабочего напряжения конденсатора.
2. Определить величину сопротивления из соображений длительности разряда более 20 секунд, иначе измерение времени будет неточным. R1 должно быть меньше входного сопротивления вольтметра в 10 раз.
3. Собрать схему и подключить к конденсатору вольтметр с пределом измерений немного большим, чем U входное.
4. Определить конечное напряжение разряда из формулы Uк. = 0,35 U вход.
Раза рядить конденсатор, кратковременно замкнув его выводы.
5. Зарядить конденсатор, включив ключ Кл. и проверить напряжение заряда по вольтметру.
6. Одновременно включить секундомер и выключить Кл. наблюдая за снижением напряжения по вольтметру.
7. Выключить секундомер при снижении напряжения до Uк.
8. Провести эксперимент три раза и взять среднее значение.
9.Провести эксперимент при другом напряжении.
| U (Вольт) | 10 | 10 | 10 | 15 | 15 | 15 | 20 | 20 | 20 |
| t (сек.) |
10. Увеличить сопротивление в два раза и повторить измерения.
Запишите результаты измерений и свои выводы в тетрадку.
ВОПРОСЫ:
1. Какой элемент электрической цепи называется конденсатором?
2. Назовите основные характеристики конденсатора.
3. Что произойдет если увеличить разрядное сопротивление в два раза?
4. Что произойдет, если входное сопротивление вольтметра будет равно разрядному сопротивлению?
Что произойдет, если входное сопротивление вольтметра будет равно разрядному сопротивлению?
5. Одинаково ли время разряда при разных напряжениях, и неизменных емкости и сопротивлении резистора.
6. Что называется постоянной времени заряда (разряда) и от чего зависит ее величина?
7.Что такое «емкость конденсатора»?
8.Каковы основные свойства конденсатора?
9.В каких единицах измеряется емкость конденсатора?
10.Что называется обкладками конденсатора, сколько их?
11. Какая электрическая цепь называется пассивной?
Используемое оборудование
1. Вольтметр (Ампервольтомметр) — один.
2. Блок питания постоянного напряжения с регулированием.
3. Калькулятор.
4. Секундомер.
5. Резистор постоянный — 1 шт.
6. Конденсатор постоянной емкости не менее 50 мкФ. — 1 шт.
7. Соединительные концы.
8. Ключ соединительный (тумблер)
9. Макетная плата.
10.Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 16
Определение емкости конденсатора методом измерения времени заряда и разряда.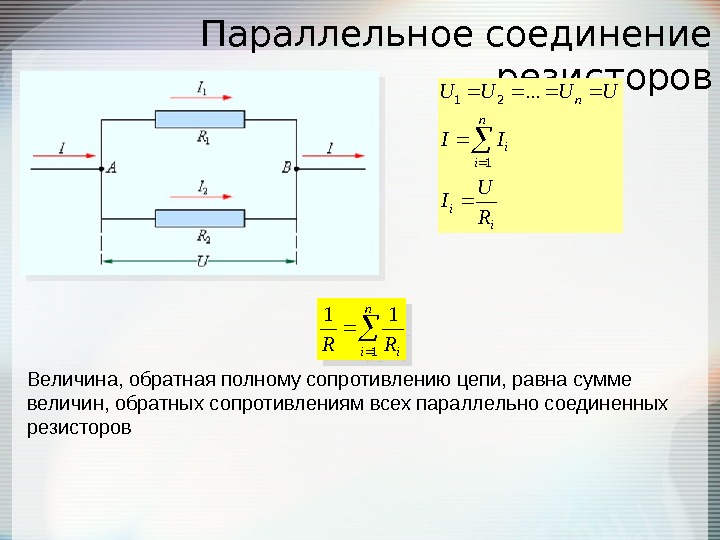
Сведения из теории. Емкость конденсатора – характеристика его свойства накапливать электрические заряды на своих обкладках. Единица измерения емкости – Фарада (микроФарада, наноФарада, пикоФарада). Накопление электрических зарядов конденсатором называется зарядом, а расход зарядов – разрядом. В момент разряда конденсатор становится источником электрического тока. Время разряда конденсатора на пассивную электрическую цепь называется постоянной времени разряда. Пассивной электрической цепью называется соединение элементов не имеющее источников питания. Постоянная времени заряда и разряда конденсатора не зависит от величины напряжения заряда и тока, а зависит только от сопротивления и емкости конденсатора. t = C x R t — в секундах. С — в Фарадах. R — в Омах. Тогда измерив величину сопротивления разрядной цепи и времени разряда конденсатора можно определить его емкость
С(Фарад) = t(сек)/R(Ом).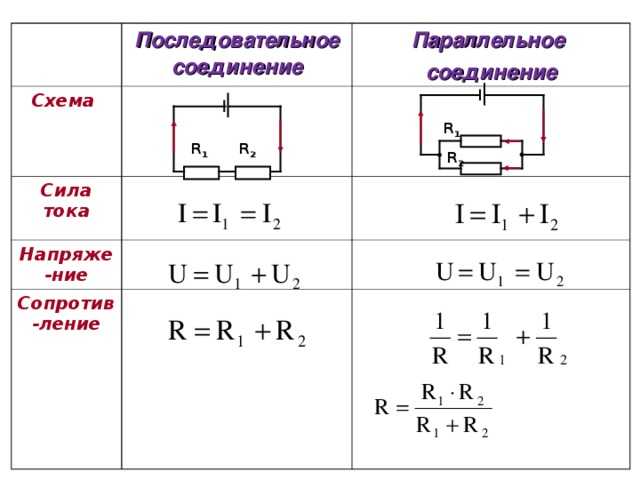
Этот метод измерения, при котором измеряются величины входящие в формулу, а затем рассчитывается нужная величина называется косвенным методом измерения. Подобный метод измерения применим для конденсаторов большой емкости (в основном полярных), потому, что измерение времени с помощью секундомера возможно только более 5 секунд. Чем меньше время разряда, тем менее точно измерение.
Цель работы: Закрепить навыки работы с мультиметром по измерению напряжений, освоить метод измерения емкости конденсатора методом измерения времени разряда и разрядного сопротивления. Практика соединения деталей методом пайки.
1. Выбрать напряжение и источник питания для заряда конденсатора. U вход. должно быть меньше рабочего напряжения конденсатора. R1 должно быть меньше входного сопротивления вольтметра в 10 раз.
2. Определить величину сопротивления из соображений длительности разряда в пределах 10-100 секунд, иначе измерение времени будет неточным. R1 должно быть меньше входного сопротивления вольтметра в 10 раз.
R1 должно быть меньше входного сопротивления вольтметра в 10 раз.
3. Собрать схему и подключить к конденсатору вольтметр с пределом измерений немного большим, чем U вход.
4. Определить конечное напряжение разряда из формулы Uк. = 0,35 U вход.
Разрядить конденсатор, кратковременно замкнув его выводы.
5. Зарядить конденсатор, включив ключ Кл. и проверить напряжение заряда по вольтметру.
6. Включить секундомер и выключить Кл. наблюдая за снижением напряжения по вольтметру.
7. Выключить секундомер при снижении напряжения до Uк. Записать результат измерений. Повторить измерения дважды. Если время разряда при неизменных условиях сильно отличается, повторить измерения третий раз, учесть в расчете близкие значения.
8. Рассчитать емкость конденсатора по формуле
9. Провести эксперимент три раза и взять среднее значение.
10.Запишите результаты измерений и свои выводы в тетрадку.
ВОПРОСЫ:
1. Какой метод измерения называется косвенным?
Какой метод измерения называется косвенным?
2.Что такое «емкость конденсатора»?
3. Какая электрическая цепь называется пассивной?
4. В каких единицах измеряется емкость?
5. Что произойдет если увеличить разрядное сопротивление в два раза?
6. Что произойдет если увеличить напряжение заряда конденсатора в два раза?
7. Что произойдет, если входное сопротивление вольтметра будет равно разрядному сопротивлению?
8. В каких единицах необходимо подставить значения времени и сопротивления в формулу, чтобы получить значение емкости в Фарадах?
9. Для каких конденсаторов применим метод измерения емкости по времени заряда и разряда конденсатора.
10. Что называется «постоянной времени разряда» конденсатора.
Используемое оборудование
1. Вольтметр (Ампервольтомметр) — один.
2. Блок питания постоянного напряжения.
3. Калькулятор.
4. Секундомер.
5. Резистор постоянный — 1 штука
6. Конденсатор постоянной емкости — 1 штука
7. Соединительные концы.
Соединительные концы.
8. Ключ соединительный (тумблер)
9. Макетная плата.
10.Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 17
Параллельное соединение емкостей. Определение суммарной емкости конденсаторов методом измерения времени разряда.
Сведения из теории. Основное свойство конденсатора накопление электрических зарядов при подключении к источнику питания — заряд и разряд – уравновешивание количества разноименных зарядов на обкладках. Способность накапливать заряды оценивается емкостью конденсатора. Емкость — это количество зарядов, отнесенное к напряжению между обкладками конденсатора, измеряется в Фарадах (микрофарадах, нанофарадах, пикофарадах). Емкость конденсатора зависит от площади его обкладок и расстояния между ними. Изменение площади обкладок, следовательно, емкости, возможно механическим путем (сдвиганием и раздвиганием обкладок) или параллельным соединением отдельных конденсаторов. Механическое изменение площади обкладок применяется в конденсаторах переменной емкости, но их емкость сравнительно невелика 10-500пФ. Для изменения большой емкости используется параллельное соединение конденсаторов.
Механическое изменение площади обкладок применяется в конденсаторах переменной емкости, но их емкость сравнительно невелика 10-500пФ. Для изменения большой емкости используется параллельное соединение конденсаторов.
Время заряда и разряда емкости не зависит от величины напряжения заряда и тока, а зависит только от сопротивления цепи и емкости конденсатора, поэтому называется постоянной времени заряда для данных емкости и сопротивления. t = C x R t -в секундах. С -в Фарадах. R — в Омах. При параллельном соединении конденсаторов их величины их емкостей складываются, время разряда увеличивается пропорционально суммарной емкости.
Цель работы: Закрепить навыки работы с мультиметром по измерению напряжений, освоить метод измерения суммы емкостей конденсаторов методом измерения времени разряда. Убедится, что общая емкость конденсаторов, при параллельном соединении, равна сумме емкостей отдельных конденсаторов.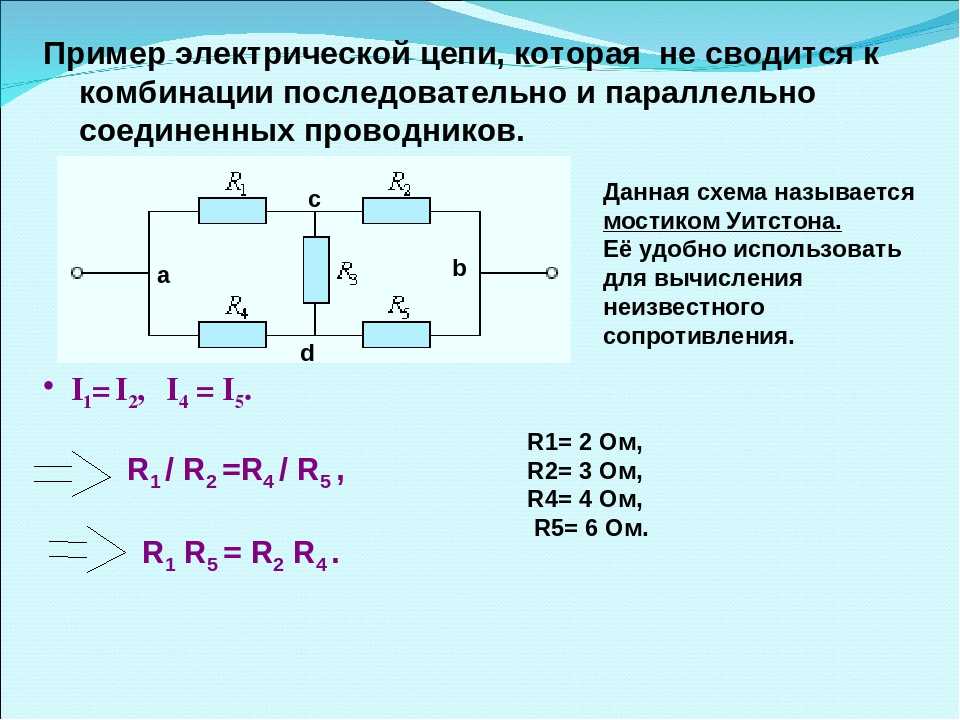 Убедится, что постоянная времени разряда получившейся емкости на одно и тоже сопротивление — равна сумме отдельных постоянных времени. Попрактиковаться в соединении деталей методом пайки.
Убедится, что постоянная времени разряда получившейся емкости на одно и тоже сопротивление — равна сумме отдельных постоянных времени. Попрактиковаться в соединении деталей методом пайки.
1. Выбрать напряжение и источник питания для заряда конденсаторов. U вход. должно быть меньше рабочего напряжения конденсатора.
2. Определить величину сопротивления из соображений длительности разряда в пределах 10-100 секунд, иначе измерение времени будет неточным. R1 должно быть меньше входного сопротивления вольтметра в 10 раз. R1 = ……….
3. Собрать схему с одним конденсатором С1наименьшим по емкости и подключить к нему вольтметр с пределом измерений немного большим, чем U вход.
4. Определить конечное напряжение разряда из формулы Uк. = 0,35 U вход.
5. Зарядить конденсатор, включив ключ Кл. и проверить заряд по вольтметру.
6. Одновременно включить секундомер и выключить Кл. наблюдая за снижением напряжения по вольтметру.
наблюдая за снижением напряжения по вольтметру.
7. Выключить секундомер при снижении напряжения до Uк. Записать результаты измерений в таблицу. Повторить измерения дважды. Если время разряда при неизменных условиях сильно отличается, повторить измерения третий раз, записать близкие значения.
| Конденсатор | С1 | С1+С2 | С1+С2 | С1+С2+С3 | С1+С2+С3 |
| U (Вольт) | |||||
| t (сек.) | |||||
| Емкость(мкФ) |
8. Рассчитать емкость цепи конденсаторов по формуле:
9. Повторить пункты 5, 6, 7, 8 подсоединяя дополнительные конденсаторы и сравнивая расчетные значения с суммой емкостей указанных на корпусе подсоединенных конденсаторов.
10.Запишите результаты измерений и свои выводы в тетрадку.
ВОПРОСЫ:
1. Можно ли сказать, что время разряда увеличивается пропорционально общей емкости конденсаторов?
2. Что произойдет, если входное сопротивление вольтметра будет равно разрядному сопротивлению?
3. Что произойдет, если зарядное напряжение превысит значение напряжения указанное на одном из конденсаторов?
4. Можно ли сказать, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей включенных конденсаторов?
5. Можно ли сказать, что постоянная времени разряда параллельно соединенных конденсаторов равна сумме постоянных разряда отдельных конденсаторов?
6. В каких единицах измеряется электрическая емкость?
7. Как называется конденсатор, изменяющий свою емкость?
Используемое оборудование
1. Вольтметр (Ампервольтомметр) — один.
2. Калькулятор.
3. Блок питания постоянного напряжения.
4. Секундомер.
5. Резистор постоянный — 1 штука
Резистор постоянный — 1 штука
6. Конденсатор постоянной емкости — 3 штуки
7. Соединительные концы.
8. Ключ соединительный (тумблер)
9. Макетная плата.
10.Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 18
Диод. Выпрямление переменного тока.
Сведения из теории. Диод – элемент электрических схем имеющий свойство пропускать ток в только одном (прямом) направлении. Под «прямым» направлением тока понимается движение зарядов от «плюса» к «минусу». Это свойство диодов используется для преобразования переменного тока, меняющего как направление, так и величину, в пульсирующий, который изменяет свою величину, но течет в одном направлении. На диод, включенный последовательно с нагрузкой, из источника переменного тока подается ЭДС. Когда полярность ЭДС совпадает с направлением пропускания тока диодом, ток течет через диод в нагрузку и возвращается к источнику тока. Когда полярность ЭДС не совпадает с направлением пропускания тока диодом, ток практически не течет. Устройства, преобразующие переменный ток в пульсирующий называются выпрямителями. Время полного цикла изменения направления тока называется периодом. Время, когда ток течет только в одном направлении, называется полупериодом. Схема выпрямителя, пропускающая ток только при одном полу периоде переменного напряжения называется однополупериодной. Для уменьшения пульсаций напряжения (Uвых.) после выпрямления подключают конденсатор Сф. который сглаживает пульсацию на выходе за счет имеющегося в нем заряда. Конкретный тип диода имеет предел по максимально пропускаемому тока и обратному напряжению, эти характеристики указываются в его техническом паспорте или справочнике.
Когда полярность ЭДС совпадает с направлением пропускания тока диодом, ток течет через диод в нагрузку и возвращается к источнику тока. Когда полярность ЭДС не совпадает с направлением пропускания тока диодом, ток практически не течет. Устройства, преобразующие переменный ток в пульсирующий называются выпрямителями. Время полного цикла изменения направления тока называется периодом. Время, когда ток течет только в одном направлении, называется полупериодом. Схема выпрямителя, пропускающая ток только при одном полу периоде переменного напряжения называется однополупериодной. Для уменьшения пульсаций напряжения (Uвых.) после выпрямления подключают конденсатор Сф. который сглаживает пульсацию на выходе за счет имеющегося в нем заряда. Конкретный тип диода имеет предел по максимально пропускаемому тока и обратному напряжению, эти характеристики указываются в его техническом паспорте или справочнике.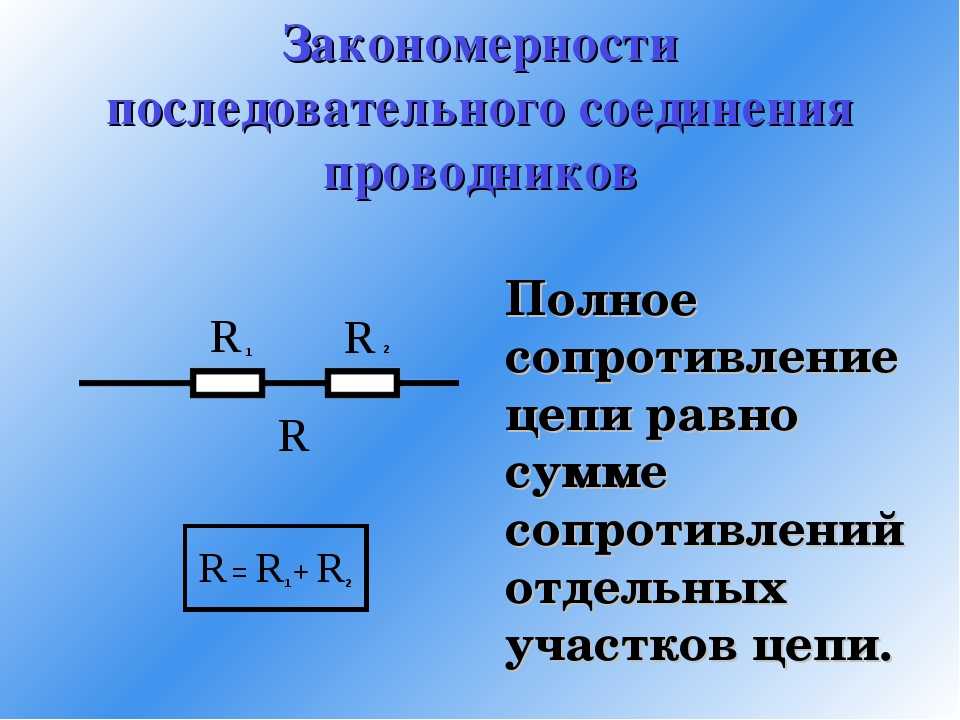 Обратное напряжение, прикладываемое к диоду равно максимальному (амплитудному) напряжению половины периода, плюс напряжение на конденсаторе, поэтому обратное напряжение диода должно определяться из условия:
Обратное напряжение, прикладываемое к диоду равно максимальному (амплитудному) напряжению половины периода, плюс напряжение на конденсаторе, поэтому обратное напряжение диода должно определяться из условия:
Uобр > 1,41 x Uвх + Uo
где Uобр — обратное напряжение диода
Uвх — входное напряжение на выпрямитель
Uo — выходное напряжение с выпрямителя при наличии в цепи емкости, при отсутствии емкости Uo = 0.
При отсутствии в цепи емкости, однополупериодный выпрямитель вдвое уменьшает входное напряжение переменного тока, потому, что пропускает только одну половину периода напряжения и тока.
При выборе диода используют два условия:
1. Обратное напряжение Uобр. должно быть меньше или равно допустимому для данного диода обратному напряжению из справочных данных.
2. Ток, проходящий по диоду должен быть меньше или равен току допустимому для данного диода из справочных данных.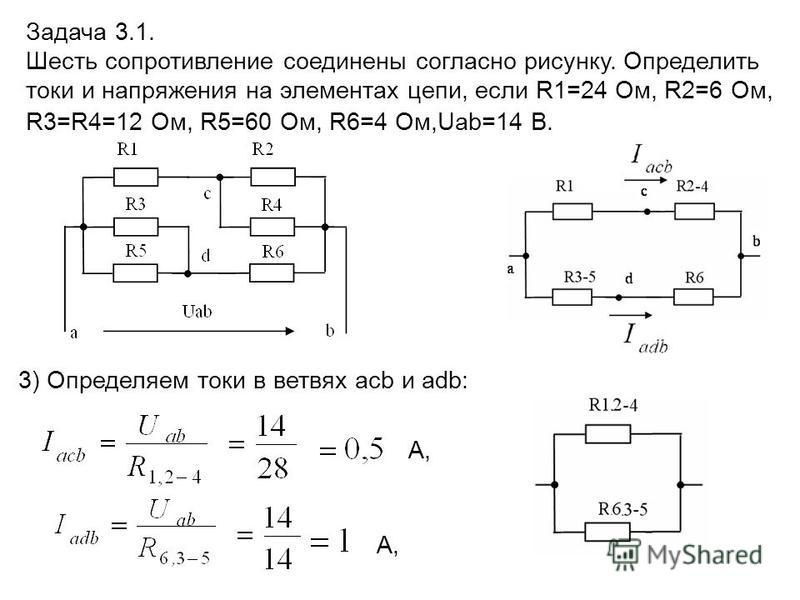
Цель работы: Закрепить навыки работы с мультиметром по измерению напряжений, закрепить знание свойств диодов. Познакомится с использованием диодов для уменьшения напряжения, свойствами однополупериодной схемы выпрямителя. Попрактиковаться в соединении деталей методом пайки.
1.Собрать схему с лампочкой на плате, предъявить преподавателю перед включением для проверки правильности монтажа. Зарисовать схему, записывать результаты и выводы в тетрадь.
2.Подключить схему к источнику питания переменного тока, измерить напряжение на лампочке ней (Uлн). Измерить напряжение на диоде (Uобр.д) и входе схемы (Uвх). Объяснить результат.
3. Подключить схему к источнику питания постоянного тока с напряжением равным напряжению лампочки, вначале «плюс к плюсу», а потом «минус к плюсу». Объяснить полученный результат.
4.Подключить схему к источнику питания переменного тока, заменив лампочку и подключив конденсатор параллельно ей, измерить напряжение на лампочке ней (Uлн). Измерить напряжение на диоде (Uобр. д) и входе схемы (Uвх). Объяснить результат.
д) и входе схемы (Uвх). Объяснить результат.
5. Подключить схему к источнику питания постоянного тока с напряжением равным напряжению лампочки «плюс к плюсу», с конденсатором. Объяснить полученный результат.
ВОПРОСЫ
1. Как называется элемент электрической схемы пропускающий ток в одном направлении?
2. Какое направление электрического тока считается «прямым», а какое «обратным»?
3. Как протекают токи в выпрямителе (показать по схеме)?
4. Какие характеристики диода тебе известны?
5. Из каких условий подбирается диод по характеристикам?
6. Какие виды электрического тока тебе известны, чем они отличаются друг от друга?
7. Где образуется падение напряжения при «прямом» полупериоде, а где при «обратном»?
8. Можно ли использовать диод в качестве делителя напряжения при переменном токе на активной нагрузке? Возможно ли это при постоянном токе?
9. Почему при подключении схемы к источнику постоянного тока лампочка при совпадении полярности горит, а при несовпадении не горит?
10. Повысится ли напряжение на лампочке, если параллельно ей подключить конденсатор большой емкости при источнике питания переменного напряжения. Если да, то почему?
Повысится ли напряжение на лампочке, если параллельно ей подключить конденсатор большой емкости при источнике питания переменного напряжения. Если да, то почему?
Используемое оборудование
1. Ампервольтомметр — один.
2. Лампочка накаливания. — одна
3. Диоды выпрямительные — 1 шт.
4. Соединительные концы.
5. Макетная плата.
6. Паяльник, припой, флюс.
7. Источник переменного тока — 1 шт.
8.Источник постоянного тока — 1 шт.
ЛАБОРАТОРНАЯ РАБОТА 18А
Диод. Выпрямление переменного тока.
Сведения из теории. Диод – элемент электрических схем имеющий свойство пропускать ток в только одном (прямом) направлении. Под «прямым» направлением тока понимается движение зарядов от «плюса» к «минусу». Это свойство диодов используется для преобразования переменного тока, меняющего как направление, так и величину, в пульсирующий, который изменяет свою величину, но течет в одном направлении. На диод, включенный последовательно с нагрузкой, из источника переменного тока подается ЭДС. Когда полярность ЭДС совпадает с направлением пропускания тока диодом, ток течет через диод в нагрузку и возвращается к источнику тока. Когда полярность ЭДС не совпадает с направлением пропускания тока диодом, ток практически не течет. Устройства, преобразующие переменный ток в пульсирующий называются выпрямителями. Время полного цикла изменения направления тока называется периодом. Время, когда ток течет только в одном направлении, называется полупериодом. Схема выпрямителя, пропускающая ток только при одном полу периоде переменного напряжения называется однополупериодной. Для уменьшения пульсаций напряжения (Uвых.) после выпрямления подключают конденсатор Сф. который сглаживает пульсацию на выходе за счет имеющегося в нем заряда.
На диод, включенный последовательно с нагрузкой, из источника переменного тока подается ЭДС. Когда полярность ЭДС совпадает с направлением пропускания тока диодом, ток течет через диод в нагрузку и возвращается к источнику тока. Когда полярность ЭДС не совпадает с направлением пропускания тока диодом, ток практически не течет. Устройства, преобразующие переменный ток в пульсирующий называются выпрямителями. Время полного цикла изменения направления тока называется периодом. Время, когда ток течет только в одном направлении, называется полупериодом. Схема выпрямителя, пропускающая ток только при одном полу периоде переменного напряжения называется однополупериодной. Для уменьшения пульсаций напряжения (Uвых.) после выпрямления подключают конденсатор Сф. который сглаживает пульсацию на выходе за счет имеющегося в нем заряда.
Конкретный тип диода имеет предел по максимально пропускаемому тока и обратному напряжению, эти характеристики указываются в его техническом паспорте или справочнике.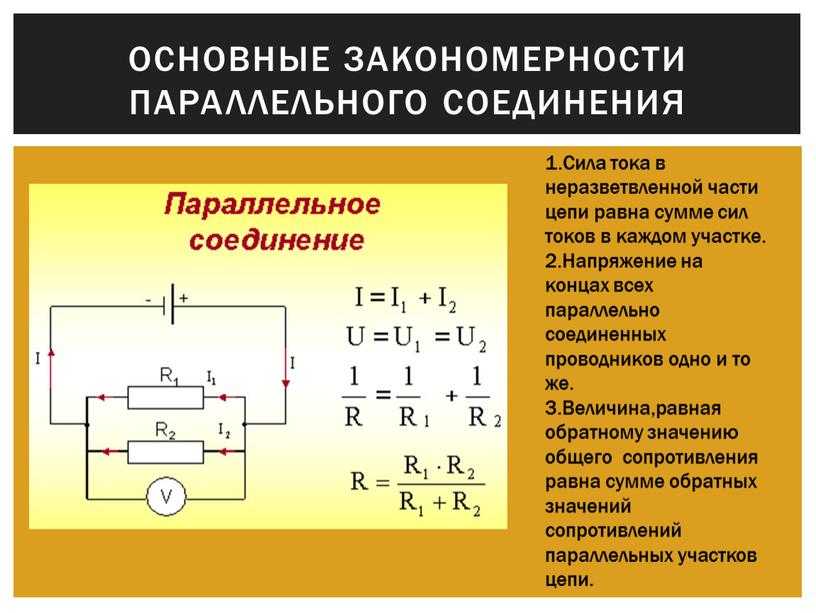
При отсутствии в цепи емкости, однополупериодный выпрямитель вдвое уменьшает входное напряжение переменного тока, потому, что пропускает только одну половину периода напряжения и тока.
При выборе диода используют два условия:
1. Обратное напряжение Uобр. должно быть меньше или равно допустимому для данного диода обратному напряжению из справочных данных.
2. Ток, проходящий по диоду должен быть меньше или равен току допустимому для данного диода из справочных данных
Цель работы: Закрепить навыки работы с мультиметром по измерению напряжений, закрепить знание свойств диодов. Познакомится с использованием диодов для уменьшения напряжения, свойствами однополупериодной схемы выпрямителя. Попрактиковаться в соединении деталей методом пайки.
1.Собрать схему для исследования свойств, предъявить преподавателю перед включением для проверки правильности монтажа. Зарисовать схему, записывать результаты и выводы в тетрадь.
2. Подключить схему к источнику питания постоянного тока с напряжением равным напряжению лампочки, вариант 1, а потом вариант 2. Объяснить полученный результат
3.Подключить схему к источнику питания переменного тока, измерить напряжение на лампочках 1 и 2, а затем напряжение на источнике питания. Объяснить результат.
4.Подключить схему к источнику питания переменного тока, подключив конденсатор параллельно Лн1 или Лн2, измерить напряжение на лампочке. Объяснить результат.
ВОПРОСЫ
1. Как называется элемент электрической схемы пропускающий ток в одном направлении?
2. Какое направление электрического тока считается «прямым», а какое «обратным»?
3. Как протекают токи в выпрямителе (показать по схеме)?
4. Какие характеристики диода тебе известны?
5. Из каких условий подбирается диод по характеристикам?
6. Какие виды электрического тока тебе известны, чем они отличаются друг от друга?
7. Почему при подключении схемы к источнику постоянного тока лампочка при совпадении полярности горит, а при несовпадении не горит?
8. Повысится ли напряжение на лампочке, если параллельно ей подключить конденсатор большой емкости при источнике питания переменного напряжения. Если да, то почему?
Повысится ли напряжение на лампочке, если параллельно ей подключить конденсатор большой емкости при источнике питания переменного напряжения. Если да, то почему?
Используемое оборудование
1. Ампервольтомметр — один.
2. Лампочка накаливания. — одна
3. Диоды выпрямительные — 1 шт.
4. Соединительные концы.
5. Макетная плата.
6. Паяльник, припой, флюс.
7. Источник переменного тока — 1 шт.
8.Источник постоянного тока — 1 шт.
ЛАБОРАТОРНАЯ РАБОТА 19
Использование электромагнитного и электрического полей. » Мигалка на реле»
Сведения из теории. В схеме используется свойство диода пропускать ток в одном направлении для преобразования переменного тока в пульсирующий, который изменяет свою величину, но течет в одном направлении. В реле используются также свойство катушки с проводом возбуждать (индуцировать) в пространстве магнитное поле при прохождении по проводу электрического тока.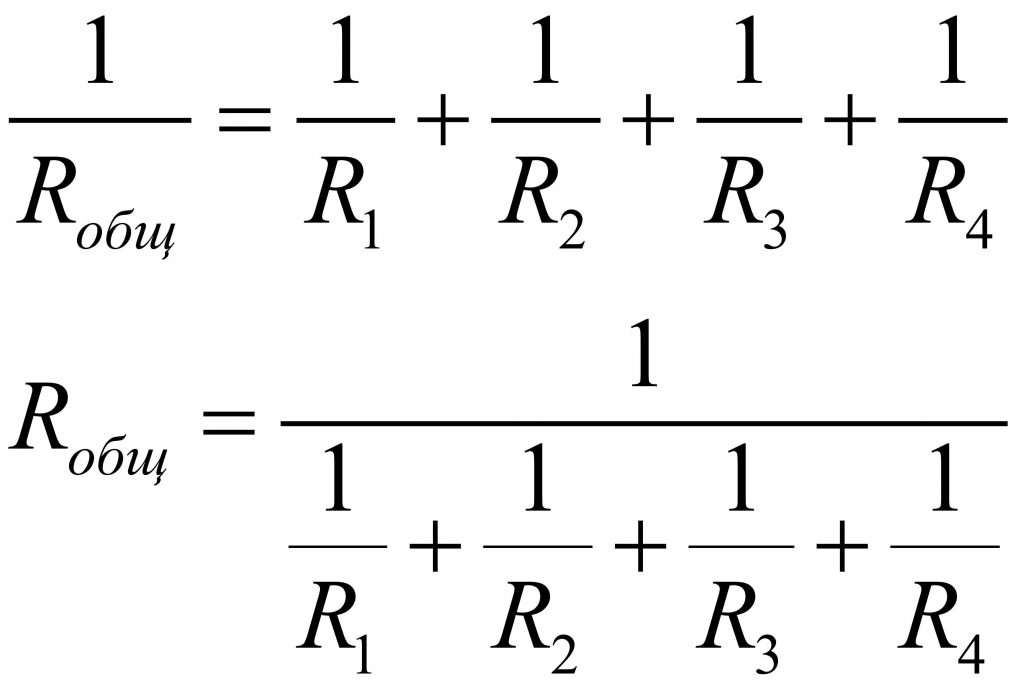 Магнитное поле – это среда, через которую осуществляется взаимодействие между магнитами. Такая катушка называется электромагнитом или индуктивностью. Свойство электромагнита — притягивать к себе магнитные материалы. В реле электромагнит притягивает к себе железную пластинку (якорь), которая в свою очередь, механически соединена с электрическими контактами, включающими и выключающими электрическую цепь. Реле – устройство, включающее или переключающее электрическую цепь под действием электрического тока. Конденсатор используется для накопления электрического заряда, необходимого для поддержания тока в катушке реле при отключении от источника от источника питания. Время заряда, или разряда конденсатора зависит только от его емкости и сопротивления цепи, по которой течет ток. Меняя емкость или сопротивление цепи можно изменять время заряда-разряда, а следовательно частоту включения и выключения реле.
Магнитное поле – это среда, через которую осуществляется взаимодействие между магнитами. Такая катушка называется электромагнитом или индуктивностью. Свойство электромагнита — притягивать к себе магнитные материалы. В реле электромагнит притягивает к себе железную пластинку (якорь), которая в свою очередь, механически соединена с электрическими контактами, включающими и выключающими электрическую цепь. Реле – устройство, включающее или переключающее электрическую цепь под действием электрического тока. Конденсатор используется для накопления электрического заряда, необходимого для поддержания тока в катушке реле при отключении от источника от источника питания. Время заряда, или разряда конденсатора зависит только от его емкости и сопротивления цепи, по которой течет ток. Меняя емкость или сопротивление цепи можно изменять время заряда-разряда, а следовательно частоту включения и выключения реле. .
.
Работа схемы: На вход устройства поступает переменная ЭДС. Диод, пропуская ток в одном направлении, одновременно заряжает конденсатор и подпитывает электромагнитную катушку реле. В начальный момент времени, ток заряжает конденсатор, постепенно повышая на нем и электромагнитной катушке реле напряжение. Балластный резистор R ограничивает ток заряда. После заряда конденсатора до напряжения срабатывания реле, электромагнит реле притянет якорь, и реле переключит свои контакты. Контакты реле бывают трех видов — нормально-замкнутые, нормально-разомкнутые и переключающие. В данной схеме используется переключающий контакт, но можно совместно использовать нормально-замкнутые и нормально-разомкнутые. Переключающий контакт, при срабатывании реле, замкнет цепь питания лампочки, и разорвет цепь питания электромагнита и конденсатора. Катушка реле питается энергией запасенной в конденсаторе, до тех пор, пока конденсатор не разрядится на до напряжения отпускания якоря реле. После разряда, катушка «отпустит» якорь, и он, с помощью соединенных с ним контактов, подключит цепь питания электромагнита реле и конденсатора, а также отключит лампочку. Далее процесс будет циклически повторяться до отключения устройства от источника питания.
После разряда, катушка «отпустит» якорь, и он, с помощью соединенных с ним контактов, подключит цепь питания электромагнита реле и конденсатора, а также отключит лампочку. Далее процесс будет циклически повторяться до отключения устройства от источника питания.
Цель работы: Познакомиться с практическим использованием свойств диода для выпрямления переменного тока, использованием электромагнитных реле и конденсаторов в электронных схемах. Усвоить понятия индуктивность, якорь, реле, наименования контактов реле, принцип его работы, характеристики. Попрактиковаться в соединении деталей методом пайки, получить навык в работе с авометром.
Порядок работы:
1. Измерить сопротивление обмотки катушки электромагнита реле Rр.
2. Подключить реле к блоку питания и определить напряжение (Uср) срабатывания реле, или узнать его из паспортных данных.
3. Определить ток срабатывания реле по закону Ома. Iср. = Uср./ Rр.
4. Определить напряжение используемого источника питания.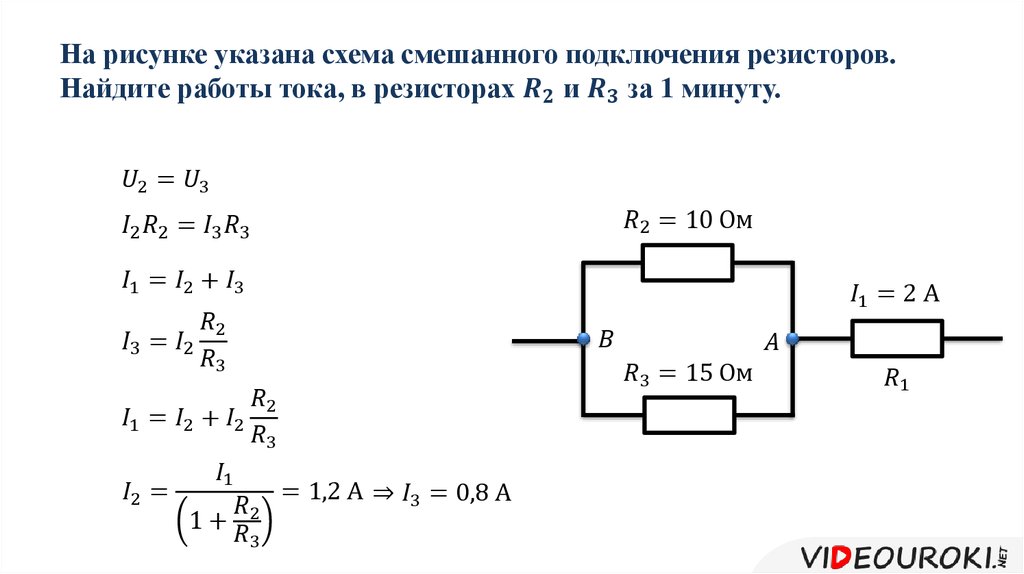
5. Подобрать сопротивление балластного резистора исходя из условия :
Rб = Uпит./5*Iср , рассчитать его мощность Р = Uпит. * I ср.
6. Подобрать ближайшее по номиналу балластное сопротивление.
7.Подобрать диод исходя из условия Uобр. д > Uпит + Uср. Iд > 2*Iср.
8. Подобрать конденсатор исходя из условия Uc > Uср , С = Rб./ t где t — время заряда конденсатора (переключения реле).
9.Собрать схему на плате, предъявить преподавателю перед включением для проверки правильности монтажа.
10.Подключить схему к источнику питания, пронаблюдать за ее работой. Измерить напряжение вольтметром на входе (Uпит.), Лн1 и С. Объяснить результаты измерений .
ВОПРОСЫ
1. Какой выпрямитель используется в схеме одно или двухполупериодный?
2. Что называется электрическим полем?
3. В каком элементе схемы используются свойство электрических зарядов притягиваться через электрическое поле? Какие заряды притягиваются, одноименные или разноименные?
4. Что такое постоянная времени заряда, как она используется в работе схемы?
Что такое постоянная времени заряда, как она используется в работе схемы?
5. Через сопротивление, каких элементов схемы происходит заряд и разряд конденсатора?
6. Что называется магнитным полем?
7. Как используется в работе схемы электромагнит? При каком токе притяжение электромагнита сильнее, а когда слабее?
8. Что такое электромагнитное реле?
9. Какие основные характеристики диода, конденсатора и реле тебе известны?
10. Когда время заряда конденсатора будет равно времени его разряда?
11. Найди и покажи на схеме электрические узлы.
12. Какие виды контактов реле (по назначению) тебе известны?
13. По каким основным параметрам подбирается диод?
Используемое оборудование
1. Ампервольтомметр — один.
2. Реле электромагнитное переключающим контактом — одно.
3. Лампочка накаливания. — одна
4. Диоды выпрямительные — 1 шт.
5. Конденсаторы полярные — 1 шт.
6. Соединительные концы.
7. Макетная плата.
8. Паяльник, припой, флюс.
ЛАБОРАТОРНАЯ РАБОТА 20
Общее сопротивление цепи — правила, формулы и примеры вычисления
Величина, благодаря которой проводник способен не пропускать через себя ток или ограничивать его прохождение, называется электрическим сопротивлением цепи. Общее её значение для замкнутой схемы определяется с помощью формул. Их вид зависит от типа соединения элементов. Кроме того, если известны определённые характеристики, найти параметр можно, используя закон Ома для участка цепи.
Содержание
- Общие сведения
- Последовательное подключение
- Параллельное соединение
- Решение задач
Общие сведения
Прохождение электрического тока через проводник зависит от его проводимости. Это параметр пропорционален силе тока. Другими словами, он определяет способность вещества пропускать через себя электричество без потерь. Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Связь между фундаментальными параметрами электротока экспериментально установил Симон Ом. Он выяснил, что сила тока в замкнутой цепи пропорциональна разности потенциалов (напряжению) и обратно пропорциональна сопротивлению: I = U / R. Так, если R равно нулю, то сила тока будет бесконечной.
Способность веществ препятствовать прохождению электротока используется при построении электрических цепей. Так, радиоэлемент, который называется резистором, установленный в определённом месте электроцепи, позволяет получить на нагрузке нужное значение напряжения или тока. Радиодеталь представляет собой двухполюсник, который имеет установленное значение сопротивления или может изменять его.
Реальная замкнутая электрическая цепь состоит из множества активных и пассивных радиоэлементов.
Каждый из них обладает каким-то значением сопротивления. В этом случае говорят о внутреннем сопротивлении прибора.
Расчёт выходных характеристик цепи, а именно величин тока и напряжения, требует знания общего сопротивления всей замкнутой цепочки. Иными словами, все элементы, начиная от источника питания и заканчивая нагрузкой, заменяются эквивалентными резисторами. Для цепи сначала считают общее значение сопротивления, а затем вычисляют нужные характеристики. Относительно источника тока, нагрузки и других элементов каждый резистор может быть подключён:
- последовательно;
- параллельно.
Вид подключения влияет на общее сопротивление. Формула для его нахождения может быть довольно громоздкой из-за смешанного соединения, поэтому чаще расчёт ведётся в несколько этапов, на каждом из которых выполняется объединение одного или нескольких элементов.
Последовательное подключение
Для удобства при изображении разветвлённой электрической цепи все сопротивления чертят в виде прямоугольников, которые являются резисторами. У любого такого элемента можно выделить два вывода. Один является началом, а другой — концом. С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.
У любого такого элемента можно выделить два вывода. Один является началом, а другой — концом. С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.
Любой проводник обладает электрическим сопротивлением. Целью преобразования является замена чередующейся последовательности одним резистором. При этом по своим электрическим свойствам он должен не отличаться от всей цепочки. Простыми словами это можно пояснить так: если взять два чёрных ящика, у которых есть по паре выводов, причём один будет содержать всю электроцепь, а другой быть её эквивалентом, то определить, в каком из них находится схема, а где эквивалент, будет невозможно.
При последовательном соединении происходят следующие явления. Пусть имеется прямая цепочка, содержащая n резисторов: R1 + R2 + … +Rn. Сила тока — это величина, которая равняется заряду, протекающему за единицу времени. Можно представить, что в первом резисторе значение электротока будет больше, чем во втором. В результате возникнет «пробка», и скорость движения зарядов замедлится.
Можно представить, что в первом резисторе значение электротока будет больше, чем во втором. В результате возникнет «пробка», и скорость движения зарядов замедлится.
В точке соединения элементов произойдёт накопление электронов, что приведёт в ней к росту напряжения. Соответственно, сила тока на первом резисторе будет уменьшаться, а на втором, наоборот, увеличиваться. Это приведёт к выравниванию количества проходящих через резисторы зарядов, поэтому сила тока практически за мгновение во всей последовательной цепи станет одинаковой.
Напряжение — это работа, выполняемая по переносу заряда. По закону сохранения энергии общее её значение равняется их сумме на различных этапах. Общую разность потенциалов можно будет определить, сложив напряжения на каждом элементе. Такой вид подключения описывается следующими выражениями:
- I = I 1 = I 2 = … = In;
- U = U1 + U2 + … +Un.
Эти равенства являются фундаментальными для нахождения параметров при повторении резисторов в цепи.
Используя закон Ома, можно найти, чему будет равняться сопротивление цепи. Формула для его нахождения будет выглядеть так: Rпос = R 1 + R 2 +… + Rn.
Параллельное соединение
По распространённости такой вид соединения чаще встречается, чем последовательное подключение. При нём проводники соединены так, что начала всех резисторов сводятся в одну точку электрической цепи, а концы — в другую. Для того чтобы заменить разветвлённое подключение одним эквивалентным элементом, нужно знать, как правильно рассчитать ток и напряжение.
Пусть имеется цепь, состоящая из R1 + R2 + … +Rn параллельно включённых радиоэлементов. На неё подаётся напряжение U. На вход схемы поступает ток с силой I. Используя закон сохранения зарядов, можно выполнить следующие рассуждения: ток втекает в узел, к которому подсоединены начала всех резисторов, затем он растекается по их выводам.
В результате через первую ветвь потечёт ток I1, вторую — I2, в энную — In. Поскольку заряд не может пропасть, то какое его количество втекло в узел, такое же должно разойтись по всем ветвям для одного и того же момента времени. Значит, сумма токов на всех выводах будет равняться поступающему на них значению.
Поскольку заряд не может пропасть, то какое его количество втекло в узел, такое же должно разойтись по всем ветвям для одного и того же момента времени. Значит, сумма токов на всех выводах будет равняться поступающему на них значению.
Электростатическое поле является потенциальным, то есть работа по перемещению заряда из одной точки в другую не зависит от траектории, по которой перемещается носитель. Следовательно, при переносе одного кулона по любой ветви нужно будет совершить одинаковую работу. Из приведённых рассуждений следует, что при параллельном соединении формулы, с помощью которых можно рассчитать характеристики электрической цепи, будут следующими:
- I = I1 + I2 + … +In;
- U1 = U2 = … = Un.
Таким образом, вычисление эквивалентного сопротивления, которым можно будет заменить всю цепь в соответствии с законом Ома, выполняется по формуле: 1 / R пар = 1 / R 1 + 1 / R 2 + … + 1 / Rn. Для одинаковых проводников при вычислении сопротивления можно использовать приведённую формулу.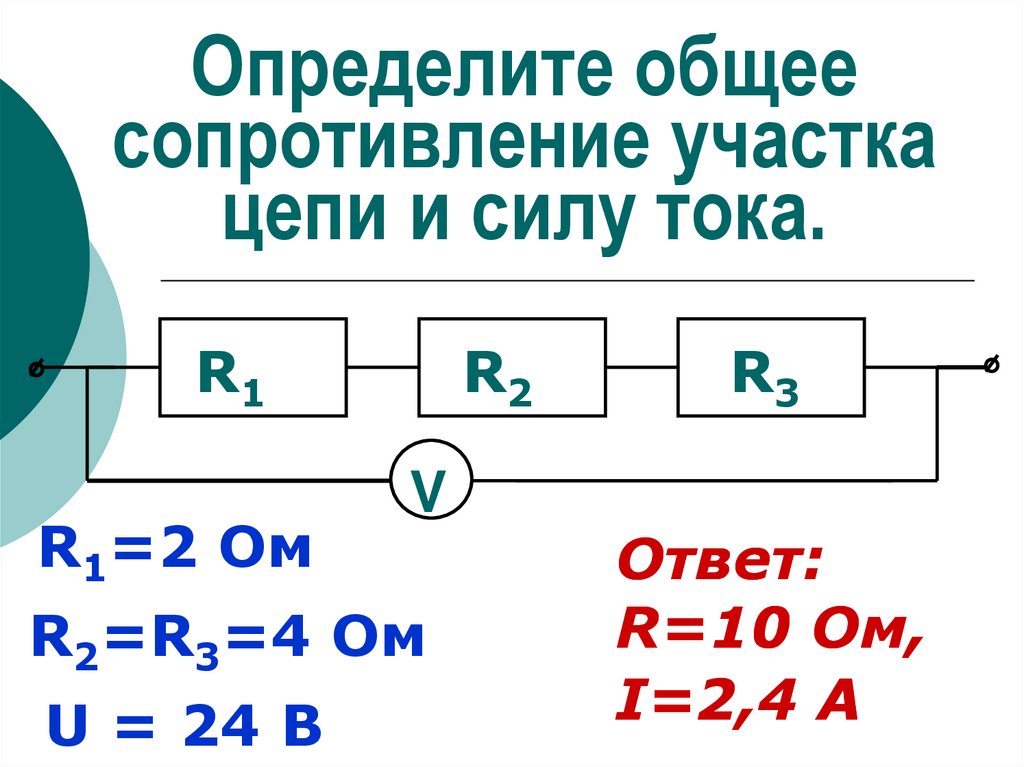 Это позволяет в некоторых случаях упростить расчёт.
Это позволяет в некоторых случаях упростить расчёт.
Согласно правилу сложения дробей c одинаковым знаменателем можно записать равенство: 1 / R1 + 1 / R2 + … + 1 / Rn = N / R1. Отсюда следует, что Rпар = R1 / N, где N равно числу резисторов. По аналогии можно посчитать общее сопротивление по упрощённой формуле для двух элементов: (1 / R1) + (1 / R2) = (R 2 + R 1) / R 1 * R 2. Это довольно удобные формулы для практического применения.
Решение задач
Для вычисления сопротивления любого смешанного соединения нужно запомнить всего две формулы — выражения для нахождения величины при последовательном и параллельном подключении. Поочерёдно комбинируя их применение, сложную схему можно заменить одним сопротивлением. Но не всегда приходится применять формулы. Есть задания, в которых неизвестную величину можно вычислить в уме.
Например, пусть имеется параллельное подключение из четырёх резисторов. Сопротивления проводников равняются 10 Ом, 12 Ом, 15 Ом, 20 Ом. Нужно образовать из них резистор, не изменяющий характеристики электрической цепи. Чтобы выполнить расчёт в уме, следует каждый элемент представить в виде комбинации из 60-омных резисторов. Тогда к первому нужно будет добавить шесть, ко второму — пять, к третьему — четыре, к четвёртому — три. Общее количество резисторов получится 18. Значит, Rобщ = 60 / 18 = 10 / 3 = 3,3 Ом.
Сопротивления проводников равняются 10 Ом, 12 Ом, 15 Ом, 20 Ом. Нужно образовать из них резистор, не изменяющий характеристики электрической цепи. Чтобы выполнить расчёт в уме, следует каждый элемент представить в виде комбинации из 60-омных резисторов. Тогда к первому нужно будет добавить шесть, ко второму — пять, к третьему — четыре, к четвёртому — три. Общее количество резисторов получится 18. Значит, Rобщ = 60 / 18 = 10 / 3 = 3,3 Ом.
Из типовых задач, в которых необходимо найти сопротивление цепи, предлагающихся в школе на уроках физики, можно привести следующие:
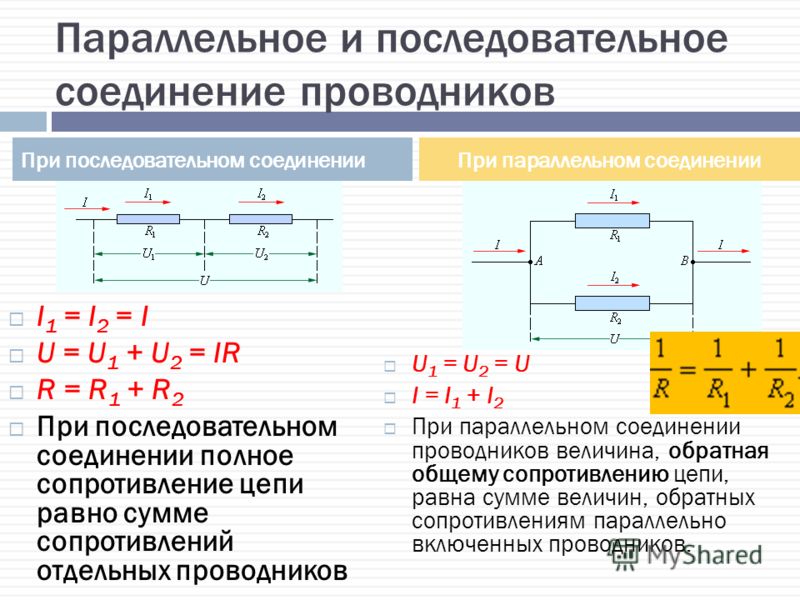
Каково будет сопротивление каждого из резисторов, если при их последовательном соединении ток равен 3A, а при параллельном — 16A. Напряжение в сети составляет 120 В. При первом способе соединения Iпосл = U / (R1 + R2), при втором Iпар = U / Rпар = U * (R1 + R2) / R1 * R2. Из первой формулы следует, что R1 + R2 = U / Iпос. Тогда: I пар = U 2 / Iпос * R 1 * R 2 → R 1 * R 2 = U 2 / I пар * I пос. Используя теорему Виета, можно составить квадратное уравнение. После его решения искомые величины будут равны: R 1 = 30 Ом, R 2 = 10 Ом.
Следует отметить, что приборы для измерения тока, напряжения и даже ёмкости используют особенности вычисления сопротивления цепи. Так, вольтметр имеет бесконечно большой внутренний импеданс, что позволяет подключать его параллельно к измеряемым точкам без внесения изменения в протекающий сигнал.
Амперметр же, наоборот, характеризуется пренебрежимо малой величиной внутреннего сопротивления, поэтому и подключают его в разрыв линии, на которой выполняют измерения.
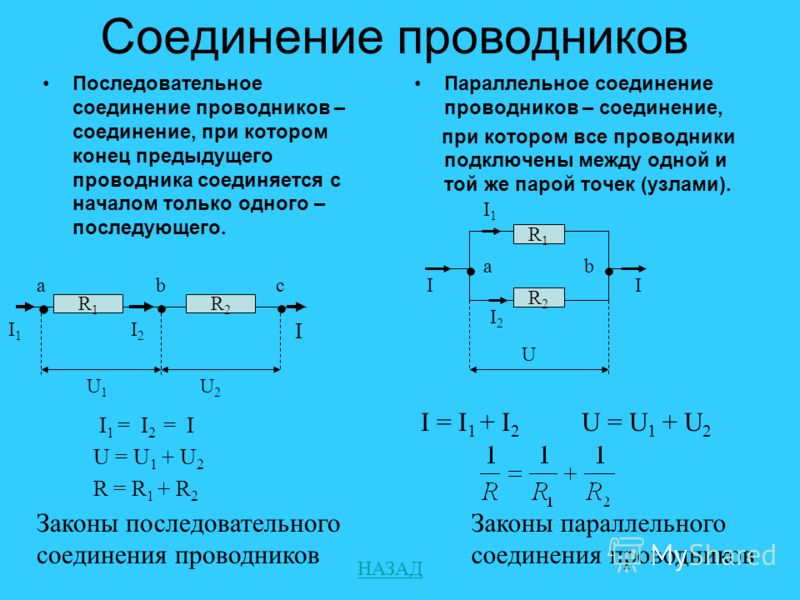
Предыдущая
ФизикаУдельное электрическое сопротивление — формула, обозначение и физический смысл
Следующая
ФизикаДоклад на тему: «Траектория, путь и перемещение» — пример реферата
Метод расчета сопротивления последовательного и параллельного сопротивления
Примечание: Расчет сопротивления Формула 1 / R общей = 1 / R1 + 1 / R2,
Сопротивление может образовывать сложные схемы сопротивления вместе с неограниченным количеством серий количества и в линии комбинационного
В предыдущем уроке мы узнали, как соединить отдельные резисторы вместе, чтобы сформировать ряд резисторов сетей или параллельной резистивной сеть Мы используем закон Ома, чтобы найти напряжение различных токов и каждую комбинацию резисторов.
Но что, если мы хотим, чтобы соединить различные резисторы параллельно и последовательно? В той же схеме, более сложная сеть сопротивления в сочетании, как мы рассчитать сопротивление цепи, ток и напряжение этих резисторов.
Резистор цепи в сочетании с серией и параллельной сети сопротивления обычно называют как комбинация резистора или гибридной схемы резистора. Метод расчета цепи эквивалентное сопротивление такое же, как метод какой-либо одной последовательной или параллельной схеме, и мы надеемся, что теперь мы знаем, что резистор последовательно выполняет один и тот же ток, а параллельные резисторы имеют точно такие же напряжения.
Например, суммарный ток (I T), полученный от источника питания 12В рассчитывается в следующей схеме.
На первый взгляд, кажется, что задача сложная, но если присмотреться, то можно увидеть два резистора, R 2 и R 3 фактически соединены в «серии», так что мы можем добавить их. Сформировать такое же сопротивление вместе , как мы сделать в серии сопротивления учебника. Таким образом, синтетическое сопротивление комбинации:
R 2 + R 3 =8Ω+4Ω=12Ω
Таким образом, мы можем заменить резисторы R 2 и R 3 на вершине значения сопротивления 12Ω
>>
Таким образом, наша схема сейчас находится в «Parallel» есть резистор R A, резистор R 4. Используя сопротивление в программе параллельно, мы можем использовать следующие два параллельные формулы сопротивления, чтобы уменьшить эту параллельную комбинацию с одной эквивалентной величиной сопротивления R (комбинация).
Используя сопротивление в программе параллельно, мы можем использовать следующие два параллельные формулы сопротивления, чтобы уменьшить эту параллельную комбинацию с одной эквивалентной величиной сопротивления R (комбинация).
Результат Схема сопротивления теперь выглядит следующим образом:
Мы можем увидеть оставшиеся два сопротивления, R 1 и R (рассортировать) соединены друг с другом в «серии», и они могут сложить (в серии), так, что точки А и В, следовательно, с учетом:
R = R comb + R 1 =6Ω+6Ω= 12Ω
Одно сопротивление 12Ω может быть использовано для замены оригинальных четыре резисторов, соединенных вместе в исходной схеме.
Теперь использовать закон Ома, значение схемы схемы просто вычисляется следующим образом:
Таким образом, любая сложная схема сопротивления может быть упрощена только один эквивалентным резистор, состоящего заменой всех резисторов, соединенных между собой последовательно или параллельно, используя описанные выше шаги.
Мы можем найти две ветви течения, я 1, и я 2, как показано на рисунке.
V (r 1) = I * R 1 = 1 * 6 = 6 вольт
В (га) = v = r4 (12 — v r 1) = 6 вольт
следовательно:
I 1 = 6В ÷ р а = 6 ÷ 12 = 0.5a или 500mA
I 2 = 6V ÷ R 4 = 6 ÷ 12 = 0.5a или 500mA
Так как значения сопротивления двух ветвей являются одинаковыми в 12 Ом, I 1 и I 2, также равны 0.5A (или 500 мА). Таким образом, общий ток питания I T: 0,5 + 0,5 = 1,0 ампер, как описано выше.
После этих изменений, использовать сложные комбинации сопротивления и сети сопротивления рисовать или перерисовывать новые схемы иногда легче, потому что это помогает математике визуальной помощи. Затем продолжить замену последовательно или параллельно, пока эквивалентное сопротивление R экв не найдено. Давайте попробуем еще более сложную комбинацию сопротивления цепи.
Последовательное сопротивление и параллельное сопротивление NO 2
Чтобы найти эквивалентный резистор, R EQ используется для следующей комбинации резистора цепи.
Опять же, на первый взгляд, кажется, имеют сложную задачу, но в то же самое, это просто сочетание последовательного и параллельного сопротивления, соединенных вместе. С правой стороны, можно использовать упрощенные формулы двух параллельных резисторов, мы можем найти эквивалентное сопротивление / суб> сочетание R 8 и R 10 <последовательных и R A.
R A и R 7, таким образом, таким образом, общее сопротивление R A + R 7 = 4 + 8 = 12Ω показано, как показано на рисунке.
Значение 12Ω сопротивления теперь параллельно R 6, которая может быть вычислена как R B.
R B и R 5, таким образом, общее сопротивление R B + R 5 = 4 + 4 = 8Ω, как показано на рисунке.
Значение сопротивления 8Ω теперь параллельно с R 4 и может быть вычислена как R C, как показано на рисунке.
R C в серии с R 3, так что общее сопротивление R C + R 3 = 8Ω показано на рисунке.
Значения сопротивления 8 Ом теперь параллельно с R 2, мы можем вычислить R D, как:
R D и R 1 соединены последовательно, так что общее сопротивление R D + R 1 = 4 + 6 = 10 Ом, показан на рисунке.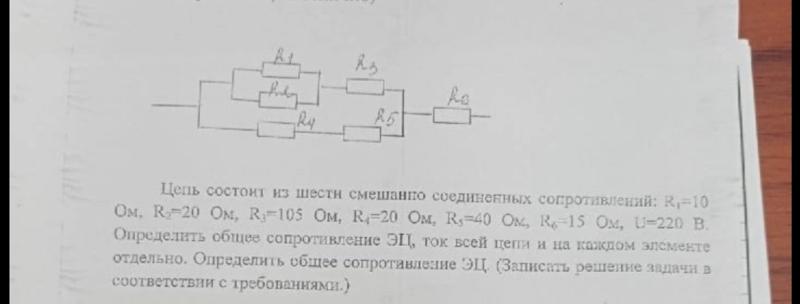
Затем сложная комбинация Резистор сеть включает в себя отдельный резистор, соединенный последовательно, параллельно комбинации, может быть заменен эквивалентным сопротивлением (R EQ) 10 Ω.
Когда какое-нибудь сочетания сопротивляться, или с помощью схемы, состоящей из сопротивления серии и параллельных ветвей, первый шаг, который мы должны быть приняты, чтобы определить простые ряды и параллельные ветви сопротивления, и заменить их с эквивалентным сопротивлением.
Этот шаг позволит уменьшить сложность схемы, чтобы помочь нам преобразовать сложную комбинацию резистор цепь в один эквивалентный резистор, помните, что последовательная цепь представляет собой делитель напряжения, а параллельная цепь тока делитель.
Однако вычисление более сложный Т-площадка аттенюатора и резистивный мост сети не может быть упрощено, чтобы использовать эквивалентное сопротивление простых параллельно или последовательно схему, и различные методы необходимы. Эти более сложные схемы необходимо использовать Кирхгофа действующий закон и закон напряжения Кирхгофа для ее решения, который будет обсуждаться в другом учебнике.
В следующем уроке о сопротивлении, мы увидим разницу потенциалов (напряжение) двух точек (включая резисторы).
21.1: Резисторы последовательно и параллельно
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2688
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Нарисовать цепь с параллельными и последовательными резисторами.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Сравните способ расчета общего сопротивления резисторов, включенных последовательно и параллельно.
- Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.

- Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.
Большинство цепей имеют более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке \(\PageIndex{1}\). Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
Рисунок \(\PageIndex{1}\): (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.Резисторы серии
Когда резисторы серии относятся к серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то \(R_{1}\) на рисунке \(\PageIndex{1}\)(a) может быть сопротивлением стержня отвертки, \ (R_{2}\) сопротивление его ручки, \(R_{3}\) сопротивление тела человека и \(R_{4}\) сопротивление ее обуви.
На рисунке \(\PageIndex {2}\) показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.)
Рисунок \(\PageIndex{2}\): Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа). Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения , в каждом резисторе на рисунке \(\PageIndex {2}\).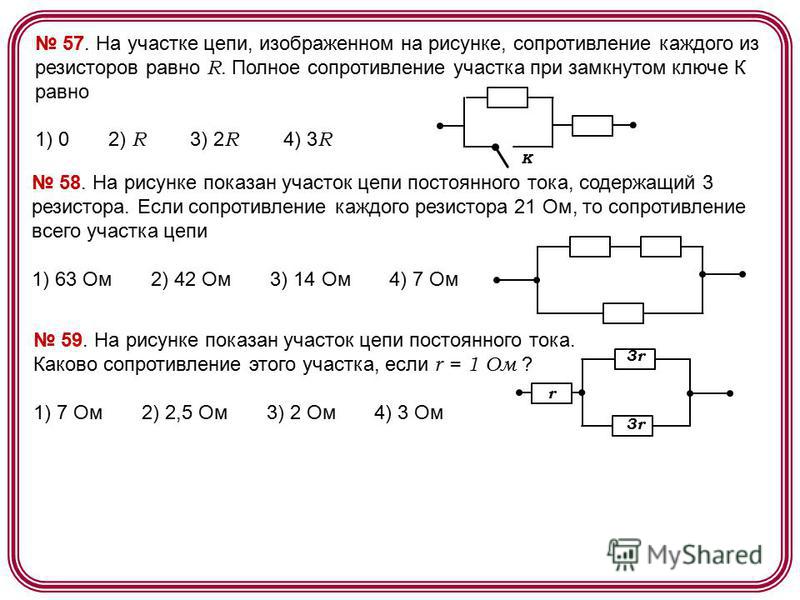
В соответствии с законом Ома падение напряжения \(V\) на резисторе при протекании через него тока рассчитывается по уравнению \(V=IR\), где \(I\) равно току в амперах (А) и \(R\) сопротивление в омах\((\Омега)\). Другой способ думать об этом состоит в том, что \(V\) — это напряжение, необходимое для того, чтобы ток \(I\) протекал через сопротивление \(R\).
Таким образом, падение напряжения на \(R_{1}\) равно \(V_{1}=IR_{1}\), на \(V_{2}=IR_{2}\) и на \ (R_{3}\) равно \(V_{3}=IR_{3}\). Сумма этих напряжений равна выходному напряжению источника; то есть
\[V=V_{1}+V_{2}+V_{3}.\]
Это уравнение основано на законах сохранения энергии и заряда. Электрическая потенциальная энергия может быть описана уравнением \(\mathrm{PE}=qV\), где \(q\) — электрический заряд, а \(V\) — напряжение. Таким образом, энергия, подаваемая источником, равна \(qV), а энергия, рассеиваемая резисторами, равна
\[qV_{1}+qV_{2}+qV_{3}.\]
СОЕДИНЕНИЯ: ЗАКОНЫ СОХРАНЕНИЯ
Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе.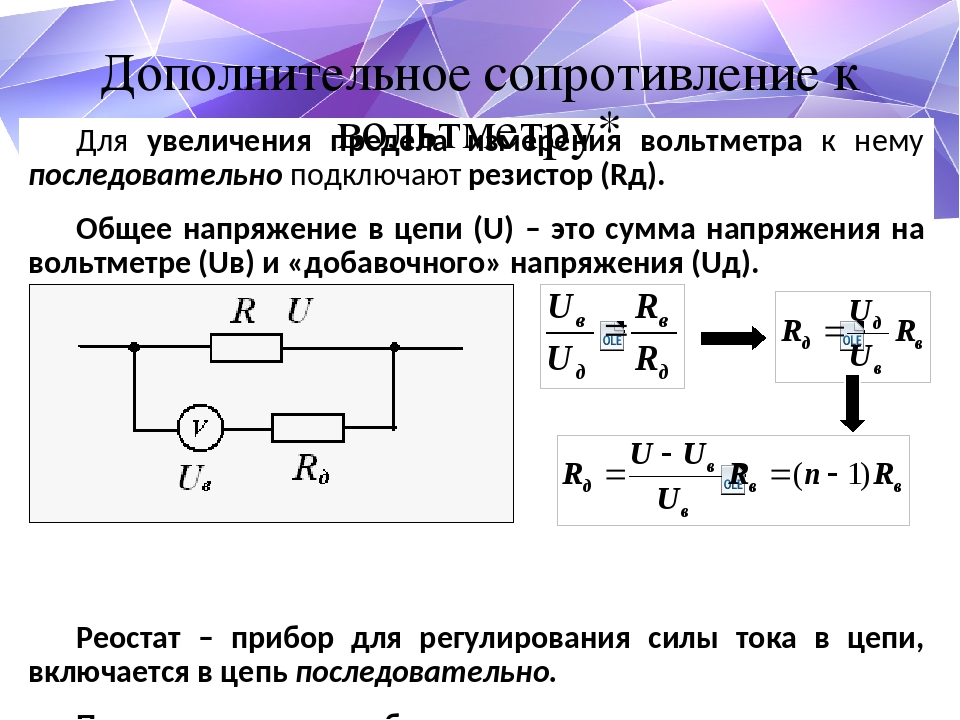 Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого места назначения энергии. Таким образом, \(qV=qV_{1}+qV_{2}+qV_{3}\). Заряд \(q\) отменяется, что дает \(V=V_{1}+V_{2}+V_{3}\), как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
\[V=IR_{1}+IR_{2}+IR_{3}=I(R_{1}+R_{2}+R_{3}). \]
Обратите внимание, что для эквивалентного последовательного сопротивления \(R_{\mathrm{S}}\) мы имеем
\[V=IR _{\mathrm{S}}.\]
Это означает, что общее или эквивалентное последовательное сопротивление \(R_{\mathrm{S}}\) трех резисторов равно \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}\).
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, полное сопротивление \(R_{\mathrm{S}}\) последовательного соединения равно
\[R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots ,\]
как предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример \(\PageIndex{1}\): расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке \(\PageIndex{2}\) равно \(12,0\mathrm{V}\), а сопротивления равны \(R_{1}=1,00\Омега\), \(R_{2}=6,00\Омега\) и \(R_{3}= 13.0\Омега\). а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую следующим уравнением:
\[R_{\mathrm{S}}=R_{1}+R_ {2}+R_{3}\]
\[=1,00\Омега + 6,00\Омега + 13,0\Омега\]
\[=20,0 \Омега.\]
Стратегия и решение для (b)
Ток определяется по закону Ома \(V=IR\). Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
\[I=\dfrac{V}{R_{\mathrm{S}}}=\dfrac{12,0\Omega}{20,0\Omega}=0,600 \mathrm{A}.\]
Стратегия и решение для (c)
Падение напряжения или \(IR\) на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
\[V_{1}=IR_{1}=(0,600\mathrm{A})(1,0\Omega)=0,600\mathrm{V}.\]
Аналогично,
\[V_{2}=IR_{2}=(0,600\mathrm{A})(6,0\Omega)=3,60\mathrm{V}\]
и
\[V_{3}= IR_{3}=(0,600\mathrm{A})(13,0\Omega)=7,80\mathrm{V}.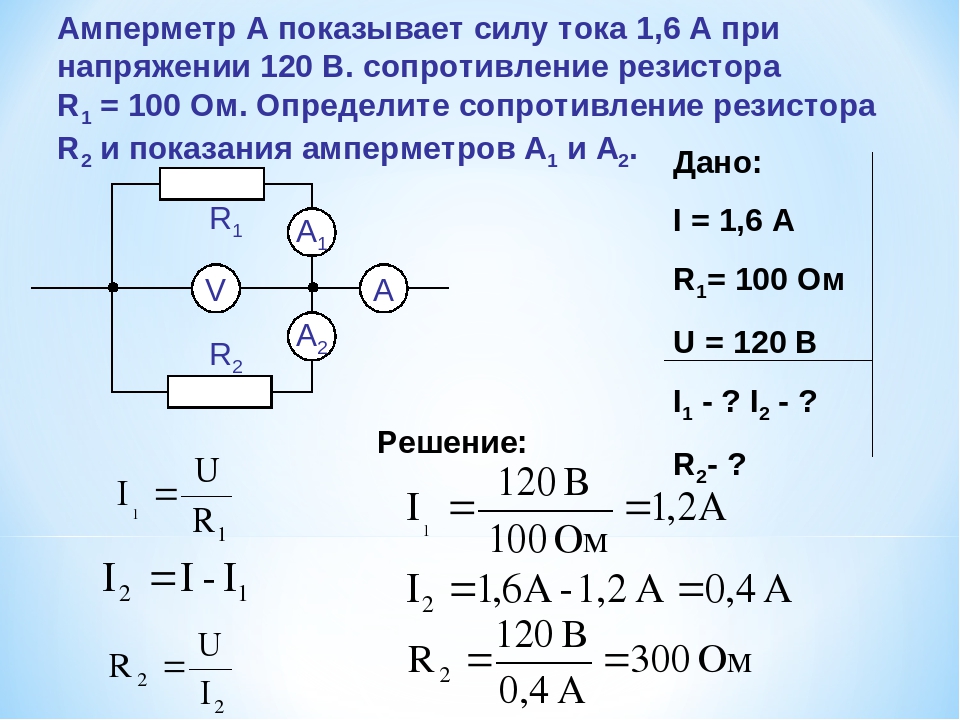 \]
\]
Обсуждение для (c)
Три капли \(IR\) добавляются к \(12.0\mathrm{V}\), как и предполагалось:
\[V_{1}+V_{2}+V_ {3}=(0,600+3,60+7,80)\mathrm{V}=12,0\mathrm{V}.\]
Стратегия и решение для (d)
Самый простой способ расчета мощности в ваттах (Вт) рассеивается на резисторе в цепи постоянного тока, чтобы использовать закон Джоуля , \(P=IV\), где \(P\) — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток. Подставив закон Ома \(V=IR\) в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как 9{2}}{R}\), где \(V\) — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать \(P=IV\), где \(V\) — напряжение источника. Это дает
\[P=(0,600\mathrm{A})(12,0\mathrm{V})=7,20 \mathrm{W}. \]
\]
Обсуждение для (e)
Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. то есть
\[P_{1}+P_{2}+P_{3}=(0,360 +2,16+4,68)\mathrm{W}=7,20\mathrm{W}.\]
Мощность – это энергия в единицу времени ( Вт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ В СЕРИИ
- Последовательные сопротивления добавляют: \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots\)
- Один и тот же ток протекает через каждый резистор последовательно.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
Резисторы, включенные параллельно
На рисунке \(\PageIndex{3}\) показаны резисторы, соединенные параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рисунок \(\PageIndex{3}\)(b).)
Рисунок \(\PageIndex{3}\): (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление. (b) Установка электроснабжения в доме. (кредит: Dmitry G, Wikimedia Commons) Чтобы найти выражение для эквивалентного параллельного сопротивления \(R_{\mathrm{p}}\), давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением.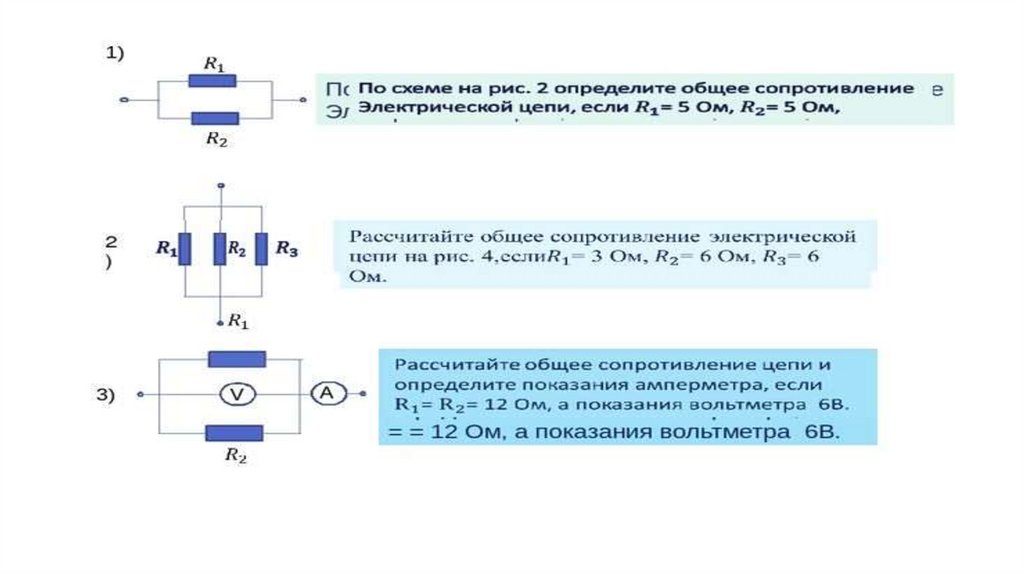 Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны \(I_{1}=\dfrac{V}{R_{1}}\), \(I_{2}=\dfrac{ V}{R_{2}}\) и \(I_{3}=\dfrac{V}{R_{3}}\). Сохранение заряда подразумевает, что полный ток \(I\), производимый источником, представляет собой сумму этих токов:
Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны \(I_{1}=\dfrac{V}{R_{1}}\), \(I_{2}=\dfrac{ V}{R_{2}}\) и \(I_{3}=\dfrac{V}{R_{3}}\). Сохранение заряда подразумевает, что полный ток \(I\), производимый источником, представляет собой сумму этих токов:
\[I=I_{1}+I_{2}+I_{3}.\]
Подстановка выражений для отдельных токов дает
\[I=\dfrac{V}{R_{1}} +\dfrac{V}{R_{2}}+\dfrac{V}{R_{3}}=V(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}} +\dfrac{1}{R_{3}}).\]
Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает
\[I=\dfrac{V}{R_{\mathrm{p}}}= V(\dfrac{1}{R_{\mathrm{p}}}).\]
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление \(R_{\mathrm{p}}\) параллельного соединения связано с отдельными сопротивлениями как
\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{ R_{3}}+\dots\]
Это соотношение дает общее сопротивление \(R_{\mathrm{p}}\), которое меньше наименьшего из отдельных сопротивлений.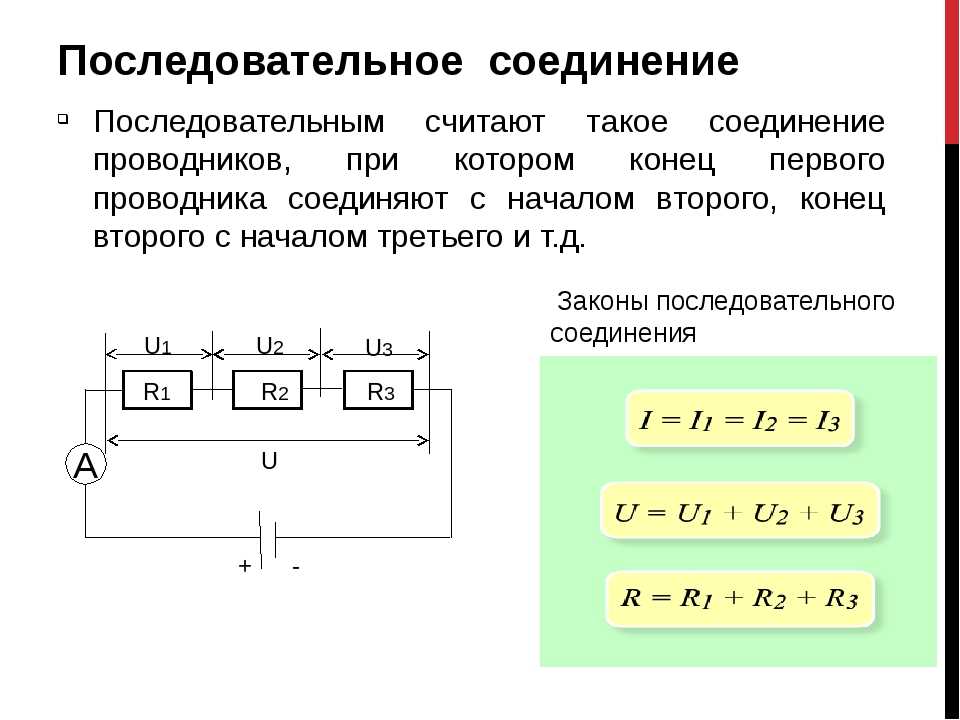 (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
(Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
Пример \(\PageIndex{2}\): расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рисунке \(\PageIndex{3}\) будут такими же, как при рассмотренном ранее последовательном соединении: \(V=12.0\mathrm{V},\: R_ {1}=1,00\Омега\: R_{2}=6,00\Омега\) и \(R_{3}=13,0\Омега\). а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения.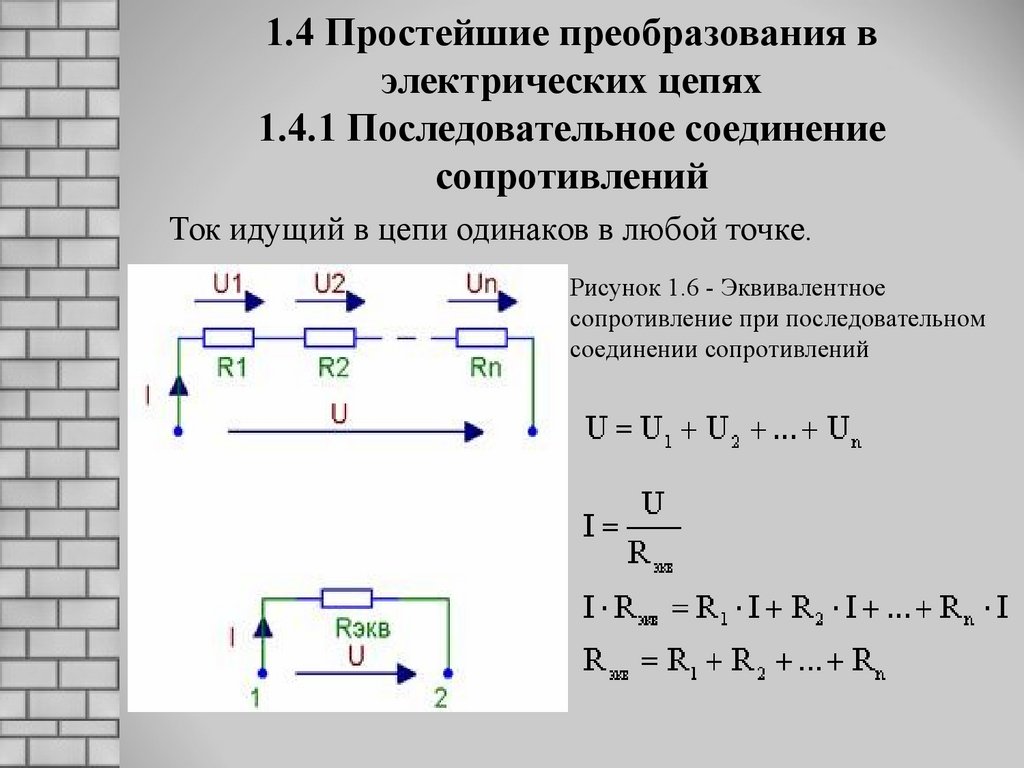 Ввод известных значений дает
Ввод известных значений дает
\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac {1}{R_{3}}=\dfrac{1}{1.00\Omega}+\dfrac{1}{6.00\Omega}+\dfrac{1}{13.0\Omega}.\]
Таким образом,
\[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1,00}{\Omega}+\dfrac{0,1667}{\Omega}+\dfrac{0,07692}{\Omega}=\ dfrac{1.2436}{\Omega}.\]
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ показан с дополнительной цифрой.)
Мы должны инвертировать это, чтобы найти полное сопротивление \(R_{\mathrm{p}}\). Это дает
\[R_{\mathrm{p}}=\dfrac{1}{1,2436}\Omega=0,8041\Omega.\]
Общее сопротивление с правильным количеством значащих цифр равно \(R_{\ матрм{р}}=0,804\Омега\).
Обсуждение для (a)
\(R_{\mathrm{p}}\), как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив \(R_{\mathrm{p}}\) вместо полного сопротивления. Это дает
Это дает
\[I=\dfrac{V}{R_{\mathrm{p}}}=\dfrac{12,0\mathrm{V}}{0,8041 \Omega}=14,92 \mathrm{A}.\]
Обсуждение для (б)
Ток \(i\) для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
\[I_{1}=\dfrac{V}{R_{1}}=\dfrac{12.0\mathrm{V}}{1.00\Omega}=12.0\mathrm{A}.\]
Аналогично,
\[I_{2}=\dfrac{V}{R_{2}}=\dfrac{12.0\mathrm{V}}{6.00\Omega}=2.00\mathrm{A}\]
и
\[I_{3}=\dfrac{V}{R_{3}}=\dfrac{12.0\mathrm{V}}{13.0\Omega}=0,92\mathrm{A}.\]
9{2}}{13.0\Omega}=11.1\mathrm{W}.\]Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же напряжению. источник.
источник.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбор \(P=IV\) и ввод общего тока дает
\[P=IV=(14,92\mathrm{A})(12,0\mathrm{V})=179\mathrm{W}.\]
Обсуждение для (д)
Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:
\[P_{1}+P_{2}+P_{3}=144\mathrm{W}+24.0\mathrm{W}+11.1\mathrm {W}=179\mathrm{W}.\]
Это согласуется с законом сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ, ПОДКЛЮЧЕННЫХ ПАРАЛЛЕЛЬНО
- Параллельное сопротивление находится из \(\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1 }{R_{2}}+\dfrac{1}{R_{3}}+\dots\), и оно меньше любого отдельного сопротивления в комбинации.
- К каждому параллельно подключенному резистору приложено одинаковое полное напряжение источника.
 (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
(Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.) - Параллельные резисторы не получают суммарный ток каждый; они его делят.
Комбинации последовательного и параллельного соединения
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединений можно привести к одному эквивалентному сопротивлению с помощью метода, показанного на рисунке \(\PageIndex{4}\). Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.
Процесс скорее трудоемкий, чем сложный.
Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рисунке \(\PageIndex{5}\), также является наиболее поучительной, поскольку она встречается во многих приложениях. Например, \(R_{1}\) может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, которые включены параллельно. \(R_{2}\) и \(R_{3}\) могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример \(\PageIndex{3}\): расчет сопротивления, падения \(IR\), тока и рассеиваемой мощности: объединение последовательных и параллельных цепей
На рисунке \(\PageIndex{5}\) показаны резисторы из предыдущие два примера подключены по-другому — комбинация последовательного и параллельного. Мы можем рассматривать \(R_1\) как сопротивление проводов, ведущих к \(R_2\) и \(R_3\). а) Найдите полное сопротивление. (б) Что такое падение \(IR\) в \(R_1\)? (c) Найдите ток от \(I_2\) до \(R_2\). (d) Какая мощность рассеивается \(R_2\)?
Мы можем рассматривать \(R_1\) как сопротивление проводов, ведущих к \(R_2\) и \(R_3\). а) Найдите полное сопротивление. (б) Что такое падение \(IR\) в \(R_1\)? (c) Найдите ток от \(I_2\) до \(R_2\). (d) Какая мощность рассеивается \(R_2\)?
Стратегия и решение для (a)
Чтобы найти общее сопротивление, заметим, что \(R_2\) и \(R_3\) параллельны, а их комбинация \(R_p\) последовательно с \(R_1 \). Таким образом, полное (эквивалентное) сопротивление этой комбинации равно \[R_{tot} = R_1 + R_2.\]
Сначала находим \(R_p\), используя уравнение для параллельных резисторов и вводя известные значения: \[\ dfrac{1}{R_p} = \dfrac{1}{R_2} + \dfrac{1}{6,00 \, \Omega} + \dfrac{1}{13,0 \, \Omega} = \dfrac{0,2436}{\ Омега}.\]
Инвертирование дает \[R_p = \dfrac{1}{0,2436}\Omega = 4,11 \, \Omega. \] Таким образом, общее сопротивление равно \[R_{tot} = R_1 + R_p = 1,00 \Omega + 4,11 \Omega. = 5,11 \, \Омега.\]
\] Таким образом, общее сопротивление равно \[R_{tot} = R_1 + R_p = 1,00 \Omega + 4,11 \Omega. = 5,11 \, \Омега.\]
Обсуждение для (а)
Суммарное сопротивление этой комбинации является промежуточным между чисто последовательными и чисто параллельными значениями (\(20,0 \, \Омега\) и \(0,804 \, \Omega\) соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение \(IR\) в \(R_1\), заметим, что полный ток \(I\) протекает через \(R_1\). Таким образом, его \(IR\) падение равно \[V_1 = IR_1.\]. Мы должны найти \(I\), прежде чем мы сможем вычислить \(V_1\). Полный ток \(I\) находится по закону Ома для цепи. То есть \[I = \dfrac{V}{R_{tot}} = \dfrac{12,0 \, V}{5,11 \, \Omega} = 2,35 \, A.\]. Вводя это в выражение выше, мы получить \[V_1 = IR_1 = (2,35 \, A)(1,00 \, \Omega) = 2,35 \, V.\]
Обсуждение для (б)
Напряжение на \(R_2\) и \(R_3\) меньше общего напряжения на величину \(V_1\).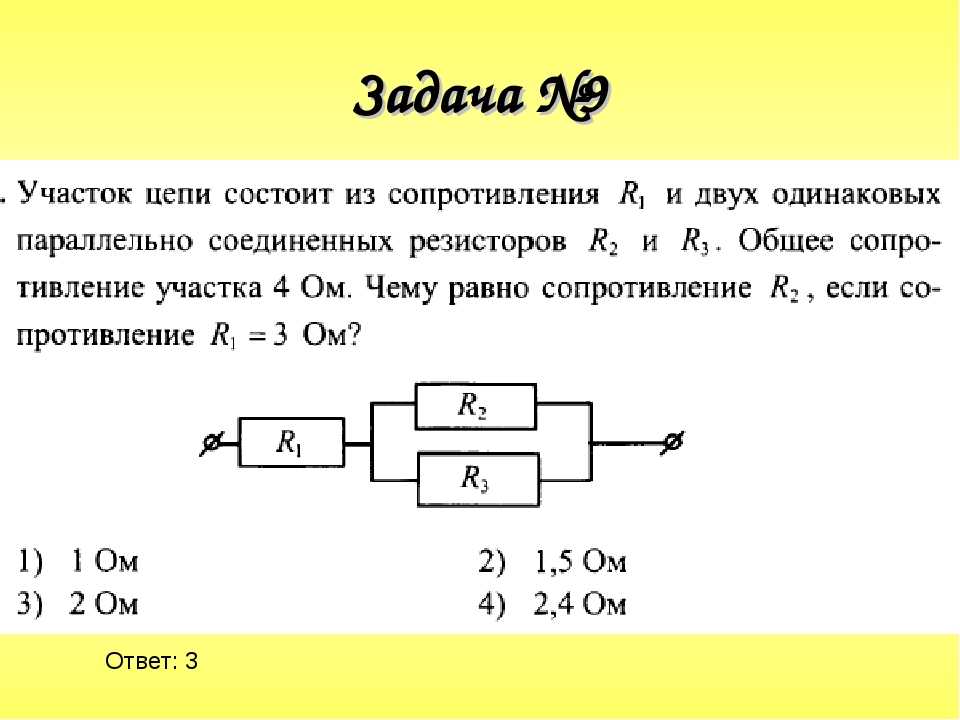 Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных \(R_2\) и \(R_3\).
Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных \(R_2\) и \(R_3\).
Стратегия и решение для (c)
Чтобы найти ток через \(R_2\), мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение \(V_p\), потому что оно применяется к параллельной комбинации резисторов. Напряжение, подаваемое как на \(R_2\), так и на \(R_3\), уменьшается на величину \(V_1\), поэтому оно равно \[V_p = V — V_1 = 12,0 \, V — 2,35 \, V = 9.65 \, В.\] Теперь ток \(I_2\) через сопротивление \(R_2\) находится по закону Ома: \[I_2 = \dfrac{V_p}{R_2} = \dfrac{9,65 \, V} {6,00 \, \Омега} = 1,61 \, А.\]
Обсуждение для (c)
Ток меньше 2,00 А, которые протекали через \(R_2\), когда он был подключен параллельно к батарея в предыдущем примере с параллельной схемой.
Стратегия и решение для (d)
Мощность, рассеиваемая \(R_2\), определяется выражением \[P_2 = (I_2)^2 R_2 = (1 61 \, A)^2(6,00 \, \ омега) = 15,5\, Вт.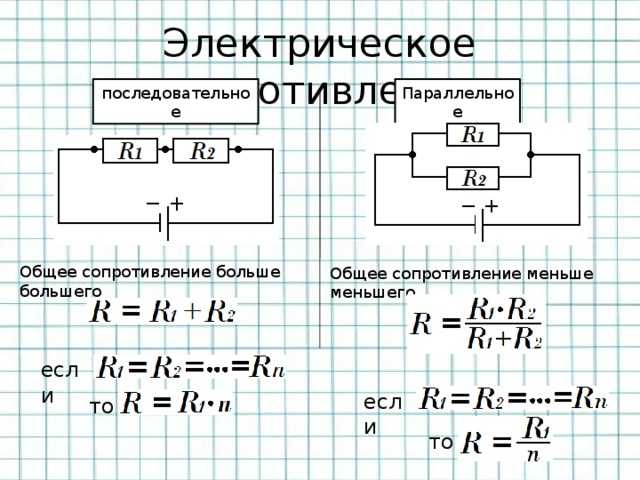 \]
\]
Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Практические выводы
Одним из следствий последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение \(IR\) в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в таких сильноточных ситуациях, показано на рисунке \(\PageIndex{6}\). Устройство, представленное \(R_3\), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение \(IR\) в проводах, представленных \(R_1\), уменьшая напряжение на лампочке (которое равно \(R_2\)), которая затем заметно тускнеет.
Этот увеличенный ток вызывает большее падение \(IR\) в проводах, представленных \(R_1\), уменьшая напряжение на лампочке (которое равно \(R_2\)), которая затем заметно тускнеет.
Упражнение \(\PageIndex{1}\)
Можно ли любую произвольную комбинацию резисторов разбить на последовательные и параллельные комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательных и параллельных соединений.
- Ответить
-
Нет, существует множество способов соединения резисторов, не являющихся комбинациями последовательного и параллельного соединения, включая петли и соединения. В таких случаях правила Кирхгофа, которые будут представлены в Правилах Кирхгофа, позволят вам проанализировать схему.

Стратегии решения проблем для последовательных и параллельных резисторов
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
- Определите, что именно нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах.
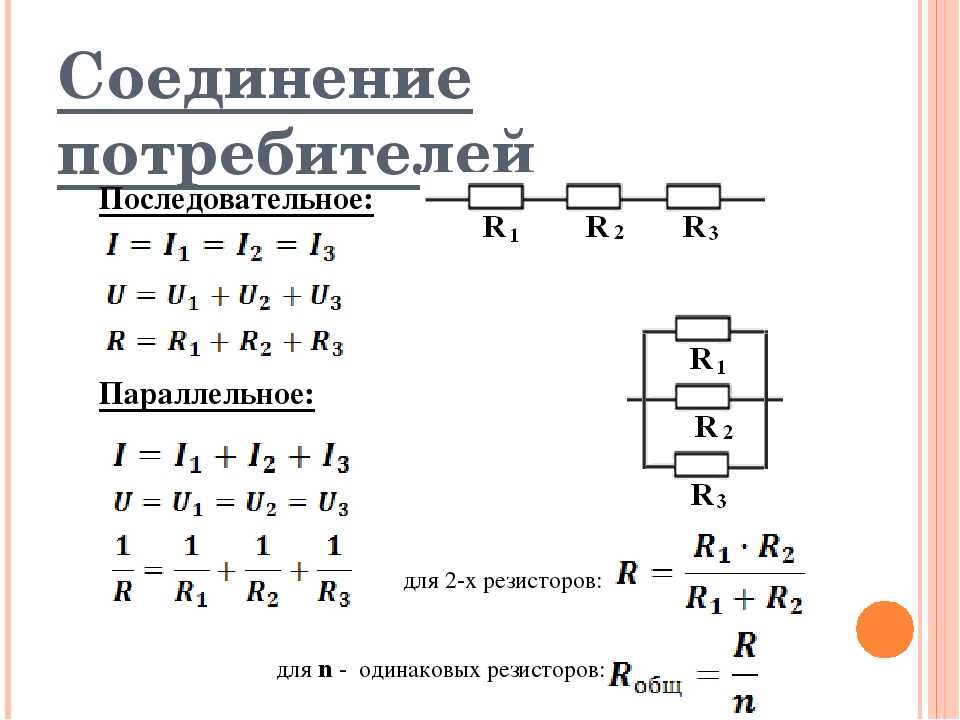 Специальное примечание: при нахождении \(R_p\) необходимо соблюдать осторожность.
Специальное примечание: при нахождении \(R_p\) необходимо соблюдать осторожность. - Проверить разумность и последовательность ответов. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
Резюме
- Общее сопротивление электрической цепи с последовательно соединенными резисторами представляет собой сумму отдельных сопротивлений: \(R_s = R_1 + R_2 + R_3 + ….\)
- Через каждый резистор в последовательной цепи протекает одинаковый ток.
- Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различны, и их общая сумма составляет входную мощность источника питания.
- Общее сопротивление электрической цепи с параллельно соединенными резисторами меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле: \(\dfrac{1}{R_p} = \dfrac{1}{R_1 } +\dfrac{1}{R_2} + \dfrac{1}{R_3} + .
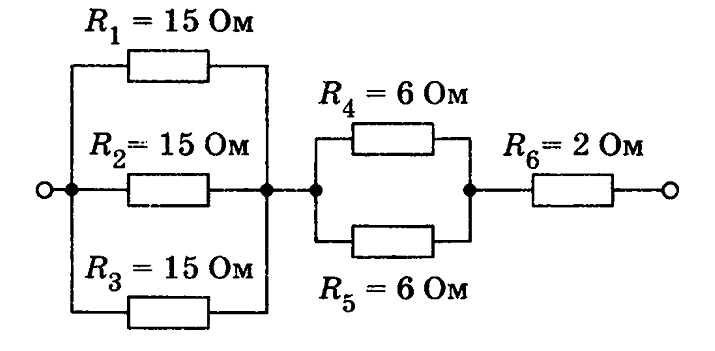 …\)
…\) - К каждому резистору в параллельной цепи приложено одинаковое полное напряжение источника.
- Ток, протекающий через каждый резистор в параллельной цепи, различен в зависимости от сопротивления.
- Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного сопротивления, его можно свести к единому эквивалентному сопротивлению, обозначив различные его части как последовательные или параллельные, сведя каждую к эквиваленту и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление .
Глоссарий
- Серия
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор
- Компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
- сопротивление
- , вызывающий потерю электроэнергии в цепи
- Закон Ома
- соотношение между током, напряжением и сопротивлением в электрической цепи: V=IR
- напряжение
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например батареей
- падение напряжения
- потеря электроэнергии при протекании тока через резистор, провод или другой компонент
- текущий
- поток заряда через электрическую цепь, проходящий через заданную точку измерения
- Закон Джоуля
- Соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое как: \(P_e = IV\)
- параллельный
- соединение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
-
- Теги
-
- Текущий
- Закон Джоуля
- Закон Ома
- параллель
- сопротивление
- Резистор
- Резисторы параллельно Резисторы
- серии
- серия
- падение напряжения
Как рассчитать полное сопротивление в последовательно-параллельной цепи?
Если ваша цепь снова и снова отключается, вам необходимо рассчитать сопротивление. Если вы часто видите короткие замыкания в своем доме, вы должны рассчитать сопротивление.
Если вы часто видите короткие замыкания в своем доме, вы должны рассчитать сопротивление.
С помощью этого расчета вы можете узнать, как устройство или материал уменьшают поток электрического тока. Определите состояние вашей цепи или компонента, рассчитав общее сопротивление! Но как рассчитать полное сопротивление в последовательно-параллельной цепи! У нас есть самые простые решения!
Пошаговый расчет сопротивления в последовательной цепи
Ну, определить последовательную цепь проще всего. Если вы видите цепь с одной единственной петлей, это последовательная цепь. В отличие от параллельных или комбинированных цепей, эта не имеет ответвлений или ответвляющихся частей.
В этой цепи есть резисторы, но они не расположены здесь и там. В последовательной цепи резисторы цепи расположены в линию. Рассчитав сопротивление, можно узнать о состоянии цепи. Если он слабый, посмотрите, как предотвратить срабатывание автоматического выключателя!
Метод 1: добавление сопротивлений
Как мы уже говорили, последовательные схемы проще, чем другие схемы. Итак, как рассчитать полное сопротивление в последовательной цепи? Просто, сложите их все! Все, что вам нужно сделать, это добавить все сопротивления вашей цепи. Здесь через каждый резистор проходит один и тот же ток. И так, сумма всех сопротивлений будет общим сопротивлением последовательной цепи.
Итак, как рассчитать полное сопротивление в последовательной цепи? Просто, сложите их все! Все, что вам нужно сделать, это добавить все сопротивления вашей цепи. Здесь через каждый резистор проходит один и тот же ток. И так, сумма всех сопротивлений будет общим сопротивлением последовательной цепи.
Давайте облегчим вам задачу. Предположим, у вас есть последовательная цепь с тремя резисторами соответственно 2 Ом, 5 Ом и 7 Ом. И так, общее сопротивление будет суммой всех этих сопротивлений.
Сопротивление R= 2+5+7= 14 Ом
Метод 2: Суммарный ток и напряжение
Есть вероятность, что вы не знаете сопротивления отдельных резисторов. Если вы думаете, что без этого не сможете узнать сопротивление, вы ошибаетесь! Вы также можете работать с полным током и полным напряжением и узнать сопротивление!
Шаг 1. Подсчитайте общий ток
Последовательные цепи имеют одинаковую величину тока во всех точках. Итак, узнать об общем токе здесь несложно. Все, что вам нужно, это знать ток в любой точке цепи, и вы готовы! Вы можете просто использовать его как общий ток в своей формуле, чтобы узнать сопротивление. Как только вы его нашли, переходите к напряжению.
Все, что вам нужно, это знать ток в любой точке цепи, и вы готовы! Вы можете просто использовать его как общий ток в своей формуле, чтобы узнать сопротивление. Как только вы его нашли, переходите к напряжению.
Шаг 2: Подсчитайте общее напряжение
Хотя общий ток последовательной цепи равен току в любой точке, напряжение нельзя измерить таким же образом. В случае напряжения напряжение на компоненте не равно общему напряжению.
Итак, когда дело доходит до подсчета общего напряжения, вы можете полагаться на напряжение питания аккумулятора. Напряжение батареи или источника питания будет таким же, как общее напряжение последовательной цепи. После того, как вы это узнали, приготовьтесь к подсчету сопротивления.
Шаг 3. Выполните вычисления
Теперь, когда вы нашли и общий ток, и полное напряжение, приготовьтесь к работе с формулой. Поскольку вы не знаете сопротивление отдельных резисторов, вы можете просто воспользоваться законом Ома и найти сопротивление R.
V = IR
R = V/I
Вот все, что вам нужно. заключается в том, чтобы поставить значение полного тока вместо I и полного напряжения вместо V. Если последовательная цепь имеет
Общий ток питания последовательной цепи I = 8 ампер
Питание от батареи V = 12 Вольт
Согласно формуле-
R = V/I = 12/8 = 1,5 Ом
Таким образом, полное сопротивление здесь равно 1,5 Ом.
Поэтапный расчет сопротивления в параллельной цепи
Прежде всего, вы должны пройти через параллельную цепь и понять ее. Есть несколько путей параллельной цепи.
Особенность параллельного контура в том, что все множественные пути контура в конце концов снова соединяются в одной точке. И электричество будет течь по всем ветвям вашей параллельной цепи. Есть две точки, где параллельная цепь может иметь резистор.
- Иногда цепь может иметь резисторы на основном пути.
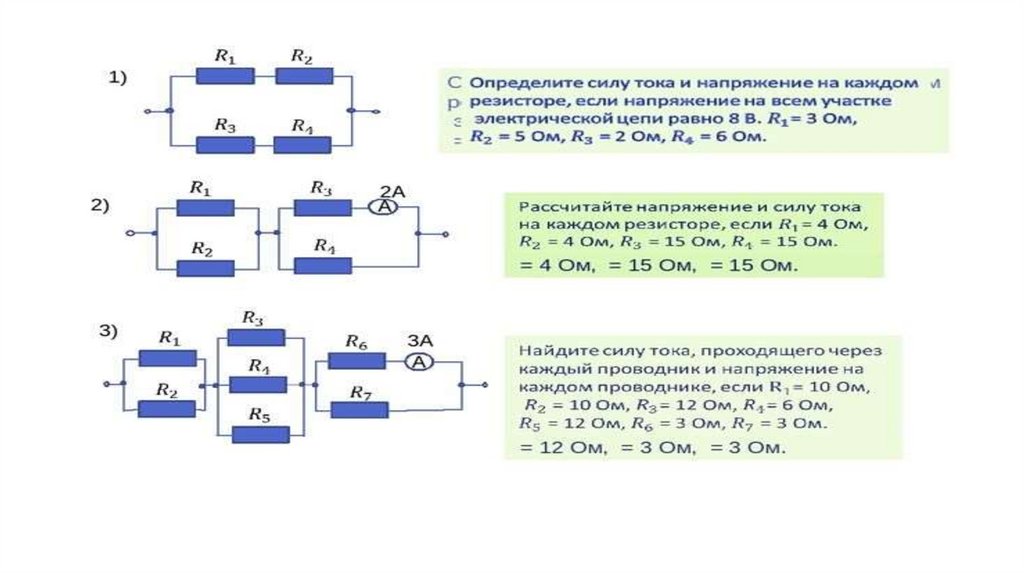 Эта область находится сразу после или перед разветвленной областью схемы.
Эта область находится сразу после или перед разветвленной областью схемы. - С другой стороны, можно добавить два или более резистора. Эти резисторы добавляются в одну ветвь.
Для двух типов резисторов существуют разные методы расчета общего сопротивления цепи.
Метод 1. Добавление отдельных сопротивлений
Ваша первая задача здесь — рассчитать сопротивление каждой ветви. Как мы уже говорили вам, будет более одного резистора, каждый резистор будет замедлять прохождение электричества. Однако каждый из них будет работать только с одной веткой.
А если посчитать объем замедления одной ветви или одного резистора, то это не слишком сильно повлияет на общее сопротивление цепи. Для подсчета общего сопротивления каждой ветви существует формула. Сначала проверьте формулу.
1/R T = 1/R 1 + 1/R 2 + 1/R 3 +….+ 1/R n 7 R
2 9 В этой формуле — это сопротивление первой марки схемы. Здесь 2, 3, 4 и n относятся к сопротивлению всех ветвей. Например, R 1 и R 2 — сопротивление первой и второй ветви, R 3 — сопротивление третьей марки и, наконец, R n — сопротивление последней марки. Неважно, сколько там ветвей, все, что вам нужно сделать, это сосчитать их и установить там формулу.
Здесь 2, 3, 4 и n относятся к сопротивлению всех ветвей. Например, R 1 и R 2 — сопротивление первой и второй ветви, R 3 — сопротивление третьей марки и, наконец, R n — сопротивление последней марки. Неважно, сколько там ветвей, все, что вам нужно сделать, это сосчитать их и установить там формулу.
Здесь мы дадим вам пример параллельной цепи. Мы берем параллельную схему с тремя ответвлениями. The resistances of the branches respectively are-
R 1 = 10 Ω or Ohm
R 2 = 2 Ω or Ohm
R 3 = 1 Ω or Ohm
Подставим все эти числа в нашу формулу и узнаем сопротивление.
1/R T = 1/R 1 + 1/R 2 + 1/R 3 +….+ 1/R n
1/R T = 1/10 + 1/2 9031 1/r T = 0,1 + 0,5 + 1 1/R T = 1,6 R T = 1/1,6 925 T = 1/1,6
2 90,620 ОР 2 900 природа r r r r r r ro = 1/1,6 r .
Метод 2: Суммарный ток и напряжение
Иногда вы можете не знать индивидуальное сопротивление. Ну, не волнуйтесь; у нас есть способы помочь вам! В этом случае лучшее, что вы можете сделать, это пойти на общий ток. И тогда, вы должны посчитать общее напряжение.
Шаг 1: Подсчитайте напряжение
Поскольку мы имеем дело с параллельной схемой, это упрощает нам одну задачу. Если известно общее напряжение на одной ветви, легко узнать и общее напряжение на блоке. Оба напряжения одинаковы. Это означает, что величина напряжения на устройстве будет такой же величиной напряжения на ветви, и наоборот. Так что для получения результата будет достаточно узнать напряжение одной ветки.
Шаг 2. Подсчитайте ток
Как мы уже говорили, вам несложно посчитать общее напряжение на одной ветке; все не так просто, когда дело доходит до подсчета тока. В параллельной цепи ток на каждой ветви может быть разным. В этом случае необходим подсчет общего тока.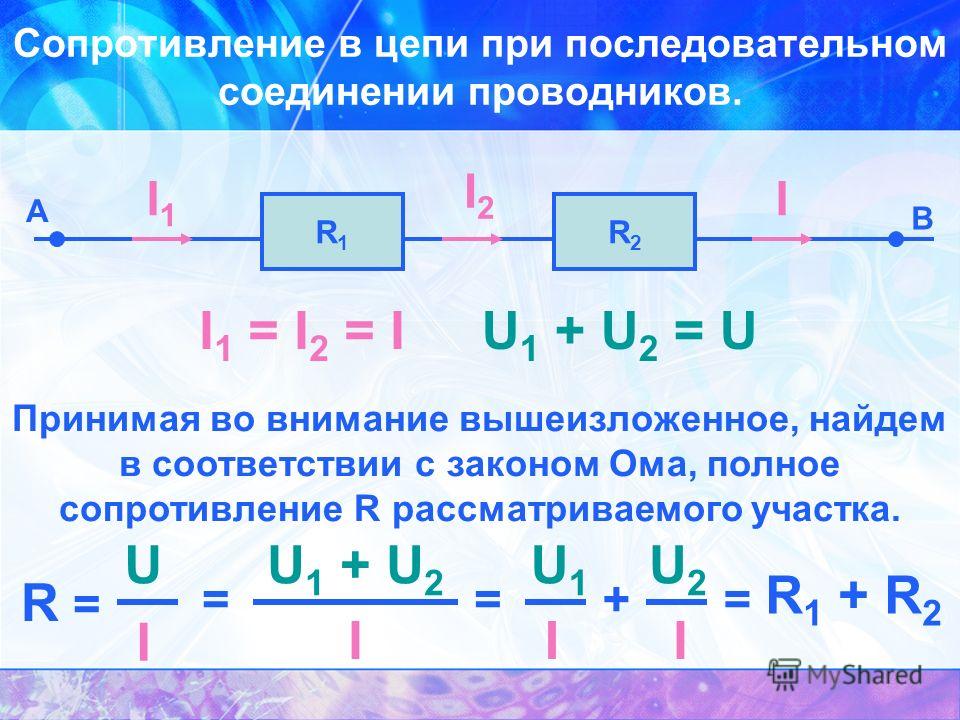 Если вы хотите узнать о сопротивлении, посчитайте общий ток, а затем вы можете двигаться дальше.
Если вы хотите узнать о сопротивлении, посчитайте общий ток, а затем вы можете двигаться дальше.
Шаг 3. Выполните расчеты
После того, как вы подсчитали общее напряжение и общий ток, пришло время следовать формуле. Чтобы найти сопротивление, здесь вы можете следовать закону Ома. По закону Ома, если вы знаете общее напряжение или V и общий ток или I, вы можете легко получить сопротивление или R.
V= IR
R= V/I
Здесь if-
Суммарное напряжение параллельной цепи V= 9 вольт и,
1 Суммарная сила тока параллельной цепи 9 I = 3 ампераТогда сопротивление R по формуле будет: Итак, общее сопротивление или R T здесь равно 3 Ом.
Результат
Теперь давайте поговорим о случаях, когда вы видите нулевое сопротивление (0). В некоторых случаях одна ветвь вашей параллельной цепи может вообще не иметь сопротивления! Да, это возможно. И если это произойдет, весь ток будет протекать через эту конкретную ветвь с нулевым сопротивлением. В этом случае сопротивление цепи будет равно нулю Ом.
В этом случае сопротивление цепи будет равно нулю Ом.
Примечание: Итак, к чему относится сопротивление цепи при нулевом оме? Ну, если вы про резистор вашей параллельной схемы, то должны понимать, что резистор вышел из строя.
Будет понятнее сказать, что он закорочен или зашунтирован. Поскольку этот имеет нулевое сопротивление, обязательно будет большой ток. В результате это в конечном итоге повредит другие части схемы, добавленные туда.
Подведение итогов
Подсчет сопротивления в последовательных цепях проще, чем в параллельных цепях. Однако, если вы знаете сопротивление для последовательных цепей, все, что вам нужно, это сложить их. В случае параллельного вы должны добавить людей, а затем следовать формуле. Но опять же, здесь вам может помочь знание общего тока и напряжения. Воспользуйтесь любым из этих способов!
Как рассчитать полное сопротивление в последовательной цепи?
Для расчета общего сопротивления используем формулу: RT = R1 + R2 + R3.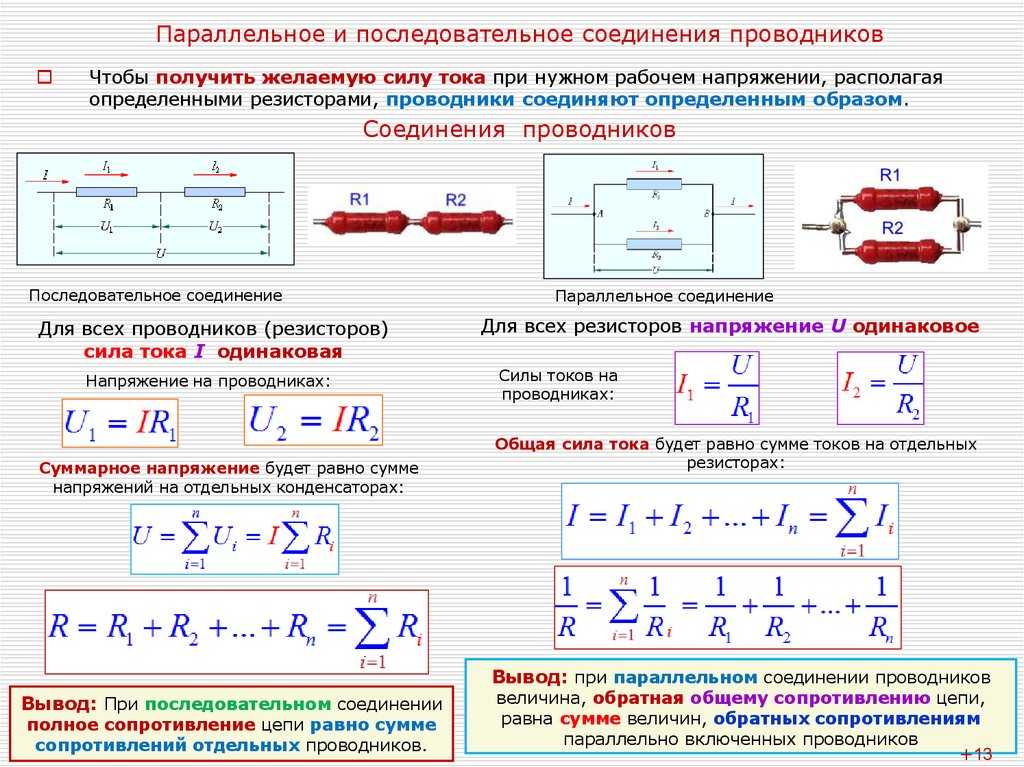
…
Если у нас уже есть сила тока и мы хотим узнать напряжение, мы также можем использовать закон Ома.
- V = I x Rобщ.
- В = 1,7 А x 7 Ом.
- В = 12 В.
Вид полный ответ на wikihow.com
Как рассчитать общее сопротивление?
Если вы знаете общий ток и напряжение во всей цепи, вы можете найти общее сопротивление, используя закон Ома: R = V / I. Например, параллельная цепь имеет напряжение 9вольт и общий ток 3 ампера. Общее сопротивление R T = 9 вольт / 3 ампера = 3 Ом.
Вид полный ответ на wikihow.com
Какова формула последовательного замыкания?
Напряжение для каждого элемента цепи в последовательной цепи можно рассчитать, применяя закон Ома: V=R*I. Кроме того, если сопротивление элемента неизвестно, правило петли Кирхгофа помогает рассчитать напряжение на таком элементе цепи.
Вид
полный ответ
на сайте Study. com
com
Как найти общее сопротивление в последовательно-параллельной цепи PDF?
Суммарное сопротивление в параллельной цепи меньше любого из сопротивлений в отдельности: R Total = 1 / (1/R 1 + 1/R 2 + … 1/R n ) Суммарный ток в параллельная цепь равна сумме токов отдельных ветвей: I Всего = I 1 + I 2 + . . . я n .
Вид полный ответ на allaboutcircuits.com
Каково общее сопротивление?
Общее сопротивление R двух или более резисторов, соединенных последовательно, равно сумме сопротивлений отдельных резисторов.
Вид полный ответ на bbc.co.uk
Расчет полного сопротивления в последовательных и параллельных цепях
Что такое общее сопротивление *?
Расчет полного сопротивления: пример вопроса №7
Каково общее сопротивление? Объяснение: Для последовательно соединенных резисторов общее сопротивление равно сумме сопротивлений каждого отдельного резистора.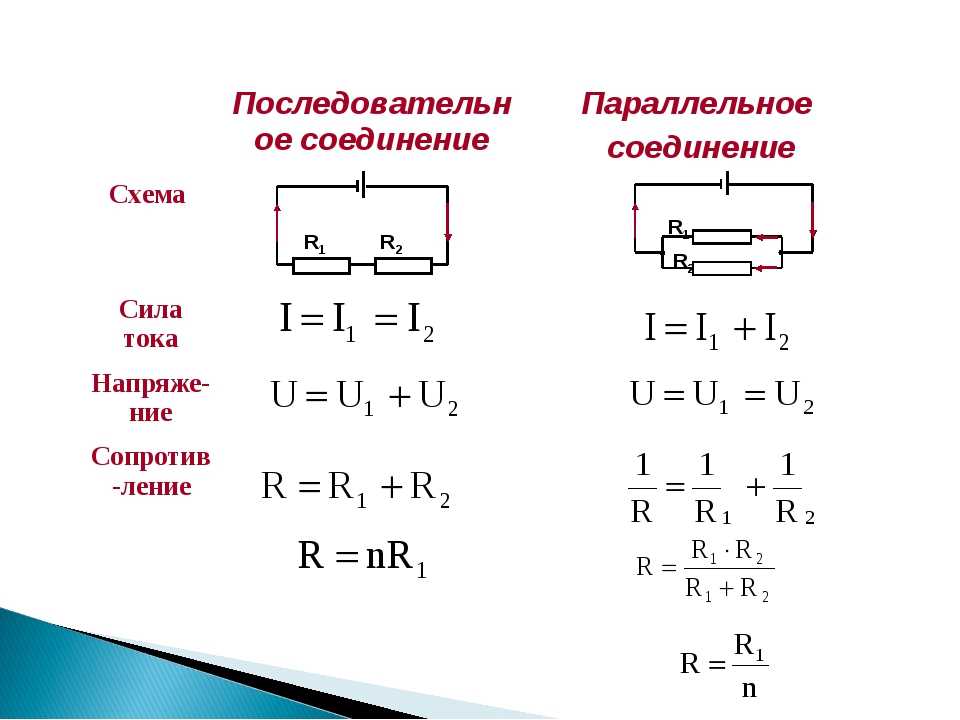 Мы можем использовать индивидуальные сопротивления из вопроса, чтобы найти общее сопротивление.
Мы можем использовать индивидуальные сопротивления из вопроса, чтобы найти общее сопротивление.
Посмотреть полный ответ на varsitytutors.com
Каково общее сопротивление между a и B в цепи?
∴ Эквивалентное сопротивление между A и B RAB=4∥4=4+44×4=2Ω
Вид полный ответ на toppr.com
Как найти сопротивление между двумя точками?
Определите, является ли это последовательной, параллельной или последовательно-параллельной цепью. Один трюк, который используется, заключается в том, чтобы поместить источник тока между двумя узлами, между которыми вам нужно знать сопротивление, затем найти напряжение на этих двух узлах, затем R = V / I.
Посмотреть полный ответ на quora.com
Чему равно полное сопротивление в параллельной цепи?
Уравнение параллельного резистора
Если два параллельных сопротивления или импеданса равны и имеют одинаковое значение, то общее или эквивалентное сопротивление R T равно половине значения одного резистора. Это равно R/2, а для трех одинаковых резисторов, включенных параллельно, R/3 и т. д.
Это равно R/2, а для трех одинаковых резисторов, включенных параллельно, R/3 и т. д.
Вид полный ответ на electronics-tutorials.ws
Что означает последовательное сопротивление?
Говорят, что два или более резистора соединены последовательно, если через все резисторы протекает одинаковый ток. В таких схемах напряжение на каждом резисторе разное.
Вид полный ответ на byjus.com
Что такое формула ряда и параллели?
Резисторы, включенные последовательно и параллельно Пример №2
R Резистор включен последовательно с R 7 , поэтому общее сопротивление будет R A + R 7 = 4 + 8 = 12 Ом, как показано. Это значение сопротивления 12 Ом теперь параллельно с R 6 и может быть рассчитано как R B . R B включен последовательно с R 5 , поэтому общее сопротивление будет R B + R 5 = 4 + 4 = 8 Ом, как показано.
Вид полный ответ на electronics-tutorials.ws
Что такое формула резистора?
Формула для расчета сопротивления по закону Ома выглядит следующим образом: R = V I. где R — сопротивление резистора R в омах (Ом) V — падение напряжения на резисторе в вольтах.
Посмотреть полный ответ на byjus.com
Одинаково ли сопротивление в последовательной цепи?
Общее сопротивление последовательной цепи равно сумме всех отдельных сопротивлений цепи. Поскольку в последовательной цепи есть только один путь для потока электронов, ток имеет одинаковую величину в любой точке цепи.
Вид полный ответ на pressbooks.bccampus.ca
Каково сопротивление двух параллельных резисторов?
Два одинаковых резистора, включенных параллельно, имеют эквивалентное сопротивление, равное половине значения сопротивления любого резистора. Ток делится поровну между ними.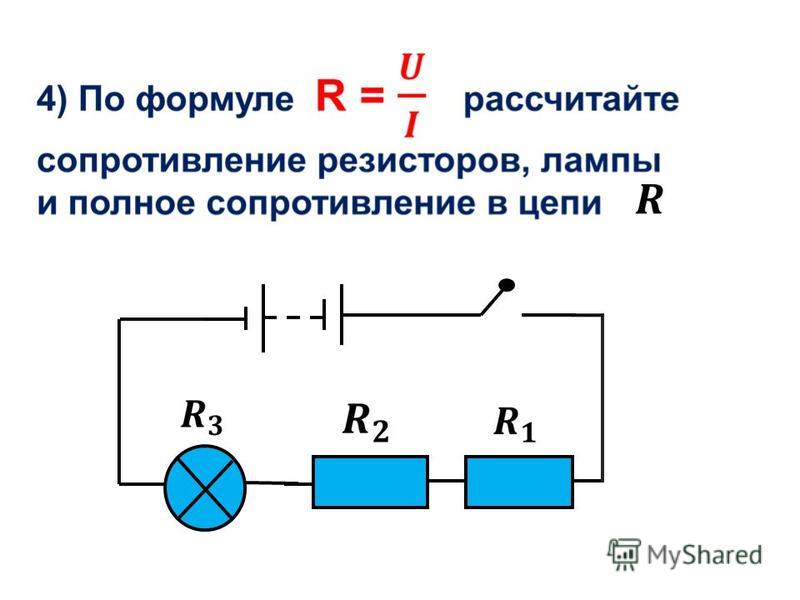
Вид полный ответ на khanacademy.org
Как рассчитать сопротивление между A и B?
Решение: На (рис. 3.22) (а) полное сопротивление на пути «ACB», т. е. «R_1 = 8,5 Омега + 3,5 Омега = 12 Омега»
Поскольку «R_1 и R_2» параллельны, эффективное сопротивление между точками `A и B`, т. е.
`R = (R_1 R_2)/(R_1 + R_2) = (3 x x 12)/(3 + 12) Omega = 2,4 Omega`
In ( Инжир.
Посмотреть полный ответ на questionnut.com
Каково общее сопротивление двух последовательно соединенных резисторов?
Ответ: Если два одинаковых резистора соединены последовательно, то общее сопротивление равно: R + R = 2R.
Вид полный ответ на byjus.com
Что такое последовательное и параллельное сопротивление?
В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков.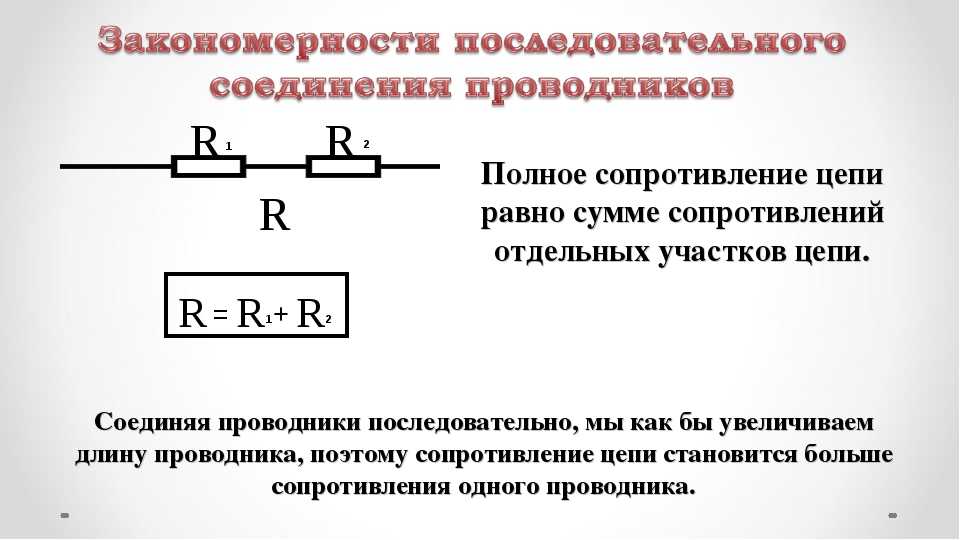 В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе.
В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе.
Посмотреть полный ответ на openpress.usask.ca
Как найти сопротивление резистора?
Эта формула говорит вам, что ваше сопротивление всегда равно вашему напряжению, деленному на ток. Вы также можете сказать, что ваше напряжение равно вашему току, умноженному на ваше сопротивление, или V = IR в форме уравнения, где R = V / I.
Вид полный ответ на сайте Study.com
Как рассчитать серию?
Сумма первых n членов арифметической последовательности равна (n/2)⋅(a₁+aₙ). Она называется формулой арифметического ряда.
Посмотреть полный ответ на сайте khanacademy.org
← Предыдущий вопрос
Водка вызывает сонливость?
Следующий вопрос →
Могут ли психопаты быть жестокими?
Как рассчитать общее сопротивление последовательной цепи?
от Veerendra
Как рассчитать общее сопротивление последовательной цепи?
Эффективное сопротивление резисторов, соединенных последовательно
- Цепь серии имеет три важные характеристики. :
(a) Ток, проходящий через каждый резистор, одинаков.
(b) Разность потенциалов на каждом резисторе напрямую зависит от его сопротивления.
(c) Сумма разности потенциалов на каждом резисторе равна полной разности потенциалов источника.
- Когда два или более сопротивления соединены встык так, что через каждое из них протекает одинаковый ток, говорят, что они соединены последовательно. Когда к батарее подключена последовательная комбинация сопротивлений, через каждое из них протекает одинаковый ток (I).
Когда к батарее подключена последовательная комбинация сопротивлений, через каждое из них протекает одинаковый ток (I). - Закон последовательного соединения сопротивлений: Закон последовательного соединения сопротивлений гласит, что при последовательном соединении нескольких сопротивлений их эквивалентное сопротивление равно сумме сопротивлений отдельных элементов.
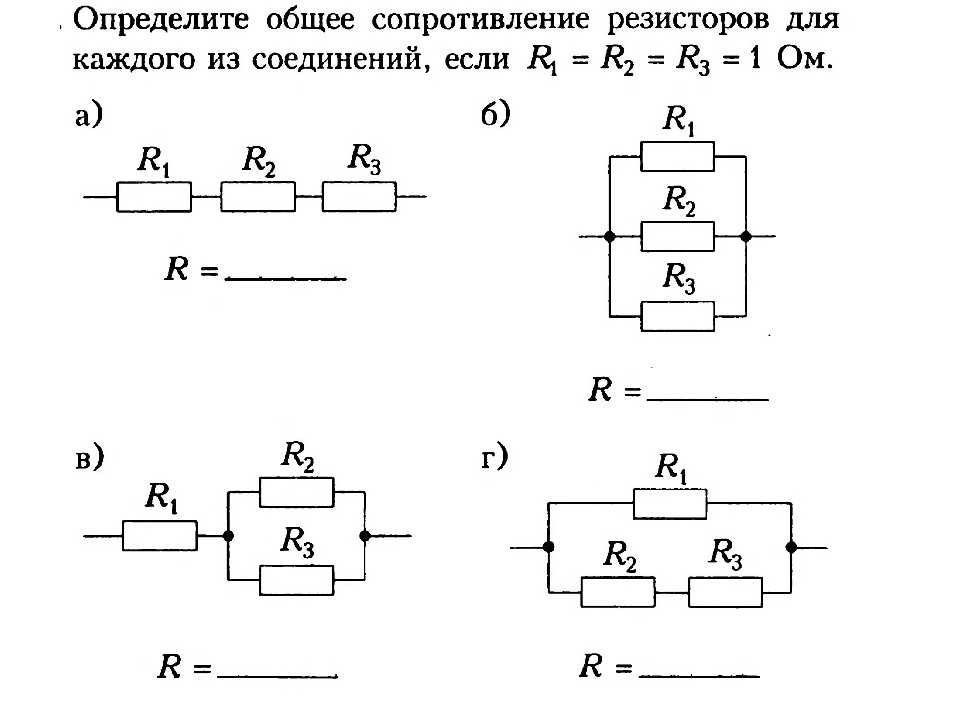 Таким образом, если R 1 , R 2 , R 3 … и т. д. соединены последовательно, то эквивалентное сопротивление (R) определяется выражением,
Таким образом, если R 1 , R 2 , R 3 … и т. д. соединены последовательно, то эквивалентное сопротивление (R) определяется выражением,
R = R 1 + R 2 + R 3 + … …. (i) - Вывод математического выражения сопротивлений при последовательном соединении :
Пусть R 1 , R 2 и R 3 будут сопротивлениями, соединенными последовательно, I будет током, протекающим через цепь, т. е. проходя через каждое сопротивление, а V 1 , V 2 и V 3 — разность потенциалов на R 1 , R 2 и R 3 соответственно. Тогда по закону Ома
В 1 = IR 1 , В 2 = IR 2 и V 3 = IR 3 3 0 , 90 0 … (ii) Комбинация сопротивлений тогда,
V = V 1 + V 2 + V 3 … (iii) - , если, r — эквивалентное сопротивление цепи, затем
V = (iv) - Используя уравнения (i)–(iv), можно записать
IR = I (R 1 + R 2 + R 3 )
R = R 1 + R 2 + R 3 9925 2 + R 3 99999999999998889888988998999999999999999999999998999899988 2 . серии, эквивалентное сопротивление выше, чем каждое отдельное сопротивление.
серии, эквивалентное сопротивление выше, чем каждое отдельное сопротивление. - Эквивалентная схема показана на рис.
Некоторые результаты о последовательном соединении:
- Когда два или более резистора соединены последовательно, общее сопротивление комбинации равно сумме всех сопротивлений по отдельности.
- Когда два или более резистора соединены последовательно, через каждый резистор протекает одинаковый ток.
- Когда несколько резисторов соединены последовательно, напряжение на комбинации
(т. е. напряжение батареи в цепи) равно сумме падений напряжения
(или разность потенциалов) на каждом отдельном резисторе.
Люди также спрашивают
- Чем отличаются последовательные и параллельные цепи?
- Как рассчитать общее сопротивление параллельной цепи?
- Что такое электрический ток?
- Что такое электрическое поле и как оно создается?
- Какая связь между электрическим током и разностью потенциалов?
- Электродвижущая сила, внутреннее сопротивление и разность потенциалов элемента/батареи
- Взаимосвязь между переданной энергией, током, напряжением и временем
- Номинальная мощность и энергопотребление различных электроприборов
Задачи серии с решениями
- Три резистора, R 9 2 7 2 90 907 2 и 5 3 , соединены последовательно с батареей 6 В, как показано на рисунке.
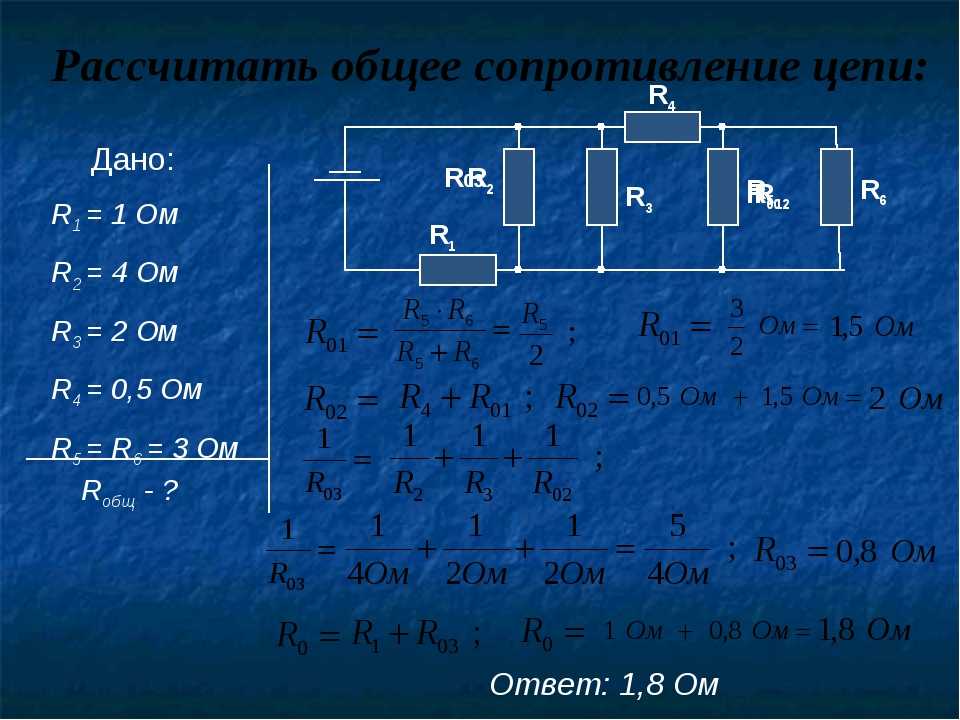
Рассчитать
(а) эффективное сопротивление, R цепи,
(б) ток, I в цепи,
(c) разности потенциалов на каждом резисторе, В 1 , В 2 и В 3 .
Решение:
Обратите внимание, что чем больше сопротивление, тем больше разность потенциалов на нем. Сумма разности потенциалов на каждом резисторе равна разности потенциалов на батарее.
Рубрики: Физика С тегами: рабочий лист комбинированных цепей с ответами, задачи сложных последовательных и параллельных цепей, последовательный и параллельный ток, вывод последовательностей, формула эффективного сопротивления, электричество, определение эквивалентного сопротивления, задачи эквивалентного сопротивления, Как рассчитать общее сопротивление последовательной цепи ?, как найти эквивалентное сопротивление, как решить задачи последовательно-параллельной цепи, определение параллельной цепи, примеры параллельных цепей, задачи с параллельными цепями с решениями, резисторы в последовательном и параллельном, последовательном и параллельном проблемы с цепями и ответы, определение последовательной цепи, схема последовательной цепи, проблемы с последовательной цепью с решениями, последовательная цепь против параллельной цепи. примеры последовательных цепей, последовательное сочетание, последовательное сочетание сопротивления, примеры последовательно-параллельных цепей, рабочий лист задач последовательно-параллельных цепей, эффективное сопротивление резисторов, соединенных последовательно, напряжение последовательно и параллельно
примеры последовательных цепей, последовательное сочетание, последовательное сочетание сопротивления, примеры последовательно-параллельных цепей, рабочий лист задач последовательно-параллельных цепей, эффективное сопротивление резисторов, соединенных последовательно, напряжение последовательно и параллельно
Эквивалентное сопротивление сложных, последовательных и параллельных цепей
Базовая электроника
Энгр Фахад Отправить письмо 2 января 2021 г.
0 4 877 6 минут чтения
Допустим, если у вас есть два резистора R1 = 10 и R2 = 20, соединенных последовательно.
Допустим, это резистор на 10 Ом, а это резистор на 20 Ом. Чему равно эквивалентное сопротивление или полное сопротивление цепи? В последовательной цепи общее сопротивление равно сумме всех сопротивлений. Таким образом, 10 + 20 равно 30. Таким образом, мы можем описать это как резистор на 30 Ом. Таким образом, эти две схемы эквивалентны. Вы можете просто заменить два резистора одним резистором.
Таким образом, эти две схемы эквивалентны. Вы можете просто заменить два резистора одним резистором.
Теперь, что если у нас есть два резистора параллельно. Допустим, это резистор на 10 Ом, а это резистор на 10 Ом. Мы назовем их R1 и R2. Так каково эквивалентное сопротивление этой цепи? Теперь, когда у вас есть два резистора, подключенных параллельно, и если они имеют одинаковое значение, эквивалентное сопротивление будет просто равно половине этого значения, поэтому эквивалентное сопротивление будет равно 5 Ом. Чтобы рассчитать общее сопротивление двух резисторов в параллельной цепи, это (1/R1 + 1/R2) -1 . Так что это будет (1/10 + 1/10) -1 . Теперь 1 + 1 равно 2, так что это становится 2 из 10, и когда вы возводите дробь в отрицательную степень 1, вы в основном переворачиваете дробь, и получается половина 10 или 10, деленное на 2, что равно 5.
А что, если мы подключим три резистора параллельно. Допустим, это резистор на четыре Ома, резистор на шесть Ом и резистор на 8 Ом.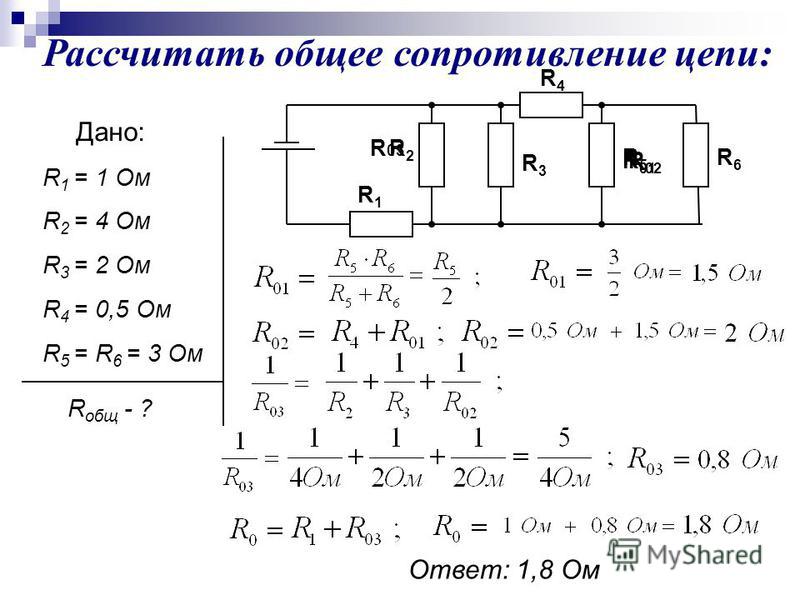 Каково эквивалентное сопротивление этой цепи?
Каково эквивалентное сопротивление этой цепи?
Назовем это R1, R2 и R3. Таким образом, мы можем использовать эту формулу, чтобы получить ответ, который будет (1/R1 + 1/R2 + 1/R3) -1 . Итак, это (1/4 + 1/6 + 1/8) -1 , и поэтому для этой схемы эквивалентное сопротивление составляет 1,846 Ом, и это ответ.
Вот еще один пример. Рассчитайте эквивалентное сопротивление этой цепи. Допустим, у нас есть два резистора на 20 Ом, которые соединены параллельно, и еще один резистор на 15 Ом. Обратите внимание, что эти два резистора параллельны друг другу и имеют одинаковое значение, поэтому эквивалентное сопротивление этих двух резисторов вы можете заменить на резистор 10 Ом. Итак, в этот момент вы можете заменить два резистора одним резистором на 10 Ом. Теперь это создаст последовательную цепь с резистором 15 Ом. Теперь резисторы 10 Ом и 15 Ом соединены последовательно, и теперь вы можете просто добавить два сопротивления, и вы получите общее сопротивление.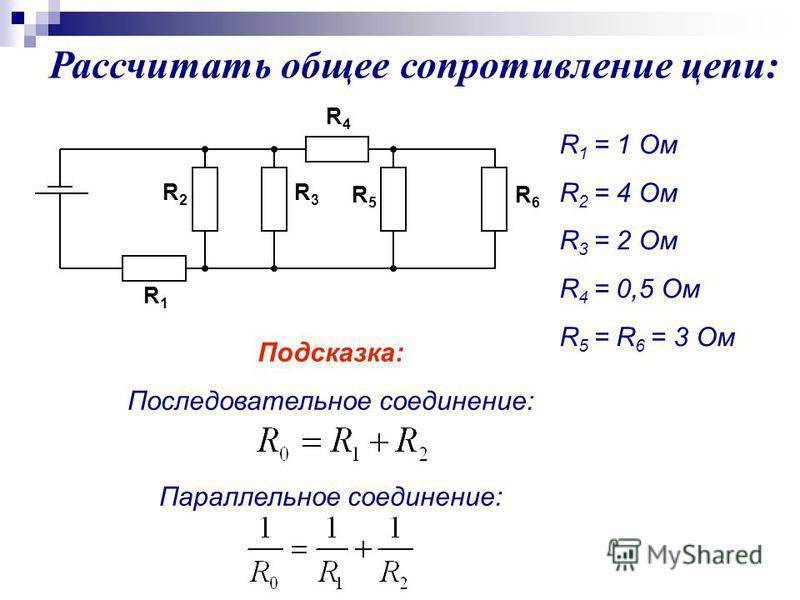 Итак, 15 + 10 = 25 Ом. Таким образом, эквивалентное сопротивление для этой цепи составляет 25 Ом, и на этом все.
Итак, 15 + 10 = 25 Ом. Таким образом, эквивалентное сопротивление для этой цепи составляет 25 Ом, и на этом все.
Вот еще один, допустим, три резистора 40 Ом, 40 Ом и 20 Ом соединены параллельно, и в той же цепи есть еще три резистора 5 Ом, 15 Ом и 30 Ом. Как объяснялось ранее, если два резистора соединены параллельно и имеют одинаковые значения, мы можем просто уменьшить значение вдвое. Итак, как вы можете видеть, два резистора по 40 Ом соединены параллельно, поэтому мы просто заменим его резистором на 20 Ом, другим резистором на 20 Ом, так что если эти два резистора вместе составляют 20, и это становится одним резистором, а это 20, то эти два становятся 10. Таким образом, эквивалентное сопротивление для всех трех резисторов равно 10, и чтобы подтвердить это, вы можете ввести его (1/40 + 1/40 + 1/20) -1 Это даст вам 10 Ом.
Итак, я могу заменить всю эту параллельную цепь резистором на 10 Ом, так что теперь оставшиеся четыре резистора замечают, что они все последовательно, и есть только один путь для протекания тока, так что это будет 5 плюс 15, что 20 плюс 10 плюс 30, поэтому эквивалентное сопротивление для этой цепи составляет 60 Ом, и это все для этой проблемы.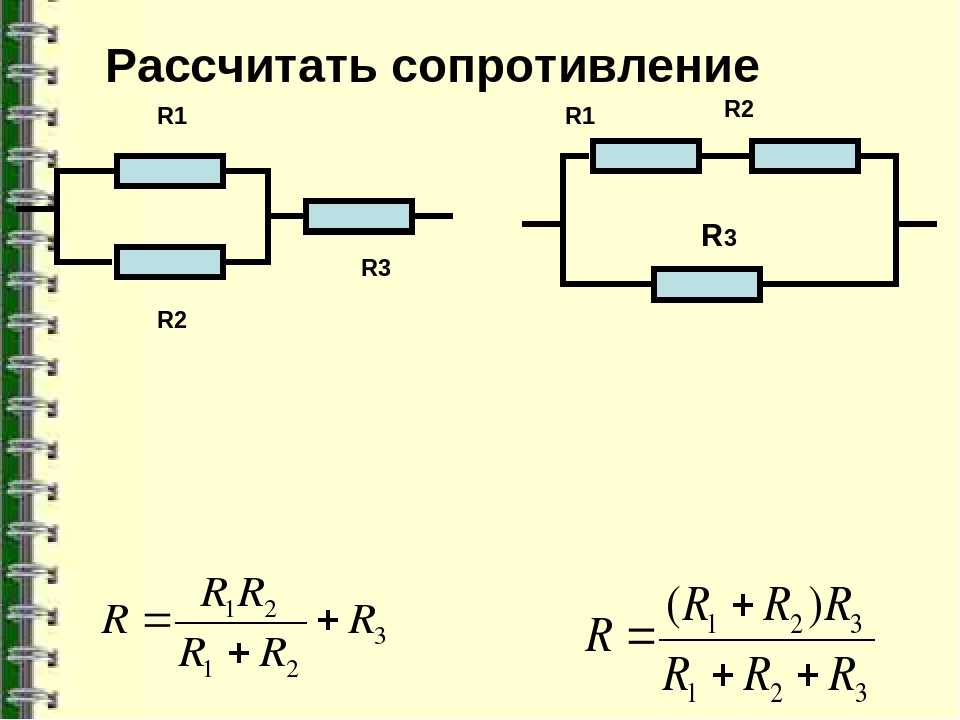
Давайте попробуем этот пример. Итак, скажем, это резистор 10 Ом, это 20, а это 30, поэтому не стесняйтесь остановиться здесь и вычислить эквивалентное сопротивление цепи. Обратите внимание, что эти два элемента соединены последовательно, потому что ток течет только по одному пути, поэтому 10 + 20 равно 30 Ом. так что я могу заменить эти два резистора резистором 30 м, теперь я могу написать этот резистор, как показано внизу, или если вы нарисуете его как-то иначе, не имеет значения, что важно, это понять, что эти два, когда вы их комбинируете в один резистор, они параллельны другому резистору на 30 Ом, поэтому, как только вы это осознаете, и тот факт, что у вас есть два параллельных резистора с одинаковым значением, вы знаете, что эквивалентное сопротивление будет половина от 30, так что это 15 Ом и это ответ.
Теперь давайте попробуем аналогичный пример, но с большим количеством шагов. Резисторы обведены красным, если это 10, это 20, и это всего лишь 30, мы собираемся сказать, что это 60.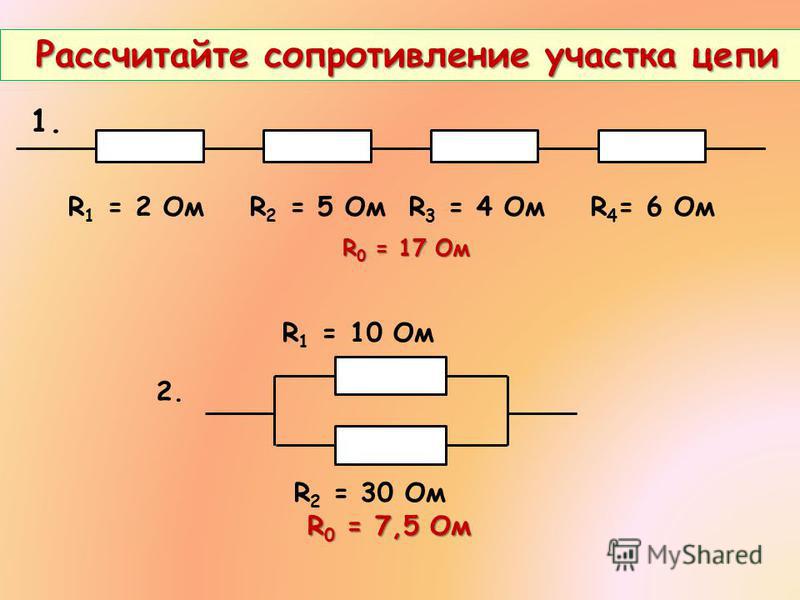 Во-первых, мы должны понять, что эти три резистора всерьез, есть только один путь для тока, протекающего в этой ветви, поэтому мы можем добавить 10, 20 и 30, чтобы получить 60, поэтому давайте заменим его собственным резистором 60. Итак, когда вы замените все три резистора одним резистором на 60 Ом, вы обнаружите, что этот резистор будет подключен параллельно резистору на 60 Ом. Таким образом, резисторы одинакового номинала соединены параллельно, и вы знаете, что если резисторы одного номинала, просто половина номинала, то есть это будет 30 Ом.
Во-первых, мы должны понять, что эти три резистора всерьез, есть только один путь для тока, протекающего в этой ветви, поэтому мы можем добавить 10, 20 и 30, чтобы получить 60, поэтому давайте заменим его собственным резистором 60. Итак, когда вы замените все три резистора одним резистором на 60 Ом, вы обнаружите, что этот резистор будет подключен параллельно резистору на 60 Ом. Таким образом, резисторы одинакового номинала соединены параллельно, и вы знаете, что если резисторы одного номинала, просто половина номинала, то есть это будет 30 Ом.
Теперь у нас есть три резистора в сериях 10, 30 и 20, что дает нам эквивалентное сопротивление или общее сопротивление 60 Ом для этой цепи.
Давайте рассмотрим еще один пример. Это будет сложнее, чем другие, но вы обязательно должны попробовать. Слишком много резисторов подключены параллельно и последовательно. Всякий раз, когда вы пытаетесь решить схему, подобную той, которую вы видите на экране, прежде всего, посмотрите на схему и попытайтесь понять, какие резисторы соединены последовательно, а какие резисторы подключены параллельно.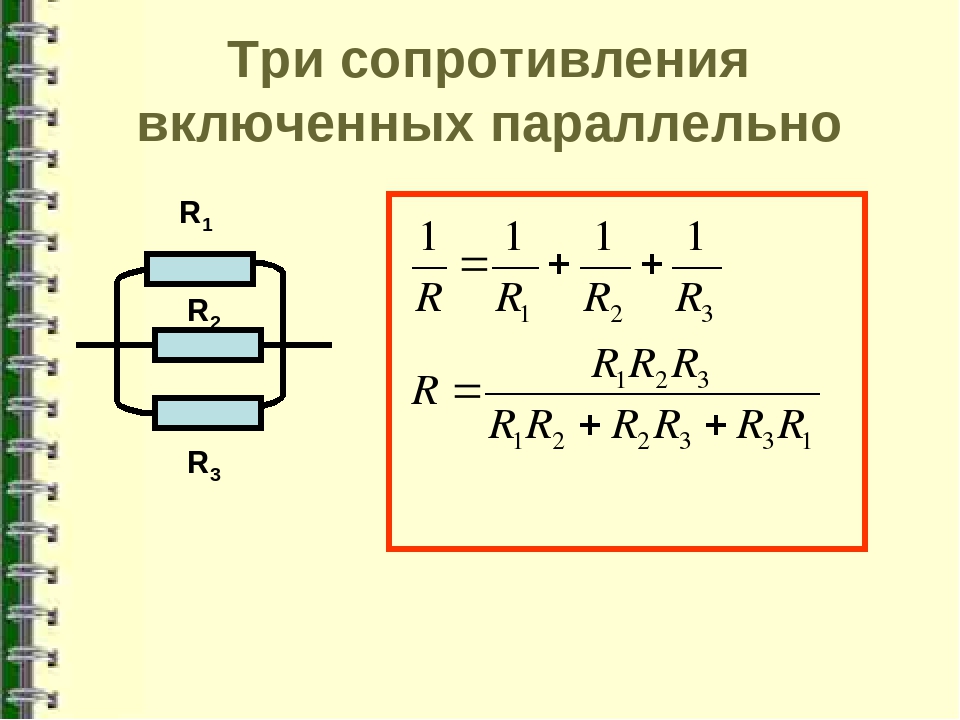 Если вам все еще трудно понять, вы можете перерисовать схему, чтобы лучше понять соединения. На изображении выше вы можете видеть, что другая схема представляет собой упрощенную версию исходной схемы, которую довольно легко понять.
Если вам все еще трудно понять, вы можете перерисовать схему, чтобы лучше понять соединения. На изображении выше вы можете видеть, что другая схема представляет собой упрощенную версию исходной схемы, которую довольно легко понять.
Итак, в правой части схемы вы можете видеть резисторы 15 Ом и 5 Ом, соединенные последовательно, поэтому решите, 15 + 5 = 20. Вы можете заменить эти два резистора одним резистором 20 Ом. Теперь можно перерисовать схему.
Теперь вы можете видеть, что два резистора имеют одинаковое значение и подключены параллельно. Вы знаете, что если два резистора подключены параллельно и имеют одинаковые значения, то просто разделите значение на 2 или простыми словами просто половина значения, которое будет составлять 10 Ом. Теперь можно дополнительно перерисовать схему и заменить два резистора одним резистором на 10 Ом между точками D и E.
Теперь вы обнаружите, что резистор на 10 Ом включен последовательно с резисторами на 20 Ом. Вы можете добавить два резистора, и вы получите 30 Ом.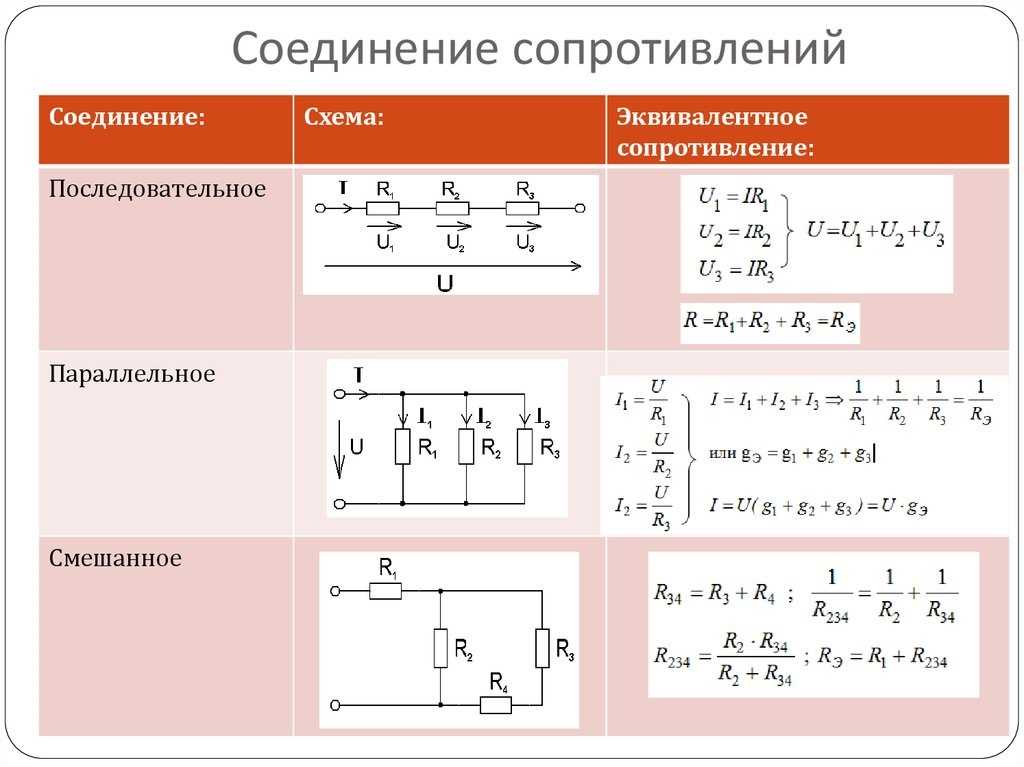
Далее вы обнаружите, что резистор на 30 Ом теперь подключен параллельно другому резистору на 30 Ом. Так как резисторы одинаковые и подключены параллельно, то половина значения и вы получите 15 Ом.
Теперь вы обнаружите, что резисторы 5, 15 и 20 включены последовательно. Итак, продолжайте и добавьте их 5 + 15 + 20 = 40.
Теперь этот резистор, который составляет 40 Ом, теперь будет параллелен резистору, подключенному между точками A и B. Так как оба резистора подключены параллельно и того же значения, поэтому мы просто уменьшим вдвое значение. Таким образом, мы получим 20 Ом. Теперь можно перерисовать схему.
Теперь все три резистора соединены последовательно, и теперь вы знаете, что вам нужно сделать, это просто добавить эти резисторы. Итак, 30+20+50=100 Ом.
Как рассчитать сопротивление при буксировке и эвакуации
Во второй части этой серии статей, состоящей из пяти частей, мы повторяем подход WreckMaster к повышению безопасности и эффективности в сфере буксировки и эвакуации, а затем сосредоточимся на втором шаге: расчете сопротивления.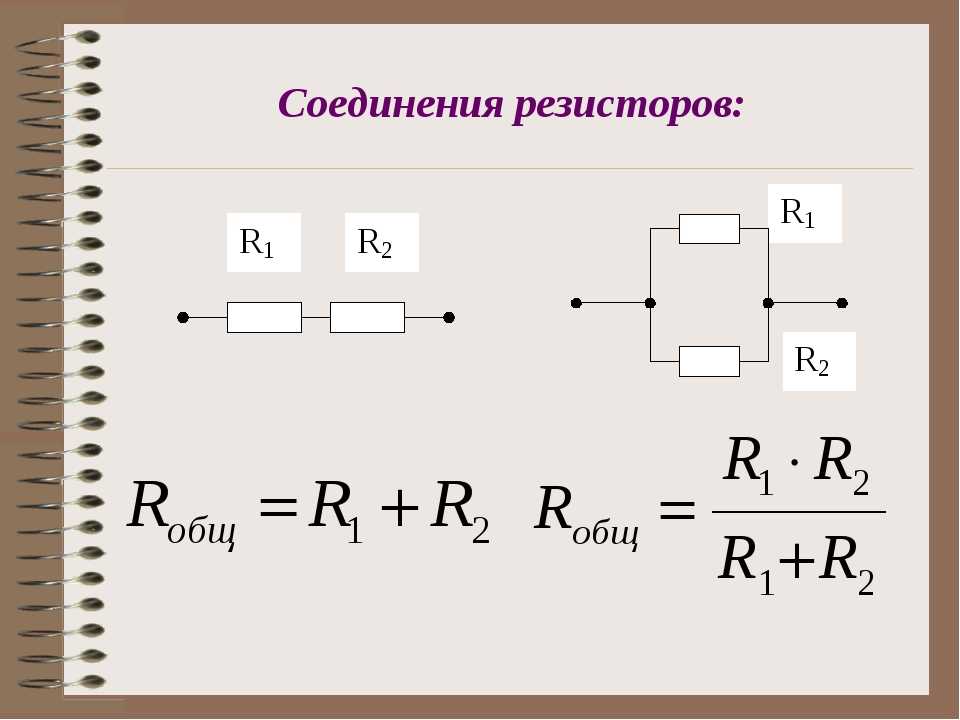 Мы расскажем вам о четырех типах сопротивления, а затем покажем, как рассчитать каждое из них, чтобы вы могли вычислить общее сопротивление, необходимое для спасения пострадавшего. Давайте начнем.
Мы расскажем вам о четырех типах сопротивления, а затем покажем, как рассчитать каждое из них, чтобы вы могли вычислить общее сопротивление, необходимое для спасения пострадавшего. Давайте начнем.
ДИСЦИПЛИНА
Буксировка, эвакуация и управление транспортными средствами – все это по своей сути рискованные действия. WreckMaster обучает операторов буксировки и эвакуации и аварийно-спасательных служб использовать рутину, которая сводит к минимуму их риск и повышает их эффективность и результативность. Мы называем этот подход «Дисциплиной».
Дисциплина состоит из пяти этапов, каждый из которых соответствует одной из букв в слове «СЦЕНА». Практикуя их вместе, эти шаги значительно уменьшат количество опасных, неприятных, трудоемких и дорогостоящих аварий, связанных с буксировкой и восстановлением. Наша цель — успех с первого раза, каждый раз.
S СОДЕРЖАНИЕ СОДЕРЖАНИЕ «ОБСЛЕ. ВЫПОЛНИТЬ»
В прошлом месяце мы рассмотрели шаг 1: «ОПРОС». На этом этапе оператор представляет себя ответственному лицу на месте происшествия, осматривает состояние пострадавшего и груза, устанавливает статические веса и оценивает окружающую среду и местность для разработки плана.
На этом этапе оператор представляет себя ответственному лицу на месте происшествия, осматривает состояние пострадавшего и груза, устанавливает статические веса и оценивает окружающую среду и местность для разработки плана.
СИМВОЛ ДЛЯ РАСЧЕТА
Для успешного перемещения груза необходимо приложить определенное усилие. Чтобы приложить правильное количество силы в первый раз, вам придется посчитать сопротивление. Расчет может показаться сложным, но крайне важно сделать его правильно. Неправильно рассчитайте ее, и вы можете перегрузить свой такелаж, трос и спасательное оборудование. Вы также можете переоценить способность своего грузовика выдерживать тяговое усилие.
Хорошая новость заключается в том, что вам не нужно заниматься расчетами самостоятельно. Калькуляторы сопротивления доступны в магазине WreckMaster, Google Play и App Store.
Что такое сопротивление? Сопротивление – это сила, необходимая для перемещения объекта с учетом его состояния и окружающей среды.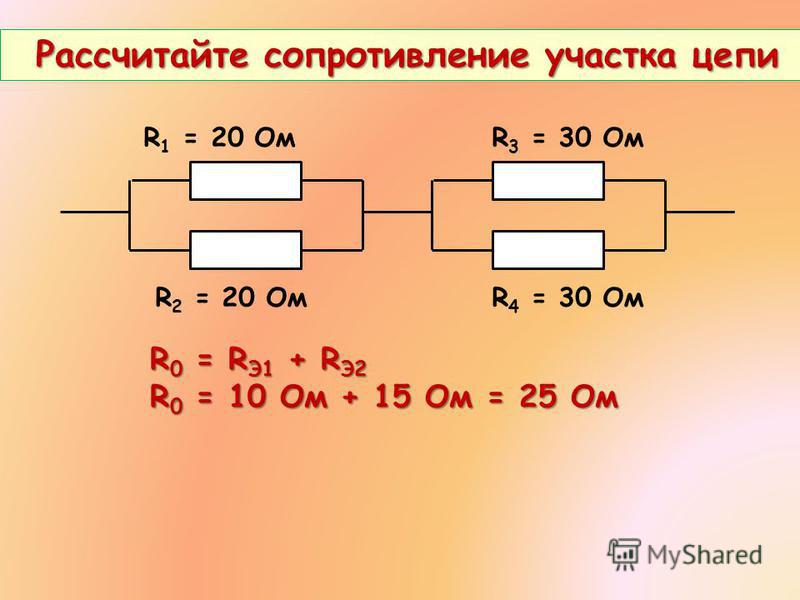 Он записывается в процентах от перемещаемого веса, который может быть меньше или больше веса объекта, в зависимости от условий. Это связано с тем, что различные поверхностные условия, состояние груза и пострадавшего, а также рельеф местности могут увеличивать или уменьшать сопротивление. Пострадавший застрял в грязи? Вы должны переместить пострадавшего в гору? Обе эти ситуации увеличат сопротивление вашим усилиям и, таким образом, увеличат количество силы, которую вам придется применить.
Он записывается в процентах от перемещаемого веса, который может быть меньше или больше веса объекта, в зависимости от условий. Это связано с тем, что различные поверхностные условия, состояние груза и пострадавшего, а также рельеф местности могут увеличивать или уменьшать сопротивление. Пострадавший застрял в грязи? Вы должны переместить пострадавшего в гору? Обе эти ситуации увеличат сопротивление вашим усилиям и, таким образом, увеличат количество силы, которую вам придется применить.
В нашей отрасли встречается 4 типа сопротивления.
- СОПРОТИВЛЕНИЕ КАЧЕНИЮ
- СОПРОТИВЛЕНИЕ БОЛЕЗНИ
- СОПРОТИВЛЕНИЕ ГРАДИЕНТУ
- СОПРОТИВЛЕНИЕ ПОВРЕЖДЕНИЯМ
Что такое сопротивление качению? Сопротивление качению — это сила, необходимая для перемещения катящегося объекта, например колеса. (Помните, когда вы были ребенком, когда вы спускались на велосипеде по инерции? В конце концов вы бы замедлились — и это из-за сил, которые способствуют сопротивлению качению.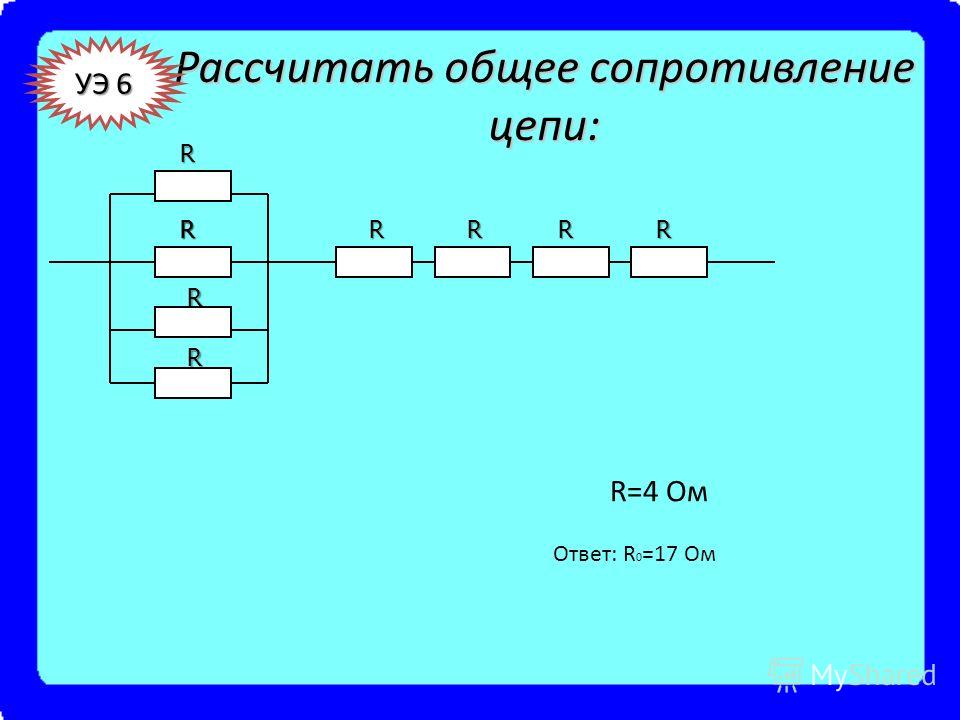 ) Силы, влияющие на сопротивление качению, включают деформацию колес, поверхности, катится объект, диаметр колеса, скорость и нагрузка на колесо. В индустрии буксировки мы называем транспортное средство либо «катящимся жестко», либо «мягко катящимся». Транспортное средство считается «тяжело катящимся», если оно стоит на твердой, плоской, ровной поверхности, такой как бетон, и все его шины накачаны, колеса свободно катятся, а трансмиссия находится в нейтральном положении. Требуется 5% от общего веса пострадавшего, чтобы переместить что-то, что сильно катится. Автомобиль «мягко катится», если он находится на мягкой поверхности, такой как трава или гравий. Для перемещения мягко катящегося объекта требуется больше силы — 15% от общего веса пострадавшего.
) Силы, влияющие на сопротивление качению, включают деформацию колес, поверхности, катится объект, диаметр колеса, скорость и нагрузка на колесо. В индустрии буксировки мы называем транспортное средство либо «катящимся жестко», либо «мягко катящимся». Транспортное средство считается «тяжело катящимся», если оно стоит на твердой, плоской, ровной поверхности, такой как бетон, и все его шины накачаны, колеса свободно катятся, а трансмиссия находится в нейтральном положении. Требуется 5% от общего веса пострадавшего, чтобы переместить что-то, что сильно катится. Автомобиль «мягко катится», если он находится на мягкой поверхности, такой как трава или гравий. Для перемещения мягко катящегося объекта требуется больше силы — 15% от общего веса пострадавшего.
ОБЩИЙ ВЕС x 0,05 = СОПРОТИВЛЕНИЕ «СИЛЬНОМУ КАЧЕНИЮ»
ОБЩИЙ ВЕС x 0,15 = «СОПРОТИВЛЕНИЕ МЯГКОМУ КАЧЕНИЮ»
1 2
2 Что такое сопротивление? Сопротивление болоту создается, когда колесо или груз погружаются в грязь, гравий, грязь, песок или другую мягкую поверхность.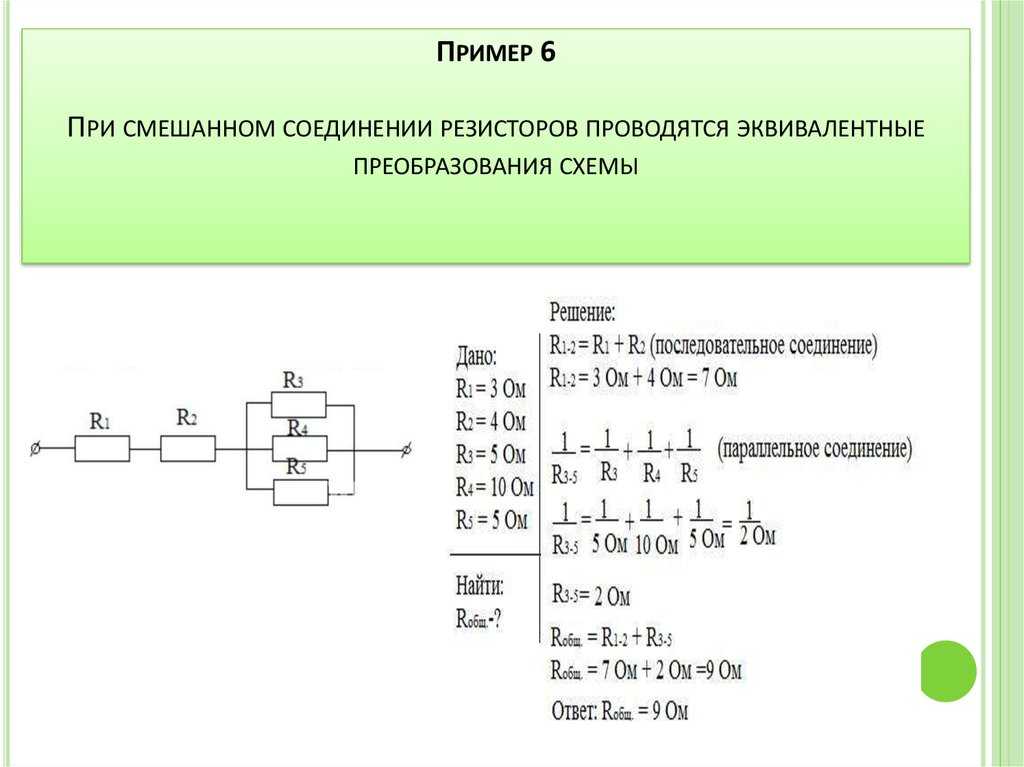 Чем глубже он утонул, тем больше силы потребуется, чтобы его сдвинуть. Если он утонул до нижней части колеса («грязь от шин»), вы добавите силу, равную 75% веса пострадавшего. Если оно утонуло до основания колесных дисков («колесная грязь»), добавьте 100% веса пострадавшего. Если он утонул по самое тело («тело трясется»), добавьте 150% веса пострадавшего.
Чем глубже он утонул, тем больше силы потребуется, чтобы его сдвинуть. Если он утонул до нижней части колеса («грязь от шин»), вы добавите силу, равную 75% веса пострадавшего. Если оно утонуло до основания колесных дисков («колесная грязь»), добавьте 100% веса пострадавшего. Если он утонул по самое тело («тело трясется»), добавьте 150% веса пострадавшего.
Общий вес x 0,75 = «Tire Mire» Сопротивление
Всего веса x 1,0 = «колесо колеса» Сопротивление
Общий вес x 1,5 = «боготворе сопротивление? Градиентное сопротивление — это сила, создаваемая гравитацией при перемещении груза вверх или вниз по уклону. Его необходимо прибавить или вычесть из общего поверхностного сопротивления. Добавьте его, когда вы перемещаете объект в гору, и вычтите его, когда вы перемещаете объект вниз.
TOTAL WEIGHT x 0.25 = RESISTANCE AT GRADIENT OF 15°
TOTAL WEIGHT x 0.50 = RESISTANCE AT GRADIENT OF 30°
TOTAL WEIGHT x 0. 75 = RESISTANCE AT GRADIENT OF 45°
75 = RESISTANCE AT GRADIENT OF 45°
Что такое сопротивление урону? Сопротивление повреждениям — это сила, которая сопротивляется движению, когда катящийся объект поврежден, например, колеса не вращаются свободно или у объекта отсутствуют колеса. Сопротивление повреждениям всегда рассчитывается по одной и той же норме, независимо от состояния поверхности. Это две трети от общего веса объекта, который вы перемещаете.
ОБЩИЙ ВЕС x 0,666 = СОПРОТИВЛЕНИЕ ПОВРЕЖДЕНИЯМ
Используя все приведенные выше расчеты, мы можем рассчитать общее сопротивление, необходимое для перемещения пострадавшего.
КАК РАСЧЕТ ОБЩЕЕ СОПРОТИВЛЕНИЕ
1. Рассчитайте статический вес груза. Статический вес включает все оборудование, багаж, топливо и все остальное, что может перевозить транспортное средство. Возможно, вам придется отрегулировать свой статический вес, чтобы компенсировать перенос веса, если имеется более одной поверхности, например, пострадавший увяз в грязи, а затем окажется на траве.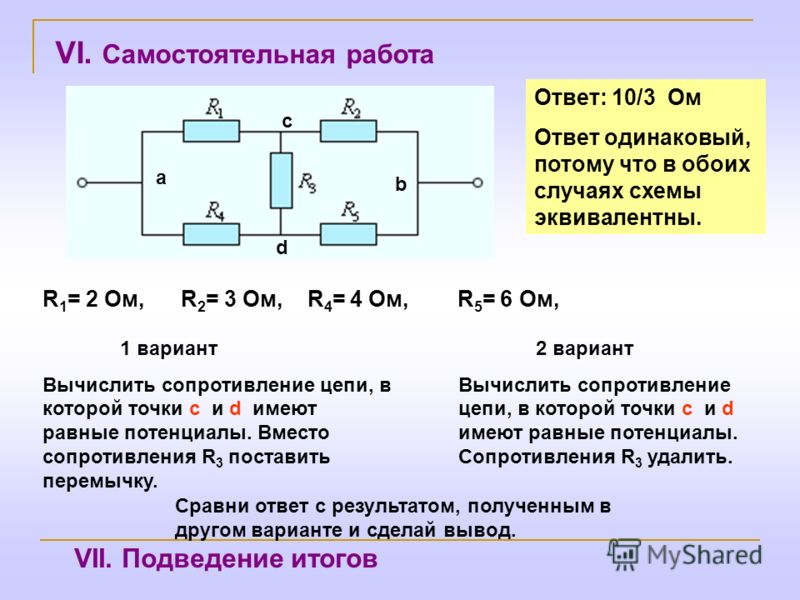 Число переноса веса добавляется к статическому весу и рассчитывается с использованием тех же показателей сопротивления градиенту, которые мы показали выше (например, умножьте статический вес на 0,25 для уклона 15°). Это скорректированное число следует использовать для расчета сопротивления поверхности и уклона на шагах 2 и 3 ниже.
Число переноса веса добавляется к статическому весу и рассчитывается с использованием тех же показателей сопротивления градиенту, которые мы показали выше (например, умножьте статический вес на 0,25 для уклона 15°). Это скорректированное число следует использовать для расчета сопротивления поверхности и уклона на шагах 2 и 3 ниже.
2. Рассчитайте поверхностное сопротивление. Поверхностное сопротивление равно или качению или повреждению или сопротивлению грязи, в зависимости от того, какое число больше.
3. Добавьте или вычтите сопротивление градиента. Добавьте его, если вы перевозите пострадавшего в гору. Вычтите его, если вы перемещаете пострадавшего вниз по склону.
ТРИ ПРОСТЫХ ПРИМЕРА
Транспортное средство массой 20 000 фунтов с четырьмя полностью функционирующими колесами необходимо буксировать вверх по склону под углом 45° по дороге с твердым покрытием.