Как рассчитать общее сопротивление при параллельном соединении резисторов. Какие формулы используются для расчета параллельного соединения. Каковы основные характеристики параллельного соединения резисторов. Как правильно применять параллельное соединение в электрических схемах.
Что такое параллельное соединение резисторов
Параллельное соединение резисторов — это способ подключения, при котором начала всех резисторов соединены в одной точке, а концы — в другой. При таком соединении напряжение на всех резисторах одинаково, а общий ток распределяется между ними.
Основные характеристики параллельного соединения резисторов:
- Напряжение на всех резисторах одинаково и равно напряжению источника питания
- Общий ток равен сумме токов через отдельные резисторы
- Общее сопротивление всегда меньше сопротивления наименьшего из параллельно соединенных резисторов
Формулы для расчета параллельного соединения
Для расчета параллельного соединения резисторов используются следующие основные формулы:
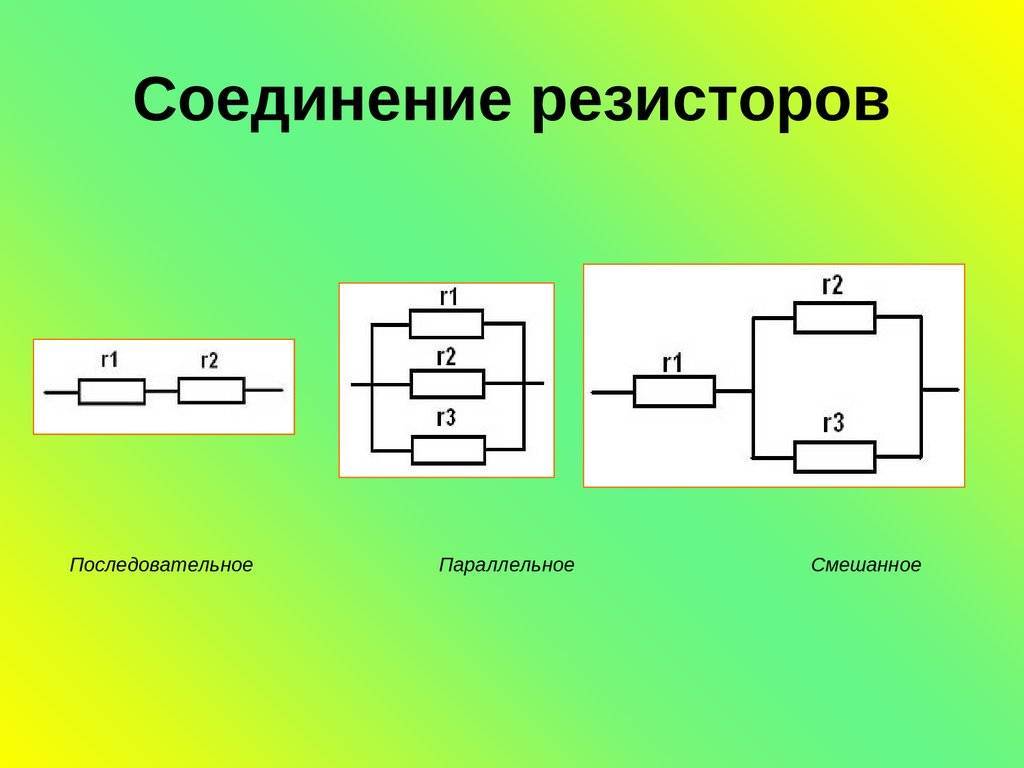
Формула общего сопротивления
Общее сопротивление при параллельном соединении резисторов рассчитывается по формуле:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, R1, R2, R3, …, Rn — сопротивления отдельных резисторов.
Формула для двух параллельных резисторов
Для случая двух параллельно соединенных резисторов формула упрощается:
R = (R1 * R2) / (R1 + R2)
Формула общего тока
Общий ток равен сумме токов через отдельные резисторы:
I = I1 + I2 + I3 + … + In
Как рассчитать параллельное соединение резисторов
Рассмотрим пошаговый алгоритм расчета параллельного соединения резисторов:
- Записать значения сопротивлений всех параллельно соединенных резисторов
- Подставить значения в формулу 1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
- Привести дроби к общему знаменателю
- Сложить числители полученных дробей
- Записать результат в виде дроби
- Вычислить обратное значение полученной дроби
Полученное значение и будет общим сопротивлением параллельно соединенных резисторов.
Пример расчета параллельного соединения
Рассчитаем общее сопротивление для трех параллельно соединенных резисторов: 10 Ом, 20 Ом и 30 Ом.
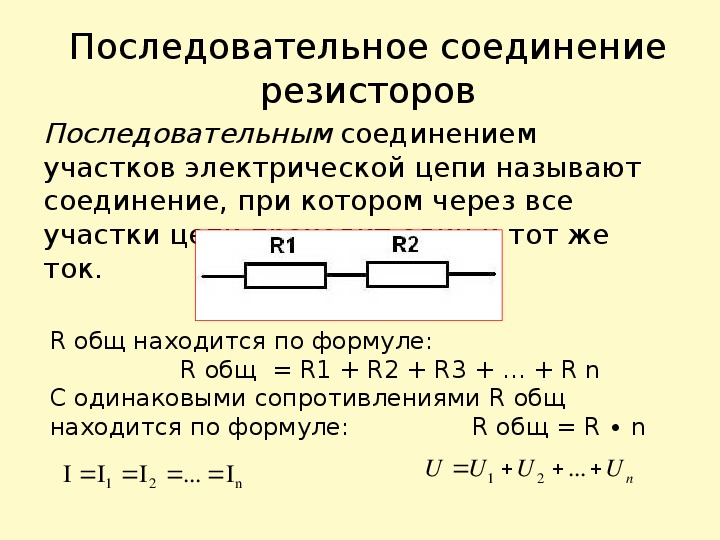
1/R = 1/10 + 1/20 + 1/30
1/R = 6/60 + 3/60 + 2/60 = 11/60
R = 60/11 = 5,45 Ом
Таким образом, общее сопротивление параллельного соединения трех резисторов составляет 5,45 Ом.
Особенности применения параллельного соединения
При использовании параллельного соединения резисторов следует учитывать некоторые важные особенности:
- Параллельное соединение позволяет уменьшить общее сопротивление цепи
- Чем больше параллельно соединенных резисторов, тем меньше общее сопротивление
- Общее сопротивление всегда меньше сопротивления наименьшего из резисторов
- При параллельном соединении увеличивается общая рассеиваемая мощность
Преимущества параллельного соединения резисторов
Параллельное соединение резисторов имеет ряд важных преимуществ:
- Возможность уменьшения общего сопротивления цепи
- Распределение тока между несколькими ветвями
- Увеличение общей рассеиваемой мощности
- Возможность получения нестандартных номиналов сопротивлений
- Повышение надежности схемы за счет резервирования
Применение параллельного соединения в электронике
Параллельное соединение резисторов широко применяется в различных областях электроники:
- Делители тока
- Шунты для измерительных приборов
- Схемы согласования импедансов
- Регулировка яркости светодиодов
- Схемы защиты от перенапряжения
- Получение нестандартных номиналов сопротивлений
Сравнение последовательного и параллельного соединения
Рассмотрим основные отличия последовательного и параллельного соединения резисторов:
| Параметр | Последовательное соединение | Параллельное соединение |
|---|---|---|
| Общее сопротивление | Увеличивается | Уменьшается |
| Ток | Одинаковый во всех резисторах | Различный, суммарный ток делится |
| Напряжение | Различное, суммарное напряжение делится | Одинаковое на всех резисторах |
| Мощность | Суммарная мощность делится | Суммарная мощность увеличивается |
Типичные ошибки при расчете параллельного соединения
При расчете параллельного соединения резисторов следует избегать некоторых распространенных ошибок:
- Суммирование сопротивлений вместо обратных величин
- Забывание о том, что общее сопротивление всегда меньше наименьшего из резисторов
- Неправильное применение формулы для двух резисторов к большему их количеству
- Ошибки в преобразовании дробей при расчетах
- Неучет погрешностей реальных резисторов
Заключение
Параллельное соединение резисторов — важный инструмент в электронике, позволяющий гибко управлять параметрами электрических цепей. Правильное понимание принципов работы и методов расчета параллельного соединения позволяет эффективно проектировать и анализировать различные электронные схемы.

общие сведения, формулы расчета • Мир электрики
Содержание
- Видео: Последовательное и параллельное соединение проводников
- Параллельное соединение: общая информация
- Расчет сопротивления
- Видео: Пример расчёта сопротивления
- Пример расчёта
- Важные нюансы
- Видео: Правильное подключение светодиодов
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Видео: Последовательное и параллельное соединение проводников
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).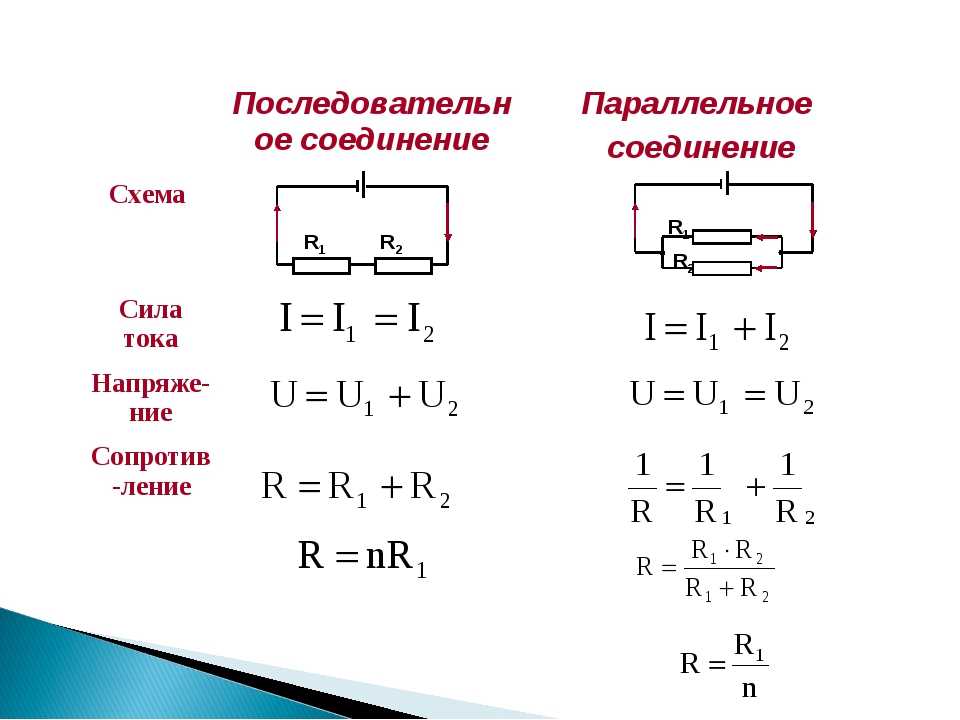
причем :
- R(общ) – суммарное значение сопротивления;
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
причем:
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
R(общ)=R1n.
причем :
- R(общ) – суммарное значение сопротивления;
- n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения.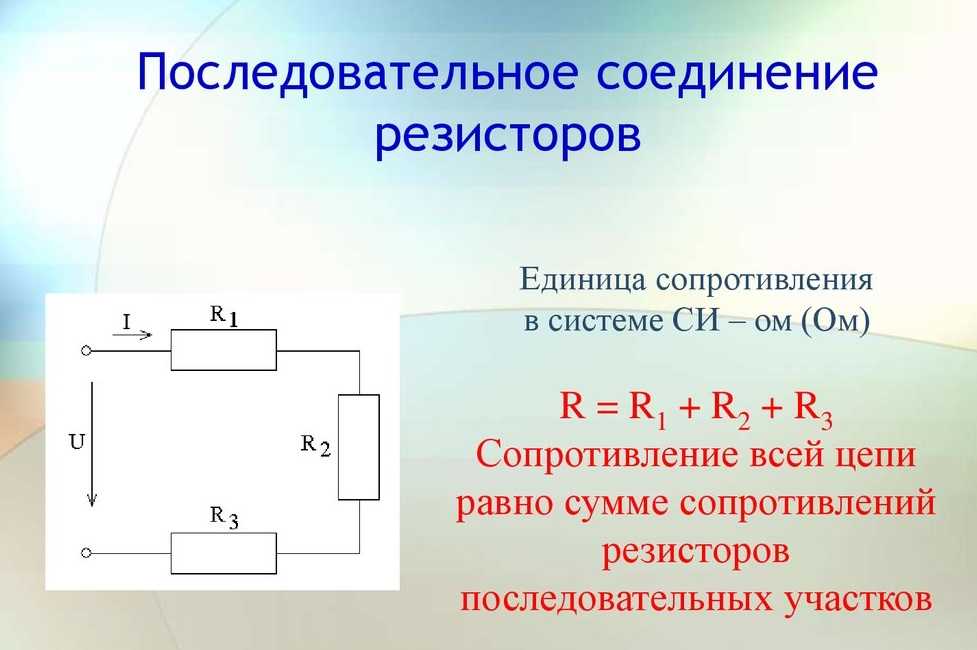 При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.
При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Закон ома для параллельного соединения схема
Автор admin На чтение 13 мин Просмотров 1 Опубликовано Обновлено
Содержание
- Параллельное соединение резисторов. Калькулятор для расчета
- Параллельное соединение резисторов — онлайн калькулятор
- Формула параллельного соединения резисторов
- Параллельное соединение резисторов — расчет
- Пример №1
- Пример расчета №2
- Как рассчитать сложные схемы соединения резисторов
- Ток, протекающий в цепи параллельно соединенных резисторах
- Подведем итог
- Последовательное и параллельное соединение резисторов.

- Последовательное соединение резисторов.
- Параллельное соединение резисторов.
- Смешанное соединение резисторов.
- Последовательное и параллельное соединение
- Последовательное соединение проводников
- Сопротивление при последовательном соединении проводников
- Сила тока через последовательное соединение проводников
- Напряжение при последовательном соединении проводников
- Параллельное соединение проводников
- Сопротивление при параллельном соединении проводников
- Напряжение при параллельном соединении проводников
- Сила тока при параллельном соединении проводников
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.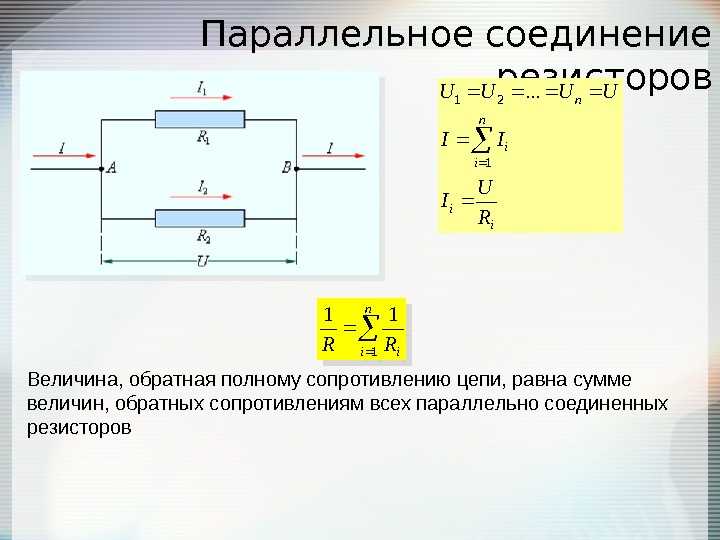 Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов.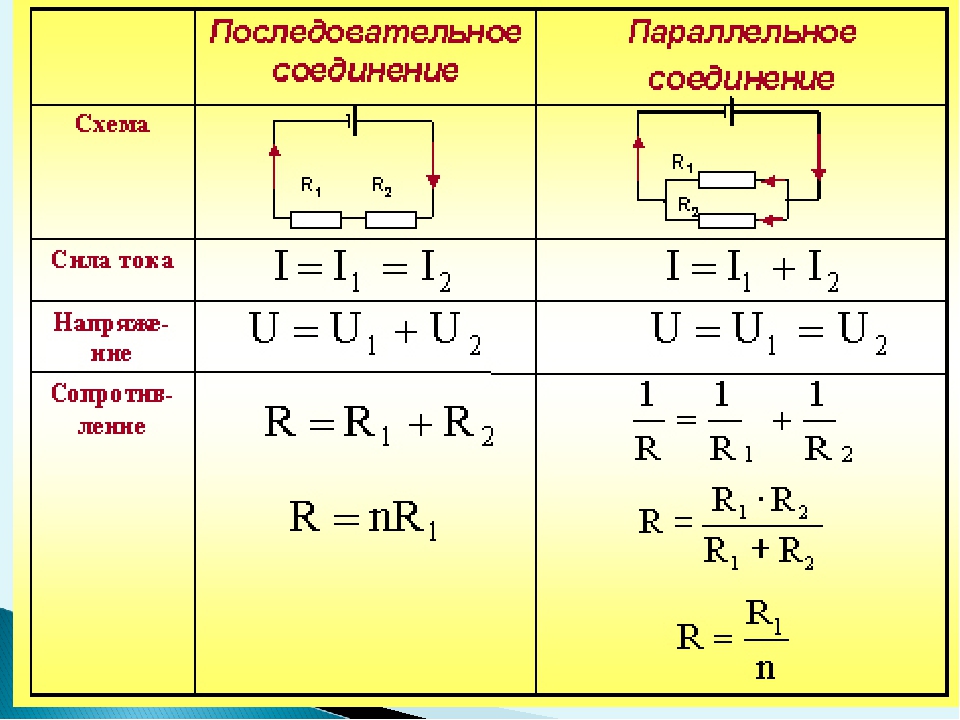 Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.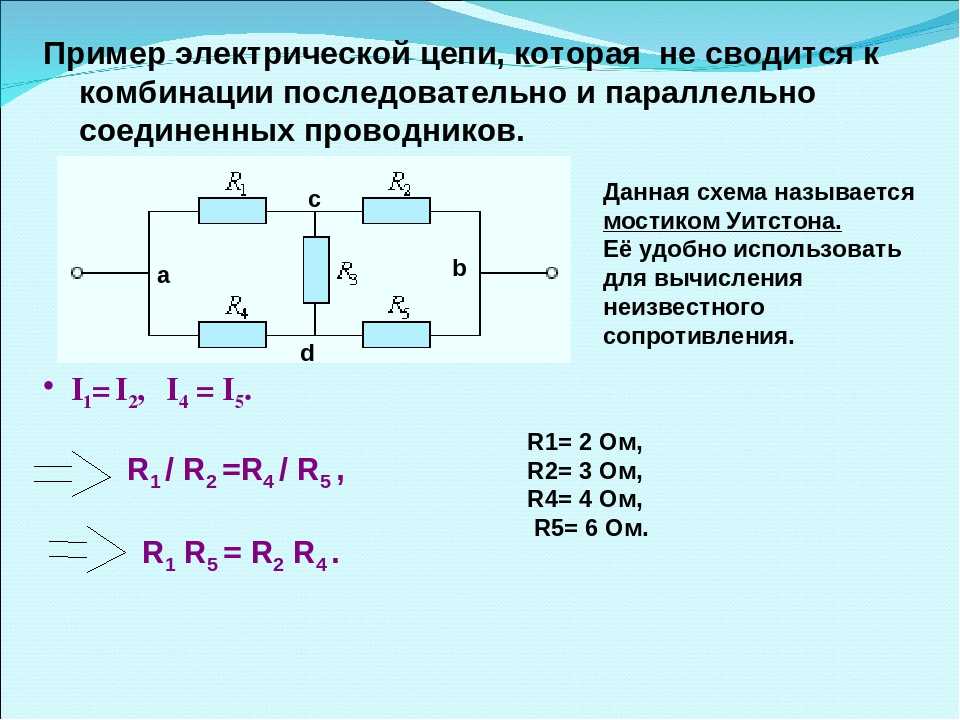
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.
Источник
Последовательное и параллельное соединение резисторов.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно.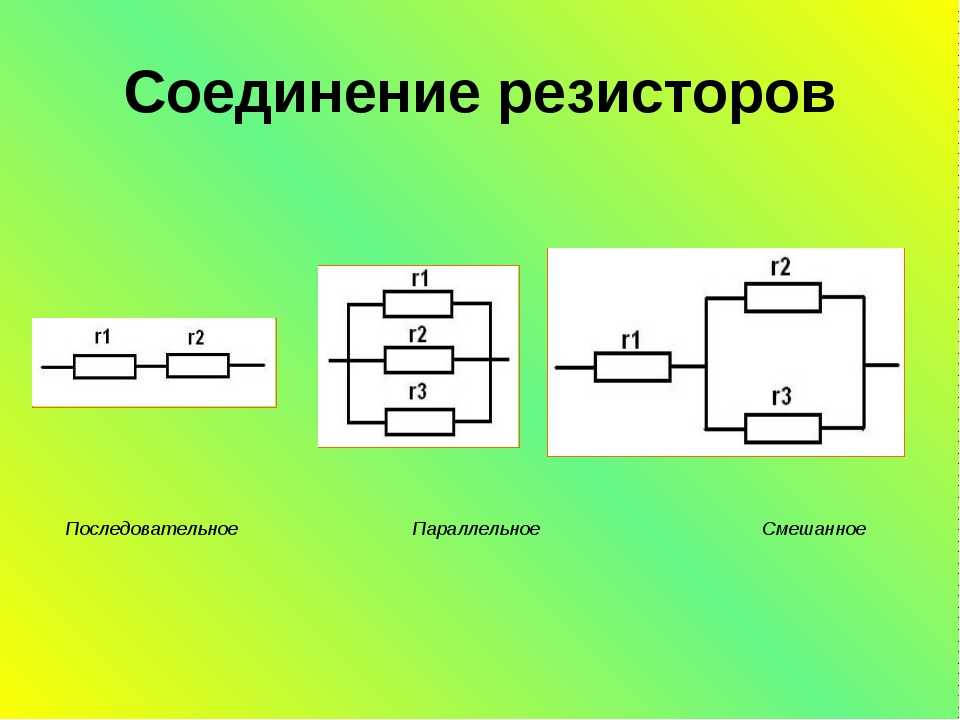 И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях, будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях, будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения — два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно использовать следующее выражение:
Но для общего напряжения также справедлив закон Ома:
Здесь R_0 — это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.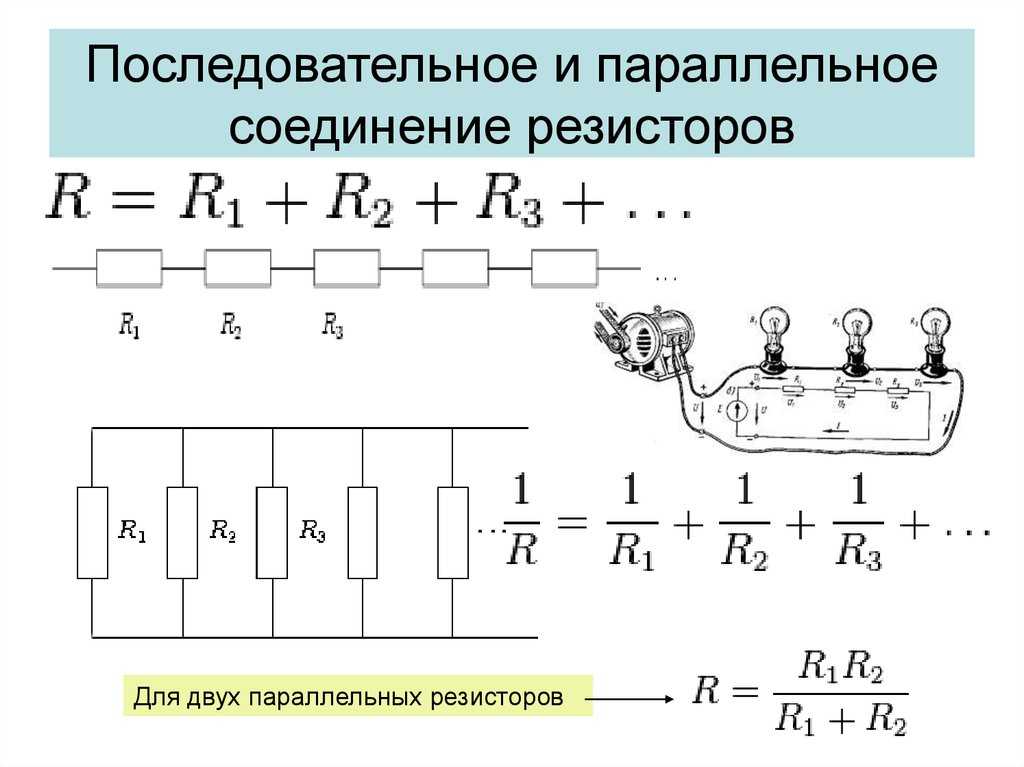
Например, для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление, будет работать в любом случае. А если при последовательном соединении все сопротивления равны ( R_1 = R_2 = . = R ), то общее сопротивление цепи составит:
В данной формуле n равно количеству элементов. С последовательным соединением резисторов разобрались, логичным образом переходим к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление. Начнем с резисторов R_1 и R_2 — они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_ :
Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой. Заменим группу параллельно соединенных резисторов R_ и R_ одним резистором R_ :
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к банальнейшему последовательному соединению двух резисторов. Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление — для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте 🤝
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление — для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте 🤝
Источник
Последовательное и параллельное соединение
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.
Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м 2
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
параллельное соединение резисторов
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.
Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет.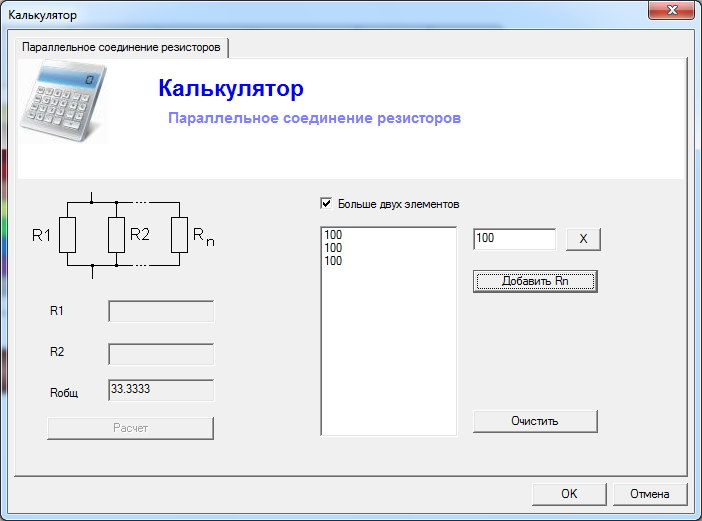 Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
Если бы у нас еще были резисторы, соединенные параллельно, то для них
В этом случае, сила тока в цепи будет равна:
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.
Воспользуемся формулами, которые приводили выше.
Если бы у нас еще были резисторы, соединенные параллельно, то для них
Далее, воспользуемся формулой
чтобы найти силу тока, которая течет в цепи
2-ой способ найти I
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.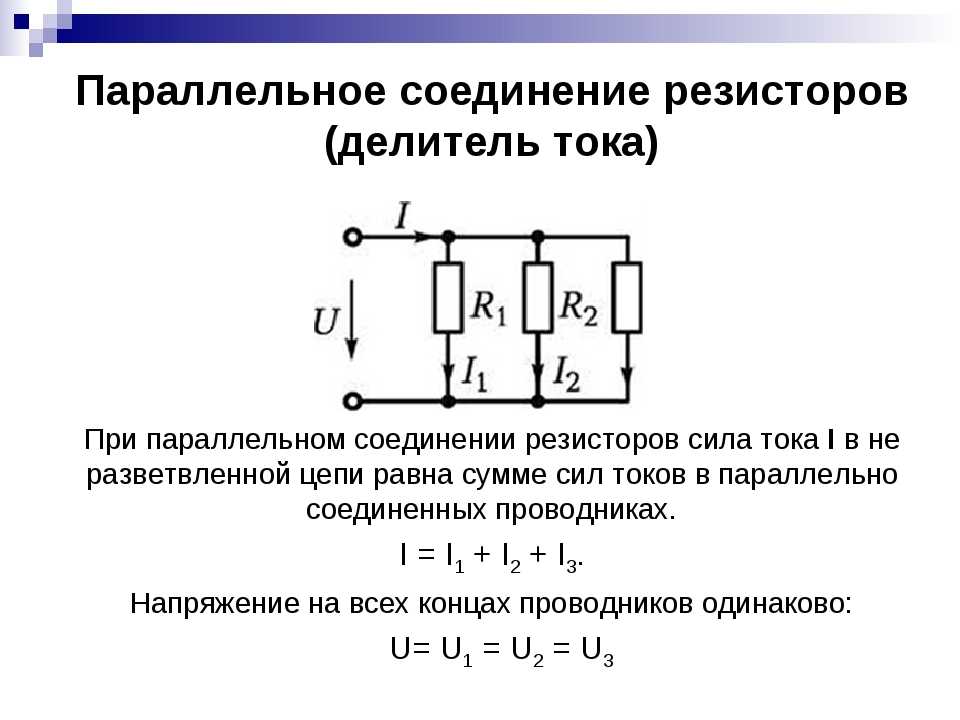
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Подробное объяснение на видео:
Источник
Калькулятор параллельного резистора
Наш калькулятор параллельного резистора вычисляет эквивалентное сопротивление до нескольких резисторов, и, кроме того, вы также можете рассчитать отсутствующий резистор в цепи.
Как пользоваться этим калькулятором параллельных резисторов?
Вы можете использовать этот калькулятор последовательной параллельной схемы, выполнив следующие действия.
- Выберите режим, т. е. расчет эквивалентного сопротивления или отсутствие резистора.
- Чтобы рассчитать эквивалентное сопротивление, введите значение резистора 1 и 2 в соответствующих единицах измерения.
- Для расчета отсутствующего резистора введите значение желаемого общего сопротивления, резистора 1 и резистора 2.

- Нажмите кнопку «Рассчитать», чтобы получить результаты.
Примечание : Вы можете добавить более 2 резисторов, чтобы рассчитать эквивалентное сопротивление или найти недостающий резистор.
Что такое параллельное сопротивление и формула параллельного сопротивления?
Резистор, оба вывода которого подключены к одному и тому же узлу, называется параллельным сопротивлением. Чтобы вычислить значение параллельного резистора, вы можете использовать онлайн-калькулятор параллельного резистора.
При этом формула параллельного сопротивления выглядит следующим образом:
$$ R_{eq} = \frac{V}{I_{total}} = \frac{V}{(\frac{V}{R_1} + \frac{V}{R_2} + \frac{V}{R_3} + … + \frac{V}{R_n})} $$
Взяв НОК приведенного выше выражения, его можно привести к простейшему виду как:
$$ R_{eq} = \frac{1}{(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … + \frac{1} {R_n})} $$
А наиболее упрощенную запись приведенного выше выражения можно записать так:
$$ \frac{1}{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
Калькулятор сопротивления параллельного подключения также учитывает следующую формулу для расчета эквивалентного сопротивления всей электрической сети.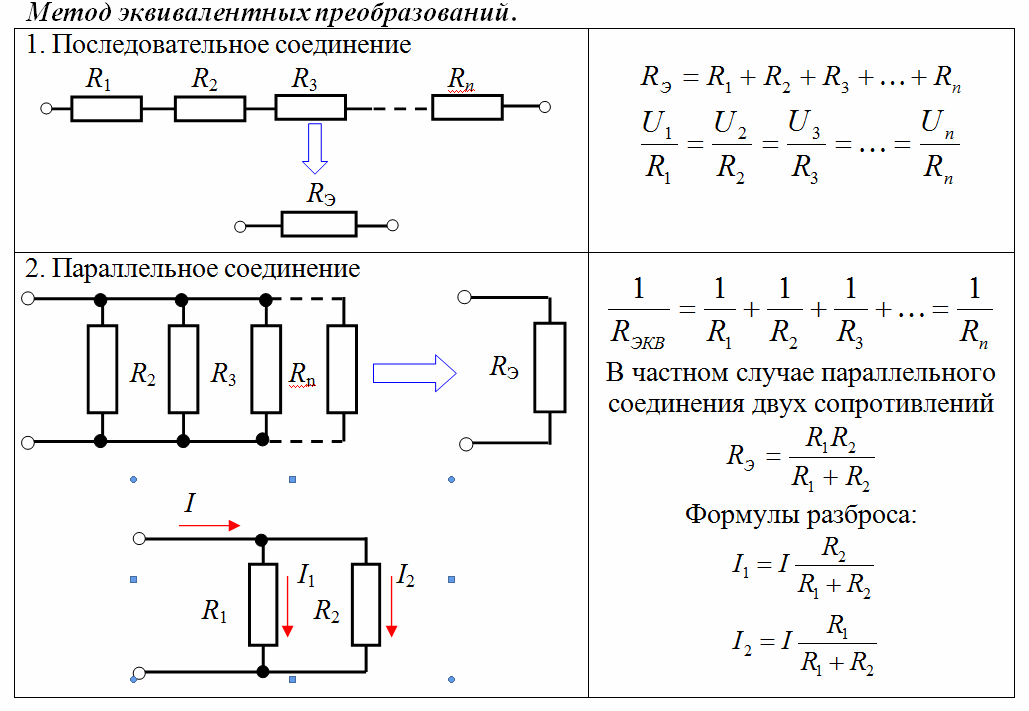
Как рассчитать параллельное сопротивление, используя формулу параллельного резистора?
Чаще всего при работе со сложными электрическими сетями на ум приходит вопрос «как решить сложные параллельные схемы». Единственный ответ на эту проблему состоит в том, чтобы использовать любую формулу параллельного резистора для этого калькулятора комбинированной схемы.
Здесь мы собираемся использовать формулу параллельного сопротивления в приведенном ниже примере, не прибегая к помощи калькулятора сложной цепи:
Пример:
В этой цепи три резистора соединены параллельно, чтобы отклонить путь тока , тем самым снижая его потенциал. Предполагая, что к нему подключена идеальная нагрузка, как рассчитать сопротивление в параллельной цепи по заданной схеме?
Решение:
Используя формулу параллельного сопротивления:
$$ \frac{1}{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
$ $ \frac{1}{R_{eq}} = \frac{1}{10 + 2 + 1} $$
$$ \frac{1}{R_{eq}} = \frac{1}{10 } + \frac{1}{2} +\frac{1}{1} $$
$$ \frac{1}{R_{eq}} = 0,1 + 0,5 + 1 $$
$$ \frac {1}{R_{eq}} = 1,6 кОм $$
Это требуемый ответ, который также можно проверить с помощью этого калькулятора параллельного сопротивления.
Часто задаваемые вопросы
Как узнать, параллельны ли два резистора?
Два сопротивления будут считаться соединенными параллельно, если узлы на обоих концах резисторов одинаковы. В таком случае сопротивления R_1 и R_2 будут параллельны, так что (R_1||R_2). А если есть еще общее сопротивление R_3, то оно будет последовательно с параллельным соединением этих двух резисторов.
Параллельное напряжение одинаковое?
Да, при параллельной схеме общее напряжение сети всегда одинаково. Вы можете лучше понять соотношение между напряжением и током любой цепи или отдельного проводника, используя резистор в калькуляторе полного сопротивления или используя калькулятор закона Ома.
Как найти неизвестный резистор в параллельной цепи?
Используйте следующую формулу для расчета неизвестного резистора в параллельной цепи:
Rn = (1/R – 1/R₁ + 1/R₂ + …)-1
Эта формула может быть получена перестановкой следующей формулы:
1/R = 1/R₁ + 1/R₂ + … + 1/Rn
Ссылки:
Из источника Wikipedia: Series и параллельные схемы, Параллельные схемы, Объединение проводимостей, Обозначения, Приложения
Из источника Академии Хана: Резисторы последовательно и параллельно, Резисторные сети, резисторная схема с двумя батареями
Калькулятор параллельных резисторов — Soldering Mind
Легко рассчитать параллельный подключенный резистор сопротивление с помощью этого онлайн-калькулятора параллельного резистора.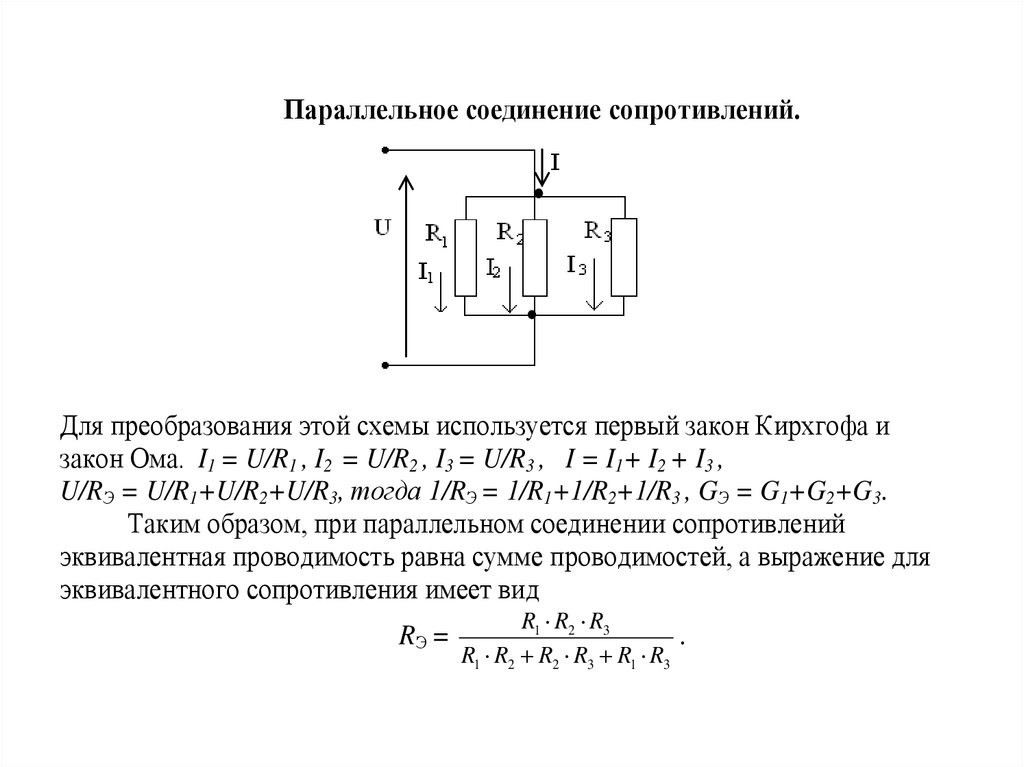 Вы можете рассчитать сопротивление параллельной цепи до 10 резисторов одновременно. Найдите правильные кодовые значения резисторов и введите их в данное поле калькулятора параллельного сопротивления, указанное ниже. Если вам сложно проверить значение резистора, воспользуйтесь онлайн-калькулятором цветового кода резистора
Вы можете рассчитать сопротивление параллельной цепи до 10 резисторов одновременно. Найдите правильные кодовые значения резисторов и введите их в данное поле калькулятора параллельного сопротивления, указанное ниже. Если вам сложно проверить значение резистора, воспользуйтесь онлайн-калькулятором цветового кода резистора
Также проверьте: Калькулятор цветового кода резистора
( You can even enter the total resistance R total and one known resistance R 1 or R 2 ).
Расчет нескольких резисторов в параллельном калькуляторе
Пожалуйста, введите несколько параллельных резисторов (в омах) для расчета параллельного сопротивления
Резистор
Резисторы — это крошечные электронные компоненты, хорошо знакомые большинству людей.
Резистор изготовлен из полупроводникового материала, который препятствует прохождению тока через одну клемму на другую. У резистора всего две клеммы. Сопротивление резистора обозначается цветовым кодом на самом резисторе. Цвет кольца на резисторе меняется, значение сопротивления тоже меняется. Высокое значение означает самое высокое сопротивление потенциальному току. Пройти через него очень сложно.
Резисторы в параллельном соединении
Резистор в параллельном соединении означает, что 2 или более резисторов подключены обоими концами с одинаковой ориентацией или параллельно к каждой клемме. Легко определить, соединены ли резисторы параллельно или последовательно? Если резисторы соединены встык друг с другом, как тележки поезда, это называется последовательным соединением.
Если вы подключаете много резисторов параллельно, общее сопротивление резистора всегда будет меньше наименьшего значения резистора. Согласно уравнению,
P = VI и Резистор, подключенный параллельно, имеет одинаковое напряжение на них все время. Но меняющимся фактором является ток, протекающий через него. Многие резисторы соединены параллельно, крошечный ток, протекающий через каждый из транзисторов, создает огромный ток, возрождающийся на другом конце.
Пример: у вас есть батарея 10 В и резистор 1 кОм. Вы ставите резистор на последовательное соединение с полюсами батареи, измеряя протекающий ток, он показывает 1 мА. Если вы поместите резистор 10 кОм параллельно резистору 1 кОм, ток не изменится через батарею и цепь. Но резистор на 10 кОм потребляет ток всего 0,1 мА через батарею. Из уравнения V =IR оно общее для всех электронных устройств. Напряжение, ток и сопротивление также коррелируют друг с другом.

