Как рассчитать индукцию магнитного поля соленоида. Какие факторы влияют на силу магнитного поля. Формулы для расчета поля внутри и снаружи соленоида. Примеры решения задач по теме.
Что такое соленоид и как он создает магнитное поле
Соленоид представляет собой катушку из проводника, намотанного на цилиндрический каркас. При пропускании электрического тока через обмотку соленоида внутри него возникает магнитное поле. Основные характеристики соленоида, влияющие на создаваемое им магнитное поле:
- Число витков обмотки N
- Длина соленоида l
- Сила тока I, протекающего через обмотку
- Площадь поперечного сечения S
Магнитное поле внутри длинного соленоида является практически однородным и направлено вдоль его оси. Снаружи соленоида поле значительно слабее.
Формула для расчета индукции магнитного поля внутри соленоида
Индукция магнитного поля B внутри бесконечно длинного соленоида рассчитывается по формуле:
B = μ0nI
где:
- μ0 — магнитная постоянная (4π×10^-7 Гн/м)
- n — число витков на единицу длины соленоида (n = N/l)
- I — сила тока в обмотке
Для соленоида конечной длины индукция поля в его центре определяется как:
B = μ0NI / l
где N — общее число витков обмотки, l — длина соленоида.
Факторы, влияющие на силу магнитного поля соленоида
На величину индукции магнитного поля соленоида влияют следующие факторы:
- Сила тока I — прямо пропорциональная зависимость
- Число витков N — прямо пропорциональная зависимость
- Длина соленоида l — обратно пропорциональная зависимость
- Наличие сердечника — ферромагнитный сердечник усиливает поле
- Форма соленоида — длинный тонкий соленоид создает более однородное поле
Чем больше сила тока и число витков, тем сильнее магнитное поле соленоида. При увеличении длины поле ослабевает.
Расчет магнитного поля внутри и снаружи соленоида
Для расчета индукции магнитного поля внутри соленоида конечной длины в произвольной точке на его оси используется формула:
B = (μ0NI/2l) * (cosα1 + cosα2)

где α1 и α2 — углы между осью соленоида и прямыми, соединяющими рассматриваемую точку с краями соленоида.
Снаружи соленоида индукция поля быстро убывает с расстоянием. На оси соленоида вне его концов:
B = (μ0NI/2) * (1/r1 — 1/r2)
где r1 и r2 — расстояния от рассматриваемой точки до концов соленоида.
Примеры расчета магнитного поля соленоида
Рассмотрим несколько типовых задач на расчет магнитного поля соленоида:
Пример 1. Расчет индукции в центре соленоида
Соленоид длиной 20 см содержит 400 витков. Найти индукцию магнитного поля в его центре при силе тока 2 А.
Решение:
- Используем формулу B = μ0NI / l
- Подставляем значения: B = 4π×10^-7 * 400 * 2 / 0.2
- Получаем: B ≈ 5.03 мТл
Пример 2. Определение числа витков соленоида
Какое число витков должен иметь соленоид длиной 25 см, чтобы при токе 0.5 А индукция поля в его центре была 2 мТл?
Решение:
- Из формулы B = μ0NI / l выражаем N
- N = Bl / (μ0I)
- Подставляем значения: N = 0.002 * 0.25 / (4π×10^-7 * 0.5)
- Получаем: N ≈ 796 витков
Практическое применение соленоидов
Соленоиды широко используются в различных областях техники благодаря своей способности создавать управляемое магнитное поле:

- Электромагниты в подъемных кранах и сортировочных устройствах
- Электромагнитные реле и пускатели
- Электромагнитные клапаны
- Линейные актуаторы в автоматике
- Электромагнитные ускорители частиц
- Магнитно-резонансные томографы
Понимание принципов работы и расчета соленоидов необходимо для их эффективного применения в инженерной практике.
Особенности расчета реальных соленоидов
При практических расчетах соленоидов необходимо учитывать ряд факторов, влияющих на создаваемое ими магнитное поле:
- Конечная длина соленоида — приводит к неоднородности поля у краев
- Многослойная намотка — усложняет расчет эффективного числа витков
- Магнитные свойства сердечника — существенно усиливают поле
- Рассеяние магнитного потока — снижает эффективность соленоида
- Нагрев обмотки при протекании тока — изменяет ее сопротивление
Для точных расчетов часто применяют компьютерное моделирование магнитных полей методом конечных элементов.
Сравнение соленоида с другими источниками магнитного поля
Рассмотрим, как соленоид соотносится с другими устройствами, создающими магнитное поле:
| Устройство | Преимущества | Недостатки |
|---|---|---|
| Соленоид | Однородное поле внутри, легко управляемое | Слабое поле снаружи |
| Постоянный магнит | Не требует питания | Фиксированная напряженность поля |
| Тороид | Замкнутое магнитное поле | Сложность изготовления |
| Электромагнит | Сильное регулируемое поле | Большие габариты и вес |
Выбор типа источника магнитного поля зависит от конкретной задачи и требований к характеристикам поля.
Курс физики (Грабовский Р.И.)
Курс физики (Грабовский Р.И.)
ОглавлениеПредисловиеВведение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 10. Силы упругости § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III. 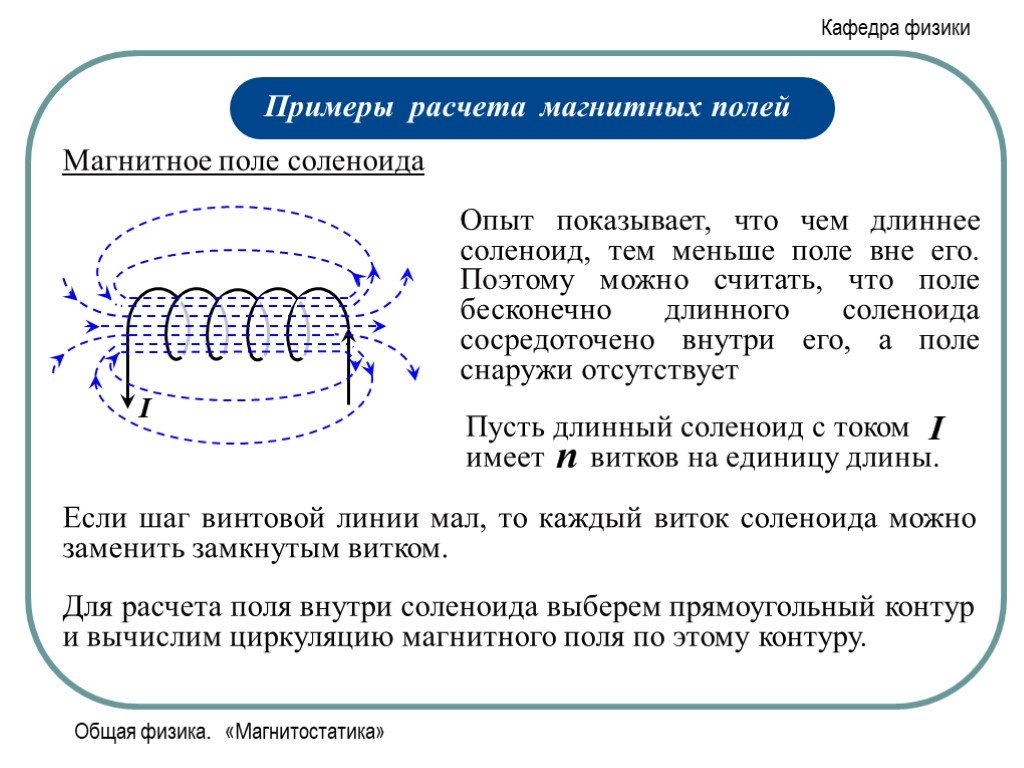 Работа и энергия Работа и энергия§ 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35. 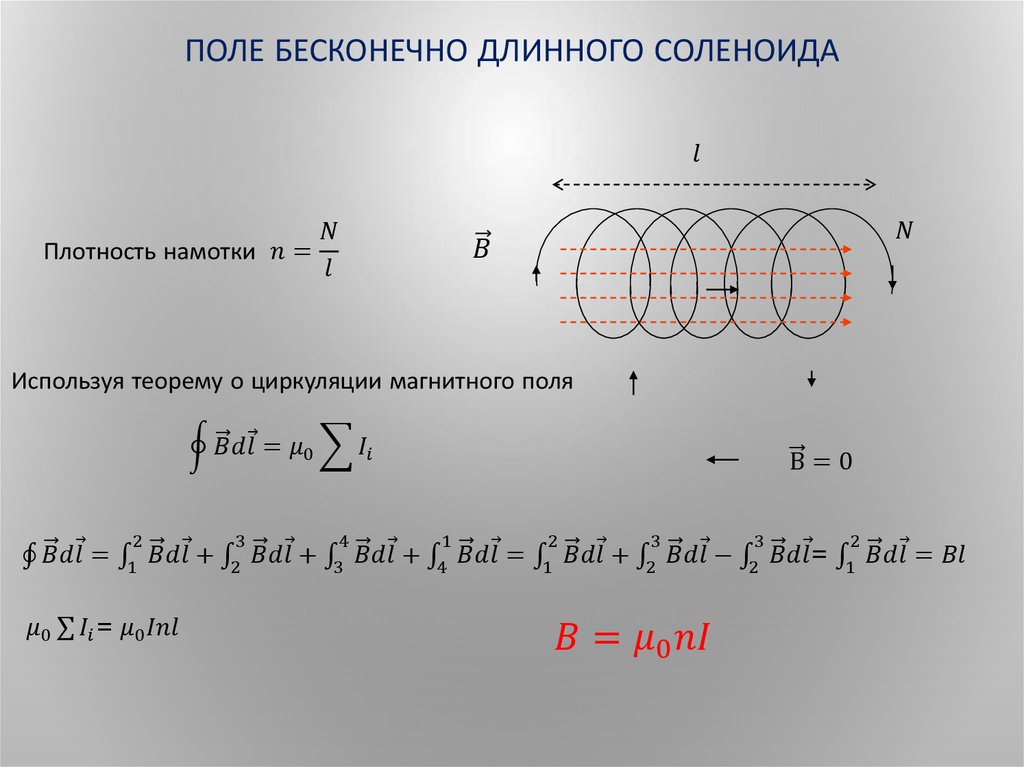 Основные положения молекулярно-кинетической теории Основные положения молекулярно-кинетической теории§ 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 43. О числе степеней свободы. Внутренняя энергия газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50.  Внутреннее трение (вязкость) Внутреннее трение (вязкость)Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. Тепловое расширение твердых и жидких тел § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67.  Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором§ 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле. 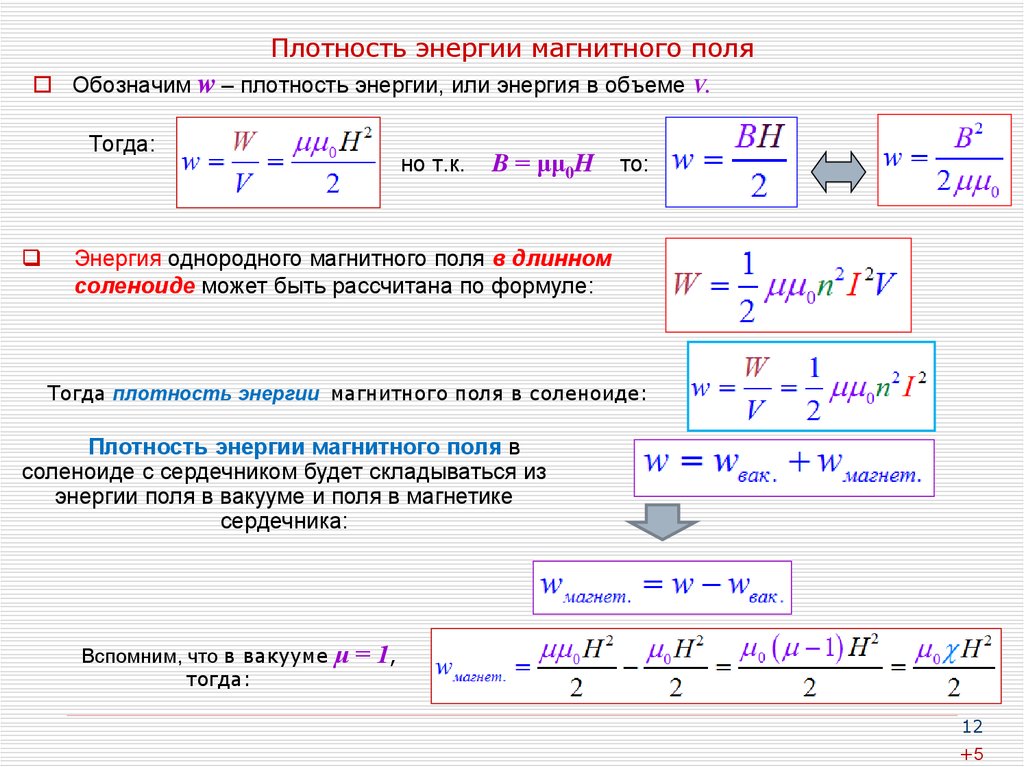 Поляризация диэлектриков Поляризация диэлектриков§ 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток.  Магнитные поля магнитов и токов
Магнитные поля магнитов и токов§ 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла 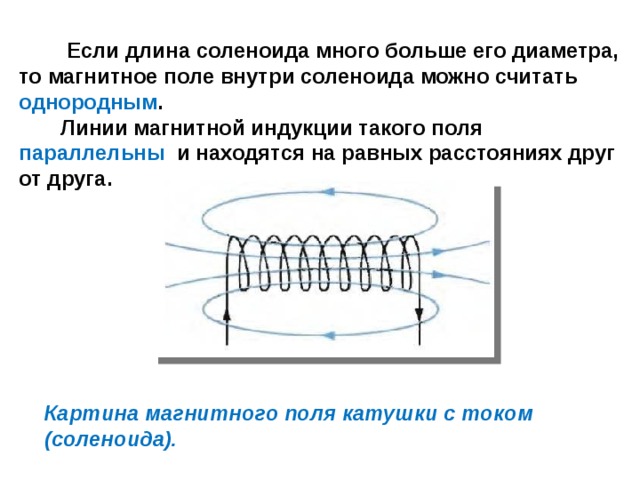 Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока§ 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122. 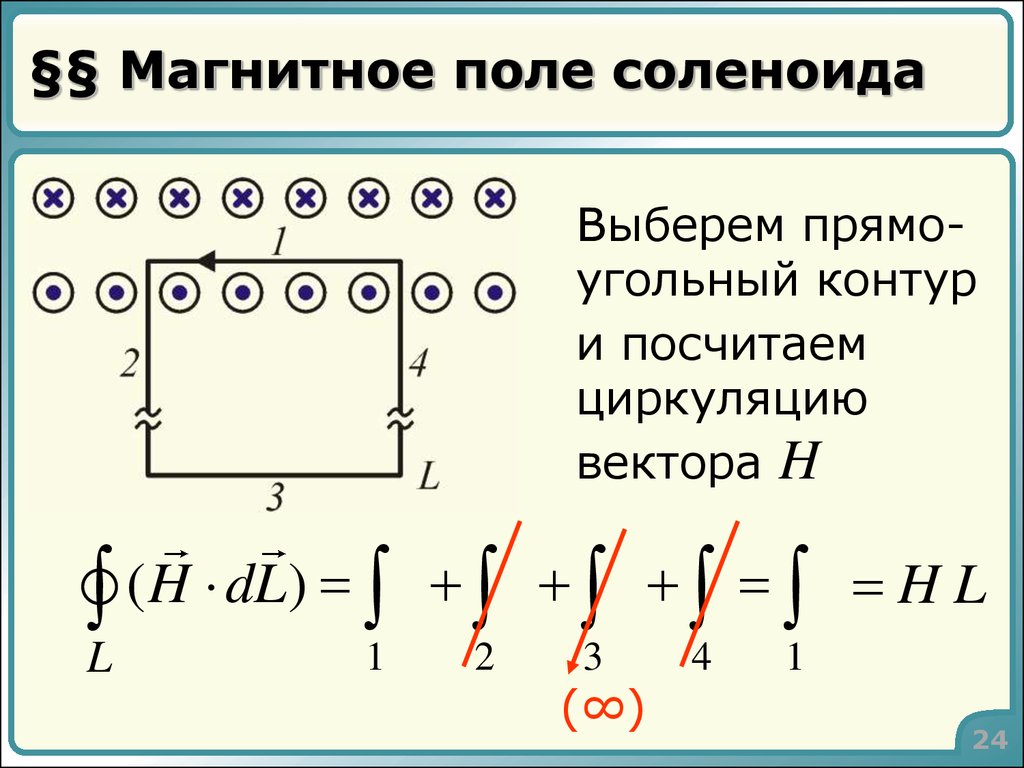 Об интерференции света, отраженного от прозрачных пленок Об интерференции света, отраженного от прозрачных пленок§ 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору).  Объяснение спектров излучения и поглощения водорода Объяснение спектров излучения и поглощения водорода§ 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии |
Вопрос 26.
 Расчет магнитных полей соленоида и тороида с использованием теоремы о циркуляции вектора h.
Расчет магнитных полей соленоида и тороида с использованием теоремы о циркуляции вектора h. Магнитное поле соленоида
Пусть на единицу длины соленоида
приходится п-витков провода с током
I. Если шаг винтовой
линии достаточно мал, то каждый виток
можно приблизительно считать замкнутым
витком с током I (как
круговой ток). Будем также считать, что
сечение провода очень мало, и ток в
соленоиде течет по его наружной
поверхности, т. е. по каркасу катушки
Dк. Опыт
показывает, что чем длиннее соленоид
(Lк >>
Dк), тем
меньше индукция магнитного поля снаружи.
В пределе – для бесконечно длинного
соленоида – снаружи В = 0 и все
поле сосредоточено внутри соленоида;
причем силовые линии В внутри
расположены равномерно и параллельно
оси соленоида, т. е. поле в соленоиде
однородно В = const
при I = const.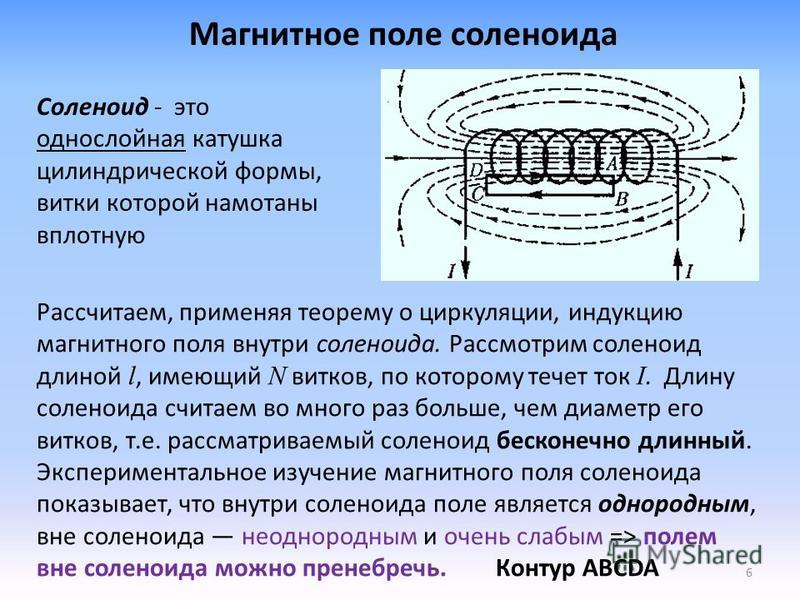
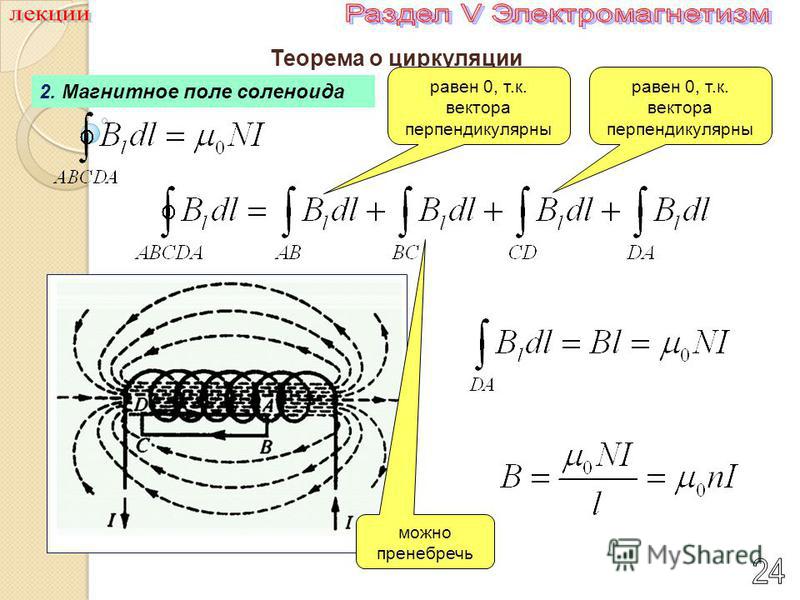
Поэтому, если выбрать контур в виде прямоугольника (см рис.) со стороной l, охватывающий ток (n∙I∙l), то циркуляция В в этом случае будет: B∙l = μ0∙n∙I∙l. Отсюда получаем искомую индукцию в соленоиде:
B = μ0∙n∙I (12)
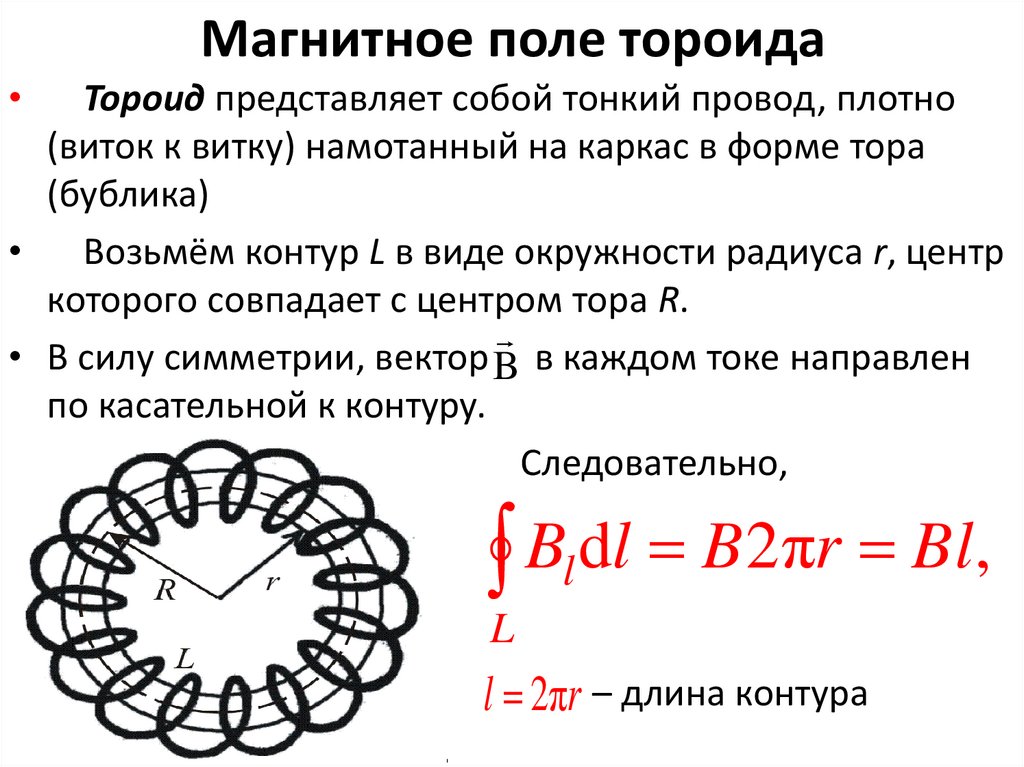
Магнитное поле тороида
Тороид представляет собой магнитную
систему в форме катушки с проводом,
плотно навитым на тороидальный каркас
круглого сечения. Пусть Rср
– средний радиус тора, N
– число витков в обмотке тороида, I
– ток в обмотке тогда из соображений
симметрии следует, что линии магнитной
индукции В здесь будут представлять
собой окружности с центрами на оси ОО’
тороида. Поэтому в качестве контура
интегрирования следует выбрать одну
из этих окружностей (с радиусом r).
Т акой контур охватывает общий ток величиной (N∙I), а циркуляция В в этом случае будет В∙2π∙r = μ0∙N∙I. Из последнего уравнения определяем искомое поле, которое из-за своей конфигурации принято называть азимутальным:
Е сли круглый контур проходит вне тора (за пределами его сечения), то никаких токов он не охватывает, циркуляция В∙2π∙r = 0 и, следовательно, вне тороида В = 0. Если устремить число витков N и радиус тора Rср в бесконечность, то в пределе из формулы (13) получим выражение для поля соленоида, т. е.
Для реального тороида, у которого витки не параллельны оси ОО’, образуется наряду с азимутальным еще и полоидальное поле.
Вопрос 27. Намагниченность вещества. Циркуляция вектора намагниченности. Магнитная восприимчивость и магнитная проницаемость. Связь векторов магнитного поля: b, j, h.

Намагниченность вещества.
Всякое вещество является магнетиком, т.е. способно под действием внешнего магнитного поля намагничиваться – приобретать магнитный момент.
Намагниченное вещество создает свое магнитное поле В’, которое вместе с исходным полем В0, обусловленным токами проводимости, образует результирующее поле (в пространстве, занятом магнетиком): В = В0 + B’ (1)
Д ля объяснения явления намагничения тел Ампер предположил, что в молекулах вещества циркулируют элементарные круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом pmi и создает в пространстве магнитное поле. В отсутствие поля В0 моменты отдельных молекул ориентированы беспорядочно, поэтому их результирующее поле равно 0; соответственно:
Под действием внешнего поля
В0
магнитные моменты молекул приобретают
преимущественную ориентацию в одном
направлении, вещество – намагничивается,
т. е. и образуется поле B’.
е. и образуется поле B’.
С тепень намагничивания магнетика характеризуют суммарным магнитным моментом единицы объема вещества и называют эту величину вектором намагниченности:
Вектор намагниченности можно также представить как: J=n.<pmi>, где n – концентрация молекул, <pmi> — средний магнитный момент одной молекулы.
П оле B’, также как и поле В0, не имеет источников («магнитных зарядов»), поэтому для результирующего поля В при наличии магнетика справедлива теорема Гаусса:
т.е. силовые линии В всегда замкнуты.
Намагничивание вещества также связано с преимущественной ориентацией (а для ряда магнетиков – индуцированием) молекулярных токов, которые могут образовывать, так называемые, макроскопические токи намагничивания I’.
Обычные токи, текущие по
проводникам и связанные с дрейфом в
веществе носителей тока, называют токами
проводимости I.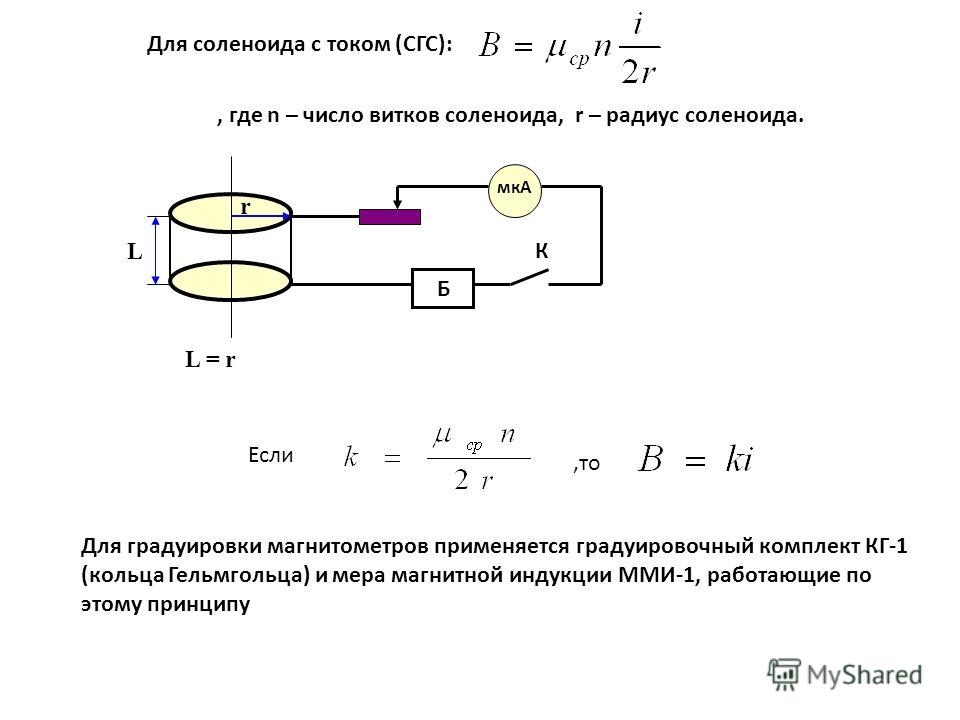
Рассмотрим некоторый цилиндр из однородного магнетика, намагниченность J которого однородна и направлена вдоль оси. Молекулярные токи в магнетике ориентированы как показано на рисунке. Причем у соседних молекул токи в местах их соприкосновения взаимно компенсируются. Неском-пенсированными остаются только токи, которые выходят на боковую поверхность цилиндра.
Эти токи образуют макроскопический поверхностный ток намагничивания I‘пов, который для длинного магнетика определяют через линейную плотность тока i’ [А/м]: I‘пов = i’.l
В неоднородном магнетике
под действием внешнего магнитного поля
молекулярные токи «выстраиваются»
аналогичным образом, но так как их
величина различна (на рисунке эти токи
растут вдоль оси х),
то полной взаимной компенсации этих
токов в объеме магнетика – не происходит
и образуется (наряду с поверхностным
током I’пов)
макроскопический
объемный ток намагничивания I’об
, который
течет вдоль оси y
и может быть определен через поверхностную
плотность тока j’
[А/м2]:
I’об
= j’. ∆S
, где ∆S
– сечение магнетика в плоскости zx.
∆S
, где ∆S
– сечение магнетика в плоскости zx.
Ц иркуляция вектора намагниченности
Докажем следующую теорему:
т.е. циркуляция намагниченности J по произвольному замкнутому контуру Γ равна алгебраической сумме токов намагничивания I’, охватываемых данным контуром.Вычислим алгебраическую сумму молекулярных токов, охватываемых контуром Γ; причем, как видно из рисунка, только те молекулярные токи, которые обвиваются вокруг контура и пересекают натянутую поверхность S один раз, учитываются в этой сумме.
Если каждый молекулярный
ток равен Iм
, а площадь его
контура Sм,
то, как видно из следующего рисунка,
элемент dl
контура Γ
обвивают те молекулярные
токи, центры которых попадают внутрь
косого цилиндра с объемом dV=Sм. cosα.dl,
где α
— угол между dl
и намагниченностью J
в данном месте. Эти токи пересекают
поверхность S
один раз, и их вклад в общий ток I’
составляет: dI’=Iм.n.dV, где
n
– концентрация молекул магнетика.
cosα.dl,
где α
— угол между dl
и намагниченностью J
в данном месте. Эти токи пересекают
поверхность S
один раз, и их вклад в общий ток I’
составляет: dI’=Iм.n.dV, где
n
– концентрация молекул магнетика.
П одставив в последнюю формулу выражение для dV, получаем: dI´= IM.SM.n.cosα.dl = J.cosα.dl = , где учтено, что IM.SM = рm, а рm.n = J. Проинтегрировав последнее выражение для dI´по контуру Г, приходим к доказываемому положению
В
оспользовавшись
теоремой Стокса (переход от циркуляции
по контуру к потоку ротора через
поверхность, натянутую на контур) ,
преобразуем интегральную форму теоремы
о циркуляции вектора J
в дифференциальную форму.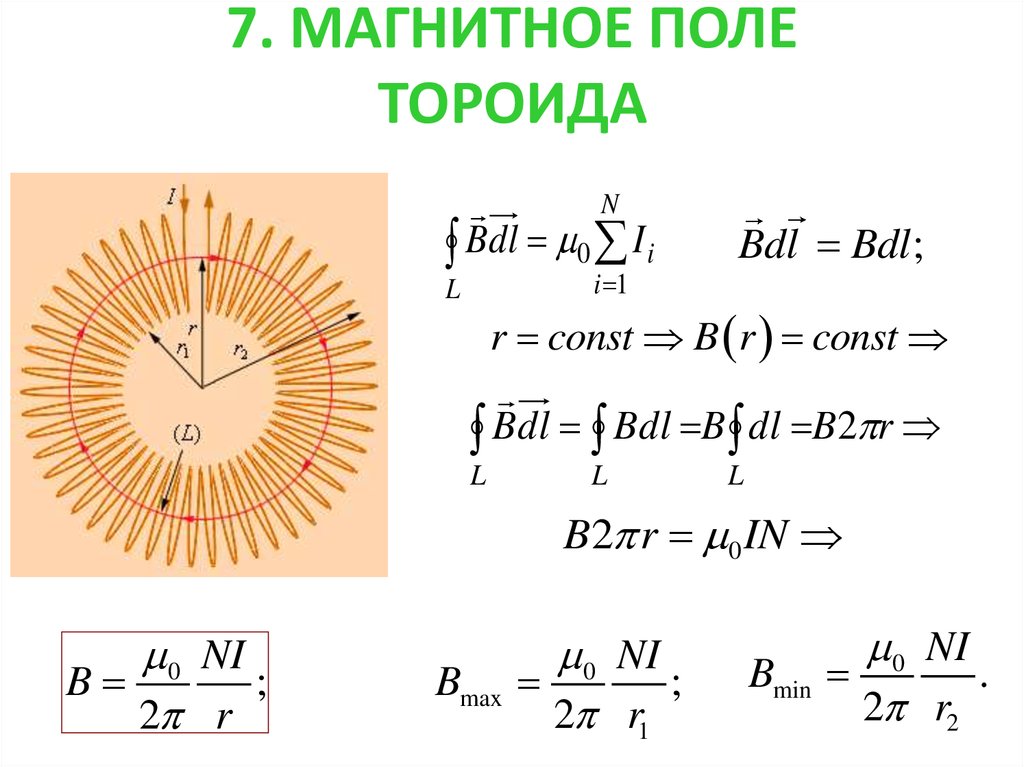 Соответствующее
уравнение
Соответствующее
уравнение
д олжно выполняться для любого контура с площадкой dS в случае, когда его подынтегральные выражения равны, т. е.
Ротор намагниченности равен плотности тока намагничивания в той же точке вещества. Циркуляция вектора магнитной индукции в веществе.
В магнетиках, помещенных во внешнее магнитное поле В0, возникают, как уже установлено, токи намагничивания I´и, следовательно, для результирующего поля можно записать:
где I – ток проводимости и I´— ток намагничивания, охватываемые заданным контуром Г.
Т ак как определение токов намагничивания в общем случае задача сложная, то использование формулы (5) для нахождения В становится крайне трудным. Поэтому следует установить некоторый вспомогательный вектор, циркуляция которого определяется только токами проводимости. Заменив в (5) ток I´через циркуляцию ,
получаем после деления на μ0 уравнение (5) в виде:
Величину, стоящую под
интегралом в скобках, называют
напряженностью
магнитного поля.
Ц иркуляция вектора Н по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром, т. е.
Д ифференциальная форма получается с помощью теоремы Стокса
Ротор вектора Н равен плотности тока проводимости в той же точке вещества.
С вязь между векторами J и H
где χ – магнитная восприимчивость вещества (величина безразмерная, характеризует магнитные свойства вещества).
Связь между векторами В и H
Д ля изотропных магнетиков, для которых выполняется (9), определение напряженности (6) может быть записано как
или представлено в виде
В водя понятие магнитной проницаемости среды как μ=1+ χ получаем прямую связь двух основных векторов магнитного поля:
Так как для вакуума имеем
В0=
μ0. Н0,
то вследствие (10) магнитная проницаемость
μ
показывает, во сколько раз магнитное
поле токов проводимости усиливается
за счет намагничения среды.
Н0,
то вследствие (10) магнитная проницаемость
μ
показывает, во сколько раз магнитное
поле токов проводимости усиливается
за счет намагничения среды.
Объяснение урока: Магнитное поле, создаваемое током в соленоиде
В этом объяснении мы узнаем, как рассчитать магнитное поле, создаваемое ток в соленоиде.
Вспомнить направление магнитного поля в петле провода с током. В центре петли магнитное поле имеет одно направление, как видно на схема ниже. Оранжевая линия — направление магнитного поля, черная линия — направление магнитного поля. петля.
Та же петля, вид спереди, с указанием направления магнитного поля вне экрана, будет выглядеть как на диаграмме ниже.
Помните, что приведенные ниже символы используются для обозначения того, что направление выходит из или в экран.
Напряженность магнитного поля в центре петли можно увеличить, поместив
больше петель в соответствии с ним.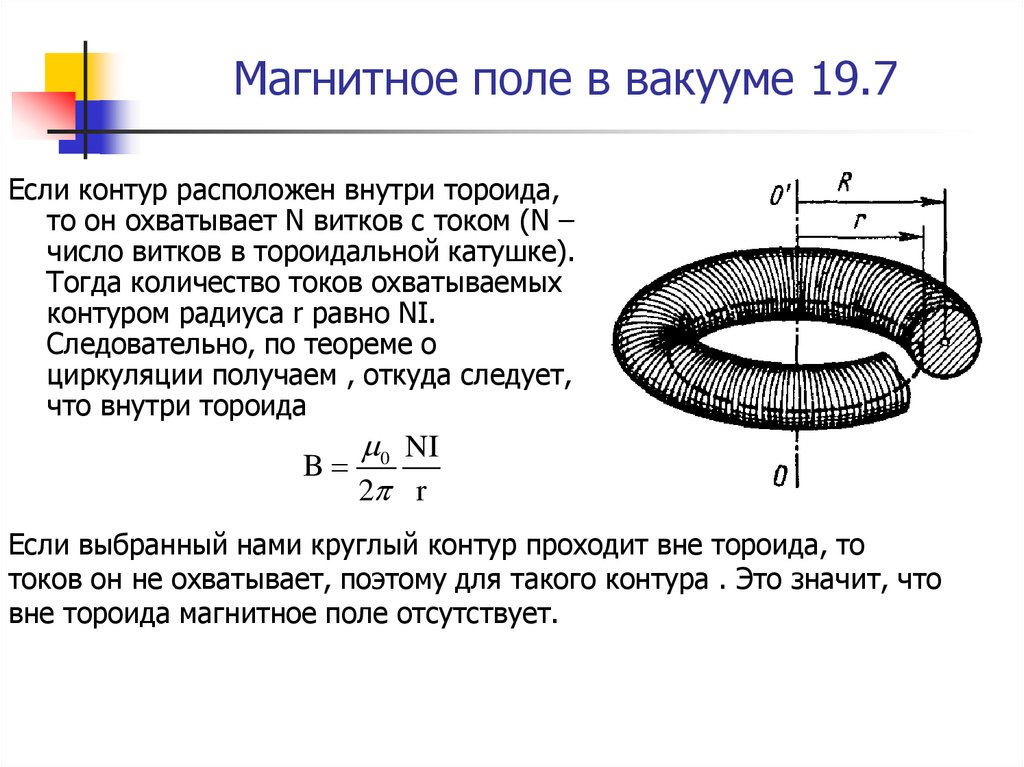 На диаграмме ниже показаны два набора петель с одинаковыми
тока и того же радиуса выстроились таким образом.
На диаграмме ниже показаны два набора петель с одинаковыми
тока и того же радиуса выстроились таким образом.
Набор петель справа имеет более сильное магнитное поле, потому что в нем больше петли.
Вместо набора петель усиление магнитного поля в центре может быть достигнуто с помощью одного провода с несколькими витками. На приведенной ниже диаграмме показано такой провод, с видом сбоку и спереди.
Провод с таким набором витков называется соленоидом. Каждый ход соленоид вносит свой вклад в силу магнитного поля в центре точно так же, как дополнительная петля будет.
Напряженность и направление магнитного поля в самом центре соленоида униформа. Он имеет одно направление и величину. Другие точки вокруг соленоида имеют различные направления и величины магнитного поля.
Прежде чем рассматривать силовые линии магнитного поля соленоида, давайте рассмотрим
угол, с которого мы будем смотреть, используя один цикл. На приведенной ниже диаграмме показан
одиночный виток провода с током и его результирующее магнитное поле от двух
разные углы.
На приведенной ниже диаграмме показан
одиночный виток провода с током и его результирующее магнитное поле от двух
разные углы.
Вид сбоку этой петли показывает направление, в котором смотрит наблюдатель, обозначенное глазом, чтобы получить вид сверху вниз. Вид сверху вниз по-прежнему показывает направление тока, входящего и выходящего из экрана, но не показать нижнюю часть петли.
Теперь давайте посмотрим на вид сверху вниз на одну петлю с ее магнитным линии поля, выделенные серым цветом, на диаграмме ниже.
Когда силовые линии магнитного поля расположены близко друг к другу, это означает, что более сильное магнитное поле. Мы видим, что в самом центре петли силовые линии магнитного поля расположены очень близко друг к другу с одинаковым направлением, что означает в этой точке у него сильное магнитное поле.
Вне контура силовые линии магнитного поля напоминают стержневой магнит,
как показано ниже.
Теперь посмотрим на соленоид с семью витками под этим углом. Диаграмма ниже показано это с соответствующим магнитным полем.
Обратите внимание, что силовые линии магнитного поля постоянны и прямые в самом центре эти провода поворачиваются, но становятся менее последовательными по направлению к концам соленоида. ближе к этим концам, тем менее однородны силовые линии.
Теперь давайте рассмотрим теоретически очень длинный соленоид. Это так долго, что мы можем относиться к нему так, как если бы у него не было концов. Это означало бы, что он имеет совершенно однородный магнитное поле внутри витков во всех точках.
Если бы мы измерили напряженность магнитного поля в разных точках в пределах витков
этот теоретический соленоид, в каждом случае величина и направление магнитного
напряженность поля была бы такой же. На приведенной ниже диаграмме показан теоретический соленоид.
с тремя точками, обозначенными красными точками, которые имеют эквивалентное магнитное поле
сильные стороны и направления.
Напряженность магнитного поля внутри витков этого теоретического соленоида может быть определяется с помощью уравнения.
Уравнение: напряженность магнитного поля в центре соленоида
Напряженность магнитного поля, 𝐵, внутри центра соленоида находится с помощью уравнения 𝐵=𝜇𝑁𝐼𝐿, где 𝐼 — ток соленоида, 𝑁 — количество витков соленоида, 𝐿 — длина соленоида, а 𝜇 — проницаемость свободного пространства, 4𝜋×10 Т⋅м/А.
Для реального соленоида с ограниченной длиной это уравнение по-прежнему полезно для описывают напряженность магнитного поля точно в центре витков, так как это там, где она однородна. На диаграмме ниже показаны точки с одинаковыми магнитными напряженность и направление поля как на теоретическом, так и на реальном соленоиде.
Реальные соленоиды имеют достаточно постоянное направление магнитного поля внутри витков,
но не напряженность магнитного поля. Только центр имеет постоянное магнитное поле. сила.
сила.
Глядя на уравнение, мы видим, что длина соленоида имеет значение, когда найти напряженность магнитного поля в центре. В частности, это магнитное напряженность поля обратно пропорциональна длине. На схеме ниже показаны два соленоиды с одинаковым током и числом витков, но с разным длины.
Так как нижний соленоид в два раза длиннее, он будет иметь вдвое меньшую длину. напряженность магнитного поля в его центре.
Давайте рассмотрим пример с использованием этого уравнения.
Пример 1: Напряженность магнитного поля в центре соленоида с витками и Длина
Соленоид имеет длину
3,2 см
и состоит из 90 витков провода. По проводу течет постоянный ток
1,2 А. Рассчитайте напряженность магнитного поля в центре соленоида. Дайте свой ответ в
тесла
выражается в научной записи с точностью до одного десятичного знака. Используйте значение
4𝜋×10 Т⋅м/А
для 𝜇.
Ответ
Мы будем использовать уравнение 𝐵=𝜇𝑁𝐼𝐿 найти напряженность магнитного поля в центре этого соленоида.
Прежде чем мы сможем подставить значения, которые нам даны, мы должны убедиться, что единицы все совпадают. Проницаемость свободного пространства использует метры, поэтому нам нужна длина 3,2 см в метров.
Есть 100 сантиметров в 1 метр: 1100 мкм
Итак, чтобы преобразовать 3,2 см в метры, умножаем на соотношение 1100×3,2=0,032 мкм см
Таким образом, 3,2 см составляет 0,032 м.
Теперь мы можем подставить значения в уравнение. Длина 0,032 м, ток 1,2 А, 90 витков, а проницаемость свободного пространства 4𝜋×10 Т⋅м/А. Это дает нам 𝐵=𝜇𝑁𝐼𝐿𝐵=4𝜋×10⋅/(90)(1,2)0,032.TmAAm
Умножим в числителе. Это отменяет единицы
Ампер там,
давать
𝐵=1,36×10⋅0,032. Tмм
Tмм
Итак, теперь, когда мы разделим эти два числа, единицы метры отменить, оставив только тесла: 1,36×10⋅0,032=4,24×10,TmmT
Округлив до одного десятичного знака, напряженность магнитного поля в центре соленоид 4,2×10 T.
Напряженность магнитного поля в центре уравнения соленоида можно использовать для нахождения другие переменные в уравнении, если напряженность магнитного поля в центре соленоид известен. Чтобы показать это, давайте посмотрим на основное уравнение и положим все значения с точки зрения 𝐼. Начиная с уравнения 𝐵=𝜇𝑁𝐼𝐿, мы можем умножить обе части на 𝐿: 𝐵×𝐿=𝜇𝑁𝐼𝐿×𝐿.
Это отменяет 𝐿 справа, оставляя позади 𝐵𝐿=𝜇𝑁𝐼.
Из этой формы мы можем разделить обе части на 𝜇 и 𝑁: 𝐵𝐿𝜇𝑁=𝜇𝑁𝐼𝜇𝑁.
Это отменяет 𝜇 и 𝑁 с правой стороны, оставив только 𝐼: 𝐵𝐿𝜇𝑁=𝐼.
Давайте рассмотрим пример, используя эту форму уравнения.
Пример 2: Определение тока в соленоиде с витками и длиной
Соленоид состоит из 35 витков провода на длине 42 мм. Магнитное поле в центре соленоида измеряется как 4.9×10 Тл. Рассчитайте силу тока в проводе. Дайте ответ в амперах на 2 десятичных разряда. Используйте значение 4𝜋×10 Т⋅м/А для 𝜇.
Ответ
Напомним, что уравнение 𝐵=𝜇𝑁𝐼𝐿 можно представить в виде, связывающем переменные с текущим: 𝐼=𝐵𝐿𝜇𝑁.
Перед тем, как мы непосредственно подставим полученные значения в эту форму уравнение, мы должны убедиться, что единицы совпадают. Проницаемость свободного пространства использует метры, поэтому нам нужна длина соленоида, 42 мм, чтобы также быть в с точки зрения метров.
1 000 миллиметров в 1 метр: 11000.mmm
Таким образом, умножая это отношение на
42 мм
даст нам значение в
метров:
11000×42=0,042. мммммм
мммммм
Длина соленоида в метрах составляет 0,042 м.
Теперь мы можем подставить значения в уравнение. Длина 0,042 м, магнитный напряженность поля 4,9×10 Т, витков 35, а проницаемость свободного пространства равна 4𝜋×10 Т⋅м/А. Это дает нам 𝐼=𝐵𝐿𝜇𝑁𝐼=4,9×10(0,042)(4𝜋×10⋅/)(35).TmTmA
Умножение на числитель дает единицы Т⋅м: 𝐼=2,06×10⋅(4𝜋×10⋅/)(35).TmTmA
Количество витков в соленоиде безразмерно, поэтому умножение на знаменатель не меняет единицы измерения: 𝐼=2,06×10⋅4,39×10⋅/.TmTmA
Разделение верхней части на нижнюю полностью аннулирует единицы Т⋅м и уходи за амперами на вершина. Глядя только на единицы, деление на дробь такое же, как умножение на обратное: (⋅)(⋅/)=(⋅)×(⋅)=.TmTmATmATmA
Итак, деление чисел дает
2,06×10⋅4,39×10⋅/=0,468. TmTmAA
TmTmAA
Округлив до двух знаков после запятой, ответ будет таким образом 0,47 A.
Уравнение можно записать и в терминах других переменных. Допустим, у нас есть соленоид с неизвестной длиной, но с другими известными переменные. Начиная с основного уравнения 𝐵=𝜇𝑁𝐼𝐿, мы можем получить длину одной стороны уравнения, умножив обе части на 𝐿: 𝐵×𝐿=𝜇𝑁𝐼𝐿×𝐿.
Отменяет 𝐿 справа, давая 𝐵𝐿=𝜇𝑁𝐼.
Затем мы делим обе части на 𝐵, чтобы получить 𝐵𝐿𝐵=𝜇𝑁𝐼𝐵, который отменяет 𝐵 слева, оставляя только 𝐿: 𝐿=𝜇𝑁𝐼𝐵.
Давайте рассмотрим пример, использующий эту форму уравнения.
Пример 3: Длина соленоида
Соленоид, образованный из отрезка проволоки, имеет 80 витков. Соленоид несет
постоянный ток 13 А
и сила создаваемого магнитного поля измеряется как
7,3×10 Т
в его центре. Вычислите длину соленоида, ответив на вопрос
Ближайшая
сантиметр.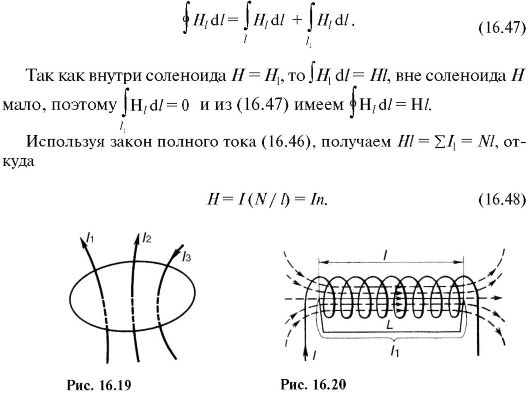 Используйте значение
4𝜋×10 Т⋅м/А
для 𝜇.
Используйте значение
4𝜋×10 Т⋅м/А
для 𝜇.
Ответ
Напомним, что уравнение 𝐵=𝜇𝑁𝐼𝐿 можно представить в виде, связывающем переменные с длиной соленоида: 𝐿=𝜇𝑁𝐼𝐵.
Давайте подставим полученные значения в эту форму уравнение. Текущий 13 А, количество витков 80, напряженность магнитного поля в центре 7,3×10 Т, а проницаемость свободного пространства 4𝜋×10 Т⋅м/А. Это дает нам 𝐿=𝜇𝑁𝐼𝐵𝐿=4𝜋×10⋅/(80)(13)7,3×10.TmAAT
Умножая на числитель, единицы Ампер отменить, осталось только T⋅m: 𝐿=1,306×10⋅7,3×10.TmT
Деление этих чисел отменяет тесла, оставляя позади только метры: 1,306×10⋅7,3×10=0,179.TmTm
Итак, длина этого соленоида равна
0,179 метра. Мы еще не закончили, так как нам нужен окончательный ответ на проблему в
сантиметры.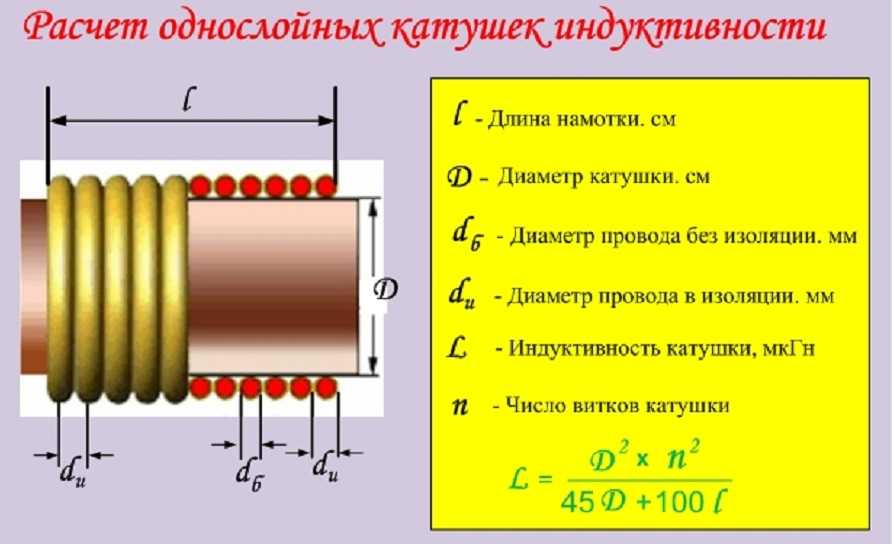
Чтобы выразить этот ответ в сантиметрах, напомнить, что есть 100 сантиметров в 1 метре: 1001.см
Умножив это на наш ответ в метров даст нам ответ в сантиметрах: 1001×0,179=17,9.смммсм
Итак, округляем до ближайшего сантиметр, этот соленоид имеет длину 18 сантиметров. Ответ 18 см.
Напомним, что длина соленоида обратно пропорциональна магнитному полю сила в его центре. Более длинной длине можно противодействовать, добавляя больше витков в провод, как показано на схеме ниже.
Оба соленоида имеют одинаковую напряженность магнитного поля, так как более длинный соленоид имеет пропорционально большее количество оборотов. Мы также можем видеть, что более длинный соленоид по сути то же самое, что и первое, но его просто больше.
Это означает, что добавление большего количества витков провода, увеличение длины соленоида в процессе,
вообще не увеличивает напряженность магнитного поля в центре. Что увеличивает
напряженность магнитного поля — это число витков на заданной длине. Это
доказано, глядя на уравнение
𝐵=𝜇𝑁𝐼𝐿.
Что увеличивает
напряженность магнитного поля — это число витков на заданной длине. Это
доказано, глядя на уравнение
𝐵=𝜇𝑁𝐼𝐿.
Если предположить, что ток одинаков для двух соленоидов, то единственный непостоянными переменными, влияющими на напряженность магнитного поля, являются число витков 𝑁 и длина 𝐿: 𝑁𝐿.
Мы видим, что удвоение витков до 2𝑁 и длины до 2𝐿 вообще не меняет эту пропорцию. Удвоенные значения исключают друг друга: 2𝑁2𝐿=𝑁𝐿.
Для упрощения уравнения эту пропорцию часто сокращают до простой строчной буквы. 𝑛, 𝑁𝐿=𝑛, единицами которых являются витки на единицу длины. Внутри полного уравнения это выглядит следующим образом.
Уравнение: магнитное поле в центре соленоида с числом оборотов на Длина блока
Напряженность магнитного поля, 𝐵, внутри центра соленоида
находится с помощью уравнения
𝐵=𝜇𝑛𝐼,
где 𝐼 — ток соленоида,
𝑛 — количество витков на единицу длины, а
𝜇 — проницаемость свободного пространства,
4𝜋×10 Т⋅м/А.
Единицы 𝑛 выражены на единицу длины. Например, рассмотрите соленоид на диаграмме ниже.
Значение 𝑛 — это общее количество витков по всей длине: 𝑛=𝑁𝐿.
Итак, 6 витков и 3 см длины дает 63=2.turnscmturnspercentimetre
Если бы мы удвоили количество витков до 12 и удвоили длину до 6 см, мы бы увидели значение 𝑛 все тот же 126=2.оборотсмоборотовпроцентиметр
Только путем изменения пропорции витков к длине соленоида изменение напряженности магнитного поля.
Давайте рассмотрим пример.
Пример 4: Изменения магнитного поля в соленоиде
Отрезок проволоки превращается в соленоид с 𝑛 витков провода на миллиметр. По проводу течет постоянный ток 𝐼. В результате магнитное поле напряженностью 𝐵 может быть измеряется в центре соленоида. Какое из следующих изменений в системе увеличит магнитное напряженность поля в центре соленоида, при условии, что все остальное остается постоянным?
- Уменьшение длины соленоида путем удаления витков провода при сохраняя 𝑛 постоянным
- Уменьшая 𝐼, ток в проводе
- Уменьшая 𝑛, количество витков провода на миллиметр
- Увеличение 𝐼, тока в проводе
- Увеличение длины соленоида добавлением витков провода при сохраняя 𝑛 постоянным
Ответ
Вспомним форму уравнения с
𝑛 оборотов на единицу длины:
𝐵=𝜇𝑛𝐼.
Если 𝑛 не изменяется в этом уравнении, магнитное поле сила не меняется. Добавление или удаление частей соленоида, но сохранение постоянной 𝑛 означает напряженность магнитного поля остается такой же.
Уменьшение 𝑛, однако, уменьшит магнитное поле сила. Точно так же уменьшение тока также уменьшит магнитное поле. напряженность поля. Это связано с тем, что напряженность магнитного поля напрямую пропорциональна как 𝑛, так и 𝐼.
Единственный способ увеличить напряженность магнитного поля — увеличить 𝑛 или 𝐼. Единственный ответ с этим увеличение D, увеличение 𝐼.
Правильный ответ D, при увеличении тока в проводе будет увеличиваться напряженность магнитного поля.
При использовании 𝑛 для выполнения вычислений обороты безразмерны,
поэтому единицы 𝑛 указаны только на единицу длины. Это значит, что
хотя мы бы сказали 5 оборотов в
метр,
внутри уравнения мы бы просто написали
5. м
м
Давайте рассмотрим пример.
Пример 5: Напряженность магнитного поля в центре соленоида
Провод, по которому течет постоянный ток 0,15 А представляет собой соленоид с 11 витками на сантиметр. Вычислите напряженность магнитного поля в центре соленоид. Дайте свой ответ в тесла выражается в научной записи с точностью до одного десятичного знака. Используйте значение 4𝜋×10 Т⋅м/А для 𝜇.
Ответ
Соленоид выглядит так, как показано на рисунке ниже.
Вспомните уравнение для напряженности магнитного поля в центре соленоид с использованием оборотов на единицу длины: 𝐵=𝜇𝑛𝐼.
Прежде чем подставлять значения в это уравнение, мы должны убедиться,
единицы совпадают. Проницаемость использования свободного пространства
метры,
поэтому нам нужно поставить 𝑛 с точки зрения
метров также.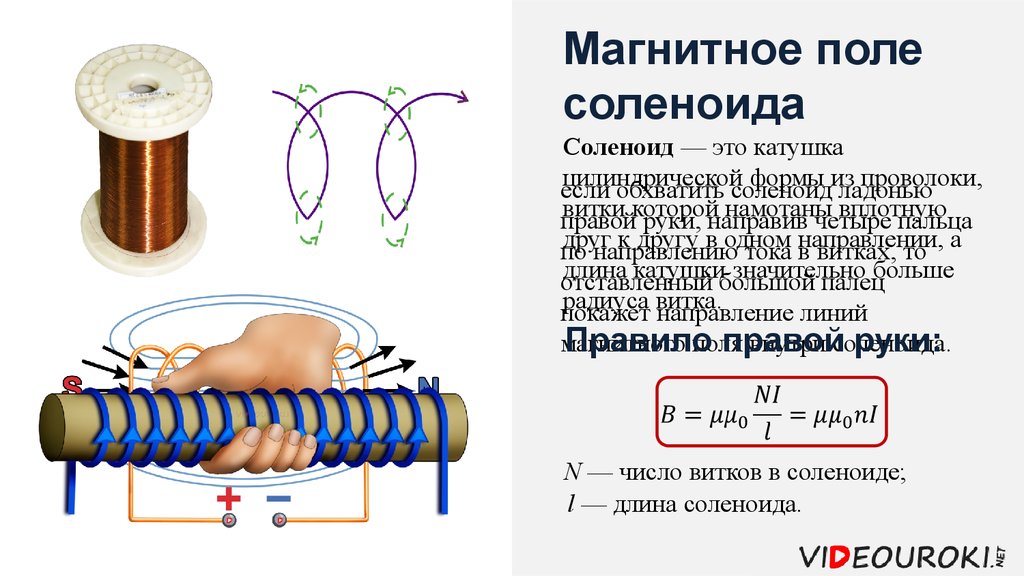
Значение 𝑛 составляет 11 витков на сантиметр, а там 100 сантиметров в 1 метре: 1001.см
Умножив это соотношение на 11 витков на сантиметр превратит его в число оборотов в метр: 1001×11=1100.cmcmm
Теперь мы можем подставить значения в уравнение. Текущий 0,15 А, 𝑛 составляет 1 100 оборотов в метр, и 𝜇 4𝜋×10 Т⋅м/А. Это дает нам 𝐵=𝜇𝑛𝐼𝐵=4𝜋×10⋅/1100(0,15).TmAmA
Умножая проницаемость свободного пространства на обороты на метр отменяет счетчики, оставляя позади 𝐵=1,38×10/(0,15).ТАА
Умножение двух последних чисел отменяет единицы измерения. ампер, оставив тесла, чтобы дать 1,38×10/(0,15)=2,07×10,TAAT
Таким образом, округляя до одного десятичного знака, напряженность магнитного поля в
центр этого соленоида
2,1×10 T.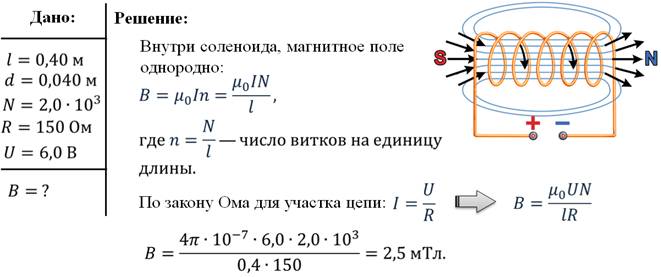
Как и в случае с другой версией уравнения напряженности магнитного поля, мы можем изолировать конкретные неизвестные переменные. Например, если нам дан соленоид с неизвестный ток, мы можем определить его, составив уравнение 𝐵=𝜇𝑛𝐼 с точки зрения 𝐼.
Для этого разделим обе части на 𝜇𝑛: 𝐵𝜇𝑛=𝜇𝑛𝐼𝜇𝑛.
Отменяет 𝜇𝑛 с правой стороны, оставляя позади только 𝐼: 𝐵𝜇𝑛=𝐼.
Давайте рассмотрим пример, в котором используется эта форма уравнения.
Пример 6: Определение тока в соленоиде с числом витков на длину
Соленоид состоит из отрезка провода, по которому течет постоянный ток 𝐼. Соленоид имеет 430 витков провода на метр. Магнитное поле в центре соленоида измеряется как 3,2×10 Т. Рассчитаем ток, 𝐼, в амперах. Дайте ответ с точностью до 1 знака после запятой. Использовать 𝜇=4𝜋×10⋅/TmA.
Ответ
Напомним, что уравнение
𝐵=𝜇𝑛𝐼
можно выразить в терминах 𝐼 следующим образом:
𝐼=𝐵𝜇𝑛.
Используя эту форму, подставим известные значения. Напряженность магнитного поля 3,2×10 Т, 𝑛 составляет 430 витков на метр, и 𝜇 4𝜋×10 Т⋅м/А. Это дает нам 𝐼=𝐵𝜇𝑛𝐼=3,2×10(4𝜋×10⋅/).TTmAm
Умножение на знаменатель удаляет единицы метров, дача 𝐼=3,2×105,4×10/.ТТА
Деление на дробь равносильно умножению на ее обратную величину. Это означает, что единственным юнитом после деления будет ампер: ТТАТАТА/=×=.
Итак, при делении чисел ответ становится 3,2×105,4×10/=5,92.TTAA
Округлив до ближайшего десятичного знака, ответ будет 5.9 A.
Давайте обобщим то, что мы узнали из этого объяснения.
Основные положения
- Соленоид представляет собой провод, состоящий из ряда витков или петель.
- Когда по соленоиду течет ток, он создает магнитное поле, которое
сильнее всего в центре своих петель.

- В петлях соленоида напряженность магнитного поля 𝐵 дается уравнением 𝐵=𝜇𝑁𝐼𝐿, где 𝑁 — число витков в соленоиде, 𝐼 — ток в соленоиде, 𝐿 — длина соленоида, а 𝜇 — проницаемость свободной пространство, 4𝜋×10 Т⋅м/А.
- Уравнение для напряженности магнитного поля 𝐵 в центре соленоид с использованием оборотов на единицу длины 𝐵=𝜇𝑛𝐼, где 𝑛 — количество витков на единицу длины, 𝐼 — ток соленоида, а 𝜇 — проницаемость свободного пространства, 4𝜋×10 Т⋅м/А.
Калькулятор магнитного поля соленоида
Калькулятор магнитного поля соленоида может помочь вам найти магнитное поле внутри соленоида по его длине, количеству витков и току, циркулирующему через него.
Вы когда-нибудь задумывались, какова сила магнитного поля в центре соленоида? В этой короткой статье мы объясним уравнение магнитного поля соленоида и соединим его с некоторыми примерами, чтобы вы могли легко понять эту тему.
Магнитное поле формулы соленоида. Магнитное поле приближения бесконечного соленоида.
Соленоид — это просто провод, обернутый вокруг нескольких петель. Когда по этому проводу циркулирует ток, внутри него создается магнитное поле В.
🙋 Если вы ничего не знаете об электричестве и его понятиях, калькулятор закона Ома — идеальное место для начала!
Если длина соленоида намного больше его радиуса , мы можем считать магнитное поле внутри него однородным и попытаться найти магнитное поле бесконечного соленоида.
Таким образом, используя закон Ампера , мы можем получить магнитное поле уравнения соленоида :
B=µINLB = \frac{\mu I N}{L}B=LµIN
, где:
- III – сила тока;
- NNN – общее количество витков;
- LLL — общая длина соленоида; и
- мк\мк — проницаемость материала внутри соленоида (или проницаемость свободного пространства).
Мы также можем заменить это следующей формулой, если мы знаем количество витков на метр nnn, но не расстояние:
B=µInB = \mu I nB=µIn
Это все, что вам нужно знать, чтобы начать использовать калькулятор магнитного поля соленоида! Как видите, найти магнитное поле в центре соленоида довольно просто.


