Расчет соленоида: Индуктивность длинного соленоида

Содержание

Расчет переходных процессов в соленоиде размагничивающего устройства рельсовых плетей при включении его на импульсное воздействие

АННОТАЦИЯ

В статье рассматриваются переходный процесс при включении соленоида с сердечником на первую гармонику напряжения, используя метод последовательных приближений и применением метода наложения для основного действия и первой и третьей гармонических составляющих тока определены вебер амперные характеристики соленоида с сердечником.

ABSTRACT

The article discusses the transient process when a solenoid with a core is turned on to the first harmonic of the voltage, using the method of successive approximations and applying the superposition method for the main action and the first and third harmonic components of the current determined the Weber ampere characteristics of the solenoid with a core.

Ключевые слова: переходный процесс; соленоид; размагничивающее устройство; импульсное воздействие; метод последовательных приближений; метод наложения.

Keywords: transitional process; solenoid; demagnetizing device; impulse impact; method of successive approximations; overlay method.

Любое импульсное воздействие представляет собой периодические несинусоидальные напряжения, токи, потокосцепление. Поэтому необходимо раскладывать в ряд Фурье импульсы в виде прямоугольника, треугольника, полуволны синусоид, следующих периодически. Для качественного размагничивающего устройства необходимо учесть импульсы в виде прямоугольника и треугольника[4-7]. Формы показаны на рис.1.

Для расчетов используем реальные значения прямоугольного импульса параметрами: частота ; период ; длительность импульса ; напряжение .

а) б)

Рисунок 1. Периодические функции несинусоидального напряжения в устройстве размагничивания. а) прямоугольный импульс; б) треугольный импульс

Вначале рассмотрим разложение в ряд прямоугольного импульса, который запишется в виде:

. (1)

С учетом цифровых данных можно записать:

(2)

Переходный процесс в соленоиде с сердечником на подачу напряжения прямоугольного импульса включает в себя расчет на постоянную, первую, третью и пятую гармонические составляющие разложенного в ряд Фурье напряжения[1-3]. Кроме того, надо учесть, что переходный процесс на импульсное воздействие учитывает включение соленоида с сердечником до промежутка времени от и отключение цепи при . Рассмотрим процесс включения соленоида с сердечником на промежутке времени . Расчет включает постоянную составляющую, первую, третью и пятую гармонические составляющие напряжения. Затем применим метод наложения. Используем основную кривую намагничивания нелинейной индуктивности, аппроксимирую её выражением:

. (3)

Кривая намагничивания представлена на рисунке 2.

Рисунок 2. График функции ψ(t) включения соленоида с сердечником на постоянное напряжение

i, А

Рисунок 3. График функции i (t) включения соленоида с сердечником на постоянное напряжение

Для определения времени используем известное выражение:

. (4)

Расчет проведем по программе Excel, используя при этом данные: , =4,33Ом; .

При этом получены следующие результаты: ; L=0,154Гн.

Рассмотрим переходный процесс при включении соленоида с сердечником на первую гармонику напряжения, используя метод последовательных приближений:

. (5)

Используем дифференциальное уравнение:

. (6)

Примем , тогда уравнение (3.44) преобразуется в новое:

. (7)

Решением уравнения (3.45) будет:

. (8)

Потокосцепления , где , то есть мы получили цифровой ответ.

При уравнение (8) будет: ,

откуда . Решение уравнения запишется:

, .

Полученные результаты предслены в таблице 1 и рис. 4 и 5.

Таблица 1.

Для первой гармонической составляющей графика

	, c	i, A
0	0	0
-0,67	0,066	-4,35868
0,77	0,077	5,059136
-1,16	0,112	-7,58595
-1,30	0,172	-8,48683
1,32	0,263	8,581039

, c

Рисунок 4.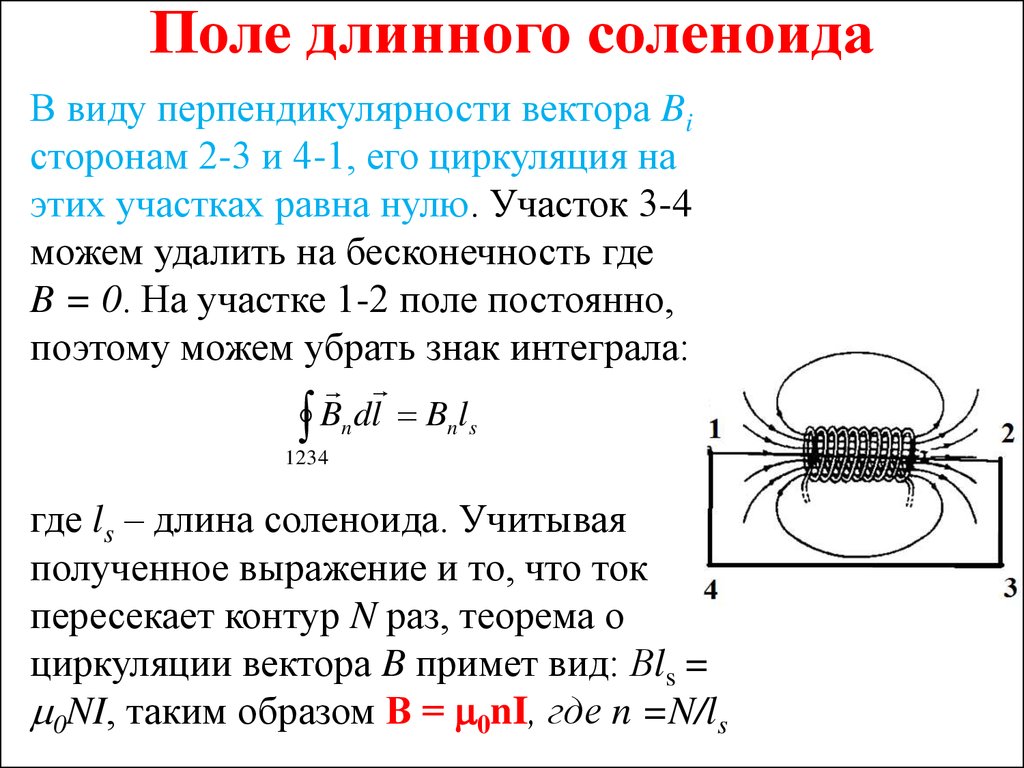 График для первой гармонической составляющей

i, A

, c

Рисунок 5. График для первой гармонической составляющей

Для третьей гармонической составляющей напряжения имеем уравнение:

(9)

Решением данного уравнения будет:

. (10)

Уравнение (10) преобразуем в следующий вид: , где . Общее решение уравнения для переходного процесса имеем вид: , где .

Результаты расчетов по 3-ей гармонической составляющей представлены в таблице 2. и на рис.6 и 7.

Таблица 2.

Для третьей гармонической составляющей графика

, c		i, A
0	0	0
0,066	46,70394	303,2724
0,077	-41,8647	-271,849
0,112	-5,67574	-36,8554
0,172	-32,3708	-210,2

, c

Рисунок 6. График для третьей гармонической составляющей

i, A

, c

Рисунок 7

. График для третьей гармонической составляющей

Применим метод наложения для основного действия и первой и третьей гармонических составляющих:

(11)

в интервале , где , для постоянной составляющей;, для первой гармонической составляющей; , для третьей гармонической составляющей [9,10].

Таблица 3.

Для интервала , гармонической составляющей

				i₀, A	i₁, A	i₃, A
0	0	0	0	0	0	0
0,066	1,008	-0,67	46,70394	0,78	-4,35868	303,2724
0,077	2,016	0,77	-41,8647	1,3	5,059136	-271,849
0,112	3,024	-1,16	-5,67574	3,64	-7,58595	-36,8554
0,172	3,276	-1,30	-32,3708	5,2	-8,48683	-210,2
0,263	3,299	1,32	44,44006	5,49	8,581039	288,5718

Таблица 4.

Для переходного процесса при включении соленоида с сердечником

		i, A
0	0	0
0,066	47,04194	299,6937
0,077	-39,0787	-265,49
0,112	-3,81174	-40,8014
0,172	-30,3948	-213,487
0,263	49,05906	302,6428

, c

Рисунок 8.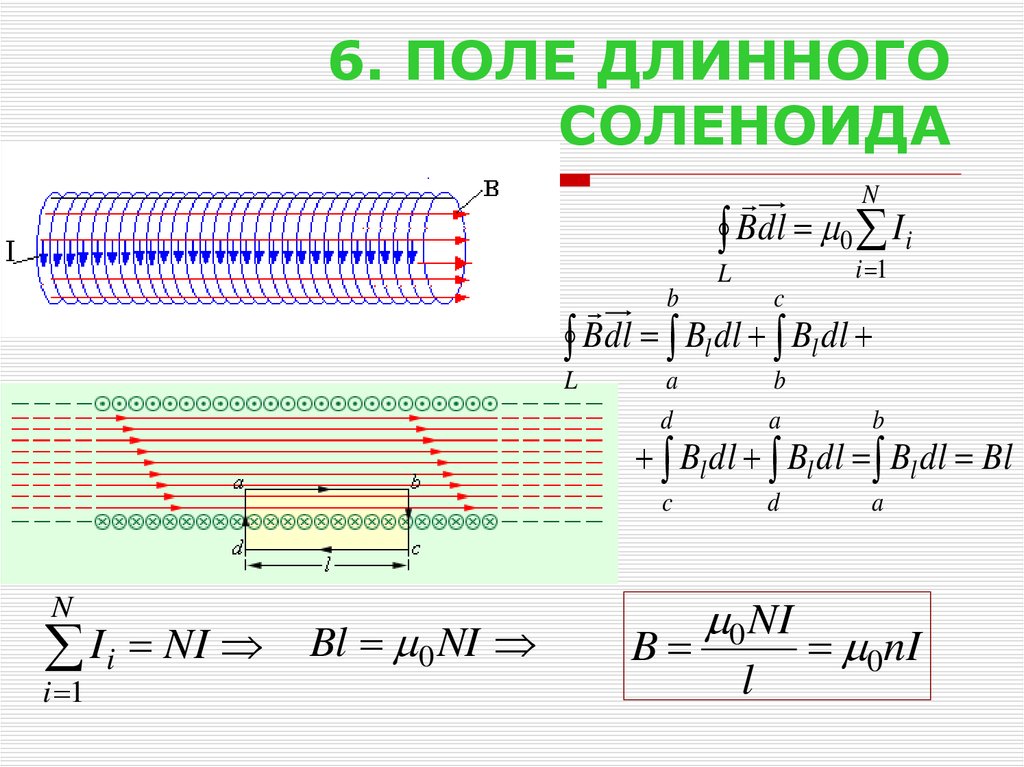 Общий график переходного процесса при включении соленоида с сердечником

Рисунок 9. Общий график переходного процесса при включении соленоида с сердечником

Рисунок 10. Вебер амперная характеристика соленоида с сердечником а-первоначальная кривая намагничивания; б-нисходящая ветвь убывания потока до остаточного значения .

Переходный процесс на участке будем рассматривать, как замыкание накоротко соленоида с сердечником, используя при этом нисходящую ветвь вебер-амперной характеристики (рис.10). Нисходящую ветвь намагничивания выразим в аналитическом виде:

. (12)

Обозначим: , . При замыкания накоротко соленоида сердечника, уравнение короткого замыкания будет иметь вид:

. (13)

Рисунок 11. Переходный процесс в соленоиде с сердечником

Решением данного уравнения является:

. (14)

t,c	i,A
0	0
0,066	299,6937
0,077	-265,49
0,112	-40,8014
0,172	-213,487
0,263	302,6428
0,3	2,727105
0,4	1,275773
0,466	299,6937
0,543	-265,49
0,655	-40,8014
0,827	-213,487
1,09	302,6428
1,39	2,727105
1,79	1,275773
2,256	299,6937

Для соленоида с сердечником нисходящая характеристика удовлетворяется,

если представить: ; , при этих значениях коэффициентов будем иметь: ; ; . Переходный процесс для потокосцепления записывается уравнением:

. (15)

Общий график переходного процесса в соленоиде с сердечником, при включении на прямоугольный импульс показан на рис.11.

Общий переходный процесс в соленоиде с сердечником для тока показан на рис.12.

i, A t,c

Рисунок 12. Переходный процесс в соленоиде с сердечником

Заключение

На основании полученных результатов можно сделать заключение о том, что оптимальным для размагничивания будет применение импульсных воздействий, так как получается большое количество максимумов и минимумов токов, как в отрицательных, так и в положительных областях. Понижение тока равносильно уменьшению насыщения стали сердечника, и экономии электроэнергии а следовательно приводит к размагничиванию стали рельсовых плетей.

Список литературы:

Колесников И. К., Курбанов Ж.Ф. Программное обеспечение системы управления единым пространственным полем // Современные состояние и перспективы применения информационных технологий в управлении, доклады республиканской научно-технической конференции,5-6сентябрь 2016г., Джизак.
Халиков А.А., Колесников И.К., Курбанов Ж.Ф. Исследование и разработка единого пространственного электромагнитного поля и устройств на их основе. / Монография. Издательства «Фан ва технология», 2019. – С.238.
Халиков А.А., Колесников И.К., Кадыров О.Х., Яронова Н.В. Влияния электромагнитного поля на свойства жидких и твердых тел // Наука образование техника №4, 2007г. Ош, Киргизия, – С.104-106.
Халиков А.А., Курбанов Ж.Ф., Ортиков М.С. Устройства намагничивания и размагничивания рельсовых плетей и их сравнительный анализ. // UNIVERSUM Технические науки. Москва– 2019. №10 (67) – С.78-80. Электронный научный журнал [email protected] .
Халиков А.А., Курбанов Ж.Ф., Ортиков М. С. Параметры магнетизма, намагничивания и размагничивания материалов и рельсовых плетей. // UNIVERSUM Технические науки. Москва– 2019. №10 (67). – С.81-83. Электронный научный журнал. [email protected] .
Халиков А.А., Мирсагдиев О.А. Разработка информационно-измерительных систем на основе волоконно-оптических датчиков. //ПРОБЛЕМЫ ПОЛУЧЕНИЯ, ОБРОБОТКИ И ПЕРЕДАЧИ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ. II Международная научно-техническая конференция, посвященная 90-летию со дня рождения профессора Зарипова Мадияра Фахритдиновича. Уфа-2019. – С.207-212.
Халиков А.А., Ибрагимова О.А. Исследование устройств систем управления единым пространственным электромагнитным полем. Монография. / Под ред.проф. ХаликоваА.А. Ташкент–Тамбов: Консальтинговая компания Юком, 2020. 102с. https: //ukonf.com/doc/mon.2020.05.01.pdf. E-mail: [email protected].
Khalikov A.A. Analysis of methods for determining the characteristics of a single spatial electromagnetic field. // Индонезия. Icon Beat 2019. [email protected]. International Conference on Bioinergy and Environmtntally Sustainable Agriculture Technology. (Международная конференция)
Kurbanov J.F. The spectral characteristics of the new functional materials based on a single device spatial field // «American Journal of Science and Tehnologies» International collaboration in Eurasia // American Journal of Science and Tehnologies, «Hrinceton University Press», 2015, №2(20). –P.11-16.
Kurbanov J.F., Khalikov A.A., Ortikov M.S. Devices for magnetization and demagnization of rail lashes and their comparative analysis with existing. Сборник статьей XXVIII международной научно-практической конференции «Технические науки: проблемы и решения». Сайт https://internauka.org/ .

4.2.Расчет магнитостатического поля соленоида

Поле на оси элементарного витка с током рассчитывается по формуле

, (4.0) где B – индукция магнитного поля, Тл; I – ток элементарного витка, А; a – радиус витка и z – расстояние от центра витка вдоль оси, м.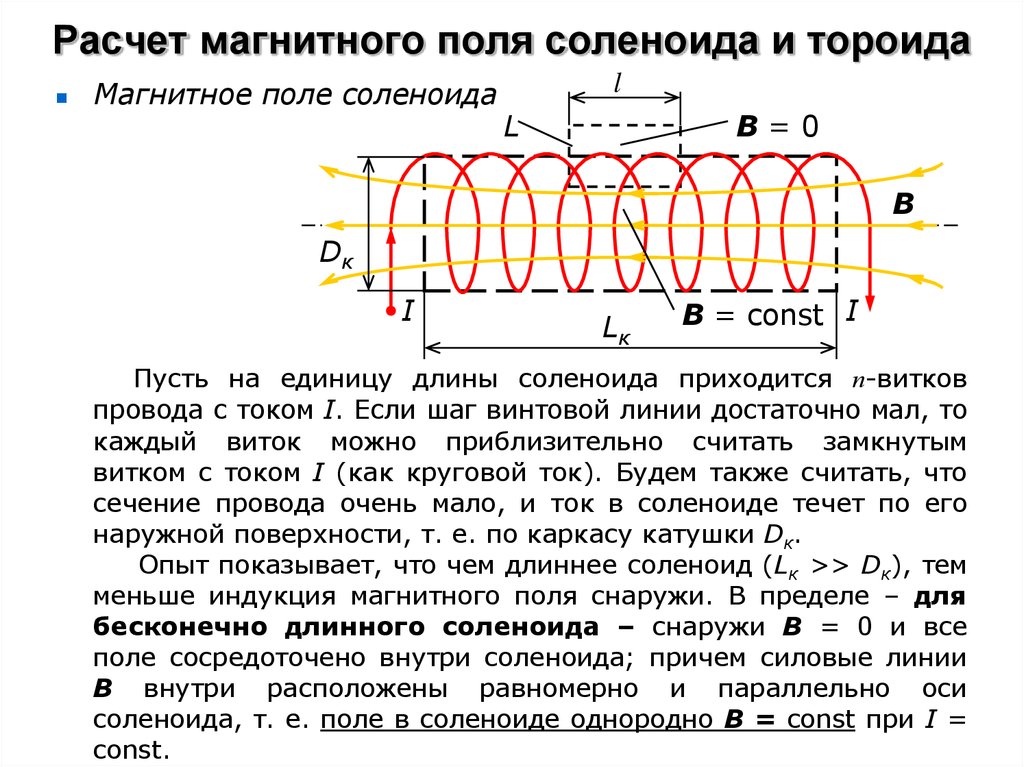

Подставляя в (4.3) значение магнитной постоянной вакуума ₀ и выражая линейные размеры в сантиметрах, получим для поля B₀ в центре витка при z = 0

. (4.0)

Используя такие же обозначения, как в (4.4), выражение (4.3) можно привести к виду

, (4.0) где B_z – индукция магнитного поля, Гс; a – радиус витка и z – расстояние от центра витка вдоль оси, см.

Выражение (4.5) можно использовать в качестве основы для расчета поля соленоида. Так, например, в центре тонкого однослойного соленоида, длина которого 2b, значение поля получается в результате интегрирования (4.5) по цилиндрической поверхности радиуса a от –b до +b:

(4.0) где N – число витков;   b/a.

Далее, интегрируя по радиусу от a₁ до a₂ выражение (4.6), получим поле в центре толстого соленоида

, где j – плотность тока, определяемая как отношение суммарного тока через осевое сечение соленоида к площади осевого сечения S_сеч 2b(a₂ a₁),   a₂/a₁ и   b/a₁.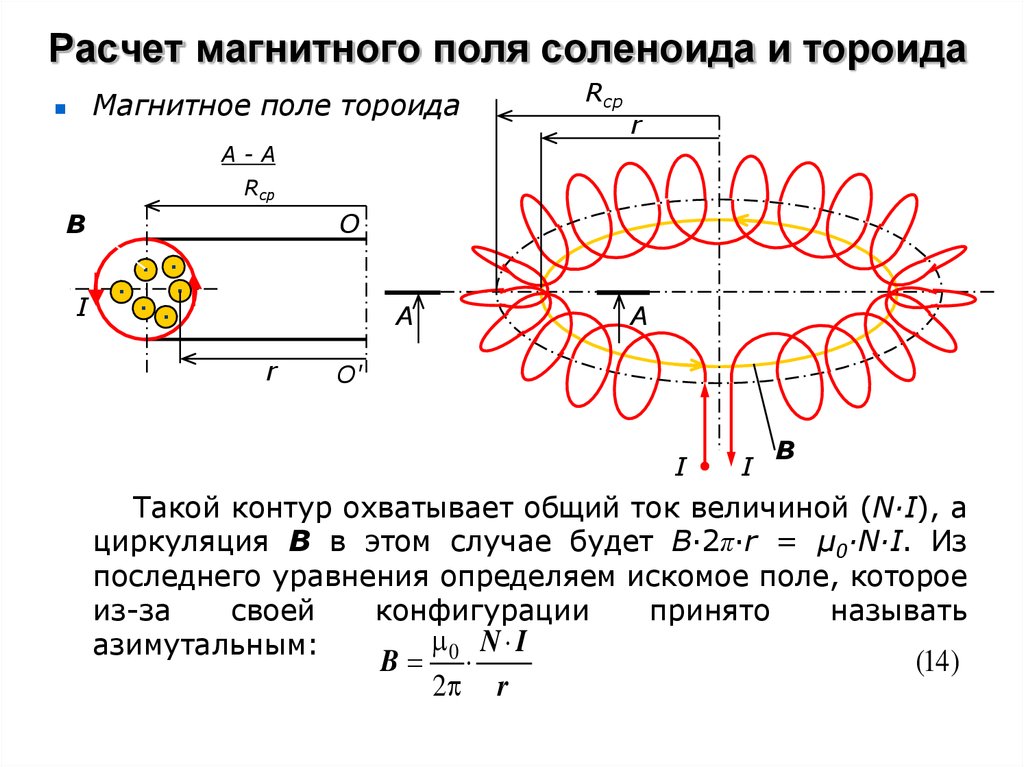

Последнюю формулу можно упростить, обозначив произведение всех безразмерных сомножителей, зависящих только от формы соленоида, как F( ) и назвав это произведение “коэффициентом поля”:

Тогда поле в центре толстого соленоида будет рассчитываться по формуле

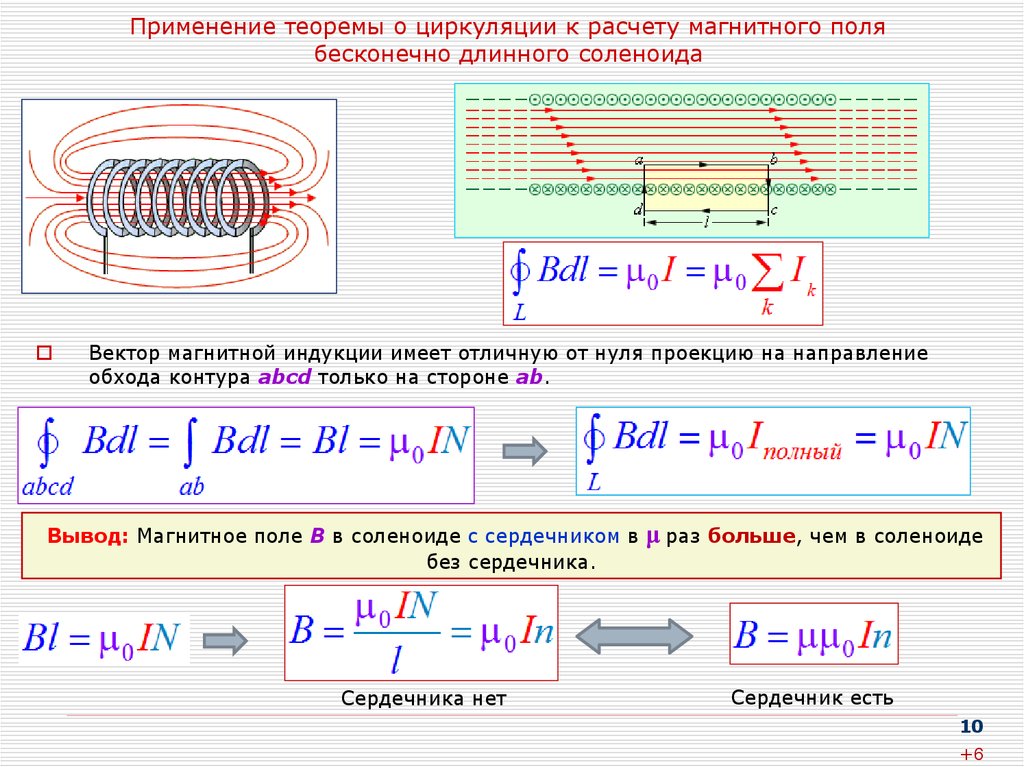
Рис. 4.2. Представление соленоидов в виде двух соленоидов половинной длины

Это означает, что поле на конце любой катушки равно половине центрального поля катушки удвоенной длины (рис. 4.2). Тогда для расчета поля в произвольной точке z на оси соленоида можно заменить исходный соленоид двумя вспомогательными (изображены сплошными линиями), длины которых зависят от величины смещения точки z вдоль оси и вычисляются по формулам (  z/a₁) и ( – z/a₁). При этом интересующее нас поле определяется как результат суперпозиции полей на концах этих соленоидов, расположенных по разные стороны от точки A, т.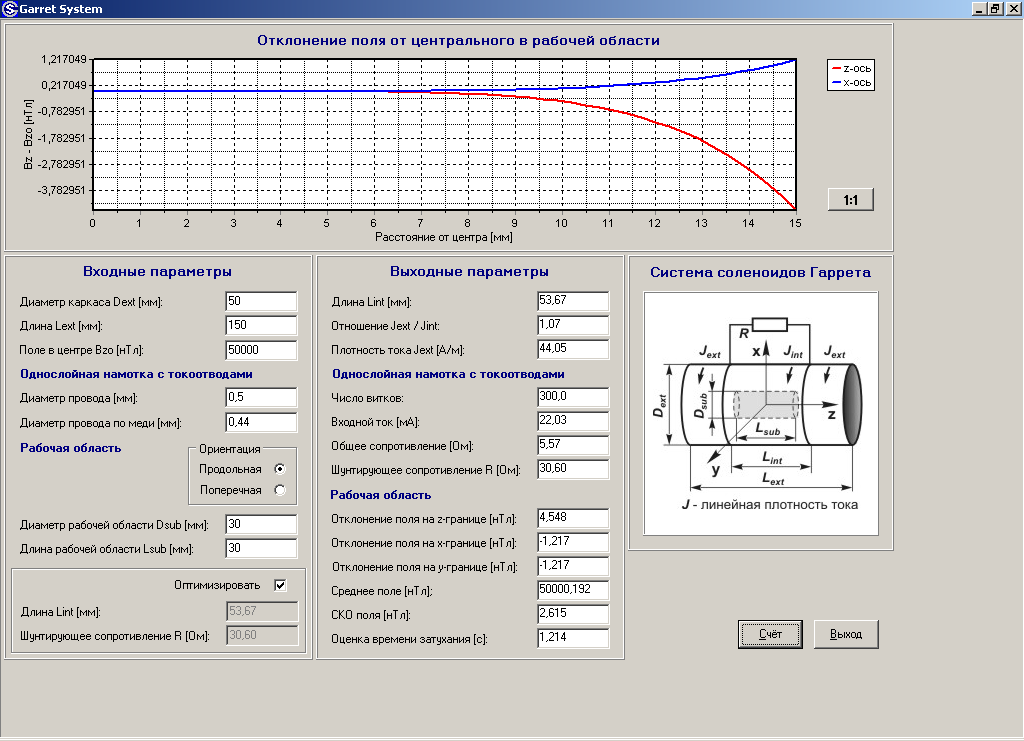 е.

, где

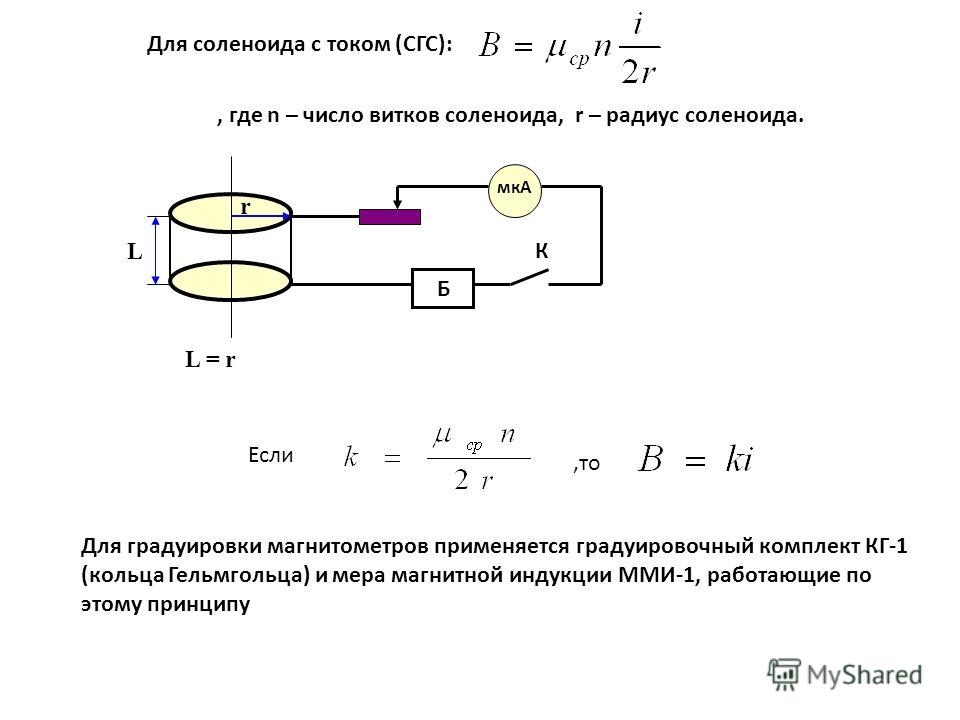
Поле на оси системы соленоидов, разделенных воздушным промежутком G, можно рассчитать по аналогичной методике, используя 4 соленоида (рис. 4.3) и 4 “коэффициента поля”:

Рис. 4.3. Представление двух соленоидов в виде четырех половинок

В этом случае результирующее поле рассчитывается по формуле

Составить программу для расчета магнитного поля двух соленоидов и построить с ее помощью график B_z(z, 0) в пределах от –(2b + G/2) до (2b + G/2). Подготовить данные для тестовой задачи, получив однородность магнитного поля в пределах –(b + G/2) до (b + G/2) путем изменения расстояния G между соленоидами. Записать значение индукции в центральной точке зазора B_z(0, 0).
Изучить инструкцию по работе с программой “Тесла”.
Заполнить шаблон исходных данных для магнитной системы двух соленоидов, соответствующих тестовой задаче. На границах сеточной области использовать следующие условия: на S границе , на E, N и W границах . Использовать сетку с постоянным шагом.
Решить задачу на двух сетках с количеством узлов 400 и 1600 для различных значений коэффициента верхней релаксации , фиксируя каждый раз количество проведенных итераций N_ит. Построить графики для каждой из двух сеток и найти для них _opt.
Исследовать погрешность численных расчетов. Для этого просчитать пять вариантов задач с количеством узлов n_уз= 100, 400, 900, 1600 и 2500, записывая каждый раз значение индукции в центральной точке зазора B_z(0, 0). Построить график . На графике провести горизонтальную линию, соответствующую значению B_z(0, 0) из решения тестовой задачи.
Исследовать погрешность численных расчетов, связанных с неточностью задания условий на границе сеточной области. Для этого на границах сеточной области E, N и W задать условие . Выбрать сетку с количеством узлов n_уз=1600. Получить решение задачи для 5 вариантов расположения границы сеточной области: z_гр= (mb + G/2), r_гр = na₂, используя для пары чисел (m, n) значения (3, 1.2), (4, 1.5), (6, 2), (10, 4) и (15, 6) и записывая каждый раз значения индукции в центральной точке зазора B_z(0, 0). Построить график . На графике провести горизонтальную линию, соответствующую значению B_z(0, 0) из решения тестовой задачи.
Задать исходные данные для половины магнитной системы, используя условие симметрии на границе E. Задать количество узлов сетки n_уз= 400. Провести расчеты, как в п. 4. Дополнить график этим вариантом.

12.7: Соленоиды и тороиды — Физика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 4426

OpenStax
OpenStax

Цели обучения

К концу этого раздела вы сможете:

Установить зависимость того, как магнитное поле соленоида изменяется в зависимости от расстояния и силы тока, используя как закон Био-Савара, так и закон Ампера
Установите зависимость того, как магнитное поле тороида изменяется в зависимости от расстояния и силы тока, используя закон Ампера

Два наиболее распространенных и полезных электромагнитных устройства называются соленоидами и тороидами. В том или ином виде они входят в состав многочисленных инструментов, как больших, так и малых. В этом разделе мы исследуем магнитное поле, характерное для этих устройств.

Соленоиды

Длинный провод, намотанный в виде спиральной катушки, известен как соленоид . Соленоиды обычно используются в экспериментальных исследованиях, требующих магнитных полей. Соленоид, как правило, легко наматывается, и вблизи его центра его магнитное поле довольно однородно и прямо пропорционально току в проводе.

На рисунке $\PageIndex{1}$ показан соленоид, состоящий из N витков проволоки, намотанной на длину L . ток I течет по проводу соленоида. Количество витков на единицу длины N / L ; следовательно, число витков бесконечно малой длины dy равно ( N / L ) dy витков. Это дает ток

\[dI = \frac{NI}{L} dy. \label{12.24}\]

Сначала вычислим магнитное поле в точке P на рисунке $\PageIndex{1}$. Эта точка находится на центральной оси соленоида. По сути, мы разрезаем соленоид на тонкие ломтики размером 9{\theta_2} cos \, \theta \, d\theta = \frac{\mu_0 I N}{2L} (sin \, \theta_2 — sin \, \theta_1)\hat{j}, \label{12.27}\ ]

— магнитное поле вдоль центральной оси конечного соленоида.

Особый интерес представляет бесконечно длинный соленоид, для которого $L \rightarrow \infty$. С практической точки зрения бесконечный соленоид — это соленоид, длина которого намного больше его радиуса $(L >> R)$. В этом случае $\theta_1 = \frac{-\pi}{2}$ и $\theta_2 = \frac{\pi}{2}$. Тогда из уравнения \ref{12.27} магнитное поле вдоль центральной оси бесконечного соленоида равно

\[\vec{B} = \frac{\mu_0 IN}{2L} \hat{j} [sin(\pi/2) — sin(-\pi/2)] = \frac{\mu_0 IN }{L} \hat{j}\] или

\[\vec{B} = \mu_0 n I \hat{j}, \label{12.28}\]

, где n — количество витков на единицу длины.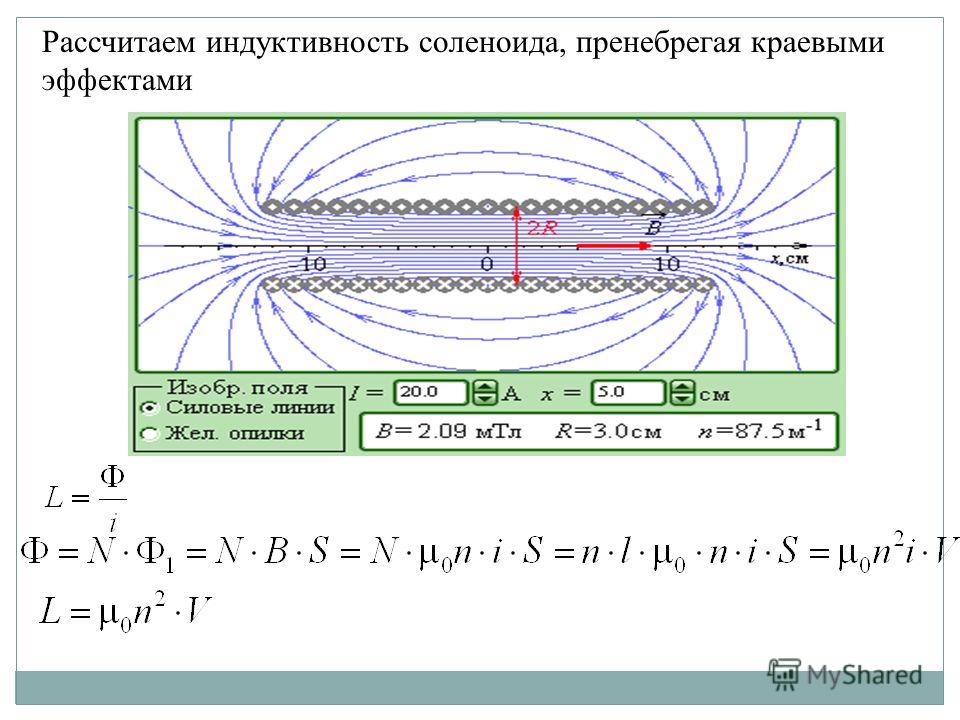 Вы можете найти направление $\vec{B}$ с помощью правила правой руки: согните пальцы в направлении тока, и ваш большой палец будет указывать вдоль магнитного поля внутри соленоида.

Теперь мы используем эти свойства вместе с законом Ампера для расчета величины магнитного поля в любом месте внутри бесконечного соленоида. Рассмотрим закрытый путь на рисунке $\PageIndex{2}$. Вдоль сегмента 1 $\vec{B}$ является равномерным и параллельным пути. Вдоль отрезков 2 и 4 $\vec{B}$ перпендикулярно части пути и обращается в нуль на остальной его части. Следовательно, отрезки 2 и 4 не дают вклада в линейный интеграл в законе Ампера. Вдоль сегмента 3 $\vec{B} = 0$, потому что магнитное поле равно нулю вне соленоида. Если вы рассматриваете петлю закона Ампера вне соленоида, ток течет в противоположных направлениях на разных сегментах провода. Следовательно, по закону Ампера замкнутого тока и магнитного поля нет. Таким образом, вклада в линейный интеграл от отрезка 3 нет. В результате находим

\[\oint \vec{B} \cdot d\vec{l} = \int_1 \vec{B} \cdot d\vec{l} = Bl. \label{12.29}\]

Рисунок $\PageIndex{2}$: Путь интегрирования, используемый в законе Ампера для оценки магнитного поля бесконечного соленоида.

Соленоид имеет n витков на единицу длины, поэтому ток, который проходит через поверхность, ограниченную путем, равен nlI . Следовательно, по закону Ампера

\[Bl = \mu_0 n lI\] и

Примечание

\[B = \mu_0 n I \label{12.30}\]

внутри соленоида. Это согласуется с тем, что мы нашли ранее для B на центральной оси соленоида. Однако здесь расположение сегмента 1 произвольно, поэтому мы нашли, что это уравнение дает магнитное поле везде внутри бесконечного соленоида.

Снаружи соленоида можно нарисовать петлю закона Ампера вокруг всего соленоида. Это будет охватывать ток, протекающий в обоих направлениях. Следовательно, чистый ток внутри петли равен нулю. Согласно закону Ампера, если чистый ток равен нулю, магнитное поле должно быть равно нулю. Следовательно, для мест вне радиуса соленоида магнитное поле равно нулю.

Когда пациент проходит магнитно-резонансную томографию (МРТ), человек ложится на стол, который перемещается в центр большого соленоида, который может генерировать очень сильные магнитные поля. Соленоид способен создавать эти сильные поля от больших токов, протекающих по сверхпроводящим проводам. Большое магнитное поле используется для изменения спина протонов в теле пациента. Время, необходимое для выравнивания или расслабления спинов (возвращения к исходной ориентации), является характеристикой различных тканей, которую можно проанализировать, чтобы определить, является ли структура тканей нормальной (рис. $\PageIndex{3}$).

Рисунок $\PageIndex{3}$: . В аппарате МРТ сильное магнитное поле создается цилиндрическим соленоидом, окружающим пациента. (кредит: Лиз Уэст)

Пример $\PageIndex{1}$: Магнитное поле внутри соленоида

Соленоид имеет 300 витков, намотанных на цилиндр диаметром 1,20 см и длиной 14,0 см. Если ток через катушки равен 0,410 А, какова величина магнитного поля внутри и вблизи середины соленоида?

Стратегия 9о\)? Соленоид имеет 1000 витков на 50 см с током 1,0 А, протекающим через катушки

Решение: а. 1.00382; б. 1.00015

Тороиды

Тороид представляет собой кольцевидную катушку, плотно намотанную одним непрерывным проводом, как показано в части (a) рисунка $\PageIndex{4}$. Если тороид имеет N обмоток и ток в проводе равен I , то каково магнитное поле как внутри, так и снаружи тороида?

Рисунок $\PageIndex{4}$: (a) Тороид представляет собой катушку, намотанную на объект в форме пончика. (b) Свободно намотанный тороид не имеет цилиндрической симметрии. (c) В туго намотанном тороиде цилиндрическая симметрия является очень хорошим приближением. г) несколько путей интегрирования закона Ампера.
Начнем с предположения о цилиндрической симметрии вокруг оси OO ’. На самом деле это предположение не совсем верно, поскольку, как показывает часть (b) рисунка $\PageIndex{4}$, вид тороидальной катушки меняется от точки к точке (например, $P_1, \, P_2 $ и $P_3$) по круговому пути с центром вокруг ОО ’. Однако, если тороид намотан туго, все точки на окружности становятся по существу эквивалентными [часть (c) рисунка $\PageIndex{4}$], и цилиндрическая симметрия является точным приближением.
При такой симметрии магнитное поле должно быть касательным и постоянным по величине вдоль любого кругового пути с центром в точке OO ’. Это позволяет нам писать для каждого из путей $D_1, \, D_2$ и $D_3$, показанных в части (d) рисунка $\PageIndex{4}$,
\[\oint \ vec{B} \cdot d\vec{l} = B(2\pi r). \метка{12.31}\]
Закон Ампера связывает этот интеграл с чистым током, проходящим через любую поверхность, ограниченную путем интегрирования. Для пути, внешнего по отношению к тороиду, либо ток не проходит через охватывающую поверхность (путь $D_1$), либо ток, проходящий через поверхность в одном направлении, точно уравновешивается током, проходящим через нее в противоположном направлении. (путь $D_3$). В любом случае через поверхность не проходит чистый ток, поэтому
\[\oint B(2\pi r) = 0\] и
\[B = 0 \, (снаружи \, \, тороид). \label{12.32}\]
Витки тороида образуют спираль, а не круговые петли. В результате внешнее по отношению к катушке небольшое поле; однако приведенный выше вывод верен, если катушки были круглыми.
Для кругового пути внутри тороида (путь $D_2$), ток в проводе пересекает поверхность N раз, что приводит к чистому току NI через поверхность. Теперь находим по закону Ампера
\[B(2\pi r) = \mu_0 NI\] и
Примечание
\[B = \frac{\mu_0 NI}{2\pi r} \, (внутри \, \, тороид) . \label{12.33}\]
Магнитное поле для показанных обмоток направлено против часовой стрелки. Когда ток в катушках меняется на противоположный, меняется и направление магнитного поля.
Магнитное поле внутри тороида неоднородно, так как изменяется обратно пропорционально расстоянию r от оси OO ’. Однако если центральный радиус R (радиус посередине между внутренним и внешним радиусами тороида) намного больше, чем диаметр поперечного сечения катушек r , изменение довольно мало, и величина магнитного поля может быть рассчитана по формуле Уравнение \ref{12. 33} где $r = R$.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта страница под названием 12.7: Соленоиды и тороиды распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать оглавление
нет
Теги
Закон Ампера
Закон Ампера
Соленоиды
источник@https://openstax. org/details/books/university-physics-volume-2
Тороиды
электромагнетизм — Как рассчитать Силу (в Ньютонах), создаваемую соленоидом?
спросил 2 года, 4 месяца назад
Изменено 2 месяца назад
Просмотрено 572 раза
$\begingroup$
Как рассчитать силу, действующую на объект (в ньютонах), который находится под воздействием электромагнитного поля, создаваемого соленоидом? Я знаю, что это потребует использования уравнения $B=(μNI)/L$, чтобы найти силу магнитного поля в Тесле, однако я не уверен, что делать дальше.
электромагнетизм
силы
электрические цепи
индуктивность
$\endgroup$
3
$\begingroup$
Используйте выражение для силы Лоренца. Если объект является точечным объектом (то есть заряженной частицей), сила Лоренца равна
$$\vec{F}=q(\vec{E}+\vec{v}\times\vec{B}).$ $
Если объект расширен, то вам придется интегрировать 93x.$$
Обратите внимание, что объект должен быть заряжен, чтобы на него воздействовала электромагнитная сила. Магнитное поле внутри очень длинного соленоида действительно равно $B=(µNI)/L$ и направлено параллельно оси соленоида. Так что, думаю, остается только спросить себя: есть ли в этом сценарии $\vec{E}$?
$\endgroup$
$\begingroup$
Хорошо, вы имеете в виду расчет. (Вы бы измерили пружинными весами — легко).
Вы хотите начать с $H$, а не с $B$, но это всего лишь множитель $\mu_0$.
Тогда вам понадобится намагниченность $M$. Для диа/парамагнетиков это просто $\chi H$, где $\chi$ — магнитная восприимчивость. Для ферромагнетиков это сложнее из-за насыщения и гистерезиса.
Если объект большой и/или чувствительный (опять же ферромагнетики), вы должны учитывать влияние намагниченного объекта на внешнее поле и на себя самого, и расчеты усложняются. Итак, давайте предположим, что он достаточно мал, чтобы не искажать картину.
Тогда энергия просто $-M.B$ интегрирована по объему, какой бы ни была форма. $M$ и $B$ здесь коллинеарны, поэтому вам не нужно беспокоиться о скалярном произведении.
Итак, сила — это просто градиент энергии, и ее можно рассчитать как функцию положения, если вы знаете поле. В стволе соленоида сила отсутствует там, где поле однородно, но появляется на концах, где линии поля расходятся.
$\endgroup$
$\begingroup$
Соленоид с током будет оказывать силу на ферромагнитный материал, который находится сразу за концом соленоида. Расчет будет сложным. Величина и направление силы, действующей на каждый небольшой сегмент материала, будут варьироваться от точки к точке и зависеть от расхождения поля и существующей или индуцированной намагниченности внутри материала.