Как рассчитать общее сопротивление при параллельном соединении резисторов. Какие формулы использовать для расчета параллельных сопротивлений. Как работает онлайн калькулятор для расчета параллельных резисторов. Какие особенности у параллельного соединения по сравнению с последовательным.
Что такое параллельное соединение резисторов
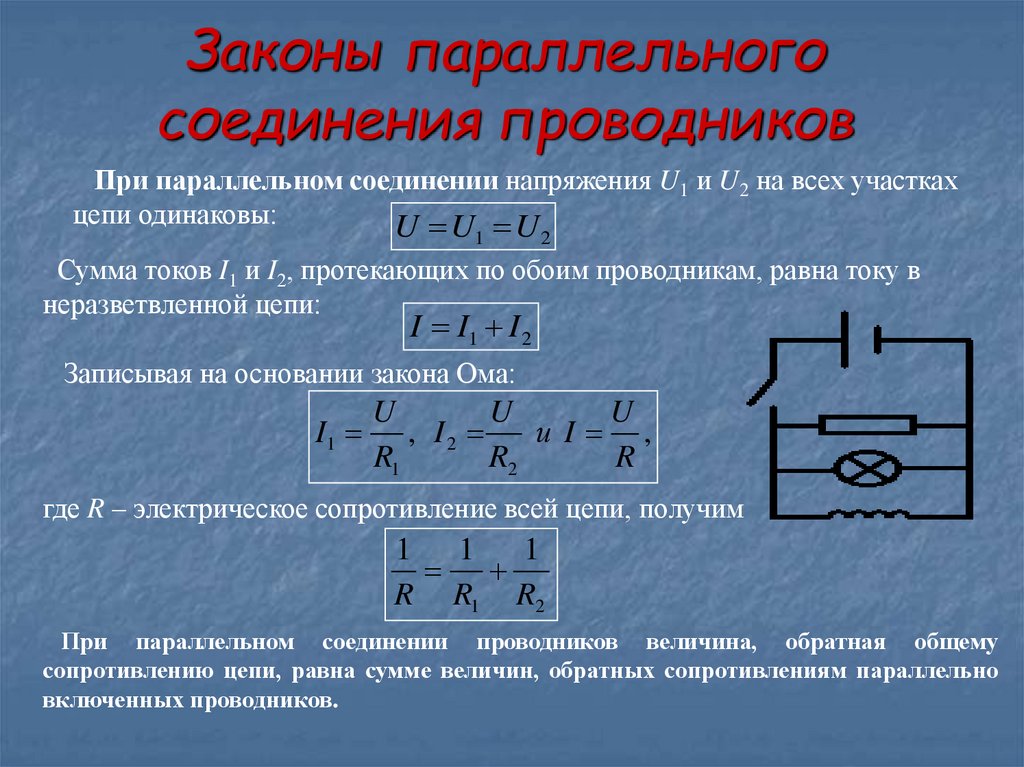
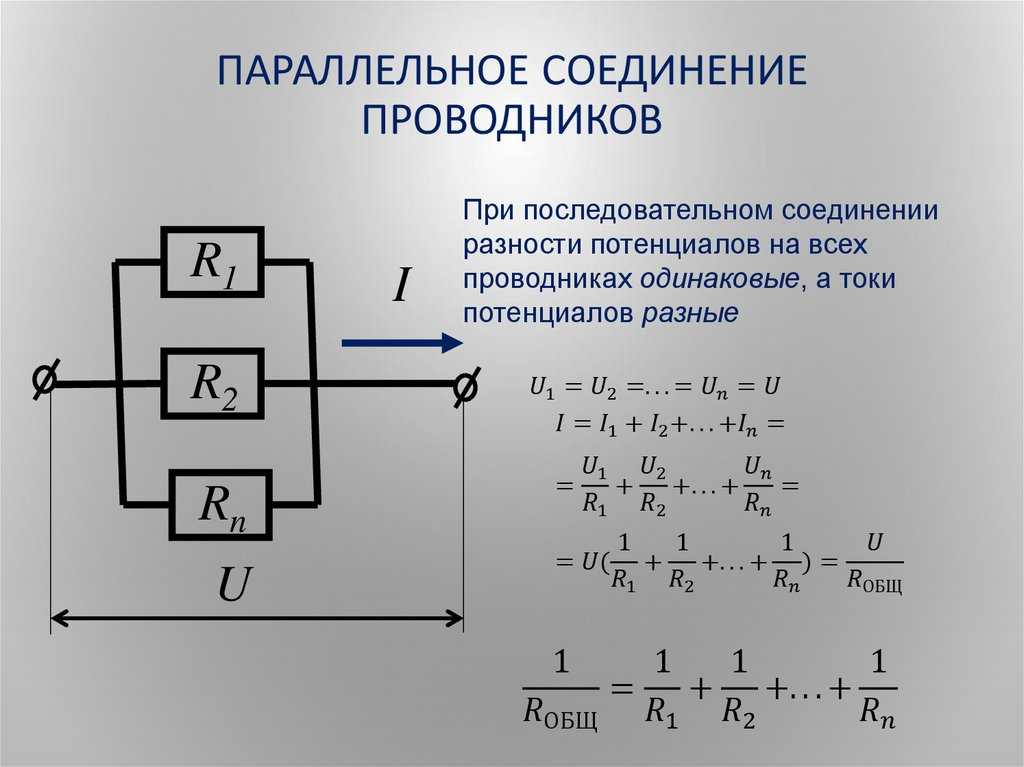
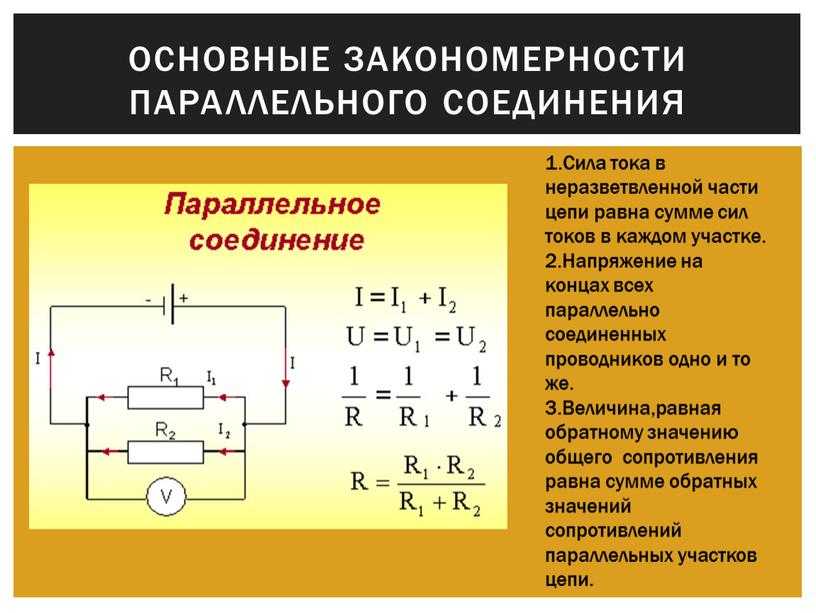
Параллельное соединение резисторов — это такой способ подключения, при котором все резисторы подсоединены к одним и тем же двум точкам электрической цепи. При этом:
- Напряжение на всех резисторах одинаково и равно напряжению на участке цепи
- Общий ток равен сумме токов через каждый резистор
- Общее сопротивление всегда меньше сопротивления наименьшего из резисторов
Параллельное соединение широко применяется в электротехнике, так как позволяет уменьшить общее сопротивление участка цепи.
Формула расчета общего сопротивления при параллельном соединении
Для расчета общего сопротивления при параллельном соединении используется следующая формула:
1/R = 1/R1 + 1/R2 + 1/R3 + …
где R — общее сопротивление, R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Эта формула выводится из закона Ома и первого закона Кирхгофа. Она показывает, что при параллельном соединении складываются величины, обратные сопротивлениям.
Пример расчета параллельного соединения двух резисторов
Рассмотрим простой пример с двумя параллельно соединенными резисторами:
R1 = 10 Ом R2 = 20 Ом
Подставляем в формулу:
1/R = 1/10 + 1/20 = 0.1 + 0.05 = 0.15
R = 1/0.15 = 6.67 Ом
Таким образом, общее сопротивление двух параллельно соединенных резисторов 10 Ом и 20 Ом равно 6.67 Ом.
Онлайн калькулятор для расчета параллельных сопротивлений
Для быстрого расчета общего сопротивления при параллельном соединении удобно использовать онлайн калькуляторы. Они позволяют:
- Рассчитать общее сопротивление для любого количества параллельно соединенных резисторов
- Вычислить токи через каждый резистор
- Определить мощность, рассеиваемую на каждом резисторе
Достаточно ввести значения отдельных сопротивлений и напряжение на участке цепи. Калькулятор мгновенно выполнит все необходимые вычисления.
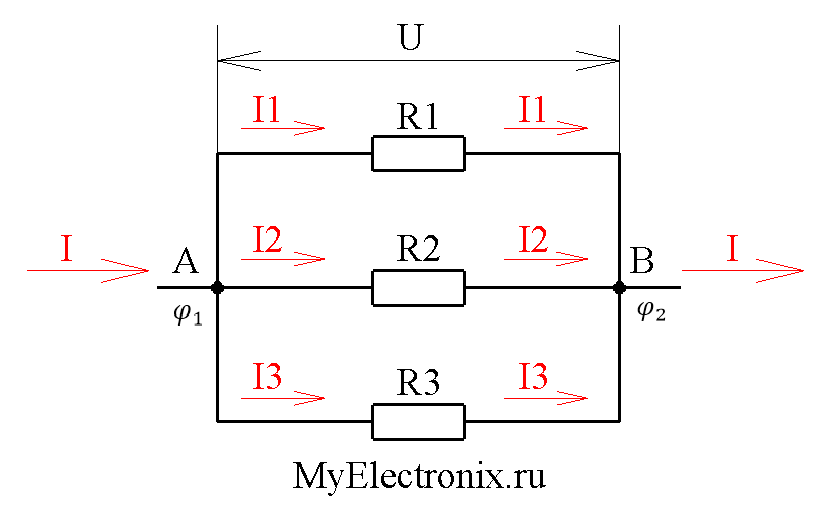
Особенности параллельного соединения по сравнению с последовательным
Основные отличия параллельного соединения от последовательного:
- При параллельном соединении общее сопротивление уменьшается, а при последовательном — увеличивается
- Напряжение на всех элементах при параллельном соединении одинаково, а при последовательном — разное
- Общий ток при параллельном соединении равен сумме токов через элементы, а при последовательном — одинаков для всех элементов
- Формула расчета общего сопротивления для параллельного соединения сложнее, чем для последовательного
Применение параллельного соединения резисторов
Параллельное соединение резисторов широко используется в электронике и электротехнике для:
- Уменьшения общего сопротивления участка цепи
- Создания делителей тока
- Подключения нескольких потребителей к одному источнику питания
- Увеличения допустимой мощности рассеивания
- Получения нестандартных номиналов сопротивлений
Например, параллельное соединение применяется для подключения осветительных приборов и розеток в квартирах.

Расчет сложных схем с параллельно-последовательным соединением
В реальных электрических схемах часто встречается смешанное параллельно-последовательное соединение резисторов. Для расчета таких схем используют следующий алгоритм:
- Разбить схему на группы параллельно и последовательно соединенных элементов
- Рассчитать эквивалентное сопротивление для каждой группы
- Заменить группы эквивалентными резисторами
- Повторять шаги 1-3, пока вся схема не сведется к одному эквивалентному резистору
Такой подход позволяет рассчитать сопротивление даже для очень сложных схем.
Законы Кирхгофа для расчета параллельных цепей
При расчете параллельных соединений важную роль играют законы Кирхгофа:
- Первый закон Кирхгофа: сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла
- Второй закон Кирхгофа: алгебраическая сумма напряжений в любом замкнутом контуре равна нулю
Эти законы позволяют составить систему уравнений для нахождения токов в ветвях сложных параллельных цепей.
Проверка формул для расчёта эквивалентных сопротивлений при последовательном, параллельном и смешанном соединении
СОДЕРЖАНИЕ
1. Цель работы 2
2. Приборы и оборудование 2
3. Техника безопасности 2
4. Порядок выполнения работы 2
5. Содержание отчета 4
6. Контрольные вопросы 4
7. Рекомендуемая литература 4
Приложение 1.
 Теоретические сведения 5
Теоретические сведения 5 Приложение 2. Задание для домашней подготовки к работе. 7
1. цель работы
1.1 Приобрести навыки выполнения различных видов соединений резисторов.
1.2 Произвести опытную проверку формул для расчёта эквивалентных сопротивлений при последовательном, параллельном и смешанном их соединениях.
2. приборы и оборудование
Таблица 1
|
№ п/п |
Наименование прибора |
Услов. обозн. |
Тип |
Завод. номер |
Измерительная система |
Класс точно-сти |
Род тока |
Пре-делы измер. |
Цена дел. |
|
|
|
Усл. обозн. |
|||||||||
|
1 |
Амперметр |
РА1 |
||||||||
|
2 |
Амперметр |
РА2 |
||||||||
|
3 |
Вольтметр |
PV |
||||||||
3. техника безопасности
техника безопасности
3.1 Сборку схем и переключения в них, производить только при отключенной от источника цепи.
3.2 Электрическую цепь или стенд включать только с разрешения преподавателя.
3.3 При сборке схем использовать только соединительные провода с исправной изоляцией.
3.4 По окончании работы отключить цепь от источника, показать преподавателю результаты измерений и расчета для проверки, привести рабочее место в порядок.
4. порядок выпонения работы
4.1 Измерение тока и напряжения. Расчёт сопротивлений резисторов R1, R2, R3.
4.1.1 На базе стенда ЛЭС-4 собрать электрическую цепь (рис. 1) и показать ее преподавателю для проверки.
4.1.2 Начертить схему замещения электрической цепи (рис.1).
4.1.3 Поочерёдно
подключая к зажимам 1, 2 используемые в опыте резисторы произвести замеры тока
и напряжения. Используя закон Ома рассчитайте их сопротивления. Результаты
измерений и расчёта занесите в табл.2.
Результаты
измерений и расчёта занесите в табл.2.
Таблица 2
Резистор |
Измерено |
Вычислено |
|
|
U, B |
I, A |
R, Oм |
|
|
R1 |
|||
|
R2 |
|||
|
R3 |
|||
4. 2. Последовательное
соединение резисторов R1, R2, R3. Измерение
тока и напряжения.
2. Последовательное
соединение резисторов R1, R2, R3. Измерение
тока и напряжения.
4.2.1. Соединить последовательно резисторы R1, R2, R3 и подключить к зажимам 1, 2 электрической цепи (рис.1).
4.2.2. Включить стенд, измерить ток и напряжение. Показания вольтметра и амперметра записать в табл.3.
4.2.3. Начертить схему замещения цепи с последовательно соединёнными резисторами R1, R2, R3.
Таблица 3
|
Вид соединения резисторов |
Измерено |
Вычислено |
||
|
U, B |
I, A |
По закону Ома RЭ |
По формуле RЭ |
|
Последовательное |
||||
|
Параллельное |
||||
|
Смешанное |
||||
4. 2.4.
Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя
из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.
2.4.
Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя
из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.
4.3. Параллельное соединение резисторов R1, R2, R3. Измерение тока и напряжения.
4.3.1. Соединить параллельно резисторы R1, R2, R3 и подключить к зажимам 1, 2 электрической цепи (рис.1).
4.3.2. Включить стенд , измерить ток и напряжение. Показания вольтметра и амперметра записать в таблицу 3.
4.3.3.Начертить схему замещения цепи с параллельно соединёнными резисторами R1, R2, R3.
4.3.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.
4.4. Смешанное соединение резисторов R1, R2, R3. Измерение тока и напряжения.
4.4.1. Соединить
резисторы R2, R3 параллельно и
подключить их к резистору R1 последовательно. Смешанное соединение
резистора R1, R2, R3 подключить к
зажимам 1, 2 электрической цепи (рис. 1).
1).
4.4.2. Включить стенд , измерить ток и напряжение. Показания вольтметра и амперметра записать в таблицу 3.
4.4.3. Начертить схему замещения цепи с смешанным соединением резисторов R1, R2, R3.
4.4.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.
4.5. По результатам работы сделать вывод, отвечающий на вопросы цели работы.
5. СОДЕРЖАНИЕ ОТЧЕТА
5.1 Цель работы.
5.2 Приборы и оборудование.
5.3 Выполнение рабочего задания.
5.3.1. Наименование задания.
5.3.2. Схемы электрических цепей.
5.3.3. Схема замещения.
5.3.4. Таблицы результатов измерений и вычислений.
5.3.5. Основные расчетные формулы.
5.4 Выводы по работе.
6. контрольные вопросы
6.1 Что называют последовательным и параллельным соединением?
6. 2
Запишите
формулы для расчёта эквивалентного сопротивления при последовательном и
параллельном соединении.
2
Запишите
формулы для расчёта эквивалентного сопротивления при последовательном и
параллельном соединении.
6.3 На каком из 2-х последовательно соединённых разных по величине резисторов будет больше падение напряжения?
6.4 В какой из 2-х параллельных ветвей, имеющих разное сопротивление будет больше ток?
6.5 Как рассчитать проводимость ветвей?
7. рекомендуемая литература
7.1 Евдокимов Ф.Е. «Теоретические основы электротехники», М. «Высшая школа», 1975.
приложение 1
Теоретические сведения
Последовательное соединение резисторов – это такое соединение, когда к концу одного резистора присоединяется начало второго, к концу второго начало третьего и т.д. и при этом образуется неразветвлённая цепь или участок цепи. При последовательном соединении ток во всех резисторах одинаков.
Рис.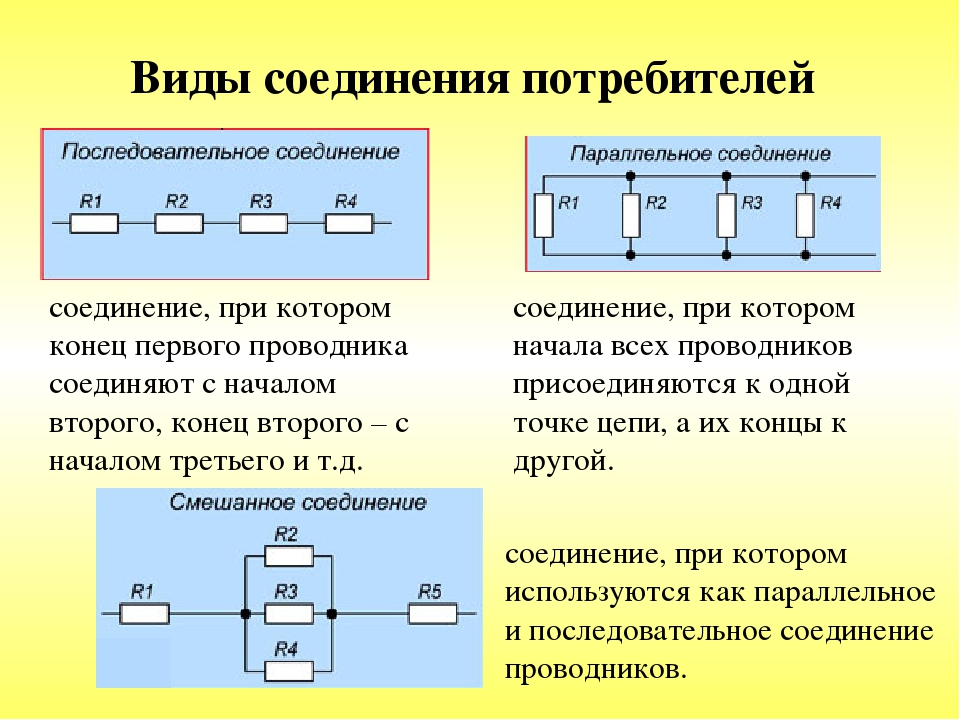 5
5
Для последовательного соединения выполняется:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
Параллельное
соединение резисторов – это такое соединение, когда начала всех резисторов
соединены в одну точку, а их концы в другую.
Рис.6
Для параллельного соединения характерно одинаковое падение напряжения на каждом резисторе и всём участке: U = U1 = U2 = U3
При параллельном соединении резисторов выполняется:
(10)
(11)
(12)
(13)
(14)
(15)
(16)
На рис.7 изображено смешанное соединение резисторов.
Рис.
 7
7Резисторы R2, R3, R4 соединены параллельно, для них выполняются закономерности параллельного соединения, а резисторы R1, R2,3,4 и R5 соединены последовательно.
приложение 2
задание для домашней подготовки к работе
Ознакомиться по учебнику, конспекту с материалом о последовательном
Параллельное соединение резисторов: формула расчета общего сопротивления
Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Расчет общего сопротивления при параллельном соединении резисторов
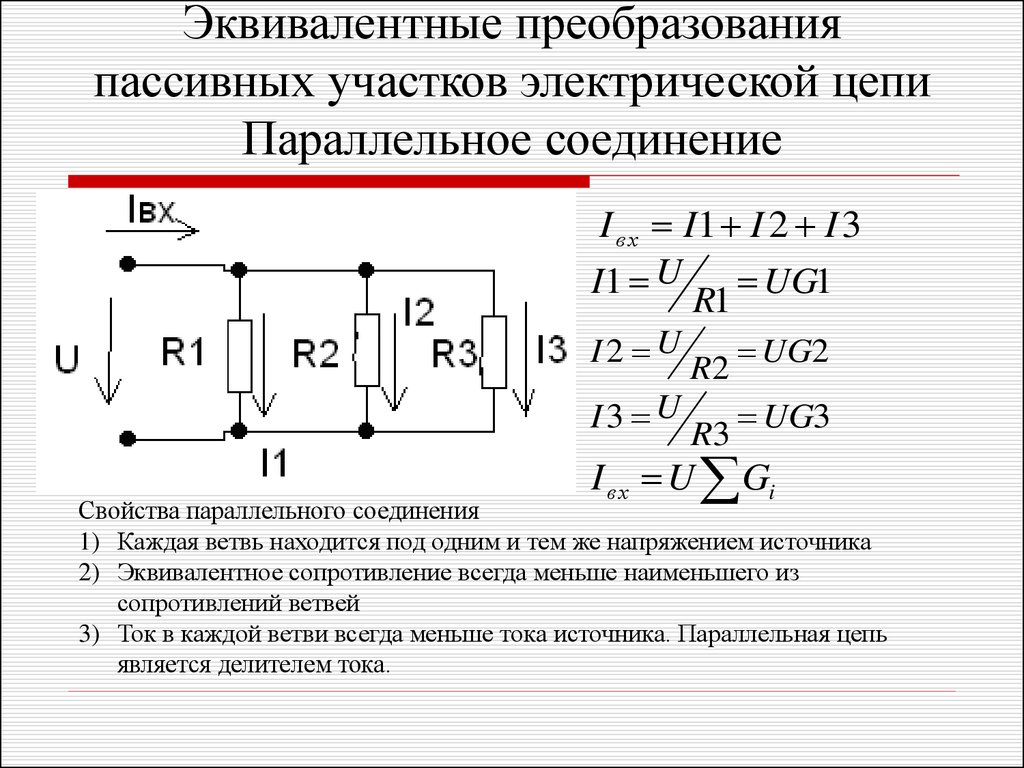
В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:
Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.
Сила тока и напряжение
При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока.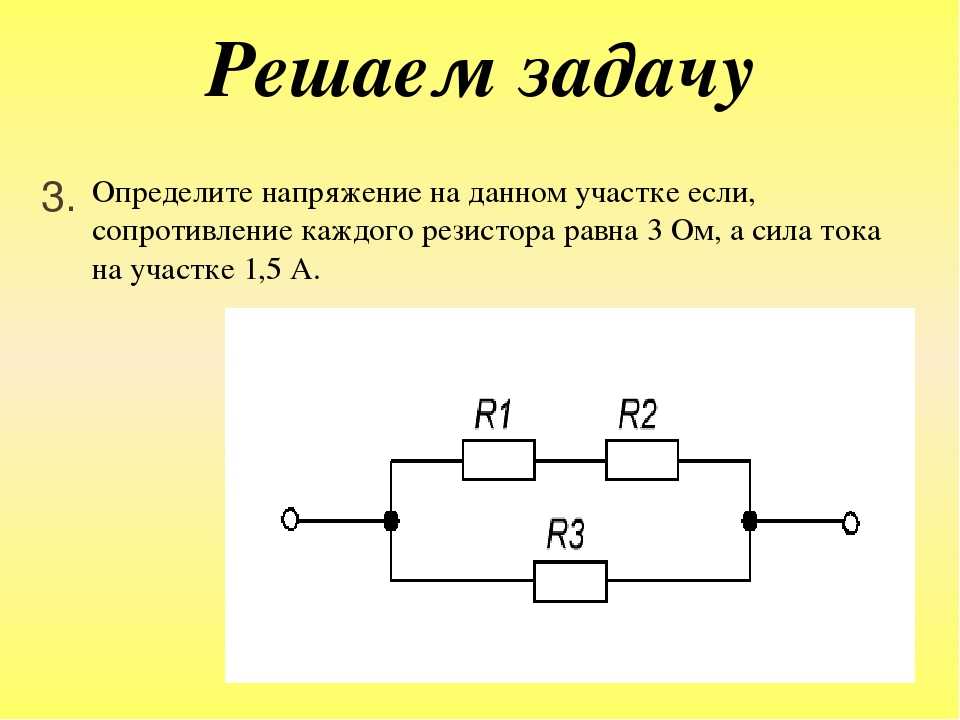 В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.
Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.
Пример расчета
В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:
По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.
Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.
Второй пример
Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:
Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.
Пример смешанного соединения
Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.
Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.
Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным.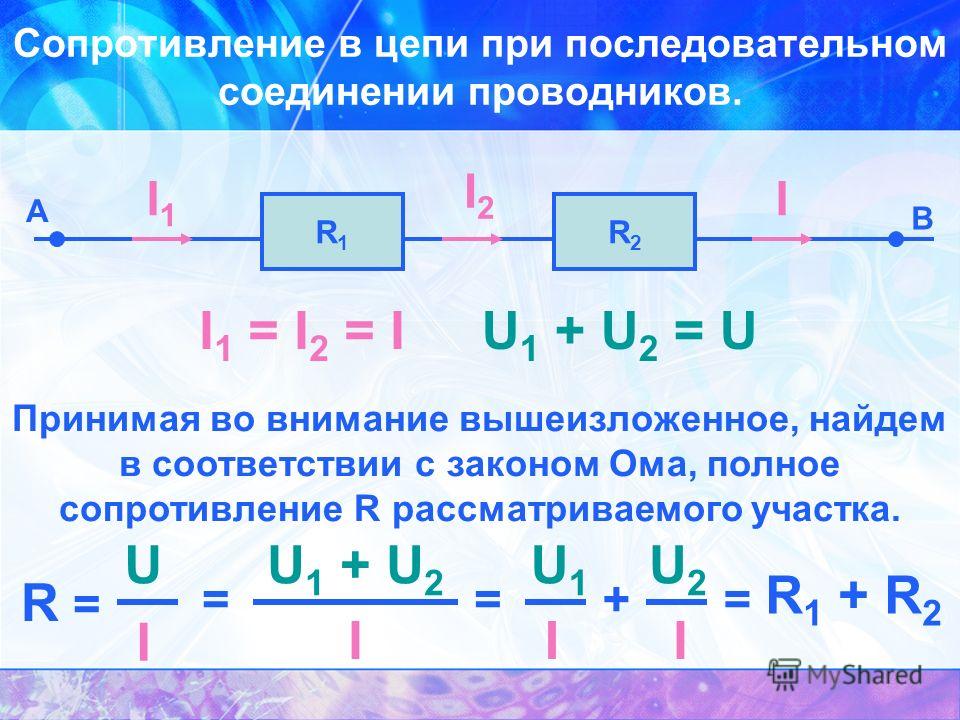 А далее то же самое, что и в примере выше.
А далее то же самое, что и в примере выше.
Применение параллельной схемы
Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.
Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.
Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.
Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.
Итог
При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.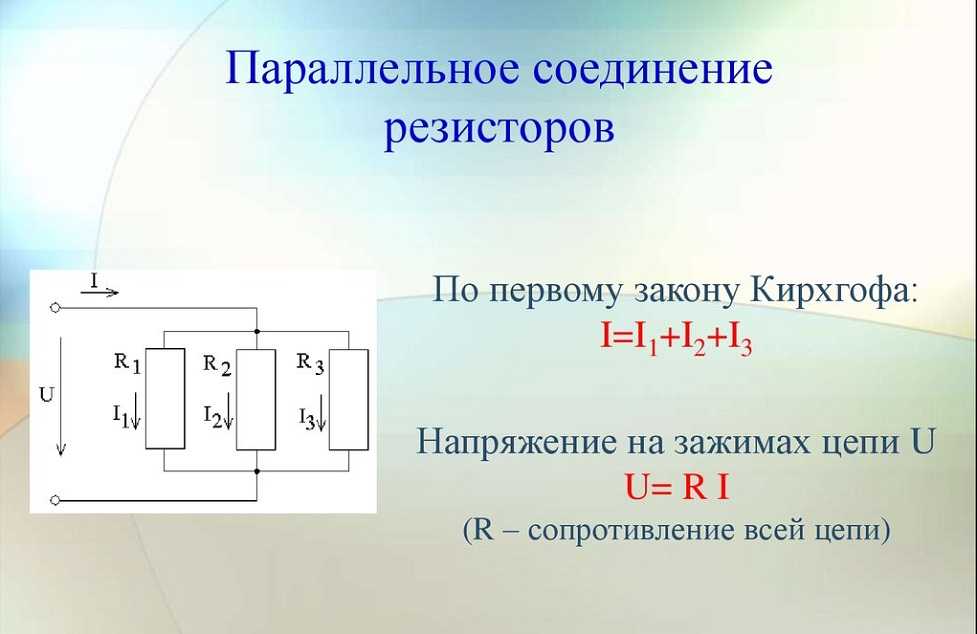
Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.
Расчет резистора для светодиода: онлайн калькулятор
Определение параллельного соединения
При таком виде, все проводники устанавливаются параллельно друг с другом. Они соединены в одну общую точку и все концы также скрепляются вместе. Если рассматривать энное количество одинаковых проводников, соединенных по данному принципу, то он будет называться разветвленным.
Какие виды подключений бывают
В каждом отсеке располагается один проводник. Поток электронов в виде тока, доходит до отметки ветвления, переходит на каждый проводник, и будет равен суммарным токам на всех сопротивлениях. Напряжение при таком подключении также будет равное.
Все проводники можно сменить одним общим резистором. Если применить правило Ома, то можно получить параметры сопротивления. При параллельном сопротивлении складываются показатели обратные их значениям.
Если применить правило Ома, то можно получить параметры сопротивления. При параллельном сопротивлении складываются показатели обратные их значениям.
Формулы для разных последовательностей
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения. Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).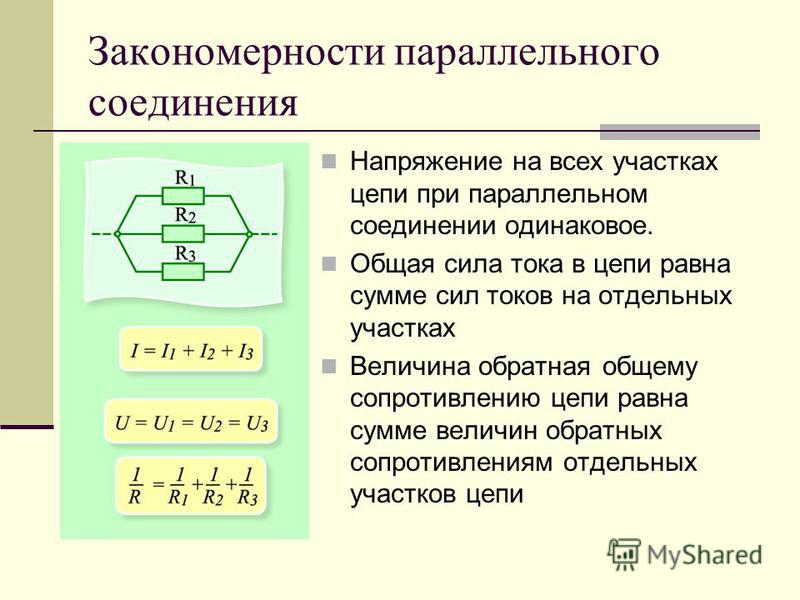
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.

Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
О разнице подключения звезда и треугольник читайте здесь.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.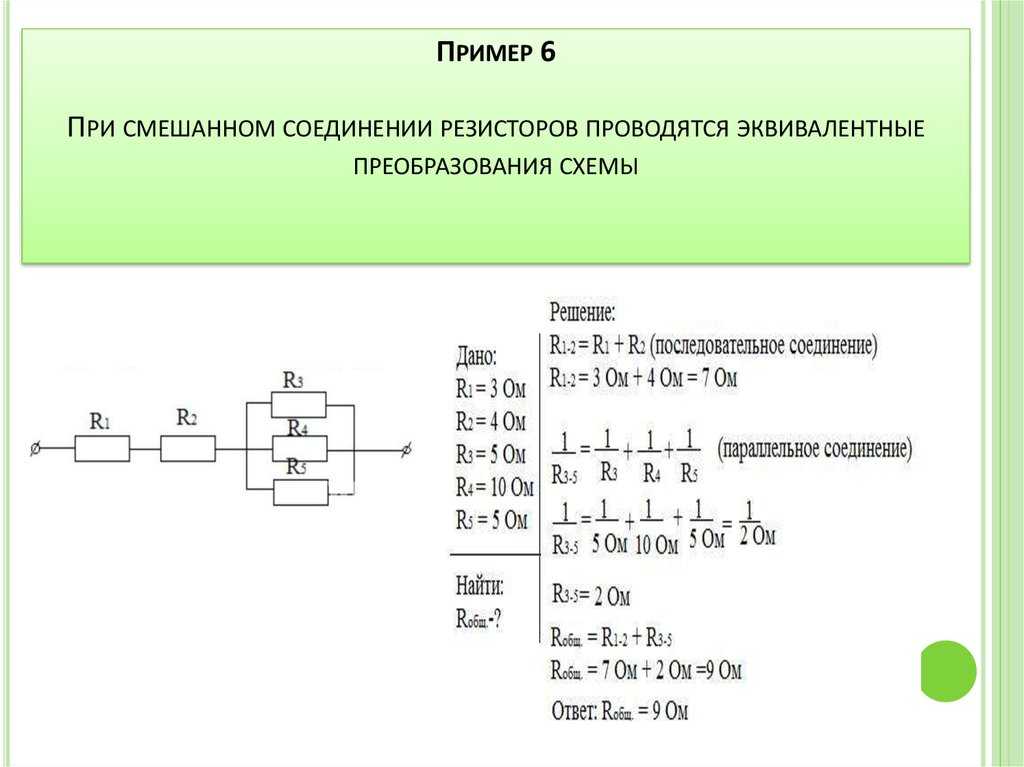
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.
Решение задачи производится путем разделения резистивных элементов на системные группы.
Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Выделяем вторую группу из последовательных элементов R1, R5, R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
Источник
Параллельное включение резисторов — схема и расчет. Как отличается параллельное и последовательное соединение резисторов?
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда.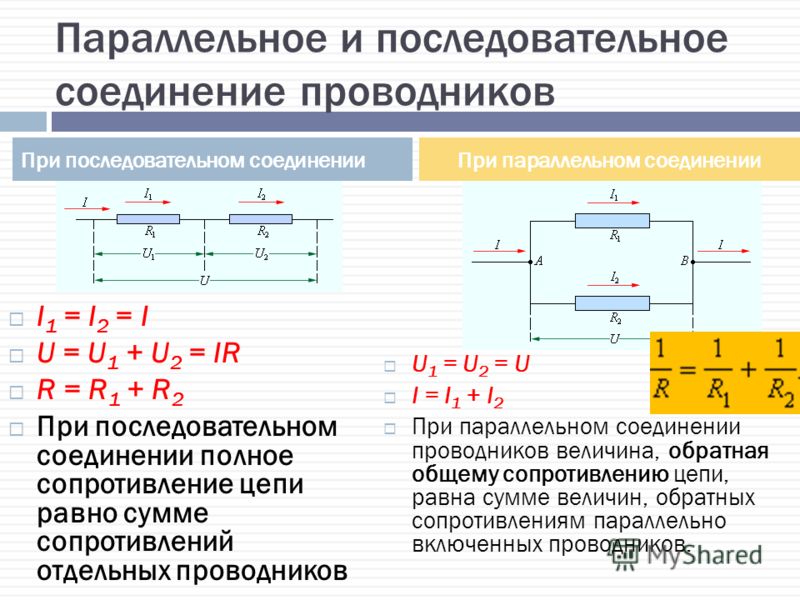 При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.

- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Общее сопротивление
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Схема
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Будет интересно➡ Переменный резистор
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.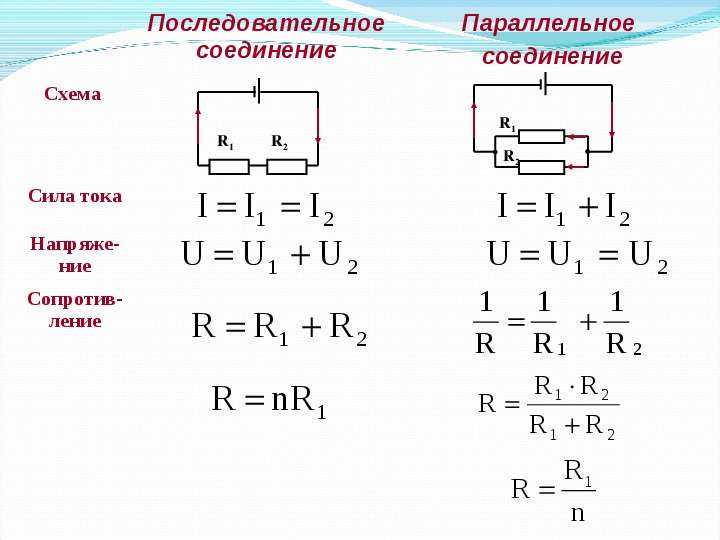
Как высчитывать
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Как выглядит формула Георга Ома
Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.
Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:
U1 = U2 = U.
Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:
I = I1 + I2.
Расчет силы тока при помощи закона Ома записывается как:
I = U/R;
I1 = U1/R1;
I2 = U2/R2.
Из формулы следует:
U/R = U1/R1 + U2/R2;
U = U1 = U2;
1/R = 1/R1 + 1/R2.
Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное.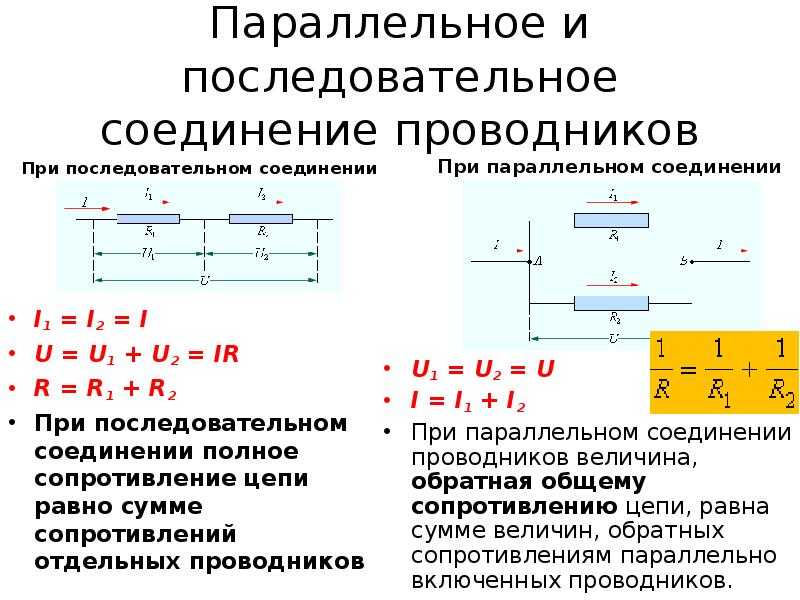 Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Отличия от последовательного и смешанного подключений
Параллельное соединение проводников
Иные способы соединения понятны из показанных на картинке примеров. Без специальных вычислений понятно, что параллельное включение резисторов создает несколько путей прохождения тока. Следовательно, в отдельных цепях его сила будет меньше, по сравнению с контрольными точками на входе и выходе. Вместе с тем напряжение в отмеченных местах остается неизменным.
Последовательное соединение резисторов увеличивает общее электрическое сопротивление. Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.
Смешанный вариант – это объединение представленных выше соединений. Различные комбинации используют для деления напряжения, решения других задач. Для упрощения расчетов суммируют последовательность соединенных сопротивлений в отдельных цепях:
Rобщ = R1 + R2 + … + Rn.
Вне зависимости от сложности схемы, на входе и выходе по первому закону Кирхгофа токи будут одинаковыми.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками.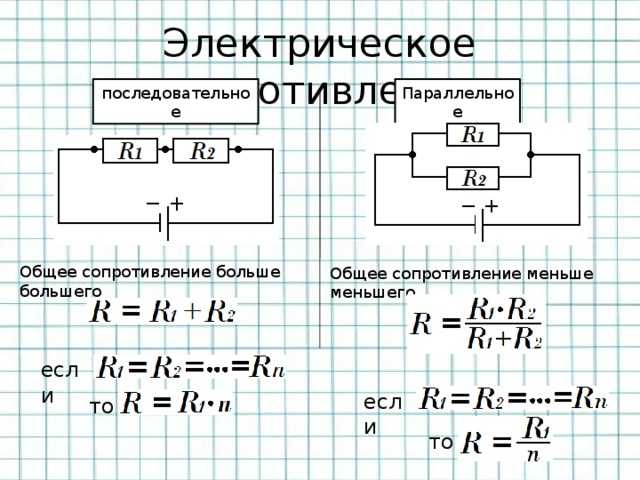 Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения.
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.
Источники
- https://rusenergetics.
 ru/praktika/raschet-soprotivleniya-rezistorov
ru/praktika/raschet-soprotivleniya-rezistorov - https://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html
- https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
- https://rusenergetics.ru/polezno-znat/parallelnoe-soedinenie
- https://www.RusElectronic.com/serial-and-parallel/
- https://amperof.ru/teoriya/parallelnoe-soedinenie-rezistorov.html
- https://www.translatorscafe.com/unit-converter/ru-RU/calculator/parallel-resistance/
- http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/
Соединение резисторов последовательное, параллельное, смешанное. Пример расчета
Соединение резисторов — это взаимное расположение данных элементов в цепи относительно друг друга и источника питания. Можно по отдельности выделить последовательное и параллельное соединение резисторов. Когда в схеме присутствуют оба варианта, то такое соединение называется смешанным.
Нам известно, что резистор — это электронный компонент, который обладает электрическим сопротивлением и мощностью рассеивания. Если в цепи имеется несколько резисторов, то для получения общего сопротивления прибегают к расчетам по правилам последовательного или параллельного соединения. Помимо общего сопротивления, группы резисторов по закону Ома влияют на напряжение и силу тока на участках цепи. И в данном обзоре будет доступно рассмотрена методика расчета общего сопротивления при различных видах соединения резисторов. Также будет рассмотрен наглядный пример со смешанным соединением резисторов, где помимо сопротивлений будут просчитаны напряжения и сила тока на разных участках.
Стоит сразу отметить, что в данной теме рассеивающая мощность резисторов вынесена за скобки. Мощность важна при подборе и комбинировании резисторов в схеме, но это уже отдельная тема. К тому же все рассмотренные примеры взяты с учетом источника переменного напряжения 220 В. Почему так? Об этом вы узнаете в последнем пункте публикации.
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
R = R1 + R2 + R3 + … + Rn.
R = 20 + 70 + 10 = 100 Ом.
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
I = U / R = U / (R1 + R2 + R3 + … + Rn).
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
- U1 = I × R1.
- U2 = I × R2.
- U3 = I × R3.
- Un = I × Rn.
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Схемы соединения конденсаторов — расчет емкости
В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.
Последовательное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.
Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.
Схема последовательного соединения конденсаторов будет иметь следующий вид:
Фактически последовательное соединение конденсаторов имеет следующий вид:
При данной схеме соединения заряды на конденсаторах будут одинаковы:
где: Q1, Q2, Q3 — соответственно заряд на первом, втором, третьем и т.д. конденсаторах
Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:
- U 1, U2, U3 — соответственно напряжение на первом, втором, третьем конденсаторах
- C 1, C2, C3 — соответственно емкости первого, второго, третьего конденсаторов
При этом общее напряжение составит:
Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:
При последовательном соединении двух конденсаторов:
При последовательном соединении трех и более конденсаторов:
Параллельное соединение конденсаторов
Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.
В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.
Схема параллельного соединения конденсаторов будет иметь следующий вид:
Таким образом параллельное соединение конденсаторов будет иметь следующий вид:
При данной схеме напряжение на всех конденсаторах будет одинаково:
Заряд же на каждом из конденсаторов будет зависеть от его емкости:
При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:
Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:
Смешанное соединение конденсаторов
Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.
Приведем пример такой схемы:
Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.
Для наглядности приведем пример расчета общей емкости данной схемы.
Пример расчета
Условно разделив схему на группы получим следующее:
Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.
Произведем расчет каждой группы:
Группа 1 — последовательное соединение трех конденсаторов:
Группа 2 — последовательное соединение двух конденсаторов:
Группа 3 — параллельное соединение трех конденсаторов:
В результате расчета схема упрощается:
Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:
Группа 4 — параллельное соединение двух групп конденсаторов:
В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:
Теперь можно определить общую емкость схемы:
Не нашли на сайте статьи на интересующую Вас тему касающуюся электрики? Напишите нам здесь. Мы обязательно Вам ответим.
Мы обязательно Вам ответим.
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
R ≈ 1 / 0,164 ≈ 6,097 Ом.
Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):
Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.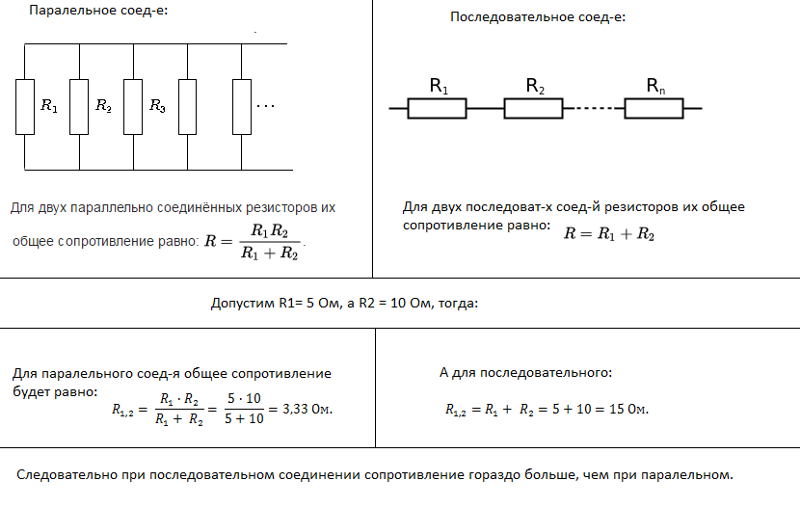
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
| Определяется общее сопротивление участков с параллельным соединением резисторов. | |
| Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление. | |
| После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений. | |
| Далее рассчитывается сопротивление полученной простой схемы. |
Краткие теоретические сведения
При расчете электрических цепей часто возникает целесообразность преобразования схем этих цепей в более простые и удобные для расчета. Различают следующие способы соединения элементов: последовательное, параллельное и смешанное.
Последовательным соединением
элементов электрической цепи называется такое, при котором начало последующего элемента соединяется с концом предыдущего (на рис. 1.1.а показано последовательное соединение резисторов). Часто такая цепь (или участок цепи) называется
1.1.а показано последовательное соединение резисторов). Часто такая цепь (или участок цепи) называется
неразветвленной
. Отличительной особенностью такого соединения элементов является то, что в них протекает один и тот же ток. Общее (эквивалентное) сопротивление последовательно включенных сопротивлений (приемников электрической энергии) равно сумме этих сопротивленийи напряжение, приложенное к цепи, равно сумме падений напряжений на отдельных элементах:
(1.1)
Мощность, потребляемая последовательной цепью:
(1.2)
При изменении величины сопротивления одного из приемников в последовательной электрической цепи происходит изменение тока и перераспределение падений напряжений на элементах, т. е. изменяется режим работы всех приемников. Это является существенным недостатком последовательного соединения элементов.
Рис. 1.1. Соединения сопротивлений:
а последовательное, бпараллельное, всмешанное
Параллельным соединением
элементов электрической цепи называется такое, при котором начала всех элементов соединены в один узел, а концы в другой (на рис.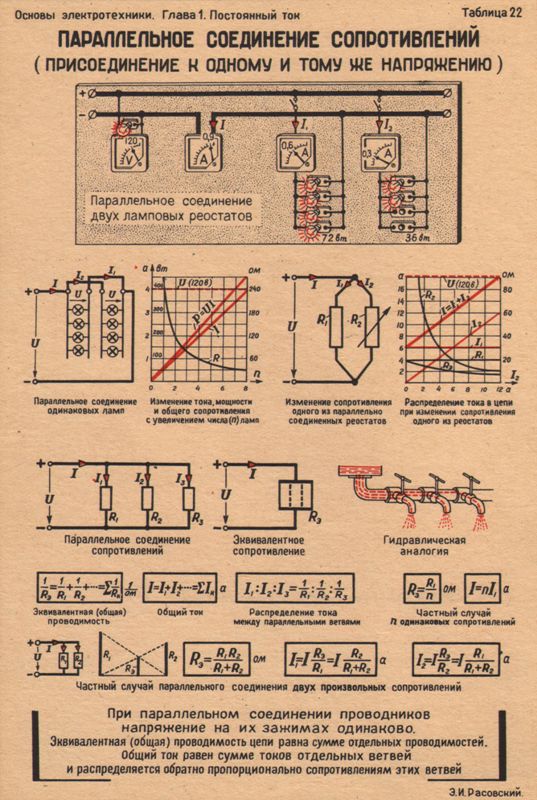 1.1.б показано последовательное соединение резисторов). При таком соединении цепь получается
1.1.б показано последовательное соединение резисторов). При таком соединении цепь получается
разветвленной
. Отличительной особенностью параллельного соединения элементов является то, что все они находятся под одним и тем же напряжением. Общая (эквивалентная) проводимость параллельно включенных сопротивлений равна сумме этих проводимостейгде проводимости отдельных приемников. Ток в неразветвленной части такой цепи равен:
(1.3)
Мощность, потребляемая параллельной электрической цепью:
(1.4)
При параллельном включении приемников режим работы каждого из них не влияет на режим работы остальных.
Смешанное соединение
приемников представляет собой цепь, которая состоит из последовательно и параллельно соединенных элементов. Для расчета таких цепей выделяют отдельные участки с последовательным и параллельным соединением и к ним применяют выше указанные соотношения.
Для смешанного соединения резисторов приведенного на рис. 1.1.в эквивалентное сопротивление находится следующим образом. Сначала определяется эквивалентное сопротивление параллельной цепи. ПосколькутоСопротивлениесоединено последовательно с сопротивлениемпоэтому эквивалентное сопротивление всей цепи равно
Сначала определяется эквивалентное сопротивление параллельной цепи. ПосколькутоСопротивлениесоединено последовательно с сопротивлениемпоэтому эквивалентное сопротивление всей цепи равно
Ток в неразветвленной части цепи равенНапряжение на сопротивленииравноНапряжение на зажимах параллельных ветвей равноТоки в параллельных ветвях равныи
Мощность, потребляемая изображенной на рис. 1.1.в смешанной электрической цепью:
(1.5)
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.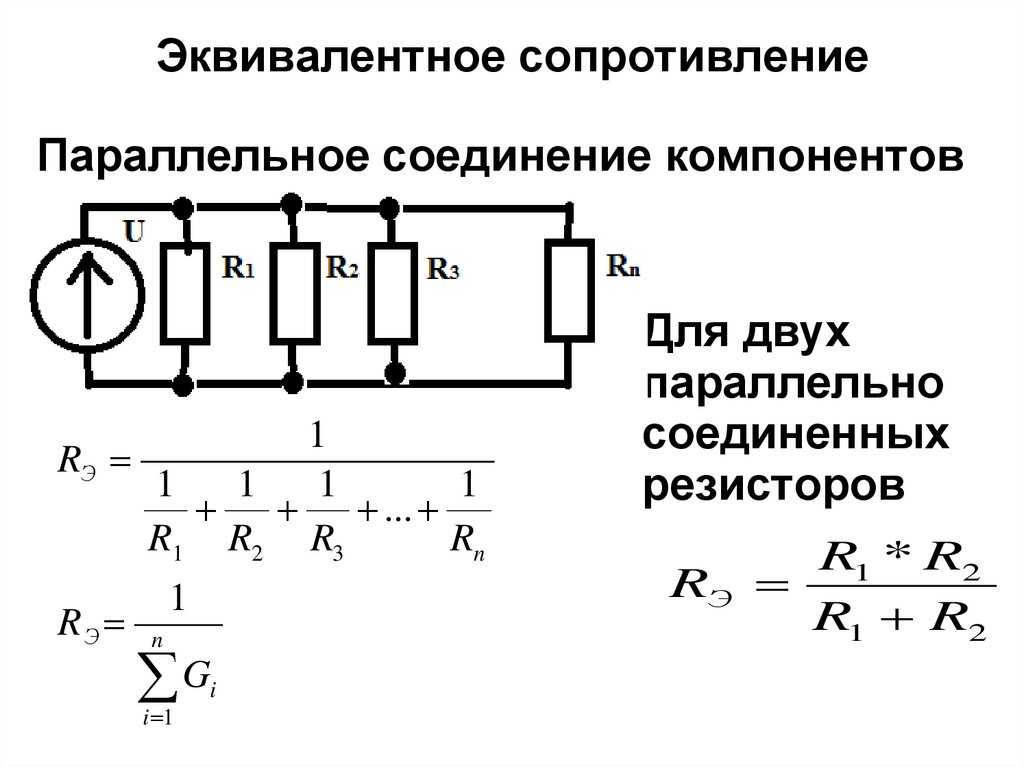
Смешанное соединение проводников. Расчёт электрических цепей 8 класс онлайн-подготовка на Ростелеком Лицей
Введение
На прошлых уроках мы рассмотрели электрические цепи только с последовательным или только с параллельным соединением проводников. Но существуют такие цепи, в которых присутствует как параллельное, так и последовательное соединение. Этот урок посвящён рассмотрению таких цепей со смешанным соединением проводников, а также расчёту различных электрических цепей.
Повторение. Факты про последовательное и параллельное соединение проводников.
1. При последовательном соединении проводников общее сопротивление участка равно сумме сопротивлений проводников:
2. При последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи:
3. При последовательном соединении проводников сумма напряжений равна общему напряжению на участке цепи:
4. При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:
При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:
5. При параллельном соединении проводников сумма сил токов равна общей силе тока на участке цепи:
6. При параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи:
Задача 1
Четыре одинаковые лампы подключены к источнику постоянного напряжения (см. рис. 1). Определите силу тока в каждой лампе, если напряжение на источнике составляет 30 В.
Дано: ;
Найти: , , ,
Решение
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображена электрическая цепь со смешанным соединением проводников: лампы 2 и 3 соединены параллельно, а лампы 2 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3.
Проводимость участка цепи, состоящего из ламп 2 и 3, равна:
Следовательно, сопротивление этого участка равно:
Так как лампы 1 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3, то общее сопротивление ламп будет равно:
Согласно закону Ома, сила тока всей цепи равна:
Так как при последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи, то:
Необходимо найти силу тока на лампах 2 и 3. Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:
Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:
Так как лампы 2 и 3 соединены параллельно, то напряжения на этих лампах равны:
Отсюда сила тока в каждой лампе равна:
Ответ: ;
Задача 2
Участок цепи, который состоит из четырёх резисторов, подключён к источнику с напряжением 40 В (см. рис. 2). Вычислите силу тока в резисторах 1 и 2, напряжение на резисторе 3. Сопротивление первого резистора равно 2,5 Ом, второго и третьего – по 10 Ом, четвёртого – 20 Ом.
Дано: ; ; ;
Найти: , ,
Решение
Рис. 2. Иллюстрация к задаче
Через резистор течёт такой же ток, как и через весь участок (), следовательно, согласно закону Ома:
То есть для нахождения нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором , другая часть с резисторами :
Резистор соединён параллельно резисторам и , следовательно:
Резисторы и соединены последовательно, поэтому:
Следовательно, сопротивление всей цепи равно:
Подставим данное значение в формулу для нахождения тока в резисторе :
Так как при параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи, то:
Отсюда:
При последовательном соединении силы тока одинаковы, поэтому:
Получили систему уравнений:
Решив эту систему получим, что:
Так как и соединены последовательно:
Напряжение на резисторе равно:
Ответ: ; ;
Задача 3
Найдите полное сопротивление цепи (см. рис. 3), если сопротивление резисторов , , . Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
рис. 3), если сопротивление резисторов , , . Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
Дано: ; ; ;
Найти: , , , , , ;
Решение
Рис. 3. Иллюстрация к задаче
Резисторы , , соединены последовательно, поэтому сопротивление на этом участке равно:
Резистор подключён параллельно участку с резисторами , , , поэтому сопротивление на участке с резисторами ,, , равно:
Резисторы и соединены с участком цепи с резисторами ,, , последовательно, то есть общее сопротивление цепи равно:
Через резистор и () неразветвлённой цепи течёт весь ток цепи, поэтому:
По закону Ома этот ток равен:
Общее напряжение цепи будет состоять из напряжений , так как ,, соединены последовательно (, потому что и параллельны):
Согласно закону Ома:
Резисторы , , соединены последовательно, следовательно:
Ответ: ; ; ;
Задача на бесконечную электрическую цепь
Найдите сопротивление R бесконечной цепи, показанной на рисунке 4.
Рис. 4. Иллюстрация к задаче
Решение
Поскольку рассматриваемая в задаче цепь бесконечна, удаление одной «ячейки», состоящей из резисторов и , не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена , тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. рис. 5) и записать для неё уравнение.
Рис. 5. Иллюстрация к задаче
Получили квадратное уравнение относительно R. Решая это уравнение и отбрасывая отрицательный корень (отрицательного сопротивления не существует), получаем формулу для общего сопротивления цепи:
Проанализировав данную формулу, можно заметить, что если , то общее сопротивление цепи . То есть резистор с малым сопротивление практически закоротит всю последующую бесконечную цепь.
Ответ:
Задача из ЕГЭ
Сопротивление каждого резистора в цепи (см. рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами A и B. Напряжение на резисторе равно 12 В. Найти напряжение между выводами схемы на участке A–B (варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В).
рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами A и B. Напряжение на резисторе равно 12 В. Найти напряжение между выводами схемы на участке A–B (варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В).
Дано: ;
Найти:
Решение
Рис. 6. Иллюстрация к задаче
Резисторы расположены последовательно, значит, силы тока на этих резисторах равны:
Так как, по условию, , то и напряжения на этих резисторах будут равны:
Следовательно, общее напряжения на участке, состоящем из резисторов , будет равно:
Так как участок с резисторами соединён с участком с резисторами параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:
Ответ: г) 36 В
Данную задачу, как видим, можно решить, не зная значений сопротивления, а зная только то, что они равны. Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.
Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.
Итоги урока
На этом уроке мы рассмотрели различные задачи на смешанное сопротивление проводников, а также на расчёт электрических цепей.
Список литературы
- Генденштейн Л. Э, Кайдалов А. Б., Кожевников В. Б. / Под ред. Орлова В. А., Ройзена И. И. Физика 8. – М.: Мнемозина.
- Перышкин А. В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А. А., Засов А. В., Киселев Д. Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «school56.pips.ru» (Источник)
- Интернет-портал «clck.ru» (Источник)
- Интернет-портал «clck.ru» (Источник)
Домашнее задание
- П. 49, стр. 117, задание 23 (5). Перышкин А. В. Физика 8. – М.
 : Дрофа, 2010.
: Дрофа, 2010. - Участок электрической цепи состоит из трех сопротивлений: ; ; (см. рис. 7). Определите показания вольтметров и амперметров , если амперметр показывает силу тока 2 А.
Рис. 7. Иллюстрация к задаче (Источник)
-
Как нужно соединить четыре резистора, сопротивления которых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее сопротивление было 1 Ом?
21.1 Резисторы, включенные последовательно и параллельно – College Physics
Глава 21 Цепи и приборы постоянного тока
Резюме
- Нарисуйте цепь с параллельными и последовательными резисторами.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.
Большинство цепей имеют более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены.
Рис. 1. (а) Последовательное соединение резисторов. (б) Параллельное соединение резисторов. Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то [латекс]{R_1}[/латекс] на рис.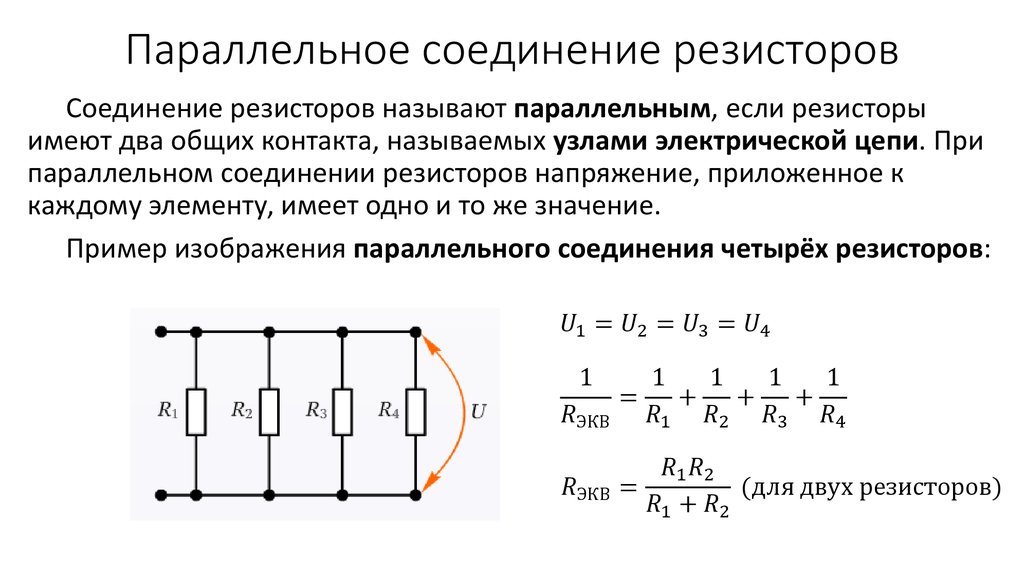 1(а) может быть сопротивлением стержня отвертки, [латекс]{R_2}[ /latex] сопротивление ручки, [latex]{R_3}[/latex] сопротивление тела человека и [latex]{R_4}[/latex] сопротивление его обуви.
1(а) может быть сопротивлением стержня отвертки, [латекс]{R_2}[ /latex] сопротивление ручки, [latex]{R_3}[/latex] сопротивление тела человека и [latex]{R_4}[/latex] сопротивление его обуви.
На рис. 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.)
Рисунок 2. Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа). Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения , в каждом резисторе на рисунке 2.
В соответствии с законом Ома , падение напряжения, [латекс]{В}[/латекс], на резисторе, когда через него протекает ток, рассчитывается по уравнению [латекс]{В = IR}[/латекс], где [латекс]{I}[/латекс] равен току в амперах (А), а [латекс]{R}[/латекс] — сопротивление в омах [латекс]{(\Omega )}[/латекс]. Другой способ представить это так: [латекс]{V}[/латекс] — это напряжение, необходимое для протекания тока [латекс]{I}[/латекс] через сопротивление [латекс]{R}[/латекс] .
Таким образом, падение напряжения на [латексе]{R_1}[/латексе] равно [латексу]{V_1 = IR_1}[/латексу], а на [латексе]{R_2}[/латексе] равно [латексу]{V_2 = IR_2 }[/latex], а через [latex]{R_3}[/latex] — [latex]{V_3 = IR_3}[/latex]. Сумма этих напряжений равна выходному напряжению источника; то есть
[латекс] {V = V_1 + V_2 + V_3}.[/латекс]
Это уравнение основано на законах сохранения энергии и сохранения заряда. Электрическая потенциальная энергия может быть описана уравнением [латекс]{РЕ = qV}[/латекс], где [латекс]{q}[/латекс] — электрический заряд, а [латекс]{В}[/латекс] — Напряжение.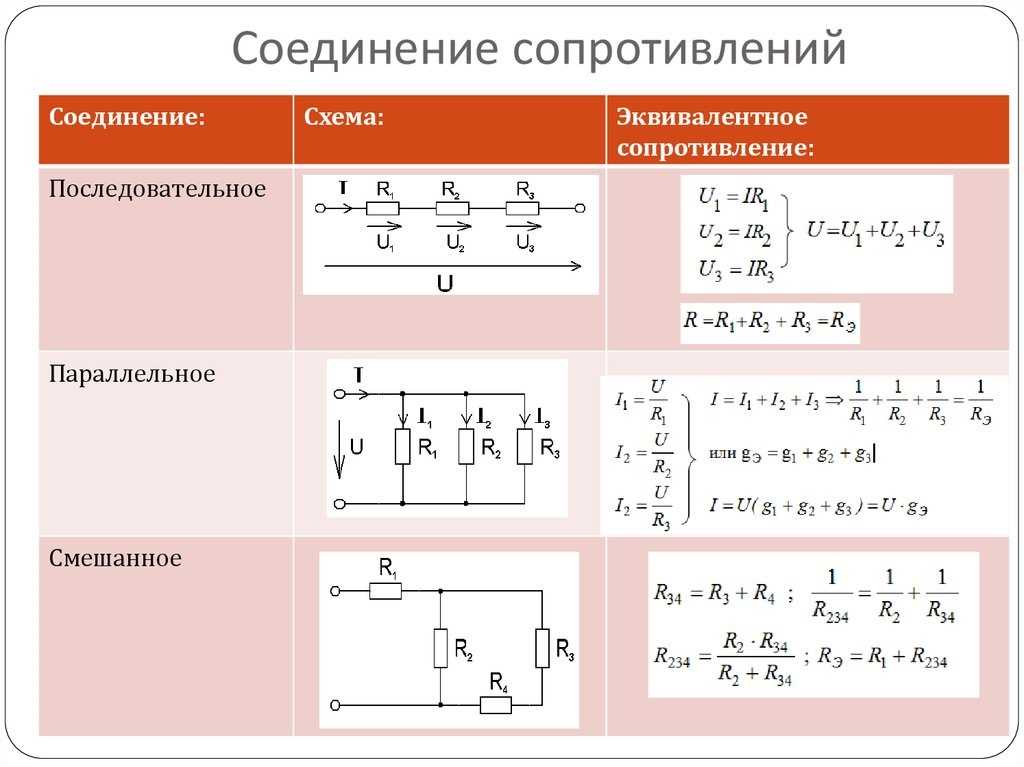 Таким образом, энергия, подаваемая источником, равна [латекс]{qV}[/латекс], а энергия, рассеиваемая резисторами, равна
Таким образом, энергия, подаваемая источником, равна [латекс]{qV}[/латекс], а энергия, рассеиваемая резисторами, равна
[латекс]{qV_1 + qV_2 + qV_3}.[/латекс]
Соединения: законы сохранения
Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого места назначения энергии. Таким образом, [латекс]{qV = qV_1 + qV_2 + qV_3}[/латекс]. Заряд [латекс]{q}[/латекс] отменяется, что дает [латекс]{V = V_1 + V_2 + V_3}[/латекс], как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.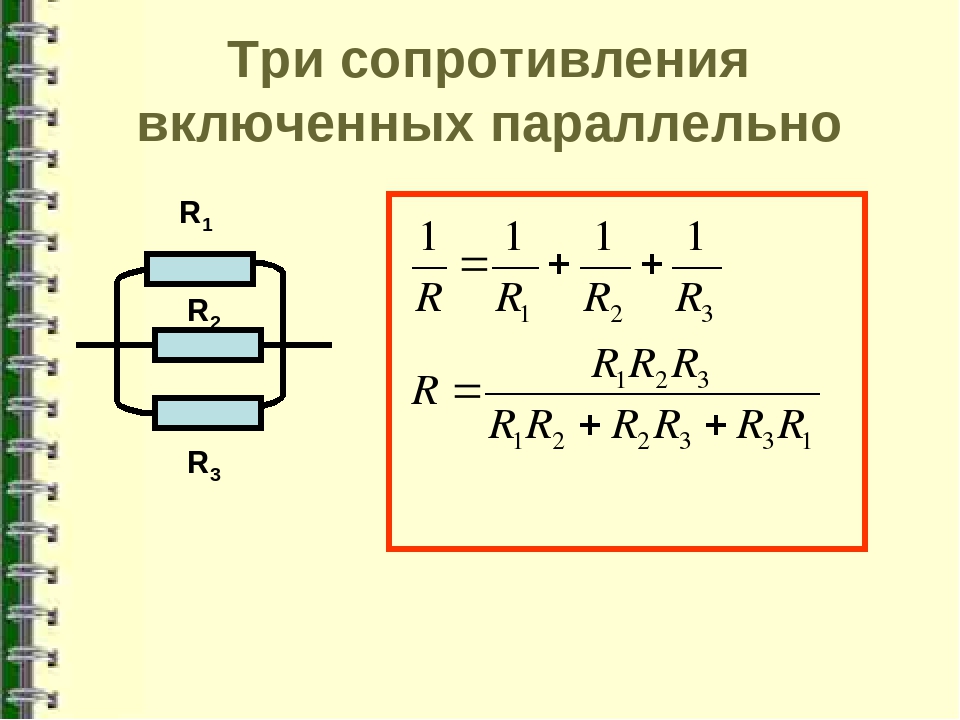 )
)
Теперь подстановка значений отдельных напряжений дает
[латекс] {V = IR_1 + IR_2 + IR_3 = I(R_1+R_2+R_3)}.[/латекс]
Обратите внимание, что для эквивалентного последовательного сопротивления [латекс]{R_s}[/латекс] мы имеем
[латекс]{V = IR_s}.[/латекс]
Это означает, что общее или эквивалентное последовательное сопротивление [латекс]{R_s}[/латекс] трех резисторов равно
.[латекс]{R_s = R_1 + R_2 + R_3}[/латекс].
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, общее сопротивление [латекс]{R_s}[/латекс] последовательного соединения равно
[латекс]{R_s = R_1 + R_2 + R_3 + \dots}[/латекс]
, как было предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример 1: расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рис. ], а сопротивления равны [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/латекс] и [латекс]{R_3 = 13,0 \; \Омега }[/латекс]. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
], а сопротивления равны [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/латекс] и [латекс]{R_3 = 13,0 \; \Омега }[/латекс]. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление — это просто сумма индивидуальных сопротивлений, определяемая следующим уравнением:
[латекс]\begin{array}{r @{{}={} } l} {R_s} & {R_1 + R_2 + R_3} \\[1em] & {1.00 \;\Omega + 6.00 \;\Omega + 13.0 \;\Omega} \\[1em] & {20.0 \;\ Омега}. \end{array}[/latex]
Стратегия и решение для (b)
Ток определяется по закону Ома, [latex]{V = IR}[/latex]. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {R_s}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {12,0 \; \text{V}}{20,0 \;\Omega}}[/latex] [латекс]{= 0,600 \;\textbf{A}}. [/latex]
[/latex]
Стратегия и решение для (c)
Падение напряжения — или [латекс] {IR} [/латекс] — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
[латекс]{V_1 = IR_1 = (0,600 \;\textbf{A})(1,0 \;\Omega) = 0,600 \;\text{V}}.[ /латекс]
Аналогично,
[латекс]{V_2 = IR_2 = (0,600 \;\textbf{A})(6,0 \;\Omega) = 3,60 \;\text{V}}[/латекс]
и
[латекс]{ V_3 = IR_3 = (0,600 \;\textbf{A})(13,0 \;\Omega) = 7,80 \;\text{V}}.[/latex]
Обсуждение для (c)
Три [ латекс] {ИК}[/латекс] капли добавляют к [латексу]{12,0 \;\текст{V}}[/латекс], как и прогнозировалось:
[латекс]{V_1 + V_2 + V_3 = (0,600 + 3,60 + 7.80) \;\text{V} = 12,0 \;\text{V}}.[/latex]
Стратегия и решение для (d) 92}{R}}[/latex], где [latex]{V}[/latex] — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать [латекс]{P = IV}[/латекс], где [латекс]{V}[/латекс] является напряжением источника.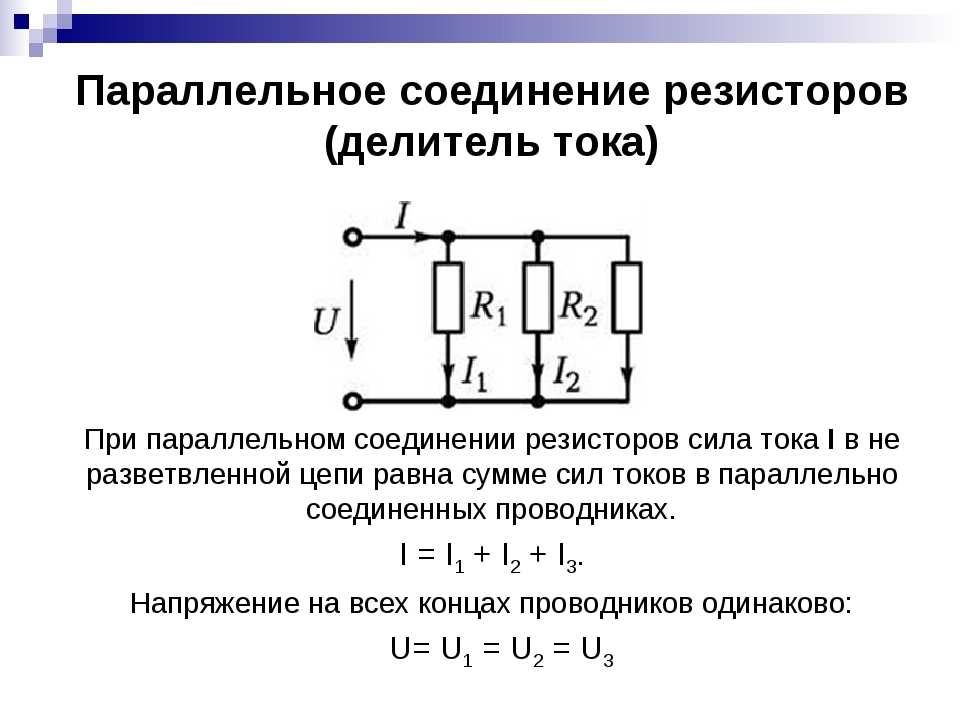 Это дает
Это дает
[латекс]{P = (0,600 \;\textbf{A})(12,0 \;\text{V}) = 7,20 \;\text{W}}.[/latex]
Обсуждение для д)
Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. То есть
[латекс]{P_1 + P_2 + P_3 = (0,360 + 2,16 + 4,68) \;\text{W} = 7,20 \;\text{W}}.[/latex]
Мощность – это энергия на единицу единица времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Сопротивления серии добавить: [латекс]{R_s = R_1 + R_2 + R_3 + \dots}[/латекс] .
- Один и тот же ток протекает через каждый последовательно соединенный резистор.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
На рис. 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рис. 3(b).)
Рисунок 3. (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление. (b) Установка электроснабжения в доме. (кредит: Дмитрий Г., Wikimedia Commons) Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс]{R_{\textbf{p}}}[/латекс], давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [latex]{I_1 = \frac{V}{R_1}}[/latex], [latex]{I_2 = \frac{V} {R_2}}[/latex] и [латекс]{I_3 = \frac{V}{R_3}}[/latex]. Сохранение заряда подразумевает, что полный ток [латекс]{I}[/латекс], производимый источником, представляет собой сумму этих токов:
Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [latex]{I_1 = \frac{V}{R_1}}[/latex], [latex]{I_2 = \frac{V} {R_2}}[/latex] и [латекс]{I_3 = \frac{V}{R_3}}[/latex]. Сохранение заряда подразумевает, что полный ток [латекс]{I}[/латекс], производимый источником, представляет собой сумму этих токов:
[латекс]{I = I_1 + I_2 + I_3}.[/латекс]
Подстановка выражений для отдельных токов дает
[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {R_1}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {V} {R_2 }}[/латекс] [латекс]{+}[/латекс] [латекс]{\ гидроразрыва {V} {R_3}}[/латекс] [латекс] {= V}[/латекс] [латекс] {(\ frac{1}{R_1}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{R_2}}[/latex] [латекс]{+}[/latex] [ латекс] {\ гидроразрыва {1} {R_3})}. [/латекс]
Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает
[латекс] {I =}[/латекс] [латекс]{\ гидроразрыва {V} {R_p}} [/ латекс] [латекс] {= V} [/латекс] [латекс] {(\ гидроразрыва {1} {R_p})}. [/латекс]
[/латекс]
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая любое количество резисторов, общее сопротивление [латекс]{R_p}[/латекс] параллельного соединения относится к отдельным сопротивлениям на
[латекс] {\ гидроразрыва {1} {R_p}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {R_1}} [/ латекс] [латекс] {+ } [/латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3}} [/ латекс] [ латекс]{+ \cdots}[/латекс]
Это соотношение приводит к тому, что общее сопротивление [латекс]{R_p}[/латекс] меньше, чем наименьшее из отдельных сопротивлений. (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
Пример 2: расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рис.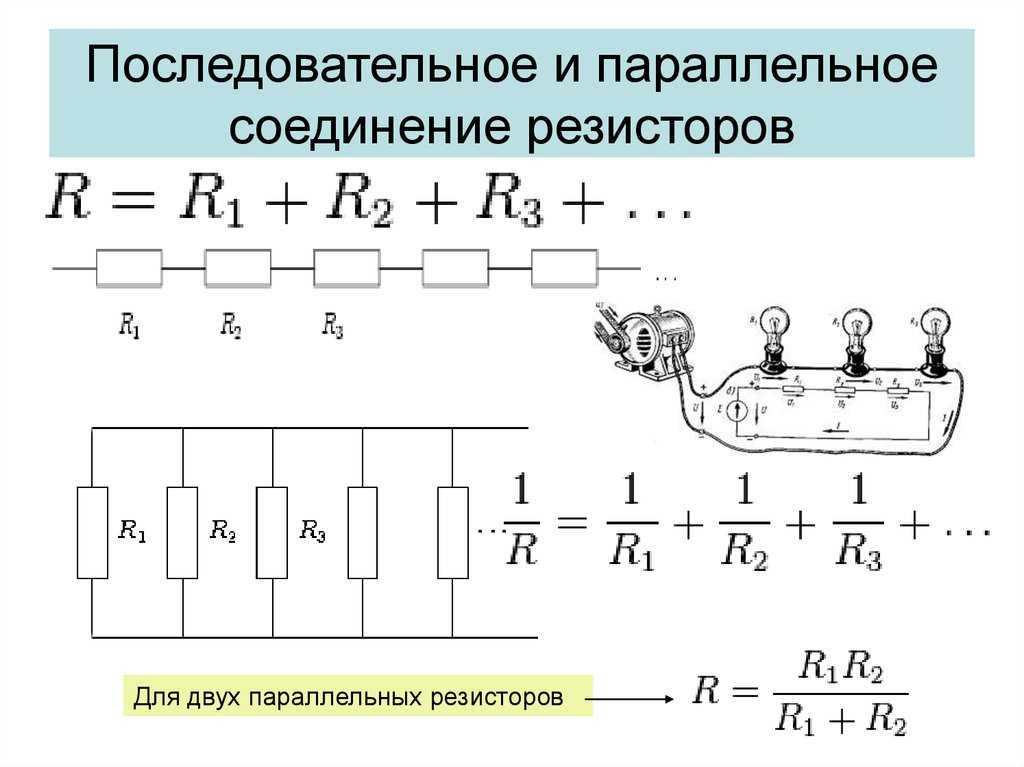 3 будут такими же, как и при последовательном соединении, рассмотренном ранее: [ латекс]{V = 12,0 \;\text{V}}[/латекс], [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/ латекс] и [латекс]{R_3 = 13,0 \;\Omega}[/латекс]. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
3 будут такими же, как и при последовательном соединении, рассмотренном ранее: [ латекс]{V = 12,0 \;\text{V}}[/латекс], [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/ латекс] и [латекс]{R_3 = 13,0 \;\Omega}[/латекс]. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает
[латекс] {\ гидроразрыва {1} {R_p}} [/латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1} {R_1}} [/латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {1,00 \; \ Omega}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ frac{1}{6. 00 \;\Omega}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{13.0 \;\Omega}}.[/latex]
00 \;\Omega}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{13.0 \;\Omega}}.[/latex]
Таким образом,
[латекс] {\ гидроразрыва {1} {R_p}} [/латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1.00} {\ Omega}} [/латекс ] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {0,1667} {\ Omega}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {0,07692} {\ Omega}}[/latex] [latex]{=}[/latex] [latex]{\frac{1.2436}{\Omega}}[/latex]
(Обратите внимание, что в этих расчетах каждый промежуточный ответ показан с лишняя цифра.)
Мы должны инвертировать это, чтобы найти общее сопротивление [латекс]{R_p}[/латекс]. Это дает
[латекс] {R_p =} [/латекс] [латекс] {\ гидроразрыва {1} {1.2436}} [/ латекс] [латекс] {\ Omega = 0,8041 \; \ Omega}. [/latex]
Общее сопротивление с правильным количеством значащих цифр равно [латекс]{R_p = 0,804 \;\Omega}[/latex]
Обсуждение для (a)
[латекс]{R_p}[/латекс] как и предсказывалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив [латекс]{R_p}[/латекс] вместо полного сопротивления. Это дает
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {R_p}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {12,0 \;\text{V}}{0,8041 \;\Omega}}[/latex] [латекс]{= 14,92 \;\textbf{A}}[/latex]
Обсуждение для (b)
Ток [latex]{I}[/latex] для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно ( см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
[латекс] {I_1 =} [/латекс] [латекс] {\ гидроразрыва {V} {R_1}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {12,0 \; \text{V}}{1. 00 \;\Omega}}[/latex] [латекс]{= 12.0 \;\textbf{A}}.[/latex]
00 \;\Omega}}[/latex] [латекс]{= 12.0 \;\textbf{A}}.[/latex]
Аналогично,
[латекс]{I_2 =} [/латекс] [латекс] {\ гидроразрыва {V} {R_2}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {12,0 \; \ текст {V}} {6,00 \ ;\Omega}}[/латекс] [латекс]{= 2,00 \;\textbf{A}}[/латекс]
и
[латекс]{I_3 =}[/латекс] [латекс]{\ гидроразрыва{ V} {R_3}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {12,0 \; \ текст {V}} {13,0 \; \ Омега}} [/ латекс] [латекс ] {= 0,92 \;\textbf{A}}.[/latex]
Обсуждение для (c)
Общий ток представляет собой сумму отдельных токов:
[латекс]{I_1 + I_2 + I_3 = 14,92 \ ;\textbf{A}}.[/latex]
Это соответствует закону сохранения заряда.
Стратегия и решение для (d)
Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. 2}{R}}[/latex], поскольку на каждый резистор подается полное напряжение. Таким образом, 92}{13.0 \;\Omega}}[/latex] [latex]{= 11.1 \;\text{W}} .[/latex]
2}{R}}[/latex], поскольку на каждый резистор подается полное напряжение. Таким образом, 92}{13.0 \;\Omega}}[/latex] [latex]{= 11.1 \;\text{W}} .[/latex]
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении значительно выше, чем при последовательном подключении к одному и тому же источнику напряжения.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбор [латекс]{P = IV}[/латекс] и ввод общего тока дает
[латекс]{P = IV = (14,92 \;\textbf{A})(12,0 \;\text{V} ) = 179\;\text{W}}.[/latex]
Обсуждение для (e)
Общая мощность, рассеиваемая резисторами, также составляет 179 Вт:
[латекс]{P_1 + P_2 + P_3 = 144 \; \text{W} + 24,0 \;\text{W} + 11,1 \;\text{W} = 179 \;\text{W}}.[/latex]
Это согласуется с законом сохранения энергии .
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.
Основные характеристики резисторов, соединенных параллельно
- Параллельное сопротивление находится из [латекс] {\ гидроразрыва {1} {R_p} = \ гидроразрыва {1} {R_1} + \ гидроразрыва {1} {R_2} + \ гидроразрыва {1 }{R_3} + \cdots }[/latex], и оно меньше любого отдельного сопротивления в комбинации.
- К каждому резистору, подключенному параллельно, приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они его делят.
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения могут быть сведены к одному эквивалентному сопротивлению с помощью метода, показанного на рис. 4. Различные части обозначены как последовательные или параллельные, приведены к их эквивалентам и далее уменьшены до тех пор, пока не останется одно сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок 4. Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление. Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рис. 5, также является наиболее поучительной, поскольку она встречается во многих приложениях. Например, [латекс]{R_1}[/латекс] может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, которые включены параллельно. [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс] могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
[латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс] могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления, [латекс]{IR}[/латекс] падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей последовательно и параллельно. Мы можем рассматривать [латекс]{R_1}[/латекс] как сопротивление проводов, ведущих к [латексу]{R_2}[/латексу] и [латексу]{R_3}[/латексу]. а) Найдите полное сопротивление. (b) Каково снижение [латекса]{IR}[/латекса] в [латексе]{R_1}[/латекс]? (c) Найдите текущий [латекс]{I_2}[/латекс] через [латекс]{R_2}[/латекс]. (d) Какая мощность рассеивается [латексом]{R_2}[/латексом]?
Рисунок 5. Эти три резистора подключены к источнику напряжения таким образом, что R 2 и R 3 соединены параллельно друг другу, а эта комбинация 40346 последовательно с R .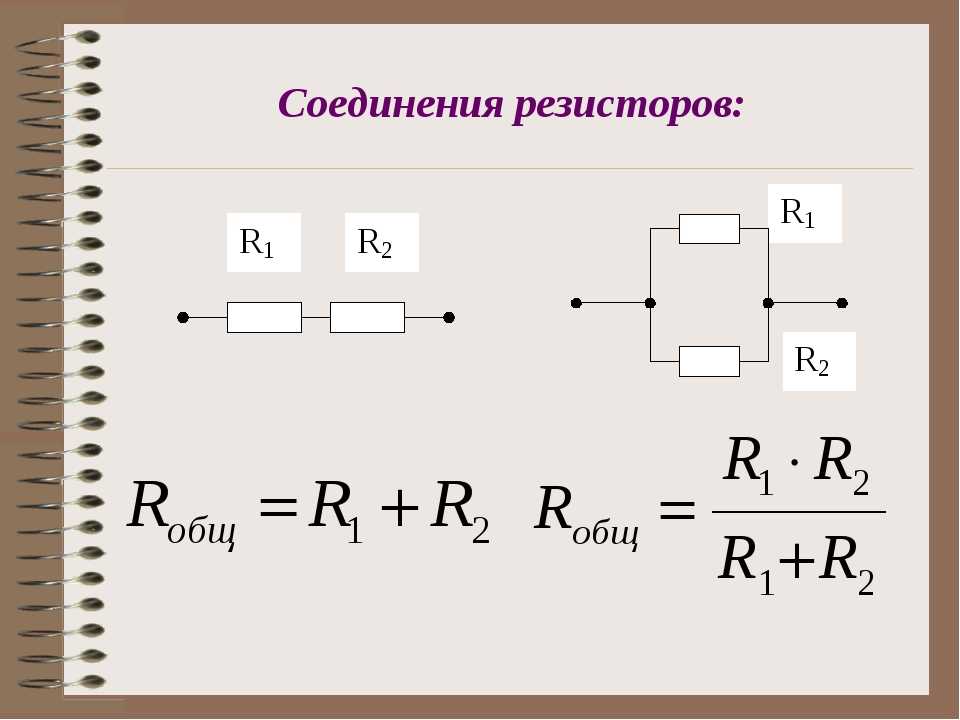 1 .
1 . Стратегия и решение для (a)
Чтобы найти полное сопротивление, заметим, что [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс] параллельны, и их комбинация [латекс ]{R_p}[/latex] идет последовательно с [latex]{R_1}[/latex]. Таким образом, общее (эквивалентное) сопротивление этой комбинации равно
[латекс]{R_{\text{tot}} = R_1 + R_p}.[/latex]
Сначала находим [латекс]{R_p}[/латекс], используя уравнение для параллельных резисторов и вводя известные значения:
[латекс]{\ гидроразрыва {1} {R_p}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/латекс] [латекс ] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {6,00 \; \ Омега }}[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{1}{13,0 \;\Омега}}[/латекс] [латекс]{=}[/латекс] [латекс] {\ гидроразрыва {0,2436} {\ Omega}}.[/латекс]
Инвертирование дает
[латекс] {R_p =} [/латекс] [латекс] {\ гидроразрыва {1} {0,2436}} [/латекс] [латекс] {\ Омега = 4,11 \; \ Омега}.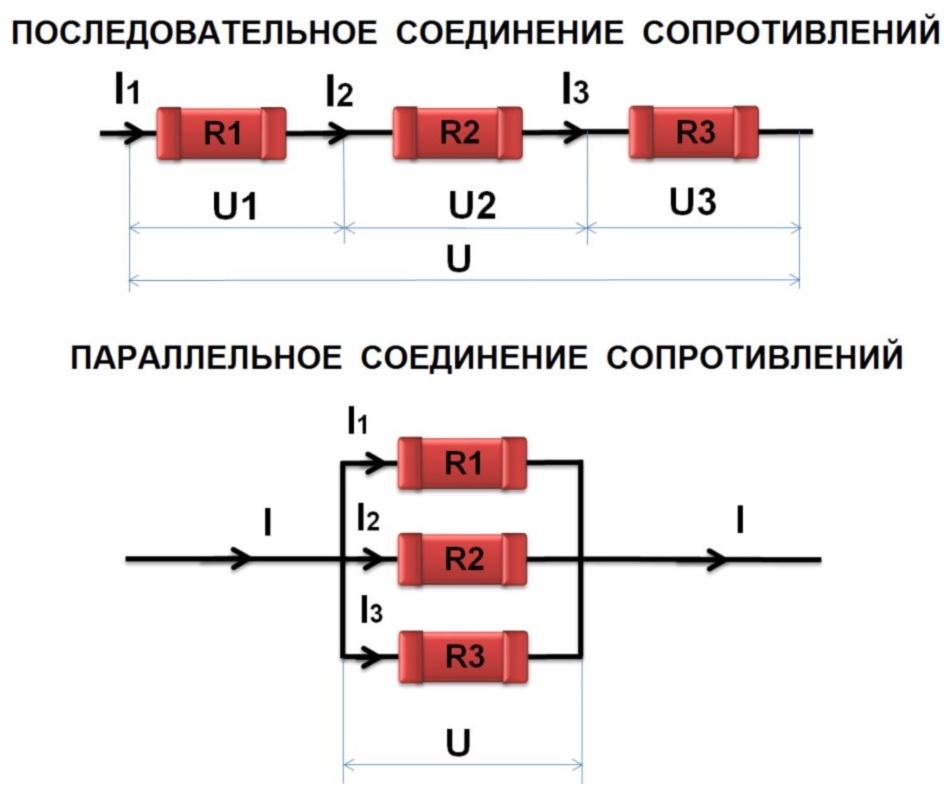 [/ латекс]
[/ латекс]
Таким образом, общее сопротивление равно
[латекс]{R_{\text{tot}} = R_1 + R_p = 1,00 \;\Omega + 4,11 \;\Omega = 5,11 \;\Omega}.[/latex ]
Обсуждение для (a)
Суммарное сопротивление этой комбинации является промежуточным между чисто последовательными и чисто параллельными значениями ([латекс]{20,0 \;\Омега}[/латекс] и [латекс]{0,804 \ ;\Omega}[/latex] соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение [latex]{IR}[/latex] в [latex]{R_1}[/latex], заметим, что полный текущий [latex]{I }[/latex] проходит через [latex]{R_1}[/latex]. Таким образом, его [латекс]{IR}[/латекс] равен
[латекс]{V_1 = IR_1}.[/латекс]
Мы должны найти [латекс]{I}[/латекс], прежде чем мы сможем вычислить [латекс ]{V_1}[/латекс]. Полный ток [латекс]{I}[/латекс] находится по закону Ома для цепи. То есть
[латекс] {I =}[/латекс] [латекс] {\ гидроразрыва {V} {R _ {\ текст {tot}}}} [/латекс] [латекс] {=}[/латекс] [латекс]{\ гидроразрыва {12,0 \;\текст{V}}{5,11 \;\Омега}}[/латекс] [латекс]{= 2,35 \;\textbf{A}}.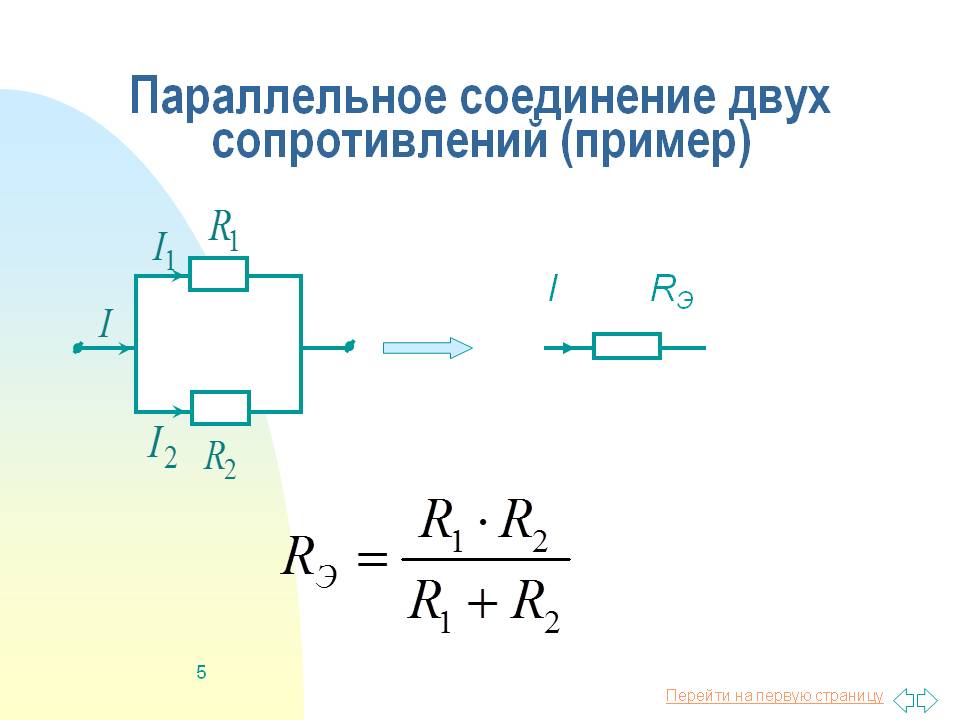 [/латекс]
[/латекс]
Подставив это в выражение выше, мы получим
[латекс]{V_1 = IR_1 = (2,35 \;\textbf{A})(1,00 \;\Omega) = 2,35 \;\text{V}}.[ /latex]
Обсуждение для (b)
Напряжение, подаваемое на [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс], меньше общего напряжения на величину [латекс ]{V_1}[/латекс]. Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс].
Стратегия и решение для (c)
Чтобы найти ток через [латекс]{R_2}[/латекс], мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение [латекс] {V _ {\ textbf {p}}} [/латекс], потому что оно приложено к параллельной комбинации резисторов. Напряжение, подаваемое как на [латекс]{R_2}[/латекс], так и на [латекс]{R_3}[/латекс], уменьшается на величину [латекс]{V_1}[/латекс], поэтому оно составляет
[латекс]. ]{V_p = V — V_1 = 12,0 \;\text{V} — 2,35 \;\text{V} = 9,65 \;\text{V}}. [/latex]
[/latex]
Теперь ток [латекс]{I_2}[/латекс] через сопротивление [латекс]{R_2}[/латекс] находится по закону Ома:
[латекс]{I_2 =}[/латекс] [латекс]{ \frac{V_p}{R_2}}[/latex] [латекс]{=}[/latex] [латекс]{\frac{9,65 \;\text{V}}{6,00 \;\Omega}}[/latex ] [latex]{ = 1,61 \;\textbf{A}}[/latex]
Обсуждение для (c)
Ток меньше, чем 2,00 A, протекающих через R2R2 размера 12{R rSub { размера 8 {2} } } {} при параллельном подключении к аккумулятору в предыдущем примере с параллельной схемой. 92(6,00 \;\Omega) = 15,5 \;\text{W}}.[/latex]
Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источник 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах уменьшает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение [латекс]{ИК}[/латекс] в проводах также может быть значительным.
Если потребляется большой ток, падение [латекс]{ИК}[/латекс] в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рис. 6. Устройство, представленное [латекс]{R_3}[/латекс], имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Это увеличение тока вызывает большее [латекс]{IR}[/латекс] падение в проводах, представленных [латекс]{R_1}[/латекс], уменьшая напряжение на лампочке (которое составляет [латекс]{R_2}[ /latex]), который затем заметно тускнеет.
Рисунок 6. Почему гаснет свет при включении большого электроприбора? Ответ заключается в том, что большой ток, потребляемый двигателем электроприбора, вызывает значительное падение напряжения в проводах и снижает напряжение на лампе.
Стратегии решения проблем с последовательными и параллельными резисторами
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
- Определите, что именно нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах.
 Особое примечание: при поиске[/latex]латекса{R_p}[/latex] следует проявлять осторожность.
Особое примечание: при поиске[/latex]латекса{R_p}[/latex] следует проявлять осторожность. - Проверьте, разумны ли и последовательны ли ответы. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
- Общее сопротивление электрической цепи с последовательно соединенными резисторами представляет собой сумму отдельных сопротивлений: [latex]{R_s = R_1 + R_2 + R_3 + \cdots}[/latex]
- Через каждый резистор в последовательной цепи протекает одинаковый ток.
- Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различны, и их общая сумма составляет входную мощность источника питания.
- Общее сопротивление электрической цепи с параллельно соединенными резисторами меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле:
[латекс] {\ гидроразрыва {1} {R _ {\ textbf {p}}}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1} {R_1}} [/ латекс] [латекс] {+}[/ латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3 }}[/латекс] [латекс]{+ \;\cdots}[/латекс]
- К каждому резистору в параллельной цепи приложено одинаковое полное напряжение источника.

- Ток, протекающий через каждый резистор в параллельной цепи, различен в зависимости от сопротивления.
- Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного сопротивления, его можно свести к единому эквивалентному сопротивлению, обозначив различные его части как последовательные или параллельные, сведя каждую к эквиваленту и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление .
Концептуальные вопросы
1: Выключатель имеет переменное сопротивление, близкое к нулю в закрытом состоянии и очень большое в разомкнутом, и он включен последовательно с устройством, которым он управляет. Объясните влияние переключателя на рисунке 7 на ток в разомкнутом и замкнутом состоянии.
Рисунок 7. Переключатель обычно подключается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в закрытом состоянии, но чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)
(Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.) 2: Какое напряжение на разомкнутом выключателе на рисунке 7?
3: На разомкнутом ключе есть напряжение, как на рис. 7. Почему же тогда мощность, рассеиваемая разомкнутым ключом, мала?
4: Почему мощность, рассеиваемая замкнутым выключателем, как на рис. 7, мала?
5: Студент в лаборатории физики по ошибке подключил лампочку, батарею и выключатель, как показано на рис. 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и выключается, когда выключатель замкнут. (Не пытайтесь это сделать — это плохо для батареи!)
Рисунок 8. Ошибка проводки поставила этот переключатель параллельно с устройством, обозначенным R . (Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи. )
) 6: Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли быть включенным последовательно или параллельно с сопротивлением, например, с нагревательным элементом тостера, если оно поражено им? Объяснять.
7: Погасли бы фары при запуске двигателя автомобиля, если бы провода в автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объясните.
8: Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые разрывали электрическое соединение, как разомкнутый выключатель, когда они перегорали. Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампочки, у которых короткое замыкание, как у замкнутого выключателя, когда они перегорают. Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 39остальные одинаковые лампочки, какое тогда рабочее напряжение у каждой?
Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 39остальные одинаковые лампочки, какое тогда рабочее напряжение у каждой?
9: Если две бытовые лампочки мощностью 60 Вт и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10: Предположим, вы выполняете лабораторную работу по физике, в которой вас просят включить резистор в цепь, но все поставляемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее требуемое значение?
11: До Второй мировой войны некоторые радиоприемники получали питание через «резистивный шнур», который имел значительное сопротивление. Такой шнур сопротивления снижает напряжение до желаемого уровня для радиоламп и т.п., а также экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и расходуют энергию, когда радио включено.
12: Некоторые лампочки имеют три уровня мощности (не считая нуля), получаемые из нескольких нитей накала, которые включаются по отдельности и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности? 92 — \;\Omega}[/latex] a [латекс]{2.50 — \;\text{k} \Omega}[/latex] и [латекс]{4.00 — \;\text{k} \Omega }[/latex] резистор соединен последовательно? б) Параллельно?
3: Какое наибольшее и наименьшее сопротивление можно получить, соединив [латекс]{36.0 — \;\Omega}[/латекс], [латекс]{50.0 — \;\Омега}[/латекс ], и резистор [латекс]{700 — \;\Омега}[/латекс] вместе?
4: Тостер мощностью 1800 Вт, электрическая сковорода мощностью 1400 Вт и лампа мощностью 75 Вт подключены к одной розетке в сети 15 А, 120 В. (Три устройства подключены параллельно, когда они подключены к одной и той же розетке.). а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5: Фара вашего автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в системе 12,0 В. Какую мощность будет потреблять одна фара и стартер при последовательном подключении к аккумулятору 12,0 В? (Любым другим сопротивлением в цепи и любым изменением сопротивления в двух устройствах пренебречь). и [латекс]{96.0 — \;\Омега}[/латекс] резисторы, найдите ток и мощность для каждого из них при последовательном соединении. (b) Повторите, когда сопротивления параллельны.
Какую мощность будет потреблять одна фара и стартер при последовательном подключении к аккумулятору 12,0 В? (Любым другим сопротивлением в цепи и любым изменением сопротивления в двух устройствах пренебречь). и [латекс]{96.0 — \;\Омега}[/латекс] резисторы, найдите ток и мощность для каждого из них при последовательном соединении. (b) Повторите, когда сопротивления параллельны.
7: Ссылаясь на пример объединения последовательных и параллельных цепей и рисунок 5, рассчитайте [латекс]{I_3}[/латекс] двумя следующими способами: (а) по известным значениям [латекс]{I }[/латекс] и [латекс]{I_2}[/латекс]; (б) с использованием закона Ома для [латекса]{R_3}[/латекс]. В обеих частях подробно показано, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
8: Ссылаясь на рисунок 5: (a) Рассчитайте [латекс]{P_3}[/латекс] и обратите внимание, как это соотносится с [латексом]{P_3}[/латекс], обнаруженным в первых двух примерах задач в этом модуль. 9- \;\Omega}[/latex] сопротивление. Рис. 9. (а) Каково сопротивление заземления 100 таких изоляторов? б) Рассчитайте мощность, рассеиваемую 100 из них. в) Какую долю мощности несет линия? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
9- \;\Omega}[/latex] сопротивление. Рис. 9. (а) Каково сопротивление заземления 100 таких изоляторов? б) Рассчитайте мощность, рассеиваемую 100 из них. в) Какую долю мощности несет линия? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
11: Покажите, что если объединить два резистора [латекс]{R_1}[/латекс] и [латекс]{R_2}[/латекс] и один из них намного больше другого ([латекс]{R_1 >> R_2 }[/latex]): (a) Их последовательное сопротивление почти равно большему сопротивлению [latex]{R_1}[/latex]. (b) Их параллельное сопротивление почти равно меньшему сопротивлению [латекс]{R_2}[/латекс].
12: Необоснованные результаты
Два резистора, один из которых имеет сопротивление [латекс]{145 Ом;\Омега}[/латекс], соединены параллельно, чтобы получить общее сопротивление [латекс]{150 Ом; \Омега}[/латекс]. а) Какова величина второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
13: Необоснованные результаты
Два резистора, один из которых имеет сопротивление [латекс]{900 \;\text{k} \Омега}[/латекс], соединены последовательно, чтобы получить общее сопротивление [латекс ]{0,500 \;\textbf{M} \Omega}[/latex]. а) Какова величина второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
- серия
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор
- компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
- сопротивление
- , вызывающий потерю электроэнергии в цепи
- Закон Ома
- взаимосвязь между током, напряжением и сопротивлением в электрической цепи: [латекс]{V=IR}[/латекс]
- напряжение
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например батареей
- падение напряжения
- потеря электроэнергии при протекании тока через резистор, провод или другой компонент
- текущий
- поток заряда через электрическую цепь, проходящий через заданную точку измерения
- Закон Джоуля
- соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое как: [latex]{P_e = IV}[/latex]
- параллельный
- соединение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
и параллельные цепи: примеры и правила
Мы используем электрические устройства каждый день и постоянно слышим об электрических цепях. Но знаете ли вы, что на самом деле существует два основных типа схем, и что у них обоих разные правила и приложения? Это объяснение погрузится прямо в эти два типа схем, известные как последовательные и параллельные схемы, и чем именно они отличаются, и где мы применяем каждый тип!
Но знаете ли вы, что на самом деле существует два основных типа схем, и что у них обоих разные правила и приложения? Это объяснение погрузится прямо в эти два типа схем, известные как последовательные и параллельные схемы, и чем именно они отличаются, и где мы применяем каждый тип!
Определение параллельной и последовательной цепи
Если мы хотим соединить два компонента цепи вместе в цепи, то у нас есть два способа сделать это последовательно и параллельно.
Цепь серии состоит из компонентов, которые соединены последовательно , т. е. они соединены один за другим в своего рода «цепочку» компонентов.
Параллельная цепь состоит из компонентов, соединенных параллельно . Для этого мы разделяем схему на две части и размещаем компоненты рядом на нескольких разных ветвях, после чего снова объединяем ветви.
Так в чем именно разница между этими двумя типами схем и как мы видим ее на принципиальных схемах?
Разница между последовательными и параллельными цепями
На изображении ниже мы можем очень четко увидеть разницу между электрическими компонентами, которые соединены последовательно или параллельно.
Три лампы соединены слева параллельно, а справа последовательно, Wikimedia Commons CC BY-SA 4.0.
Разница между последовательной и параллельной схемой заключается в том, в какой конфигурации компоненты соединены друг с другом.
Формулы и правила для последовательных и параллельных цепей
Тремя основными величинами, соответствующими цепям, являются напряжение, ток и сопротивление. В общем, напряжение можно рассматривать как «силу», толкающую заряженные частицы через цепь, ток можно рассматривать как количество заряженных частиц, которые могут пройти через цепь, а сопротивление можно рассматривать как сужение дороги или маленькая дверь: чем больше сопротивление, тем меньше дверь, через которую должны пройти заряженные частицы.
С помощью этих сравнений мы можем понять закон Ома, если сформулируем его следующим образом:
Если мы увеличим толчок (увеличим напряжение) или сделаем дорогу шире (уменьшим сопротивление), больше частиц сможет пройти (ток увеличится).
Правила последовательной цепи
Для последовательной цепи мы находимся в ситуации, показанной на рисунке ниже, в которой два (или более) резистора с сопротивлением и соединены последовательно по напряжению.
Серийная схема A, Wikimedia Commons CC BY-SA 4.0.
Правила для последовательных цепей:
- Общее сопротивление всех резисторов равно сумме сопротивлений отдельных резисторов. Таким образом, полное сопротивление в цепи выше равно.
- Ток одинаков через все резисторы. Зная это, мы можем теперь рассчитать этот ток, используя закон Ома, чтобы быть.
- В результате предыдущего пункта мы можем рассчитать напряжение на отдельных резисторах (и) до 9 и . Таким образом, напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений равна общему напряжению.
Запомните эти правила, разбираясь в них! Вот способ взглянуть на правила и формулы для последовательных цепей.
- Если вы заряженная частица, вы должны пройти через оба барьера.
 Общий барьер, с которым вы сталкиваетесь, представляет собой сумму двух отдельных барьеров, потому что вы дважды замедляетесь на своем пути.
Общий барьер, с которым вы сталкиваетесь, представляет собой сумму двух отдельных барьеров, потому что вы дважды замедляетесь на своем пути. - Если ток не везде одинаков, то где-то будет нарастание или потеря заряда, что невозможно в идеальной цепи. Одна партия заряженных частиц не может обогнать другую, потому что ветвь только одна. Добавление большего количества резисторов увеличит общий барьер, поэтому ток будет меньше.
- Это правило следует закону Ома.
Предположим, что два резистора на самом деле являются двумя лампами. Мощность компонента в электрической цепи можно рассчитать по формуле, поэтому мощность лампы 1 равна:
и мы можем сделать аналогичный расчет для лампы 2. Мы видим, что лампа с большим сопротивлением потребляет больше энергии от последовательной цепи.
Правила параллельной цепи
Для параллельной цепи мы находимся в ситуации, показанной на рисунке ниже, в которой два (или более) резистора с сопротивлением и соединены параллельно по напряжению.
Параллельная цепь, Wikimedia Commons CC BY-SA 4.0.
Правила параллельных цепей:
- Напряжение на всех ветвях одинаковое, а именно полное напряжение, а ток через отдельные резисторы можно рассчитать по закону Ома.
- Общий ток представляет собой сумму токов отдельных резисторов. Следовательно, общее сопротивление меньше, чем сопротивление отдельных резисторов.
Вот способ понять эти правила и формулы для параллельных цепей.
- Оба резистора напрямую подключены к электрической ячейке с обоих концов, поэтому напряжение на них должно быть напряжением ячейки.
- Теперь у заряженных частиц есть несколько способов добраться до другого конца клетки: есть две двери из стороны в сторону, и частицы могут выбирать, к какой из них они хотят встать в очередь. Таким образом, через двери можно пропустить больше заряженных частиц.
- Ток — это количество заряженных частиц, проходящих контрольную точку в секунду. Эта величина везде одинакова, поэтому сумма отдельных токов должна составлять общий ток.
 Как будто два потока бегунов сливаются воедино на одной большой улице.
Как будто два потока бегунов сливаются воедино на одной большой улице.
Предположим, что два резистора на самом деле являются двумя лампами. Тогда мощность над лампой равна , и мы можем сделать аналогичный расчет для лампы. Мы видим, что лампа с меньшим сопротивлением получает большую мощность от параллельной цепи.
Мы можем рассчитать общее сопротивление параллельной цепи. Рассчитываем:
.
Проще говоря, мы можем сказать, что общее сопротивление параллельной цепи равно обратной сумме обратных величин отдельных сопротивлений. Мы видим, что действительно общее сопротивление меньше, чем сопротивление отдельных резисторов. Это приводит к большему общему току, чем если бы была только одна ветвь. Это означает, что создание параллельных ветвей в цепи уменьшит сопротивление и увеличит ток в цепи. Это имеет смысл в рамках нашей аналогии с дверьми.
Пример последовательной и параллельной цепей и расчеты
Давайте рассмотрим сложный пример, сочетающий последовательную и параллельную цепи. См. рисунок ниже для настройки. В большинстве практических ситуаций вы можете сами определить напряжение 90 343 В 90 344 90 345 1 90 346 и выбрать резисторы, которые вы используете, а ваша задача — найти другие величины. Это то, что мы будем делать.
См. рисунок ниже для настройки. В большинстве практических ситуаций вы можете сами определить напряжение 90 343 В 90 344 90 345 1 90 346 и выбрать резисторы, которые вы используете, а ваша задача — найти другие величины. Это то, что мы будем делать.
Цепь, содержащая последовательные и параллельные соединения, с сопротивлениями R i , амперметры A i и вольтметры V i , Wikimedia Commons CC BY-SA 4.0.
Обратите внимание, как напряжения на сопротивлениях измеряются прибором, подключенным параллельно сопротивлениям. Это связано с тем, что напряжение на параллельной цепи одинаково на всех ветвях, поэтому напряжение, которое измеряет вольтметр, совпадает с напряжением на сопротивлении, к которому он подключен параллельно!
Предположим, мы подключили вольтметр последовательно к сопротивлению, на котором мы хотим измерить напряжение. Тогда напряжение будет разделено между вольтметром и сопротивлением, и вольтметр будет измерять только напряжение на себе, что будет близко к общему напряжению, выдаваемому батареей, потому что вольтметры имеют чрезвычайно высокое сопротивление.
Обратите также внимание на то, как ток в цепи измеряется прибором, подключенным последовательно к сопротивлениям, через которые мы хотим измерить ток. Это связано с тем, что ток через последовательную цепь везде одинаков, поэтому ток, который измеряет амперметр, такой же, как ток через сопротивления, к которым он подключен последовательно!
Предположим, мы подключили амперметр параллельно сопротивлению, через которое мы хотим измерить ток. Тогда ток будет разделен между амперметром и сопротивлением, и амперметр будет измерять ток только через свою собственную ветвь, а не через ветвь интересующего сопротивления вообще! Этот ток будет очень высоким, потому что амперметры имеют чрезвычайно низкое сопротивление.
Вопрос дает значения , и.
Видим, что у нас параллельная цепь, но одна из ветвей параллельной цепи содержит два резистора, которые соединены последовательно. Приведем общее сопротивление резисторов и название, а общее напряжение над названием.
Из правил параллельных цепей мы знаем, что и. Мы также знаем, что сумма отдельных токов есть общий ток, т.е.
По правилам последовательного соединения мы знаем то и это. Все идет нормально.
Теперь мы можем использовать закон Ома, чтобы сделать вывод, что
И
Тогда общий ток равен
Мы снова используем закон Ома, чтобы узнать, каковы напряжения В 3 4 4
И
Теперь мы успешно выразили неизвестные величины через известные величины, так что мы закончили! В процессе мы использовали правила как для последовательных, так и для параллельных схем, потому что эта схема представляет собой комбинацию этих двух.
Идентификация последовательных и параллельных цепей
Определить последовательную цепь довольно легко, потому что последовательные цепи имеют только один провод, по которому может проходить ток: в последовательных цепях нет дополнительных ответвлений. С другой стороны, параллельная цепь — это цепь, в которой все компоненты напрямую подключены к обеим сторонам источника напряжения. Трудности возникают, когда нам нужно идентифицировать компоненты в комбинированной схеме. Короче говоря, компоненты, соединенные последовательно, расположены встречно, а компоненты, соединенные параллельно, расположены бок о бок.
Трудности возникают, когда нам нужно идентифицировать компоненты в комбинированной схеме. Короче говоря, компоненты, соединенные последовательно, расположены встречно, а компоненты, соединенные параллельно, расположены бок о бок.
Мы можем рассматривать непрерывный кусок провода как узел : разные узлы разделены компонентами внутри цепи. Два компонента соединены параллельно, если (и только если) они имеют два общих узла, т. е. они соединены с одними и теми же двумя узлами.
Два компонента соединены последовательно, если (и только если) они имеют ровно один общий узел, который не разветвляется между двумя компонентами. Это хорошее упражнение — попытаться идентифицировать узлы на всех рисунках в этой статье. Вы можете сделать это, дав им имена или цвета. Тогда посмотрите, пришли ли вы к правильным выводам о том, как все компоненты связаны на основе этого метода! См. приведенный ниже пример реализации этого метода.
Оба резистора имеют общий синий и красный узел, поэтому они соединены параллельно, адаптировано из Paulgwilliamson, Wikimedia Commons CC BY-SA 4. 0.
0.
Использование последовательных и параллельных цепей
В общем, выбор между последовательными и параллельными цепями прост. Мы подключаем выключатель последовательно с лампой так, чтобы отключение тока в выключателе путем его щелчка также отключало ток через лампу. Мы также подключаем резистор последовательно с диодами, чтобы ток через диоды не был слишком большим, предотвращая перегрев диодов.
С другой стороны, мы подключаем фары в автомобилях параллельно, так что, если одна из ветвей цепи выходит из строя, другая ветвь все еще проводит ток. Таким образом, у вас все еще будет одна рабочая фара, если другая выйдет из строя: параллельное подключение добавляет фактор безопасности. Бытовые приборы тоже подключаем параллельно, чтобы они все были под одним напряжением. Имея выключатели, соединенные последовательно с отдельными приборами, мы можем управлять током через отдельные приборы. Если бы все приборы были соединены последовательно, нам пришлось бы выбирать между всем включенным и всем выключенным!
Последовательные и параллельные цепи — основные выводы
- Последовательное соединение состоит из компонентов, расположенных один за другим.

- Параллельное соединение имеет компоненты, параллельные друг другу.
- Правила последовательного соединения:
- Общее сопротивление всех резисторов равно сумме сопротивлений отдельных резисторов.
- Ток одинаков через все резисторы.
- Напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений составляет общее напряжение.
- Правила параллельного соединения:
- Общее сопротивление всех резисторов меньше, чем сопротивление отдельных резисторов, и определяется по формуле.
- Общий ток представляет собой сумму токов отдельных резисторов.
- Напряжение на всех резисторах одинаковое, а именно общее напряжение.
- Для выявления последовательных и параллельных соединений можно использовать метод узлов.
- Всякий раз, когда ситуация требует фактора безопасности, вы обычно видите параллельные соединения, как в бытовых приборах. Последовательные соединения используются для переключения и предотвращения перегрева компонентов.

17,5 Параллельные резисторы | Электрические цепи
17.5 Параллельные резисторы (ESAFK)
Когда мы добавляем резисторы параллельно цепи:
-
Существует больше путей для протекания тока, что обеспечивает разделение тока по разным пути .
-
Напряжение то же на резисторах. Напряжение на аккумуляторе в цепи равно напряжению на каждом из параллельных резисторов:
\[{V}_{\text{батарея}} = {V}_{1} = {V}_{2} = {V}_{3} \ldots\] -
Сопротивление протеканию тока уменьшается . Общее сопротивление, \({R}_{P}\), дано автор:
\[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]
При параллельном соединении резисторов начальная и конечная точки для всех резисторов одинаковы. Эти
точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова независимо от того, что
поставить между ними. Вы можете иметь один, два или несколько резисторов между двумя точками, разность потенциалов будет
не изменить. Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы
между двумя точками.
Вы можете иметь один, два или несколько резисторов между двумя точками, разность потенциалов будет
не изменить. Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы
между двумя точками.
Посмотрите на следующие электрические схемы. Аккумулятор во всех случаях одинаков, меняется только количество резисторов. добавляются между точками, отмеченными черными точками. Если бы мы измерили разность потенциалов между две точки в этих схемах, мы получили бы один и тот же ответ для всех трех случаев.
Давайте посмотрим на два параллельных резистора более внимательно. Когда вы строите цепь, вы используете провода, и вы можете
думаю, что измерение напряжения в разных местах проводов будет иметь значение. Это неправда.
разность потенциалов или измерение напряжения будут отличаться только в том случае, если вы измеряете другой набор компонентов.
Все точки на проводах, между которыми нет компонентов схемы, дадут вам одинаковые измерения.
Все три измерения, показанные на рисунке ниже (т. е. A–B, C–D и E–F), дадут вам одинаковое напряжение. Между различными точками измерения слева нет компонентов, поэтому изменение потенциальной энергии. Точно то же самое относится к различным точкам справа. Когда вы измеряете разность потенциалов между точками слева и справа вы получите тот же ответ.
Рабочий пример 7: Напряжение I
Рассмотрим следующую электрическую схему:
Какое напряжение на резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и одним резистором. Мы знаем напряжение на аккумуляторе. Мы хотим найти это напряжение на резисторе.
\[{V}_{\text{батарея}} = \text{2}\text{V}\]
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
составные части.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
В цепи есть только один компонент — резистор.
\[{V}_{\text{всего}}={V}_{1}\]
Это означает, что напряжение на батарее равно напряжению на резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} = {V} _ {1} \\ {V}_{1} & = \text{2}\text{V} \конец{выравнивание*}
Рабочий пример 8: Напряжение II
Рассмотрим эту цепь:
Каково напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы измерения
У нас есть схема с батареей и двумя резисторами. Мы знаем напряжение на аккумуляторе и одном из резисторы. Мы хотим найти это напряжение на резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {2} \ text {V} \\ {V}_{B} & = \text{1}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
компоненты, которые находятся в последовательном соединении.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V}_{\text{всего}} = {V}_{A} + {V}_{B}\]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\\\ {V} _ {\ text {батарея}} & = {V} _ {1} + {V} _ {\ text {резистор}} \\ \text{2}\text{V} & = {V}_{1} + \text{1}\text{V} \\ {V}_{1} & = \text{1}\text{V} \конец{выравнивание*}
Рабочий пример 9: Напряжение III
Рассмотрим принципиальную схему:
Каково напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы измерения
У нас есть схема с батареей и тремя резисторами. Мы знаем напряжение на аккумуляторе и двух
резисторы. Мы хотим найти это напряжение на неизвестном резисторе.
Мы знаем напряжение на аккумуляторе и двух
резисторы. Мы хотим найти это напряжение на неизвестном резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известно}} & = {V} _ {A} + {V} _ {C} \\ & = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на аккумуляторе должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся в последовательном соединении.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V} _ {\ text {всего}} = {V} _ {B} + {V} _ {\ text {известно}} \]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {B} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{B} + \text{5}\text{V} \\ {V}_{B} & = \text{2}\text{V} \конец{выравнивание*}
Рабочий пример 10: Напряжение IV
Рассмотрим принципиальную схему:
Каково напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальное
схема аналогична предыдущей задаче.
Быстрый ответ
Схема такая же, как и в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в схема не зависит от того, что находится между ними, поэтому ответ такой же, как и выше \({V}_{\text{parallel}} = \text{2}\text{V}\).
Проверьте, что у вас есть и единицы измерения — подробный ответ
У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно). Мы знаем напряжение на аккумуляторе и двух резисторах. Мы хотим найти это напряжение на параллельном резисторы, \({V}_{\text{параллельные}}\).
\начать{выравнивать*} {V} _ {\ text {батарея}} = \ text {7} \ text {V} \\ {V}_{\text{известно}} = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
составные части.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Напряжения складываются только алгебраически для компонентов, соединенных последовательно. Параллельные резисторы можно рассматривать как один компонент, который последовательно с другими компонентами, а затем напряжения могут быть добавлены.
\[{V} _ {\ text {всего}} = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{\text{параллельно}} + \text{5}\text{V} \\ {V} _ {\ text {параллельно}} & = \ text {2} \ text {V} \конец{выравнивание*}
temp text В отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще путей вдоль
какой ток может течь. Делая это, мы уменьшаем общее сопротивление цепи!
Делая это, мы уменьшаем общее сопротивление цепи!
Взгляните на диаграмму ниже. Слева у нас такая же схема, как и в предыдущем разделе с аккумулятором и резистор. Амперметр показывает силу тока \(\text{1}\) \(\text{A}\). Справа мы добавили второй резистор параллельно первому резистору. Это увеличило количество путей (ответвлений), по которым может пройти заряд. по цепи — общее сопротивление уменьшилось. Вы видите, что ток в цепи вырос. Также обратите внимание, что ток в разных ветвях может быть разным.
Общее сопротивление ряда параллельно соединенных резисторов НЕ является суммой отдельных сопротивлений, поскольку общее сопротивление уменьшается с увеличением количества путей для тока. Общее сопротивление для параллельных резисторов дано автор:
\[\frac{1}{{R}_{P}}=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+\ldots\ ] Давайте рассмотрим случай, когда у нас есть два резистора, включенных параллельно, и выясним, каким будет конечное сопротивление. Эта ситуация показана на диаграмме ниже:
Эта ситуация показана на диаграмме ниже:
Применяя формулу полного сопротивления имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{Там всего два резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} \\ & \text{Сложите дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}}{{R}_{2 }} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}}{{R}_{1}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}}{{R}_{1}{R}_{2}} + \frac{{R} _{1}}{{R}_{1}{R}_{2}} \\ & \text{Переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2} + {R}_{1}}{{R}_{1}{R}_{2} } \\ \frac{1}{{R}_{P}} & = \frac{{R}_{1} + {R}_{2}}{{R}_{1}{R}_{2} } \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}}{{R}_{1} + {R}_{2}} \конец{выравнивание*}Теперь мы знаем, что для любых двух резисторов, включенных параллельно,
\[{R}_{P} = \frac{\text{произведение сопротивлений}}{\text{сумма сопротивлений}} = \frac{{R}_{1}{R}_{2}}{ {Р}_{1} + {Р}_{2}}\]Делители тока
Цель
Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.
Аппарат
-
Аккумулятор
Вольтметр
-
Амперметр
-
Провода
-
Резисторы
Метод
-
Подключите каждую цепь, показанную ниже
-
Измерьте напряжение на каждом резисторе в цепи.
-
Измерьте ток до и после каждого резистора в цепи, а также до и после параллельного резистора. ветви.
Результаты и выводы
-
Сравните токи через отдельные резисторы друг с другом.
-
Сравните сумму токов через отдельные резисторы с током перед параллельным ветви.

-
Сравните различные измерения напряжения на параллельных резисторах.
Рабочий пример 11: Параллельные резисторы I
Цепь содержит два резистора, включенных параллельно. Резисторы имеют значения сопротивления \(\text{15}\) \(\text{Ω}\) и \(\text{7}\) \(\text{Ω}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно рассчитать общую сопротивление. Значения двух резисторов указаны в правильных единицах, Ом.
Применение соответствующих принципов
Было показано, что общее сопротивление резисторов, включенных параллельно, представляет собой произведение сопротивлений, деленное на сумма. Мы можем использовать
\[{R}_{P} = \frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}\]
9{2}}{\текст{22}\текст{Ом}} \\ & = \text{4,77}\text{ Ом} \конец{выравнивание*}Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{4,77}\) \(\text{Ом}\)
Рабочий пример 12: Параллельные резисторы II
Мы добавляем третий параллельный резистор к конфигурации (настройке) в предыдущем примере. Дополнительный
резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\).
Дополнительный
резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно вычислить общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применить соответствующие принципы
Общее сопротивление для параллельных резисторов указано как
\[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]
У нас есть три резистора, и мы теперь сопротивления. В данном случае имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{три резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \frac{1 }{{R}_{3}} \\ & \text{сложить дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}{R}_{3}} {{R}_{2}{R}_{3}} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{3}} + \frac{1}{{R}_{3} } \times \frac{{R}_{1}{R}_{2}}{{R}_{1}{R}_{2}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3}}{{R}_{1}{R}_{2}{ Р}_{3}} + \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{2}{R}_{3}} + \frac{{R}_{ 1}{R}_{2}}{{R}_{1}{R}_{2}{R}_{3}} \\ & \текст {переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + { Р}_{2}{Р}_{3}}{{Р}_{1}{Р}_{2}{Р}_{3}} \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}{R}_{3}}{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + {R}_{2}{R}_{3}} \\ {R}_{P} & = \frac{\left(\text{15}\text{Ω} \right)\left(\text{7}\text{Ω} \right)\left(\text{3}\text{ Ω} \right)}{\left(\text{7}\text{ Ω} \right)\left(\text{3}\text{ Ω} \right) + \left(\text{15}\text{ Ω} \right)\left(\text{3}\text{ Ω}\right) + \left(\text{7}\text{ Ω} \right)\left(\text{15}\text{ Ω}\right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R}_{P} & = \text{1,84}\text{ Ом} \конец{выравнивание*}
Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{1,84}\) \(\text{Ом}\)
При расчете сопротивления для сложных конфигураций резисторов можно начать с любой комбинации двух
резисторы (последовательно или параллельно) и рассчитайте их общее сопротивление. Затем вы можете заменить их одним
резистор, который имеет общее сопротивление, которое вы рассчитали. Теперь используйте этот новый резистор в сочетании с любым другим
резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь
использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Затем вы можете заменить их одним
резистор, который имеет общее сопротивление, которое вы рассчитали. Теперь используйте этот новый резистор в сочетании с любым другим
резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь
использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Рабочий пример 13: Параллельные резисторы III
Мы добавляем третий параллельный резистор к первой параллельной рабочей конфигурации (настройка). Дополнительный резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\)
Каково общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно вычислить общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Примените соответствующие принципы
Мы можем поменять местами резисторы, не меняя схему:
Мы уже рассчитали общее сопротивление двух резисторов в пунктирной рамке, равное \(\text{4,77}\)
\(\текст{Ω}\). Мы можем заменить эти два резистора одним резистором \(\text{4,77}\)
\(\text{Ω}\), чтобы получить:
Мы можем заменить эти два резистора одним резистором \(\text{4,77}\)
\(\text{Ω}\), чтобы получить:
Рассчитайте общее сопротивление для следующей пары резисторов
Затем снова воспользуемся формулой для двух параллельных резисторов, чтобы получить общее сопротивление для этой новой цепи: 9{2}}{\текст{11,77} \Омега} \\ & = \text{1,84}\text{ Ом} \конец{выравнивание*}
Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{1,84}\) \(\text{Ом}\). Это тоже самое результат, как если бы мы добавили все три резистора одновременно.
Сопротивление
Учебник Упражнение 17.1
Как называется единица сопротивления и каково ее обозначение?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи при последовательном включении резисторов?
Решение пока недоступно
Объясните, что происходит с общим сопротивлением цепи при параллельном добавлении резисторов?
Решение пока недоступно
Почему батареи разряжаются?
Решение пока недоступно
Моделирование: VPfzj
Формула параллельного соединения резисторов — GeeksforGeeks
Параллельное соединение резисторов определяется как цепь, в которой два или более резистора соединены параллельно друг с другом так, что обе клеммы одного резистора соединены с каждой клеммой другого резистора. или резисторы. Параллельная цепь также известна как делитель тока, поскольку ток цепи в параллельной сети резисторов может проходить более чем по одному каналу, поскольку для него существует несколько путей. В результате ток не одинаков во всех ветвях параллельной сети. С другой стороны, падение напряжения на всех резисторах в параллельной резистивной сети является постоянным.
или резисторы. Параллельная цепь также известна как делитель тока, поскольку ток цепи в параллельной сети резисторов может проходить более чем по одному каналу, поскольку для него существует несколько путей. В результате ток не одинаков во всех ветвях параллельной сети. С другой стороны, падение напряжения на всех резисторах в параллельной резистивной сети является постоянным.
Формула
Общее сопротивление параллельной цепи оценивается путем расчета эквивалентного сопротивления цепи. Его формула гласит, что обратная величина эквивалентного сопротивления равна сумме обратных величин отдельных сопротивлений, соединенных параллельно. Эквивалентное сопротивление обозначается символом R eq . Его единицей измерения СИ является ом (Ом), а размерная формула определяется как [M 1 L 2 А -2 Т -3 ].
. * * eq — эквивалентное сопротивление,1/ REQ = 1/R 1 + 1/R 2 + 1/R 3 +… .
. + 1/R N
, где,
2929292959595959595959595959595929595959595959595945959595959495959549595494495944954944959444959549549549549549549549549549549549549549549549. n
R 1 — сопротивление первого резистора,
R 2 — сопротивление второго резистора,
R 3 — сопротивление третьего резистора, и так на.
Вывод
Предположим, у нас есть цепь напряжения V и тока I. Резисторы R 1 , R 2 и R 3 подключены параллельно цепи.
Известно, что в параллельной цепи ток делится на количество частей, равное количеству резисторов.
Пусть I 1 , I 2 и I 3 будут значениями, на которые делится ток I. Мы знаем,
I = I 1 + I 2 + I 3
Разделив обе части на V, получим, 3 /V
1/(V/I) = 1/(V/I 1 ) + 1/(V/I 2 ) + 1/(V/I 3 )
Согласно Закон Ома, V = IR.
Итак, приведенное выше уравнение принимает вид:
1/R eq = 1/R 1 + 1/R 2 + 1/R 3
Отсюда выводится формула для эквивалентного сопротивления в параллельной цепи.
Примеры задач
Задача 1. Вычислить эквивалентное сопротивление, если три сопротивления 5 Ом, 2 Ом и 7 Ом соединены параллельно.
Решение:
Мы имеем,
R 1 = 5 ω
R 2 = 2 ω
R 3 = 7 Ω
с помощью Formula
. 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
1/R экв. = 1/5 + 1/2 + 1/7
1/R экв. = 1/1,2
R экв. = 1,2 Ом
1 Рассчитайте задачу эквивалентное сопротивление, если три сопротивления 2 Ом, 1 Ом и 3 Ом соединены параллельно.Решение:
Мы имеем,
R 1 = 2 ω
R 2 = 1 ω
R 3 = 3 ω
с помощью Formula
.
1/р экв. = 1/R 1 + 1/R 2 + 1/R 3
1/R экв. = 1/2 + 1/1 + 1/3 50005 3/
eq = 1/0,55
R eq = 0,55 Ом
Задача 3. Вычислить эквивалентное сопротивление, если три сопротивления 4 Ом, 6 Ом и 10 Ом соединены параллельно.
Решение:
У нас есть,
R 1 = 4 Ом
R 2 = 6 Ом
R 3 = 10 Ом
Используя формулу, получаем, экв. = 1/4 + 1/6 + 1/10
1/R экв. = 1/1,9
R экв. = 1,9 Ом
5 Ом, 3 Ом и 8 Ом соединены параллельно.
Решение:
У нас есть,
R 1 = 5 ω
R 2 = 3 ω
R 3 = 8 ω
Используя формулу, которую мы получаем,
1/R EQ = 1103459 1
1/R eq = 11034541961
1111111919 11/R .
+ 1/R 2 + 1/R 3
1/R экв. = 1/5 + 1/3 + 1/8
1/R экв. eq = 1,5 Ом
Задача 5. Найдите неизвестное сопротивление, если три сопротивления 3 Ом, 8 Ом и x Ом соединены параллельно, чтобы получить эквивалентное сопротивление 1,8 Ом.
Решение:
Мы имеем,
R 1 = 3 ω
R 2 = 8 ω
R EQ = 1,8 ω
,
, EQ = 1,8 ω
, eq = 1,8 ω
, . 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
=> 1/1,8 = 1/3 + 1/8 + 1/R 3 6
=> 1/R 3 = 1/1,8 – 1/3 – 1/8
=> 1/R 3 = 1/11
=> R 3 = 11 Ом
Задача 6. Найдите неизвестное сопротивление, если три сопротивления 2,5 Ом, 1,5 Ом и x Ом соединены параллельно, что дает эквивалентное сопротивление 0,76 Ом.

Solution:
We have,
R 1 = 2.5 Ω
R 2 = 1.5 Ω
R eq = 0.76 Ω
Using the formula we get,
1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
=> 1/0,76 = 1/2,5 + 1/1,5 + 1/R 3
=> 1/R 3 = 1/0,76 – 1/2,5 – 1/1,5
25 =
5 > 1/R 3 = 1/4
=> R 3 = 4 Ом
Задача 7. Найти неизвестное сопротивление, если три сопротивления 3 Ом, 6 Ом и x Ом соединены параллельно дают эквивалентное сопротивление 1,6 Ом.
Решение:
Имеем,
R 1 = 3 Ом
R 2 = 6 Ω
R eq = 1.6 Ω
Using the formula we get,
1/R eq = 1/R 1 + 1/R 2 + 1 /R 3
=> 1/1,6 = 1/3 + 1/6 + 1/R 3
=> 1/R 3 = 1/1,6 – 1/3 – 1/6
=> 1/R 3 = 1/8
=> R 3 = 8 Ом
19.
3 Параллельные цепи | Техасский шлюз
Цели обученияПараллельное соединение резисторов. Практические задачи. Резисторы, соединенные параллельно. Практические задачи. Проверка понимания.
Цели обучения.
Расчет эквивалентного сопротивления комбинаций резисторов, содержащих последовательные и параллельные резисторы
Основные термины раздела параллельно Параллельные резисторы
В предыдущем разделе мы узнали, что последовательно соединенные резисторы — это резисторы, соединенные один за другим. Если вместо этого мы объединим резисторы, соединив их рядом друг с другом, как показано на рис. 19.19, то говорят, что резисторы соединены параллельно . Резисторы параллельны, когда оба конца каждого резистора соединены напрямую друг с другом.

Обратите внимание, что все вершины резисторов подключены к одному и тому же проводу, поэтому напряжение на вершине каждого резистора одинаково. Точно так же все основания резисторов подключены к одному и тому же проводу, поэтому напряжение внизу каждого резистора одинаково. Это означает, что падение напряжения на каждом резисторе одинаково. В этом случае падение напряжения равно номинальному напряжению В аккумулятора, потому что верхний и нижний провода подключаются к положительному и отрицательному полюсам аккумулятора соответственно.
Хотя падение напряжения на каждом резисторе одинаково, мы не можем сказать то же самое о токе, протекающем через каждый резистор. Таким образом, I1, I2, и I3I1, I2, и I3 не обязательно одинаковы, поскольку резисторы R1, R2, и R3R1, R2, и R3 не обязательно имеют одинаковое сопротивление.
Обратите внимание, что три резистора на рис. 19.19 обеспечивают три различных пути, по которым может течь ток.
Это означает, что эквивалентное сопротивление этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может протекать ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) уменьшится. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.
Рис. 19.19 На левой принципиальной схеме показано параллельное подключение трех резисторов. Напряжение В батареи приложено ко всем трем резисторам. Токи, протекающие через каждую ветвь, не обязательно равны. На правой принципиальной схеме показано эквивалентное сопротивление, которое заменяет три параллельных резистора.
Чтобы найти эквивалентное сопротивление RequivRequiv трех резисторов R1, R2, и R3R1, R2, и R3, применим закон Ома к каждому резистору.
Так как падение напряжения на каждом резисторе равно В , получаем
19.21V=I1R1, V=I2R2, V=I3R3V=I1R1, V=I2R2, V=I3R3
или
19.22I1=VR1, I2=VR2, I3=VR3.I1=VR1, I2=VR2, I3=VR3.
Из закона сохранения заряда мы также знаем, что три тока I1, I2, и I3I1, I2, и I3 должны складываться, чтобы получить ток I , проходящий через батарею. Если бы это было не так, ток должен был бы таинственным образом создаваться или уничтожаться где-то в цепи, что физически невозможно. Таким образом, мы имеем
19.23I=I1+I2+I3.I=I1+I2+I3.
Подстановка выражений для I1, I2, и I3I1, I2, и I3 в это уравнение дает
19.24I=VR1+VR2+VR3=V(1R1+1R2+1R3)I=VR1+VR2+VR3=V(1R1+1R2+1R3)
или
19,25 В=I(11/R1+1/R2+1/R3).V=I(11/R1+1/R2+1/R3).
Эта формула представляет собой просто закон Ома, где множитель в скобках означает эквивалентное сопротивление.
19,26 В=I(11/R1+1/R2+1/R3)=IRэкв.
V=I(11/R1+1/R2+1/R3)=IRэкв.
Таким образом, эквивалентное сопротивление трех резисторов, включенных параллельно, равно
19.27Requiv=11/R1+1/R2+1/R3.Requiv=11/R1+1/R2+1/R3.
Та же логика работает для любого количества параллельно соединенных резисторов, поэтому общая форма уравнения, которая дает эквивалентное сопротивление N резисторов, соединенных параллельно, равна
.19.28 Requiv=11/R1+1/R2+⋯+1/RN.Requiv=11/R1+1/R2+⋯+1/RN.
Рабочий пример
Определение тока через параллельные резисторы
Три приведенные ниже схемы эквивалентны. Если номинальное напряжение батареи Vbattery=3 VVbattery=3 V, каково эквивалентное сопротивление цепи и какой ток протекает через цепь?
СТРАТЕГИЯ
Три резистора соединены параллельно, и падение напряжения на них составляет В батарея . Таким образом, мы можем применить уравнение для эквивалентного сопротивления параллельных резисторов, которое принимает вид
19,29Requiv=11/R1+1/R2+1/R3.
Requiv=11/R1+1/R2+1/R3. .
Схема с эквивалентным сопротивлением показана ниже. Зная эквивалентное сопротивление, мы можем использовать закон Ома, чтобы найти ток в цепи.
Решение
Подставляя заданные значения сопротивления в уравнение для эквивалентного сопротивления, получаем 4,84 Ом. Requiv=11/R1+1/R2+1/R3=11/10 Ом+1/25 Ом+1/15 Ом=4,84 Ом.
Таким образом, ток в цепи равен
19,31 В=IRI=VR=3 V4,84 Ω=0,62 A.V=IRI=VR=3 V4,84 Ω=0,62 A. всей цепи, обратите внимание, что этот ток не протекает через каждый резистор. Однако, поскольку в цепи должен сохраняться электрический заряд, сумма токов, проходящих через каждую ветвь цепи, должна в сумме равняться току, проходящему через батарею. Другими словами, мы не можем волшебным образом создать заряд где-то в цепи и добавить этот новый заряд к току. Давайте проверим это рассуждение, используя закон Ома, чтобы найти ток через каждый резистор.
19.32I1=VR1=3 V10 Ω=0,30 AI2=VR2=3 V25 Ω=0,12 AI3=VR3=3 V15 Ω=0,20 AI1=VR1=3 V10 Ω=0,30 AIV2=VR2=3 3 1 VR3=3 V15 Ω=0,20 A
Как и ожидалось, эти токи в сумме дают 0,62 A, что является общим найденным током, проходящим через эквивалентный резистор.
Также обратите внимание, что через самый маленький резистор протекает наибольший ток, и наоборот.
Рабочий пример
Рассуждения с параллельными резисторами
Каково эквивалентное сопротивление трех одинаковых резисторов без каких-либо вычислений R параллельно?
СТРАТЕГИЯ
Три одинаковых резистора R , соединенные параллельно, создают три одинаковых пути, по которым может протекать ток. Таким образом, току через эти резисторы протекать в три раза легче, чем через один из них.
Раствор
Если через три одинаковых резистора R протекать в три раза легче, чем через один из них, то эквивалентное сопротивление должно быть в три раза меньше: Р /3.
Обсуждение
Проверим наши рассуждения, рассчитав эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно.
Уравнение для эквивалентного сопротивления параллельных резисторов дает
19,33Requiv=11/R+1/R+1/R=13/R=R3.Requiv=11/R+1/R+1/R=13/ Р=Р3.
Таким образом, наши рассуждения были верны. В общем, когда доступно больше путей, по которым может протекать ток, эквивалентное сопротивление уменьшается. Например, если у нас есть одинаковые резисторы R параллельно, эквивалентное сопротивление будет R /10.
Практические задачи
Три резистора, 10, 20 и 30 Ом, соединены параллельно. Чему равно сопротивление?
- Эквивалентное сопротивление 5,5 Ом
- Эквивалентное сопротивление 60 Ом
- Эквивалентное сопротивление 6 × 103 Ом
- Эквивалентное сопротивление 6 × 104 Ом
Если на R1 происходит падение напряжения 5 В, а R1 подключен параллельно R2, каково падение напряжения на R2?
- Падение напряжения 0В.

- Падение напряжения на 2,5В.
- Падение напряжения на 5В.
- Падение напряжения на 10В.
Резисторы параллельно и последовательно
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Комбинации последовательных и параллельных резисторов можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 19..20. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок 19.20 Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единое эквивалентное сопротивление.

Давайте выполним четыре шага, показанные на рис. 19.20, чтобы уменьшить количество семи резисторов до одного эквивалентного резистора. Чтобы не отвлекаться на алгебру, мы будем считать, что сопротивление каждого резистора равно 10 Ом. На шаге 1 мы уменьшаем два набора параллельных резисторов, обведенных синей пунктирной петлей. Верхний набор имеет три параллельных резистора и будет уменьшен до одного эквивалентного резистора RP1RP1. Нижний набор имеет два параллельных резистора и будет уменьшен до одного эквивалентного резистора RP2RP2. Используя уравнение для эквивалентного сопротивления параллельно включенных резисторов, получаем
19.34RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+1/10 Ом=5 Ом.RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+ 1/10 Ом=5 Ом.
Эти два эквивалентных сопротивления обведены красной пунктирной петлей после шага 1. Они соединены последовательно, поэтому мы можем использовать уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы свести их к одному эквивалентному сопротивлению RS1RS1.
.Это делается на шаге 2, в результате чего получается
19.35RS1=RP1+RP2=103 Ом+5 Ом=253 Ом. RS1=RP1+RP2=103 Ом+5 Ом=253 Ом.
Эквивалентный резистор RS1RS1 появляется в зеленой пунктирной петле после шага 2. Этот резистор включен параллельно резистору R7R7, поэтому пара может быть заменена эквивалентным резистором RP3RP3, который определяется как
.19.36RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.
Это делается на шаге 3. Резистор RP3RP3 включен последовательно с резистором R1R1, как показано фиолетовым пунктиром после шага 3. Эти два резистора объединяются на последнем шаге, чтобы сформировать окончательный эквивалентный резистор RequivRequiv, который равен
19,37Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.
Таким образом, всю комбинацию из семи резисторов можно заменить одним резистором с сопротивлением около 14,5 Ом.
Это было много работы, и вы можете спросить, почему мы это делаем.
Нам важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи. Но чтобы узнать ток, надо сначала узнать эквивалентное сопротивление.
Вот общий подход к поиску эквивалентного резистора для любой произвольной комбинации резисторов:
- Определите группу резисторов, которые включены только параллельно или только последовательно.
- Для резисторов, соединенных последовательно, используйте уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы привести их к одному эквивалентному сопротивлению. Для параллельных резисторов используйте уравнение для эквивалентного сопротивления параллельных резисторов, чтобы привести их к одному эквивалентному сопротивлению.
- Нарисуйте новую принципиальную схему, заменив резисторы из шага 1 эквивалентными им резисторами.
- Если в цепи осталось более одного резистора, вернитесь к шагу 1 и повторите.
В противном случае вам конец.
Fun In Physics
Робот
Роботы захватывают наше коллективное воображение уже более века. Теперь эта мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стал огромной областью исследований и разработок, при этом некоторые технологии уже коммерциализированы. Вспомните, например, маленькие автономные пылесосы.
На рис. 19.21 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые человекоподобные роботы умеют ходить, разливать напитки, даже танцевать (хотя и не очень грациозно). Другие роботы созданы на основе биологии, например собачий робот , показанный на средней фотографии рис. 19.21. Этот робот может перевозить сотни фунтов груза по пересеченной местности. Фотография справа на рисунке 19.
21 показано внутреннее устройство М-блока , , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться и подбрасываться в воздух, а также соединяться в различные формы. Общаясь по беспроводной связи между собой, они самособираются в различные формы, такие как столы, стулья, а когда-нибудь, возможно, даже здания.
Все роботы включают в себя огромное количество физики и техники. Роботы освоили простое действие по наливанию напитка лишь недавно, после более чем 30 лет исследований и разработок! Баланс и время, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложными действиями, требующими отличного баланса, ловкости и обратной связи. Чтобы справиться с этим, требуются датчики для определения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсационных действий, а также соединения и приводы для выполнения необходимых действий.

Помимо определения гравитации или ускорения, роботы могут иметь несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для роботизированного зрения, аналогична той, что используется в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы. Для определения температуры можно использовать простые термисторы, представляющие собой резисторы, сопротивление которых изменяется в зависимости от температуры.
Создание робота сегодня намного проще, чем несколько лет назад. Сейчас многие компании предлагают комплекты для сборки роботов. По сложности они варьируются от подходящих для детей начальной школы до задач, которые могут бросить вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать делать своего собственного робота уже сегодня.

Рис. 19.21 Роботы бывают разных форм и размеров, от классического гуманоида типа до роботов-собак в маленькие кубики, которые самостоятельно собираются для выполнения различных задач.
Watch Physics
Параллельные резисторы
В этом видео лектор обсуждает простую схему с батареей и парой резисторов, соединенных параллельно. Он подчеркивает, что электроны движутся в направлении, противоположном направлению положительного тока, а также использует тот факт, что напряжение одинаково во всех точках идеального провода. Вывод очень похож на то, что сделано в этом тексте, но лектор хорошо его проходит, объясняя каждый шаг.
Щелкните, чтобы просмотреть содержание
Проверка захвата
Верно или неверно — на принципиальной схеме мы можем предположить, что напряжение одинаково в каждой точке данного провода.
- ложный
- правда
Watch Physics
Резисторы, соединенные последовательно и параллельно
В этом видеоролике показано, как рассчитать эквивалентное сопротивление цепи, содержащей резисторы, соединенные параллельно и последовательно.
Лектор использует тот же подход, что и изложенный выше, для нахождения эквивалентного сопротивления.
Щелкните, чтобы просмотреть содержание
Проверка захвата
Представьте, что N одинаковых резистора соединены параллельно. Каждый резистор имеет сопротивление · Ом. Каково эквивалентное сопротивление этой группы параллельных резисторов?
- Эквивалентное сопротивление ( R ) Н .
- Эквивалентное сопротивление NR.
- Эквивалентное сопротивление РН.РН.
- Эквивалентное сопротивление NR.NR.
Рабочий пример
Найдите ток в цепи комплексного резистора
Батарея в схеме ниже имеет номинальное напряжение 10 В. Какой ток течет по цепи и в каком направлении?
СТРАТЕГИЯ
Примените стратегию нахождения эквивалентного сопротивления, заменив все резисторы одним эквивалентным сопротивлением, затем используйте закон Ома, чтобы найти ток через эквивалентный резистор.

Решение
Комбинация резисторов R4R4 и R5R5 может быть уменьшена до эквивалентного сопротивления 9 Ом.0005
19,38RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.
Замена R4R4 и R5R5 этим эквивалентным сопротивлением дает следующую схему.
Теперь заменим два верхних резистора R2R2 и R3R3 эквивалентным резистором RS1RS1, а два нижних резистора RP1RP1 и R6R6 эквивалентным резистором RS2RS2. Эти резисторы включены последовательно, поэтому мы складываем их вместе, чтобы найти эквивалентное сопротивление.
19,39RS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25,71 Ом+20 Ом=45,71 ОмRS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25,71 Ом +20 Ом=45,71 Ом
Замена соответствующих резисторов эквивалентными им резисторами дает следующую схему.
Теперь замените два резистора RS1 и RS2RS1 и RS2, включенных параллельно, на эквивалентный им резистор RP2RP2. Сопротивление RP2RP2 составляет
19,40RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом=29,09 Ом.
RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом =29,09 Ом.
Обновление электрической схемы путем замены RS1 и RS2RS1 и RS2 этим эквивалентным сопротивлением дает приведенную ниже схему.
Наконец, мы соединяем резисторы R1 и RP2R1 и RP2, которые включены последовательно. Эквивалентное сопротивление: RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. Окончательная схема показана ниже.
Теперь воспользуемся законом Ома, чтобы найти силу тока в цепи.
19,41 В=IRS3I=VRS3=10 V104,09 Ом=0,096 AV=IRS3I=VRS3=10 V104,09 Ом=0,096 A поэтому в этой цепи он течет по часовой стрелке.
Обсуждение
Этот расчет может показаться довольно длинным, но немного потренировавшись, вы сможете комбинировать некоторые шаги. Обратите также внимание на то, что в расчетах учитывались дополнительные значащие цифры. Только в конце окончательный результат округлялся до двух значащих цифр.
Рабочий пример
Странно выглядящие принципиальные схемы
Иногда вы можете столкнуться с не очень аккуратно нарисованными принципиальными схемами, такими как схема, показанная ниже.
Эта принципиальная схема больше похожа на то, как реальная схема может выглядеть на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если предположить, что сопротивление каждого резистора равно 10 Ом, а номинальное напряжение батареи равно 12 В?
СТРАТЕГИЯ
Давайте перерисуем эту принципиальную схему, чтобы она была понятнее. Затем мы применим описанную выше стратегию для расчета эквивалентного сопротивления.
Решение
Чтобы перерисовать диаграмму, рассмотрите рисунок ниже. В верхней схеме синие резисторы образуют путь от положительной клеммы батареи к отрицательной клемме. Параллельно этой цепи расположены красные резисторы, которые образуют еще один путь от положительного к отрицательному выводу батареи. Синие и красные пути показаны более четко на нижней принципиальной схеме. Обратите внимание, что как на верхней, так и на нижней принципиальных схемах синяя и красная дорожки соединяют положительную клемму батареи с отрицательной клеммой батареи.

Теперь легче увидеть, что R1 и R2R1 и R2 параллельны, а параллельная комбинация последовательно с R4R4. Эта комбинация, в свою очередь, параллельна последовательной комбинации R3 и R5R3 и R5. Сначала мы вычисляем синюю ветвь, которая содержит R1, R2 и R4, R1, R2 и R4. Эквивалентное сопротивление
19,42Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.
, где мы показываем вклад от параллельной комбинации резисторов и от последовательной комбинации резисторов. Теперь рассчитаем эквивалентное сопротивление красной ветви, которое равно
19,43Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.
Вставка этих эквивалентных резисторов в цепь дает следующую схему.
Эти два резистора включены параллельно, поэтому их можно заменить одним эквивалентным резистором с сопротивлением
11/Rсиний+1/Rкрасный=11/15 Ом+1/20 Ом=8,6 Ом.
Окончательная эквивалентная схема показана ниже.

Обсуждение
Найти эквивалентное сопротивление было проще, если была понятная принципиальная схема. Вот почему мы пытаемся сделать четкие принципиальные схемы, где параллельно подключенные резисторы выстроены параллельно друг другу и в одном и том же горизонтальном положении на схеме.
Теперь мы можем использовать закон Ома, чтобы найти ток, проходящий через каждую ветвь этой цепи. Рассмотрим принципиальную схему с RblueRblue и RredRred. Напряжение на каждой из этих ветвей составляет 12 В (т. е. номинальное напряжение батареи). Ток в синей ветви
19,45Iblue=VRblue=12 V15 Ω=0,80 A.Iblue=VRblue=12 V15 Ω=0,80 A
Ток в красной ветви
19,46Ired=VRVred=12 Ω=0,60 A.Ired=VRred=12 V20 Ω=0,60 A.
Ток, проходящий через батарею, должен быть суммой этих двух токов (понимаете, почему?), или 1,4 A.
Практические задачи
Какова формула эквивалентного сопротивления двух параллельных резисторов с сопротивлением Ом 1 и Ом 2 ?
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1+R2Reqv=R1+R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1×R2Reqv=R1×R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=R1-R2Reqv=R1-R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv=11/R1+1/R2Reqv=11/R1+1/R2
Рисунок 19.
22
Каково эквивалентное сопротивление двух показанных ниже резисторов?
- Эквивалентное сопротивление 20 Ом
- Эквивалентное сопротивление 21 Ом
- Эквивалентное сопротивление 90 Ом
- Эквивалентное сопротивление 1925 Ом
Проверьте свое понимание
Упражнение 6
Падение напряжения на параллельных резисторах ________.
- одинаковы для всех резисторов
- больше для больших резисторов
- меньше для больших резисторов
- больше для меньших резисторов
Упражнение 7
Рассмотрим цепь из параллельных резисторов. Минимальный резистор 25 Ом. Каков верхний предел эквивалентного сопротивления?
- Верхний предел эквивалентного сопротивления составляет 2,5 Ом.
- Верхний предел эквивалентного сопротивления составляет 25 Ом.
- Верхний предел эквивалентного сопротивления составляет 100 Ом.

- Нет верхнего предела.
- Печать
- Поделиться
Примеры проблем и подробные факты — Lambda Geeks
В этой статье мы обсудим различные методы расчета напряжения в параллельных цепях. Параллельное соединение делит цепь на ветви, чтобы ток распределялся по всем из них.
Параллельные цепи подчиняются закону сохранения энергии. Напряжение можно назвать электрической работой, совершаемой на единицу заряда. Электрические поля консервативны, что означает, что электрическая работа зависит только от начальной и конечной точек. Все ветви имеют общий начальный и конечный узел в параллельном соединении. Следовательно, напряжение равно.
Подробнее о…..Функция параллельной цепи: полная информация и ответы на часто задаваемые вопросы
Как рассчитать напряжение в параллельной цепи – числовые примеры Параллельная цепь RLC; «Файл:Example9d.
{-1} = \frac{R} {2} \Omega [/ Латекс]. Учитывая R / 2 = 15, Таким образом, значение каждого резистора = 15 × 2 = 30 Ом. Значение тока i 1 задается как 3 А.
Поскольку это параллельная цепь, напряжение на одной ветви будет таким же, как и на любой другой ветви, и это будет также напряжение питания. Следовательно, напряжение источника [Latex] V_{s} = ток\; в\; а\; филиал \раз соответствующий\; сопротивление \; значение = i_{1} \times R = 3 \times 30 = 90\; В [/латекс].
Q2. Параллельная сеть состоит из пяти резисторов R, 2R, 4R, 8R и 16R. Чистый ток в сети равен I. Найдите напряжение в ответвлении, содержащем резистор 4R. 9{-1} = \frac{16R} {31} \: \Omega [/Latex]
Полный ток в цепи дается как I Amp.
Следовательно, напряжение источника [Latex] V_{s} = I \times \frac{16R} {31} = \frac{16IR} {31}\; V [/Latex]
Мы знаем, что напряжение источника параллельной цепи такое же, как и напряжение в любой ветви цепи. Таким образом, напряжение в ответвлении, содержащем резистор 4R, равно 16IR/31 В.
.{-1} [/Latex ]
Умножить Req на общий ток. Если указано только одно сопротивление и соответствующее значение тока, умножьте их, чтобы получить напряжение.
Подробнее……Примеры параллельных цепей: полная информация и ответы на часто задаваемые вопросы
Как найти отсутствующее напряжение в параллельной цепи?
Под «отсутствующим напряжением» в параллельной цепи мы подразумеваем подаваемое напряжение, так как оно одинаково для всех ответвлений. Итак, имея какое-либо значение тока и сопротивления, мы можем узнать напряжение в параллельной цепи.
Давайте разберемся с этим на примере. Предположим, есть два резистора на 2 Ом и 4 Ом, соединенные параллельно. Ток, проходящий через резистор 2 Ом, составляет 1,5 А. Мы знаем напряжение питания В с = напряжение ответвления В 1 = напряжение ответвления В 2 . Следовательно, недостающее напряжение [Latex] V = iR = 2 \times 1,5 = 3 \times V [/Latex].

Как найти напряжение источника в последовательно-параллельной цепи?
По принципу параллельной цепи напряжение в каждой ветви одинаково и равно напряжению источника. Если напряжение источника Vs, а напряжения ветвей V 9.
Если указано напряжение источника, у нас уже есть напряжения ветвей. Если напряжение источника неизвестно, а заданы значения тока, то можно узнать напряжение с помощью закона Ома. Например, если ток в ответвлении равен 5 А, а значение сопротивления равно 2 Ом, напряжение равно 5 × 2 = 10 В.
Подробнее… Часто задаваемые вопросы
Как найти приложенное напряжение в параллельной цепи?
Приложенное напряжение в параллельной схеме относится к напряжению источника или напряжению батареи. Оно задано, или мы можем вычислить его с помощью другой предоставленной информации, такой как значения тока и сопротивления.
Приложенное напряжение означает напряжение, подаваемое на элемент.



