Силовой кабель
Промышленность
Образование
Наука
Типовые примеры
Отзывы
Пользователи
Главная >> Применение >> Типовые примеры >>
расчет Джоулевых потерь силового кабеля, калькулятор импеданса кабеля, импеданс кабеля, кабельный калькулятор, расчет сопротивления кабеля, САПР кабеля
1. Описание модели
Высоковольтный четырехпроводный кабель состоит из трех фазных проводников и одного нулевого. Фазный проводник в сечении имеет форму треугольника со скругленными углами, а нулевой проводник – круглое сечение. Все проводники алюминиевые, изолированные. Кабель в целом имеет трехслойную изоляцию – внутренняя электрическая изоляция, затем защитный слой стальной ленты и внешняя защитная изоляция. Свободное пространство между изолированными проводниками заполнено диэлектриком, в роли которого может быть и воздух.
Четырехпроводный силовой электрический кабельВысоковольтный четырехпроводный кабель состоит из трех фазных проводников и одного нулевого.
фаза Aфаза Bфаза CнольИзоляция жилВнутренняя изоляцияБроняОболочкаЗаполнитель
На практике часто требуется спроектировать кабель по заданному сечению фазных проводников. ELCUT может с успехом использоваться для анализа инженерных систем с разных точек зрения – магнитной, электрической, тепловой, прочностной. Эти взаимосвязанные виды анализа могут быть автоматизированы для конкретной технической системы.
Пример представляет из себя Word-документ со встроенными макросами. Документ содержит результаты анализа, основывающегося на заданных исходных параметрах. Содержащиеся в нем таблицы, картинки и графики сформированы в результате автоматического расчета профессиональной версией ELCUT. Управление ELCUT происходит через объектную модель.
- Полный текст документа в формате PDF.
- Скачать файлы задачи
- Видео: Четырехпроводный силовой электрический кабель
- Видео:
- Смотреть онлайн на YouTube.
2.
Исходные данные.
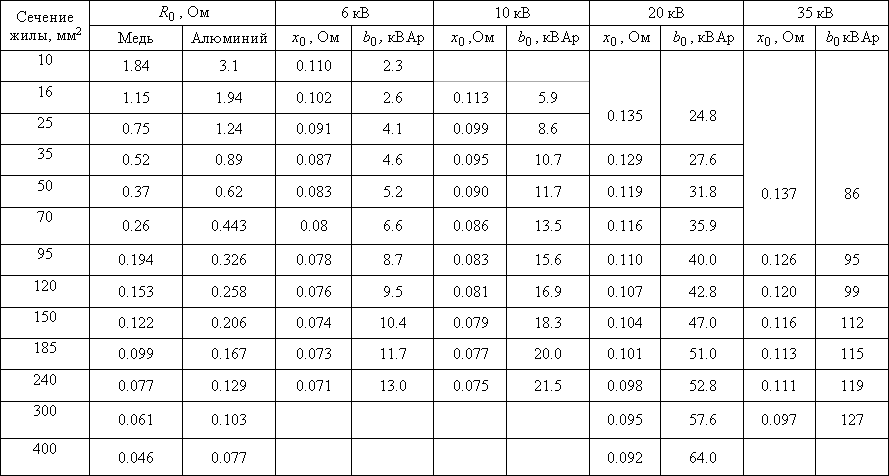
Таблица 1. Геометрические размеры проводников.
Сечение фазного провода 120 мм² Сечение нулевого провода 35 мм² Радиус скругления проводника (R) 2 мм Таблица 2. Геометрические параметры изоляции.
Толщина фазовой изоляции 2 мм Толщина внутреннего слоя изоляции кабеля 1 мм Толщина стальной ленты 1 мм Толщина внешнего слоя изоляции кабеля 3 мм Таблица 3.
Точность вычисления площади 0.001 мм². Таблица 4. Электрическая нагрузка.
Амплитуда фазного тока 200 A. Амплитуда фазного напряжения 6500 В Частота тока 50 Гц Фазовый угол тока 0 град Таблица 5. Физические свойства проводника.
Относительная магнитная проницаемость 1 Электрическая проводимость 36000000 См/м Теплопроводность 140 Вт/К•м Модуль Юнга 6. 9e+10
Н/м² Коэффициент Пуассона 0.33 Коэффициент теплового расширения 2.33e-5 1/K Плотность материала 2700 кг/м³ Таблица 6. Физические свойства стального экрана.
Относительная магнитная проницаемость 1000 6000000 См/м Теплопроводность 85 Вт/К•м Модуль Юнга 2e+11 Н/м² Коэффициент Пуассона 0. 3
Коэффициент теплового расширения 0.000012 1/K Плотность материала 7870 кг/м³ Таблица 7. Физические свойства изоляции.
Проводниковая Внутренняя Внешняя Относительная магнитная проницаемость 1 1 1 Электрическая проводимость, См/м 0 0 0 Диэлектрическая проницаемость 2.5 2.5 2.5 Теплопроводность, Вт/К•м 0. 04
0.04 0.04 Модуль Юнга, Н/м² 10000000 10000000 10000000 Коэффициент Пуассона 0.3 0.3 0.3 Коэффициент теплового расширения, 1/K 0.0001 0.0001 0.0001 Плотность материала, кг/м³ 900 900 1050 3. Результаты анализа кабеля.
Таблица 8 представляет результаты вычисления геометрических характеристик кабеля по введенным исходным данным.
Внешний диаметр кабеля рассчитывается с учетом геометрических размеров проводников и изоляции, введенных в таблицах 1 и 2. Для расчета плотности и погонной массы используются вычисленные площади сечений и плотности материалов.
Таблица 8. Физические параметры кабеля.
Внешний диаметр кабеля 4.28e+01 мм Вес (на метр длины) 2.74e+00 кг Средняя плотность кабеля 1.90e+03 кг/м² Расчет электростатического поля выполняется для определения собственных и взаимных частичных емкостей проводников. Результаты вычислений сведены в таблицу «Емкость проводников» (см. ниже). Значения емкости вычисляются в ходе анализа решения электростатических задач с использованием следующего подхода:
Каждой строке таблицы соответствует решение одной задачи ELCUT. В каждой такой задаче одному из проводников сообщается единичный заряд. После решения на всех проводниках измеряется наведенный потенциал, и частичные емкости проводников вычисляются по формуле:
Cij = Qi / Uj,
где Qi
Uj – наведенный потенциал на этом и других проводниках.
Собственная емкость проводника вычисляется как отношение его заряда к наведенному на нем самом потенциалу.
Таблица 9. Емкость проводников, Ф
Проводник 1 Проводник 2 Проводник 3 Нулевой провод Проводник 1 2.53e-10 1.02e-09 1.95e-09 8.43e-10 Проводник 2 1.02e-09 2.67e-10 1.02e-09 1.88e-09 Проводник 3 1.95e-09 1.02e-09 2.53e-10 8.42e-10 Нулевой провод 8. 43e-10
1.88e-09 8.42e-10 1.28e-10 Результаты расчета индуктивностей приведены в таблице 10. Мгновенные значения токов в фазных проводниках задаются в соответствии с фазовым углом, заданным в таблице 4. Значения в левой половине таблицы (колонки 2-5) вычислены для постоянного тока, а в правой половине (колонки 6-9) – для переменного тока заданной частоты (по умолчанию 50 Гц). Для вычисления взаимных и собственных индуктивностей использовался подход, основанный на потокосцеплениях: Lij = F
Таблица 10. Индуктивности проводников на постоянном и переменном токе.
постоянный ток переменный ток Пров.1 Пров.2 Пров.3 Нуль. пров Пров. 1
Пров.2 Пров.3 Нуль. пров Провод 1 1.15e-05 1.12e-05 1.11e-05 1.13e-05 6.17e-06 5.99e-06 5.94e-06 6.02e-06 Провод 2 1.12e-05 1.15e-05 1.12e-05 1.11e-05 5.99e-06 6.17e-06 5.99e-06 5.93e-06 Провод 3 1. 11e-05
1.12e-05 1.15e-05 1.13e-05 5.94e-06 5.99e-06 6.17e-06 6.02e-06 Нулевой провод 3.89e-10 3.84e-10 3.89e-10 4.04e-10 6.02e-06 5.93e-06 6.02e-06 6.27e-06 Импедансы отдельных проводников и соответствующие им активные сопротивления на постоянном токе сведены в таблицу 11.
На постоянном токе активное сопротивление проводника легко вычисляется через геометрические размеры сечения и электропроводность материала как:
R = ρ · l / S,
где ρ — удельное сопротивление проводника,
S – площадь поперечного сечения,
l – длина (= 1 м)Мощность джоулевых потерь на постоянном токе вычисляется как:
P = IA² · R,
где IA действующее значение тока в проводнике и R — его активное сопротивление.
Импеданс проводника на переменном токе вычисляется на основе закона Ома как отношение комплексного значения напряжения, приложенного к концам проводника, к комплексному значению полного тока в нем. Действительная часть этого отношения представляет собой активное сопротивление проводника на переменном токе (с учетом эффекта вытеснения и эффекта близости), а мнимая часть – индуктивное сопротивление. Мощность джоулевых потерь в проводнике на переменном токе вычисляется внутри ELCUT по формуле:
P = ò j²ρ ds,
где j — плотность тока, а интегрирование выполняется по сечению проводника.
Таблица 11. Импеданс проводников.
Постоянный ток Переменный ток Фазный провод Нулевой провод Пров. 1
Пров. 2 Пров. 3 Импеданс, Ом 2.31e-04 7.94e-04 2.40e-04 2.55e-04 2.80e-04 Активное сопротивление, Ом 2.31e-04 7.94e-04 2.15e-04 2.37e-04 2.59e-04 Реактивное сопротивление, Ом 0.00e+00 0.00e+00 1.08e-04 9.41e-05 1.06e-04 Мощность потерь, Вт 4. 63e+00
0.00e+00 4.71e+00 4.74e+00 4.71e+00 Распределение плотности тока по сечению проводников, вычисленное в задаче магнитного поля переменных токов, передается в качестве источника тепла в задачу расчета температурного поля.
Результаты теплового расчета приводятся в таблице 12. Это средняя температура на наружной поверхности кабеля и поток тепла с этой поверхности в окружающую среду, а также средние значения температуры по сечению каждого из проводников. Приведенные в таблице значения температур вычислены в предположении, что температура окружающей среды = 20°C.Таблица 12. Тепловые параметры кабеля.
Средняя температура внешней поверхности кабеля 23.5 °C Поток тепла в окружающее пространство 14. 2
Вт Средняя температура проводника, °C Провод 1 Провод 2 Провод 3 Нулевой провод 4.59e+01 4.68e+01 4.59e+01 3.93e+01 Анализ упруго-деформированного напряженного состояния элементов кабеля выполняется с учетом его теплового состояния, рассчитанного ранее. Также принимаются во внимание силы магнитного взаимодействия проводников друг с другом, которые рассчитаны при расчете магнитного поля переменных токов. Механические напряжения в элементах кабеля развиваются вследствие термических деформаций и магнитных сил. Результаты расчета приведены в таблице 13.
Таблица 13. Механические характеристики.
Наибольшее перемещение 5.14e-02 мм Максимальное значение критерия прочности по Мору 8.16e+07 Н/м² При анализе электрической прочности изоляционных систем кабеля, необходимо знать максимальное значение напряженности электрического поля.
Таблица 14. Напряженность электрического поля.
Максимальная напряженность в сечении 8.78e+03 В/м Раздел 4. Картина поля.
Ниже приводятся картины распределения напряженности электрического поля, плотности тока (с учетом вихревых токов), плотности энергии магнитного поля, мгновенного значения магнитной индукции на переменном токе, распределения температуры по сечению проводника и механического перемещения под действием термических деформаций и магнитных усилий.
- Видео:
Исходные данные.
9e+10
3
04
43e-10
1
11e-05
1
63e+00
2
Расчёт сопротивления нулевой последовательности линии
Величина сопротивления нулевой последовательности используется в расчетах однофазного короткого замыкания методом симметричных составляющих. Но, зачастую проблематично найти значение этой величины в справочниках для различного исполнения электрических сетей, и, следовательно, невозможно выполнить расчет. При этом значения сопротивлений фазного и нулевого проводников в справочниках присутствуют. Как же быть?
Можно использовать следующие формулы расчета сопротивления нулевой последовательности:
где R0л (X0л) – активное (индуктивное) сопротивление нулевой последовательности линии;
Rф (Xф) – активное (индуктивное) сопротивление фазного проводника;
Rн (Xн) – активное (индуктивное) сопротивление нулевого проводника.
Вывод формул смотри ниже.
Сразу следует подчеркнуть, что этими формулами следует пользоваться, если сопротивление нулевой последовательности неизвестно. Если есть выбор, использовать справочные данные, или выполнить расчет сопротивления нулевой последовательности, то, наверное, следует отдать предпочтение справочным данным.
Итак, основным документом, регламентирующим расчеты токов короткого замыкания до 1000 В, является ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ». В справочном приложении 2 этого ГОСТ, в таблицах №№ 6-14 содержатся данные о сопротивлениях прямой и нулевой последовательностей для различного исполнения кабельных линий. К сожалению, есть варианты исполнения линий, довольно распространенные, для которых нет подходящей таблицы в этом стандарте. Например, нельзя найти параметры 4-жильного кабеля с алюминиевыми жилами в непроводящей оболочке, если сечение жил одинаковое (в табл.
11 сечение нулевого провода меньше, чем сечение фазного). Также, отсутствуют аналогичные данные для кабеля с медными жилами (в табл.14 приведены данные для кабеля в стальной оболочке; да и номенклатура сечений неполная).
В то же время, в справочниках есть данные сопротивлений для любого исполнения линий. Вот только приведены эти данные в виде сопротивлений фазного и нулевого проводников (для применения в расчетах тока однофазного короткого замыкания методом петли «фаза-ноль»), а не сопротивлений прямой, обратной и нулевой последовательностей.
Логично предположить, что если результаты расчета по двум разным методам:
— методу петли «фаза-ноль»;
— методу симметричных составляющих,
приравнять, то можно сделать вывод о соотношениях сопротивлений, используемых в этих методах.
Формула расчета тока однофазного КЗ методом петли «фаза-ноль» выглядит следующим образом (см.
[2] и [3]):
где U – линейное напряжение сети;
Uф – фазное напряжение сети;
Zпт – полное сопротивление петли фаза-ноль от трансформатора до точки КЗ;
Zс.т. – сопротивление системы и трансформатора току однофазного КЗ.
где Х1т, Х2т, Х0т, R1т, R2т, R0т – индуктивные (Х) и активные (R) сопротивления трансформатора токам прямой (1), обратной (2) и нулевой (0) последовательностей;
Хс – индуктивное сопротивление питающей сети;
Rд – сопротивление электрической дуги.
Перепишем формулу (3) в более удобной форме, при этом:
— учтем, что сопротивления прямой и обратной последовательностей равны;
— умножим числитель и знаменатель на 3;
— в знаменателе будем складывать не модули полных сопротивлений, а отдельно их активные и индуктивные составляющие (это сделает расчет более точным).
где Rф (Rн) – активное сопротивление фазного (нулевого) проводника линии;
Xф (Xн) – индуктивное сопротивление фазного (нулевого) проводника линии.
Вот формула расчета тока однофазного КЗ методом симметричных составляющих (см. [1], п.8.2.1, формула 24):
где R1сум. (R0сум.) – суммарное активное сопротивление прямой (нулевой) последовательности;
X1сум. (X0сум.) – суммарное индуктивное сопротивление прямой (нулевой) последовательности.
Перепишем формулу (6), подставив в нее значение фазного напряжения, а также расписав более подробно суммарные величины сопротивлений прямой и обратной последовательностей:
где R1л (R0л) – суммарное активное сопротивление прямой (нулевой) последовательности линии;
X1л (X0л) – суммарное индуктивное сопротивление прямой (нулевой) последовательности линии.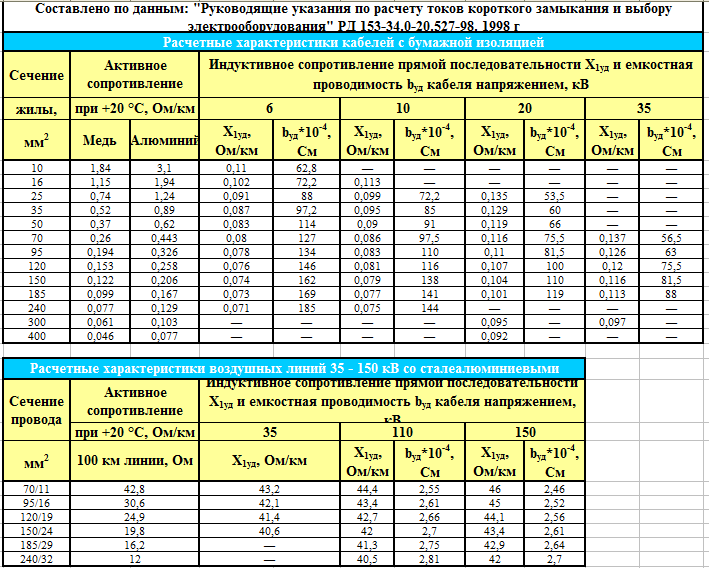
После сравнения формул (5) и (7) получим следующие выражения:
Считая, что Rф=R1л, Xф=X1л, выразим из соотношений (8) и (9) величины сопротивлений нулевой последовательности:
Итак, при отсутствии справочных значений о величине сопротивления нулевой последовательности линии, эти значения можно рассчитать, используя справочные данные сопротивлений фазного и нулевого проводников линии.
Используемая литература
ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ».
Кужеков С. Л. Практическое пособие по электрическим сетям и электрооборудованию / С.Л. Кужеков, С. В. Гончаров. – Ростов н/Д.: Феникс, 2007.
Тульчин И. К., Нудлер Г. И. Электрические сети и электрооборудование жилых и общественных зданий.
– 2-е изд., перераб. и доп. – М.: Энерготамиздат, 1990.
Значение сопротивления проводника и способы его расчета
В этой части серии «Практикующий техник» мы рассмотрим расчеты, необходимые для определения сопротивления данного проводника. Этот часто упускаемый из виду параметр может быть важен при попытке определить подходящий диаметр проволоки для данного применения. Также важно учитывать сопротивление проводника при оценке эффективности применения. Меньшее сопротивление означает меньшее рассеивание мощности проводником. Оптимизация этих двух аспектов сопротивления проводника для вашего конкретного приложения может привести к значительному снижению затрат на внедрение и эксплуатацию. Важно знать сопротивление, предлагаемое данным проводником, а также понимать, в какой степени это сопротивление влияет на приложение и его работу. По этой причине мы рассмотрим некоторые важные аспекты сопротивления проводника, кратко опишем и обсудим их.
Какие факторы определяют сопротивление данного проводника?
Есть три фактора, которые определяют величину сопротивления данного проводника.
Они проиллюстрированы здесь в соотношении, используемом для расчета сопротивления проводника.
Мы начнем с признания того очевидного факта, что длина проводника влияет на его общее сопротивление. Чем больше длина данного проводника, тем большее сопротивление будет иметь этот проводник. Это хорошо видно из соотношения, приведенного выше.
Удельное сопротивление материала проводника играет важную роль в общем сопротивлении. Это связано с тем, что разные материалы, например золото или медь, обладают разным сопротивлением постоянному току. Материалы проводников, как правило, выбираются на основе рентабельности и пригодности. Удельное сопротивление материала некоторых из наиболее распространенных проводников, используемых сегодня, указано ниже.
Последним важным фактором, определяющим сопротивление проводника, является площадь поперечного сечения данного проводника. Важно отметить обратную зависимость между площадью поперечного сечения проводника и сопротивлением проводника.
Как видно из приведенного примера, чем меньше площадь поперечного сечения проводника, тем больше становится значение сопротивления проводника. Это означает, что, хотя использование меньших размеров проводника может быть дешевле, существует компромисс с сопротивлением.
Каким образом сопротивление проводника может иметь значение?
Это соотношение позволяет определить сопротивление проводника, которое можно использовать для изучения потерь мощности, влияющих на общую эффективность приложения. Это отношение также можно изменить, чтобы решить для площади. Затем это расчетное значение площади поперечного сечения можно использовать для получения требуемого диаметра проволоки для удовлетворения конкретных потребностей применения. В видеоролике, представленном по ссылке ниже, мы рассмотрим шаги, необходимые для определения минимального диаметра провода, который можно использовать при заданных конкретных критериях, касающихся длины проводника и допустимого сопротивления проводника.
Как указывалось ранее, эти два фактора влияют на стоимость внедрения и эксплуатационные расходы и заслуживают изучения.
Если вам понравился этот пост, ознакомьтесь с нашими предыдущими статьями из серии «Практикующий техник»;
Использование естественного логарифма или функции «ln» в анализе цепей
Как создать правильные уравнения ветвей KCL по закону Ома для узлового анализа
Как решить одновременные уравнения с несколькими неизвестными
Преобразование параллельных цепей RL в их «упрощенные для работы» серии Эквиваленты
Общие правила для взвешенных систем счисления
Полезность поиска схемы, эквивалентной тевенину
Мы надеемся, что это было полезно для вас как практикующего или студента-техника. Мы ждем ваших отзывов или других идей для серии «Практикующий техник». Сообщите нам свои идеи о том, о чем вы хотели бы, чтобы мы написали, отправив нам свои мысли и вопросы по адресу support@gbctechtraining.
com.
Калькулятор импеданса коаксиального кабеля — все RF
Большинство коаксиальных кабелей RF имеют импеданс 50 Ом или 75 Ом. Они считаются стандартизированными значениями импеданса с доступными кабелями. В некоторых случаях пользователям требуется пользовательское значение импеданса. Этого можно добиться, регулируя внутренний и внешний диаметр коаксиального кабеля вместе с диэлектриком.
Примечание: Для работы этого калькулятора единицы измерения диаметра внешнего и внутреннего проводника должны совпадать. Они всегда находятся в соотношении, поэтому будут компенсировать друг друга.
- Внешний диаметр коаксиального кабеля (D)
- Внутренний диаметр кососеального кабеля (D)
- Относительная диэлектрическая проницаемость (ε R )
Результат
РЕЗУЛЬТАТ
. длина (C)
пФ
Индуктивность на единицу длины (L)
NH
Импеданс на единицу длины (z)
ω
Частота отсечения (F C )
ГГц
Формуля Формации для коаксиала.
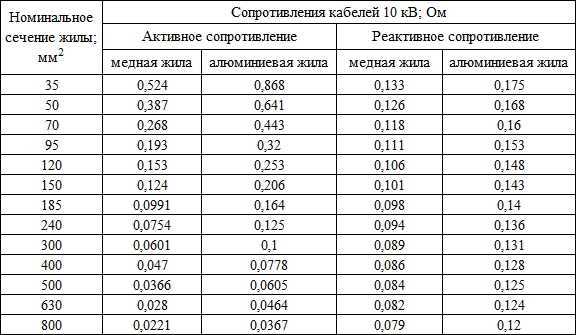Коаксиальный кабель Коаксиальный кабель имеет емкость из-за зазора между внутренним проводником и внешним экраном кабеля. Значение емкости зависит от расстояния между проводниками, диэлектрической проницаемости и импеданса кабеля. Эту емкость можно рассчитать по следующей формуле.
Где:
C = емкость в PF/метре
εR = относительная проницаемость диэлектрика между внутренним и наружным проводником
D = диаметром
D = внутренний диаметр
Индуктивность коаксиального кабеля пропорциональна длине линии и не зависит от диэлектрической проницаемости материала между жилами. Индуктивность можно рассчитать по следующей формуле.
Где:
L = индуктивность в µH / метр
D = Внешний диаметр
D = внутренний диаметр
Примечание: Расчет импеданса коаксиального кабеля
Импеданс радиочастотного коаксиального кабеля зависит от диэлектрической проницаемости кабеля и диаметра внутреннего и внешнего проводников.
